Performance Analysis of Artificial Intelligence Models for Classification of Transmission Line Losses
Abstract
1. Introduction
- (1)
- This study introduces a novel classification-based methodology using deep learning models (LSTM, GRU, BiLSTM, and hybrids) to detect and analyze transmission line losses based on real-world high-voltage network data from Nigeria, moving beyond conventional loss minimization techniques.
- (2)
- It is among the first to apply a comparative deep learning framework—including attention mechanisms (LSTM-AM)—for loss classification across multiple scenarios, with LSTM-AM achieving the highest accuracy of 83.84%.
- (3)
- The research highlights the significance of data preprocessing, feature engineering, and statistical variability analysis as diagnostic tools for identifying loss-prone lines and informing targeted interventions.
- (4)
- By providing actionable insights for intelligent transmission loss management, the study contributes to the advancement of data-driven energy systems aligned with the goals of affordable and reliable electricity access.
2. Materials and Method
2.1. Transmission Line Data Collection and Preprocessing
- Identify columns with null values:
- 2.
- Datetime Formatting: the date strings were converted to datetime objects:
- 3.
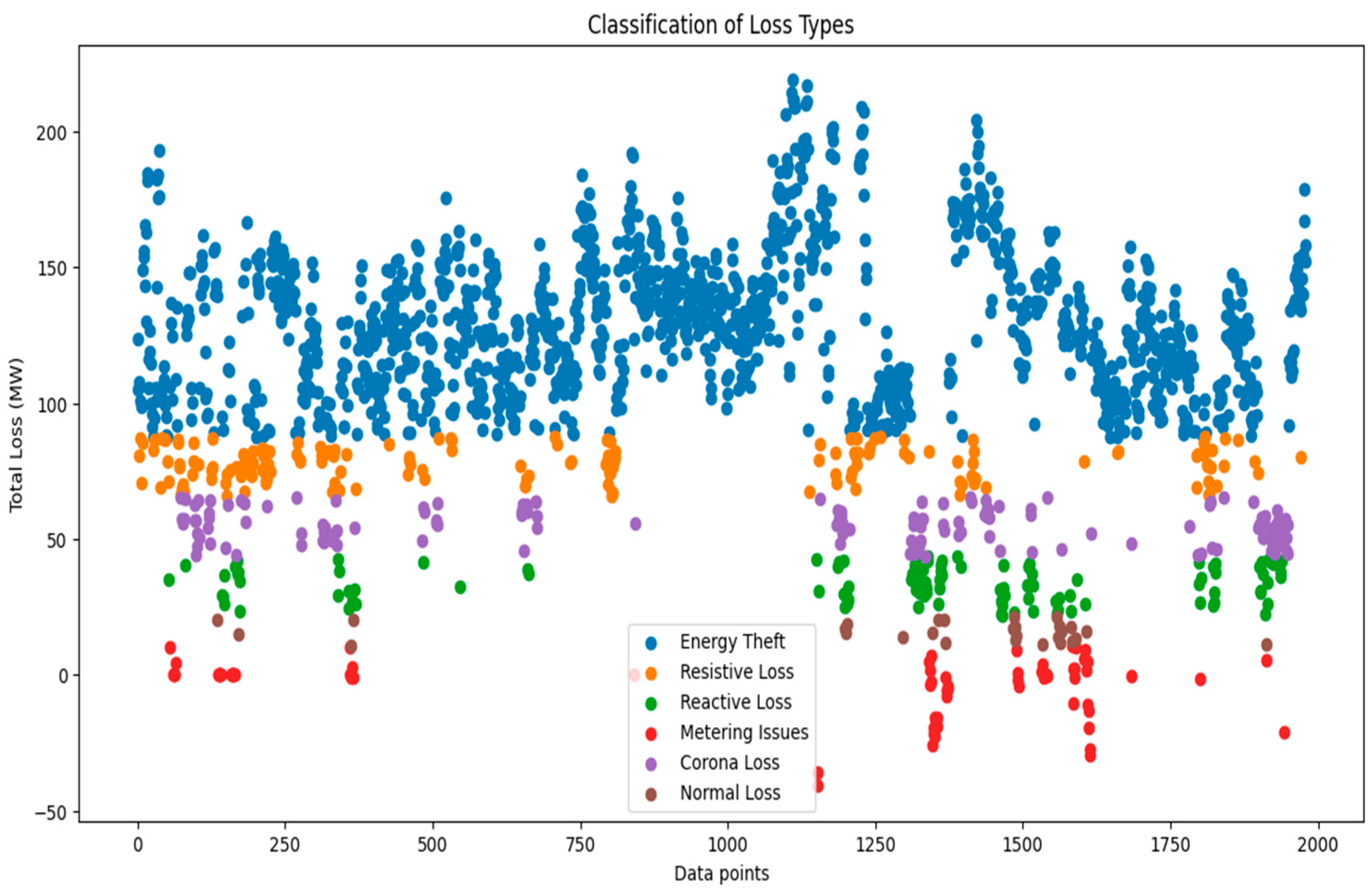
- Engineering of loss type classes: used the ‘Energy Difference’ column values to categorize the loss types into classes using the threshold values in Table 3.
- 4.
- Label Encoding: The categorical ‘loss_type’ labels were transformed into a numerical format using ‘label encoding’ to ensure compatibility with the neural network models. This was performed via this pseudocode:
- 5.
- Select all the 12 loss lines and drop less important features, such as datetime, ED, TG, TL, and BI, as shown in Table 2.
- 6.
- Feature Normalization: all numeric features were normalized to the [0, 1] range using the Min-max feature scaling, as seen in the equation below:
- 7.
- Time-series sequencing: for temporal models like LSTM, GRU, and BiLSTM, the data was reshaped into sequences using a sliding window approach:
- 8.
- Train-test splitting: shuffle data randomly and allocate 80% for training and 20% for testing.
2.2. Transmission Line Losses Modeling
2.3. Models for Transmission Losses Management System
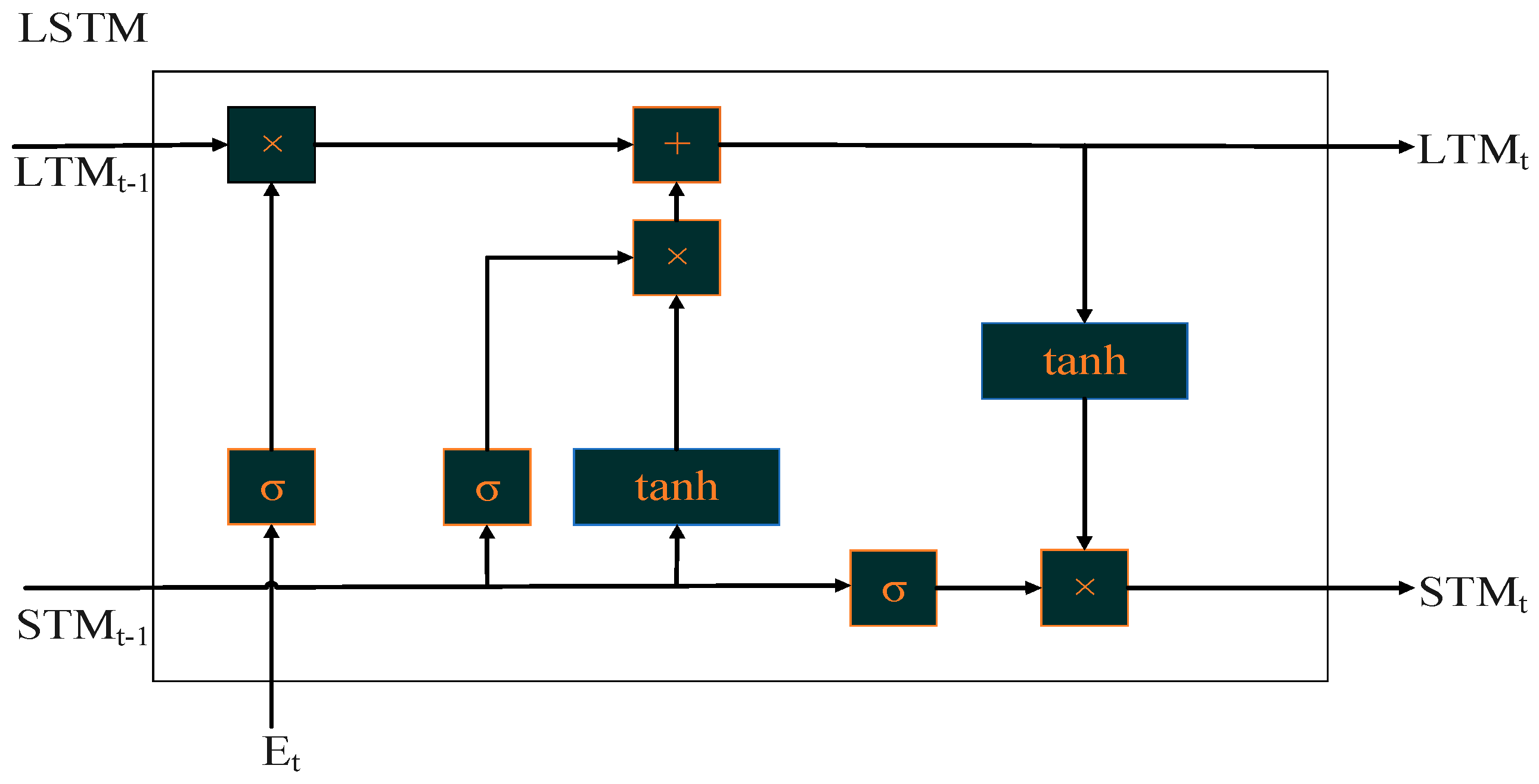
2.3.1. Long Short-Term Memory (LSTM) Model
2.3.2. Bidirectional Long Short-Term Memory (BiLSTM) Model
2.3.3. Gated Recurrent Unit (GRU) Model
2.3.4. Input–Output Design of the Models
- Input Structure
- 2.
- Output Structure
2.4. Model Training and Testing
2.5. Simulation Scenarios Transmission Loss Management System
2.6. Performance Evaluation
- i.
- Confusion matrix: The confusion matrix is a tabular summary showing the number of correct and incorrect predictions for each class, organized by true labels (rows) and predicted labels (columns). While the elements of the main diagonal represent the number of correctly classified instances, the off-diagonal elements represent the number of misclassified instances. It matrix consists of four key components, namely,
- True Positive (TP), which indicates the number of positive cases that the model correctly identified;
- False Negative (FN), representing the number of actual positive cases that the model incorrectly classified as negative;
- False Positive (FP), which refers to the number of negative cases that the model mistakenly classified as positive;
- True Negative (TN), signifying the number of negative cases that the model correctly classified.
- ii.
- Accuracy: The accuracy of the classification system refers to the ratio of correctly classified instances (TP + TN) to the total number of instances (TP + TN + FP + FN). It can be mathematically expressed as Equation (33).
- iii.
- Recall: The recall is simply defined as the ratio of correctly predicted positive instances to all the actual positive instances. The idea behind the recall is how many instances have been classified as a particular class of losses. Recall is also called sensitivity, and it can be mathematically expressed as Equation (34).
- iv.
- F1-score: The F1-score is also known as the F Measure, and it measures the harmonic mean/equilibrium between the precision and the recall, thereby balancing their trade-off. It can be mathematically expressed as Equation (35).
- v.
- Precision: The precision of a classification system simply measures the ratio of correctly predicted positive instances to the total predicted positive instances. It can be mathematically expressed as Equation (36).
3. Results and Discussions
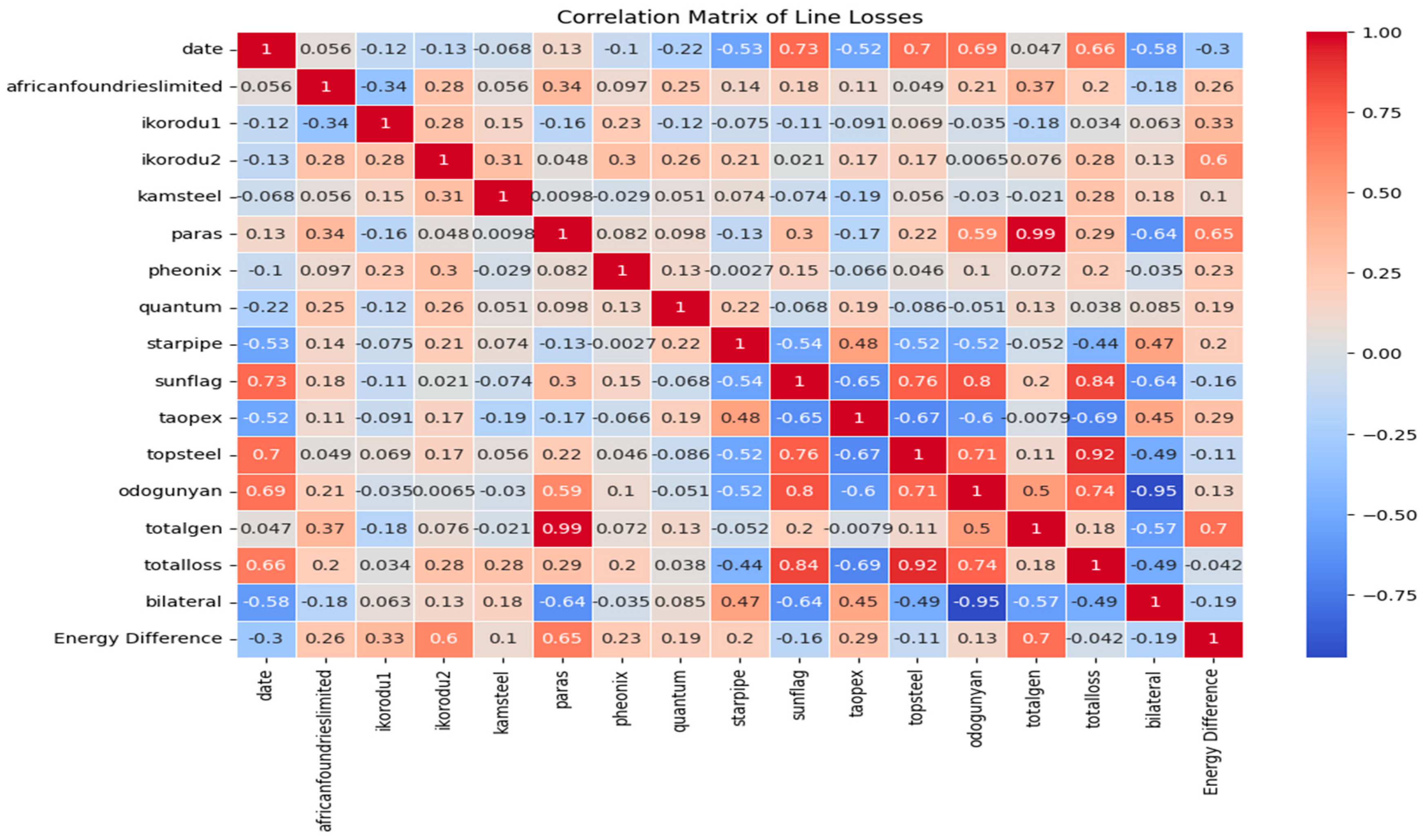
3.1. Insights from Data Preprocessing
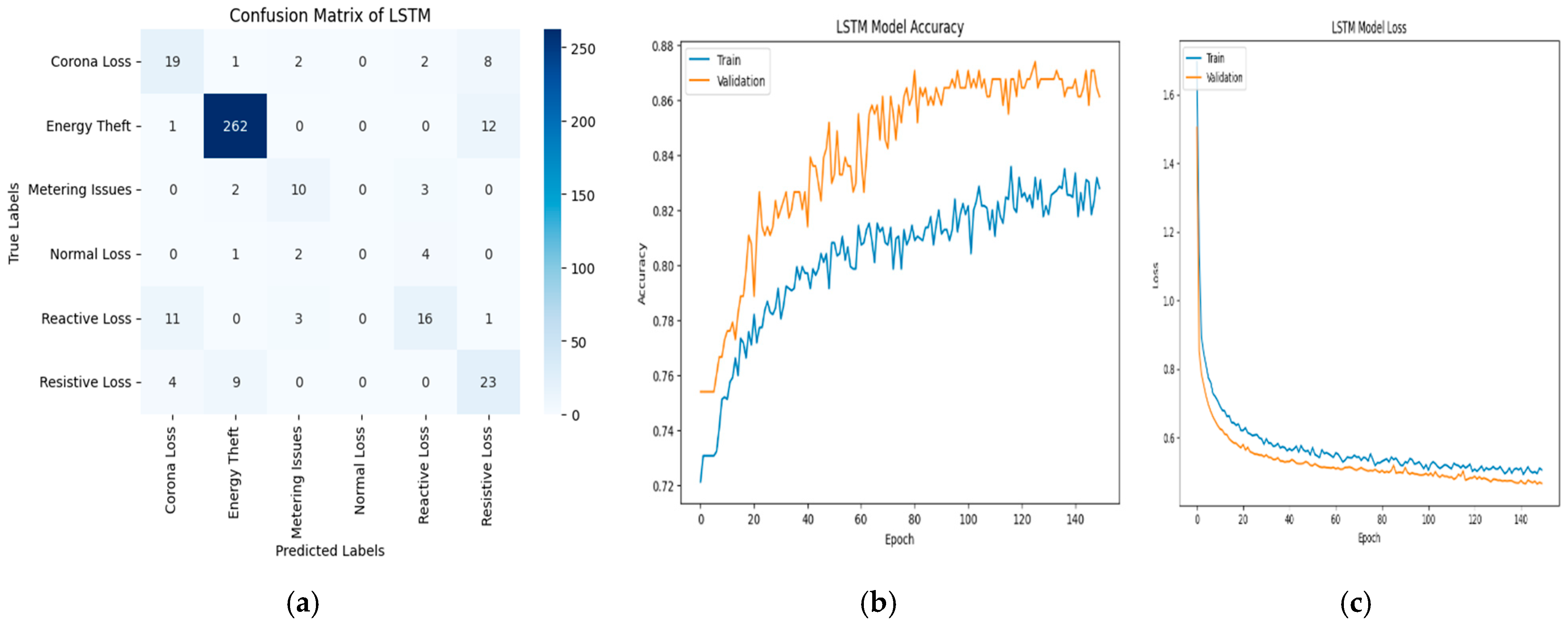
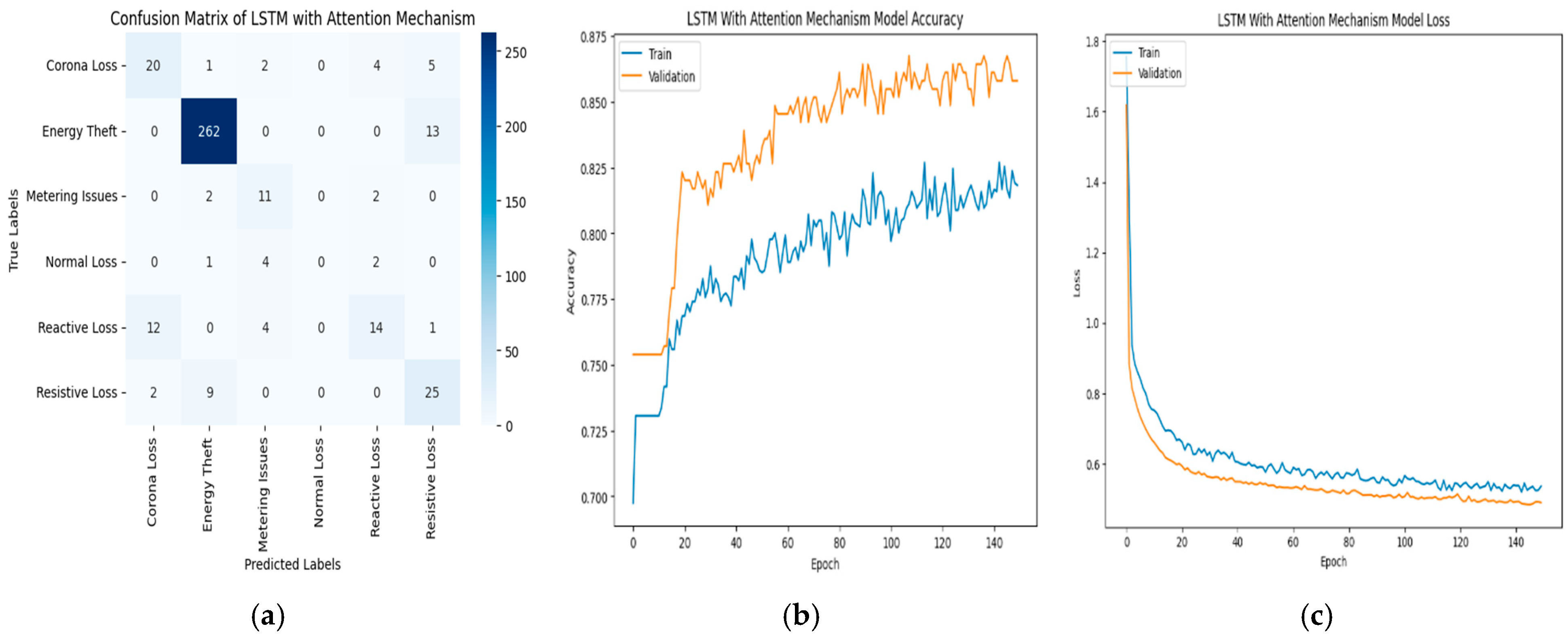
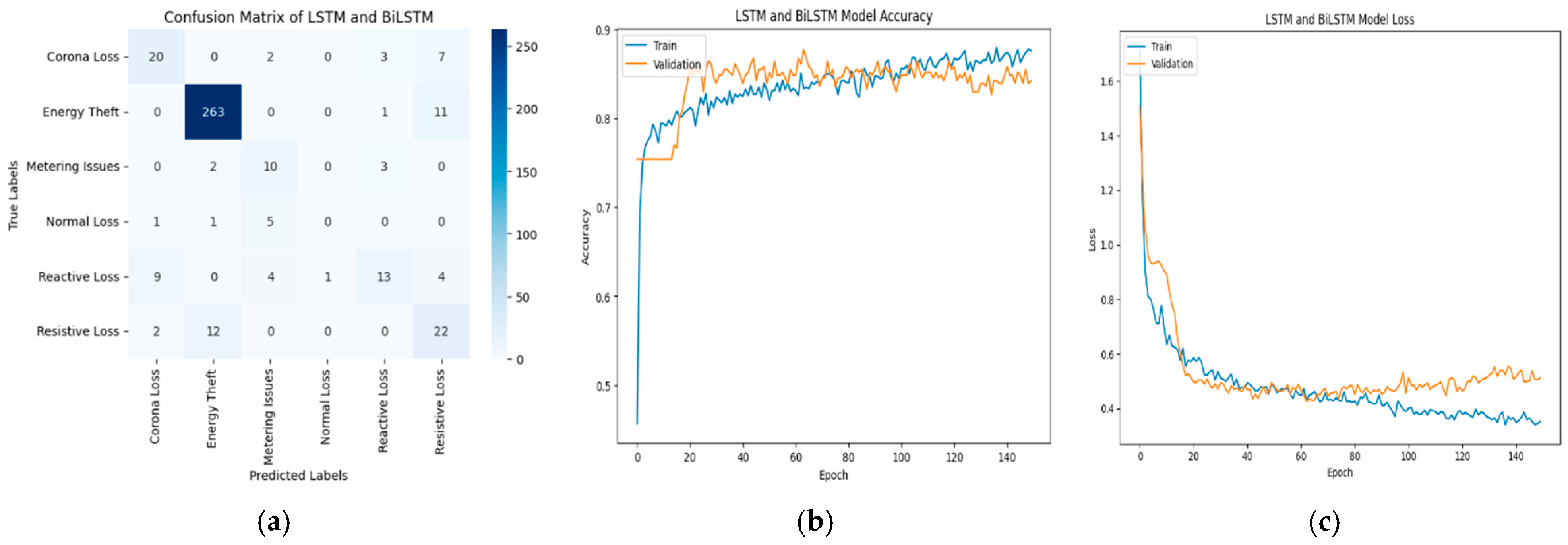
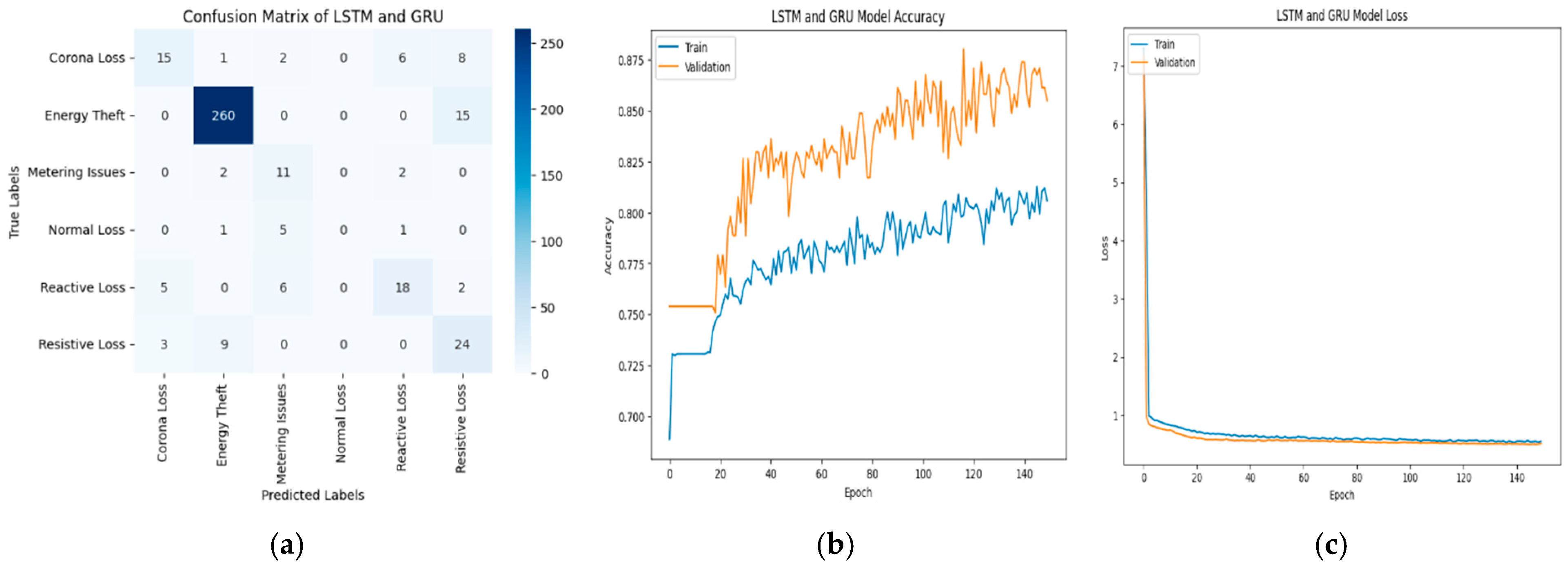
3.2. Transmission Loss Classification Result
4. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amole, A.O.; Oladipo, S.; Olabode, O.E.; Makinde, K.A.; Gbadega, P. Analysis of grid/solar photovoltaic power generation for improved village energy supply: A case of Ikose in Oyo State Nigeria. Renew. Energy Focus 2023, 44, 186–211. [Google Scholar] [CrossRef]
- Gaonwe, T.P.; Kusakana, K.; Hohne, P.A. A review of solar and air-source renewable water heating systems, under the energy management scheme. Energy Rep. 2022, 8, 1–10. [Google Scholar] [CrossRef]
- Ma, Z.; Ye, C.; Li, H.; Ma, W. Applying support vector machines to predict building energy consumption in China. Energy Procedia 2018, 152, 780–786. [Google Scholar] [CrossRef]
- Kiasari, M.; Ghaffari, M.; Aly, H.H. A Comprehensive Review of the Current Status of Smart Grid Technologies for Renewable Energies Integration and Future Trends: The Role of Machine Learning and Energy Storage Systems. Energies 2024, 17, 4128. [Google Scholar] [CrossRef]
- Akinyele, D.; Amole, A.; Olabode, E.; Olusesi, A.; Ajewole, T. Simulation and analysis approaches to microgrid systems design: Emerging trends and sustainability framework application. Sustainability 2021, 13, 11299. [Google Scholar] [CrossRef]
- Amole, A.O.; Akinyele, D.O.; Olabode, O.E.; Idogun, O.O.; Adeyeye, A.O.; Olarotimi, B.S. Comparative Analysis of Techno-Environmental Design of Wind and Solar Energy for Sustainable Telecommunications Systems in Different Regions of Nigeria. Int. J. Renew. Energy Res. 2021, 11, 1776–1792. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar] [CrossRef]
- Ehimen Airoboman, A. On the Assessment of Power System Stability Using Matlab/Simulink Model. Int. J. Energy Power Eng. 2015, 4, 51. [Google Scholar] [CrossRef]
- Salimon, S.A.; Fajinmi, I.O.; Adewuyi, O.B.; Pandey, A.K.; Adebiyi, O.W.; Kotb, H. Graph theory-enhanced integrated distribution network reconfiguration and distributed generation planning: A comparative techno-economic and environmental impacts analysis. Clean. Eng. Technol. 2024, 22, 100808. [Google Scholar] [CrossRef]
- Owusu, K.B.; Annan, J.K.; Effah, E.; Kwame Tweneboah-Koduah, F.; Bediako Owusu, K.; Kojo Annan, J. Mitigation of Technical Losses in Ghana’s Transmission Network using Optimal Capacitor Bank Allocation Technique. Glob. J. Res. Eng. Felectrical Electron. Eng. 2015, 15, 21–31. [Google Scholar]
- Alam, M.S.; Arefifar, S.A. Hybrid PSO-TS Based Distribution System Expansion Planning for System Performance Improvement Considering Energy Management. IEEE Access 2020, 8, 221599–221611. [Google Scholar] [CrossRef]
- Oyedepo, S.O.; Uwoghiren, T.; Babalola, P.O.; Nwanya, S.C.; Kilanko, O.; Leramo, R.O.; Aworinde, A.K.; Adekeye, T.; Oyebanji, J.A.; Abidakun, O.A. Assessment of Decentralized Electricity Production from Hybrid Renewable Energy Sources for Sustainable Energy Development in Nigeria. Open Eng. 2019, 9, 72–89. [Google Scholar] [CrossRef]
- Carr, D.; Thomson, M. Non-Technical Electricity Losses. Energies 2022, 15, 2218. [Google Scholar] [CrossRef]
- Gaur, B.; Ucheniya, R.; Saraswat, A. Real power transmission loss minimization and bus voltage improvement using UPFC. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2020; Volume 662, pp. 1–9. [Google Scholar]
- Kojima, M.; Trimble, C. Making Power Affordable for Africa and Viable for Its Utilities; World Bank: Washington, DC, USA, 2016. [Google Scholar]
- de Savian, F.S.; Siluk, J.C.M.; Garlet, T.B.; Do Nascimento, F.M.; Pinheiro, J.R.; Vale, Z. Non-technical Losses in Brazil: Overview, Challenges, and Directions for Identification and Mitigation. Int. J. Energy Econ. Policy 2022, 12, 93–107. [Google Scholar] [CrossRef]
- Barja-Martinez, S.; Aragüés-Peñalba, M.; Munné-Collado, Í.; Lloret-Gallego, P.; Bullich-Massagué, E.; Villafafila-Robles, R. Artificial intelligence techniques for enabling Big Data services in distribution networks: A review. Renew. Sustain. Energy Rev. 2021, 150, 111459. [Google Scholar] [CrossRef]
- Kim, S.; Sun, Y.; Lee, S.; Seon, J.; Hwang, B.; Kim, J.; Kim, J.; Kim, K.; Kim, J. Data-Driven Approaches for Energy Theft Detection: A Comprehensive Review. Energies 2024, 17, 3057. [Google Scholar] [CrossRef]
- Alzahrani, A.; Ferdowsi, M.; Shamsi, P.; Dagli, C.H. Modeling and Simulation of Microgrid. Procedia Comput. Sci. 2017, 114, 392–400. [Google Scholar] [CrossRef]
- Khan, F.A.; Pal, N.; Saeed, S.H. Optimization and sizing of SPV/Wind hybrid renewable energy system: A techno-economic and social perspective. Energy 2021, 233, 121114. [Google Scholar] [CrossRef]
- Guarda, F.G.K.; Hammerschmitt, B.K.; Capeletti, M.B.; Neto, N.K.; dos Santos, L.L.C.; Prade, L.R.; Abaide, A. Non-Hardware-Based Non-Technical Losses Detection Methods: A Review. Energies 2023, 16, 2054. [Google Scholar] [CrossRef]
- Viegas, J.L.; Esteves, P.R.; Vieira, S.M. Clustering-based novelty detection for identification of non-technical losses. Int. J. Electr. Power Energy Syst. 2018, 101, 301–310. [Google Scholar] [CrossRef]
- Saeed, M.S.; Mustafa, M.W.; Hamadneh, N.N.; Alshammari, N.A.; Sheikh, U.U.; Jumani, T.A.; Khalid, S.B.A.; Khan, I. Detection of non-technical losses in power utilities—A comprehensive systematic review. Energies 2020, 13, 4727. [Google Scholar] [CrossRef]
- Odje, M.; Uhunmwangho, R.; Okedu, K.E. Aggregated Technical Commercial and Collection Loss Mitigation Through a Smart Metering Application Strategy. Front. Energy Res. 2021, 9, 703265. [Google Scholar] [CrossRef]
- Iheukwumere Uchechukwu, M.; Ephraim, O.N.C. Evaluation of Technical and Commercial Losses on Power Distribution Networks in Nigeria Using Statistical Analytical Method. Am. J. Electr. Comput. Eng. 2021, 5, 56. [Google Scholar] [CrossRef]
- Kumar, M.; Pal, N. Machine Learning-based Electric Load Forecasting for Peak Demand Control in Smart Grid. Comput. Mater. Contin. 2023, 74, 4785. [Google Scholar] [CrossRef]
- Ahmadi, B.; Giraldo, J.S.; Hoogsteen, G.; Gerards, M.E.T.; Hurink, J.L. A multi-objective decentralized optimization for voltage regulators and energy storage devices in active distribution systems. Int. J. Electr. Power Energy Syst. 2023, 153, 109330. [Google Scholar] [CrossRef]
- Passos Júnior, L.A.; Oba Ramos, C.C.; Rodrigues, D.; Pereira, D.R.; de Souza, A.N.; Pontara da Costa, K.A.; Papa, J.P. Unsupervised non-technical losses identification through optimum-path forest. Electr. Power Syst. Res. 2016, 140, 413–423. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Symbiotic organism search algorithm applied to load frequency control of multi-area power system. Energy Syst. 2018, 9, 439–468. [Google Scholar] [CrossRef]
- Bartłomiejczyk, M.; Hołyszko, P.; Filipek, P. Measurement and analysis of transmission losses in the supply system of electrified transport. J. Ecol. Eng. 2016, 17, 64–71. [Google Scholar] [CrossRef]
- Xie, J.; Lu, Y.; Gao, R.; Zhu, S.C.; Wu, Y.N. Cooperative Training of Descriptor and Generator Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 27–45. [Google Scholar] [CrossRef]
- Velasco, J.A.; Amaris, H.; Alonso, M. Deep Learning loss model for large-scale low voltage smart grids. Int. J. Electr. Power Energy Syst. 2020, 121, 106054. [Google Scholar] [CrossRef]
- Coma-Puig, B.; Calvo, A.; Carmona, J.; Gavaldà, R. A case study of improving a non-technical losses detection system through explainability. Data Min. Knowl. Discov. 2024, 38, 2704–2732. [Google Scholar] [CrossRef]
- Almasoudi, F.M. Enhancing Power Grid Resilience through Real-Time Fault Detection and Remediation Using Advanced Hybrid Machine Learning Models. Sustainability 2023, 15, 8348. [Google Scholar] [CrossRef]
- Shafei, A.P.; Silva, J.F.A.; Monteiro, J. Convolutional neural network approach for fault detection and characterization in medium voltage distribution networks. E-Prime-Adv. Electr. Eng. Electron. Energy 2024, 10, 100820. [Google Scholar] [CrossRef]
- Chamangard, M.; Ghodrati Amiri, G.; Darvishan, E.; Rastin, Z. Transfer Learning for CNN-Based Damage Detection in Civil Structures with Insufficient Data. Shock Vib. 2022, 2022, 3635116. [Google Scholar] [CrossRef]
- Yin, X.; Zuo, Y.; Fu, G. Design of intelligent detection method for electricity transmission line equipment defect based on data mining algorithm. Int. J. Thermofluids 2024, 24, 100814. [Google Scholar] [CrossRef]
- Khan, A.Q.; Ullah, Q.; Sarwar, M.; Gul, S.T.; Iqbal, N. Transmission Line Fault Detection and Identification in an Interconnected Power Network using Phasor Measurement Units. IFAC-Pap. 2018, 51, 1356–1363. [Google Scholar] [CrossRef]
- Amole, A.O.; Oladipo, S.; Ighravwe, D.; Makinde, K.A.; Ajibola, J. Comparative Analysis of Deep Learning Techniques Based COVID-19 Impact Assessment on Electricity Consumption in Distribution Network. Niger. J. Technol. Dev. 2023, 20, 29–46. [Google Scholar] [CrossRef]
- Sehovac, L.; Nesen, C.; Grolinger, K. Forecasting building energy consumption with deep learning: A sequence to sequence approach. In Proceedings of the Proceedings-2019 IEEE International Congress on Internet of Things, ICIOT 2019-Part of the 2019 IEEE World Congress on Services, Milan, Italy, 8–13 July 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway Township, NJ, USA, 2019; pp. 108–116. [Google Scholar]
- Tunio, N.A.; Tunio, M.A.; Raza, M.A.; Faheem, M.; Hashmani, A.A.; Nadeem, R. Performance Comparison Between Deep Learning Models for Fault Classification in Transmission Lines Using Time Series Data. Energy Sci. Eng. 2025, 6, 2330–2351. [Google Scholar] [CrossRef]
- Yadav, G.K.; Kirar, M.K.; Gupta, S.C.; Rajender, J. Integrating ANN and ANFIS for effective fault detection and location in modern power grid. Sci. Technol. Energy Transit. 2025, 80, 1–20. [Google Scholar] [CrossRef]
- Klomjit, J.; Ngaopitakkul, A. Comparison of artificial intelligence methods for fault classification of the 115-kv hybrid transmission system. Appl. Sci. 2020, 10, 3967. [Google Scholar] [CrossRef]
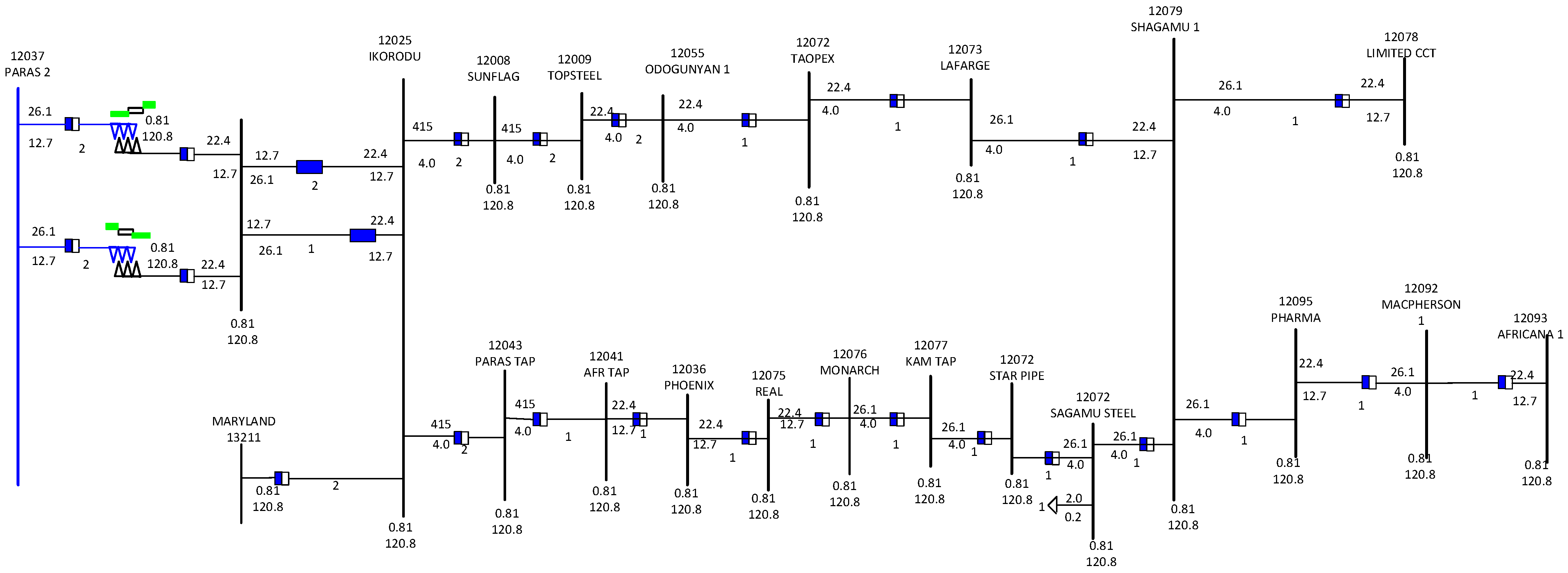









| S/N | Lines | Line Code | Circuit |
|---|---|---|---|
| 1 | Ikorodu | 12,025 | 1 |
| 2 | Sunflag | 12,008 | 1 |
| 3 | Topsteel | 12,009 | 1 |
| 4 | Odogunyan 1 | 12,055 | 1 |
| 5 | Taopex | 12,072 | 1 |
| 6 | Lafarge | 12,073 | 1 |
| 7 | Paras_1 | 12,037 | 2 |
| 8 | Paras Tap1 | 12,043 | 2 |
| 9 | AFR Tap | 12,041 | 2 |
| 10 | Phoenix | 12,036 | 2 |
| 11 | Real | 12,075 | 2 |
| 12 | Monarch | 12,076 | 2 |
| 13 | Kam Tap | 12,077 | 2 |
| 14 | Star Pipe | 12,078 | 2 |
| 15 | Sagamu Steel | 12,079 | 2 |
| AFL | I1 | I 2 | Ks | Ps | Phx | Qt | Sp | Sf | Tp | Ts | Ogy | TG | TL | Bl | ED |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.07 | 13.58 | 102.41 | 0.000 | 18.06 | 8.99 | 3.42 | 2.35 | 1.76 | 11.16 | 0.94 | 21.2 | 29.22 | 21.530 | 0.330 | 123.68 |
| 3.75 | 17.41 | 97.56 | 0.000 | 0.00 | 8.95 | 3.16 | 1.94 | 1.56 | 10.13 | 0.75 | 20.7 | 10.13 | 20.110 | −0.590 | 104.99 |
| 3.66 | 21.43 | 97.72 | 2.344 | 0.00 | 10.03 | 1.88 | 2.33 | 1.60 | 11.32 | 0.77 | 20.2 | 11.32 | 22.614 | 2.414 | 107.85 |
| 4.40 | 5.35 | 87.78 | 2.348 | 0.00 | 11.38 | 1.93 | 1.92 | 1.07 | 11.32 | 0.60 | 21.2 | 11.32 | 23.648 | 2.448 | 80.80 |
| 4.33 | 1.75 | 97.40 | 2.351 | 0.00 | 10.57 | 2.28 | 2.08 | 1.27 | 11.32 | 0.64 | 23.7 | 11.32 | 23.521 | −0.178 | 86.94 |
| Category | Description |
|---|---|
| Energy Theft | 40% and above Energy Difference |
| Resistive Loss | 30% and 40% Energy Difference |
| Corona Loss | 20% to 30% Energy Difference |
| Reactive Loss | 10% and 20% Energy Difference |
| Normal Loss | 5% to 10% Energy Difference |
| Metering Issues | Less than 5% Energy Difference |
| Parameters | Type or Value |
|---|---|
| Optimizer | Adam |
| Learning rate | 0.001 |
| Loss | sparse_categorical_crossentropy |
| Output dense layer function | softmax |
| Model activation function | ReLU |
| Epochs | 150 |
| Batch size | 32 |
| Hyperparameter | Range Tested | Best Value Found | Justification |
|---|---|---|---|
| Optimizer | Adam | Adam | Adam optimizer was chosen for its efficiency and adaptability to the model’s requirements. |
| Learning Rate | 0.0001 to 0.01 (log scale) | 0.0016 | The learning rate of 0.0016 was optimal based on validation performance. It balanced model stability and convergence speed. |
| Epochs | 50 to 200 | 150 | While 50 epochs were initially tested for quick evaluation, 150 epochs were later selected as it showed a stable convergence and optimal model performance. |
| Batch Size | 16, 32, 64 | 32 | A batch size of 32 provided a balance between computational efficiency and gradient stability during training. |
| Units (layer 1) | 32, 64, 128 | 64 | The LSTM layer 1 was tuned to have 64 units |
| Dropout Rate (Layer 1) | 0.2 to 0.5 | 0.3 | Dropout of 0.3 was found to prevent overfitting effectively without compromising performance. |
| Units (layer 2) | 32, 64, 128 | 64 | The LSTM layer 2 was tuned to have 64 units. |
| Dropout Rate (Layer 2) | 0.2 to 0.5 | 0.2 | Dropout of 0.2 was also found to prevent overfitting, just like in Layer 1 |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| lstm_1 | (None, 1, 64) | 19,712 |
| dropout_1 | (None, 1, 64) | 0 |
| lstm_2 | (None, 32) | 12,416 |
| dropout_15 (Dropout) | (None, 32) | 0 |
| dense_16 (Dense) | (None, 5) | 165 |
| Total params | 0 | 32,293 (126.14 KB) |
| Trainable params | 0 | 32,293 (126.14 KB) |
| Non-trainable params | 0 | 0 (0.00 B) |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| input_layer | (None, 1, 12) | 0 |
| lstm_1 | (None, 1, 32) | 5760 |
| dropout_1 | (None, 1, 32) | 0 |
| dense_1 | (None, 1, 64) | 2112 |
| dense_2 | (None, 1, 1) | 65 |
| reshape _1 | (None, 1) | 0 |
| dense_3 | (None, 1) | 2 |
| Reshape_2 | (None, 1, 1) | 0 |
| Multiply | (None, 1, 32) | 0 |
| lstm_2 | (None, 64) | 24,832 |
| dropout_2 | (None, 64) | 0 |
| dense_4 | (None, 5) | 325 |
| Total params | 0 | 33,096 (129.28 KB) |
| Trainable params | 0 | 33,096 (129.28 KB) |
| Non-trainable params | 0 | 0 (0.00 B) |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| bidirectional | (None, 128) | 39,424 |
| dropout | (None, 128) | 0 |
| dense_1 | (None, 32) | 4128 |
| dense_2 | (None, 6) | 198 |
| Total params | 0 | 43,750 (170.90 KB) |
| Trainable params | 0 | 43,750 (170.90 KB) |
| Non-trainable params | 0 | 0 (0.00 B) |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| gru_1 | (None, 1, 64) | 14,976 |
| dropout_1 | (None, 1, 64) | 0 |
| gru _2 | (None, 32) | 9408 |
| dropout_2 | (None, 32) | 0 |
| Dense | (None, 6) | 198 |
| Epochs | 0 | 150 |
| Batch size | 0 | 32 |
| Total params | 0 | 24,582 (96.02 KB) |
| Trainable params | 0 | 24,582 (96.02 KB) |
| Non-trainable params | 0 | 0 (0.00 B) |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| input_layer | (None, 1, 12) | 0 |
| lstm_1 | (None, 1, 64) | 19,712 |
| batch_normalization_1 | (None, 1, 64) | 256 |
| dropout_1 | (None, 1, 64) | 0 |
| bidirectional | (None, 1, 128) | 66,048 |
| batch_normalization_2 | (None, 1, 128) | 512 |
| dropout_2 | (None, 1, 128) | 0 |
| lstm_ 2 | (None, 64) | 49,408 |
| batch_normalization_3 | (None, 64) | 256 |
| dropout_3 | (None, 64) | 0 |
| Dense | (None, 6) | 390 |
| Epochs | 150 | |
| Batch size | 32 | |
| Total params | 136,582 (533.52 KB) | |
| Trainable params | 136,070 (531.52 KB) | |
| Non-trainable params | 512 (2.00 KB) |
| Layer (Type) | Output Shape | Parameters |
|---|---|---|
| input_layer | (None, 1, 12) | 0 |
| lstm_1 | (None, 1, 64) | 19,712 |
| dropout_1 | (None, 1, 64) | 0 |
| gru | (None, 1, 64) | 24,960 |
| dropout_2 | (None, 1, 64) | 0 |
| lstm_2 | (None, 32) | 12,416 |
| dropout_3 | (None, 32) | 0 |
| dense | (None, 1583) | 52,239 |
| Epochs | 0 | 150 |
| Batch size | 0 | 32 |
| Total params | 0 | 109,327 (427.06 KB) |
| Trainable params | 0 | 109,327 (427.06 KB) |
| Non-trainable params | 0 | 0 (0.00 B) |
| Statistic | AFL | I1 | I 2 | Ks | Ps | Phx | Qt | Sp | Sf | Tp | Ts | Ogy | TG | TL | Bl | ED |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 3.84 | −23.16 | 78.52 | 2.52 | 69.40 | 2.95 | 2.56 | 1.31 | 4.25 | 7.24 | 7.26 | 45.56 | 76.64 | 24.69 | −20.87 | 107.31 |
| Min | 0.00 | −67.71 | −1.37 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −1.47 | 0.00 | 0.00 | 0.00 | −100.18 | −40.74 | −40.74 |
| 25% | 3.66 | −32.54 | 69.89 | 0.00 | 43.19 | 2.21 | 2.30 | 0.39 | 0.42 | 1.01 | 0.80 | 19.12 | 55.62 | 12.76 | −40.04 | 82.23 |
| 50% (Median) | 4.04 | −24.81 | 83.64 | 0.00 | 72.58 | 2.59 | 2.63 | 1.21 | 0.92 | 7.41 | 1.05 | 24.70 | 88.75 | 16.60 | −10.20 | 113.91 |
| 75% | 4.30 | −15.34 | 93.49 | 3.18 | 96.50 | 3.49 | 2.93 | 2.00 | 7.16 | 11.90 | 16.93 | 82.70 | 104.71 | 39.72 | −2.96 | 138.99 |
| Max | 6.58 | 25.81 | 128.60 | 17.87 | 114.41 | 12.27 | 21.51 | 3.68 | 21.60 | 21.88 | 44.60 | 129.59 | 117.85 | 68.51 | 54.39 | 218.97 |
| Std Dev | 0.87 | 15.12 | 24.80 | 4.23 | 36.14 | 1.64 | 1.01 | 0.96 | 6.01 | 5.81 | 10.13 | 42.25 | 35.62 | 15.71 | 32.30 | 45.60 |
| Loss Type | Count |
|---|---|
| Energy Theft | 1440 |
| Resistive Loss | 169 |
| Corona Loss | 150 |
| Reactive Loss | 113 |
| Metering Issues | 79 |
| Normal Loss | 29 |
| Total Counts | 1980 |
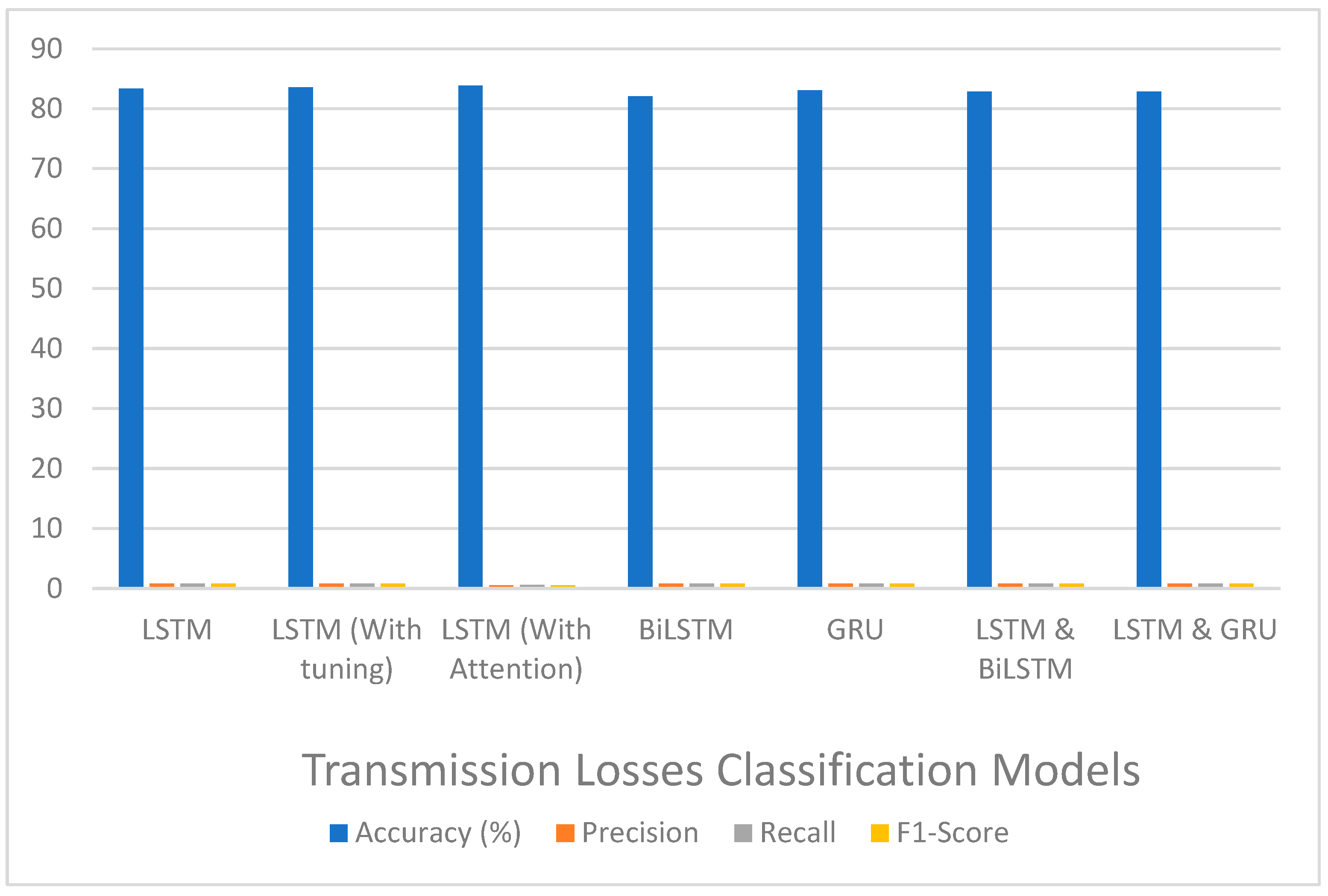
| Model | Accuracy (%) | Precision | Recall | F1-Score |
|---|---|---|---|---|
| LSTM | 83.33 | 0.83 | 0.83 | 0.83 |
| LSTM-AM | 83.84 | 0.54 | 0.58 | 0.55 |
| BiLSTM | 82.07 | 0.83 | 0.84 | 0.83 |
| GRU | 83.08 | 0.83 | 0.83 | 0.83 |
| LSTM & BiLSTM | 82.83 | 0.82 | 0.83 | 0.82 |
| LSTM & GRU | 82.83 | 0.83 | 0.83 | 0.82 |
| Authors | Focus | Models | Results |
|---|---|---|---|
| [41] | Transmission line fault classification (Jamshoro-New Karachi), Sindh, Pakistan | Temporal convolutional networks (TCN) Bidirectional Long Short-Term Memory (BiLSTM) Gated Recurrent Units (GRUs) | TCN achieves accuracy of 99.9%. BiLSTM achieves accuracy of 92.31% GRU achieves accuracy of 95.27%. |
| [42] | Fault detection and location power grid | Artificial neural network (ANN) Adaptive Neuro-fuzzy inference system (ANFIS) | ANN recorded 92–95% operational efficiency ANFIS recorded 97–99% operational efficiency |
| [43] | Fault classification in 115-kV hybrid transmission line in the Provincial Electricity Authority (PEA-Thailand) system | Probabilistic neural networks (PNNs) Back-propagation neural networks (BPNNs) Support vector machine (SVM) | PNN recorded 100% accuracy of sending end BPNN recorded 100% accuracy of sending end SVM recorded 100% accuracy of sending end |
| Present Study | Transmission line loss classification | Long short-term memory (LSTM) Bidirectional long short-term memory (BiLSTM) Gated recurrent units (GRU) Long short-term memory—Attention Mechanism (LSTM-AM) LSTM-BiLSTM LSTM-GRU | LSTM achieved accurcay of 83.33% BiLSTM achieved accurcay of 82.07% GRU achieved accurcay of 83.08% LSTM-AM achieved accurcay of 83.84% LSTM-BiLSTM achieved accurcay of 82.83% LSTM-GRU achieved accurcay of 82.83% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amole, A.O.; Ajiboye, O.E.; Oladipo, S.; Okakwu, I.K.; Giwa, I.A.; Olusanya, O.O. Performance Analysis of Artificial Intelligence Models for Classification of Transmission Line Losses. Energies 2025, 18, 2742. https://doi.org/10.3390/en18112742
Amole AO, Ajiboye OE, Oladipo S, Okakwu IK, Giwa IA, Olusanya OO. Performance Analysis of Artificial Intelligence Models for Classification of Transmission Line Losses. Energies. 2025; 18(11):2742. https://doi.org/10.3390/en18112742
Chicago/Turabian StyleAmole, Abraham O., Oluwagbemiga E. Ajiboye, Stephen Oladipo, Ignatius K. Okakwu, Ibrahim A. Giwa, and Olamide O. Olusanya. 2025. "Performance Analysis of Artificial Intelligence Models for Classification of Transmission Line Losses" Energies 18, no. 11: 2742. https://doi.org/10.3390/en18112742
APA StyleAmole, A. O., Ajiboye, O. E., Oladipo, S., Okakwu, I. K., Giwa, I. A., & Olusanya, O. O. (2025). Performance Analysis of Artificial Intelligence Models for Classification of Transmission Line Losses. Energies, 18(11), 2742. https://doi.org/10.3390/en18112742







