Networked Multi-Agent Deep Reinforcement Learning Framework for the Provision of Ancillary Services in Hybrid Power Plants
Abstract
1. Introduction
1.1. Background
1.2. Contribution and Outline
- (1).
- For optimal coordination, most of the relevant literature focuses on centralised and hierarchical control schemes such as those in [30,35]. Here, we develop a model-free HPP environment using MASAC approach to enable coordination between heterogeneous PV, WP, and ESS agents using local control inputs without global information. In addition, our MASAC approach combines MAAC and SAC schemes for handling scalability and coordination control with only local information instead of global information. Compared to existing schemes [38,39], the proposed approach efficiently reduces frequency deviations and regulates HPP frequency for real-time decision-making.
- (2).
- To facilitate decentralised coordination and improve the learning process, a centralised training and decentralised execution (CTDE) mechanism is proposed in which every agent has unique characteristics for real-time decision-making. Compared with [43,44], in which frequency deviation was considered as a cost-optimisation reward function, we propose a performance-based shared reward function for optimal dispatch of HPP assets, reserve management, and power balancing for frequency control and system stability.
- (3).
- Considering the communication complexity of HPP agents, which ultimately impacts the robustness and stability of the training model [52], we propose a networked communication model that uses partially, fully, and randomly connected communication topologies for training, testing, and validation processes without affecting performance. The proposed scheme provides robust, stable, and resilient performance regardless of communication topology and delays in real-time decision-making.
2. Problem Formulation
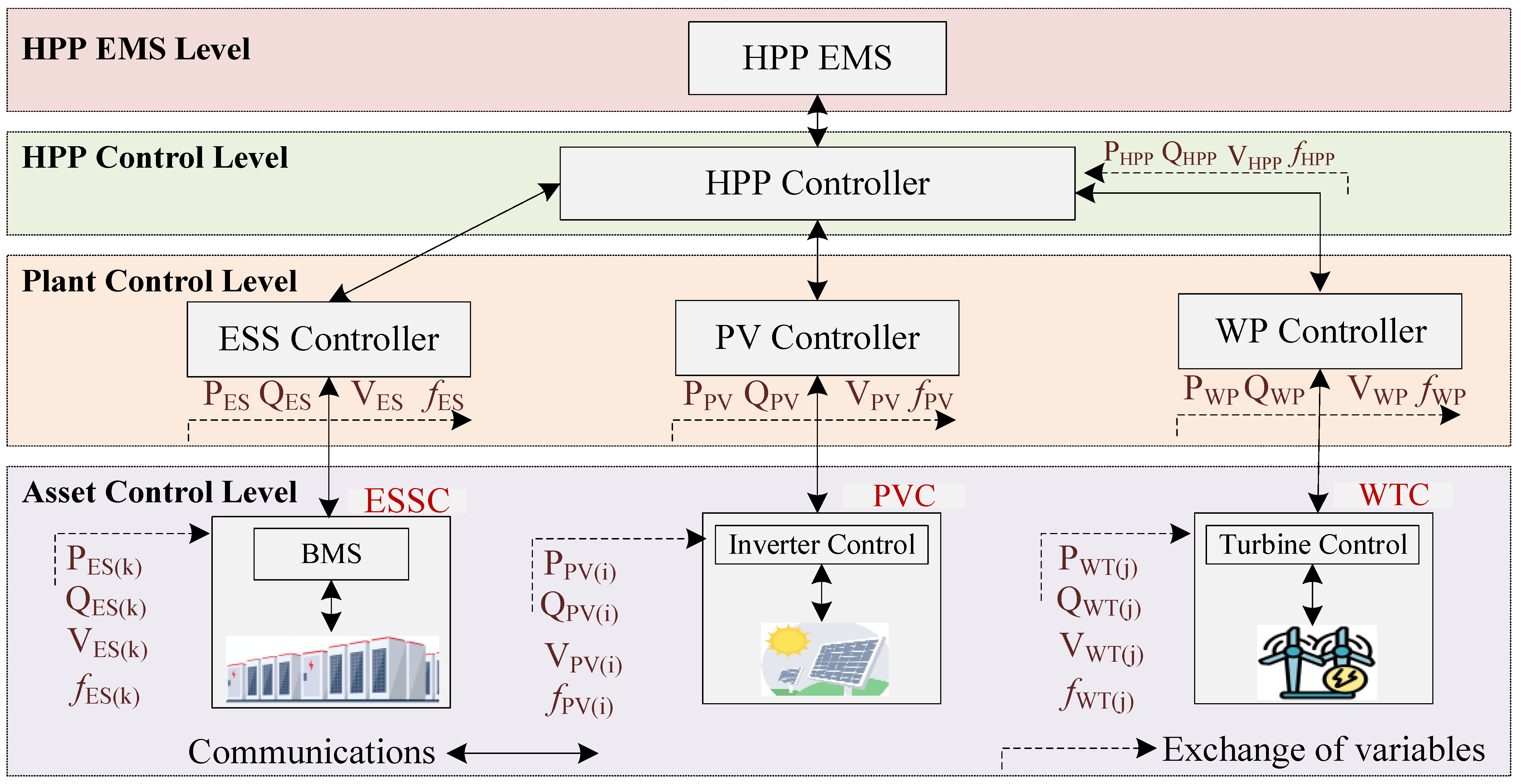
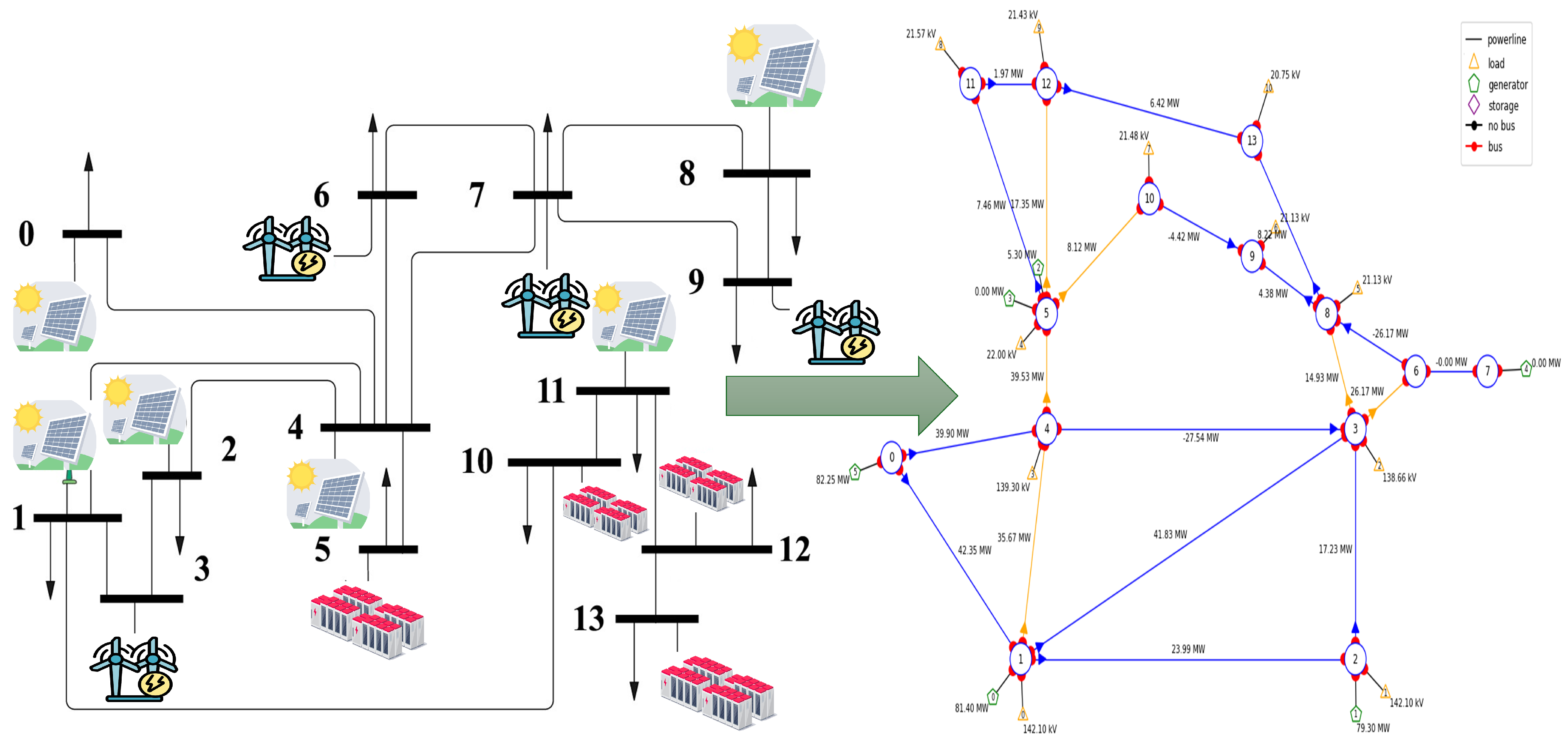
2.1. Description of the HPP Environment
2.2. Objective Function
2.3. Constraints
2.3.1. Curtailment of PV and WP Plant
2.3.2. Power Balancing of the ESS Plant
2.3.3. Energy Storage at ESS Plant
2.3.4. Frequency Control
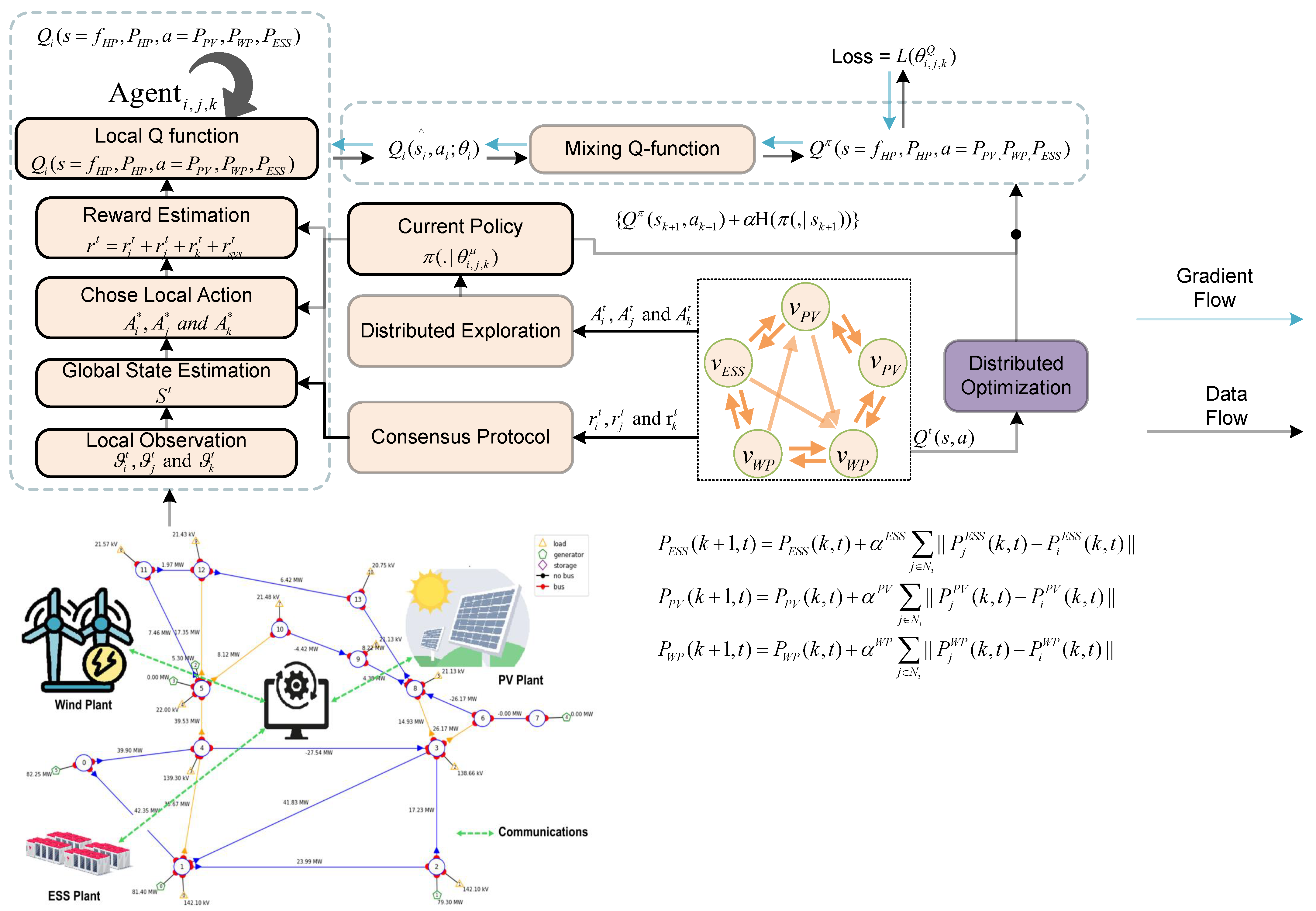
3. Proposed Networked Multi-Agent Deep Reinforcement Learning (N—MADRL) Approach
3.1. Network Representation
3.2. MADRL Preliminaries
- Agents: Agents represent PV, WP, and ESS assets, respectively.
- Region Set: The HPP environment is considered in terms of PV, WP, and ESS zones.
- System States: The system state contains the global information set of all agents, for instance .
- Agent Observation: The observation sets of PV, WP, and ESS agents are , , , respectively.
- Agent Actions: An action of agent at time t is represented as , , and , representing the optimal dispatch and frequency control. The boundary of , , and is limited within , where l represents optimal dispatch and reserve management.
- Reward Function: For optimal dispatch and frequency stability, the shared reward function accumulates the system reward and agent reward , formulated as follows:
3.3. Multi-Agent and Soft Actor–Critic (MASAC) Approach
3.4. Scalability and Heterogeneity
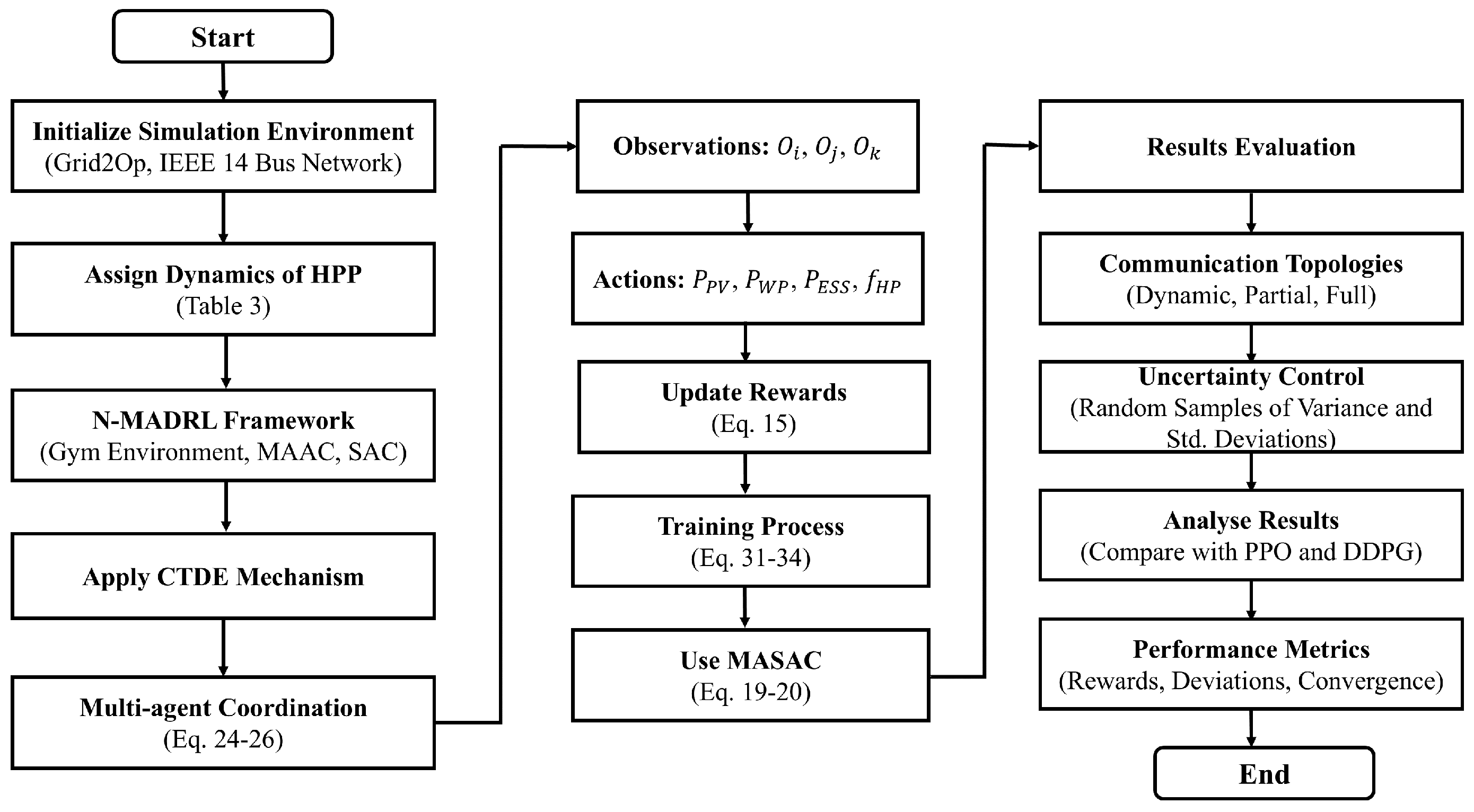
3.5. N—MADRL Implementation
| Algorithm 1 Proposed N—MADRL Scheme |
|
4. Numerical Simulations
4.1. N—MADRL Environment
4.2. Results Validation
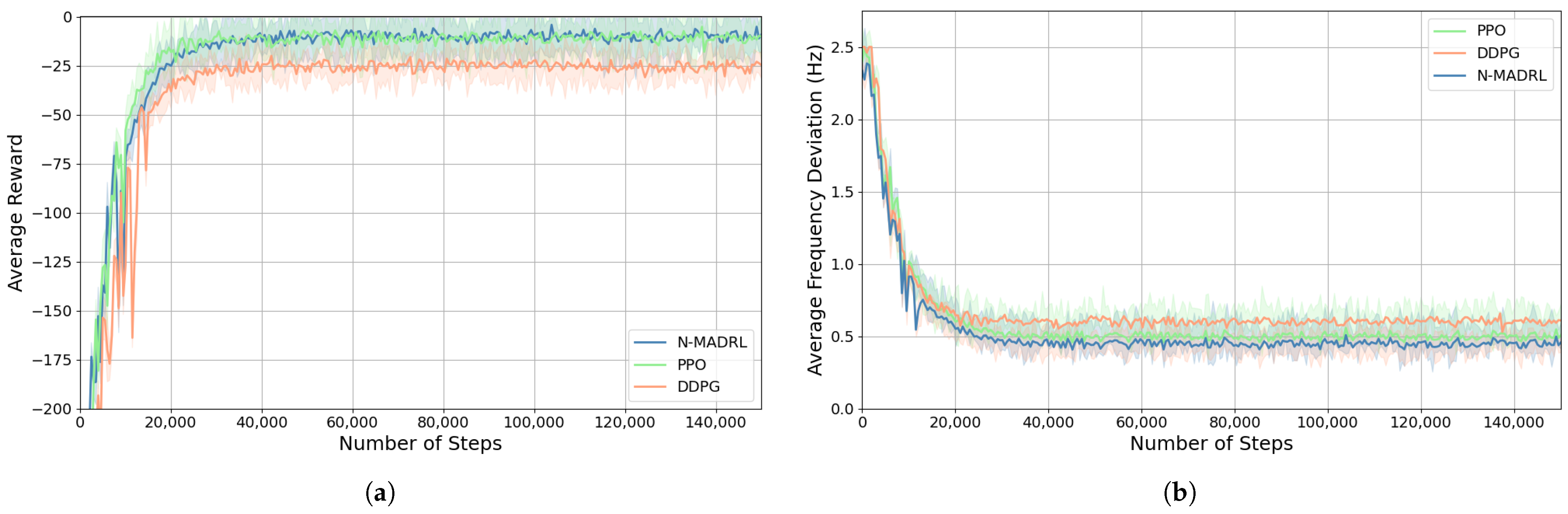
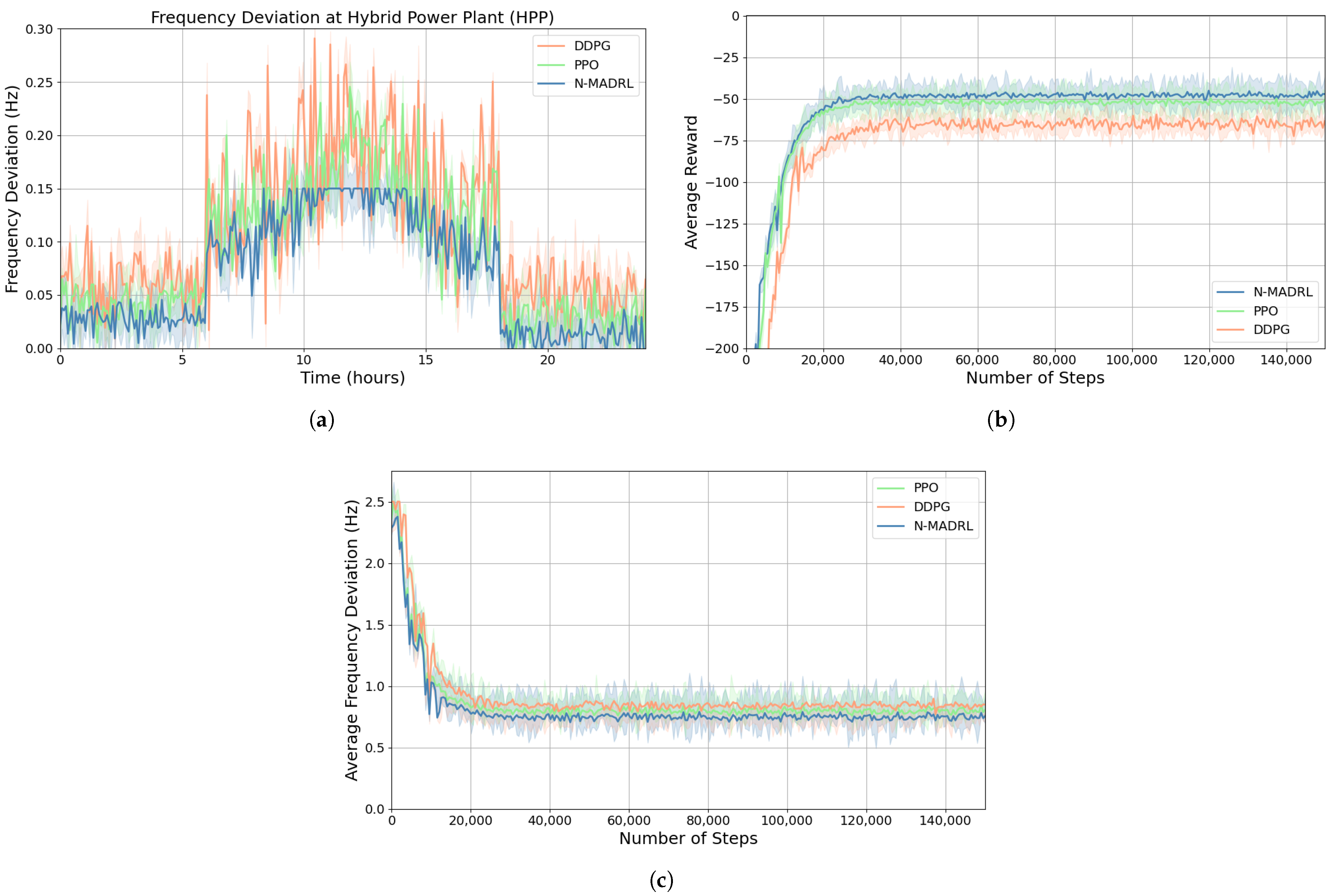
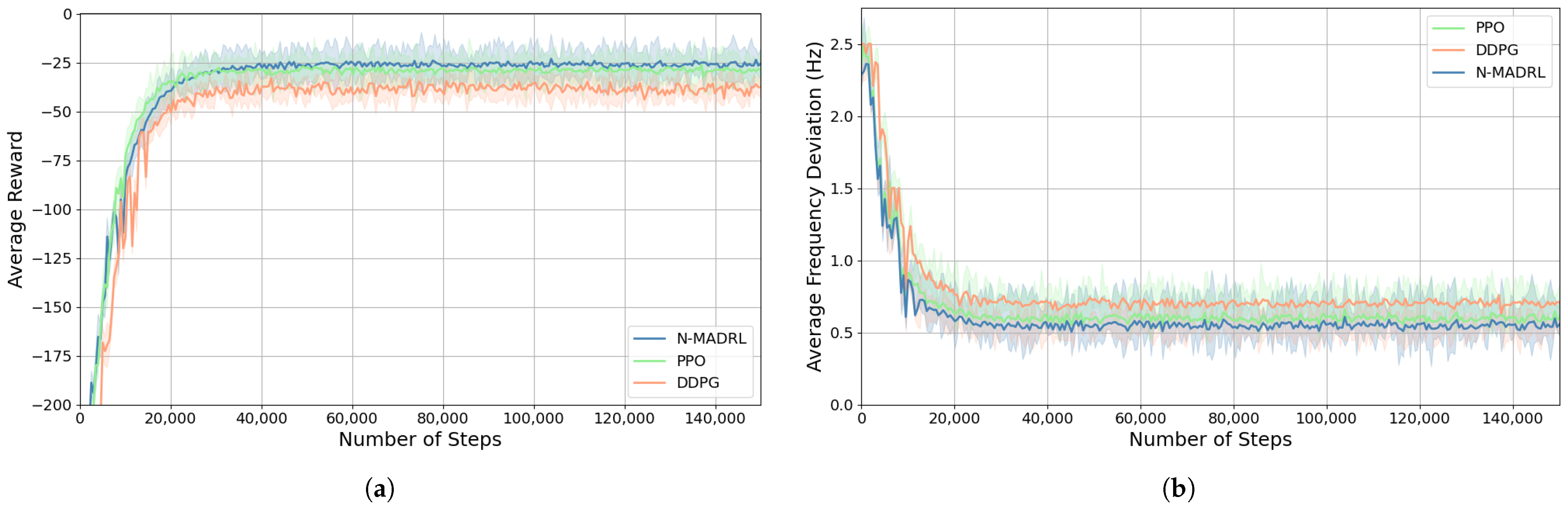
4.2.1. Training Process
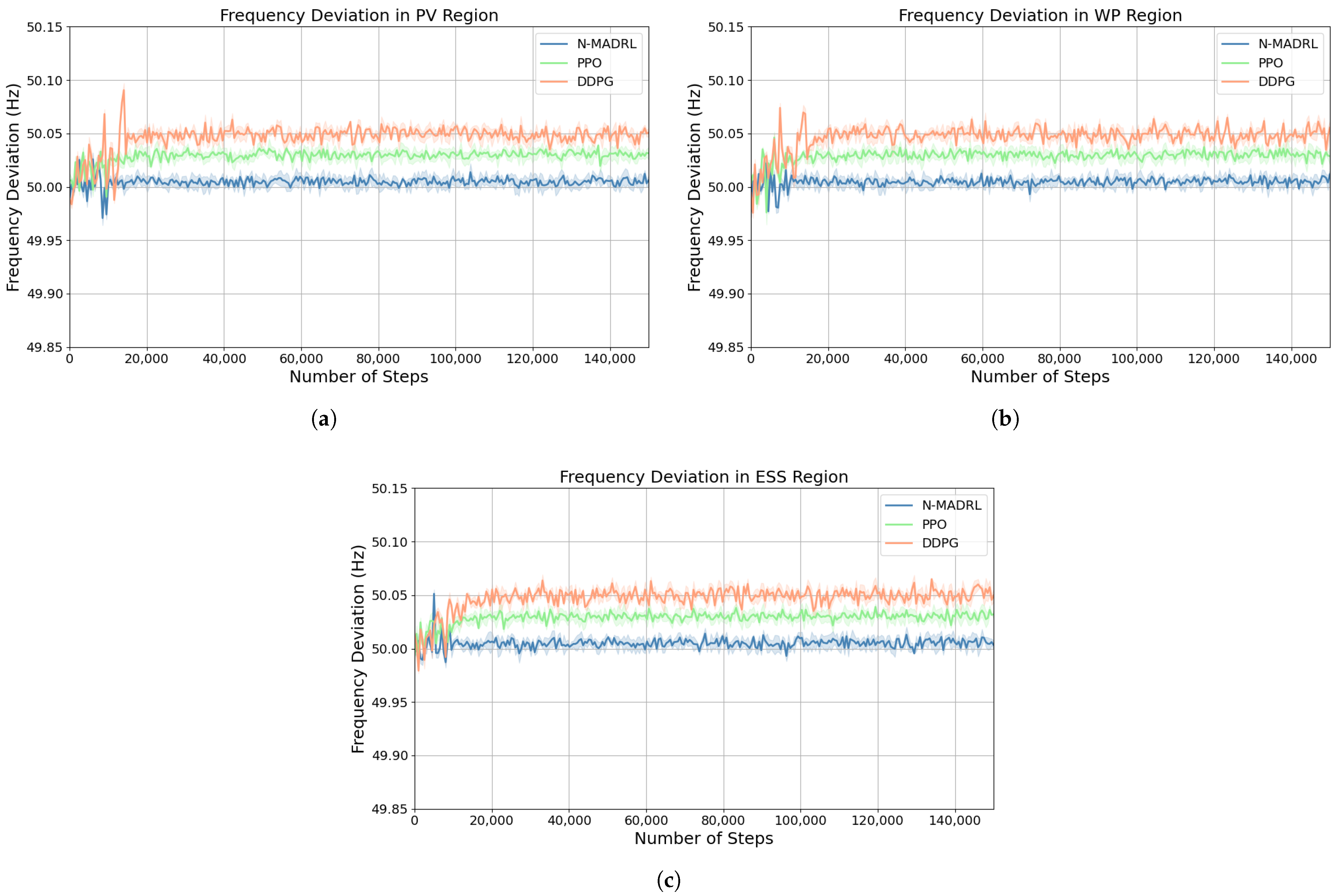
4.2.2. Comparison of DRL Algorithms
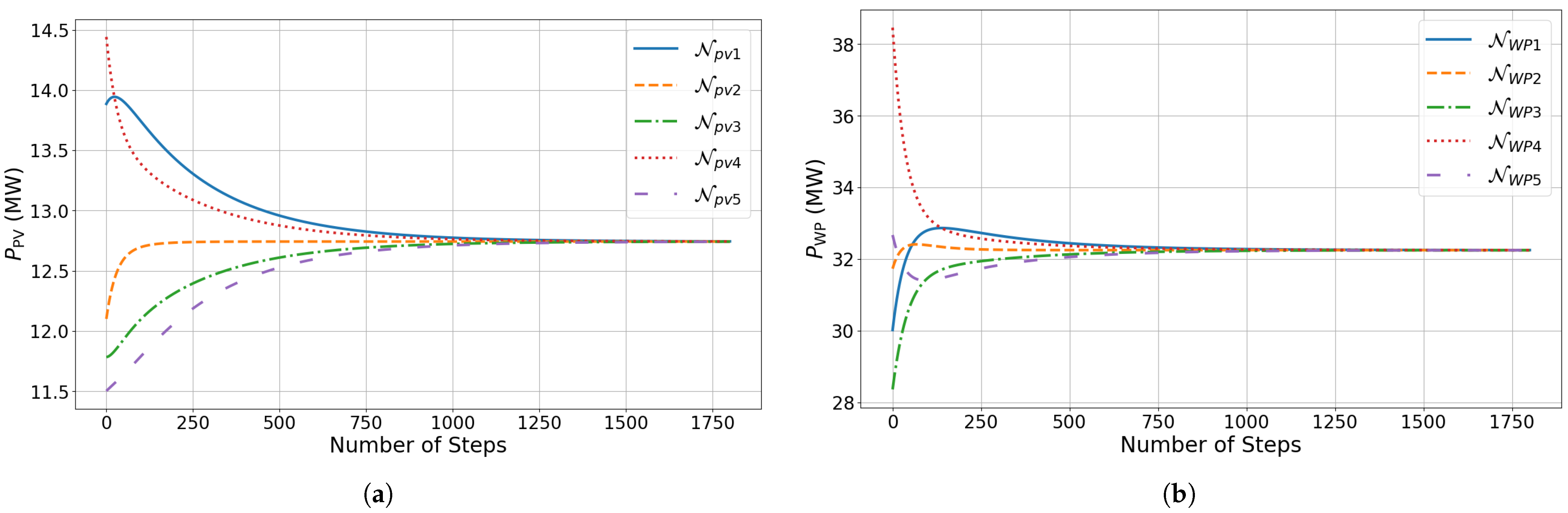
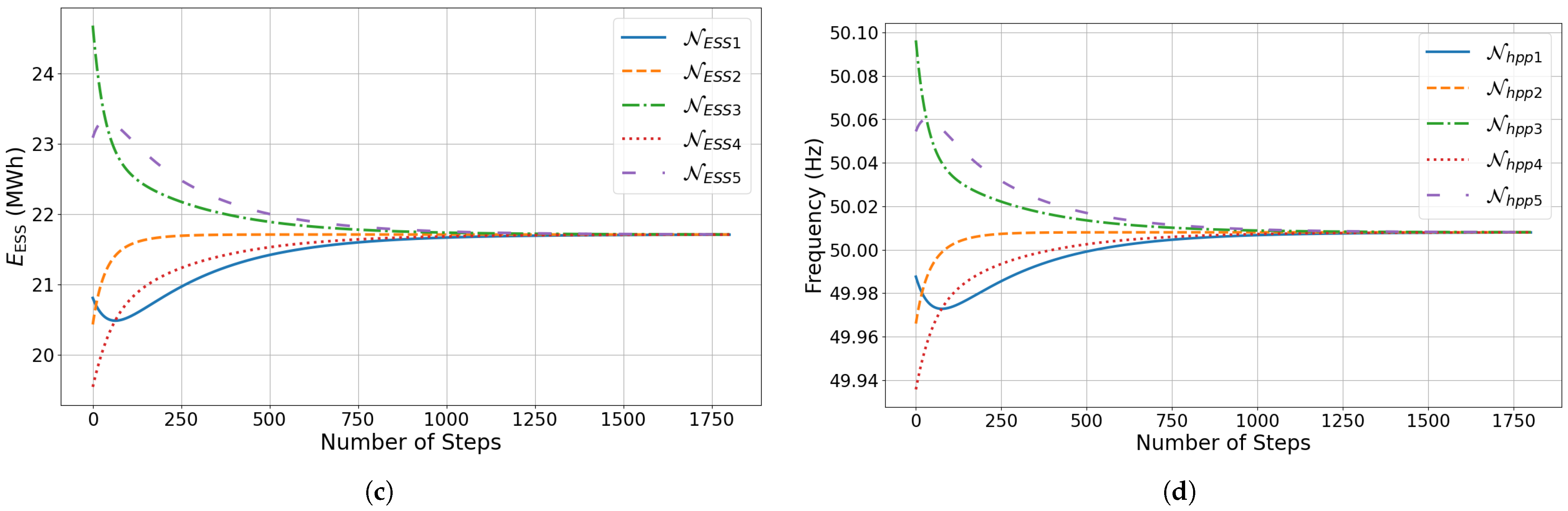
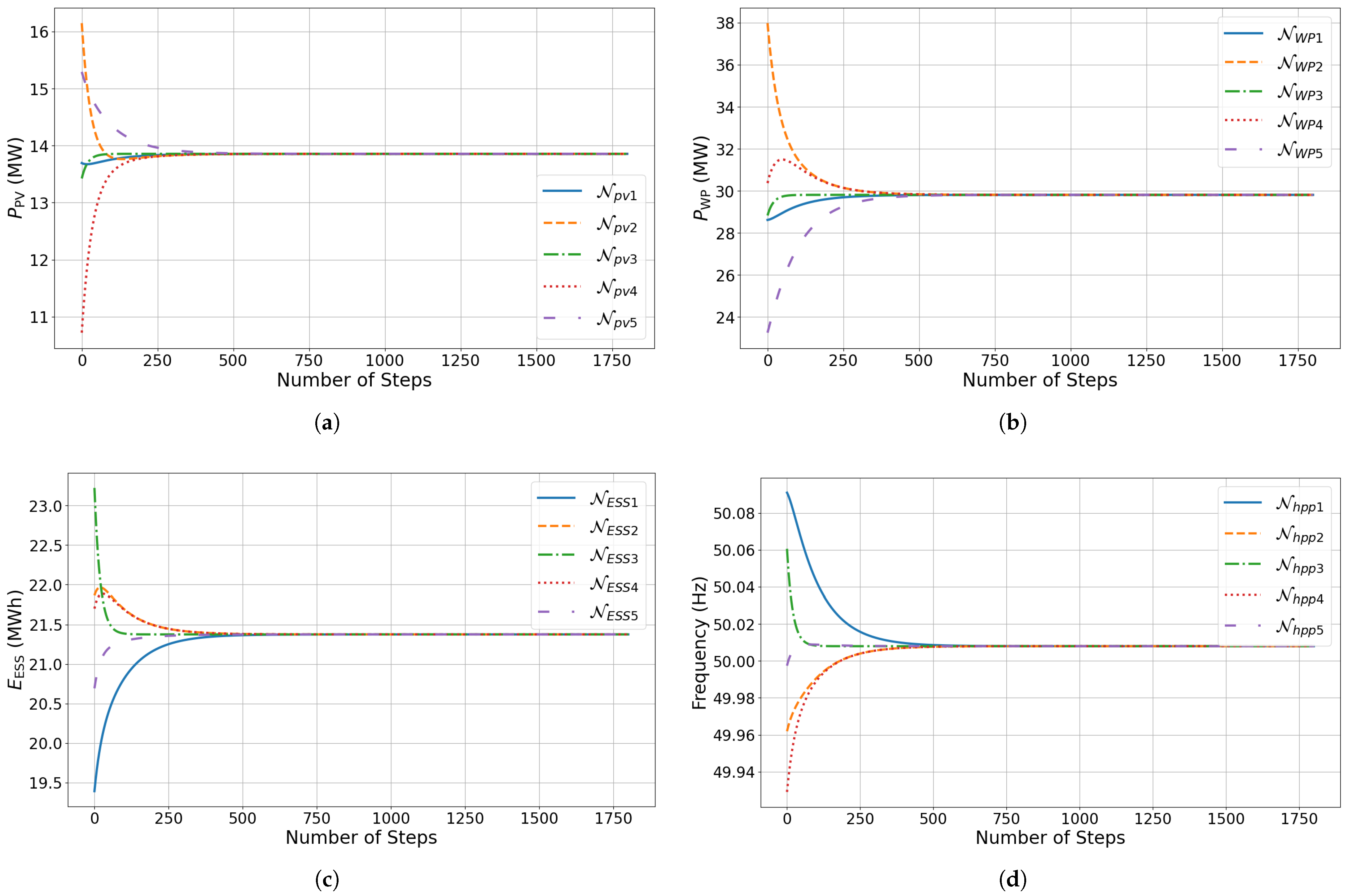
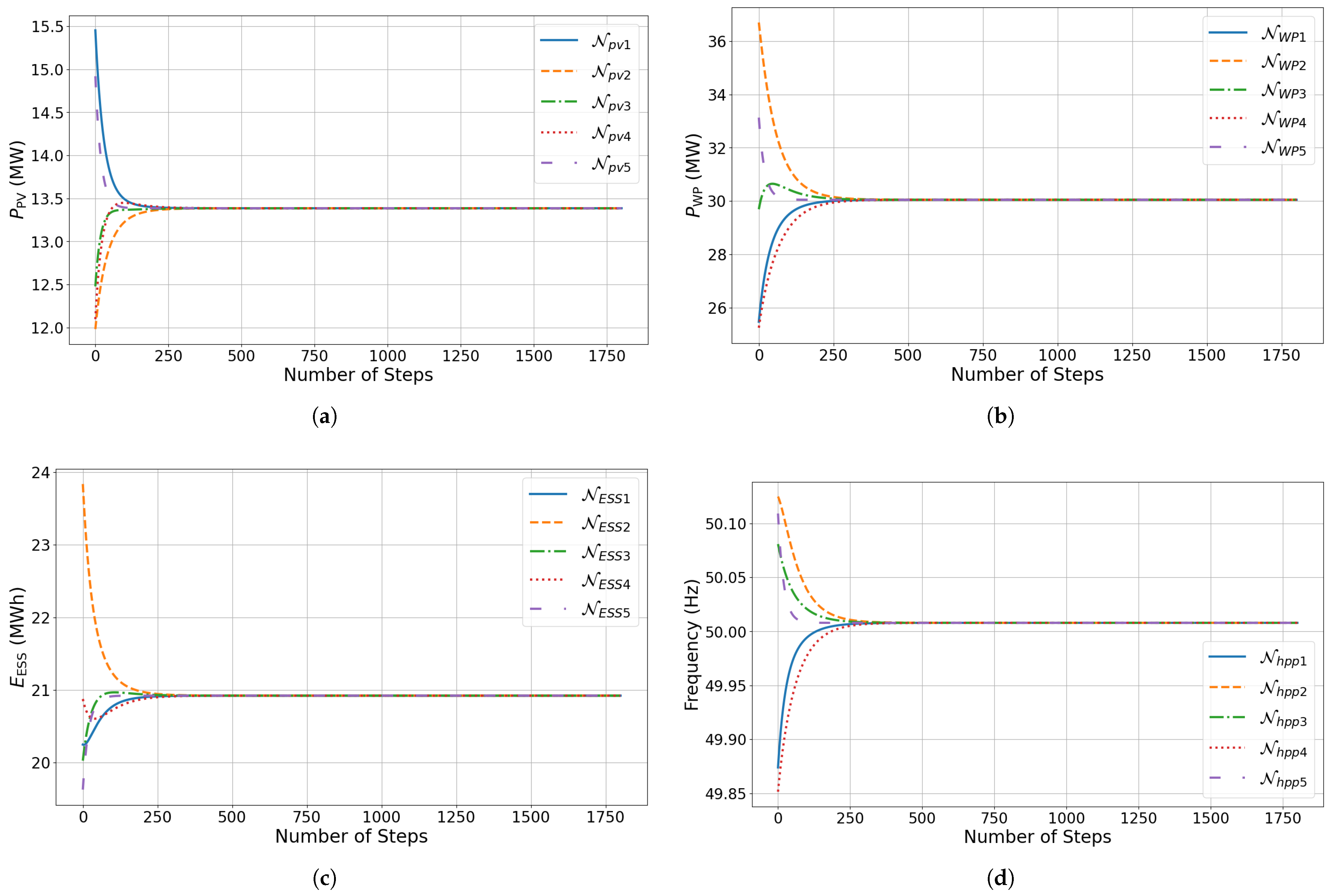
4.3. Optimal Dispatch Analysis
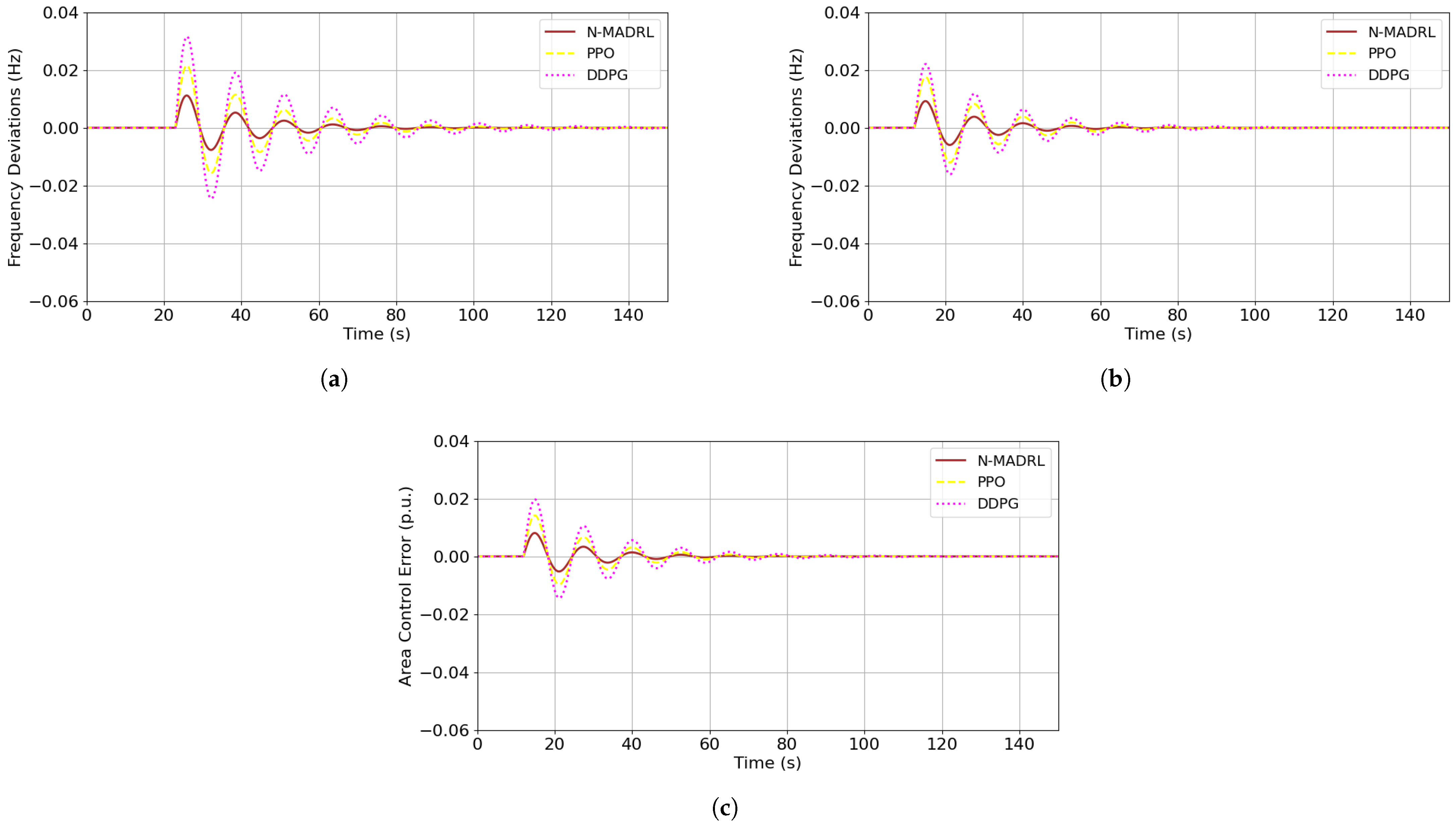
5. Discussion and Results Analysis
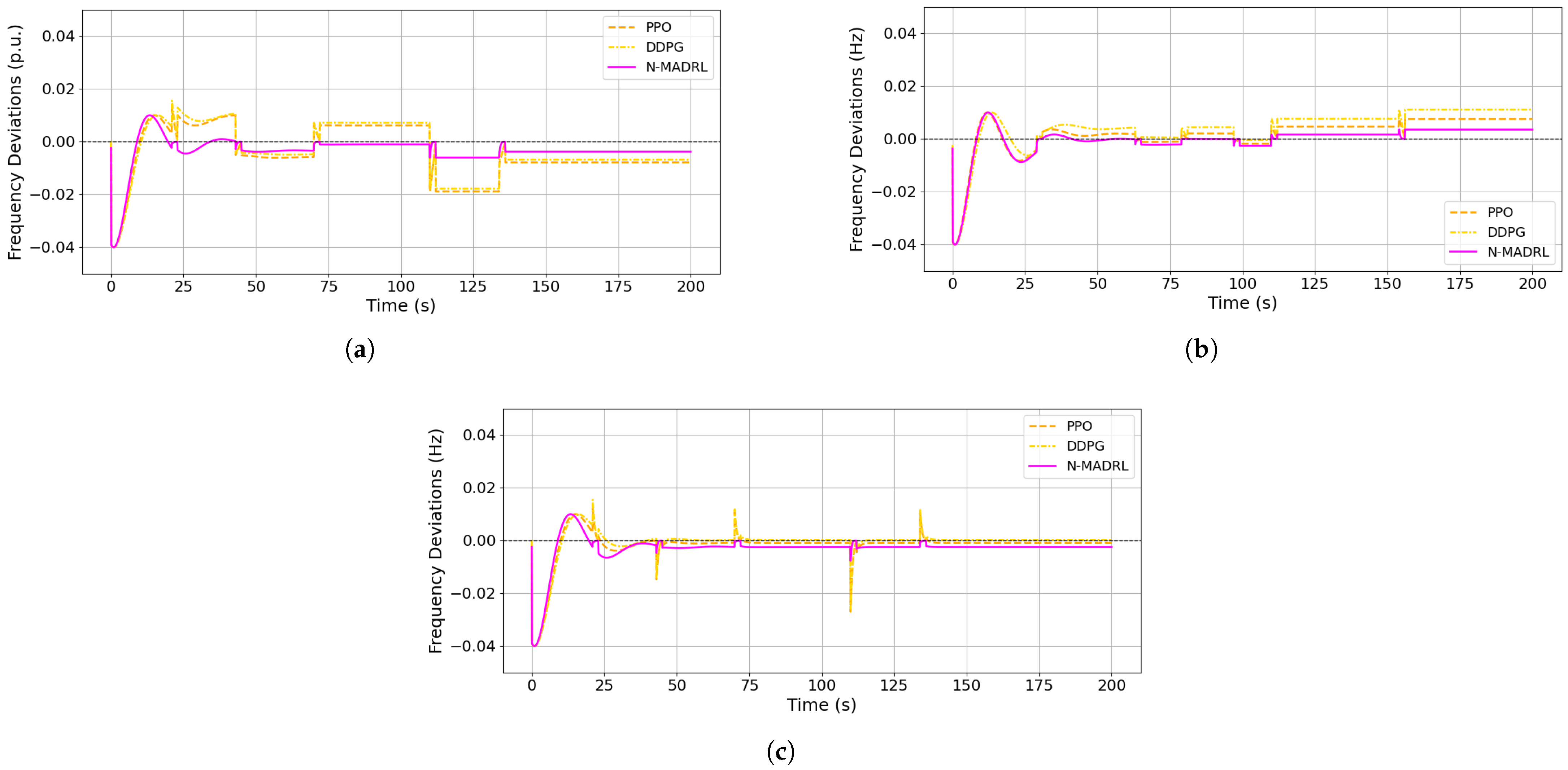
5.1. Robustness Analysis
5.1.1. Uncertainty Control
5.1.2. Communication Resiliency
- Scenario One (S 1): In this scenario, every agent , , is fully connected in each zone during the training process of the DDPG, PPO, and N—MADRL algorithms.
- Scenario Two (S 2): In this scenario, every agent in , , is partially connected in their respective zones during the training process for the DDPG, PPO, and N—MADRL algorithms.
5.2. Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IBR | Inverter-based resources |
| HPP | Hybrid power plant |
| PV | Photovoltaic |
| WP | Wind plant |
| ESS | Energy storage system |
| EMS | Energy management system |
| FFR | Fast frequency response |
| BS | Black start |
| DR | Demand response |
| EV | Electric vehicle |
| VPP | Virtual power plant |
| DER | Distributed energy resources |
| MPC | Model predictive control |
| DNN | Deep neural network |
| RL | Reinforcement learning |
| MARL | Multi-agent reinforcement learning |
| LFC | Load frequency control |
| GNN | Graph neural network |
| MG | Markov game |
| POMG | Partially-observable Markov game |
| DRL | Deep reinforcement learning |
| DDPG | Deep deterministic policy gradient |
| MADDPG | Multi-agent deep deterministic policy gradient |
| PPO | Proximal policy optimisation |
| MDP | Markov decision process |
| DQN | Deep Q-network |
| CTDE | Centralised training and decentralised execution |
| MADRL | Multi-agent deep reinforcement learning |
| SAC | Soft actor–critic |
| MAAC | Multi-agent actor–critic |
| MASAC | Multi-agent and soft actor–critic |
| MAAC | Multi-agent actor–critic |
| N—MADRL | Networked multi-agent deep reinforcement learning |
| Variables | |
| Power and frequency of hybrid power plant | |
| Power of PV, WP, and ESS plants | |
| Frequency of PV, WP, and ESS plants | |
| Indices of PV, WP, and ESS agents | |
| Number of PV, WP, and ESS agents | |
| PV, WP, and ESS plant agents | |
| Observations of PV, WP, and ESS agents | |
| States of PV, WP, and ESS agents | |
| Actions of PV, WP, and ESS agents | |
| Rewards of PV, WP, and ESS agents | |
| Optimal policy of PV, WP, and ESS agents | |
| Control input of PV, WP, and ESS agents | |
| Convergence coefficients of PV, WP, and ESS agents | |
| Collective action and observation of agents | |
| Value functions of HPP agents | |
| Parameters of actor networks for agents | |
| Proposed target value of agents | |
| Proposed loss function of agents | |
| Entropy-regularized exploration of agents | |
| Gradient of policy for agents | |
References
- Čović, N.; Pavić, I.; Pandžić, H. Multi-energy balancing services provision from a hybrid power plant: PV, battery, and hydrogen technologies. Appl. Energy 2024, 374, 123966. [Google Scholar] [CrossRef]
- Klyve, Ø.S.; Grab, R.; Olkkonen, V.; Marstein, E.S. Influence of high-resolution data on accurate curtailment loss estimation and optimal design of hybrid PV–wind power plants. Appl. Energy 2024, 372, 123784. [Google Scholar] [CrossRef]
- Kim, Y.S.; Park, G.H.; Kim, S.W.; Kim, D. Incentive design for hybrid energy storage system investment to PV owners considering value of grid services. Appl. Energy 2024, 373, 123772. [Google Scholar] [CrossRef]
- Zhang, T.; Xin, L.; Wang, S.; Guo, R.; Wang, W.; Cui, J.; Wang, P. A novel approach of energy and reserve scheduling for hybrid power systems: Frequency security constraints. Appl. Energy 2024, 361, 122926. [Google Scholar] [CrossRef]
- Askarov, A.; Rudnik, V.; Ruban, N.; Radko, P.; Ilyushin, P.; Suvorov, A. Enhanced Virtual Synchronous Generator with Angular Frequency Deviation Feedforward and Energy Recovery Control for Energy Storage System. Mathematics 2024, 12, 2691. [Google Scholar] [CrossRef]
- Leng, D.; Polmai, S. Virtual Synchronous Generator Based on Hybrid Energy Storage System for PV Power Fluctuation Mitigation. Appl. Sci. 2019, 9, 5099. [Google Scholar] [CrossRef]
- Pourbeik, P.; Sanchez-Gasca, J.J.; Senthil, J.; Weber, J.; Zadkhast, P.; Ramasubramanian, D.; Rao, S.D.; Bloemink, J.; Majumder, R.; Zhu, S.; et al. A Generic Model for Inertia-Based Fast Frequency Response of Wind Turbines and Other Positive-Sequence Dynamic Models for Renewable Energy Systems. IEEE Trans. Energy Convers. 2024, 39, 425–434. [Google Scholar] [CrossRef]
- Long, Q.; Das, K.; Pombo, D.V.; Sørensen, P.E. Hierarchical control architecture of co-located hybrid power plants. Int. J. Electr. Power Energy Syst. 2022, 143, 108407. [Google Scholar] [CrossRef]
- Ekomwenrenren, E.; Simpson-Porco, J.W.; Farantatos, E.; Patel, M.; Haddadi, A.; Zhu, L. Data-Driven Fast Frequency Control Using Inverter-Based Resources. IEEE Trans. Power Syst. 2024, 39, 5755–5768. [Google Scholar] [CrossRef]
- Jendoubi, I.; Bouffard, F. Multi-agent hierarchical reinforcement learning for energy management. Appl. Energy 2023, 332, 120500. [Google Scholar] [CrossRef]
- Guruwacharya, N.; Chakraborty, S.; Saraswat, G.; Bryce, R.; Hansen, T.M.; Tonkoski, R. Data-Driven Modeling of Grid-Forming Inverter Dynamics Using Power Hardware-in-the-Loop Experimentation. IEEE Access 2024, 12, 52267–52281. [Google Scholar] [CrossRef]
- Zhu, D.; Yang, B.; Liu, Y.; Wang, Z.; Ma, K.; Guan, X. Energy management based on multi-agent deep reinforcement learning for a multi-energy industrial park. Appl. Energy 2022, 311, 118636. [Google Scholar] [CrossRef]
- Li, Y.; Hou, J.; Yan, G. Exploration-enhanced multi-agent reinforcement learning for distributed PV-ESS scheduling with incomplete data. Appl. Energy 2024, 359, 122744. [Google Scholar] [CrossRef]
- Ochoa, T.; Gil, E.; Angulo, A.; Valle, C. Multi-agent deep reinforcement learning for efficient multi-timescale bidding of a hybrid power plant in day-ahead and real-time markets. Appl. Energy 2022, 317, 119067. [Google Scholar] [CrossRef]
- Jin, R.; Zhou, Y.; Lu, C.; Song, J. Deep reinforcement learning-based strategy for charging station participating in demand response. Appl. Energy 2022, 328, 120140. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, Y.; Zou, Y.; Yan, Z.; Zhou, N.; Chi, Y.; Wang, Q. Regional-privacy-preserving operation of networked microgrids: Edge-cloud cooperative learning with differentiated policies. Appl. Energy 2024, 370, 123611. [Google Scholar] [CrossRef]
- Sun, X.; Xie, H.; Qiu, D.; Xiao, Y.; Bie, Z.; Strbac, G. Decentralized frequency regulation service provision for virtual power plants: A best response potential game approach. Appl. Energy 2023, 352, 121987. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.I.; Vouros, G.A. Fuzzy Q-Learning for multi-agent decentralized energy management in microgrids. Appl. Energy 2018, 219, 53–67. [Google Scholar] [CrossRef]
- May, R.; Huang, P. A multi-agent reinforcement learning approach for investigating and optimising peer-to-peer prosumer energy markets. Appl. Energy 2023, 334, 120705. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, W.; Ghias, A.M.; Xu, X.; Chen, Z. Two-timescale autonomous energy management strategy based on multi-agent deep reinforcement learning approach for residential multicarrier energy system. Appl. Energy 2023, 351, 121777. [Google Scholar] [CrossRef]
- Xu, X.; Xu, K.; Zeng, Z.; Tang, J.; He, Y.; Shi, G.; Zhang, T. Collaborative optimization of multi-energy multi-microgrid system: A hierarchical trust-region multi-agent reinforcement learning approach. Appl. Energy 2024, 375, 123923. [Google Scholar] [CrossRef]
- Lv, C.; Liang, R.; Zhang, G.; Zhang, X.; Jin, W. Energy accommodation-oriented interaction of active distribution network and central energy station considering soft open points. Energy 2023, 268, 126574. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, Y.; Li, Y.; Xu, Y. Collaborative optimization of multi-microgrids system with shared energy storage based on multi-agent stochastic game and reinforcement learning. Energy 2023, 280, 128182. [Google Scholar] [CrossRef]
- Bui, V.H.; Su, W. Real-time operation of distribution network: A deep reinforcement learning-based reconfiguration approach. Sustain. Energy Technol. Assess. 2022, 50, 101841. [Google Scholar] [CrossRef]
- Li, H.; He, H. Optimal Operation of Networked Microgrids With Distributed Multi-Agent Reinforcement Learning. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024; pp. 1–5. [Google Scholar]
- Fang, X.; Wang, J.; Song, G.; Han, Y.; Zhao, Q.; Cao, Z. Multi-agent reinforcement learning approach for residential microgrid energy scheduling. Energies 2019, 13, 123. [Google Scholar] [CrossRef]
- Anjaiah, K.; Dash, P.; Bisoi, R.; Dhar, S.; Mishra, S. A new approach for active and reactive power management in renewable based hybrid microgrid considering storage devices. Appl. Energy 2024, 367, 123429. [Google Scholar] [CrossRef]
- Wu, H.; Qiu, D.; Zhang, L.; Sun, M. Adaptive multi-agent reinforcement learning for flexible resource management in a virtual power plant with dynamic participating multi-energy buildings. Appl. Energy 2024, 374, 123998. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, B.; Liu, H.; Sun, H.; Pan, Z.; Guo, Q. Exploiting the flexibility inside park-level commercial buildings considering heat transfer time delay: A memory-augmented deep reinforcement learning approach. IEEE Trans. Sustain. Energy 2021, 13, 207–219. [Google Scholar] [CrossRef]
- Ebrie, A.S.; Kim, Y.J. Reinforcement Learning-Based Multi-Objective Optimization for Generation Scheduling in Power Systems. Systems 2024, 12, 106. [Google Scholar] [CrossRef]
- Qiu, D.; Wang, Y.; Zhang, T.; Sun, M.; Strbac, G. Hybrid Multiagent Reinforcement Learning for Electric Vehicle Resilience Control Towards a Low-Carbon Transition. IEEE Trans. Ind. Inform. 2022, 18, 8258–8269. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, D.; Strbac, G.; Gao, Z. Coordinated Electric Vehicle Active and Reactive Power Control for Active Distribution Networks. IEEE Trans. Ind. Inform. 2023, 19, 1611–1622. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Distributed Multi-Agent System-Based Load Frequency Control for Multi-Area Power System in Smart Grid. IEEE Trans. Ind. Electron. 2017, 64, 5151–5160. [Google Scholar] [CrossRef]
- Yu, T.; Wang, H.Z.; Zhou, B.; Chan, K.W.; Tang, J. Multi-Agent Correlated Equilibrium Q(λ) Learning for Coordinated Smart Generation Control of Interconnected Power Grids. IEEE Trans. Power Syst. 2015, 30, 1669–1679. [Google Scholar] [CrossRef]
- Shen, R.; Zhong, S.; Wen, X.; An, Q.; Zheng, R.; Li, Y.; Zhao, J. Multi-agent deep reinforcement learning optimization framework for building energy system with renewable energy. Appl. Energy 2022, 312, 118724. [Google Scholar] [CrossRef]
- Lu, R.; Li, Y.C.; Li, Y.; Jiang, J.; Ding, Y. Multi-agent deep reinforcement learning based demand response for discrete manufacturing systems energy management. Appl. Energy 2020, 276, 115473. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Ajagekar, A.; Decardi-Nelson, B.; You, F. Energy management for demand response in networked greenhouses with multi-agent deep reinforcement learning. Appl. Energy 2024, 355, 122349. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, D.; Strbac, G. Multi-agent deep reinforcement learning for resilience-driven routing and scheduling of mobile energy storage systems. Appl. Energy 2022, 310, 118575. [Google Scholar] [CrossRef]
- Zhang, J.; Sang, L.; Xu, Y.; Sun, H. Networked Multiagent-Based Safe Reinforcement Learning for Low-Carbon Demand Management in Distribution Networks. IEEE Trans. Sustain. Energy 2024, 15, 1528–1545. [Google Scholar] [CrossRef]
- Tavakol Aghaei, V.; Ağababaoğlu, A.; Bawo, B.; Naseradinmousavi, P.; Yıldırım, S.; Yeşilyurt, S.; Onat, A. Energy optimization of wind turbines via a neural control policy based on reinforcement learning Markov chain Monte Carlo algorithm. Appl. Energy 2023, 341, 121108. [Google Scholar] [CrossRef]
- Li, J.; Yu, T.; Zhang, X. Coordinated load frequency control of multi-area integrated energy system using multi-agent deep reinforcement learning. Appl. Energy 2022, 306, 117900. [Google Scholar] [CrossRef]
- Dong, L.; Lin, H.; Qiao, J.; Zhang, T.; Zhang, S.; Pu, T. A coordinated active and reactive power optimization approach for multi-microgrids connected to distribution networks with multi-actor-attention-critic deep reinforcement learning. Appl. Energy 2024, 373, 123870. [Google Scholar] [CrossRef]
- Deptula, P.; Bell, Z.I.; Doucette, E.A.; Curtis, J.W.; Dixon, W.E. Data-based reinforcement learning approximate optimal control for an uncertain nonlinear system with control effectiveness faults. Automatica 2020, 116, 108922. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, D.; Hu, W.; Ghias, A.M.; Chen, Z. Physics-Informed Multi-Agent deep reinforcement learning enabled distributed voltage control for active distribution network using PV inverters. Int. J. Electr. Power Energy Syst. 2024, 155, 109641. [Google Scholar] [CrossRef]
- Li, S.; Hu, W.; Cao, D.; Chen, Z.; Huang, Q.; Blaabjerg, F.; Liao, K. Physics-model-free heat-electricity energy management of multiple microgrids based on surrogate model-enabled multi-agent deep reinforcement learning. Appl. Energy 2023, 346, 121359. [Google Scholar] [CrossRef]
- Abid, M.S.; Apon, H.J.; Hossain, S.; Ahmed, A.; Ahshan, R.; Lipu, M.H. A novel multi-objective optimization based multi-agent deep reinforcement learning approach for microgrid resources planning. Appl. Energy 2024, 353, 122029. [Google Scholar] [CrossRef]
- Hua, M.; Zhang, C.; Zhang, F.; Li, Z.; Yu, X.; Xu, H.; Zhou, Q. Energy management of multi-mode plug-in hybrid electric vehicle using multi-agent deep reinforcement learning. Appl. Energy 2023, 348, 121526. [Google Scholar] [CrossRef]
- Xie, J.; Ajagekar, A.; You, F. Multi-Agent attention-based deep reinforcement learning for demand response in grid-responsive buildings. Appl. Energy 2023, 342, 121162. [Google Scholar] [CrossRef]
- Xiang, Y.; Lu, Y.; Liu, J. Deep reinforcement learning based topology-aware voltage regulation of distribution networks with distributed energy storage. Appl. Energy 2023, 332, 120510. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, M.; Gong, Y.; Xu, Q. Safe multi-agent deep reinforcement learning for real-time decentralized control of inverter based renewable energy resources considering communication delay. Appl. Energy 2023, 349, 121648. [Google Scholar] [CrossRef]
- Si, R.; Chen, S.; Zhang, J.; Xu, J.; Zhang, L. A multi-agent reinforcement learning method for distribution system restoration considering dynamic network reconfiguration. Appl. Energy 2024, 372, 123625. [Google Scholar] [CrossRef]
- Tzani, D.; Stavrakas, V.; Santini, M.; Thomas, S.; Rosenow, J.; Flamos, A. Pioneering a performance-based future for energy efficiency: Lessons learnt from a comparative review analysis of pay-for-performance programmes. Renew. Sustain. Energy Rev. 2022, 158, 112162. [Google Scholar] [CrossRef]
- Donnot, B. *Grid2Op: A Testbed Platform to Model Sequential Decision Making in Power Systems*. Available online: https://github.com/Grid2op/grid2op (accessed on 31 March 2025).



| Refs. | Energy Source | Coordinations | Algorithms | Scalability | Performance |
|---|---|---|---|---|---|
| [27] | BESS, DG | Decentralized | Q-learning | Low | Improves power dispatch |
| [28] | PV, ESS, WP | Centralized | MPC | Low | Energy scheduling |
| [29] | VPP | Distributed | Q-learning | Moderate | Energy cost optimization |
| [30] | Microgrid | Centralized | SAC, DDQN | Moderate | Enhances thermal management |
| [31] | PV, ESS | Distributed | MOPS | Low | Improves cost optimization |
| [32,33] | PV, WP, EV | Distributed | Dec-POMDP | Moderate | Marginal cost optimization |
| [34,35] | Smart grid | Centralized | Dec-POMDP | Moderate | Reduces frequency deviation |
| [36,37,38] | PV, WP, ESS | Decentralized | D3Q, MADDPG | Moderate | Fast convergence |
| [39,40,41] | WP, ESS, PV | Networked | SAC, DDQN | Moderate | Optimizes energy cost |
| [42,43,44] | WP, PV | Networked | DDPG, MAAC | Moderate | Energy scheduling |
| This paper | PV, WP, ESS | Networked | SAC, MAAC | High | Optimal dispatch and Reserve |
| Algorithms | Parameters | Values |
|---|---|---|
| N—MADRL | Actors hidden units | {128, 256} |
| Actors hidden layers | {2, 5} | |
| Critic hidden units | {128, 256} | |
| Critic hidden layers | {2, 5} | |
| Learning rate | 0.0003 | |
| 0.60 | ||
| PPO & DDPG | Actors hidden units | 256 |
| Critic hidden units | 256 | |
| Optimizer | Adam | |
| Activation function | ReLU | |
| Shared | Learning rate | 0.0003 |
| Mini-batch size | 64 | |
| Reply buffer | ||
| Discount factor | 0.97 | |
| Total iterations k | ||
| Soft update | 0.10 |
| g-id | Bus | Asset | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | pv | 0.039 | 0 | 0 | 11.7 | 0 | 0 | 2.34 | 0 | 0 |
| 1 | 5 | ess | 0 | 0 | 0.032 | 0 | 0 | 21.8 | 0 | 0 | 4.36 |
| 2 | 3 | wind | 0 | 0.026 | 0 | 0 | 26.7 | 0 | 0 | 5.34 | 0 |
| 3 | 12 | ess | 0 | 0 | 0.030 | 0 | 0 | 25.75 | 0 | 0 | 5.15 |
| 4 | 2 | pv | 0.036 | 0 | 0 | 14.8 | 0 | 0 | 2.96 | 0 | 0 |
| 5 | 6 | wind | 0 | 0.023 | 0 | 0 | 41.4 | 0 | 0 | 8.28 | 0 |
| 6 | 4 | pv | 0.034 | 0 | 0 | 17.6 | 0 | 0 | 3.52 | 0 | 0 |
| 7 | 13 | ess | 0 | 0 | 0.029 | 0 | 0 | 18.6 | 0 | 0 | 3.72 |
| 8 | 9 | wind | 0 | 0.025 | 0 | 0 | 33.4 | 0 | 0 | 6.68 | 0 |
| 9 | 11 | pv | 0.037 | 0 | 0 | 10.4 | 0 | 0 | 2.08 | 0 | 0 |
| 10 | 7 | wind | 0 | 0.021 | 0 | 0 | 22.8 | 0 | 0 | 4.56 | 0 |
| 11 | 10 | ess | 0 | 0 | 0.031 | 0 | 0 | 22.7 | 0 | 0 | 4.54 |
| 12 | 8 | pv | 0.035 | 0 | 0 | 10.7 | 0 | 0 | 2.14 | 0 | 0 |
| 13 | 14 | pv | 0.038 | 0 | 0 | 12.2 | 0 | 0 | 2.44 | 0 | 0 |
| Algorithms | Training (hr) | Validation (min) | Testing (min) |
|---|---|---|---|
| N—MADRL | 6.50 | 25 | 13 |
| PPO | 8.25 | 40 | 21 |
| DDPG | 10.20 | 50 | 24 |
| Algorithms | Ave. Rewards | Ave. Deviation (Hz) | Ave. Power (MW) |
|---|---|---|---|
| N—MADRL | −9.93 | 0.013 | 0.22 |
| PPO | −12.45 | 0.041 | 0.38 |
| DDPG | −24.58 | 0.053 | 0.57 |
| Scenarios | Algorithms | Rewards | Deviation (Hz) | Std. Deviation | Convergence Rate | Threshold | Steps |
|---|---|---|---|---|---|---|---|
| Scenario 1 | N—MADRL | −25 | 0.085 | 4.37 | 0.61 | 61% | 21,100 |
| PPO | −54 | 0.098 | 7.11 | 0.64 | 64% | 28,400 | |
| DDPG | −128 | 0.106 | 9.34 | 0.62 | 62% | – | |
| Scenario 2 | N—MADRL | −35 | 0.092 | 4.37 | 0.37 | 37% | 33,200 |
| PPO | −70 | 0.103 | 6.48 | 0.41 | 41% | 41,230 | |
| DDPG | −135 | 0.160 | 7.15 | 0.39 | 39% | – |
| g-id | Bus | ||||
|---|---|---|---|---|---|
| 0 | 1 | 0.618 | 0.039 | 11.7 | 2.34 |
| 4 | 2 | 0.562 | 0.036 | 14.8 | 2.96 |
| 6 | 4 | 0.647 | 0.034 | 17.6 | 3.52 |
| 9 | 11 | 0.683 | 0.037 | 10.4 | 2.08 |
| 12 | 8 | 0.594 | 0.035 | 10.7 | 2.14 |
| 13 | 14 | 0.616 | 0.038 | 12.2 | 2.44 |
| g-id | Bus | ||||
|---|---|---|---|---|---|
| 2 | 3 | 0.594 | 0.026 | 26.7 | 5.34 |
| 5 | 6 | 0.631 | 0.023 | 41.4 | 8.28 |
| 8 | 9 | 0.658 | 0.025 | 33.4 | 6.68 |
| 10 | 7 | 0.614 | 0.021 | 22.8 | 4.56 |
| g-id | Bus | ||||
|---|---|---|---|---|---|
| 1 | 5 | 0.670 | 0.032 | 21.8 | 4.36 |
| 3 | 12 | 0.621 | 0.030 | 25.75 | 5.15 |
| 7 | 13 | 0.632 | 0.029 | 18.6 | 3.72 |
| 11 | 10 | 0.594 | 0.031 | 22.7 | 4.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikram, M.; Habibi, D.; Aziz, A. Networked Multi-Agent Deep Reinforcement Learning Framework for the Provision of Ancillary Services in Hybrid Power Plants. Energies 2025, 18, 2666. https://doi.org/10.3390/en18102666
Ikram M, Habibi D, Aziz A. Networked Multi-Agent Deep Reinforcement Learning Framework for the Provision of Ancillary Services in Hybrid Power Plants. Energies. 2025; 18(10):2666. https://doi.org/10.3390/en18102666
Chicago/Turabian StyleIkram, Muhammad, Daryoush Habibi, and Asma Aziz. 2025. "Networked Multi-Agent Deep Reinforcement Learning Framework for the Provision of Ancillary Services in Hybrid Power Plants" Energies 18, no. 10: 2666. https://doi.org/10.3390/en18102666
APA StyleIkram, M., Habibi, D., & Aziz, A. (2025). Networked Multi-Agent Deep Reinforcement Learning Framework for the Provision of Ancillary Services in Hybrid Power Plants. Energies, 18(10), 2666. https://doi.org/10.3390/en18102666







