Steady-State Model Enabled Dynamic PEMFC Performance Degradation Prediction via Recurrent Neural Network
Abstract
1. Introduction
- Modeling insufficiency: Existing semi-empirical frameworks inadequately capture coupled electrochemical–physical degradation mechanisms, particularly under transient operational regimes.
- Feature ambiguity: Data-driven approaches frequently employ heuristic feature selection without systematic quantification of degradation-relevant feature vectors, limiting their capacity to resolve high-order nonlinear degradation dynamics.
- Integration naivety: Prevailing hybrid methodologies often adopt linear additive fusion frameworks that fail to exploit synergistic interactions between physics-based models and machine learning architectures.
- Development of a self-consistent electrochemistry-explicit model integrating Nernst–Planck transport dynamics with Butler–Volmer reaction kinetics for enhanced mechanistic fidelity.
- Rather than embedding physics residuals as regularization terms, implementation of physics-informed feature engineering that systematically extracts degradation-sensitive parameters through thermodynamic irreversibility analysis.
- Creation of a nonlinear co-learning framework where semi-empirical model outputs are encoded as latent states within RNN architectures through attention-based fusion mechanisms.
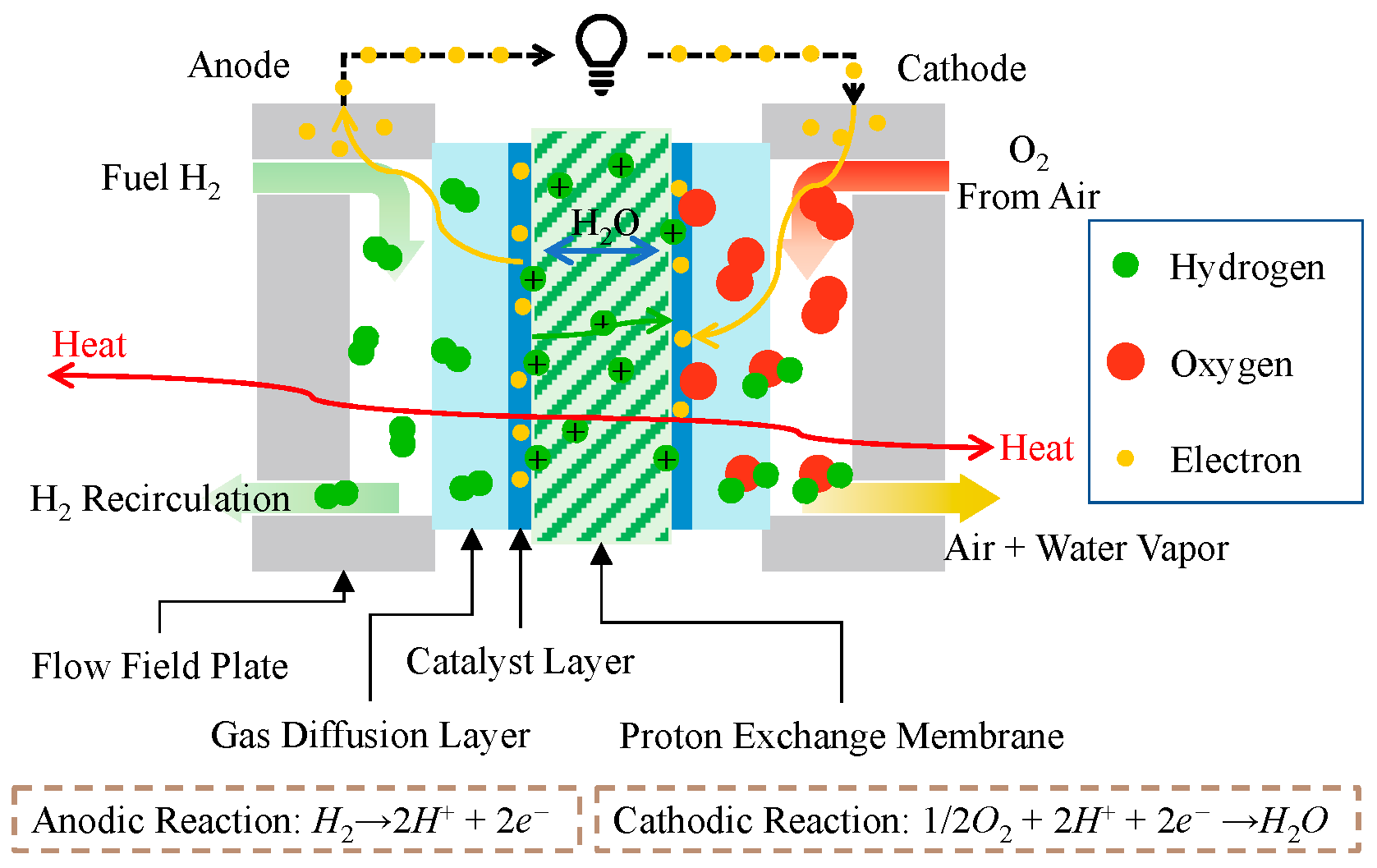
2. Self-Consistent Semi-Empirical Model
2.1. Semi-Empirical Model of PEMFC
2.1.1. Ohmic Loss
2.1.2. Concentration Loss
2.1.3. Activation Loss
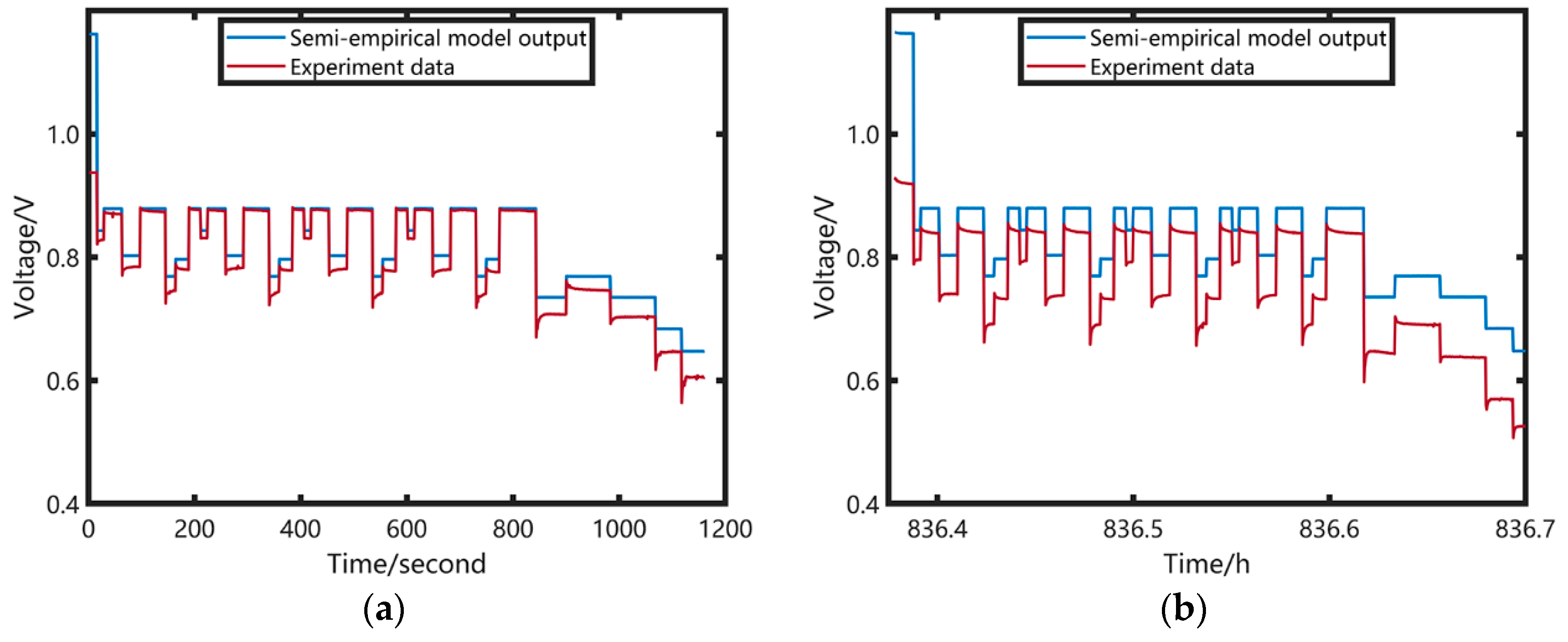
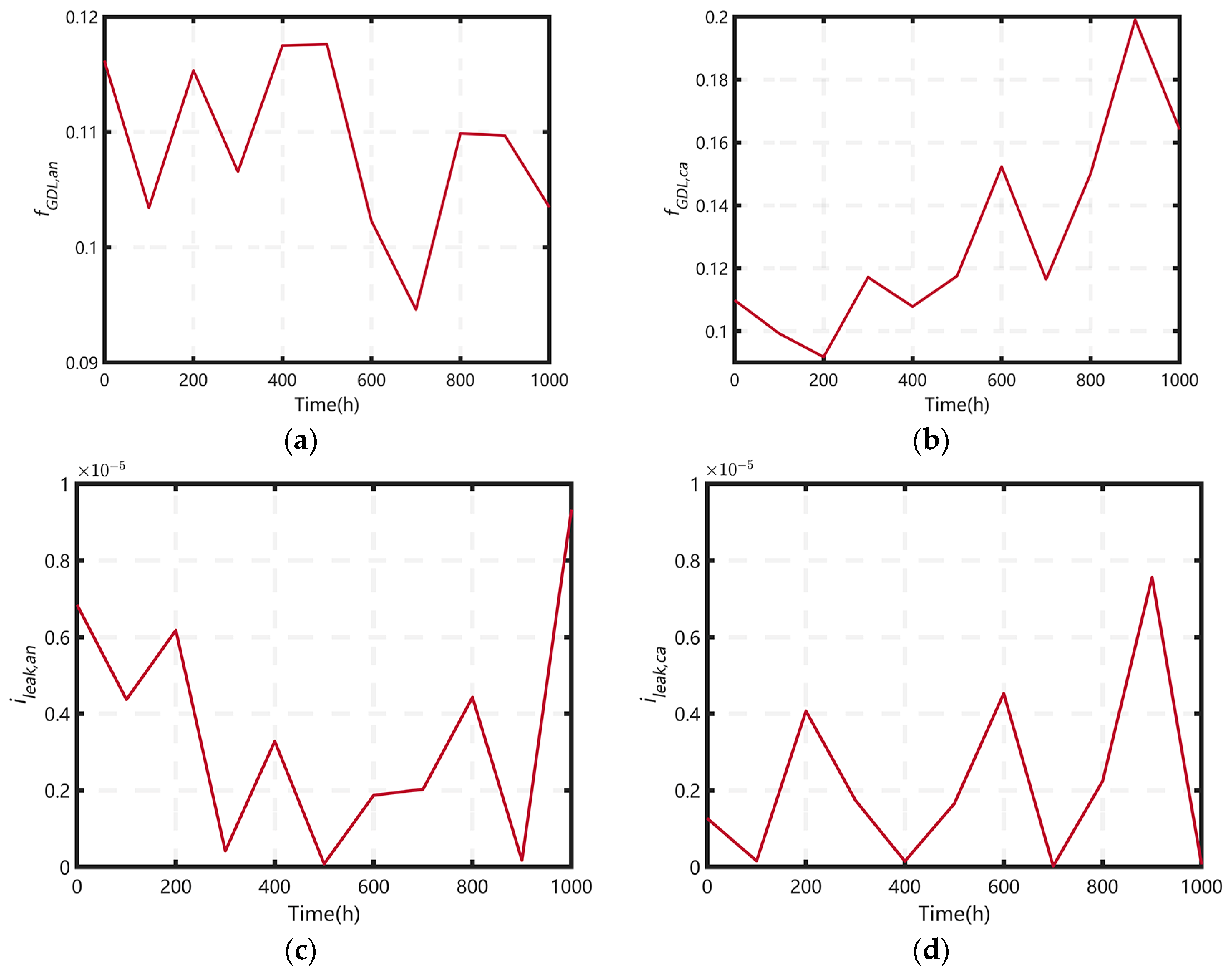
2.2. Model Parameters Identification and Analysis
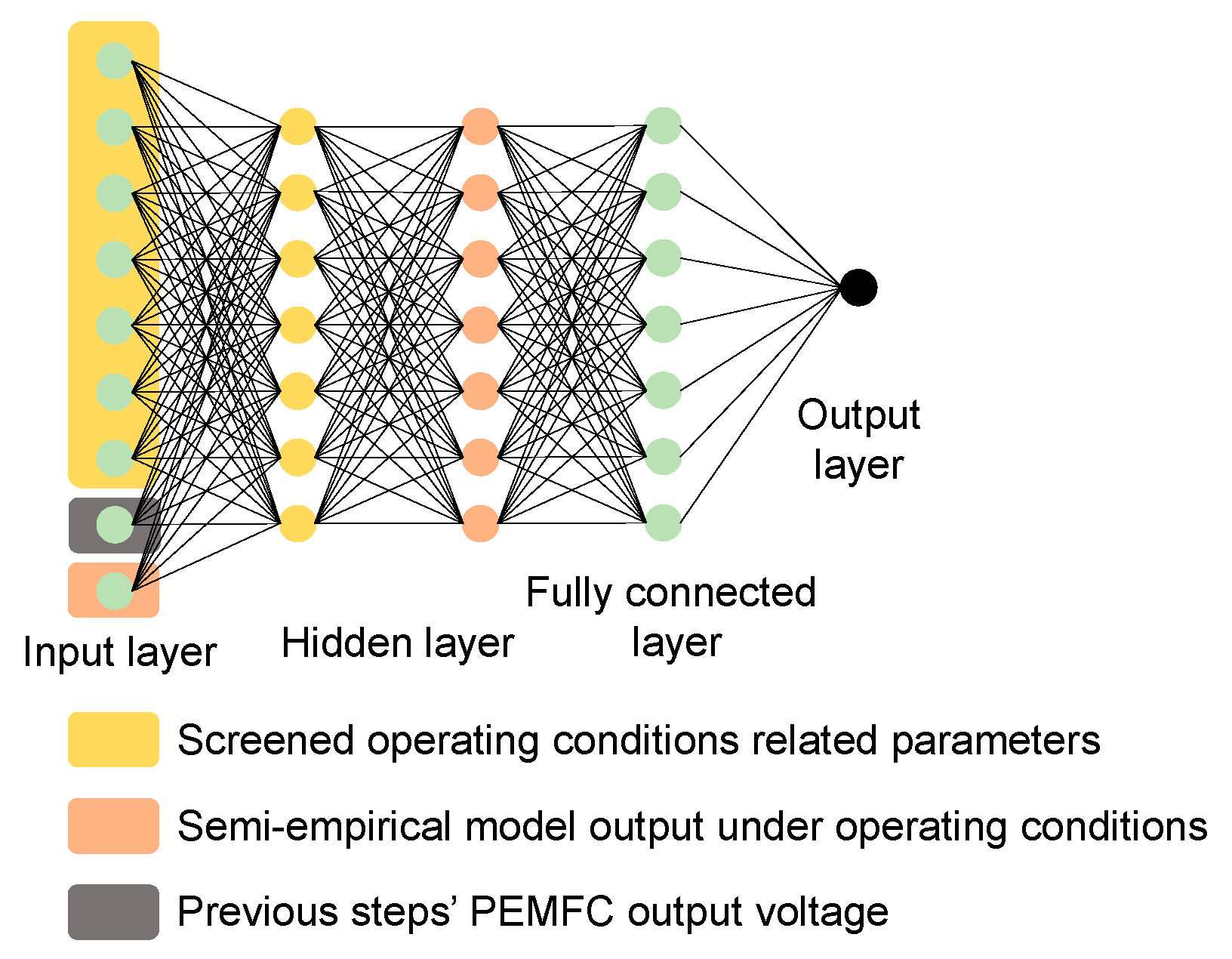
3. Semi-Empirical Model Involving RNN Methods
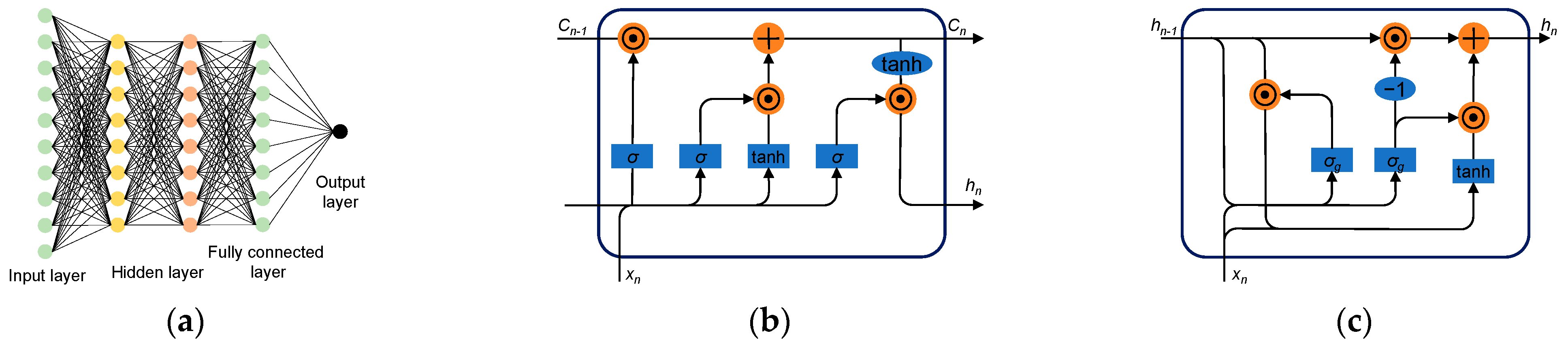
3.1. Recurrent Neural Network
3.1.1. Basics of LSTM
3.1.2. Basics of GRU
3.2. Dataset Analysis and Screening
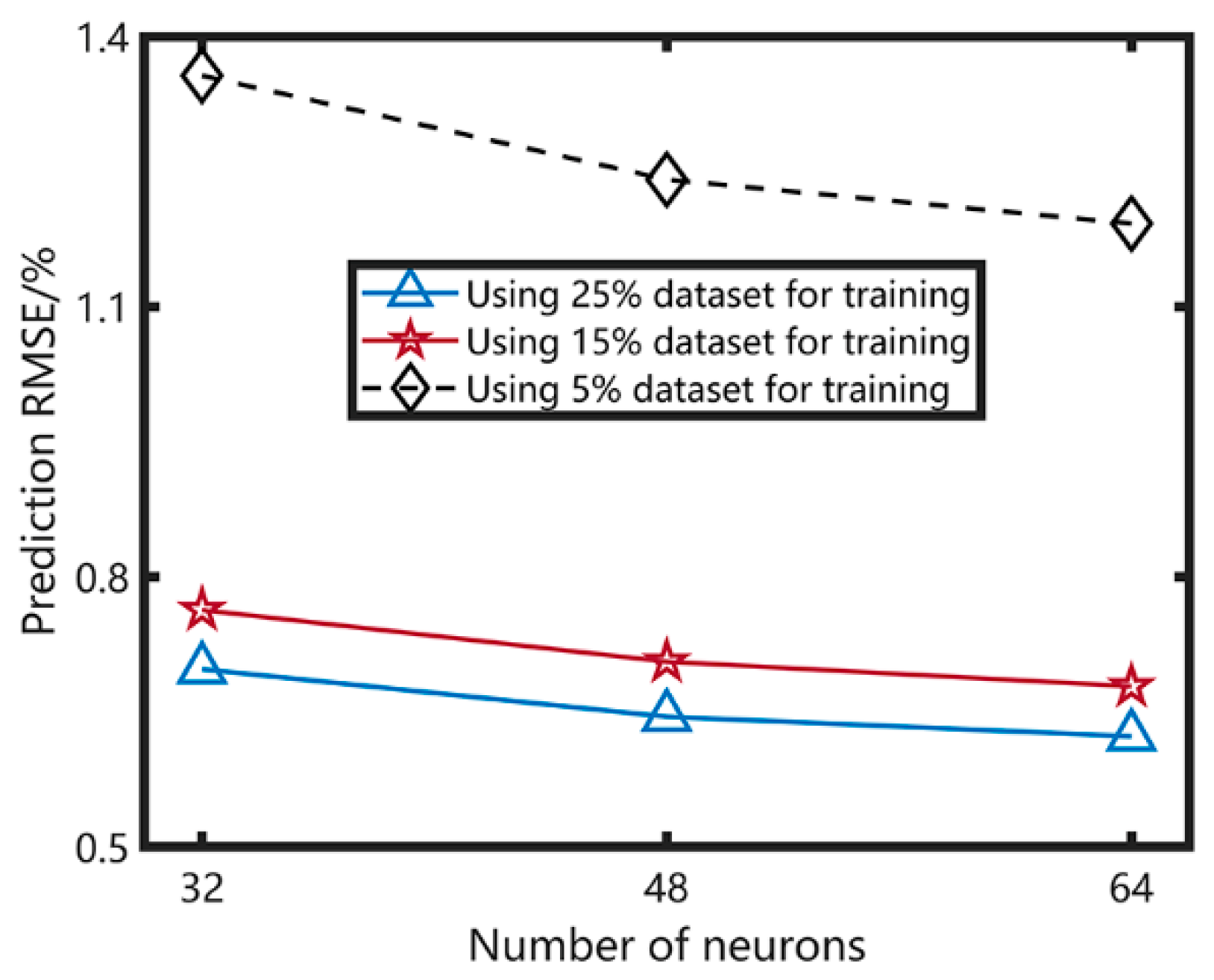
3.3. Method Development and Training
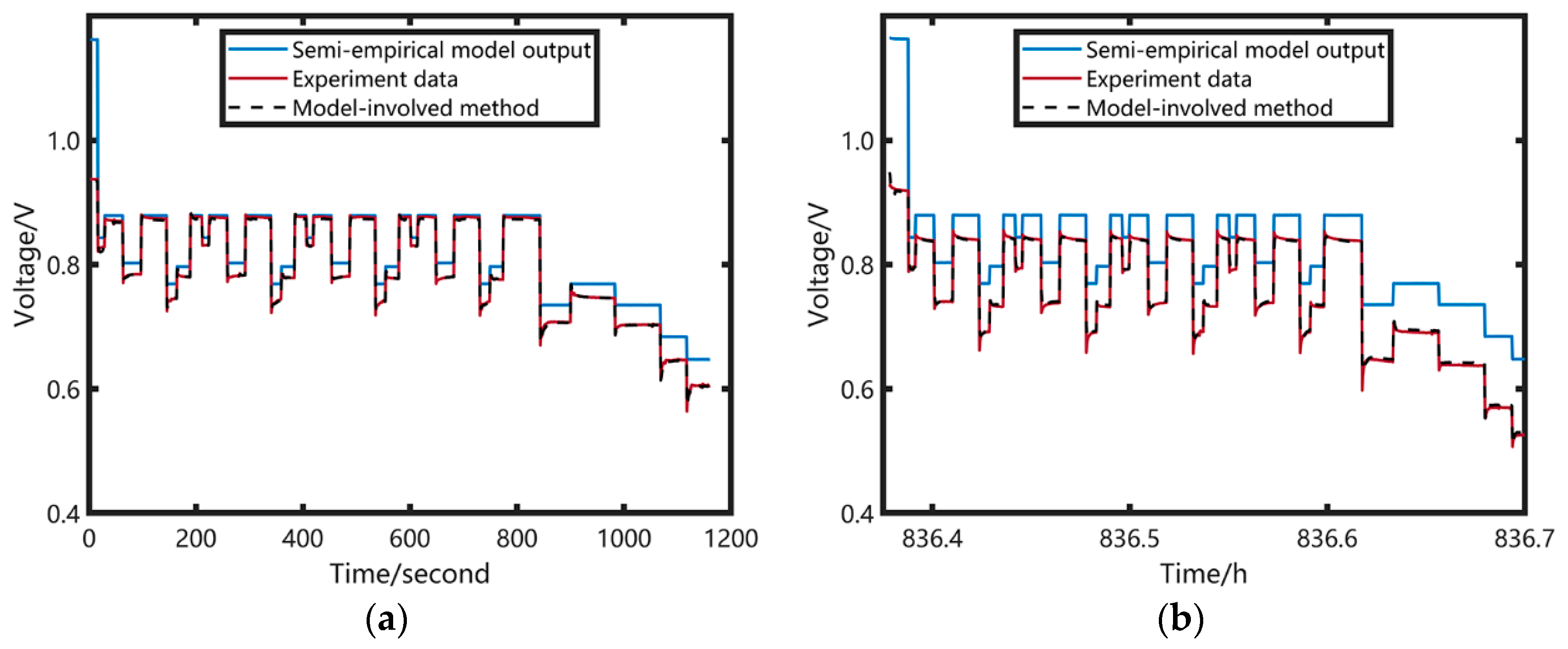
4. Discussion
5. Conclusions
- Mechanistically grounded model reformulation: The semi-empirical framework was rederived from first principles, explicitly incorporating Nernstian potential dynamics and mass transport limitations during redox reactions.
- Intelligent parameter identification: Critical model coefficients were optimized via a grey wolf optimization algorithm with adaptive convergence thresholds, calibrated against experimental polarization data.
- Physics-informed data fusion: Voltage predictions from the calibrated model were concatenated with operational boundary conditions (current density, temperature, humidity) to generate hybrid training datasets, which underwent rigorous statistical screening via cross-correlation analysis to eliminate multicollinear features.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEMFC | Proton exchange membrane fuel cells |
| RNN | Recurrent neural network |
| FCEV | Fuel cell electric vehicles |
| EMS | Energy management strategy |
| SOH | State of health |
| ECSA | Electrochemical surface area |
| LSSVM | Least square support vector machine |
| RPF | Regularized particle filter |
| LSTM | Long short-term memory |
| GRU | Gate-recurrent unit |
| RMSE | Root mean square error |
| ESN | Echo state network |
| CNN | Convolutional neural network |
| GWO | Grey wolf optimization |
| GDL | Gas diffusion layer |
| MSE | Mean square error |
| MAE | Mean absolute error |
References
- Lagioia, G.; Spinelli, M.P.; Amicarelli, V. Blue and Green Hydrogen Energy to Meet European Union Decarbonisation Objectives. An Overview of Perspectives and the Current State of Affairs. Int. J. Hydrogen Energy 2022, 48, 1304–1322. [Google Scholar] [CrossRef]
- Dirkes, S.; Leidig, J.; Fisch, P.; Pischinger, S. Prescriptive Lifetime Management for PEM Fuel Cell Systems in Transportation Applications, Part I: State of the Art and Conceptual Design. Energy Convers. Manag. 2023, 277, 116598. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, Q.; Li, Y.; Yang, J.; Dong, Z. Energy Efficiency and CO2 Emission Comparison of Alternative Powertrain Solutions for Mining Haul Truck Using Integrated Design and Control Optimization. J. Clean. Prod. 2022, 370, 133568. [Google Scholar] [CrossRef]
- Feng, Y.; Dong, Z. Comparative Lifecycle Costs and Emissions of Electrified Powertrains for Light-Duty Logistics Trucks. Transp. Res. Part D Transp. Environ. 2023, 117, 103672. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation Mechanisms of Proton Exchange Membrane Fuel Cell under Typical Automotive Operating Conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, P.; Chen, H.; Pei, P. A Review of Automotive Proton Exchange Membrane Fuel Cell Degradation under Start-Stop Operating Condition. Appl. Energy 2018, 223, 249–262. [Google Scholar] [CrossRef]
- Chen, H.; Pei, P.; Song, M. Lifetime Prediction and the Economic Lifetime of Proton Exchange Membrane Fuel Cells. Appl. Energy 2015, 142, 154–163. [Google Scholar] [CrossRef]
- Ma, R.; Chai, X.; Geng, R.; Xu, L.; Xie, R.; Zhou, Y.; Wang, Y.; Li, Q.; Jiao, K.; Gao, F. Recent Progress and Challenges of Multi-Stack Fuel Cell Systems: Fault Detection and Reconfiguration, Energy Management Strategies, and Applications. Energy Convers. Manag. 2023, 285, 117015. [Google Scholar] [CrossRef]
- Borup, R.; Meyers, J.; Pivovar, B.; Kim, Y.S.; Mukundan, R.; Garland, N.; Myers, D.; Wilson, M.; Garzon, F.; Wood, D.; et al. Scientific Aspects of Polymer Electrolyte Fuel Cell Durability and Degradation. Chem. Rev. 2007, 107, 3904–3951. [Google Scholar] [CrossRef]
- Tarasevich, M.R.; Korchagin, O.V. Rapid diagnostics of characteristics and stability of fuel cells with proton-conducting electrolyte. Russ. J. Electrochem. 2014, 50, 737–750. [Google Scholar] [CrossRef]
- Avakov, V.B.; Bogdanovskaya, V.A.; Kapustin, A.V.; Korchagin, O.V.; Kuzov, A.V.; Landgraf, I.K.; Stankevich, M.M.; Tarasevich, M.R. Lifetime prediction for the hydrogen–air fuel cells. Russ. J. Electrochem. 2014, 51, 570–586. [Google Scholar] [CrossRef]
- Pei, P.; Chen, D.; Wu, Z.; Ren, P. Nonlinear Methods for Evaluating and Online Predicting the Lifetime of Fuel Cells. Appl. Energy 2019, 254, 113730. [Google Scholar] [CrossRef]
- Bressel, M.; Hilairet, M.; Hissel, D.; Bouamama, B.O. Extended Kalman Filter for Prognostic of Proton Exchange Membrane Fuel Cell. Appl. Energy 2016, 164, 220–227. [Google Scholar] [CrossRef]
- Jouin, M.; Bressel, M.; Morando, S.; Gouriveau, R.; Hissel, D.; Péra, M.-C.; Zerhouni, N.; Jemei, S.; Hilairet, M.; Bouamama, B.O. Estimating the End-of-Life of PEM Fuel Cells: Guidelines and Metrics. Appl. Energy 2016, 177, 87–97. [Google Scholar] [CrossRef]
- Lo, J.; Hu, Z.; Xu, L.; Ouyang, M.; Fang, C.; Hu, J.; Cheng, S.; Hong, P.; Zhang, W.; Jiang, H. Fuel Cell System Degradation Analysis of a Chinese Plug-in Hybrid Fuel Cell City Bus. Int. J. Hydrogen Energy 2016, 41, 15295–15310. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, L.; Li, J.; Ouyang, M.; Song, Z.; Huang, H. A Reconstructed Fuel Cell Life-Prediction Model for a Fuel Cell Hybrid City Bus. Energy Convers. Manag. 2018, 156, 723–732. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Pahon, E.; Péra, M.-C.; Gao, F. A Review on Lifetime Prediction of Proton Exchange Membrane Fuel Cells System. J. Power Sources 2022, 529, 231256. [Google Scholar] [CrossRef]
- Cheng, Y.; Zerhouni, N.; Lu, C. A Hybrid Remaining Useful Life Prognostic Method for Proton Exchange Membrane Fuel Cell. Int. J. Hydrogen Energy 2018, 43, 12314–12327. [Google Scholar] [CrossRef]
- Ma, R.; Yang, T.; Breaz, E.; Li, Z.; Briois, P.; Gao, F. Data-Driven Proton Exchange Membrane Fuel Cell Degradation Predication through Deep Learning Method. Appl. Energy 2018, 231, 102–115. [Google Scholar] [CrossRef]
- Liu, H.; Chen, J.; Hissel, D.; Su, H. Remaining useful life estimation for proton exchange membrane fuel cells using a hybrid method. Appl. Energy 2019, 237, 910–919. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Deep Learning Based Prognostic Framework towards Proton Exchange Membrane Fuel Cell for Automotive Application. Appl. Energy 2021, 281, 115937. [Google Scholar] [CrossRef]
- Yue, M.; Li, Z.; Roche, R.; Jemei, S.; Zerhouni, N. Degradation Identification and Prognostics of Proton Exchange Membrane Fuel Cell under Dynamic Load. Control Eng. Pract. 2022, 118, 104959. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, T.; Xiao, F.; Zhang, R. Degradation prediction model of PEMFC based on multi-reservoir echo state network with Mini Reservoir. Int. J. Hydrogen Energy 2022, 47, 40026–40040. [Google Scholar] [CrossRef]
- Long, B.; Wu, K.; Li, P.; Li, M. A Novel Remaining Useful Life Prediction Method for Hydrogen Fuel Cells Based on the Gated Recurrent Unit Neural Network. Appl. Sci. 2022, 12, 432. [Google Scholar] [CrossRef]
- Tao, Z.; Zhang, C.; Xiong, J.; Hu, H.; Ji, J.; Peng, T.; Nazir, M.S. Evolutionary gate recurrent unit coupling convolutional neural network and improved manta ray foraging optimization algorithm for performance degradation prediction of PEMFC. Appl. Energy 2023, 336, 120821. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, T.; Xiao, F.; Luo, J. Bi-Directional Gated Recurrent Unit Recurrent Neural Networks for Failure Prognosis of Proton Exchange Membrane Fuel Cells. Int. J. Hydrogen Energy 2022, 47, 33027–33038. [Google Scholar] [CrossRef]
- Hua, Z.; Yang, Q.; Chen, J.; Lan, T.; Zhao, D.; Dou, M.; Liang, B. Degradation prediction of PEMFC based on BiTCN-BiGRU-ELM fusion prognostic method. Int. J. Hydrogen Energy 2024, 87, 361–372. [Google Scholar] [CrossRef]
- Li, S.; Luan, W.; Wang, C.; Chen, Y.; Zhuang, Z. Degradation Prediction of Proton Exchange Membrane Fuel Cell Based on Bi-LSTM-GRU and ESN Fusion Prognostic Framework. Int. J. Hydrogen Energy 2022, 47, 33466–33478. [Google Scholar] [CrossRef]
- Yakut, Y.B. Short-term voltage loss prediction in PEMFCs using single-step and multi-step LSTM models. Int. J. Hydrogen Energy 2025. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, X.; Dong, S.; Huang, L.; Li, Y. Degradation prediction of PEM fuel cell using LSTM based on Gini gamma correlation coefficient and improved sand cat swarm optimization under dynamic operating conditions. Appl. Energy 2025, 392, 125967. [Google Scholar] [CrossRef]
- Yang, J.; Chen, L.; Zhang, B.; Zhang, H.; Chen, B.; Wu, X.; Deng, P.; Xu, X. Remaining useful life prediction for vehicle-oriented PEMFCs based on organic gray neural network considering the influence of dual energy source synergy. Energy 2025, 322, 135578. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Yang, Y.; Zhu, W.; Xie, C.; Yu, X.; Guo, B. Reliability assessment of PEMFC aging prediction based on probabilistic Bayesian mixed recurrent neural networks. Renew. Energy 2025, 246, 122892. [Google Scholar] [CrossRef]
- Wang, F.-K.; Cheng, F.K.X.-B.; Hsiao, K.-C. Stacked Long Short-Term Memory Model for Proton Exchange Membrane Fuel Cell Systems Degradation. J. Power Sources 2020, 448, 227591. [Google Scholar] [CrossRef]
- Zuo, J.; Lv, H.; Zhou, D.; Xue, Q.; Jin, L.; Zhou, W.; Yang, D.; Zhang, C. Long-Term Dynamic Durability Test Datasets for Single Proton Exchange Membrane Fuel Cell. Data Brief 2021, 35, 106775. [Google Scholar] [CrossRef]
- Wilberforce, T.; Alaswad, A.; Garcia–Perez, A.; Xu, Y.; Ma, X.; Panchev, C. Remaining Useful Life Prediction for Proton Exchange Membrane Fuel Cells Using Combined Convolutional Neural Network and Recurrent Neural Network. Int. J. Hydrogen Energy 2022, 48, 291–303. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, K.; Zhao, H.; Li, J.; Sheng, X.; Yin, Y.; Du, Q.; Zu, B.; Han, L.; Jiao, K. Degradation Prediction of Proton Exchange Membrane Fuel Cell Stack Using Semi-Empirical and Data-Driven Methods. Energy AI 2022, 11, 100205. [Google Scholar] [CrossRef]
- Wu, K.; Du, Q.; Zu, B.; Wang, Y.; Cai, J.; Gu, X.; Xuan, J.; Jiao, K. Enabling Real-Time Optimization of Dynamic Processes of Proton Exchange Membrane Fuel Cell: Data-Driven Approach with Semi-Recurrent Sliding Window Method. Appl. Energy 2021, 303, 117659. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, H.; Xu, L.; Mao, L.; Hu, Z.; Li, J. Toward low-data and real-time PEMFC diagnostic: Multi-sine stimulation and hybrid ECM-informed neural network. Appl. Energy 2025, 391, 125959. [Google Scholar] [CrossRef]
- Ko, T.; Kim, D.; Park, J.; Lee, S.H. Physics-informed neural network for long-term prognostics of proton exchange membrane fuel cells. Appl. Energy 2025, 382, 125318. [Google Scholar] [CrossRef]
- Yuan, Y.; Qu, Z.; Wang, W.; Ren, G.; Hu, B. Illustrative Case Study on the Performance and Optimization of Proton Exchange Membrane Fuel Cell. ChemEngineering 2019, 3, 23. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2019, 69, 46–61. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Péra, M.-C.; Zerhouni, N. Degradations Analysis and Aging Modeling for Health Assessment and Prognostics of PEMFC. Reliab. Eng. Syst. Saf. 2016, 148, 78–95. [Google Scholar] [CrossRef]
- Jao, T.-C.; Jung, G.-B.; Kuo, S.-C.; Tzeng, W.-J.; Su, A. Degradation Mechanism Study of PTFE/Nafion Membrane in MEA Utilizing an Accelerated Degradation Technique. Int. J. Hydrogen Energy 2012, 37, 13623–13630. [Google Scholar] [CrossRef]
- Collette, F.; Thominette, F.; Mendil-Jakani, H.; Gebel, G. Structure and Transport Properties of Solution-Cast Nafion® Membranes Subjected to Hygrothermal Aging. J. Membr. Sci. 2013, 435, 242–252. [Google Scholar] [CrossRef]
- Hong, J.; Yang, H.; Liang, F.; Li, K.; Zhang, X.; Zhang, H.; Zhang, C.; Yang, Q.; Wang, J. State of Health Prediction for Proton Exchange Membrane Fuel Cells Combining Semi-Empirical Model and Machine Learning. Energy 2024, 291, 130364. [Google Scholar] [CrossRef]
- Hongwei, L.; Binxin, Q.; Zhicheng, H.; Junnan, L.; Yue, Y.; Guolong, L. An Interpretable Data-Driven Method for Degradation Prediction of Proton Exchange Membrane Fuel Cells Based on Temporal Fusion Transformer and Covariates. Int. J. Hydrogen Energy 2023, 48, 25958–25971. [Google Scholar] [CrossRef]


| Parameter | Value | |
|---|---|---|
| Operating conditions | RHan | 0.5 |
| RHca | 0.8 | |
| T/℃ | 85 | |
| Pan/kPa | 110 | |
| Pca/kPa | 110 | |
| λair | 3.5 | |
| PEMFC | A/cm2 | 25 |
| lthick/μm | 15 | |
| LGDL/μm | 220 | |
| Contact resistance/Ωcm2 | 12~18 | |
| Thickness of CL/μm | 6~8 | |
| Radius of Pt particle/nm | 3.2 | |
| Pt loading of the anode/mg/cm−2 | JM Pt/C 0.1 | |
| Pt loading of the cathode/mg/cm−2 | JM Pt/C 0.4 | |
| Pt/C catalyst loading/% | Pt (20~50) |
| Relec | λmem | fGDL,an | fGDL,ca |
|---|---|---|---|
| 2.964574 × 10−3 | 13.958904 | 0.116182 | 0.109845 |
| αOx,an | αRd,ca | α0,Rd,ca | ΔGOx,an |
| 0.755445 | 1.070204 | 0.899016 | 7226.240437 |
| ΔGRd,ca | ileak,an | ileak,ca | |
| 15,177.114302 | 6.852172 × 10−6 | 1.265307 × 10−6 |
| RMSE | MAE | MSE | R-Square |
|---|---|---|---|
| 0.3286% | 0.2779% | 0.0011% | 0.9996 |
| RNN Architecture | Layer Parameters | Model Involved RNN | RNN |
|---|---|---|---|
| Input layer | Number of features | 9 | 8 |
| Hidden layer | Number of neurons | 32/48/64 | 32/48/64 |
| Dropout layer | Probability | 0.5 | 0.5 |
| Fully connect layer | Number of neurons | 32/48/64 | 32/48/64 |
| Regression layer | Number of outputs | 1 | 1 |
| Training Parameters | Values |
|---|---|
| Max Epochs | 500 |
| Mini Batch Size | 4096 |
| Learning rate | 0.005 |
| Learning rate drop factor | 0.2 |
| Learning rate drop period | 50 |
| Number of Neurons | Model Involved RNN | RNN | ||
|---|---|---|---|---|
| LSTM | GRU | LSTM | GRU | |
| 32 | 0.6973 | 0.6985 | 0.7120 | 0.7113 |
| 48 | 0.6446 | 0.6444 | 0.6632 | 0.6622 |
| 64 | 0.6228 | 0.6229 | 0.6421 | 0.6422 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Zang, W.; Zhang, W.; Zhang, Y.; Tong, Y.; Feng, Y. Steady-State Model Enabled Dynamic PEMFC Performance Degradation Prediction via Recurrent Neural Network. Energies 2025, 18, 2665. https://doi.org/10.3390/en18102665
Liu Q, Zang W, Zhang W, Zhang Y, Tong Y, Feng Y. Steady-State Model Enabled Dynamic PEMFC Performance Degradation Prediction via Recurrent Neural Network. Energies. 2025; 18(10):2665. https://doi.org/10.3390/en18102665
Chicago/Turabian StyleLiu, Qiang, Weihong Zang, Wentao Zhang, Yang Zhang, Yuqi Tong, and Yanbiao Feng. 2025. "Steady-State Model Enabled Dynamic PEMFC Performance Degradation Prediction via Recurrent Neural Network" Energies 18, no. 10: 2665. https://doi.org/10.3390/en18102665
APA StyleLiu, Q., Zang, W., Zhang, W., Zhang, Y., Tong, Y., & Feng, Y. (2025). Steady-State Model Enabled Dynamic PEMFC Performance Degradation Prediction via Recurrent Neural Network. Energies, 18(10), 2665. https://doi.org/10.3390/en18102665






