Abstract
Probabilistic modeling of net load forecast errors is an important approach for reserve decision-making in power systems with a high penetration of renewable energy. However, existing probabilistic modeling methods face issues such as insufficient estimation accuracy in the small probability interval of the tails or increased complexity in probability decision-making problems. A probabilistic reserve decision-making method based on cumulative probability approximation is proposed. By using key points on the cumulative probability distribution curve of net load forecast error samples, this method enhances the fitting accuracy of the normal distribution model in the small probability interval of the tail, resulting in an optimal reserve outcome with the desired comprehensive expected profit. Using relevant renewable energy output and load data from actual transmission networks in Guangdong Province, China, the proposed method demonstrates good practical value.
1. Introduction
The demand for operating reserve capacity in power systems depends on the net load reserve capacity requirement and the contingency reserve capacity requirement [1]. The contingency reserve is generally determined based on the maximum unit generation capacity or the maximum DC import capacity, which is a fixed value independent of load power and renewable energy generation [2]. The net load reserve capacity requirement, on the other hand, depends on load forecast errors and renewable energy output forecast errors. The primary focus of operating reserve decisions lies in net load reserve decision-making [3]. Historically, China has set operating reserve capacity based on deterministic criteria, typically ranging from 2% to 5% of the system’s peak load [4]. Deterministic criteria are based on load forecasts and renewable energy forecasts to formulate generation plans, with reserve decisions being manually made. This leads to arbitrariness and blindness in the selection of reserve capacity. When the reserve capacity is too low, it becomes difficult to match the significant fluctuations in renewable energy output and load power, thus jeopardizing system security. Conversely, excessive reserve capacity results in the wastage of reserve resources, decreasing the economics of system operation [5].
With the continuous growth of electricity demand and the ongoing progress being made in renewable energy technologies, the integration of large-scale wind and solar power generation into the power system has led to a significant increase in the penetration of renewable energy in the grid [6]. The large-scale integration of wind and solar power generation increases the uncertainty of generation output, while the existing deterministic load reserve criteria lack enough theoretical support, resulting in overly conservative scenarios or risky decisions in practical applications [7]. Moreover, the combined uncertainties of renewable energy and load significantly increase the volatility of net load, making it difficult for traditional, experience-based reserve decisions to respond quickly and accurately. There is an urgent need for more precise and flexible reserve decision-making methods [8].
Application scenarios such as reserve decision-making, risk assessment, and risk dispatch for power systems with a high proportion of renewable energy rely heavily on the accuracy of the probabilistic modeling of net load forecast errors [9,10]. Since the net load less than expected reserve does not generate any load cutting and the risk of an intermediate large probability interval is nearly zero, the main factor affecting reserve decision-making is the small probability interval model of the tail where the net load exceeds the expected reserve [11].
Existing research on the probabilistic modeling of reserve decision-making can be mainly divided into two types:
- (1)
- The first method adopts uniform probability models such as normal, beta, and Weibull distributions [12,13,14], which mainly focus on the consistency of statistical indicators such as mean and variance. Among them, the normal distribution has been widely used in probabilistic modeling research of forecast errors due to its simple form and the fact that the result of the addition and subtraction operation among independent normally distributed variables is still normally distributed [15]. Probabilistic models such as normal distribution have good modeling accuracy for the intermediate large probability interval but lack accuracy in terms of fitting the small probability interval of the tail [16].
- (2)
- Another method adopts the Gaussian Mixture Model (GMM), which is based on observational data and the Expectation Maximization (EM) method to find the parameters of the Gaussian Mixture Model [17,18]. Compared with a single probability distribution model, the GMM can effectively improve the fitting effect in the full probability space, but the EM method treats all sample data equally and can’t guarantee its fitting accuracy in the small probability interval of the tail [19].
In addition, existing probabilistic reserve decision-making is typically based on a certain confidence level to determine the reserve capacity. However, the selection of the confidence level lacks theoretical justification. For example, the studies in [20,21,22] all propose opportunity constraint approaches based on a certain confidence level, but none provide a theoretical basis for determining the confidence level.
Therefore, this paper proposes a probabilistic reserve decision-making method based on cumulative probability approximation for high-penetration renewable energy power systems. Compared with existing technologies, the advantages of the proposed technical solution are mainly reflected in the following aspects:
- (1)
- This method comprehensively considers three factors: reserve cost, expected generation revenue from reserves, and expected loss due to load shedding. It provides optimal conditions for probabilistic reserve decisions and an iterative solving algorithm, achieving the optimal expected overall benefit in probabilistic reserve decision-making.
- (2)
- The method determines the parameters of the net load forecast error’s normal distribution model based on the key factors influencing the optimality of reserve decisions. By employing cumulative probability approximation at key points, the accuracy of the probabilistic reserve decision results is enhanced.
- (3)
- By selecting key points for cumulative probability approximation, the proposed method effectively improves the fitting accuracy of the cumulative probability in the small probability interval of the tail.
The remainder of this paper is arranged as follows: Section 2 presents the procedures for the proposed method. Section 3 discusses the required data and the preprocessing operations. Section 4 plots the cumulative probability distribution curve of the samples. Section 5 performs probabilistic reserve decision modeling. Section 6 estimates the parameters of the normal distribution model for net load forecasting errors. Section 7 iteratively solves the reserve results. Section 8 provides a case analysis. Section 9 concludes this paper.
2. Procedures for the Proposed Method
The flowchart of the probabilistic reserve decision method based on cumulative probability approximation for high-penetration renewable energy power systems proposed in this paper is shown in Figure 1, which includes the following steps:

Figure 1.
The flowchart of probabilistic reserve decision method.
- (1)
- Data loading and preprocessing;
- (2)
- Calculation of the cumulative probability distribution of historical net load forecast error sample data;
- (3)
- Probabilistic reserve decision modeling based on the normal distribution probability model of net load forecast errors;
- (4)
- Estimation of the normal distribution model parameters based on cumulative probability approximation at key points;
- (5)
- Probabilistic reserve decision-making based on the normal distribution model of net load forecast errors.
3. Data Loading and Preprocessing
The purpose of data loading and preprocessing is to obtain all the possible values of the net load forecast error and the parameters used for subsequent probabilistic reserve decision-making.
The data required for the reserve decision-making of high-penetration renewable energy power systems include the following:
- (1)
- Historical actual and forecasted data of renewable energy output;
- (2)
- Historical actual and forecasted data of load;
- (3)
- Unit cost of reserve capacity;
- (4)
- Unit revenue from increased power generation during reserve activation;
- (5)
- Unit cost of load shedding;
- (6)
- Load forecast value when making reverse decision;
- (7)
- Installed capacity of renewable energy sources when making reverse decision.
The power system net load forecast error can be described by Equation (1):
where ΔN denotes the net load forecast error, ΔL denotes the load forecast error, and ΔP denotes the renewable energy forecast error.
If only the historical net load forecast error data are modeled probabilistically, the reserve decision-making is operationally irrelevant and poorly rationalized. Therefore, during the data preprocess, based on the historical data of load and renewable energy sources, the following three forecast relative error indicators are defined:
where M is the number of statistical time intervals of the historical data and i is the number of time intervals. , , and are the forecast relative errors of the load, wind, and PV power in the same time interval i, respectively. is the forecasted value of the load. is the actual value of the load. is the forecasted value of the wind power. is the actual value of the wind power. is the wind power installed capacity in the corresponding time interval i. is the forecasted value of the PV power. is the actual value of the PV power. is the PV power installed capacity in the corresponding time interval i.
Based on , , and , we can calculate all of the possible values of the net load forecast error when making reserve decision for the power system:
where CW, CS, and L are the wind power installed capacity, PV power installed capacity, and load forecast value when making a reserve decision, respectively. As can be seen from the above, the load forecast value and the installed capacity of renewable energy sources are used in the calculation of the net load forecast error, which can reflect the actual operating status of the grid and improve the accuracy of the reserve decision. After that, probabilistic models such as normal distribution can be used to probabilistically model the net load forecast error.
4. Cumulative Probability Distribution Curve of the Net Load Forecast Errors
The net load forecast errors are sorted in ascending order. It is assumed that the sorted net load forecast errors are , where N represents the number of samples. Each sample corresponds to a probability of . Therefore, the cumulative probabilities for are ,,, respectively. Using the net load forecast errors as the abscissa (x-axis) and the sample cumulative probability as the ordinate (y-axis), the sample points are sequentially connected to form the sample cumulative probability curve, which is shown in Figure 2. Let γ(x) denote the sample cumulative probability function.

Figure 2.
Plot the sample cumulative probability curve.
5. Probabilistic Reserve Decision Model
The objective of probabilistic reserve decision-making is to minimize the total cost, which is the sum of the reserve configuration cost and the expected cost of power shortage per unit time after subtracting the revenue from reserve activation:
where CR represents the unit cost of reserve capacity, and R represents the reserve decision capacity. CEDNS represents the unit cost of power shortage expectation, and PEDNS(R) represents the power shortage expectation, which is a function of reserve capacity. CINC represents the unit benefit of additional generation when reserve capacity is dispatched, and PINC(R) represents the expected power generation of the reserve capacity.
The normal distribution is commonly used to describe the distribution of forecasting errors in renewable energy output and load prediction. Since the sum or difference in normal distributed random variables also follows a normal distribution, the normal distribution can be used to model the net load forecast error. The probability density function of the normal distribution can be expressed as follows:
where x represents the random variable, which refers to the net load forecast error. μ denotes the mean of the normal distribution, and σ represents the standard deviation of the normal distribution, with .
If the system’s net load forecast error exceeds the reserve capacity of the system, the portion of the load beyond the reserve capacity will be lost, and the system’s power shortage expectation is as follows:
where R represents the decision reserve capacity. PEDNS(R) denotes the power shortage expectation, which is a function of the decision reserve capacity R.
where ϕ(⋅) represents the probability density function of the standard normal distribution, and Φ(⋅) represents the cumulative distribution function of the standard normal distribution.
The standard normal distribution refers to a normal distribution with a mean of zero and a standard deviation of one, and its probability density function is as follows:
The expected generation power of the decision reserve capacity consists of two parts: when the net load forecast error x is greater than zero but less than the decision reserve capacity R, the generation power of the reserve capacity is x; when the net load forecast error x exceeds the decision reserve capacity R, the generation power of the reserve capacity is R. Therefore, the expected energy generation of the decision reserve capacity per unit time is as follows:
where PINC(R) represents the expected generation power per unit time of the decision reserve capacity, which is a function of the decision reserve capacity.
The necessary condition for the extremum of Equation (4) is as follows:
Due to the following:
By substituting Equations (12) and (13) into Equation (11), we obtain the following:
By rearranging Equation (14), we obtain the following:
6. Parameter Estimation of the Normal Distribution Model by Using Key Points
From Equation (15), we can find that the factors influencing the probabilistic reserve decision include the cumulative probability at a net load forecast error of 0, as well as the cumulative probability and probability density at a net load forecast error of R.
Since the normal distribution has only two parameters, the mean and standard deviation, it has only two degrees of freedom. Therefore, the parameters of the normal distribution can be determined by the two points on the cumulative probability distribution curve.
For actual power systems, is close to 1 and is a smaller positive number which can be ignored since CEDNS>>CINC and CEDNS>>CR. The key factors influencing the probabilistic reserve decision are the cumulative probability at a net load forecast error of 0 and at a net load forecast error of R.
To improve the accuracy of the reserve decision as much as possible, the cumulative probability values of the normal distribution probability model for net load forecast errors at 0 and R are set to be equal to the corresponding sample cumulative probability values at those positions, i.e.,
where represents the cumulative probability function of net load forecast error.
From Equations (15)–(17), we obtain the following:
Since R is a decision variable, it needs to be determined after the reserve decision and remains an unknown quantity at the time of parameter estimation for the normal distribution model. Considering that is a smaller positive number, the initial value of the decision variable R can be calculated according to Equation (19):
where the superscript 0 indicates the initial value.
The right end term of Equation (19) can be obtained from the original parameters and the sample data. Thus, R(0) can be obtained by linear interpolation of the sample cumulative probability curve.
Comparison of Equations (18) and (19) shows the following:
Since the sample cumulative probability curve is monotonically increasing,
Equation (21) shows that R(0) is a lower bound for the probabilistic reserve decision.
By applying R(0) from the alternative expression (17) of R, we obtain the following:
It can be obtained from Equation (16) that the following is true:
It can be obtained from Equation (22) that the following is true:
By solving Equations (23) and (24) simultaneously, we obtain the following:
The solution of Equations (25) and (26) requires the use of the cumulative probability curve of the standard normal distribution to obtain the quantiles from the cumulative probability.
The cumulative probability table of the standard normal distribution can be obtained through numerical integration. The cumulative probability of the standard normal distribution possesses the following properties:
Due to , it is enough in practice to construct a cumulative probability table of the standard normal distribution for the range [0, 5]. For values exceeding 5, the cumulative probability can be approximated as 1, which meets the accuracy requirements for engineering applications. When constructing the cumulative probability table of the standard normal distribution via numerical integration, it is recommended to use a small integration step size (e.g., 0.0001) to ensure numerical accuracy. When using the table lookup method, linear interpolation can be applied between the data intervals to obtain the cumulative probability corresponding to a specified value. The integral formula for the cumulative probability within the range [0, 5] is as follows:
The numerical integration formula for calculating the cumulative probability of the standard normal distribution is as follows:
where represents the integration step size and k denotes the number of integration steps.
7. Probabilistic Reserve Decision-Solving
After determining the mean and standard deviation of the forecast error normal distribution model, the reserve decision variable R can be obtained based on the optimality conditions of Equation (15).
Since the right-hand side of Equation (15) contains the decision variable R, which poses challenges for direct numerical solution, an iterative method based on Equation (31) is constructed to solve this:
where the superscript i represents the iteration number.
The solution of Equation (31) also requires the use of the standard normal distribution cumulative probability table to obtain the quantile from the cumulative probability.
If the deviation between two consecutive iteration results is smaller than the predefined allowable error, the iteration converges, and R(i+1) is taken as the probabilistic reserve decision result. The convergence criterion is set as follows:
where represents the allowable error.
8. Case Analysis
The renewable energy and load data of Guangdong Province for the whole year of 2023 are used for the example analysis. CEDNS is set to USD 1000/(MW·h), CR is set to USD 20/(MW·h), and CINC is set to USD 5/(MW·h) [23,24,25], and it is assumed that the installed capacity of wind power at the time of probabilistic reserve decision-making is 50GW, the installed capacity of PV power is 20GW, and load forecast value is 150 GW. Based on the historical data, the load forecast value, and renewable energy installed capacity at the time of reserve decision-making, all possible values of the net load forecast error are calculated, and the histogram of its probability distribution is shown in Figure 3. The cumulative probability curve for the net load forecast error sample is shown in Figure 4.
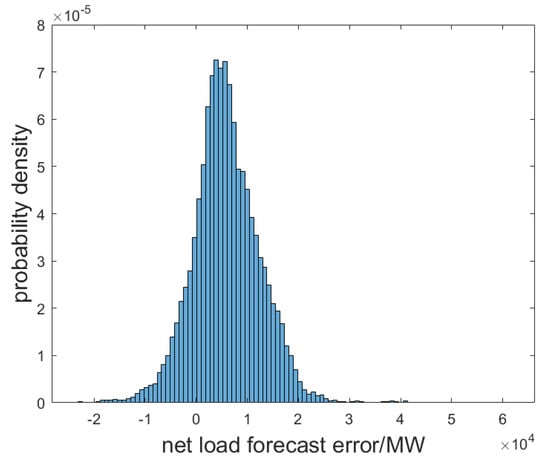
Figure 3.
Histogram of probability density of net load forecast errors.
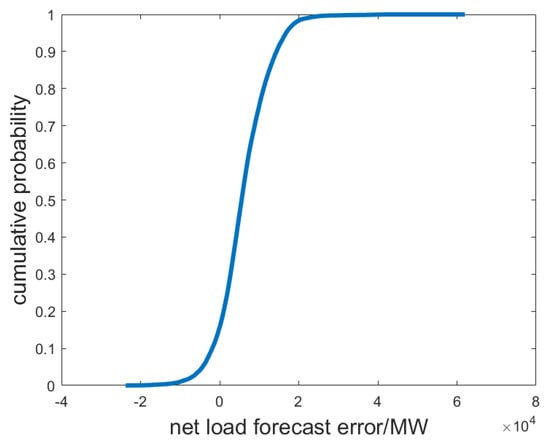
Figure 4.
Cumulative probability distribution curve of net load forecast errors.
Based on the methodology presented in this paper, we can obtain the following:
According to R(0), it can be seen that the final reserve capacity R is greater than 20,000 MW. R lies in the side-tailed small probability interval of the probabilistic model of the net load forecast error.
According to Equations (25) and (26), we can obtain the parameters of the normal distribution model:
8.1. Fitting Effects of Different Probabilistic Models
To compare the effects of different probabilistic models for fitting the small probability interval of the tail, the normal distribution model obtained in this paper is denoted as G1. The normal distribution model obtained by using the sample mean and sample variance is denoted as G2. In addition, we fit the net load forecast error by using the GMM derived from the EM algorithm. The GMM with two Gaussian components is denoted as G3. After calculation, the following expression for G2 and G3 is obtained:
The comparison of the fitting effects in the small probability interval of the tail between G1, G2, and G3 is shown in Figure 5. It can be found that the method proposed in this paper constructs a normal distribution model G1 by selecting two key points on the cumulative probability distribution curve. Compared with the normal distribution model G2 based on sample data and the Gaussian Mixture Model G3 with two Gaussian components, the method proposed in this paper significantly improves the accuracy of the probability fitting in the small probability interval of the tail.
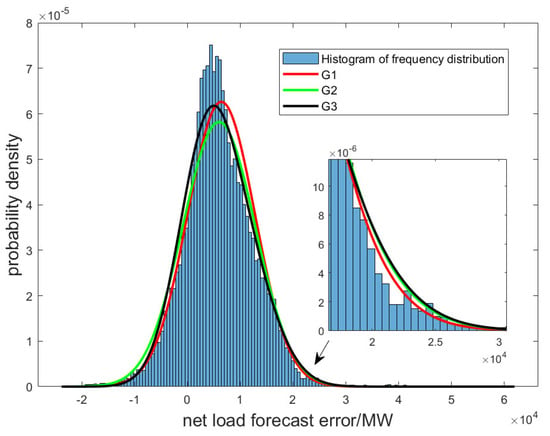
Figure 5.
Comparison of the fit between G1, G2, and G3.
8.2. Probabilistic Reserve Decision Results
The three probabilistic models, G1, G2, and G3, are substituted into the probabilistic reserve decision model proposed in this paper to solve their corresponding reserve results. Among them, since the GMM is a linear combination of multiple normal distributions, it possesses similar derivation results with the normal distribution in the process of probabilistic reserve decision-making, which will not be repeated in this paper. The final reserve results are shown in Table 1.

Table 1.
The reserve results of the three probabilistic models.
As can be seen from Table 1, the normal distribution model based on the two key points on the cumulative probability curve enhances the fitting accuracy in the small probability interval of the tail, which leads to a more accurate reserve result. The reserve value of G1 is reduced by 2.8% and 3.3% compared to G2 and G3, respectively.
8.3. Result Analysis
Based on the above, the probabilistic reserve decision-making method proposed in this paper has the following mathematical advantages:
- (1)
- The normal distribution model obtained through fitting the key points provides a better fit for the small probability interval of the tail.
- (2)
- Since the normal distribution is still used to fit the net load forecast error variable, compared to other parameter distributions, the method has a lower computational complexity and is easier to compute.
In addition, this paper is parameterized by two critical points on the sample cumulative probability curve for the normal distribution model (2 points at 0 and R for the net load forecast error). Since R is a decision variable that needs to be determined after the reserve decision, this paper virtually uses the two points at 0 and R(0) to parameterize the normal distribution model. According to the derivation process, the closer the R(0) used is to the final reserve result R, the more accurate the reserve result obtained. Therefore, subsequent research should be conducted to find out how to make R(0) approximate R as much as possible.
9. Conclusions
This paper proposes a probabilistic reserve decision-making method for high-penetration renewable energy power systems based on cumulative probability approximation. It comprehensively considers three factors: reserve cost, expected generation revenue from reserves, and expected loss due to load shedding. While using a normal distribution model to fit the net load forecast error variable, the method improves the fitting accuracy in the small probability interval of the tail and obtains a more accurate reserve capacity result, demonstrating good practical value.
It is worth noting that this paper does not consider the limitations of transmission line capacity in the power system. Moreover, with the increasing frequency of extreme weather in recent years, the power grid is prone to N-k line failures during such events. Therefore, considering transmission line capacity and N-k line failures in reserve decision-making will be a direction for future research.
Author Contributions
Conceptualization, Y.Y., Z.M. and G.W.; methodology, Y.Y., Z.Y. and R.G.; software, R.G. and Z.Y.; validation, Z.Y.; formal analysis, R.G.; investigation, Z.M. and G.W.; writing—original draft, Z.Y. and R.G.; writing—review and editing, Z.Y. and R.G.; supervision, Z.M.; resources, G.W.; data curation, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported by the Science and Technology Project of Guangdong Power Grid Corporation (Project No.: GDKJXM20230802).
Data Availability Statement
The data presented in this study are available on request from the corresponding author (limitations due to commercial and grid security reasons).
Conflicts of Interest
Authors Yun Yang, Zichao Meng, Guobing Wu were employed by the company Power Dispatching and Control Center Guangdong Power Grid Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Cai, Z.; Ding, Q.; Cui, H.; Dai, S.; Li, Q.; Li, Y.X. Configuration Scheme of Provincial Reserve Capacity in Regional Power Grid (Part II): Optimization Model. Proc. CSEE 2023, 43, 1037–1045. [Google Scholar]
- Liu, Y.K.; Tang, Z.; Wu, L. On Secured Spinning Reserve Deployment of Energy-Limited Resources Against Contingencies. IEEE Trans. Power Syst. 2022, 37, 518–529. [Google Scholar] [CrossRef]
- Li, B.; Li, H.R.; Liang, Z.C.; Bai, X.Q. Load Day-Ahead Automatic Generation Control Reserve Capacity Demand Prediction Based on the Attention-BiLSTM Network Model Optimized by Improved Whale Algorithm. Energies 2024, 17, 414. [Google Scholar] [CrossRef]
- Li, P.; Li, F.T.; Song, X.F.; Zhang, G.H. Considering the Flexible Load New Energy Access System Optimization for Spinning Reserve. Power Syst. Technol. 2021, 45, 1288–1295. [Google Scholar]
- Liu, S.; Yang, Y.; Yang, Z.F.; Chen, Q.X. Reserve Capacity Determination and Its Cost Allocation Considering Stochastic Characteristics of Renewable Energy. Autom. Electr. Power Syst. 2023, 47, 10–18. [Google Scholar]
- Shi, Y.S.; Guo, R.P.; Tang, Y.C.; Lin, Y.; Yang, Z.X. Integrated Transmission Network Planning by Considering Wind Power’s Uncertainty and Disasters. Energies 2023, 16, 5336. [Google Scholar] [CrossRef]
- Zhang, N.; Li, Y.; Ding, Q.; Zhang, X.; Jiang, H.; Li, W. An Inertia Reserve Capacity Planning Method for Power Systems Considering Risk Preference. IEEE Access 2024, 12, 87728–87741. [Google Scholar] [CrossRef]
- Huang, H.Y.; Zhou, M.; Li, G.Y. An Endogenous Approach to Quantifying the Wind Power Reserve. IEEE Trans. Power Syst. 2020, 35, 2431–2442. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Wan, C.; Liu, H.; Zhao, C.F.; Song, Y.H. Probabilistic Forecasting-Based Reserve Determination Considering Multi-Temporal Uncertainty of Renewable Energy Generation. IEEE Trans. Power Syst. 2024, 39, 1019–1031. [Google Scholar] [CrossRef]
- Parker, K.; Barooah, P. A Probabilistic Method for Reserve Sizing in Power Grids with High Renewable Penetration. IEEE Trans. Power Syst. 2021, 36, 2473–2480. [Google Scholar] [CrossRef]
- Zeng, Z.L.; Li, P.Q.; Li, Y.; Zhong, J.J.; Cao, Y.J. Low-carbon distributionally two-stage robust optimization considering conditional value-at-risk for hybrid AC/DC grids. High Volt. Eng. 2024, 50, 157–168. [Google Scholar]
- Ortega-Vazquez, M.A.; Kirschen, D.S. Estimating the Spinning Reserve Requirements in Systems with Significant Wind Power Generation Penetration. IEEE Trans. Power Syst. 2009, 24, 114–124. [Google Scholar] [CrossRef]
- Yang, H.; Yuan, J.S.; Zhang, T.F. A Model and Algorithm for Minimum Probability Interval of Wind Power Forecast Errors Based on Beta Distribution. Proc. CSEE 2015, 35, 2135–2142. [Google Scholar]
- Shirzadi, N.; Nasiri, F.; Menon, R.P.; Monsalvete, P.; Kaifel, A.; Eicker, U. Smart Urban Wind Power Forecasting: Integrating Weibull Distribution, Recurrent Neural Networks, and Numerical Weather Prediction. Energies 2023, 16, 6208. [Google Scholar] [CrossRef]
- Min, C.G.; Park, J.K.; Hur, D.; Kim, M.K. A risk evaluation method for ramping capability shortage in power systems. Energy 2016, 113, 1316–1324. [Google Scholar] [CrossRef]
- Dingec, K.D.; Hormann, W. Efficient Algorithms for Tail Probabilities of Exchangeable Lognormal Sums. Methodol. Comput. Appl. Probab. 2022, 24, 2093–2121. [Google Scholar] [CrossRef]
- Luo, P.; Yan, W.L.; Wang, Y.; Li, J.J.; Lu, Q. Robust Optimal Dispatch of Electricity-Gas-Heat Integrated Energy System Considering Carbon Capture, Utilization and Storage. High Volt. Eng. 2022, 48, 2077–2087. [Google Scholar]
- Xu, S.W.; Wu, W.C.; Zhu, T.; Wang, Z.Y. Convex relaxation based iterative solution method for stochastic dynamic economic dispatch with chance constrains. Autom. Electr. Power Syst. 2020, 44, 43–51. [Google Scholar]
- Xu, S.W.; Wu, W.C. Tractable Reformulation of Two-Side Chance-Constrained Economic Dispatch. IEEE Trans. Power Syst. 2022, 37, 796–799. [Google Scholar] [CrossRef]
- Wu, W.C.; Xu, S.W.; Yang, Y.; Wang, B.; Lin, C.H.; Shen, Y.K. Risk-Quantified Probabilistic Dispatch for Power System with High Proportion of Renewable Energy. Autom. Electr. Power Syst. 2023, 47, 3–11. [Google Scholar]
- Yang, Y.; Wu, W.; Wang, B.; Li, M. Analytical Reformulation for Stochastic Unit Commitment Considering Wind Power Uncertainty with Gaussian Mixture Model. IEEE Trans. Power Syst. 2020, 35, 2769–2782. [Google Scholar] [CrossRef]
- Möws, S.; Scheffer, V.; Becker, C. Probabilistic power forecast of renewable distributed generation for provision of control reserve using vine copulas. IET Gen. Transmiss. Distrib. 2020, 14, 6312–6318. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.N.; Ma, G.; Guo, C.X.; Zhang, J.J. Two-stage Day-ahead and Intra-day Robust Reserve Optimization Considering Demand Response. Autom. Electr. Power Syst. 2019, 43, 67–76. [Google Scholar]
- He, Y.Q.; Li, X.; Jia, H.Q.; Liu, C.X.; Liu, R.; Gu, X.D.; Lei, X. Method for Wind Power Balancing Cost Allocation Considering Spatiotemporal Characteristics of Wind Power and Relative Volatility. Electr. Power Constr. 2024, 45, 157–166. [Google Scholar]
- Sui, D.X.; Wei, Z.B.; Zhou, C.Y.; Yang, H.Q. Deviation Electricity Optimization of Microgrid Based on Hybrid Energy Storage Technology in Spot Market. Autom. Electr. Power Syst. 2021, 45, 160–169. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).