General Response Modes of Cylindrical Thermal Contact Conductance to Bidirectional Heat Flux and Temperature Variations
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Model
2.2. Governing Equations
2.3. Benchmark
2.4. Computation Parameters
3. Results and Discussion
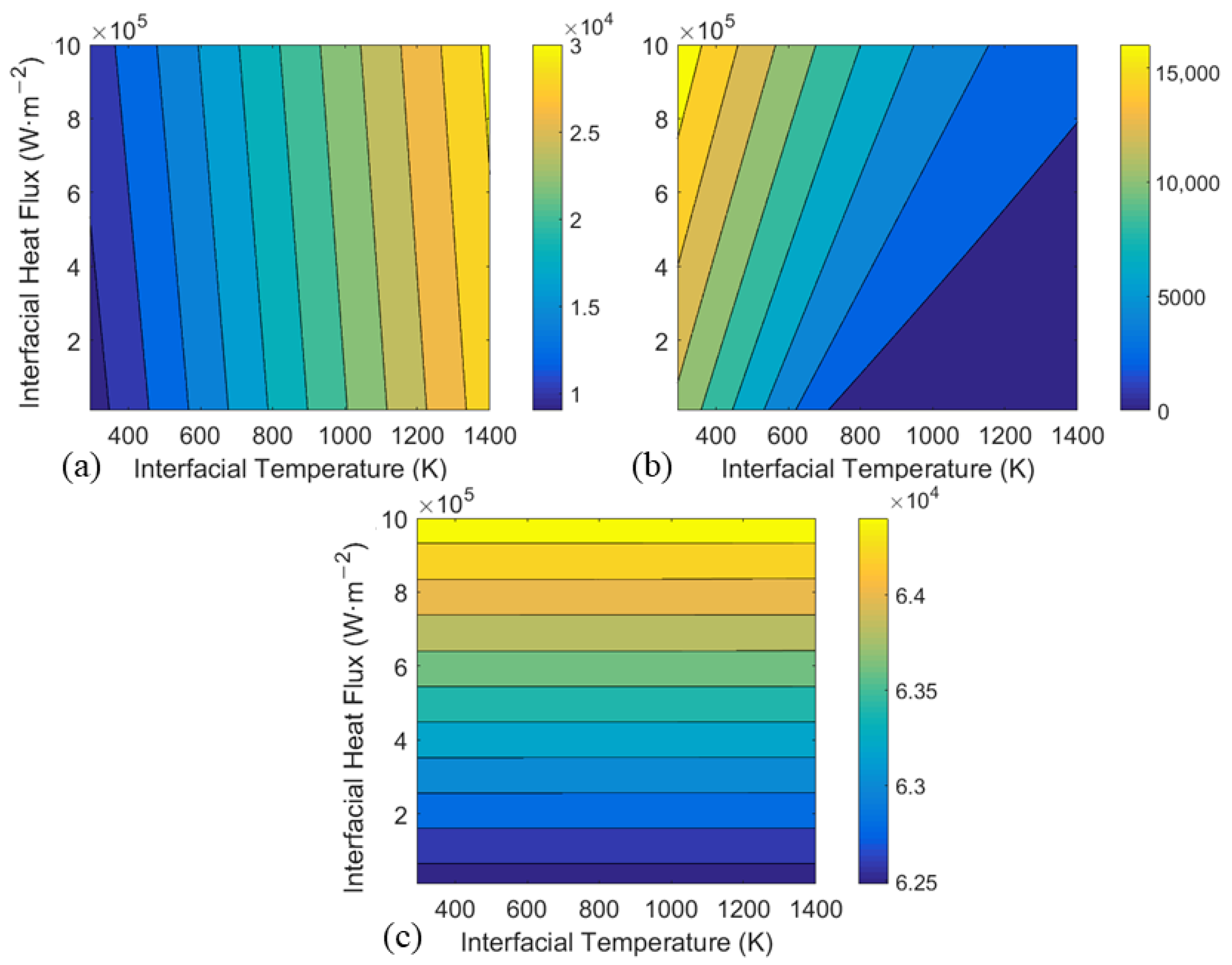
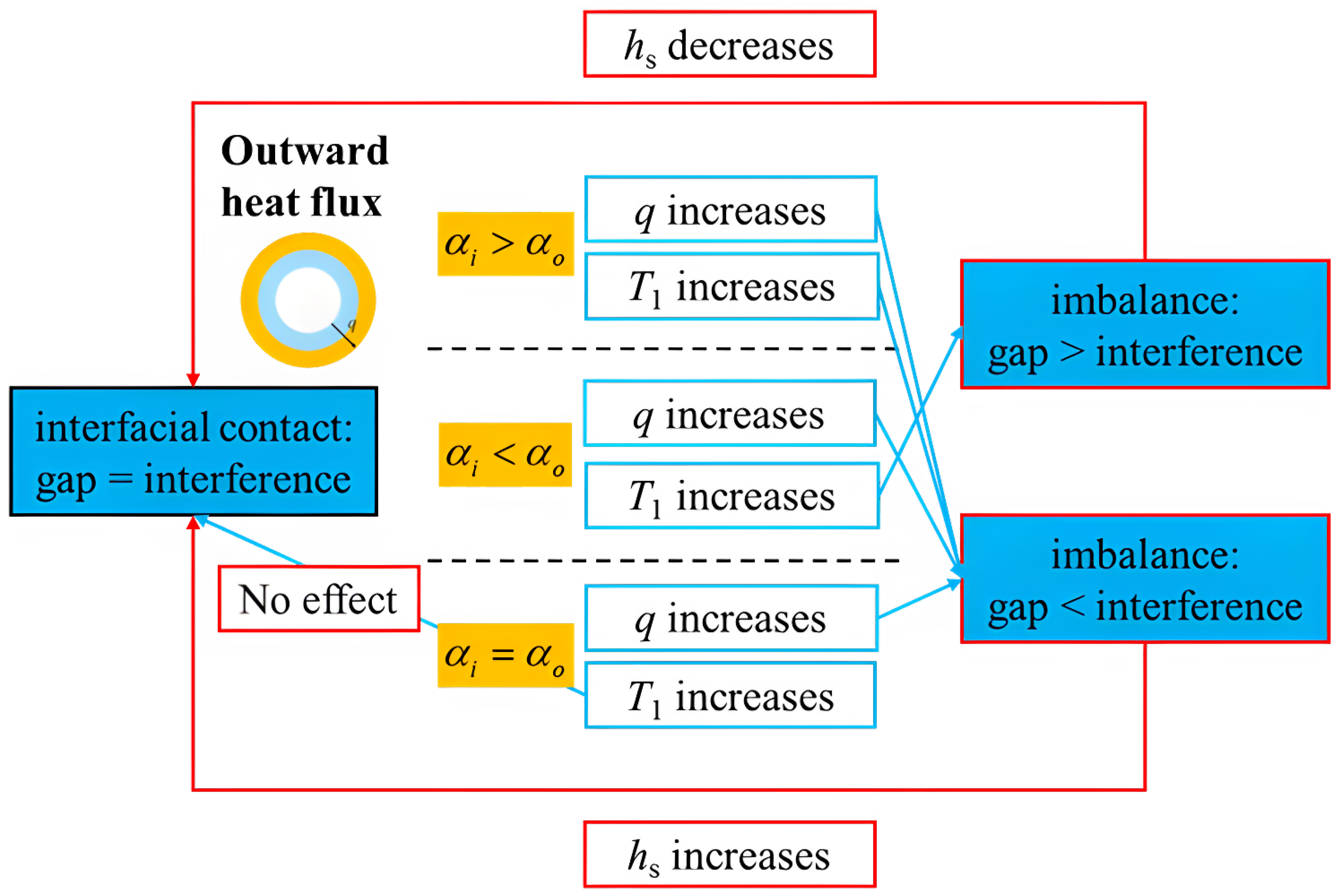
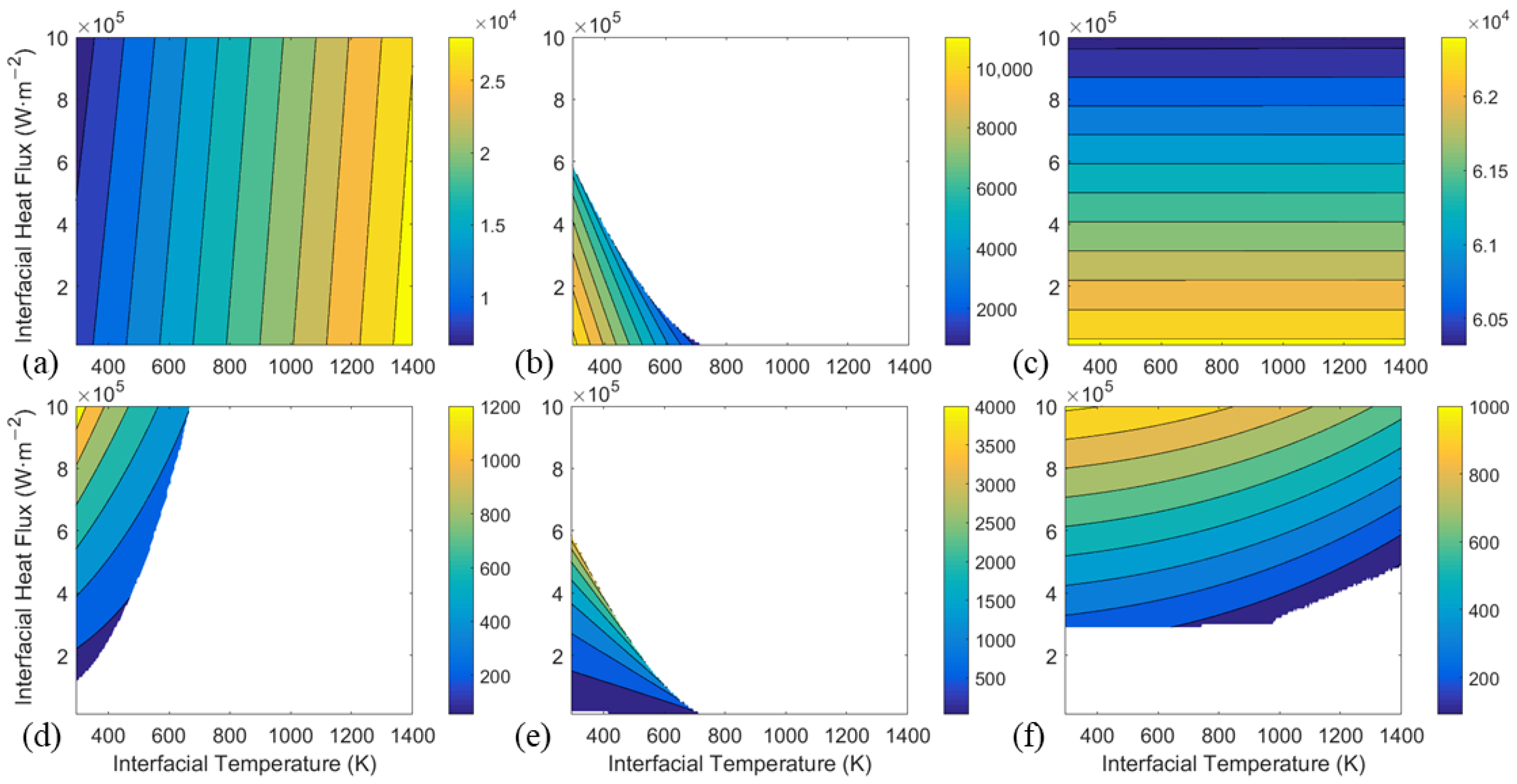
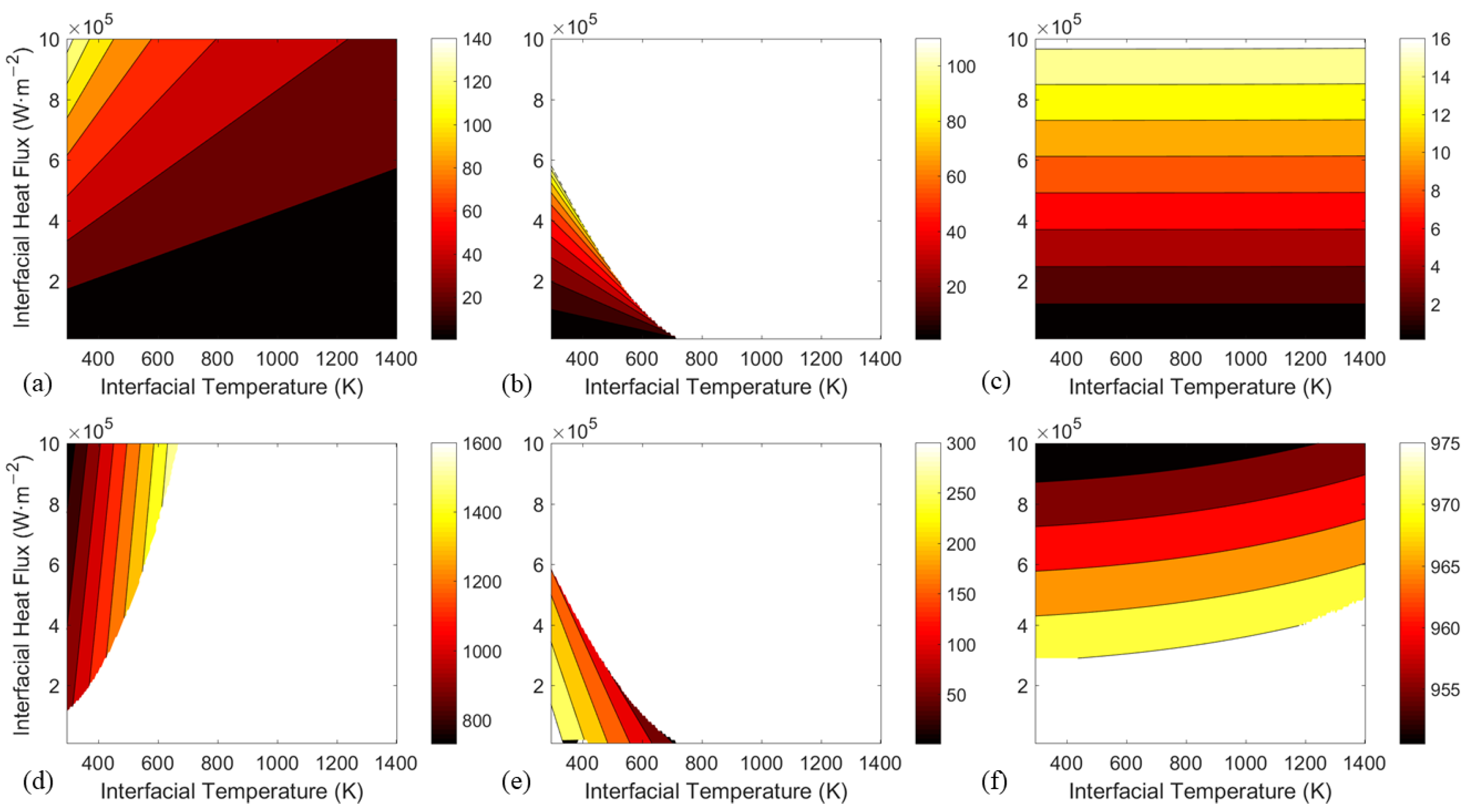
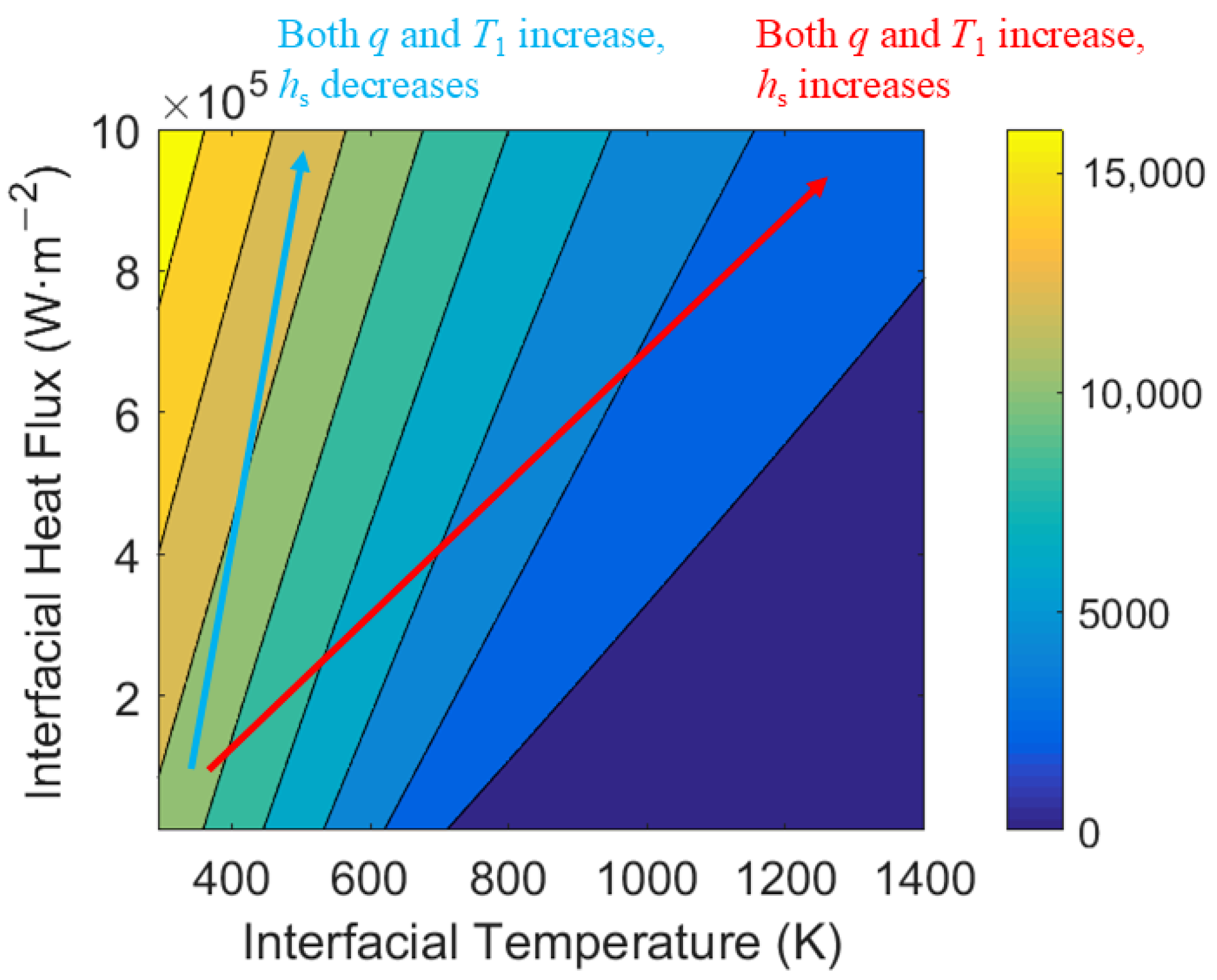
3.1. Outward Heat Flux: Three Representative Response Modes
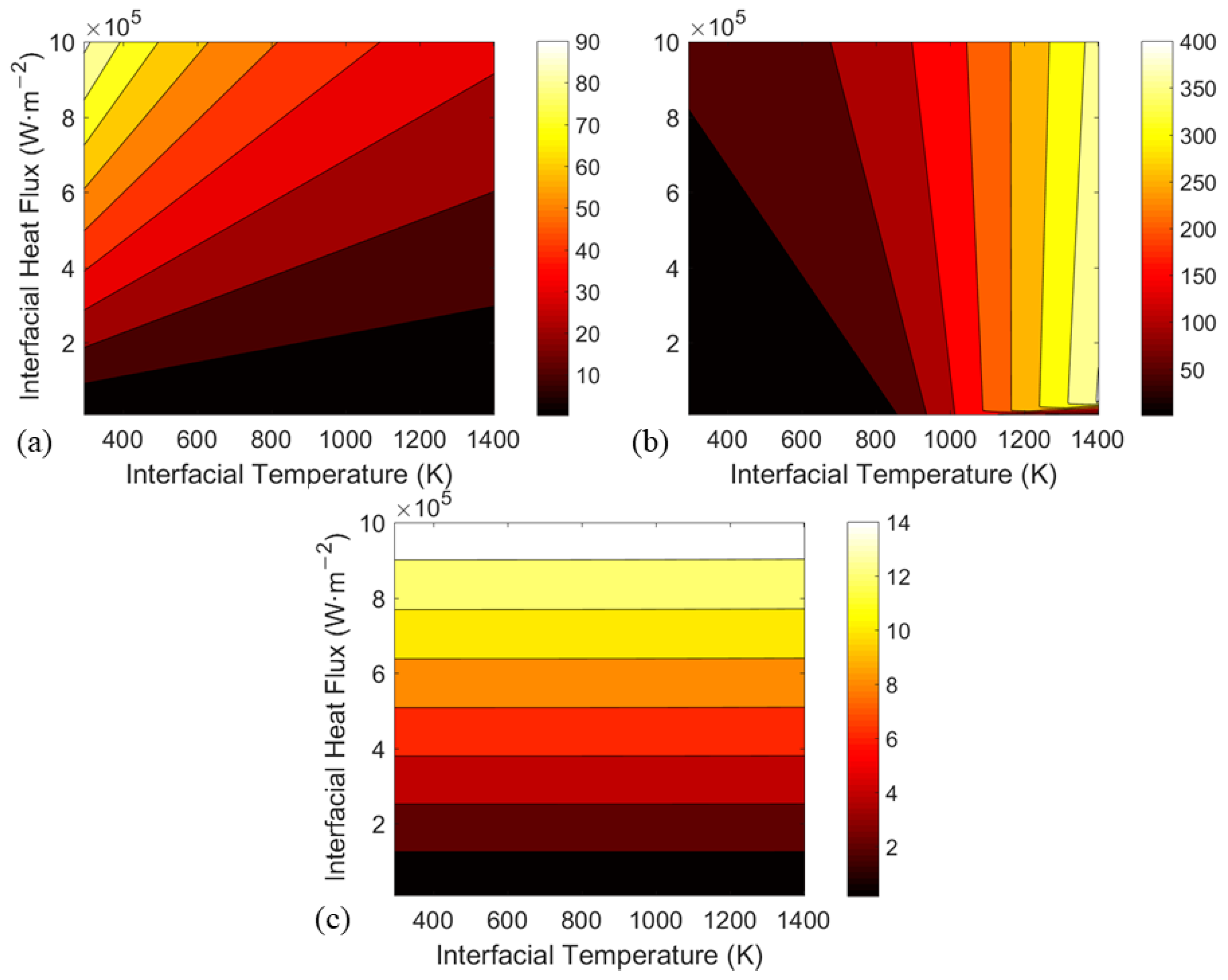
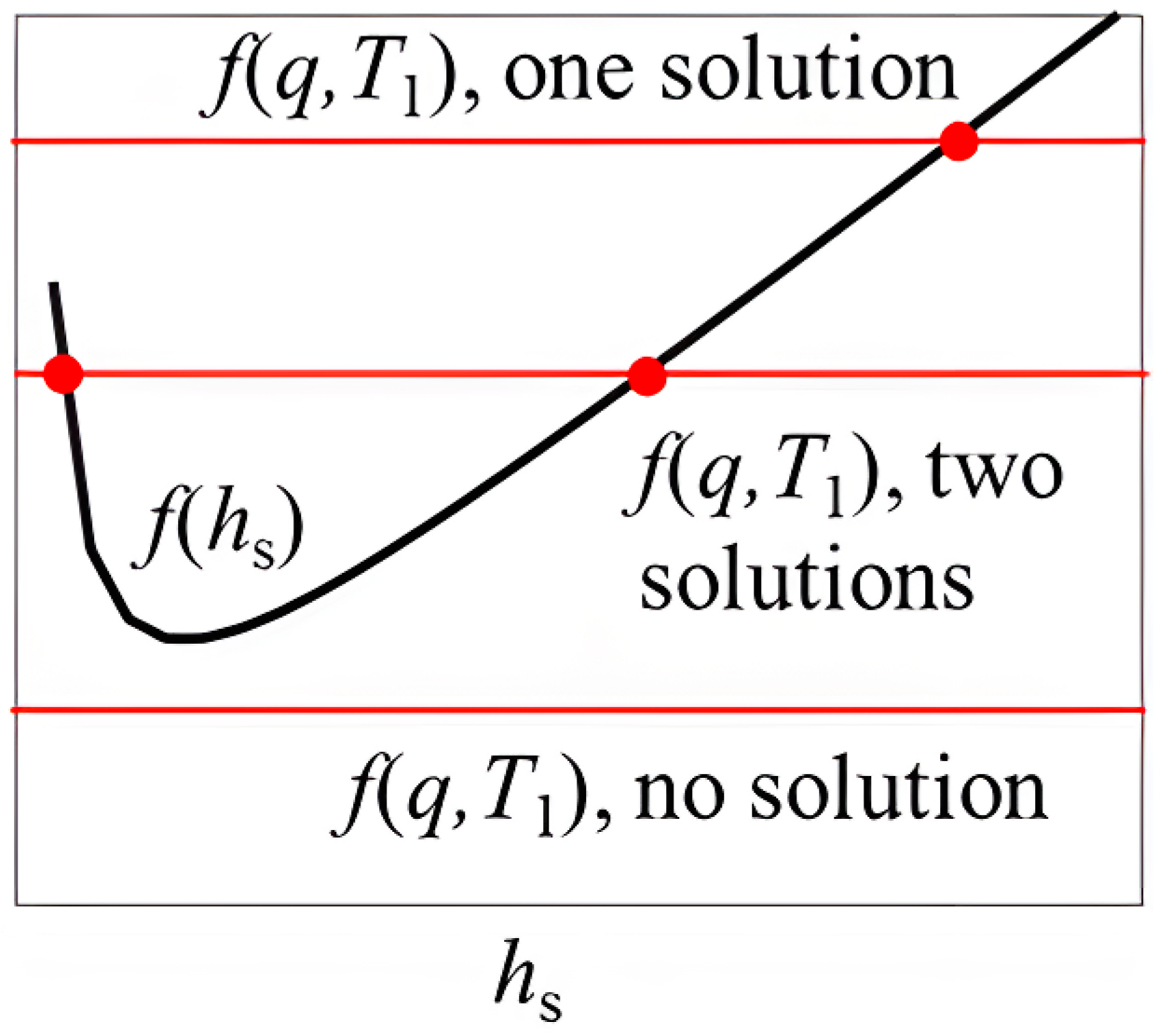
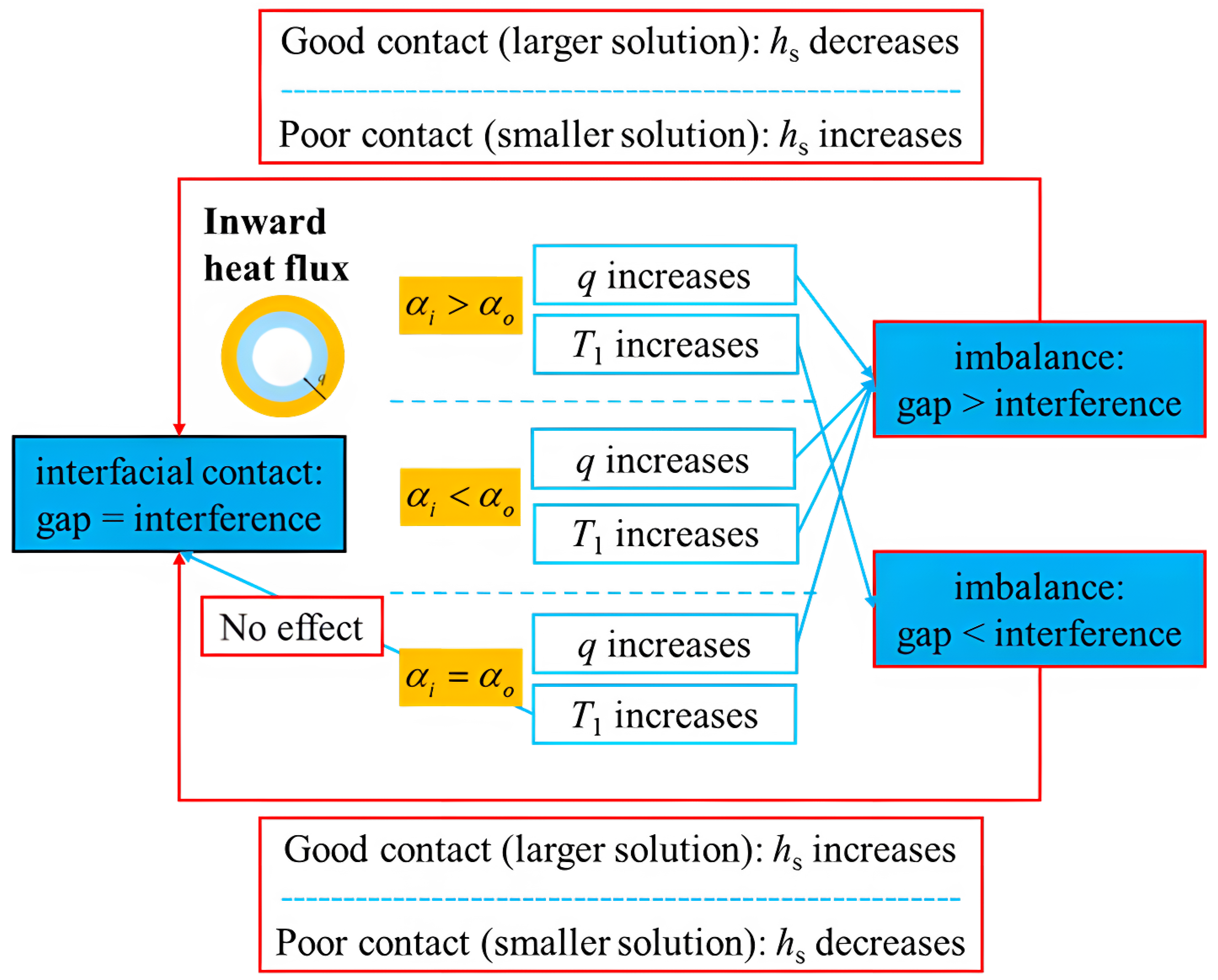
3.2. Inward Heat Flux: Six Representative Response Modes and Two Coexistent Solutions
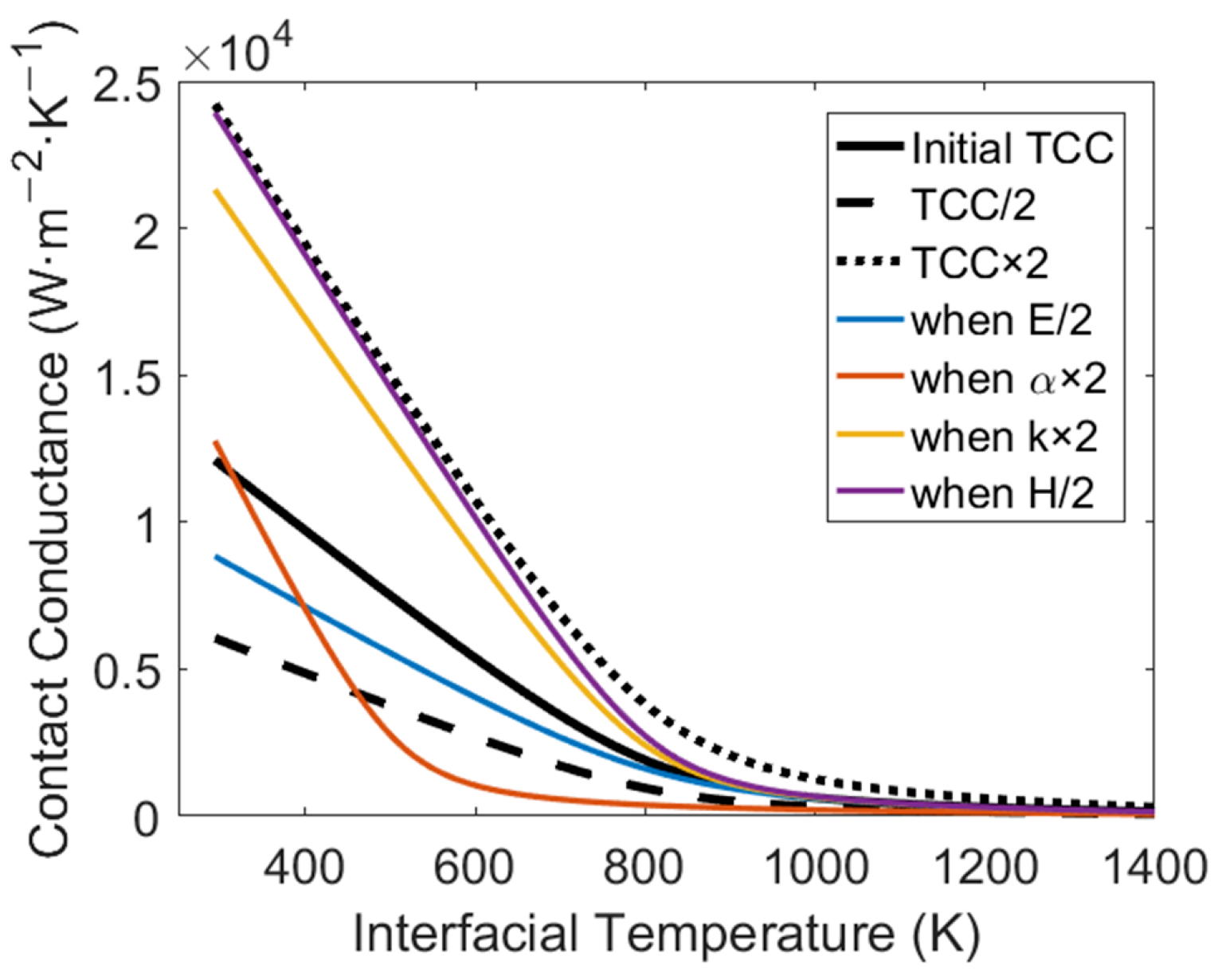
3.3. Quasi-Quantitative Discussion on Other Influencing Factors of TCC
4. Conclusions
- For outward heat flux, TCC consistently increases with heat flux and has three possible response modes to temperature changes, depending on the thermal expansion coefficients of the materials involved.
- For inward heat flux, there are six possible response modes due to the coexistence of two opposite solutions of TCC, corresponding to good and bad interfacial contact states, for the same interfacial conditions. This behavior arises from the asymmetry between the thermal expansions of the inner and outer cylinders. Results also indicate that fast heating may lead to poor contact state, and thus should be avoided.
- The qualitative response patterns are governed by the relative thermal expansion coefficients and heat flux direction, while other material properties and geometric parameters influence the quantitative response of TCC.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SS | Stainless Steel |
| TCC | Thermal Contact Conductance |
References
- Górecki, G.; Łęcki, M.; Gutkowski, A.N.; Andrzejewski, D.; Warwas, B.; Kowalczyk, M.; Romaniak, A. Experimental and numerical study of heat pipe heat exchanger with individually finned heat pipes. Energies 2021, 14, 5317. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Olabi, A.; Alami, A.H.; Al Radi, M.; Zwayyed, F.; Wilberforce, T.; Abdelkareem, M.A. Numerical simulation of heat pipes in different applications. Int. J. Thermofluids 2022, 16, 100199. [Google Scholar] [CrossRef]
- Singh, S.; Sørensen, K.; Condra, T.J. Influence of the degree of thermal contact in fin and tube heat exchanger: A numerical analysis. Appl. Therm. Eng. 2016, 107, 612–624. [Google Scholar] [CrossRef]
- Tang, S.; Wang, C.; Zhang, D.; Tian, W.; Su, G.; Qiu, S. Thermoelectric performance study on a heat pipe thermoelectric generator for micro nuclear reactor application. Int. J. Energy Res. 2021, 45, 12301–12316. [Google Scholar] [CrossRef]
- Tang, D.; Li, D.; Peng, Y.; Du, Z. A new approach in evaluation of thermal contact conductance of tube–fin heat exchanger. Appl. Therm. Eng. 2010, 30, 1991–1996. [Google Scholar] [CrossRef]
- Deng, J.; Wang, T.; Liu, X.; Zhang, T.; He, H.; Chai, X. Experimental study on transient heat transfer performance of high temperature heat pipe under temperature feedback heating mode for micro nuclear reactor applications. Appl. Therm. Eng. 2023, 230, 120826. [Google Scholar] [CrossRef]
- Gibson, M.; Schmitz, P. Higher power design concepts for NASA’s kilopower reactor. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; IEEE: New York, NY, USA, 2020; pp. 1–9. [Google Scholar]
- Merrigan, M.; Keddy, E.; Sena, J. Transient Heat Pipe Investigations for Space Power Systems; Report; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 1985.
- Madhusudana, C.; Fletcher, L.; Peterson, G. Thermal conductance of cylindrical joints—A critical review. J. Thermophys. Heat Transf. 1990, 4, 204–211. [Google Scholar] [CrossRef]
- Kumar, S.; Tariq, A. Effects of contact-nature on transient thermal contact conductance. Int. J. Therm. Sci. 2019, 137, 299–312. [Google Scholar] [CrossRef]
- Rosochowska, M.; Balendra, R.; Chodnikiewicz, K. Measurements of thermal contact conductance. J. Mater. Process. Technol. 2003, 135, 204–210. [Google Scholar] [CrossRef]
- Singhal, V.; Litke, P.J.; Black, A.F.; Garimella, S.V. An experimentally validated thermo-mechanical model for the prediction of thermal contact conductance. Int. J. Heat Mass Transf. 2005, 48, 5446–5459. [Google Scholar] [CrossRef]
- Tariq, A.; Asif, M. Experimental investigation of thermal contact conductance for nominally flat metallic contact. Heat Mass Transf. 2016, 52, 291–307. [Google Scholar] [CrossRef]
- Sun, X.; Meng, C.; Duan, T. Fractal model of thermal contact conductance of two spherical joint surfaces considering friction coefficient. Ind. Lubr. Tribol. 2022, 74, 93–101. [Google Scholar] [CrossRef]
- Kumar, A.; Rana, S.; Gori, Y.; Sharma, N.K. Thermal contact conductance prediction using FEM-based computational techniques. In Advanced Computational Methods in Mechanical and Materials Engineering; CRC Press: Boca Raton, FL, USA, 2021; pp. 183–217. [Google Scholar]
- Yang, Z.; Yi, S.; Li, J.; Ding, S. Thermal and force simulation modelling of graphene oxide nanosheets as cutting fluid additives during Ti-6Al-4V drilling process. Int. J. Therm. Sci. 2025, 210, 109608. [Google Scholar] [CrossRef]
- Brazhenko, V.; Qiu, Y.; Cai, J.; Wang, D. Thermal Evaluation of Multilayer Wall with a Hat-Stringer in Aircraft Design. Stroj. Vestn.-J. Mech. Eng. 2022, 68, 635–641. [Google Scholar] [CrossRef]
- Sunil Kumar, S.; Abilash, P.; Ramamurthi, K. Thermal contact conductance for cylindrical and spherical contacts. Heat Mass Transf. 2004, 40, 679–688. [Google Scholar] [CrossRef]
- Tio, K.K.; Chuan, T.K. Thermal resistance of two solids in contact through a cylindrical joint. Int. J. Heat Mass Transf. 1998, 41, 2013–2024. [Google Scholar] [CrossRef]
- Liu, J.; Ma, C.; Wang, S. Thermal contact conductance between rollers and bearing rings. Int. J. Therm. Sci. 2020, 147, 106140. [Google Scholar] [CrossRef]
- Tafazzoli Aghvami, K.; Shojaeefard, M.H.; Jourabian, M. Steady-state estimation of thermal contact conductance between sliding disk and stationary cylinder with similar/dissimilar materials under the isothermally heated boundary condition. Heat Transf. 2021, 50, 8012–8034. [Google Scholar] [CrossRef]
- Ayers, G.; Fletcher, L.; Madhusudana, C. Thermal contact conductance of composite cylinders. J. Thermophys. Heat Transf. 1997, 11, 72–81. [Google Scholar] [CrossRef]
- Madhusudana, C.V. Thermal conductance of cylindrical joints. Int. J. Heat Mass Transf. 1999, 42, 1273–1287. [Google Scholar] [CrossRef]
- Madhusudana, C.V.; Madhusudana, C. Thermal Contact Conductance; Springer: New York, NY, USA, 1996; Volume 79. [Google Scholar]
- Mikić, B. Thermal contact conductance; theoretical considerations. Int. J. Heat Mass Transf. 1974, 17, 205–214. [Google Scholar] [CrossRef]
- Tien, C. A correlation for thermal contact conductance of nominally flat surfaces in vacuum. In Proceedings of the Thermal Conductivity, Proceedings of the Seventh Conference, National Bureau of Standards Special Publication, Gaithersburg, MD, USA, 13–16 November 1967; Volume 302, pp. 755–759. [Google Scholar]
- Yüncü, H.; Kakaç, S. Thermal contact conductance-theory and applications. In Cooling of Electronic Systems; Springer: Dordrecht, The Netherlands, 1994; pp. 677–702. [Google Scholar]
- Hetnarski, R.B.; Eslami, M.R.; Gladwell, G. Thermal Stresses: Advanced Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009; Volume 41. [Google Scholar]
- Lurie, A.I. Theory of Elasticity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Ugural, A.C.; Fenster, S.K. Advanced Strength and Applied Elasticity; Pearson Education: Hoboken, NJ, USA, 2003. [Google Scholar]
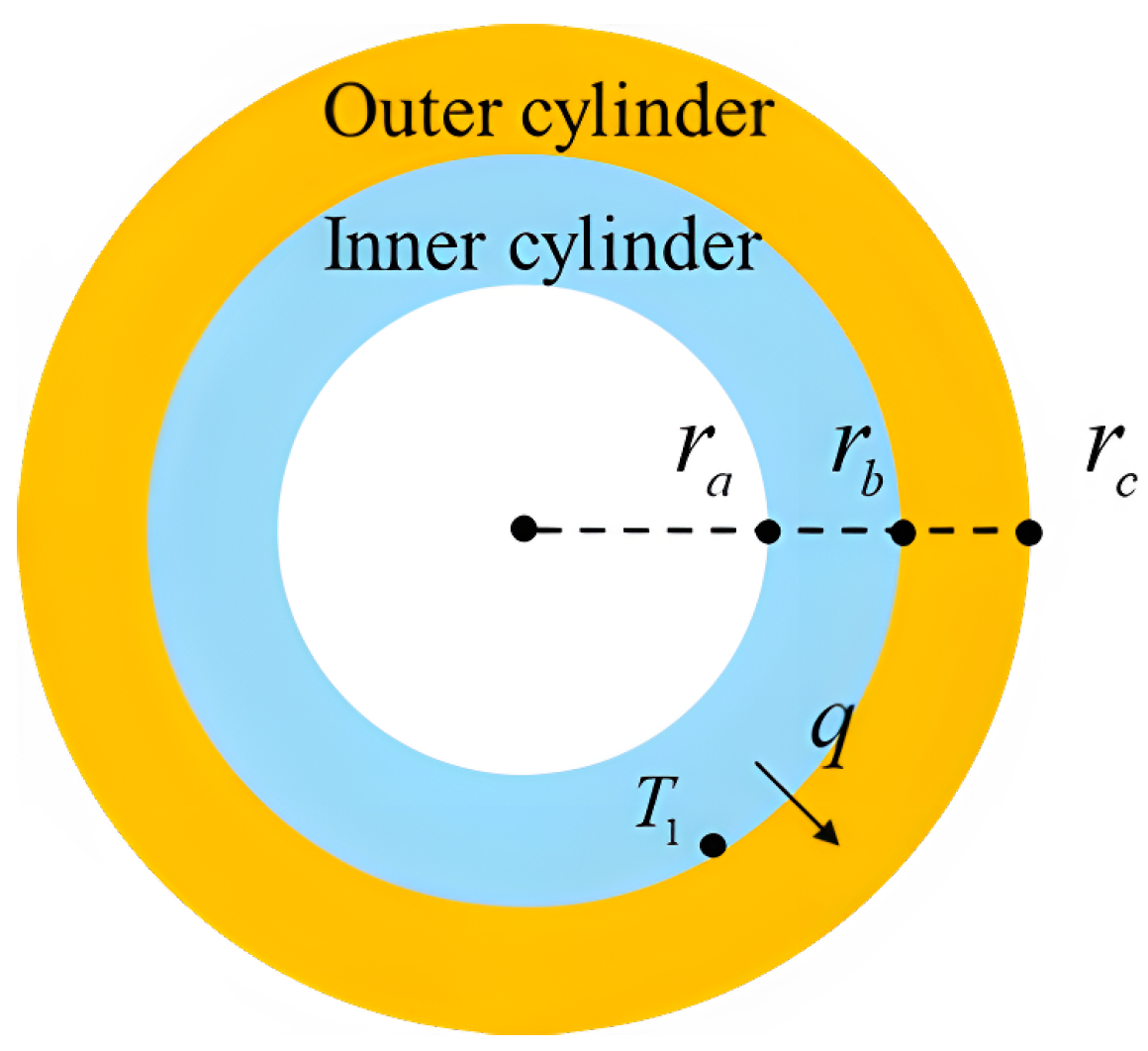
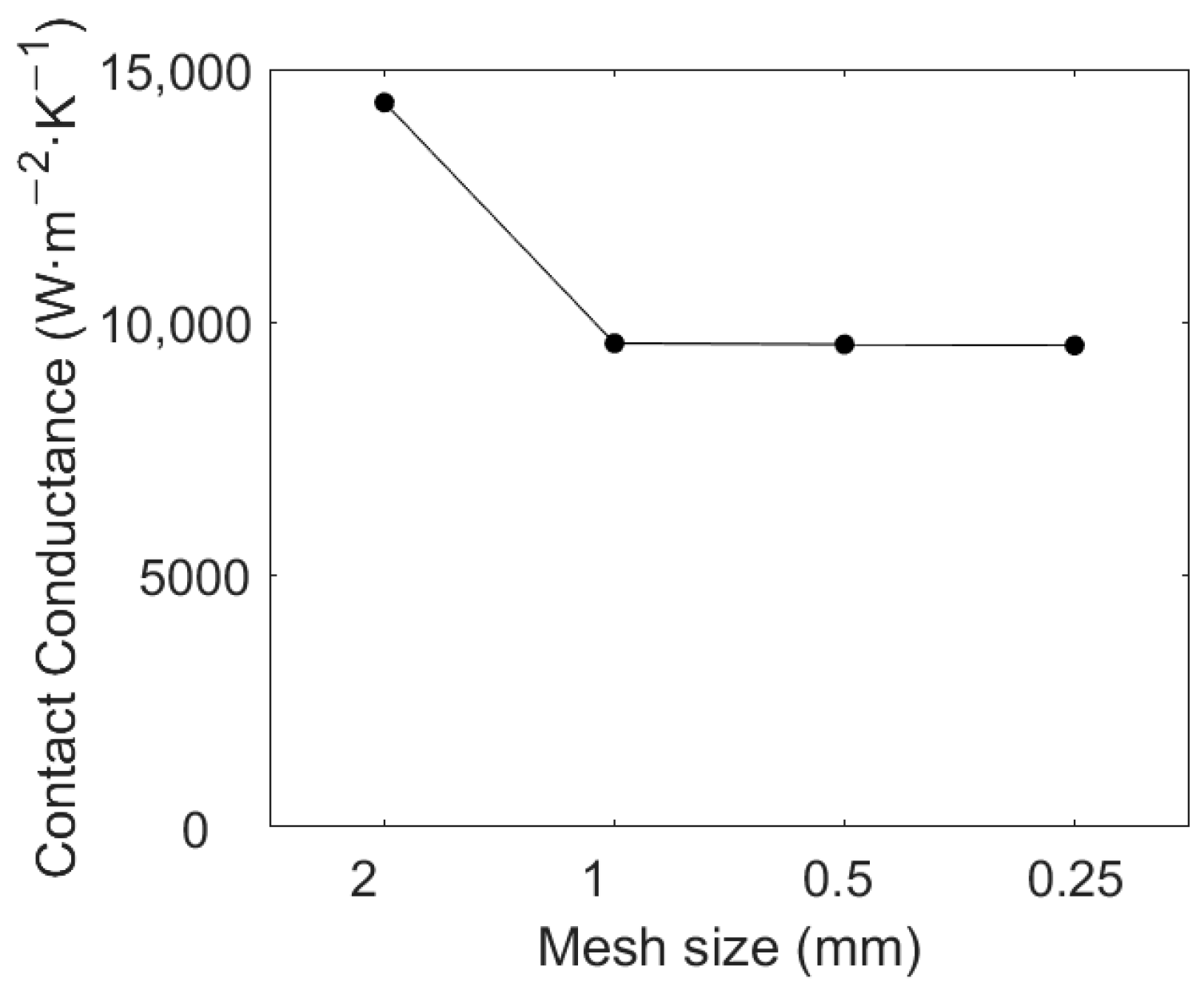
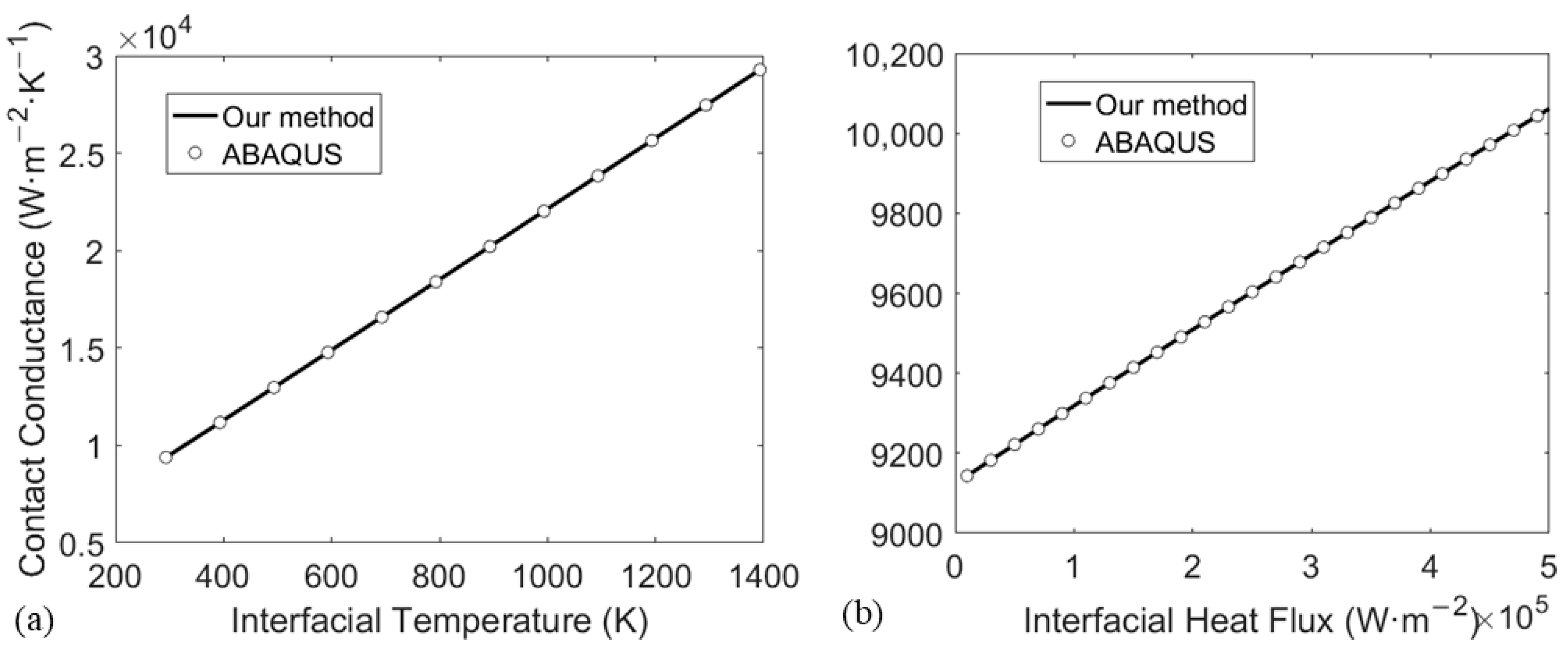
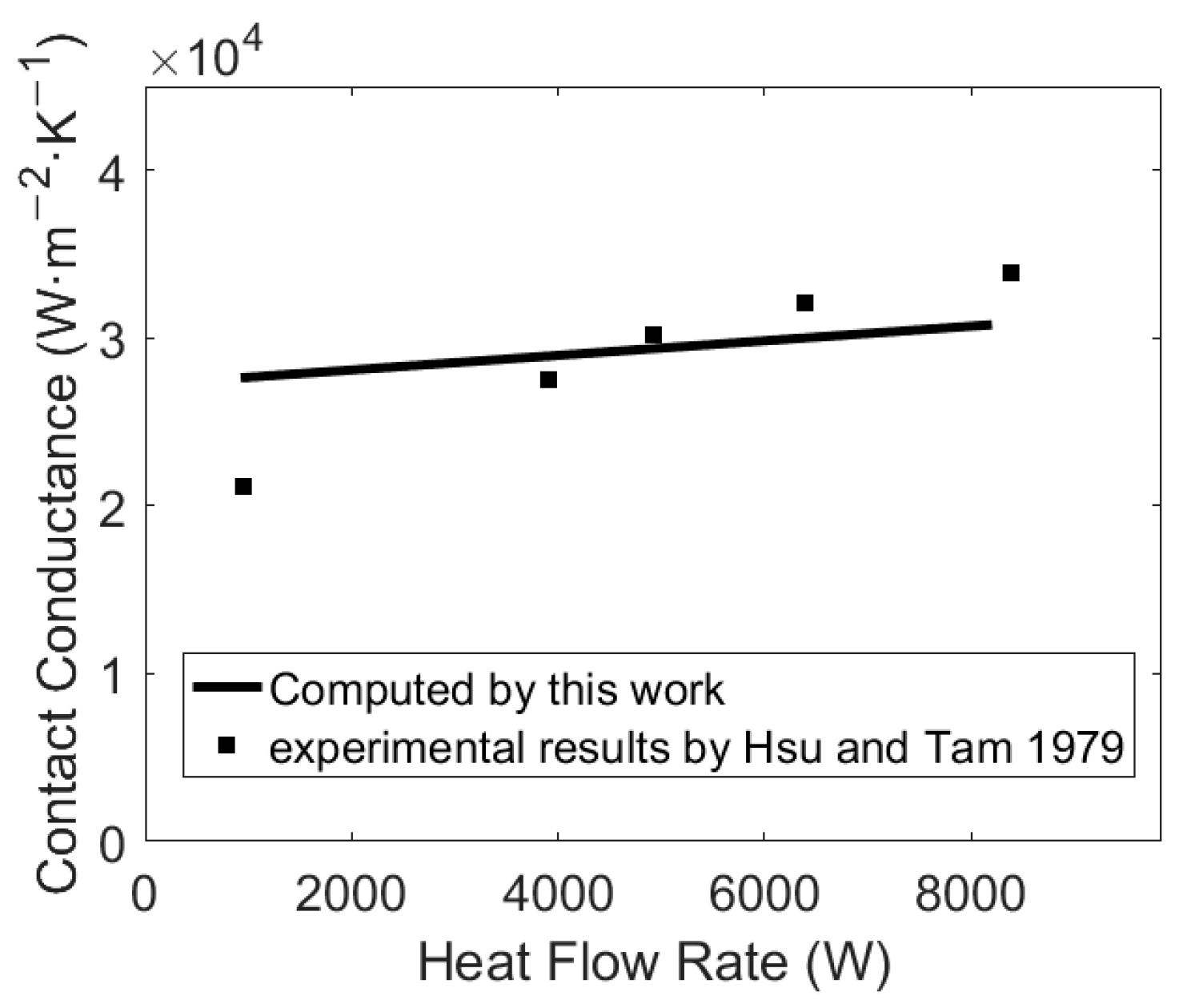
| Inner Cylinder | Outer Cylinder | |
|---|---|---|
| Material | Alclad 2011-T351 | Stainless steel AISI 304 |
| Elastic modulus (Pa) | 7.1 × 1010 | 2 × 1011 |
| Thermal expansion coefficient (K−1) | 2.28 × 10−5 | 1.73 × 10−5 |
| Thermal conductivity (W·m−1·K−1) | 155 | 16.5 |
| Poisson’s ratio | 0.28 | 0.33 |
| Hardness (Pa) | 9.33 × 108 | 2.42 × 109 |
| Surface roughness (m) | 3 × 10−6 | 1.27 × 10−6 |
| Inner radius (m) | 1.1 × 10−2 | 2.958 × 10−2 |
| Outer radius (m) | 2.958 × 10−2 | 3.626 × 10−2 |
| Material Properties | Stainless Steel | Molybdenum |
|---|---|---|
| Elastic modulus (Pa) | 2 × 1011 | 3.3 × 1011 |
| Thermal expansion coefficient (K−1) | 1.6 × 10−5 | 5.35 × 10−6 |
| Thermal conductivity (W·m−1·K−1) | 16.5 | 138 |
| Poisson’s ratio | 0.28 | 0.38 |
| Hardness (Pa) | 2.75 × 109 | 1.4 × 109 |
| Emissivity | 0.4 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Ma, M.; Zhang, Y.; Xie, Q.; Liang, W. General Response Modes of Cylindrical Thermal Contact Conductance to Bidirectional Heat Flux and Temperature Variations. Energies 2025, 18, 2454. https://doi.org/10.3390/en18102454
Liu F, Ma M, Zhang Y, Xie Q, Liang W. General Response Modes of Cylindrical Thermal Contact Conductance to Bidirectional Heat Flux and Temperature Variations. Energies. 2025; 18(10):2454. https://doi.org/10.3390/en18102454
Chicago/Turabian StyleLiu, Fanli, Mingyang Ma, Yang Zhang, Qilin Xie, and Wenfeng Liang. 2025. "General Response Modes of Cylindrical Thermal Contact Conductance to Bidirectional Heat Flux and Temperature Variations" Energies 18, no. 10: 2454. https://doi.org/10.3390/en18102454
APA StyleLiu, F., Ma, M., Zhang, Y., Xie, Q., & Liang, W. (2025). General Response Modes of Cylindrical Thermal Contact Conductance to Bidirectional Heat Flux and Temperature Variations. Energies, 18(10), 2454. https://doi.org/10.3390/en18102454





