A High-Resolution Defect Location Method for Medium-Voltage Cables Based on Gaussian Narrow-Band Envelope Signals and the S-Transform
Abstract
1. Introduction
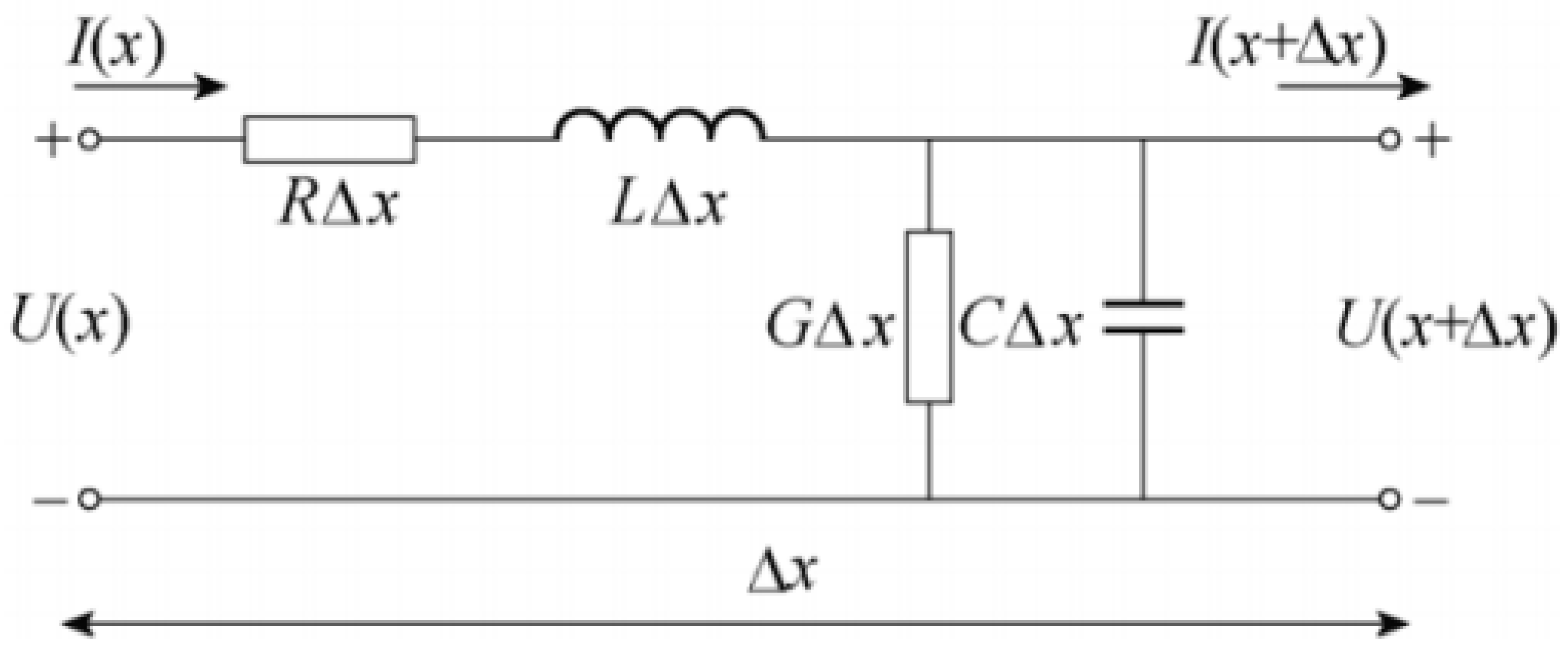
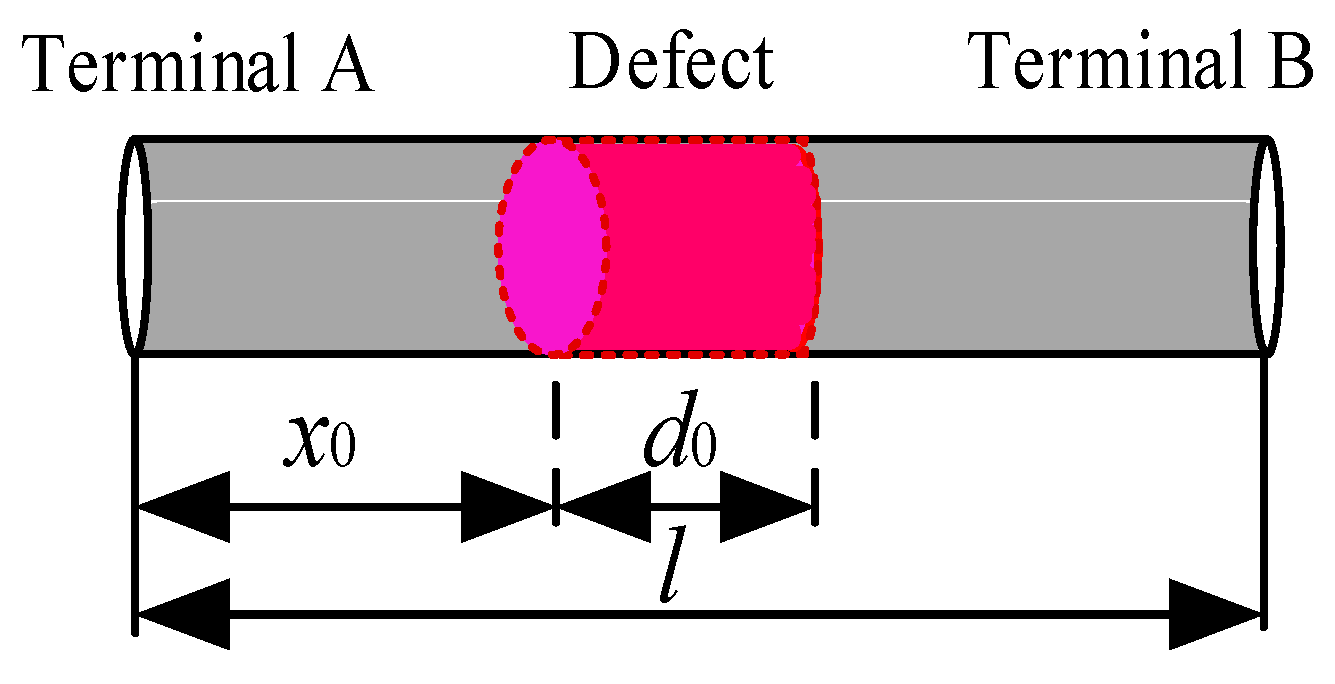
2. Medium-Voltage Cable Model and Principle of Locating Defects
3. Equivalent Frequency Estimation Based on Gaussian Narrow-Band Envelope Signals and the S-Transform
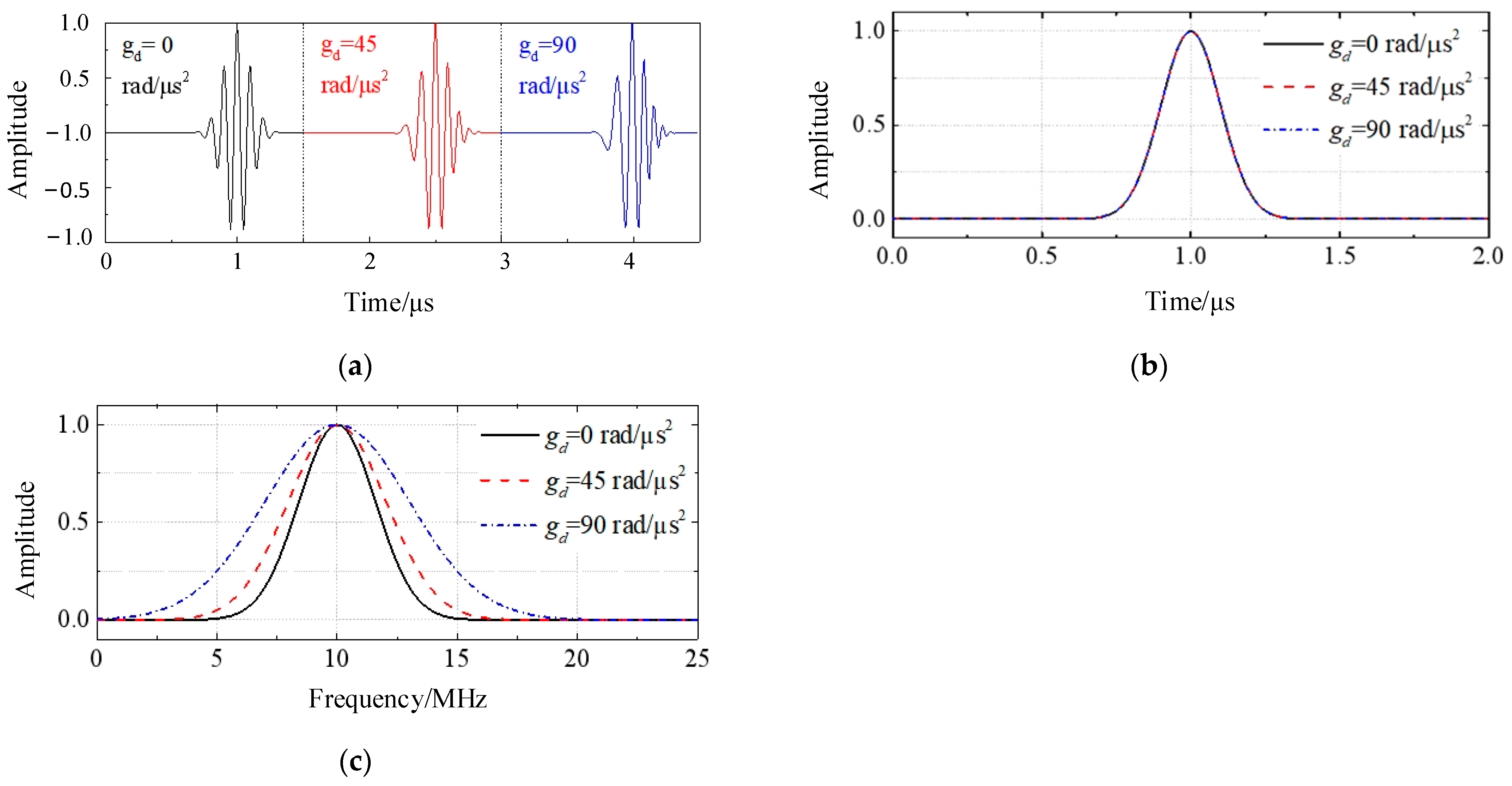
3.1. Gaussian Narrow-Band Envelope Signals
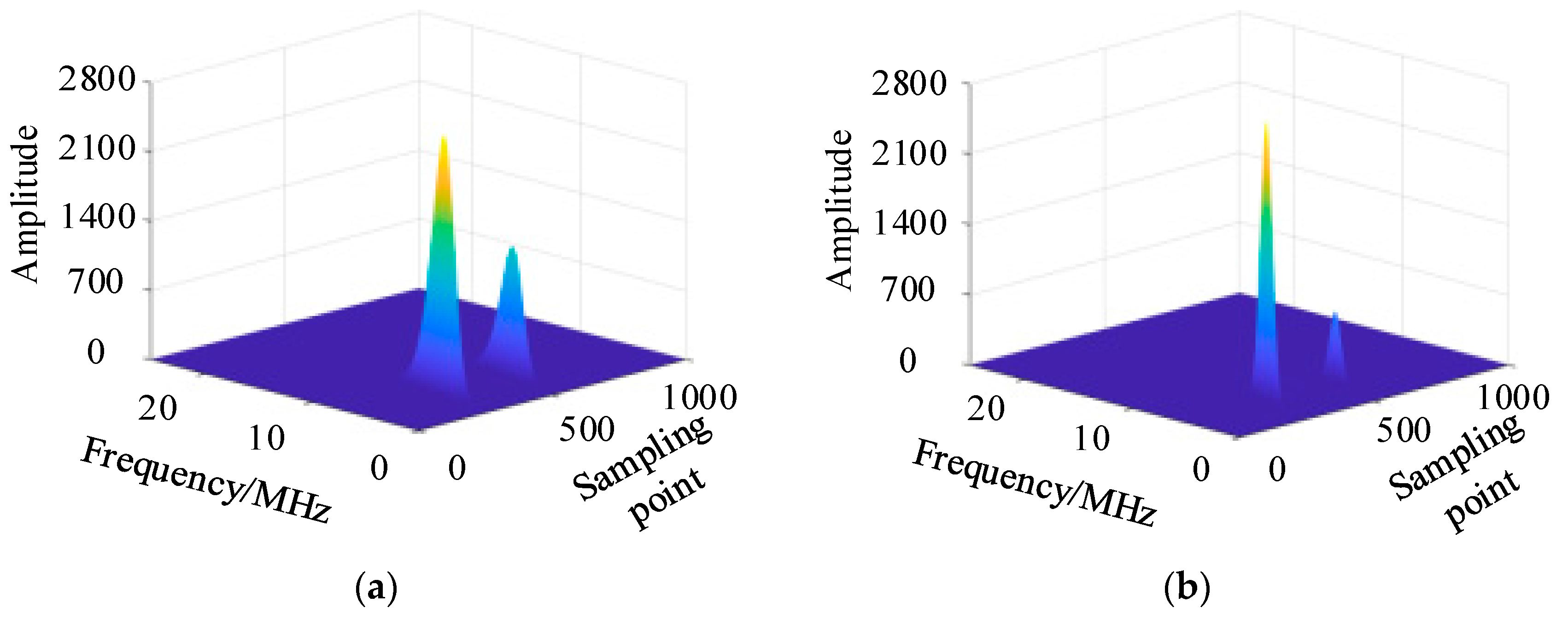
3.2. Defect Detection Based on the S-Transform
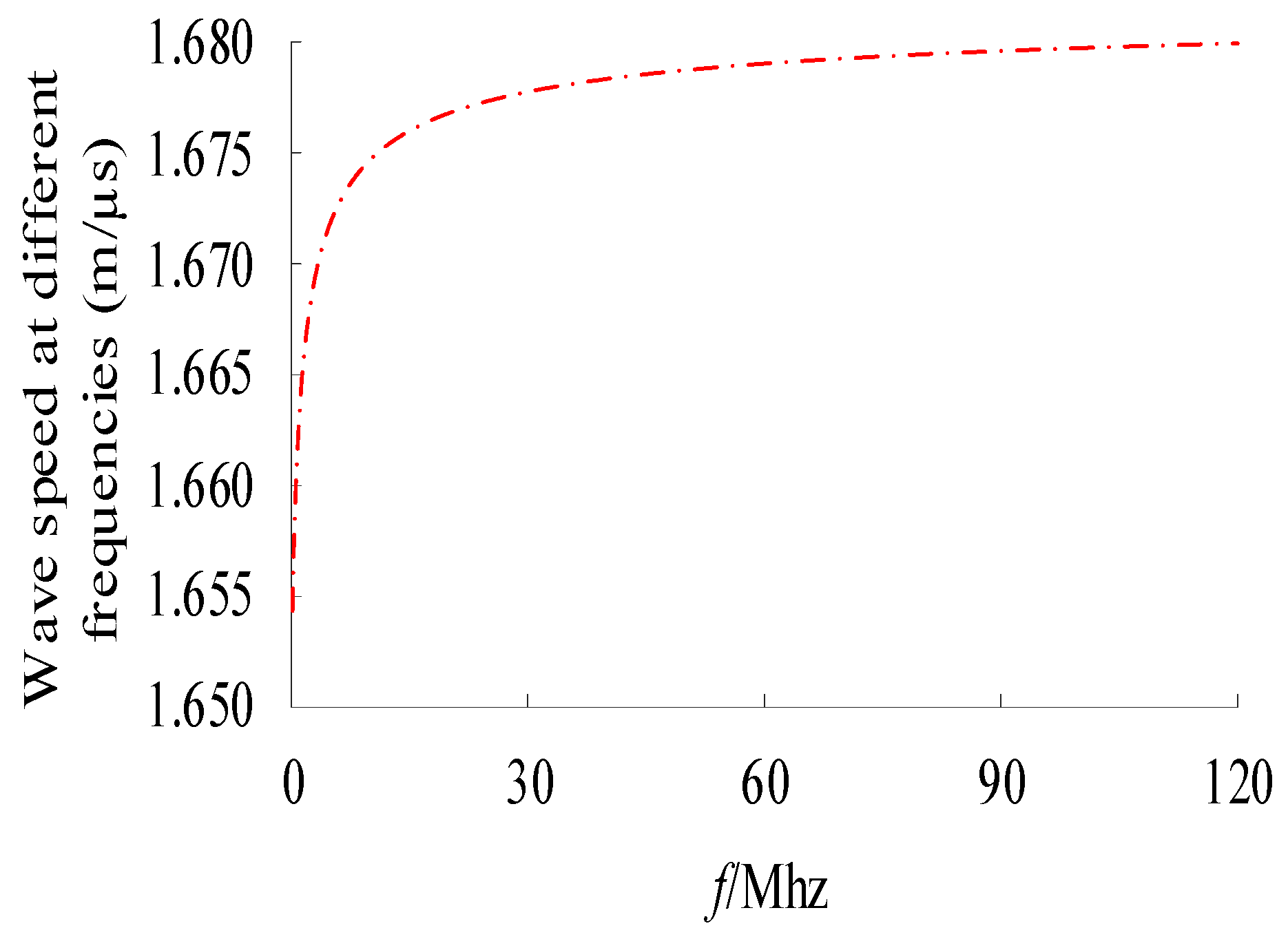
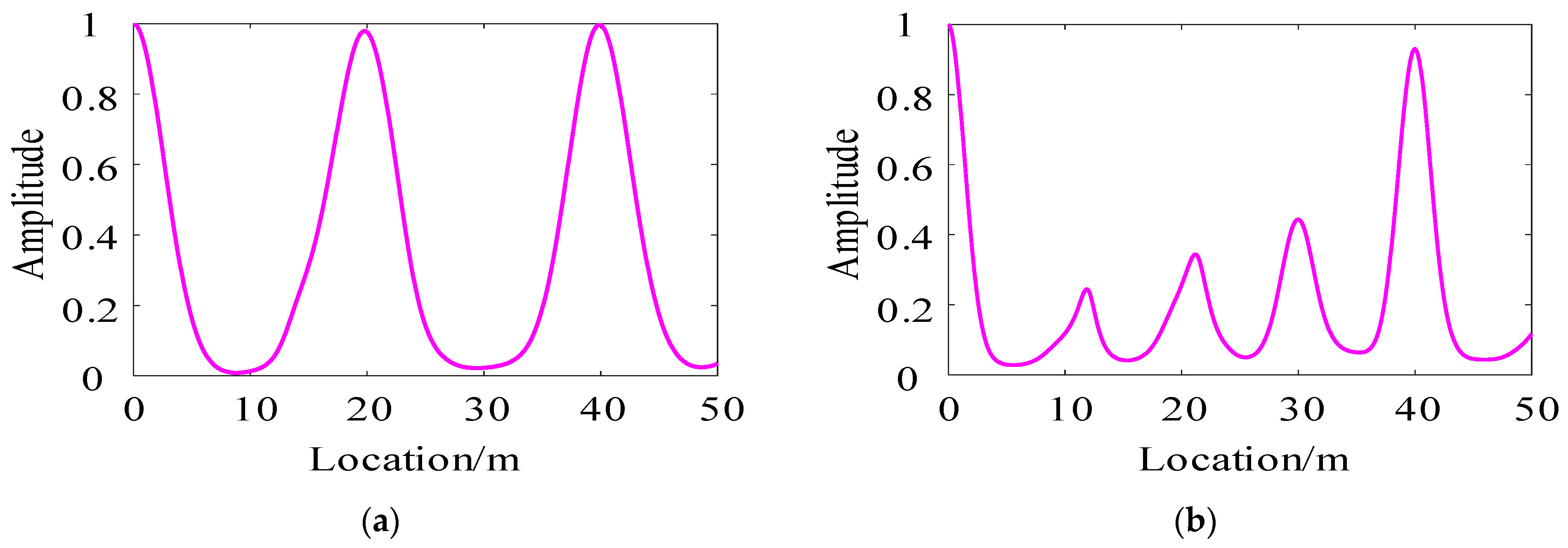
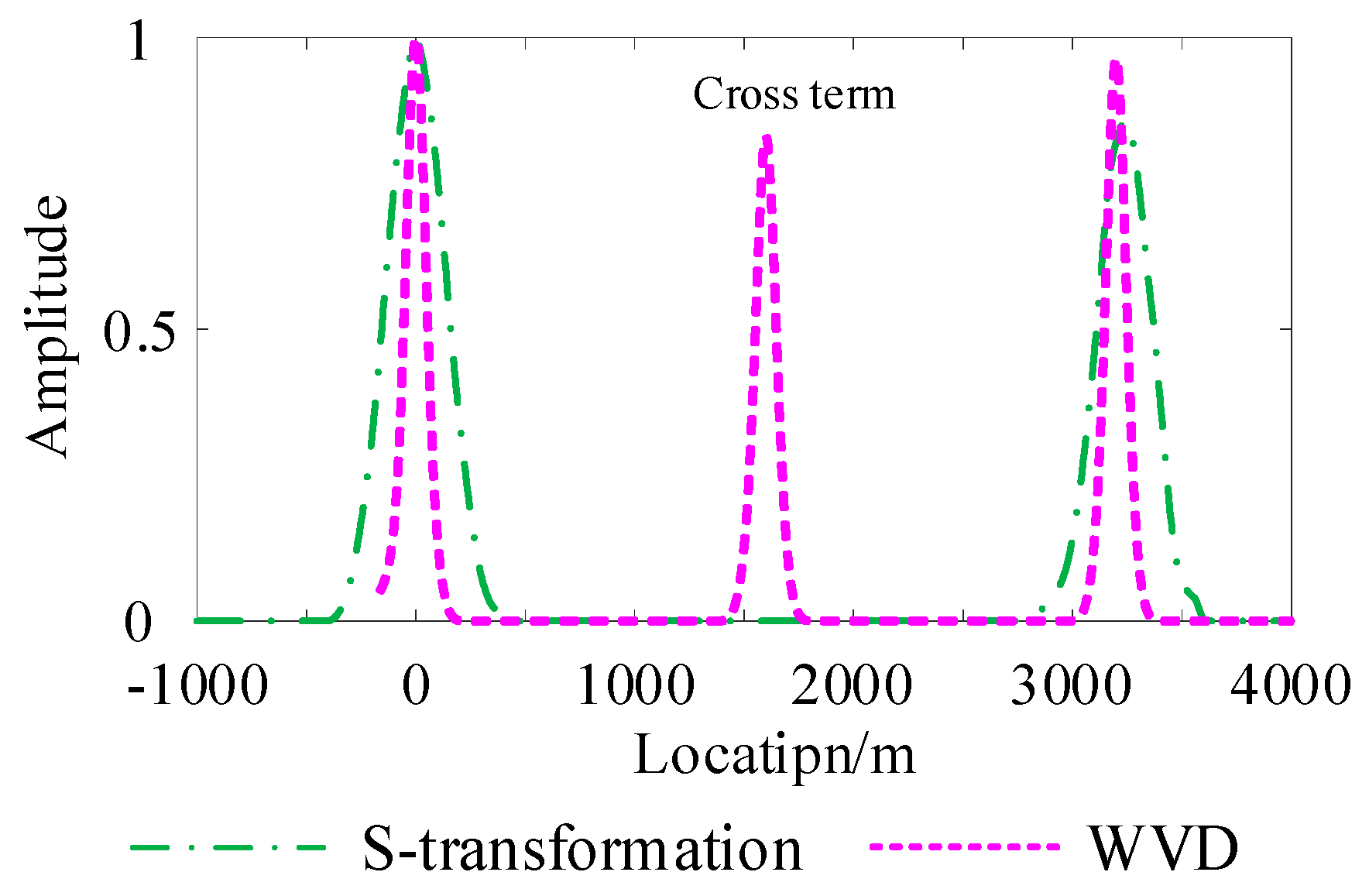
4. Simulation Analysis of Medium-Voltage Cables
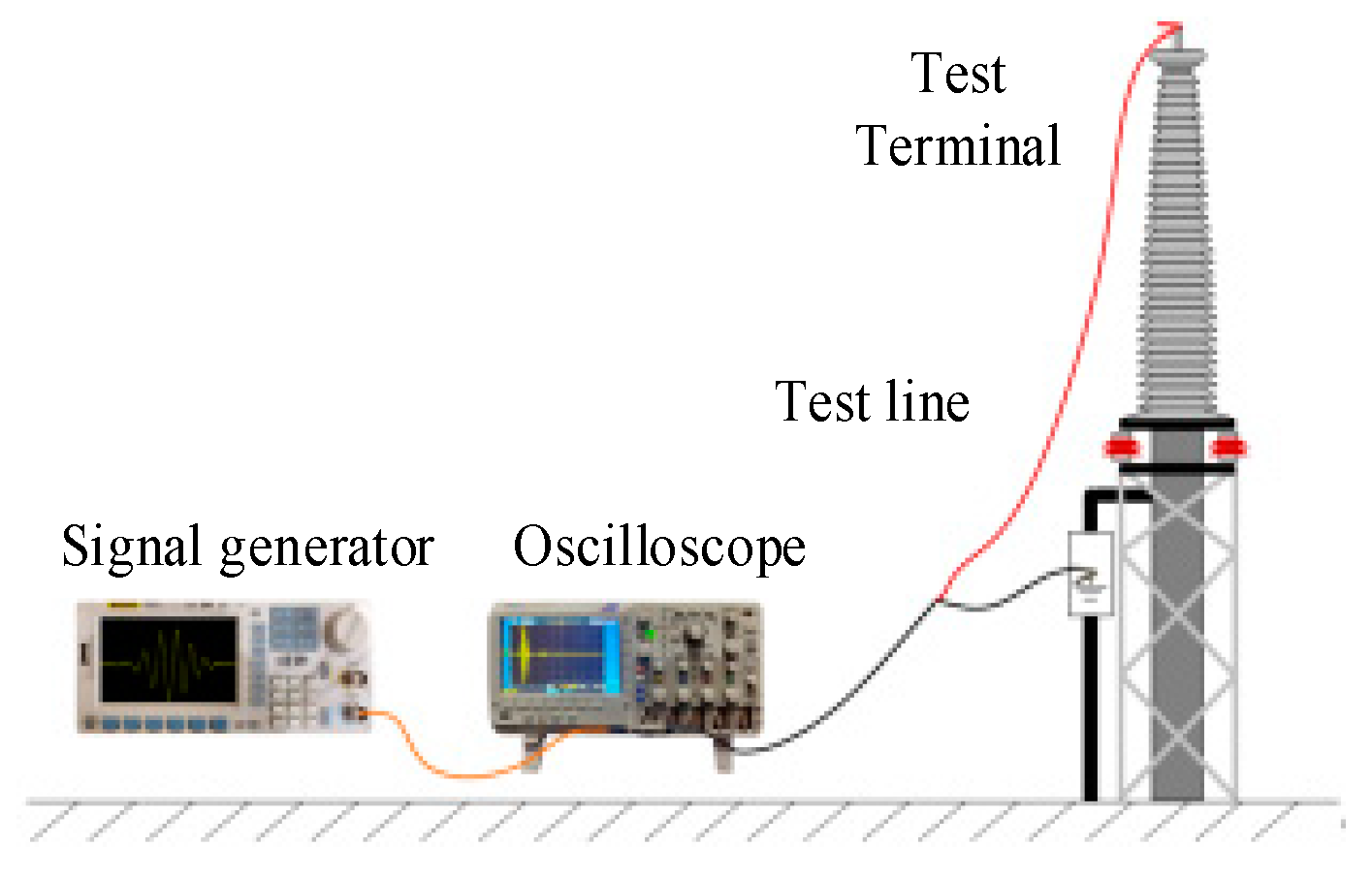
5. Actual Medium-Voltage Cable Test
5.1. Case 1
5.2. Case 2
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Full Names | Abbreviations |
| Time–frequency-domain reflection | TFDR |
| Frequency-domain reflection | FDR |
| Time-domain reflectometry | TDR |
| Broadband impedance spectroscopy | BIS |
| Wigner–Ville distribution | WVD |
| Pseudo-Wigner–Ville distribution | PWVD |
| Smooth pseudo-Wigner distribution | SPWVD |
| Cable transfer function | CTF |
| Symbols | Meaning |
| Δx | The unit length of the cable |
| R | The resistance per unit length |
| L | The inductance per unit length |
| C | The capacitance per unit length |
| G | The conductance per unit length |
| ω/f | Angular frequency/frequency |
| rc, rs | The core radius and the inner radius of the shield layer |
| ρc, ρs | The resistivity of the cable core and shield layer |
| μ0 | The vacuum permeability |
| σ, ε | The electrical conductivity and dielectric constant |
| Γ(ω) | The CTF |
| Z0, ZL | The characteristic impedance of the cable body and the load impedance at the terminal |
| r(ω) | The propagation coefficient of the signal in the cable |
| α(ω), β(ω) | The attenuation coefficient and the phase coefficient |
| v | The propagation speed of electromagnetic waves |
| x | The location of the defect |
| ga, gb, gc,, gd, fm | The amplitude factor, the time factor, the pulse width factor, the frequency modulation factor, and the central frequency |
Appendix A
| Case | Experimental Set-Up | Experimental Results |
|---|---|---|
| 1 | fm = 100 MHz, ga = 1 V, ga = 1 V, gb = 20 μs and gc = 0.4 μs | S-transform: 0.050% without cross-term WVD: 0.030% with cross-term |
| 2 | fm = 2.5 MHz, ga = 1 V, gb = 200 ns and gc = 0.4 ns | S-transform: 0.28% without cross-term WVD: 0.28% with cross-term |
References
- Xie, S.; Chen, Z.; Yan, Z.; Qiu, X.; Hu, M.; Gu, C.; Zhao, X.; Wang, K. Blending Modification Technology of Insulation Materials for Deep Sea Optoelectronic Composite Cables. Energies 2024, 17, 820. [Google Scholar] [CrossRef]
- Tang, Z.; Zhou, K.; Xu, Y.; Meng, P.; Zhang, H.; Wu, Y. A Reflection Coefficient Estimation Method for Power Cable Defects Based on Three-Point Interpolated FFT. IEEE Trans. Instrum. Meas. 2024, 73, 3505508. [Google Scholar] [CrossRef]
- Li, Z.; Dong, Y.; Wu, Y.; Meng, Z.; Song, P.; Zhu, M.; Li, X.; Du, B. Breakdown Performance Evaluation and Lifetime Prediction of XLPE Insulation in HVAC Cables. Energies 2024, 17, 1337. [Google Scholar] [CrossRef]
- Li, S.; Song, P.; Wei, Z.; Li, X.; Tang, Q.; Meng, Z.; Li, J.; Liu, S.; Wang, Y.; Li, J. Partial Discharge Detection and Defect Location Method in GIS Cable Terminal. Energies 2023, 16, 413. [Google Scholar] [CrossRef]
- Li, C.; Hu, J.; Lin, C.; Zhang, B.; Zhang, G.; He, J. Surface charge migration and dc surface flashover of surface-modified epoxy-based insulators. J. Phys. D Appl. Phys. 2017, 50, 065301. [Google Scholar] [CrossRef]
- Li, C.; Lin, C.; Chen, G.; Tu, Y.; Zhou, Y.; Li, Q.; Zhang, B.; He, J. Field-dependent charging phenomenon of HVDC spacers based on dominant charge behaviors. Appl. Phys. Lett. 2019, 114, 202904. [Google Scholar] [CrossRef]
- Ngui, Y.J.; Lin, C.-P. Self-Referencing TDR Dielectric Spectroscopy Using Reflection-Decoupled Analysis with a Mismatched Section. IEEE Trans. Instrum. Meas. 2022, 71, 1003415. [Google Scholar] [CrossRef]
- Tian, C.; Ye, D.; Xing, W. Research on Aging Performance and Mechanism Analysis of Cross-linked Polyethylene Wire and Cable Materials. In Proceedings of the 2021 IEEE International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Johor Bahru, Malaysia, 12–14 July 2021; p. 93. [Google Scholar]
- Li, W.; Zhou, W.; Fu, L.; Yuan, T. Cable Fault on-Line Monitoring Based on Transient Traveling Wave Signal Analysis Technology. In Proceedings of the 2023 IEEE 3rd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 29–31 January 2023; pp. 631–635. [Google Scholar] [CrossRef]
- Papazyan, R.; Eriksson, R. Calibration for time domain propagation constant measurements on power cables. IEEE Trans. Instrum. Meas. 2003, 52, 415–418. [Google Scholar] [CrossRef]
- Lee, C.-K.; Kwon, G.-Y.; Shin, Y.-J. Condition Assessment of I&C Cables in Nuclear Power Plants via Stepped-Frequency Waveform Reflectometry. IEEE Trans. Instrum. Meas. 2019, 68, 215–224. [Google Scholar] [CrossRef]
- Arman, A.S.; Ali, M.; Glass, S.W.; Fifield, L.S. Full-Wave and Circuit-Based Simulations of Cable Insulation Aging/Damage Using Time-Frequency Domain Reflectometry. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Vancouver, BC, Canada, 12–15 December 2021; pp. 531–534. [Google Scholar] [CrossRef]
- Zhou, K.; Tang, Z.; Meng, P.; Huang, J.; Xu, Y.; Rao, X. A Novel Method for Sign Judgment of Defects based on Phase Correction in Power Cable. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Huang, J.; Ju, D.; Chu, G.; Liang, Y.; Chen, C.; Chen, P. Localization of Typical Defects in 220kV XLPE Submarine Cable Based on Frequency Domain Reflection Technology. In Proceedings of the 2023 IEEE World Conference on Applied Intelligence and Computing (AIC), Sonbhadra, India, 29–30 July 2023; pp. 948–953. [Google Scholar] [CrossRef]
- Ohki, Y.; Hirai, N. Location attempt of a degraded portion in a long polymer-insulated cable. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 2461–2466. [Google Scholar] [CrossRef]
- Shi, Q.; Kanoun, O. Wire Fault Diagnosis in the Frequency Domain by Impedance Spectroscopy. IEEE Trans. Instrum. Meas. 2015, 64, 2179–2187. [Google Scholar] [CrossRef]
- Chen, C.; Guan, Q.; Guan, Q.; Jin, X.; Shi, Z. A Wavenumber Domain Reflectometry Approach to Locate and Image Line-Like Soft Faults in Cables. IEEE Trans. Instrum. Meas. 2023, 72, 6011012. [Google Scholar] [CrossRef]
- Tang, Z.; Zhou, K.; Meng, P.; Li, Y. A Frequency-Domain Location Method for Defects in Cables Based on Power Spectral Density. IEEE Trans. Instrum. Meas. 2022, 71, 9005110. [Google Scholar] [CrossRef]
- Lee, H.M.; Lee, G.S.; Kwon, G.-Y.; Bang, S.S.; Shin, Y.-J. Industrial Applications of Cable Diagnostics and Monitoring Cables via Time–Frequency Domain Reflectometry. IEEE Sens. J. 2021, 21, 1082–1091. [Google Scholar] [CrossRef]
- Zou, X.; Mu, H.; Wang, R.; Fan, K.; Cheng, Z.; He, Y.; Zhang, G. An efficient accuracy improvement method for cable defect location based on instantaneous filtering in time-frequency domain. Meas. J. Int. Meas. Confed. 2024, 226, 114178. [Google Scholar] [CrossRef]
- Kwon, G.-Y.; Lee, Y.H.; Bang, S.S.; Ji, G.H.; Lee, G.S.; Tamus, Z.A.; Shin, Y.-J. Assessment of Cable Aging for Nuclear Power Plants I&C Cable via Time-Frequency Domain Reflectometry. In Proceedings of the 2020 IEEE 3rd International Conference on Dielectrics (ICD), Valencia, Spain, 5–31 July 2020; pp. 77–80. [Google Scholar] [CrossRef]
- Tang, Z.; Xu, Y.; Zhou, K.; Meng, P.; Huang, J.; Liang, Z. A Frequency Sweep Location Method for Soft Faults of Power Cables Based on MUSIC-Pseudospectrum. IEEE Trans. Instrum. Meas. 2023, 72, 3510410. [Google Scholar] [CrossRef]
- Górecki, K.; Szmajda, M.; Zygarlicki, J.; Zygarlicka, M.; Mroczka, J. Zaawansowane metody analiz w pomiarach jakości energii elektrycznej. Pomiary Autom. Kontrola 2011, 57, 284–286. [Google Scholar]
- Shweta; Kishor, N. Time- Frequency Based Detection of Faulted Line and Fault Instant Using Wide Area Signals. In Proceedings of the 2019 International Conference on Electrical, Electronics and Computer Engineering, Aligarh, India, 8–10 November 2019; pp. 1–6. [Google Scholar]
- Asorza, J.E.G.; Leon Colqui, J.S.; Kurokawa, S.; Filho, J.P. Analysis of Increased Induced Voltages on the Sheath of Double-Circuit Underground Transmission Lines Guaranteeing Ampacity. Energies 2024, 17, 1637. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, K.; Xu, Y.; Meng, P.; Tang, Z.; Liang, Z. Upper Sweeping Frequency Selection for Cable Defect Location Based on STFT. IEEE Trans. Instrum. Meas. 2023, 72, 3521109. [Google Scholar] [CrossRef]
- Sathyanarayana, S.G.; Gargava, A.; Venkatesan, S.M. Parameterized transform domain computation of the Hilbert Transform applied to separation of channels in Doppler spectra. In Proceedings of the 2013 3rd IEEE International Advance Computing Conference (IACC), Ghaziabad, India, 22–23 February 2013; pp. 1189–1194. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Tian, S.; Li, Y. Fault location method of distribution network based on transient energy relative entropy of S-transform. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 2255–2259. [Google Scholar]





| Parameter | Value |
|---|---|
| Core radius rc/mm | 4 |
| Radius inside the shield rs/mm | 9.5 |
| Cable core resistivity ρc/(μΩ·mm) | 17.5 |
| Shield resistivity ρs/(μΩ·mm) | 17.5 |
| Conductivity of XLPE σ/(S·m) | 1 × 10−16 |
| Dielectric constant of XLPE ε/(F·m) | 2.4 × 10−11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Yang, Z.; Song, J.; Zhou, L.; Xiang, L.; Wang, X.; Hao, C.; Fan, X. A High-Resolution Defect Location Method for Medium-Voltage Cables Based on Gaussian Narrow-Band Envelope Signals and the S-Transform. Energies 2024, 17, 2218. https://doi.org/10.3390/en17092218
Chen W, Yang Z, Song J, Zhou L, Xiang L, Wang X, Hao C, Fan X. A High-Resolution Defect Location Method for Medium-Voltage Cables Based on Gaussian Narrow-Band Envelope Signals and the S-Transform. Energies. 2024; 17(9):2218. https://doi.org/10.3390/en17092218
Chicago/Turabian StyleChen, Wei, Zhenbao Yang, Jinyang Song, Lifu Zhou, Lingchen Xiang, Xing Wang, Changjin Hao, and Xianhao Fan. 2024. "A High-Resolution Defect Location Method for Medium-Voltage Cables Based on Gaussian Narrow-Band Envelope Signals and the S-Transform" Energies 17, no. 9: 2218. https://doi.org/10.3390/en17092218
APA StyleChen, W., Yang, Z., Song, J., Zhou, L., Xiang, L., Wang, X., Hao, C., & Fan, X. (2024). A High-Resolution Defect Location Method for Medium-Voltage Cables Based on Gaussian Narrow-Band Envelope Signals and the S-Transform. Energies, 17(9), 2218. https://doi.org/10.3390/en17092218





