Reinforcement Learning for Efficient Power Systems Planning: A Review of Operational and Expansion Strategies
Abstract
1. Introduction
- -
- Presents a detailed analysis of the most relevant publications on the use of RL and DRL in power system operation and expansion planning. The analysis is conducted using a systematic literature review methodology.
- -
- Identifies learning algorithms, function approximators, and reward functions used in the application of RL and DRL in power system operation and expansion planning. It also highlights relevant case studies to provide a comprehensive perspective on how these technologies are reshaping power system planning and operation.
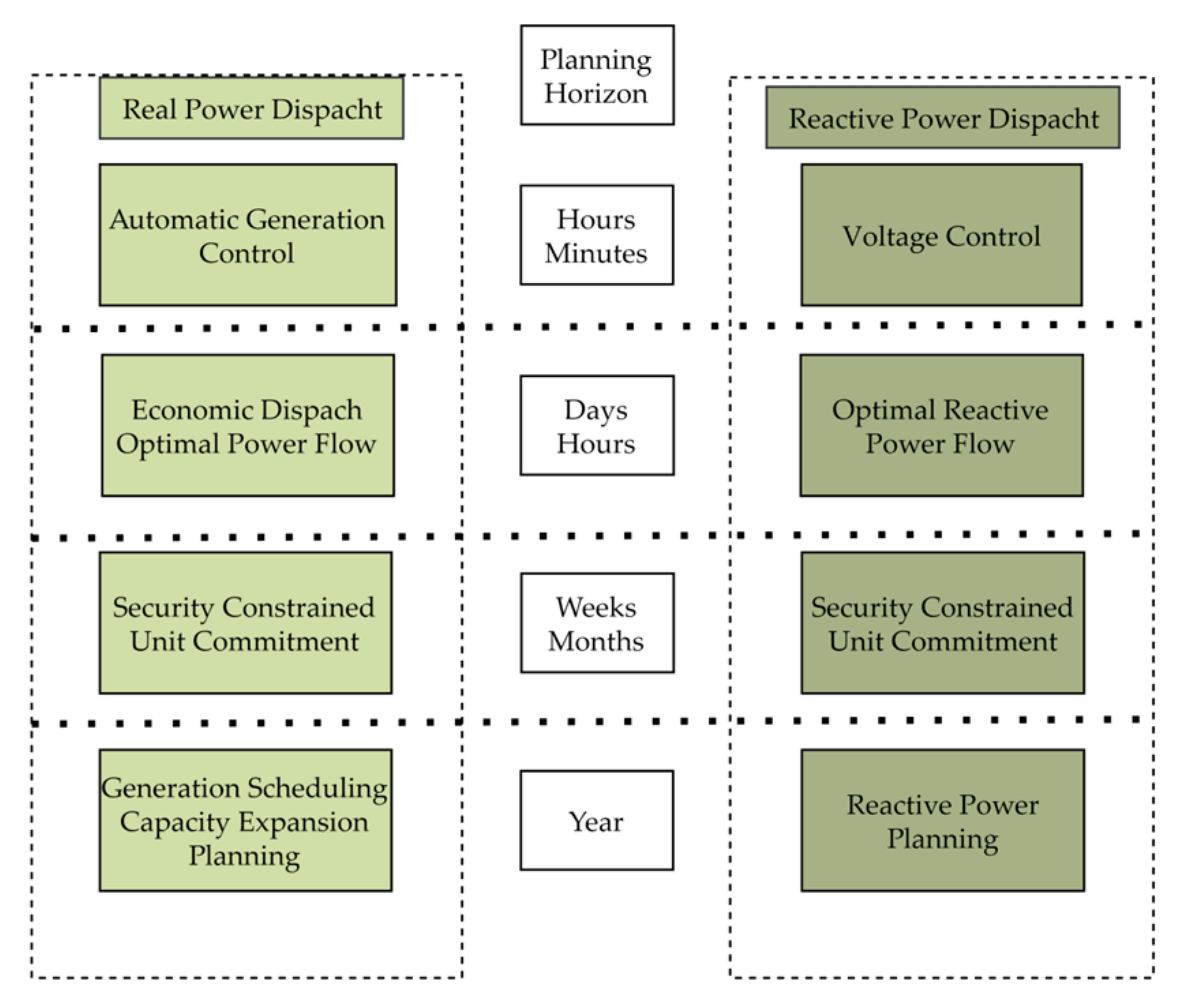
2. Reinforcement Learning (RL) Theoretical Background
2.1. Reinforcement Learning and Markov Decision Process
2.2. Classification of Reinforcement Learning Algorithms
2.3. Deep Reinforcement Learning
3. Research Methodology
- -
- The main interest of this review is the various works that implement RL and DRL to solve power system planning problems. In this study, the following research questions were addressed:
- ○
- RQ1: According to the literature, what are the applications of RL and DRL in solving the OPF problem?
- ○
- RQ2: According to the literature, what are the applications of RL and DRL in solving the ED and UC problems?
- ○
- RQ3: According to the literature, what are the applications of RL and DRL in TNEP and DNEP?
- -
- In this study, data were collected using a search string optimized to find the most relevant literature. A total of four digital repositories were selected based on the analysis presented in [27]. The selected digital repositories were:
- ○
- IEEE Xplore;
- ○
- ScienceDirect;
- ○
- Springer Link;
- ○
- Wiley Online Library;
- ○
- MDPI.
- -
- A search string was generated based on the study questions to retrieve the relevant literature from the selected digital sources, called primary studies. The following string was used to search the digital repositories: ((“Power Systems Planning” OR “OPF” OR “Economic Dispatch” OR “Generation Expansion Planning” OR “Transmission Expansion Planning” OR “Distribution Expansion Planning” OR “Grid Planning”) AND (“Reinforcement Learning” OR “Deep Reinforcement Learning”)).
- -
- For data inclusion, we adopted the following guidelines:
- Papers related to the field of Power and Energy Systems;
- English language;
- Journal papers and conference papers;
- Articles published between 2016 and 2024;
- Full text available online;
- Available in one or more of the selected databases;
- Focus on Power Systems Planning: OPF, ED, UC, TNEP, DNEP;
- RL or DRL mentioned in the abstract;
- Relationship between RL or DRL and power systems planning.
- -
- The quality assessment in this study focused on determining the usefulness of the primary studies selected to answer the research questions posed. Simultaneously, data extraction and quality assessment of the selected publications were conducted. To ensure an objective assessment, a checklist was developed (provided in Table 2). This checklist included five quality criteria (Q1–Q5) designed to examine each primary study comprehensively.
- ○
- Articles that fully met each criterion on the checklist were given a score of 1.00;
- ○
- Articles that partially met a criterion received a score of 0.50;
- ○
- Those not addressing a specific criterion on the list received a score of 0.00.
| Questions | Checklist Questions |
|---|---|
| Q1 | Does this paper address issues related to OPF, ED, or GP, whose solution is found by applying RL or DRL technique implementation methodologies? |
| Q2 | Are the learning algorithm, function approximator, agent type, metrics to evaluate algorithm performance, and reward function clearly identified? |
| Q3 | Are the contributions of the document to power system planning clearly stated? |
| Q4 | Is a case study used to validate the methodology presented? |
| Q5 | Are the limitations of the study mentioned? |
- -
- The results shown in Table 3 were obtained based on the considered inclusion criteria. Two additional specific search filters were applied: the first filter considered the search string for the abstract, and the second filter exclusively for the abstract and title, thus obtaining 55 papers.
- -
- Appendix A presents the complete list of articles reviewed and the score assigned to each, from which 45 papers were selected and classified into three groups: optimal power flow, economic dispatch and unit commitment, and power systems expansion planning, which includes TNEP and DNEP.
4. RL and DRL Applications in Power Systems Operation and Expansion Planning
4.1. Optimal Power Flow
4.2. Economic Dispatch and Unit Commitment
4.3. RL and DRL Applications in Power Systems Expansion Planning
5. Discussion
6. Conclusions
- -
- The use of RL and DRL in power system operation and planning is a relatively recent development. In this study, RL and DRL algorithms applied to problems such as OPF, ED, UC, and expansion planning have been examined in detail. In all of these areas, the results indicate that RL and DRL algorithms outperform conventional methods, especially in terms of efficiency in computational time.
- -
- The metrics used to evaluate the performance of RL and DRL algorithms in the context of electrical power systems are not uniform. Many of the studies reviewed in this paper resorted to the mean absolute error (MAE) to compare their results with solutions obtained from traditional optimization methods. In addition, the use of average reward was common, reflecting the intrinsic nature of RL problems, which seek to maximize the reward.
- -
- The strategies and approximation functions used in DRL and RL for planning electrical systems converge on a common goal: minimizing the costs associated with generation, network operation, and the construction of new infrastructure. However, there is significant potential to extend their application to additional objectives such as minimizing CO2 emissions and maximizing network reliability.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbreviations | |
| RL | Reinforcement learning |
| MDP | Markov decision process |
| DRL | Deep reinforcement learning |
| ML | Machine learning |
| SAC | Soft actor-critic |
| OPF | Optimal power flow |
| UC | Unit commitment |
| ED | Economic dispatch |
| TNEP | Transmission network expansion planning |
| PEM | Point estimate method |
| NN | Neural network |
| PPO | Proximal policy optimization |
| Sets, indices, and dimensions | |
| Set of Busbar system | |
| Set of branch | |
| Tuple containing the state space, agent, policy, and reward. | |
| Set of generators | |
| Action Space | |
| State space | |
| Rewards Space | |
| Parameters | |
| Lagrange Vector | |
| Variables | |
| (radians) | |
| (radians) | |
| (radians) | |
Appendix A
| Item | Ref. | Paper Title | Year | Data Sources | Q1 | Q2 | Q3 | Q4 | Q5 | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | [9] | Reinforcement learning-based solution to power grid planning and operation under uncertainties | 2020 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5.0 |
| 2 | [34] | Deep reinforcement learning based approach for optimal power flow of distribution networks embedded with renewable energy and storage devices | 2021 | IEEE Xplore | 1.0 | 1.0 | 0.5 | 1.0 | 0.5 | 4.0 |
| 3 | [22] | A data-driven method for fast AC optimal power flow solutions via deep reinforcement learning | 2020 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 0.0 | 4.0 |
| 4 | [35] | Deep reinforcement learning based real-time AC optimal power flow considering uncertainties | 2022 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5.0 |
| 5 | [36] | Real-time optimal power flow: A Lagrangian-based deep reinforcement learning | 2020 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5.0 |
| 6 | [37] | Distributed optimal power flow for electric power systems with high penetration of distributed energy resources | 2019 | IEEE Xplore | 1.0 | 1.0 | 0.5 | 1.0 | 0.5 | 4.0 |
| 7 | [20] | A general real-time OPF algorithm using DDPG with multiple simulation platforms | 2019 | Wiley Online Library | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | 4.0 |
| 8 | [38] | Two-level area-load modeling for OPF of power system using reinforcement learning | 2019 | Wiley Online Library | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 9 | [39] | Markov game approach for multi-agent competitive bidding strategies in the electricity market | 2016 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 0.5 | 0.0 | 3.5 |
| 10 | [46] | Distributed Q-learning-based online optimization algorithm for unit commitment and dispatch in smart grid | 2020 | IEEE Xplore | 1.0 | 1.0 | 0.50 | 1.0 | 1.0 | 4.5 |
| 11 | [47] | Day-ahead optimal dispatch strategy for active distribution network based on improved deep reinforcement learning | 2022 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5 |
| 12 | [48] | Nash-Q learning-based collaborative dispatch strategy for interconnected power systems | 2020 | IEEE Xplore | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | 4.0 |
| 13 | [45] | Solving unit commitment problems with multi-step deep reinforcement learning | 2021 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 0.0 | 4.0 |
| 14 | [49] | Optimal dispatch of PV inverters in unbalanced distribution systems using reinforcement learning | 2022 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5.0 |
| 15 | [87] | Evaluation of look-ahead economic dispatch using reinforcement learning | 2022 | ScienceDirect | 1.0 | 0.5 | 0.5 | 1.0 | 0.5 | 3.5 |
| 16 | [50] | Multi-objective optimization of the environmental-economic dispatch with reinforcement learning based on a non-dominated sorting genetic algorithm | 2019 | IEEE Xplore | 1.0 | 1.0 | 0.5 | 1.0 | 0.5 | 4.0 |
| 17 | [88] | Deep reinforcement learning for scenario-based robust economic dispatch strategy in Internet of energy | 2021 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 0.0 | 0.5 | 3.5 |
| 18 | [89] | Deep reinforcement learning for economic dispatch of virtual power plant in Internet of energy | 2020 | Wiley Online Library | 1.0 | 1.0 | 1.0 | 0.5 | 0.0 | 3.5 |
| 19 | [51] | The distributed economic dispatch of smart grid based on deep reinforcement learning | 2021 | Wiley Online Library | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 4.5 |
| 20 | [52] | Low-carbon economic dispatch of the combined heat and power-virtual power plants: An improved deep reinforcement learning-based approach | 2023 | Wiley Online Library | 1.0 | 1.0 | 0.5 | 1.0 | 1.0 | 4.5 |
| 21 | [90] | Hierarchical learning optimization method for the coordination dispatch of the inter-regional power grid considering the quality-of-service index | 2020 | Wiley Online Library | 1.0 | 1.0 | 1.0 | 0.5 | 0.0 | 3.5 |
| 22 | [39] | Markov game approach for multi-agent competitive bidding strategies in the electricity market | 2016 | Wiley Online Library | 1.0 | 1.0 | 1.0 | 0.5 | 0.5 | 4.0 |
| 23 | [70] | A deep reinforcement learning-based multi-agent framework to enhance power system resilience using shunt resources | 2021 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 0.50 | 4.5 |
| 24 | [53] | Deep-Q-network-based intelligent reschedule for power system operational planning | 2020 | IEEE Xplore | 1.0 | 1.0 | 0.50 | 1.0 | 0.50 | 4.0 |
| 25 | [71] | Transmission network dynamic planning based on a double deep-Q network with deep ResNet | 2021 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 0.50 | 4.5 |
| 26 | [72] | Reinforcement learning for active distribution network planning based on Monte Carlo tree search. | 2022 | MDPI | 1.0 | 1.0 | 1.0 | 1.0 | 0.50 | 4.5 |
| 27 | [73] | Flexible transmission network expansion planning based on DQN algorithm | 2021 | MDPI | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5.0 |
| 28 | [74] | Transmission network expansion planning considering wind power and load uncertainties based on multi-agent DDQN | 2021 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5.0 |
| 29 | [75] | A storage expansion planning framework using reinforcement learning and simulation-based optimization | 2021 | ScienceDirect | 1.0 | 1.0 | 1.0 | 0.50 | 0.50 | 4.0 |
| 30 | [91] | Machine learning approaches to the unit commitment problem: Current trends, emerging challenges, and new strategies | 2021 | IEEE Xplore | 1.0 | 0.5 | 0.5 | 0.5 | 0.0 | 2.5 |
| 31 | [49] | Optimal dispatch of PV inverters in unbalanced distribution systems using reinforcement learning | 2022 | IEEE Xplore | 1.0 | 1.0 | 1.0 | 0.50 | 0.0 | 3.5 |
| 32 | [40] | Reactive power optimization of distribution network based on deep reinforcement learning and multi-agent system | 2021 | IEEE Xplore | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 4.5 |
| 33 | [54] | A graph-based deep reinforcement learning framework for autonomous power dispatch on power systems with changing topologies | 2022 | IEEE Xplore | 1.0 | 1.0 | 0.5 | 1.0 | 0.5 | 4 |
| 34 | [92] | A new power system dispatching optimization method based on reinforcement learning | 2023 | IEEE Xplore | 1.0 | 0.5 | 0.5 | 0.0 | 1.0 | 3 |
| 35 | [41] | Reinforcement learning-based optimal power flow of distribution networks with high permeation of distributed PVs | 2023 | IEEE Xplore | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 4.5 |
| 36 | [76] | Application of improved reinforcement learning technology for real time operation and scheduling optimization of virtual power plant | 2023 | SpringerLink | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 4.5 |
| 37 | [77] | Planning for network expansion based on prim algorithm and reinforcement learning | 2023 | SpringerLink | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 38 | [78] | Integrating distributed generation and advanced deep learning for efficient distribution system management and fault detection | 2024 | MDPI | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 39 | [79] | Solving dynamic distribution network reconfiguration using deep reinforcement learning | 2021 | MDPI | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 40 | [60] | Bacteria foraging reinforcement learning for risk-based economic dispatch via knowledge transfer | 2017 | MDPI | 1.0 | 1.0 | 0.5 | 1.0 | 0.5 | 4 |
| 41 | [55] | Research on data-driven optimal scheduling of power system | 2023 | MDPI | 1.0 | 0.5 | 1.0 | 0.5 | 1.0 | 4 |
| 42 | [56] | Deep-reinforcement-learning-based low-carbon economic dispatch for community-integrated energy system under multiple uncertainties | 2023 | SpringerLink | 1.0 | 1.0 | 1.0 | 0.5 | 0.5 | 4 |
| 43 | [57] | Unlocking the flexibility of district heating pipeline energy storage with reinforcement learning | 2022 | MDPI | 1.0 | 1.0 | 1.0 | 0.0 | 1.0 | 4 |
| 44 | [58] | Towards reinforcement learning for vulnerability analysis in power-economic systems | 2021 | ScienceDirect | 1.0 | 0.5 | 1.0 | 1.0 | 1.0 | 4.5 |
| 45 | [59] | A deep reinforcement learning method for economic power dispatch of microgrid in OPAL-RT environment | 2023 | ScienceDirect | 1.0 | 1.0 | 1.0 | 0.5 | 1.0 | 4.5 |
| 46 | [61] | Deep reinforcement learning approaches for the hydro-thermal economic dispatch problem considering the uncertainties of the context | 2023 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 47 | [62] | Solving large-scale combined heat and power economic dispatch problems by using deep reinforcement learning-based crisscross optimization algorithm | 2024 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 5 |
| 48 | [63] | Adaptive look-ahead economic dispatch based on deep reinforcement learning | 2024 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 49 | [64] | Economic dispatch of industrial park considering uncertainty of renewable energy based on a deep reinforcement learning approach | 2023 | ScienceDirect | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | 4 |
| 50 | [65] | Combined heat and power system intelligent economic dispatch: A deep reinforcement learning approach | 2020 | ScienceDirect | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | 4 |
| 51 | [42] | Multi-objective solution of optimal power flow based on TD3 deep reinforcement learning algorithm | 2023 | ScienceDirect | 1.0 | 0.5 | 1.0 | 0.5 | 1.0 | 4 |
| 52 | [43] | Real-time operation of distribution network: A deep reinforcement learning-based reconfiguration approach | 2022 | ScienceDirect | 1.0 | 1.0 | 1.0 | 1.0 | 0.5 | 4.5 |
| 53 | [44] | Multi-agent deep reinforcement learning for resilience-driven routing and scheduling of mobile energy storage systems | 2022 | ScienceDirect | 1.0 | 0.5 | 1.0 | 1.0 | 0.5 | 4 |
| 54 | [93] | A scalable graph reinforcement learning algorithm based stochastic dynamic dispatch of power system under high penetration of renewable energy Junbin | 2023 | ScienceDirect | 1.0 | 0.5 | 1.0 | 1.0 | 0.0 | 3.5 |
| 55 | [94] | Emergency fault affected wide-area automatic generation control via large-scale deep reinforcement learning | 2021 | ScienceDirect | 0.0 | 1.0 | 1.0 | 1.0 | 0.5 | 3.5 |
References
- Wood, A.; Wollemberg, B.; Sheblé, G. Power Generation, Operation and Control, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; ISBN 9780471790556. [Google Scholar]
- Glover, J.D.; Overbye, T.J.; Sarma, M.S. Power System Analysis and Design, 6th ed.; Cengage Learning: Boston, MA, USA, 2017; ISBN 9781305632134. [Google Scholar]
- Natividad, L.E.; Benalcazar, P. Hybrid Renewable Energy Systems for Sustainable Rural Development: Perspectives and Challenges in Energy Systems Modeling. Energies 2023, 16, 1328. [Google Scholar] [CrossRef]
- Conejo, A.J.; Baringo Morales, L.; Kazempour, S.J.; Siddiqui, A.S. Investment in Electricity Generation and Transmission; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 9783319294995. [Google Scholar]
- Cordova-Garcia, J.; Wang, X. Robust Power Line Outage Detection with Unreliable Phasor Measurements. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 1309–1319. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, D.; Qiu, R.C. Deep Reinforcement Learning for Power System: An Overview. CSEE J. Power Energy Syst. 2019, 6, 213–225. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Zhao, J.; Zhang, G.; Zhang, B.; Liu, Z.; Chen, Z.; Blaabjerg, F. Reinforcement Learning and Its Applications in Modern Power and Energy Systems: A Review. J. Mod. Power Syst. Clean Energy 2020, 8, 1029–1042. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Asadi, S.; Abdar, B.M.-I.M.; Jebelli, H.; Sadat-Mohammadi, M. Application of Machine Learning and Deep Learning Methods to Power System Problems; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 9783030776954. [Google Scholar]
- Shang, X.; Ye, L.; Zhang, J.; Yang, J.; Xu, J.; Lyu, Q.; Diao, R. Reinforcement Learning-Based Solution to Power Grid Planning and Operation Under Uncertainties. In Proceedings of the 2020 IEEE/ACM Workshop on Machine Learning in High Performance Computing Environments (MLHPC) and Workshop on Artificial Intelligence and Machine Learning for Scientific Applications (AI4S), Atlanta, GA, USA, 12 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 72–79. [Google Scholar]
- Glavic, M.; Fonteneau, R.; Ernst, D. Reinforcement Learning for Electric Power System Decision and Control: Past Considerations and Perspectives. IFAC-PapersOnLine 2017, 50, 6918–6927. [Google Scholar] [CrossRef]
- Arwa, E.O.; Folly, K.A. Reinforcement Learning Techniques for Optimal Power Control in Grid-Connected Microgrids: A Comprehensive Review. IEEE Access 2020, 8, 208992–209007. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Kamalaruban, P. Applications of Reinforcement Learning in Energy Systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, N. Deep Reinforcement Learning in Power Distribution Systems: Overview, Challenges, and Opportunities. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–18 February 2021; pp. 1–5. [Google Scholar]
- Khodayar, M.; Liu, G.; Wang, J.; Khodayar, M.E. Deep Learning in Power Systems Research: A Review. CSEE J. Power Energy Syst. 2021, 7, 209–220. [Google Scholar] [CrossRef]
- Frank, S.; Rebennack, S. An Introduction to Optimal Power Flow: Theory, Formulation, and Examples. IIE Trans. 2016, 48, 1172–1197. [Google Scholar] [CrossRef]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. arXiv 2022, arXiv:2102.01168. [Google Scholar] [CrossRef]
- Wang, Y.; Chai, B.; Lu, W.; Zheng, X. A Review of Deep Reinforcement Learning Applications in Power System Parameter Estimation. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 8–9 December 2021. [Google Scholar] [CrossRef]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; Bach, F., Ed.; The MIT Press: Cambridge, MA, USA, 2020; ISBN 9780262039246. [Google Scholar]
- Coronado, C.A.; Figueroa, M.R.; Roa-Sepulveda, C.A. A Reinforcement Learning Solution for the Unit Commitment Problem. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), Uxbridge, UK, 4–7 September 2012; pp. 2–7. [Google Scholar] [CrossRef]
- Nie, H.; Chen, Y.; Song, Y.; Huang, S. A General Real-Time OPF Algorithm Using DDPG with Multiple Simulation Platforms. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3713–3718. [Google Scholar]
- Sanghi, N. Deep Reinforcement Learning with Python; Apress: New York, NY, USA, 2021; ISBN 9781484268087. [Google Scholar]
- Zhou, Y.; Zhang, B.; Xu, C.; Lan, T.; Diao, R.; Shi, D.; Wang, Z.; Lee, W.-J. A Data-Driven Method for Fast AC Optimal Power Flow Solutions via Deep Reinforcement Learning. J. Mod. Power Syst. Clean Energy 2020, 8, 1128–1139. [Google Scholar] [CrossRef]
- Kitchenham, B.; Charters, S. Guidelines for Performing Systematic Literature Reviews in Software Engineering; EBSE Technical Report; Version 2.3; Elsevier: Amsterdam, The Netherlands, 2007; Volume 1, pp. 1–54. [Google Scholar]
- Al Naqbi, A.; Alyieliely, S.S.; Talib, M.A.; Nasir, Q.; Bettayeb, M.; Ghenai, C. Energy Reduction in Building Energy Management Systems Using the Internet of Things: Systematic Literature Review. In Proceedings of the2021 International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Chiu, P.C.; Selamat, A.; Krejcar, O.; Kuok, K.K.; Bujang, S.D.A.; Fujita, H. Missing Value Imputation Designs and Methods of Nature-Inspired Metaheuristic Techniques: A Systematic Review. IEEE Access 2022, 10, 61544–61566. [Google Scholar] [CrossRef]
- Mendoza-Pitti, L.; Calderon-Gomez, H.; Vargas-Lombardo, M.; Gomez-Pulido, J.M.; Castillo-Sequera, J.L. Towards a Service-Oriented Architecture for the Energy Efficiency of Buildings: A Systematic Review. IEEE Access 2021, 9, 26119–26137. [Google Scholar] [CrossRef]
- Khan, R.A.; Khan, S.U.; Khan, H.U.; Ilyas, M. Systematic Literature Review on Security Risks and Its Practices in Secure Software Development. IEEE Access 2022, 10, 5456–5481. [Google Scholar] [CrossRef]
- Kim, J.Y.; Kim, K.S. Integrated Model of Economic Generation System Expansion Plan for the Stable Operation of a Power Plant and the Response of Future Electricity Power Demand. Sustainability 2018, 10, 2417. [Google Scholar] [CrossRef]
- Ebeed, M.; Kamel, S.; Jurado, F. Optimal Power Flow Using Recent Optimization Techniques; Elsevier Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780128124420. [Google Scholar]
- Guamán, W.P.; Pesántez, G.N.; Torres R․, M.A.; Falcones, S.; Urquizo, J. Optimal Dynamic Reactive Power Compensation in Power Systems: Case Study of Ecuador-Perú Interconnection. Electr. Power Syst. Res. 2023, 218, 109191. [Google Scholar] [CrossRef]
- Carpentier, J. Contribution a.’l’etude Du Dispatching Economique. Bull. Soc. Fr. Electr. 1962, 3, 431–447. [Google Scholar]
- Hasan, F.; Kargarian, A.; Mohammadi, A. A Survey on Applications of Machine Learning for Optimal Power Flow. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, J.; Xue, Y.; Dong, Z.Y.; Wong, K.P. An Adaptive Importance Sampling Method for Probabilistic Optimal Power Flow. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, D.; Hu, W.; Xu, X.; Wu, Q.; Huang, Q.; Chen, Z.; Blaabjerg, F. Deep Reinforcement Learning Based Approach for Optimal Power Flow of Distribution Networks Embedded with Renewable Energy and Storage Devices. J. Mod. Power Syst. Clean Energy 2021, 9, 1101–1110. [Google Scholar] [CrossRef]
- Zhou, Y.; Lee, W.; Diao, R.; Shi, D. Deep Reinforcement Learning Based Real-Time AC Optimal Power Flow Considering Uncertainties. J. Mod. Power Syst. Clean Energy 2022, 10, 1098–1109. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. Real-Time Optimal Power Flow: A Lagrangian Based Deep Reinforcement Learning Approach. IEEE Trans. Power Syst. 2020, 35, 3270–3273. [Google Scholar] [CrossRef]
- Al-Saffar, M.; Musilek, P. Distributed Optimal Power Flow for Electric Power Systems with High Penetration of Distributed Energy Resources. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Jiang, C.; Li, Z.; Zheng, J.H.; Wu, Q.H.; Shang, X. Two-level Area-load Modelling for OPF of Power System Using Reinforcement Learning. IET Gener. Transm. Distrib. 2019, 13, 4141–4149. [Google Scholar] [CrossRef]
- Rashedi, N.; Tajeddini, M.A.; Kebriaei, H. Markov Game Approach for Multi-agent Competitive Bidding Strategies in Electricity Market. IET Gener. Transm. Distrib. 2016, 10, 3756–3763. [Google Scholar] [CrossRef]
- Gao, Z.; Zheng, Z.; Wu, J.; Qi, L.; Li, W.; Yang, Y. Reactive Power Optimization of Distribution Network Based on Deep Reinforcement Learning and Multi Agent System. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1052–1057. [Google Scholar]
- Yao, Z.; Chen, W.; Sun, L.; Wu, X. Reinforcement Learning-Based Optimal Power Flow of Distribution Networks with High Permeation of Distributed PVs. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3421–3426. [Google Scholar]
- Sun, B.; Song, M.; Li, A.; Zou, N.; Pan, P.; Lu, X.; Yang, Q.; Zhang, H.; Kong, X. Multi-Objective Solution of Optimal Power Flow Based on TD3 Deep Reinforcement Learning Algorithm. Sustain. Energy Grids Netw. 2023, 34, 101054. [Google Scholar] [CrossRef]
- Bui, V.-H.; Su, W. Real-Time Operation of Distribution Network: A Deep Reinforcement Learning-Based Reconfiguration Approach. Sustain. Energy Technol. Assess. 2022, 50, 101841. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, D.; Strbac, G. Multi-agent deep reinforcement learning for resilience-driven routing and scheduling of mobile energy storage systems. Appl. Energy 2022, 310, 118575. [Google Scholar] [CrossRef]
- Qin, J.; Yu, N.; Gao, Y. Solving Unit Commitment Problems with Multi-Step Deep Reinforcement Learning. In Proceedings of the 2021 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aachen, Germany, 25–28 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 140–145. [Google Scholar]
- Li, F.; Qin, J.; Zheng, W.X. Distributed Q-Learning-Based Online Optimization Algorithm for Unit Commitment and Dispatch in Smart Grid. IEEE Trans. Cybern. 2020, 50, 4146–4156. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Han, X.; Yang, M. Day-Ahead Optimal Dispatch Strategy for Active Distribution Network Based on Improved Deep Reinforcement Learning. IEEE Access 2022, 10, 9357–9370. [Google Scholar] [CrossRef]
- Li, R.; Han, Y.; Ma, T.; Liu, H. Nash-Q Learning-Based Collaborative Dispatch Strategy for Interconnected Power Systems. Glob. Energy Interconnect. 2020, 3, 227–236. [Google Scholar] [CrossRef]
- Vergara, P.P.; Salazar, M.; Giraldo, J.S.; Palensky, P. Optimal Dispatch of PV Inverters in Unbalanced Distribution Systems Using Reinforcement Learning. Int. J. Electr. Power Energy Syst. 2022, 136, 107628. [Google Scholar] [CrossRef]
- Bora, T.C.; Mariani, V.C.; dos Santos Coelho, L. Multi-Objective Optimization of the Environmental-Economic Dispatch with Reinforcement Learning Based on Non-Dominated Sorting Genetic Algorithm. Appl. Therm. Eng. 2019, 146, 688–700. [Google Scholar] [CrossRef]
- Fu, Y.; Guo, X.; Mi, Y.; Yuan, M.; Ge, X.; Su, X.; Li, Z. The Distributed Economic Dispatch of Smart Grid Based on Deep Reinforcement Learning. IET Gener. Transm. Distrib. 2021, 15, 2645–2658. [Google Scholar] [CrossRef]
- Tan, Y.; Shen, Y.; Yu, X.; Lu, X. Low-carbon Economic Dispatch of the Combined Heat and Power-virtual Power Plants: A Improved Deep Reinforcement Learning-based Approach. IET Renew. Power Gener. 2023, 17, 982–1007. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Qiu, G.; Gu, Y.; Li, H.; Liu, J. Deep-Q-Network-Based Intelligent Reschedule for Power System Operational Planning. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Zhao, Y.; Liu, J.; Liu, X.; Yuan, K.; Ren, K.; Yang, M. A Graph-Based Deep Reinforcement Learning Framework for Autonomous Power Dispatch on Power Systems with Changing Topologies. In Proceedings of the 2022 IEEE Sustainable Power and Energy Conference (iSPEC), Perth, Australia, 4–7 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Luo, J.; Zhang, W.; Wang, H.; Wei, W.; He, J. Research on Data-Driven Optimal Scheduling of Power System. Energies 2023, 16, 2926. [Google Scholar] [CrossRef]
- Mo, M.; Xiong, X.; Wu, Y.; Yu, Z. Deep-Reinforcement-Learning-Based Low-Carbon Economic Dispatch for Community-Integrated Energy System under Multiple Uncertainties. Energies 2023, 16, 7669. [Google Scholar] [CrossRef]
- Stepanovic, K.; Wu, J.; Everhardt, R.; de Weerdt, M. Unlocking the Flexibility of District Heating Pipeline Energy Storage with Reinforcement Learning. Energies 2022, 15, 3290. [Google Scholar] [CrossRef]
- Wolgast, T.; Veith, E.M.; Nieße, A. Towards Reinforcement Learning for Vulnerability Analysis in Power-Economic Systems. Energy Inform. 2021, 4, 21. [Google Scholar] [CrossRef]
- Lin, F.-J.; Chang, C.-F.; Huang, Y.-C.; Su, T.-M. A Deep Reinforcement Learning Method for Economic Power Dispatch of Microgrid in OPAL-RT Environment. Technologies 2023, 11, 96. [Google Scholar] [CrossRef]
- Han, C.; Yang, B.; Bao, T.; Yu, T.; Zhang, X. Bacteria Foraging Reinforcement Learning for Risk-Based Economic Dispatch via Knowledge Transfer. Energies 2017, 10, 638. [Google Scholar] [CrossRef]
- Arango, A.R.; Aguilar, J.; R-Moreno, M.D. Deep Reinforcement Learning Approaches for the Hydro-Thermal Economic Dispatch Problem Considering the Uncertainties of the Context. Sustain. Energy Grids Netw. 2023, 35, 101109. [Google Scholar] [CrossRef]
- Meng, A.; Rong, J.; Yin, H.; Luo, J.; Tang, Y.; Zhang, H.; Li, C.; Zhu, J.; Yin, Y.; Li, H.; et al. Solving Large-Scale Combined Heat and Power Economic Dispatch Problems by Using Deep Reinforcement Learning Based Crisscross Optimization Algorithm. Appl. Therm. Eng. 2024, 245, 122781. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, H.; Zhang, G.; Ruan, G.; He, Y.; Yu, Z. Adaptive Look-Ahead Economic Dispatch Based on Deep Reinforcement Learning. Appl. Energy 2024, 353, 122121. [Google Scholar] [CrossRef]
- Feng, J.; Wang, H.; Yang, Z.; Chen, Z.; Li, Y.; Yang, J.; Wang, K. Economic Dispatch of Industrial Park Considering Uncertainty of Renewable Energy Based on a Deep Reinforcement Learning Approach. Sustain. Energy Grids Netw. 2023, 34, 101050. [Google Scholar] [CrossRef]
- Zhou, S.; Hu, Z.; Gu, W.; Jiang, M.; Chen, M.; Hong, Q.; Booth, C. Combined Heat and Power System Intelligent Economic Dispatch: A Deep Reinforcement Learning Approach. Int. J. Electr. Power Energy Syst. 2020, 120, 106016. [Google Scholar] [CrossRef]
- Ahrari Nouri, M.; Hesami, A.; Seifi, A. Reactive Power Planning in Distribution Systems Using a Reinforcement Learning Method. In Proceedings of the 2007 International Conference on Intelligent and Advanced Systems, Kuala Lumpur, Malaysia, 25–28 November 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 157–161. [Google Scholar]
- MingKui, W.; ShaoRong, C.; Quan, Z.; Xu, Z.; Hong, Z.; YuHong, W. Multi-Objective Transmission Network Expansion Planning Based on Reinforcement Learning. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2348–2353. [Google Scholar]
- Choi, J.; Lee, K. Probabilistic Power System Expansion Planning with Renewable Energy Resources and Energy Storage Systems; IEEE Press Editorial Board, Ed.; Wiley: Hoboken, NJ, USA, 2022; ISBN 9781119684138. [Google Scholar]
- Papadimitrakis, M.; Giamarelos, N.; Stogiannos, M.; Zois, E.N.; Livanos, N.A.-I.; Alexandridis, A. Metaheuristic Search in Smart Grid: A Review with Emphasis on Planning, Scheduling and Power Flow Optimization Applications. Renew. Sustain. Energy Rev. 2021, 145, 111072. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Duan, J.; Shi, D.; Benidris, M. A Deep Reinforcement Learning-Based Multi-Agent Framework to Enhance Power System Resilience Using Shunt Resources. IEEE Trans. Power Syst. 2021, 36, 5525–5536. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Zhou, H.; Chen, L.; Zheng, Z.; Zeng, Q.; Cai, S.; Wang, Q. Transmission Network Dynamic Planning Based on a Double Deep-Q Network With Deep ResNet. IEEE Access 2021, 9, 76921–76937. [Google Scholar] [CrossRef]
- Zhang, X.; Hua, W.; Liu, Y.; Duan, J.; Tang, Z.; Liu, J. Reinforcement Learning for Active Distribution Network Planning Based on Monte Carlo Tree Search. Int. J. Electr. Power Energy Syst. 2022, 138, 107885. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Zhou, H.; Zhou, X.; Zheng, Z.; Zeng, Q.; Jiang, L.; Lu, L. Flexible Transmission Network Expansion Planning Based on DQN Algorithm. Energies 2021, 14, 1944. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Shi, Y.; Zheng, Z.; Zeng, Q.; Chen, L.; Xiang, B.; Huang, R. Transmission Network Expansion Planning Considering Wind Power and Load Uncertainties Based on Multi-Agent DDQN. Energies 2021, 14, 6073. [Google Scholar] [CrossRef]
- Tsianikas, S.; Yousefi, N.; Zhou, J.; Rodgers, M.D.; Coit, D. A Storage Expansion Planning Framework Using Reinforcement Learning and Simulation-Based Optimization. Appl. Energy 2021, 290, 116778. [Google Scholar] [CrossRef]
- Chao, F.A.Z.; Ying, S.B.Z.; Yu, T.C.J. Application of Improved Reinforcement Learning Technology for Real Time Operation and Scheduling Optimization of Virtual Power Plant. In Proceedings of the 2023 IEEE Sustainable Power and Energy Conference (iSPEC), Chongqing, China, 28–30 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Dong, F.; Li, Z.; Xu, Y.; Zhu, D.; Huang, R.; Zou, H.; Wu, Z.; Wang, X. Planning for Network Expansion Based on Prim Algorithm and Reinforcement Learning. In Proceedings of the 2023 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chongqing, China, 7–9 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 252–258. [Google Scholar]
- Bhatnagar, M.; Yadav, A.; Swetapadma, A. Integrating Distributed Generation and Advanced Deep Learning for Efficient Distribution System Management and Fault Detection. Arab. J. Sci. Eng. 2024, 49, 7095–7111. [Google Scholar] [CrossRef]
- Kundačina, O.B.; Vidović, P.M.; Petković, M.R. Solving Dynamic Distribution Network Reconfiguration Using Deep Reinforcement Learning. Electr. Eng. 2022, 104, 1487–1501. [Google Scholar] [CrossRef]
- Davis, J.V.; Dhillon, I.S. Structured Metric Learning for High Dimensional Problems. In Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 195–203. [Google Scholar] [CrossRef]
- Hossin, M.; Sulaiman, M. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Koltsaklis, N.E.; Dagoumas, A.S. State-of-the-Art Generation Expansion Planning: A Review. Appl. Energy 2018, 230, 563–589. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sabillon Antunez, C.; Ajalli, M.; Romero, R. Transmission Expansion Planning: Literature Review and Classification. IEEE Syst. J. 2019, 13, 3129–3140. [Google Scholar] [CrossRef]
- Chatzos, M.; Mak, T.W.K.; Vanhentenryck, P. Spatial Network Decomposition for Fast and Scalable AC-OPF Learning. IEEE Trans. Power Syst. 2021, 37, 2601–2612. [Google Scholar] [CrossRef]
- Woo, J.H.; Wu, L.; Park, J.B.; Roh, J.H. Real-Time Optimal Power Flow Using Twin Delayed Deep Deterministic Policy Gradient Algorithm. IEEE Access 2020, 8, 213611–213618. [Google Scholar] [CrossRef]
- Benalcazar, P.; Kamiński, J.; Stós, K. An Integrated Approach to Long-Term Fuel Supply Planning in Combined Heat and Power Systems. Energies 2022, 15, 8339. [Google Scholar] [CrossRef]
- Yu, Z.; Ruan, G.; Wang, X.; Zhang, G.; He, Y.; Zhong, H. Evaluation of Look-Ahead Economic Dispatch Using Reinforcement Learning. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 11–13 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1708–1713. [Google Scholar]
- Fang, D.; Guan, X.; Hu, B.; Peng, Y.; Chen, M.; Hwang, K. Deep Reinforcement Learning for Scenario-Based Robust Economic Dispatch Strategy in Internet of Energy. IEEE Internet Things J. 2021, 8, 9654–9663. [Google Scholar] [CrossRef]
- Lin, L.; Guan, X.; Peng, Y.; Wang, N.; Maharjan, S.; Ohtsuki, T. Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things J. 2020, 7, 6288–6301. [Google Scholar] [CrossRef]
- Lv, K.; Tang, H.; Bak-Jensen, B.; Radhakrishna Pillai, J.; Tan, Q.; Zhang, Q. Hierarchical Learning Optimisation Method for the Coordination Dispatch of the Inter-regional Power Grid Considering the Quality of Service Index. IET Gener. Transm. Distrib. 2020, 14, 3673–3684. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, L. Machine Learning Approaches to the Unit Commitment Problem: Current Trends, Emerging Challenges, and New Strategies. Electr. J. 2021, 34, 106889. [Google Scholar] [CrossRef]
- Wang, D. A New Power System Dispatching Optimization Method Based on Reinforcement Learning. In Proceedings of the 2023 2nd Asian Conference on Frontiers of Power and Energy (ACFPE), Chengdu, China, 20–22 October 2023; IEEE: Piscataway, NJ, USA, 2023; Volume 4, pp. 145–149. [Google Scholar]
- Chen, J.; Yu, T.; Pan, Z.; Zhang, M.; Deng, B. A Scalable Graph Reinforcement Learning Algorithm Based Stochastic Dynamic Dispatch of Power System under High Penetration of Renewable Energy. Int. J. Electr. Power Energy Syst. 2023, 152, 109212. [Google Scholar] [CrossRef]
- Li, J.; Yu, T.; Zhang, X. Emergency Fault Affected Wide-Area Automatic Generation Control via Large-Scale Deep Reinforcement Learning. Eng. Appl. Artif. Intell. 2021, 106, 104500. [Google Scholar] [CrossRef]


| Phases | Steps |
|---|---|
| Research questions |
| Data sources | |
| Search strings | |
| Inclusion criteria | |
| Quality criteria for study selection | |
| Primary study selection |
| Data extraction | |
| Data synthesis | |
| Documenting the extracted results |
| Data Sources | Filter 1 | Filter 2 |
|---|---|---|
| IEEE Xplore | 49 | 23 |
| ScienceDirect | 37 | 15 |
| SpringerLink | 62 | 3 |
| Wiley Online Library | 24 | 7 |
| MDPI | 19 | 7 |
| Ref. | Application | Learning Algorithm | Function Approximator | Reward Function | Metrics | Test System |
|---|---|---|---|---|---|---|
| [34] | OPF of distribution networks | PPO algorithm with clipped surrogate loss | Value function and policy function with DNN. The actor and critic networks have three hidden layers with 200, 100, and 100 neurons, respectively. | Penalties associated with voltage restrictions, power capacity, and storage limits. | Proportion of satisfied constraints (PSC). | Modified IEEE 33-bus system trained by a 5500 dataset. |
| [22] | AC OPF | PPO algorithm with clipped surrogate loss | Value function and policy function with DNN. The actor-critic structure: Three hidden layers with (380, 195, 100) neurons are applied in the actor NN, and three hidden layers with (380, 44, 5) are applied in the critic NN in PPO. | Negative reward (−5000) if the OPF does not converge. Also, penalties are associated with the total number of violations of active power, voltage, and line loading constraints. | Cost comparison in percentage as an MAE, feasibility rate, and running time. | IEEE 14-bus: 55,000 training dataset, 17,364 testing dataset I, 2000 testing dataset II. Illinois 200-bus systems: 60,000 training dataset, 17,364 testing dataset I, 2000 testing dataset II. |
| [35] | ||||||
| [36] | AC OPF | Modified DDPG with Lagrangian-based gradient | At the offline stage, a policy model optimizes the augmented cost and iteratively updates the parameters of a deep neural network (DNN) agent using the deep deterministic policy gradient. | Penalties are in the form of coefficients that correspond to equality and inequality constraints. | Generation power average as MAE, generation cost, operating cost comparison of different OPF methods. | IEEE 118-bus system |
| [37] | OPF in a multi-objective optimization | Combination of Monte Carlo tree search and reinforcement learning MCTS-RL | Q-value: The tree state is randomly built up, and the accumulated experience in each state is updated by random sampling during the optimization and exploration policy process. | is a discount factor that indicates the effect of the current decision on the long-term reward. | Power transfer distribution factor (PTDF). | IEEE 33-bus test system. |
| [20] | Real-time OPF solution | Deep deterministic policy gradient (DDPG) | DQN: The actor is updated by following the applying the chain rule to the expected return from the start distribution concerning the actor parameters | and the quadratic number of violations, the reward is determined. | Network losses, batch average critic training cost. | IEEE 9-bus system. |
| [38] | Distributed optimal power flow | Inverse reinforcement learning (IRL) | represents the experience value of the agent acting is the learning rate | A general indicator is defined based on the self-fitting error to evaluate the model’s accuracy. | A general indicator is defined based on the self-fitting error, which is obtained from the lower-level optimization and denoted as an optimization error. | IEEE 57-bus power system is utilized in the model, and OPF considers N − 1 static security constraints. |
| [39] | OPF | Multi-agent reinforcement learning (MARL) | The Q-value of the player is defined as a function of all players’ actions | A reward function of the agent after bidding at the demand level (payoff of each generator after clearing the market). | Learning rate, the cost function. | IEEE-30-bus power system. |
| [40] | Distribution network planning | Deep Q-network (DQN) | Neural network trained by Q-values | Minimum network loss and voltage deviation are taken as the reward function. | Network loss distribution. | IEEE-37 bus distribution network |
| [41] | Distribution network | Traditional and accelerated Q learning | Deep neural network | Node voltage | Convergence time. | IEEE 33-bus system. |
| [42] | Optimal power flow | Twin delayed deep deterministic policy gradient (TD3) | Deep neural networks | The value is determined by calculating the following factors: (1) line current exceeding the limit, (2) consumption of renewable energy units, (3) balanced unit power exceeding the limit, (4) unit operating costs, and (5) reactive power output exceeding the limit. | Renewable energy consumption under different weights. | IEEE-30 bus networks. |
| [43] | Operation of distribution networks | Double deep Q network | Deep neural network | It is determined by running a power flow with input state information and selected actions. | Output power. | IEEE 33-bus networks. |
| [44] | Optimal power flow | Partially observable Markov game (POMG) | Q-value | The penalty function is analogous to the reward function and employs active power load and active power loss. | Daily routing and scheduling decisions. | 6-bus and 33-bus power networks. |
| Ref. | Application | Learning Algorithm | Function Approximator | Reward Function | Metrics | Study Case |
|---|---|---|---|---|---|---|
| [46] | Unit commitment | Q-learning-based | Adjust power output with ε-greedy. | Reflects the negative of the operation cost. | Generation cost. | New England 10-unit system. |
| [47] | Unit commitment and dispatch with multistage stochastic programming | Q-learning-based | DNN with state action value function to minimize operation. | Penalty ratios associated with violations of voltage and current limits, respectively. | Energy cost, Network losses cost, curtailment penalty, total cost, and CPU time. | Modified IEEE 39-bus two-region system. |
| [48] | Optimal dispatch | Nash-Q learning | Q-value function incorporating a Nash equilibrium. | . | Mean value of the objective function, variance, standard deviation, and relative standard deviation. | IEEE 39-bus two-region system. |
| [45] | Optimal dispatch | Multi-step deep Q-learning | DQN using stochastic gradient descent. | Penalties associated with generation operating costs. | MAE, mean-squared temporal difference error. | 5-unit UC test case. |
| [49] | Economic dispatch model | Least square policy iteration (LSPI) | Radial basis functions (RBFs). | Two terms for each PV agent: the first reduces the amount of PV active power constrained, and the second penalizes actions that cause a voltage magnitude violation. | Total power curtailed PV, total reward, and voltage magnitude. | 25-node unbalanced distribution system test. |
| [50] | Economic dispatch | NSGA-RL, an enhancement of the non-dominated sorting genetic algorithm II (NSGA-II) | Q-value function using NSGA. | The NSGA-RL uses an implicit reward function, rewarding efficient parameter values during its evolutionary process. | Generational distance for convergence, extent of spread achieved among the obtained solutions. | IEEE 30-bus system model. |
| [51] | Economic dispatch | Adam algorithm | The DQN (deep Q-network) algorithm computes the action-state value function. | It is defined by the scale constraint, upper and lower limit constraints of the generators, and the power balancing compensation, which is added together to obtain the reward. | The mean square error is used to define the error function in DQN training. | The IEEE-14 and IEEE-162 node systems are analyzed. |
| [52] | Economic dispatch | Multi-level backtracking prioritized experience replay-twin delayed deep deterministic policy gradient (MBEPR-TD3) | An actor neural network which maps the environment states of combined heat and power-virtual power plant. | The reward function is composed of the operation cost of virtual power plants and the penalty cost. | The metrics evaluated in the study include the increase in profits and reduction in carbon emissions due to the incorporation of power-to-gas in CHP-VPP. | Proposed 4-bus CHP-VPP system considering carbon capture and P2G technologies. |
| [53] | Power grid operational planning | Intelligent reschedule algorithm Q-learning based | DQN, which approximates the value function of the rescheduled action through the Q network. | It includes three aspects of rescheduling: the average node voltage fluctuation, the system fragile line load safety margin, and the generation cost. | Voltage fluctuation, the variance between the line load and the base value power generation cost index. | 9-bus radial distribution feeder. 34-bus radial distribution feeders. |
| [54] | Economic dispatch | Novel graph-based deep reinforcement learning | GraphSAGE network. | Correlation between power loss and operating costs. | Correlation between power loss and operating costs. | IEEE 118-bus system |
| [55] | Economic dispatch | Proximal policy optimization (PPO) | Neural network. | Renewable energy consumption, line overload, unit operating cost penalties, penalties for power imbalances, penalties for exceeding the unit power limit, and penalties for exceeding the thermal unit power limit. | Renewable energy output. | The grid has 126 nodes, 35 thermal power units, 18 renewable energy units, 1 balancing unit, 91 loads, and 185 load lines. |
| [56] | Economic dispatch | A soft actor-critic | Neural network. | Minimization of carbon emissions costs and carbon dioxide emissions during dispatch operations. | Electric load curtailment. | Community-integrated energy system with electricity–gas–cooling coupling. |
| [57] | CHP economic dispatch | Q-learning | Q-value. | Linear sum of profit, unserved heat, maximum inlet supply temperature, minimum inlet supply temperature, minimum inlet return temperature, and maximum mass flow. | Profit. | System constructed with data obtained online. |
| [58] | Economic dispatch | Twin-delayed deep deterministic policy gradient (TD3) | Q-value or neural network. | Total market profit. Defined as the sum of the profits of all attacker generators. It can be employed in the reward function as an incentive for the agent. | The summed market profits, the attacker market share, and constraint violations are categorized by undervoltage, overvoltage, and branch overload. | 97-bus rural MV Simbench system. |
| [59] | Economic dispatch | Deep deterministic policy gradient | Deep neural networks. | Negative equivalent of the microgrid operational cost. | Fuel cost and power limits of generators in microgrid. | Cimei Island power system. |
| [60] | Economic dispatch | Bacteria foraging reinforcement learning | Neural network. | Fuel cost. | Calculation time. | IEEE RTS-79 system. |
| [61] | Hydro-thermal economic dispatch | DQN and A2C | Neural network. | An aggregate level of volume water stored in the reservoir in the system. | MAPE and Pearson’s correlation coefficient. | Hydro-thermal economic dispatch case study. |
| [62] | Economic Dispatch | Based crisscross optimization (CSO) | Neural network. | The reward function includes the cost of all units while considering the balance constraints. | Discount factor. | 48 units, 96 units as well as 192 units |
| [63] | Economic dispatch | Deep deterministic policy gradient (DDPG) | Q-network. | Consists of two components: look-ahead economic dispatch model and total generation cost of generators. | Power generation costs. | IEEE30-bus and SG126-bus systems. |
| [64] | Economic dispatch | Distributed proximal policy optimization (DPPO) | Neural network. | The reward function is divided into two aspects: objective function and power deviation reward. | Total training time (s). | Real data from a region in the Liaoning Province of China to build a test system. |
| [65] | Economic dispatch | Distributed proximal policy optimization (DPPO) | Neural network. | The reward consists of 3 sub-targets: total operating costs, power mismatch, and storage tank status. | Economic performance. | Two different systems with four decision variables (gas turbine (GT), gas boiler (GB), power grid, and thermal storage tank (TST)) and four random variables (wind turbine, energy price, heat load, and electricity load), which was adopted to test whether our method could cope with variable operating states without recalculation. |
| Ref. | Application | Learning Algorithm | Function Approximator | Reward Function | Metrics | Study Case |
|---|---|---|---|---|---|---|
| [70] | Plan for the deployment of shunts for power system resilience enhancement | Multi-agent based hybrid soft actor critic (HSAC) algorithm | Policy Q-function with Monte Carlo estimator | Penalties are associated with bus voltage magnitude deviation, energy not supplied, and transmission cost during contingencies. | Amount of rewards of training episodes. | IEEE 57-bus and IEEE 300-bus systems. |
| [9] | Power grid planning and operation under uncertainties | SAC algorithm with automated temperature coefficient calculation is adopted for training effective SAC agent | Q-function with the batch normalization technique is applied. | Contingency reward and base case reward consider the power flow through the line and the line capacity impact ratio. | Average reward and training step curves. | SGCC Zhejiang Electric Power Company study cases. |
| [71] | Transmission network expansion planning | Double deep-Q network with deep ResNet | The deep learning has two main branches: the deep convolutional networks and the deep confidence networks. | The reward is based on expected energy not supplied, electrical interconnection, and global cost. | Total cost, EENS, increase in load, and generator capacity. | IEEE New England 39-bus test system. IEEE RTS 24-bus test system. |
| [72] | Distribution network planning | Monte Carlo tree search-based reinforcement learning | Policy network function with DNN. | The reward is a function of the total investment cost and device installation investment. | Investment cost, load curtailment, and PV curtailment. | IEEE 33-bus test system. The nodes 14, 22, and 33 are equipped with ESS, gas generator, and CB. |
| [73] | Transmission network expansion planning | Deep Q-network (DQN) | The action’s Q-value can be calculated based on the feedback of the action. | The final benchmark cost is appropriately increased on this basis, and the N-1 security constraints are considered so that the reward. | Comparison of network loss after cutting different lines. | IEEE 24-bus reliability test system is selected for calculation and analysis. |
| [74] | Transmission network expansion planning | Multi-agent double deep Q network (DDQN) based on deep reinforcement learning. | The value function can be calculated iteratively through dynamic programming. | The reward is considered based on meeting the upper and lower bounds of the constraints of the TNEP optimization model. | Accumulation and change rate as indicators to measure the data uncertainty. | Modified IEEE 24-bus system and New England 39-bus system. |
| [75] | Transmission network expansion planning | Q-learning-based with a preprocessing step | Random forest based algorithm using synthetic dataset. | A storage expansion planning framework using reinforcement learning and simulation-based optimization. | Monetary savings. The number of episodes required for convergence. | The microgrid is in Westhampton, NY. |
| [76] | Power grid planning and operation | Deep Q-network (MDQN) | Neural network for action value function Q. | Minimization of overall operational expenses. | Cumulative Unbalance (kW). | Virtual power plant consisting of photovoltaic (PV), energy storage, and three micro gas turbines as distributed energy resources. |
| [77] | Power planning for distribution network | Q-learning | Q-table. | Rewards include: construction, operation costs, and constraint function. | Voltage node. | IEEE-18 system. |
| [78] | Power planning for distribution network | Q-learning | Convolutional neural network (CNN). | Active power loss. | Accuracy, security, and dependability. | IEEE 33 bus radial distribution networks. |
| [79] | Power planning for distribution network | Dynamic distribution network reconfiguration (DDNR) | Q-table. | Active energy losses, price of the switching, penalty value, | Losses reduction | IEEE 33-bus radial system. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesántez, G.; Guamán, W.; Córdova, J.; Torres, M.; Benalcazar, P. Reinforcement Learning for Efficient Power Systems Planning: A Review of Operational and Expansion Strategies. Energies 2024, 17, 2167. https://doi.org/10.3390/en17092167
Pesántez G, Guamán W, Córdova J, Torres M, Benalcazar P. Reinforcement Learning for Efficient Power Systems Planning: A Review of Operational and Expansion Strategies. Energies. 2024; 17(9):2167. https://doi.org/10.3390/en17092167
Chicago/Turabian StylePesántez, Gabriel, Wilian Guamán, José Córdova, Miguel Torres, and Pablo Benalcazar. 2024. "Reinforcement Learning for Efficient Power Systems Planning: A Review of Operational and Expansion Strategies" Energies 17, no. 9: 2167. https://doi.org/10.3390/en17092167
APA StylePesántez, G., Guamán, W., Córdova, J., Torres, M., & Benalcazar, P. (2024). Reinforcement Learning for Efficient Power Systems Planning: A Review of Operational and Expansion Strategies. Energies, 17(9), 2167. https://doi.org/10.3390/en17092167








