Non-Contact Wind Turbine Blade Crack Detection Using Laser Doppler Vibrometers
Abstract
1. Introduction
2. Finite Element Method
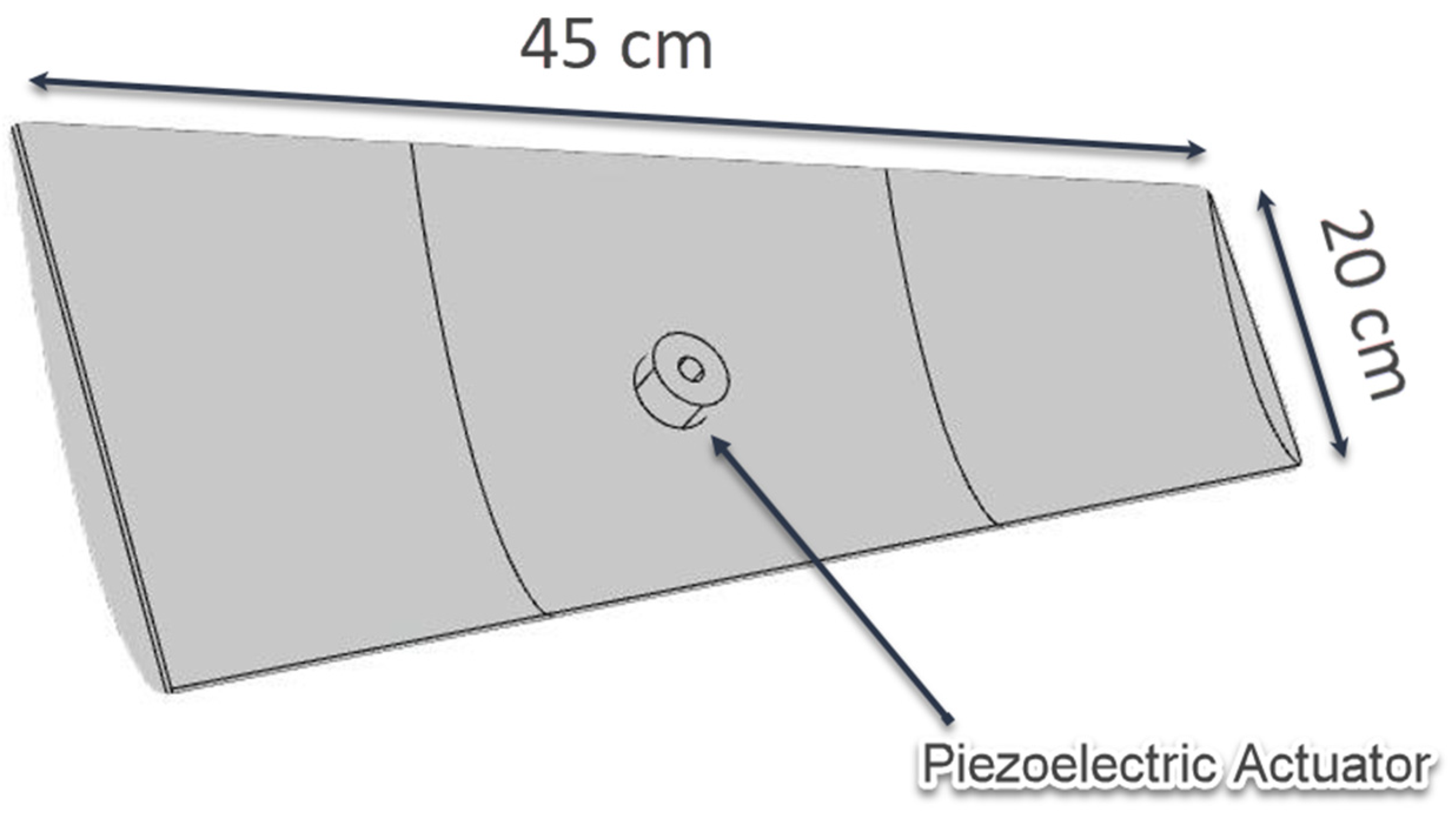
2.1. Structural Design
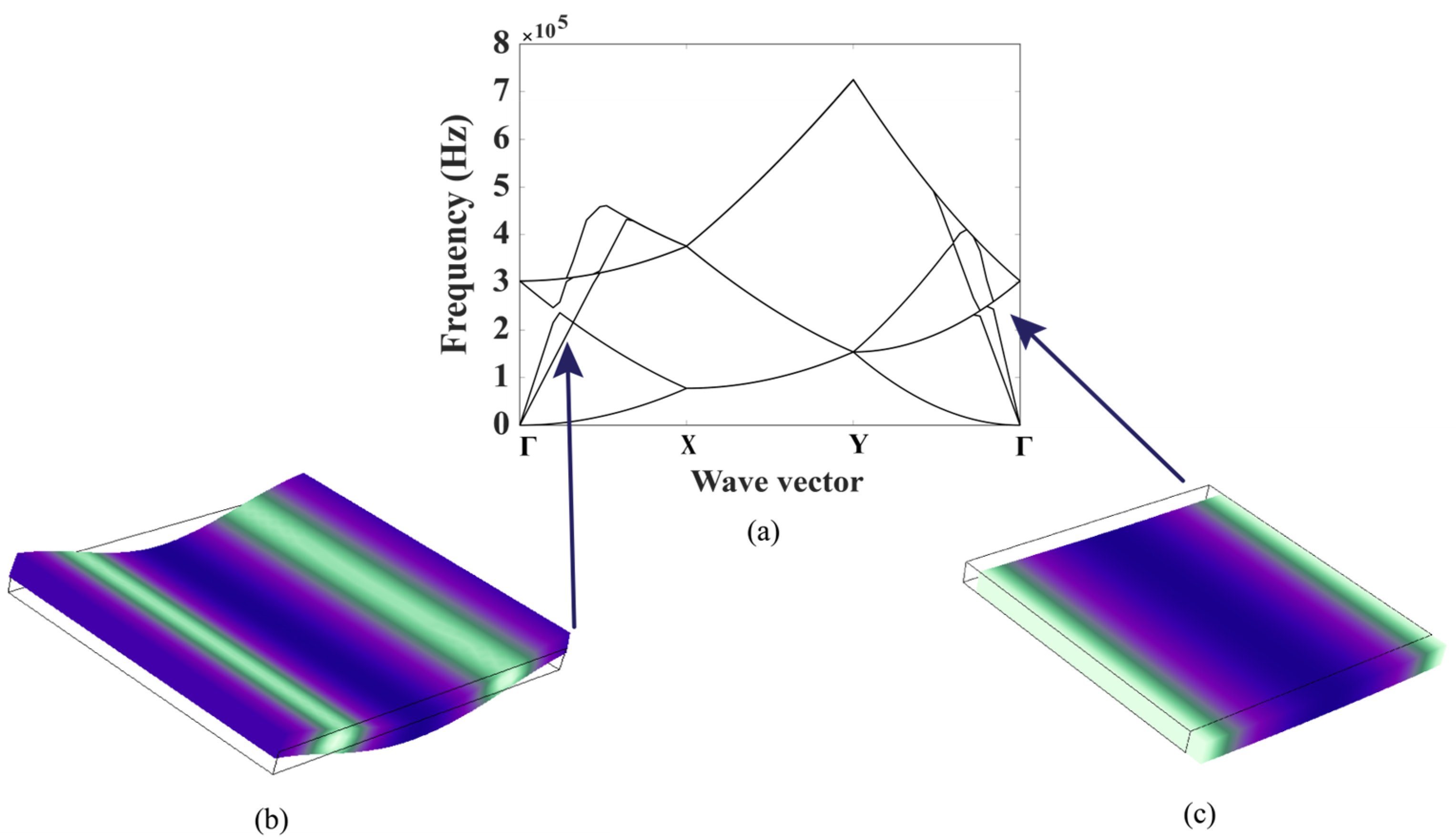
2.2. Band Structure
3. Experimental Procedure
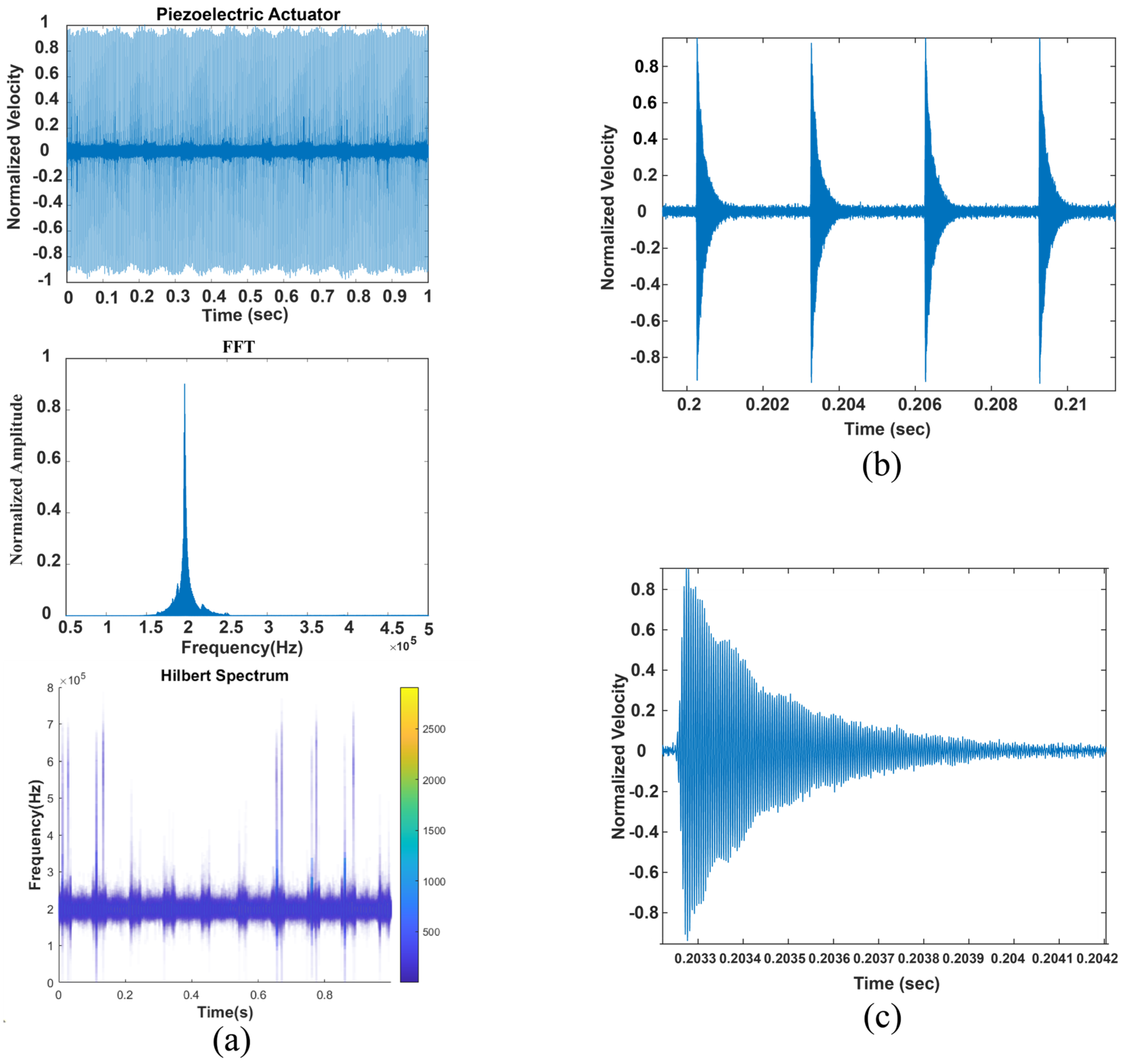
3.1. Experimental Setup
3.2. Correlation Factor
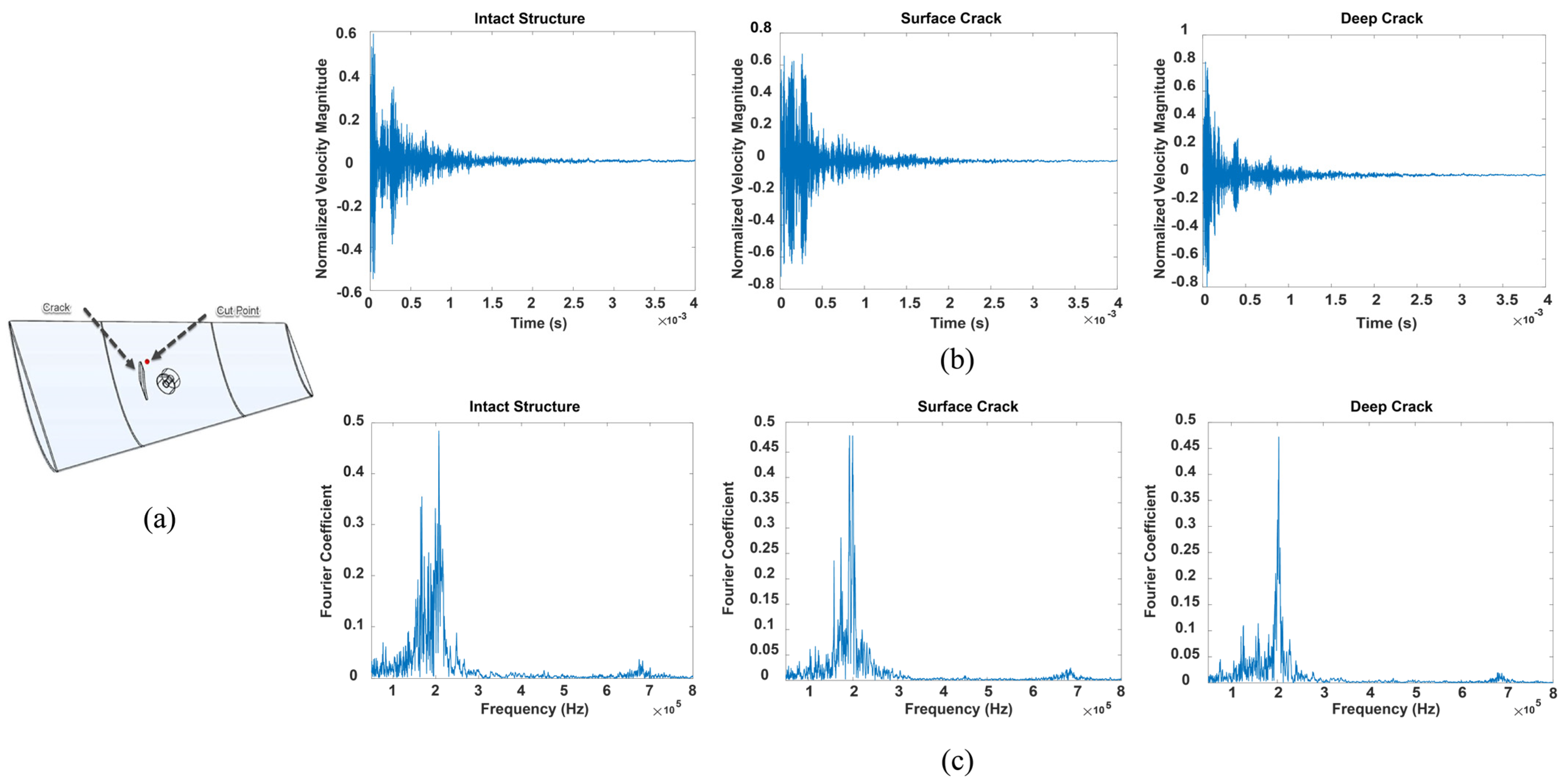
4. Simulation and Experiment
5. Conclusions
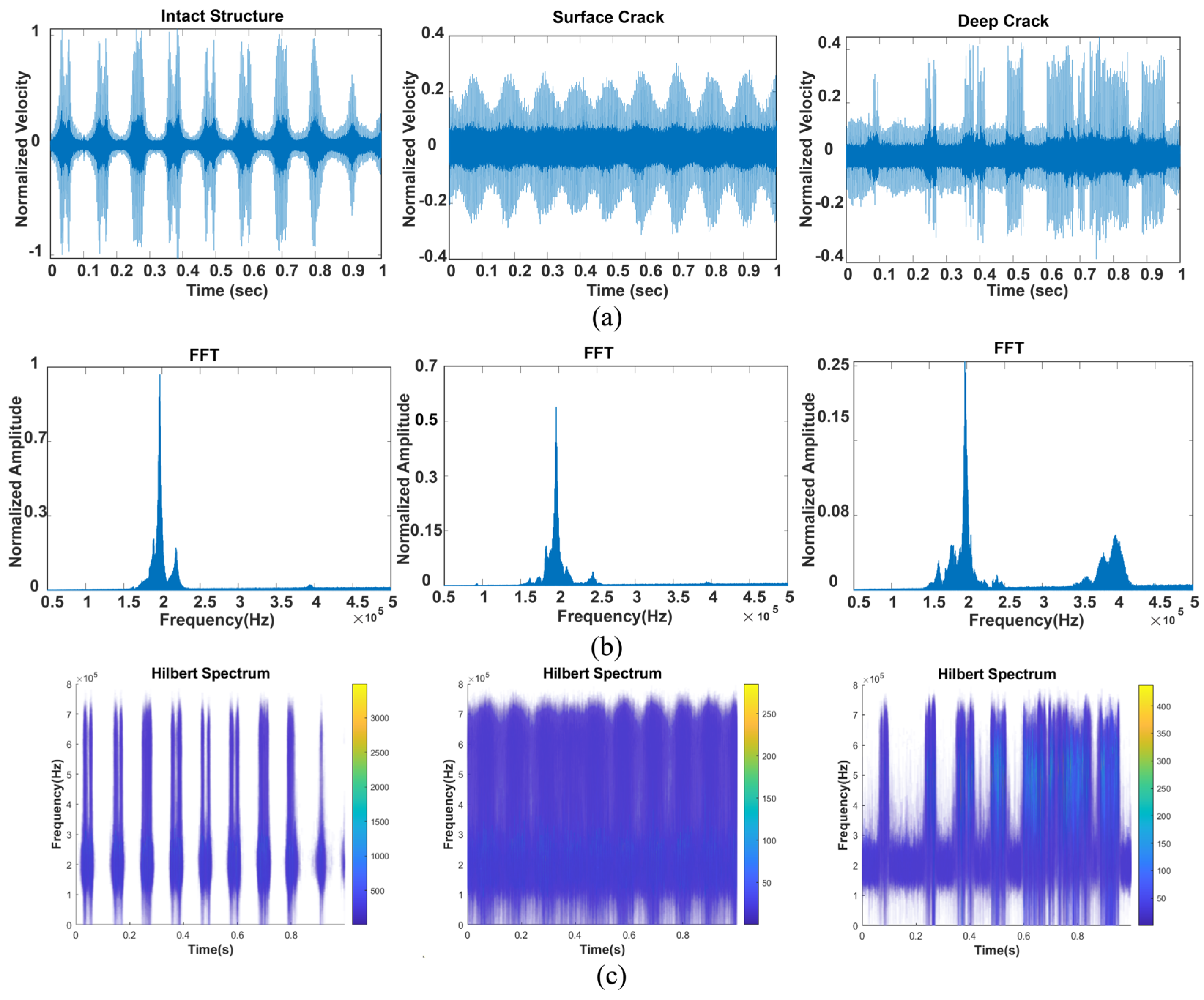
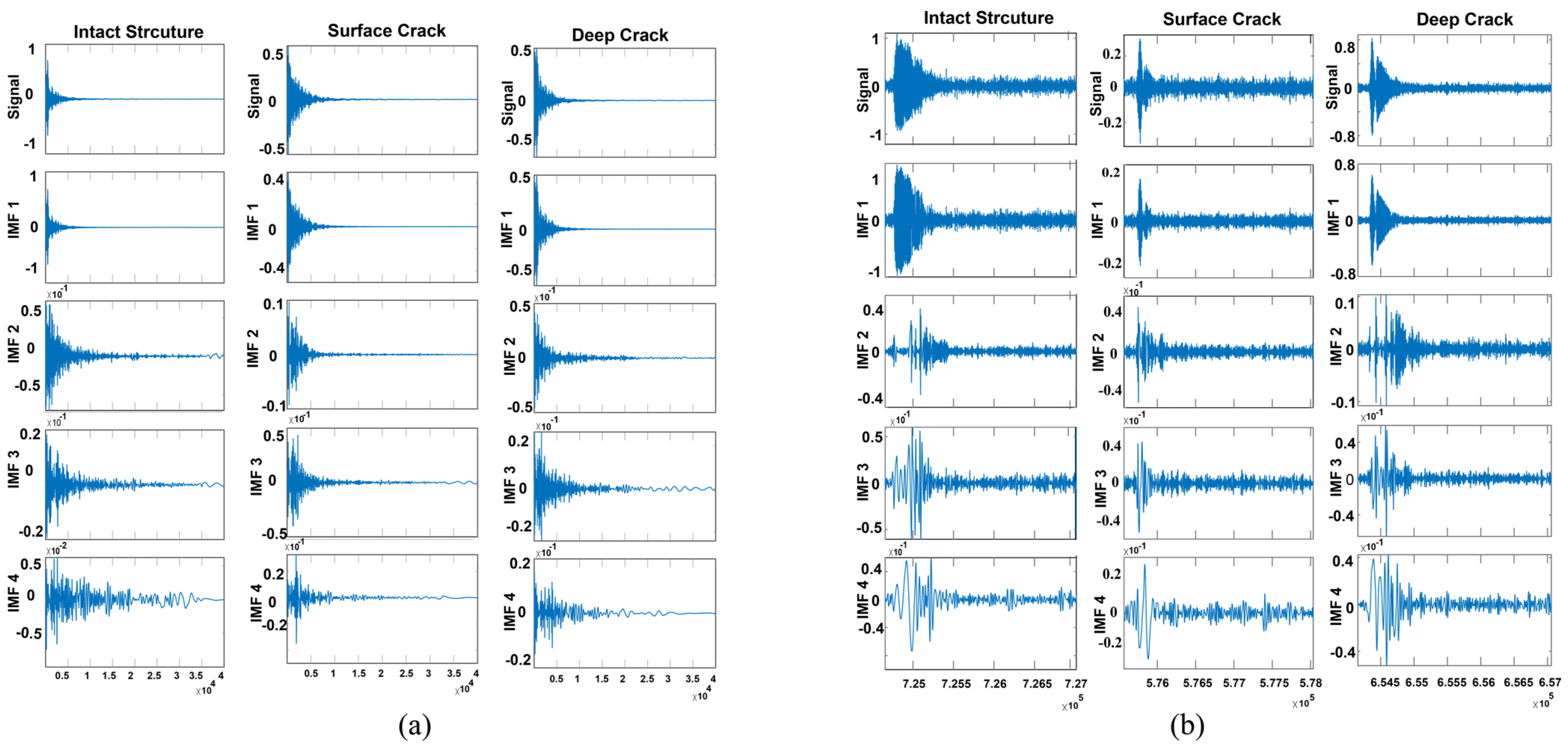
- The investigation into the IMFs, namely the first, second, third, and forth IMF, showed great potential as a reliable marker for identifying signal irregularities.
- IMF1 has the highest correlation factor.
- IMF2 can serve as a viable indicator of short pulses when the signal is noisy.
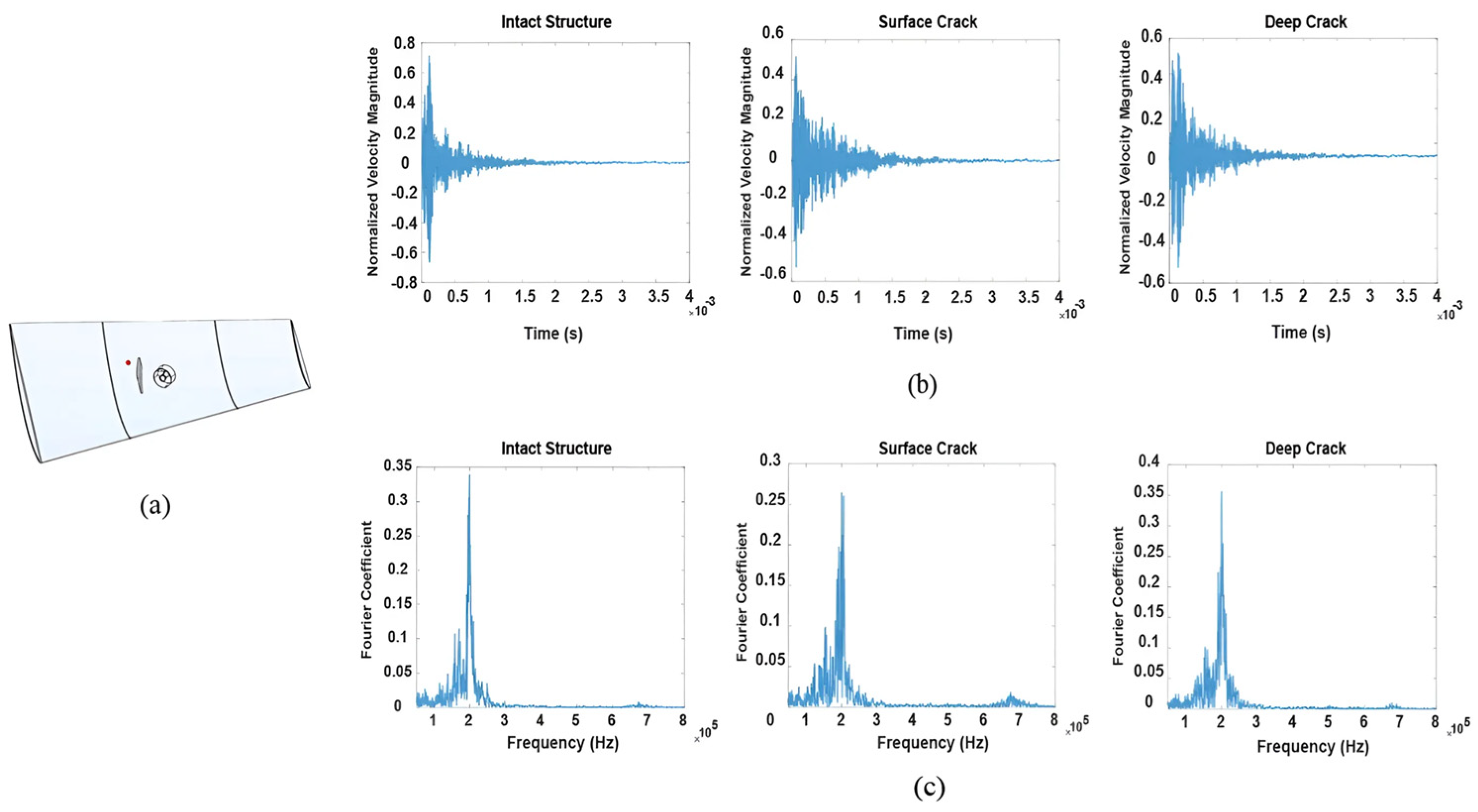
- In the damaged structure, the FFT exhibits variations and higher-frequency components compared to the intact structure.
- Increasing the crack depth distorts the signal more in the time domain.
- The similarities and differences between simulation and experiment were analyzed, which could be helpful for future structural inspection studies of WTBs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paraschiv, L.S.; Paraschiv, S. Contribution of Renewable Energy (Hydro, Wind, Solar and Biomass) to Decarbonization and Transformation of the Electricity Generation Sector for Sustainable Development. Energy Rep. 2023, 9, 535–544. [Google Scholar] [CrossRef]
- Elgendi, M.; AlMallahi, M.; Abdelkhalig, A.; Selim, M.Y.E. A Review of Wind Turbines in Complex Terrain. Int. J. Thermofluids 2023, 17, 100289. [Google Scholar] [CrossRef]
- Dimitrova, M.; Aminzadeh, A.; Meiabadi, M.S.; Sattarpanah Karganroudi, S.; Taheri, H.; Ibrahim, H. A Survey on Non-Destructive Smart Inspection of Wind Turbine Blades Based on Industry 4.0 Strategy. Appl. Mech. 2022, 3, 1299–1326. [Google Scholar] [CrossRef]
- Algolfat, A.; Wang, W.; Albarbar, A. The Sensitivity of 5MW Wind Turbine Blade Sections to the Existence of Damage. Energies 2023, 16, 1367. [Google Scholar] [CrossRef]
- Leon, M., Jr. Recycling of Wind Turbine Blades: Recent Developments. Curr. Opin. Green Sustain. Chem. 2023, 39, 100746. [Google Scholar] [CrossRef]
- Gao, R.; Yang, J.; Yang, H.; Wang, X. Wind-Tunnel Experimental Study on Aeroelastic Response of Flexible Wind Turbine Blades under Different Wind Conditions. Renew. Energy 2023, 219, 119539. [Google Scholar] [CrossRef]
- Sun, S.; Wang, T.; Yang, H.; Chu, F. Condition Monitoring of Wind Turbine Blades Based on Self-Supervised Health Representation Learning: A Conducive Technique to Effective and Reliable Utilization of Wind Energy. Appl. Energy 2022, 313, 118882. [Google Scholar] [CrossRef]
- Liu, S.; Ren, S.; Jiang, H. Predictive Maintenance of Wind Turbines Based on Digital Twin Technology. Energy Rep. 2023, 9, 1344–1352. [Google Scholar] [CrossRef]
- Kaewniam, P.; Cao, M.; Alkayem, N.F.; Li, D.; Manoach, E. Recent Advances in Damage Detection of Wind Turbine Blades: A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2022, 167, 112723. [Google Scholar] [CrossRef]
- Reddy, A.; Indragandhi, V.; Ravi, L.; Subramaniyaswamy, V. Detection of Cracks and Damage in Wind Turbine Blades Using Artificial Intelligence-Based Image Analytics. Measurement 2019, 147, 106823. [Google Scholar] [CrossRef]
- Denhof, D.; Staar, B.; Lütjen, M.; Freitag, M. Automatic Optical Surface Inspection of Wind Turbine Rotor Blades Using Convolutional Neural Networks. Procedia CIRP 2019, 81, 1166–1170. [Google Scholar] [CrossRef]
- He, Y.; Li, M.; Meng, Z.; Chen, S.; Huang, S.; Hu, Y.; Zou, X. An Overview of Acoustic Emission Inspection and Monitoring Technology in the Key Components of Renewable Energy Systems. Mech. Syst. Signal Process. 2021, 148, 107146. [Google Scholar] [CrossRef]
- Niezrecki, C.; Poozesh, P.; Aizawa, K.; Heilmann, G. Wind Turbine Blade Health Monitoring Using Acoustic Beamforming Techniques. J. Acoust. Soc. Am. 2014, 135, 2392–2393. [Google Scholar] [CrossRef]
- Groth, E.B.; Clarke, T.G.R.; Schumacher da Silva, G.; Iturrioz, I.; Lacidogna, G. The Elastic Wave Propagation in Rectangular Waveguide Structure: Determination of Dispersion Curves and Their Application in Nondestructive Techniques. Appl. Sci. 2020, 10, 4401. [Google Scholar] [CrossRef]
- Li, Y.; Dieussaert, E.; Baets, R. Miniaturization of Laser Doppler Vibrometers—A Review. Sensors 2022, 22, 4735. [Google Scholar] [CrossRef] [PubMed]
- Dilek, A.U.; Oguz, A.D.; Satis, F.; Gokdel, Y.D.; Ozbek, M. Condition Monitoring of Wind Turbine Blades and Tower via an Automated Laser Scanning System. Eng. Struct. 2019, 189, 25–34. [Google Scholar] [CrossRef]
- Zieger, T.; Nagel, S.; Lutzmann, P.; Kaufmann, I.; Ritter, J.; Ummenhofer, T.; Knödel, P.; Fischer, P. Simultaneous Identification of Wind Turbine Vibrations by Using Seismic Data, Elastic Modeling and Laser Doppler Vibrometry. Wind Energy 2020, 23, 1145–1153. [Google Scholar] [CrossRef]
- Vuye, C.; Vanlanduit, S.; Presezniak, F.; Steenackers, G.; Guillaume, P. Optical Measurement of the Dynamic Strain Field of a Fan Blade Using a 3D Scanning Vibrometer. Opt. Lasers Eng. 2011, 49, 988–997. [Google Scholar] [CrossRef]
- Yu, L.; Tian, Z. Lamb Wave Structural Health Monitoring Using a Hybrid PZT-Laser Vibrometer Approach. Struct. Health Monit. 2013, 12, 469–483. [Google Scholar] [CrossRef]
- Allen, M.S.; Sracic, M.W. A New Method for Processing Impact Excited Continuous-Scan Laser Doppler Vibrometer Measurements. Mech. Syst. Signal Process. 2010, 24, 721–735. [Google Scholar] [CrossRef]
- Chen, Y.; Griffith, D.T. Experimental and Numerical Full-Field Displacement and Strain Characterization of Wind Turbine Blade Using a 3D Scanning Laser Doppler Vibrometer. Opt. Laser Technol. 2023, 158, 108869. [Google Scholar] [CrossRef]
- Chen, Y.; Escalera Mendoza, A.S.; Griffith, D.T. Experimental Dynamic Characterization of Both Surfaces of Structures Using 3D Scanning Laser Doppler Vibrometer. Exp. Tech. 2023, 47, 989–1006. [Google Scholar] [CrossRef]
- Liu, J.; Wang, X.; Yuan, S.; Li, G. On Hilbert-Huang Transform Approach for Structural Health Monitoring. J. Intell. Mater. Syst. Struct. 2006, 17, 721–728. [Google Scholar] [CrossRef]
- Dehina, W.; Boumehraz, M.; Kratz, F. Detectability of Rotor Failure for Induction Motors through Stator Current Based on Advanced Signal Processing Approaches. Int. J. Dyn. Control 2021, 9, 1381–1395. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Sun, Y.; Gao, L.; Yue, Y. Hilbert–Huang Transform Based Method for Monitoring the Crack of Concrete Arch by Using FBG Sensors. Optik 2016, 127, 3417–3422. [Google Scholar] [CrossRef]
- Al-hababi, T.; Alkayem, N.F.; Asteris, P.G.; Wang, J.; Hu, S.; Cao, M. Time-Frequency Domain Methods for the Identification of Breathing Cracks in Beam-like Structures. Tribol. Int. 2023, 180, 108202. [Google Scholar] [CrossRef]
- Chen, B.; Zhao, S.; Li, P. Application of Hilbert-Huang Transform in Structural Health Monitoring: A State-of-the-Art Review. Math. Probl. Eng. 2014, 2014, 317954. [Google Scholar] [CrossRef]
- Hamdi, S.E.; Le Duff, A.; Simon, L.; Plantier, G.; Sourice, A.; Feuilloy, M. Acoustic Emission Pattern Recognition Approach Based on Hilbert–Huang Transform for Structural Health Monitoring in Polymer-Composite Materials. Appl. Acoust. 2013, 74, 746–757. [Google Scholar] [CrossRef]
- Xiaoming, N.; Jian, Z.; Xingwu, L. Application of Hilbert–Huang Transform to Laser Doppler Velocimeter. Opt. Laser Technol. 2012, 44, 2197–2201. [Google Scholar] [CrossRef]
- Teng, F.; Wei, J.; Lv, S.; Geng, X.; Peng, C.; Zhang, L.; Ju, Z.; Jia, L.; Jiang, M. Damage Localization in Carbon Fiber Composite Plate Combining Ultrasonic Guided Wave Instantaneous Energy Characteristics and Probabilistic Imaging Method. Measurement 2023, 221, 113443. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, L.; Chhibber, R.; Dixit, A.; Singhal, R. Environmental Degradation of Glass Fiber-Reinforced Nanocomposites with Self-Healing Reinforcement in Polymer Matrix for Wind Turbine Blade Application. Trans. Indian Inst. Met. 2021, 74, 3119–3133. [Google Scholar] [CrossRef]
- Amano, R.S.; Lewinski, G.; Shen, R. Imprinted Glass Fiber-Reinforced Polymer Vascular Networks for Creating Self-Healing Wind Turbine Blades. J. Energy Resour. Technol. 2022, 144, 062107. [Google Scholar] [CrossRef]
- Cousins, D.S.; Suzuki, Y.; Murray, R.E.; Samaniuk, J.R.; Stebner, A.P. Recycling Glass Fiber Thermoplastic Composites from Wind Turbine Blades. J. Clean. Prod. 2019, 209, 1252–1263. [Google Scholar] [CrossRef]
- Rawat, P.; Singh, N.K.; Singh, K.K.; Agrhari, N. Influence of Oblique Impact on Glass Fiber-Reinforced Polymer Composites: A Numerical Approach. In Trends in Materials Engineering; Springer Nature: Singapore, 2019; pp. 77–86. [Google Scholar]
- Kuppusamy, R.R.P.; Rout, S.; Kumar, K. Advanced Manufacturing Techniques for Composite Structures Used in Aerospace Industries. In Modern Manufacturing Processes; Elsevier: Amsterdam, The Netherlands, 2020; pp. 3–12. [Google Scholar]
- Xin, H.; Liu, Y.; Mosallam, A.S.; He, J.; Du, A. Evaluation on Material Behaviors of Pultruded Glass Fiber Reinforced Polymer (GFRP) Laminates. Compos. Struct. 2017, 182, 283–300. [Google Scholar] [CrossRef]
- He, Y.; Chen, H.; Liu, D.; Zhang, L. A Framework of Structural Damage Detection for Civil Structures Using Fast Fourier Transform and Deep Convolutional Neural Networks. Appl. Sci. 2021, 11, 9345. [Google Scholar] [CrossRef]
- Yang, S.; Allen, M.S. Output-Only Modal Analysis Using Continuous-Scan Laser Doppler Vibrometry and Application to a 20 KW Wind Turbine. Mech. Syst. Signal Process. 2012, 31, 228–245. [Google Scholar] [CrossRef]




| IMF | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Correlation Coefficient | 0.9948 | 0.0538 | 0.0021 | 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabihi, A.; Aghdasi, F.; Ellouzi, C.; Singh, N.K.; Jha, R.; Shen, C. Non-Contact Wind Turbine Blade Crack Detection Using Laser Doppler Vibrometers. Energies 2024, 17, 2165. https://doi.org/10.3390/en17092165
Zabihi A, Aghdasi F, Ellouzi C, Singh NK, Jha R, Shen C. Non-Contact Wind Turbine Blade Crack Detection Using Laser Doppler Vibrometers. Energies. 2024; 17(9):2165. https://doi.org/10.3390/en17092165
Chicago/Turabian StyleZabihi, Ali, Farhood Aghdasi, Chadi Ellouzi, Nand Kishore Singh, Ratneshwar Jha, and Chen Shen. 2024. "Non-Contact Wind Turbine Blade Crack Detection Using Laser Doppler Vibrometers" Energies 17, no. 9: 2165. https://doi.org/10.3390/en17092165
APA StyleZabihi, A., Aghdasi, F., Ellouzi, C., Singh, N. K., Jha, R., & Shen, C. (2024). Non-Contact Wind Turbine Blade Crack Detection Using Laser Doppler Vibrometers. Energies, 17(9), 2165. https://doi.org/10.3390/en17092165








