Research on Off-Design Characteristics and Control of an Innovative S-CO2 Power Cycle Driven by the Flue Gas Waste Heat
Abstract
1. Introduction
1.1. Background
1.2. Study on S-CO2 Cycle Layout and Performance
1.3. Study on Off-Design Performance of S-CO2 Cycle
1.4. Purpose of This Work
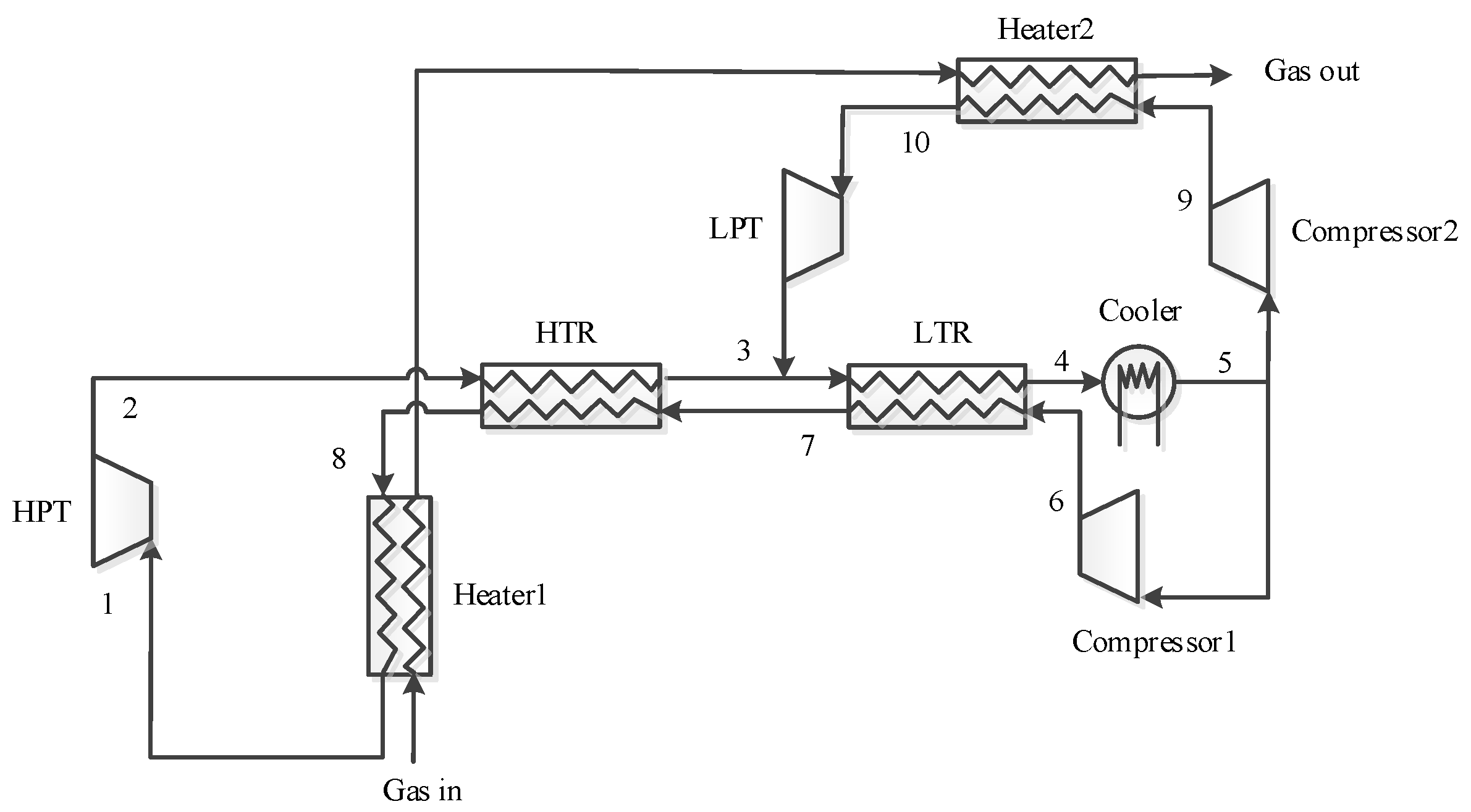
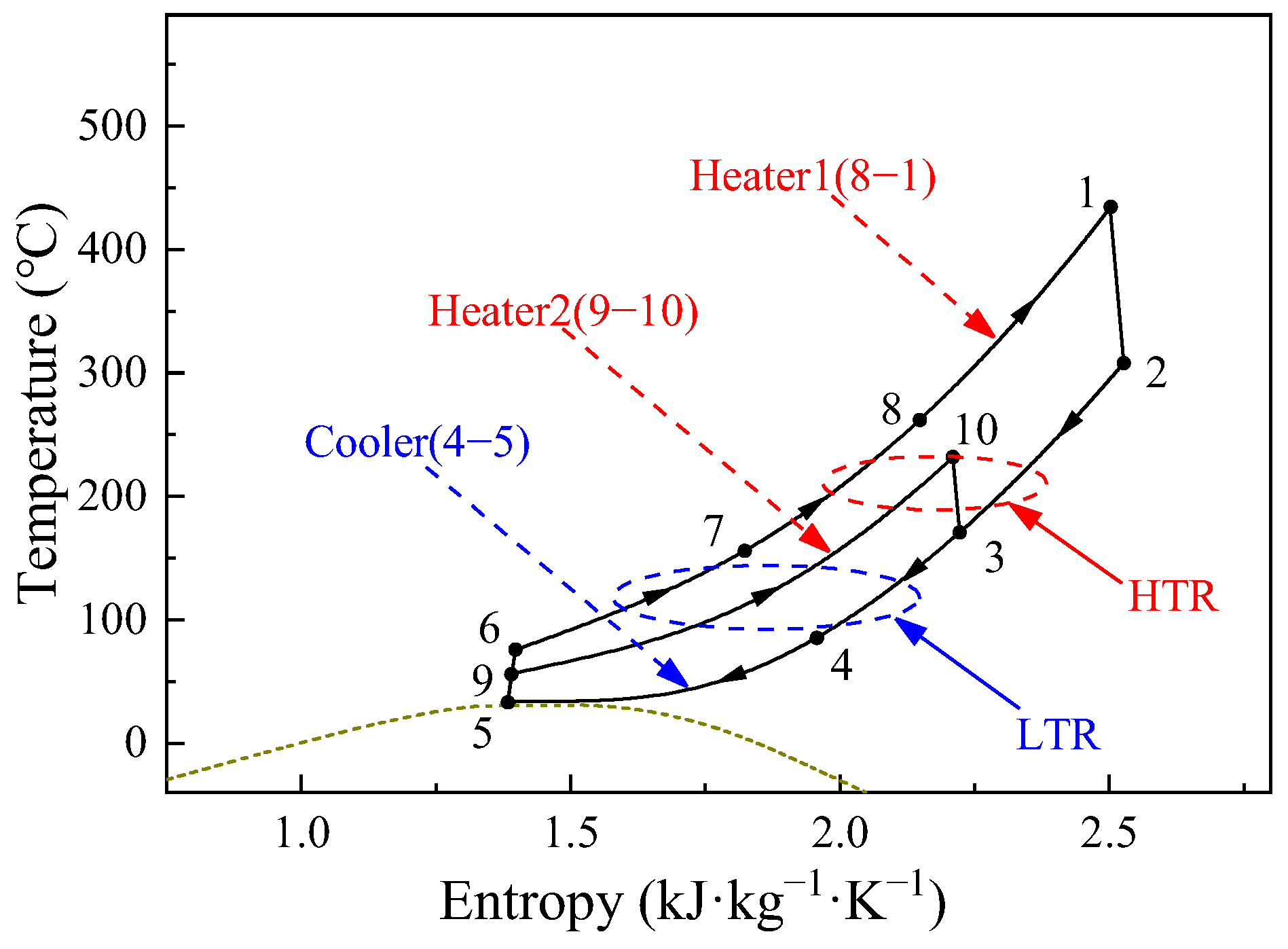
2. System Layout and Design Parameters
3. Structural Design and Off-Design Models of Heat Exchangers
- The pressure drop of the heat exchangers caused by inlet losses, outlet losses and acceleration effects is neglected.
- The fluids are fully mixed in the tube and flow one-dimensionally.
- The heat conduction between the fluids and the tube wall along the axial direction is ignored.
- The heat transfer with the external environment is ignored.
3.1. Structural Design of Heat Exchangers
3.2. Off-Design Models of Heat Exchangers
3.2.1. Off-Design Models of PCHEs
3.2.2. Off-Design Models of Shell-and-Tube Heat Exchangers
4. Off-Design Models of the Power Machinery
4.1. Modeling of Compressor
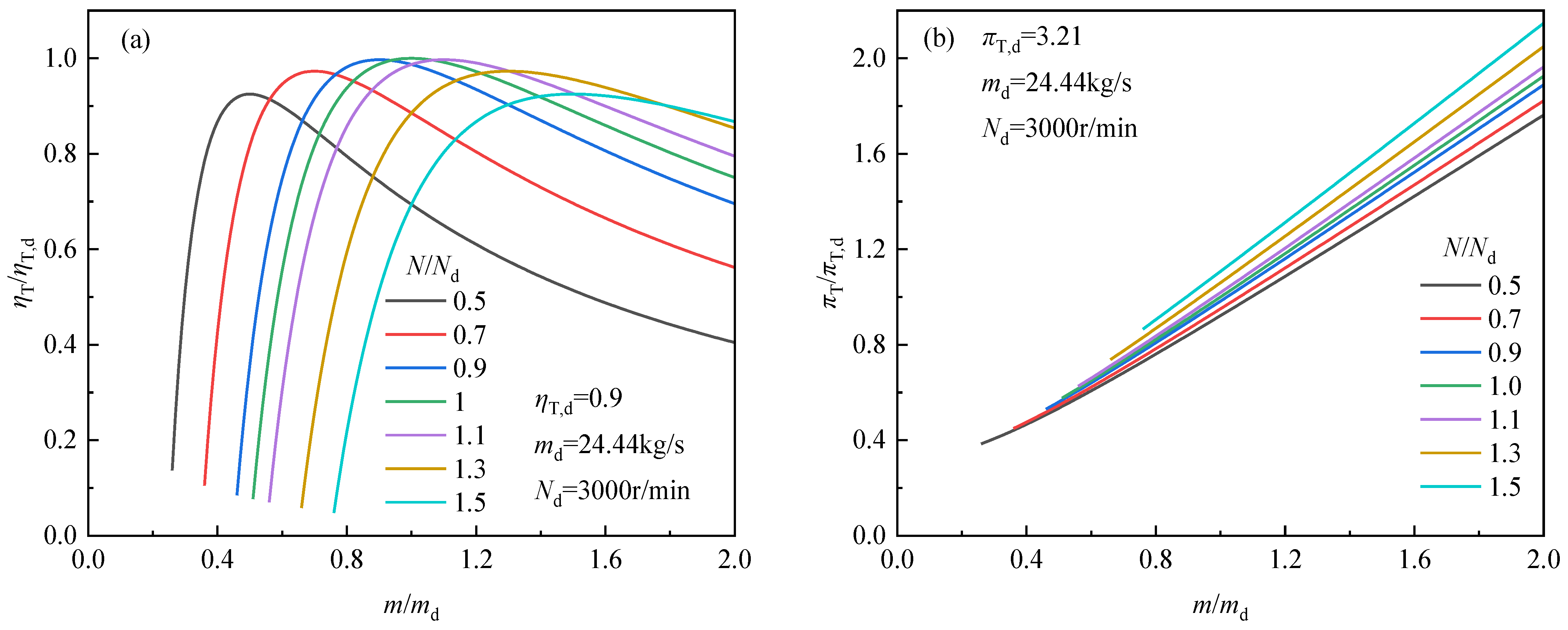
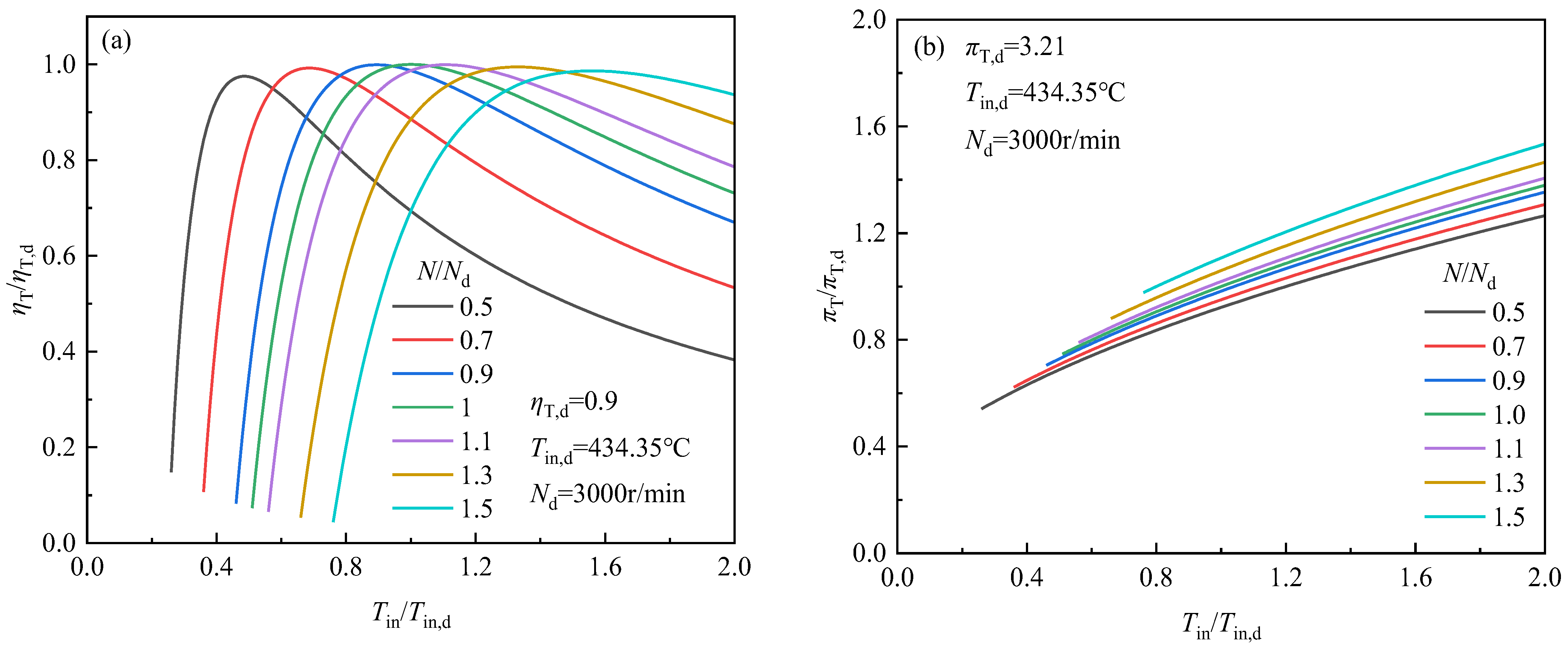
4.2. Modeling of Turbine
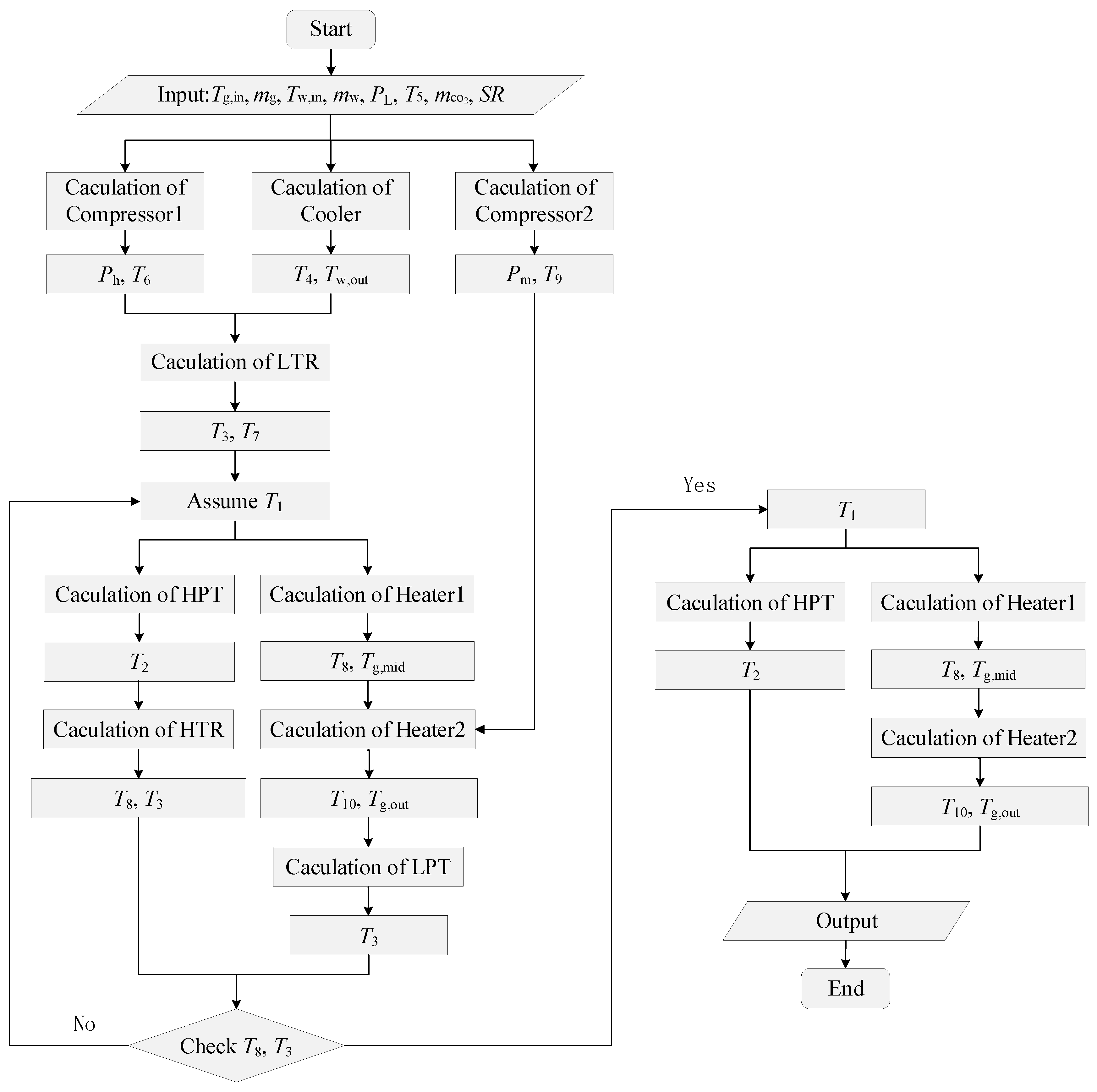
5. Off-Design Performance Calculation of S-CO2 Cycle
6. Effects of Key System Parameters
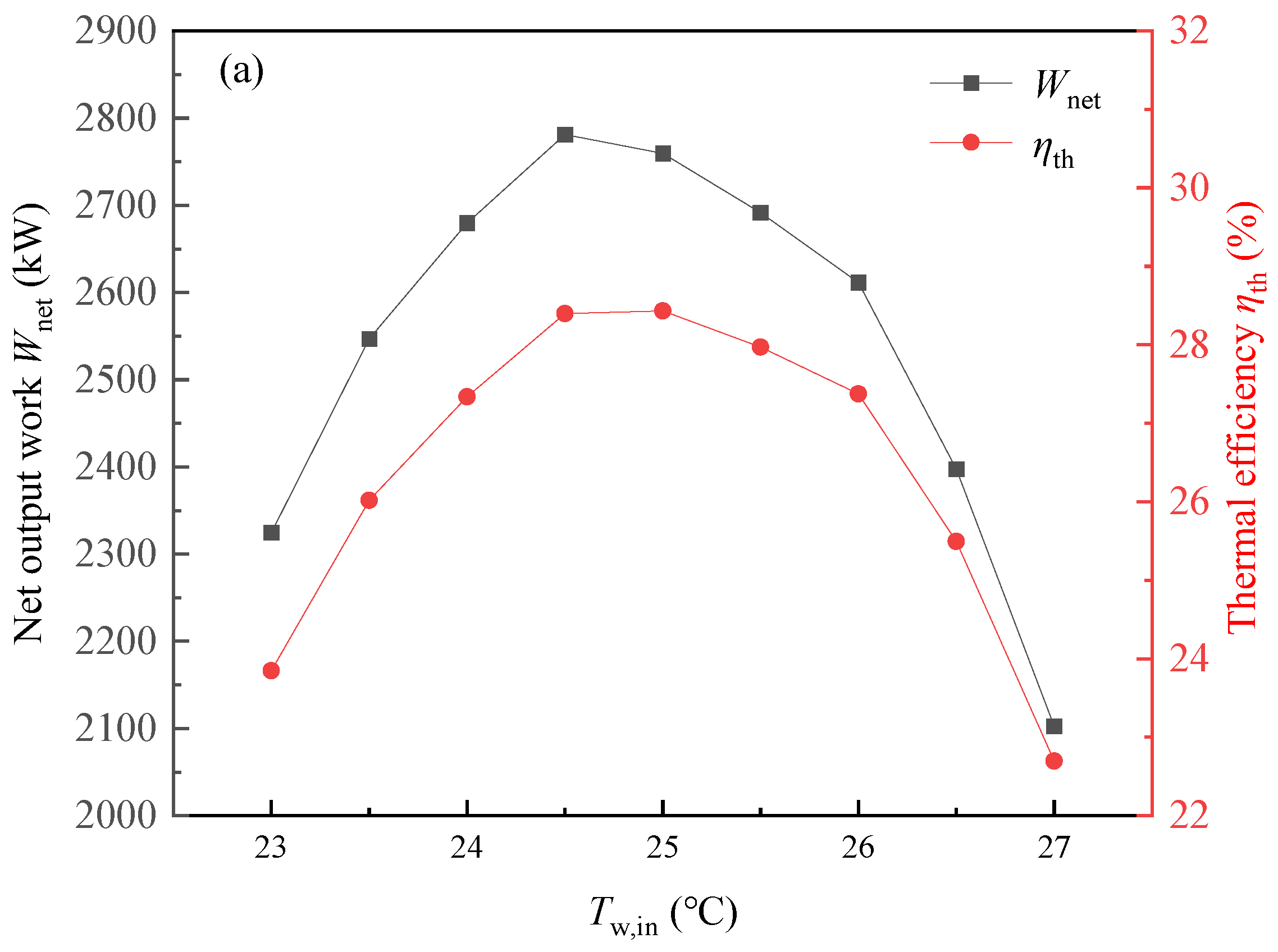
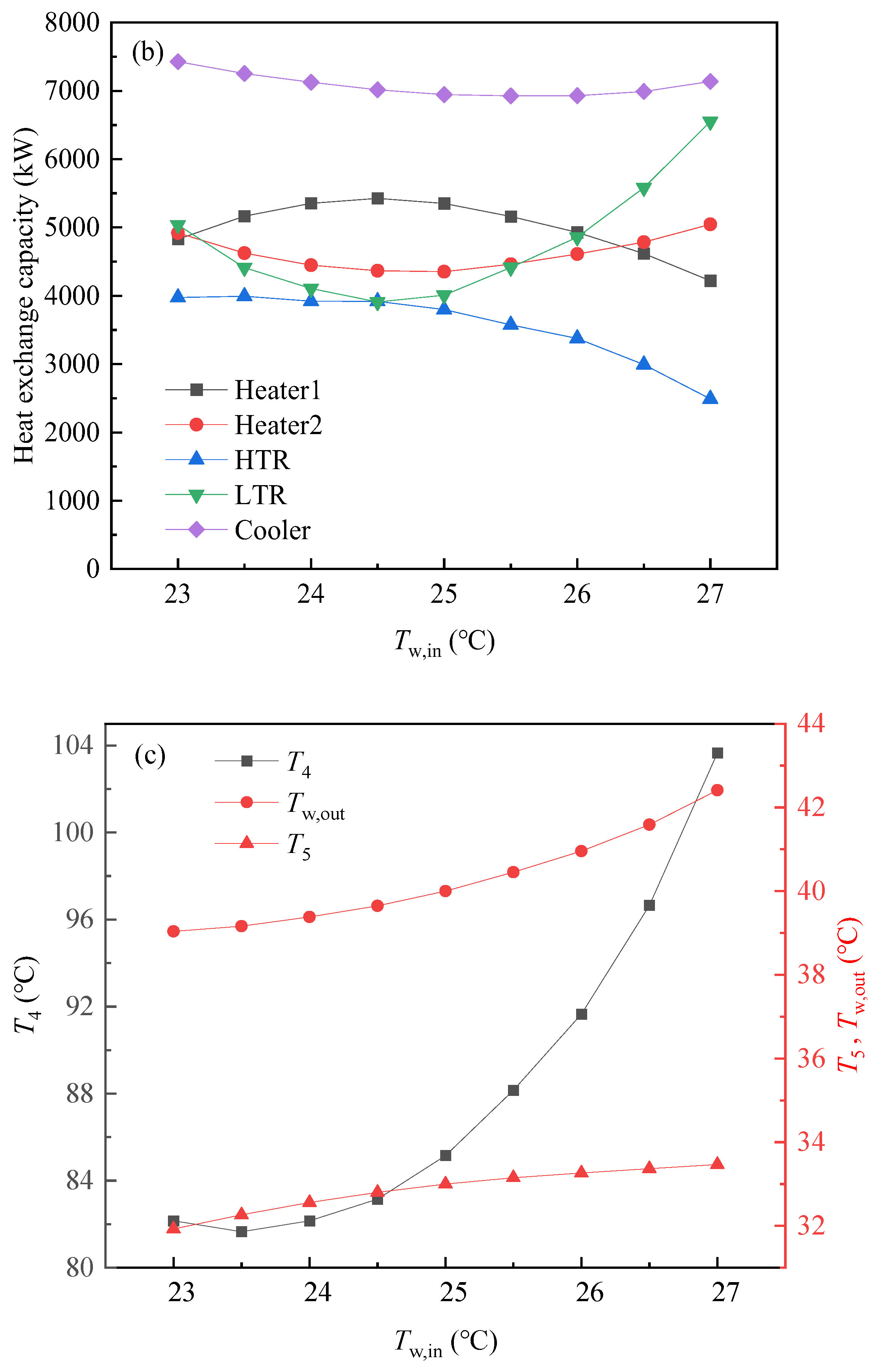
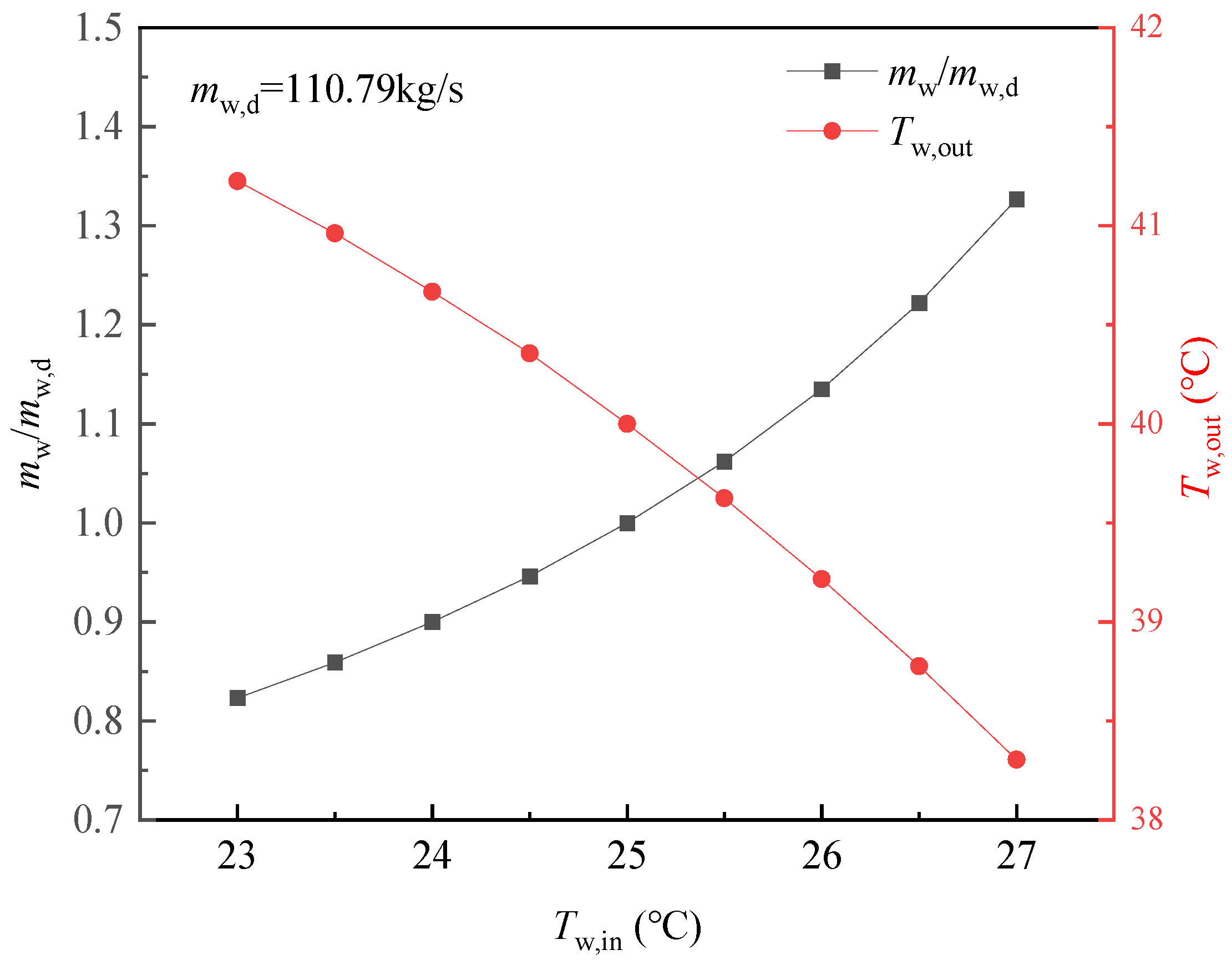
6.1. Effects of Cold Source Parameters
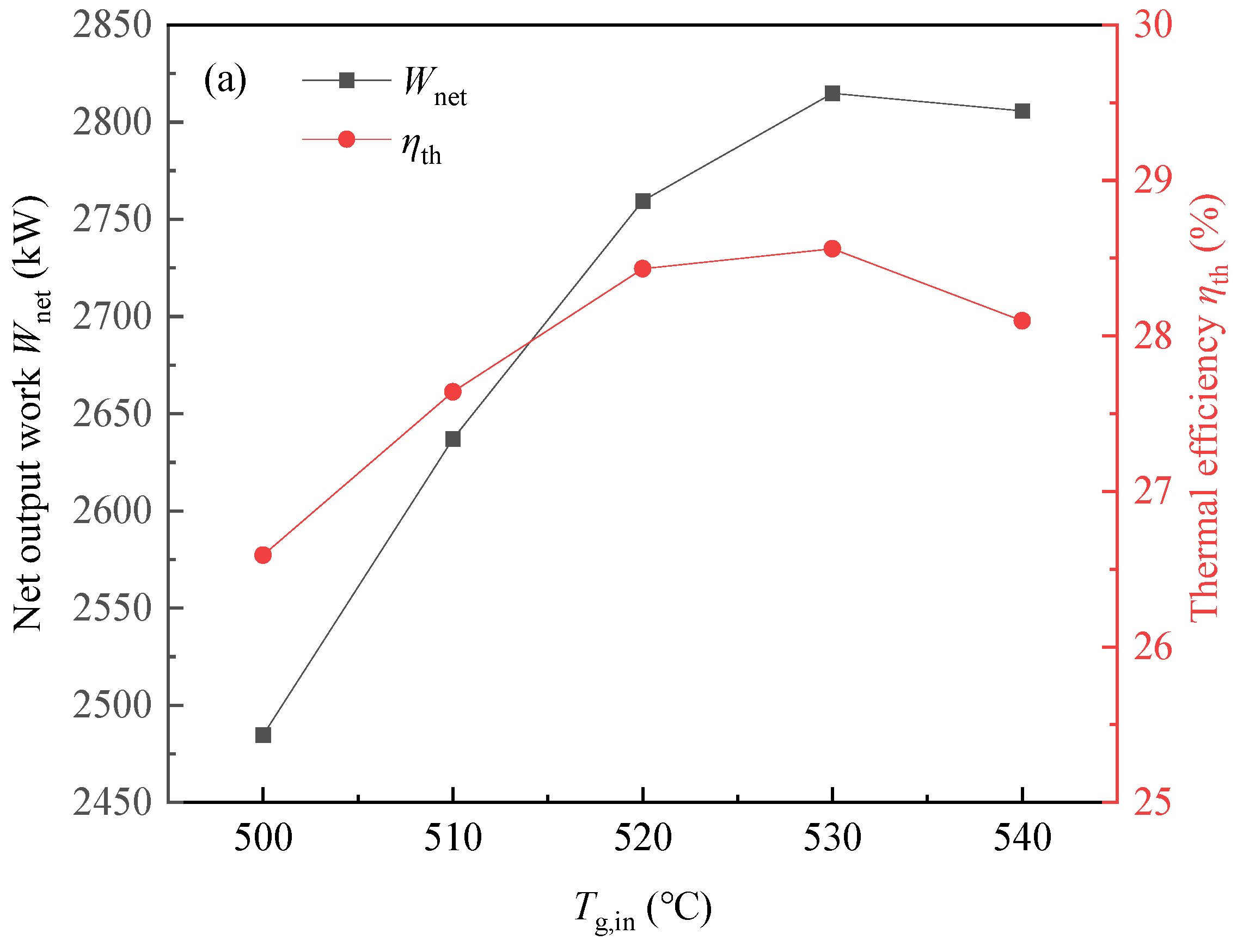
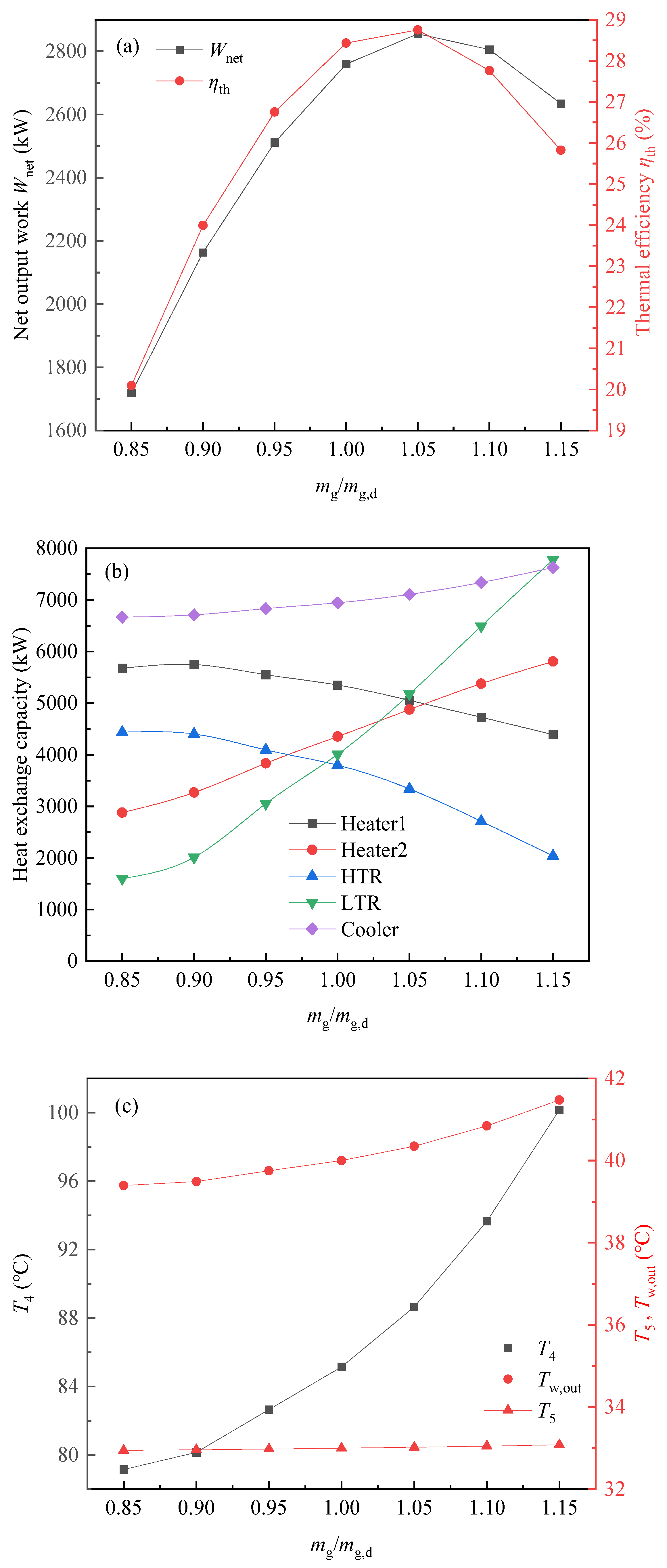
6.2. Effects of Heat Source Parameters
7. Control Strategy of the Cooling Process
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| S-CO2 | Supercritical carbon dioxide |
| PCHE | Printed circuit heat exchanger |
| ORC | Organic rankine cycle |
| SRC | Simple recuperative cycle |
| PC | Precompression cycle |
| RC | Recompression cycle |
| PCC | Partial cooling cycle |
| ICC | Intermediate cooling cycle |
| T-CO2 | Transcritical carbon dioxide |
| LTR | Low-temperature recuperator |
| HTR | High-temperature recuperator |
| HPT | High-pressure turbine |
| LPT | Low-pressure turbine |
| PPTD | Pinch point temperature difference (°C) |
| Wnet | Net output work (kW) |
| T | Temperature (°C) |
| P | Pressure (MPa) |
| s | Specific entropy (kJ/(kg·K)) |
| m | Mass flow rate (kg/s) |
| h | Specific enthalpy (kJ/kg) or convective heat transfer coefficients (kW/(m2·K)) |
| Q | Heat transfer rate (kW) |
| a | Number of channels |
| n | Number of single channel unit elements |
| A | Heat exchange area (m2) |
| k | Local heat transfer coefficient (kW/(m2·K)) |
| Rw | Conductive thermal resistance of the channel wall ((m2·K)/kW) |
| dhy | Hydraulic diameter (mm) |
| Nu | Nusselt number |
| Re | Reynold number |
| Pr | Prandtl number |
| uo | The flow velocity passing through the maximum cross-sectional area between pipes (m/s) |
| wch | Channel width (mm) |
| dch | Channel height (mm) |
| tp | Plate thickness (mm) |
| wf | Fin width (mm) |
| Aflow | Flow area of the channel (m2) |
| K | Total heat transfer coefficient (kW/(m2·K)) |
| Ai | Inside heat transfer area of heat transfer tube (m2) |
| Ao | Outside heat transfer area of heat transfer tube (m2) |
| Am | Average heat transfer area of heat transfer tube (m2) |
| d | Diameter (m) |
| de | Feature size (m) |
| Pt | Center distance of the tubes (m) |
| As | Maximum cross-sectional area between tubes (m2) |
| lb | Baffle spacing (m) |
| Di | Inner diameter of the shell (m) |
| nc | Number of tubes across the centerline of the bundle |
| Nt | Number of the tubes |
| Af | Shell side flow area (m2) |
| N | Rotor speed (r/min) |
| SR | Split ratio |
| Greek symbols | |
| ηth | Thermal efficiency (%) |
| λ | Thermal conductivity of the fluid (kW/(m·K)) |
| λw | Thermal conductivity of the channel wall or tube wall, (kW/(m·K)) |
| αi | Heat transfer coefficient inside the tube (kW/(m2·K)) |
| αo | Heat transfer coefficient outside the tube (kW/(m2·K)) |
| δ | Thickness of the tube wall (m) |
| ρ | Density (kg/m3) |
| μ | Dynamic viscosity (kg/(m·s)) |
| πC | Compression ratio |
| πT | Expansion ratio |
| Subscripts | |
| c | Critical or cold fluid |
| ch | Channel |
| h | Hot fuid or high pressure |
| i | Inside |
| o | Outside |
| in | Inlet |
| w | Wall or water |
| out | Outlet |
| L | Low pressure |
| m | Medium pressure |
| g | Flue gas |
| mid | Flue gas outlet of Heater1 |
| C | Compressor |
| d | Design condition |
| T | Turbine |
References
- Chen, S.; Zheng, Y.; Wu, M.; Hu, J.; Xiang, W. Thermodynamic analysis of oxy-fuel combustion integrated with the sCO2 Brayton cycle for combined heat and power production. Energy Convers. Manag. 2021, 232, 113869. [Google Scholar] [CrossRef]
- Kareem, P.H.; Ali, M.; Tursoy, T.; Khalifa, W. Testing the Effect of Oil Prices, Ecological Footprint, Banking Sector Development and Economic Growth on Energy Consumptions: Evidence from Bootstrap ARDL Approach. Energies 2023, 16, 3365. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M. The Thermal Economy of a Circulating Medium and Low Temperature Waste Heat Recovery System of Industrial Flue Gas. Int. J. Heat Technol. 2021, 39, 1680–1688. [Google Scholar] [CrossRef]
- Gao, B.; Sun, Z. Marginal CO2 and SO2 Abatement Costs and Determinants of Coal-Fired Power Plants in China: Considering a Two-Stage Production System with Different Emission Reduction Approaches. Energies 2023, 16, 3488. [Google Scholar] [CrossRef]
- Larjola, J. Electricity from industrial waste heat using high-speed organic Rankine cycle (ORC). Int. J. Prod. Econ. 1995, 41, 227–235. [Google Scholar] [CrossRef]
- Wang, E.; Peng, N. A Review on the Preliminary Design of Axial and Radial Turbines for Small-Scale Organic Rankine Cycle. Energies 2023, 16, 3423. [Google Scholar] [CrossRef]
- Loni, R.; Najafi, G.; Bellos, E.; Rajaee, F.; Mazlan, M. A review of industrial waste heat recovery system for power generation with Organic Rankine Cycle: Recent Challenges and Future Outlook. J. Clean. Prod. 2020, 287, 125070. [Google Scholar] [CrossRef]
- Carrillo Caballero, G.; Cardenas Escorcia, Y.; Venturini, O.J.; Silva Lora, E.E.; Alviz Meza, A.; Mendoza Castellanos, L.S. Unidimensional and 3D Analyses of a Radial Inflow Turbine for an Organic Rankine Cycle under Design and Off-Design Conditions. Energies 2023, 16, 3383. [Google Scholar] [CrossRef]
- Zhang, R.; Su, W.; Lin, X.; Zhou, N.; Zhao, L. Thermodynamic analysis and parametric optimization of a novel S–CO2 power cycle for the waste heat recovery of internal combustion engines. Energy 2020, 209, 118484. [Google Scholar] [CrossRef]
- Guo, J.; Li, M.; He, Y.; Jiang, T.; Ma, T.; Xu, J.; Cao, F. A systematic review of supercritical carbon dioxide(S-CO2) power cycle for energy industries: Technologies, key issues, and potential prospects. Energy Convers. Manag. 2022, 258, 115437. [Google Scholar] [CrossRef]
- Yu, A.; Xing, L.; Su, W.; Liu, P. State-of-the-art review on the CO2 combined power and cooling system: System configuration, modeling and performance. Renew. Sustain. Energy Rev. 2023, 188, 113775. [Google Scholar] [CrossRef]
- White, M.T.; Bianchi, G.; Chai, L.; Tassou, S.A.; Sayma, A.I. Review of supercritical CO2 technologies and systems for power generation. Appl. Therm. Eng. 2021, 185, 116447. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, X.; Su, W.; Xing, L.; Zhou, N. Thermal-economic analysis of a novel solar power tower system with CO2-based mixtures at typical days of four seasons. Energy 2023, 276, 127602. [Google Scholar] [CrossRef]
- Rahbari, H.R.; Mandø, M.; Arabkoohsar, A. A review study of various High-Temperature thermodynamic cycles for multigeneration applications. Sustain. Energy Technol. Assess. 2023, 57, 103286. [Google Scholar] [CrossRef]
- Liao, J.; Liu, X.; Zheng, Q.; Zhang, H. Analysis of supercritical CO2 power generation cycle characteristics. Therm. Power Eng. 2016, 31, 40−46+149−150. [Google Scholar] [CrossRef]
- Fang, Z.; Dong, X.; Tang, X. Research on gas engine waste heat recovery system based on S-CO2. Combust. Sci. Technol. 2023, 29, 543–551. [Google Scholar]
- Fu, J. Research on Optimization of Supercritical Carbon Dioxide Brayton Cycle Thermodynamic System. Master’s Thesis, North China Electric Power University, Beijing, China, 2020. [Google Scholar]
- Lock, A.; Bone, V. Off-design operation of the dry-cooled supercritical CO2 power cycle. Energy Convers. Manag. 2022, 251, 114903. [Google Scholar] [CrossRef]
- Duniam, S.; Veeraragavan, A. Off-design performance of the supercritical carbon dioxide recompression Brayton cycle with NDDCT cooling for concentrating solar power. Energy 2019, 187, 115992. [Google Scholar] [CrossRef]
- Xiao, G.; Yu, A.; Lin, X.; Su, W.; Zhou, N. Constructing a novel supercritical carbon dioxide power cycle with the capacity of process switching for the waste heat recovery. Int. J. Energy Res. 2022, 46, 5099–5118. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.-S.; Bai, K.-L.; Li, J. Thermodynamic analysis and parametric optimization of CDTPC-ARC based on cascade use of waste heat of heavy-duty internal combustion engines (ICEs). Appl. Therm. Eng. 2016, 106, 661–673. [Google Scholar] [CrossRef]
- Huang, J.; Han, Z.; Guo, J.; Huai, X. Research progress of supercritical CO2 microchannel heat exchangers. J. Refrig. 2023, 44, 1–14. [Google Scholar]
- Rao, Z.; Xue, T.; Huang, K.; Liao, S. Multi-objective optimization of supercritical carbon dioxide recompression Brayton cycle considering printed circuit recuperator design. Energy Convers. Manag. 2019, 201, 112094. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, Y.; Wang, F.; Wang, P.; Liu, J. In Proceedings of the 11th International Symposium on Heating, Ventilation and Air Conditioning (ISHVAC 2019): Volume III: Buildings and Energy; Springer: Berlin/Heidelberg, Germany, 2020.
- Ngo, T.L.; Kato, Y.; Nikitin, K.; Tsuzuki, N. New printed circuit heat exchanger with S-shaped fins for hot water supplier. Exp. Therm. Fluid Sci. 2006, 30, 811–819. [Google Scholar] [CrossRef]
- Gnielinski, V. New equations for heat and mass transfer in the turbulent flow in pipes and channels. In NASA STI/Recon Technical Report A; NASA/ADS: Washington, DC, USA, 1975; Volume 41. [Google Scholar]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 1985, 12, 3–22. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, J.; Wang, S.; Zheng, W. Thermodynamic calculation and numerical simulation of shell-and-tube heat exchangers. Non-Ferr. Metall. Energy Effic. 2012, 28, 34−38+28. [Google Scholar]
- Tun, C.M.; Fane, A.G.; Matheickal, J.T.; Sheikholeslami, R. Membrane distillation crystallization of concentrated salts-Flux and crystal formation. J. Membr. Sci. 2005, 257, 144–155. [Google Scholar] [CrossRef]
- Qi, F. Advances in heat transfer calculation methods for shell-and-shell heat exchangers without phase change. Pharm. Eng. 2002, 23, 29–36. [Google Scholar]
- Jeong, Y.; Son, S.; Cho, S.K.; Baik, S.; Lee, J.I. Evaluation of supercritical CO2 compressor off-design performance prediction methods. Energy 2020, 213, 119071. [Google Scholar] [CrossRef]
- Wang, W.; Cai, R.; Zhang, N. General characteristics of single shaft microturbine set at variable speed operation and its optimization. Appl. Therm. Eng. 2004, 24, 1851–1863. [Google Scholar] [CrossRef]
- Zhang, N.; Cai, R. Analytical solutions and typical characteristics of part-load performance of single shaft gas turbine and its cogeneration. Energy Convers. Manag. 2002, 43, 1323–1337. [Google Scholar] [CrossRef]
- Poškas, R.; Sirvydas, A.; Kulkovas, V.; Poškas, P.; Jouhara, H.; Miliauskas, G.; Puida, E. Flue Gas Condensation in a Model of the Heat Exchanger: The Effect of the Cooling Water Flow Rate and Its Temperature on Local Heat Transfer. Appl. Sci. 2022, 12, 12650. [Google Scholar] [CrossRef]
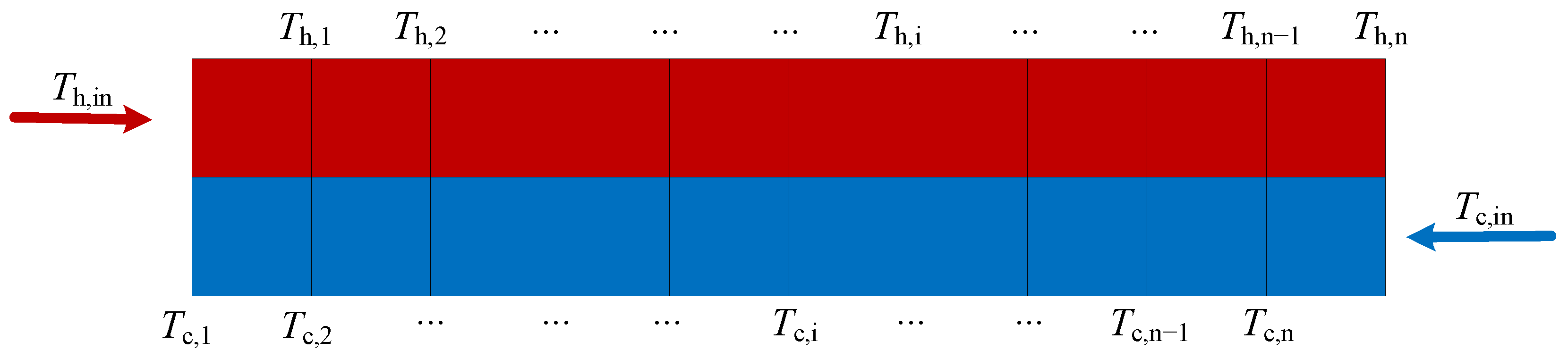

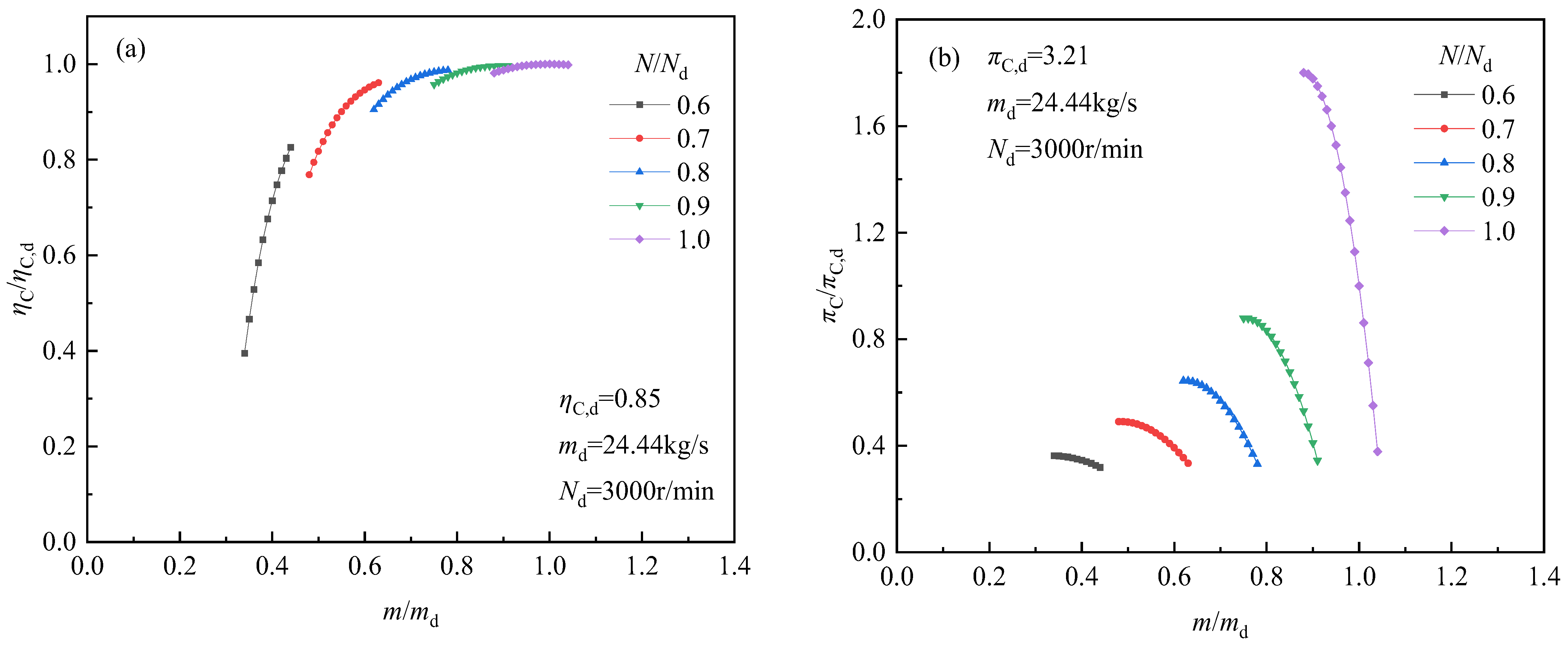




| Flue Gas Components | Value | Flue Gas Parameters | Value |
|---|---|---|---|
| N2 (%) | 71.6 | Flue gas inlet temperature (°C) | 520 |
| CO2 (%) | 15.1 | Flue gas mass flow (kg/s) | 20 |
| O2 (%) | 7.8 | Flue gas pressure (MPa) | 0.1 |
| H2O (%) | 5.5 |
| Design Parameters | Value |
|---|---|
| HPT inlet temperature (°C) | 434.35 |
| Compressor inlet temperature (°C) | 33 |
| HPT inlet pressure (MPa) | 25 |
| LPT inlet pressure (MPa) | 15 |
| Compressor inlet pressure (MPa) | 7.8 |
| PPTD of Heater1 (°C) | 20 |
| PPTD of Heater2 (°C) | 20 |
| PPTD of HTR (°C) | ≥5 |
| PPTD of LTR (°C) | ≥5 |
| Isentropic efficiency of Compressor [20] | 0.85 |
| Isentropic efficiency of Turbine [20] | 0.9 |
| Energy efficiency coefficient of heat exchanger [20] | 0.9 |
| State Point | m (kg/s) | P (MPa) | T (°C) | s (kJ/(kg·K)) | h (kJ/kg) |
|---|---|---|---|---|---|
| 1 | 24.44 | 25 | 434.35 | 2.5 | 887.36 |
| 2 | 24.44 | 7.8 | 307.9 | 2.53 | 762.17 |
| 3 | 37.94 | 7.8 | 170.52 | 2.22 | 606.76 |
| 4 | 37.94 | 7.8 | 85.16 | 1.96 | 501.11 |
| 5 | 37.94 | 7.8 | 33 | 1.38 | 318.06 |
| 6 | 24.44 | 25 | 75.32 | 1.4 | 349.02 |
| 7 | 24.44 | 25 | 155.6 | 1.82 | 513.01 |
| 8 | 24.44 | 25 | 261.73 | 2.15 | 668.43 |
| 9 | 13.5 | 15 | 55.66 | 1.39 | 331.95 |
| 10 | 13.5 | 15 | 231.66 | 2.21 | 654.43 |
| Flue gas inlet | 20 | 0.1 | 520 | 7.2 | 959.9 |
| Flue gas outlet of Heater1 | 20 | 0.1 | 281.73 | 6.8 | 692.32 |
| Flue gas outlet | 20 | 0.1 | 75.69 | 6.31 | 474.63 |
| cooling water inlet | 110.79 | 0.1 | 25 | 0.37 | 104.92 |
| cooling water outlet | 110.79 | 0.1 | 40 | 0.57 | 167.62 |
| Parameters | HTR | LTR | Cooler |
|---|---|---|---|
| Channel width (mm) | 1 | 1 | 1 |
| Channel depth (mm) | 1 | 1 | 1 |
| Plate thickness (mm) | 1.5 | 1.5 | 1.5 |
| Fin width (mm) | 0.5 | 0.5 | 0.5 |
| Number of channels per layer | 300 | 300 | 300 |
| Number of plies | 300 | 300 | 300 |
| Single channel heat transfer area (m2) | 0.025 | 0.05 | 0.036 |
| Parameters | Heater1 | Heater2 |
|---|---|---|
| Number of one-way tubes | 484 | 237 |
| One way tube length (m) | 16.64 | 40.44 |
| Length of tube (m) | 5 | 7 |
| Number of tube sides | 4 | 6 |
| Number of shell sides | 2 | 2 |
| Number of centerline tubes | 48 | 41 |
| Calculated nominal diameter (m) | 1.77 | 1.51 |
| Nominal diameter (m) | 1.8 | 1.6 |
| Inside diameter of tube (m) | 0.02 | 0.02 |
| Outer diameter of tube (m) | 0.025 | 0.025 |
| Tube wall thickness (m) | 0.0025 | 0.0025 |
| Tube pitch (m) | 0.032 | 0.032 |
| Pipe flow area (m2) | 0.0003 | 0.0003 |
| Baffle thickness (m) | 0.012 | 0.012 |
| Baffle spacing (m) | 0.3 | 0.3 |
| Number of baffles | 52 | 126 |
| Total heat transfer area (m2) | 596.97 | 706.9 |
| Area margin | 17.20% | 1.65% |
| CO2 tube velocity (m/s) | 0.75 | 0.75 |
| Flue gas center velocity (m/s) | 204.26 | 142.83 |
| Pipe pressure drop (kPa) | 7.93 | 17.41 |
| Pipe volume (m3) | 3.04 | 3.13 |
| Heat transfer coefficient of CO2 (W/(m2·k)) | 535.34 | 575.07 |
| Heat transfer coefficient of flue gas (W/(m2·k)) | 380.22 | 324.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Liang, Y.; Ding, R.; Xing, L.; Su, W.; Lin, X.; Zhou, N. Research on Off-Design Characteristics and Control of an Innovative S-CO2 Power Cycle Driven by the Flue Gas Waste Heat. Energies 2024, 17, 1871. https://doi.org/10.3390/en17081871
Hu S, Liang Y, Ding R, Xing L, Su W, Lin X, Zhou N. Research on Off-Design Characteristics and Control of an Innovative S-CO2 Power Cycle Driven by the Flue Gas Waste Heat. Energies. 2024; 17(8):1871. https://doi.org/10.3390/en17081871
Chicago/Turabian StyleHu, Shaohua, Yaran Liang, Ruochen Ding, Lingli Xing, Wen Su, Xinxing Lin, and Naijun Zhou. 2024. "Research on Off-Design Characteristics and Control of an Innovative S-CO2 Power Cycle Driven by the Flue Gas Waste Heat" Energies 17, no. 8: 1871. https://doi.org/10.3390/en17081871
APA StyleHu, S., Liang, Y., Ding, R., Xing, L., Su, W., Lin, X., & Zhou, N. (2024). Research on Off-Design Characteristics and Control of an Innovative S-CO2 Power Cycle Driven by the Flue Gas Waste Heat. Energies, 17(8), 1871. https://doi.org/10.3390/en17081871





