Abstract
This paper presents the results of a comprehensive investigation into the comparative analysis and design optimization of ferrite-based surface permanent magnet vernier machines (SPMVMs). While SPMVMs boast a simple mechanical structure and enhanced torque density attributed to the flux modulation effect, they suffer from a persistent challenge of low power factor. Several factors hinder the adoption of low-cost ferrite magnets in SPMVMs. First, ferrite magnets are prone to irreversible demagnetization, constraining the allowable range of magnet thickness. Second, the reduced residual magnetic flux density of ferrite magnets exacerbates the decrease in power factor and machine efficiency. Thus, achieving optimal performance in ferrite-based SPMVMs necessitates the careful selection of various design parameters. To address these issues, this study employs a surrogate-based metaheuristic optimization algorithm with adaptive sampling to identify the optimal solution. Additionally, the integration of a Halbach array is explored to further enhance the performance of the three-slot/two-pole SPMVM topology. Subsequently, two ferrite-based SPMVM baseline models—one with a conventional SPM structure and another with a Halbach magnet array—are thoroughly designed, optimized, and subjected to detailed performance analysis using the 2D finite element method.
1. Introduction
The demand for compact designs and high-torque, high-efficiency characteristics of electric machines has driven research into new machine topologies in recent years. Among the various topologies, machine types that utilize the flux modulation principle have gained significant attention due to their high torque density characteristics. In the last decade, a significant number of research papers on flux modulation machines have been reported on a variety of topics, including working principles [1,2,3], various topologies [4,5,6], and application-specific performance characteristics [7,8,9].
Among the flux modulation machines, surface permanent magnet vernier machine (SPMVM) is quite popular due to its simple mechanical structure and higher torque density owing to the flux modulation effect. Flux modulation machines have the potential to generate higher power compared to conventional PM machines because they have relatively higher shear stress at the same airgap volume and rotational speed [1,3]. Nevertheless, the low power factor of SPMVM is one of its major limiting factors. In addition, it is difficult to avoid using expensive NdFeB magnets when considering the risk of magnet demagnetization because the flux modulation effect is based on the slot harmonics of the airgap permeance, leading to the use of thin magnets [10,11]. Hence, the design of a ferrite-based SPMVM poses many challenges in light of these factors.
Several past studies have discussed the unique design challenges of ferrite-based SPMVM designs in more detail. One prominent issue is the low power factor associated with these motors, which is a problem that is exacerbated when replacing NdFeB magnets with low-cost ferrite alternatives due to their low residual flux density [12]. Achieving higher machine efficiency is also a challenge due to the relatively low residual flux density of ferrite magnets [13]. Another problem is mitigating the risk of demagnetization, which limits the minimum allowable dimensions of permanent magnets. In addition, depending on the application, considerations such as torque ripple and fault tolerance emerge as critical design factors. Careful design is also essential to avoid localized magnetic saturation, which can reduce shear stress and consequently output power.
Several studies have presented design techniques to improve the performance of ferrite-based SPMVM. For example, ref. [14] shows that the consequent pole vernier machine is a proper type to utilize low-cost ferrite magnets because of its advantage in increasing the magnet thickness. Halbach magnet arrays are known to have magnetic self-shunting characteristics, which means that the magnetic field on one side of the Halbach array can be enhanced while the magnetic field on the other side can be significantly reduced. This allows the power factor of the SPMVM to be improved without sacrificing magnet flux and torque [15,16]. To achieve high torque density at reasonable cost, a hybrid-excited SPMVM [17] utilizing both NdFeB and ferrite magnets has been proposed.
In most cases, machine designers need to solve multiple design issues simultaneously. The process of identifying the optimal solution considering these conflicting design goals involves tradeoff analysis, which simultaneously evaluates various design requirements, goals, and constraints to determine the most desirable design that is physically feasible. Unfortunately, this important issue has received little attention to date, especially in the family of vernier PM machines. This paper aims to fill this research gap by utilizing multi-objective design optimization techniques to compensate for the inherent shortcomings of the ferrite-based SPMVM. The main contributions of this paper are summarized as follows:
- (1)
- Step-by-step analysis of the systematic design optimization process of ferrite-based SPMVMs using a metaheuristic algorithm with adaptive sampling;
- (2)
- Comprehensive comparative study of ferrite-based SPMVMs with and without Halbach magnet array;
- (3)
- Thorough performance analysis of ferrite-based SPMVMs over a wide range of operating regions.
Presenting an approach to solve this complex problem, we first describe the basic operating principles of SPMVMs and the key design variables. Then, a thorough performance analysis of ferrite-based SPMVM is performed with and without the Halbach magnet array, considering the operational safety margin and reasonable design constraints. The main design focus was kept on the torque density, power factor, and efficiency. The results of the design optimization demonstrate the challenges inherent in achieving satisfactory power factor and efficiency for ferrite-based SPMVMs compared to NdFeB-based SPMVMs. As a result, we explore the potential benefits of incorporating a Halbach magnet array to improve machine performance. Finally, two baseline ferrite-based SPMVMs were designed and optimized, and their detailed performance characteristics, including demagnetization risk, performance map analysis, and material cost, were comprehensively evaluated using 2D finite element analysis (FEA).
2. Basic Operation Principles and Baseline Designs
Similar to other flux modulation machines, SPMVMs work based on the principle of magnetic gearing effect, which is also known as the flux modulation effect. The basic operating principle may be best described by the permeance distribution theory [1]. To help the reader’s understanding, this section explains the torque mechanism of SPMVM based on analytical expressions and provides an explanation of the trade-off relationship between output torque and power factor.
Rotating electrical machines generate output power by creating a shear stress in the airgap. The shear stress of a vernier PM machine can be expressed as follows:
where Ks is the surface current density, B0 and B1 are the main and the modulation fluxes, and Gr is the gear ratio of the flux modulation machine. As shown in (2), the gear ratio depends on the ratio between the number of rotor pole pairs Zr and the number of modulation pole pairs Pmod. The number of modulation pole pairs can be expressed as the absolute difference between the number of modulation teeth Zs and the number of rotor pole pairs Zr [4].
The surface current density Ks is proportional to the series winding turns Nph and the amplitude of phase current Iph and inversely proportional to the airgap diameter Dg, as shown in the following [4]:
Using (1), the output torque To of SPM vernier machine can be derived as
where Vg is the airgap volume of the machine. Alternatively, the output torque can be expressed as follows [1]:
where Br is the residual flux density, μr is the recoil permeability of permanent magnet, k1q is the fundamental winding factor, lstk is the stack length, gm is the magnet thickness, g is the effective airgap length, Kconv is the torque coefficient for a conventional SPM machine, and Kadd is the additional torque coefficient for a SPMVM. As shown in (1), the additional torque component associated with Kadd is proportional to the product of Ks, Gr, and B1 [1].
The power factor of SPMVM can be expressed as follows [3]:
where ωe is the synchronous angular frequency, Lq is the q-axis inductance, iq is the q-axis current, Rs is the stator resistance, and λpm is the magnet flux linkage. Neglecting the resistive voltage drop, (6) can be further simplified as:
It was discussed in [3] that the power factor generally increases when magnetic loading is high and electrical loading is low, as shown in (7). It was also pointed out that there is a trade-off between power factor and gear ratio, and that balancing the power factor and output torque requires some sacrifice of additional torque due to magnetic gearing effects. While many analytical approaches have been proposed to overcome this problem, the use of numerical analysis is indispensable to clearly define the trade-offs between different objective functions and constraints that consider magnetic saturation and complex machine geometries.
The remainder of this section describes the 2D FEA model setup for SPMVM performance analysis. The basic structure of the SPMVM with outer rotor configuration used in this study is shown in Figure 1a. The nomenclature of the main design variables shown in Figure 2 is given in Table 1. Considering the benefits associated with employing a Halbach array, a second baseline design utilizing a Halbach PM array was investigated, as shown in Figure 1b. The stator structure shown in Figure 1 is equipped with the most common fractional slot winding configuration with a ratio of three-slot/two-pole, or 1/2 slot-per-pole-per-phase (SPP). Figure 2 shows a cross-section of the baseline SPMVM with key design parameters, and Table 1 provides information about the key constants and parameters of the baseline machine shown in Figure 1.
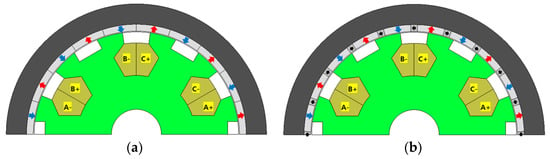
Figure 1.
Two baseline SPMVM designs and conventional SPM counterpart. (a) Design I (without Halbach), (b) Design II (with Halbach).
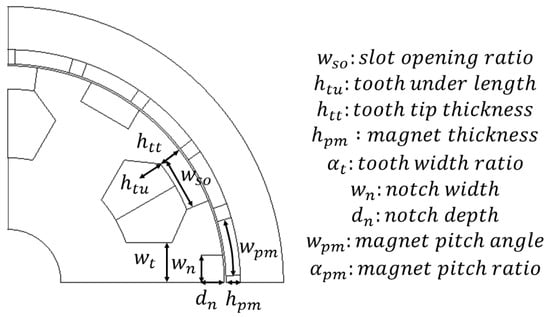
Figure 2.
Key design variables.

Table 1.
Key design constants and variables information.
3. Initial Performance Comparison: NdFeB SPMVM vs. Ferrite SPMVM
As mentioned in Section 1, there are several design issues associated with the ferrite-based SPMVM. To better highlight these issues, an SPM vernier generator based on NdFeB magnets designed in [11] is taken as a reference. The main design parameters and simulation conditions of the reference machine are given in Table 2. It is worth noting that due to the presence of the stator notches, the number of stator modulation teeth was counted as twice the number of slots.

Table 2.
Main design parameters of reference machine [11].
The key electromagnetic performance parameters of the reference model shown in Table 2 were obtained using 2D FEA. For the sake of comparison, a counterpart reference model is additionally designed with ferrite magnets. The electromagnetic performances of the original reference model (labeled as Design A) and its counterpart ferrite-based machine (labeled as Design B) are comparatively presented in Table 3. Figure 3 shows the B–H curve characteristics at 20 °C for the NdFeB and ferrite magnets used in the simulation, respectively. Both curves are very linear in the second quadrant, while the knee point for the ferrite magnet appears as it enters the third quadrant. This curve shows that ferrite magnets can be easily demagnetized by an external H-field of much smaller amplitude compared to NdFeB magnets.

Table 3.
Key performance comparisons between reference NdFeB model and ferrite model.
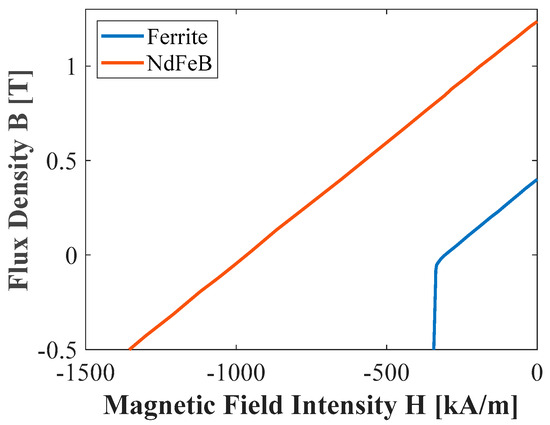
Figure 3.
Magnet B-H curves: NdFeB (red) vs. ferrite (blue) at 20 °C.
As given in Table 3, at the same surface current density, the torque per airgap volume of Design B is approximately 33% of that of Design A. This is clearly due to the much lower residual flux density of the ferrite magnets. In addition, the lower residual flux density of Design B adversely affects the power factor as well as the overall machine efficiency. Moreover, the fact that Design B’s magnets are more susceptible to irreversible demagnetization indicates that Design B’s performance may degrade further under the influence of large d-axis currents (e.g., fault conditions or deep flux-weakening operations).
The following sections detail the optimal design process for improving conflicting design goals while meeting challenging constraints. To maximize the performance of the ferrite SPMVM, two variants are considered for Design B. The machine without the Halbach array is denoted as Design I and the machine with the Halbach array is denoted as Design II.
4. Design Optimization
4.1. Surrogate-Based Optimization Algorithm
For the efficient design optimization of the baseline ferrite SPMVMs, the surrogate-based stochastic optimization process introduced in [18] was used. This process has been proven to save approximately 93% of computational time compared to traditional FEA-based optimization methods while maintaining accuracy to within 1%. Moreover, the Gaussian process upper confidence bound (GP-UCB)-based adaptive sampling technique was also used to further improve the performance of the stochastic optimization process.
The presented process in Figure 4 presents an optimal design method for an electric machine, comprising (1) selecting key design variables and setting the scope so as to improve an objective function, such as torque density, power factor, and efficiency, (2) constructing a mathematical approximation model (i.e., surrogate model) that defines the correlation between design variables and objective functions to efficiently perform design space exploration, (3) using the surrogate model to reduce the computation time of the metaheuristic optimization algorithm, and (4) using an adaptive sampling technique to select samples to add to the training set for surrogate model training when the results in (2) and (3) do not satisfy the convergence conditions. As described in [18], the presented adaptive sampling technique is applied to both phase 2 and phase 3 to maximize the benefits of balancing exploration–exploitation.
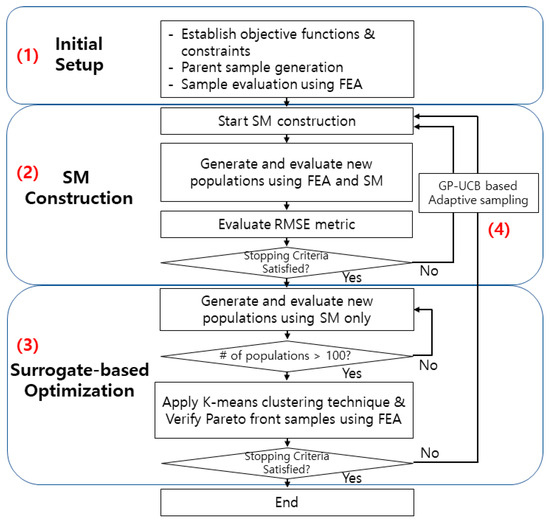
Figure 4.
Surrogate-based design optimization process using GP-UCB-based adaptive sampling.
The results of using the presented multi-objective, multi-variable design optimization procedure to identify global optimal solutions for the baseline SPMVMs are thoroughly analyzed in this section. The objective functions and constraint conditions of the optimization process can be described as follows:
where Tpk is the maximum output torque and mtotal is the total active material mass. The definition of torque ripple is as follows:
where Tavg is the average value, Tmin is the lowest value, and Tmax is the greatest value of the instantaneous torque waveform. It was reported in [19] that the SPMVMs exhibit inherently low torque ripple due to harmonic flux interactions. The range of input design variables considered in the optimization is summarized in Table 4.
| maximize: | 1. Tpk/mtotal [N·m/kg] |
| 2. Power factor | |
| 3. Efficiency [%] | |
| subject to: | 1. Active material cost ≤ $135 |
| 2. Torque ripple ≤ 7% | |

Table 4.
Summary of design variable ranges and optimal values.
The multi-objective optimization problems for the two baseline SPMVMs were solved using NSGA-II, which is a metaheuristic method based on genetic algorithms. In this study, the population of 30 samples and 40 evolutionary generations, with a crossover probability of 0.9 and a mutation probability of 0.05, are used in the NSGA-II algorithm. Table 4 summarizes the initial values and variable ranges for the eight design variables (as in Table 1) considered in the design optimization. The range of each parameter is refined by examining the impact of each parameter on the objective functions using the sensitivity study introduced in [18].
4.2. Optimization Results
In the preceding section, both the ferrite-based SPMVMs with and without a Halbach PM array are optimally designed, and the detailed design parameters are provided in Table 4. Figure 5 shows the optimized machine geometry for both Design I and Design II. To compare the performance of the optimized SPMVMs to the conventional SPM design, we also prepare and analyze an SPM machine with SPP = ½ by removing the stator notches and reducing the number of poles from 20 to 4, as shown in Figure 5c. As summarized in Table 4, the optimized designs show noticeable changes in most of the design parameters, including decreasing the slot opening ratio, increasing the modulation pole dimensions, increasing the magnet thickness, widening and deepening the notch width and depth, and decreasing the magnet pitch ratio. The results of these changes were significant improvements in all the objective functions while satisfying the constraints, as will be shown in Table 5.

Figure 5.
Baseline designs after optimization and conventional SPM counterpart. (a) Design I (without Halbach), (b) Design II (with Halbach), (c) Design III (SPM counterpart).

Table 5.
Summary of optimization results.
Figure 6 shows the flux density distribution for Design I and Design II at the rated load condition. As shown in the figure, the overall saturation of the core for both designs is relaxed with a noticeable reduction in localized saturation along the main flux path through the stator teeth and back yoke region. This improved core utilization leads to reduced core losses and mitigated temperature rise.
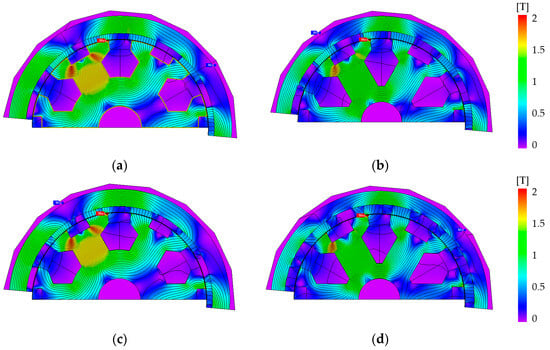
Figure 6.
Flux density contour and flux lines at rated load condition. (a) Design I: before optimization, (b) Design I: after optimization, (c) Design II: before optimization, (d) Design II: after optimization.
Achieving a sinusoidal back-emf waveform is a key factor in improving the performance of rotating electrical machines. It is well known that harmonic components in the back-emf waveform contribute to torque ripple, losses, noise, and vibration [20]. There are several techniques to improve the quality of the back-emf waveform, but most methods have drawbacks. For example, winding short pitching and rotor skewing are very effective at suppressing undesirable harmonic components but at the expense of output torque degradation. The problem of achieving a sinusoidal waveform becomes even more complex when conflicting objective functions such as torque capability and manufacturing cost are considered.
The advantage of applying the proposed optimization process is that it can consider thousands of combinations of design variables over a wide design space to find the optimal design that balances the various objective functions and constraints. Although the back-emf harmonic component was not explicitly included as a design objective or constraint, the process of maximizing output torque and efficiency and suppressing torque ripple to 7% or less naturally shifted the waveshape of back-emf voltage closer to sinusoidal. This is clearly shown in Figure 7, which compares the back-emf waveforms and FFT spectrum for both Design 1 and Design 2 before and after optimization.
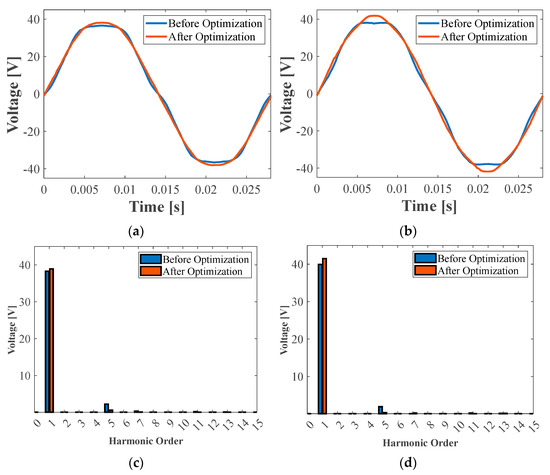
Figure 7.
Comparison of no-load back-emf waveforms. (a) Back-emf waveform: Design I. (b) Back-emf waveform: Design II. (c) FFT spectrum: Design I. (d) FFT Spectrum: Design II.
Figure 8 compares the output torque waveform under the rated load condition at 214 r/min for both Design I and II before and after the optimization. The results in Figure 8a show that the average torque as well as torque ripple of Design I have been noticeably improved after optimization by approximately 9% and 40%, respectively. Similarly, the average torque and torque ripple of Design II have been improved by approximately 12% and 51%, respectively. In conclusion, machine geometry optimization successfully improved output torque and torque ripple characteristics by maximizing the combined torque components in (5) and generating sinusoidal back-emf voltage waveforms for both the baseline SPMVM designs. Further details of the electromagnetic performance summary of Design I and Design II are compared and summarized in Table 5.
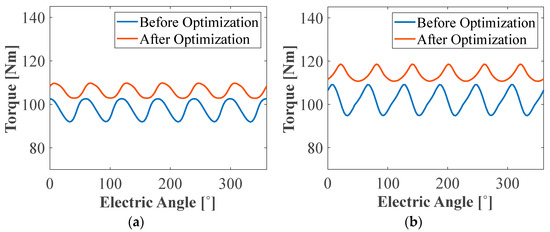
Figure 8.
Output torque waveforms of the two baseline machines at rated condition. (a) Design I (without Halbach). (b) Design II (with Halbach).
Figure 9 and Figure 10 show the 2D and 3D projections of sample distributions and the Pareto front for Design I and Design II, showing the optimal set of solutions between the conflicting objective functions. Referring to the strategy described in [18], the approach used in this paper is to prioritize the maximization of torque density and power factor while balancing other objectives and constraints to solve common design problems related to PMVMs.
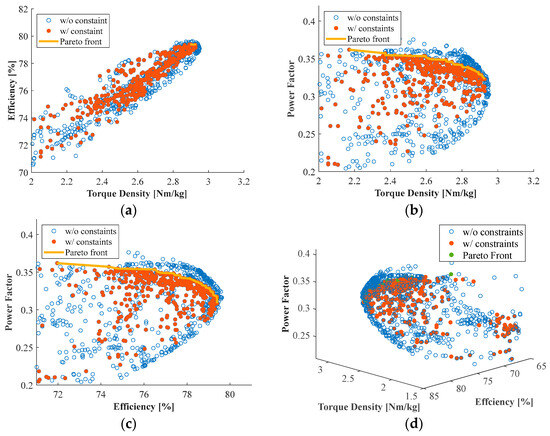
Figure 9.
Two-dimensional (2D) and 3D objective space projections of the sample distribution and Pareto front: Design I (without Halbach). (a) Efficiency vs. torque density. (b) Power factor vs. torque density. (c) Power factor vs. efficiency. (d) PF vs. efficiency vs. torque density.
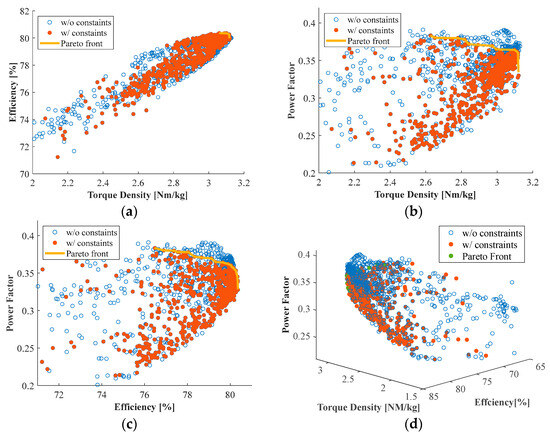
Figure 10.
Three-dimensional (3D) objective space projections of the sample distribution and Pareto front: Design II (with Halbach) performance metrics indicate superiority in the SPMVMs, which is likely due to the additional torque component in SPMVM. (a) Efficiency vs. torque density. (b) Power factor vs. torque density. (c) Power factor vs. efficiency. (d) PF vs. efficiency vs. torque density.
Figure 9a–c show the correlations between the three objectives: torque density, power factor, and efficiency. Interestingly, a counter-intuitive linear relationship is observed between torque density and efficiency. This is mainly because of the improved core utilization shown in Figure 6, which helps to improve both torque performance and core losses. However, the Pareto fronts of torque density vs. power factor and power factor vs. efficiency generally show an inverse relationship as expected. The details of the final optimal design for Design I are shown in Table 5.
Figure 10a–c show the correlations between the three objectives of Design II. Similar to the results in Figure 9, a linear relationship is observed between torque density and efficiency, while inverse relationships are observed between torque density and power factor as well as between power factor and efficiency. The maximum values for each of the three objectives are slightly higher than the values in Figure 9 because of the Halbach PM array. The details of the final optimal design for Design II are summarized in Table 5.
Table 5 presents the results of the design optimization for both Design I and Design II. Compared to the initial results, significant improvements are observed in the performance metrics including torque density, power factor, and efficiency for both models. Moreover, both models show acceptable torque ripple characteristics, meeting the targeted 7%. Despite a very slight increase in material costs, both designs stayed under the specified target of USD 135. Detailed cost analysis findings are presented in Table 6 and Table 7. Due to the low ferrite cost, Design II was optimized to significantly increase magnet usage. However, the torque increase was not directly proportional because the additional torque component decreased as the effective airgap length increased. Finally, a comparison is drawn between the performance characteristics of the traditional SPM design with the optimized SPMVM designs. As shown in Table 5, except for the power factor, all performance metrics indicate superiority in the SPMVMs, which is likely due to the additional torque component in SPMVM.
5. Discussion
This section provides a detailed analysis of efficiency and power factor for the entire operation area as well as other important performance metrics such as demagnetization and cost analysis.
5.1. Performance Characteristics of Efficiency and Power Factor
The analysis results for efficiency and power factor studied in Section 3 and Section 4 were limited to a single operating point (rated condition). In this subsection, the performance characteristics of efficiency and power factor over the entire operating region is investigated to extend the previously obtained results. Assuming a 58.7 Arms peak current amplitude and a dc bus voltage of 400 V, the efficiency and power factor for the entire torque-speed region are calculated using FEA.
Figure 11a,b show a comparison of the efficiency maps for Design 1 before and after optimization. Comparing the two figures, the maximum torque value for a given maximum current has increased by approximately 19.6%, and the high-efficiency region above 95% is more extensive. The improvement in power factor can also be seen by comparing Figure 11c,d. The power factor is plotted as a function of torque except for the very low-speed region, and the power factor drops below 0.5 for medium torque and above. In conclusion, ferrite SPMVMs have attractive performance characteristics under lightly loaded conditions, but the benefits diminish as torque increases.
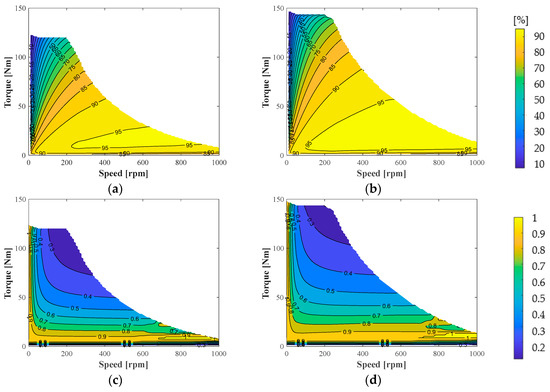
Figure 11.
Comparison of efficiency maps and power factor before and after optimization for Design I (without Halbach). (a) Efficiency map: before optimization. (b) Efficiency map: after optimization. (c) Power factor: before optimization. (d) Power factor: after optimization.
Figure 12a,b show a comparison of the efficiency maps for Design 2 before and after optimization. Similar to the results of Design I, both an improvement in maximum torque and an expansion of the high-efficiency region were observed. The adoption of the Halbach array resulted in a 33.5% increase in peak torque, which is a greater improvement than that shown in Design I.
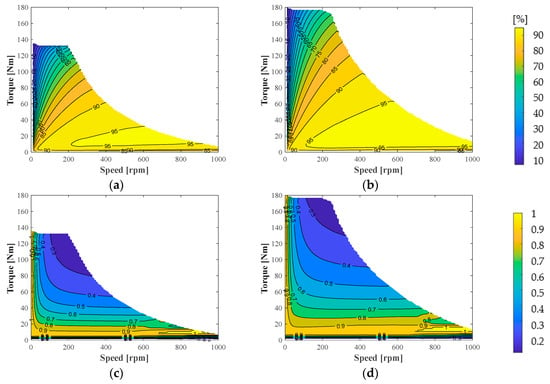
Figure 12.
Comparison of efficiency maps and power factor before and after optimization for Design II (with Halbach). (a) Efficiency map: before optimization. (b) Efficiency map: after optimization. (c) Power factor: before optimization. (d) Power factor: after optimization.
5.2. Chamfering Effect on Notch
As pointed out in Section 1, magnetic saturation can adversely affect the performance of SPMVMs because it contributes to the degradation of the magnetic gearing effect. To mitigate this saturation effect, various design techniques have been studied in several papers. One effective approach to minimize saturation in the modulation pole region is to adopt fluidic pole shape [21].
Figure 13 shows a comparison of a traditional rectangular notch with a chamfered notch geometry with two chamfering ratios as examples. As the chamfering ratio increases, the corners of the notch become increasingly rounded. Figure 14 shows a comparison of flux density contours with and without chamfering, showing the reduction in magnetic saturation when introducing fluidic geometry through chamfers. Figure 15 shows the results of a parametric study that examined the correlation between the three objectives and the chamfering ratio. The results show that the adoption of fluidic geometry improves torque performance and efficiency by about 6% and 2%, respectively, compared to rectangular pole geometry. However, the chamfering ratio is not included as one of the design variables because it only influences very narrow flux paths and further increases computational time.
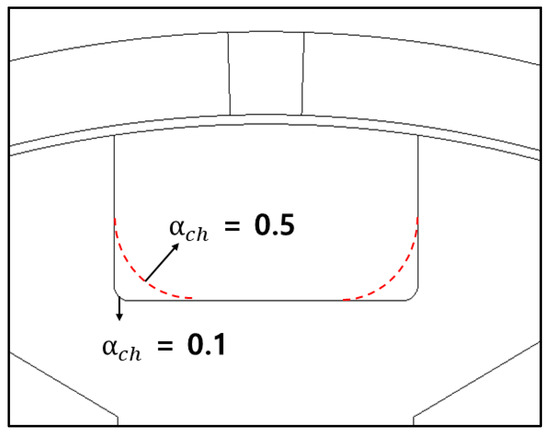
Figure 13.
Stator modulation pole with notch chamfering (αch: chamfering ratio).
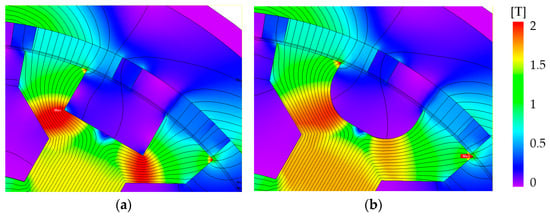
Figure 14.
Comparison of flux density contours. (a) Design I without chamfering. (b) Design I with chamfering.
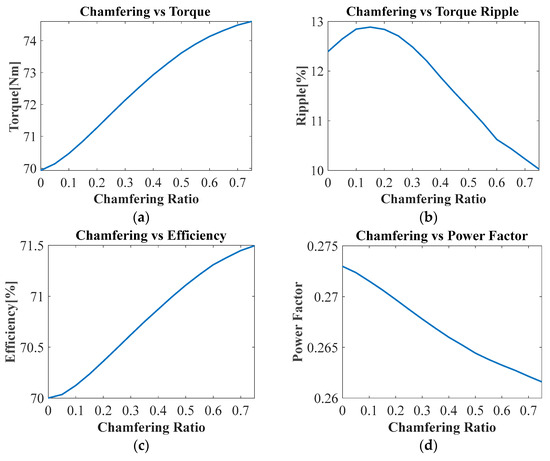
Figure 15.
Parametric study results of chamfering. (a) Torque vs. chamfering ratio. (b) Torque ripple vs. chamfering ratio. (c) Efficiency vs. chamfering ratio. (d) Power factor vs. chamfering ratio.
5.3. Rotor Demagnetization
The demagnetization characteristics of the baseline ferrite SPMVMs can be visually inspected from the analysis of color contour plots of remanence ratio of the rotor magnets. The magnet remanence ratio represents the reduction in remanent magnetic flux density in the rotor magnets and is given by the following:
where Bro is the initial remanent flux density and Br is the post-demagnetization value.
Because the rotor magnets are directly exposed in the airgap area without being protected by an iron core, SPM machines are known to have the worst magnetization characteristics of the various PM machine configurations [22]. Figure 16 shows a comparison of the remanence ratio of the two rotor pole units of Design 1 and Design 2 when the rated current is aligned with the negative d-axis for one electrical cycle. As shown in Figure 16a,c, the magnet strength losses in both initial (before optimization) SPMVM designs are extensive, especially near the edges of each magnet, with remanence ratio values typically in the 70–100% range. In contrast, after the optimization, the rotor magnets in Design I showed little demagnetization, and Design II also showed little loss of magnet strength except at localized magnet edges near the rotor back yoke, as shown in Figure 16b,d. This is due to the increased demagnetization resistance as the magnet thickness increases and the magnet span decreases.
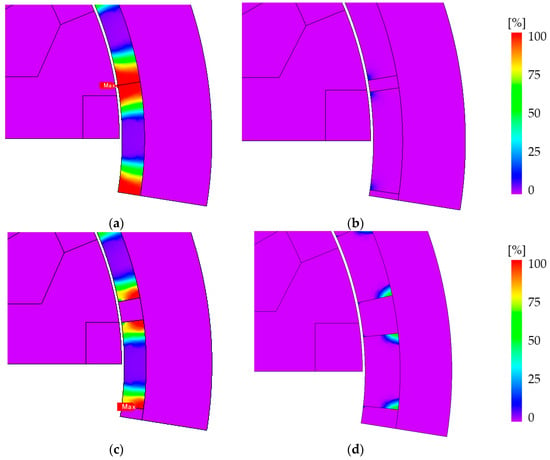
Figure 16.
Comparison of magnet demagnetization states. (a) Design I: before optimization. (b) Design I: after optimization. (c) Design II: before optimization. (d) Design II: after optimization.
5.4. Cost Analysis
Finally, we present a comparison of the results of the active material mass and cost breakdown for the two machines with and without a Halbach array. Table 6 shows the material costs used in the cost analysis. It is shown in Table 7 that after optimization, the total mass of both machines decreases slightly while the cost increases. This is because the mass reduction is more pronounced for steel, which has a relatively lower price per kg compared to the other materials. Based on the results, both designs were optimized by increasing the ferrite magnet content, which is much cheaper compared to rare earth magnets.

Table 6.
Material cost.
Table 6.
Material cost.
| Material | Cost |
|---|---|
| Steel [23] | $1.08/kg |
| Copper [23] | $10.78/kg |
| Ferrite [24] | $7/kg |
| NdFeB [25] | $71.6/kg |

Table 7.
Mass and cost breakdown.
Table 7.
Mass and cost breakdown.
| Material | Design I (w/o Halbach) | Design II (w/Halbach) | ||
|---|---|---|---|---|
| Initial | Optimized | Initial | Optimized | |
| Steel | 28.32 kg/ $30.59 | 25.97 kg/ $28.05 (–8.3%) | 28.32 kg/ $30.59 | 24.41 kg/ $26.36 (–13.8%) |
| Copper | 5.52 kg/ $59.51 | 6.23 kg/ $67.16 (+12.9%) | 5.52 kg/ $59.51 | 6.23 kg/ $67.16 (+12.9%) |
| Magnet | 3.55 kg/ $24.85 | 4.06 kg/ $28.42 (+14.1%) | 3.55 kg/ $24.85 | 5.84 kg/ $40.88 (+64.2%) |
| Total | 37.39 kg/ $114.95 | 36.26 kg/ $123.63 (+7.55%) | 37.39 kg/ $114.95 | 36.5 kg/ $134.4 (+13.4%) |
6. Conclusions
This paper presents an analysis and optimal design of ferrite-based SPMVMs both with and without Halbach magnet arrays. Initially, it demonstrates that SPMVMs utilizing ferrite magnets encounter significant challenges including lower efficiency and inferior power factor compared to traditional NdFeB-based counterparts alongside restricted usable PM thickness due to demagnetization risks. To maximize the performance of ferrite-based SPMVMs, a multi-objective optimization algorithm using a surrogate model and adaptive sampling is employed with emphasis placed on torque density, power factor, and efficiency enhancement.
Results indicate noticeable improvements in harmonic components of the back-emf voltage waveform and reduced magnetic saturation post-optimization. Consequently, torque density, efficiency, and power factor all improve by more than 10 to 20%; however, achieving comparable performance to NdFeB-based SPMVMs remains challenging for ferrite-based counterparts. The application of Halbach magnet arrays is observed to partially bridge this performance gap.
Detailed performance evaluations of two ferrite-based SPMVMs, including demagnetization risks and performance mapping, are conducted via comprehensive 2D Finite Element Analysis (FEA). Optimization efforts effectively mitigate demagnetization risks by bolstering resistance through increased magnet thickness and reduced span. In addition, all three objective functions—torque, power factor, and efficiency—show improvement post-optimization. Furthermore, while ferrite SPMVMs demonstrate favorable performance under light loads, diminishing benefits are observed at higher torque levels.
Despite notable performance enhancements achieved through the proposed design approach for ferrite-based SPMVMs, it remains insufficient in comparison to NdFeB-based counterparts. The search for new PMVM topologies will continue to facilitate the integration of ferrite-based PMVMs across diverse industries.
Author Contributions
Conceptualization, A.R. and G.C.; methodology, G.C. A.R. and G.-H.J.; software, G.J, A.R. and G.C.; validation, G.C., A.R. and G.-H.J.; formal analysis, G.-H.J., A.R. and G.C.; investigation, G.-H.J., A.R. and G.C.; data curation, G.-H.J., A.R. and G.C.; writing—original draft preparation, G.C., A.R. and G.-H.J.; writing—review and editing, G.C.; visualization, G.-H.J., G.C. and A.R.; supervision, G.C.; project administration, G.C.; funding acquisition, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Inha University Research Grant.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kim, B.; Lipo, T. Operation and design principles of a PM vernier motor. IEEE Trans. Ind. Appl. 2014, 50, 3656–3663. [Google Scholar] [CrossRef]
- Zhu, X.; Lee, C.H.T.; Chan, C.C.; Xu, L.; Zhao, W. Overview of Flux-Modulation Machines Based on Flux-Modulation Principle: Topology, Theory, and Development Prospects. IEEE Trans. Transp. Electrif. 2020, 6, 612–623. [Google Scholar] [CrossRef]
- Zhu, J.; Zuo, Y.; Chen, H.; Chen, J.; Lee, C.H.T. Deep-Investigated Analytical Modeling of a Surface Permanent Magnet Vernier Motor. IEEE Trans. Ind. Electron. 2022, 69, 12336–12347. [Google Scholar] [CrossRef]
- Kim, B.; Lipo, T. Analysis of a PM vernier motor with spoke type structure. IEEE Trans. Ind. Appl. 2016, 52, 217–225. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, G.; Zhao, W.; Ji, J.; Zhou, H.; Zhao, W.; Jiang, T. Quantitative comparison of integral and fractional slot permanent magnet vernier motors. IEEE Trans. Energy Convers. 2015, 30, 1483–1495. [Google Scholar] [CrossRef]
- Zou, T.; Li, D.; Qu, R.; Li, J.; Jiang, D. Analysis of a dual-rotor, toroidal-winding, axial-flux vernier permanent magnet machine. IEEE Trans. Ind. Appl. 2017, 53, 1920–1930. [Google Scholar] [CrossRef]
- Yang, H.; Liu, H.; Zhu, Z.Q.; Fang, S.; Huang, Y. Novel flux-regulatable dual-magnet vernier memory machines for electric vehicle propulsion. IEEE Trans. Appl. Supercond. 2014, 24, 1–5. [Google Scholar]
- Liu, G.; Yang, J.; Zhao, W.; Ji, J.; Chen, Q.; Gong, W. Design and analysis of a new fault-tolerant permanent magnet vernier machine for electrical vehicles. IEEE Trans. Magn. 2012, 48, 4176–4179. [Google Scholar] [CrossRef]
- Zheng, P.; Bai, J.; Tong, C.; Sui, Y.; Song, Z.; Zhao, Q. Investigation of a novel radial magnetic field-modulated brushless double-rotor machine used for HEVs. IEEE Trans. Magn. 2013, 49, 1231–1241. [Google Scholar] [CrossRef]
- Kim, B. Design method of a direct-drive permanent magnet vernier generator for a wind turbine system. IEEE Trans. Ind. Appl. 2019, 55, 4665–4675. [Google Scholar] [CrossRef]
- Rehman, A.; Kim, B. Design and Analysis of 15 MW SPM Vernier Generator for Direct-Drive Wind Turbine Applications. Energies 2023, 16, 1094. [Google Scholar] [CrossRef]
- Du, Z.; Lipo, T. Design of an Improved Dual-Stator Ferrite Magnet Vernier Machine to Replace an Industrial Rare-Earth IPM Machine. IEEE Trans. Energy Convers. 2019, 34, 2062–2069. [Google Scholar] [CrossRef]
- Du, Z.; Lipo, T. Torque Performance Comparison Between a Ferrite Magnet Vernier Motor and an Industrial Interior Permanent Magnet Machine. IEEE Trans. Ind. Appl. 2017, 53, 2088–2097. [Google Scholar] [CrossRef]
- Rehman, A.; Kim, B. Characteristics analysis of consequent pole ferrite magnet vernier machine using novel equivalent magnetic circuit. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 1823–1833. [Google Scholar] [CrossRef]
- Xu, L.; Liu, G.; Zhao, W.; Ji, J.; Fan, X. High-performance fault tolerant Halbach permanent magnet vernier machines for safety-critical applications. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Xie, K.; Li, D.; Qu, R.; Gao, Y. A novel permanent magnet vernier machine with Halbach array magnets in stator slot opening. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Kang, M.; Xu, L.; Ji, J.; Zhu, X. Design and Analysis of a High Torque Density Hybrid Permanent Magnet Excited Vernier Machine. Energies 2022, 15, 1723. [Google Scholar] [CrossRef]
- Choi, G.; Jang, G.-H.; Choi, M.; Kang, J.; Kang, Y.G.; Kim, S. Optimal Design of a Surface Permanent Magnet Machine for Electric Power Steering Systems in Electric Vehicle Applications Using a Gaussian Process-Based Approach. Actuators 2024, 13, 13. [Google Scholar] [CrossRef]
- Li, D.; Qu, R.; Li, J.; Xiao, L.; Wu, L.; Xu, W. Analysis of torque capability and quality in vernier permanent-magnet machines, IEEE Trans. Ind. Appl. 2016, 52, 125–135. [Google Scholar] [CrossRef]
- Li, D.; Qu, R. Sinusoidal Back-EMF of Vernier Permanent Magnet Machines. J. Int. Conf. Electr. Mach. Syst. 2014, 3, 40–47. [Google Scholar] [CrossRef][Green Version]
- Cinti, L.; Conto, C.; Bianchi, N. Fluid Dynamic-based Pole Shaping for Electrically Excited Synchronous Motor. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 4016–4021. [Google Scholar]
- Choi, G. Analysis and Experimental Verification of the Demagnetization Vulnerability in Various PM Synchronous Machine Configurations for an EV Application. Energies 2021, 14, 5447. [Google Scholar] [CrossRef]
- Du-Bar, C.; Mann, A.; Wallmark, O.; Werke, M. Comparison of Performance and Manufacturing Aspects of an Insert Winding and a Hairpin Winding for an Automotive Machine Application. In Proceedings of the 2018 Eighth International Electric Drives Production Conference (EDPC), Schweinfurt, Germany, 4–5 December 2018; pp. 1–8. [Google Scholar]
- Ormerod, J. Permanent Magnet Material Options: Why $/kg and (BH)max Are Misleading Metrics. In Proceedings of the International Forum on Magnetic Applications, Technologies & Materials, Orlando, FL, USA, 8–9 February 2018. [Google Scholar]
- Hemsen, J.; Nowak, N.; Eckstein, L. Production cost modeling for permanent magnet synchronous machines for electric vehicles. Automot. Engine Technol. 2023, 8, 109–126. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).