A Method for Evaluating Coalbed Methane Reservoir Productivity Considering Drilling Fluid Damage
Abstract
1. Introduction
2. Physical Model and Related Assumptions
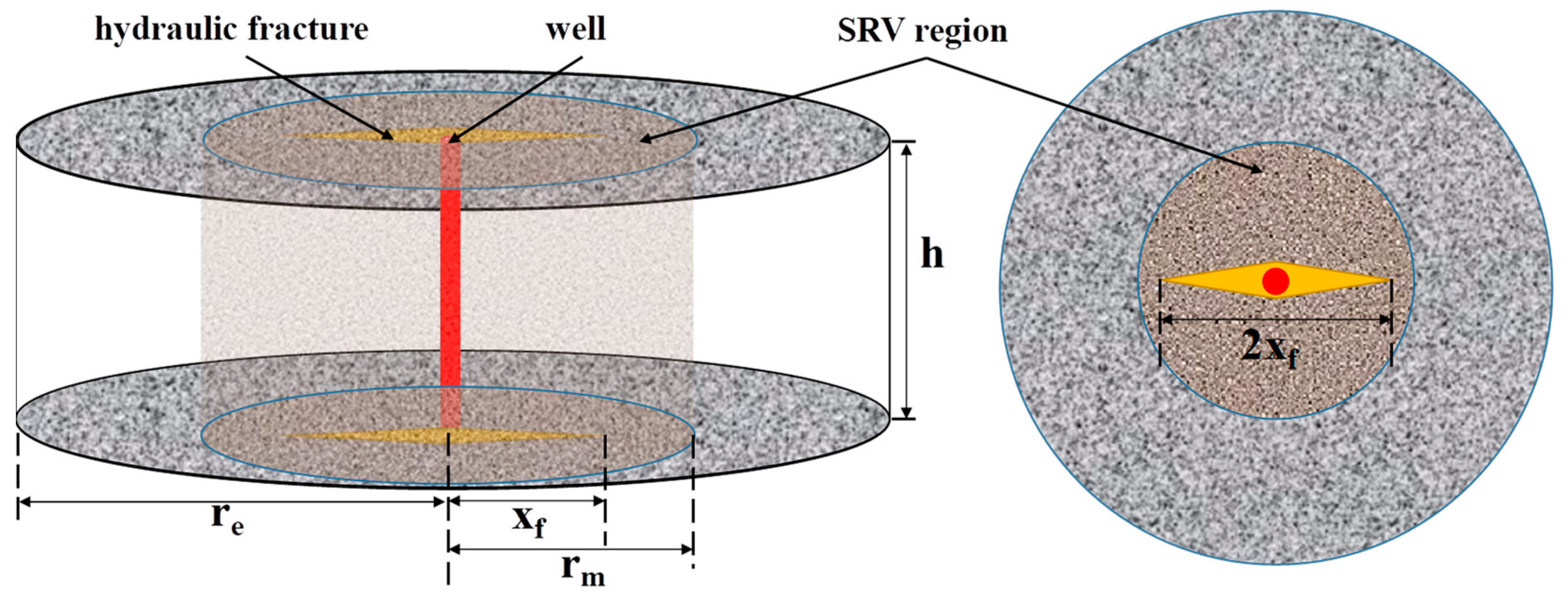
- The fracture of a fractured vertical well in the center of the circular boundary is an infinite conductivity fracture (Figure 1).
- The gas reservoir is a constant temperature gas reservoir.
- The permeability in the inner and outer areas of the gas reservoir is inconsistent, and the vertical permeability is 0 (Figure 1).
- The inner boundary is the fixed production or constant pressure production, and the circular outer boundary is the closed boundary or constant pressure boundary.
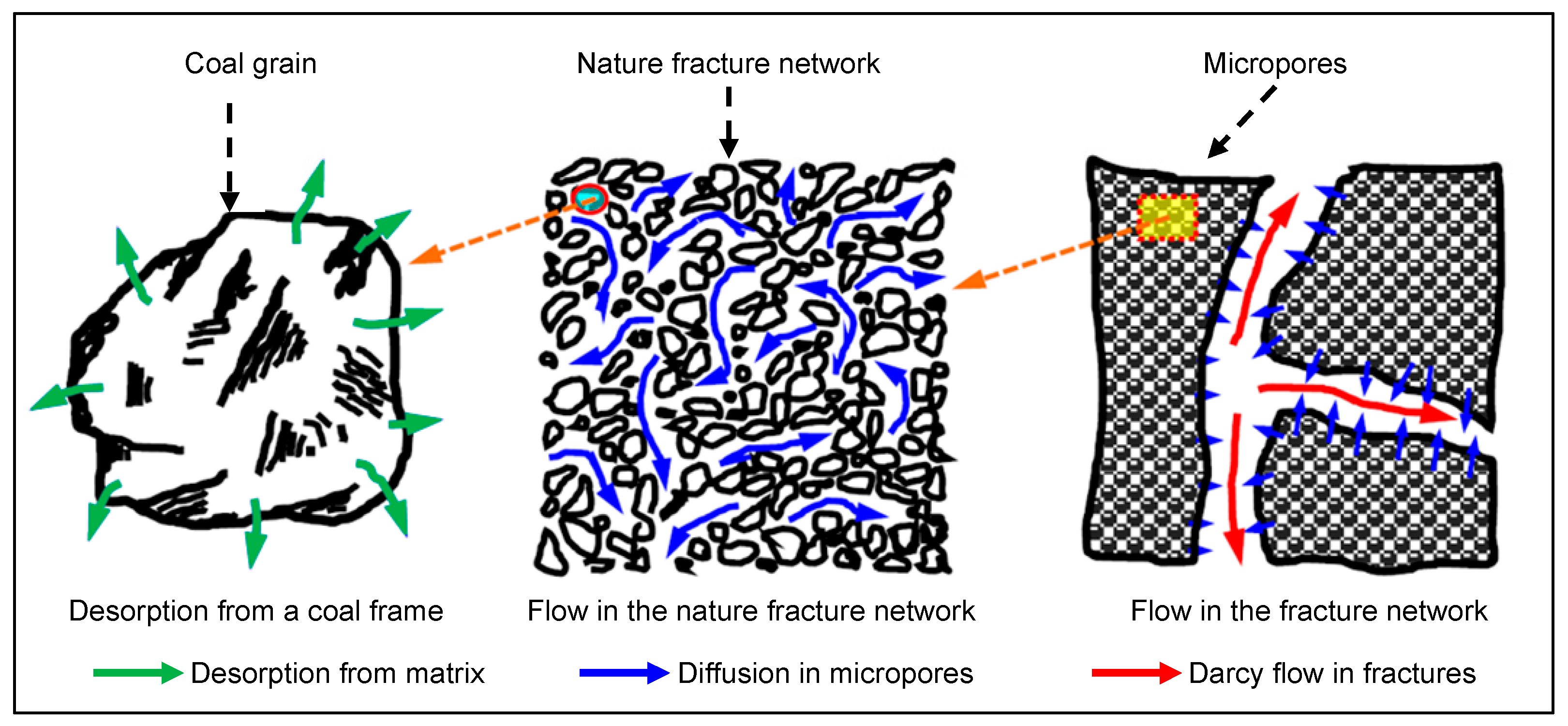
- Gas diffusion and flow occur in the matrix and cracks, respectively, and steady-state diffusion occurs (Figure 2).
- The flow in the natural fracture system is called Darcy seepage (Figure 2).
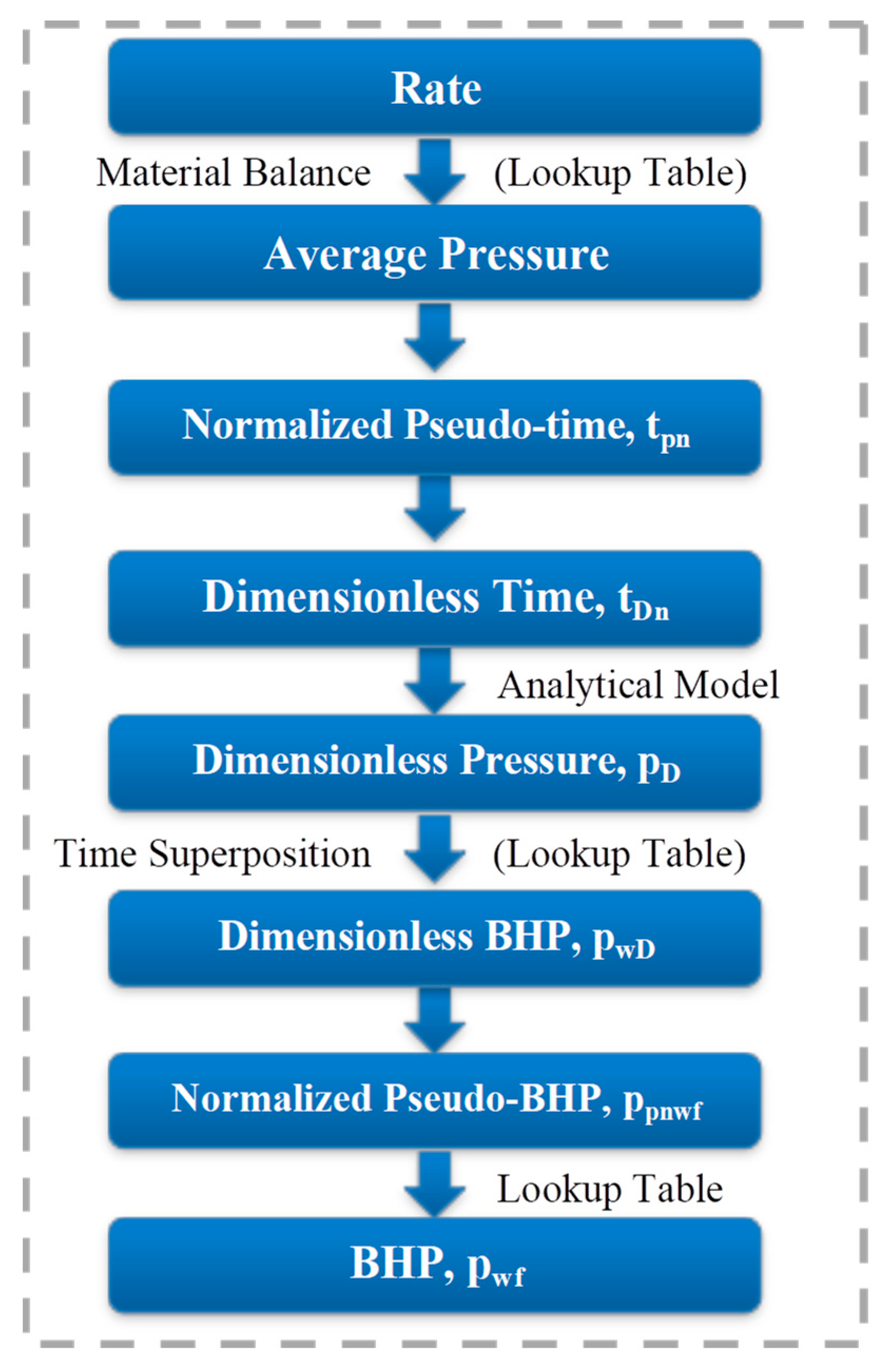
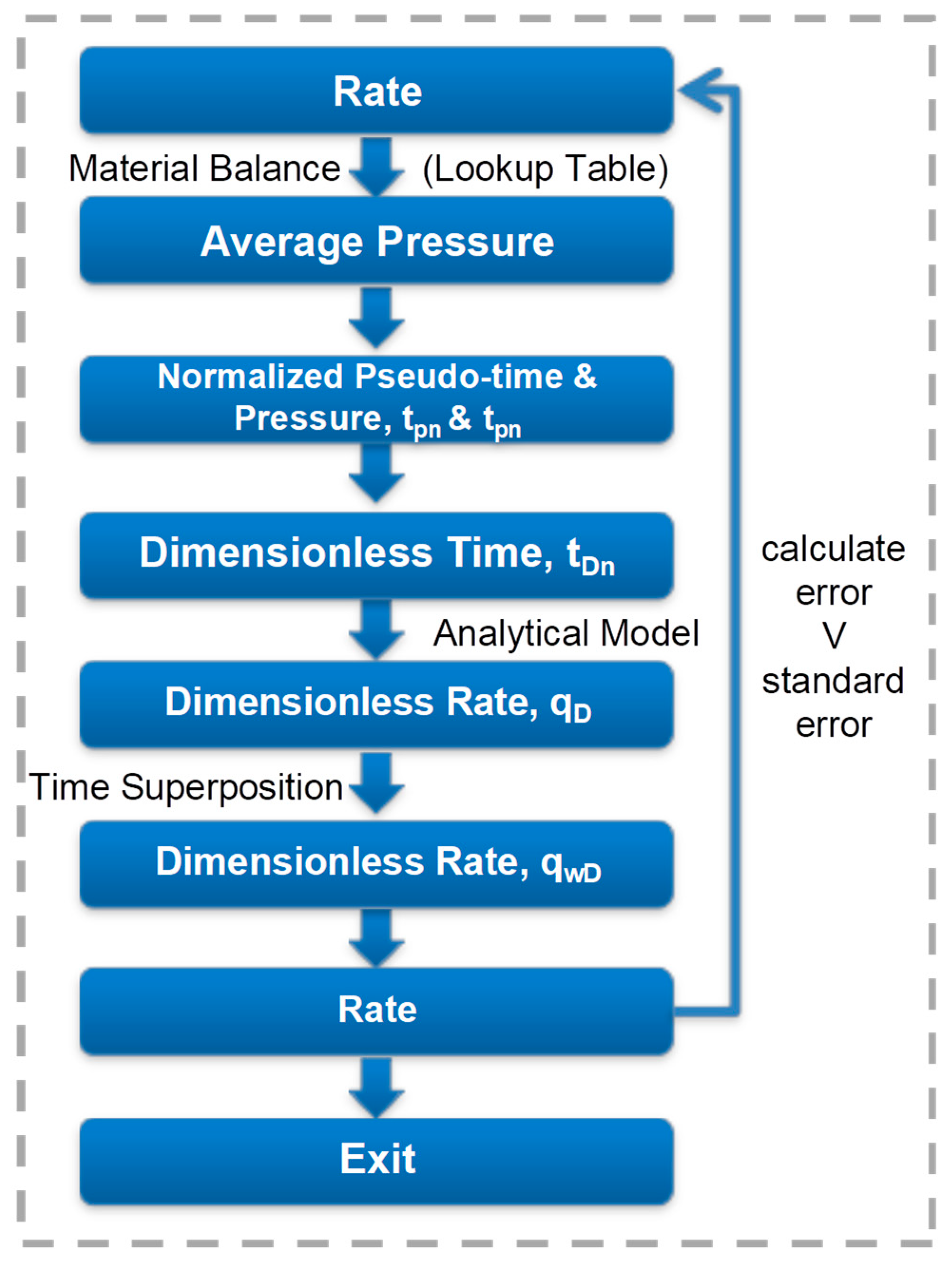
3. Mathematical Model
4. Historical Fitting Analysis
5. Verifying the Accuracy of the Calculation Results
6. Gas Field Application
7. Result Analysis
8. Conclusions
- Compared with the classical analytical solution, the green function is more accurate in solving the fracture model and has a better fitting effect with the numerical solution. The accuracy of the result calculated by the green function is 97%, while the accuracy of the result calculated by the classical analytical solution is 89%. Please refer to the section titled Verifying the Accuracy of the Calculation Results in this article for the demonstration process.
- In the process of coalbed methane mining, the improper use of fracturing fluid and pollution caused by filtration loss in the drilling process will have a great impact on the productivity of a single well in a later stage. The pollution of working fluid in the reservoir is greater than the permeability increase effect caused by hydraulic fracturing in the later stage. The main function of hydraulic fracturing is to form a flow channel with high permeability, but it cannot increase the permeability of all areas around the wellbore. In the process of increasing the permeability ratio from 0.25 to 1, the gas production year increased from 3 million square meters to 7 million square meters, demonstrating a growth rate of 133%. Please refer to the Result Analysis Section of this article for the demonstration process.
- During the evaluation of coal bed methane productivity, the pollution caused by working fluid filtration loss and the permeability increase effect of late fracturing need to be considered. Considering the permeability difference between internal and external regions and the skin effect will greatly improve the fitting degree of the predicted value and the actual value in the productivity prediction, making the productivity prediction more accurate. As seen in the fitting data of the actual wells, the fitting error of daily gas production was reduced from 28.9% to 17.3%, and the error of cumulative gas production was reduced from 17.3% to 3.3% when considering drilling fluid pollution. The demonstration process is shown in the section titled Gas Field Application in this paper.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols in Article | |
| radial radius of gas reservoir, m | |
| pressure, MPa | |
| gas viscosity, mpa·s | |
| gas deviation factor, dimensionless | |
| porosity, decimal | |
| compressibility, MPa−1 | |
| permeability, D | |
| time variable, h | |
| reference length, L, which is equal to half of the fracture length, m | |
| pseudo-pressure, MPa2/cp | |
| temperature, K | |
| Bessel function of order 0 | |
| ratio of permeability between SRV region and outer region | |
| s | image variable of Laplace transformation |
| dimensionless wellbore storage coefficient | |
| skin factor | |
| Langmuir pressure, MPa | |
| Langmuir volume, m3/m3 | |
| gas flow rate, m3/d | |
| compressibility, MPa−1 | |
| R | external radius of matrix, m |
| D | diffusion coefficient, m3/s |
| fracture half length, m | |
| Subscripts and Superscripts | |
| D | dimensionless property |
| e | boundary property |
| g | gas property |
| L | factor of Langmuir equation |
| i | initial condition |
| sc | standard condition |
| f | fracture property |
| 1 | inner region property |
| 2 | outer region property |
| ~ | image function of Laplace transform |
| Intermediate Variables | |
| Dimensionless Variables | |
References
- Seidle, J. Principle of Coalbed Gas Reservoir Engineering; Shi, X., Ed.; Petroleum Industry Press: Beijing, China, 2016. [Google Scholar]
- Scott, A.R.; Kaiser, W.R. Hydrogeologic factor affecting dynamic open-hole cavity complections in the San Juan basin. In Proceedings of the 1995 Coalbed Methane Symposium, Tuscaloosa, AL, USA, 14–20 May 1995. [Google Scholar]
- Harrington, L.J.; Whitsitt, N.F.; Hannah, R.R. Prediction of the Location and Movement of Fluid Interfaces in a Fracture. In Proceedings of the Southwestern Petroleum Short Course, Lubbock, TX, USA, 20–23 April 1973; pp. 26–27. [Google Scholar]
- Cinco-Ley, H.; Samaniego, V.F. Transient Pressure Analysis: Finite Conductivity Fracture Versus Damaged Fracture Case. In Proceedings of the 58th Annual Fall Technical Conference and Exhibition of the Petroleum Engineers of AIME, San Antonio, TX, USA, 5–7 October 1981; Volume 10179. [Google Scholar]
- Jiao, G.; Zhao, L.; Liu, P.; Pei, P.; Lin, Y. An Analytical Model for Predicting Prudctivity of Frac and Packed Completion. Offshore Oil 2005, 25, 38–40. [Google Scholar]
- Yekeen, N.; Padmanabhan, E.; Idris, A.K. A review of recent advance in foma-based fracturing fluid application in unconventional reservoirs. J. Ind. Eng. Chem. 2018, 66, 45–71. [Google Scholar] [CrossRef]
- Ying, H.; Liu, Y.; Fu, C. Productivity analysis for fractured well in low permeability reservoir. Spec. Oil Gas Reserv. 2005, 12, 55–56. [Google Scholar]
- Len, V.; Brent, K.; Thanos, A. State of the art in coalbed methane drilling fluids. SPE Drill. Complet. 2008, 23, 250–257. [Google Scholar]
- Barr, K. A guideline to optimization drilling fluids for coalbed methane reservoirs. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Denver, CO, USA, 14–16 April 2009; Volume SPE 123175-MS. [Google Scholar]
- Zhao, J.; Guo, J. Dynamic prediction of hydraulic fracturing effects. Oil Drill. Prod. Technol. 1995, 17, 55–61. [Google Scholar]
- Gao, S.; Liu, H.; Ye, L.; Hu, Z.; Chang, J. A coupling model for gas diffusion and seepage in SRV section of shale gas reservoirs. Nat. Gas Ind. 2017, 37, 97–104. [Google Scholar] [CrossRef]
- An, Q.; Yang, F.; Yang, R.; Huang, Z.; Li, G.; Gong, L.; Yu, W. Practice and Understanding of Deep Coalbed Methane Massive Hydraulic Fracturing in Shenfu Block, Ordos Basin. J. China Coal Soc. 2024, 1, 1–18. [Google Scholar]
- Liu, Y.; Zhu, H.; Tang, H.; Sun, H.; Zhang, B.; Chen, Z. Four-dimensional in-situ stress model of CBM reservoirs based on geology-engineering integration. Nat. Gas Ind. 2022, 42, 82–92. [Google Scholar]
- Li, F.; Huang, W.; Chen, H.; Zhong, X. Coalbed methane well productivity prediction model considering pore compressibility and coal matrix shrinkage effect and influencing factors analysis of well productivity. Pet. Geol. Oilfield Dev. Daqing 2023, 42, 168–174. [Google Scholar]
- Thamas, G.; Neithan, D.; Richard, J. Effect of drilling fluids on coal permeability: Impact on horizontal wellbore stability. Int. J. Coal Geol. 2009, 78, 177–191. [Google Scholar]
- Li, H.; Cao, Y.; Zhou, D.; Cai, X.; Liu, T.; Feng, P.; Shi, B.; Tian, L. Fracturing parameters analysis and productivity evaluation of vertical coalbed methane wells with nitrogen foam. Coal Geol. Explor. 2020, 48, 65–74. [Google Scholar]
- Zhang, X.; Zhang, S.; Sun, Q.; Yang, Y.; Yang, Y. Evaluating the influence of geological structure to CBM productivity based on AHP and fuzzy mathematics. J. China Coal Soc. 2017, 42, 2385–2392. [Google Scholar]
- Reng, J. Effect of dynamic permeability variation on production of coalbed methane wells. Nat. Gas Ind. 2018, 38, 62–64. [Google Scholar]
- Sun, H.; Wang, C. Damage mechanism of cement slurry to CBM reservoirs with developed fractures and cleats: A case study from eastern Yunnan and western Guizhou in China. Nat. Gas Ind. 2018, 38, 82–87. [Google Scholar] [CrossRef]
- Zheng, L.; Li, X.; Su, G.; Zhao, W.; Gong, X.; Tao, X. Applicability of working fluid damage assessment methods for coalbed methane reservoirs. Nat. Gas Ind. 2018, 38, 28–39. [Google Scholar]
- Tian, S.; Huang, Z.; Li, G.; Lu, P.; Zhang, H.; Wang, T. Laboratory experiments on blockage removing and stimulation of CBM reservoirs by composite pulsating fracturing of radial horizontal wells. Nat. Gas Ind. 2018, 38, 88–94. [Google Scholar] [CrossRef]
- Ji, C.; Hao, C.; Xin, K.; Yu, Z.; Chang, H.; Yang, C. Study on cementing damage mechanism for reservoir of CBM well. Coal Eng. 2017, 49, 116–119. [Google Scholar]
- Wang, W.; Xiao, N.; Huang, L.; Zou, L.; Tian, Z.; Yang, H. Damage in coal reservoir caused by coal swelling after drilling fluid invasion. Drill. Fluid Complet. Fluid 2010, 27, 20–22. [Google Scholar]
- Cai, J.; Yuan, Y.; Wang, J.; Li, X.; Cao, W. Experimental research on decreasing coalbed methane formation damage using micro-foam mud stabilized by nanoparticles. J. China Coal Soc. 2013, 38, 1640–1645. [Google Scholar]
- Wang, D.; Shi, Y.; Wu, X.; Wu, C. Experimental research on decreasing coalbed methane formation damage by using low density cement slurry. Coal Geol. Explor. 2015, 43, 105–109. [Google Scholar]
- Zheng, L.; Meng, S.; Cao, Y.; Li, Z. Laboratory studies on control coalbed methane formation damage by fuzzy-ball based drilling fluids. J. China Coal Soc. 2010, 35, 439–442. [Google Scholar]
- Wang, W.; Tao, S.; Huang, L.; Zou, L.; Tian, Z.; Yang, H. Experimental research on the scaling damage in coalbed methane reservoir caused by drilling fluid. Oil Drill. Prod. Technol. 2010, 32, 35–38. [Google Scholar]
- Tao, T.; Lin, X.; Fang, X.; Cao, C.; Zhang, T. Fracturing Damage Mechanism and Fracturing Fluid with Low Damage of Coalbed Methane Well. J. Chongqing Univ. Sci. Technol. (Nat. Sci. Ed.) 2011, 13, 21–23. [Google Scholar]
- Chen, J. Reservoir damage-problems that should be paid attention to in CBM drilling. Coal Technol. 1998, 2, 18–19. [Google Scholar]
- Wei, Y.; Li, C.; Cao, D.; Cui, B.; Xiang, X. Effect of pulverized coal dispersant on coal in the CBM well-washing technology. J. China Coal Soc. 2018, 43, 1951–1958. [Google Scholar]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef]
- AI-Hussainy, R.; Ramey, H.J.; Crawford, P.B. The flow of real gas through porous media. J. Pet. Technol. 1966, 18, 625–636. [Google Scholar]
- Everdingen, V.; Hust, A.F. The Application of the Laplace Transformation to Flow Problems in Reservoirs. J. Pet. Technol. 1949, 1, 305–324. [Google Scholar] [CrossRef]
- Anbarci, K.; Ertekin, T. A comprehensive study of pressure transient analysis with sorption phenomena for single-phase gas flow in coal seams. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990; Volume SPE-20568-MS. [Google Scholar]
- Anbarci, K.; Ertekin, T. Pressure transient behavior of fractured wells in coalbed reservoirs. In Proceedings of the Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992; Volume SPE-24703-MS. [Google Scholar]
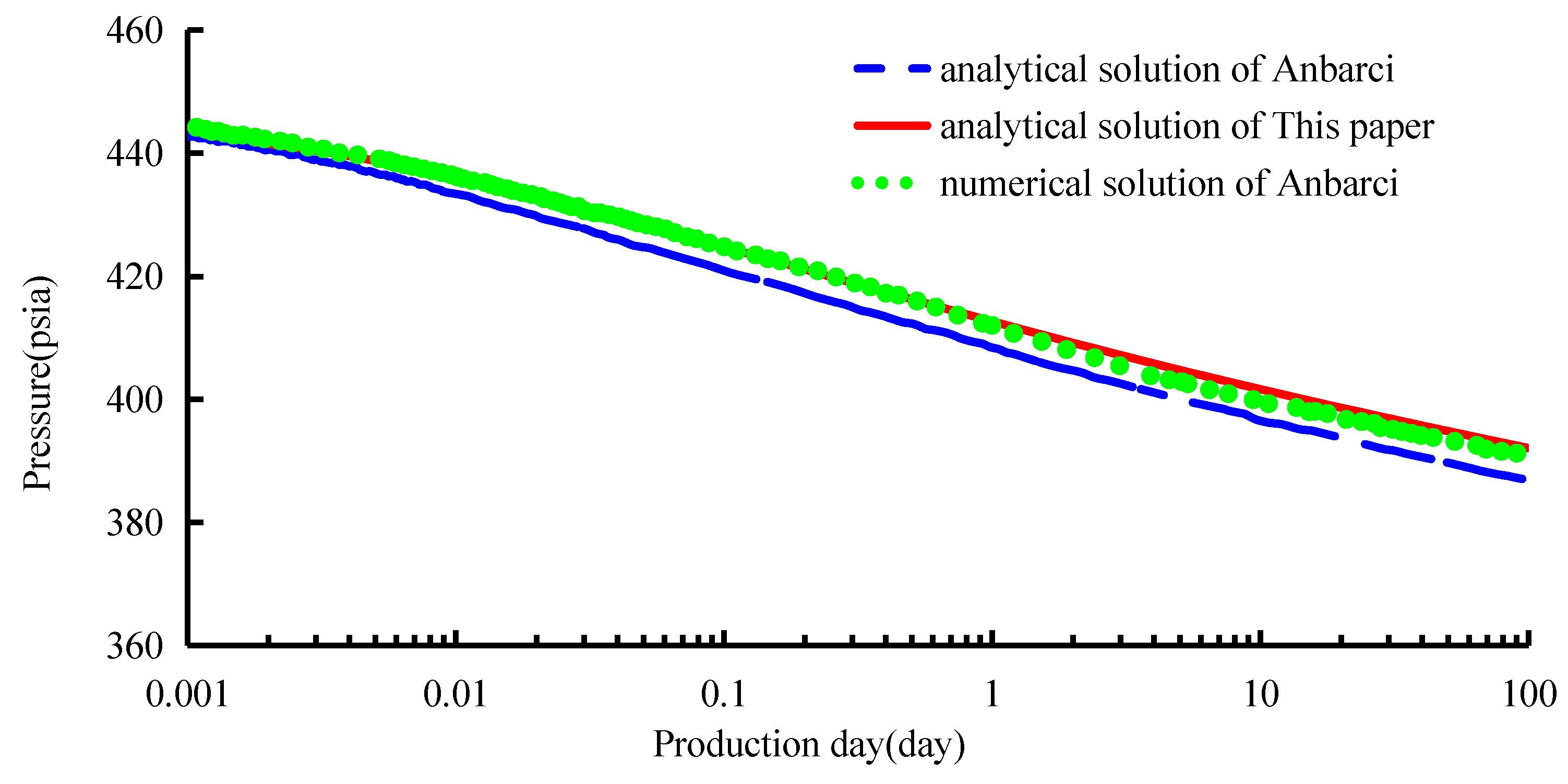

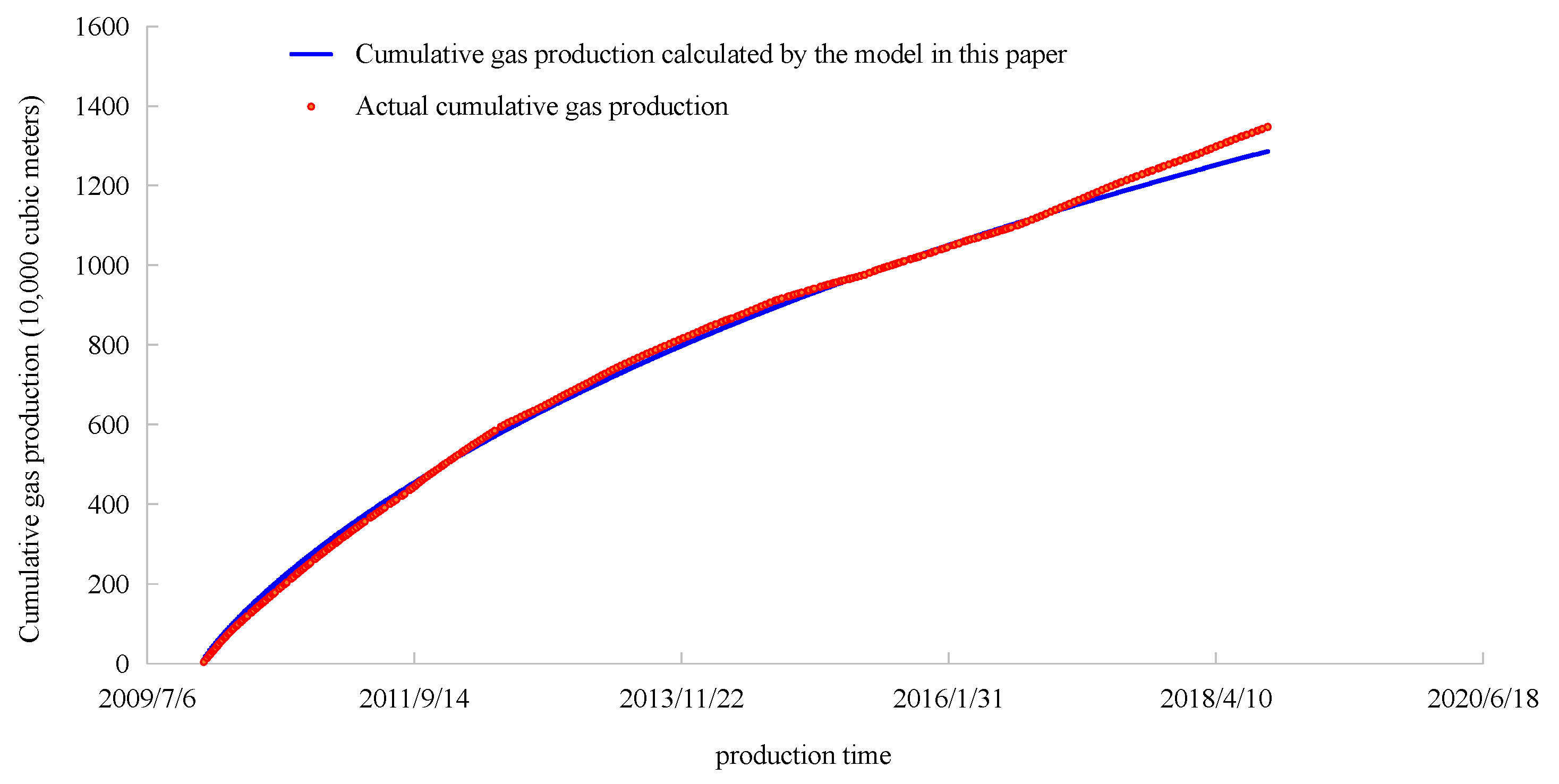
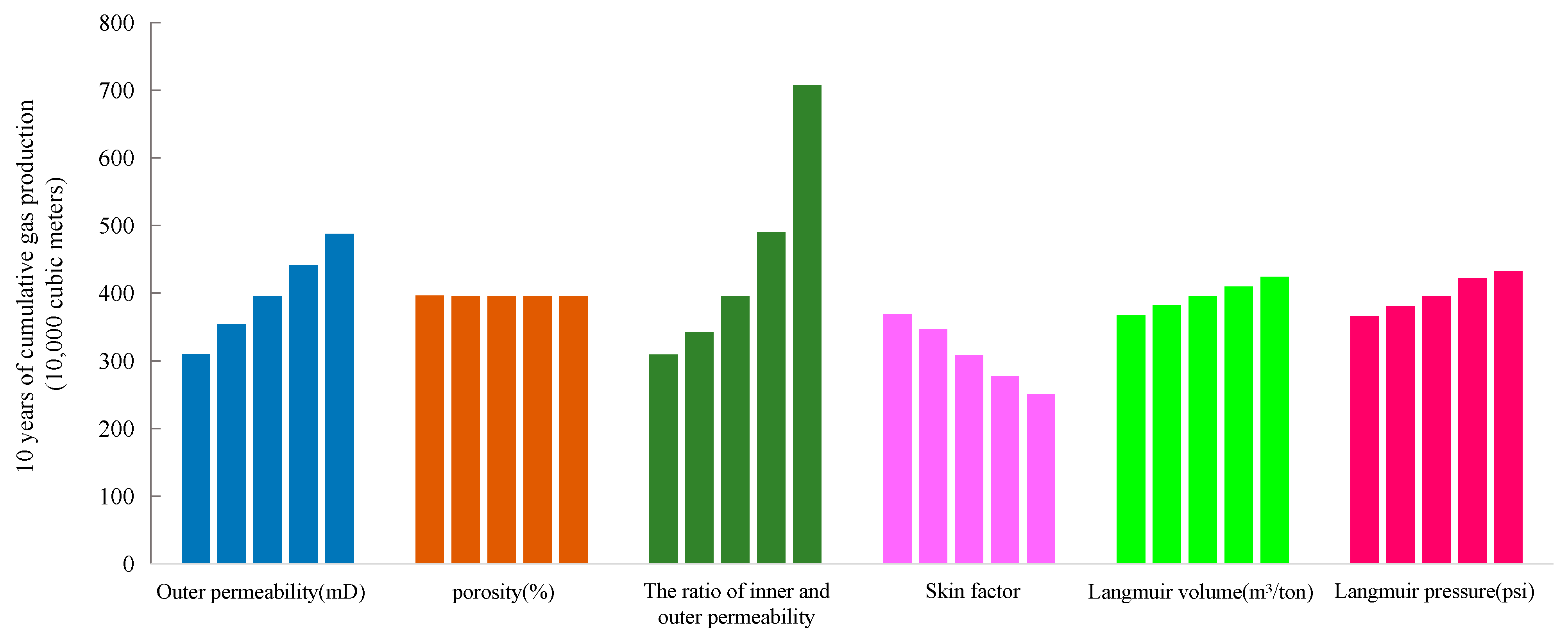

| τ/h | μ/cp | T/R | qsc/MMscf·d−1 | pic/psi | φ |
|---|---|---|---|---|---|
| 328,990 | 0.01082 | 530 | 0.2 | 447.7 | 0.01 |
| rw/ft | c/psia−1 | z | VL/scf·ft−3 | k/md | h/ft |
| 0.5 | 0.002234 | 0.94 | 18.6 | 26 | 6 |
| Pic/MPa | s | k/md | ρg/g·m−3 | re/m | Cf/e−6kp−1 |
|---|---|---|---|---|---|
| 3.1 | 0.4 | 0.88 | 1.47 | 400 | 5 |
| h/m | M12 | φ | VL/cm3·g−1 | Lf/m | PL/Mpa |
| 4.5 | 6 | 0.02 | 60 | 90 | 1.4 |
| Inner Permeability (mD) | Outer Permeability (mD) | Ratio of Outer to Inner Permeability | Simulation | Daily Gas Volume Fitting Error | Cumulative Gas Production Fitting Error |
|---|---|---|---|---|---|
| 0.88 | 0.88 | M12 = 1 | A * | 28.9% | 17.3% |
| 1.76 | 0.88 | M12 = 0.5 | B * | 23.5% | 13.1% |
| 0.44 | 0.88 | M12 = 2 | 21.5% | 11.6% | |
| 0.15 | 0.88 | M12 = 6 | 17.3% | 3.3% | |
| 0.09 | 0.88 | M12 = 10 | 20.7% | 12.3% |
| Parameters | Basic | Max | Min | Step Size |
|---|---|---|---|---|
| k (mD) | 0.6 | 1 | 0.2 | 0.2 |
| φ (%) | 2 | 3 | 1 | 0.5 |
| M12 | 1/3 | 1 | 1/5 | |
| SK | 0 | 3.2 | 0 | 0.8 |
| VL (m3/ton) | 60 | 70 | 50 | 5 |
| PL (Mpa) | 1.3 | 1.5 | 1.1 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Sun, L.; Zhao, Z.; Zhang, J.; Li, Y.; Meng, Y.; Wang, L. A Method for Evaluating Coalbed Methane Reservoir Productivity Considering Drilling Fluid Damage. Energies 2024, 17, 1686. https://doi.org/10.3390/en17071686
Li C, Sun L, Zhao Z, Zhang J, Li Y, Meng Y, Wang L. A Method for Evaluating Coalbed Methane Reservoir Productivity Considering Drilling Fluid Damage. Energies. 2024; 17(7):1686. https://doi.org/10.3390/en17071686
Chicago/Turabian StyleLi, Chen, Lichun Sun, Zhigang Zhao, Jian Zhang, Yong Li, Yanjun Meng, and Lei Wang. 2024. "A Method for Evaluating Coalbed Methane Reservoir Productivity Considering Drilling Fluid Damage" Energies 17, no. 7: 1686. https://doi.org/10.3390/en17071686
APA StyleLi, C., Sun, L., Zhao, Z., Zhang, J., Li, Y., Meng, Y., & Wang, L. (2024). A Method for Evaluating Coalbed Methane Reservoir Productivity Considering Drilling Fluid Damage. Energies, 17(7), 1686. https://doi.org/10.3390/en17071686







