Evaluation and Bias Correction of the ERA5 Reanalysis over the United States for Wind and Solar Energy Applications
Abstract
1. Introduction
2. Data Sets
2.1. ERA5
2.2. Solar Observations
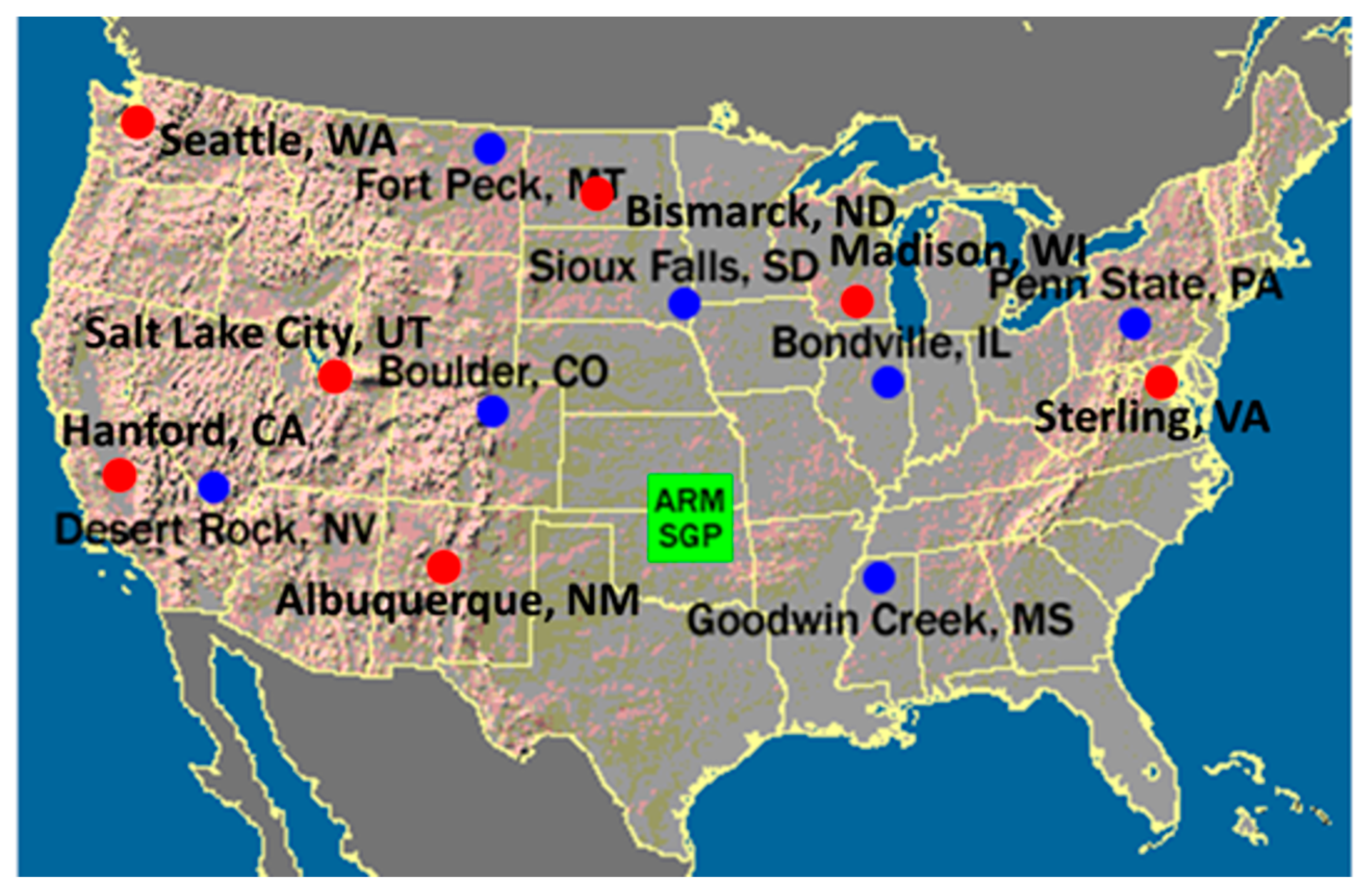
2.3. Wind Observations
3. Converting Wind Speed and Solar Irradiance to Power
3.1. Solar Power Using Pvlib
3.2. Wind Turbine Power Curves
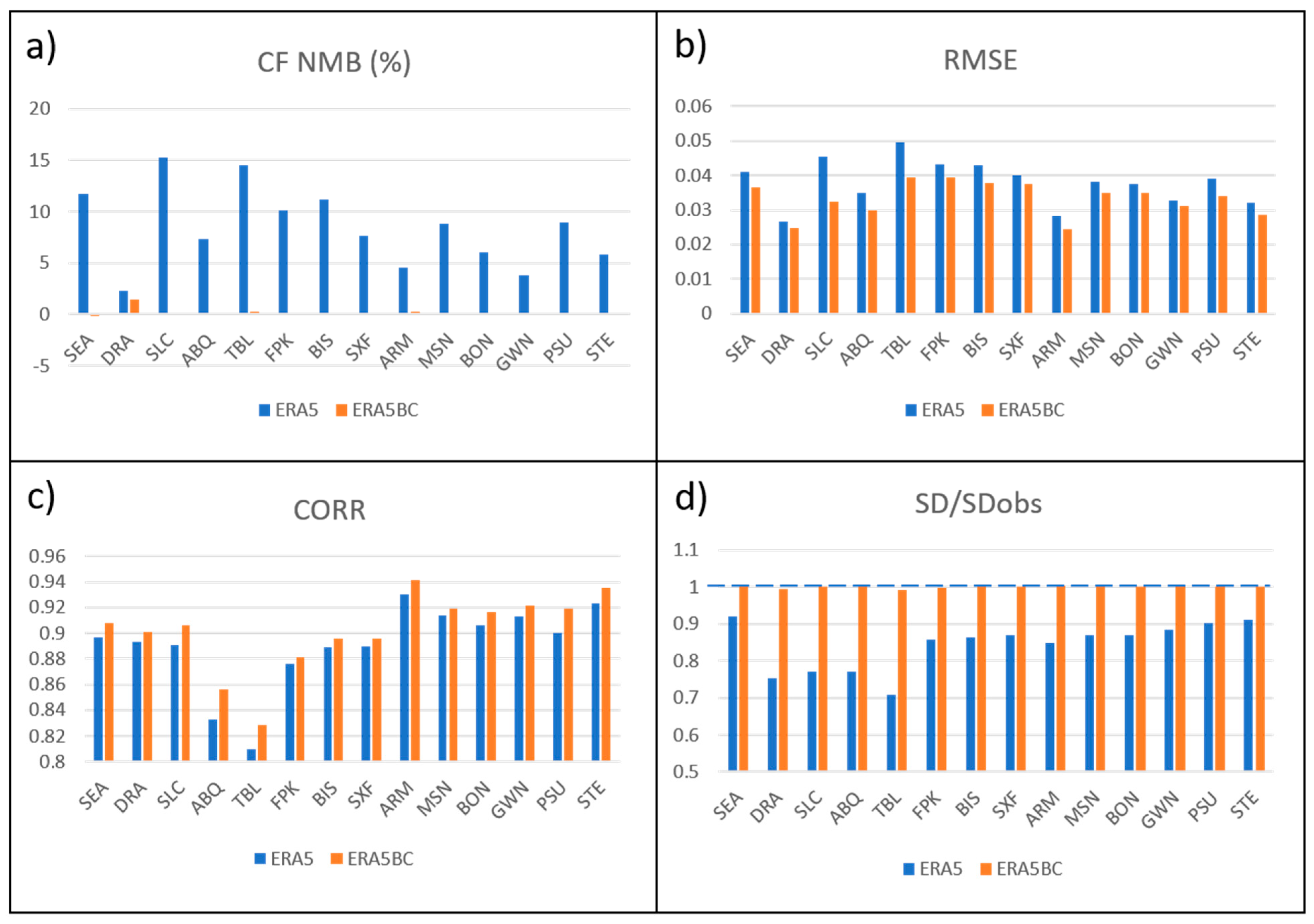
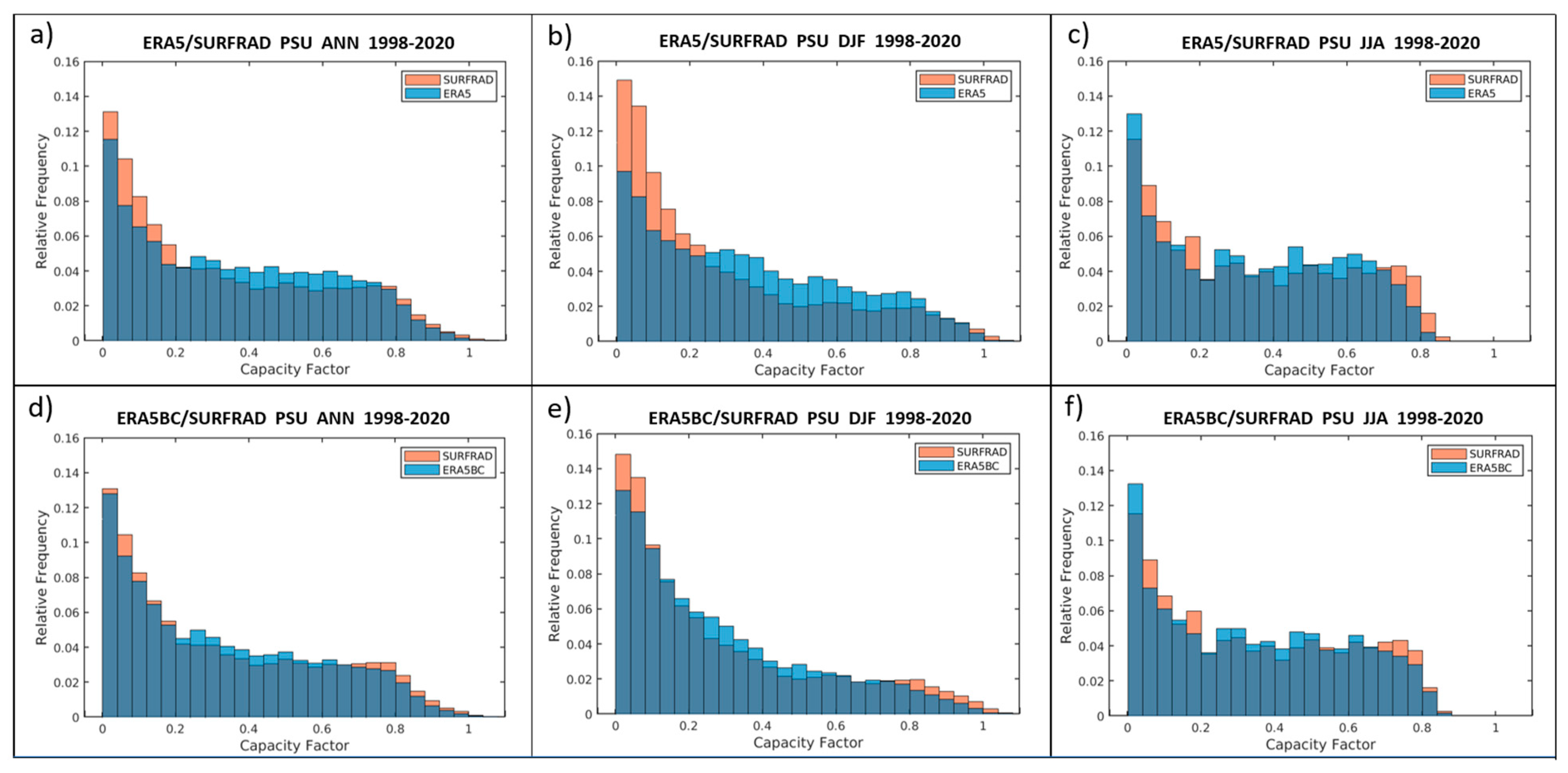
4. Evaluation and Bias Correction of ERA5-Derived Solar Capacity Factor Systematic Errors
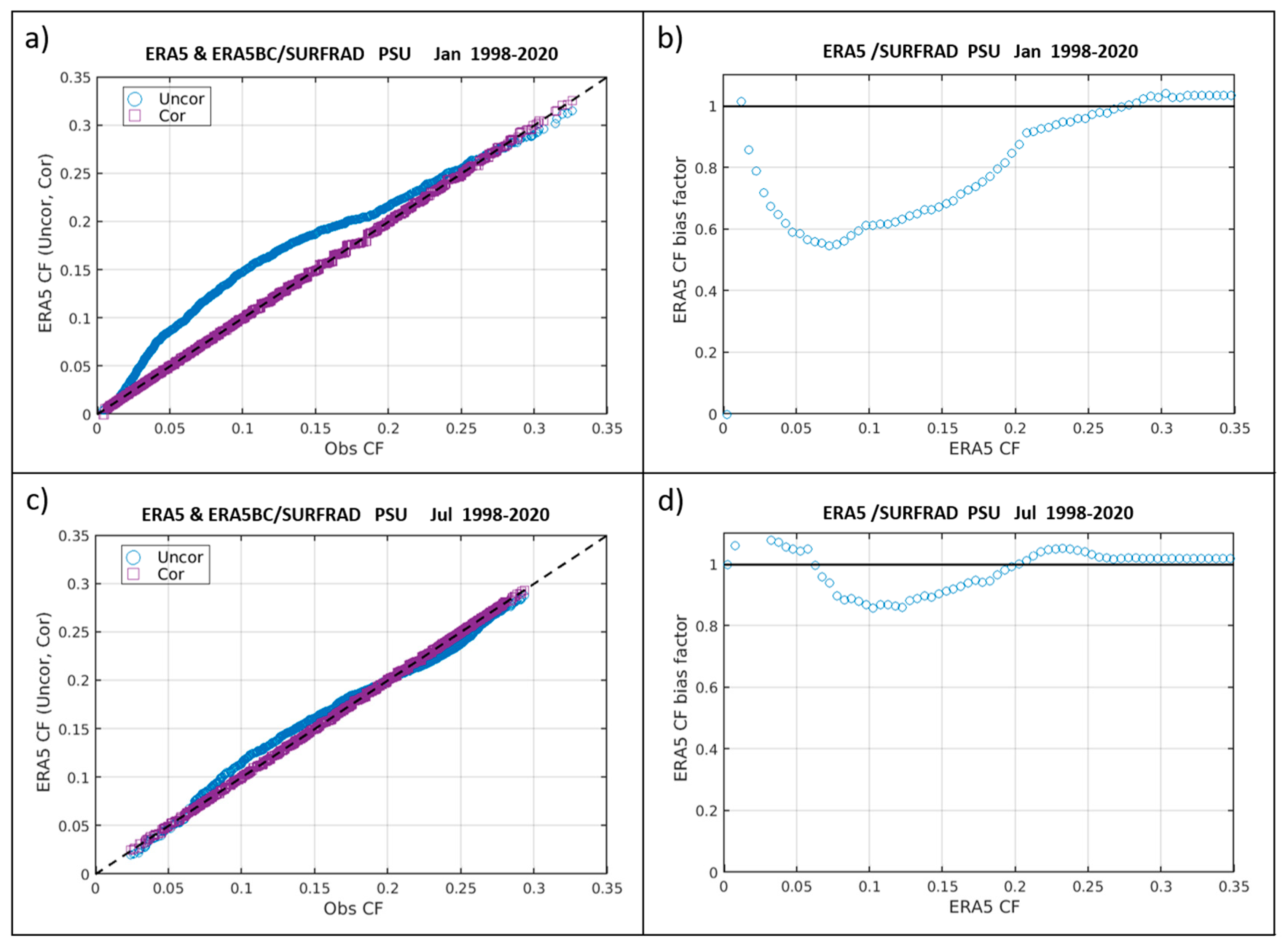
4.1. Quantile–Quantile Correction of Solar Power
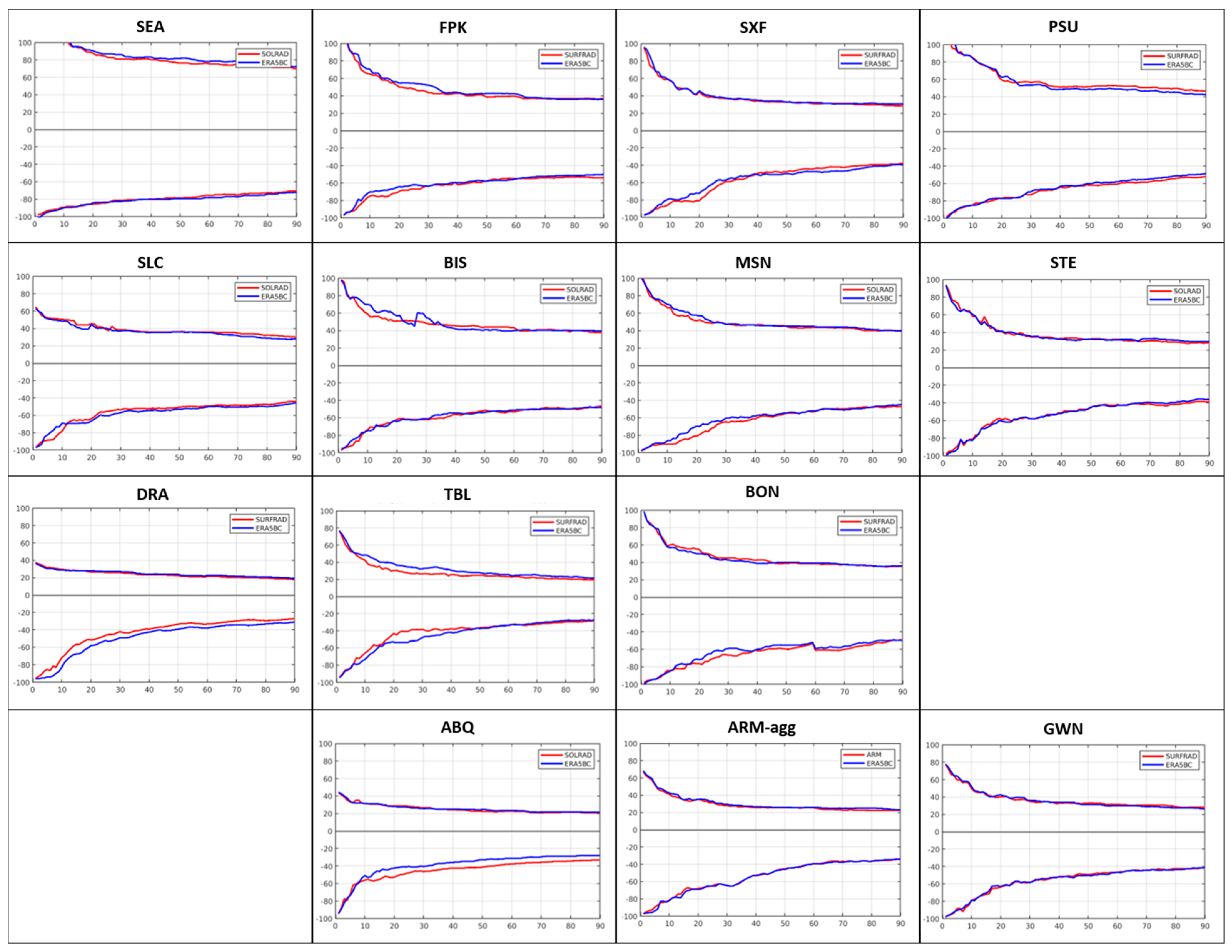
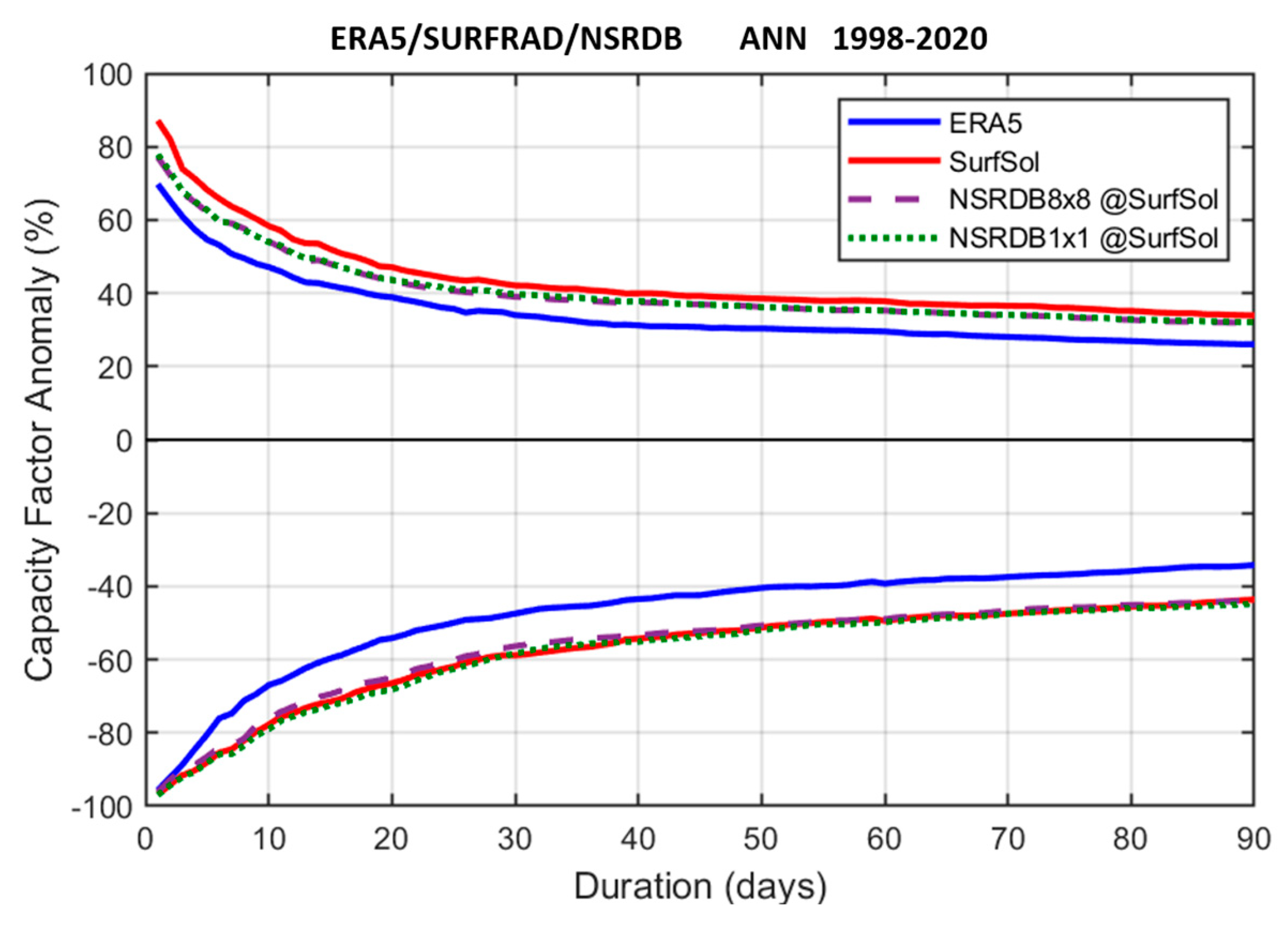
4.2. Intensity–Duration Curves
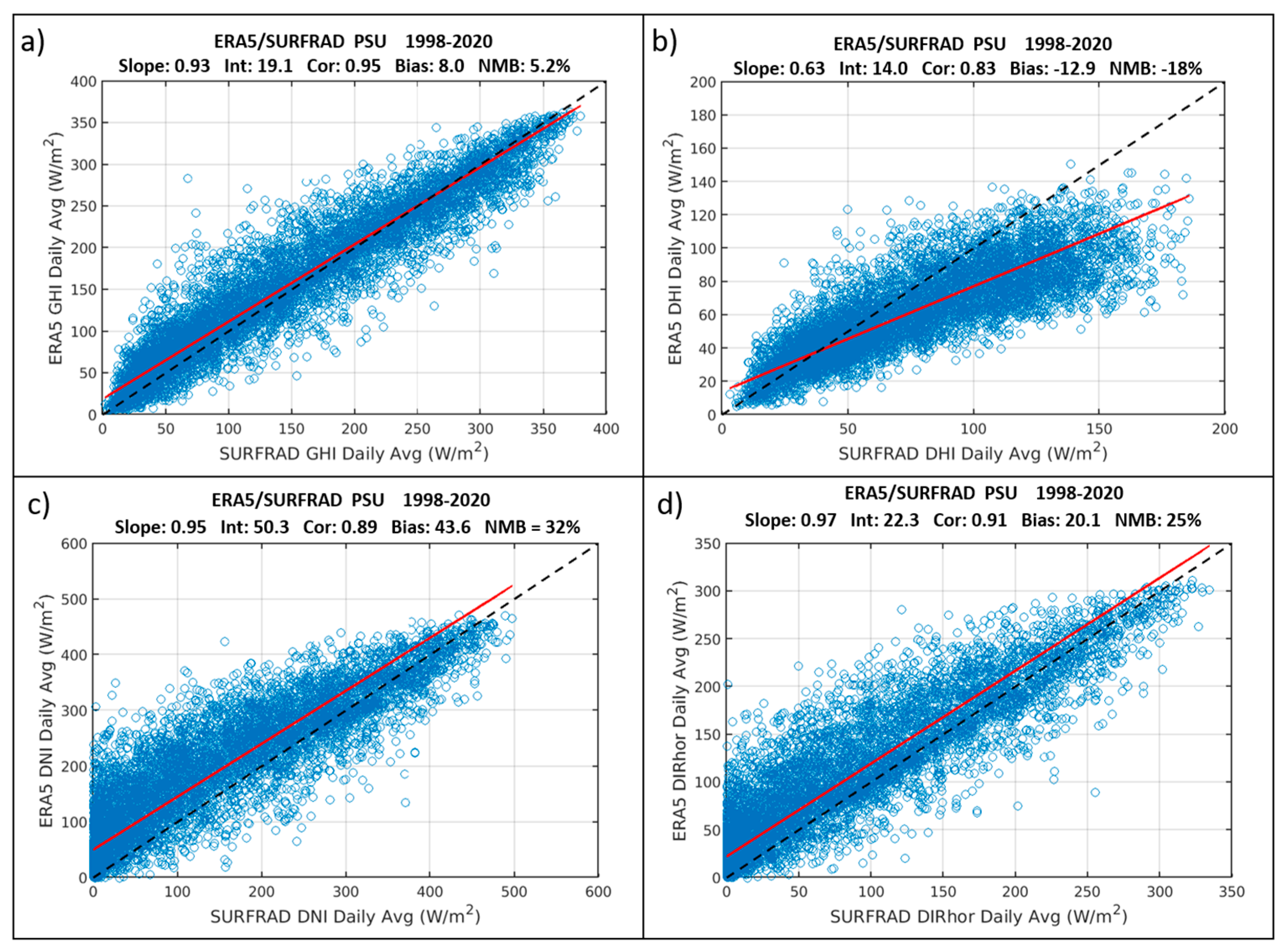
4.3. NSRDB and SURFRAD
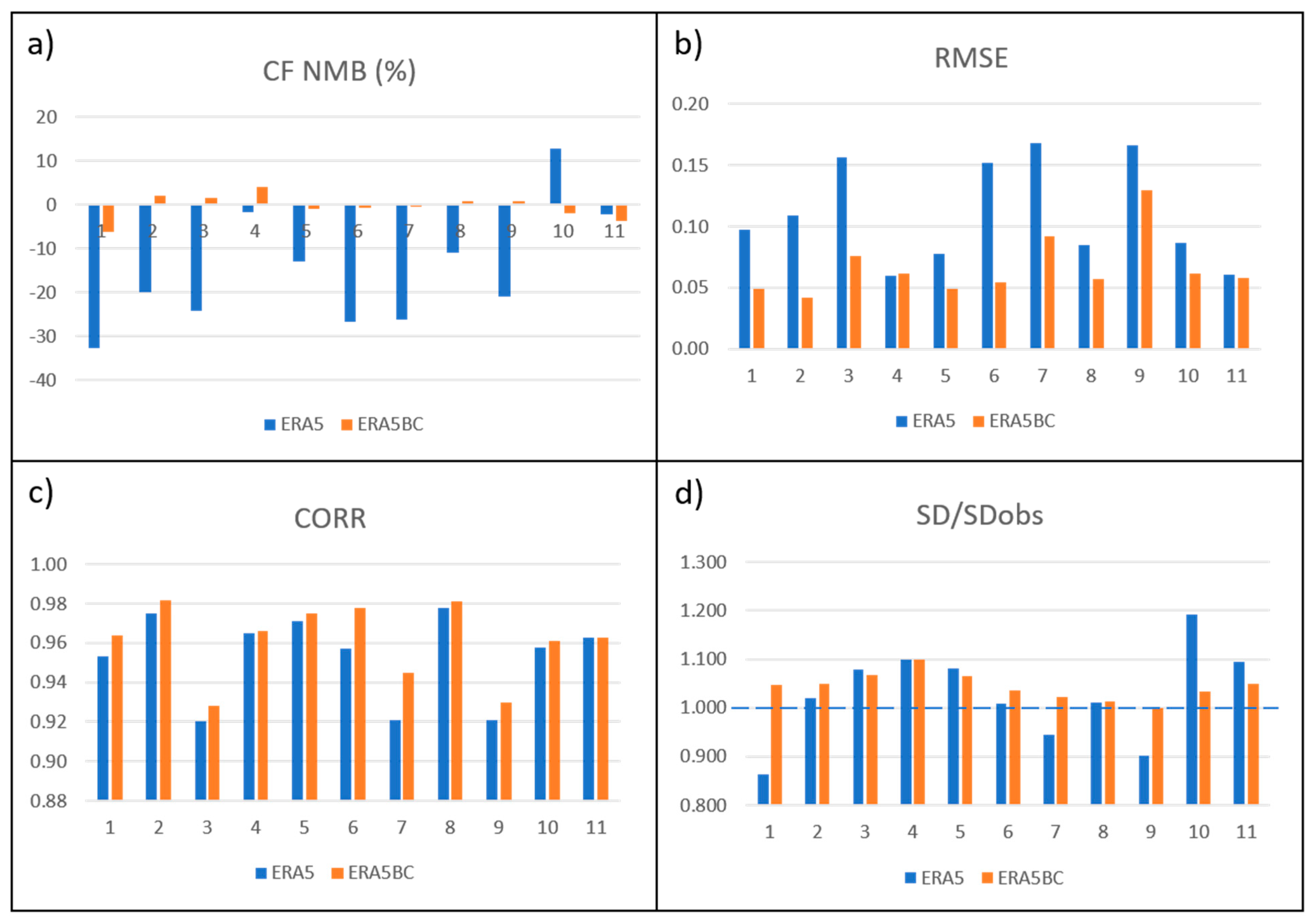
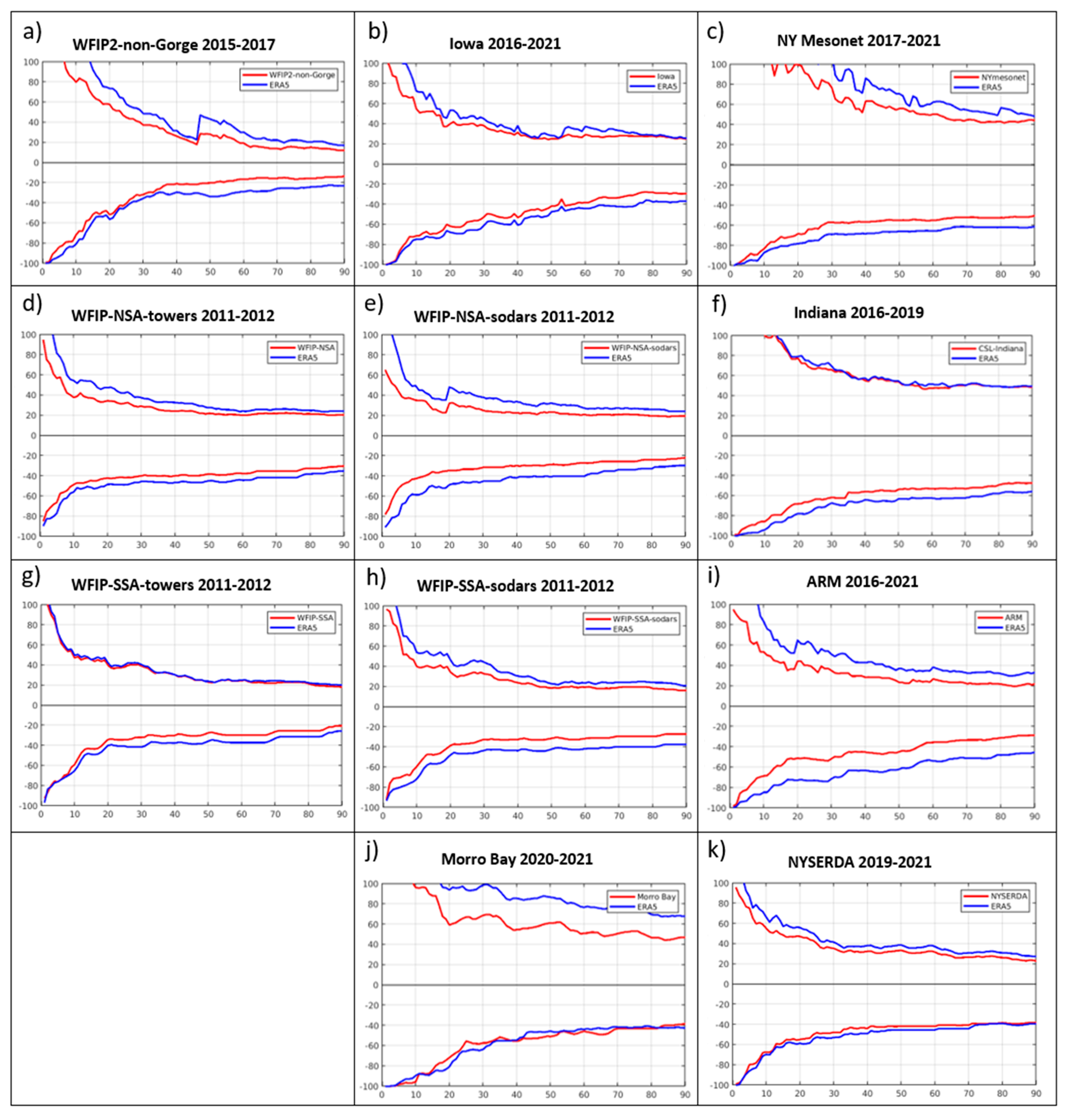
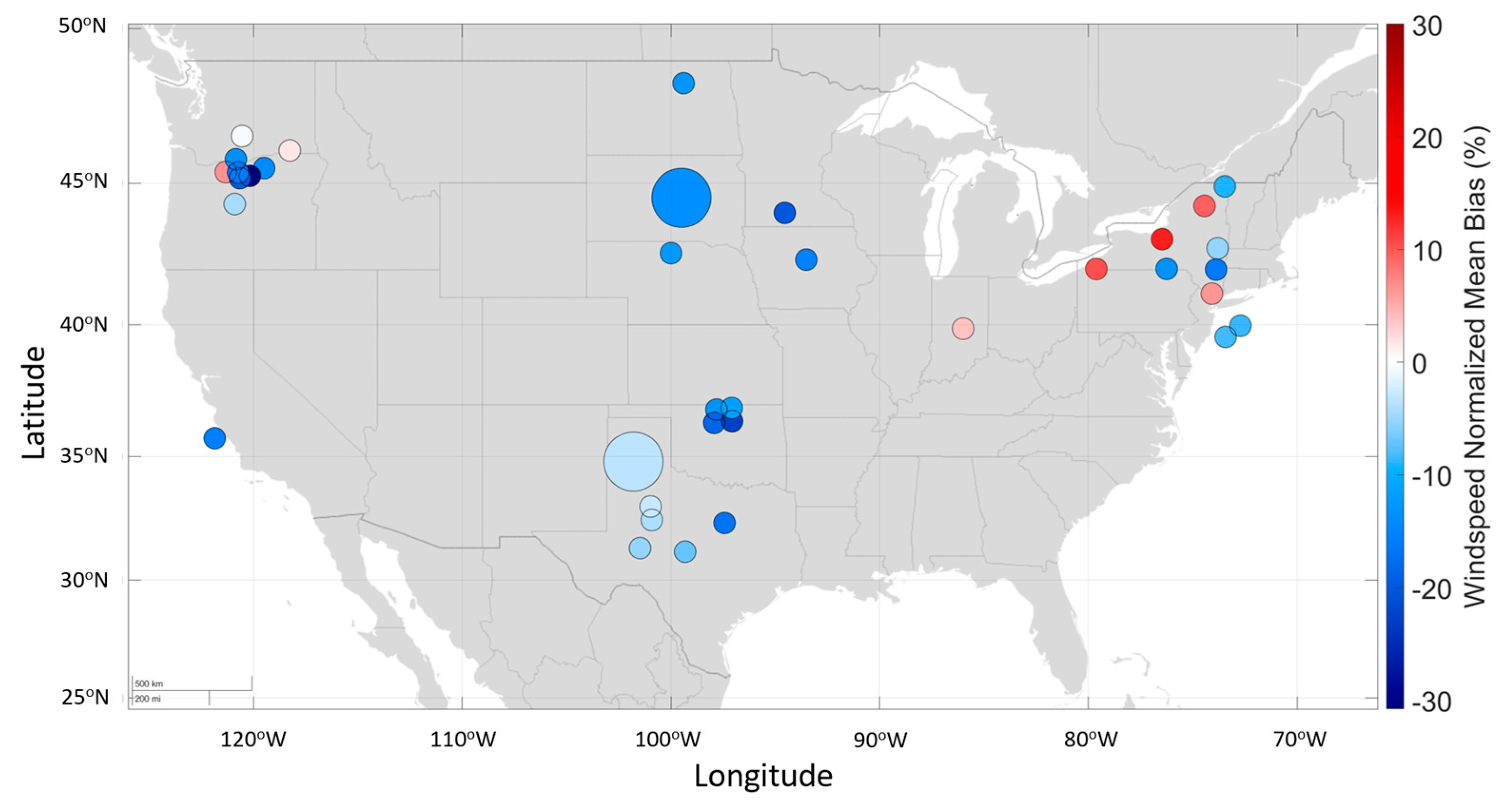
5. Evaluation of ERA5-Derived Wind Capacity Factor Systematic Errors
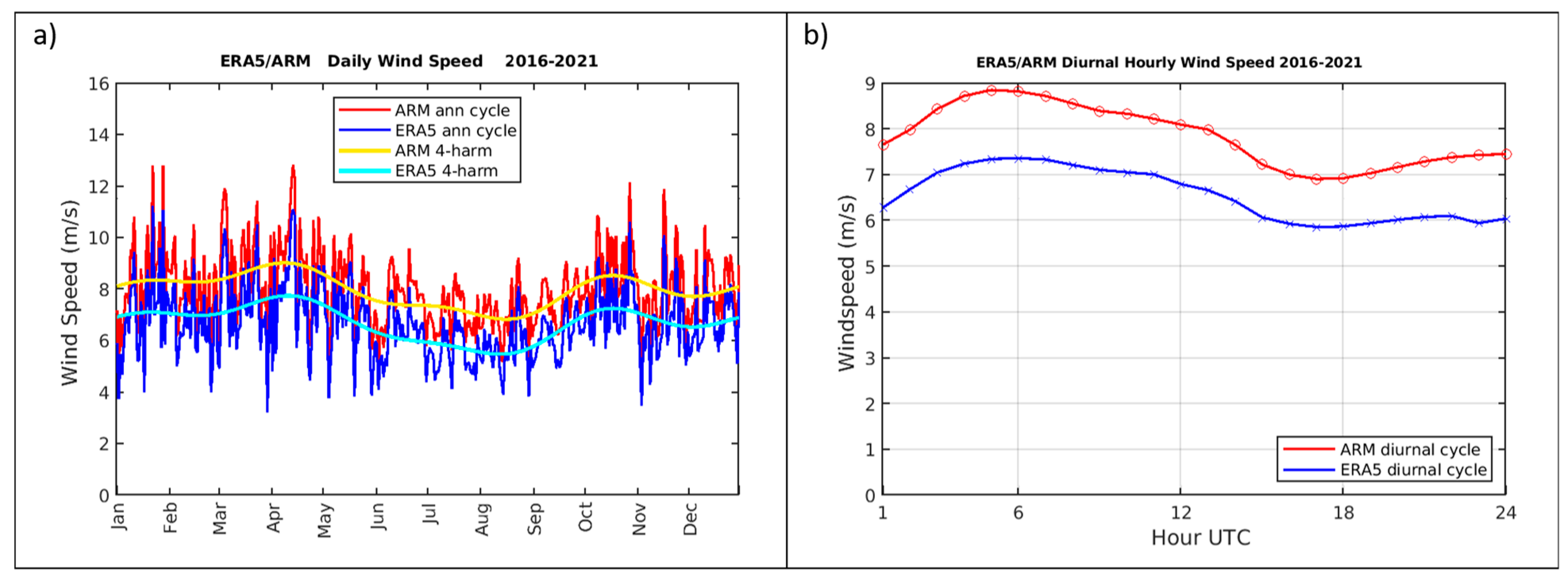
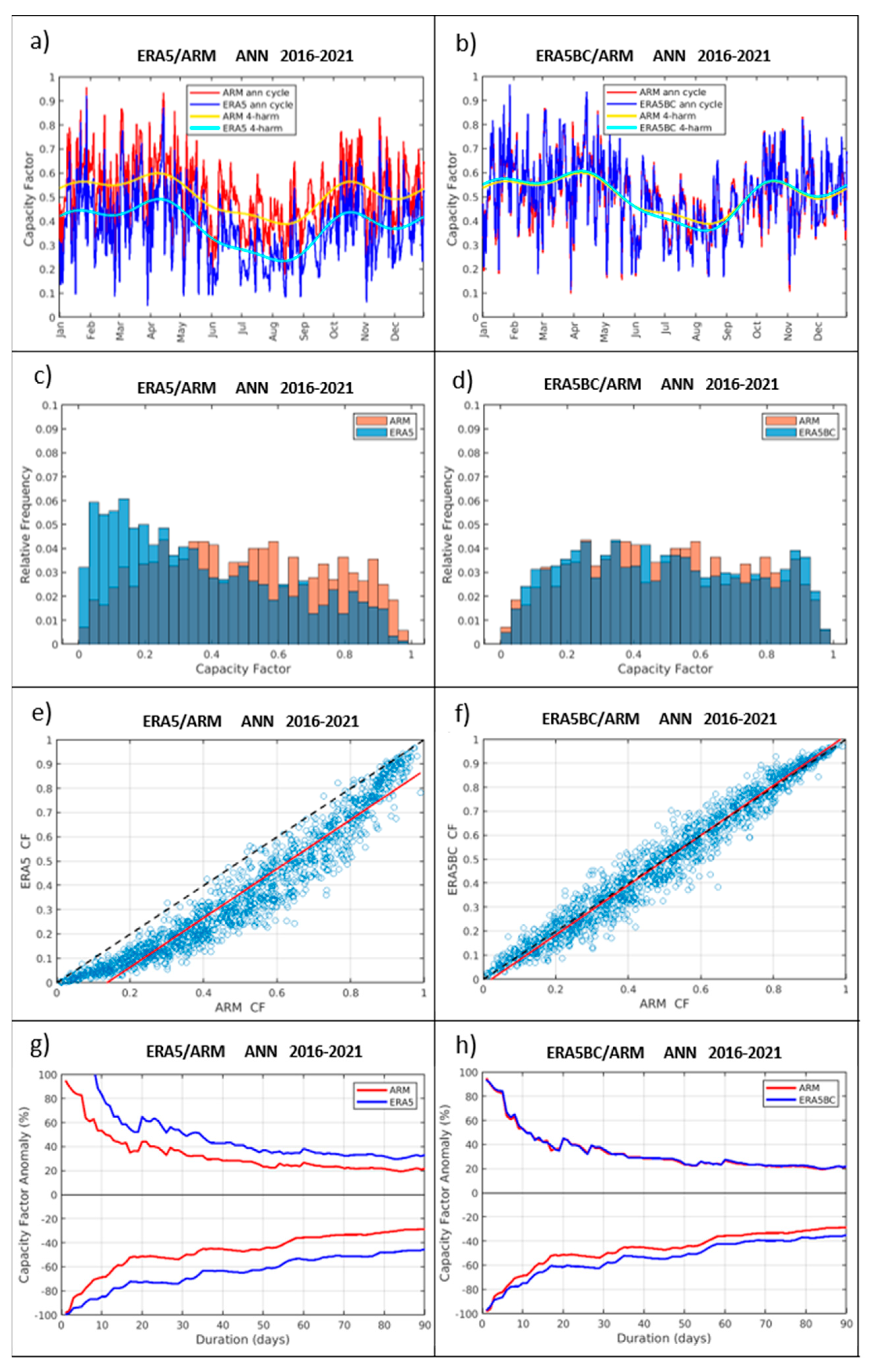
5.1. ARM-SGP Lidars
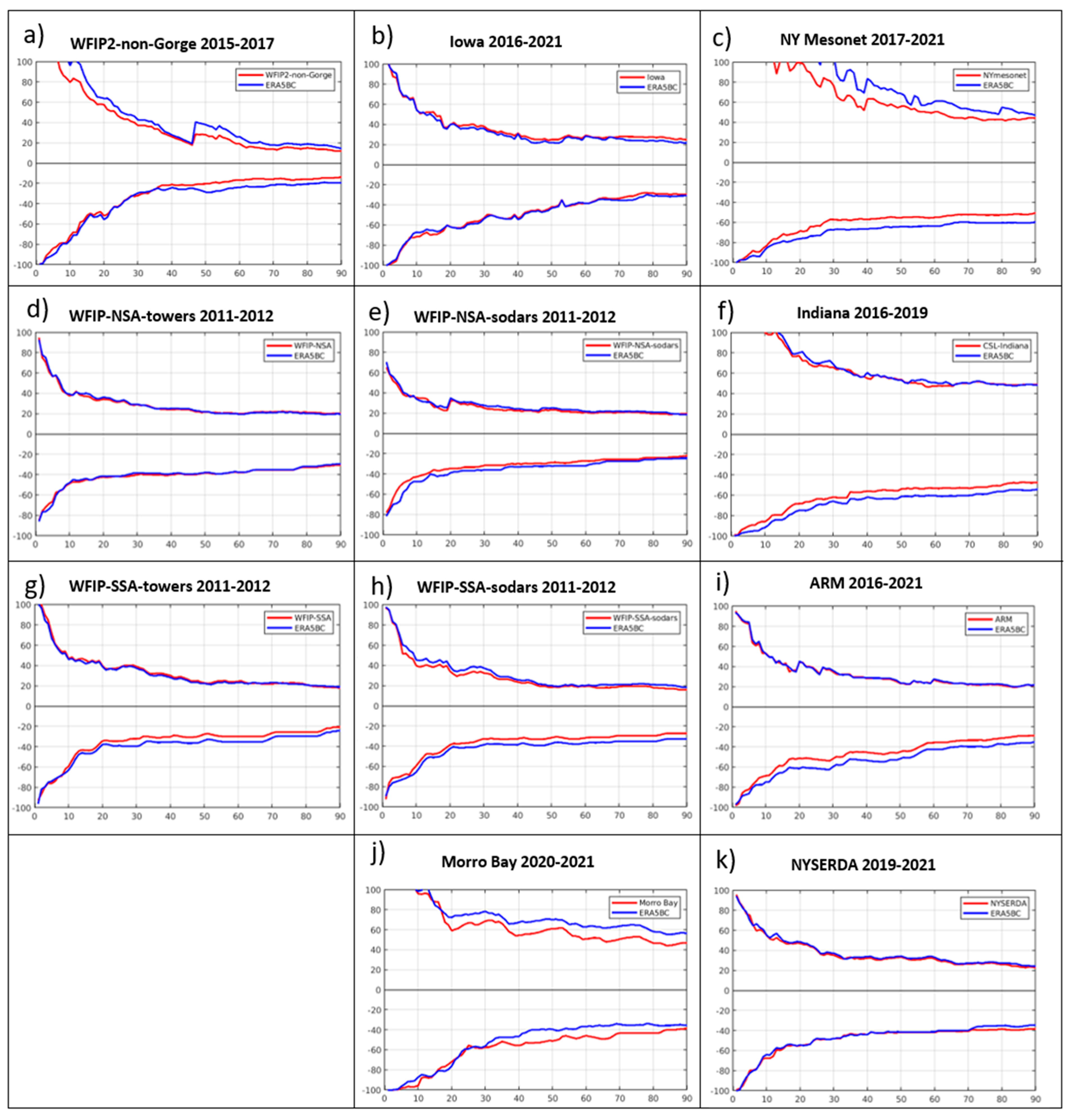
5.2. Corrections to the Remaining Wind Data Sets
6. Summary and Discussion
- (1)
- Instrumentation errors: Although this possibility can never be completely ruled out, this seems unlikely, as only the highest quality observational data sets available have been used, and for wind, similar errors are found whether using sodars, lidars, or tall tower in situ observations.
- (2)
- Non-representative siting within a grid associated with topography or land surface conditions: For solar, similar systematic errors are found for all sites, indicating that non-representative siting can be ruled out. For wind, in the central and western U.S., similar systematic errors are found whether in extremely flat (Iowa), flat but uniformly sloping (ARM-SGP) terrain, or more moderate rolling terrain (WFIP1, WFIP2). This indicates that it is unlikely that siting and terrain effects are a dominant source of the wind speed errors.
- (3)
- Turbine wake effects: Since the ERA5 does not account for turbine wake effects, the effect of wakes, if they are present, would be to bias the ERA5 winds higher than the observations, while instead they are found to have a low bias. Wind turbine wakes cannot therefore explain the ERA5 biases, and the true ERA5 biases, relative to unwaked flow, would be larger by some unknown amount if wind turbine wakes did not exist. The magnitude of the ERA5 wind speed negative bias, therefore, can be considered to be a lower bound and may be greater.
- (4)
- Model physical parameterization errors: Wind speed errors are not found to be a strong function of season or diurnal cycle, suggesting that stability impacts are not important, but also increase with wind speed, leaving surface roughness as a more likely source. Wind biases are larger for non-forested regions, and are smaller on average for the northeastern U.S., which is heavily treed, again suggesting a surface roughness parameterization error. For solar, ERA5 errors are smallest in summer months, while winter days that are partially cloudy are the most difficult, which may help identify aspects of cloud parameterizations that could be the source of these errors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
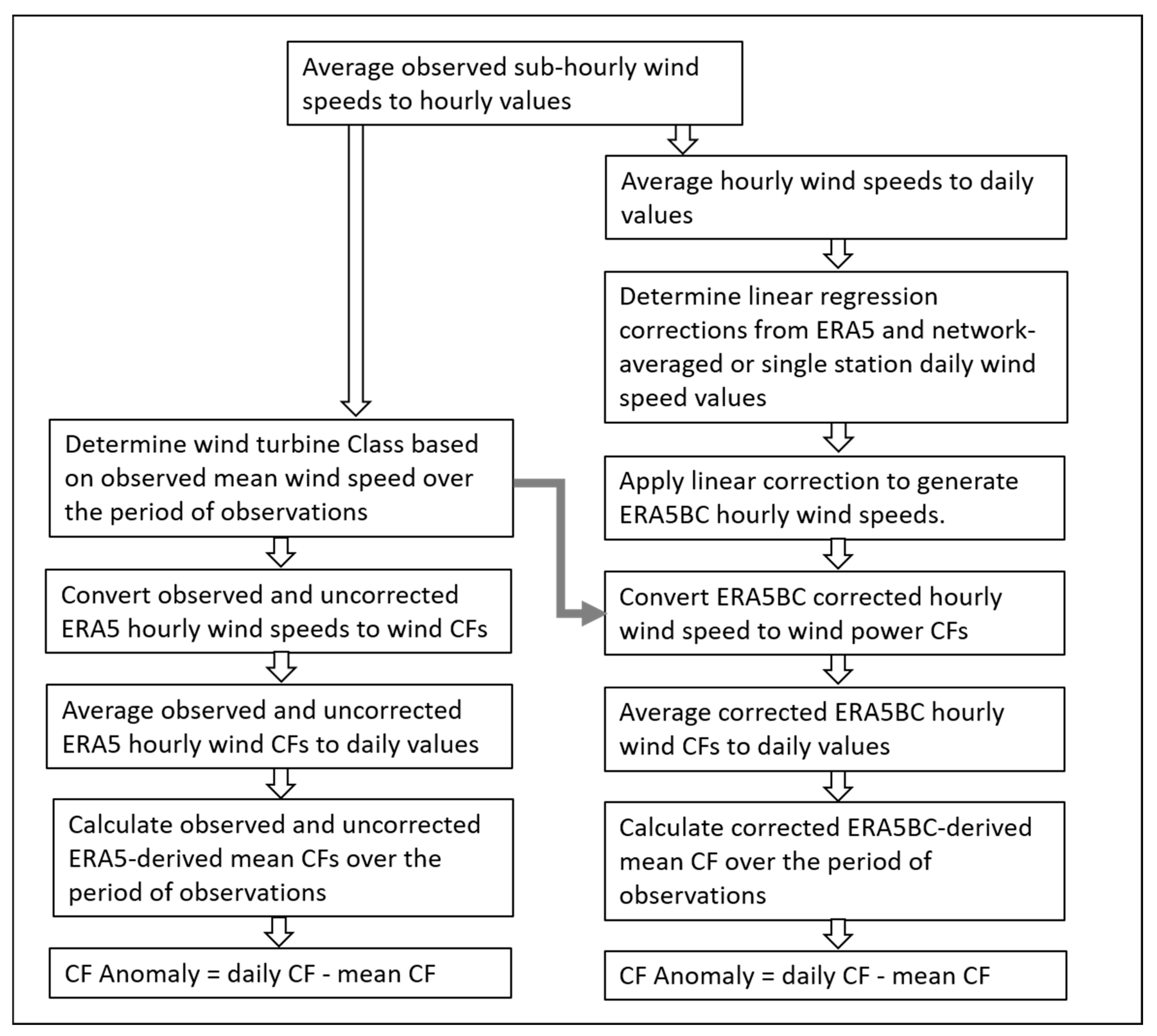
Appendix A. Processing Methods for Solar Power and Summary Statistics
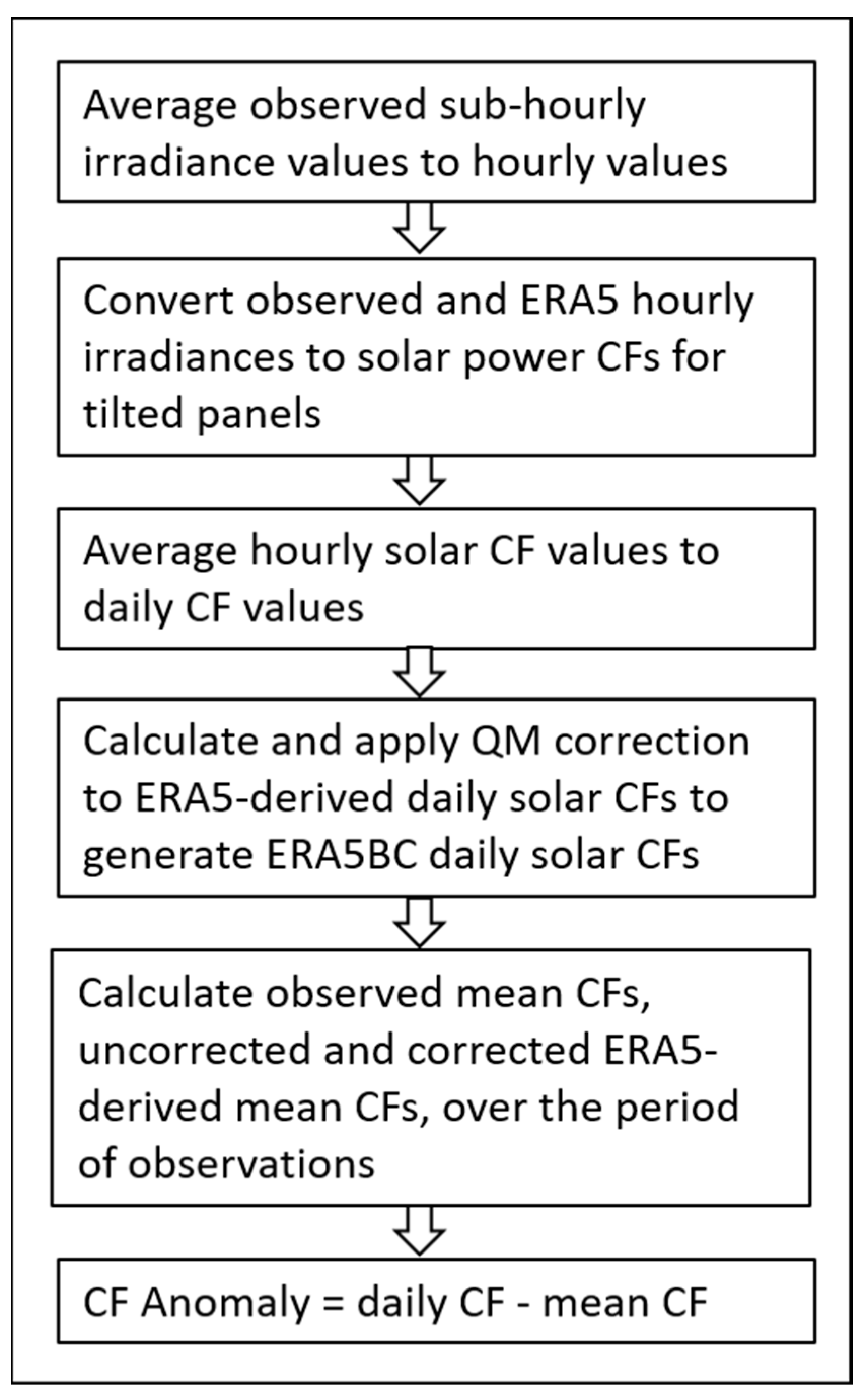




- Processing Methods for Wind Power and Summary Statistics

References
- Sharp, J. Meteorology 101: Meteorological Data Fundamentals for Power System Planning. Available online: https://www.esig.energy/weather-data-for-power-system-planning (accessed on 15 November 2023).
- Gualtieri, G. Analysing the uncertainties of reanalysis data used for wind resource assessment: A critical review. Renew. Sust. Energ. Rev. 2022, 167, 112741. [Google Scholar] [CrossRef]
- Kies, A.; Schyska, B.U.; Bilousova, M.; El Sayed, O.; Jurasz, J.; Stoecker, H. Critical review of renewable generation datasets and their implications for European power system models. Renew. Sustain. Energy Rev. 2021, 152, 111614. [Google Scholar] [CrossRef]
- Dörenkämper, M.; Olsen, B.T.; Witha, B.; Hahmann, A.N.; Davis, N.N.; Barcons, J.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; et al. The Making of the New European Wind Atlas—Part 2: Production and evaluation. Geosci. Model. Dev. 2020, 13, 5079–5102. [Google Scholar] [CrossRef]
- Jourdier, B. Evaluation of ERA5, MERRA-2, COSMO-REA6, NEWA and AROME to simulate wind power production over France. Adv. Sci. Res. 2020, 17, 63–77. [Google Scholar] [CrossRef]
- Gualtieri, G. Reliability of ERA5 Reanalysis Data for Wind Resource Assessment: A Comparison against Tall Towers. Energies 2021, 14, 4169. [Google Scholar] [CrossRef]
- Brune, S.; Keller, J.D.; Wahl, S. Evaluation of wind speed estimates in reanalyses for wind energy applications. Adv. Sci. Res. 2021, 18, 115–126. [Google Scholar] [CrossRef]
- Pronk, V.; Bodini, N.; Optis, M.; Lundquist, J.K.; Moriarty, P.; Draxl, C.; Purkayastha, A.; Young, E. Can reanalysis products outperform mesoscale numerical weather prediction models in modeling the wind resource in simple terrain? Wind. Energy Sci. 2022, 7, 487–504. [Google Scholar] [CrossRef]
- Sheridan, L.M.; Krishnamurthy, R.; Gorton, A.M.; Shaw, W.J.; Newsom, R.K. Validation of Reanalysis-Based Offshore Wind Resource Characterization Using Lidar Buoy Observations. Mar. Technol. Soc. J. 2020, 54, 44–61. [Google Scholar] [CrossRef]
- Sheridan, L.M.; Krishnamurthy, R.; Medina, G.G.; Gaudet, B.J.; Gustafson, W.I.; Mahon, A.M.; Shaw, W.J.; Newsom, R.K.; Pekour, M.; Yang, Z.Q. Offshore reanalysis wind speed assessment across the wind turbine rotor layer off the United States Pacific coast. Wind. Energy Sci. 2022, 7, 2059–2084. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Babar, B.; Graversen, R.; Boström, T. Solar radiation estimation at high latitudes: Assessment of the CMSAF databases, ASR and ERA5. Sol. Energy 2019, 182, 397–411. [Google Scholar] [CrossRef]
- Sianturi, Y.; Marjuki, M.; Sartika, K. Evaluation of ERAS and MERRA2 Reanalyses to Estimate Solar Irradiance Using Ground Observations over Indonesia Region. AIP Conf. Proc. 2020, 2223, 020002. [Google Scholar] [CrossRef]
- He, Y.Y.; Wang, K.C.; Feng, F. Improvement of ERA5 over ERA-Interim in Simulating Surface Incident Solar Radiation throughout China. J. Clim. 2021, 34, 3853–3867. [Google Scholar] [CrossRef]
- Khamees, A.S.; Khalil, S.A.; Morsy, M.; Hassan, A.H.; Rahoma, U.A.; Sayad, T. Evaluation of global solar radiation estimated from (ECMWF-ERA5) and validation with measured data over Egypt. Turk. J. Comp. Math. Educ. 2021, 12, 3996–4012. [Google Scholar]
- Tong, L.; He, T.; Ma, Y.C.; Zhang, X.T. Evaluation and intercomparison of multiple satellite-derived and reanalysis downward shortwave radiation products in China. Int. J. Digit. Earth 2023, 16, 1853–1884. [Google Scholar] [CrossRef]
- Wu, J.Y.; Fang, H.J.; Qin, W.M.; Wang, L.C.; Song, Y.; Su, X.; Zhang, Y.J. Constructing High-Resolution (10 km) Daily Diffuse Solar Radiation Dataset across China during 1982-2020 through Ensemble Model. Remote Sens. 2022, 14, 3695. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, Y.P.; Bai, Y.Q.; Wang, H.Z. Evaluation of the Total, Direct, and Diffuse Solar Radiations From the ERA5 Reanalysis Data in China. IEEE Geosci. Remote Sens. 2020, 17, 47–51. [Google Scholar] [CrossRef]
- Li, Z.G.; Yang, X.; Tang, H. Evaluation of the hourly ERA5 radiation product and its relationship with aerosols over China. Atmos. Res. 2023, 294, 106941. [Google Scholar] [CrossRef]
- Mathews, D.; Gallachóir, B.O.; Deane, P. Systematic bias in reanalysis-derived solar power profiles & the potential for error propagation in long duration energy storage studies. Appl. Energy 2023, 336, 120819. [Google Scholar] [CrossRef]
- Qin, Y.; McVicar, T.R.; Huang, J.; West, S.; Steven, A.D.L. On the validity of using ground-based observations to validate geostationary-satellite-derived direct and diffuse surface solar irradiance: Quantifying the spatial mismatch and temporal averaging issues. Remote Sens. Environ. 2022, 280, 113179. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. SURFRAD—A national surface radiation budget network for atmospheric research. B Am. Meteorol. Soc. 2000, 81, 2341–2357. [Google Scholar] [CrossRef]
- Augustine, J.A.; Hodges, G.B.; Cornwall, C.R.; Michalsky, J.J.; Medina, C.I. An update on SURFRAD—The GCOS Surface Radiation budget network for the continental United States. J. Atmos. Ocean. Technol. 2005, 22, 1460–1472. [Google Scholar] [CrossRef]
- Riihimaki, L.; Shi, Y.; Zhang, D. Data Quality Assessment for ARM Radiation Data (QCRAD1LONG). 1997-03-21 to 2020-05-25, Southern Great Plains (SGP) Facility. Atmospheric Radiation Measurement (ARM) User Facility. ARM Data Center, 1997. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::qcrad1long/dataLevel::c2 (accessed on 23 March 2022). [CrossRef]
- Michalsky, J.J.; Gueymard, C.; Kiedron, P.; McArthur, L.J.B.; Philipona, R.; Stoffel, T. A proposed working standard for the measurement of diffuse horizontal shortwave irradiance. J. Geophys. Res.-Atmos. 2007, 112, D16112. [Google Scholar] [CrossRef]
- Holmgren, W.; Hansen, C.; Mikofski, M. pvlib Python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling Daylight Availability and Irradiance Components from Direct and Global Irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Jadhav, V. World estimates of PV optimal tilt angles and ratios of sunlight incident upon tilted and tracked PV panels relative to horizontal panels. Sol. Energy 2018, 169, 55–66. [Google Scholar] [CrossRef]
- Draxl, C.; Clifton, A.; Hodge, B.M.; McCaa, J. The Wind Integration National Dataset (WIND) Toolkit. Appl. Energy 2015, 151, 355–366. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Polo, J.; Wilbert, S.; Ruiz-Arias, J.A.; Meyer, R.; Gueymard, C.; Súri, M.; Martín, L.; Mieslinger, T.; Blanc, P.; Grant, I.; et al. Preliminary survey on site-adaptation techniques for satellite-derived and reanalysis solar radiation datasets. Sol. Energy 2016, 132, 25–37. [Google Scholar] [CrossRef]
- Harmsen, E.W.; Tosado-Cruz, P.; Mecikalski, J.R. Calibration of selected pyranometers and satellite derived solar radiation in Puerto Rico. Int. J. Renew. Energy Technol. 2014, 5, 43–54. [Google Scholar] [CrossRef]
- Polo, J.; Martín, L.; Vindel, J.M. Correcting satellite derived DNI with systematic and seasonal deviations: Application to India. Renew. Energy 2015, 80, 238–243. [Google Scholar] [CrossRef]
- Bender, G.; Davidson, F.; Eichelberger, F.; Gueymard, C.A. The road to bankability: Improving assessments for more accurate financial planning. In Proceedings of the Solar 2011 Conference American Solar Energy Society, Raleigh, NC, USA, 19 May 2011. [Google Scholar]
- Gueymard, C.A.; Gustafson, W.T.; Bender, G.; Etringer, A.; Storck, P. Evaluation of procedures to improve solar resource assessments: Optimum use of short-term data from a local weather station to correct bias in long-term satellite derived solar radiation time series. In Proceedings of the World Renewable Energy Forum, Denver, CO, USA, 13–17 May 2012. [Google Scholar]
- Schumann, K.; Beyer, H.G.; Chhatbar, K.; Meyer, R. Improving satellite-derived solar resource analysis with parallel ground-based measurements. In Proceedings of the ISES Solar World Congress, Kasel, Germany, 28 August–2 September 2011. [Google Scholar]
- Ruiz-Arias, J.A.; Quesada-Ruiz, S.; Fernández, E.F.; Gueymard, C.A. Optimal combination of gridded and ground-observed solar radiation data for regional solar resource assessment. Sol. Energy 2015, 112, 411–424. [Google Scholar] [CrossRef]
- Wood, A.W.; Maurer, E.P.; Kumar, A.; Lettenmaier, D.P. Long-range experimental hydrologic forecasting for the eastern United States. J. Geophys. Res.-Atmos. 2002, 107, ACL 6-1–ACL 6-15. [Google Scholar] [CrossRef]
- Wood, A.W.; Lettenmaier, D.P. A test bed for new seasonal hydrologic forecasting approaches in the western United States. B Am. Meteorol. Soc. 2006, 87, 1699–1712. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Clim. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Hopson, T.M.; Webster, P.J. A 1-10-Day Ensemble Forecasting Scheme for the Major River Basins of Bangladesh: Forecasting Severe Floods of 2003-07. J. Hydrometeorol. 2010, 11, 618–641. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Costoya, X.; Rocha, A.; Carvalho, D. Using bias-correction to improve future projections of offshore wind energy resource: A case study on the Iberian Peninsula. Appl. Energy 2020, 262, 114562. [Google Scholar] [CrossRef]
- Campos, R.M.; Gramcianinov, C.B.; de Camargo, R.; Dias, P.L.D. Assessment and Calibration of ERA5 Severe Winds in the Atlantic Ocean Using Satellite Data. Remote Sens. 2022, 14, 4918. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Augustine, J.A.; Capotondi, A. Forcing for Multidecadal Surface Solar Radiation Trends Over Northern Hemisphere Continents. J. Geophys. Res.-Atmos. 2022, 127, e2021JD036342. [Google Scholar] [CrossRef]
- MacDonald, A.E.; Clack, C.T.M.; Alexander, A.; Dunbar, A.; Wilczak, J.; Xie, Y.F. Future cost-competitive electricity systems and their impact on US CO emissions. Nat. Clim. Chang. 2016, 6, 526–531. [Google Scholar] [CrossRef]
- Phadke, A.; Paliwal, U.; Abhyankar, N.; McNair, T.; Paulos, B.; Wooley, D.; O’Connell, R. The 2035 Report: Plummeting Solar, Wind, and Battery Costs Can. Accelerate Our Clean. Electricity Future; Goldman School of Public Policy, University of California Berkeley: Berkeley, CA, USA, 2020. [Google Scholar]
- Brown, P.; Botterud, A. The Value of Inter-Regional Coordination and Transmission in Decarbonizing the US Electricity System. Joule 2021, 5, 115–134. [Google Scholar] [CrossRef]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sust. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Shippert, T.; Newsom, R.; Riihimaki, L.; Zhang, D. Doppler Lidar Horizontal Wind Profiles (DLPROFWIND4NEWS), Southern Great Plains (SGP) Facility; Atmospheric Radiation Measurement (ARM) User Facility; ARM Data Center, 2010. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::dlprofwind4news/dataLevel::c1 (accessed on 22 March 2022). [CrossRef]
- Jensen, M.P.; Toto, T.; Troyan, D.; Ciesielski, P.E.; Holdridge, D.; Kyrouac, J.; Schatz, J.; Zhang, Y.; Xie, S. The Midlatitude Continental Convective Clouds Experiment (MC3E) sounding network: Operations, processing and analysis. Atmos. Meas. Technol. 2015, 8, 421–434. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- DNV-GL. NYSERDA Floating LiDAR Buoy Data. Available online: https://oswbuoysny.resourcepanorama.dnv (accessed on 13 September 2023).
- Bodini, N.; Lundquist, J.K.; Moriarty, P. Wind plants can impact long-term local atmospheric conditions. Sci. Rep. 2021, 11, 22939. [Google Scholar] [CrossRef]
- Wilczak, J.; Finley, C.; Freedman, J.; Cline, J.; Bianco, L.; Olson, J.; Djalalova, I.; Sheridan, L.; Ahlstrom, M.; Manobianco, J.; et al. The Wind Forecast Improvement Project (WFIP) A Public-Private Partnership Addressing Wind Energy Forecast Needs. Bull. Am. Meteorol. Soc. 2015, 96, 1699–1718. [Google Scholar] [CrossRef]
- Takle, E.S.; Rajewski, D.A.; Purdy, S.L. The Iowa Atmospheric Observatory: Revealing the Unique Boundary Layer Characteristics of a Wind Farm. Earth Interact. 2019, 23, 1–27. [Google Scholar] [CrossRef]
- Rajewski, D.A.; Takle, E.S.; VanLoocke, A.; Purdy, S.L. Observations Show That Wind Farms Substantially Modify the Atmospheric Boundary Layer Thermal Stratification Transition in the Early Evening. Geophys. Res. Lett. 2020, 47, e2019GL086010. [Google Scholar] [CrossRef]
- Shaw, W.J.; Berg, L.K.; Cline, J.; Draxl, C.; Djalalova, I.; Grimit, E.P.; Lundquist, J.K.; Marquis, M.; McCaa, J.; Olson, J.B.; et al. The Second Wind Forecast Improvement Project (WFIP2): General Overview. Bull. Am. Meteorol. Soc. 2019, 100, 1687–1699. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Stoelinga, M.; Berg, L.K.; Sharp, J.; Draxl, C.; McCaffrey, K.; Banta, R.M.; Bianco, L.; Djalalova, I.; Lundquist, J.K.; et al. The Second Wind Forecast Improvement Project (WFIP2): Observational Field Campaign. Bull. Am. Meteorol. Soc. 2019, 100, 1701–1723. [Google Scholar] [CrossRef]
- Sharp, J.M.; Mass, C. Columbia Gorge gap flow—Insights from observational analysis and ultra-high-resolution simulation. Bull. Am. Meteorol. Soc. 2002, 83, 1757–1762. [Google Scholar] [CrossRef]
- Brotzge, J.A.; Wang, J.; Thorncroft, C.D.; Joseph, E.; Bain, N.; Bassill, N.; Farruggio, N.; Freedman, J.M.; Hemker, K.; Johnston, D.; et al. A Technical Overview of the New York State Mesonet Standard Network. J. Atmos. Ocean. Technol. 2020, 37, 1827–1845. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczak, J.M.; Akish, E.; Capotondi, A.; Compo, G.P. Evaluation and Bias Correction of the ERA5 Reanalysis over the United States for Wind and Solar Energy Applications. Energies 2024, 17, 1667. https://doi.org/10.3390/en17071667
Wilczak JM, Akish E, Capotondi A, Compo GP. Evaluation and Bias Correction of the ERA5 Reanalysis over the United States for Wind and Solar Energy Applications. Energies. 2024; 17(7):1667. https://doi.org/10.3390/en17071667
Chicago/Turabian StyleWilczak, James M., Elena Akish, Antonietta Capotondi, and Gilbert P. Compo. 2024. "Evaluation and Bias Correction of the ERA5 Reanalysis over the United States for Wind and Solar Energy Applications" Energies 17, no. 7: 1667. https://doi.org/10.3390/en17071667
APA StyleWilczak, J. M., Akish, E., Capotondi, A., & Compo, G. P. (2024). Evaluation and Bias Correction of the ERA5 Reanalysis over the United States for Wind and Solar Energy Applications. Energies, 17(7), 1667. https://doi.org/10.3390/en17071667





