Joint Estimation of SOC and SOH for Lithium-Ion Batteries Based on Dual Adaptive Central Difference H-Infinity Filter
Abstract
1. Introduction
2. Battery Modeling and Parameter Identification
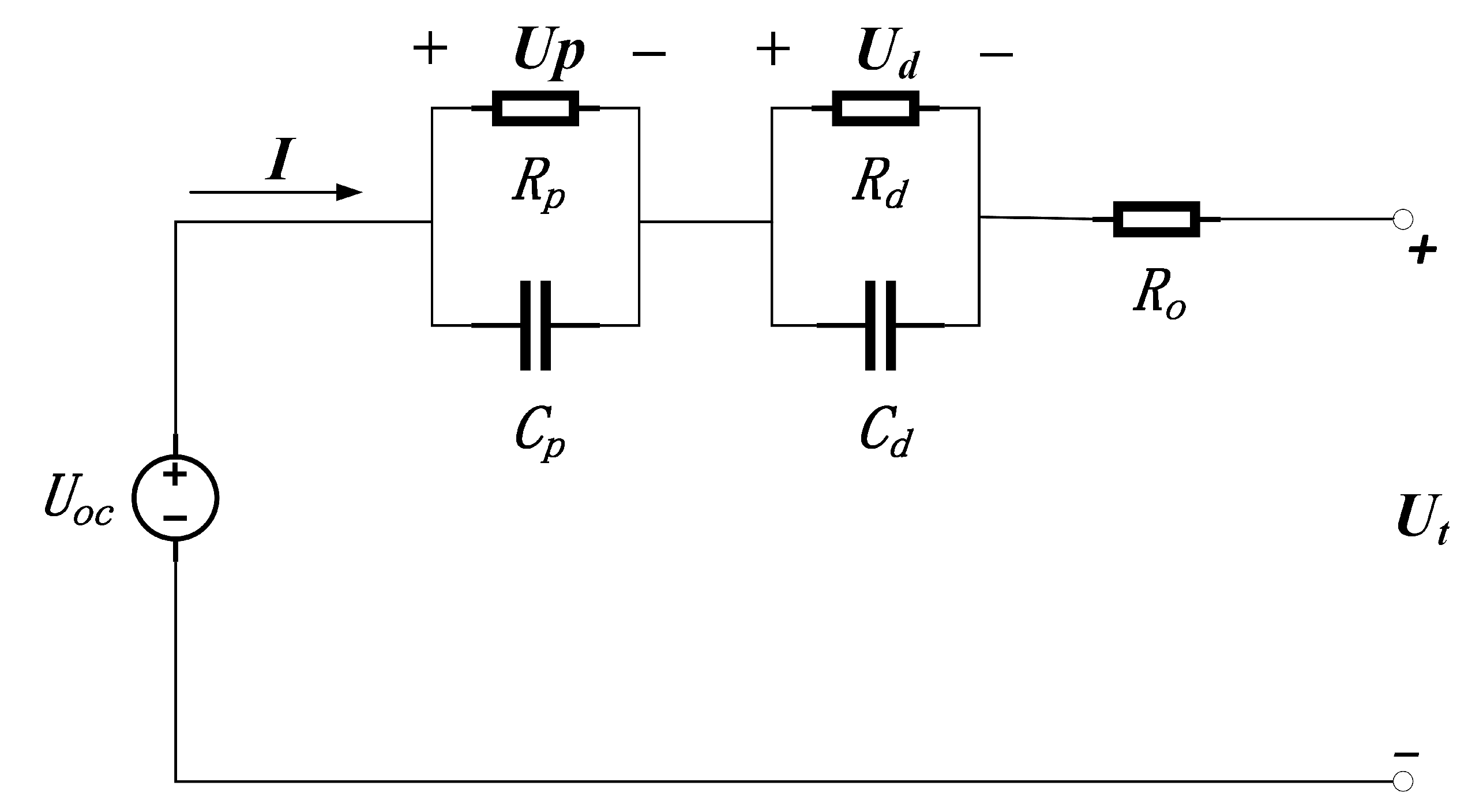
2.1. Battery Modeling
2.2. The Relationship between the State-of-Charge and Open-Circuit Voltage
2.3. Improved FFRLS
2.4. Model Parameter Identification
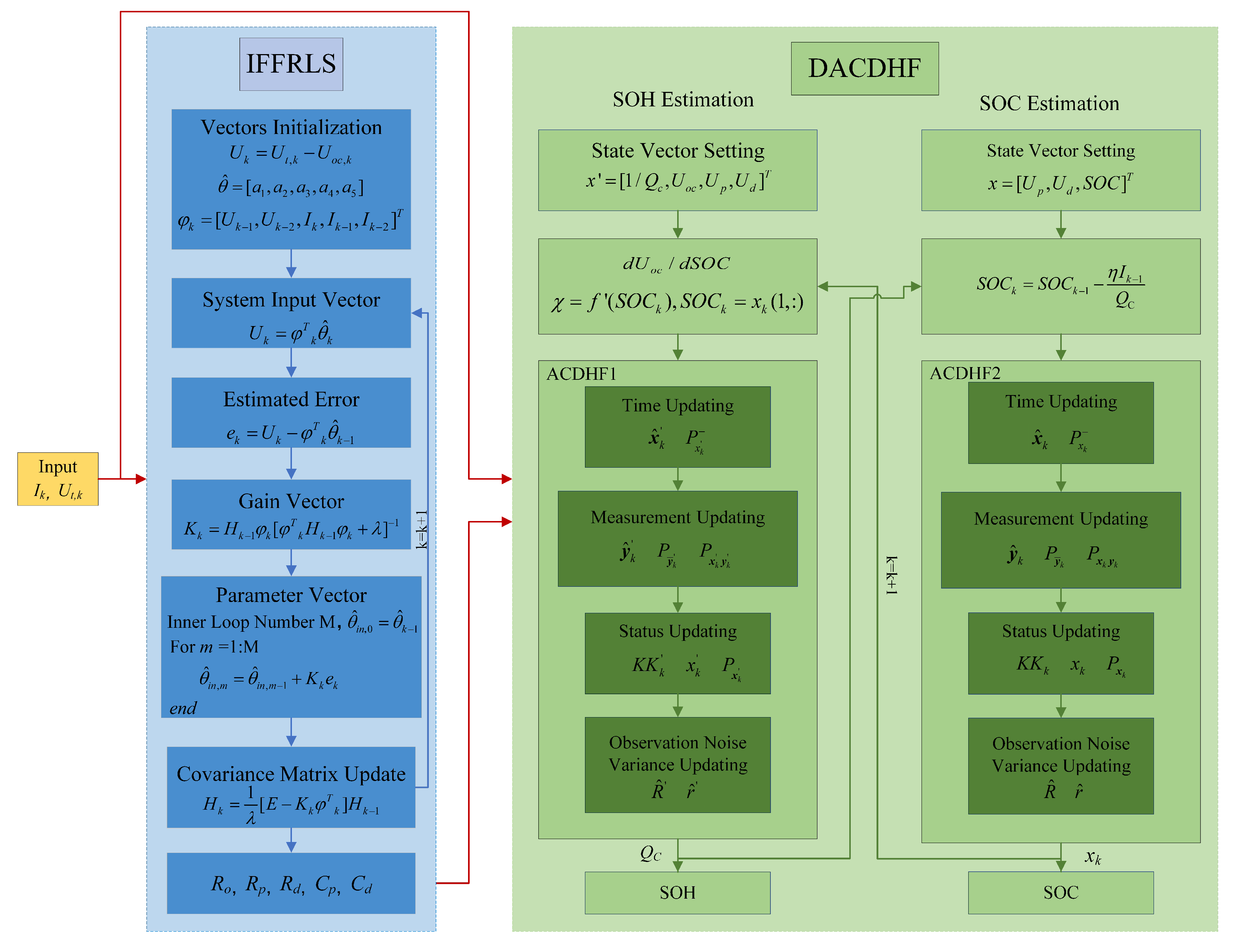
3. Joint Estimation of SOC and SOH Based on DACDHF
3.1. Joint Estimation of SOC and SOH
3.2. Adaptive Center Difference H∞ Filtering (ACDHF) Algorithm
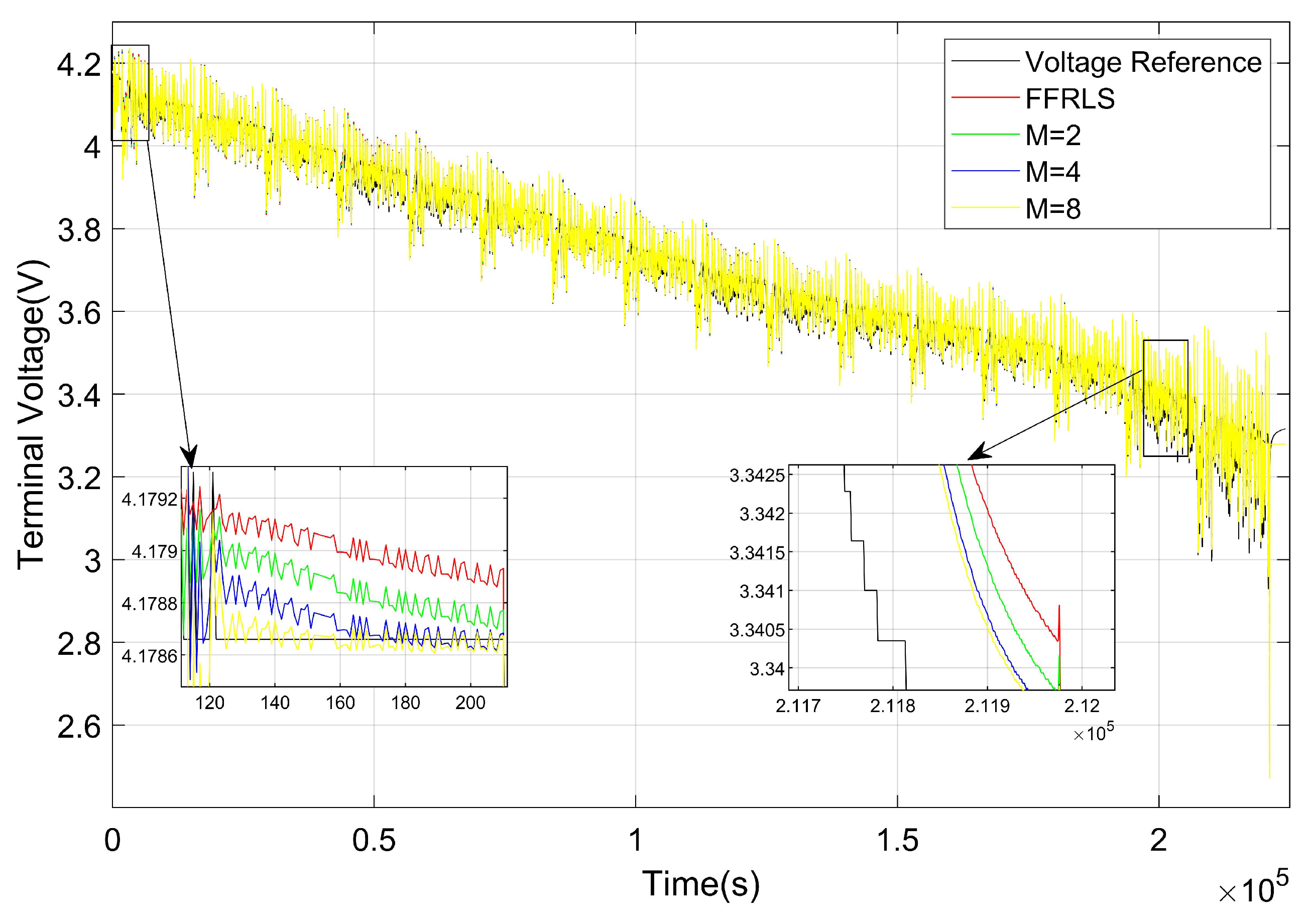
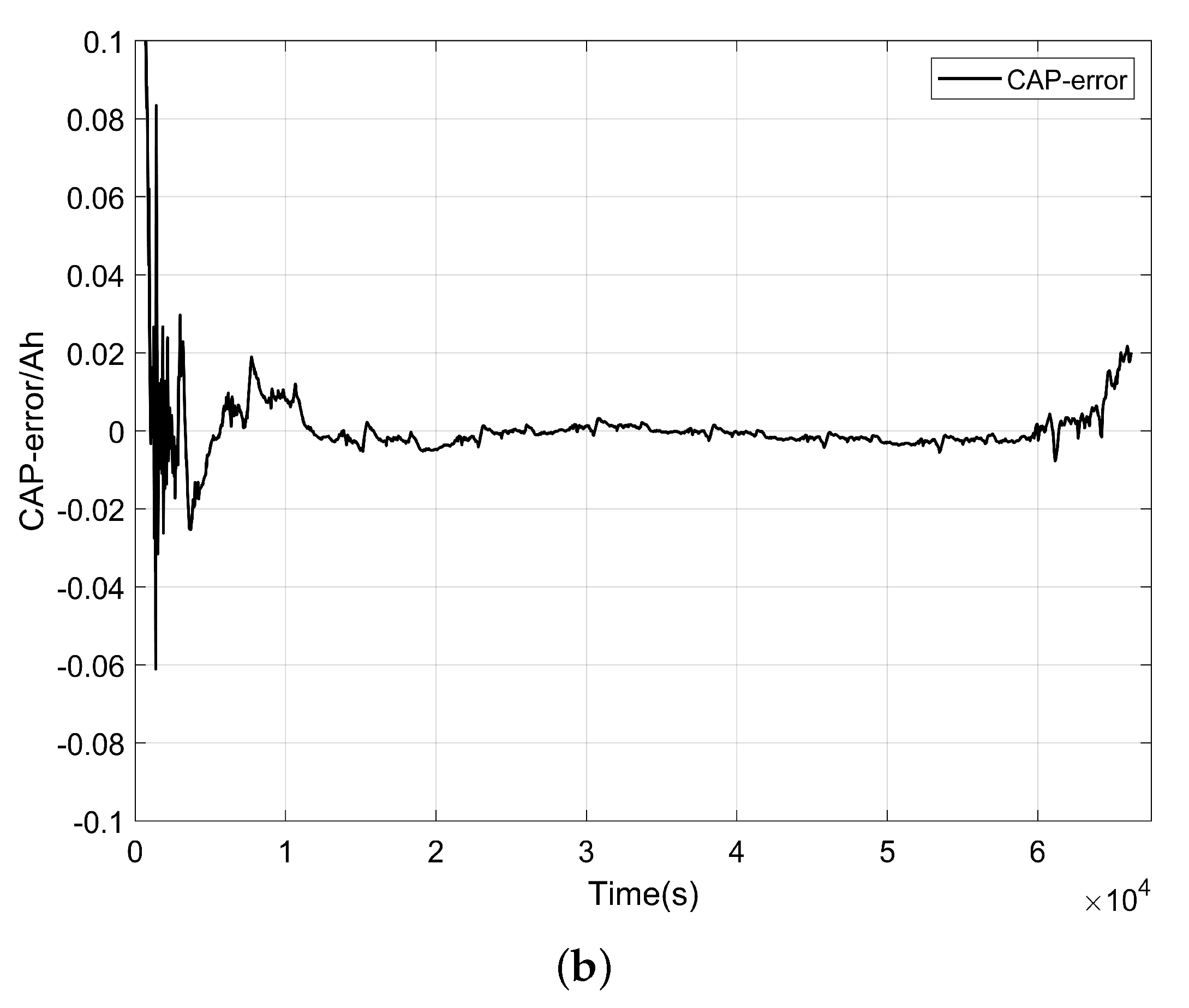
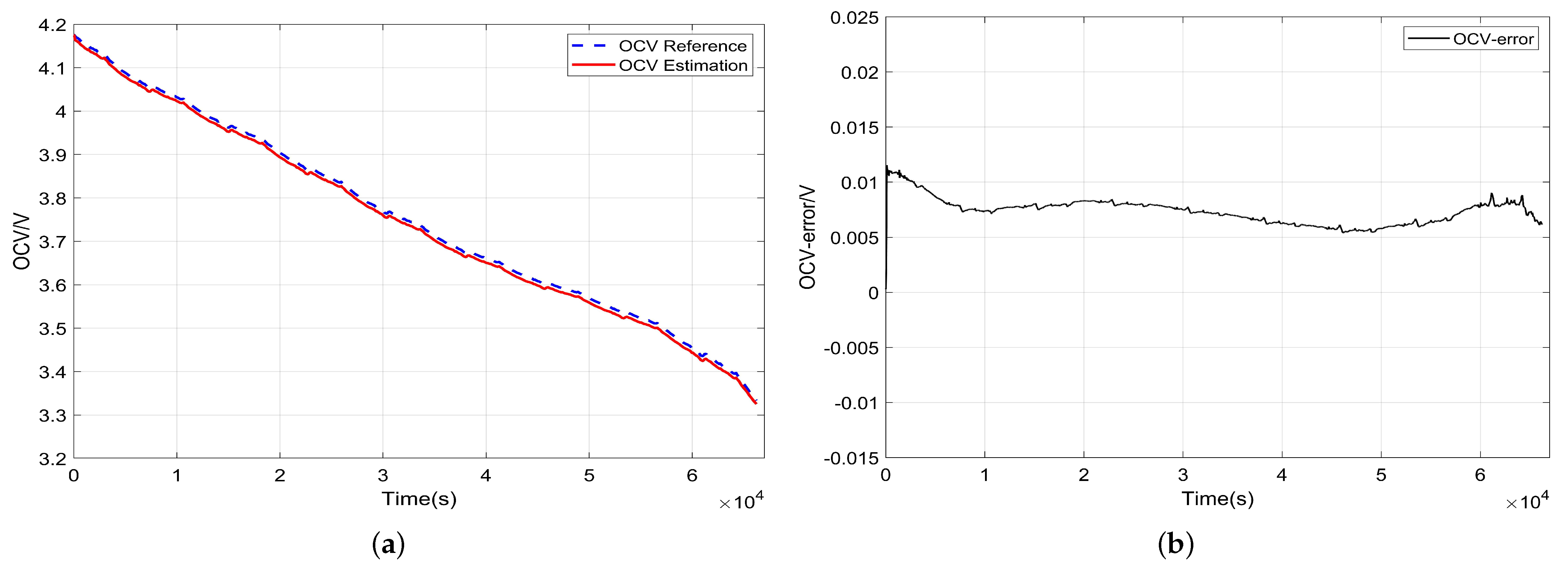
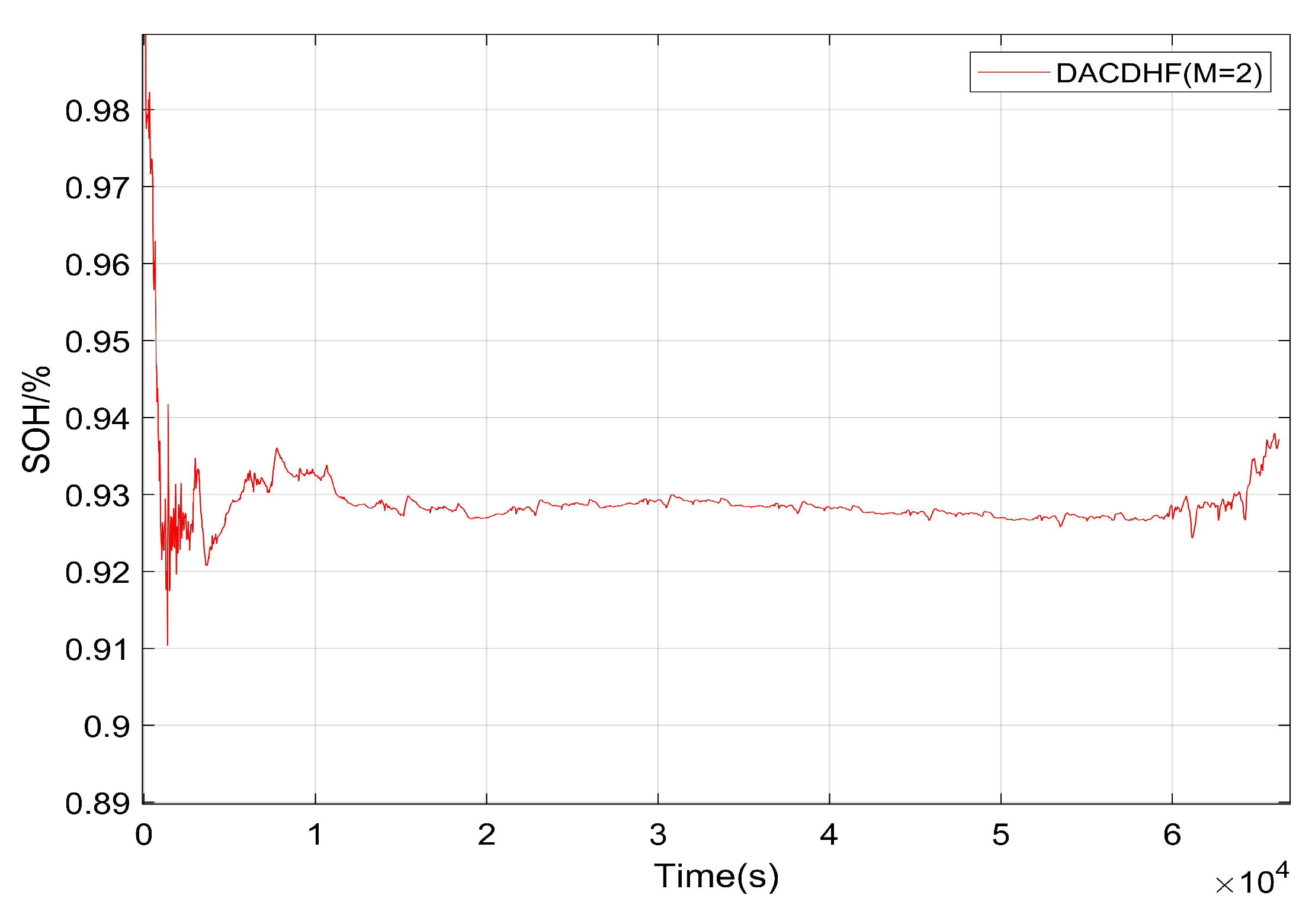
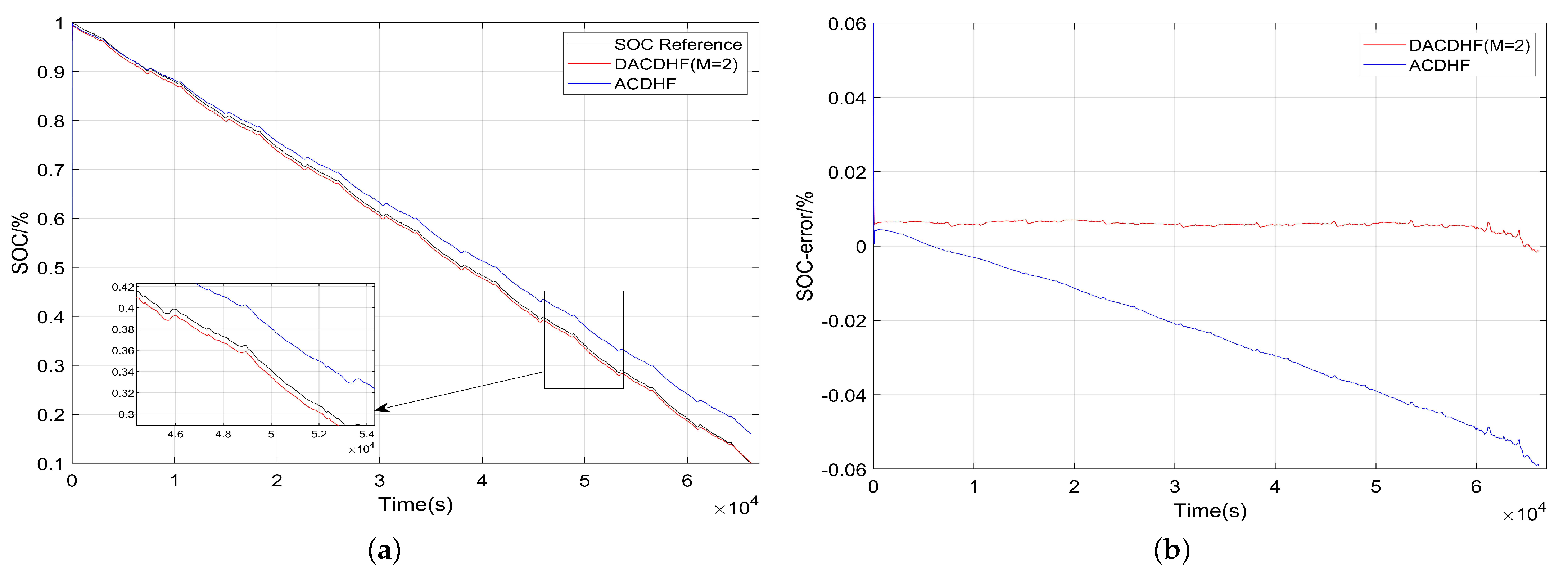
4. Experimental Verifications and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lai, X.; Yuan, M.; Tang, X.; Yao, Y.; Weng, J.; Gao, F.; Ma, W.; Zheng, Y. Co-Estimation of State-of-Charge and State-of-Health for Lithium-Ion Batteries Considering Temperature and Ageing. J. Energies 2022, 15, 7416. [Google Scholar] [CrossRef]
- Yihuan, L.; Kang, L.; James, Y.U. Estimation Approaches for States of Charge and Health of Lithium-ion Battery. J. Power Gener. Technol. 2021, 42, 537–546. [Google Scholar]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. J. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Pei, L.; Lu, R.; Zhu, C. Relaxation model of the open-circuit voltage for state-of-charge estimation in lithium-ion batteries. J. IET Electr. Syst. Transp. 2013, 3, 112–117. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- How, D.N.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.; Ker, P.J.; Muttaqi, K.M. State-of-charge estimation of Li-ion battery in electric vehicles: A deep neural network approach. J. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
- Xiao, F.; Li, C.; Fan, Y.; Yang, G.; Tang, X. State of charge estimation for lithium-ion battery based on Gaussian process regression with deep recurrent kernel. J. Int. J. Electr. Power Energy Syst. 2021, 124, 106369. [Google Scholar] [CrossRef]
- Wang, W.; Fu, R. Stability Analysis of EKF-Based SOC Observer for Lithium-Ion Battery. Energies 2023, 16, 5946. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Xia, J.; Zhang, Y. Estimation of the SOC of lithium batteries based on an improved CDKF algorithm. J. Energy Storage Sci. Technol. 2021, 10, 1454–1462. [Google Scholar]
- Xiong, R.; Yu, Q.; Lin, C. A novel method to obtain the open circuit voltage for the state of charge of lithium-ion batteries in electric vehicles by using H infinity filter. Appl. Energy 2017, 207, 346–353. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, L.; Gong, Q.; Wang, Y.; Song, H. State of charge estimation for lithium-ion battery based on adaptive extended Kalman filter with improved residual covariance matrix estimator. J. Power Sources 2024, 589, 233758. [Google Scholar] [CrossRef]
- Xiang, L.; Cai, L.; Dai, N.; Gao, L.; Lei, G.; Li, J.; Deng, M. State of Charge Estimation of Lithium-Ion Batteries Based on an Improved Sage-Husa Extended Kalman Filter Algorithm. World Electr. Veh. J. 2022, 13, 220. [Google Scholar] [CrossRef]
- Zhao, J.; Tian, L.; Cheng, L. Review on State Estimation and Remaining Useful Life Prediction Methods for Lithium-ion Battery. Power Gener. Technol. 2023, 44, 5014. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The Co-estimation of State of Charge, State of Health, and State of Function for Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 92–103. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Hu, P.; Tang, W.F.; Li, C.H.; Mak, S.L.; Li, C.Y.; Lee, C.C. Joint State of Charge (SOC) and State of Health (SOH) Estimation for Lithium-Ion Batteries Packs of Electric Vehicles Based on NSSR-LSTM Neural Network. J. Energies 2023, 16, 5313. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, L.; Sun, X.M. State of Charge and State of Health Estimation of Li-ion Batteries Based on Adaptive Square-root Unscented Kalman Filters. J. Proc. CSEE 2018, 38, 2384–2393+2548. [Google Scholar]
- Yiqi, L.; Wanjun, L.; Qian, L.; Yichao, G.; Ming, D. Joint State Estimation of Lithium-Ion Battery Based on Dual Adaptive Extended Particle Filter. J. Trans. China Electrotech. Soc. 2024, 39, 607–616. [Google Scholar]
- Ruoqi, W.; Xiaojia, W.; Qi, Y. Joint Estimation of Lithium Battery SOC/SOH Based on Double Adaptive Untracked Kalman Filtering Algorithm. Mach. Des. Manuf. 2023, 1, 1–4. [Google Scholar]
- Yu, Q.; Xiong, R.; Yang, R.; Pecht, M.G. Online capacity estimation for lithium-ion batteries through joint estimation method. J. Appl. Energy 2019, 255, 113817. [Google Scholar] [CrossRef]
- Tan, Z.; Peng, T.; Dai, N.; Cai, L.; Wei, J.; Chen, H. Joint estimation of lithium battery SOC and SOH based on improved DAEKF. J. Chongqing Univ. Posts Telecommun. (Nat. Sci. Ed.) 2023, 35, 760–766. [Google Scholar]
- Ren, B.; Xie, C.; Sun, X.; Zhang, Q.; Yan, D. Parameters Identification of Lithium-ion Battery Based on the Improved Forgetting Factor Recursive Least Squares Algorithm. J. IET Power Electron. 2020, 3, 2531–2537. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
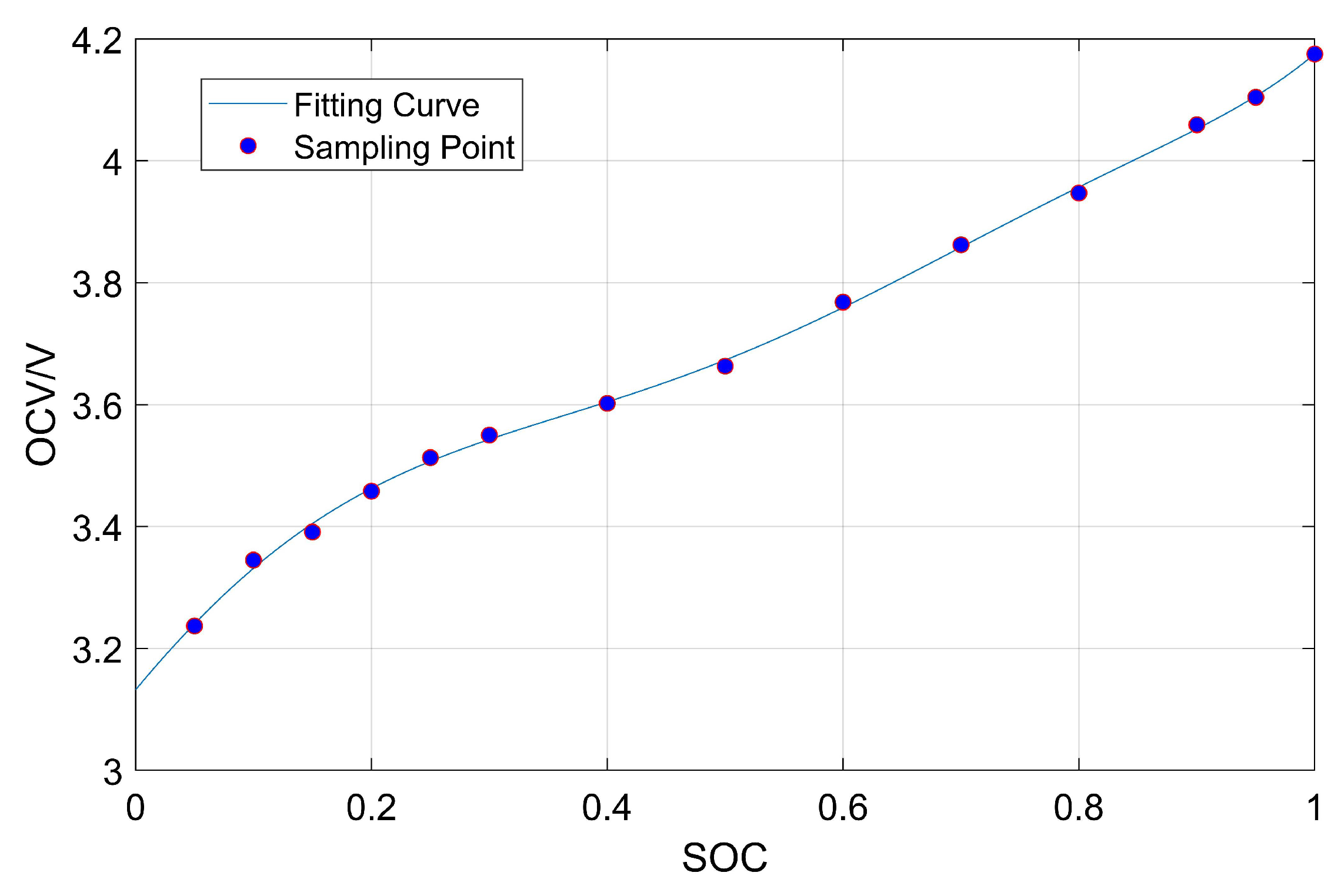

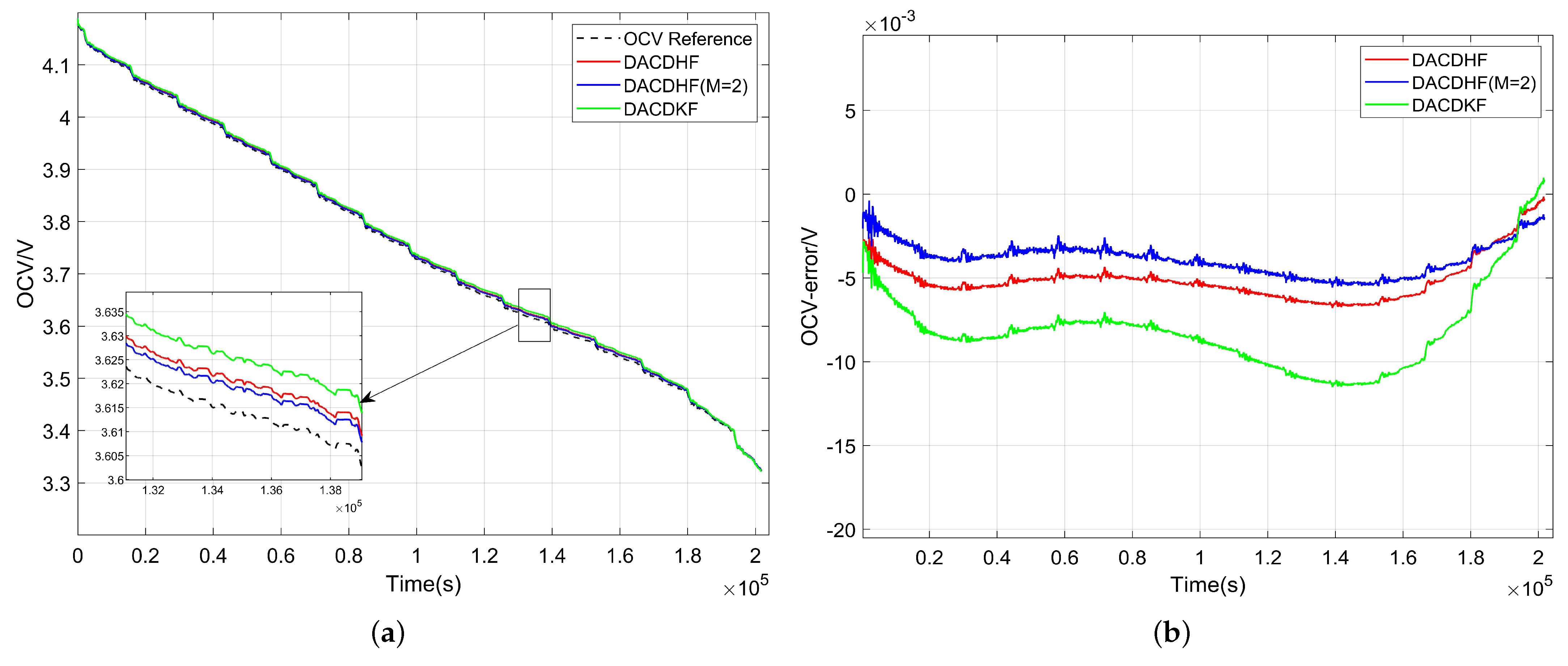
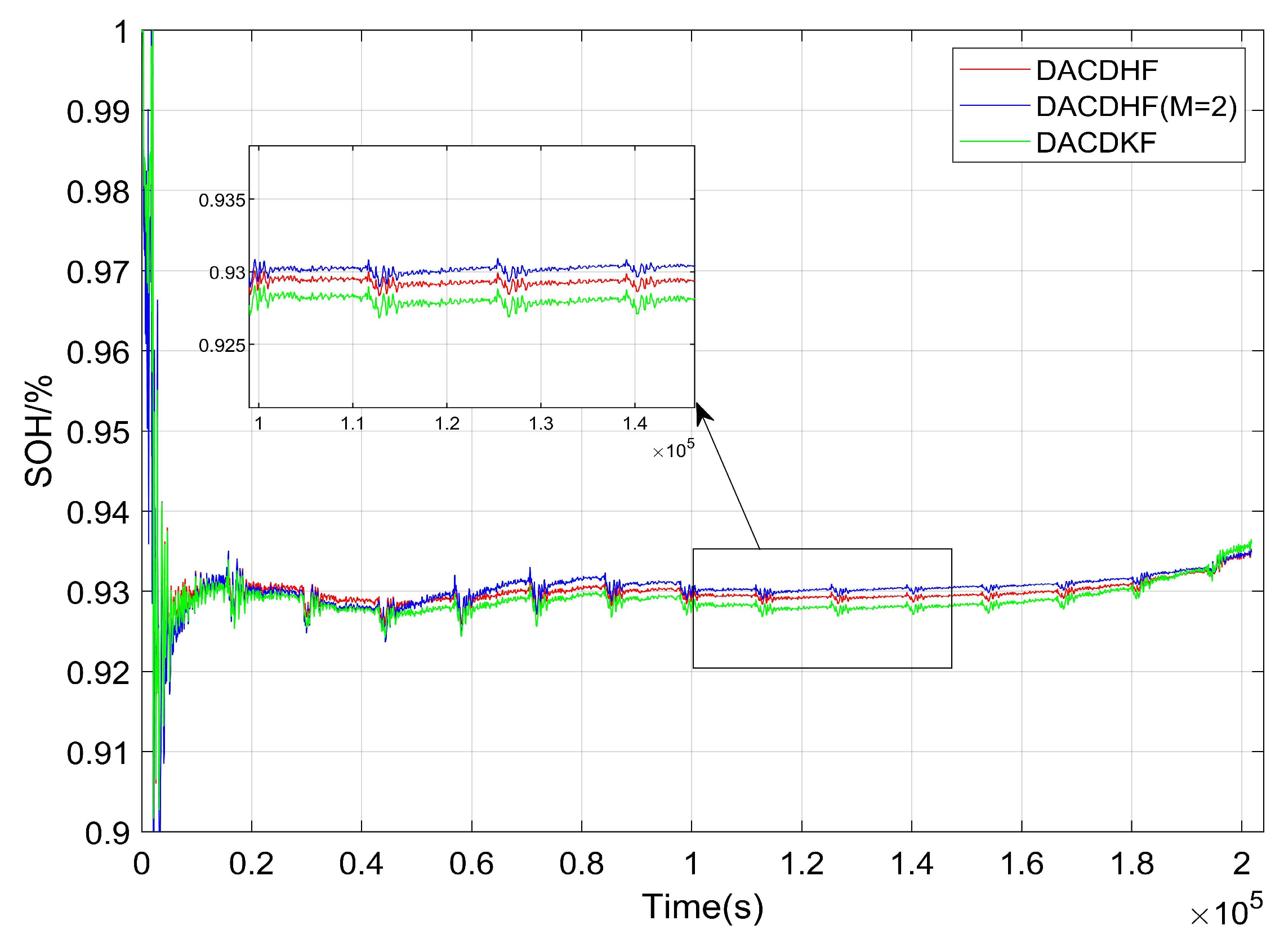

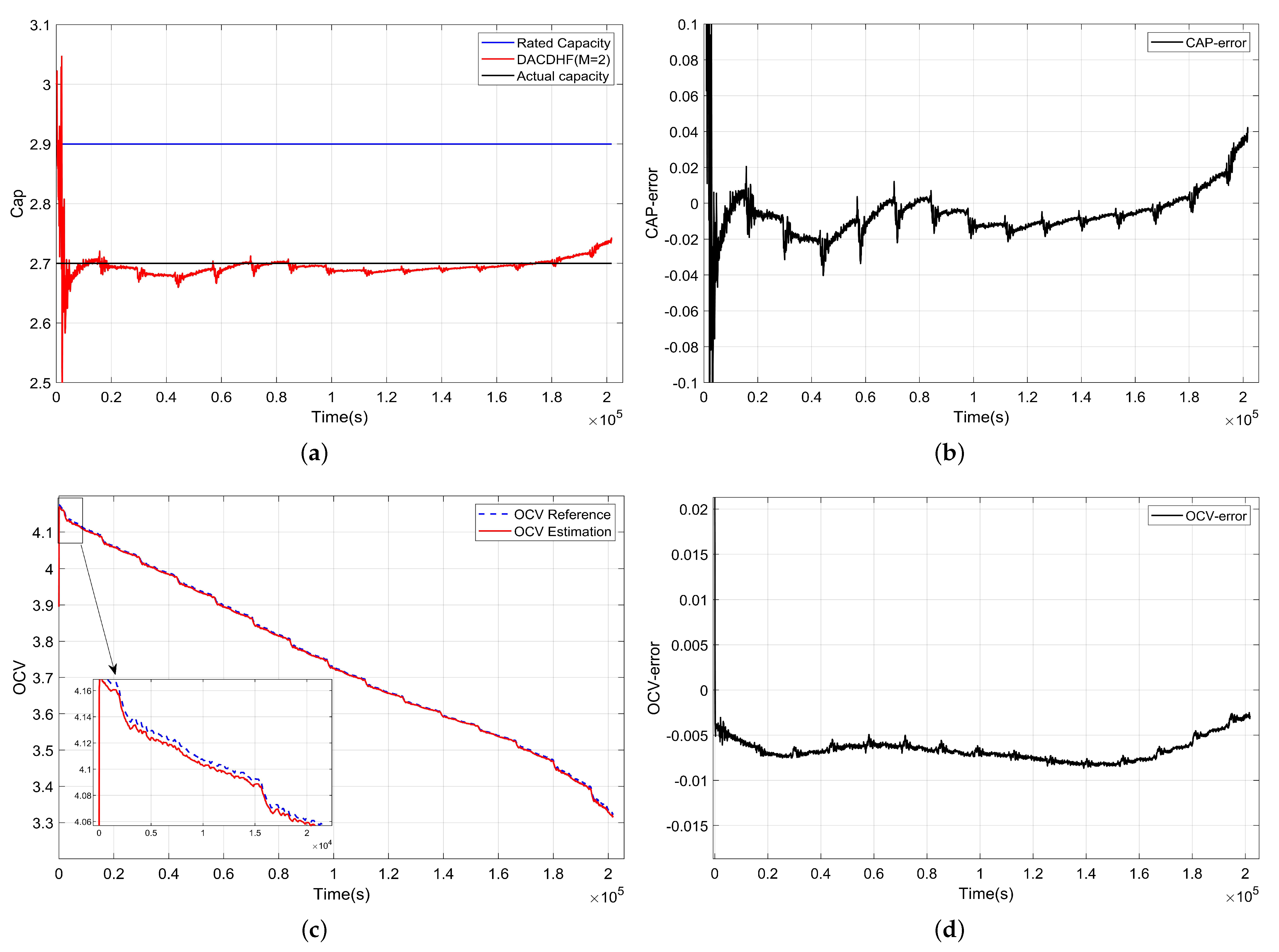
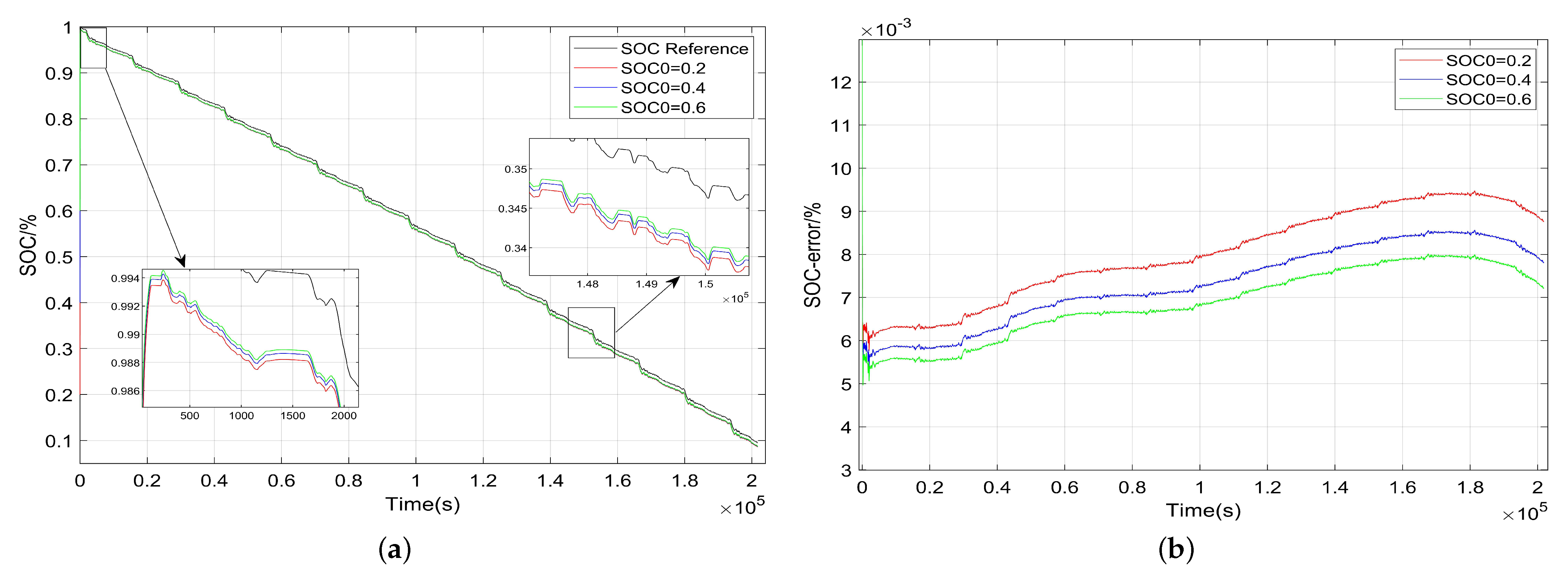

| SOC/% | 100 | 90 | 80 | 70 | 60 |
| OCV/V | 4.175 | 4.059 | 3.947 | 3.862 | 3.768 |
| 50 | 40 | 30 | 20 | 10 | 5 |
| 3.663 | 3.602 | 3.55 | 3.458 | 3.345 | 3.237 |
| MRE (%) | MAE (V) | RMSE (V) | t/s | |
|---|---|---|---|---|
| FFRLS (M = 0) | 0.26023 | 0.0093640 | 0.013023 | 1.74 |
| M = 2 | 0.24618 | 0.0088864 | 0.011873 | 1.79 |
| M = 4 | 0.23972 | 0.0086771 | 0.011361 | 1.96 |
| M = 8 | 0.23855 | 0.0086541 | 0.011293 | 2.23 |
| Estimation Algorithm | Initial Capacity Value | Convergence Time |
|---|---|---|
| DACDHF (M = 2) | 2.9 Ah | <8 min |
| DEKF [23] | 2.9 Ah | <140 min |
| Multiscale DEKF [23] | 2.9 Ah | <140 min |
| Estimation Algorithm | Capacity Estimation | OCV Estimation | SOC Estimation | |||
|---|---|---|---|---|---|---|
| MAE/% | RMSE/% | MAE/% | RMSE/% | MAE/% | RMSE/% | |
| DACDKF | 0.9 | 1.778 | 0.813 | 0.848 | 1.11 | 1.24 |
| DACDHF | 0.823 | 1.737 | 0.507 | 0.523 | 0.577 | 0.592 |
| DACDHF (M = 2) | 0.542 | 1.621 | 0.384 | 0.397 | 0.501 | 0.516 |
| Initial Capacity | Initial OCV | Capacity Estimation Error | OCV Estimation Error |
|---|---|---|---|
| 3.1 Ah | 3.9 V | 0.089 Ah | 15 mv |
| 3.1 Ah | 3.7 V | 0.108 Ah | 24 mv |
| 3.2 Ah | 3.7 V | 0.14 Ah | 29 mv |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, B.; Wu, Z.; Yang, B.; Wei, J.; Wan, Y. Joint Estimation of SOC and SOH for Lithium-Ion Batteries Based on Dual Adaptive Central Difference H-Infinity Filter. Energies 2024, 17, 1640. https://doi.org/10.3390/en17071640
Sang B, Wu Z, Yang B, Wei J, Wan Y. Joint Estimation of SOC and SOH for Lithium-Ion Batteries Based on Dual Adaptive Central Difference H-Infinity Filter. Energies. 2024; 17(7):1640. https://doi.org/10.3390/en17071640
Chicago/Turabian StyleSang, Bingyu, Zaijun Wu, Bo Yang, Junjie Wei, and Youhong Wan. 2024. "Joint Estimation of SOC and SOH for Lithium-Ion Batteries Based on Dual Adaptive Central Difference H-Infinity Filter" Energies 17, no. 7: 1640. https://doi.org/10.3390/en17071640
APA StyleSang, B., Wu, Z., Yang, B., Wei, J., & Wan, Y. (2024). Joint Estimation of SOC and SOH for Lithium-Ion Batteries Based on Dual Adaptive Central Difference H-Infinity Filter. Energies, 17(7), 1640. https://doi.org/10.3390/en17071640





