Thermodynamic Reactivity Study during Deflagration of Light Alcohol Fuel-Air Mixtures with Water
Abstract
1. Introduction
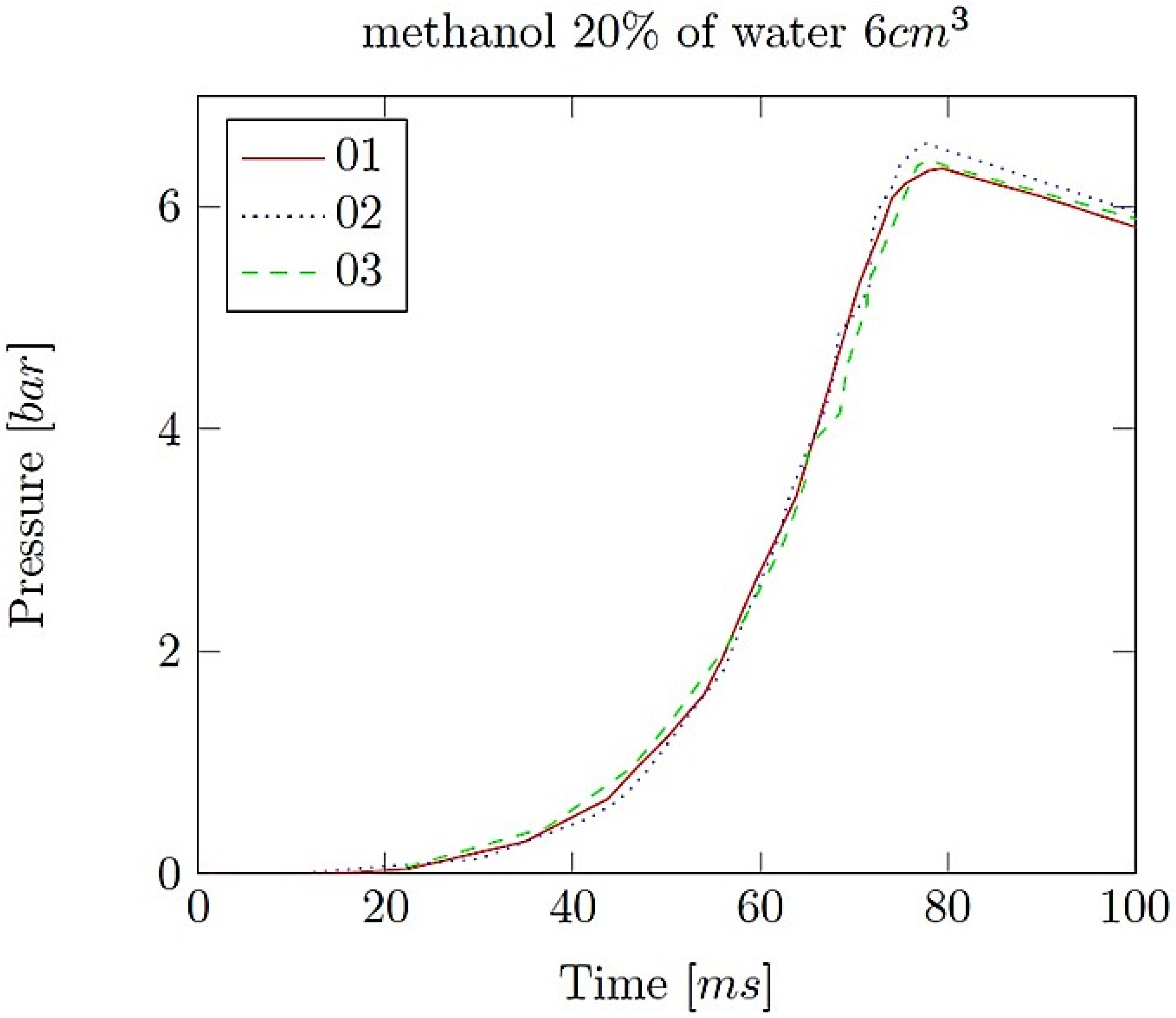
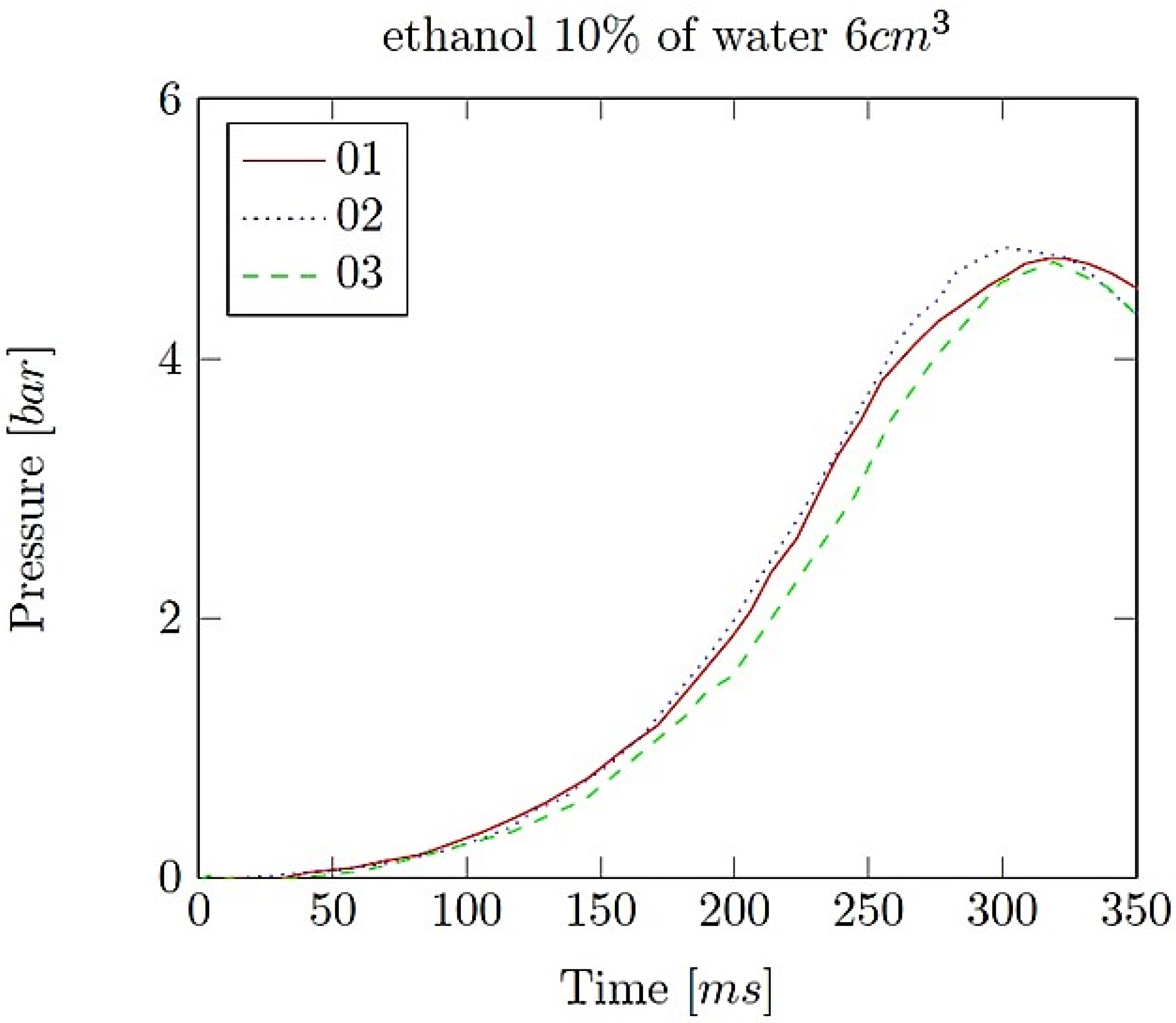
2. Experimental Study
- ➢
- Explosion pressure (Pex): This is typically the peak pressure reached during the explosion, measured relative to the initial atmospheric pressure. It is an excess pressure that is additional to the atmospheric baseline.
- ➢
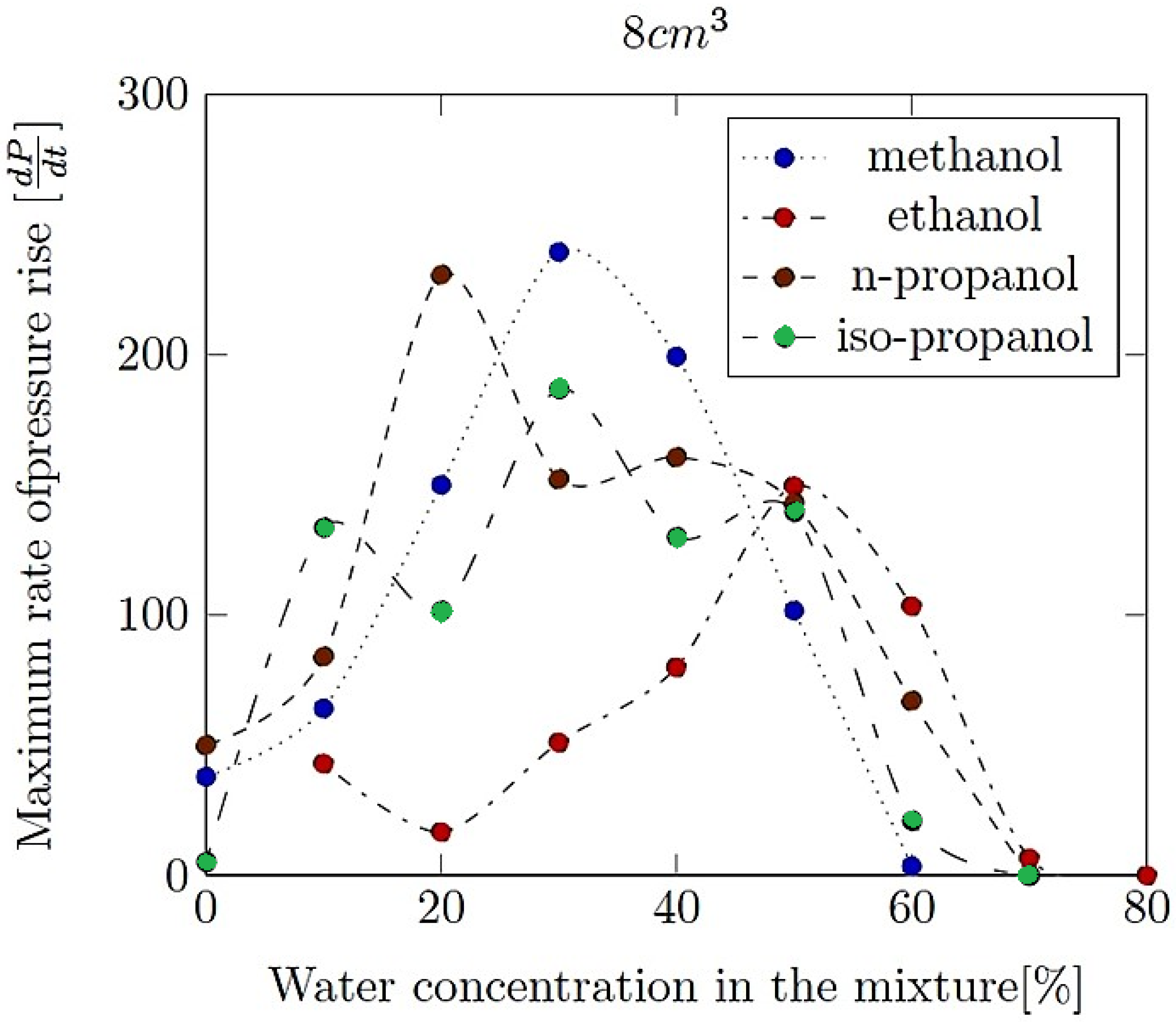
- Maximum rate of pressure rise (dP/dt)max: This is the highest rate at which pressure increases inside the vessel or engine during the combustion event. It is often associated with the intensity of the explosion and is a critical parameter for safety and engine design.
- ➢
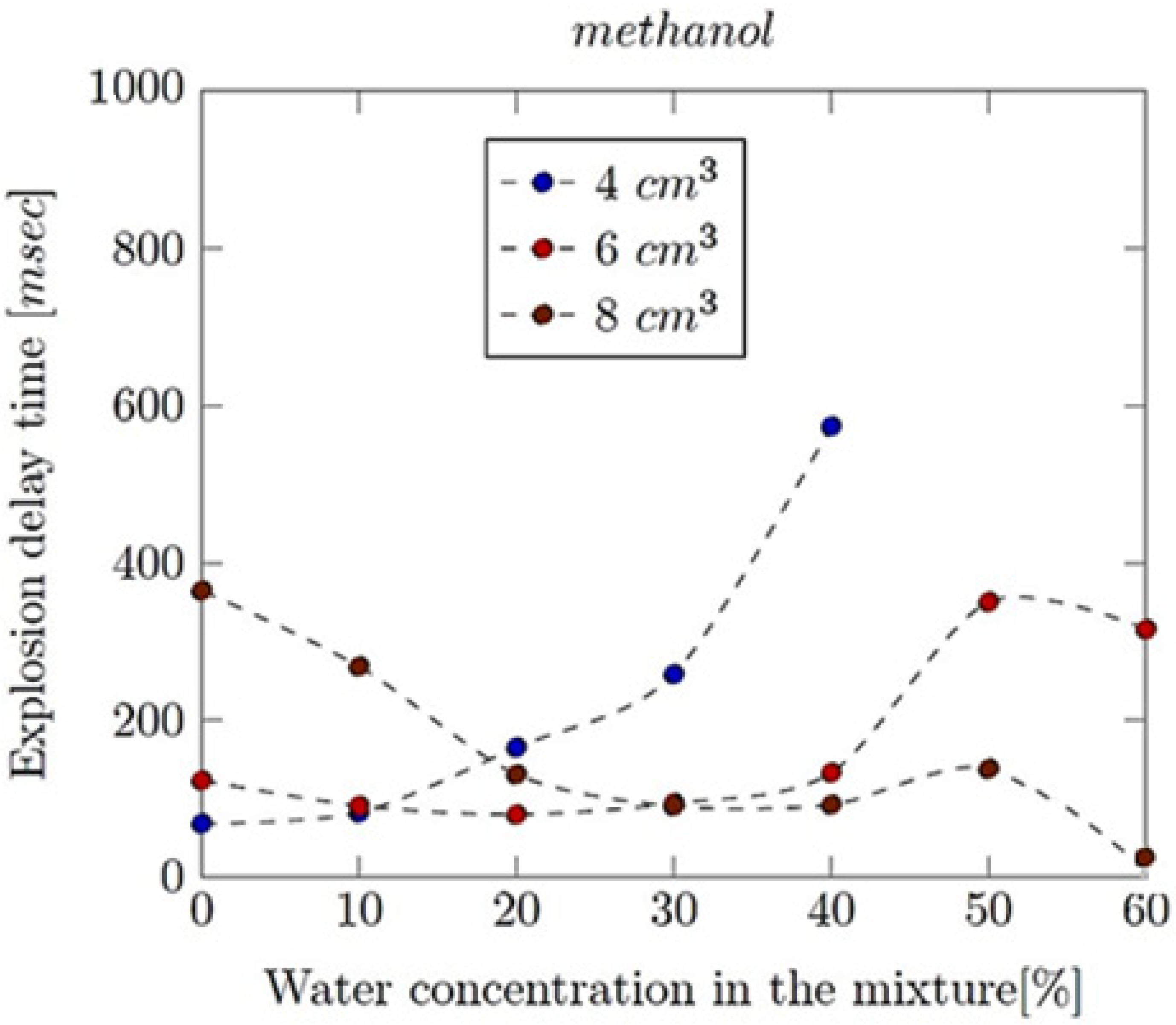
- Explosion delay time (tdel): This is the time interval between the initiation of the combustion process (such as the introduction of a spark or reaching the auto-ignition temperature) and the occurrence of the maximum explosion pressure. It reflects the reactivity of the fuel–air mixture and is influenced by the composition of the mixture, the temperature, the pressure and the presence of any diluents like water vapour.
- methanol, ethanol, n-propanol and iso-propanol at ϕ = 0.3–0.7;
- mixtures of alcohols and water, such that the volumetric content of the latter ranged from 10 to 60 vol%.
3. Liquid Phase Composition of the Alcohol–Water Mixtures
- ➢
- Equations (1)–(3) become invalid for calculating mixture properties such as the liquid sample density and specific volume. Instead, Equation (5) should be applied, provided that VE is known on an a priori basis from experiments or theoretical predictions.
- ➢
- The partial molar volumes of the species in the mixture are no longer equal to the molar volumes of the pure species: ≠ VAlc and ≠ . Furthermore, for real mixtures, and become nonlinear functions of and . Equation (12), further on, establishes a thermodynamic relationship between the partial molar volume of a species, , and the total volume V of a mixture as a function of varying composition. Hence, although Equation (4) remains valid for both ideal and real mixtures, its application to the latter requires precise a priori knowledge of the nonlinear dependence of ), i.e., ), in Equation (12), on the mixture composition [18].
- ➢
- The application of models that predict ρS directly.
- ➢
- The deployment of Equation (5) in conjunction with models that predict VE.
4. Density of the Liquid Samples and the Excess Volume of Liquid Mixtures
5. Vapour Pressures of the Pure Liquids
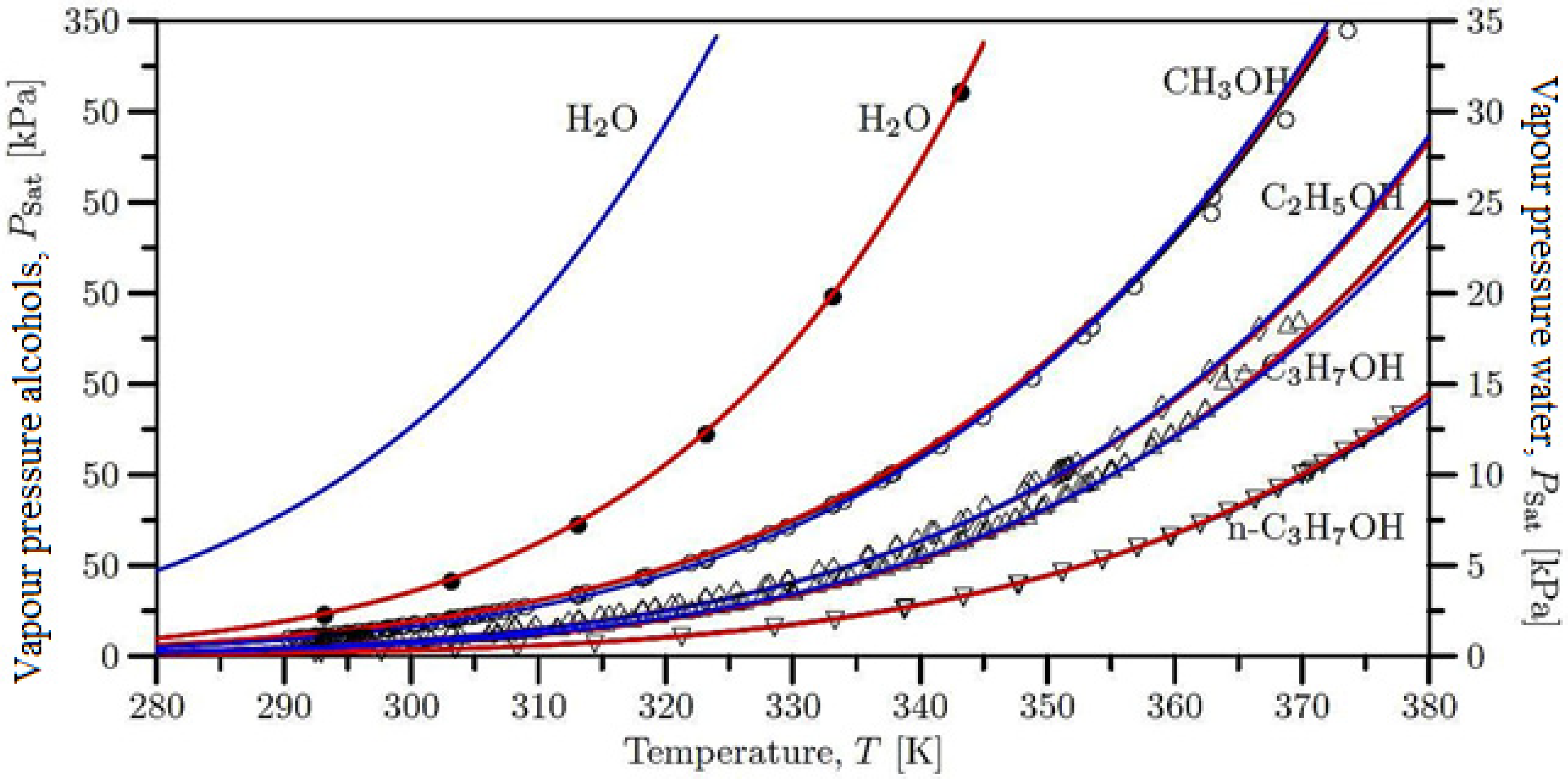
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Thermodynamic Quantities and Properties
| Methanol–Water | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (cm3) | q (vol%) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (cm3 mol−1) | ρs (kg m−3) | Ignition |
| 4.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 4.0 | 10 | 0.888 | 0.112 | - | - | 0.817 | 0.183 | - | - | - | - | 3 × y |
| 4.0 | 20 | 0.798 | 0.202 | - | - | 0.691 | 0.309 | - | - | - | - | 3 × y |
| 4.0 | 30 | 0.725 | 0.275 | - | - | 0.599 | 0.401 | - | - | - | - | 3 × y |
| 4.0 | 40 | 0.664 | 0.336 | - | - | 0.528 | 0.472 | - | - | - | - | 3 × y |
| 4.0 | 50 | 0.612 | 0.388 | - | - | 0.472 | 0.528 | - | - | - | - | 2 × n |
| 4.0 | 60 | 0.568 | 0.432 | - | - | 0.427 | 0.573 | - | - | - | - | 3 × n |
| 6.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 6.0 | 10 | 0.888 | 0.112 | - | - | 0.817 | 0.183 | - | - | - | - | 3 × y |
| 6.0 | 20 | 0.798 | 0.202 | - | - | 0.691 | 0.309 | - | - | - | - | 3 × y |
| 6.0 | 30 | 0.725 | 0.275 | - | - | 0.599 | 0.401 | - | - | - | - | 3 × y |
| 6.0 | 40 | 0.664 | 0.336 | - | - | 0.528 | 0.472 | - | - | - | - | 3 × y |
| 6.0 | 50 | 0.612 | 0.388 | - | - | 0.472 | 0.528 | - | - | - | - | 3 × y |
| 6.0 | 60 | 0.568 | 0.432 | - | - | 0.427 | 0.573 | - | - | - | - | 3 × y |
| 8.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 8.0 | 10 | 0.888 | 0.112 | - | - | 0.817 | 0.183 | - | - | - | - | 3 × y |
| 8.0 | 20 | 0.798 | 0.202 | - | - | 0.691 | 0.309 | - | - | - | - | 3 × y |
| 8.0 | 30 | 0.725 | 0.275 | - | - | 0.599 | 0.401 | - | - | - | - | 3 × y |
| 8.0 | 40 | 0.664 | 0.336 | - | - | 0.528 | 0.472 | - | - | - | - | 3 × y |
| 8.0 | 50 | 0.612 | 0.388 | - | - | 0.472 | 0.528 | - | - | - | - | 3 × y |
| 8.0 | 60 | 0.568 | 0.432 | - | - | 0.427 | 0.573 | - | - | - | - | 3 × y |
| Ethanol–Water | ||||||||||||
| (cm3) | q (vol%) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (cm3 mol−1) | ρs (kg m−3) | Ignition |
| 4.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 4.0 | 10 | 0.888 | 0.112 | - | - | 0.757 | 0.243 | - | - | - | - | 3 × y |
| 4.0 | 20 | 0.798 | 0.202 | - | - | 0.609 | 0.391 | - | - | - | - | 3 × y |
| 4.0 | 30 | 0.725 | 0.275 | - | - | 0.509 | 0.491 | - | - | - | - | 3 × y |
| 4.0 | 40 | 0.664 | 0.336 | - | - | 0.438 | 0.562 | - | - | - | - | 3 × y |
| 4.0 | 50 | 0.612 | 0.388 | - | - | 0.384 | 0.616 | - | - | - | - | 2 × y |
| 4.0 | 60 | 0.568 | 0.432 | - | - | 0.341 | 0.659 | - | - | - | - | 3 × n |
| 6.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 6.0 | 10 | 0.888 | 0.112 | - | - | 0.757 | 0.243 | - | - | - | - | 3 × y |
| 6.0 | 20 | 0.798 | 0.202 | - | - | 0.609 | 0.391 | - | - | - | - | 3 × y |
| 6.0 | 30 | 0.725 | 0.275 | - | - | 0.509 | 0.491 | - | - | - | - | 3 × y |
| 6.0 | 40 | 0.664 | 0.336 | - | - | 0.438 | 0.562 | - | - | - | - | 3 × y |
| 6.0 | 50 | 0.612 | 0.388 | - | - | 0.384 | 0.616 | - | - | - | - | 3 × y |
| 6.0 | 60 | 0.568 | 0.432 | - | - | 0.341 | 0.659 | - | - | - | - | 3 × y |
| 8.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 8.0 | 10 | 0.888 | 0.112 | - | - | 0.757 | 0.243 | - | - | - | - | 3 × y |
| 8.0 | 20 | 0.798 | 0.202 | - | - | 0.609 | 0.391 | - | - | - | - | 3 × y |
| 8.0 | 30 | 0.725 | 0.275 | - | - | 0.509 | 0.491 | - | - | - | - | 3 × y |
| 8.0 | 40 | 0.664 | 0.336 | - | - | 0.438 | 0.562 | - | - | - | - | 3 × y |
| 8.0 | 50 | 0.612 | 0.388 | - | - | 0.384 | 0.616 | - | - | - | - | 3 × y |
| 8.0 | 60 | 0.568 | 0.432 | - | - | 0.341 | 0.659 | - | - | - | - | 3 × y |
| n-Propanol–Water | ||||||||||||
| (cm3) | q (vol%) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (cm3 mol−1) | ρs (kg m−3) | Ignition |
| 4.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 4.0 | 10 | 0.888 | 0.112 | - | - | 0.708 | 0.292 | - | - | - | - | 3 × y |
| 4.0 | 20 | 0.798 | 0.202 | - | - | 0.548 | 0.452 | - | - | - | - | 3 × y |
| 4.0 | 30 | 0.725 | 0.275 | - | - | 0.447 | 0.553 | - | - | - | - | 3 × y |
| 4.0 | 40 | 0.664 | 0.336 | - | - | 0.378 | 0.622 | - | - | - | - | 3 × y |
| 4.0 | 50 | 0.612 | 0.388 | - | - | 0.327 | 0.673 | - | - | - | - | 2 × n |
| 4.0 | 60 | 0.568 | 0.432 | - | - | 0.288 | 0.712 | - | - | - | - | 3 × n |
| 6.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 6.0 | 10 | 0.888 | 0.112 | - | - | 0.708 | 0.292 | - | - | - | - | 3 × y |
| 6.0 | 20 | 0.798 | 0.202 | - | - | 0.548 | 0.452 | - | - | - | - | 3 × y |
| 6.0 | 30 | 0.725 | 0.275 | - | - | 0.447 | 0.553 | - | - | - | - | 3 × y |
| 6.0 | 40 | 0.664 | 0.336 | - | - | 0.378 | 0.622 | - | - | - | - | 3 × y |
| 6.0 | 50 | 0.612 | 0.388 | - | - | 0.327 | 0.673 | - | - | - | - | 3 × y |
| 6.0 | 60 | 0.568 | 0.432 | - | - | 0.288 | 0.712 | - | - | - | - | 3 × y |
| 8.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 8.0 | 10 | 0.888 | 0.112 | - | - | 0.708 | 0.292 | - | - | - | - | 3 × y |
| 8.0 | 20 | 0.798 | 0.202 | - | - | 0.548 | 0.452 | - | - | - | - | 3 × y |
| 8.0 | 30 | 0.725 | 0.275 | - | - | 0.447 | 0.553 | - | - | - | - | 3 × y |
| 8.0 | 40 | 0.664 | 0.336 | - | - | 0.378 | 0.622 | - | - | - | - | 3 × y |
| 8.0 | 50 | 0.612 | 0.388 | - | - | 0.327 | 0.673 | - | - | - | - | 3 × y |
| 8.0 | 60 | 0.568 | 0.432 | - | - | 0.288 | 0.712 | - | - | - | - | 3 × y |
| i-Propanol–Water | ||||||||||||
| (cm3) | q (vol%) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (cm3 mol−1) | ρs (kg m−3) | Ignition |
| 4.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 4.0 | 10 | 0.888 | 0.112 | - | - | 0.703 | 0.297 | - | - | - | - | 3 × y |
| 4.0 | 20 | 0.798 | 0.202 | - | - | 0.542 | 0.458 | - | - | - | - | 3 × y |
| 4.0 | 30 | 0.725 | 0.275 | - | - | 0.441 | 0.559 | - | - | - | - | 3 × y |
| 4.0 | 40 | 0.664 | 0.336 | - | - | 0.372 | 0.628 | - | - | - | - | 3 × y |
| 4.0 | 50 | 0.612 | 0.388 | - | - | 0.322 | 0.678 | - | - | - | - | 2 × n |
| 4.0 | 60 | 0.568 | 0.432 | - | - | 0.283 | 0.717 | - | - | - | - | 3 × n |
| 6.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 6.0 | 10 | 0.888 | 0.112 | - | - | 0.703 | 0.297 | - | - | - | - | 3 × y |
| 6.0 | 20 | 0.798 | 0.202 | - | - | 0.542 | 0.458 | - | - | - | - | 3 × y |
| 6.0 | 30 | 0.725 | 0.275 | - | - | 0.441 | 0.559 | - | - | - | - | 3 × y |
| 6.0 | 40 | 0.664 | 0.336 | - | - | 0.372 | 0.628 | - | - | - | - | 3 × y |
| 6.0 | 50 | 0.612 | 0.388 | - | - | 0.322 | 0.678 | - | - | - | - | 3 × y |
| 6.0 | 60 | 0.568 | 0.432 | - | - | 0.283 | 0.717 | - | - | - | - | 3 × y |
| 8.0 | 0 | 1.000 | 0.000 | - | - | 1.000 | 0.000 | - | - | - | - | 3 × y |
| 8.0 | 10 | 0.888 | 0.112 | - | - | 0.703 | 0.297 | - | - | - | - | 3 × y |
| 8.0 | 20 | 0.798 | 0.202 | - | - | 0.542 | 0.458 | - | - | - | - | 3 × y |
| 8.0 | 30 | 0.725 | 0.275 | - | - | 0.441 | 0.559 | - | - | - | - | 3 × y |
| 8.0 | 40 | 0.664 | 0.336 | - | - | 0.372 | 0.628 | - | - | - | - | 3 × y |
| 8.0 | 50 | 0.612 | 0.388 | - | - | 0.322 | 0.678 | - | - | - | - | 3 × y |
| 8.0 | 60 | 0.568 | 0.432 | - | - | 0.283 | 0.717 | - | - | - | - | 3 × y |
References
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook, 7th ed.; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- The Dortmund Data Bank. Thermophysical Properties of Pure Components and Their Mixtures. 2018. Available online: http://www.ddbst.com/ (accessed on 6 September 2023).
- Arce, A.; Blanco, A.; Soto, A.; Vidal, I. Densities, refractive indices, and excess molar volumes of the ternary systems water + methanol + 1-octanol and water + ethanol + 1-octanol and their binary mixtures at 298.15 K. J. Chem. Eng. Data 1993, 38, 336–340. [Google Scholar] [CrossRef]
- Vilcu, R.; Simion, A. Grandeurs d’exces par des Mesures Acoustiques, dans les Systemes Binaires de Liquides. Rev. Roum. Chim. 1976, 21, 177–186. [Google Scholar]
- Sarathy, S.M.; Oßwald, P.; Hansen, N.; Kohse-Hoinghaus, K. Alcohol combustion chemistry. Prog. Energy Combust. Sci. 2014, 44, 40–102. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, Y.; Huang, Z. Comparative assessment of the explosion characteristics of alcohol-air mixtures. J. Loss Prev. Process Ind. 2015, 37, 91–100. [Google Scholar] [CrossRef]
- Bryan, W.W.; Kumar, K.; Zhang, Y.; Sung, C.-J. Autoignition of n-butanol at elevated pressure and low to intermediate temperature. Combust. Flame 2011, 158, 809–819. [Google Scholar]
- Zhu, Y.; Davidson, D.F.; Hanson, R.K. 1-butanol ignition delay times at low temperatures: An application of the constrained-reaction-volume strategy. Combust. Flames 2013, 161, 634–643. [Google Scholar] [CrossRef]
- Douheret, G.; Khadir, A.; Pal, A. Thermodynamic characterization of the water + methanol system, at 298.15 K. Thermochim. Acta 1989, 142, 219–243. [Google Scholar] [CrossRef]
- Grolier, J.-P.E.; Wilhelm, E. Excess volumes and excess heat capacities of water + ethanol at 298.15 K. Fluid Phase Equilibria 1981, 6, 283–287. [Google Scholar] [CrossRef]
- Ott, J.B.; Sipowska, J.T.; Gruszkiewicz, M.S.; Woolley, A.T. Excess volumes for (ethanol + water) at the temperatures (298.15 and 348.15) K and pressures (0.4, 5, and 15) MPa and at the temperature 323.15 K and pressures (5 and 15) MPa. J. Chem. Thermodyn. 1993, 25, 307–318. [Google Scholar] [CrossRef]
- Davis, M.I.; Ham, E.S. Part 2. Comparisons of the propanol isomers in their aqueous mixtures. Thermochim. Acta 1991, 190, 251–258. [Google Scholar] [CrossRef]
- Langdon, W.M.; Keyes, D.B. Isopropyl alcohol-water system. Ind. Eng. Chem. 1943, 35, 459–464. [Google Scholar] [CrossRef]
- Yamamoto, H.; Ichikawa, K.; Tokunaga, J. Solubility of helium in methanol + water, ethanol + water, 1-propanol + water, and 2-propanol + water solutions at 25 °C. J. Chem. Eng. Data 1994, 39, 155–157. [Google Scholar] [CrossRef]
- Benson, G.C.; Kiyohara, O. Thermodynamics of aqueous mixtures of nonelectrolytes. I. Excess volumes of water—N-alcohol mixtures at several temperatures. J. Solut. Chem. 1980, 9, 791–804. [Google Scholar] [CrossRef]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics, 7th ed.; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Battino, R. Volume changes on mixing for binary mixtures of liquids. Chem. Rev. 1971, 71, 5–45. [Google Scholar] [CrossRef]
- Abbott, M.M.; Van Ness, H.C. Theory and Problems of Thermodynamics; Schaum’s Outline Series; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes, The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Dahoe, A.E.; Skjold, T.; Roekaerts, D.J.E.M.; Pasman, H.J.; Eckho, R.K.; Hanjalic, K.; Donze, M. On the application of the Levenberg-Marquardt method in conjunction with an explicit Runge-Kutta and an implicit Rosenbrock method to assess burning velocities from confined deflagrations. Flow Turbul. Combust. 2013, 91, 281–317. [Google Scholar] [CrossRef]
- Rackett, H.G. Equation of state for saturated liquids. J. Chem. Eng. Data 1970, 15, 514–517. [Google Scholar] [CrossRef]
- Lydersen, A.L.; Greenkorn, R.A.; Hougen, O.A. Generalized thermodynamic properties of pure fluids. In Engineering Experiment Station Report 4; College of Engineering, University of Wisconsin: Madison, WI, USA, 1955. [Google Scholar]
- Gunn, R.D.; Yamada, T. A corresponding states correlation of saturated liquid volumes. AIChE J. 1971, 17, 1341–1345. [Google Scholar] [CrossRef]
- Yen, L.C.; Woods, S.S. A generalized equation for computer calculation of liquid densities. AIChE J. 1966, 12, 95–99. [Google Scholar] [CrossRef]
- Yamada, T.; Gunn, R. Saturated liquid molar volumes. Rackett Equ. J. Chem. Eng. Data 1973, 18, 234–236. [Google Scholar] [CrossRef]
- The National Institute of Standards and Technology (NIST). The NIST ChemistryWebBook. Data Compiled under the Standard Reference Data Program. 2018. Available online: https://webbook.nist.gov/ (accessed on 6 September 2023).
- Kotsarenko, A.A.; Yarym-Agaev, N.L. Sättigungsdampfdruck von Methanol im Temperaturbereich von 251.9 bis 298.15 k. Izv. Vyss. Uchebnykh Zaved. Neft Gaz 1990, 6, 59–61. [Google Scholar]
- Gibbard, H.F.; Creek, J.L. Vapor pressure of methanol from 288.15 to 337.65 k. J. Chem. Eng. Data 1974, 19, 308–310. [Google Scholar] [CrossRef]
- Dever, D.F.; Finch, A.; Grunwald, E. The Vapor Pressure of Methanol. J. Phys. Chem. 1955, 59, 668–669. [Google Scholar] [CrossRef]
- Chun, K.W.; Davison, R.R. Thermodynamic properties of binary mixtures of triethylamine with methyl and ethyl alcohol. J. Chem. Eng. Data 1972, 17, 307–310. [Google Scholar] [CrossRef]
- Ambrose, D.; Sprake, C.H.S. Thermodynamic properties of organic oxygen compounds. XXV. Vapour pressures and normal boiling temperatures of aliphatic alcohols. J. Chem. Thermodyn. 1970, 2, 631–645. [Google Scholar] [CrossRef]
- Ambrose, D.; Sprake, C.H.S.; Townsend, R. Thermodynamic properties of organic oxygen compounds. XXXVII. Vapour pressures of methanol, ethanol, pentan-1-ol, and octan-1-ol from the normal boiling temperature to the critical temperature. J. Chem. Thermodyn. 1975, 7, 185–190. [Google Scholar] [CrossRef]
- Hirata, M.; Suda, S. Vapor pressure on methanol in high pressure regions. J. Chem. Thermodyn. 1967, 31, 339–342. [Google Scholar] [CrossRef][Green Version]
- Mishchenko, K.P.; Subbotina, V.V. Dampfdruck von Ethanol bei Temperaturen von 4 bis 46 °C. Zhurnal Pikladnoi Khimii 1967, 40, 1156–1159. [Google Scholar]
- Kahlbaum, G.W.A.; von Wirkner, C.G. Studien uber Dampfspannkraftsmessungen. Monograph, 1897; Reprint in 2012 under ISBN-9785883729552. [Google Scholar]
- Scatchard, G.; Raymond, C.L. II. Chloroform-ethanol mixtures at 35, 45 and 55 °C. J. Am. Chem. Soc. 1938, 60, 1278–1287. [Google Scholar] [CrossRef]
- Scatchard, G.; Satkiewicz, F.G. XII. The system ethanol-cyclohexane from 5 to 65 °C. J. Am. Chem. Soc. 1964, 86, 130–133. [Google Scholar] [CrossRef]
- Kretschmer, C.B.; Wiebe, R. Liquid-vapor equilibrium of ethanol-toluene solutions. J. Am. Chem. Soc. 1949, 71, 1793–1797. [Google Scholar] [CrossRef]
- Dejoz, A.; Gonzalez-Alfaro, V.; Miguel, P.J.; Vazquez, M.I. Isobaric vapor-liquid equilibria of tetrachloroethylene + 1-propanol and + 2-propanol at 20 and 100 kpa. J. Chem. Eng. Data 1996, 41, 1361–1365. [Google Scholar] [CrossRef]
- Shulgin, I.L.; Belousov, V.P.; Baglai, A.K. Eine tensimetrische Untersuchungsmethode des Dampf-flussig-Gleichgewichtes in binaren Systemen. Termodin. Org. Soedin. 1989, 32, 32–35. [Google Scholar]
- Daubert, T.E.; Jalowka, J.W.; Goren, V. Vapor pressure of 22 pure industrial chemicals. AIChE Symp. Ser. 1987, 32, 128–156. [Google Scholar]
- Ambrose, D.; Townsend, R. Thermodynamic properties of organic oxygen compounds. the critical properties and vapour pressures, above five atmospheres, of six aliphatic alcohols. Part IX. J. Chem. Soc. 1963, 54, 3614–3625. [Google Scholar] [CrossRef]
- Biddiscombe, D.P.; Collerson, R.R.; Handley, R.; Herington, E.F.G.; Martin, J.F.; Sprake, C.H.S. Thermodynamic properties of organic oxygen compounds. Part XIII. J. Chem. Soc. 1963, 54, 1954–1957. [Google Scholar] [CrossRef]
- Kemme, H.R.; Kreps, S.I. Vapor pressure of primary n-alkyl chlorides and alcohols. J. Chem. Eng. Data 1969, 14, 98–102. [Google Scholar] [CrossRef]
- Gudkov, A.N.; Fermor, N.A.; Smirnov, N.I. Communication I. Zurnal Prikl. Chim. 1964, 37, 2204–2210. [Google Scholar]
- Bridgeman, O.C.; Aldrich, E.W. Vapor pressure tables for water. J. Heat Transf. 1964, 86, 279–286. [Google Scholar] [CrossRef]
- Stull, D.R. Vapor pressure of pure substances. Organic and inorganic compounds. Ind. Eng. Chem. 1947, 39, 517–540. [Google Scholar] [CrossRef]
- Clapeyron, E. M’emoire sur la Puissance Motrice de la Chaleur. J. L’ecole R. Polytech. 1834, 14, 153–191. [Google Scholar]
- Wisniak, J. Historical development of the vapor pressure equation from Dalton to Antoine. J. Phase Equilibria 2001, 22, 622–630. [Google Scholar] [CrossRef]
- Wagner, W. New vapour pressure measurements for argon and nitrogen and a new method for establishing rational vapour pressure equations. Cyrogenics 1973, 13, 470–482. [Google Scholar] [CrossRef]
- Wagner, W. A New Correlation Method for Thermodynamic Data Applied to the Vapor-Pressure Curve of Argon, Nitrogen, and Water; Watson, J.T.R., Ed.; IUPAC Thermodynamic Tables Project Centre: London, UK, 1977. [Google Scholar]
- Ambrose, D. The corelation and estimation of vapour pressures IV. Observations on Wagner’s method of fitting equations to vapour pressures. J. Chem. Thermodyn. 1986, 18, 45–51. [Google Scholar] [CrossRef]
- Ambrose, D. Vapour pressures and critical temperatures and critical pressures of some alkanoic acids: C1 to C10. J. Chem. Thermodyn. 1987, 19, 505–519. [Google Scholar] [CrossRef]
- Lee, B.I.; Kesler, M.G. A generalized thermodynamic correlation based on three-parameter corresponding states. AIChE J. 1975, 21, 510–527. [Google Scholar] [CrossRef]
- Barr-David, F.; Dodge, B.F. The systems ethanol–water and 2-propanol–water. J. Chem. Eng. Data 1959, 4, 107–121. [Google Scholar] [CrossRef]
- Alduchov, O.A.; Eskridge, R.E. Improved Magnus form approximation of saturation vapor pressure. J. Appl. Meteorol. 1996, 35, 601–619. [Google Scholar] [CrossRef]
- Alduchov, O.A.; Eskridge, R.E. Über einige meteorologische Begriffe. Z. Fur Geophys. 1930, 6, 207–309. [Google Scholar]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Murphy, D.M.; Koop, T. Review of the vapour pressures of ice and supercooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005, 131, 1539–1565. [Google Scholar] [CrossRef]
- Dethlefsen, C.; Sørensen, P.G.; Hvidt, A. Excess volumes of propanol-water mixtures at 5, 15, and 25 °C. J. Solut. Chem. 1984, 13, 191–202. [Google Scholar] [CrossRef]
- Soetens, J.C.; Bopp, P.A. Water-methanol mixtures: Simulations of mixing properties over the entire range of mole fractions. J. Phys. Chem. B 2015, 119, 8593–8599. [Google Scholar] [CrossRef]
- McGlashan, M.L.; Williamson, A. Isothermal liquidvapor equilibria for system methanol-water. J. Chem. Eng. Data 1976, 21, 196–199. [Google Scholar] [CrossRef]
- Van Ness, H.C. Thermodynamics in the treatment of vapor/liquid equilibrium (VLE) data. Pure Appl. Chem. 1995, 67, 859–872. [Google Scholar] [CrossRef]

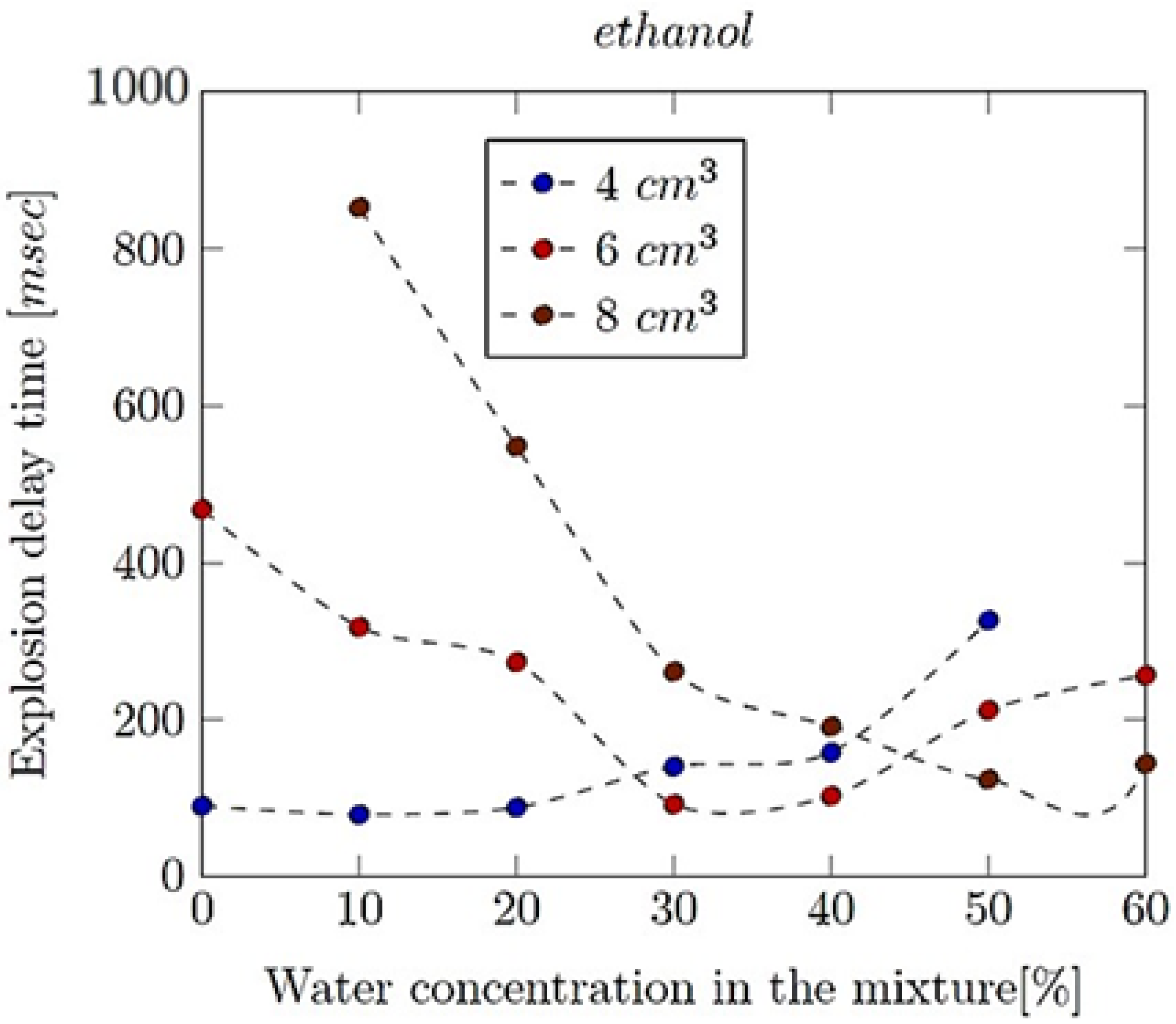
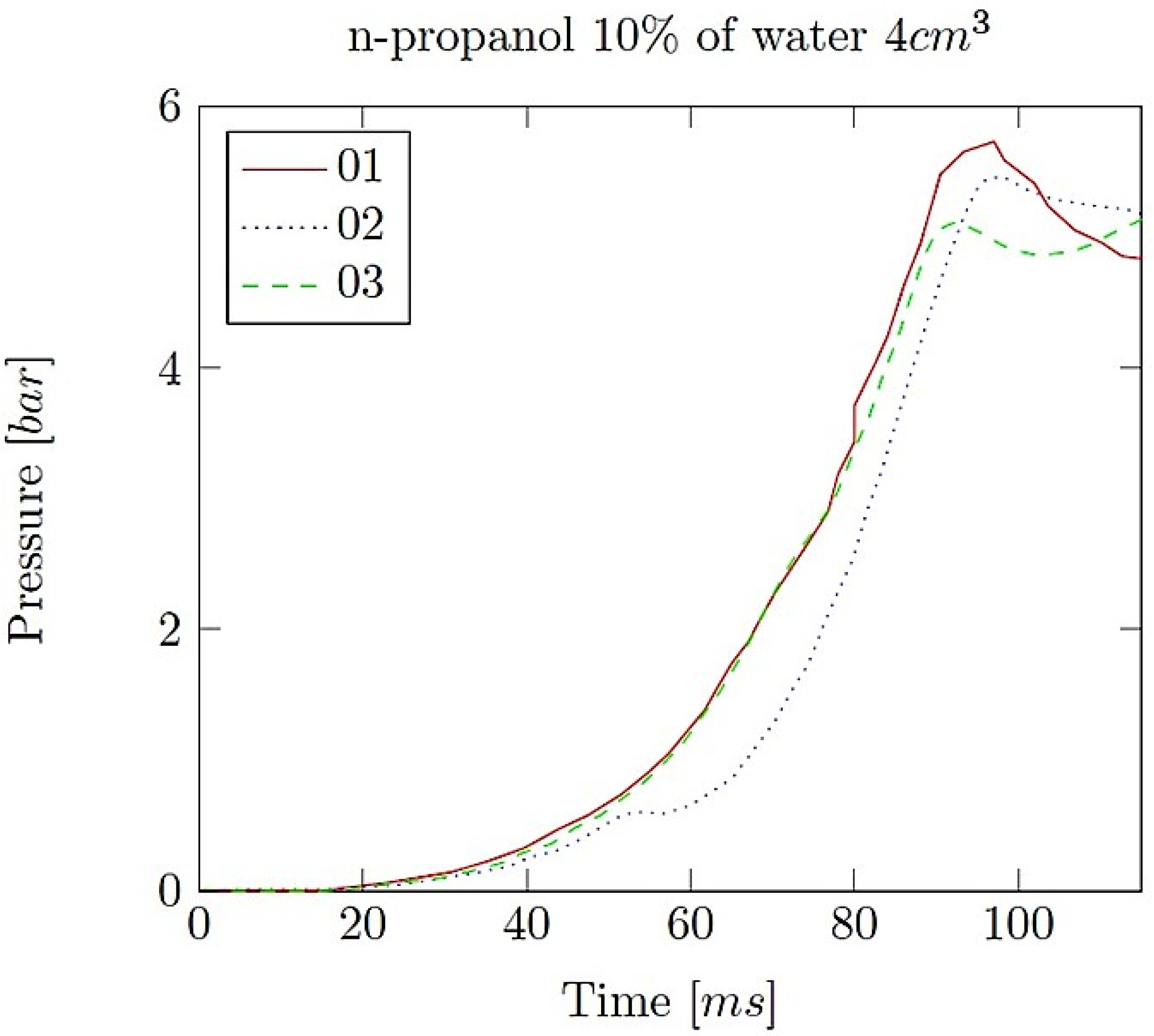
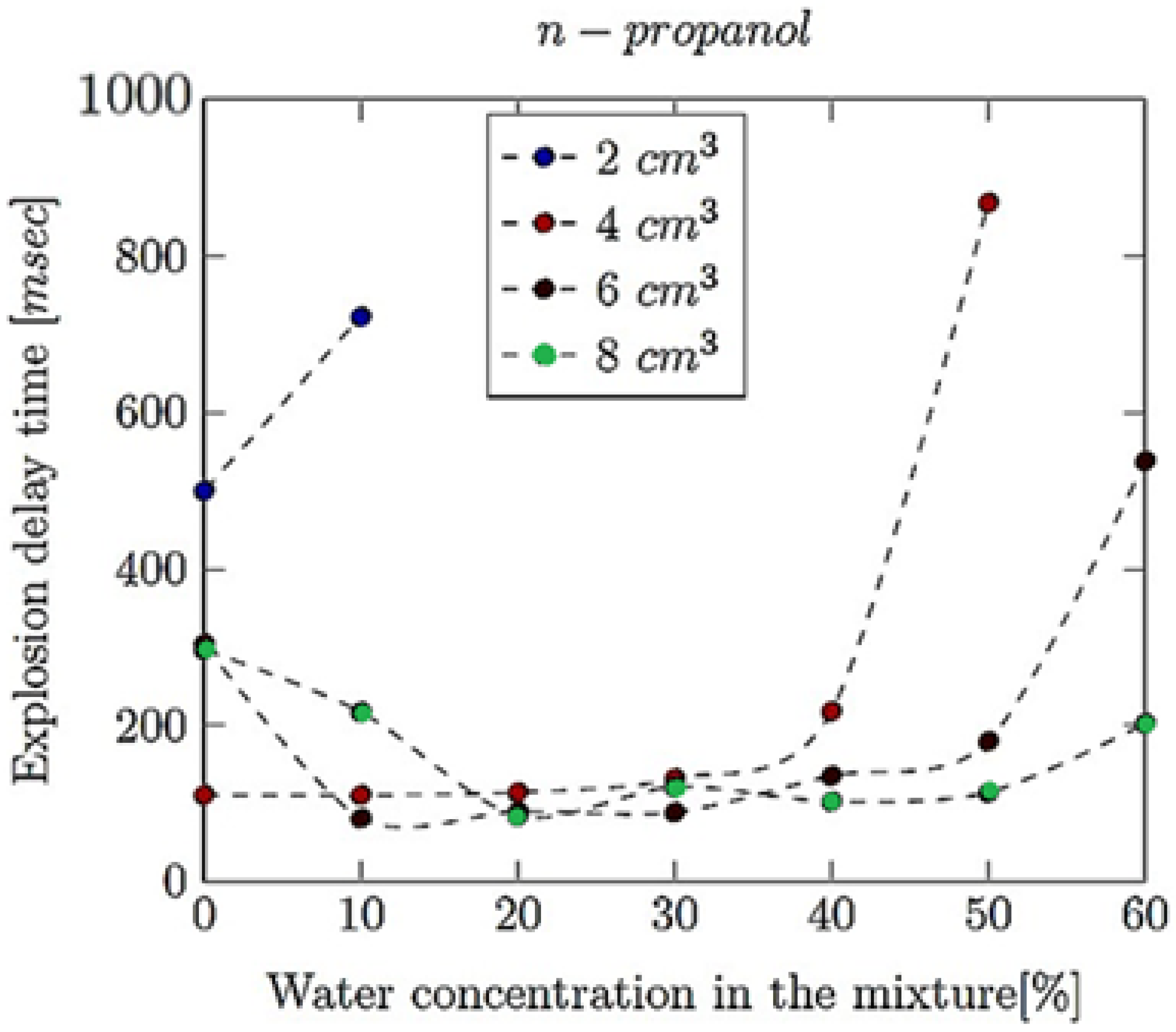
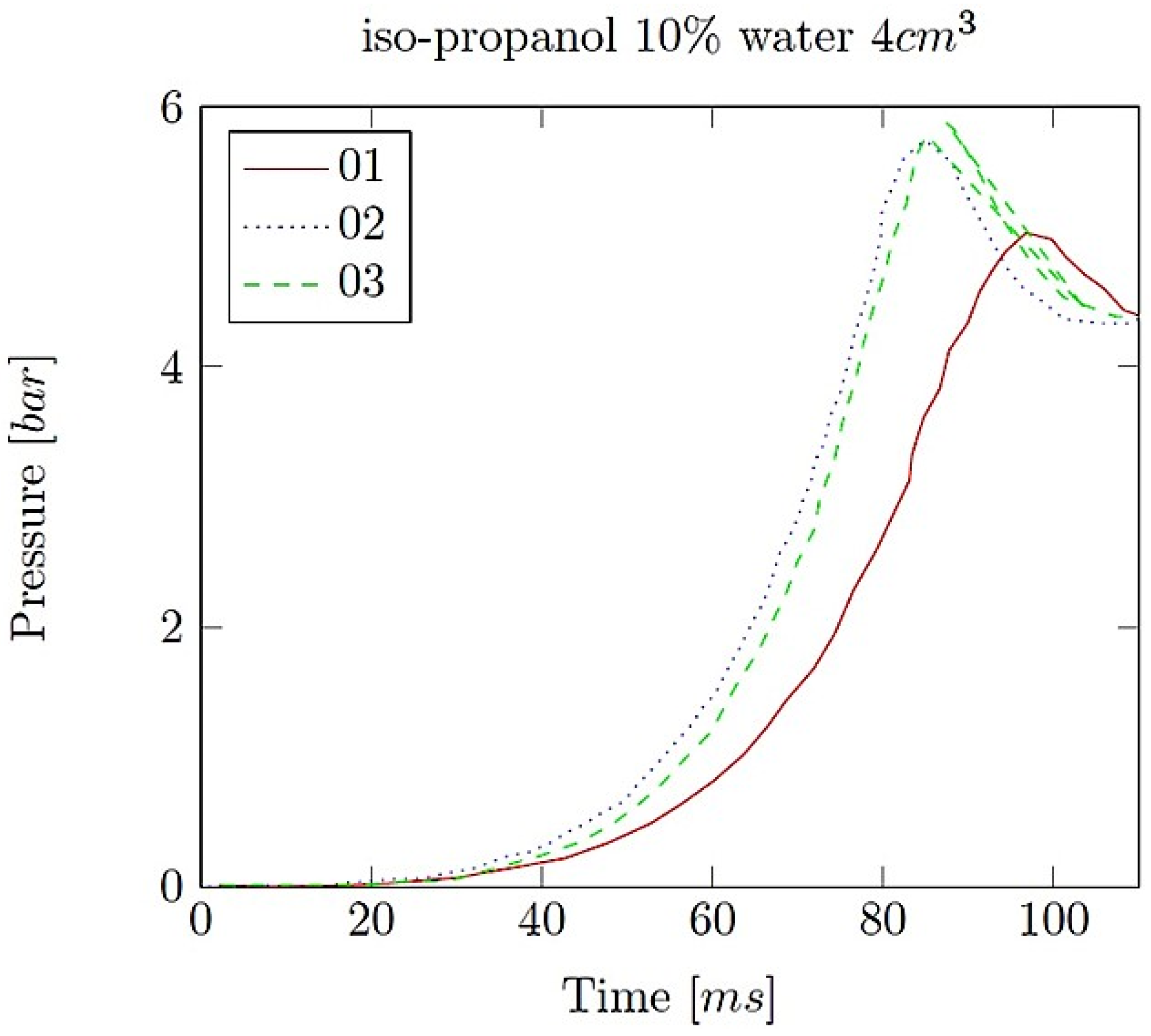
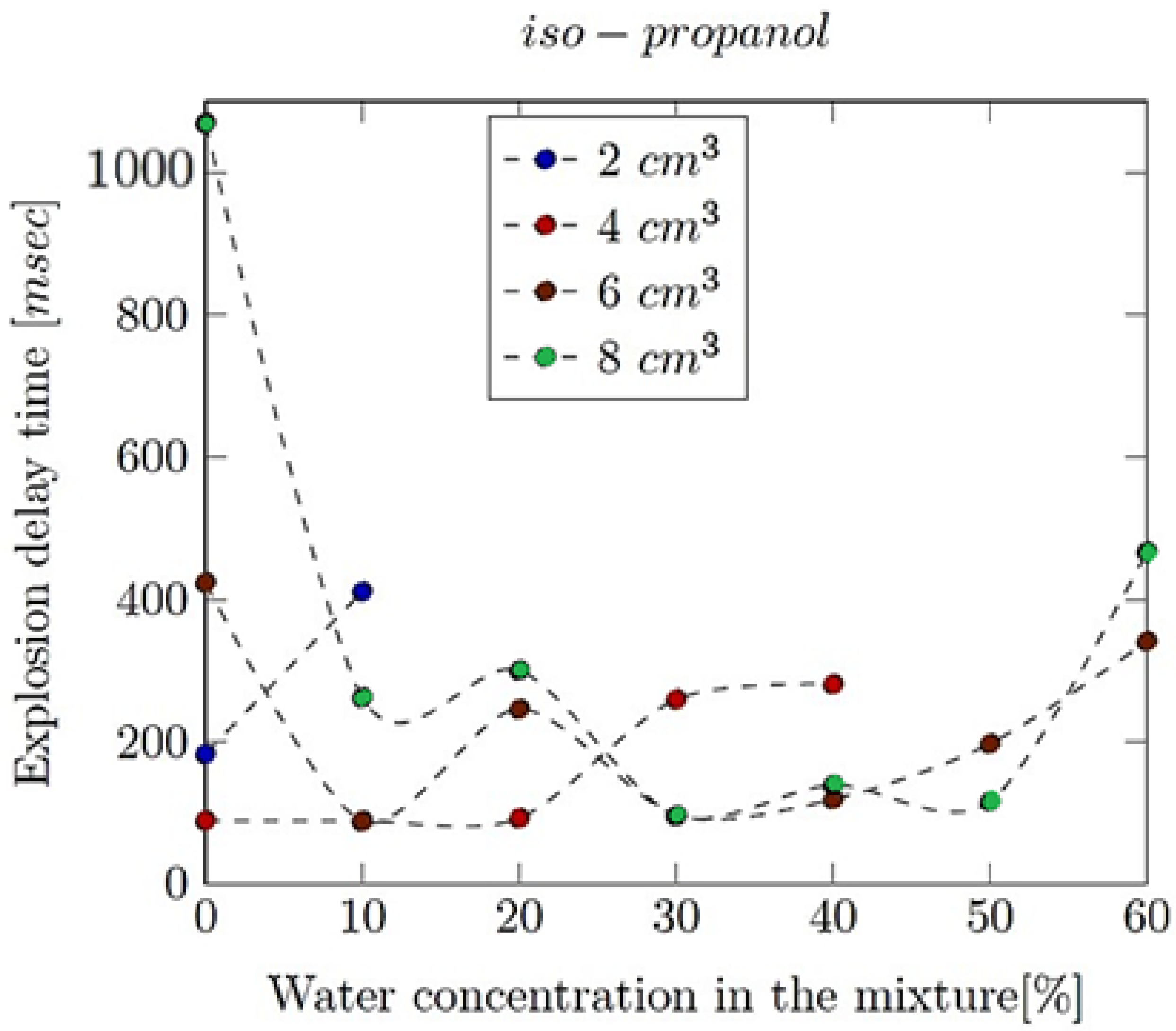
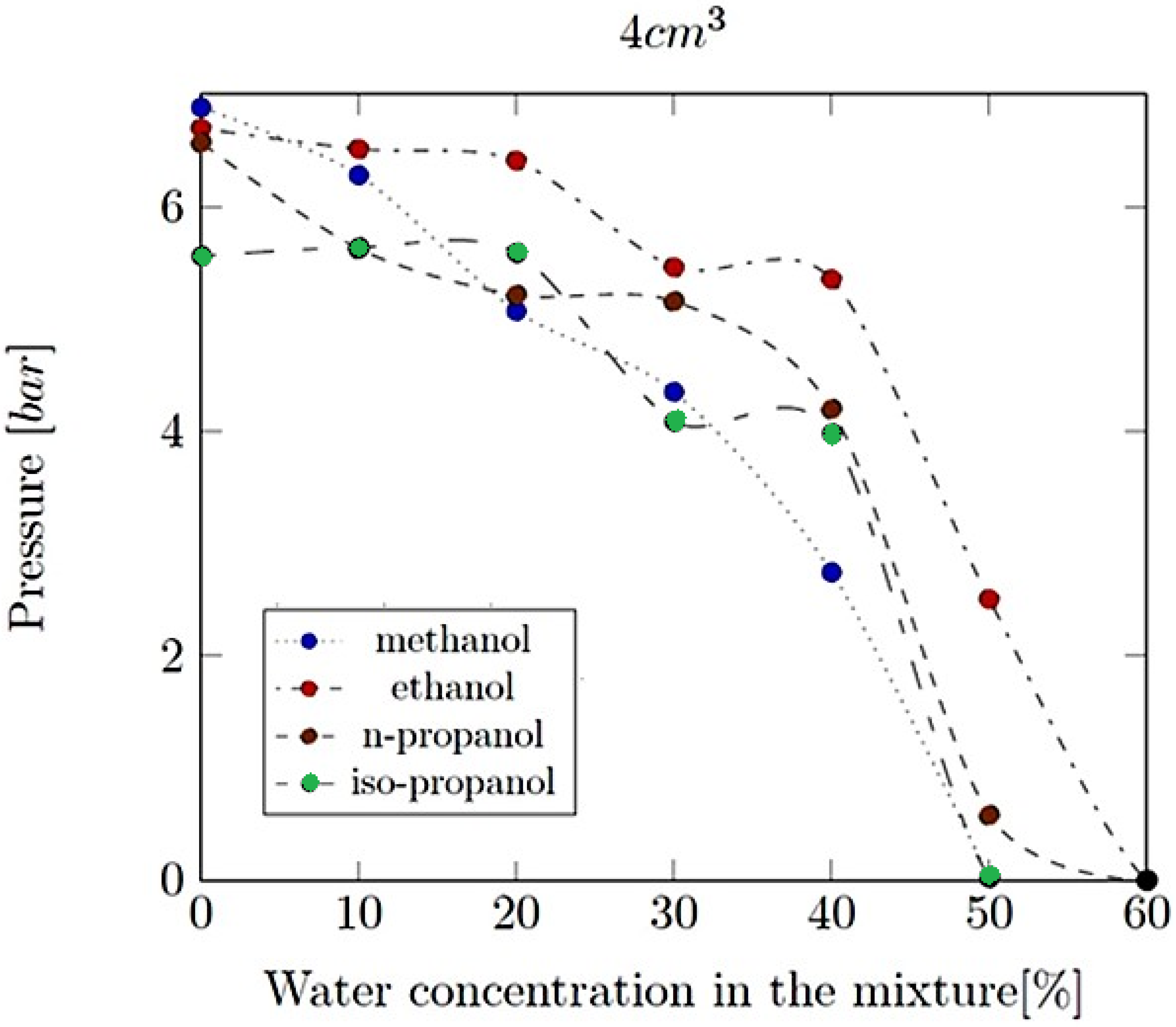
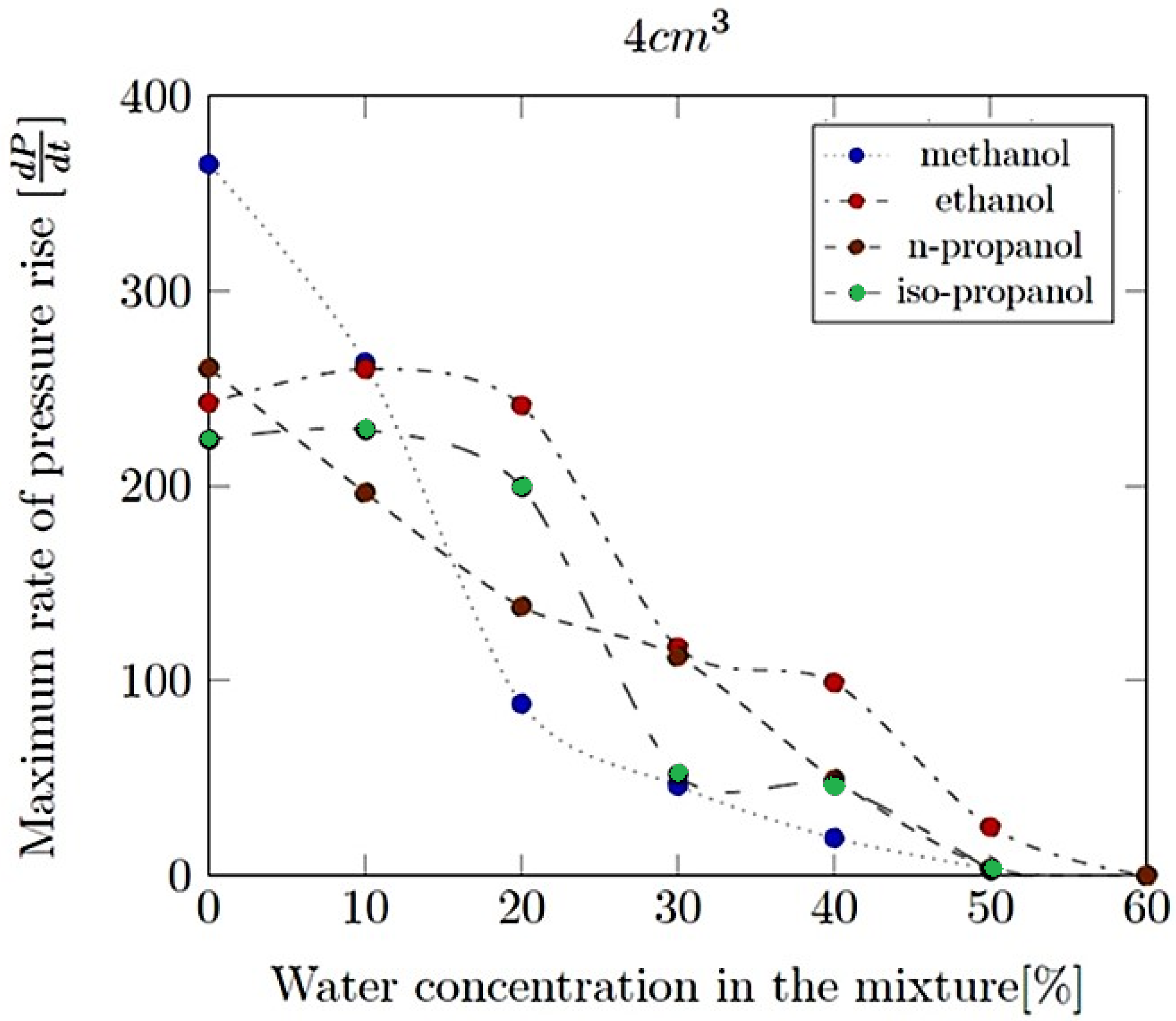
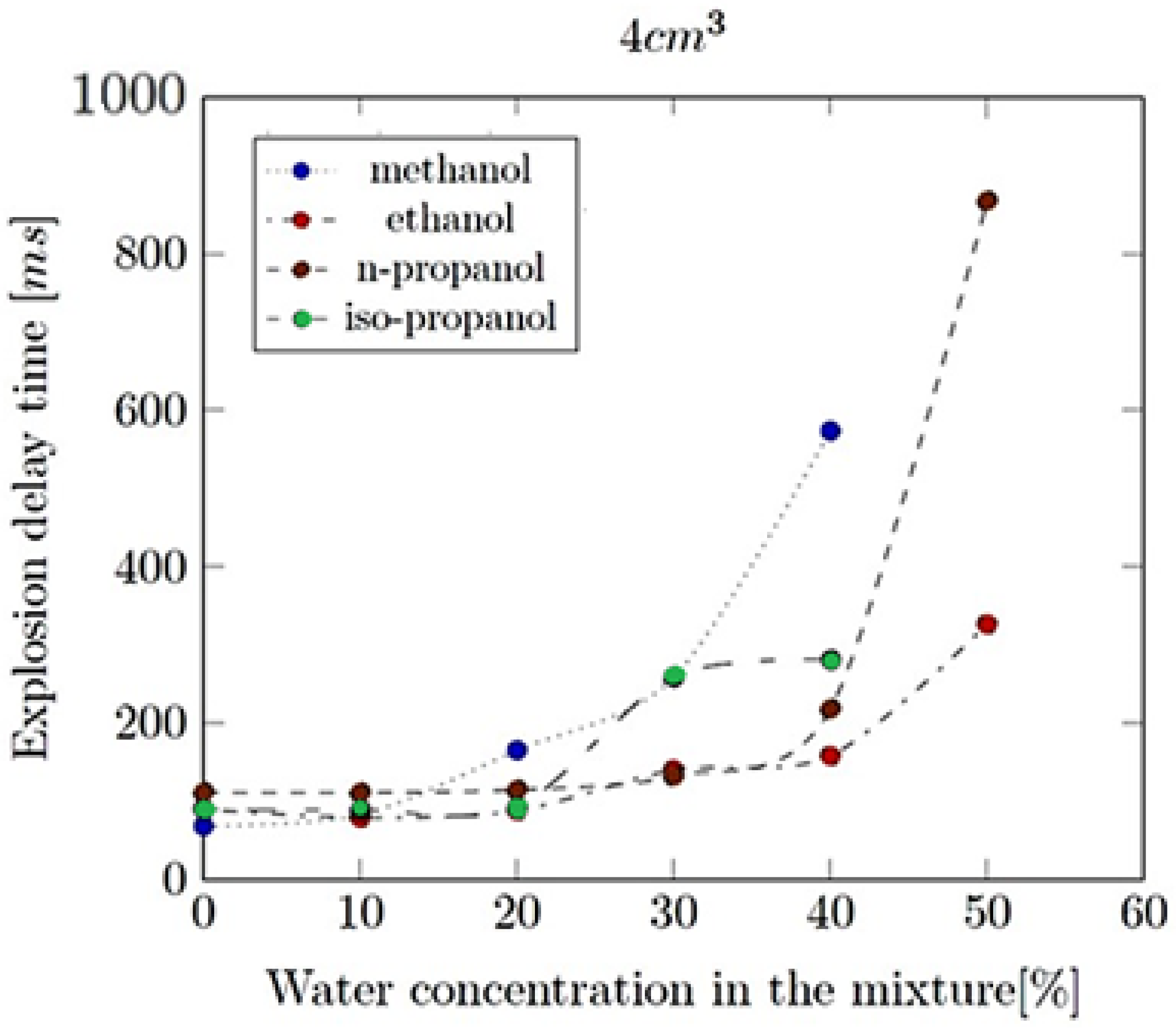
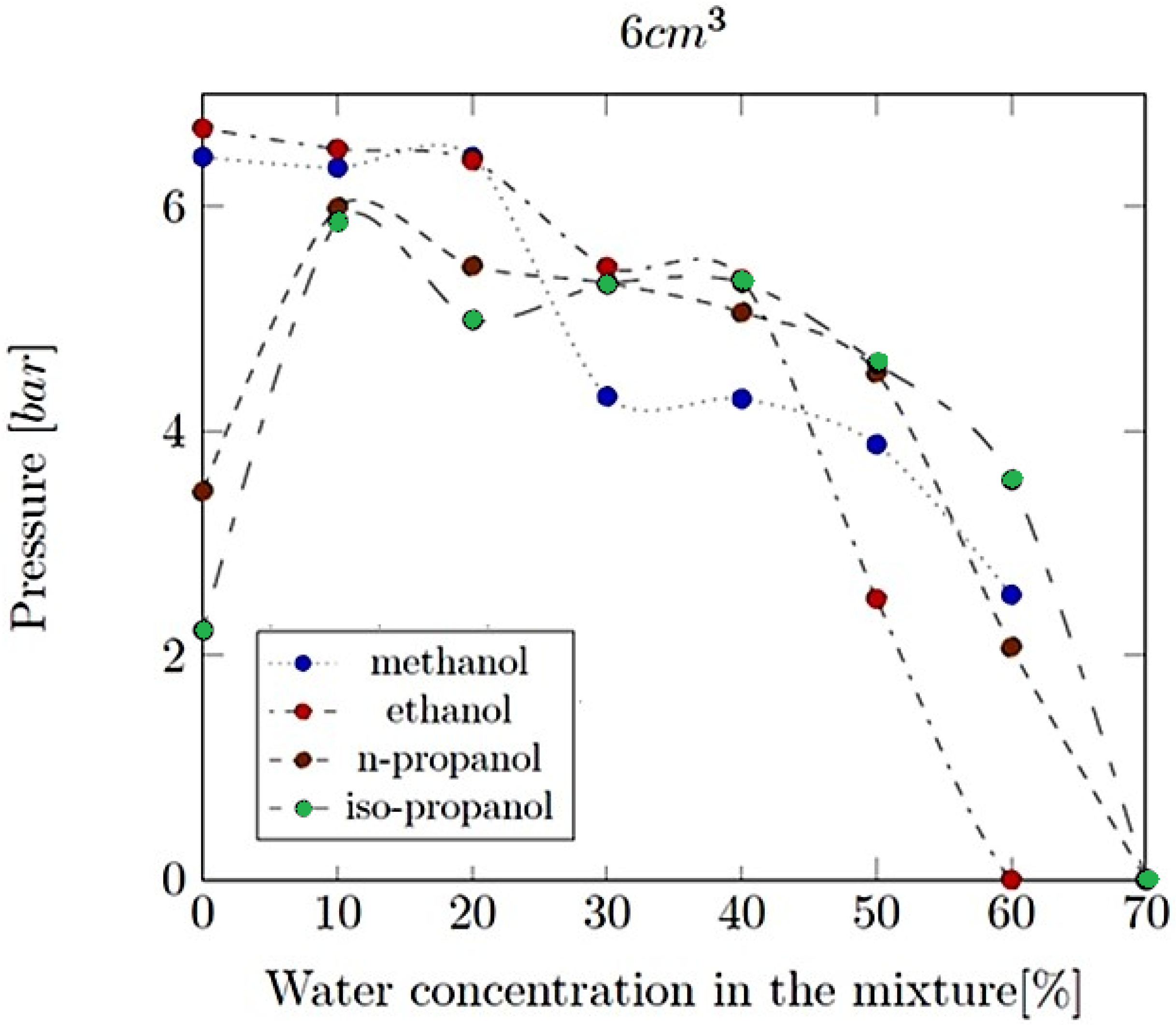
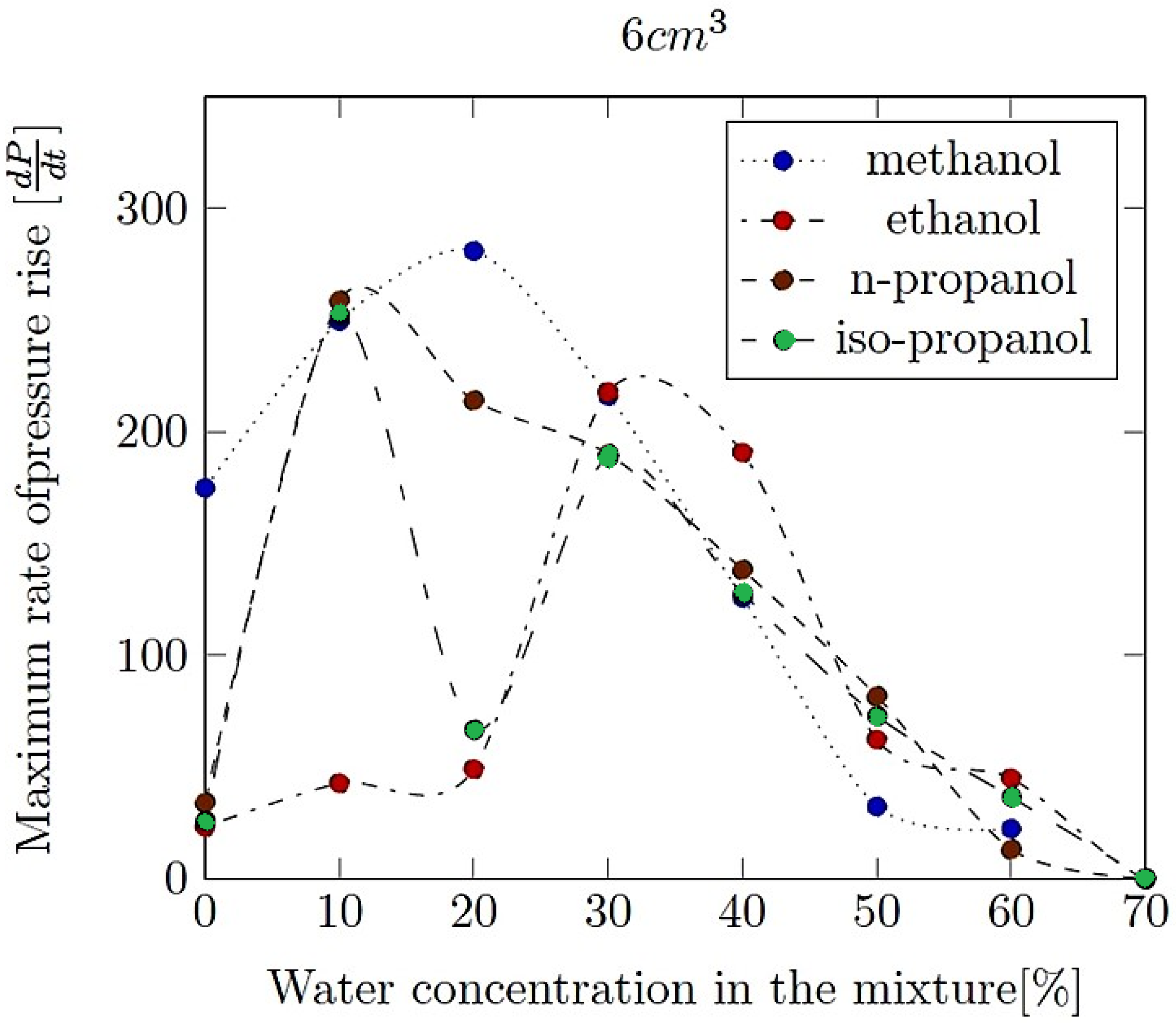
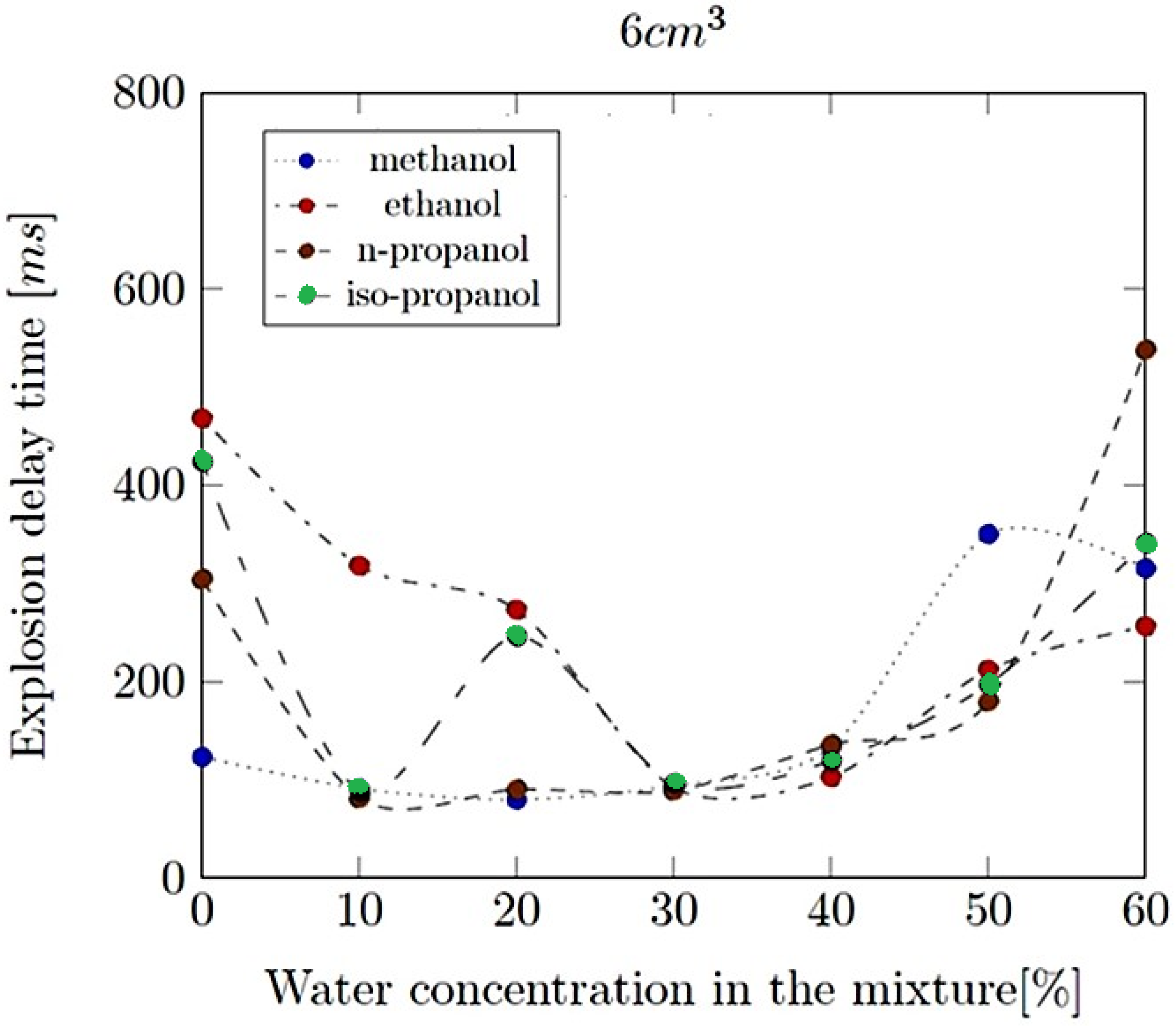
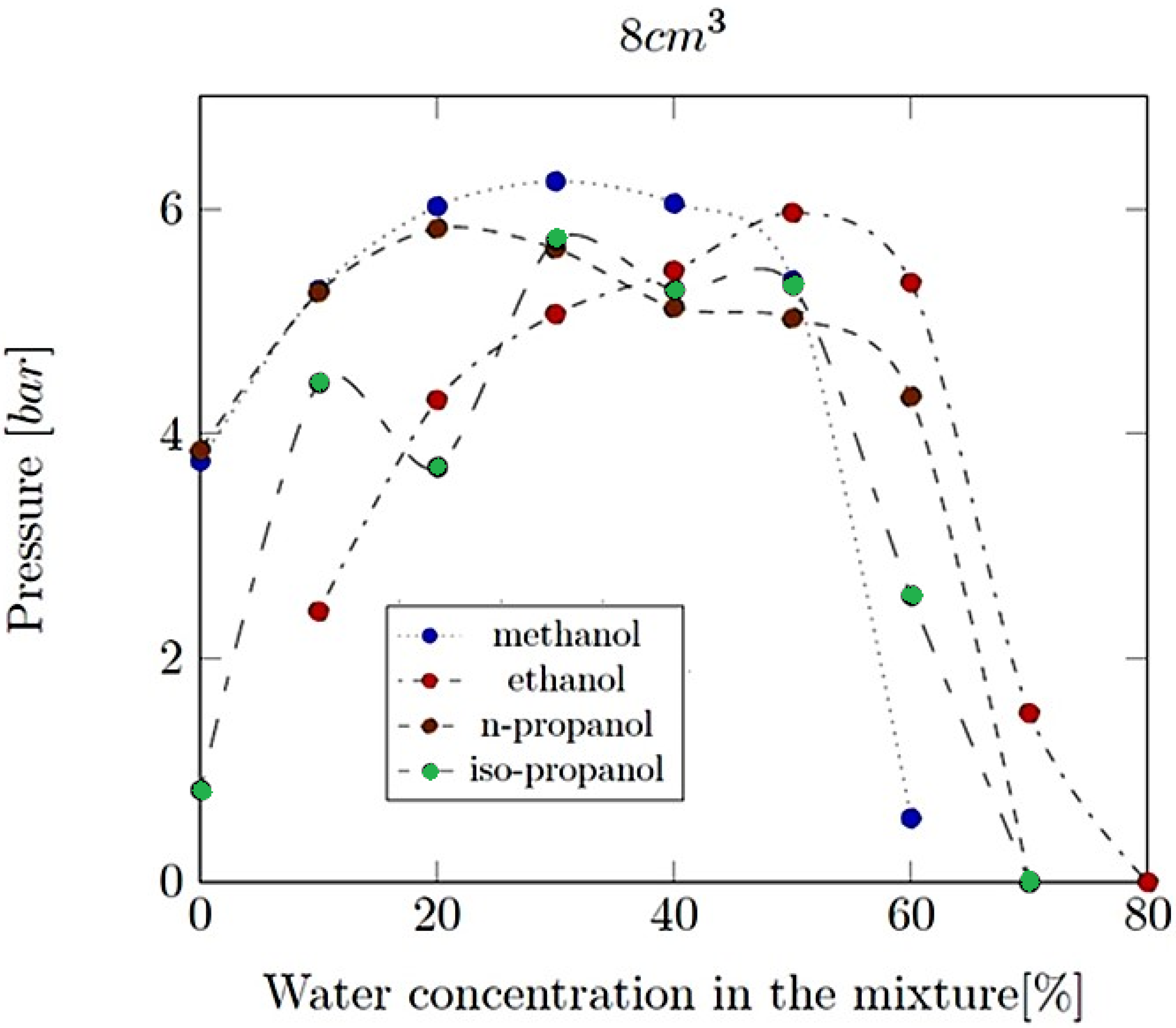
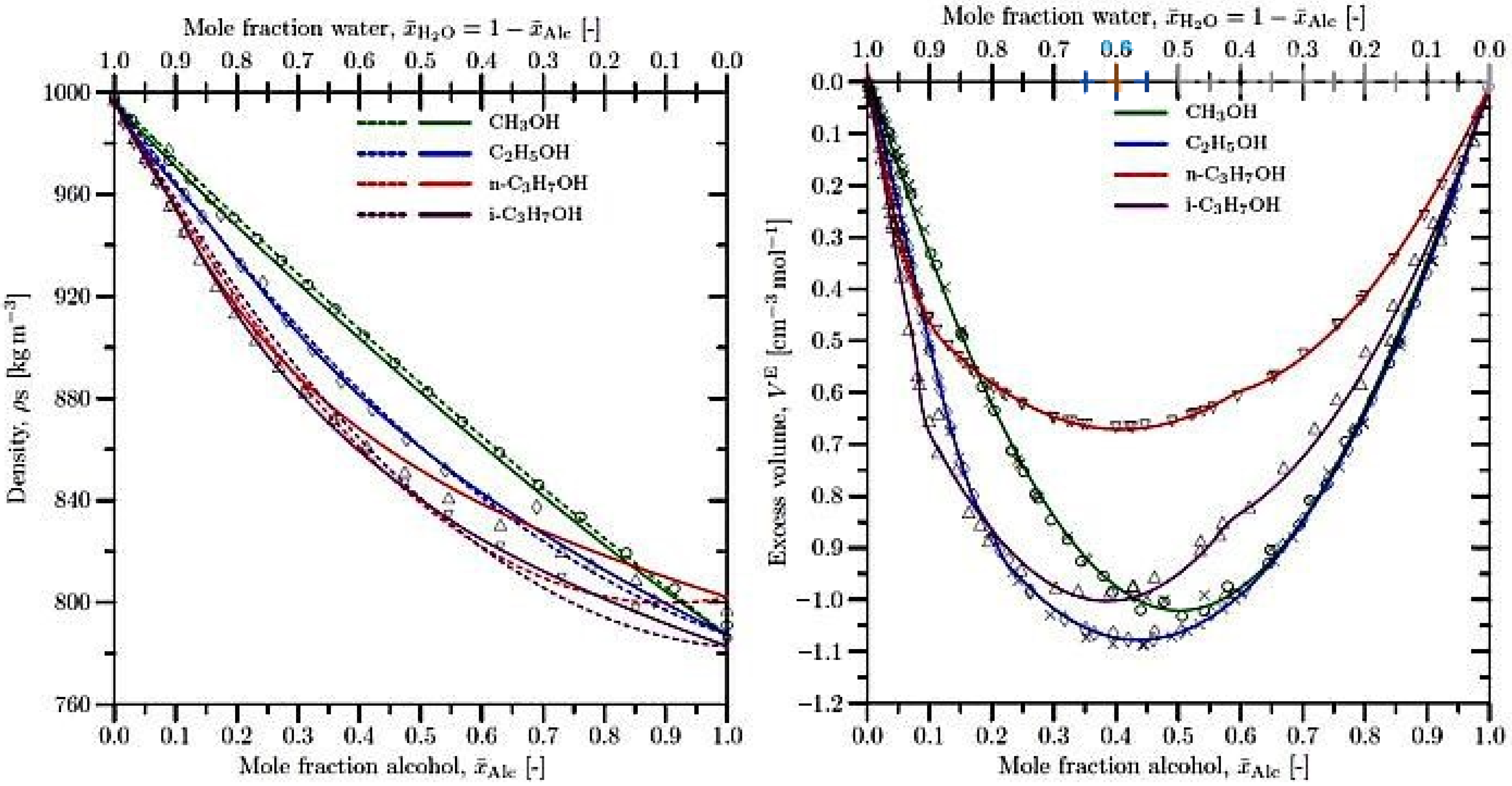
| Substance | M (kg mol−1) | Ρ (†) (kg m−3) | Tc(⊕) (K) | Pc(⊕) (bar) | Vc(⊕) (cm3 mol−1) | ω (-) | Tb (‡) (K) | PSat (*) (bar) | Fl. lim. (y) (vol%) |
|---|---|---|---|---|---|---|---|---|---|
| CH3OH | 32.04 × 10−3 | 787.2 | 512.16 | 80.92 | 117.88 | 0.565 | 338.15 | 0.17 | 6–37 |
| C2H5OH | 46.07 × 10−3 | 787.3 | 513.9 | 61.37 | 167.10 | 0.649 | 351.15 | 0.079 | 3–19 |
| n-C3H7OH | 60.10 × 10−3 | 802.0 | 536.8 | 51.70 | 218.41 | 0.629 | 370.15 | 0.028 | 2–14 |
| i-C3H7OH | 60.10 × 10−3 | 782.7 | 508.3 | 47.62 | 220.10 | 0.665 | 355.15 | 0.061 | 2–12 |
| H2O | 18.015 × 10−3 | (a) 997.05 | 647.10 | 220.64 | 56.02 | 0.344 | (a) 373.13 | (a) 0.0317 | |
| Air | (b) 28.964 × 10−3 | 1.161 | (c) 132.63 | (c) 37.858 | 92.35 |
| Polynomial: VE = ρAlc Alc + ρH2O(1 − Alc) + a0 Alc(1 − Alc) | |||||
| Mixture | Range | a0 | |||
| CH3OH–H2O | 0.0 ≤ Alc ≤ 1.0 | −25.2 × 100 | |||
| C2H5OH–H2O | 0.0 ≤ Alc ≤ 1.0 | −124.7 × 100 | |||
| n-C3H7OH–H2O | 0.0 ≤ Alc ≤ 1.0 | −242.1 × 100 | |||
| i-C3H7OH–H2O | 0.0 ≤ Alc ≤ 1.0 | −19.6 × 101 | |||
| Polynomial: VE = a0 Alc + a1(1 − Alc) + a2 Alc(1 − Alc) + a3 2 (1 − Alc)2 | |||||
| Mixture | Range | a0 | a1 | a2 | a3 |
| CH3OH–H2O | 0.0 ≤ Alc ≤ 1.0 | 0.3 × 10−3 | 17.0 × 10−3 | −370.1 × 10−2 | −16.7 × 10−1 |
| C2H5OH–H2O | 0.0 ≤ Alc < 0.2 0.2 ≤ Alc ≤ 1.0 | 25.2 × 100 1.3 × 10−3 | 8.0 × 10−3 −41.6 × 10−2 | −29.5 × 100 −36.3 × 10−1 | −46.6 × 100 8.1 × 10−1 |
| n-C3H7OH–H2O | 0.0 ≤ Alc < 0.1 0.1 ≤ Alc < 0.6 0.6 ≤ Alc ≤ 1.0 | 20.7 × 100 5.9 × 10−2 −10.1 × 10−3 | 25.6 × 10−3 −324.8 × 10−3 16.0 × 10−2 | −28.4 × 100 −208.3 × 10−2 −27.3 × 10−1 | 0.0 0.0 0.0 |
| i-C3H7OH–H2O | 0.0 ≤ Alc < 0.1 0.1 ≤ Alc < 0.6 0.6 ≤ Alc ≤ 1.0 | 2.4 × 100 5.0 × 10−1 −1.9 × 10−2 | 12.3 × 10−3 −41.1 × 10−2 −1.4 × 10−1 | −10.2 × 100 −39.8 × 10−1 −31.9 × 10−1 | 0.0 0.0 0.0 |
| Species | Extended Antoine Equation | Wagner Equation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | E | F | t0 | n | p | q | a | b | c | d | |
| CH3OH | 5.20277 | 1580.080 | 239.500 | – | – | – | – | 8 | 12 | −8.63571 | 1.17982 | −2.4790 | −1.0240 |
| C2H5OH | 5.33675 | 1648.220 | 230.918 | – | – | – | – | 8 | 12 | −8.68587 | 1.17831 | −4.8762 | 1.5880 |
| n-C3H7OH | 4.99991 | 512.940 | 205.807 | – | – | – | – | 8 | 12 | −8.53706 | 1.96214 | −7.6918 | 2.9450 |
| i-C3H7OH | 5.24268 | 1580.920 | 219.610 | – | – | – | – | 8 | 12 | −8.73656 | 2.16240 | −8.70785 | 4.77927 |
| H2O | 5.11564 | 1687.537 | 230.17 | – | – | – | – | 3 | 6 | −7.77224 | 1.45684 | −2.71942 | −1.41336 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porowski, R.; Dahoe, A.; Kowalik, R.; Sosnowa, J.; Zielinska, K. Thermodynamic Reactivity Study during Deflagration of Light Alcohol Fuel-Air Mixtures with Water. Energies 2024, 17, 1466. https://doi.org/10.3390/en17061466
Porowski R, Dahoe A, Kowalik R, Sosnowa J, Zielinska K. Thermodynamic Reactivity Study during Deflagration of Light Alcohol Fuel-Air Mixtures with Water. Energies. 2024; 17(6):1466. https://doi.org/10.3390/en17061466
Chicago/Turabian StylePorowski, Rafał, Arief Dahoe, Robert Kowalik, Joanna Sosnowa, and Katarzyna Zielinska. 2024. "Thermodynamic Reactivity Study during Deflagration of Light Alcohol Fuel-Air Mixtures with Water" Energies 17, no. 6: 1466. https://doi.org/10.3390/en17061466
APA StylePorowski, R., Dahoe, A., Kowalik, R., Sosnowa, J., & Zielinska, K. (2024). Thermodynamic Reactivity Study during Deflagration of Light Alcohol Fuel-Air Mixtures with Water. Energies, 17(6), 1466. https://doi.org/10.3390/en17061466






