Quantitative Analysis of Balancing Range for Single-Phase 3L-NPC Converters
Abstract
1. Introduction
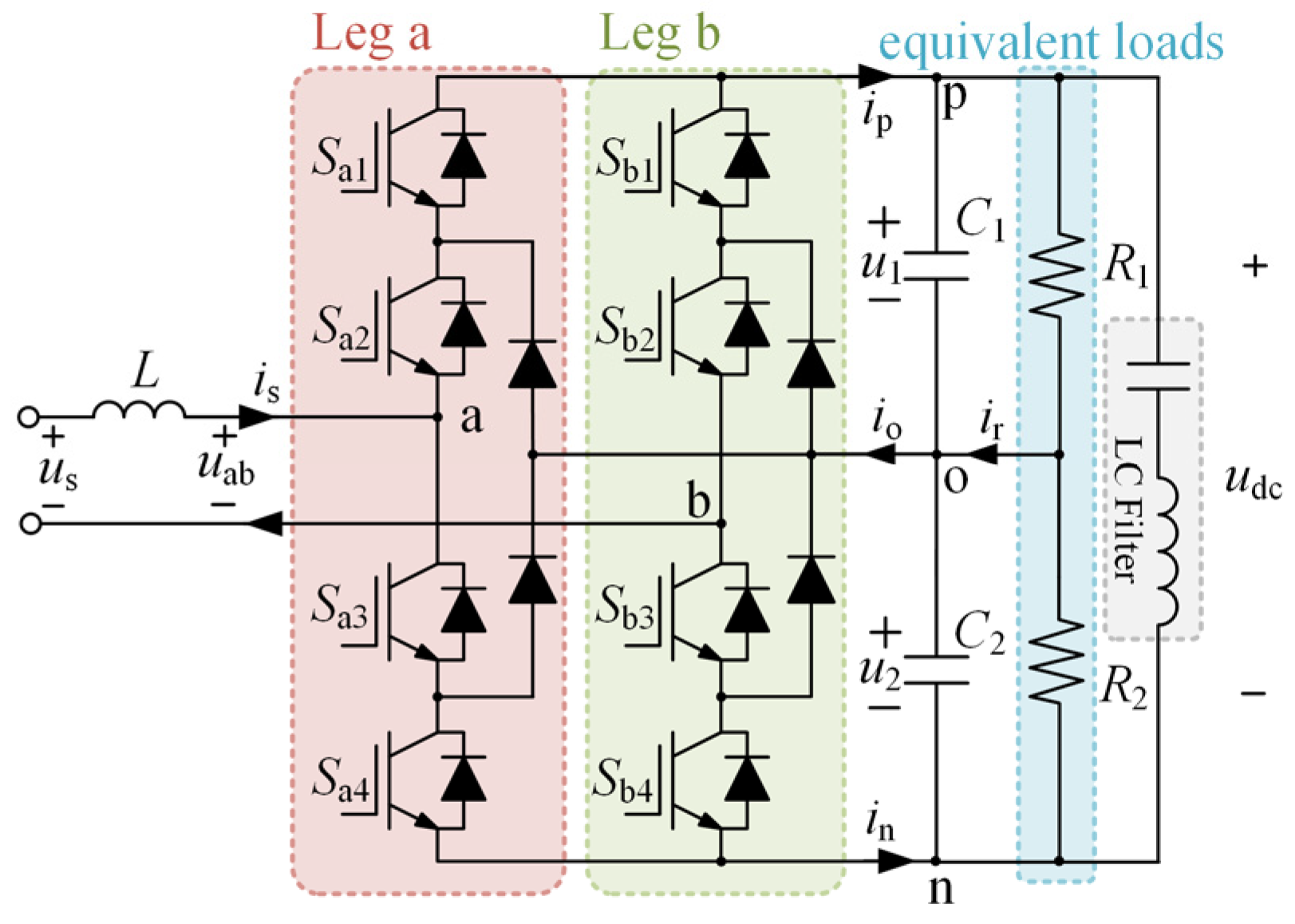
2. System Description
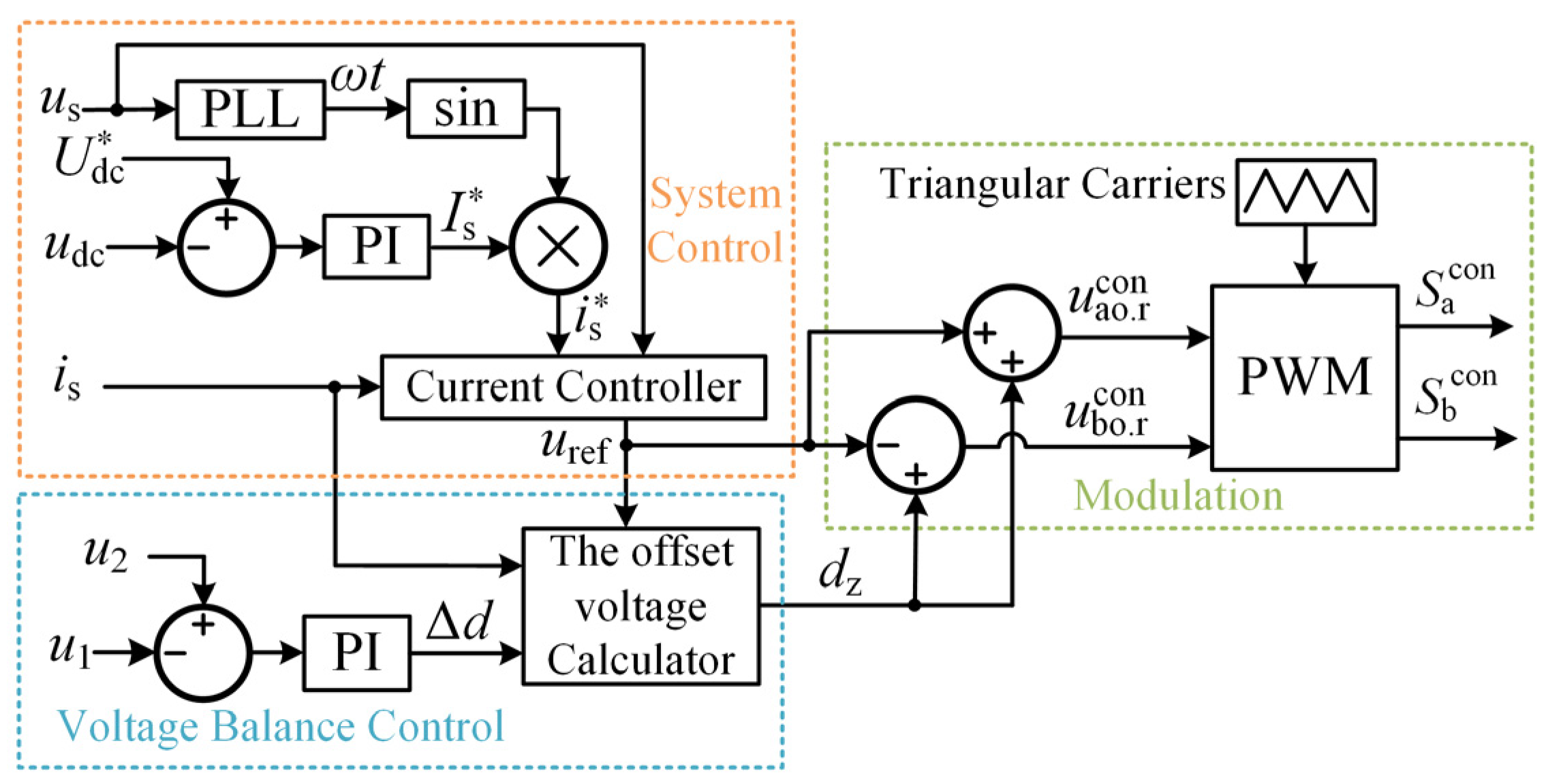
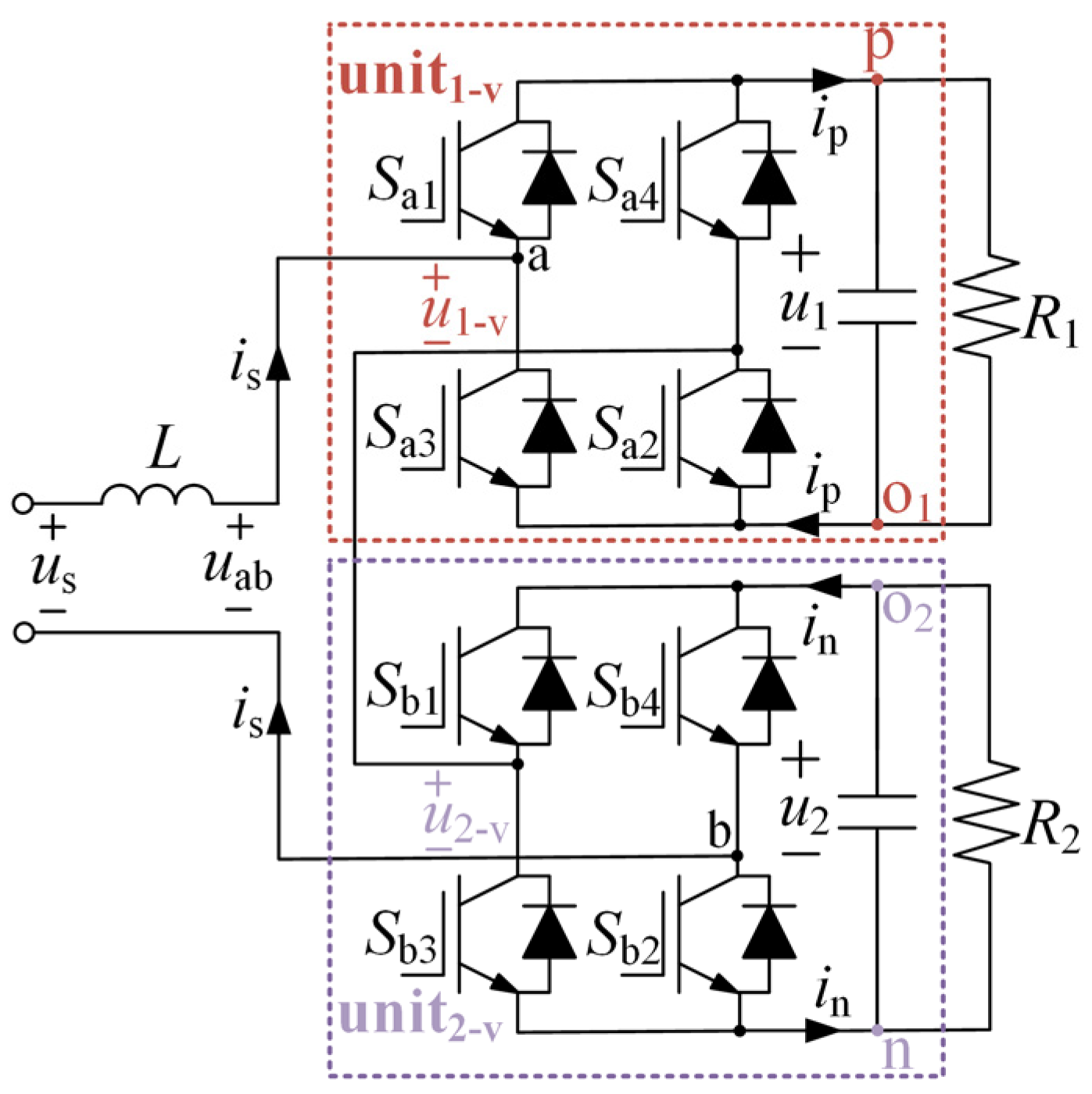
2.1. Operational Principles
2.2. Mathematical Model
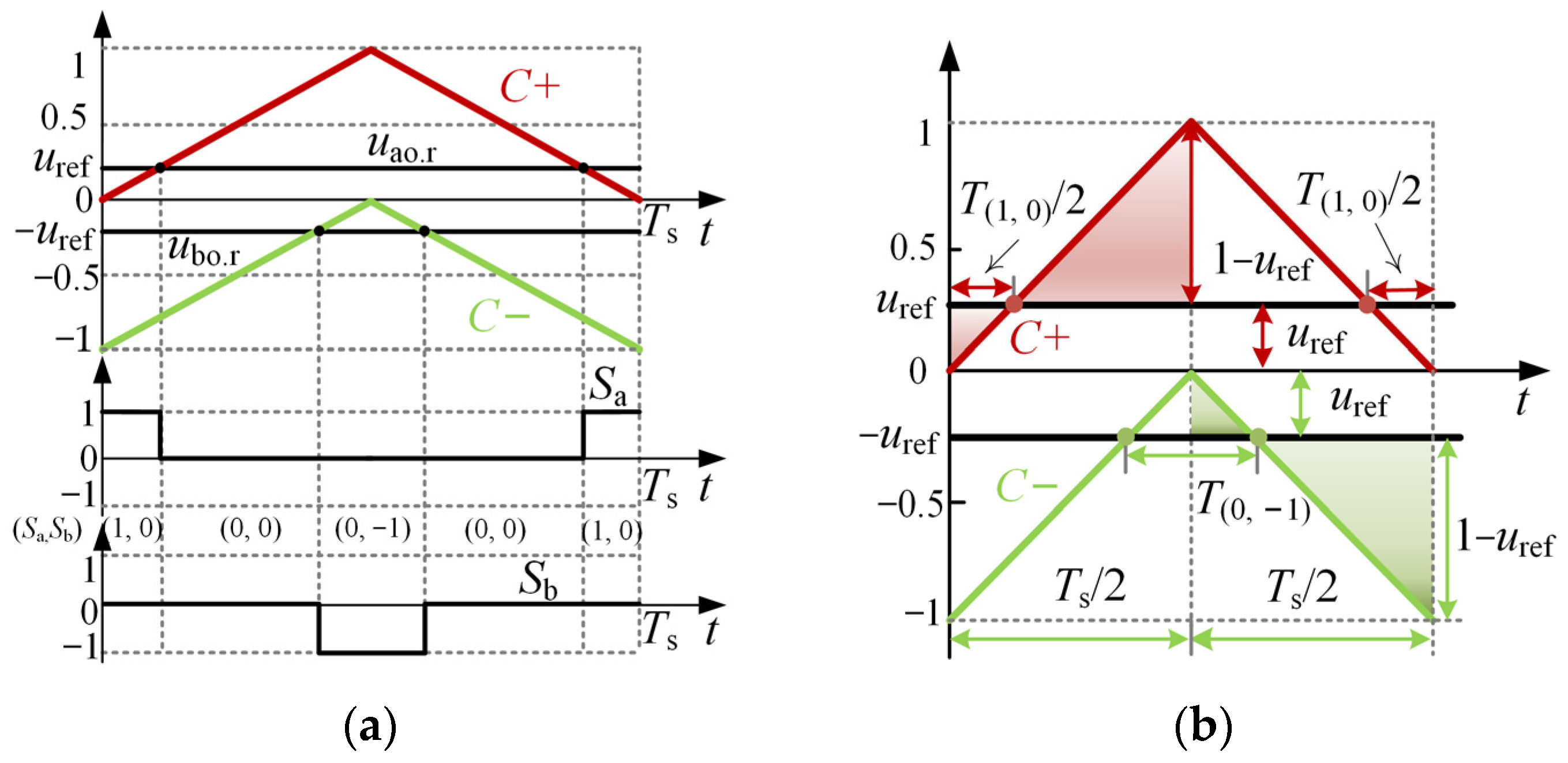
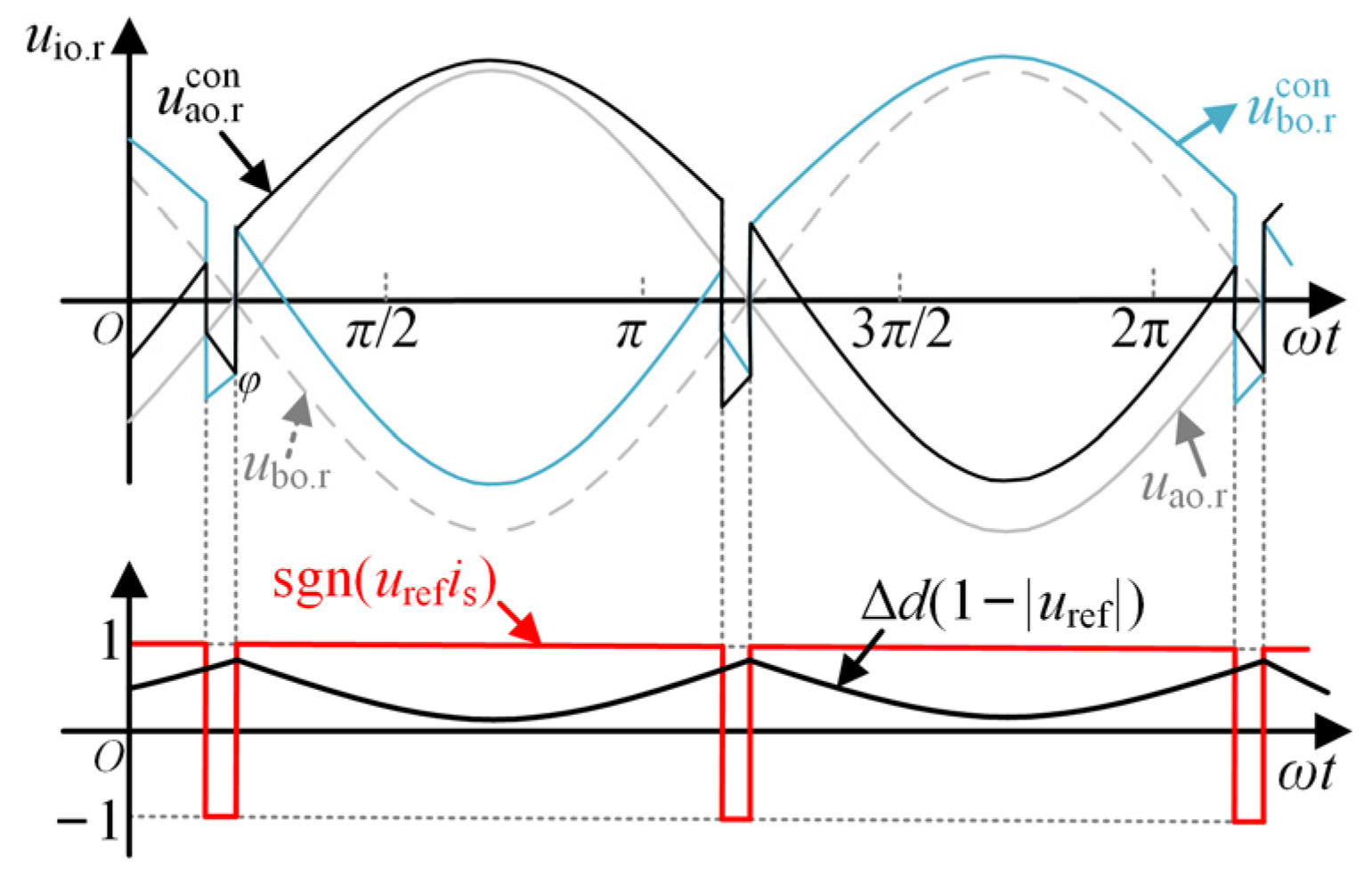
2.3. Voltage Balancing
3. Quantitative Analysis of Voltage Balancing Range
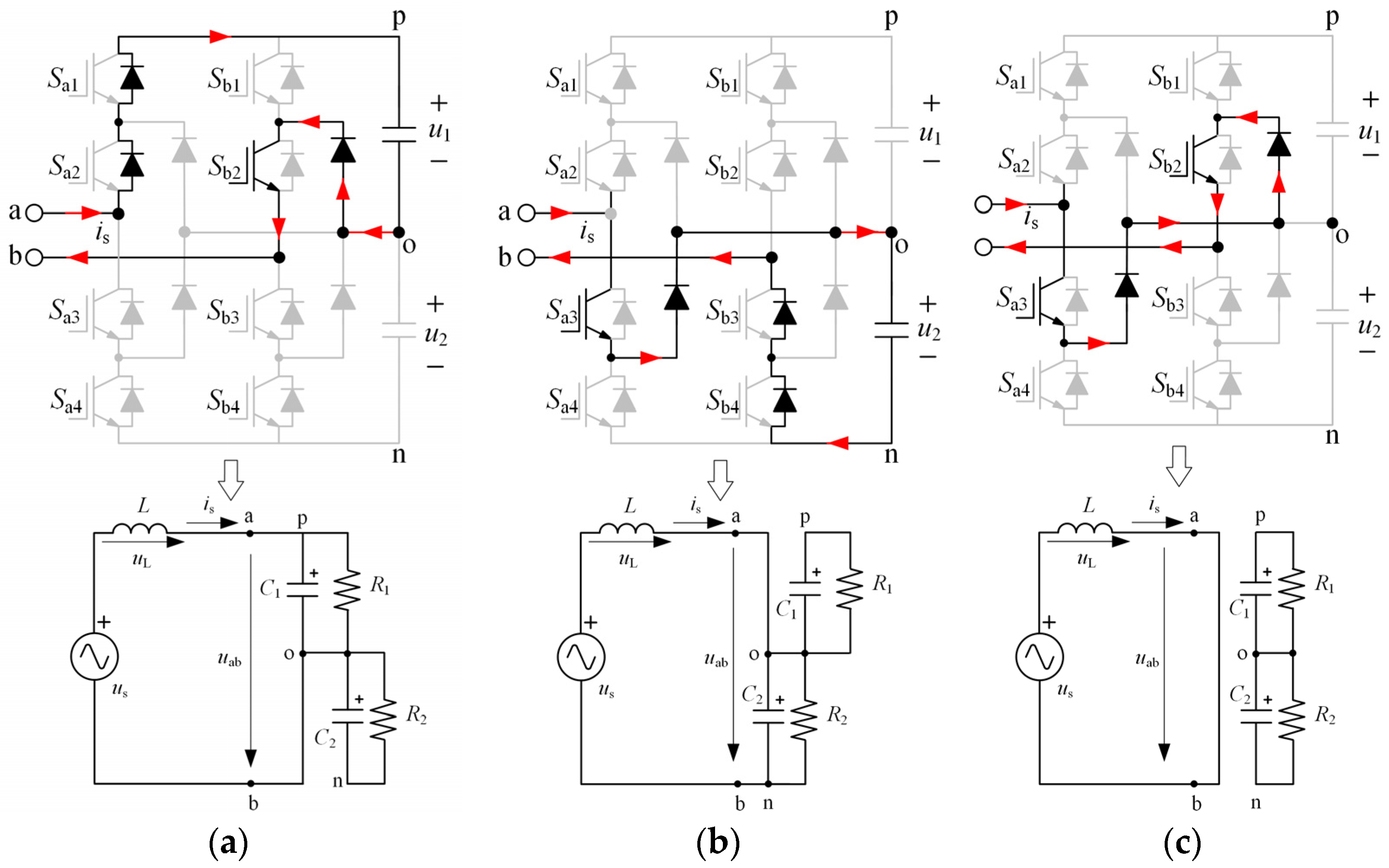
3.1. The Two-Unit H-Bridge Equivalence
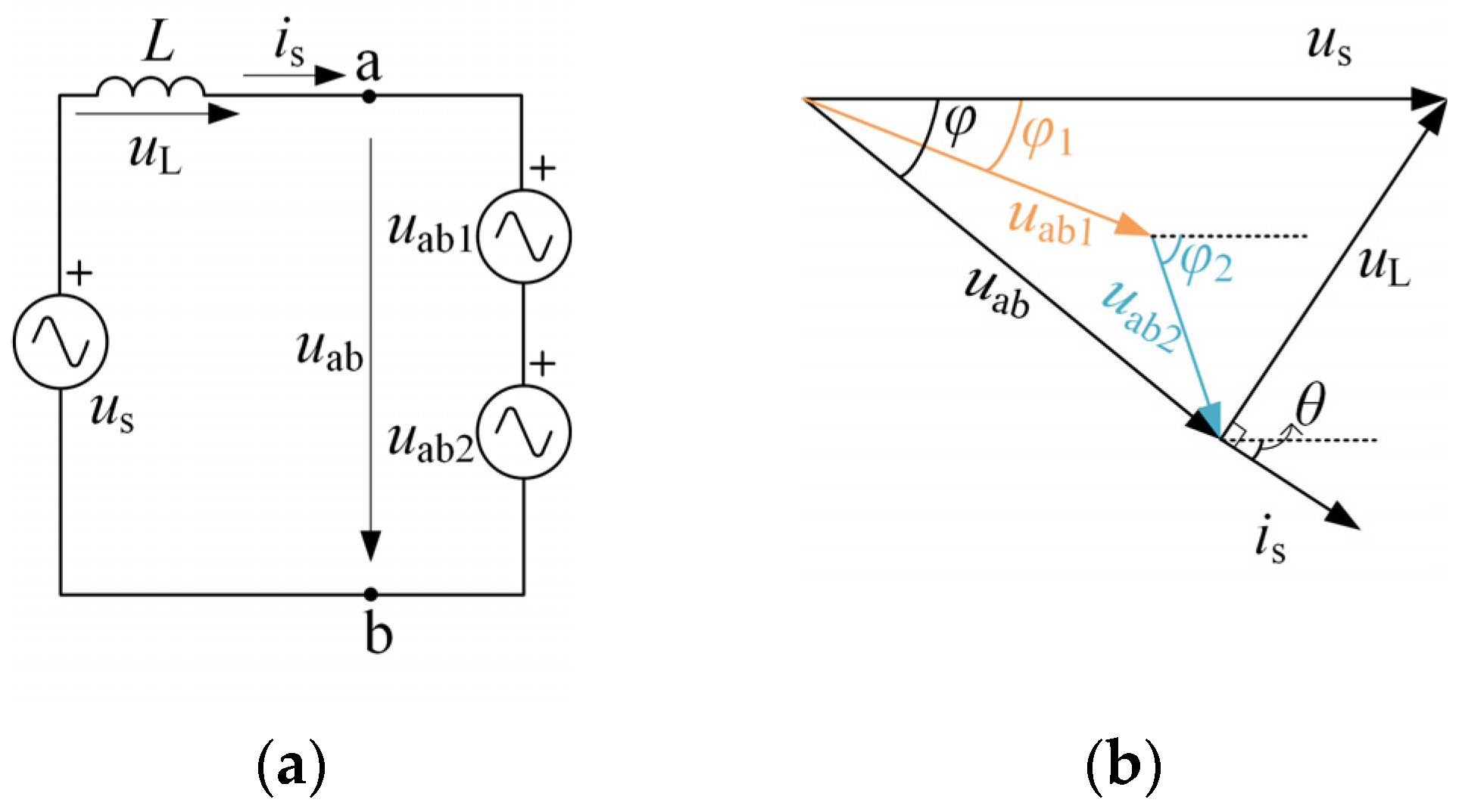
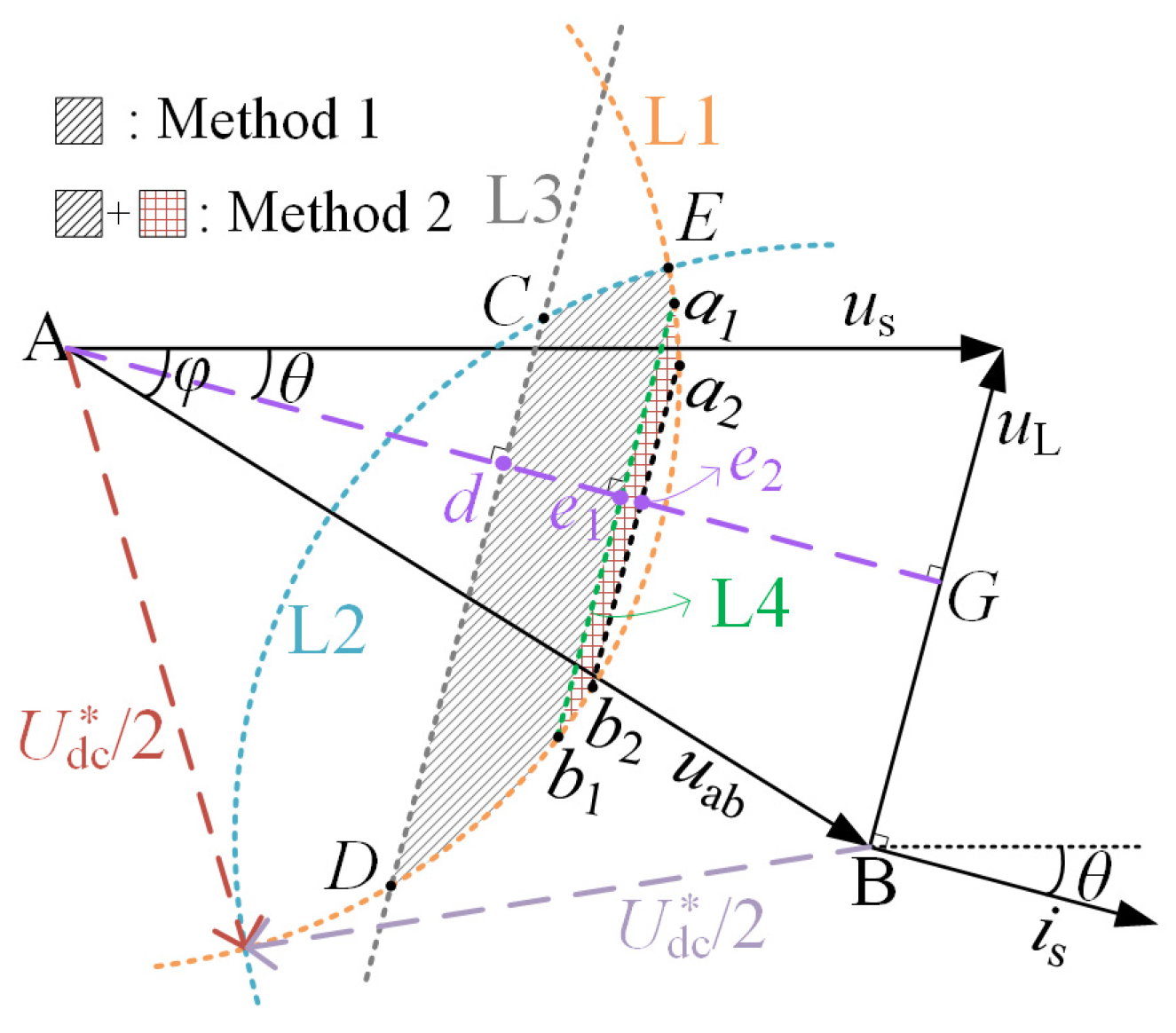
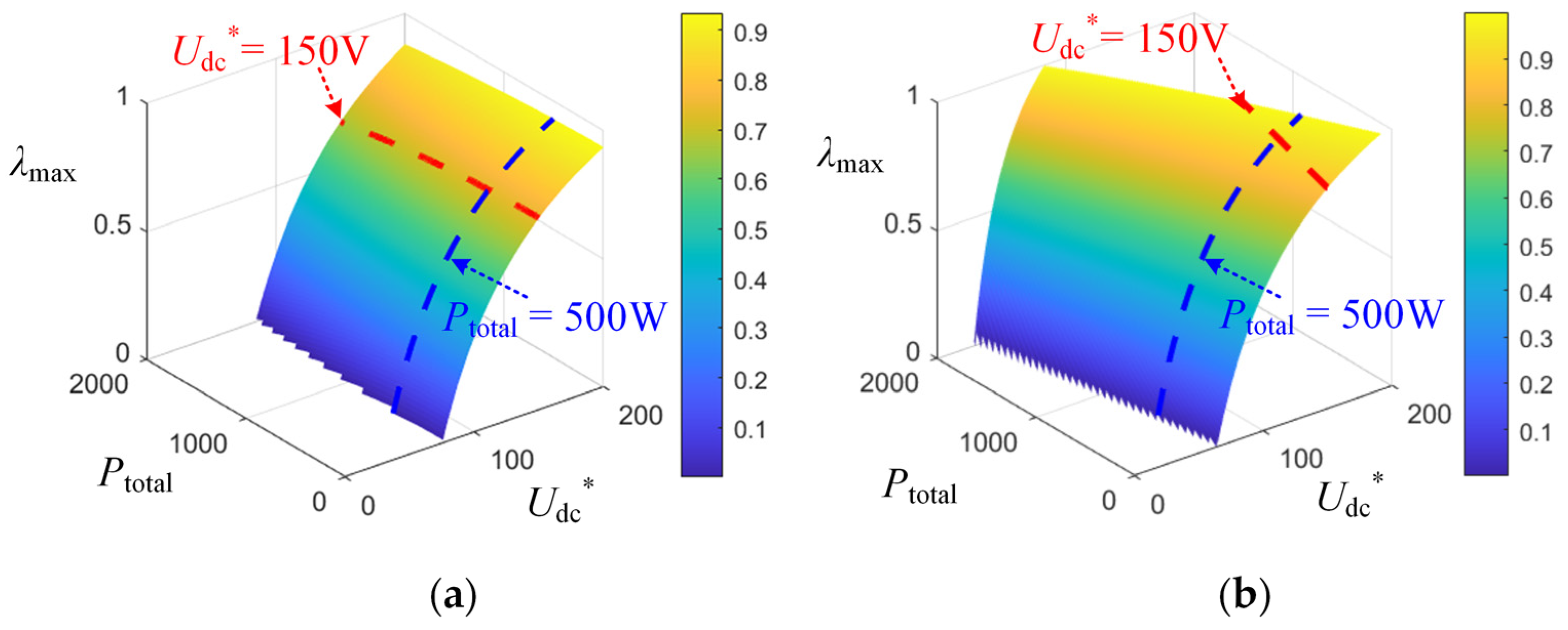
3.2. Deriving the Voltage Balancing Range
4. Methods to Increase Balance Abilities
4.1. Method 1: The Basic Form
4.2. Method 2
4.3. Method 3: Increasing the Reference DC Voltage
4.4. Method 4: Reducing the Total Input Active Power
5. Comparing Different Approaches for Enhancing Load Balancing Capabilities
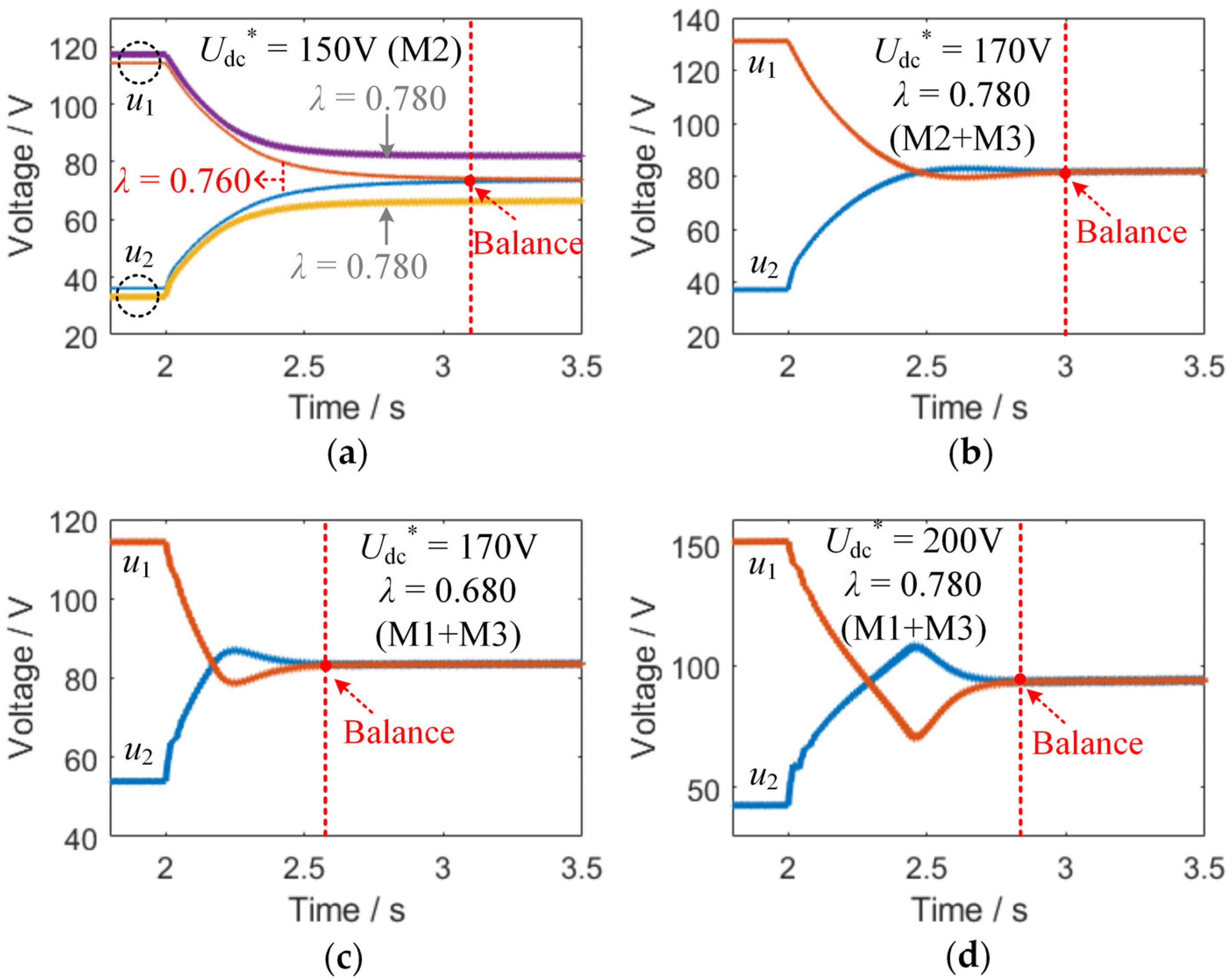
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aghabali, I.; Bauman, J.; Kollmeyer, P.J.; Wang, Y.; Bilgin, B.; Emadi, A. 800-V Electric Vehicle Powertrains: Review and Analysis of Benefits, Challenges, and Future Trends. IEEE Trans. Transp. Electrific. 2021, 7, 927–948. [Google Scholar] [CrossRef]
- Rafi, M.A.H.; Bauman, J. A Comprehensive Review of DC Fast-Charging Stations with Energy Storage: Architectures, Power Converters, and Analysis. IEEE Trans. Transp. Electrific. 2021, 7, 345–368. [Google Scholar] [CrossRef]
- Yaramasu, V.; Dekka, A.; Kouro, S. Chapter 6—Multilevel Converters for Renewable Energy Systems; Academic Press: Cambridge, MA, USA, 2021; ISBN 978-0-323-90217-5. [Google Scholar]
- Emissions of Carbon Dioxide in the Transportation Sector. Available online: https://www.cbo.gov/publication/58861#_idTextAnchor051 (accessed on 3 March 2024).
- Emadi, A. Advanced Electric Drive Vehicles; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Blaabjerg, F. Control of Power Electronic Converters and Systems; Academic Press: London, UK, 2018; Volume 2, ISBN 978-0-12-805245-7. [Google Scholar]
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power Electronics Technology for Large-Scale Renewable Energy Generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Blaabjerg, F. Power Electronics-the Enabling Technology for Renewable Energy Integration. CSEE J. Power Energy Syst. 2021, 8, 39–52. [Google Scholar] [CrossRef]
- Ma, J.; Song, W.; Wang, S.; Feng, X. Model Predictive Direct Power Control for Single Phase Three-Level Rectifier at Low Switching Frequency. IEEE Trans. Power Electron. 2018, 33, 1050–1062. [Google Scholar] [CrossRef]
- Han, P.; He, X.; Ren, H.; Wang, Y.; Peng, X.; Shu, Z.; Gao, S.; Wang, Y.; Chen, Z. Fault Diagnosis and System Reconfiguration Strategy of Single-Phase Three Level Neutral-Point-Clamped Cascaded Inverter. IEEE Trans. Ind. Applicat. 2019, 55, 3863–3876. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, S.-J.; Lee, K.-B. Novel Switching Method for Single-Phase NPC Three-Level Inverter with Neutral-Point Voltage Control. Int. J. Electron. 2018, 105, 303–323. [Google Scholar] [CrossRef]
- Faraji, F.; Mousavi, G.S.M.; Hajirayat, A.; Birjandi, A.A.M.; Al-Haddad, K. Single-Stage Single-Phase Three-Level Neutral-Point-Clamped Transformerless Grid-Connected Photovoltaic Inverters: Topology Review. Renew. Sustain. Energy Rev. 2017, 80, 197–214. [Google Scholar] [CrossRef]
- Shults, T.E.; Husev, O.; Blaabjerg, F.; Roncero-Clemente, C.; Romero-Cadaval, E.; Vinnikov, D. Novel Space Vector Pulsewidth Modulation Strategies for Single-Phase Three-Level NPC Impedance-Source Inverters. IEEE Trans. Power Electron. 2019, 34, 4820–4830. [Google Scholar] [CrossRef]
- Osawa, C.; Matsumoto, Y.; Mizukami, T.; Ozaki, S. A State-Space Modeling and a Neutral Point Voltage Control for an NPC Power Converter. In Proceedings of the Power Conversion Conference—PCC ’97, Nagaoka, Japan, 6 August 1997. [Google Scholar]
- Cobreces, S.; Bordonau, J.; Salaet, J.; Bueno, E.J.; Rodriguez, F.J. Exact Linearization Nonlinear Neutral-Point Voltage Control for Single-Phase Three-Level NPC Converters. IEEE Trans. Power Electron. 2009, 24, 2357–2362. [Google Scholar] [CrossRef]
- Stala, R. Application of Balancing Circuit for DC-Link Voltages Balance in a Single-Phase Diode-Clamped Inverter withTwo Three-Level Legs. IEEE Trans. Ind. Electron. 2011, 58, 4185–4195. [Google Scholar] [CrossRef]
- Wang, S.; Song, W.; Ma, J.; Zhao, J.; Feng, X. Study on Comprehensive Analysis and Compensation for the Line Current Distortion in Single-Phase Three-Level NPC Converters. IEEE Trans. Ind. Electron. 2018, 65, 2199–2211. [Google Scholar] [CrossRef]
- Salaet, J.; Alepuz, S.; Gilabert, A.; Bordonau, J.; Peracaula, J. D-Q Modeling and Control of a Single-Phase Three-Level Boost Rectifier with Power Factor Correction and Neutral-Point Voltage Balancing. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference, Cairns, QLD, Australia, 23–27 June 2002. [Google Scholar]
- Cobreces, S.; Bueno, E.J.; Rodriguez, F.J.; Salaet, J.; Bordonau, J. A New Neutral-Point Voltage Control for Single-Phase Three-Level NPC Converters. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006. [Google Scholar]
- Song, W.; Feng, X.; Smedley, K.M. A Carrier-Based PWM Strategy with the Offset Voltage Injection for Single-Phase Three-Level Neutral-Point-Clamped Converters. IEEE Trans. Power Electron. 2013, 28, 1083–1095. [Google Scholar] [CrossRef]
- Jun, E.; Sangshin-Kwak; Baek, J. Model Predictive Control Method with NP Voltage Balance by Offset Voltage Injection for Single-Phase NPC Converters. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019. [Google Scholar]
- Etxeberria-Otadui, I.; Lopez-de-Heredia, A.; San-Sebastian, J.; Gaztanaga, H.; Viscarret, U.; Caballero, M. Analysis of a H-NPC Topology for an AC Traction Front-End Converter. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; IEEE: Poznan, Poland, 2008; pp. 1555–1561. [Google Scholar]
- De Freitas, I.S.; Bandeira, M.M.; Barros, L.D.M.; Jacobina, C.B.; Dos Santos, E.C.; Salvadori, F.; Da Silva, S.A. A Carrier-Based PWM Technique for Capacitor Voltage Balancing of Single-Phase Three-Level Neutral-Point-Clamped Converters. IEEE Trans. Ind. Applicat. 2015, 51, 3227–3235. [Google Scholar] [CrossRef]
- Chen, X.; Huang, S.; Jiang, D.; Li, B. Fast Voltage-Balancing Scheme for a Carrier-Based Modulation in Three-Phase and Single-Phase NPC Three-Level Inverters. J Electr Eng Technol. 2018, 13, 1986–1995. [Google Scholar] [CrossRef]
- Jun, E.-S.; Kwak, S. A Highly Efficient Single-Phase Three-Level Neutral Point Clamped (NPC) Converter Based on Predictive Control with Reduced Number of Commutations. Energies 2018, 11, 3524. [Google Scholar] [CrossRef]
- Lahooti Eshkevari, A.; Mosallanejad, A.; Sepasian, M.S. Design and Analysis of a Simple Predictive Power Controller for a 1.0-kV Single-phase NPC PWM Rectifier. Circuit Theory Apps. 2018, 46, 2495–2511. [Google Scholar] [CrossRef]
- Lee, J.-S.; Kwak, R.; Lee, K.-B. Novel Discontinuous PWM Method for a Single-Phase Three-Level Neutral Point Clamped Inverter with Efficiency Improvement and Harmonic Reduction. IEEE Trans. Power Electron. 2018, 33, 9253–9266. [Google Scholar] [CrossRef]
- Ma, J.; Song, W.; Wang, X.; Blaabjerg, F.; Feng, X. Low-Complexity Model Predictive Control of Single-Phase Three-Level Rectifiers with Unbalanced Load. IEEE Trans. Power Electron. 2018, 33, 8936–8947. [Google Scholar] [CrossRef]
- Guemez, J.G. Modelling and Control of Grid-Tied NPC Inverters. Ph.D. Thesis, University of Southampton, Southampton, UK, 2020. [Google Scholar]
- Jun, E.-S.; Nguyen, M.H.; Kwak, S. Model Predictive Control Method Based on Deterministic Reference Voltage for Single-Phase Three-Level NPC Converters. Appl. Sci. 2020, 10, 8840. [Google Scholar] [CrossRef]
- Vazquez, S.; Acuna, P.; Aguilera, R.P.; Pou, J.; Leon, J.I.; Franquelo, L.G. DC-Link Voltage-Balancing Strategy Based on Optimal Switching Sequence Model Predictive Control for Single-Phase H-NPC Converters. IEEE Trans. Ind. Electron. 2020, 67, 7410–7420. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, X.; Ning, G.; Dan, H.; Wang, H.; Su, M. Model Predictive-Based Voltage Balancing Control for Single-Phase Three-Level Inverters. IEEE Trans. Power Electron. 2021, 36, 12177–12182. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Chowdhury, S.; Rahman, M.A.; Islam, M.R. Advanced Switching Sequences Based Model-Predictive Control for Single-Phase NPC Converters. IEEE Trans. Ind. Electron. 2022, 69, 3515–3526. [Google Scholar] [CrossRef]
- Pou, J.; Pindado, R.; Boroyevich, D. Voltage-Balance Limits in Four-Level Diode-Clamped Converters with Passive Front Ends. IEEE Trans. Ind. Electron. 2005, 52, 190–196. [Google Scholar] [CrossRef]
- Rivera, S.; Wu, B.; Kouro, S.; Yaramasu, V.; Wang, J. Electric Vehicle Charging Station Using a Neutral Point Clamped Converter with Bipolar DC Bus. IEEE Trans. Ind. Electron. 2015, 62, 1999–2009. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Carrasco, J.M.; Franquelo, L.G.; Galvan, E.; Reyes, M.; Sanchez, J.A.; Dominguez, E. Analysis of the Power Balance in the Cells of a Multilevel Cascaded H-Bridge Converter. IEEE Trans. Ind. Electron. 2010, 57, 2287–2296. [Google Scholar] [CrossRef]



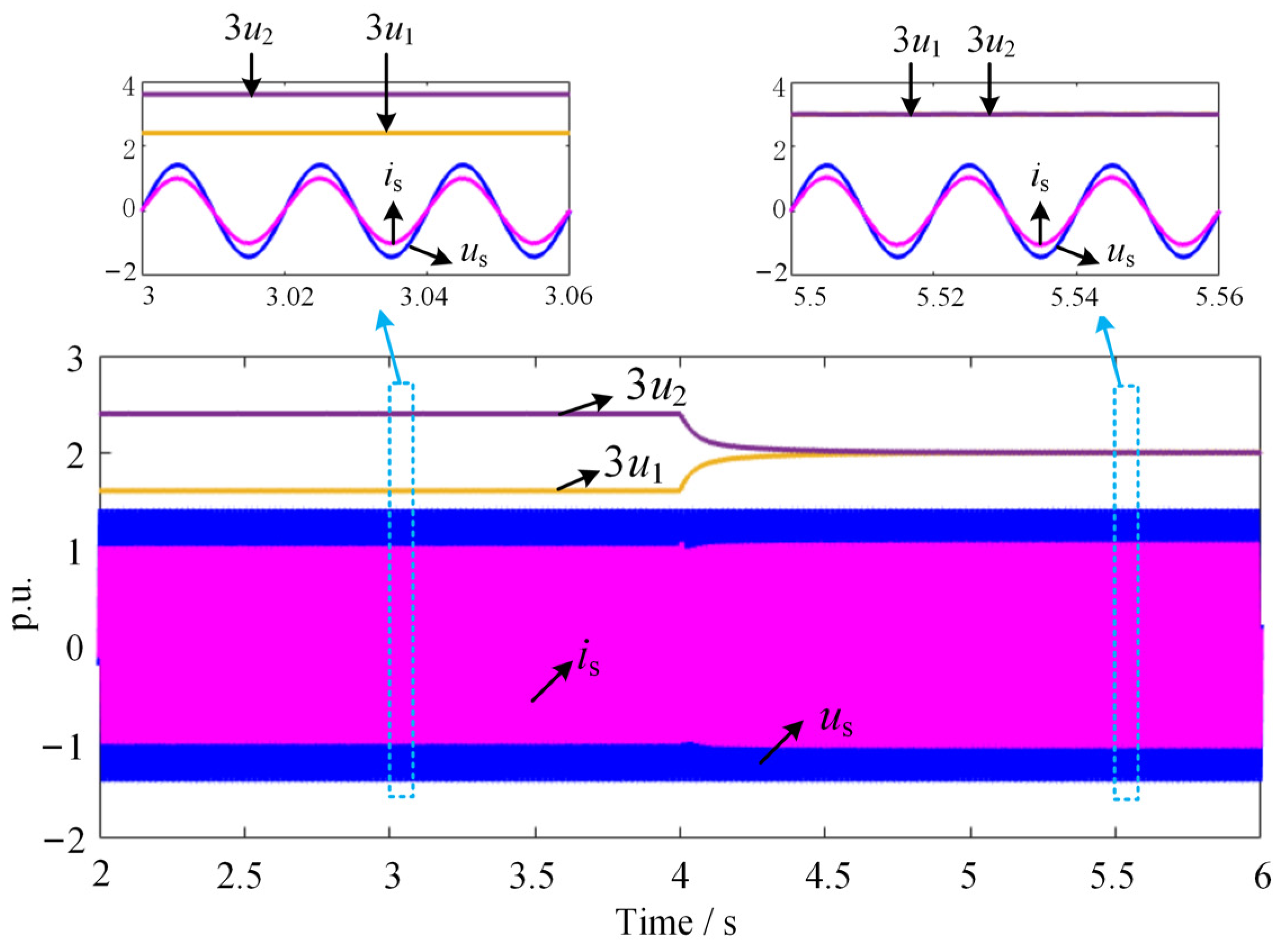

| Method | Upper Limit of DC Load Imbalance Level (λmax) |
|---|---|
| Method 1 | |
| Method 2 | |
| Method 1 + Method 3 | |
| Method 2 + Method 3 | |
| Method 1 + Method 4 | |
| Method 2 + Method 4 |
| Parameters | Value |
|---|---|
| Switching frequency fs/Hz | 5000 |
| AC voltage source Us/V | |
| AC side inductance L/mH | 5 |
| Load (R1 + R2)/Ω | 50 |
| DC link capacitor C/mF | 4.4 |
| Proportional term of balance control Kp | 1 |
| Integral term of balance control Ki | 10 |
| Method | Udc* | λ | The Theoretical Value of λmax | Balance Results |
|---|---|---|---|---|
| M1 | 150 V | 0.600 | 0.665 | Balanced |
| M1 | 150 V | 0.680 | 0.665 | Not Balanced |
| M1 + M3 | 170 V | 0.680 | 0.755 | Balanced |
| M1 + M3 | 200 V | 0.780 | 0.855 | Balanced |
| M2 | 150 V | 0.600 | 0.770 | Balanced |
| M2 | 150 V | 0.680 | 0.770 | Balanced |
| M2 | 150 V | 0.760 | 0.770 | Balanced |
| M2 | 150 V | 0.780 | 0.770 | Not Balanced |
| M2 + M3 | 170 V | 0.780 | 0.830 | Balanced |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Jiao, N.; Wang, S.; Ma, J.; Zhang, R.; Liu, T. Quantitative Analysis of Balancing Range for Single-Phase 3L-NPC Converters. Energies 2024, 17, 1464. https://doi.org/10.3390/en17061464
Wang Z, Jiao N, Wang S, Ma J, Zhang R, Liu T. Quantitative Analysis of Balancing Range for Single-Phase 3L-NPC Converters. Energies. 2024; 17(6):1464. https://doi.org/10.3390/en17061464
Chicago/Turabian StyleWang, Ziying, Ning Jiao, Shunliang Wang, Junpeng Ma, Rui Zhang, and Tianqi Liu. 2024. "Quantitative Analysis of Balancing Range for Single-Phase 3L-NPC Converters" Energies 17, no. 6: 1464. https://doi.org/10.3390/en17061464
APA StyleWang, Z., Jiao, N., Wang, S., Ma, J., Zhang, R., & Liu, T. (2024). Quantitative Analysis of Balancing Range for Single-Phase 3L-NPC Converters. Energies, 17(6), 1464. https://doi.org/10.3390/en17061464






