Active Disturbance Rejection Control Design with Sensitivity Constraint for Drum Water Level
Abstract
1. Introduction
- (1)
- An MADRC is proposed, and the convergence of the proposed MADRC is proven;
- (2)
- An MWOA with sensitivity constraint is applied to optimize the parameters of the MADRC, where the bandwidths of the controller and ESO can be selected with sensitivity constraint;
- (3)
- The effectiveness of the proposed MADRC optimized by the MWOA is verified by comparative simulations.
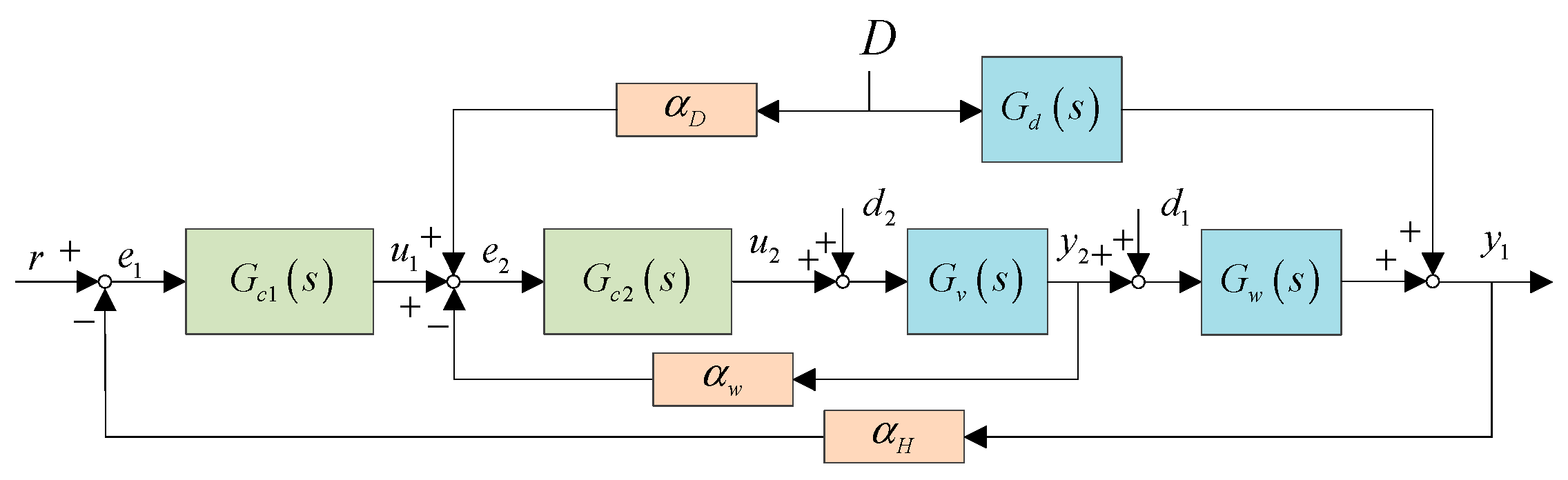
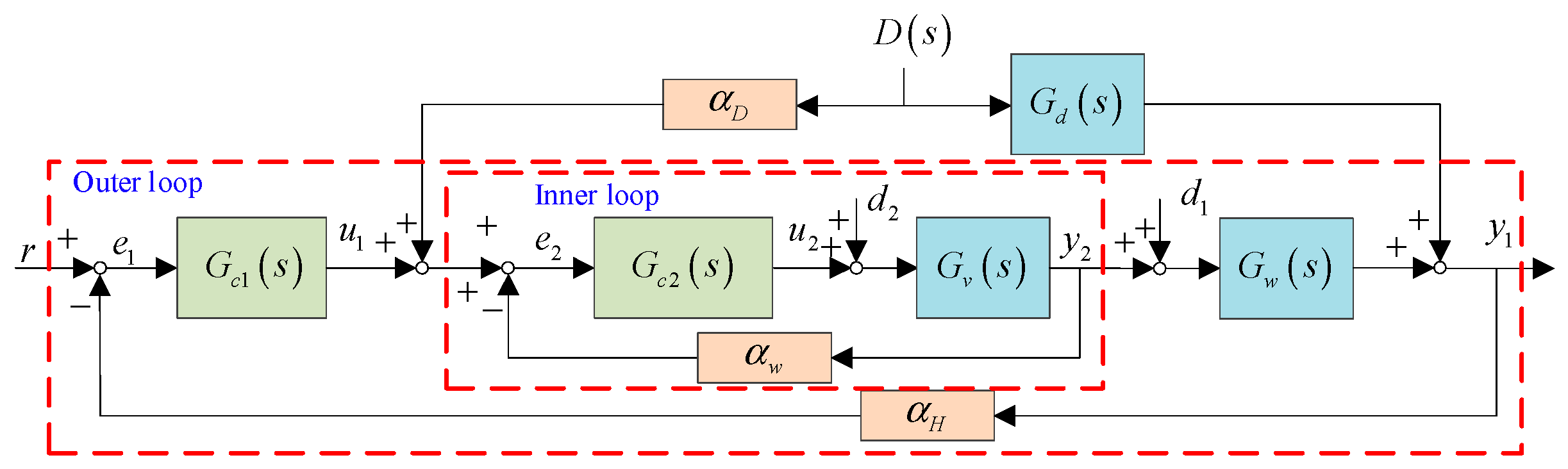
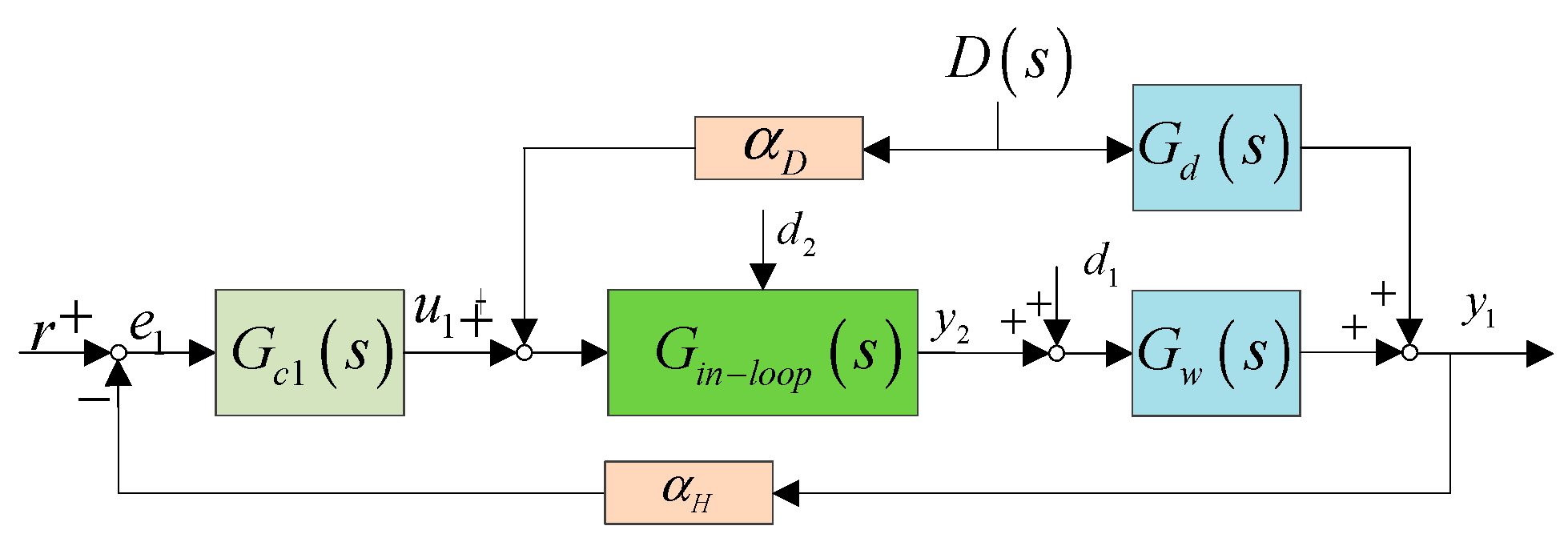
2. Control Structure of Drum Water Level and Control Objective
- tracks as fast as possible with small overshoot;
- The closed-loop system can quickly recover to the steady state when , or occurs;
- The closed-loop system should have a strong ability to handle system uncertainties.
3. Modified Active Disturbance Rejection Control and Convergence Analysis
3.1. Regular Active Disturbance Rejection Control
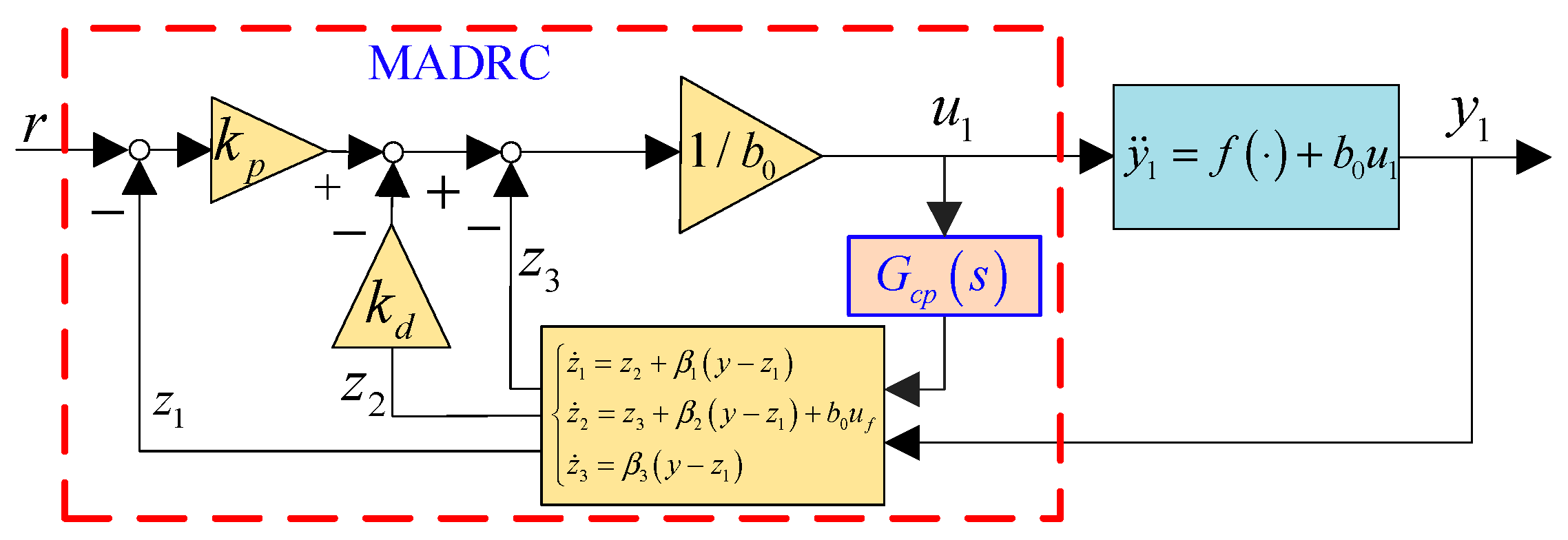
3.2. Modified Active Disturbance Rejection Control
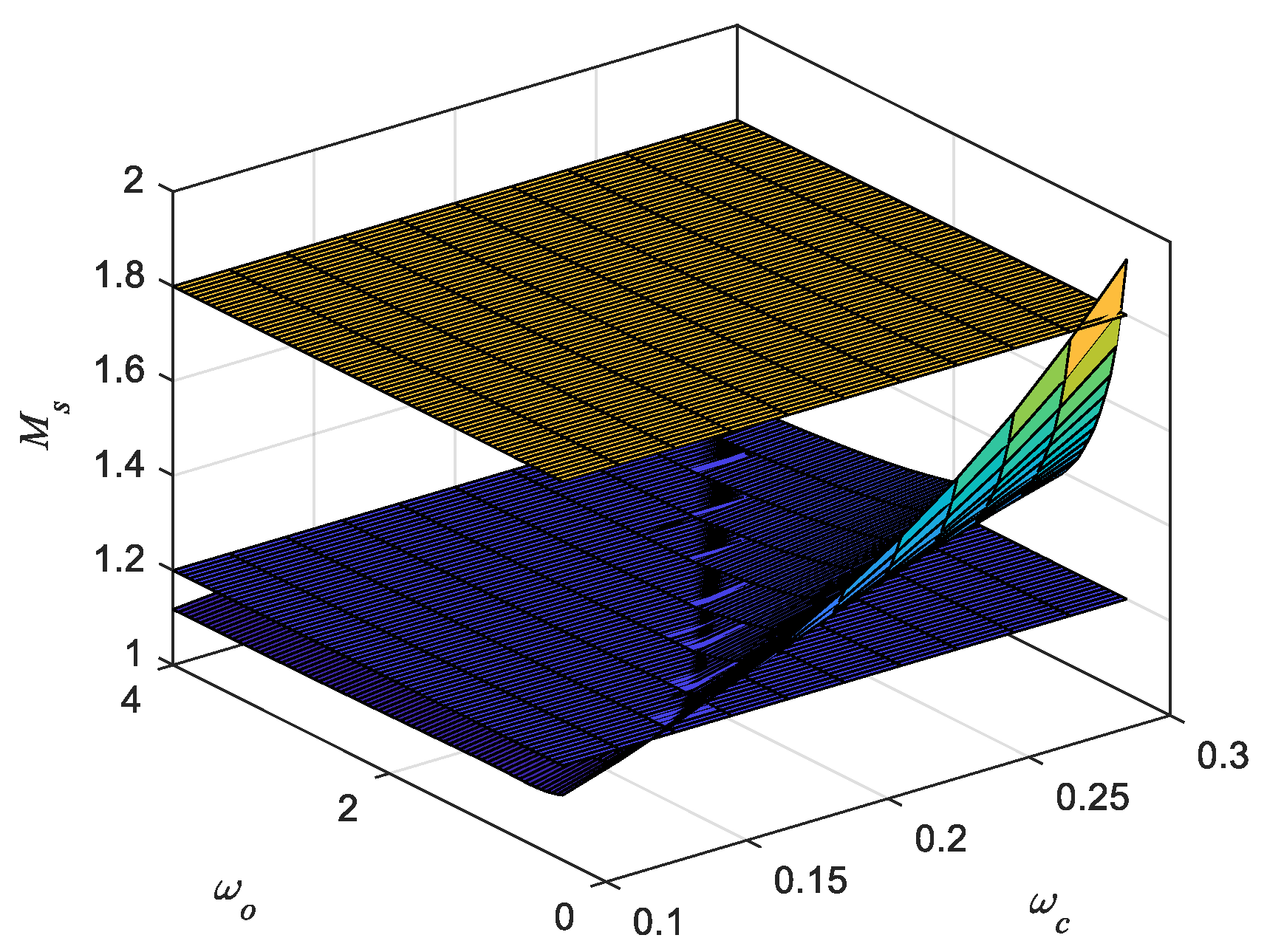
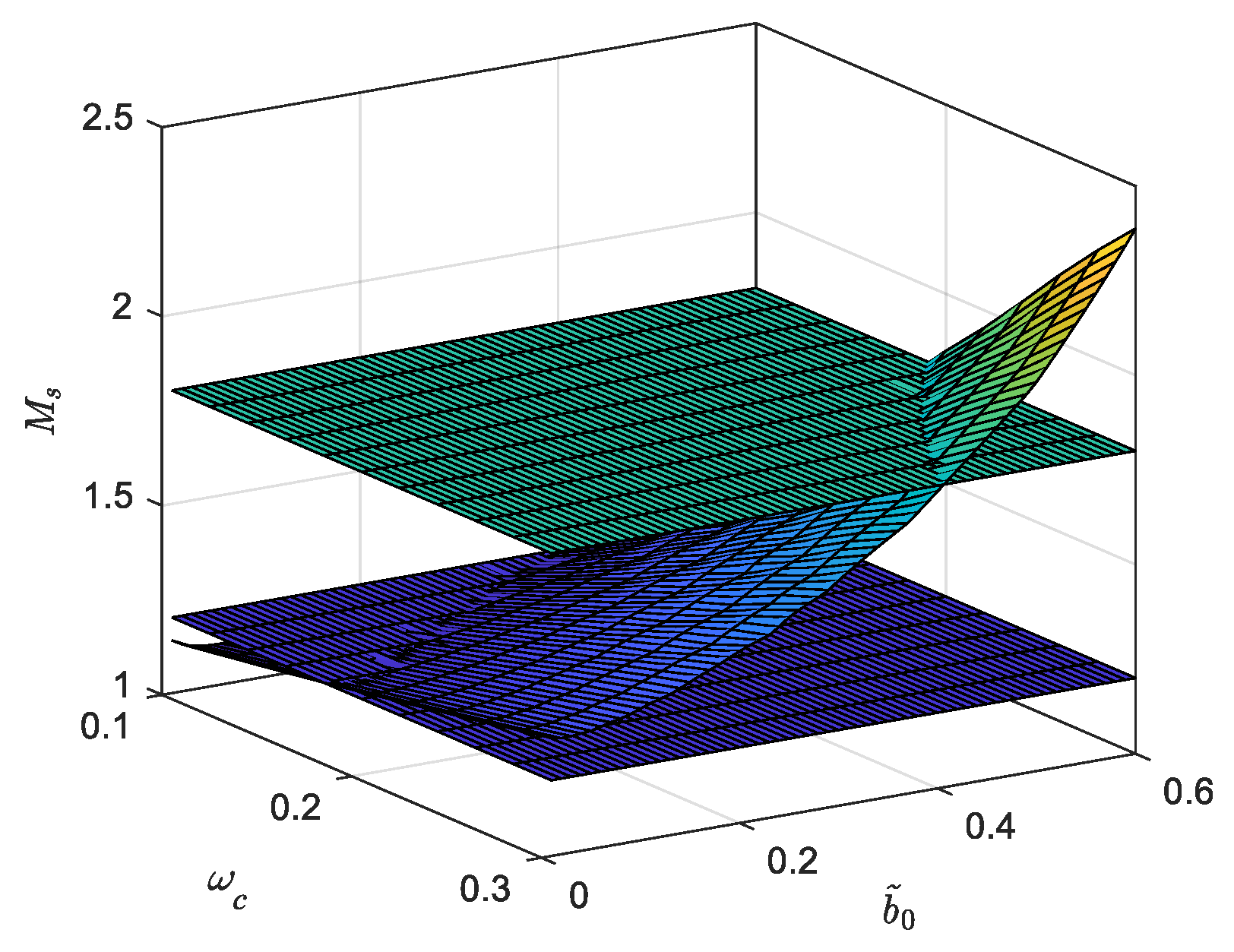
3.3. Distributions of Ms for MADRC
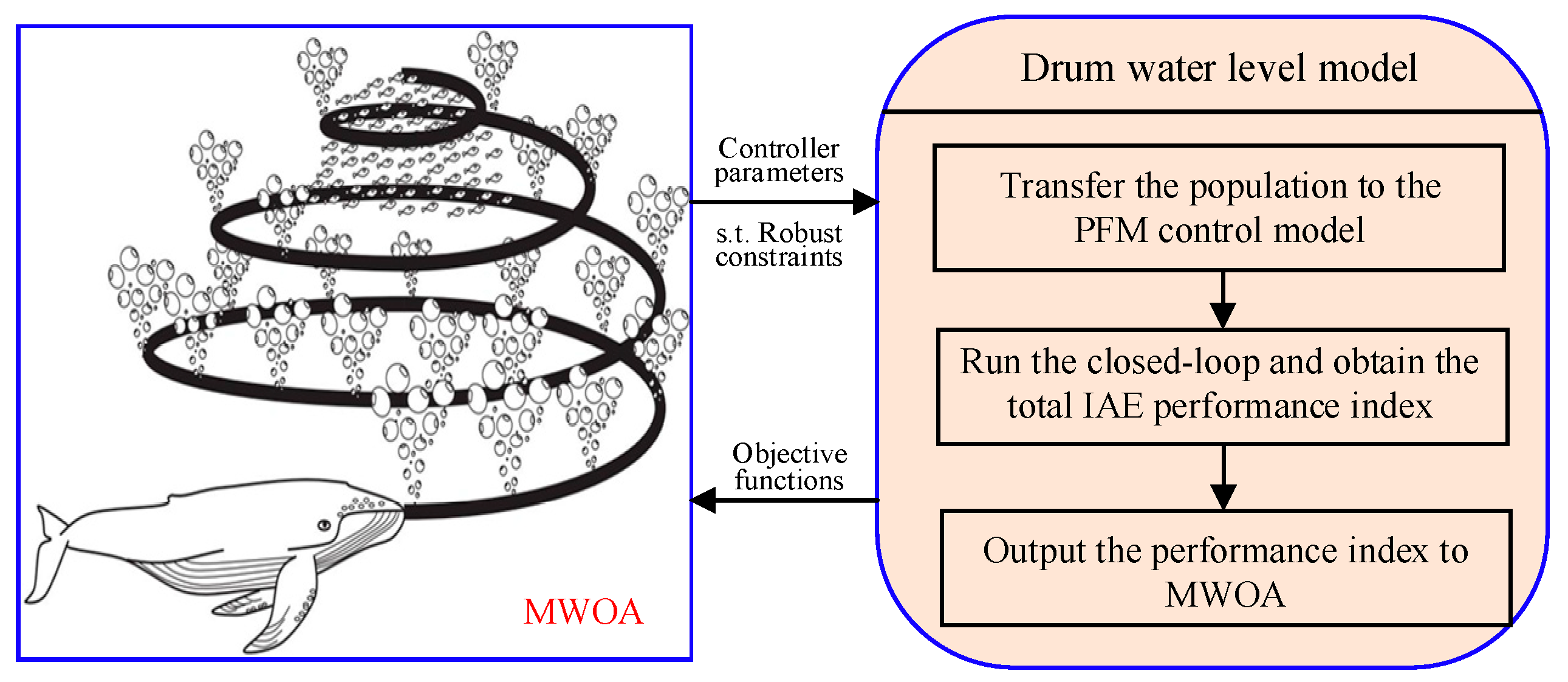
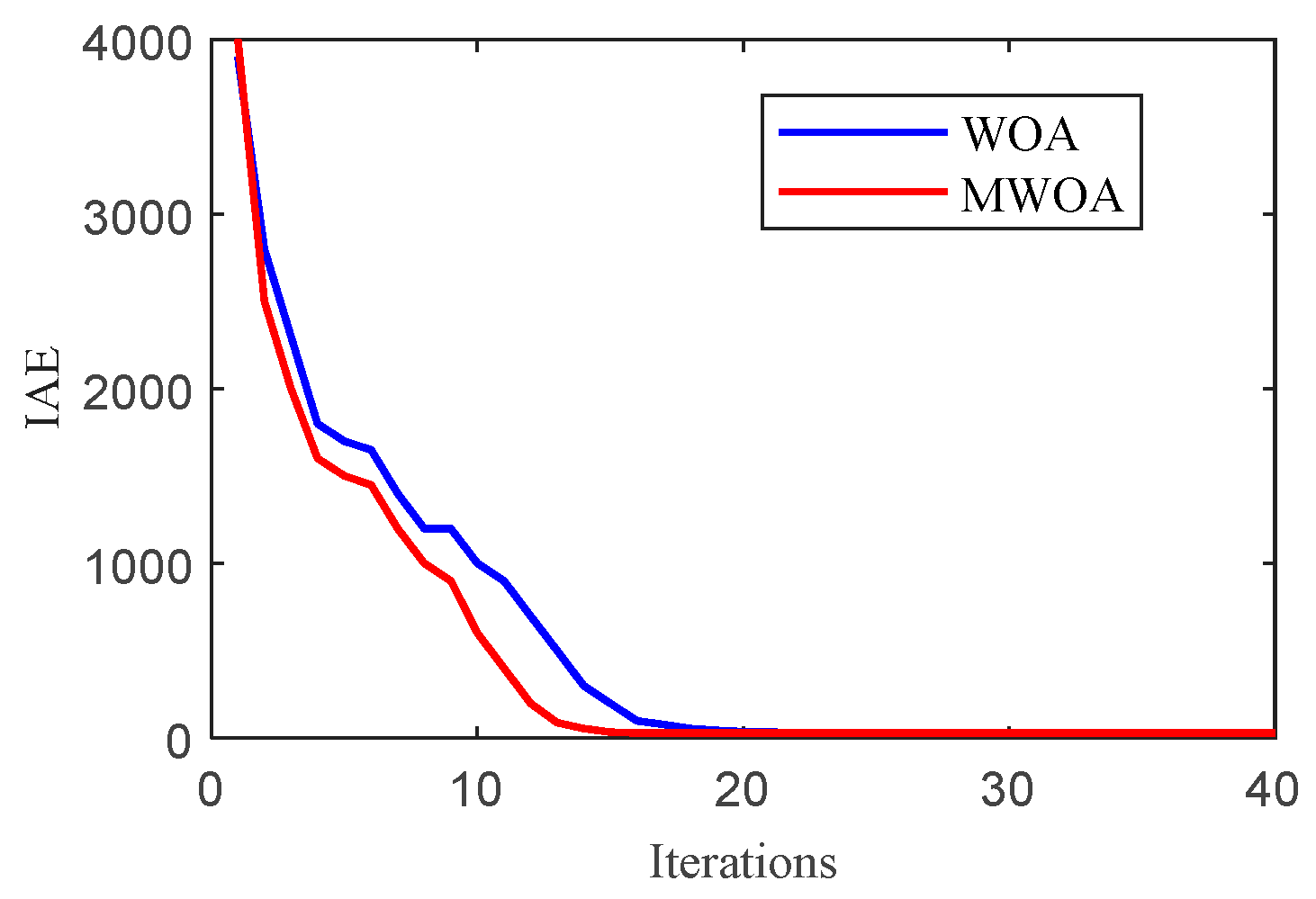
4. Modified Whale Optimization Algorithm with Sensitivity Constraint for MADRC
- 1.
- Heuristic probability
- 2.
- Linear control parameter
- 3.
- Lévy flight strategy
- 4.
- Elementary knowledge-acquisition-sharing algorithm
- 5.
- Position update method based on correction spiral
- 6.
- Quadratic interpolation method
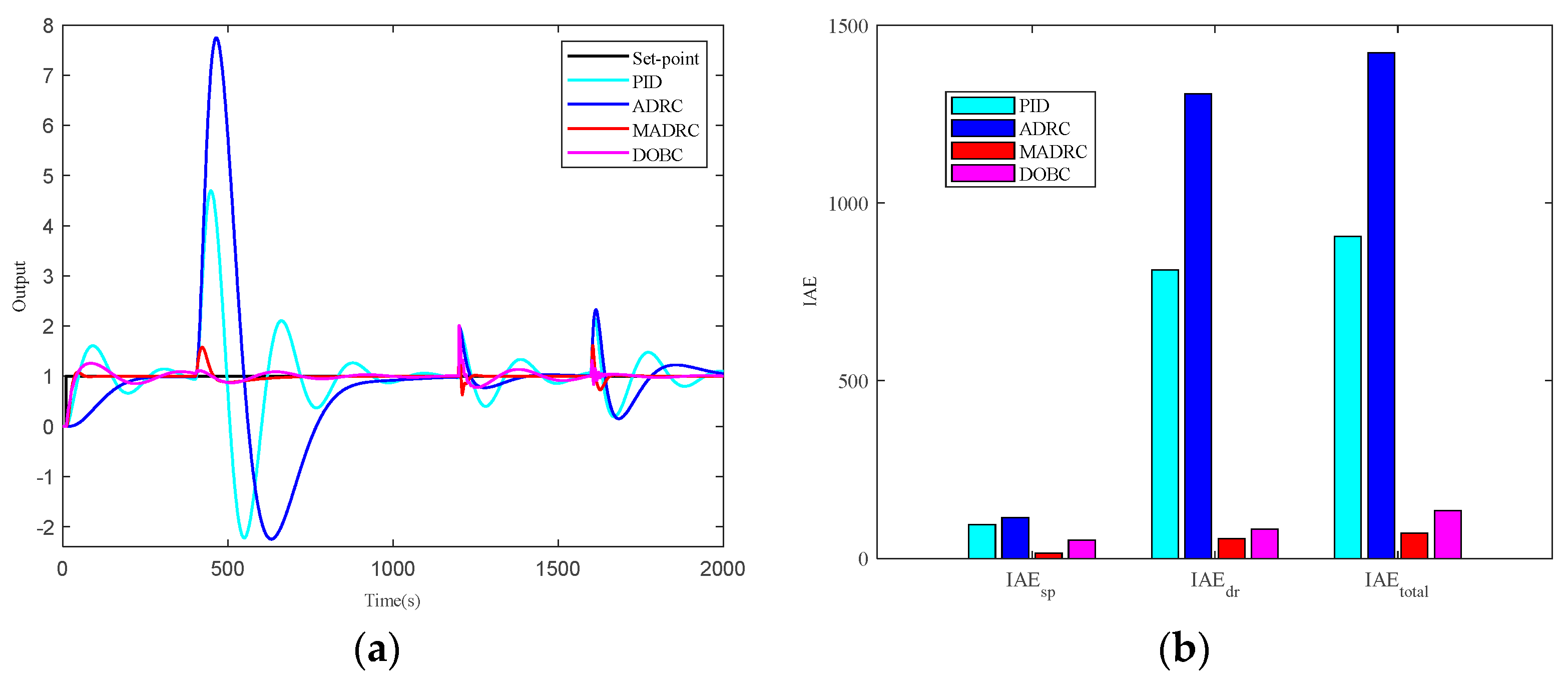
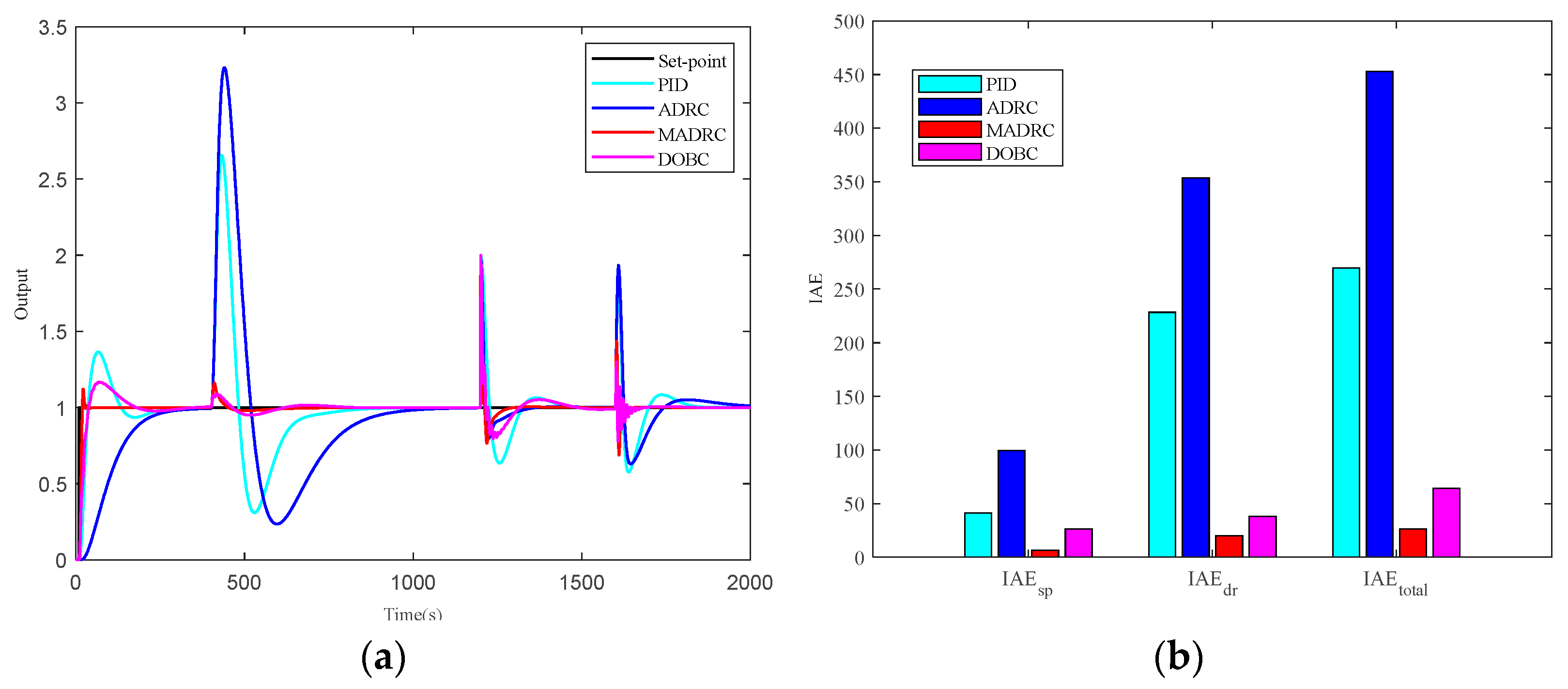
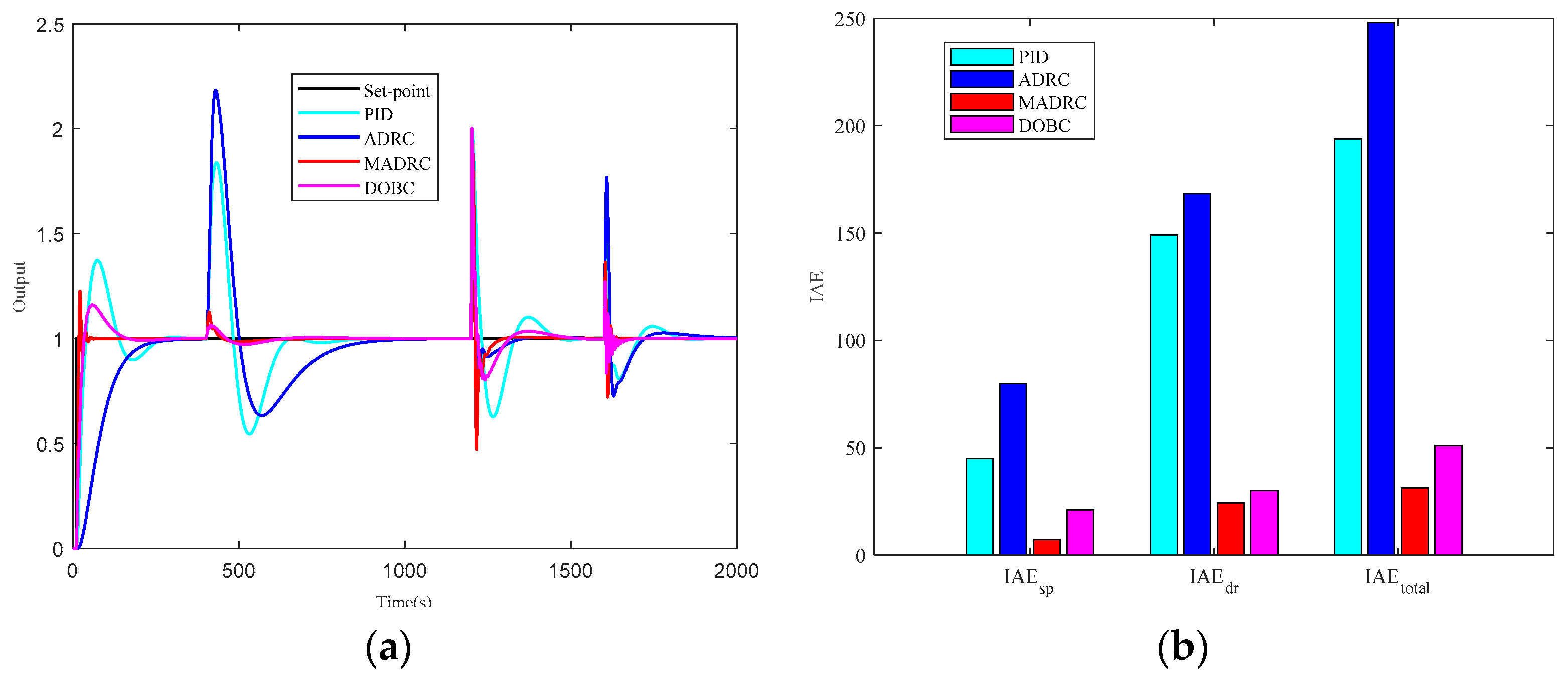
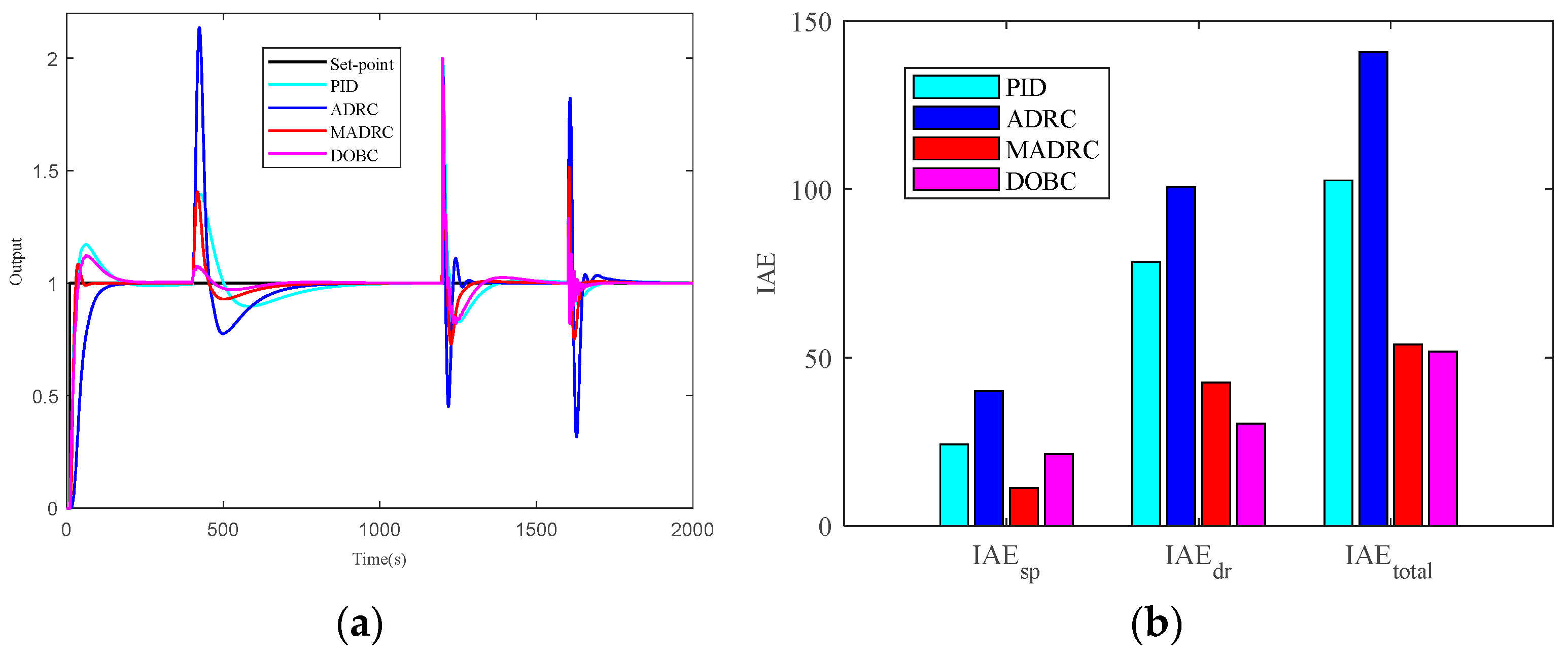
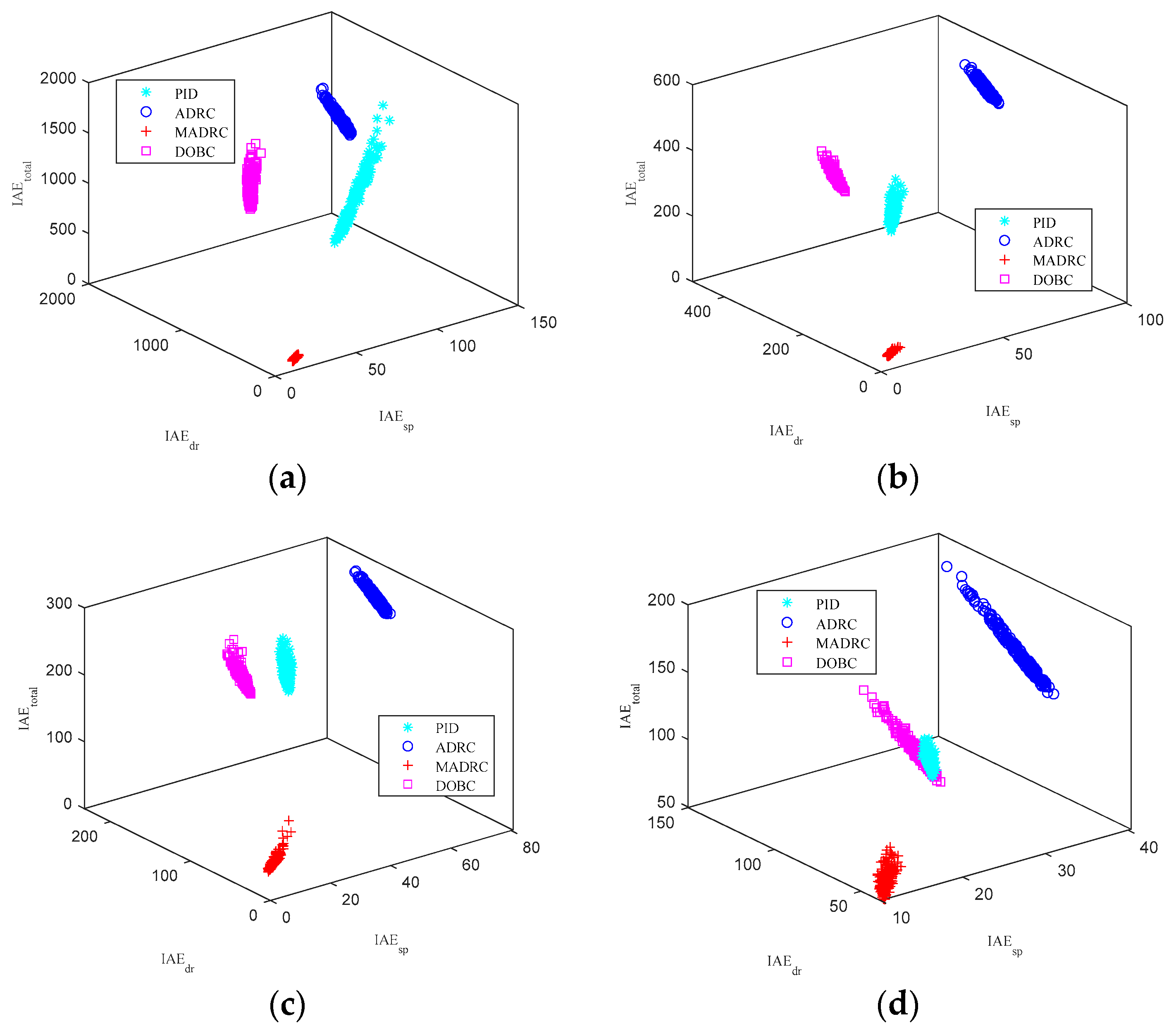
5. Simulation Illustrations
5.1. Scenario 1: Fixed Sensitivity Constraint
5.2. Scenario 2: Sensitivity Constraint with a Range
5.3. Scenario 3: Uncertain Systems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arpit, S.; Das, P.K. A state-of-the-art review of heat recovery steam generators and waste heat boilers. Energy Effic. 2023, 16, 99. [Google Scholar] [CrossRef]
- Moradi, H.; Saffar-Avval, M.; Bakhtiari-Nejad, F. Sliding mode control of drum water level in an industrial boiler unit with time varying parameters: A comparison with H∞-robust control approach. J. Process Control 2013, 22, 1844–1855. [Google Scholar] [CrossRef]
- Xiao, B.; Xie, A.; Xiao, M.; Zhou, M.; Su, S.; Xiao, Z.; Li, X. Optimal design of boiler drum water level control system. In Proceedings of the Third International Conference on Mechanical, Electronics, and Electrical and Automation Control (METMS 2023), Hangzhou, China, 17–19 February 2023. [Google Scholar] [CrossRef]
- Thampi, M.S.P.; Raghavendra, G. Intelligent model for automating PID controller tuning for industrial water level control system. In Proceedings of the 2021 International Conference on Design Innovations for 3Cs Compute Communicate Control (ICDI3C), Bangalore, India, 10–11 June 2021. [Google Scholar] [CrossRef]
- Liu, J.; Sun, W.; Zhang, S. Particle swarm optimization-based PID control of drum water level. Comput. Eng. App. 2009, 45, 239–241. [Google Scholar]
- Zhao, X. Chaos optimization strategy on fuzzy adaptive PID control of boiler drum water level. In Proceedings of the Annual Conference of China-Institute-of-Communications, Guangzhou, China, 26 November 2009. [Google Scholar]
- Liu, C.; Chen, M. Research on fuzzy PID control of boiler drum water level. J. Eng. Therm. Energy Power 2021, 36, 100–105. [Google Scholar]
- Precup, R.E.; Nguyen, A.T.; Blazic, S. A survey on fuzzy control for mechatronics applications, Int. J. Syst. Sci. 2023, 55, 771–813. [Google Scholar] [CrossRef]
- Elhosseini, M.A.; El-din, A.S.; Ali, H.A.; Abraham, A. Heat recovery steam generator (HRSG) three-element drum level control utilizing fractional order PID and fuzzy controllers. ISA Trans. 2022, 122, 281–293. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Ahooghalandari, N.; Shadi, R.; Fakharian, A. Hinfinity robust control design for three-element industrial boiler supervisory system. In Proceedings of the 2022 8th International Conference on Control, Instrumentation and Automation (ICCIA), Tehran, Iran, 2–3 March 2022. [Google Scholar] [CrossRef]
- Moradi, H.; Bakhtiari-Nejad, F.; Saffar-Awal, M. Robust control of an industrial boiler system; a comparison between two approaches: Sliding mode control & H∞ technique. Energy Conv. Manag. 2009, 50, 1401–1410. [Google Scholar]
- Panda, S.K.; Subudhi, B. A review on robust and adaptive control schemes for microgrid. J. Mod. Power Syst. Clean Energy 2023, 11, 1027–1040. [Google Scholar] [CrossRef]
- Wu, Z.L.; Li, D.H.; Chen, Y.Q. Active Disturbance rejection control design based on probabilistic robustness for uncertain systems. Ind. Eng. Chem. Res. 2020, 59, 18070–18087. [Google Scholar] [CrossRef]
- Pu, C.P.; Ren, J.; Su, J.B. The sliding mode control of the drum water level based on extended state observer. IEEE Access 2019, 7, 135942–135948. [Google Scholar] [CrossRef]
- Aliakbari, S.; Ayati, M.; Osman, J.H.S.; Sam, Y.M. Second-order sliding mode fault-tolerant control of heat recovery steam generator boiler in combined cycle power plants. Appl. Therm. Eng. 2013, 50, 1326–1338. [Google Scholar] [CrossRef]
- Li, B.; Guo, F.; Jia, W.; Zhao, Q. Application research on grey generalized prediction control in boiler drum water level. Comput. Meas. Control 2010, 18, 370–406. [Google Scholar]
- Sun, L.F.; Li, J.C.; Zhao, X. Predictive control of drum water level based on ant colony optimization algorithm. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010. [Google Scholar]
- Urrea, C.; Paez, F. Design and comparison of strategies for level control in a nonlinear tank. Processes 2021, 9, 735. [Google Scholar] [CrossRef]
- Quan, Y.L.; Yang, X.H. A method for alarming water level of boiler drum on nuclear power plant based on BP neural network. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014. [Google Scholar]
- Panjapornpon, C.; Chinchalongporn, P.; Bardeeniz, S.; Makkayatorn, R.; Wongpunnawat, W. Reinforcement learning control with deep deterministic policy gradient algorithm for multivariable ph process. Processes 2022, 10, 2514. [Google Scholar] [CrossRef]
- Wu, Z.L.; Gao, Z.Q.; Li, D.H.; Chen, Y.Q.; Liu, Y.H. On transitioning from PID to ADRC in thermal power plants. Control Theory Technol. 2021, 19, 3–18. [Google Scholar] [CrossRef]
- Xue, W.C.; Huang, Y. Performance analysis of active disturbance rejection tracking control for a class of uncertain LTI systems. ISA Trans. 2015, 58, 133–154. [Google Scholar] [CrossRef]
- Gao, B.W.; Zheng, L.T.; Shen, W.; Zhang, W. A summary of parameter tuning of active disturbance rejection controller. Recent. Adv. Electr. Electron. Eng. 2023, 16, 180–196. [Google Scholar]
- Fareh, R.; Khadraoui, S.; Abdallah, M.Y.; Baziyad, M.; Bettayeb, M. Active disturbance rejection control for robotic systems: A review. Mechatronics 2021, 80, 102671. [Google Scholar] [CrossRef]
- Wu, Z.L.; Li, D.H.; Liu, Y.H.; Chen, Y.Q. Performance analysis of improved ADRCs for a class of high-order processes with verification on main steam pressure control. IEEE Trans. Ind. Electron. 2023, 70, 6180–6190. [Google Scholar] [CrossRef]
- Wu, Z.L.; He, T.; Li, D.H.; Xue, Y.L.; Sun, L.; Sun, L.M. Superheated steam temperature control based on modified active disturbance rejection control. Control Eng. Pract. 2019, 83, 83–97. [Google Scholar] [CrossRef]
- Wang, P.Y.; Zhang, C.R.; Zhu, L.K.; Wang, C.C. The research of improved active disturbance rejection control algorithm for particleboard glue system based on neural network state observer. Algorithms 2020, 12, 259. [Google Scholar] [CrossRef]
- Xu, F.R.; Chen, M.Q.; Liang, X.L.; Liu, W.S. PSO optimized active disturbance rejection control for aircraft anti-skid braking system. Algorithms 2022, 15, 158. [Google Scholar] [CrossRef]
- Wu, Z.L.; Liu, Y.H.; Li, D.H.; Chen, Y.Q. Multivariable active disturbance rejection control for compression liquid chiller system. Energy 2023, 262, 125344. [Google Scholar] [CrossRef]
- Pu, C.; Zhu, Y.; Su, J. Drum water level control based on improved ADRC. Algorithms 2019, 12, 132. [Google Scholar] [CrossRef]
- Wang, D.; Li, H.Y.; Xie, X.Y.; Liu, D.Y. Boiler drum water level control based on linear active disturbance rejection and gray correlation compensation. Control Eng. Appl. Inform. 2020, 22, 42–49. [Google Scholar]
- Hu, C.M.; Ren, J. Study and application of LADRC for drum water-level cascade three-element control. Electr. Power 2014, 47, 28–31. [Google Scholar]
- Sun, Y.J.; Wang, X.L.; Chen, Y.H.; Liu, Z.J. A modified whale optimization algorithm for large-scale global optimization problems. Expert Syst. Appl. 2018, 114, 563–577. [Google Scholar] [CrossRef]
- Astrom, K.J.; Panagopoulos, H.; Hagglund, T. Design of PI controllers based on non-convex optimization. Automatica 1998, 34, 585–601. [Google Scholar] [CrossRef]
- Wu, Z.L.; Li, D.H.; Xue, Y.L. A new PID controller design with constraints on relative delay margin for first-order plus dead-time systems. Processes 2019, 7, 713. [Google Scholar] [CrossRef]
- Gao, Z.Q. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]


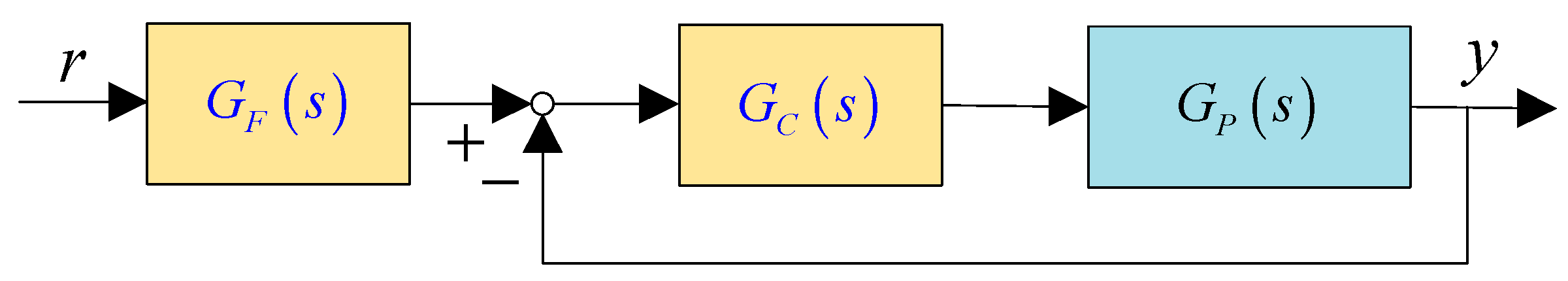



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, A.; Cui, X. Active Disturbance Rejection Control Design with Sensitivity Constraint for Drum Water Level. Energies 2024, 17, 1438. https://doi.org/10.3390/en17061438
Gao A, Cui X. Active Disturbance Rejection Control Design with Sensitivity Constraint for Drum Water Level. Energies. 2024; 17(6):1438. https://doi.org/10.3390/en17061438
Chicago/Turabian StyleGao, Aimin, and Xiaobo Cui. 2024. "Active Disturbance Rejection Control Design with Sensitivity Constraint for Drum Water Level" Energies 17, no. 6: 1438. https://doi.org/10.3390/en17061438
APA StyleGao, A., & Cui, X. (2024). Active Disturbance Rejection Control Design with Sensitivity Constraint for Drum Water Level. Energies, 17(6), 1438. https://doi.org/10.3390/en17061438






