A Distributed Multi-Timescale Dispatch Strategy for a City-Integrated Energy System with Carbon Capture Power Plants

Abstract

In city-integrated energy systems containing electric–thermal multi-energy sources, the uncertainty of renewable energy sources and the fluctuation of loads challenge the safe, efficient, economic and stable operation of the integrated energy systems. This paper introduces a novel approach for the operation of a carbon capture plant/CHP with PV accommodation within a city-integrated energy system. The proposed strategy aims to maximize the utilization of photovoltaic (PV) power generation and carbon capture equipment, addressing issues related to small-scale CHP climbing constraints and short-term output regulation. Additionally, this paper presents a multi-timescale optimal scheduling strategy, which effectively addresses deviations caused by PV fluctuations and load changes. This was achieved through a detailed analysis of the CHP climbing constraints, carbon capture equipment operation and real-time characteristics of PV power generation. This paper introduces a fully distributed neural dynamics-based optimization algorithm designed to address multi-timescale optimization challenges. Utilizing rolling cycles, this algorithm computes both day-ahead and real-time scheduling outcomes for urban integrated energy systems. Theoretical analyses and numerical simulations were conducted to validate the precision and efficacy of the proposed model and algorithm. These analyses quantitatively evaluate the scheduling performance of PV power generation and carbon capture CHP systems across various timescales.

1. Introduction

Energy is an important basis for supporting social life, economic development, and scientific and technological innovation. The economic dispatch problem in city-integrated energy systems pertains to the strategic management and scheduling of multiple energy resources. Currently, the requirements of the modern energy industry imply not only increasing the capacity and efficiency of energy production, but also minimizing harmful emissions into the atmosphere. It has become crucial to increase the proportion of renewable energy sources, reduce carbon emissions from power plants and improve the efficiency of energy conversion. Low-carbon power generation utilizing carbon capture systems combined with photovoltaics has received widespread attention [1,2,3]. Meanwhile, figuring out how to effectively deal with the coupling of attributes and timescales between different energy types and different equipment has become a new challenge.

Photovoltaic (solar) energy is one of the most environmentally friendly ways of generating electricity by utilizing solar panels to convert sunlight directly into electricity. With no harmful emissions during the power generation process, photovoltaics plays a crucial role in mitigating climate change and reducing carbon emissions. As of the close of 2021, China’s installed PV capacity surpassed 250 gigawatts, solidifying its status as the globe’s foremost producer of PV power [4]. For several years, China has maintained a leadership role in the global PV market, actively fostering the growth and utilization of PV power generation. This form of energy generation has emerged as a pivotal component in China’s transition to a more diverse energy mix. In some cases, the power generated by PV power generation installations exceeds the load demand of the system, resulting in part of the PV power not being absorbed by the system and ultimately being discarded [5]. Regarding scheduling, the inherent uncertainty and randomness associated with renewable energy sources contribute to increased instability within the energy network. This instability often results in significant levels of unused or abandoned wind and photovoltaic power. To address this issue of renewable energy wastage, scholars globally have proposed a variety of solutions, each offering unique perspectives and approaches. Some scholars [6,7] proposed a coordinated operation strategy for an off-grid combined wind and PV power generation system, where excess wind and PV power is used to make hydrogen. Ref. [8] proposed a PV consumption method based on voltage sensitivity to reduce the impact of PV fluctuations on the grid by regulating the control parameters of the inverter. In terms of optimal scheduling, some scholars [9] established a robust optimal scheduling model for wind power in response to the impact of wind power prediction errors on the network, which improved the utilization of wind power. Ref. [10] also addressed the uncertainty of photovoltaics and gave an operating cost function for photovoltaic power generation based on confidence intervals and error compensation, so that photovoltaic and fuel power plants could participate in optimal scheduling at the same time. Ref. [11] incorporated renewable energy into electric boilers and introduced a multi-timescale optimal scheduling method for electric power and district heating systems. This method emphasizes the thermal comfort of users, enhancing the integration of the energy system while ensuring heating demands are met. Furthermore, ref. [12] discussed optimal dispatch through price and penalty mechanisms, constructing a multi-timescale optimization model specifically for wind power. Additionally, refs. [13,14,15] each developed a rolling coordinated dispatch model that analyzed the role of renewable energy in demand response. Ref. [16] used dynamics programming to implement day-ahead scheduling for a sustainable residential micro-cogeneration system. This analysis took into account the uncertainty of renewable energy and the prediction error across different timescales, namely day-ahead, intraday and real-time. These studies collectively highlight that, beyond expanding renewable energy application scenarios, multi-timescale optimal scheduling strategies can significantly enhance the utilization of renewable energy.

With the growing concern for environmental protection and sustainable development, reducing carbon emissions has become an important goal on a global scale [17]. The operation and scheduling of integrated energy systems need to consider how to minimize carbon emissions, including by increasing the proportion of renewable energy sources, improving the efficiency of energy use and adopting clean energy technologies. Carbon capture and storage (CCS) is a key technology for capturing carbon dioxide produced in industrial processes. CCS reduces the concentration of greenhouse gases in the atmosphere by storing carbon in underground repositories through a series of steps. This technology plays an important role in mitigating climate change and is considered one of the solutions to the global carbon emission challenge. Currently, CCS equipment is often used in conjunction with energy production equipment in integrated urban energy systems to reduce carbon emissions and increase the utilization of renewable energy.

In the realm of carbon capture equipment application, contemporary research predominantly concentrates on analyzing its low-carbon attributes and carbon removal efficiency. There is limited utilization of such equipment in enhancing renewable energy usage. However, ref. [18] delineated that the high-power capacity and rapid regulation capability of carbon capture devices are effectively instrumental in mitigating prediction errors associated with renewable energy sources. Consequently, these devices emerge as ideal auxiliary power sources or payloads for photovoltaic power generation, offering a synergistic approach to harnessing renewable energy more efficiently. According to ref. [19], fuel-fired power plants containing carbon capture equipment can reduce the efficiency of carbon removal in real time, improving grid fluctuations and increasing the utilization of wind power. Ref. [20] provided an analytical exploration of the interplay between the environmental benefits of decarbonization and the operational costs of relevant equipment. This analysis incorporated the operational characteristics of carbon capture equipment, wind power and a CHP within the energy system framework. This integrative approach facilitates a nuanced understanding of the cost–benefit dynamics in the pursuit of decarbonization and sustainability in energy systems. Ref. [21] provided a coordinated operation scheme for renewable energy and carbon capture-containing power plants through a day-ahead–real-time two-stage optimal dispatch model. Ref. [22] quantified the risk of load shedding and power limitation based on probability-distributed conditional risk values, which reduce the operational risk under the multi-timescale dispatch of renewable energy. The above study found that the fluctuation in renewable energy in a power grid can be effectively mitigated by the high load and high-speed regulation capability of carbon capture equipment. However, with the current stage of integrated energy optimization and scheduling methods gradually shifting from being centralized to distributed, there is no effective distributed optimization strategy to regulate renewable energy and carbon capture equipment operation status.

This paper proposes an operation strategy for a carbon capture CHP system that accommodates PV power generation, aiming to enhance the utilization of solar energy. Additionally, it delves into the energy scheduling challenges of an integrated energy system across multiple timescales, employing a distributed optimization approach.

The primary contributions of this study are the following:

• Considering the characteristics of a city-integrated energy system and the working mode of a carbon capture CHP, a carbon capture CHP operation strategy with PV accommodation is proposed. It makes full use of PV power generation and carbon capture equipment to make up for the problems of small CHP climbing constraints and the difficulty of adjusting a short-time output. At the same time, it effectively reduces the abandoned PV and maximizes social welfare.
• A multi-timescale optimal scheduling strategy is proposed by analyzing the climbing constraint limit of a CHP, the working process of carbon capture equipment and the real-time characteristics of PV power generation. Based on the optimization results of the previous day, the deviation problems caused by PV fluctuations and load changes are adjusted intraday.
• A fully distributed neural dynamics optimization algorithm is proposed for solving the multi-timescale optimization problem presented in this paper. It employs a rolling cycle approach to compute both day-ahead and real-time scheduling for an urban integrated energy system. The algorithm’s efficacy was substantiated through rigorous theoretical analysis and comprehensive simulation experiments, confirming its accuracy and effectiveness.

In Section 2, we analyzed the working mode of the carbon capture CHP and propose a carbon capture CHP operation strategy with PV accommodation. The system optimization process in multiple timescales was also analyzed. Section 3 gives the cost model of the infrastructure equipment in the city-integrated energy system. A neural dynamics optimization algorithm is also proposed, and the proof of convergence and optimality is given. Section 4 verifies the accuracy of the model and algorithm through simulation experiments. Section 5 summarizes the main contents of this paper.

2. A Carbon Capture Plant/CHP Operation Strategy with PV Accommodation

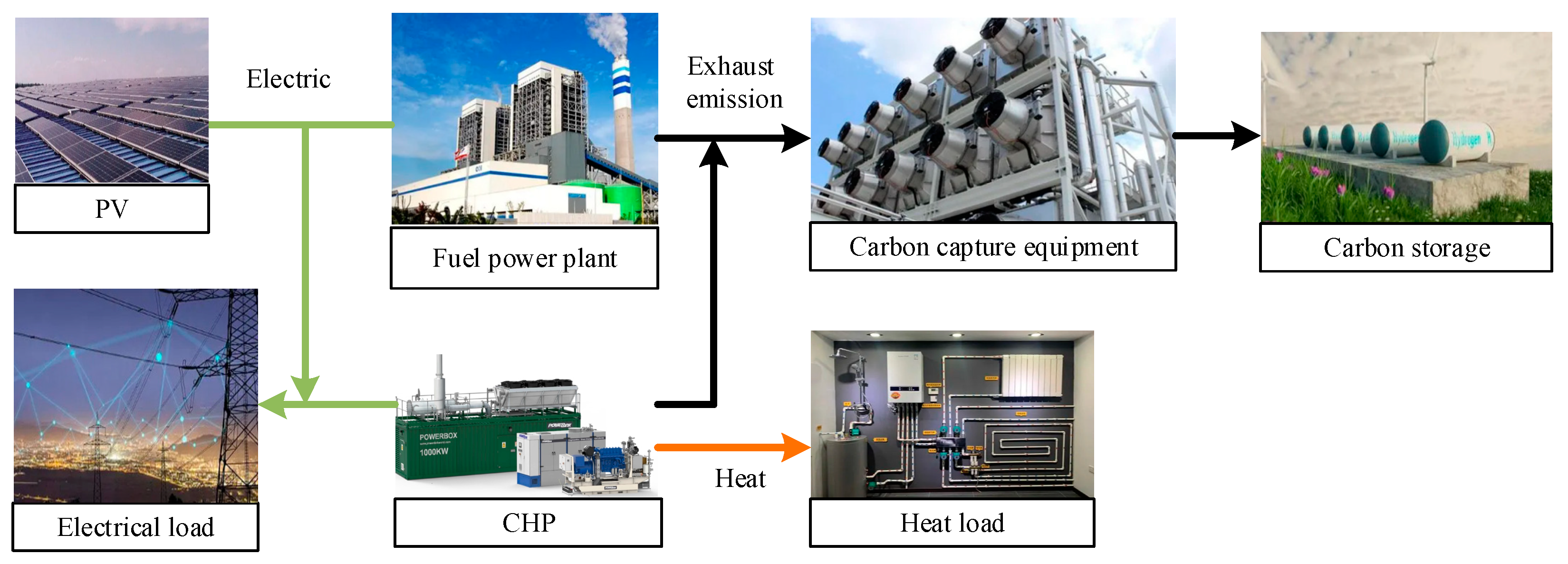
Carbon capture CHP equipment is a decarbonization modification of traditional fuel-fired power plants and cogeneration equipment, to reduce the high concentration of carbon tail gas emissions from the equipment and achieve the purpose of reducing the system’s carbon emissions. The carbon capture plant/CHP with PV accommodation operation process proposed in this paper is shown in Figure 1.

City power and heat supply are mainly created by fuel power plants, PV power plants and CHPs. Carbon capture equipment can be installed at the tail end of fuel power plants and CHP equipment, which reduces a large amount of carbon emissions for the equipment. In addition to exporting electricity to the outside world, fuel-fired power plants and CHPs also deliver a portion of their electricity and exhaust gases to carbon capture devices, which are used to reduce carbon emissions. Therefore, the net power output of fuel-fired power plants and CHPs with carbon capture is equal to the output of the energy-producing equipment minus the energy consumption of the carbon capture equipment. This type of energy transfer allows the capture device to be considered as an internal adjustable load for the fuel power plant and CHP. When system demand decreases, the excess output of the capacity plant is shared. When system demand increases, the amount of carbon capture is reduced and prioritized to ensure a balance between supply and demand. With this capacity management strategy, the impact of capacity equipment subject to creep constraints can be reduced. The access to PV power further improves the capacity equipment’s ability to respond to transient changes. It can namely supply energy to the carbon capture equipment and directly connect to the grid. Meanwhile, the linear adjustable characteristic of carbon capture equipment can also effectively improve the volatility of PV power generation.

Further, the integration of carbon capture systems and photovoltaic power generation can be viewed as creating an integrated power plant that fully utilizes the clean performance of photovoltaic power generation and the fact that carbon capture devices can capture carbon dioxide produced by other conventional power plants. This integration can enhance the utilization of renewable energy, radically reduce CO₂ emissions and lower the environmental impact of carbon emissions. In addition, the electricity market can optimize the cost of electricity production by reducing the cost of carbon credits and incentivizing customers to use solar resources.

2.1. An Analysis of Carbon Capture Devices

Carbon capture equipment plays a crucial role in the regulation of power plants and CHP systems by facilitating rapid energy output adjustments. The fast regulation capability of carbon capture devices allows them to function as adjustable loads, effectively consuming energy to regulate the net production of fuel power plants and CHP systems. This, in turn, enhances the power output adjustment rate of capacity equipment. The carbon capture CHP follows the law of conservation of energy and its operation is modeled as the following:

$$P^{\mathit{chp}}=P^{chpe}+P^c+P^d$$

(1)

$$P^c={\lambda }^c{E}^{{co}_2}$$

(2)

$$E^{{co}_2}={\theta }^c{\delta }^c{C}^g{P}^{\mathit{chp}}$$

(3)

$$e_m{P}^{chp}+f_m{H}^{chp}+z_m\ge 0,(m=1,2,3,4)$$

(4)

where $P^{chp}$ and $H^{chp}$ are the electrical and thermal output of the CHP, respectively; $P^{chpe}$ is the net electrical power output of the CHP; $P^c$ is the energy consumption of the carbon capture equipment, which is the key to regulating the net output of capacity devices; $P^d$ is the fixed operating load; ${\lambda }^c$ is the energy consumption per unit of carbon captured; $E^{{co}_2}$ is the mass of CO₂ captured; ${\theta }^c$ is the carbon capture efficiency; $C^g$ is the amount of CO₂ released from the unit of electricity produced; ${\delta }^c$ is the flue gas split ratio; and $e_{i,m}$, $f_{i,m}$ and $z_{i,m}$ are the coefficients for linear inequality constraints, which are used to compose the inequality box constraints for the CHP. In this paper, since fuel-fired power plants differed from the CHP only in their cost function and box constraints, the CHP plant was mainly taken as an example when analyzing the operational status of a carbon capture plant. As shown in Equations (1)–(4), the net electric output power and gross output power of the CHP are the following:

$$P^e=(1-C^g{\delta }^c{\lambda }^c{\theta }^c)P^{chp}-P^d$$

(5)

From this, it can be seen that the CHP with carbon capture equipment has a lower net lower output limit, which allows for lower power supply or even zero-output operation. In terms of energy, because of the use of carbon capture devices, the lower net output lower limit of the CHP can enable more PV power to be consumed: when the total load is suddenly reduced, PV power generation feeds carbon capture devices, i.e., it effectively realizes PV consumption and avoids a wide range of adjustment of the CHP’s output. The carbon capture device, functioning as a significant controllable load, can be conceptualized as an auxiliary energy source. In instances of abrupt electrical load surges, the energy consumption of these devices can be curtailed or temporarily halted to prioritize meeting the emergent load requirements. However, this adjustment may lead to an increase in the carbon emissions generated by the CHP system.

Regarding temporal dynamics, the modulation rate of carbon capture CHP systems is intricately linked to the energy acquisition method of the carbon capture device. This device’s operational state can be altered by varying the vapor absorption rate, integrating a photovoltaic power supply and modulating the volume of carbon sequestered. These adjustments collectively influence the net power output of the CHP system. Compared with the traditional CHP response time of 5–10 min, the response time of a carbon capture-containing CHP can be within 5 min. Moreover, for a 5 min PV forecast, conventional fuel-fired power plants and CHPs cannot realize a fast response, while power plants and CHPs with carbon capture equipment can meet this requirement. This coordinated energy supply method can simultaneously satisfy the fast response of energy and increase the utilization of PV power generation.

2.2. A Rapid Regulation Volume Analysis of a Carbon Capture CHP

The net output power range of the CHP system is expanded due to the rapid adaptability in the energy consumption of carbon capture equipment and the diversification of its energy supply methods. The details are the following:

$$\Delta P^{chp,up}=P^c$$

(6)

$$\Delta P^{chp,low}=P^{c\max }-P^c+P^{\mathrm{c}pv}$$

(7)

where $\Delta P^{chp,up}$ is the maximum value at which the carbon capture CHP can upregulate the power output in real time; $\Delta P^{chp,low}$ is the maximum value at which the carbon capture CHP can adjust the power output downward in real time; $P^{c\max }$ is the maximum operational energy consumption of the carbon capture device; and $P^{\mathrm{c}pv}$ is the power of the PV connected to the carbon capture device. Therefore, the net output electric power of the CHP can be expressed as the following:

$$\Delta P^{chp,up}=C^g{\delta }^c{\lambda }^c{\theta }^c{P}^{chp}$$

(8)

$$\Delta P^{chp,low}=P^{c\max }+P^{\mathrm{c}pv}-C^g{\delta }^c{\lambda }^c{\theta }^c{P}^{chp}$$

(9)

From the above equation, it can be seen that the regulation range of the net electric power output of the CHP is related to the PV power access and the total CHP power generation. In turn, the regulation range of the real-time net electric power output of the CHP with carbon capture can be obtained as the following:

$$P^{c\max }+P^{\mathrm{c}pv}-C^g{\delta }^c{\lambda }^c{\theta }^c{P}^{chp}\le P^{chpe}\le C^g{\delta }^c{\lambda }^c{\theta }^c{P}^{chp}$$

(10)

Since the lower limit of the net electric power output of the CHP is related to the amount of PV power access, to ensure real-time PV power consumption, it is necessary to adjust the value of the flue gas diversion ratio ${\delta }^c$ in real time according to the short-term PV power forecast value. Assuming that the total load remains unchanged, there is a case of deviation in the PV generation forecast value. When the real-time PV power generation increases, the traditional CHP without carbon capture equipment is unable to reduce the electric power output quickly, which leads to discarding part of the PV power generation. A carbon capture CHP can increase the flue gas split ratio, which in turn increases the energy consumption of the carbon capture equipment and reduces the net electrical power output of the carbon capture CHP. This in turn increases the amount of PV connected to the grid and reduces the amount of discarded PV.

2.3. Device Operating Cost Modeling

The cost function and local operation constraints for the combined heat and power (CHP) units are expressed as the following [23]:

$$C(p_i^{chp},h_i^{chp})=a_i{(p_i^{chp})}^2+b_i{p}_i^{chp}+{\alpha }_i{(h_i^{chp})}^2+{\beta }_i{h}_i^{chp}+c_i{p}_i^{chp}{h}_i^{chp}+d_i,$$

(11)

$$e_{i,m}{p}_i^{chp}+f_{i,m}{h}_i^{chp}+z_{i,m}\ge 0,(m=1,2,3,4),$$

(12)

$$-p_i^{chp,ramp}\le p_i^{chp}(t+1)-p_i^{chp}(t)\le p_i^{chp,ramp},$$

(13)

In this model, $p_i^{chp}$ and $h_i^{chp}$ represent the power and heat outputs of the $i$-th CHP units, while $a_i$, $b_i$, ${\alpha }_i$, ${\beta }_i$, $c_i$ and $d_i$ are part of the cost function, which is related to the hard metrics of the equipment. Because the CHP is a dual-energy coupled device, it is subject to both electrical and thermal constraints. Therefore, the capacity constraints of the CHP are not the upper and lower limits, but box constraints. The values $e_{i,m}$, $f_{i,m}$ and $z_{i,m}$ are the coefficients for linear inequality constraints, and $p_i^{chp,ramp}$ denotes the ramp rate.

Distributed fuel generators (DFGs) utilize the heat from burning flammable substances to heat and pressurize liquid water, converting it into water vapor. The steam drives a turbine connected to a generator, producing electricity. Thermal power plants are a common type of power generation facility due to their ability to provide large amounts of electricity consistently. In order to address and investigate the ramping rate constraints of distributed fuel generators, the discrete version is often reformulated as a knapsack problem [24]. The cost function of a DFG is the following:

$$C(p_i^{fg})=a_i{(p_i^{fg})}^2+b_i{p}_i^{fg}+c_i,$$

(14)

$$p_i^{fg,\min }\le p_i^{fg}\le p_i^{fg,\max },$$

(15)

$$-p_i^{fg,ramp}\le p_i^{fg}(t+1)-p_i^{fg}(t)\le p_i^{fg,ramp},$$

(16)

where $p_i^{fg}$ is the power outputs of $i$-th traditional power plants; $a_i$, $b_i$ and $c_i$ are the non-negative constants; $p_i^{fg,\min }$ and $p_i^{fg,\max }$ are the minimum and maximum power plants outputs, respectively; and the positive constant $p_i^{fg,ramp}$ serves as the ramp rate constraint, signifying the need for the DFG to remain within a specific range in order to regulate the rate of generation over time.

Photovoltaic power generation is a technology that utilizes solar energy to generate electricity by converting sunlight into electricity through solar panels. A solar panel consists of photovoltaic cells, which generate a photovoltaic voltage when sunlight hits the panel, and converts solar energy into direct current electrical energy. Photovoltaic power generation is a renewable energy source that is environmentally friendly and sustainable. In order to add PV to the economic dispatch problem, we used forecasting techniques to obtain an approximation of how the PV was likely to be generated. The prediction mean was derived from the day-ahead prediction curves provided in [25], which were used as a reference for each dispatch level.

$$p_{i,t}^{PV,f}=\frac{1}{T}{\displaystyle {\int }_t^{t+T}{p}_{i,\tau }^{PV,f}}d\tau$$

(17)

where $p_{i,t}^{PV,f}$ is the forecasting output of $i$-th PV at time $t$ and $T$ is the forecast period. Due to the existence of prediction error, the true output value of the PV may fluctuate up and down from the predicted value. Therefore, we assume that the PV error obeys a Gaussian distribution [21]. We then define the effective confidence interval of the PV as $\left[{\overline{p}}_{i,t}^{PV},{\underset{\_}{p}}_{i,t}^{PV}\right]$, where ${\underset{\_}{p}}_{i,t}^{PV}=p_{i,t}^{PV}-3\sigma$ and ${\overline{p}}_i^{PV}=p_{i,t}^{PV}+3\sigma$. The cost function of the PV is modeled based on the previous discussion and the characterization of the Gaussian distribution as the following:

$$C(p_{i,t}^{PV})=a_i{p}_{i,t}^{PV}-b_i\exp (c_i\frac{{\overline{p}}_{i,t}^{PV}-p_{i,t}^{PV}}{p_{i,t}^{PV}-{\underset{\_}{p}}_{i,t}^{PV}})$$

(18)

where $a_i$, $b_i$ and $c_i$ are the non-negative constants. The first item pertains to the operation and maintenance cost of the PV, while the second item involves compensating for PV generation uncertainty. The compensation term increases as the prediction results become more inaccurate. In photovoltaic systems, Gaussian distribution is usually used to describe the change pattern of photovoltaic power generation. Therefore, a function similar to the Gaussian distribution is used to describe the cost of PV power generation. This description is consistent with the trend of temperature, irradiance and the variation in PV power generation.

Carbon capture equipment is a technological device used to capture and store carbon dioxide. It is commonly used in industrial processes to capture emitted carbon dioxide and store it underground or elsewhere to reduce emissions to the atmosphere. Carbon capture devices help to reduce greenhouse gas emissions and are important for combating climate change and mitigating global warming. We consider that the operating cost of carbon capture equipment is proportional to the flue gas split ratio and the power output of the CHP, which is modeled as the following:

$$C(p_i^{\mathrm{c}})=a_i^c{\delta }^{\mathrm{c}}{p}_i+b_i^c,$$

(19)

$$p_i^{\mathrm{cmin}}\le p_i^{\mathrm{c}}\le p_i^{\mathrm{cmax}}$$

(20)

where $p_i^{\mathrm{cmin}}$ and $p_i^{\mathrm{cmax}}$ are the maximum and minimum energy consumption of the carbon capture device, respectively, and $a_i^c$ and $b_i^c$ are the cost coefficients.

2.4. Multi-Timescale Optimization

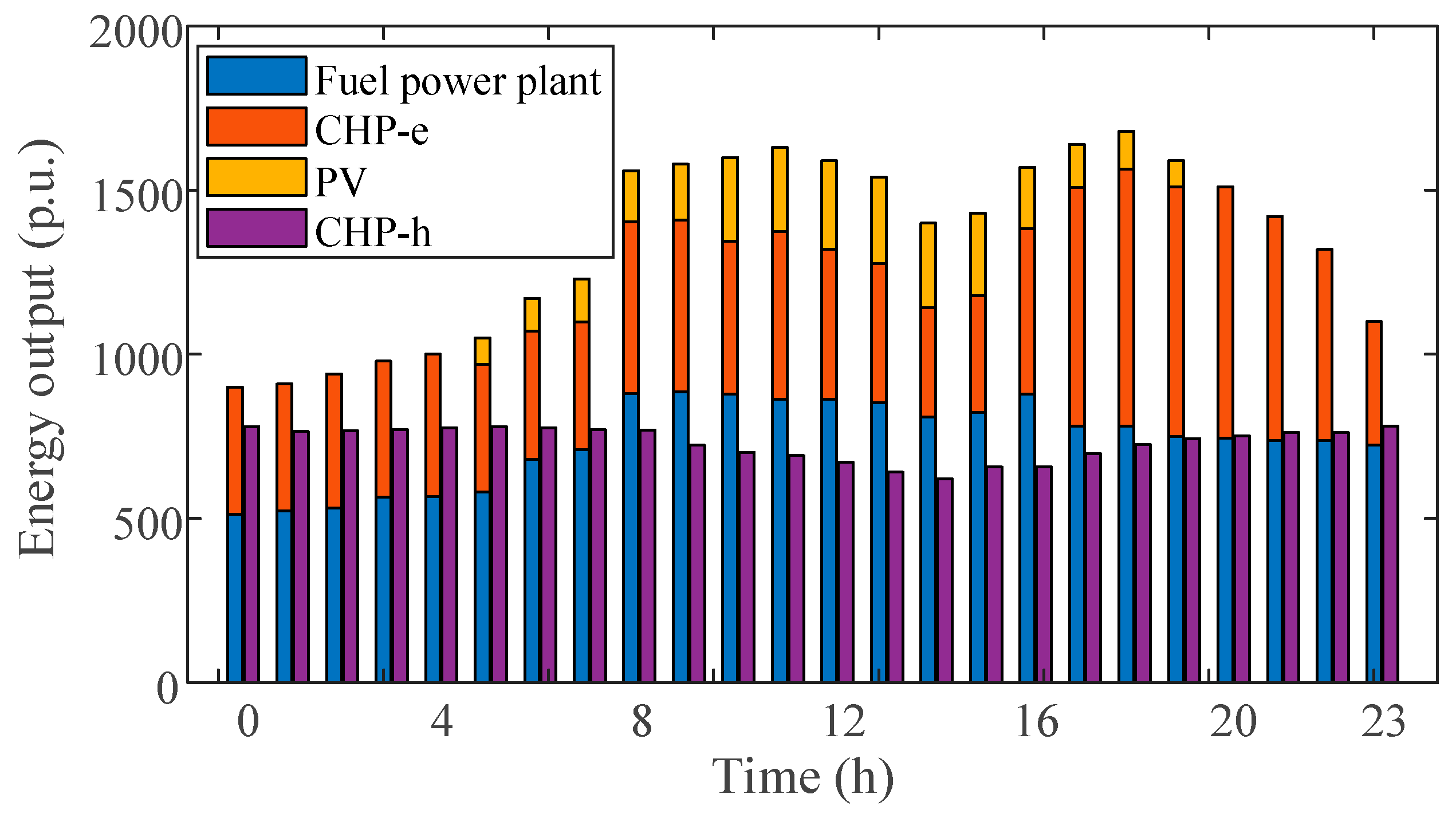
In response to the challenges posed by the large-scale integration of renewable energy sources, traditional day-ahead single dispatch methods fall short of ensuring the economic and safe operation of integrated energy systems. This paper introduces a novel three-phase dispatch approach that spans day-ahead, intraday and real-time periods, offering a multi-timescale solution tailored to the specific characteristics of carbon capture devices and PV power generation.

The scheduling model fully considers the energy output method of a carbon capture CHP, so that it has a wider regulation range and a faster regulation rate. Among them, the deeper regulation range can be involved in the consumption of abandoned light in the intraday scheduling before the day, while the faster regulation rate can be used to consume abandoned light in the real-time scheduling. To mitigate the impact of the predetermined flue gas diversion ratio on real-time scheduling, this study introduces a strategy that imposes constraints on the flue gas diversion ratio during the pre-day-ahead scheduling stage. To summarize, this is the three-phase scheduling strategy of this paper, i.e., day-ahead-intraday-real-time scheduling. First, day-ahead scheduling specifies the energy output plan for the subsequent 24 h in advance, with large deviations in all renewable generation and load forecasts. Intraday dispatch allows corrections to be made to the output of the capacity plant for the next 4 h based on the load changes at this stage. Real-time dispatch is based on 5–15 min ultra-short-term forecasts, with real-time attention to load changes and PV generation fluctuations. The net output of fuel power plants and CHP systems can be rapidly modulated by regulating the energy consumption of carbon capture equipment. The multi-timescale scheduling intervals of the integrated energy system are shown in Figure 2.

2.4.1. Day-Ahead Dispatch

Day-ahead dispatch of an integrated energy system is the process of scheduling and managing the energy of various energy facilities (e.g., solar, wind, conventional thermal, storage facilities, etc.) in an energy system over the next few days or the coming week. This approach is designed to ensure the efficient utilization of energy resources, maintain the safety and stability of the system, and maximize economic benefits. The day-ahead dispatch strategy was formulated with the primary objective of optimizing the welfare of the integrated urban energy system, specifically focusing on minimizing operational costs. The objective function and conventional constraints are the following:

$$\min Obj=f(p),$$

(21)

$$f(p)={\displaystyle {\sum }_1^n{C}_i(p_i^{pv})}+{\displaystyle {\sum }_1^m{C}_i(p_i^{fg})+}{\displaystyle {\sum }_1^q{C}_i(p_i^{chp},h_i^{chp})}+{\displaystyle {\sum }_1^w{C}_i(p_i^c)}$$

(22)

$$\mathrm{s}.\mathrm{t}. {\displaystyle {\sum }_{i=1}^{n+m+w+q}{p}_i}={\displaystyle {\sum }_{i=1}^{n+m+w+q}{d}_i^e},$$

(23)

$$P^e=(1-C^g{\delta }^c{\lambda }^c{\theta }^c)P^{chp}-P^d$$

(24)

$${\displaystyle {\sum }_{i=1}^q{h}_i^{chp}}={\displaystyle {\sum }_{i=1}^{n+m+w+q}{d}_i^h}$$

(25)

$$e_{i,m}{p}_i^{chp}+f_{i,m}{h}_i^{chp}+z_{i,m}\ge 0,(m=1,2,3,4),$$

(26)

$$h_i^{\mathit{chp},\min }\le h_i^{chp}\le h_i^{\mathit{chp},\max }$$

(27)

$$p_i^{\mathrm{cmin}}\le p_i^{\mathrm{c}}\le p_i^{\mathrm{cmax}}$$

(28)

$$p_i^{\min }\le p_i(t)\le p_i^{\max },$$

(29)

$$\left|p_i(t+1)-p_i(t)\right|\le p_i^{ramp},$$

(30)

where f(P) is the total operating cost of the system, and since the objective function $f(P)$ is obtained by summing the operating cost functions, $f(P)$ is linear, convex and satisfies the Lipschitz continuum; $n$, $m$, $q$ and $w$ are the numbers of PV, fuel-fired, CHP and carbon capture devices, respectively; $d_i^{\mathrm{e}}$ and $d_i^h$ are the electrical and thermal loads at each node, respectively; $p_i^{ramp}$ is the hill-climbing constraint for each device; $P_i^{\min }$ and $P_i^{\max }$ are the minimum and maximum outputs of the devices, respectively; and $h_i^{\mathit{chp},\max }$ and $h_i^{\mathit{chp},\min }$ are the maximum and minimum thermal power outputs of the CHP, respectively. The minimum start–stop time constraints for the fuel power plant and CHP are the following:

$$(T_{i,t-1}^{up}-T_{i,\min }^{up})(u_{i,t-1}-u_{i,t})\ge 0$$

(31)

$$(T_{i,t-1}^{down}-T_{i,\min }^{down})(u_{i,t-1}-u_{i,t})\ge 0$$

(32)

where $T_{t-1}^{up}$ and $T_{t-1}^{down}$ are the times when the fuel power plant and the CHP have been continuously turned on and off at the time period $t-1$; $T_{i,\min }^{up}$ and $T_{i,\min }^{down}$ are the minimum turn-on and turn-off times of the fuel power plant and the CHP; and $u_{i,t-1}$ and $u_{i,t}$ denote the start–stop state of the equipment at the time periods $t-1$ and $t$, respectively.

2.4.2. Intraday Dispatch

Intraday dispatch of an integrated energy system requires consideration of the characteristics and operating conditions of the various energy facilities, as well as real-time energy demand conditions. This includes rationalizing the use of PV and carbon capture equipment based on the day’s weather forecasts and load forecasts, in conjunction with fuel-fired power plants and CHPs to meet the system’s energy needs. The intraday scheduling of the integrated urban energy system does not consider the start and stop of the unit, but only the operating cost of the capacity equipment and the sudden change in the load, so the objective function is the following:

$$\min Obj=\stackrel{-}{f}(p),$$

(33)

$$\stackrel{-}{f}(p)={\displaystyle {\sum }_1^n{C}_i(p_i^{pv})}+{\displaystyle {\sum }_1^m{C}_i(p_i^{fg})+}{\displaystyle {\sum }_1^q{C}_i(p_i^{chp},h_i^{chp})}+{\displaystyle {\sum }_1^w{C}_i(p_i^c)}$$

(34)

$$\mathrm{s}.\mathrm{t}. P^e=(1-C^g{\delta }^c{\lambda }^c{\theta }^c)P^{chp}-P^d$$

(35)

$$h_i^{\mathit{chp},\min }\le h_i^{chp}\le h_i^{\mathit{chp},\max }$$

(36)

$$p_i^{\mathrm{cmin}}\le p_i^{\mathrm{c}}\le p_i^{\mathrm{cmax}}$$

(37)

$$p_i^{\min }\le p_i(t)\le p_i^{\max },$$

(38)

Unit startup and shutdown constraints are not considered during the day. Unit climb constraints and rotating standby constraints need to be adjusted due to the change in the timescale:

$$\left|p_i(t+1)-p_i(t)\right|\le p_i^{ramp}/4,$$

(39)

Due to the possibility of load imbalance, the load equation constraints need to be corrected. Therefore, the load equation constraints were adjusted to the following:

$${\displaystyle {\sum }_{i=1}^q{h}_i^{chp}}={\displaystyle {\sum }_{i=1}^{n+m+w+q}{d}_i^h}+{\displaystyle {\sum }_{i=1}^{n+m+w+q}\Delta d_i^h}$$

(40)

$${\displaystyle {\sum }_{i=1}^{n+m+w+q}{p}_i}={\displaystyle {\sum }_{i=1}^{n+m+w+q}{d}_i^e+{\displaystyle {\sum }_{i=1}^{n+m+w+q}\Delta d_i^e}},$$

(41)

where $\Delta d_i^e$ and $\Delta d_i^h$ are the sudden change in the power/heat load.

2.4.3. Real-Time Dispatch

Real-time scheduling of integrated energy systems refers to the process of real-time energy scheduling and management of various energy facilities based on real-time information on energy production, load demand and market prices during the operation of the energy system. This approach is designed to ensure the efficient utilization of energy resources, maintain the safety and stability of the system, and maximize economic benefits. So, the objective function is the following:

$$\min Obj=f(p),$$

(42)

$$f(p)={\displaystyle {\sum }_1^n{C}_i(p_i^{pv})}+{\displaystyle {\sum }_1^m{C}_i(p_i^{fg})+}{\displaystyle {\sum }_1^q{C}_i(p_i^{chp},h_i^{chp})}+{\displaystyle {\sum }_1^w{C}_i(p_i^c)}$$

(43)

$$\mathrm{s}.\mathrm{t}. P^e=(1-C^g{\delta }^c{\lambda }^c{\theta }^c)P^{chp}-P^d$$

(44)

$${\displaystyle {\sum }_{i=1}^q{h}_i^{chp}}={\displaystyle {\sum }_{i=1}^{n+m+w+q}{d}_i^h}$$

(45)

$$e_{i,m}{p}_i^{chp}+f_{i,m}{h}_i^{chp}+z_{i,m}\ge 0,(m=1,2,3,4),$$

(46)

During real-time scheduling, adjustments can be made to the supply and demand equity of the power system based on the results of real-time forecasts of PV power generation:

$$e_{i,m}{p}_i^{chp}+f_{i,m}{h}_i^{chp}+z_{i,m}\ge 0,(m=1,2,3,4),$$

(47)

where $\Delta P_i^{pv}$ is the PV forecast error. When the adjustment of the system net electric power demand is within the adjustment range of the carbon capture device, i.e.,

$${\displaystyle {\sum }_{i=1}^{m+w+q}{p}_i^{cmin}\le }{\displaystyle {\sum }_{i=1}^{n+m+w+q}\Delta d_i^e}+{\displaystyle {\sum }_i^n\Delta P_i^{pv}}\le {\displaystyle {\sum }_{i=1}^{m+w+q}{p}_i^{cmax}}$$

(48)

The system adjustment amount takes the total carbon capture equipment load of the fuel power plant and CHP and expands the upper and lower output limits of the fuel power plant and CHP so that they are constrained to be the following:

$$\left|p_i(t+1)-p_i(t)\right|\le p_i^{ramp}+{\displaystyle {\sum }_{i=1}^{m+w+q}{p}_i^{\mathrm{cmax}}}$$

(49)

3. Distributed Optimization Algorithm

3.1. Preliminary Definitions

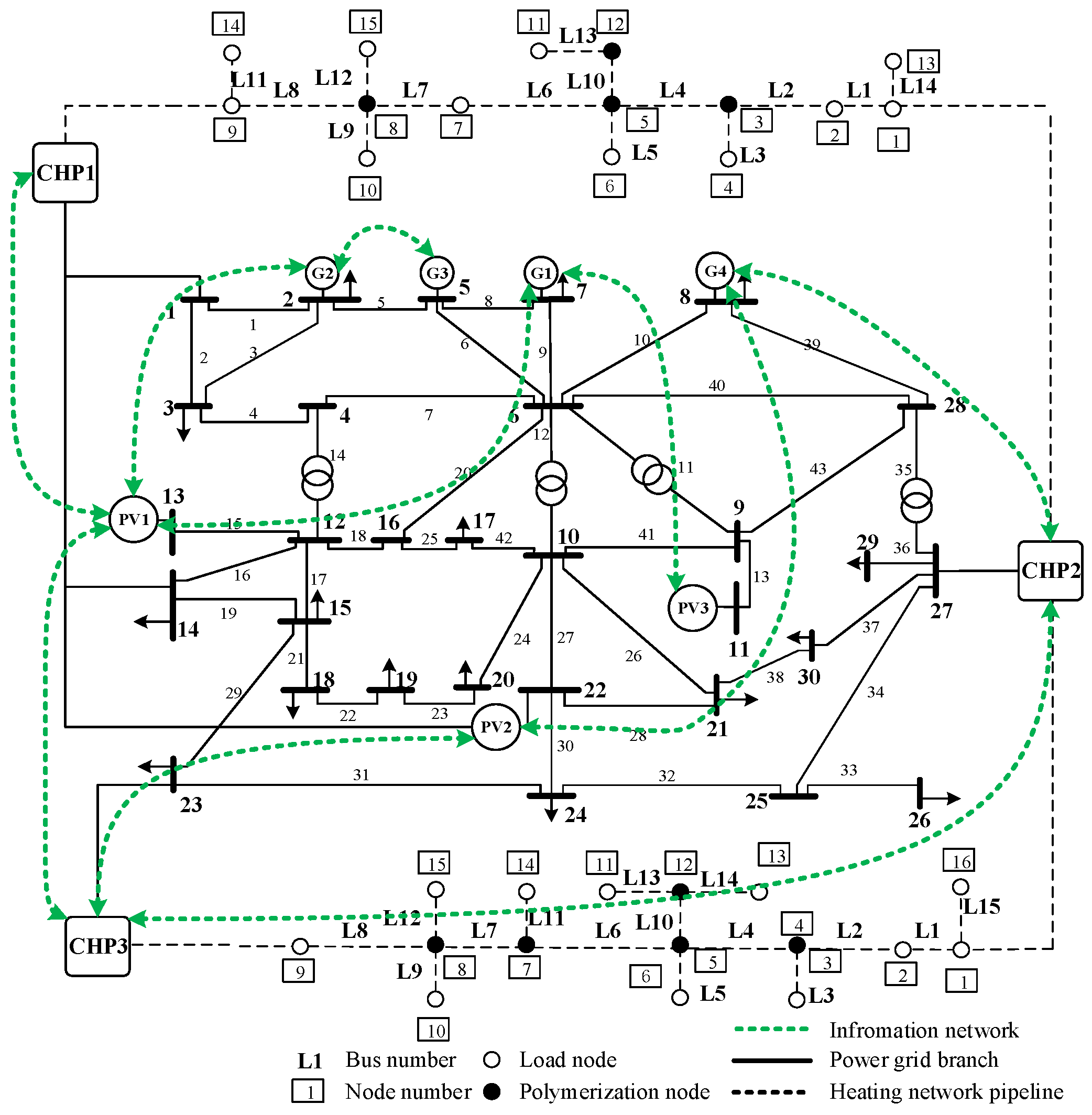
This subsection starts with a mathematical definition for the network topology of an integrated energy system. We can consider that fuel power plants, CHPs, carbon capture devices, photovoltaics, electrical loads and thermal loads are set up with communication nodes and can be regarded as intelligence which can be independently computed and information-transferred.

Consider an undirected fully connected topology graph $\mathcal{G}=(\mathcal{V},\zeta ,\mathcal{A})$. We assume that each device and bus load has an agent that can transmit data and compute independently, denoted by the set of nodes $\mathcal{V}=\{v_1,v_2,\dots ,v_n\}$. The set $\zeta \subseteq \mathcal{V}\times \mathcal{V}$ represents the edges and communication lines, while $\mathcal{A}\in {ℝ}^{n\times n}$ is the adjacency matrix. Define $D=\mathrm{diag}\{d_1,d_2,\dots ,d_n\}$ to be the degree matrix and $d_i={\displaystyle {\sum }_{j=1,i\ne j}^n{\mathrm{a}}_{ij}}$. Thus, the Laplace matrix of figure $\mathcal{G}$ is $ℒ=D-\mathcal{A}\in {ℝ}^{n\times n}$, which is symmetric semipositive definite. The smallest nonzero eigenvalue ${\lambda }_2$ of $ℒ$ is the algebraic connectivity of the graph.

For convenience, all vectors in the paper without any special expression are considered as column vectors, e.g., $x=[x_1;x_2;x_3]={[x_1,x_2,x_3]}^T$. The Kronecker product is denoted by $\otimes$. The Euclidean norm is represented by $\Vert •\Vert$. The derivative of a differentiable function $g(x)$ is denoted by $g^{\prime }(x)={(\nabla g_1(x),\nabla g_2(x),\dots ,\nabla g_m(x))}^T$, where $\nabla g(x)={(𝜕g(x)/𝜕x_1,𝜕g(x)/𝜕x_2,\dots ,𝜕g(x)/𝜕x_n)}^T$ is the gradient vector. We use ${[a]}^{+}=\max \{0,a\}$ to represent the projection of a positive number. To account for local constraints and feasible region constraints, we define $P_{\mathsf{\Omega }}$ as a projection operator. Within the feasible domain range $\mathsf{\Omega }=\{u\in R^n:l_i\le u_i\le h_i,i=1,\dots ,n\}$, the $P_{\mathsf{\Omega }}$ can be defined as $P_{\mathsf{\Omega }}(u)=\arg \underset{v\in \mathsf{\Omega }}{\min }\left|\right|u-v\left|\right|$.

3.2. A Fully Distributed Neural Dynamics Optimization Algorithm

We propose a new distributed neural dynamics optimization algorithm in order to solve the problem (1)–(2). This algorithm is based on the neurodynamic algorithm in [26], which uses intelligences instead of recurrent neurons in the RNN network to achieve global distributed optimization. This distributed neural dynamics optimization algorithm is designed as the following:

$${\dot{x}}_i=2\{P_{\mathsf{\Omega }}[x_i-\nabla f_i(x_i)-g{\prime }_i^T(x_i){\lambda }_i+{{\overline{A}}_i}^T{\mu }_i]-x_i\},$$

(50)

$${\dot{\mu }}_i=-{\overline{L}}_i{\mu }_i-{\eta }_i-({\overline{A}}_i{x}_i-{\overline{d}}_i),$$

(51)

$${\dot{\lambda }}_i={[{\lambda }_i+g_i(x_i)]}^{+}-{\lambda }_i,$$

(52)

$${\dot{\eta }}_i={\overline{L}}_i{\mu }_i,$$

(53)

where $x_i$ is both a neuron of the RNN network and a target variable that replaces $p_i^{pv}$, $p_i^{fg}$, $p_i^{chp}$, $h_i^{chp}$ and $p_i^c$, and ${\lambda }_i$, ${\mu }_i$ and ${\eta }_i$ are the shared variables. Since the inequality constraint $g_i(x_i)$ can be expressed as a box constraint, define ${\mathsf{\Omega }}_i$ as the feasible domain of $x_i$. Additionally, $f_i(x_i)\in {ℝ}^n$ represents the local objective function. The value $g{\prime }_i^T(x_i)$ is the transpose of the derivative of the inequality bound $g_i(x_i)$ and the number of inequality constraints is $r$. Furthermore, since the target variable $x_i$ is multidimensional, we define $\overline{L}=ℒ\otimes I_p$ and ${\overline{L}}_i$ represents the $i$-th row. $\overline{A}$ is the block matrix to represent the equation constraints and the number of equation constraints is $p$.

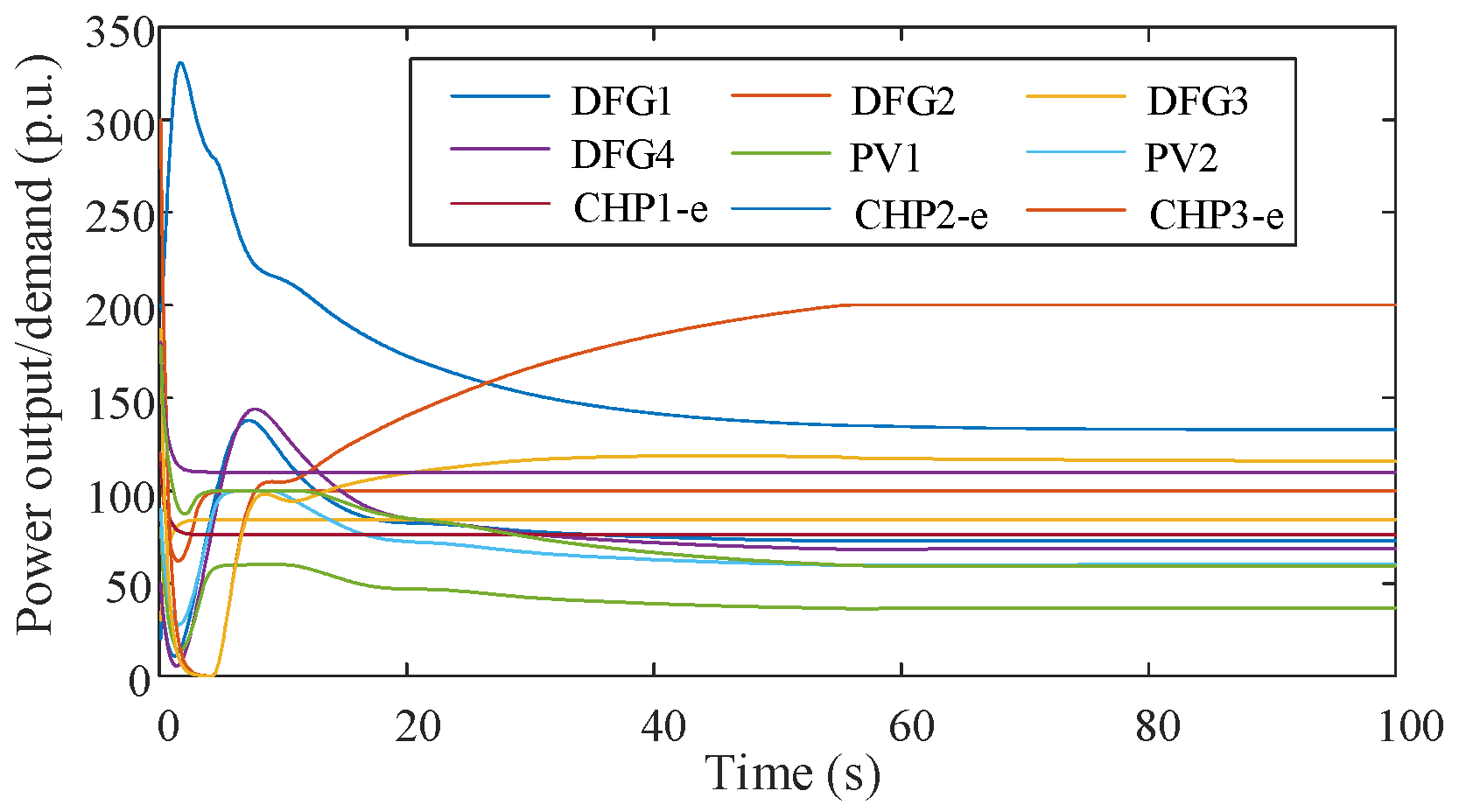
The pseudocode of this algorithm is shown in Algorithm 1. This distributed neural dynamics optimization algorithm enhances reliability, robustness, flexibility and privacy in the economic dispatch process of integrated energy systems. First, it is computed in a distributed manner, where the intelligence of all nodes can be computed independently, thus reducing the impact of single-point failures on the system. Second, since there is no central control center, any single point or channel is allowed to join the system at any time, matching the hot-plugging characteristic of the integrated energy system and enhancing the flexibility of the system. Third, auxiliary variables are passed as shared variables among neighboring nodes and target variables are computed locally. This information transfer method protects the privacy of the target variables and reduces the possibility of privacy leakage.

Algorithm 1: Distributed neural dynamics optimization algorithm
Day-ahead dispatch
Input	Initial values of all variables $x_i(0)$, ${\mu }_i(0)$, ${\lambda }_i(0)$, ${\eta }_i(0)$; device operating range ${\mathsf{\Omega }}_i$, local power loads $d_i^e$ and local heat load $d_i^h$; forecasted PV output $p_{i,t}^{PV,f}$; flue gas split ratio ${\delta }^c$.
Output	The optimal output of each device.
While	unconvergence does the following
	Exchanges data $\mu$, $\eta$ with neighboring nodes.
	The neural dynamics optimization algorithm (50)–(53) is applied to find the optimal solution for day-ahead optimization.
End
Intraday dispatch
Input	Sudden change in the power load $\Delta d_i^e$ and heat load $\Delta d_i^h$.
Output	The optimal output of each device.
While	unconvergence does the following
	Exchanges data $\mu$, $\eta$ with neighboring nodes.
	The neural dynamics optimization algorithm (50)–(53) is applied to find the optimal solution for day-ahead optimization.
End
Real-time dispatch
Input	PV forecast error $\Delta P_i^{pv}$; sudden change in power load $\Delta d_i^e$ and heat load $\Delta d_i^h$.
Output	The optimal output of each device.
While	unconvergence does the following:
	Exchanges data $\mu$, $\eta$ with neighboring nodes.
	The neural dynamics optimization algorithm (50)–(53) is applied to find the optimal solution for day-ahead optimization.
End
End

3.3. Optimality and Convergence Analysis

In order to prove the convergence and optimality of the present algorithm, we first define three auxiliary variables as the following:

$$\tilde{x}=P_{\mathsf{\Omega }}[x-\nabla f(x)-g{\prime }^T(x)\lambda +{\overline{A}}^T\mu ],$$

(54)

$$\tilde{\mu }=\dot{\mu }+\mu =\mu -L_p\mu -\eta -(\overline{A}x-d),$$

(55)

$$\tilde{\lambda }=\dot{\lambda }+\lambda ={[\lambda +g(x)]}^{+}.$$

(56)

Next, we define $z={(x^T,{\mu }^T,{\lambda }^T,{\eta }^T)}^T$ and assume $z^{*}={({(x^{*})}^T,{({\mu }^{*})}^T,{({\lambda }^{*})}^T,{({\eta }^{*})}^T)}^T$ is the optimal solution of algorithm (50)–(53). The Lyapunov equation is established as the following:

$$V(z)={(z^{*}-z)}^T\nabla \psi (z^{*})+\frac{1}{2}{\Vert z-z^{*}\Vert }^2-\psi (z^{*})+\psi (z),$$

(57)

$$\psi (z)=f(x)+\frac{1}{2}({\Vert \tilde{\mu }\Vert }^2+{\Vert \tilde{\lambda }\Vert }^2+{\Vert \eta \Vert }^2).$$

(58)

From the previous definition of the objective function, f is convex and Lipschitz continuous. So, a is also convex and Lipschitz continuous. Using Equations (57) and (58) and the definition of a convex function, one has $\psi (z)-\psi (z^{*})\ge {(z-z^{*})}^T\nabla \psi (z)$. Thus, the z is positively fixed for all $z^{*}$. Further, we give Lemma 1 and show that the derivative of the Lyapunov equation $\dot{V}(z)\le 0$.

Lemma 1.

Supposing $f(x)$ and  $g(x)$ are convex and Lipschitz continuous, the neural dynamics algorithm (1) can converge asymptotically over a large range to $z^{*}$.

Proof of Lemma 1.

We can define the Lagrange equation according to the objective function (1) as the following:

$$L(x,\lambda ,\mu )=f(x)+{\lambda }^{T}g(x)-{\mu }^T(\overline{A}x-\overline{d}).$$

(59)

Based on the saddle point theorem, one obtains

$$L(x^{*},\lambda ,\mu )\le L(x^{*},{\lambda }^{*},{\mu }^{*})\le L(x,{\lambda }^{*},{\mu }^{*}).$$

(60)

According to the left-side inequality of (60), we can obtain

$${(\lambda -{\lambda }^{*})}^{T}g(x^{*})-{(\mu -{\mu }^{*})}^T(\overline{A}{x}^{*}-\overline{d})\le 0.$$

(61)

Taking the directional derivative of the right-side inequality of (60) yields

$$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t$}\right.[L(x^{*},{\lambda }^{*},{\mu }^{*})-L(x^{*}+t(x-x^{*}),{\lambda }^{*},{\mu }^{*})]\le 0.$$

(62)

To satisfy inequality (61) and (62), the following inequality holds as

$${(x-x^{*})}^{T}L(x^{*},{\lambda }^{*},{\mu }^{*})\ge 0.$$

(63)

$${\lambda }^{*}\ge 0, \overline{A}{x}^{*}=\overline{d}, {({\lambda }^{*})}^{T}g(x^{*})=0, \overline{g}(x^{*})\le 0,$$

(64)

By the projection theorem and inequality (63) and (64), we obtain

$$\begin{array}{ll}\dot{V}(z)& =\nabla \phi (z)-\nabla \phi (z^{*})+z-z^{*}\\ & =-2{(x-\tilde{x})}^T(\nabla f(x)+g{\prime }^T(x)\tilde{\lambda }-{\overline{A}}^T\tilde{\mu }-\nabla f(x^{*})-g{\prime }^T(x){\lambda }^{*}+{\overline{A}}^T{\mu }^{*}+x-x^{*})\\ & \hspace{1em}-{(\mu -\tilde{\mu })}^T((1-L_p)\tilde{\mu }-(1-L_p){\mu }^{*}+\mu -{\mu }^{*})+{(\tilde{\lambda }-\lambda )}^T(\tilde{\lambda }-{\lambda }^{*}+\lambda -{\lambda }^{*})\\ & \hspace{1em}+{(L_p\mu )}^T(-\tilde{\mu }+\eta +{\mu }^{*}-{\eta }^{*}+\eta *-\eta )\\ & \le -2{(x^{*}-x)}^2+2{(\tilde{x}-x^{*})}^T(2x-x^{*}-\tilde{x})+2{\overline{A}}^T{(x^{*}-x)}^T(-\tilde{\mu }+{\mu }^{*})\\ & \hspace{1em}+2{(x^{*}-x)}^T(g{\prime }^T(x)\tilde{\lambda }-g{\prime }^T(x){\lambda }^{*})+{(\tilde{\mu }-u)}^2+2{(\tilde{\mu }-u)}^T(-u*+u)\\ & \hspace{1em}-{\tilde{\mu }}^T{L}_p\tilde{\mu }+{(\tilde{\lambda }-\lambda )}^T(\tilde{\lambda }-2{\lambda }^{*}+\lambda )\\ & \le 2{(x^{*}-x)}^T(\nabla \overline{g}{(x)}^T\tilde{\lambda }-\nabla \overline{g}{(x^{*})}^T{\lambda }^{*})-{(\tilde{\mu }-\mu )}^2-{(\tilde{\lambda }-\lambda )}^2\\ & \hspace{1em}+2{(\tilde{\lambda }-{\lambda }^{*})}^T(\tilde{\lambda }-\lambda )-{\tilde{\mu }}^T{L}_p\tilde{\mu }-2{(x-\tilde{x})}^2\\ & \le 2{\tilde{\lambda }}^T({[-\lambda -\overline{g}(x)]}^{+}+\overline{g}(x)+{(x^{*}-x)}^T\nabla \overline{g}{(x)}^T)\\ & \hspace{1em}-2{\lambda *}^T({[-\lambda -\overline{g}(x)]}^{+}+\overline{g}(x)+{(x^{*}-x)}^T\nabla \overline{g}{(x^{*})}^T)\\ & \hspace{1em}-{\tilde{\mu }}^T{L}_p\tilde{\mu }-2{(\tilde{x}-x)}^2-{(\tilde{\mu }-\mu )}^2-{(\tilde{\lambda }-\lambda )}^2\\ & \le -2{(\tilde{x}-x)}^2-{(\tilde{\mu }-\mu )}^2-{(\tilde{\lambda }-\lambda )}^2\le 0.\end{array}$$

(65)

□

This proof is thus completed. Also, according to inequality (63) and (64), we can obtain the algorithm (50)–(53) that satisfies the KKT condition, i.e.,

$$\{\begin{array}{l}\exists {\mu }^{*}\in R^{np},\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\exists {\lambda }^{*}\in R^r,\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{x}^{*}\in \mathsf{\Omega }\\ \overline{A}{x}^{*}=\overline{d}\\ {(x-x^{*})}^T[\nabla f(x*)+g_{i^{\prime }}^T(x^{*}){\lambda }^{*}-{\overline{A}}^T\mu ]\ge 0,\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall x\in \mathsf{\Omega }\\ {\lambda }^{*}\ge 0,\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}g(x^{*})\le 0,\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{({\lambda }^{*})}^{T}g(x^{*})=0\end{array}$$

(66)

Therefore, according to Lemma 1 and Equation (66), algorithm (50)–(53) can converge asymptotically to $z^{*}$ on a large scale and $z^{*}$ is the optimal solution. Further, using $z^{*}$, we can obtain the optimal solution $P^{*}$ for all power generators. The proof process is the same for the objective functions (33)–(41) and (42)–(49) for intraday scheduling and real-time scheduling.

4. Simulation and Results

In this paper, we took an integrated energy system in a city in northern China as an example, whose energy transmission network and information communication network are shown in Figure 3. The system realizes the electricity–heat supply of the city, which mainly includes 30-bus electricity nodes and 15-bus heat nodes. The capacity equipment includes four fuel power plants, three PV power plants and three CHPs, and this paper assumes that all fuel power plants and CHPs have carbon capture equipment. Operating cost parameters for all equipment were derived from ref. [27]. The operating cost factors for the carbon capture equipment are shown in

Table 1. The parameters of the carbon capture equipment.

	${\mathit{a}}_{\mathit{i}}^{\mathit{c}}$	${\mathit{b}}_{\mathit{i}}^{\mathit{c}}$	${\mathit{\delta }}_{\mathit{i}}^{\mathit{c}}$
CC 1	0.021	7.88	0.80
CC 2	0.01	7.85	0.85
CC 3	0.022	7.8	0.10
CC4	0.031	7.82	0.43
CC 5	0.025	7.79	0.73
CC 6	0.019	7.87	0.56
CC 7	0.29	4.5	0.40

. To ensure consistency in units, we define 1 p.u. as 1 MW for power, 1 p.u. as 1 MW for heat and 1 p.u. as 1 USD/MWh for price. In addition, the data involved in the experiments were sampled using the random balance method to obtain diverse, real-time, integration capability and system stability data to provide more accurate and comprehensive information for optimization decisions [28].

4.1. The Results and Analysis of the Neural Dynamics Optimization Algorithm

In this paper, we employed Algorithm 1 to conduct a cyclical optimization of the integrated energy system, ensuring that the outcomes of each optimization cycle were precise and valid. This subsection delves into the convergence properties of the proposed distributed neural dynamics optimization method. We set the initial electrical load at 1150 (p.u.) and the thermal load at 770 (p.u.), applying Algorithm 1 for a single instance of real-time scheduling in the integrated energy system, as illustrated in Figure 3. The results of the calculations are shown in Figure 4 and Figure 5.

Figure 4 illustrates the supply and demand balance of electricity and heat for an integrated energy system. The two curves represent electricity mismatch $={\displaystyle {\sum }_{i=1}^{n+m+w}{p}_i}-{\displaystyle {\sum }_{i=1}^{n+m+w}{d}_i^e}$ and heat mismatch $={\displaystyle {\sum }_{i=1}^q{h}_i^{chp}}-{\displaystyle {\sum }_{i=1}^{n+m+w+q}{d}_i^h}$. When t = 40 s, the two curves reach 0, indicating that the system has reached supply and demand equilibrium at this time, but the output of the capacity equipment is not the optimal value. Figure 5 demonstrates the results of power production optimization for fuel power plants, PV, and CHPs. Figure 6 demonstrates the heat production optimization results for a CHP. When t = 60 s, the optimization results of all capacity devices gradually stabilize, which shows that this algorithm operates in a distributed manner and the optimal solution can be obtained within 1 min in a single run.

4.2. Multi-Timescale Dispatching

In this subsection, we use Algorithm 1 for optimal scheduling of integrated energy systems on multiple timescales. Due to the limitation of regional development, not all heat loads are equipped with temperature sensors to intuitively measure whether the users reach a satisfactory temperature. So, to demonstrate the advantages of the algorithm and the effectiveness of the multi-timescale regulation, we did not take into account the loss of the heat pipeline. By default, the system reaches thermal supply–demand equilibrium when the heat output value of the CHP is equal to the load demand value. The day-ahead scheduling was performed first, and the electrical and thermal loads of the system are shown in Figure 7. The day-ahead scheduling results are shown in Figure 8.

It can be seen that the day-ahead scheduling well realizes the balance of electricity and heat supply and demand in the system. The thermal energy is supplied by CHP heat production. Electricity is mainly supplied by fuel power plants and the CHP. When the irradiance is strong, PV power generation joins the network to share the supply pressure of fuel power plants and CHPs.

Intraday dispatch mainly considers the instantaneous variation in loads and is compensated by photovoltaic generation and carbon capture devices. We assume that the instantaneous variation in the electric load conforms to a Gaussian distribution. The instantaneous variation in load for the intraday dispatch is shown in Figure 9.

As can be seen in Figure 9, short-term electrical load variations can be compensated by PV power generation and lowering of the energy consumption of the carbon capture equipment without the need for instantaneous regulation of fuel power generation from a CHP. As time continues, the fuel generation and CHP gradually increase the turbine speed to gradually compensate for the amount of electrical load variation and reopen the carbon capture equipment.

The purpose of real-time dispatch is to utilize more accurate forecast information to adjust for sudden load changes and PV generation uncertainty, while correcting the energy consumption of carbon capture equipment without changing the total output of the fuel-fired power plant and CHP, thus changing the net output profile of the capacity equipment for the purpose of consuming photovoltaic power and reducing the loss-of-load scenario. The intraday dispatch results are shown in Figure 10.

5. Conclusions

The combination of carbon capture and PV power generation is a promising direction for energy development, with the potential to make energy production cleaner, more efficient and cost-effective. However, this technology requires the development of efficient and affordable carbon capture technologies, reduction in the cost of using PV panels and power generation efficiency, and creation of a regulatory framework to regulate the activities of power plants using CCS and photovoltaic generation. Therefore, this paper proposes a carbon capture plant/CHP with a PV accommodation operation strategy from the perspective of reducing the operating cost of the system. First, the authors propose a carbon capture CHP operation strategy that aims to fully utilize PV power generation and carbon capture equipment, which compensates the problems of small-scale CHP climbing constraints and short-term output regulation difficulties. Second, the authors propose a multi-timescale optimal scheduling strategy, which solves the deviation problems caused by PV fluctuations and load changes by analyzing the climbing constraint limit of a CHP, the working process of carbon capture equipment and the real-time characteristics of PV power generation, and realizes the adjustment of the optimization results of the previous day to the scheduling of the same day. Finally, the authors propose an event-triggered fully distributed neural dynamics-based optimization algorithm for solving the multi-timescale optimization problem presented in this paper. The algorithm effectively computes both day-ahead and real-time scheduling results for the urban integrated energy system using rolling cycles. Theoretical analysis and simulation experiments were conducted to validate the accuracy and reliability of the algorithm.