Numerical Analysis of Three Vertical Axis Turbine Designs for Improved Water Energy Efficiency
Abstract
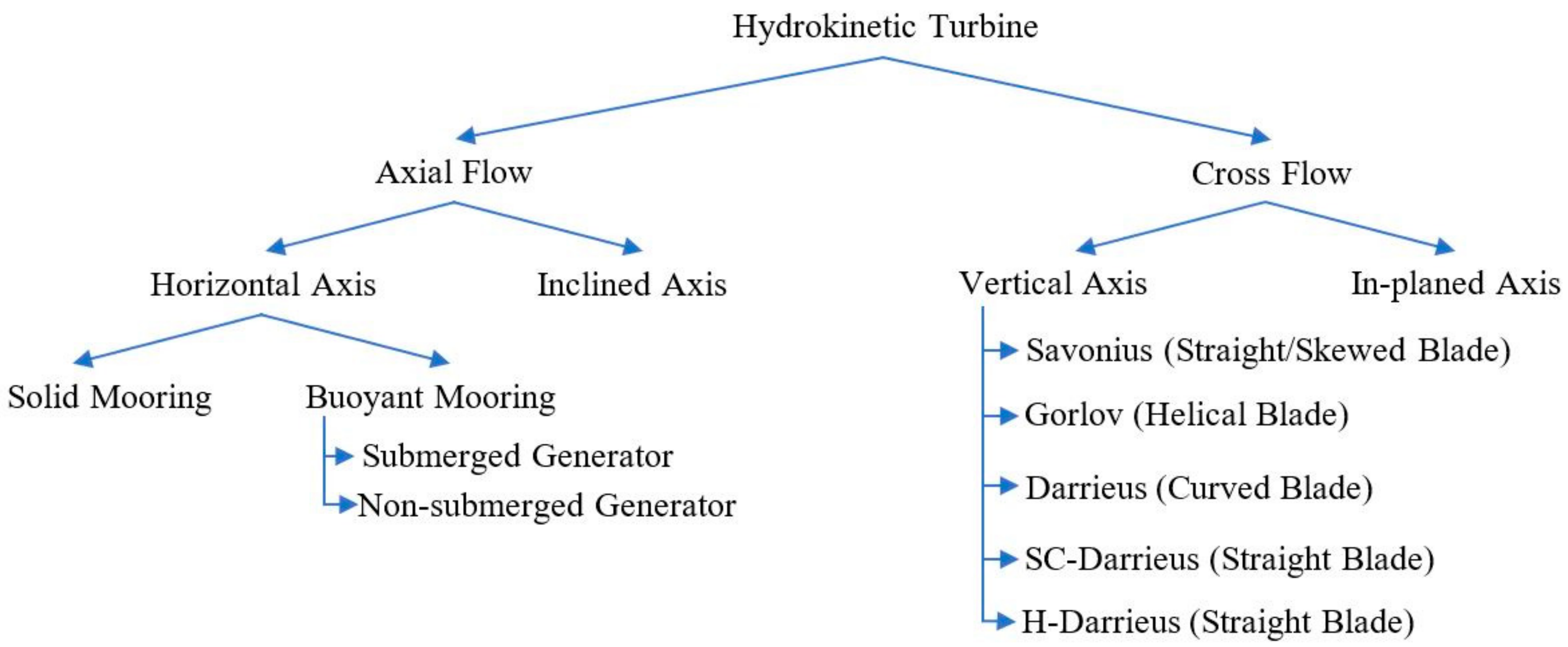
1. Introduction
2. Design of the Turbines
3. Performance Parameters
4. Modeling and Numerical Analysis
4.1. Turbulence Model and Governing Equations
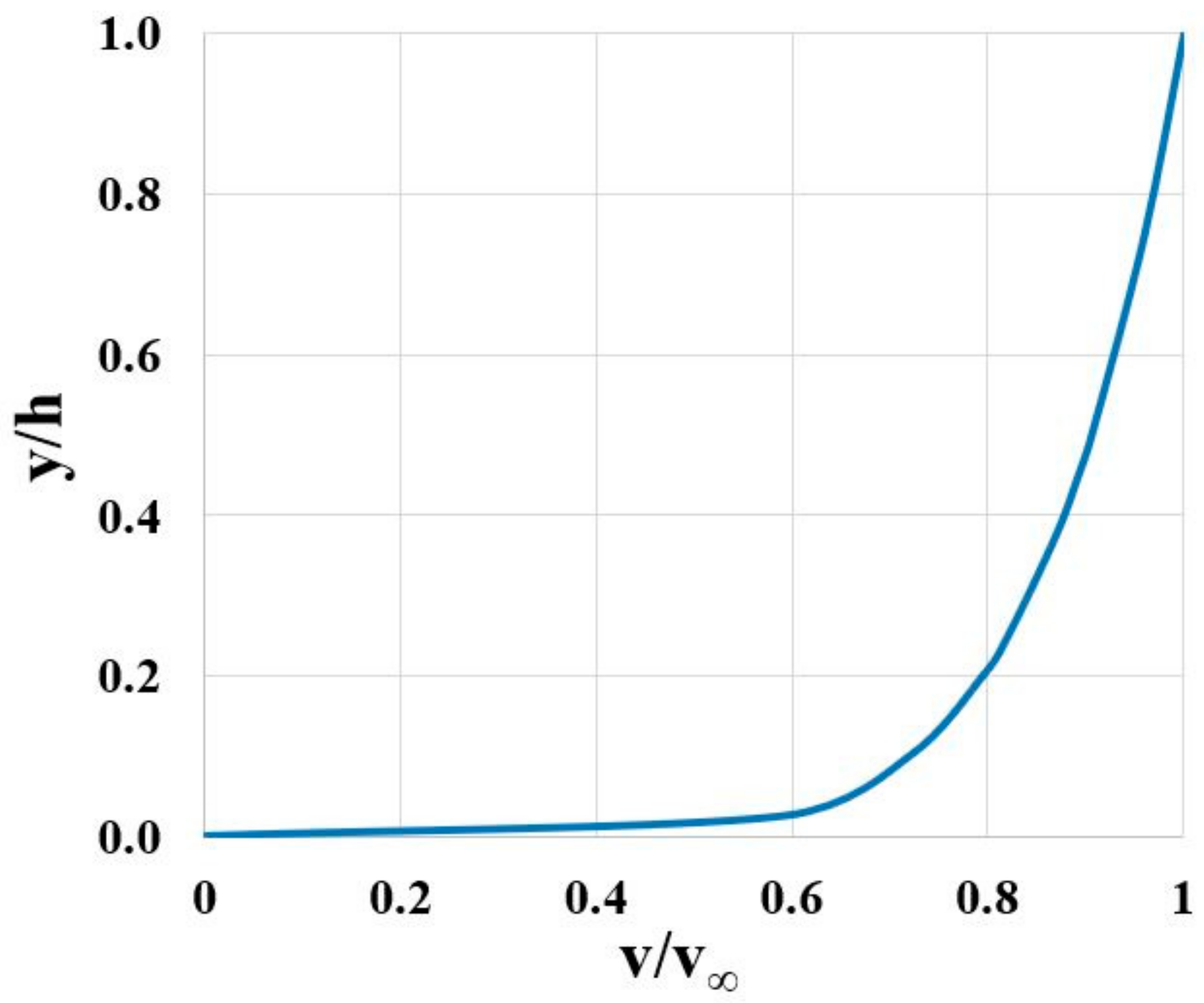
4.2. Model Domain and Boundary Conditions
4.3. Mesh Generation and Mesh Independency Testing
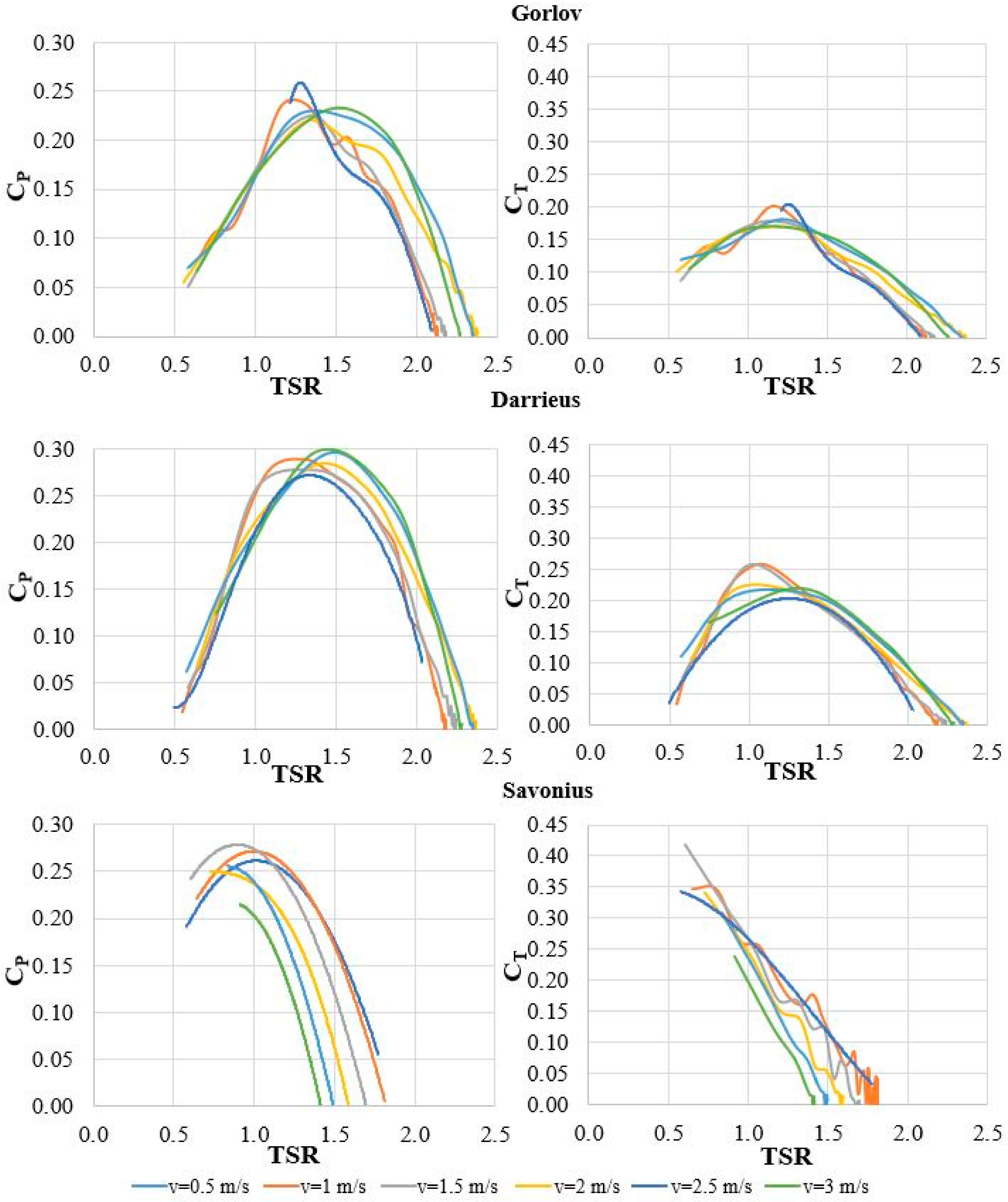
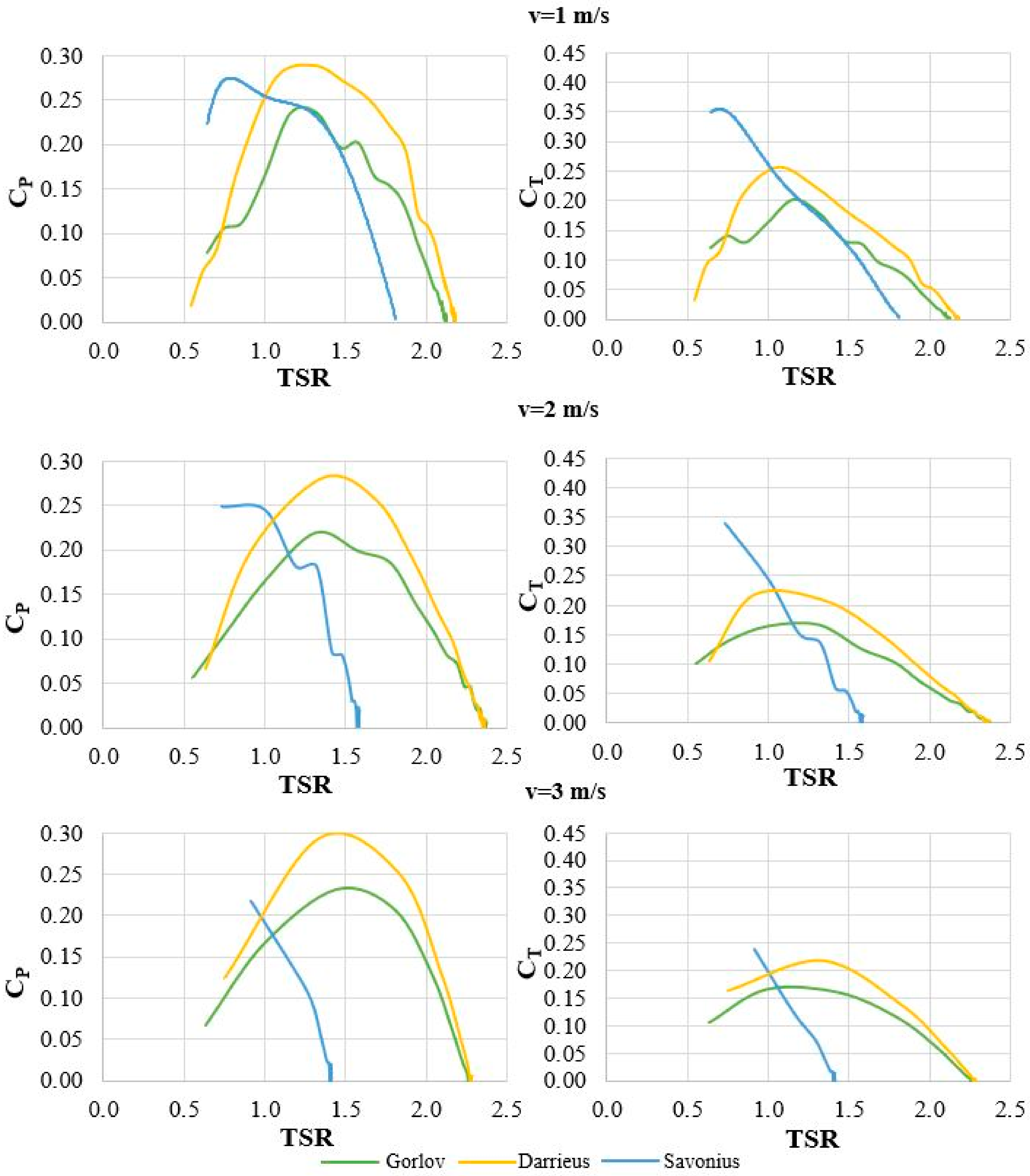
5. Results and Discussion
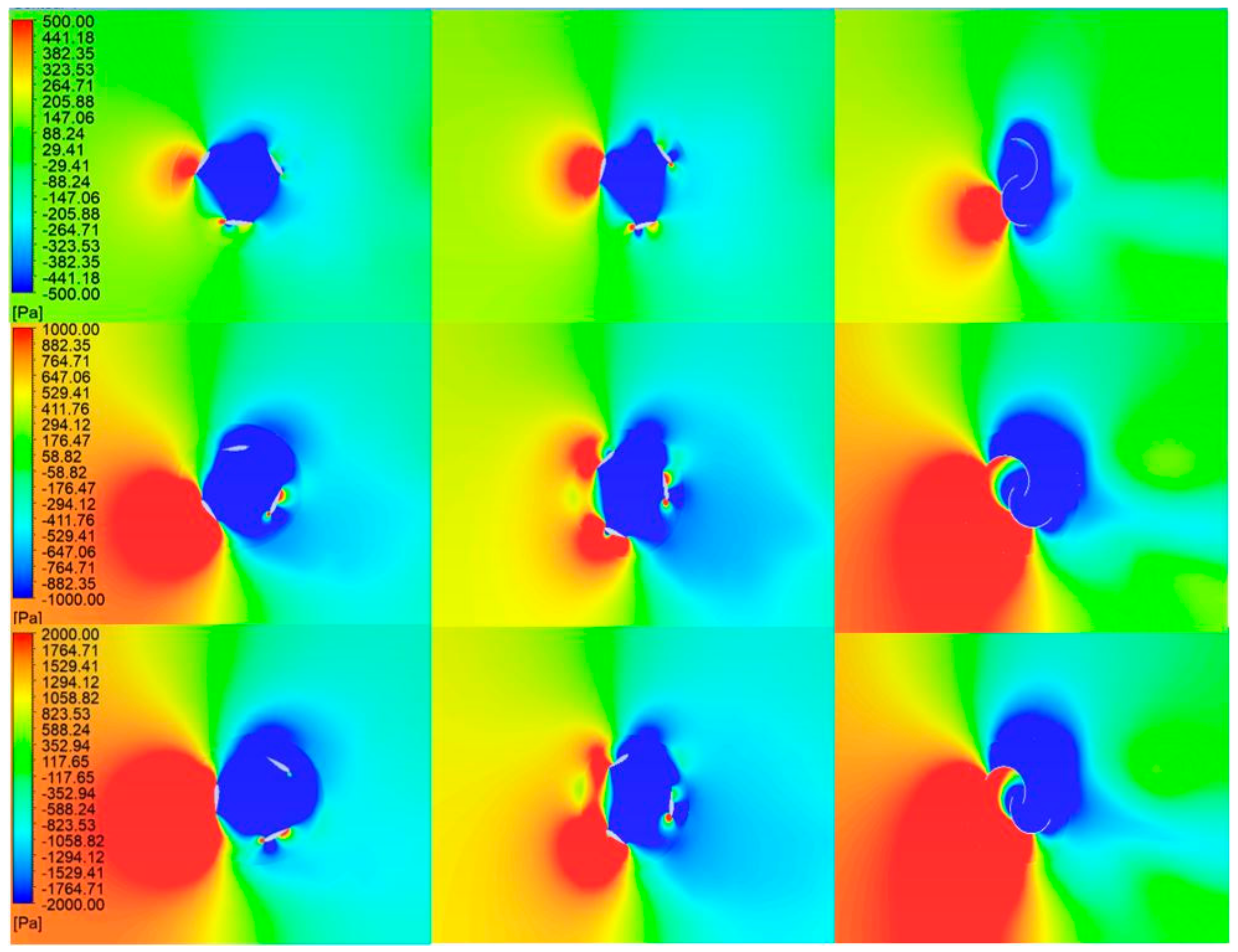
5.1. Pressure Contours
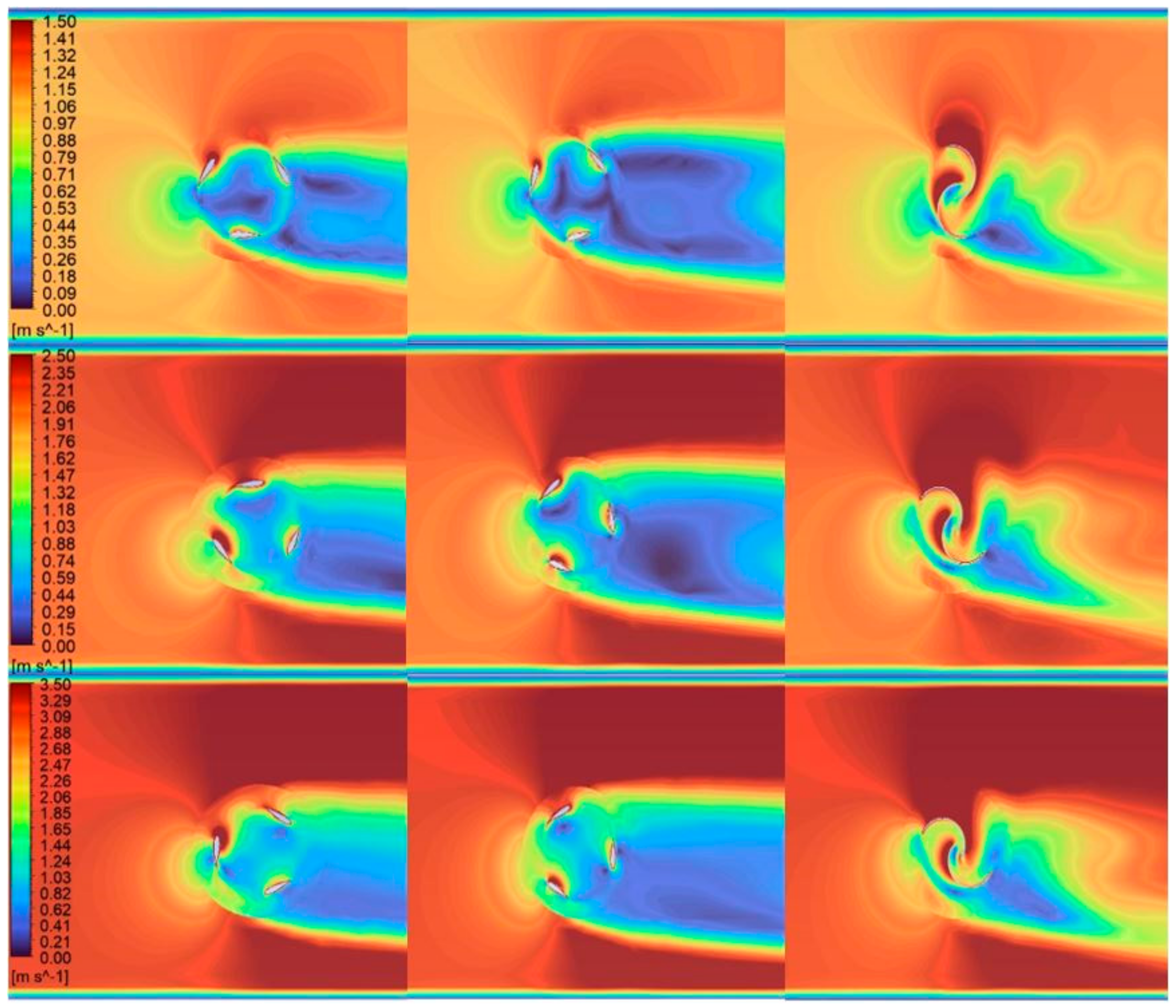
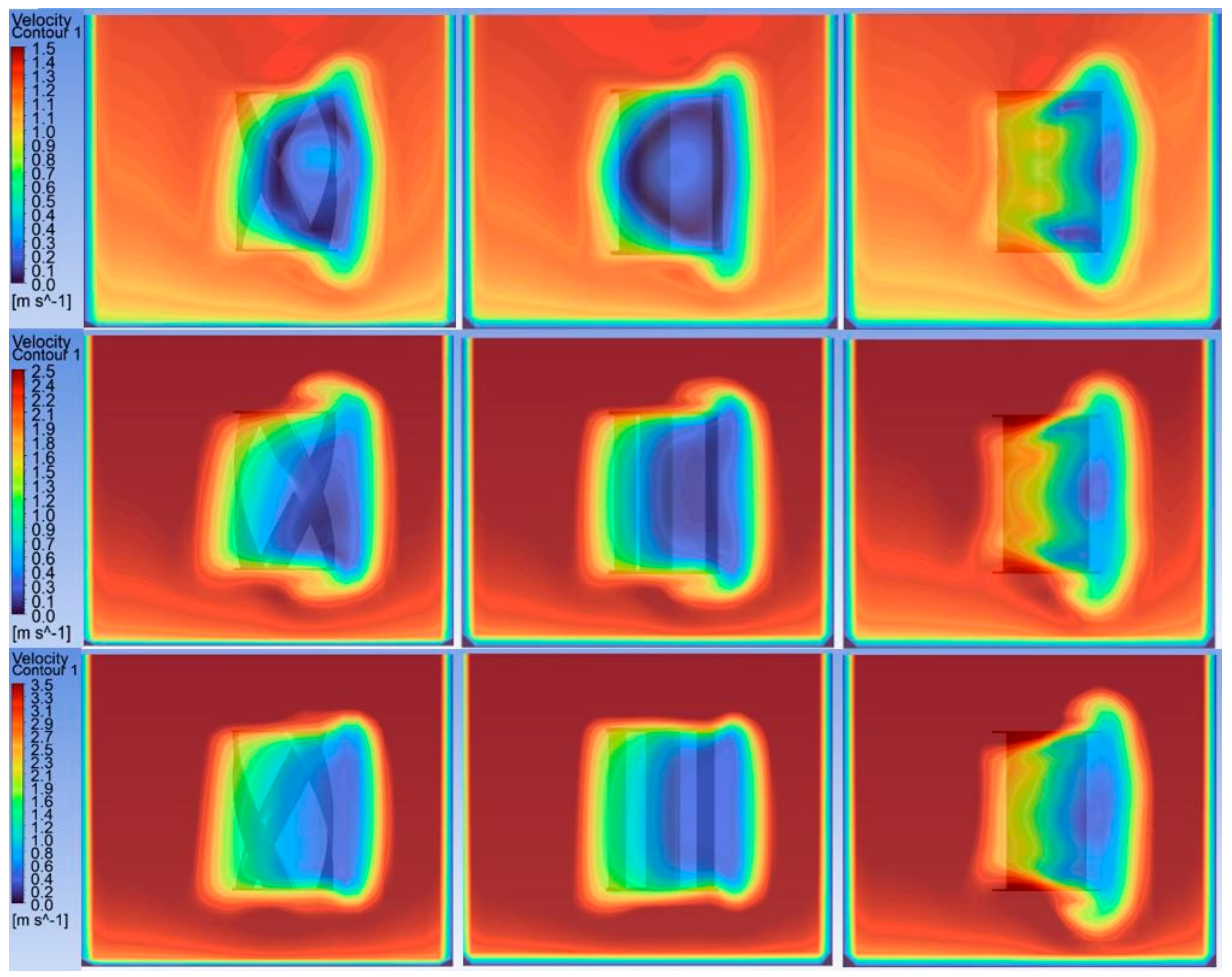
5.2. Velocity Contours
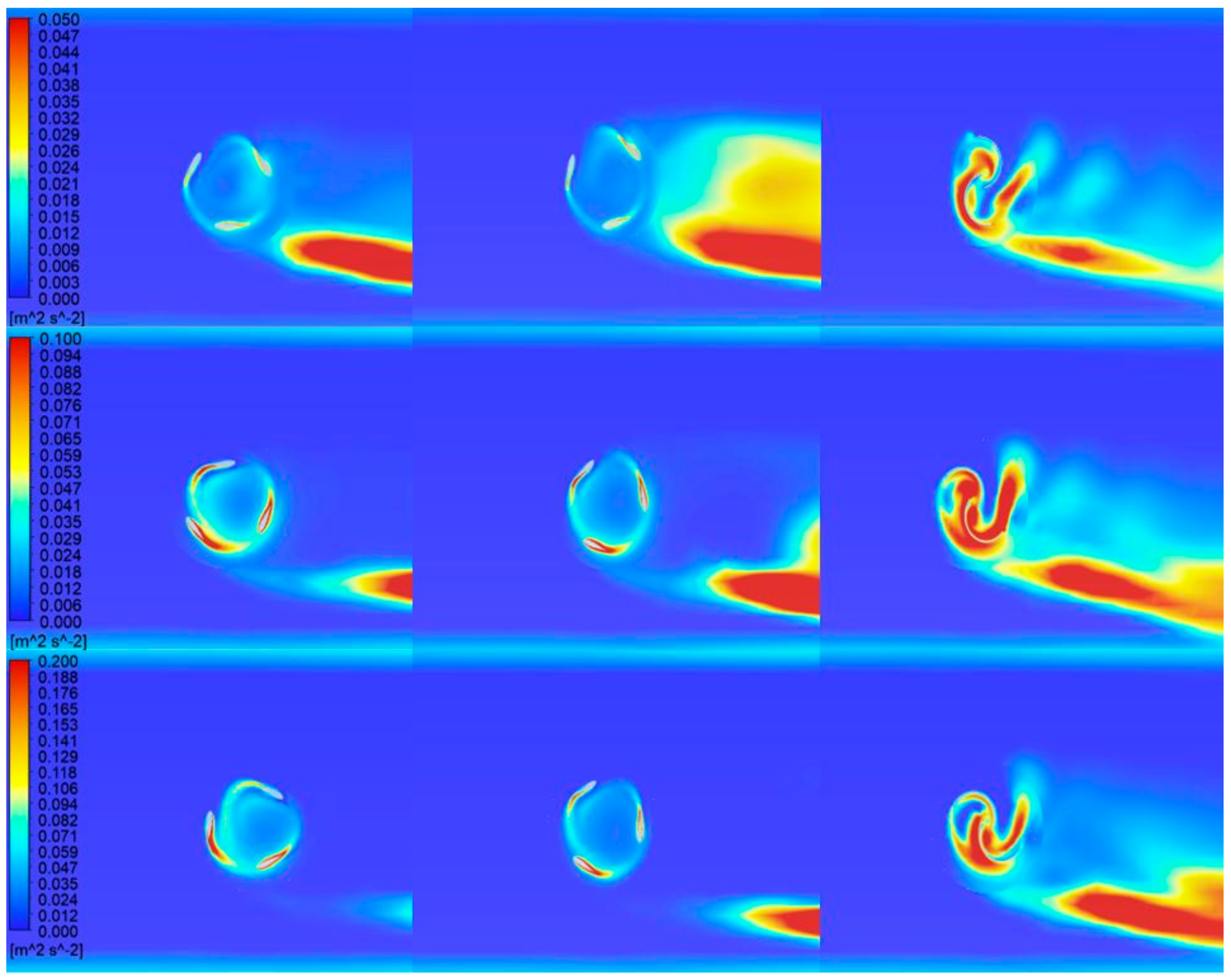
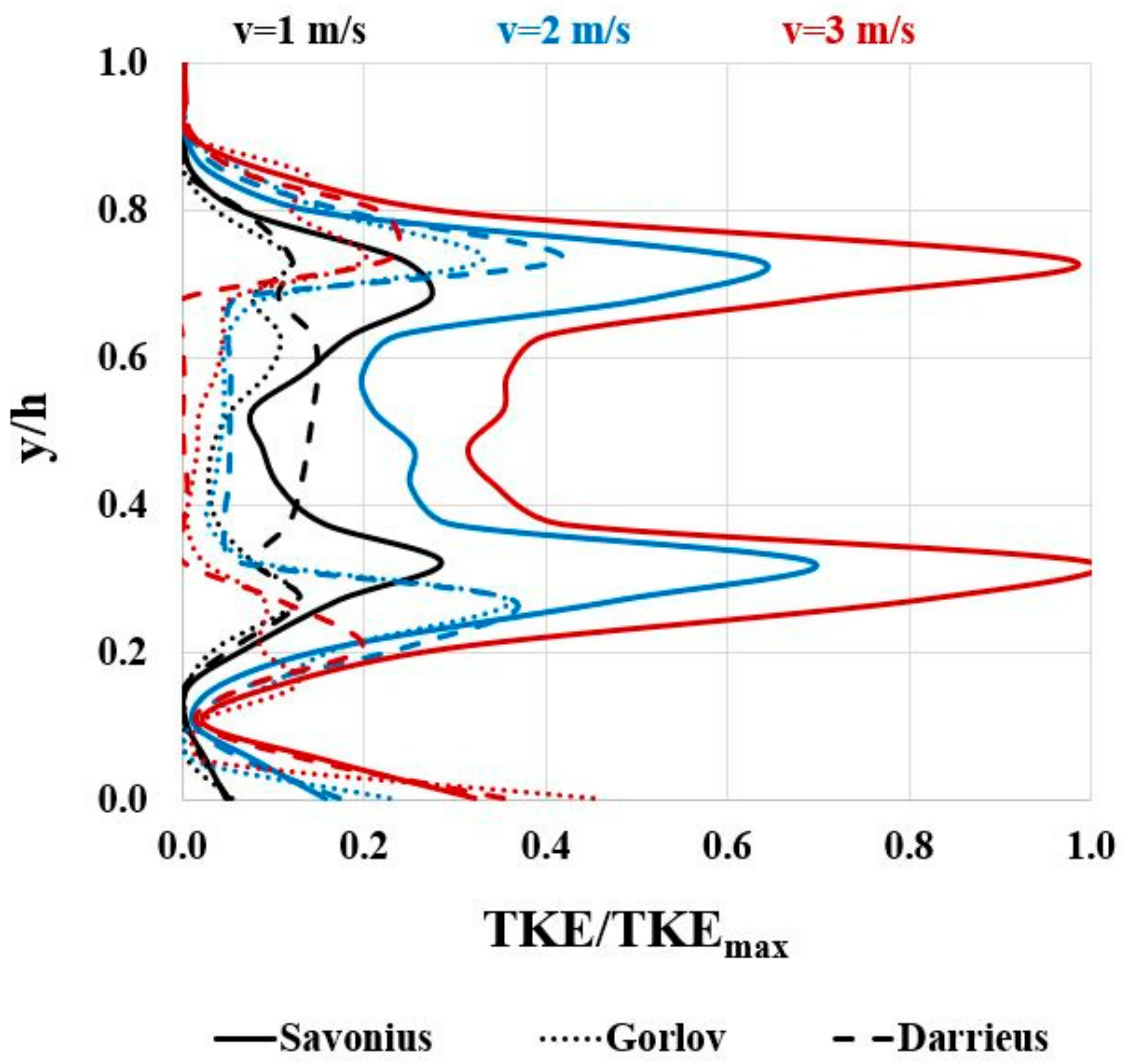
5.3. Turbulence Kinetic Energy Contours
6. Conclusions
- The maximum power coefficient value of 0.293 was obtained for the model with a Darrieus turbine corresponding to a water velocity of 3 m/s and a TSR value of 1.34.
- The Savonius turbine achieved the lowest maximum power of coefficient value at a velocity of 3 m/s.
- The maximum torque coefficient value obtained from the turbines is 0.419 at 0.60 TSR for 1.5 m/s water velocity, achieved by the Savonius turbine.
- The Darrieus and Gorlov turbines were found to have a more comprehensive operating range than Savonius.
- The minimum pressure values around the Savonius turbine swept area increase with higher flow velocities and are observed in the turbine downstream.
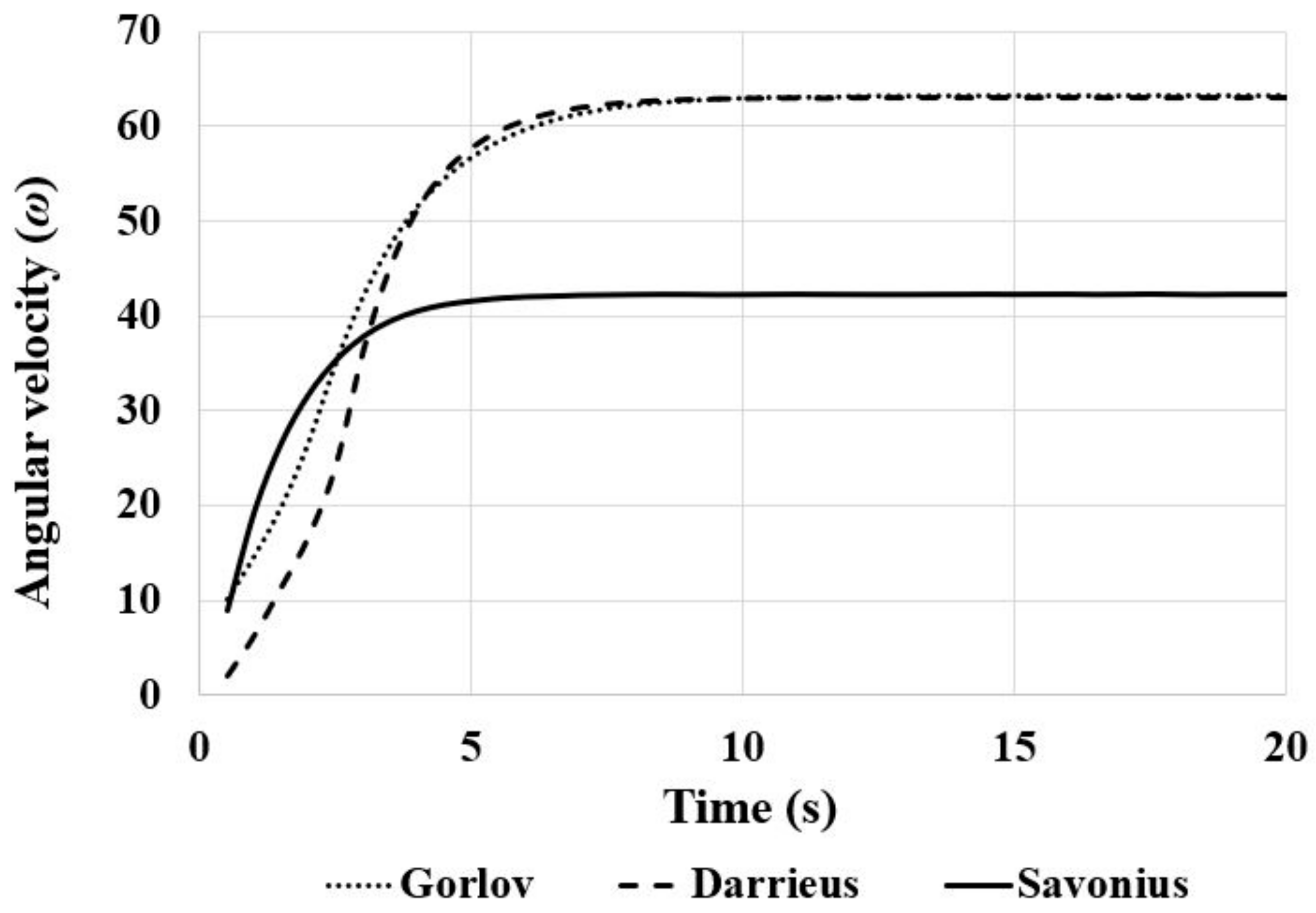
- The Savonius blade exhibited the most effective self-starting capability.
- It is essential to use the dynamic mesh technique for optimal turbine rotation display in 3D modeling.
- Simulated flow around the Savonius turbine indicated a relatively higher turbulent flow, resulting in increased energy dissipation downstream.
- The straight blade (Darrieus) turbine performed better than the helical blade (Gorlov).
- Hydrokinetic turbines can produce significant energy even in water depths as low as 40 cm and, therefore, have great potential as a renewable energy source.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- REN21. Renewables 2020 Global Status Report. 2020. p. 367. Available online: https://www.ren21.net/wp-content/uploads/2019/05/gsr_2020_full_report_en.pdf (accessed on 21 November 2023).
- Singh, D.; Power, M.H. Resource Assessment Handbook; Asian and Pacific Centre for Transfer of Technology of the United Nations, Economic and Social Commission for Asia and the Pacific (ESCAP): New Delhi, India, 2009; pp. 16–34. [Google Scholar]
- Hoq, T.; Nawshad, U.A.; Islam, N.; Syfullah, K.; Rahman, R. Micro hydro power: Promising solution for off-grid renewable energy source. Int. J. Sci. Eng. Res. 2011, 2, 2–6. [Google Scholar]
- Ashok, S. Optimised model for community-based hybrid energy system. Renew. Energy 2007, 32, 1155–1164. [Google Scholar] [CrossRef]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Vermaak, H.J.; Kusakana, K.; Koko, S.P. Status of micro-hydrokinetic river technology in rural applications: A review of literature. Renew. Sustain. Energy Rev. 2014, 29, 625–633. [Google Scholar] [CrossRef]
- Khan, M.J.; Iqbal, M.T.; Quaicoe, J.E. River current energy conversion systems: Progress, prospects and challenges. Renew. Sustain. Energy Rev. 2008, 12, 2177–2193. [Google Scholar] [CrossRef]
- Grabbe, M.; Yuen, K.; Goude, A.; Lalander, E.; Leijon, M. Design of an experimental setup for hydro-kinetic energy conversion. Int. J. Hydropower Dams 2009, 16, 112–116. [Google Scholar]
- Kuschke, M.; Strunz, K. Modeling of tidal energy conversion systems for smart grid operation. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–3. [Google Scholar]
- Cada, G.; Ahlgrimm, J.; Bahleda, M.; Bigford, T.; Stavrakas, S.D.; Hall, D.; Moursund, R.; Sale, M. Potential impacts of hydrokinetic and wave energy conversion technologies on aquatic environments. Fisheries 2007, 32, 174–181. [Google Scholar] [CrossRef]
- Van Arkel, R.; Owen, L.; Allison, S.; Tryfonas, T.; Winter, A.; Entwistle, R.; Keane, E.; Parr, J. Design and preliminary testing of a novel concept low depth hydropower device. In Proceedings of the OCEANS’11 MTS/IEEE KONA, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–10. [Google Scholar]
- Hermann, S. Design of a Micro-Hydro Powered Battery Charging System for Rural Village Electrification; Carl von Ossietzky University: Oldenburg, Germany, 2006. [Google Scholar]
- Elghali, S.B.; Benbouzid, M.E.H.; Charpentier, J.F. Marine tidal current electric power generation technology: State of the art and current status. In Proceedings of the 2007 IEEE International Electric Machines and Drives Conference, Antalya, Turkey, 3–5 May 2007; Volume 2, pp. 1407–1412. [Google Scholar]
- Johnson, J.B.; Pride, D.J. River, Tidal, and Ocean Current Hydrokinetic Energy Technologies: Status and Future Opportunities in Alaska; Alaska Center for Energy and Power: Fairbanks, AK, USA, 2010. [Google Scholar]
- Kusakana, K.; Vermaak, H.J. Hydrokinetic power generation for rural electricity supply: Case of South Africa. Renew. Energy 2013, 55, 467–473. [Google Scholar] [CrossRef]
- Lago, L.I.; Ponta, F.L.; Chen, L. Advances and trends in hydrokinetic turbine systems. Energy Sustain. Dev. 2010, 14, 287–296. [Google Scholar] [CrossRef]
- Güney, M.S.; Kaygusuz, K. Hydrokinetic energy conversion systems: A technology status review. Renew. Sustain. Energy Rev. 2010, 14, 2996–3004. [Google Scholar] [CrossRef]
- Kumar, A.; Nikhade, A. Hybrid kinetic turbine rotors: A review. Int. J. Eng. Sci. Adv. Technol. 2014, 4, 453–463. [Google Scholar]
- Kumar, D.; Sarkar, S. A review on the technology, performance, design optimization, reliability, techno-economics and environmental impacts of hydrokinetic energy conversion systems. Renew. Sustain. Energy Rev. 2016, 58, 796–813. [Google Scholar] [CrossRef]
- Niebuhr, C.M.; Van Dijk, M.; Neary, V.S.; Bhagwan, J.N. A review of hydrokinetic turbines and enhancement techniques for canal installations: Technology, applicability and potential. Renew. Sustain. Energy Rev. 2019, 113, 109240. [Google Scholar] [CrossRef]
- Saini, G.; Saini, R.P. A review on technology, configurations, and performance of cross-flow hydrokinetic turbines. Int. J. Energy Res. 2019, 43, 6639–6679. [Google Scholar] [CrossRef]
- Sood, M.; Singal, S.K. Development of hydrokinetic energy technology: A review. Int. J. Energy Res. 2019, 43, 5552–5571. [Google Scholar] [CrossRef]
- Ibrahim, W.I.; Mohamed, M.R.; Ismail, R.M.T.R.; Leung, P.K.; Xing, W.W.; Shah, A.A. Hydrokinetic energy harnessing technologies: A review. Energy Rep. 2021, 7, 2021–2042. [Google Scholar] [CrossRef]
- Kamal, M.M.; Saini, R.P. A review on modifications and performance assessment techniques in cross-flow hydrokinetic system. Sustain. Energy Technol. Assess. 2022, 51, 101933. [Google Scholar] [CrossRef]
- Li, L.; Xu, W.; Tan, Y.; Yang, Y.; Yang, J.; Tan, D. Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method. Mech. Syst. Signal Process. 2023, 189, 110058. [Google Scholar] [CrossRef]
- Li, L.; Li, Q.; Ni, Y.; Wang, C.; Tan, Y.; Tan, D. Critical penetrating vibration evolution behaviors of the gas-liquid coupled vortex flow. Energy 2024, 292, 130236. [Google Scholar] [CrossRef]
- Shiono, M.; Suzuki, K.; Kiho, S. Output characteristics of Darrieus water turbine with helical blades for tidal current generations. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Kitakyushu, Japan, 26–31 May 2002; p. ISOPE-I. [Google Scholar]
- Niblick, A.L. Experimental and Analytical Study of Helical Cross-Flow Turbines for a Tidal Micropower Generation System; University of Washington: Seattle, WA, USA, 2012. [Google Scholar]
- Yang, B.; Shu, X.W. Hydrofoil optimization and experimental validation in helical vertical axis turbine for power generation from marine current. Ocean Eng. 2012, 42, 35–46. [Google Scholar] [CrossRef]
- Wenlong, T.; Baowei, S.; Zhaoyong, M. Conceptual design and numerical simulations of a vertical axis water turbine used for underwater mooring platforms. Int. J. Nav. Archit. Ocean Eng. 2013, 5, 625–634. [Google Scholar] [CrossRef]
- Sahim, K.; Santoso, D.; Radentan, A. Performance of combined water turbine with semielliptic section of the Savonius rotor. Int. J. Rotating Mach. 2013, 2013, 985943. [Google Scholar] [CrossRef]
- Demircan, E. Design and Analysis of a Vertical Axis Water Turbine for River Applications Using Computational Fluid Dynamics. Master’s Thesis, Middle East Technical University, Ankara, Türkiye, 2014. [Google Scholar]
- Bachant, P.; Wosnik, M. Performance measurements of cylindrical-and spherical-helical cross-flow marine hydrokinetic turbines, with estimates of exergy efficiency. Renew. Energy 2015, 74, 318–325. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R.P. Performance analysis of a Savonius hydrokinetic turbine having twisted blades. Renew. Energy 2017, 108, 502–522. [Google Scholar] [CrossRef]
- Basumatary, M.; Biswas, A.; Misra, R.D. CFD analysis of an innovative combined lift and drag (CLD) based modified Savonius water turbine. Energy Convers. Manag. 2018, 174, 72–87. [Google Scholar] [CrossRef]
- Saini, G.; Saini, R.P. A numerical analysis to study the effect of radius ratio and attachment angle on hybrid hydrokinetic turbine performance. Energy Sustain. Dev. 2018, 47, 94–106. [Google Scholar] [CrossRef]
- Mejia, O.D.L.; Quiñones, J.J.; Laín, S. RANS and hybrid RANS-LES simulations of an H-type Darrieus vertical axis water turbine. Energies 2018, 11, 2348. [Google Scholar] [CrossRef]
- Mosbahi, M.; Ayadi, A.; Chouaibi, Y.; Driss, Z.; Tucciarelli, T. Performance study of a Helical Savonius hydrokinetic turbine with a new deflector system design. Energy Convers. Manag. 2019, 194, 55–74. [Google Scholar] [CrossRef]
- Alizadeh, H.; Jahangir, M.H.; Ghasempour, R. CFD-based improvement of Savonius type hydrokinetic turbine using optimized barrier at the low-speed flows. Ocean Eng. 2020, 202, 107178. [Google Scholar] [CrossRef]
- Saini, G.; Saini, R.P. A computational investigation to analyze the effects of different rotor parameters on hybrid hydrokinetic turbine performance. Ocean Eng. 2020, 199, 107019. [Google Scholar] [CrossRef]
- Kumar, R.; Sarkar, S. Effect of design parameters on the performance of helical Darrieus hydrokinetic turbines. Renew. Sustain. Energy Rev. 2022, 162, 112431. [Google Scholar] [CrossRef]
- Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Kumar, A.; Saini, R.P. Performance parameters of Savonius type hydrokinetic turbine—A Review. Renew. Sustain. Energy Rev. 2016, 64, 289–310. [Google Scholar] [CrossRef]
- Maldar, N.R.; Ng, C.Y.; Oguz, E. A review of the optimization studies for Savonius turbine considering hydrokinetic applications. Energy Convers. Manag. 2020, 226, 113495. [Google Scholar] [CrossRef]
- Talukdar, P.K.; Sardar, A.; Kulkarni, V.; Saha, U.K. Parametric analysis of model Savonius hydrokinetic turbines through experimental and computational investigations. Energy Convers. Manag. 2018, 158, 36–49. [Google Scholar] [CrossRef]
- Guo, F.; Song, B.; Mao, Z.; Tian, W. Experimental and numerical validation of the influence on Savonius turbine caused by rear deflector. Energy 2020, 196, 117132. [Google Scholar] [CrossRef]
- Ramadan, A.; Hemida, M.; Abdel-Fadeel, W.A.; Aissa, W.A.; Mohamed, M.H. Comprehensive experimental and numerical assessment of a drag turbine for river hydrokinetic energy conversion. Ocean Eng. 2021, 227, 108587. [Google Scholar] [CrossRef]
- Mohamed, M.H. Performance investigation of H-rotor Darrieus turbine with new airfoil shapes. Energy 2012, 47, 522–530. [Google Scholar] [CrossRef]
- Alqurashi, F.; Mohamed, M.H. Aerodynamic forces affecting the H-rotor Darrieus wind turbine. Model. Simul. Eng. 2020, 2020, 1368369. [Google Scholar] [CrossRef]
- Dominy, R.; Lunt, P.; Bickerdyke, A.; Dominy, J. Self-starting capability of a Darrieus turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 111–120. [Google Scholar] [CrossRef]
- Hill, N.; Dominy, R.; Ingram, G.; Dominy, J. Darrieus turbines: The physics of self-starting. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 21–29. [Google Scholar] [CrossRef]
- Douak, M.; Aouachria, Z.; Rabehi, R.; Allam, N. Wind energy systems: Analysis of the self-starting physics of vertical axis wind turbine. Renew. Sustain. Energy Rev. 2018, 81, 1602–1610. [Google Scholar] [CrossRef]
- Menet, J.L. A double-step Savonius rotor for local production of electricity: A design study. Renew. Energy 2004, 29, 1843–1862. [Google Scholar] [CrossRef]
- Khan, M.N.I.; Iqbal, M.T.; Hinchey, M. Sea-floor power generation system. In Proceedings of the 17th IEEE NECEC Conference, St. John’s, NL, Canada, 8 November 2007. [Google Scholar]
- Alam, M.J.; Iqbal, M.T. Design and development of hybrid vertical axis turbine. In Proceedings of the 2009 Canadian Conference on Electrical and Computer Engineering, St. John’s, NL, Canada, 3–6 May 2009; pp. 1178–1183. [Google Scholar]
- Anyi, M.; Kirke, B. Hydrokinetic turbine blades: Design and local construction techniques for remote communities. Energy Sustain. Dev. 2011, 15, 223–230. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, G.; Gao, K.; Ju, W. Darrieus vertical axis wind turbine: Basic research methods. Renew. Sustain. Energy Rev. 2015, 42, 212–225. [Google Scholar] [CrossRef]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. Three-dimensional numerical simulations of straight-bladed vertical axis tidal turbines investigating power output, torque ripple and mounting forces. Renew. Energy 2015, 83, 67–77. [Google Scholar] [CrossRef]
- Rogowski, K. CFD Computation of the H-Darrieus wind turbine—The impact of the rotating shaft on the rotor performance. Energies 2019, 12, 2506. [Google Scholar] [CrossRef]
- Patel, V.; Patel, R. Free energy-extraction using Savonius hydrokinetic rotor with dual splitters. Mater. Today Proc. 2021, 45, 5354–5361. [Google Scholar] [CrossRef]
- Balduzzi, F.; Bianchini, A.; Maleci, R.; Ferrara, G.; Ferrari, L. Critical issues in the CFD simulation of Darrieus wind turbines. Renew. Energy 2016, 85, 419–435. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. CFD simulation of a vertical axis wind turbine operating at a moderate tip speed ratio: Guidelines for minimum domain size and azimuthal increment. Renew. Energy 2017, 107, 373–385. [Google Scholar] [CrossRef]
- Kamal, M.M.; Saini, R.P. A numerical investigation on the influence of savonius blade helicity on the performance characteristics of hybrid cross-flow hydrokinetic turbine. Renew. Energy 2022, 190, 788–804. [Google Scholar] [CrossRef]
- Ansys Fluent. ANSYS Fluent UDF Manual; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Marsh, P.; Ranmuthugala, D.; Penesis, I.; Thomas, G. The influence of turbulence model and two and three-dimensional domain selection on the simulated performance characteristics of vertical axis tidal turbines. Renew. Energy 2017, 105, 106–116. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Tutorial Guide R18; ANSYS Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Maître, T.; Amet, E.; Pellone, C. Modeling of the flow in a Darrieus water turbine: Wall grid refinement analysis and comparison with experiments. Renew. Energy 2013, 51, 497–512. [Google Scholar] [CrossRef]
- Saini, G.; Saini, R.P. Numerical investigations on hybrid hydrokinetic turbine for electrification in remote area. In Proceedings of the All India Seminar on Renewable Energy for Sustainable Development (Institution of Engineers), Ghaziabad, India, 27–28 July 2018; pp. 27–28. [Google Scholar]
- Cavagnaro, R.J.; Polagye, B. Field performance assessment of a hydrokinetic turbine. Int. J. Mar. Energy 2016, 14, 125–142. [Google Scholar] [CrossRef]
- National Energy Action. Electricity Consumption around the Home: A Simple Guide to Understanding the Typical Usage of Electrical Appliances and Equipment in the Home. 2022. Available online: https://www.nea.org.uk/wp-content/uploads/2022/03/Electricity-Consumption-Around-the-Home.pdf (accessed on 18 February 2024).







| Authors | Turbine Type | Methodology | Turbine Properties | Flow Velocity (m/s) | Turbulence Model | Experimental Technique and Channel Size | Max. CP Value Achieved |
|---|---|---|---|---|---|---|---|
| Shiono et al. [28] | Helical Darrieus | Experimental | D = 300, H = 300 c = 62.8, 94.2, 125.7, 157.1 | 0.6, 1.0, and 1.4 | - | Tow tank method W = 3, Hw = 1.5, L = 30 | ≈0.35 |
| Niblick [29] | Gorlov | Experimental | D = 172, H = 234 | 0.8 | - | Tow tank method W = 0.757, Hw = 0.47, L = 3 | 0.24 |
| Yang and Shu [30] | Gorlov | Experimental and Numerical | D = 300, H = 400, c = 90 | 0.5, 1.0, and 1.5 | SST k-ω | W = 1.450, Hw = 1.450 | 0.416 |
| Wenlong et al. [31] | Darrieus | Numerical | D = 1220, 1600, and 2000 H = 1000, c = 150 | 0.5 | Standard k-ε | - | 0.1 |
| Sahim et al. [32] | Hybrid Darrieus–Savonius | Experimental | Darrieus D = 300, H = 300, c = 63 Savonius D = 30, H = 240 | 0.61 | - | Irrigation canal W = 1, Hw = 0.6 | 0.12 |
| Demircan [33] | Darrieus | Numerical | D = 175, H = 175, c = 32, d = 22 | 2.8 | SST k-ω | - | ≈0.35 |
| Bachant and Wosnik [34] | Gorlov | Experimental | D = 1000, H = 1320 | 0.5–1.5 | - | Tow tank method W = 3.66, Hw = 2.44, L = 36.6 | 0.35 |
| Kumar and Saini [35] | Savonius | Numerical | D = 160, H = 253 | 0.5–2 | Realizable k-ε | - | 0.39 |
| Basumatary et al. [36] | Savonius | Numerical | D = 260, d = 14 | 0.3–0.9 | SST k-ω | - | 0.284 |
| Saini and Saini [37] | Hybrid Darrieus–Savonius | Numerical | Darrieus D = 1500, c = 220 Savonius D = 300 | 0.5–2.5 | Realizable k-ε | - | 0.34 |
| Mejia et al. [38] | Darrieus | Numerical | D = 175, H = 175, c = 32, d = 22 | 2.8 | SST k-ω | - | 0.457 |
| Mosbahi et al. [39] | Helical Savonius | Experimental and Numerical | D = 182, H = 160, d = 10 | 0.86 | Realizable k-ε | İrrigation channel W = 0.6, Hw = 0.5 | 0.125 |
| Alizadeh et al. [40] | Savonius | Numerical | D = 970, H = 1000 | 0.48 | SST Transition | - | 0.29 |
| Saini and Saini [41] | Hybrid Darrieus–Savonius | Numerical | Darrieus D = 175, H = 160, c = 55 Savonius H = 160 | 0.5–2.0 | RNG k-ε | - | 0.109 |
| Kumar and Sarkar [42] | Helical Darrieus | Experimental and Numerical | D = 200, H = 200 | 0.5 | SST k-ω | Tow tank method W = 0.6, Hw = 0.7, L = 6 | 0.316 |
| General Characteristics | Axial Flow | Cross Flow |
|---|---|---|
| Efficiency | High | Low |
| Self-starting capability | Have | Depends on rotor type |
| Debris control | Highly effected | Less effected |
| Airfoil requirement | Yes | No |
| Manufacturing cost | High | Low |
| Torque produce | Stable | Fluctuating |
| Depth requirement | High | Low |
| Rotor shape | Circular disc | Cylindrical |
| Power transmission | Complex | Simple |
| Application | Ocean and tidal currents | River currents |
| Parameters | Gorlov | Darrieus | Savonius |
|---|---|---|---|
| Turbine height, H | 200 mm | 200 mm | 200 mm |
| Turbine diameter, D | 150 mm | 150 mm | 150 mm |
| Aspect ratio, AR | 1.33 | 1.33 | 1.33 |
| Shaft diameter, d | 12 mm | 12 mm | 12 mm |
| Solidity, σ | 0.35 | 0.32 | - |
| Blade number, n | 3 | 3 | 2 |
| Length of chord, c | 50 mm | 50 mm | - |
| Airfoil | S-1046 | S-1046 | - |
| Rotor type | Helical blade | Straight blade | Semi-circular |
| Overlap ratio, | - | - | 0.256 |
| Blockage ratio, BR | 0.136 | 0.136 | 0.136 |
| Blade inclination angle, φ (deg) | 43.7 | - | - |
| Overlap distance | - | - | 22 mm |
| Blade diameter | - | - | 86 mm |
| Location | Boundary Condition | Value |
|---|---|---|
| Inlet | Velocity | Velocity profile with UDF |
| Outlet | Pressure | 1 atm |
| Bottom and side walls | No-slip walls | - |
| Top surface | Symmetry | - |
| Turbine | No-slip walls | Variable depending on flow conditions |
| Refinement Level | Number of Elements | Number of Nodes | Quality Aspects (Average) | Mesh Size (mm) | CP | |||
|---|---|---|---|---|---|---|---|---|
| Skewness | Orthogonal Quality | Aspect Ratio | Rotating Part | Stationary Part | ||||
| Gorlov | ||||||||
| 1 | 333,189 | 186,708 | 0.15 | 0.86 | 1.91 | 10 | 20 | 0.054 |
| 2 | 421,726 | 279,518 | 0.13 | 0.89 | 1.70 | 10 | 15 | 0.079 |
| 3 | 745,051 | 341,202 | 0.17 | 0.84 | 1.76 | 10 | 15 | 0.118 |
| 4 | 812,752 | 215,958 | 0.22 | 0.79 | 1.88 | 12 | 20 | 0.204 |
| 5 | 880,997 | 283,737 | 0.20 | 0.80 | 1.87 | 10 | 20 | 0.199 |
| 6 | 1,050,528 | 315,311 | 0.21 | 0.80 | 1.86 | 10 | 20 | 0.184 |
| 7 | 1,259,805 | 350,862 | 0.21 | 0.79 | 1.86 | 10 | 20 | 0.197 |
| 8 | 1,467,147 | 633,013 | 0.17 | 0.84 | 2.00 | 6 | 15 | 0.177 |
| 9 | 1,760,138 | 773,086 | 0.17 | 0.84 | 2.09 | 5 | 15 | 0.178 |
| 10 | 2,207,172 | 1,129,430 | 0.16 | 0.86 | 1.80 | 6 | 10 | 0.177 |
| Darrieus | ||||||||
| 1 | 325,272 | 183,411 | 0.15 | 0.86 | 1.92 | 10 | 20 | 0.120 |
| 2 | 418,465 | 280,809 | 0.12 | 0.89 | 1.69 | 10 | 15 | 0.120 |
| 3 | 619,392 | 181,633 | 0.23 | 0.79 | 1.89 | 12 | 25 | 0.201 |
| 4 | 688,167 | 249,604 | 0.19 | 0.81 | 1.88 | 10 | 20 | 0.190 |
| 5 | 751,805 | 343,636 | 0.17 | 0.84 | 1.76 | 10 | 15 | 0.192 |
| 6 | 888,048 | 268,220 | 0.21 | 0.80 | 1.85 | 10 | 20 | 0.209 |
| 7 | 921,690 | 292,002 | 0.21 | 0.80 | 1.87 | 10 | 20 | 0.204 |
| 8 | 1,101,723 | 574,058 | 0.15 | 0.86 | 2.05 | 6 | 15 | 0.179 |
| 9 | 1,342,820 | 615,333 | 0.17 | 0.84 | 2.01 | 6 | 15 | 0.211 |
| 10 | 1,470,951 | 638,738 | 0.17 | 0.84 | 2.00 | 6 | 15 | 0.192 |
| Savonius | ||||||||
| 1 | 375,180 | 193,733 | 0.16 | 0.85 | 1.91 | 10 | 20 | 0.157 |
| 2 | 464,396 | 287,057 | 0.22 | 0.79 | 1.71 | 10 | 25 | 0.252 |
| 3 | 717,770 | 240,603 | 0.20 | 0.80 | 1.85 | 10 | 20 | 0.269 |
| 4 | 805,740 | 351,739 | 0.18 | 0.83 | 1.77 | 10 | 15 | 0.268 |
| 5 | 826,944 | 354,991 | 0.18 | 0.83 | 1.77 | 10 | 15 | 0.268 |
| 6 | 1,101,456 | 273,390 | 0.22 | 0.78 | 1.87 | 10 | 25 | 0.276 |
| 7 | 1,156,280 | 332,171 | 0.21 | 0.79 | 1.87 | 10 | 20 | 0.276 |
| 8 | 1,248,353 | 427,577 | 0.20 | 0.81 | 1.79 | 10 | 15 | 0.276 |
| 9 | 1,464,115 | 726,120 | 0.15 | 0.86 | 2.14 | 5 | 15 | 0.272 |
| 10 | 1,765,381 | 690,370 | 0.18 | 0.82 | 1.98 | 6 | 15 | 0.271 |
| Settings | Parameter |
|---|---|
| Water density | 1000 kg/m3 |
| Water viscosity | 0.001002 kg/m.s |
| Water velocity | 0.5–3 m/s |
| Turbulent model | SST k-ω |
| Pressure–velocity coupling | SIMPLE |
| Convergence criteria | 10−5 |
| Output frequency | Every time step |
| Time step size | 0.01 s |
| Maximum Power Harvested (Watts) | |||
|---|---|---|---|
| v = 1 m/s | v = 2 m/s | v = 3 m/s | |
| Gorlov | 3.52 | 26.39 | 93.9 |
| Darrieus | 4.33 | 33.78 | 118.64 |
| Savonius | 4.14 | 29.81 | 98.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakaya, D.; Bor, A.; Elçi, S. Numerical Analysis of Three Vertical Axis Turbine Designs for Improved Water Energy Efficiency. Energies 2024, 17, 1398. https://doi.org/10.3390/en17061398
Karakaya D, Bor A, Elçi S. Numerical Analysis of Three Vertical Axis Turbine Designs for Improved Water Energy Efficiency. Energies. 2024; 17(6):1398. https://doi.org/10.3390/en17061398
Chicago/Turabian StyleKarakaya, Derya, Aslı Bor, and Sebnem Elçi. 2024. "Numerical Analysis of Three Vertical Axis Turbine Designs for Improved Water Energy Efficiency" Energies 17, no. 6: 1398. https://doi.org/10.3390/en17061398
APA StyleKarakaya, D., Bor, A., & Elçi, S. (2024). Numerical Analysis of Three Vertical Axis Turbine Designs for Improved Water Energy Efficiency. Energies, 17(6), 1398. https://doi.org/10.3390/en17061398








