Author Contributions
Conceptualization, J.E. and S.G.; methodology, R.M., T.D., J.E. and S.G.; software, R.M., T.D., J.E. and S.G.; validation, R.M., T.D., J.E. and S.G.; formal analysis, R.M., T.D., J.E. and S.G.; investigation, R.M., T.D., J.E. and S.G.; resources, R.M., T.D., J.E. and S.G.; data curation, R.M. and T.D.; writing—original draft preparation, R.M. and T.D.; writing—review and editing, J.E. and S.G.; visualization, J.E. and S.G.; supervision, J.E. and S.G.; project administration, S.G.; funding acquisition, J.E. and S.G. All authors have read and agreed to the published version of the manuscript.
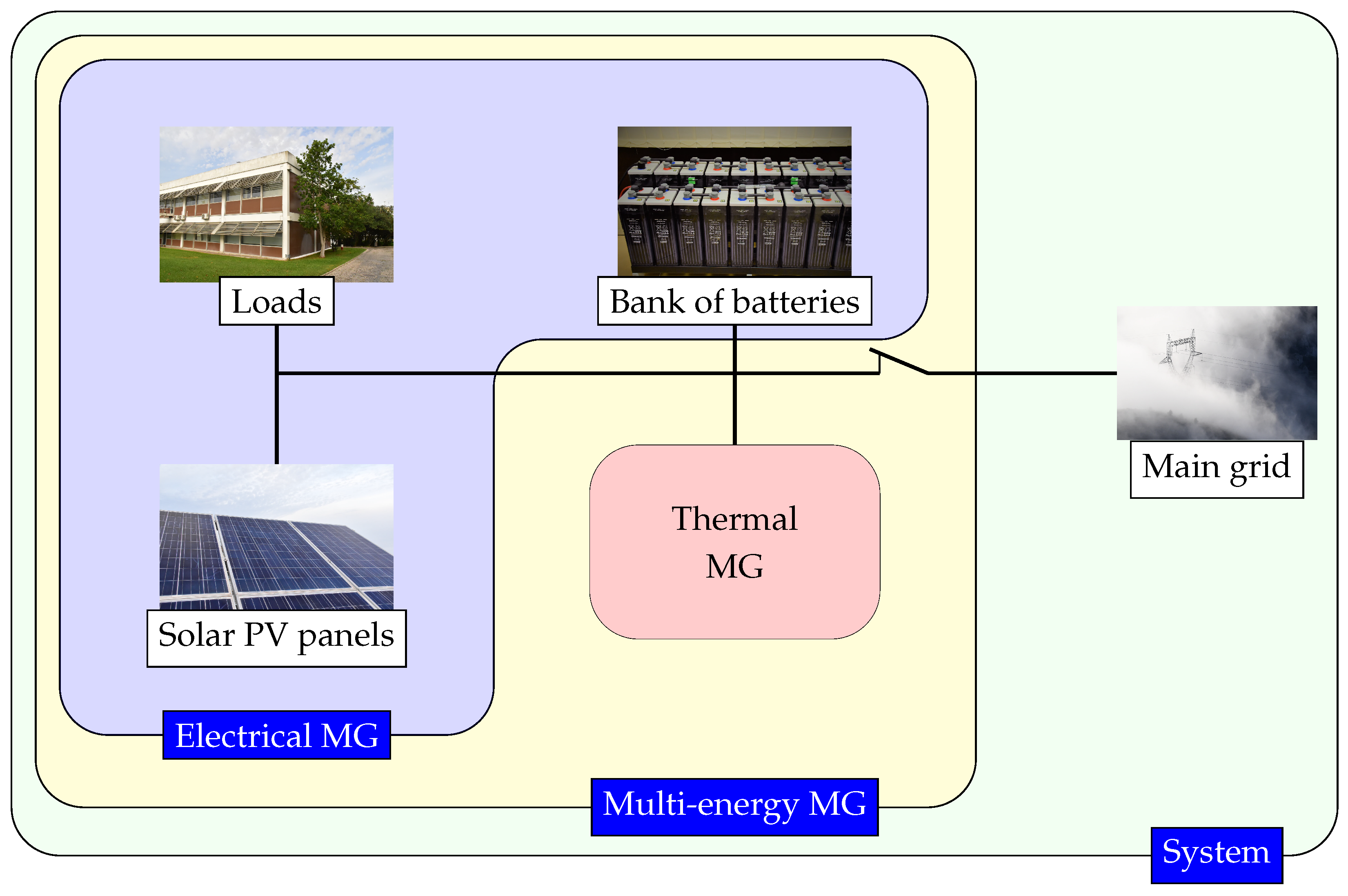
Figure 1.
Schematic of the LNEG building-integrated MG. The thermal MG is shown in
Figure 2.
Figure 1.
Schematic of the LNEG building-integrated MG. The thermal MG is shown in
Figure 2.
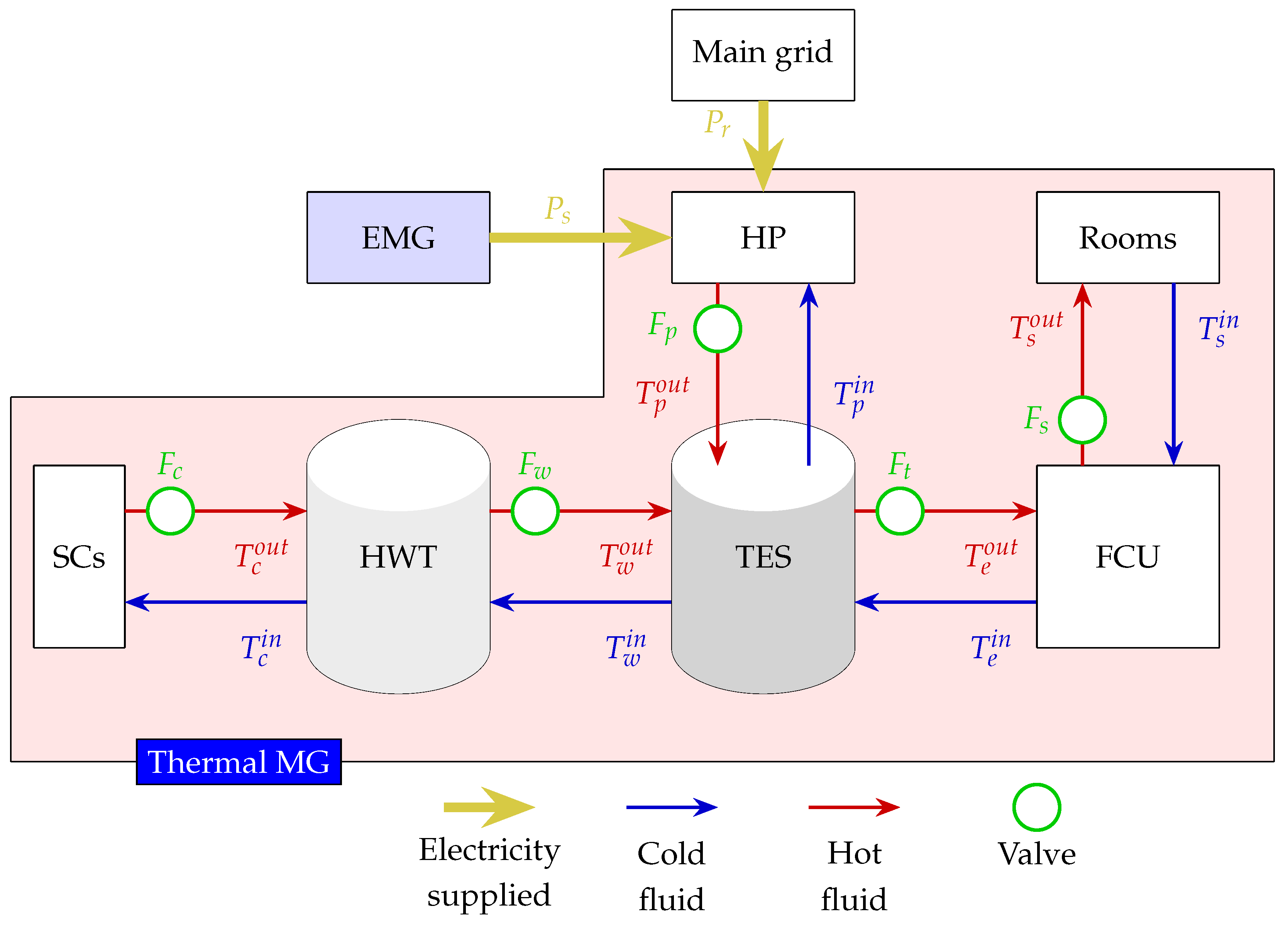
Figure 2.
Schematic of the LNEG thermal MG operated in economic mode. EMG: electrical MG (see
Figure 1). HP: heat pump. SCs: solar collectors. HWT: hot water tank. TES: thermal energy storage. FCU: fan coil unit.
: temperature of the water entering/leaving the SCs.
: temperature of the water entering/leaving the HWT.
: temperature of the water entering/leaving the TES.
: temperature of the water entering/leaving the HP.
: temperature of the water entering/leaving the FCUs.
: flow rate of the fluid circulating between the SCs and the HWT.
: flow rate of the water circulating between the HWT and the TES.
: flow rate of the water circulating between the TES and the FCUs.
: flow rate of the water circulating between the TES and the HP.
: supply air flow rate.
: electricity bought from the main grid.
: PV power generation surplus.
Figure 2.
Schematic of the LNEG thermal MG operated in economic mode. EMG: electrical MG (see
Figure 1). HP: heat pump. SCs: solar collectors. HWT: hot water tank. TES: thermal energy storage. FCU: fan coil unit.
: temperature of the water entering/leaving the SCs.
: temperature of the water entering/leaving the HWT.
: temperature of the water entering/leaving the TES.
: temperature of the water entering/leaving the HP.
: temperature of the water entering/leaving the FCUs.
: flow rate of the fluid circulating between the SCs and the HWT.
: flow rate of the water circulating between the HWT and the TES.
: flow rate of the water circulating between the TES and the FCUs.
: flow rate of the water circulating between the TES and the HP.
: supply air flow rate.
: electricity bought from the main grid.
: PV power generation surplus.
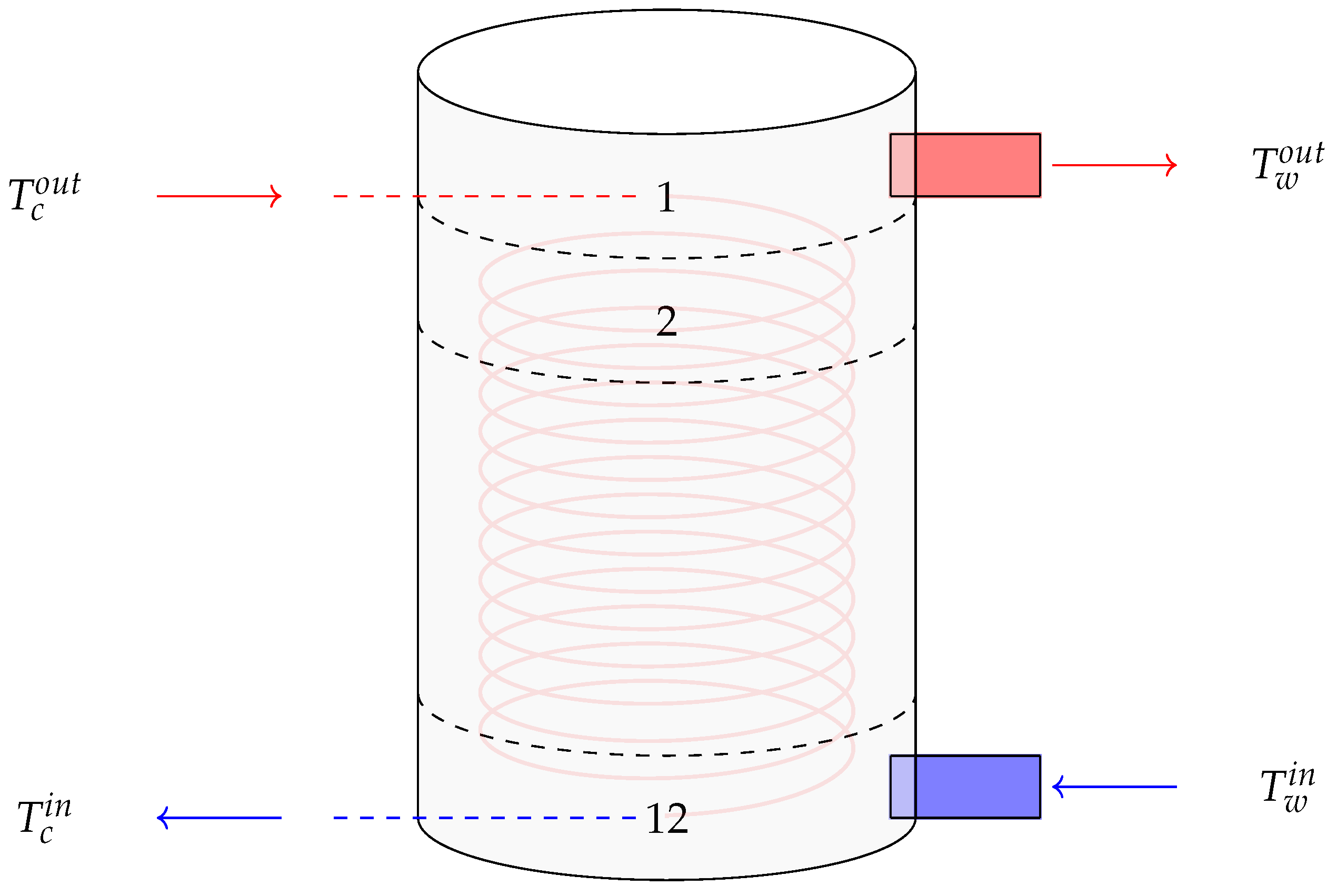
Figure 3.
Schematic of the 300 L HWT. : temperature of the water entering/leaving the SCs. : temperature of the water entering/leaving the HWT. The heat exchanger (layer 1 to layer 12) is depicted by the coil in red.
Figure 3.
Schematic of the 300 L HWT. : temperature of the water entering/leaving the SCs. : temperature of the water entering/leaving the HWT. The heat exchanger (layer 1 to layer 12) is depicted by the coil in red.
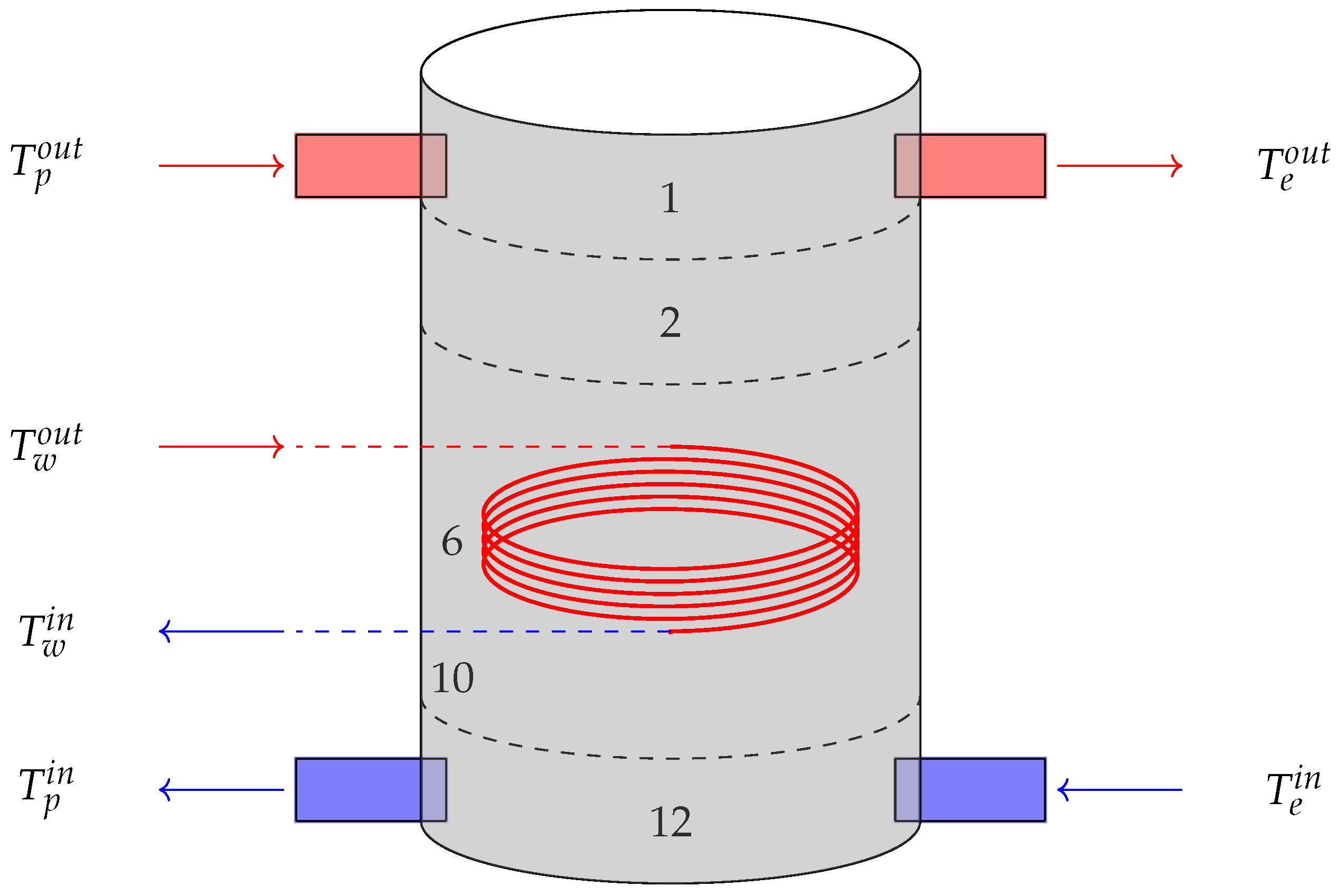
Figure 4.
Schematic of the 1000 L TES. : temperature of the water entering/leaving the HWT. : temperature of the water entering/leaving the TES. : temperature of the water entering/leaving the HP. The heat exchanger (layer 6 to layer 10) is depicted by the red coil.
Figure 4.
Schematic of the 1000 L TES. : temperature of the water entering/leaving the HWT. : temperature of the water entering/leaving the TES. : temperature of the water entering/leaving the HP. The heat exchanger (layer 6 to layer 10) is depicted by the red coil.
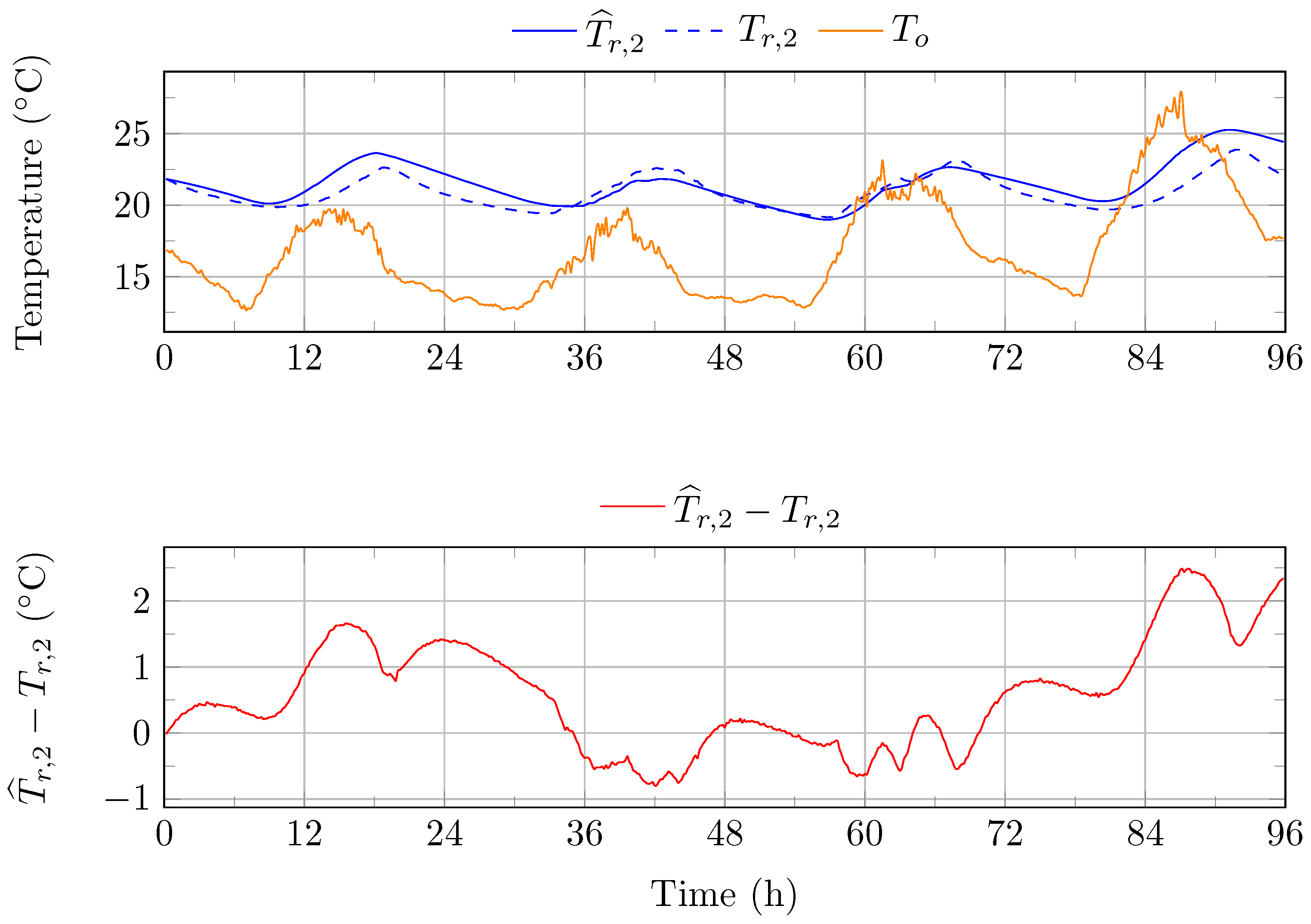
Figure 5.
Air temperature in room R2, from May 1 to May 4. : simulated air temperature in room R2. : measured air temperature in room R2. : outdoor temperature.
Figure 5.
Air temperature in room R2, from May 1 to May 4. : simulated air temperature in room R2. : measured air temperature in room R2. : outdoor temperature.
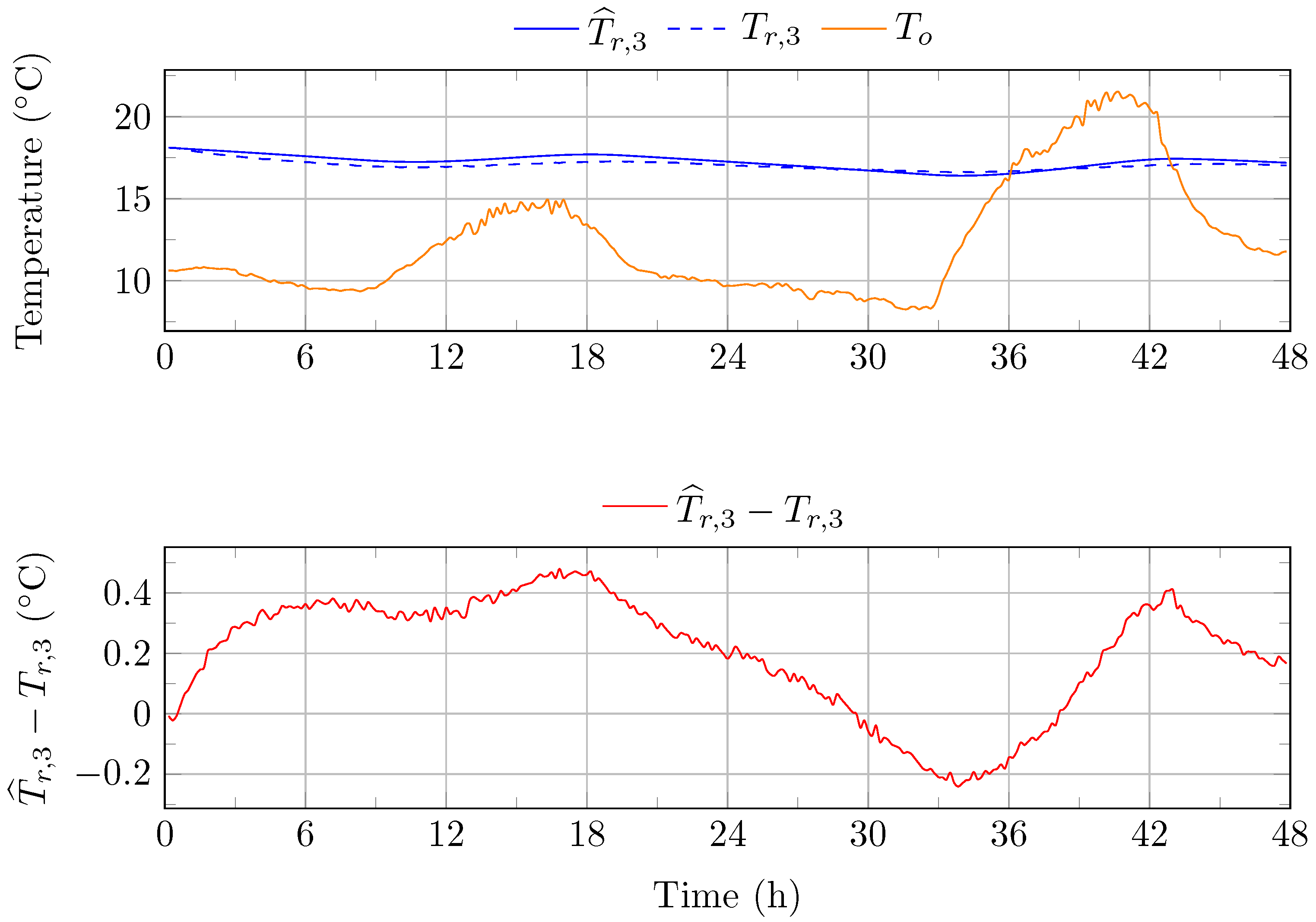
Figure 6.
Air temperature in room R3, from May 1 to May 4. : simulated air temperature in room R3. : measured air temperature in room R3. : outdoor temperature.
Figure 6.
Air temperature in room R3, from May 1 to May 4. : simulated air temperature in room R3. : measured air temperature in room R3. : outdoor temperature.
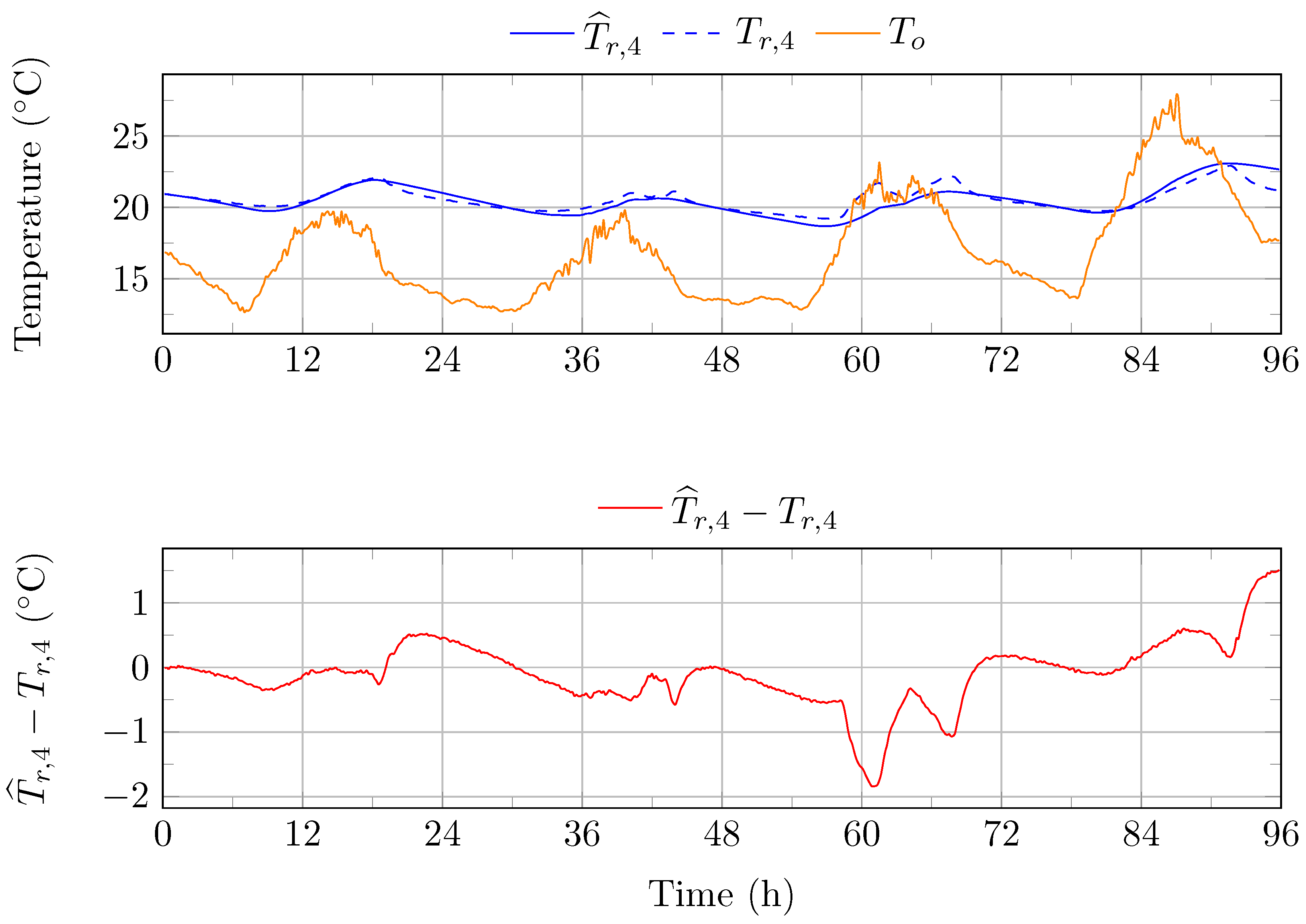
Figure 7.
Air temperature in room R4, from May 1 to May 4. : simulated air temperature in room R4. : measured air temperature in room R4. : outdoor temperature.
Figure 7.
Air temperature in room R4, from May 1 to May 4. : simulated air temperature in room R4. : measured air temperature in room R4. : outdoor temperature.
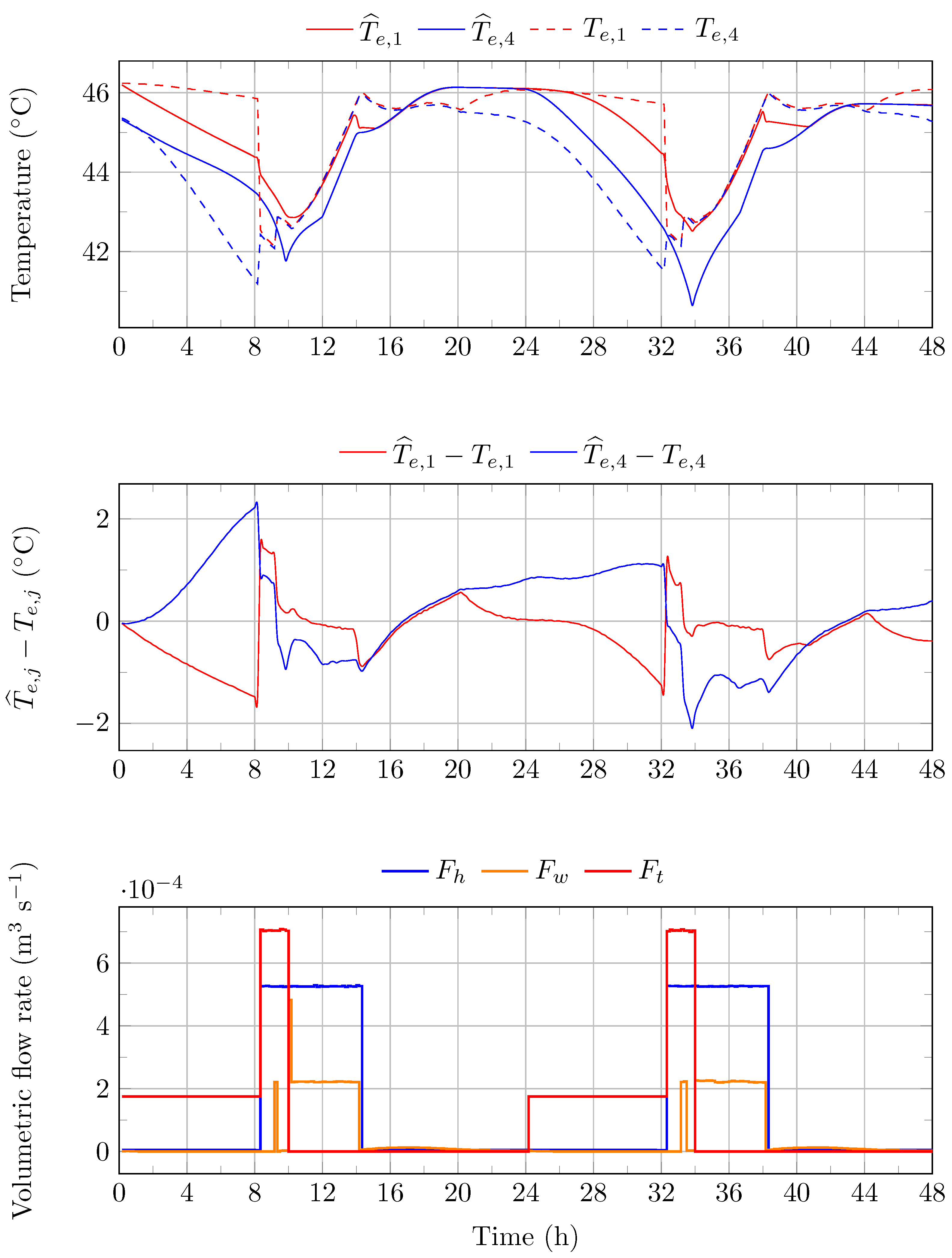
Figure 8.
Water temperatures and volumetric flow rates (TES), from May 11 to May 12. : simulated/measured temperature of the water in layer 1 of the TES. : simulated/measured temperature of the water in layer 4 of the TES. : volumetric flow rate of the water circulating between the HP and the TES. : volumetric flow rate of the water circulating between the HWT and the TES. : volumetric flow rate of the water circulating between the TES and the FCUs.
Figure 8.
Water temperatures and volumetric flow rates (TES), from May 11 to May 12. : simulated/measured temperature of the water in layer 1 of the TES. : simulated/measured temperature of the water in layer 4 of the TES. : volumetric flow rate of the water circulating between the HP and the TES. : volumetric flow rate of the water circulating between the HWT and the TES. : volumetric flow rate of the water circulating between the TES and the FCUs.
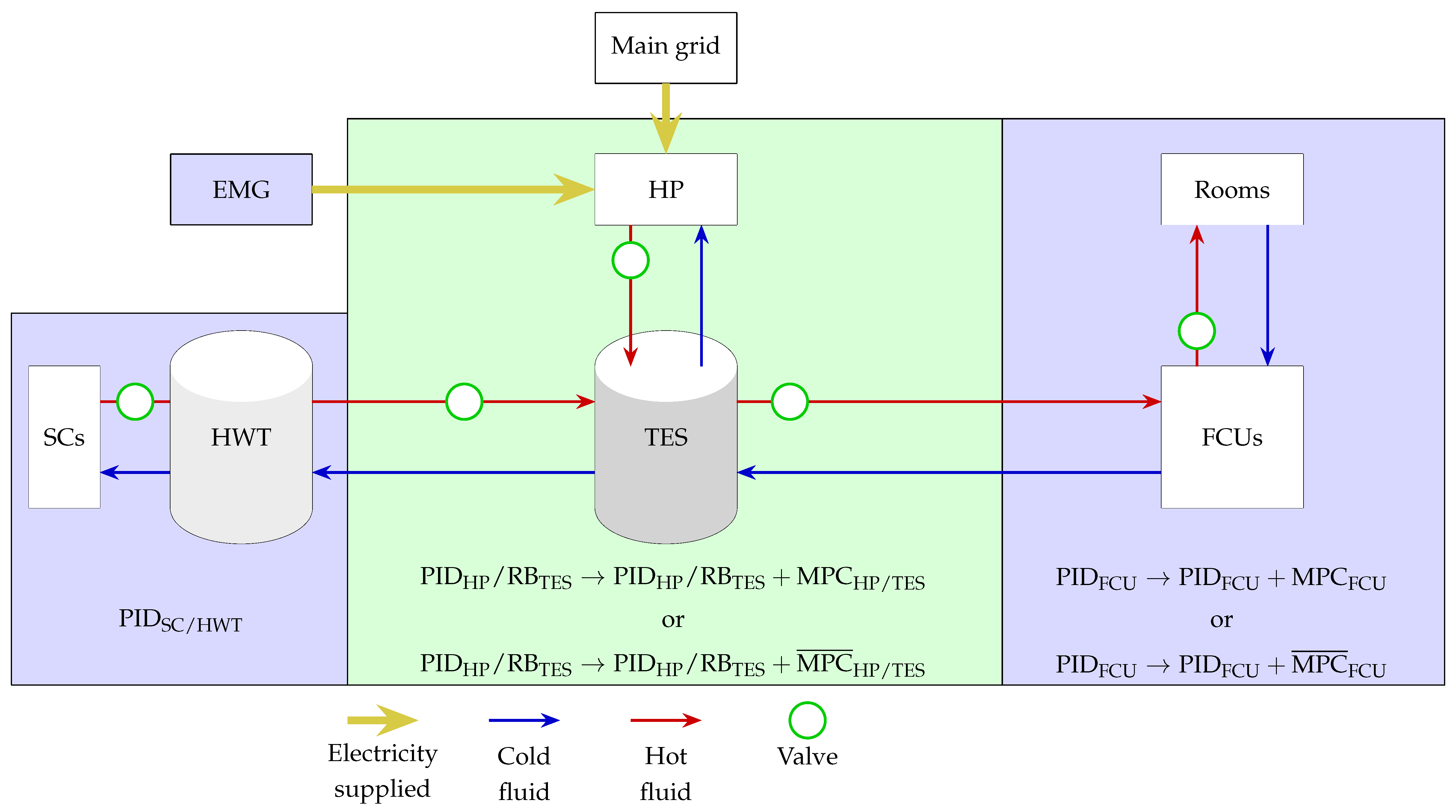
Figure 9.
Synoptic of the IMPROVEMENT EMS. EMG: electrical microgrid. HP: heat pump. SCs: solar collectors. HWT: hot water tank. TES: thermal energy storage. FCU: fan coil unit. : SC/HWT PID controller. : HP PID controller. : TES rule-based controller. : HP/TES optimization-based MPC controller. : HP/TES optimization-free MPC controller. : FCU PID controller. : FCU optimization-based MPC controller. : FCU optimization-free MPC controller.
Figure 9.
Synoptic of the IMPROVEMENT EMS. EMG: electrical microgrid. HP: heat pump. SCs: solar collectors. HWT: hot water tank. TES: thermal energy storage. FCU: fan coil unit. : SC/HWT PID controller. : HP PID controller. : TES rule-based controller. : HP/TES optimization-based MPC controller. : HP/TES optimization-free MPC controller. : FCU PID controller. : FCU optimization-based MPC controller. : FCU optimization-free MPC controller.
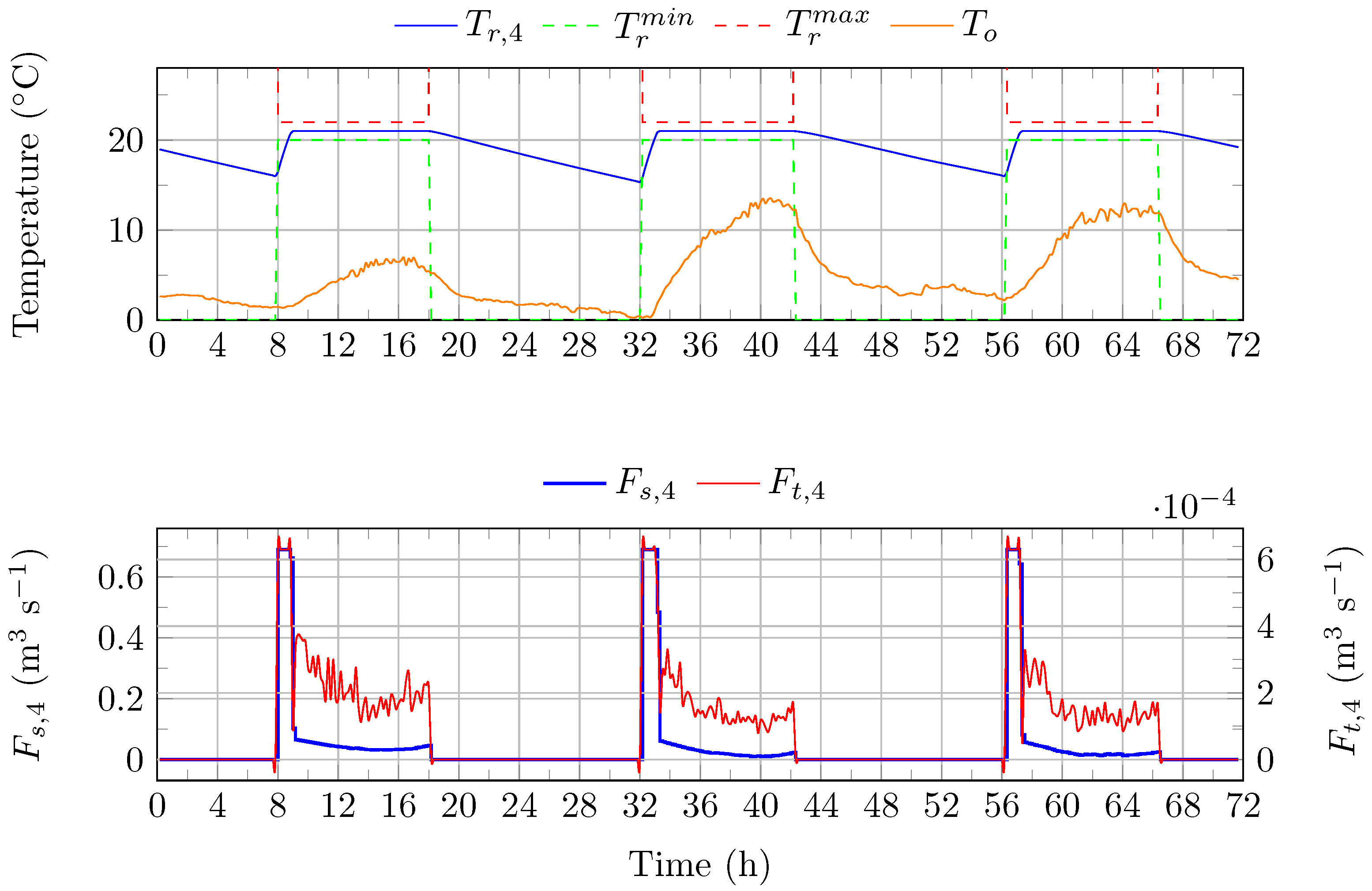
Figure 10.
PID-based strategy () for the management of thermal comfort in room R4 (3-day simulation). : air temperature in room R4. : outdoor temperature. : supply air flow rate of FCU 4. : flow rate of the water circulating between the TES and FCU 4.
Figure 10.
PID-based strategy () for the management of thermal comfort in room R4 (3-day simulation). : air temperature in room R4. : outdoor temperature. : supply air flow rate of FCU 4. : flow rate of the water circulating between the TES and FCU 4.
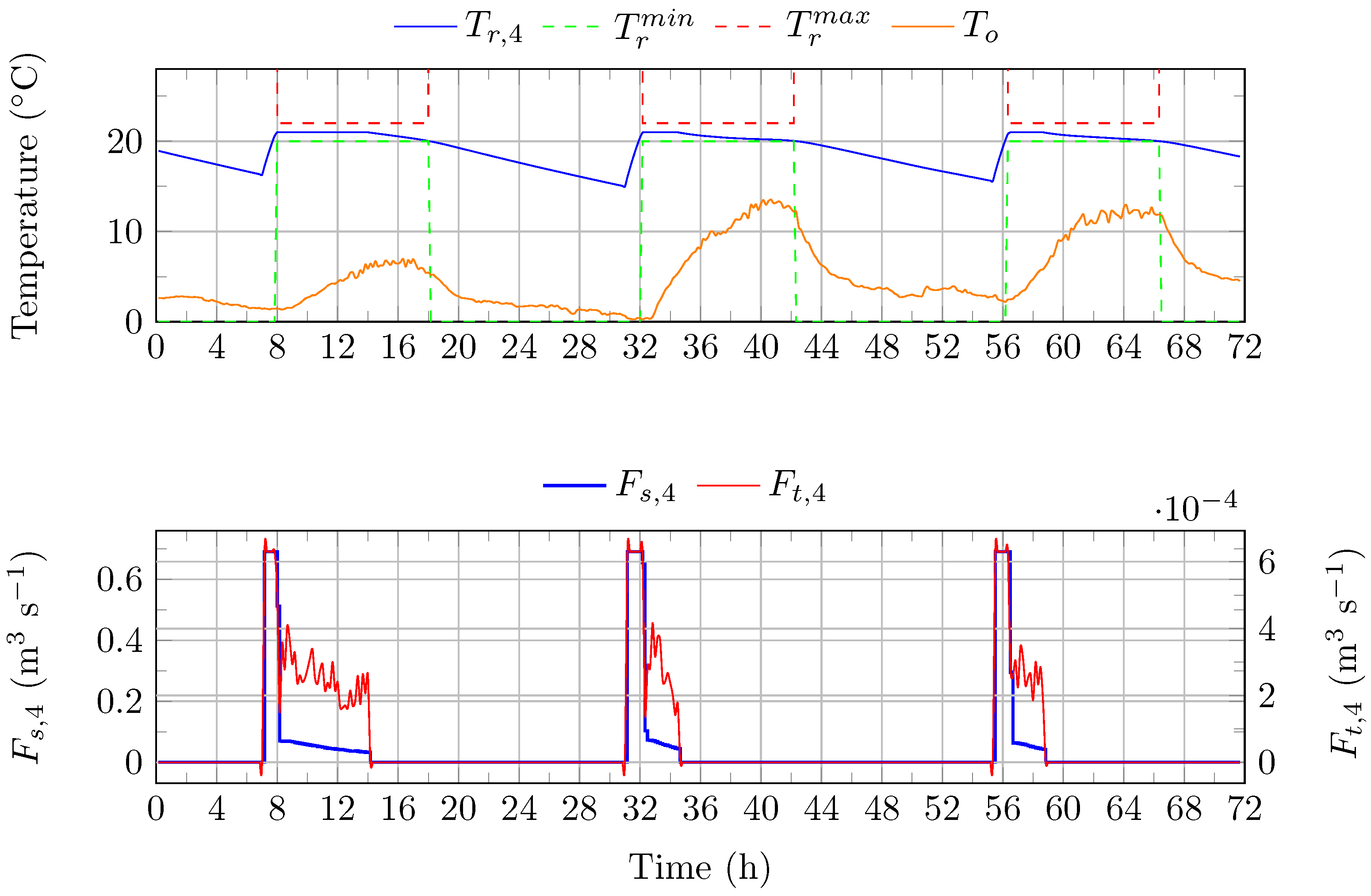
Figure 11.
Optimization-free/based MPC strategy () for the management of thermal comfort in room R4 (3-day simulation). : air temperature in room R4. : outdoor temperature. : supply air flow rate of FCU 4. : flow rate of the water circulating between the TES and FCU 4.
Figure 11.
Optimization-free/based MPC strategy () for the management of thermal comfort in room R4 (3-day simulation). : air temperature in room R4. : outdoor temperature. : supply air flow rate of FCU 4. : flow rate of the water circulating between the TES and FCU 4.
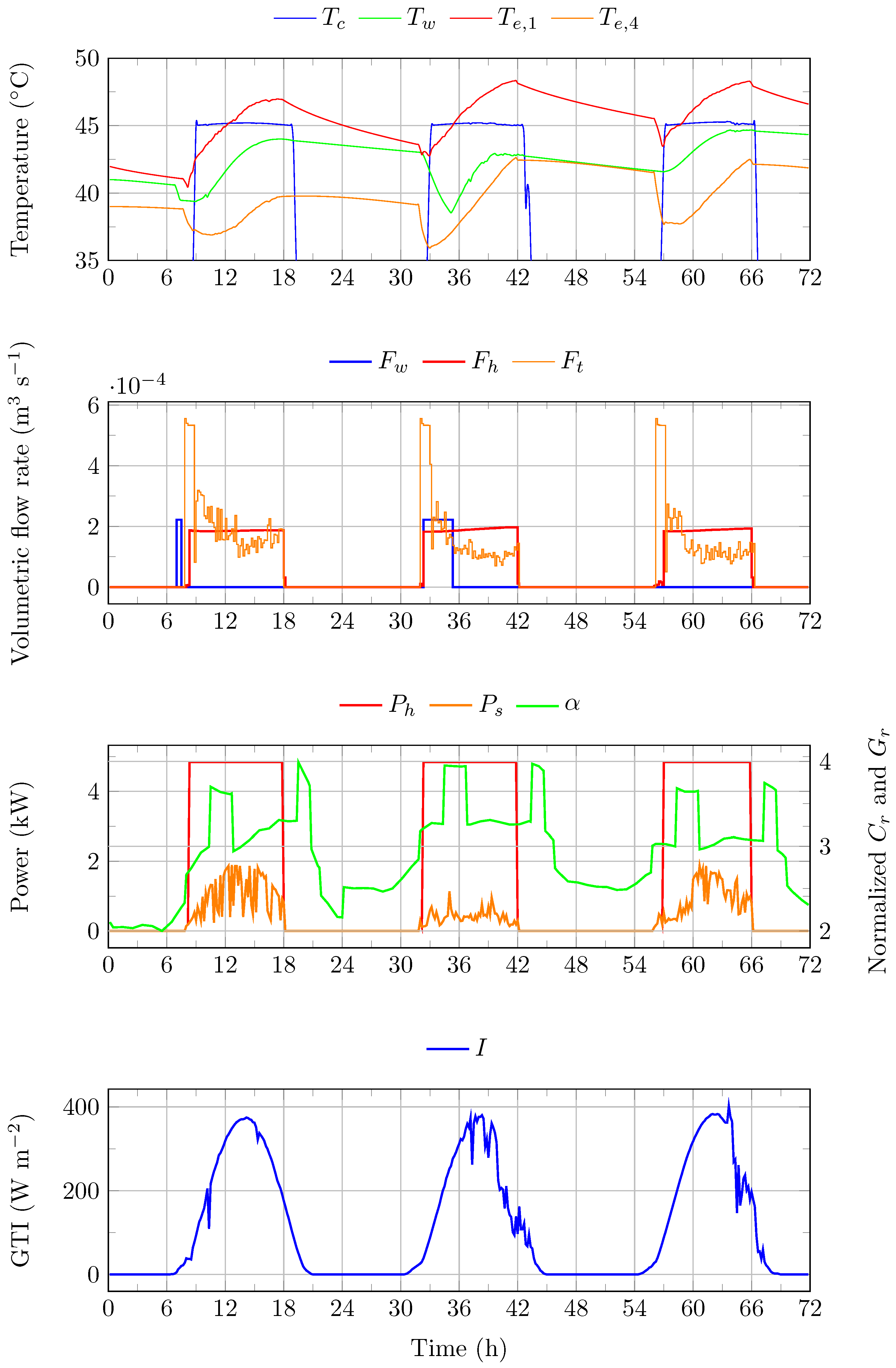
Figure 12.
strategy (3-day simulation). : temperature of the water in the hot water tank (HWT). : temperature of the fluid circulating in the SCs. : temperature of the water in the layer j of the TES. : flow rate of the water circulating between the HP and the TES. : flow rate of the water circulating between the HWT and the TES. : flow rate of the water circulating between the TES and the FCUs. : PV power generation surplus. : sum of normalized electricity tariffs and normalized emissions. : global tilted irradiance.
Figure 12.
strategy (3-day simulation). : temperature of the water in the hot water tank (HWT). : temperature of the fluid circulating in the SCs. : temperature of the water in the layer j of the TES. : flow rate of the water circulating between the HP and the TES. : flow rate of the water circulating between the HWT and the TES. : flow rate of the water circulating between the TES and the FCUs. : PV power generation surplus. : sum of normalized electricity tariffs and normalized emissions. : global tilted irradiance.
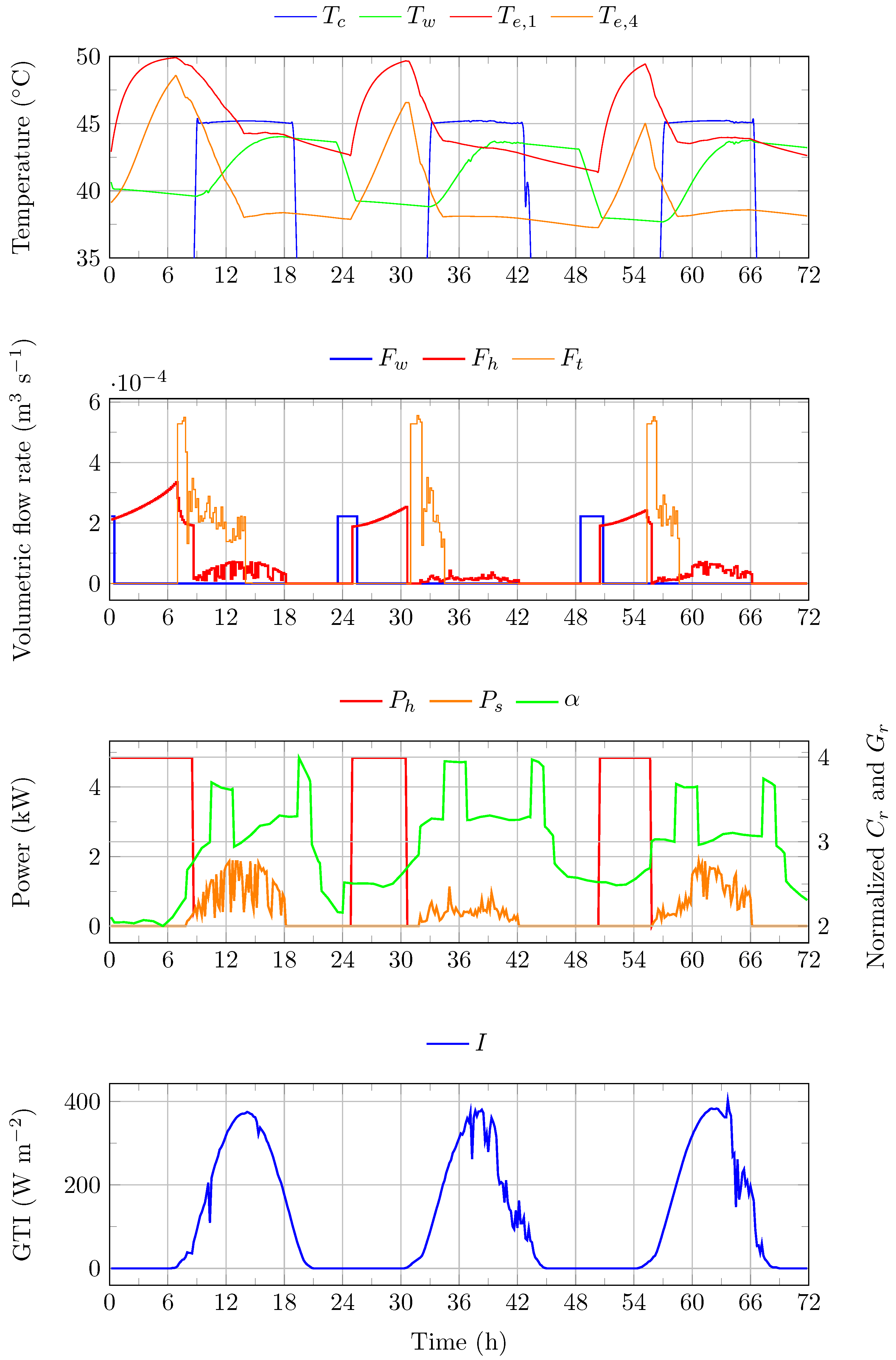
Figure 13.
strategy (3-day simulation). : temperature of the water in the hot water tank (HWT). : temperature of the fluid circulating in the SCs. : temperature of the water in the layer j of the TES. : flow rate of the water circulating between the HP and the TES. : flow rate of the water circulating between the HWT and the TES. : flow rate of the water circulating between the TES and the FCUs. : PV power generation surplus. : sum of normalized electricity tariffs and normalized emissions. : global tilted irradiance.
Figure 13.
strategy (3-day simulation). : temperature of the water in the hot water tank (HWT). : temperature of the fluid circulating in the SCs. : temperature of the water in the layer j of the TES. : flow rate of the water circulating between the HP and the TES. : flow rate of the water circulating between the HWT and the TES. : flow rate of the water circulating between the TES and the FCUs. : PV power generation surplus. : sum of normalized electricity tariffs and normalized emissions. : global tilted irradiance.
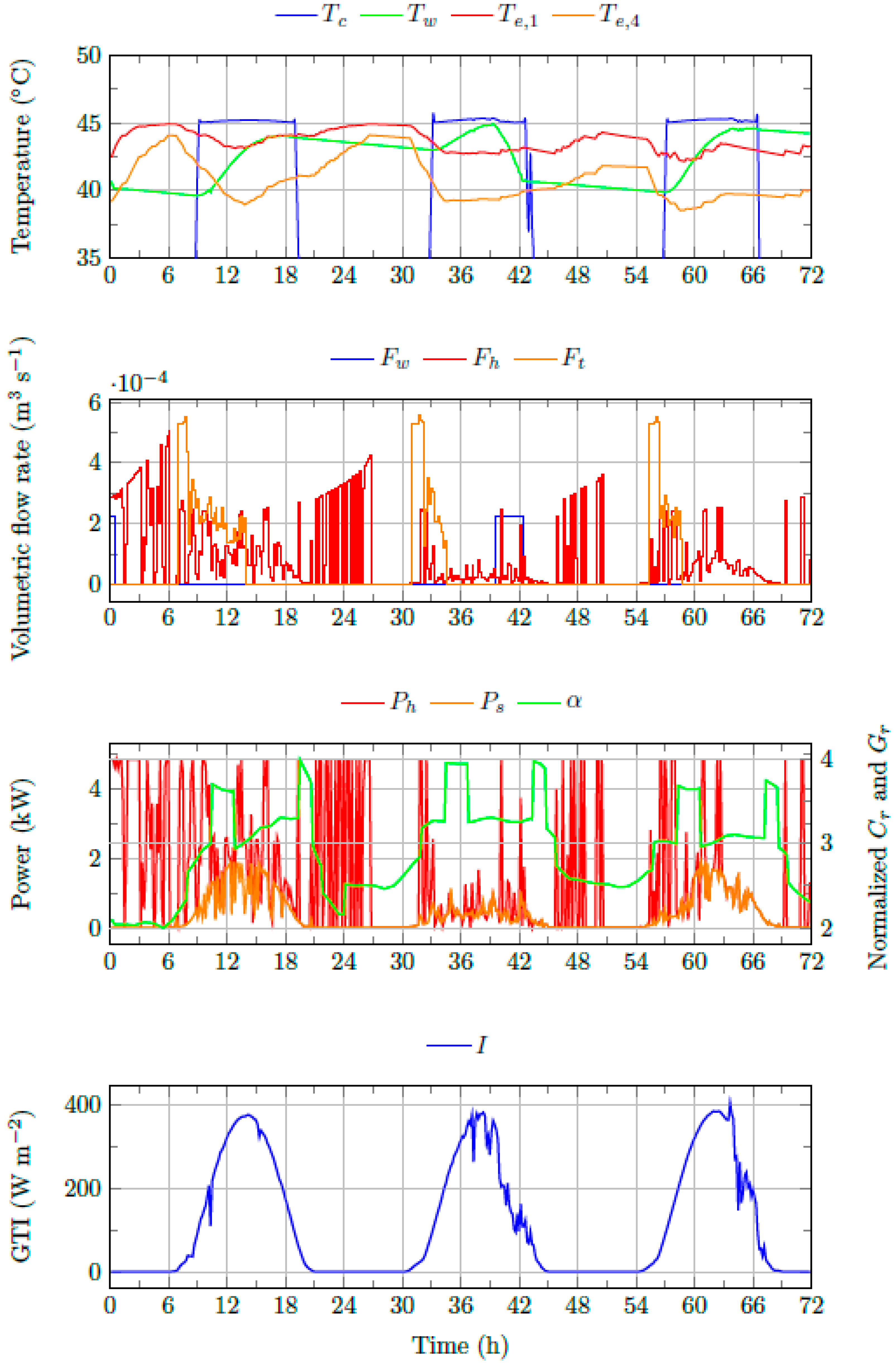
Figure 14.
strategy (3-day simulation). : temperature of the water in the hot water tank (HWT). : temperature of the fluid circulating in the SCs. : temperature of the water in the layer j of the TES. : flow rate of the water circulating between the HP and the TES. : flow rate of the water circulating between the HWT and the TES. : flow rate of the water circulating between the TES and the FCUs. : PV power generation surplus. : sum of normalized electricity tariffs and normalized emissions. : global tilted irradiance.
Figure 14.
strategy (3-day simulation). : temperature of the water in the hot water tank (HWT). : temperature of the fluid circulating in the SCs. : temperature of the water in the layer j of the TES. : flow rate of the water circulating between the HP and the TES. : flow rate of the water circulating between the HWT and the TES. : flow rate of the water circulating between the TES and the FCUs. : PV power generation surplus. : sum of normalized electricity tariffs and normalized emissions. : global tilted irradiance.
Table 1.
Modeling results. : air temperature in room z. : temperature of the water in the TES (layer j). RMSE: root-mean-square error. nRMSE: normalized root-mean-square error.
Table 1.
Modeling results. : air temperature in room z. : temperature of the water in the TES (layer j). RMSE: root-mean-square error. nRMSE: normalized root-mean-square error.
| | Thermal Zones (R2, R3 and R4) | TES |
|---|
| | February | May | May |
| | | | | | | | | |
| RMSE | | | | | | | | |
| nRMSE | | | | | | | | |
Table 2.
PID controllers for the management of thermal comfort. TES: thermal energy storage. FCU: fan coil unit. : proportional gain. : integral gain. : derivative gain. N: filter coefficient.
Table 2.
PID controllers for the management of thermal comfort. TES: thermal energy storage. FCU: fan coil unit. : proportional gain. : integral gain. : derivative gain. N: filter coefficient.
| PID Controller | | | | N |
|---|
| TES-FCU R1 | | | | |
| TES-FCU R2 | | | | |
| TES-FCU R3 | | | | |
| TES-FCU R4 | | | | |
| FCU R1/R2/R3 | | | | |
| FCU R4 | | | | |
Table 3.
Simulation parameters.
Table 3.
Simulation parameters.
| Room | R1 | R2 | R3 | R4 |
|---|
| Number of people | 1 | 1 | 4 | 16 |
| Beginning/end of the occupancy period | 8 AM/6 PM |
| Air temperature set point (occupancy/nonoccupancy period) | 21 /none |
| Minimum/maximum air temperature (occupancy period) | 20 /22 |
Table 4.
Air temperature constraint violation (3-day simulation). : PID-based strategy. : optimization-based MPC strategy. : optimization-free MPC strategy.
Table 4.
Air temperature constraint violation (3-day simulation). : PID-based strategy. : optimization-based MPC strategy. : optimization-free MPC strategy.
| | [] |
|---|
| Season | Strategy | R1/R2 | R3 | R4 |
| | | 0.20 | 0.05 | 0.66 |
| Winter | | 0 | 0 | 0 |
| | | 0 | 0 | 0 |
| | | 0.05 | 0.01 | 0.20 |
| Spring | | 0 | 0 | 0 |
| | | 0 | 0 | 0 |
Table 5.
Heat delivered by the FCUs (3-day simulation). : PID-based strategy. : optimization-based MPC strategy. : optimization-free MPC strategy.
Table 5.
Heat delivered by the FCUs (3-day simulation). : PID-based strategy. : optimization-based MPC strategy. : optimization-free MPC strategy.
| | [kWh] |
|---|
| Season | Strategy | R1/R2 | R3 | R4 |
| | | 2.2 | 2.2 | 15.6 |
| Winter | | 1.5 | 1.3 | 11.4 |
| | | 1.5 | 1.3 | 11.4 |
| | | 1.3 | 1.5 | 7.6 |
| Spring | | 0.6 | 1.2 | 3.2 |
| | | 0.6 | 1.2 | 3.2 |
Table 6.
Computational cost (3-day simulation). : PID-based strategy. : optimization-based MPC strategy (18 workers are used in parallel). : optimization-free MPC strategy. Calculation server used: two processors, Intel Xeon Gold 6230 @ 2.10 GHz with 20 cores and 40 threads, 512 Go of RAM, and an average CPU mark of 26,657.
Table 6.
Computational cost (3-day simulation). : PID-based strategy. : optimization-based MPC strategy (18 workers are used in parallel). : optimization-free MPC strategy. Calculation server used: two processors, Intel Xeon Gold 6230 @ 2.10 GHz with 20 cores and 40 threads, 512 Go of RAM, and an average CPU mark of 26,657.
| | Computational Cost |
|---|
| Season | Strategy | R1/R2 | R3 | R4 |
| | | 34 | 47 | 23 |
| Winter | | 203,940 | 283,518 | 162,846 |
| | | 5185 | 2754 | 2848 |
| | | 36 | 81 | 22 |
| Spring | | 132,192 | 143,136 | 95,940 |
| | | 2891 | 2827 | 3072 |
Table 7.
PID controllers for the management of thermal resources. SCs: solar collectors. HWT: hot water tank. HP: heat pump. : proportional gain. : integral gain. : derivative gain. N: filter coefficient.
Table 7.
PID controllers for the management of thermal resources. SCs: solar collectors. HWT: hot water tank. HP: heat pump. : proportional gain. : integral gain. : derivative gain. N: filter coefficient.
| System | | | | N |
|---|
| SCs/HWT | | | | |
| HP | | | | |
Table 8.
Electricity bought from the main grid (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy.
Table 8.
Electricity bought from the main grid (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy.
| | Electricity Bought from the Main Grid [![Energies 17 01355 i001 Energies 17 01355 i001]() ] ] |
|---|
| Season | Strategy | No Use of PV Power Generation Surplus | Use of PV Power Generation Surplus |
| | | 26.36 | 21.91 |
| Winter | | 14.08 | 12.34 |
| | | 13.54 | 11.08 |
| | | 13.41 | 7.53 |
| Spring | | 0.42 | 0.42 |
| | | 0.31 | 0.35 |
Table 9.
emissions related to the electricity bought from the main grid (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy.
Table 9.
emissions related to the electricity bought from the main grid (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy.
| | Emissions [] |
|---|
| Season | Strategy | No Use of PV Power Generation Surplus | Use of PV Power Generation Surplus |
| | | 55.8 | 46.5 |
| Winter | | 35.6 | 31.7 |
| | | 32.3 | 27.8 |
| | | 25.9 | 14.4 |
| Spring | | 0.9 | 0.9 |
| | | 0.7 | 0.7 |
Table 10.
Hourly average temperature () constraint deviation (3-day simulation). : PID/rule-based strategy.
Table 10.
Hourly average temperature () constraint deviation (3-day simulation). : PID/rule-based strategy.
| | [] |
|---|
| Season | Strategy | No Use of PV Power Generation Surplus | Use of PV Power Generation Surplus |
| Winter | | 1.43 | 1.41 |
| Spring | | 0.19 | 0.06 |
Table 11.
Objective function (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy.
Table 11.
Objective function (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy.
| | Objective Function [] |
|---|
| Season | Strategy | No Use of PV Power Generation Surplus | Use of PV Power Generation Surplus |
| | | 1167.2 | 1080.1 |
| Winter | | 252.7 | 222.0 |
| | | 240.5 | 206.7 |
| | | 310.9 | 150.9 |
| Spring | | 6.7 | 6.7 |
| | | 4.9 | 5.5 |
Table 12.
Computational cost (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy. Calculation server used: two processors Intel Xeon Gold 6230 @ 2.10 GHz with 20 cores and 40 threads, 512 Go of RAM and an average CPU mark of 26,657. ★ 18 workers in the parallel pool.
Table 12.
Computational cost (3-day simulation). : PID/rule-based strategy. : optimization-free MPC strategy. : optimization-based MPC strategy. Calculation server used: two processors Intel Xeon Gold 6230 @ 2.10 GHz with 20 cores and 40 threads, 512 Go of RAM and an average CPU mark of 26,657. ★ 18 workers in the parallel pool.
| | Computational Cost |
|---|
| Season | Strategy | No Use of PV Power Generation Surplus | Use of PV Power Generation Surplus |
| | | 126 | 179 |
| Winter | | 2824 | 2566 |
| | | 3,280,284 ★ | 3,229,758 ★ |
| | | 157 | 176 |
| Spring | | 1950 | 2669 |
| | | 2,788,524 ★ | 2,589,102 ★ |
 ]
]






