Influence of Background Voltage Distortion on Operation of Passive Harmonic Compensation Devices
Abstract
1. Introduction
2. Materials and Methods
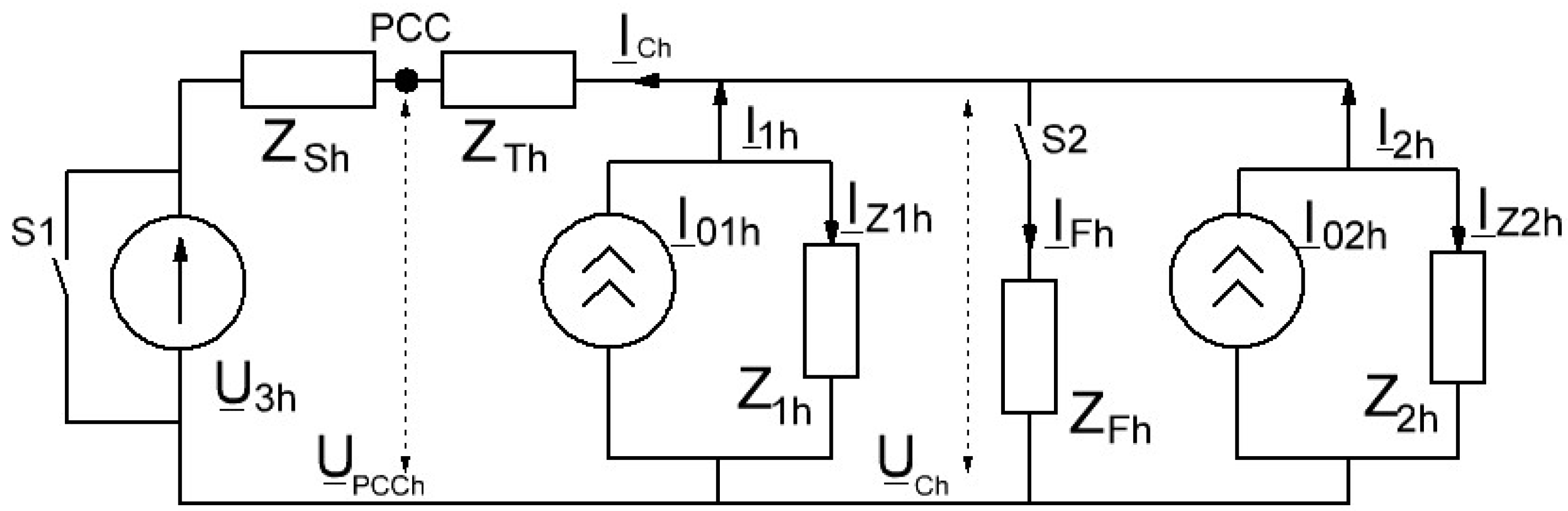
2.1. Method for Determination the Share Contribution of Harmonic Sources
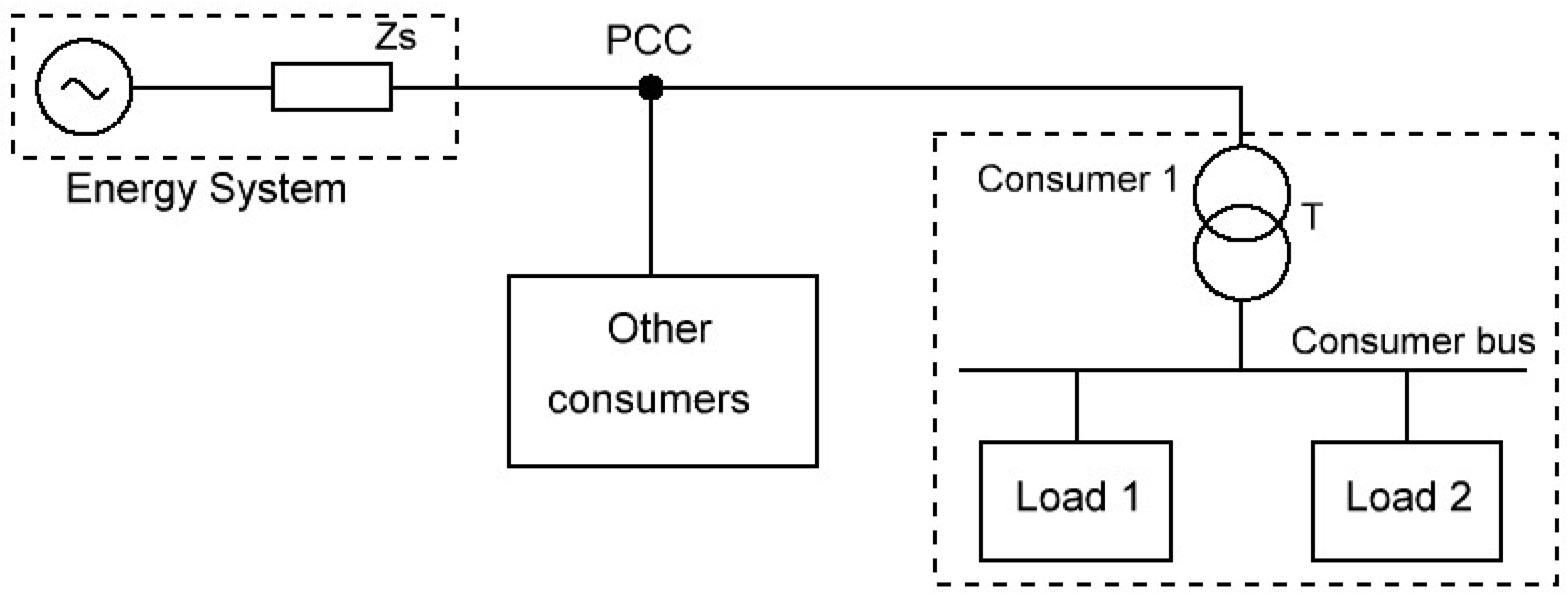
2.2. Description of Simulation Model and Parameters
- -
- The SPHF harmonic current when external distortion source TR is disconnected and all consumer loads are connected for the corresponding mode (IFh_0);
- -
- The SPHF harmonic current when external distortion source TR is connected and all consumer loads are connected for the corresponding mode (IFh_1);
- -
- The SPHF harmonic current when external distortion source TR is connected and all consumer loads (except SPHF) are disconnected (IFh_2).
3. Results and Discussion
3.1. Simulation Results
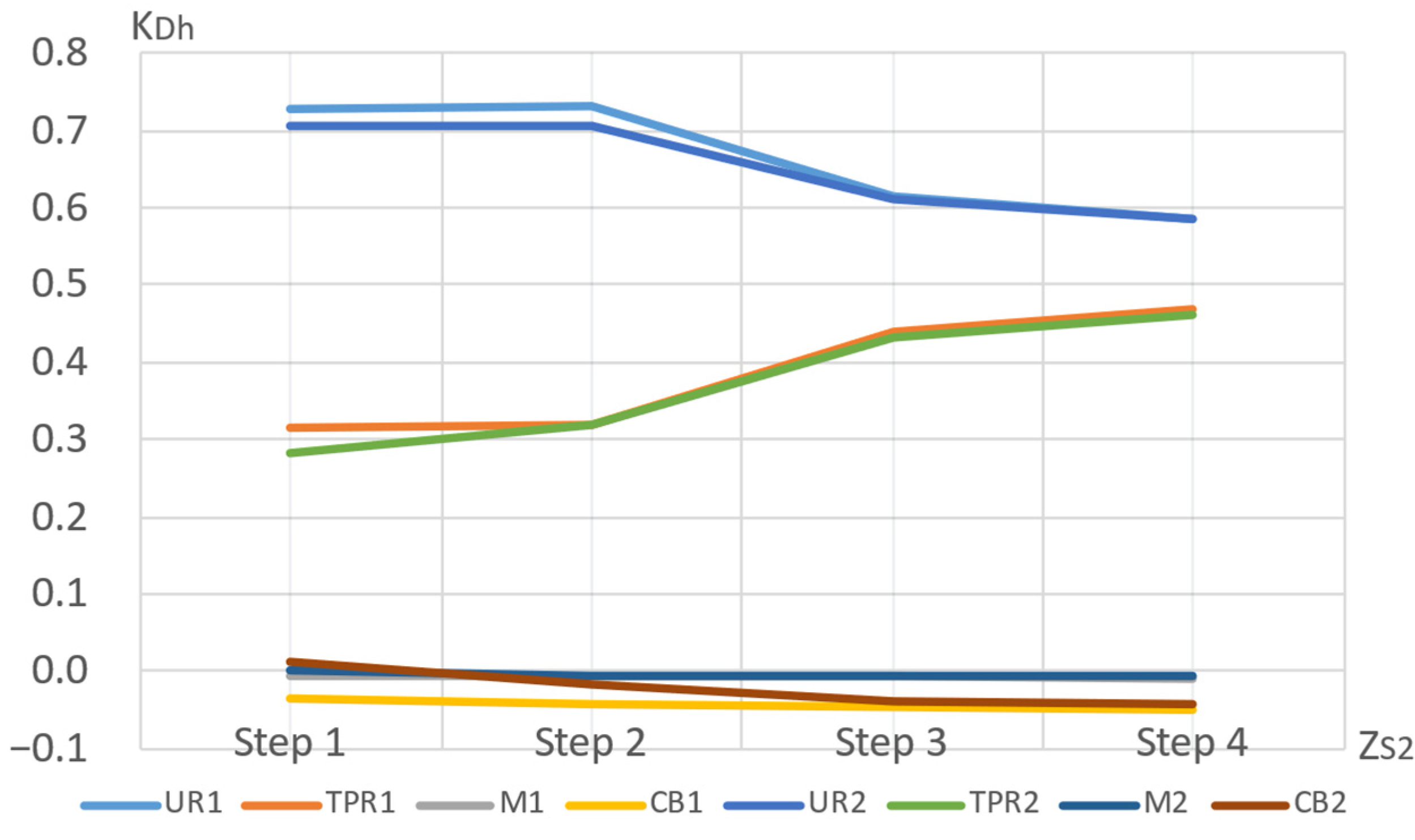
3.1.1. Contribution of Internal Distortion Sources Depending on the Parameters of the External Source and the Supply Feeder
3.1.2. Contribution of External Distortion Sources Depending on the Parameters of the Supply Feeder
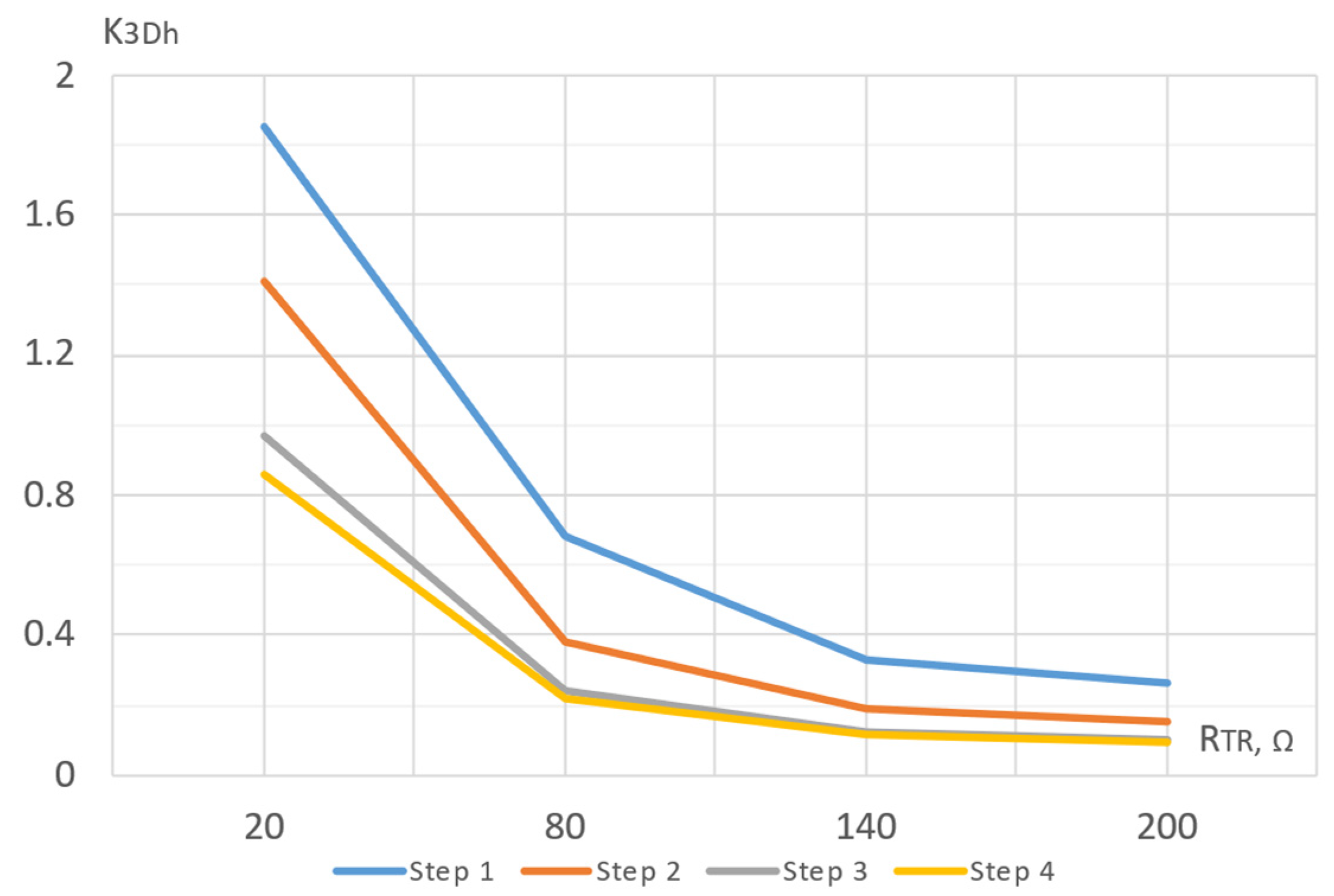
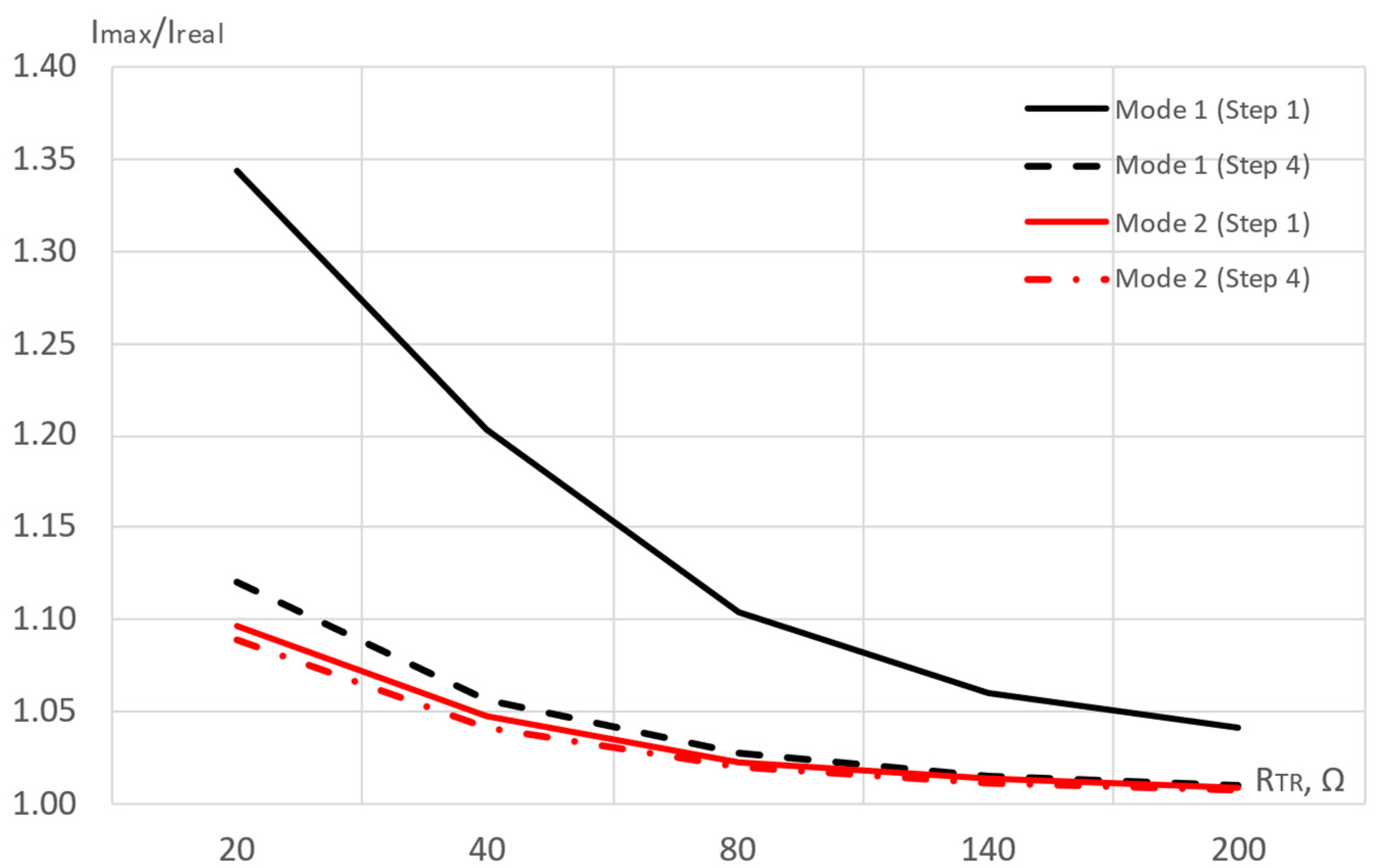
3.1.3. Assessment of SPHF Overload by Currents from an External Distortion Source
3.2. Analytical Calculation of SPHF Overload by Background Harmonic Currents
- -
- Power of the external distortion source;
- -
- Short circuit power at the consumer buses;
- -
- Short circuit power at the point of external nonlinear load connection;
- -
- Parameters of the passive harmonic filter.
- -
- The parameters of the linear load connected in parallel to the passive filter are not taken into account at the hth harmonic because the equivalent impedance of the passive filter at the hth harmonic (near the resonant frequency) is very low;
- -
- The parameters of the power system and the supply transformer are assumed to be inductive;
- -
- The resistance of the SPHF is not taken into account.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bagheri, A.; de Oliveira, R.A.; Bollen, M.H.J.; Gu, I.Y.H. A Framework Based on Machine Learning for Analytics of Voltage Quality Disturbances. Energies 2022, 15, 1283. [Google Scholar] [CrossRef]
- Kanálik, M.; Margitová, A.; Beňa, Ľ.; Kanáliková, A. Power System Impedance Estimation Using a Fast Voltage and Current Changes Measurements. Energies 2020, 14, 63. [Google Scholar] [CrossRef]
- Bogdanov, I.; Abramovich, B. Improving the efficiency of autonomous electrical complexes of oil and gas enterprises. J. Min. Inst. 2021, 249, 408–416. [Google Scholar] [CrossRef]
- Morenov, V.; Leusheva, E.; Lavrik, A.; Lavrik, A.; Buslaev, G. Gas-Fueled Binary Energy System with Low-Boiling Working Fluid for Enhanced Power Generation. Energies 2022, 15, 2551. [Google Scholar] [CrossRef]
- Khalifa, A.; Bazhin, V.; Ustinova, Y.; Shalabi, M. Study of the Kinetics of the Process of Producing Pellets from Red Mud in a Hydrogen Flow. J. Min. Inst. 2022, 254, 261–270. [Google Scholar] [CrossRef]
- Ustinov, D.A.; Aysar, A.R. Development of a New Working Algorithm for Improving the Efficiency of the Remote Protection in the Distributed Generation Networks. Occup. Saf. Ind. 2023, 5, 20–27. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Cobben, S.; Ribeiro, P.; Kling, W. Harmonic Emission Limits and Responsibilities at a Point of Connection. IET Gener. Transm. Distrib. 2012, 6, 256–264. [Google Scholar] [CrossRef]
- Crepaldi, J.; Amoroso, M.M.; Ando, O.H. Analysis of the Topologies of Power Filters Applied in Distributed Generation Units—Review. IEEE Lat. Am. Trans. 2018, 16, 1892–1897. [Google Scholar] [CrossRef]
- Belsky, A.; Glukhanich, D.; Sutikno, T.; Hatta Jopri, M. Estimation of Hourly Solar Irradiation on Tilted Surfaces. Bull. Electr. Eng. Inform. 2023, 12, 3202–3214. [Google Scholar] [CrossRef]
- Ustinov, D.A.; Aysar, A.R. Analysis of the Impact of the Distributed Generation Facilities on Protection Systems and Voltage Mode: Review. Occup. Saf. Ind. 2023, 2, 15–20. [Google Scholar] [CrossRef]
- Buslaev, G.; Lavrik, A.; Lavrik, A.; Tcvetkov, P. Hybrid System of Hydrogen Generation by Water Electrolysis and Methane Partial Oxidation. Int. J. Hydrogen Energy 2023, 48, 24166–24179. [Google Scholar] [CrossRef]
- Fujita, H.; Yamasaki, T.; Akagi, H. A Hybrid Active Filter for Damping of Harmonic Resonance in Industrial Power Systems. IEEE Trans. Power Electron. 2000, 15, 215–222. [Google Scholar] [CrossRef]
- Bai, H.; Wang, X.; Loh, P.C.; Blaabjerg, F. Harmonic Analysis and Mitigation of Low-Frequency Switching Voltage Source Inverter with Series LC Filtered VSI. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3299–3306. [Google Scholar] [CrossRef]
- Srivastava, M.; Goyal, S.K.; Saraswat, A.; Shekhawat, R.S.; Gangil, G. A Review on Power Quality Problems, Causes and Mitigation Techniques. In Proceedings of the 2022 1st International Conference on Sustainable Technology for Power and Energy Systems (STPES), Srinagar, India, 4–6 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kazmierkowski, M.P. Power Quality: Problems and Mitigation Techniques [Book News]. IEEE Ind. Electron. Mag. 2015, 9, 62. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.; Korolev, N.; Malkova, Y. Monitoring of Grinding Condition in Drum Mills Based on Resulting Shaft Torque. J. Min. Inst. 2022, 256, 686–700. [Google Scholar] [CrossRef]
- Karadeniz, A.; Balci, M.E. Comparative Evaluation of Common Passive Filter Types Regarding Maximization of Transformer’s Loading Capability under Non-Sinusoidal Conditions. Electr. Power Syst. Res. 2018, 158, 324–334. [Google Scholar] [CrossRef]
- Gimenes, T.K.; da Silva, M.P.C.; Ledesma, J.J.G.; Ando, O.H. Impact of Distributed Energy Resources on Power Quality: Brazilian Scenario Analysis. Electr. Power Syst. Res. 2022, 211, 108249. [Google Scholar] [CrossRef]
- Jopri, M.H.; Ghani, M.A.; Abdullah, A.; Sutikno, T.; Manap, M.; Too, J. Naïve Bayes and Linear Discriminate Analysis Based Diagnostic Analytic of Harmonic Source Identification. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 1626–1633. [Google Scholar] [CrossRef]
- Martinez, R.; Castro, P.; Arroyo, A.; Manana, M.; Galan, N.; Moreno, F.S.; Bustamante, S.; Laso, A. Techniques to Locate the Origin of Power Quality Disturbances in a Power System: A Review. Sustainability 2022, 14, 7428. [Google Scholar] [CrossRef]
- Shcherbakova, P.; Senderovych, G.; Abramovitz, A. Revisiting the Active Power Direction Method. IET Gener. Transm. Distrib. 2021, 15, 1056–1069. [Google Scholar] [CrossRef]
- Mohamed, I.F.; Abdel Aleem, S.H.E.; Ibrahim, A.M.; Zobaa, A.F. Optimal Sizing of C -Type Passive Filters under Non-Sinusoidal Conditions. Energy Technol. Policy 2014, 1, 35–44. [Google Scholar] [CrossRef]
- Abdel Aleem, S.H.E.; Elmathana, M.T.; Zobaa, A.F. Different Design Approaches of Shunt Passive Harmonic Filters Based on IEEE Std. 519-1992 and IEEE Std. 18-2002. Recent Patents Electr. Electron. Eng. 2013, 6, 68–75. [Google Scholar] [CrossRef]
- Ko, W.; Tuomainen, M. Design and Application of a Single-tuned Passive Harmonic Filter to Suppress Harmonic Distortion and Resonance for Railway Traction Power Systems—A Case Study. IET Electr. Syst. Transp. 2022, 12, 153–164. [Google Scholar] [CrossRef]
- AbdelAziz, M.M.; AbouEl-Zahab, E.E.-D.; Ibrahim, A.M.; Zobaa, A.F. Practical Considerations Regarding Power Factor for Nonlinear Loads. IEEE Trans. Power Deliv. 2004, 19, 337–341. [Google Scholar] [CrossRef]
- Aziz, M.M.A.; Zobaa, A.F.; Ibrahim, A.M.; Monem, A.M.A. Effect of Time Variation of System Impedance and Voltage Harmonics on LC Compensation for Nonlinear Loads. In Proceedings of the 2004 11th International Conference on Harmonics and Quality of Power (IEEE Cat. No.04EX951), Lake Placid, NY, USA, 12–15 September 2004; pp. 77–82. [Google Scholar] [CrossRef]
- Azebaze Mboving, C.S.; Hanzelka, Z.; Firlit, A. Analysis of the Factors Having an Influence on the LC Passive Harmonic Filter Work Efficiency. Energies 2022, 15, 1894. [Google Scholar] [CrossRef]
- Aleem, S.H.E.A.; Balci, M.E.; Zobaa, A.F.; Sakar, S. Optimal Passive Filter Design for Effective Utilization of Cables and Transformers under Non-Sinusoidal Conditions. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 626–630. [Google Scholar] [CrossRef]
- Abdul Kahar, N.H.B.; Zobaa, A.F. Application of Mixed Integer Distributed Ant Colony Optimization to the Design of Undamped Single-Tuned Passive Filters Based Harmonics Mitigation. Swarm Evol. Comput. 2019, 44, 187–199. [Google Scholar] [CrossRef]
- Nassif, A.; Xu, W.; Freitas, W. An Investigation on the Selection of Filter Topologies for Passive Filter Applications. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; p. 1. [Google Scholar] [CrossRef]
- Almutairi, M.S.; Hadjiloucas, S. Harmonics Mitigation Based on the Minimization of Non-Linearity Current in a Power System. Designs 2019, 3, 29. [Google Scholar] [CrossRef]
- Filho da Costa Castro, J.; Lima, L.R.; Belchior, F.N.; Ribeiro, P.F. A Novel Approach to the Design of Passive Filters in Electric Grids. Int. J. Emerg. Electr. Power Syst. 2016, 17, 693–701. [Google Scholar] [CrossRef]
- Menti, A.; Zacharias, T.; Milias-Argitis, J. Optimal Sizing and Limitations of Passive Filters in the Presence of Background Harmonic Distortion. Electr. Eng. 2009, 91, 89–100. [Google Scholar] [CrossRef]
- Benaouadj, M.; Boumous, Z.; Boumous, S. Active Harmonic Filtering for Improving Power Quality of an Electrical Network. J. Eur. Syst. Autom. 2022, 55, 397–403. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd Radzi, M.; Hassan, M.; Mailah, N. Control Algorithms of Shunt Active Power Filter for Harmonics Mitigation: A Review. Energies 2017, 10, 2038. [Google Scholar] [CrossRef]
- Davi Curi Busarello, T.; Vendrusculo, E.A.; Pomilio, J.A.; da Silva, N. Analysis of a Derivative Hybrid Power Filter in Distorted Voltage Grid. In Proceedings of the 2013 IEEE PES Conference on Innovative Smart Grid Technologies (ISGT Latin America), Sao Paulo, Brazil, 15–17 April 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Mahmoud, M.O.; Mamdouh, W.; Khalil, H. Source Current Harmonic Mitigation of Distorted Voltage Source by Using Shunt Active Power Filter. Int. J. Electr. Comput. Eng. 2020, 10, 3967–3977. [Google Scholar] [CrossRef]
- Skamyin, A.; Belsky, A.; Dobush, V.; Gurevich, I. Computation of Nonlinear Load Harmonic Currents in the Presence of External Distortions. Computation 2022, 10, 41. [Google Scholar] [CrossRef]
- Zhukovskiy, Y.L.; Vasilev, B.Y.; Korolev, N.A.; Malkova, Y.M. Analysis of the behavior of asynchronous electric drive with a closed scalar control system when changing the inductance of the magnetizing circuit. Indones. J. Sci. Technol. 2022, 8, 65–78. [Google Scholar] [CrossRef]
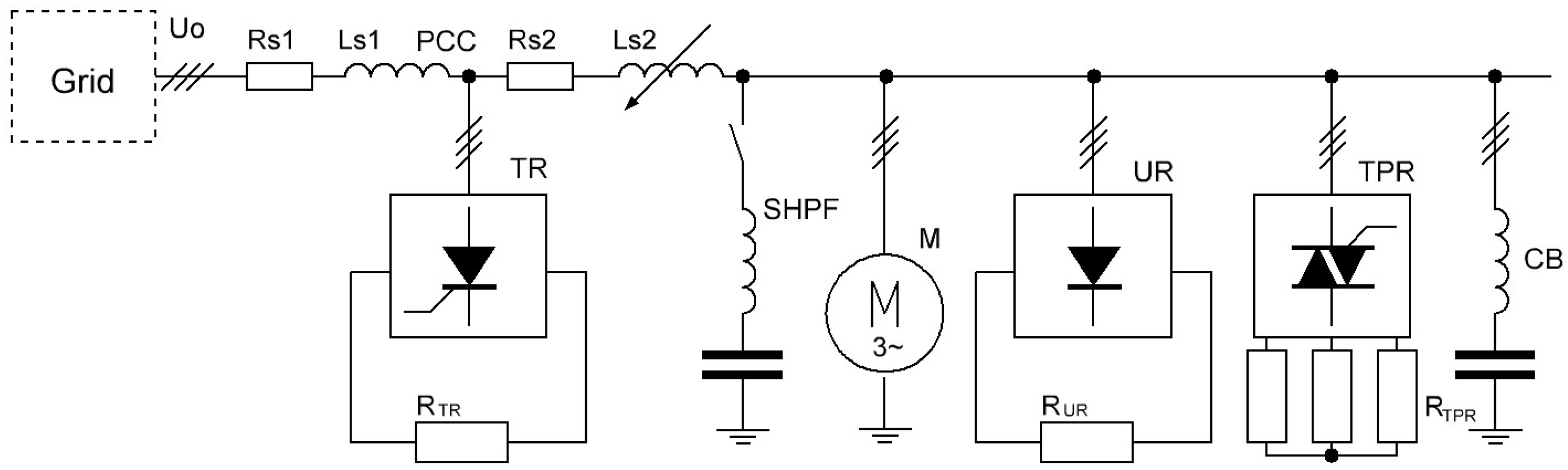


| Elements of the Scheme | Parameters and Values |
|---|---|
| Grid | U0 = 0.4 kV, RS1 = 0.18 Ω, LS1 = 1.75 mH |
| Supply feeder ZS2 (step 1) | Step 1: RS2 = 0.22 Ω, LS2 = 1.71 mH Step 2: RS2 = 0.83 Ω, LS2 = 4.8 mH Step 3: RS2 = 1.0 Ω, LS2 = 10.96 mH Step 4: RS2 = 1.49 Ω, LS2 = 14.73 mH |
| Induction motor (M) | UM = 0.38 kV, PM = 1.5 kW, η = 76%, cosφ = 0.74 |
| Thyristor rectifier (TR) | UTR = 0.38 kV, RTR = [20; 200] Ω |
| Thyristor power regulator (TPR) | UTPR = 0.38 kV, RTPR = 32.3 Ω |
| Uncontrolled rectifier (UR) | UUR = 0.38 kV, RUR = 96.8 Ω |
| Capacitor banks (CB) | 4 step of regulation, QCB1 = 0.5 kvar, ftuned = 134 Hz |
| Passive harmonic filter (SPHF) | LF = 14.1 mH, CF = 31 μF, ftuned = 241 Hz |
| Stage Number | TR | UR | TPR | M | CB | Variation Parameters | |
|---|---|---|---|---|---|---|---|
| ZS2 | RTR, Ω | ||||||
| 1 and 2 | + | + | + | + | + | Step 1–Step 4 | [20; 200] |
| 3 (mode 1) | + | + | + | + | + | ||
| 3 (mode 2) | + | − | + | + | + | ||
| 3 (mode 3) | + | + | − | + | + | ||
| RTR | δKDh (UR), % | δKDh (TPR), % | ||||||
|---|---|---|---|---|---|---|---|---|
| Step 1 | Step 2 | Step 3 | Step 4 | Step 1 | Step 2 | Step 3 | Step 4 | |
| 20 | 3.0 | 3.6 | 0.8 | 0.2 | 9.7 | 0.6 | 1.4 | 1.1 |
| 80 | 0.4 | 0.8 | 0.2 | 0.1 | 2.1 | 0.3 | 0.1 | 0.2 |
| 140 | 0.2 | 0.4 | 0.1 | 0.1 | 1.2 | 0.2 | 0.1 | 0.1 |
| 200 | 0.1 | 0.3 | 0.1 | 0.1 | 0.9 | 0.2 | 0.1 | 0.1 |
| RTR | IFh_0, A | IFh_2, A | IFh_0 + IFh_2, A | IFh_1, A | δ1, % | δ 4, % | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Step 1 | Step 4 | Step 1 | Step 4 | Step 1 | Step 4 | Step 1 | Step 4 | Step 1 | Step 4 | |
| 20 | 1.611 | 1.751 | 1.761 | 0.446 | 3.372 | 2.197 | 3.271 | 2.016 | 3.00 | 8.24 |
| 40 | 0.902 | 0.23 | 2.513 | 1.981 | 2.450 | 1.860 | 2.51 | 6.11 | ||
| 80 | 0.457 | 0.117 | 2.068 | 1.868 | 2.031 | 1.787 | 1.79 | 4.34 | ||
| 140 | 0.263 | 0.067 | 1.874 | 1.818 | 1.851 | 1.764 | 1.23 | 2.97 | ||
| 200 | 0.185 | 0.047 | 1.796 | 1.798 | 1.779 | 1.758 | 0.95 | 2.22 | ||
| KSC | Ssc1, kVA | I3h_meas, A | fr | IFh_meas, A | IFh_calc, A | δI, % |
|---|---|---|---|---|---|---|
| 2.00 | 250 | 4.82 | 0.966 | 1.855 | 1.938 | −4.48 |
| 3.97 | 4.78 | 1.092 | 1.083 | 0.83 | ||
| 7.19 | 4.76 | 0.601 | 0.628 | −4.49 | ||
| 9.40 | 4.75 | 0.470 | 0.488 | −3.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skamyin, A.; Shklyarskiy, Y.; Gurevich, I. Influence of Background Voltage Distortion on Operation of Passive Harmonic Compensation Devices. Energies 2024, 17, 1342. https://doi.org/10.3390/en17061342
Skamyin A, Shklyarskiy Y, Gurevich I. Influence of Background Voltage Distortion on Operation of Passive Harmonic Compensation Devices. Energies. 2024; 17(6):1342. https://doi.org/10.3390/en17061342
Chicago/Turabian StyleSkamyin, Aleksandr, Yaroslav Shklyarskiy, and Ilya Gurevich. 2024. "Influence of Background Voltage Distortion on Operation of Passive Harmonic Compensation Devices" Energies 17, no. 6: 1342. https://doi.org/10.3390/en17061342
APA StyleSkamyin, A., Shklyarskiy, Y., & Gurevich, I. (2024). Influence of Background Voltage Distortion on Operation of Passive Harmonic Compensation Devices. Energies, 17(6), 1342. https://doi.org/10.3390/en17061342








