Abstract
Power quality improvement and Power quality disturbance (PQD) detection are two significant concerns that must be addressed to ensure an efficient power distribution within the utility grid. When the process to analyze PQD is migrated to real-time platforms, the possible occurrence of a phase mismatch can affect the algorithm’s accuracy; this paper evaluates phase shifting as an additional stage in signal acquisition for detecting and classifying eight types of single power quality disturbances. According to their mathematical models, a set of disturbances was generated using an arbitrary waveform generator BK Precision 4064. The acquisition, detection, and classification stages were embedded into a BeagleBone Black. The detection stage was performed using multiresolution analysis. The feature vectors of the acquired signals were obtained from the combination of Shannon entropy and log-energy entropy. For classification purposes, four types of classifiers were trained: multilayer perceptron, K-nearest neighbors, probabilistic neural network, and decision tree. The results show that incorporating a phase-shifting stage as a preprocessing stage significantly improves the classification accuracy in all cases.
1. Introduction
The recent population growth has led to an accelerated increase in supply demand. This situation, coupled with the use of traditional and obsolete power grids, has resulted in the current problem of energy unsustainability []. Other factors contributing to power deterioration include using new electronic devices and non-linear loads, renewable energies, and environmental factors [,].
Power quality (PQ) is related to the parameters defining a power supply signal in magnitude, waveform, frequency, symmetry, and continuity. The improvement of power quality is an aspect that concerns both the power supplier and the power consumer [], and the high penetration of renewable sources has implied studies that contribute to the mitigation of PQ issues [], mainly because renewable energy is highly unpredictable []. Therefore, new equipment and devices have been proposed to allow prompt monitoring [].
One of the leading causes of poor power quality is the occurrence of anomalies within the supply signals, known as power quality disturbances (PQD). Identifying the occurrence of these phenomena in the supply systems is a critical step because poor PQ can cause equipment malfunction and damage, a decreasing AC motor speed, relay malfunction, and the downtime of computers, among others [,]. In addition, real-time PQD monitoring can help to take faster actions to mitigate PQ issues, and it is a way of knowing the PQD propagation along the grid []. The identification of PQD is usually divided into three main stages: detection, feature extraction, and classification [].
For the detection of PQDs, several approaches have been proposed using different signal processing techniques, such as Kalman filters, Stockwell transform, and wavelet transform, among others, to obtain some information from analyzing their waveforms. This information is generally inadequate for classification purposes, so it is optimized using feature extraction methods. In this sense, the classification is usually evaluated through different classifiers such as neural networks, Bayesian classifiers, support vector machines, fuzzy logic, deep learning, and many others [,,].
In the case of wavelet transform, it has been widely used as a suitable tool for analyzing signals with abrupt contours and small discontinuities in their waveforms, as in the case of power quality disturbances [].
Most of the related works involve the detection and classification of these disturbances in simulation. However, migrating and evaluating these methods on a hardware platform remains a research challenge []; for instance, [] proposes a real-time PQD recognition algorithm based on the deep belief network, showing a good accuracy but compromising time. In [], the authors proposed an algorithm to analyze PQD using an FPGA; the FPGA was only used for data acquisition and processing to classify the disturbances developed in a computer.
Although the phase mismatch between signals may impact classification purposes [], there is a lack of studies showing this effect by using phase-shifted signals acquired with a previous phase-shifting stage, compared to non-phase-shifted signals.
This work presents an evaluation of phase shifting as an additional stage in signal acquisition for the detection and classification of eight types of single power quality disturbances, including sag, swell, interrupt, harmonics, flicker, notching, oscillatory transient, and impulsive transient. The disturbances were generated through an arbitrary waveform generator to be acquired and analyzed in a real-time scenario. The detection stage was performed by multiresolution analysis (MRA) using the wavelet Daubechies 4 (db4) function as the mother wavelet at nine resolution levels. Later, the feature vectors of the acquired phase-shifted and non-phase-shifted disturbances were obtained from the combination of Shannon entropy and log-energy entropy, which, in turn, served as the input for four types of classifiers such as multilayer perceptron (MLP), K-nearest neighbors (KNN), probabilistic neural network (PNN), and decision tree (DT).
The contributions of the present work are as follows:
- The novelty of the proposed algorithm is that it uses phase shifting as an additional stage in signal acquisition for the detection and classification of eight types of single power quality disturbances;
- An algorithm to analyze disturbances in electrical signals was developed on the BeagleBone Black and probed its capability to acquire and classify the signals in real time;
- Four classifiers, MLP, KNN, PNN, and DT, were compared in the classification stage.
The work is organized as follows: Section 2 presents the materials and methods applied, the signals analyzed, the experiments performed, and the software and hardware used. Section 3 contains the results, a comparison of the methods used, and the use of hardware for the analysis. Finally, the conclusions are addressed in Section 4, the results are interpreted, and future work is proposed.
2. Materials and Methods
Power quality disturbances represent any deviation in the waveform of a supply signal, both in terms of voltage and current regarding its nominal values []. This topic has been a significant focus of interest within the power grid environment, given the incorporation of the new smart grid and smart meter technologies [].
In this section, the scheme proposed to analyze the PQDs is presented. The block diagram corresponding to the whole process is shown in Figure 1. At first, the disturbances are generated using an arbitrary function generator. The signals are sent to BeagleBone, and phase shifting is applied as preprocessing. Then, the signal is analyzed to detect and classify PQD; these stages are developed in BeagleBone. In the rest of this section, all the individual blocks are described in detail.
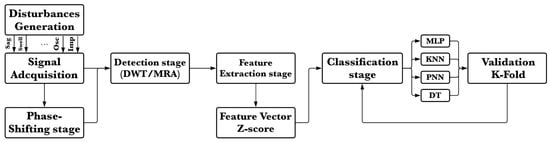
Figure 1.
Block diagram of the proposed method.
- A.
- Disturbances Generation
The power quality disturbances imply a momentary increase or decrease in the magnitude of the signals and the presence of harmonics, interruptions, and transients, among others. PQDs can be classified according to the number of disturbances present. Thus, if only one deviation in the waveform is present, they are classified as single disturbances. In contrast, when two or more deviations are present, they are classified as combined or complex disturbances. They can also be classified according to their duration as short-term, long-term, or stationary.
The primary single power quality disturbances are sag, swell, interrupt, flicker, harmonics, notching, oscillatory transient, and impulsive transient [], as shown in Figure 2. Their behavior can be described through mathematical models such as those shown in Table 1, and their typical parameters and limits are regulated by the IEEE 1159-2009 standard [].
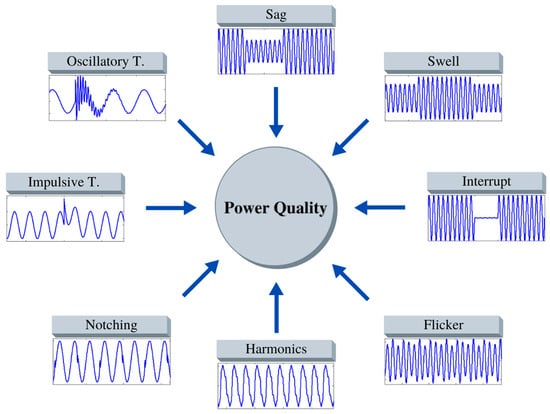
Figure 2.
Main single disturbances.

Table 1.
Main disturbances, their mathematical models, and typical parameters.
An arbitrary waveform generator, BK Precision 4064, as shown in Figure 3, was used to generate the disturbances. The generator operates at 120 MHz and has two high-impedance output channels and USB communication. It supports the generation of waveforms using comma-separated value files. For this purpose, the signals were generated in MATLAB according to their mathematical models and had 16,384 samples with a duration of 0.5 s. Each of the eight types of generated disturbances has 500 examples, whose typical parameters were randomly determined so that the dataset is composed of 4000 examples stored as a comma-separated value file, where each row represents a different disturbance. At the same time, the columns correspond to the samples of that specific signal.

Figure 3.
Arbitrary Waveform Generator BK Precision 4064.
- B.
- Signal Acquisition and Phase-Shifting Stage
Phase shifting is a term related to the displacement of two signals in a given time interval, as shown in Figure 4. This phase mismatch involves a high level of randomness between signals. It may have an impact on a further classification process since the classifier would need to be trained with a large number of signals to cover every possible phase, which would also increase the complexity of the algorithm so that, to solve this problem, a hardware or software zero-crossing detector could be implemented [].
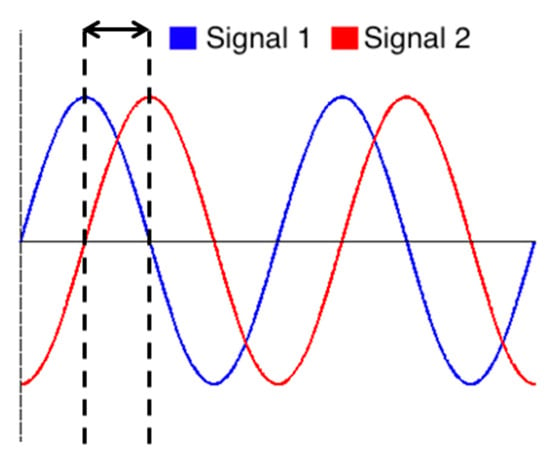
Figure 4.
Phase shifting.
A zero crossing is a point in a graph of a mathematical function where the value of the axis is zero, which means changing the sign of the function from positive to negative. The point without instant voltage is commonly known as the zero crossing. This occurs twice each cycle in a sinusoidal wave or another simple waveform. It is an instrument that determines where the voltage in any direction crosses zero [].
For this work, a software phase-shifting stage based on zero-crossing detection was programmed in Python and implemented within signal acquisition as a preprocessing stage.
A BeagleBone Black was used for signal acquisition and classification. BeagleBone Black is a low-cost, community-supported, single-board computer (SBC) compatible with different Linux distributions, such as Debian or Ubuntu, as operating system. It has a 1 GHz AM335x processor and two 200 MHz co-processors that can act as Programmable Real-Time Units (PRUs). The significant advantage of this device is that it has a 12-bit analog-to-digital converter (ADC) available on seven analog pins of 1.8 V, so it does not require an additional module for signal acquisition.
Communication between the generator and the computer to send the disturbances via USB was carried out through the EasyWave software, revision 1.1.1.36. Moreover, the generator has controls for modifying the amplitude and offset of the signals, so it was possible to condition the signals to connect an output channel of the generator to one of the analog pins. The detection and classification algorithms were programmed in Python. A general diagram of the acquisition and classification process of the PQDs can be seen in Figure 5. On the other hand, Figure 6 shows the experimental setup.
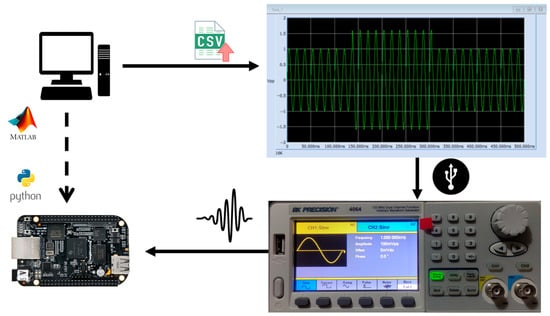
Figure 5.
General process of the proposed method.
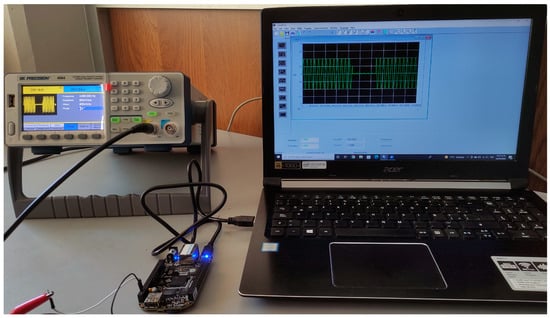
Figure 6.
Experimental setup.
Five hundred examples of each type of disturbance were sampled, giving a total of 4000 signals, and an ideal sinusoidal signal was also sampled for use in the feature vector extraction. Each signal has 5000 samples with a duration of 0.5 s, which provides a sampling frequency of 10 kHz. Some examples of acquired phase-shifted and non-phase-shifted signals are shown in Figure 7 and Figure 8, respectively.
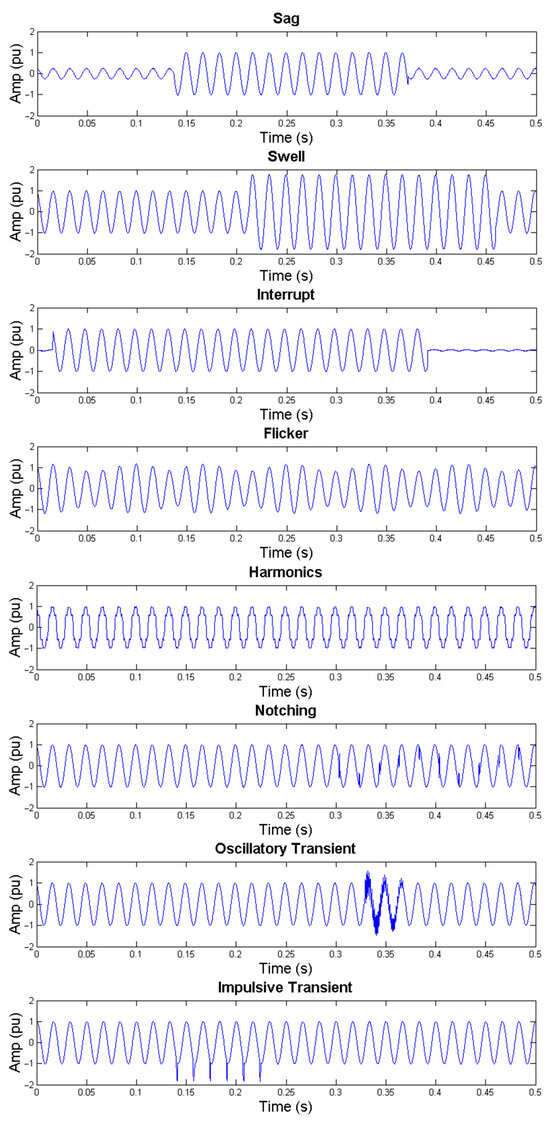
Figure 7.
Phase-shifted signals.
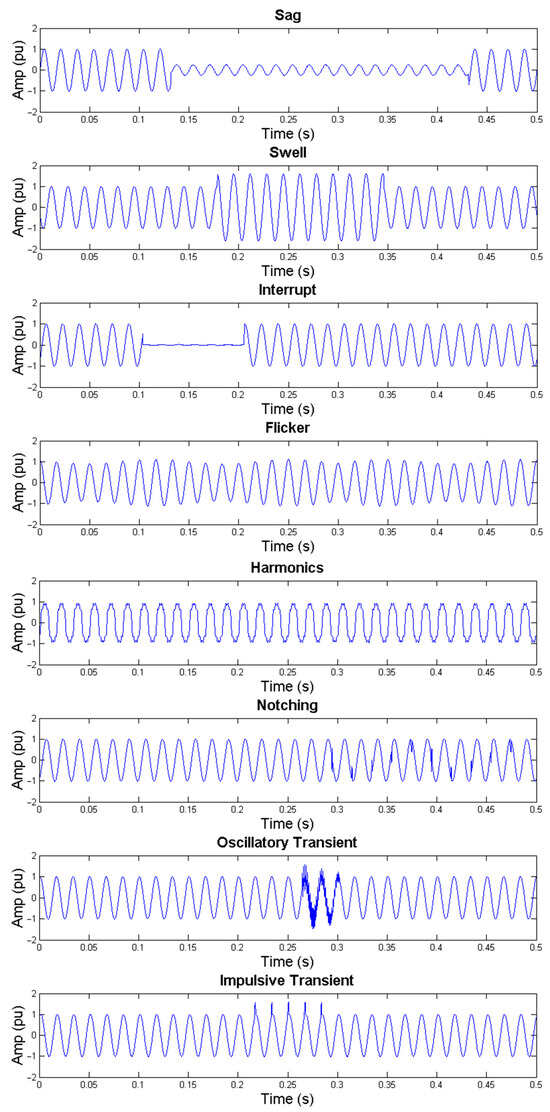
Figure 8.
Non-phase-shifted signals.
- C.
- Detection and Feature Extraction
The multiresolution analysis (MRA), derived from applying discrete wavelet transform (DWT) to the acquired signals, was used for disturbance detection. The application of MRA involves decomposing the signals into two different versions by applying complementary high-pass and low-pass filters: a detailed version, which contains information from the high-frequency components, and another smoothed version, which includes information from the low-frequency components. This information is obtained within a series of detail and approximation coefficients, cD and cA, respectively []. Applying this process multiple times results in new details and approximation coefficients. Each iteration is referred to as a resolution level, where cD1 and cA1 are known as the detail and approximation coefficients of the first resolution level. In contrast, cDn and cAn then correspond to the coefficients of the n-th resolution level, as can be seen in Equations (1) and (2), where g and h correspond to the coefficients of the high-pass and low-pass filters, respectively, which are determined by the wavelet function used.
The wavelet transform represents how much a given signal resembles a mother wavelet function. Therefore, the choice of the latter is an essential aspect. In the case of applications related to power quality, the Daubechies 4 function (db4) is one of the most used functions because it has characteristics analogous to those presented by the PQDs [], so it was considered for this work.
Likewise, the information obtained through MRA depends on the number of resolution levels analyzed. However, increasing the number of levels implies increasing the computational expense, so the key is to choose several levels significant enough to obtain relevant information without compromising the computational performance. In this sense, decomposing the signals into nine resolution levels results in an appropriate number of decomposition levels for the case of power quality disturbances [], so it was chosen for this work.
The detail and approximation coefficients obtained by MRA can be optimized to serve as input to a classifier through wavelet-based feature extraction methods, reducing them dimensionally. For the formation of the feature vector, a combination of Shannon entropy and log-energy entropy was considered from the obtained coefficients since this combination is suitable for the classification of power quality disturbances []. Equations (3) and (4) show the mathematical definition of Shannon entropy and log-energy entropy, respectively, where Ci,j are the N coefficients of the i-th resolution level.
On the other hand, Equations (5) and (6) show the features for classification, where SEcAn, SEcDn and LOEcAn, and LOEcDn represent the Shannon entropy and log-energy entropy of the approximation and detail coefficients, respectively.
Since the features for classification present a long variation, the feature vector of each disturbance was extracted using the features of an ideal sine signal as a reference, as shown in the Equation (7), where SESin and LOESin correspond to the Shannon entropy and log-energy entropy proper to this signal.
Subsequently, each vector was normalized by Z-score to obtain a new range of values closer to each other, improving the classification accuracy []. Equation (8) shows the normalization by cap Z-score, where corresponds to the data to be normalized, to the mean, and to the standard deviation. This normalization gives the data the properties of a normal distribution, i.e., a mean of zero and a standard deviation equal to one [].
Finally, the normalized vectors are the input features for the classifiers; for this purpose, a matrix of binary coded targets was used so that a 1 means that it belongs to the class and 0 is the opposite case.
- D.
- Classification
The classification process was tested using four different classifiers whose parameters were empirically set according to [] so that they were iteratively evaluated to obtain the highest accuracy. The classifiers at issue were as follows:
- Multilayer perceptron (MLP) has 12 neurons in the hidden layer, and SoftMax is used for the activation function;
- K-nearest neighbors (KNN), with the number of neighbors, K, is set to 3;
- Probabilistic neural network (PNN) with a propagation of the radial basis function (smoothing factor ) of 0.02;
- Decision tree (DT).
MLP is one of the well-known and most widely used feedforward subclasses of ANNs, and the learning process is accomplished by employing multilayers of neurons. MLP models utilize the error back-propagation technique, one of the well-known training schemes, to maximize network accuracy and achieve a superior outcome []. The nearest neighbor is a non-parametric technique that finds application in pattern recognition, text classification, or ranking the models. KNN uses an input vector with the K-closest training samples in feature space. The algorithm requires training to define the neighbors based on the distance from the test samples and a testing step to determine the class to which these test samples belong [].
A PNN is a feedforward neural network, which was proven to be extremely useful in classification and pattern recognition applications. The PNN utilizes the concepts used in classical pattern recognition problems, where it implements the Bayesian classifier concepts. The Bayesian strategies rely on procedures that minimize the “expected risk” of assigning a pattern to a wrong category, known as misclassification. PNNs are closely related to the Parzen estimator window of probability density functions []. DTs are machine-learning models used for classification and regression tasks. These models are composed of inner nodes, which contain logical tests, and leaves, which contain predictions. In the inference step, an observation follows a path from the root to one of the leaves, determined by the results of each logical test applied to the tested observation. These tests (often called ‘‘splits’’) can be univariate or multivariate [].
Classification validation was performed through the K-fold method, in which the data are randomly separated into K subsets such that one of them is used for validation. In contrast, the remaining K − 1 subsets are used for training. Subsequently, the performance is evaluated based on the accuracy average after K rounds of training and validation []. For this work, K = 10 was taken so that out of 4000 examples available, 3600 were used for training and 400 for validation in each round. The accuracy average for each round was obtained by Equation (9).
3. Results
The proposed method was tested using the acquired phase-shifted and non-phase-shifted disturbances, and its performance was evaluated through the K-fold cross-validation method on the BeagleBone Black. Table 2 shows the accuracy percentage of each classifier in each K-round for the non-phase-shifted signals. Table 3 is similar to Table 2 but for the case of phase-shifted signals. In both tables, the last row shows the average accuracy percentage for all rounds. In all cases, phase shifting improves the algorithm’s performance, giving results with an accuracy higher than 94% for all cases; the better case was 99.1% with PNN, which is an excellent classifier for analyzing disturbances.

Table 2.
Accuracy on BeagleBone Black for each round K (non-phase-shifted signals).

Table 3.
Accuracy on BeagleBone Black for each round K (phase-shifted signals).
Table 4 compares the classification accuracy with the acquired phase-shifted and non-phase-shifted signals. It is possible to observe that incorporating the phase-shifting stage in obtaining the signals considerably improves the accuracy percentage.

Table 4.
Comparison of classification with phase-shifted and non-phase-shifted signals.
In all cases, the K-nearest neighbors and probabilistic neural network classifiers, followed by the decision tree, show a similar performance with the highest accuracy. On the other hand, the multilayer perceptron presents a lower accuracy. In the case of non-phase-shifted signals, the accuracy is considerably lower than that of the other classifiers.
As an example of the algorithm’s performance in a noisy environment, it was tested with two different noise amplitudes, SNR 30 dB and 50 dB, as shown in Table 5. Although in a noisy environment, the accuracy is higher than 90% in all cases, except for MLP with SNR 30 dB.

Table 5.
Comparison of classification with phase-shifted and different noise amplitudes.
A comparative analysis of the results obtained in other related works and the proposed method is shown in Table 6. The table shows the detection method, the number of features considered for classification purposes, the hardware used, and their respective accuracy with phase-shifted and non-phase-shifted signals.

Table 6.
Comparative analysis between related works and the proposed method.
For example, a real-time implementation of an optimized power quality events classifier for detecting and classifying six single and fourteen complex types of PQDs is presented in []. The optimized classifier was embedded into a myRIO-1900 device using the LabVIEW interface. In this context, 21 features were extracted from the coefficients obtained by decomposing the signals into six resolution levels through MRA, which, in turn, served as inputs for the classification algorithm using three random forest classifiers (RF). The accuracy is then based on the overall performance of the classifiers. The performance was tested using phase-shifted and non-phase-shifted signals, and it can be observed that the accuracy is slightly lower in the case of phase-shifted signals; however, the authors in [] consider only the effect of applying a random phase shift to the signal, but not attend to this issue; this is the reason why the accuracies appear to be backwards, and the better performance was obtained without a phase shift.
S. He, in [], presents a hybrid method based on S-transform and dynamics for the real-time detection and classification of power quality disturbances. The hybrid method was implemented on a DSP-FPGA system; in this case, FPGA Xilinx Spartan XC2S200PQ208 was used for signal acquisition, and DSP TMS320C6713 was used to run the algorithm. All the signals were acquired with the same phase using a zero-crossing circuit detector. A decision tree (DT) was trained using five different features for classification purposes. However, a performance comparison using phase-shifted and non-phase-shifted signals is not given.
According to [,], the proposed method can be completed if complex PQDs are considered, although the present work demonstrates the usefulness of phase shifting.
With the proposed method, it can be evidenced that including a software phase-shifting stage increases the accuracy in all the classifiers tested. In addition, it is a reliable solution to the problem of the high randomness present between signals acquired with different phases, which would lead to misclassification.
4. Conclusions
This paper analyzed the effect of phase shifting as an additional stage in signal acquisition for detecting and classifying eight types of single power quality disturbances. The detection was based on the multiresolution analysis technique derived from applying DWT to the acquired signals. The disturbances were generated using an arbitrary waveform generator and subsequently acquired, processed, and classified within a BeagleBone Black, as it does not require an additional module for signal acquisition. For this purpose, four different types of classifiers such as MLP, KNN, PNN, and DT were trained using a combination of Shannon Entropy and Log-Energy Entropy features extracted from the detail and approximation coefficients obtained by decomposing the signals into nine resolution levels. The classification process was validated using the K-fold cross-validation method. From the results, it is clear that incorporating a software phase-shifting stage as a preprocessing stage significantly improves the classification accuracy in all cases.
The process of this work can be applied to analyze complex PQDs, and it is an issue for future work. The results obtained in a noisy environment can be improved if the number of details and approximations are optimized to work in appropriate frequency ranges.
Author Contributions
Conceptualization, E.R.-A.; methodology, A.V.R.-M.; software, J.C.O.-R.; validation, J.R.-H.; formal analysis, J.A.G.G.; resources, W.Y.; writing—original draft preparation, E.R.-A. and A.V.R.-M.; supervision, J.A.G.G.; project administration, E.R.-A.; funding acquisition, W.Y.; writing—revised draft preparation, E.R.-A. and J.R.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science, Technology, and Innovation Institute of Michoacan, grant number ICTI-PICIR23-164, and the University of Manchester funded the APC.
Data Availability Statement
The datasets used and analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yoldas, Y.; Önen, A.; Muyeen, S.; Vasilakos, A.V.; Alan, I. Enhancing smart grid with microgrids: Challenges and opportunities. Renew. Sustain. Energy Rev. 2017, 72, 205–214. [Google Scholar] [CrossRef]
- Junior, W.L.R.; Borges, F.A.S.; Rabelo, R.A.L.; Rodrigues, J.J.P.C.; Fernandes, R.A.S.; da Silva, I.N. A methodology for detection and classification of power quality disturbances using a real-time operating system in the context of home energy management systems. Int. J. Energy Res. 2021, 45, 203–219. [Google Scholar] [CrossRef]
- Naidu, T.A.; Albeshr, H.M.A.A.; Al-Sabounchi, A.; Sadanandan, S.K.; Ghaoud, T. A Study on Various Conditions Impacting the Harmonics at Point of Common Coupling in On-Grid Solar Photovoltaic Systems. Energies 2023, 16, 6398. [Google Scholar] [CrossRef]
- Herman, L.; Špelko, A. New Reference Current Calculation Method of a Hybrid Power Filter Based on Customer Harmonic Emission. Energies 2023, 16, 7876. [Google Scholar] [CrossRef]
- Jha, K.; Shaik, A.G. A comprehensive review of power quality mitigation in the scenario of solar PV integration into utility grid. e-Prime Adv. Electr. Eng. Electron. Energy 2023, 3, 100103. [Google Scholar] [CrossRef]
- Beniwal, R.K.; Saini, M.K.; Nayyar, A.; Qureshi, B.; Aggarwal, A. A Critical Analysis of Methodologies for Detection and Classification of Power Quality Events in Smart Grid. IEEE Access 2021, 9, 83507–83534. [Google Scholar] [CrossRef]
- WJunior, L.R.; Borges, F.A.D.S.; de AL Rabelo, R.; Rodrigues, J.J. A methodology for detection of power quality disturbances in the context of demand side management. In Proceedings of the 2019 4th International Conference on Smart and Sustainable Technologies (SpliTech), Split, Croatia, 18–21 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Kumar, C.S.; Ramesh, P.; Kasilingam, G.; Ragul, D.; Bharatiraja, C. The power quality measurements and real time monitoring in distribution feeders. Mater. Today Proc. 2021, 45 Pt 2, 2987–2992. [Google Scholar] [CrossRef]
- Oubrahim, Z.; Amirat, Y.; Benbouzid, M.; Ouassaid, M. Power Quality Disturbances Characterization Using Signal Processing and Pattern Recognition Techniques: A Comprehensive Review. Energies 2023, 16, 2689. [Google Scholar] [CrossRef]
- Caicedo, J.E.; Agudelo-Martínez, D.; Rivas-Trujillo, E.; Meyer, J. A systematic review of real-time detection and classification of power quality disturbances. Prot. Control. Mod. Power Syst. 2023, 8, 2–37. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H. A novel deep learning method for the classification of power quality disturbances using deep convolutional neural network. Appl. Energy 2019, 235, 1126–1140. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G.; Shaik, M.; Padmanaban, S.; Holm-Nielsen, J.B.; Mahela, O.P.; Kaliannan, P. Comprehensive review on detection and classification of power quality disturbances in utility grid with renewable energy penetration. IEEE Access 2020, 8, 146807–146830. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Zia, M.F.; Benbouzid, M.; El Hani, S. Overview of Signal Processing and Machine Learning for Smart Grid Condition Monitoring. Electronics 2021, 10, 2725. [Google Scholar] [CrossRef]
- Turović, R.; Dragan, D.; Gojić, G.; Petrović, V.B.; Gajić, D.B.; Stanisavljević, A.M.; Katić, V.A. An End-to-End Deep Learning Method for Voltage Sag Classification. Energies 2022, 15, 2898. [Google Scholar] [CrossRef]
- Jandan, F.; Khokhar, S.; Memon, Z.A.; Shah, S.A.A. Wavelet-based simulation and analysis of single and multiple power quality disturbances. Eng. Technol. Appl. Sci. Res. 2019, 2, 3909–3914. [Google Scholar] [CrossRef]
- Igual, R.; Medrano, C. Research challenges in real-time classification of power quality disturbances applicable to microgrids: A systematic review. Renew. Sustain. Energy Rev. 2020, 132, 110050. [Google Scholar] [CrossRef]
- Chen, Z.; Li, M.; Ji, T.; Wu, Q. Real-Time Recognition of Power Quality Disturbance-Based Deep Belief Network Using Embedded Parallel Computing Platform. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 519–526. [Google Scholar] [CrossRef]
- Ribeiro, E.G.; Mendes, T.M.; Dias, G.L.; Faria, E.R.; Viana, F.M.; Barbosa, B.H.; Ferreira, D.D. Real-Time System for Automatic Detection and Classification of Single and Multiple Power Quality Disturbances. Measurement 2018, 128, 276–283. [Google Scholar] [CrossRef]
- Markovska, M.; Taskovski, D.; Kokolanski, Z.; Dimchev, V.; Velkovski, B. Real-time implementation of optimized power quality events classifier. IEEE Trans. Ind. Appl. 2020, 56, 3431–3442. [Google Scholar] [CrossRef]
- Junior, W.L.R.; Borges, F.A.; Veloso AF, D.S.; de ALRabêlo, R.; Rodrigues, J.J. Rodrigues. Low voltage smart meter for monitoring of power quality disturbances applied in smart grid. Measurement 2019, 147, 106890. [Google Scholar] [CrossRef]
- IEEE 1159-2009; IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE Transmission and Distribution Committee: Piscataway, NJ, USA, 2009.
- Rahman, D.; Awal, M.A.; Islam, M.S.; Yu, W.; Husain, I. Low-latency High-speed Saturable Transformer based Zero-Crossing Detector for High-Current High-Frequency Applications. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3266–3272. [Google Scholar] [CrossRef]
- Eristi, B.; Yildirim, O.; Eristi, H.; Demir, Y. A real-time power quality disturbance detection system based on the wavelet transform. In Proceedings of the 2016 51st International Universities Power Engineering Conference (UPEC), Coimbra, Portugal, 6–9 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Rico-Medina, A.V.; Reyes-Archundia, E.; Gutiérrez-Gnecchi, J.A.; Olivares-Rojas, J.C.; García-Ramírez, M.D.C. Analysis of the appropriate decomposition level based on discrete wavelet transform for detection of power quality disturbances. In Proceedings of the 2022 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 9–11 November 2022; IEEE: Piscataway, NJ, USA, 2022; Volume 6, pp. 1–6. [Google Scholar]
- Rico-Medina, A.V.; Reyes-Archundia, E.; Gutiérrez-Gnecchi, J.A.; Chávez-Báez, M.V.; Olivares-Rojas, J.C.; del C García-Ramírez, M. Evaluation of wavelet-based feature extraction methods for detection and classification of power quality disturbances. World J. Adv. Eng. Technol. Sci. 2022, 07, 220–229. [Google Scholar] [CrossRef]
- Patro, S.; Sahu, K.K. Normalization: A preprocessing stage. arXiv 2015, arXiv:1503.06462. [Google Scholar] [CrossRef]
- Jo, J.-M. Effectiveness of normalization pre-processing of big data to the machine learning performance. J. Korea Inst. Electron. Commun. Sci. 2019, 14, 547–552. [Google Scholar]
- Ansari, S.; Alnajjar, K.A.; Saad, M.; Abdallah, S.; El-Moursy, A.A. Automatic Digital Modulation Recognition Based on Genetic-Algorithm-Optimized Machine Learning Models. IEEE Access 2022, 10, 50265–50277. [Google Scholar] [CrossRef]
- Kumar, H.S.; Upadhyaya, G. Fault diagnosis of rolling element bearing using continuous wavelet transform and K- nearest neighbour. Mater. Today Proc. 2023, 92, 56–60. [Google Scholar] [CrossRef]
- Baroud, D.H.; Hasan, A.N.; Shongwe, T. The Use of Multiclass Support Vector Machines and Probabilistic Neural Networks for Signal Classification and Noise Detection in PLC/OFDM Channels. In Proceedings of the 2020 30th International Conference Radioelektronika (RADIOELEKTRONIKA), Bratislava, Slovakia, 15–16 April 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Costa, V.G.; Salcedo-Sanz, S.; Pedreira, C.E. Efficient evolution of decision trees via fully matrix-based fitness evaluation. Appl. Soft Comput. 2024, 150, 111045. [Google Scholar] [CrossRef]
- Jamali, S.; Farsa, A.R.; Ghaffarzadeh, N. Identification of optimal features for fast and accurate classification of power quality disturbances. Measurement 2018, 116, 565–574. [Google Scholar] [CrossRef]
- He, S.; Li, K.; Zhang, M. A real-time power quality disturbances classification using a hybrid method based on s-transform and dynamics. IEEE Trans. Instrum. Meas. 2013, 62, 2465–2475. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).