Dynamic Modeling and Control of Supercritical Carbon Dioxide Power Cycle for Gas Turbine Waste Heat Recovery
Abstract
1. Introduction
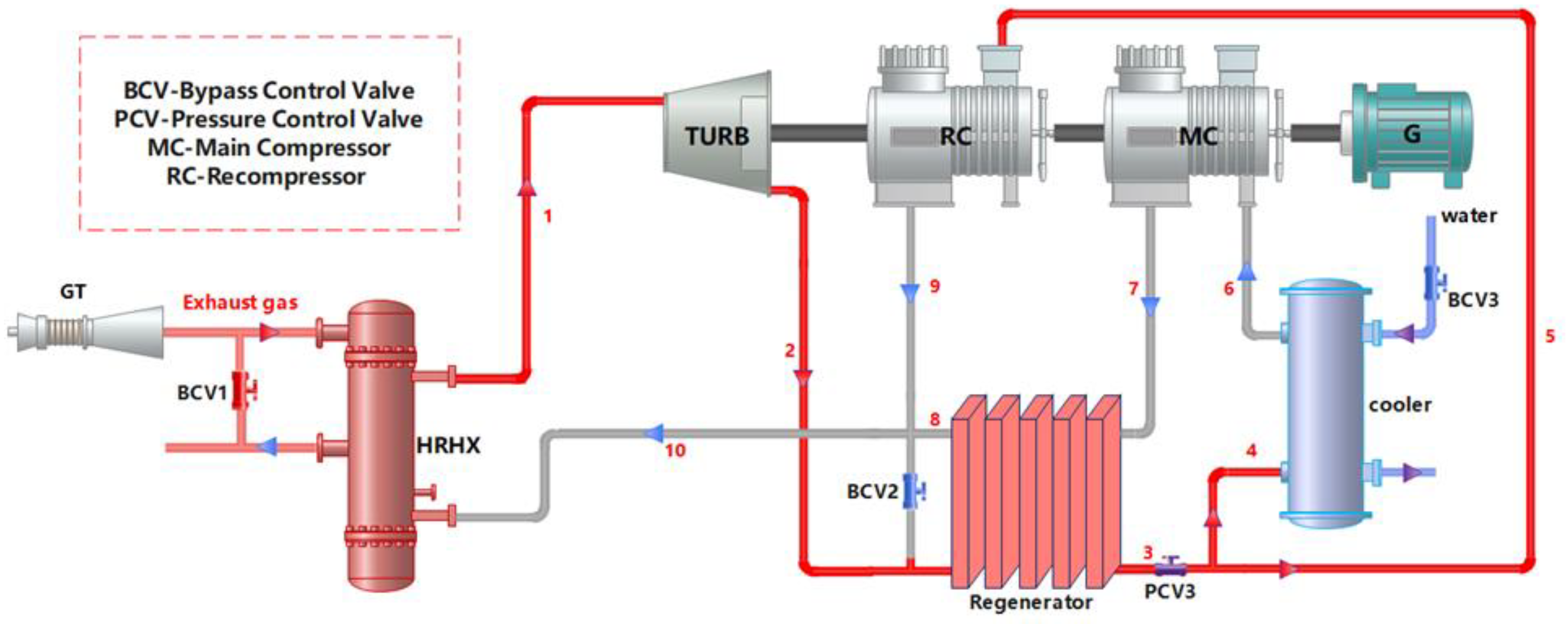
2. System Configuration and Description
2.1. Printed Circuit Heat Exchanger
2.2. Turbomachinery
2.2.1. Compressor
2.2.2. Turbine
3. Model Simulation and Validation
3.1. Steady-State Numerical Validation
3.2. Dynamic Response Experiment
4. Control Strategy and Controller Design for the System
4.1. Control Strategy
4.2. Controller Design
4.2.1. The Design of PI Controller
4.2.2. The Design of the ADRC Controller
5. Simulations and Results
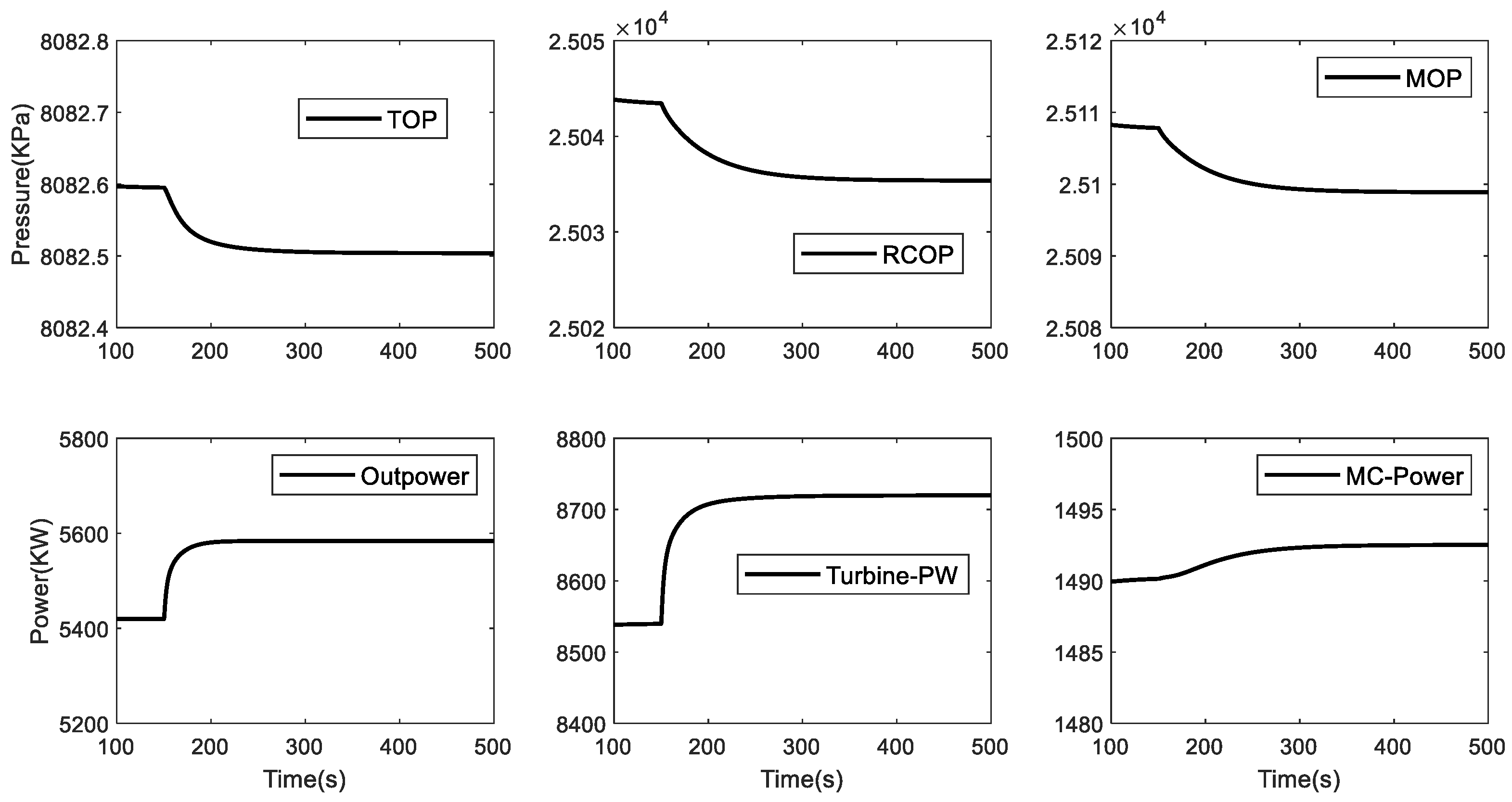
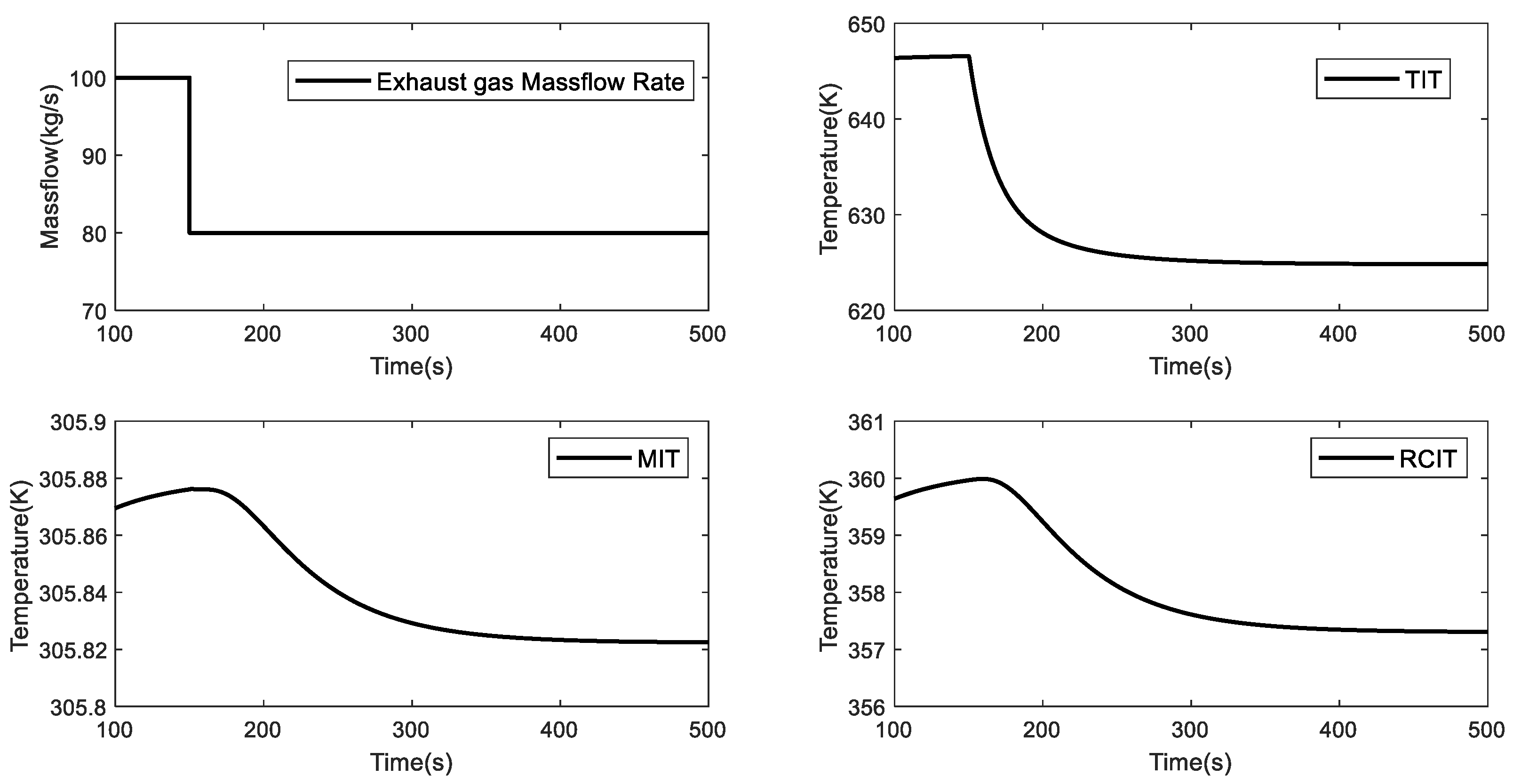
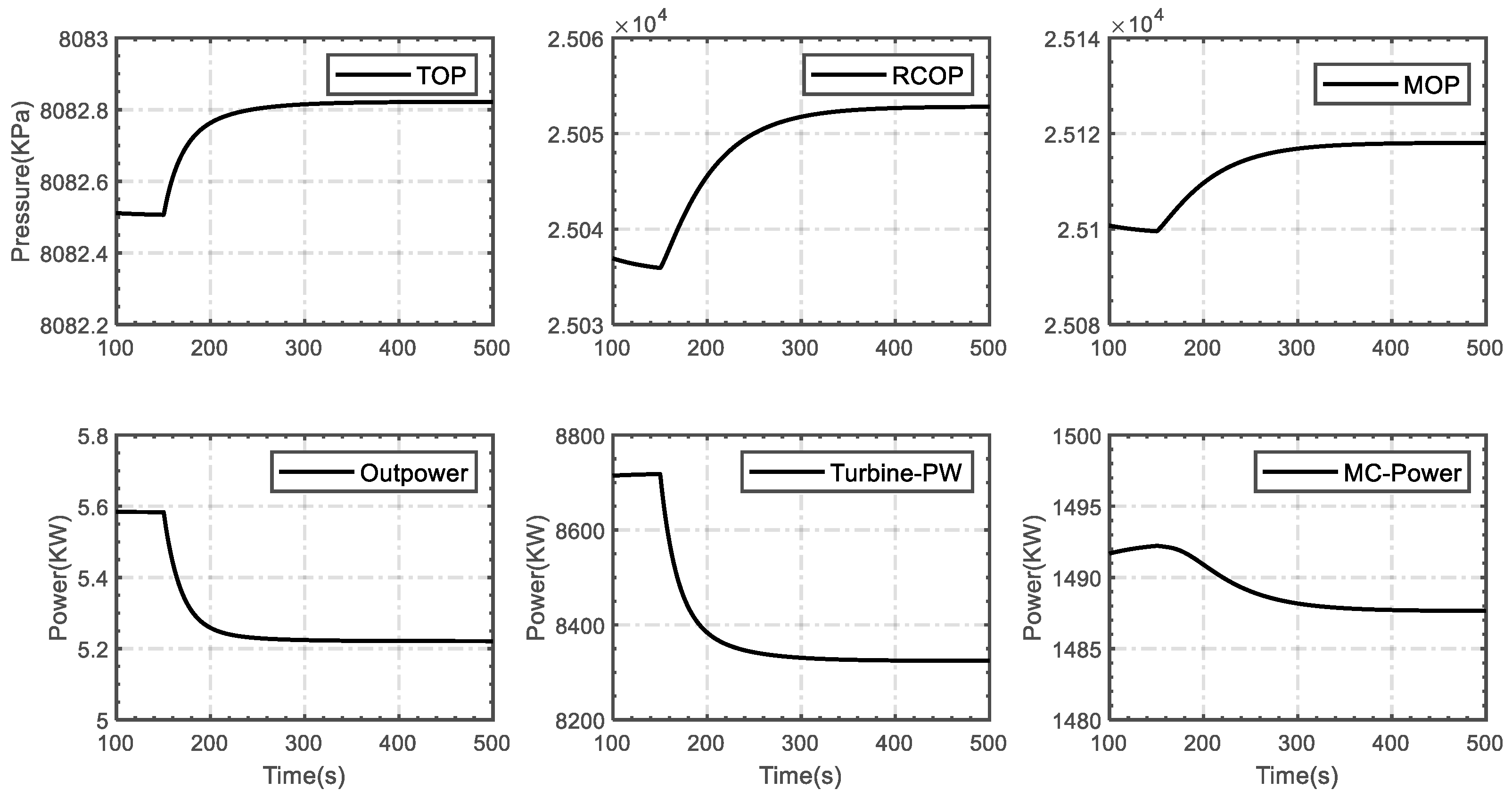
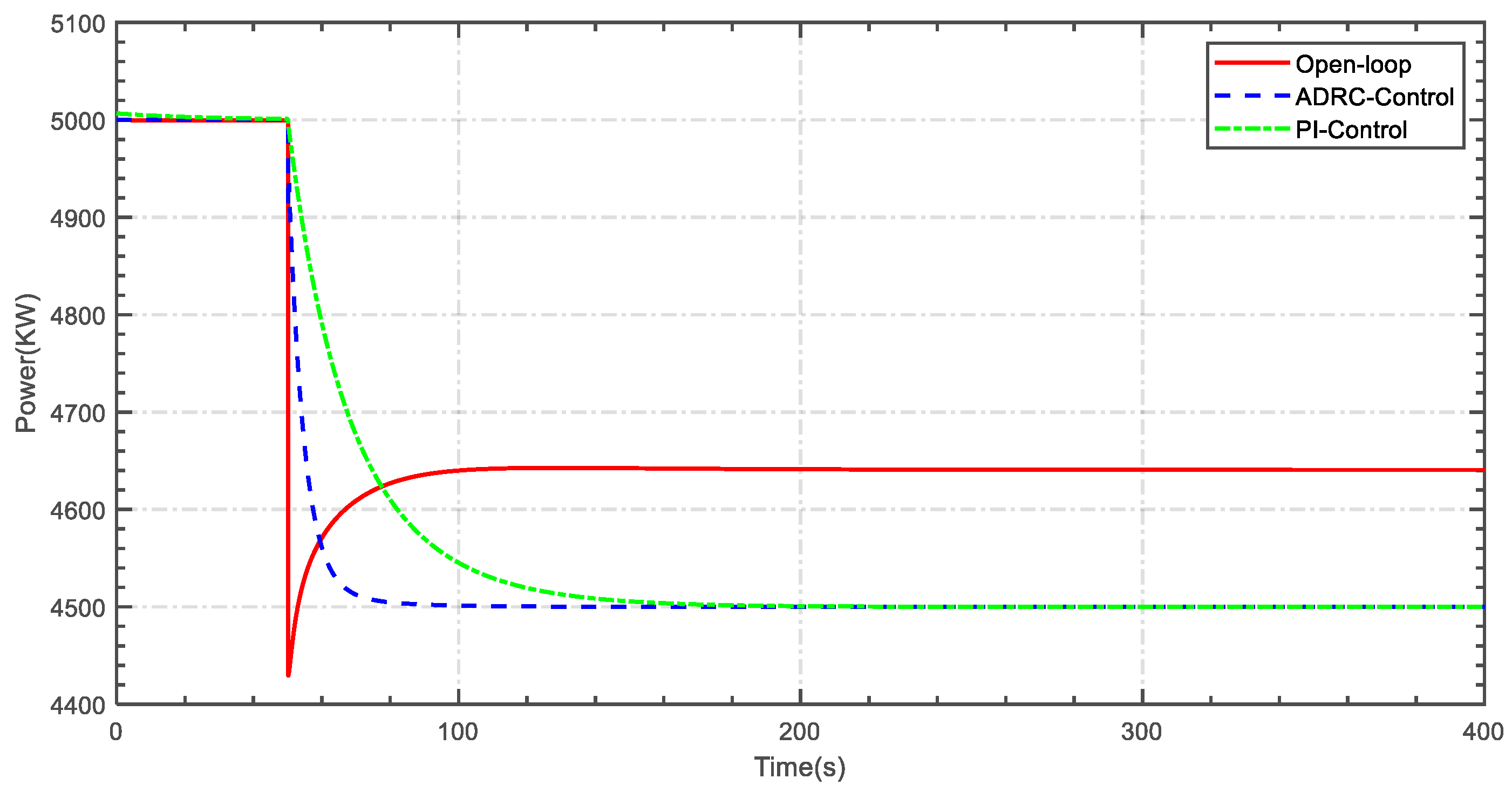
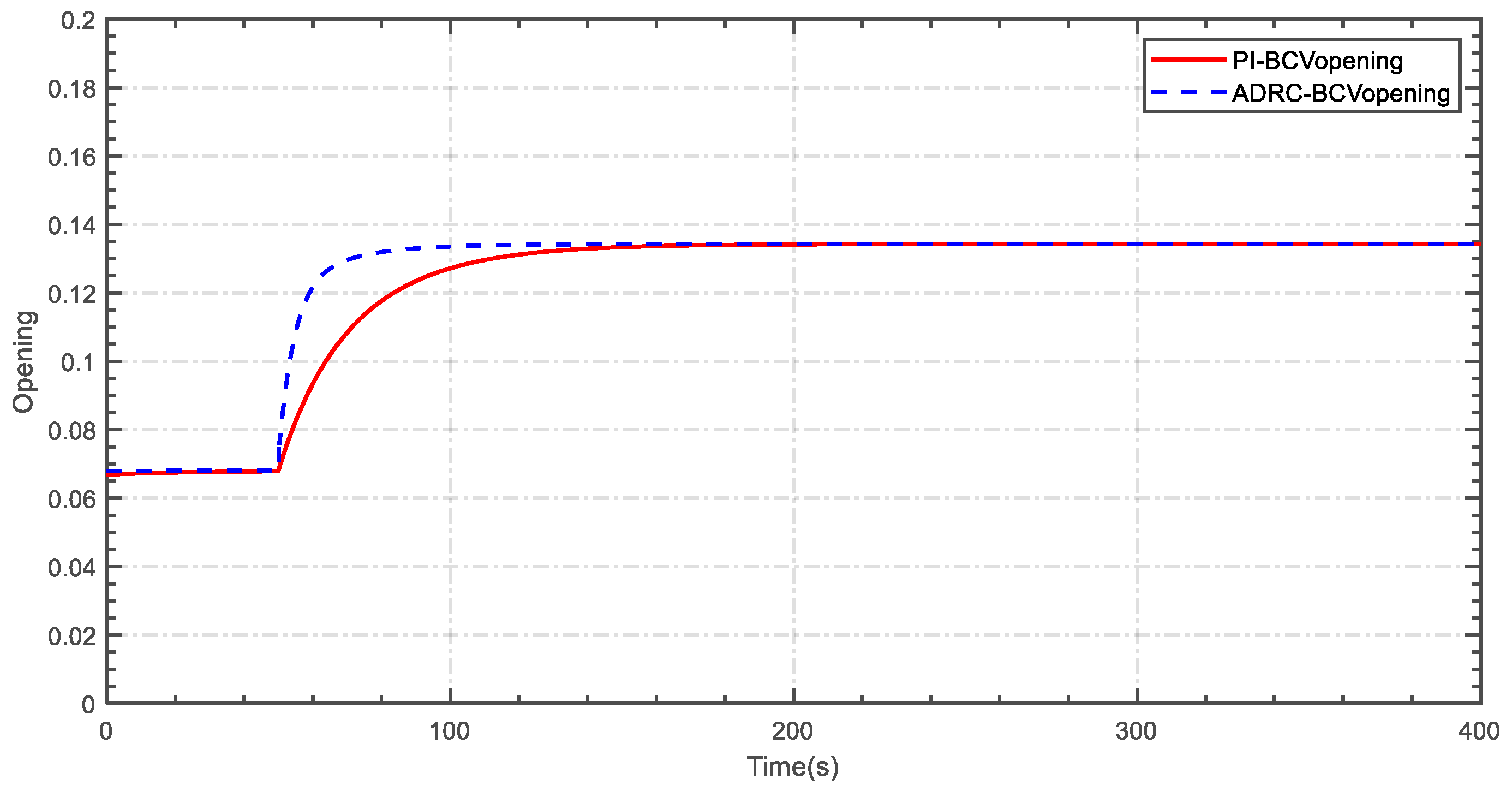
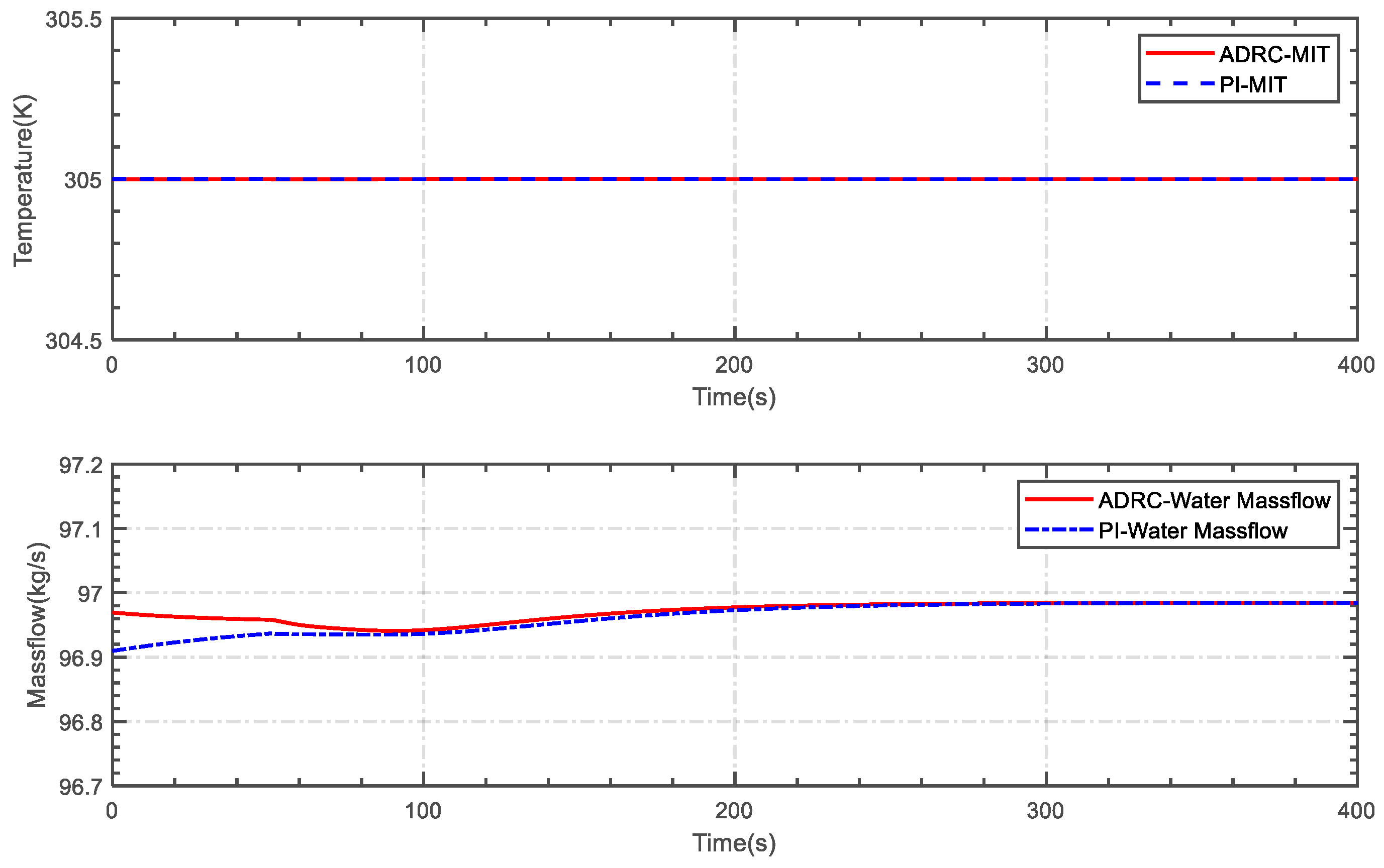
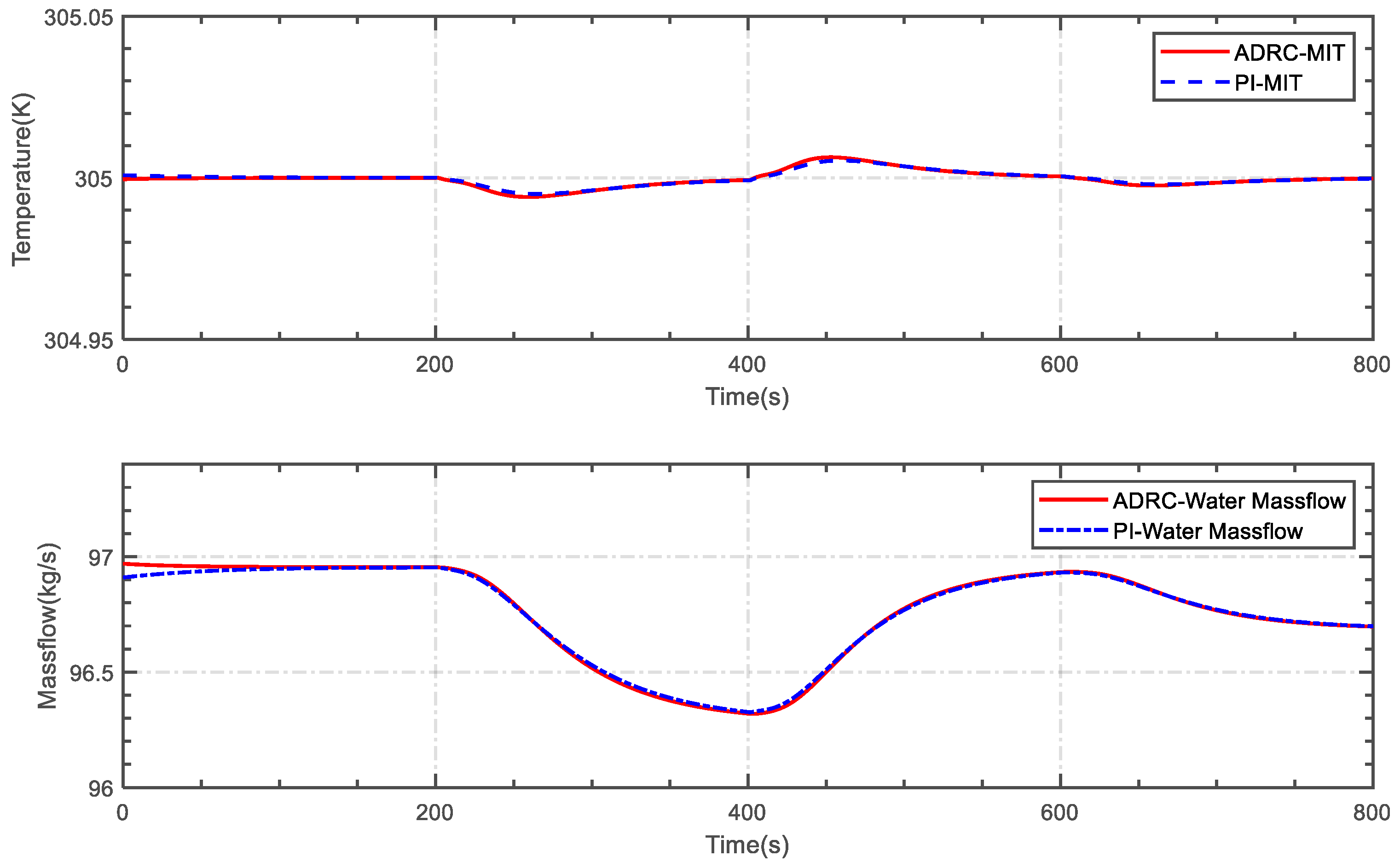
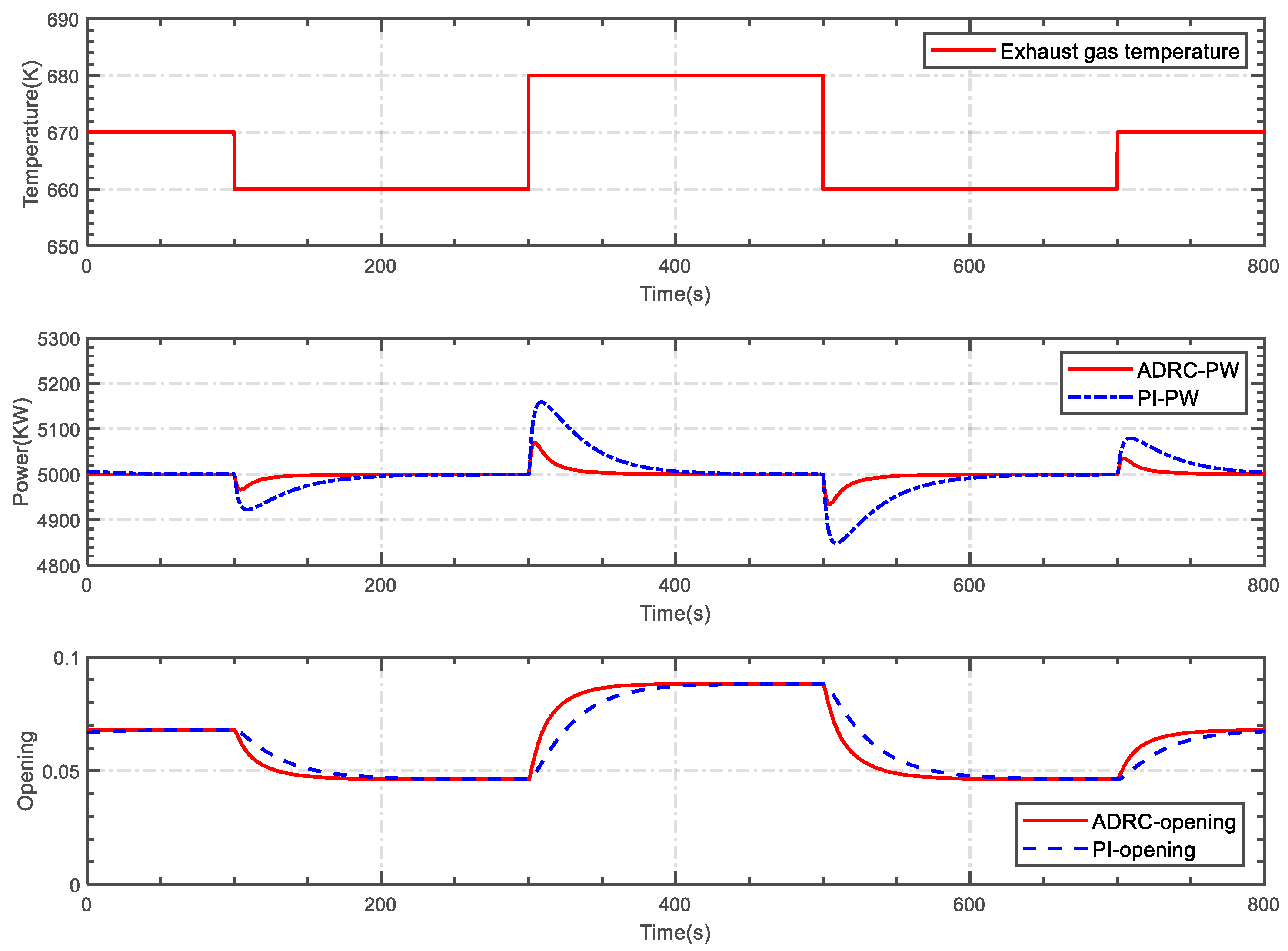
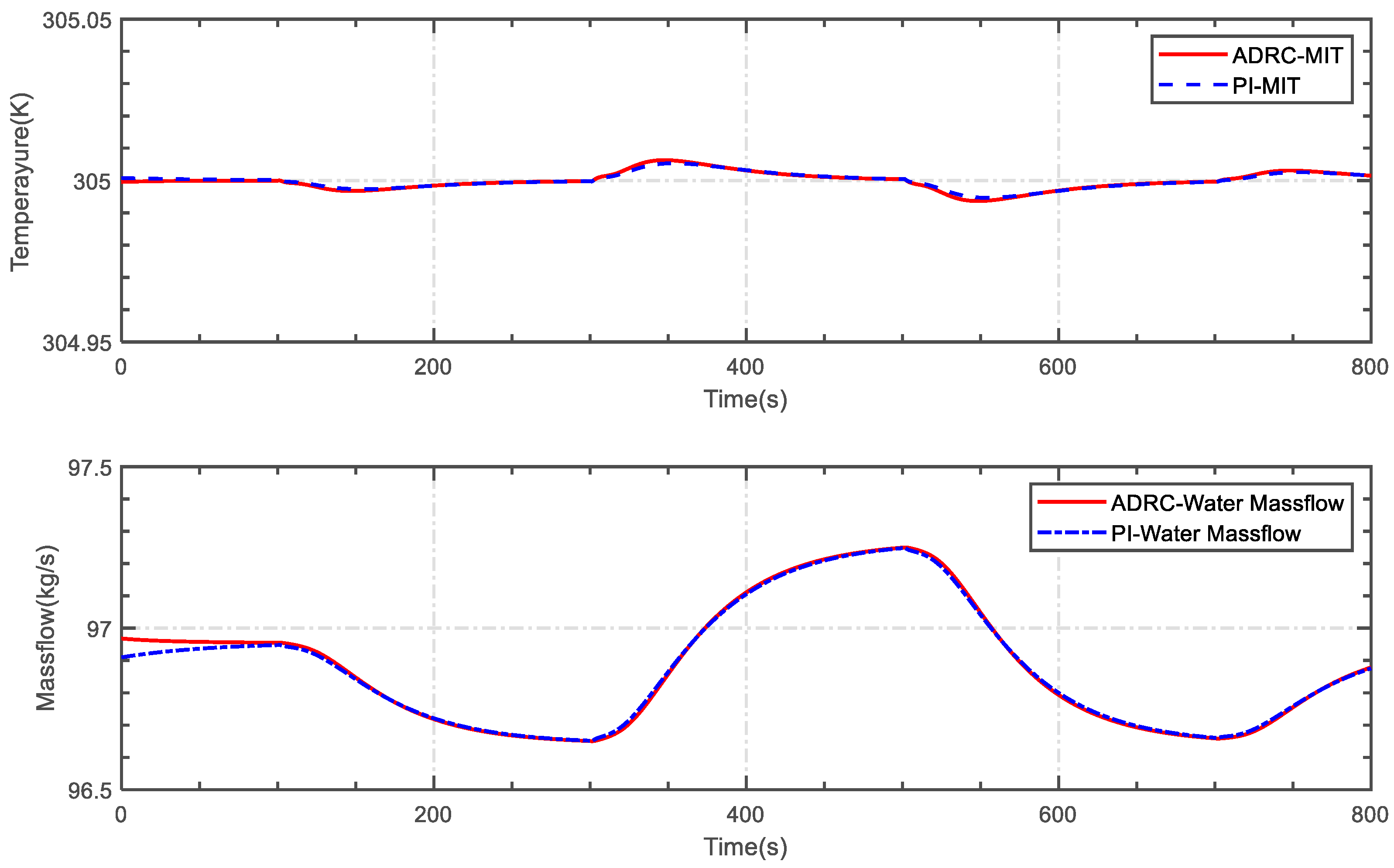
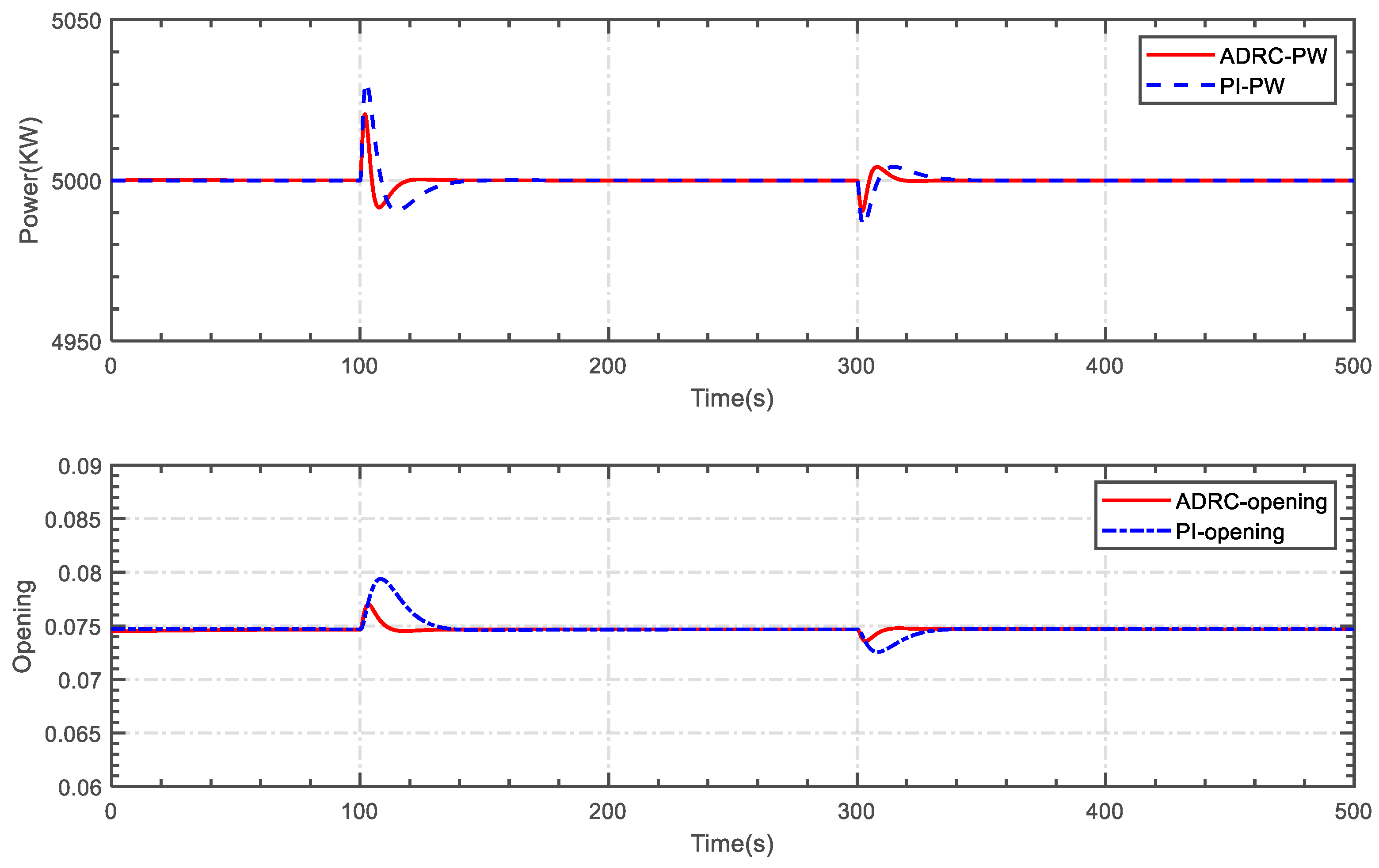
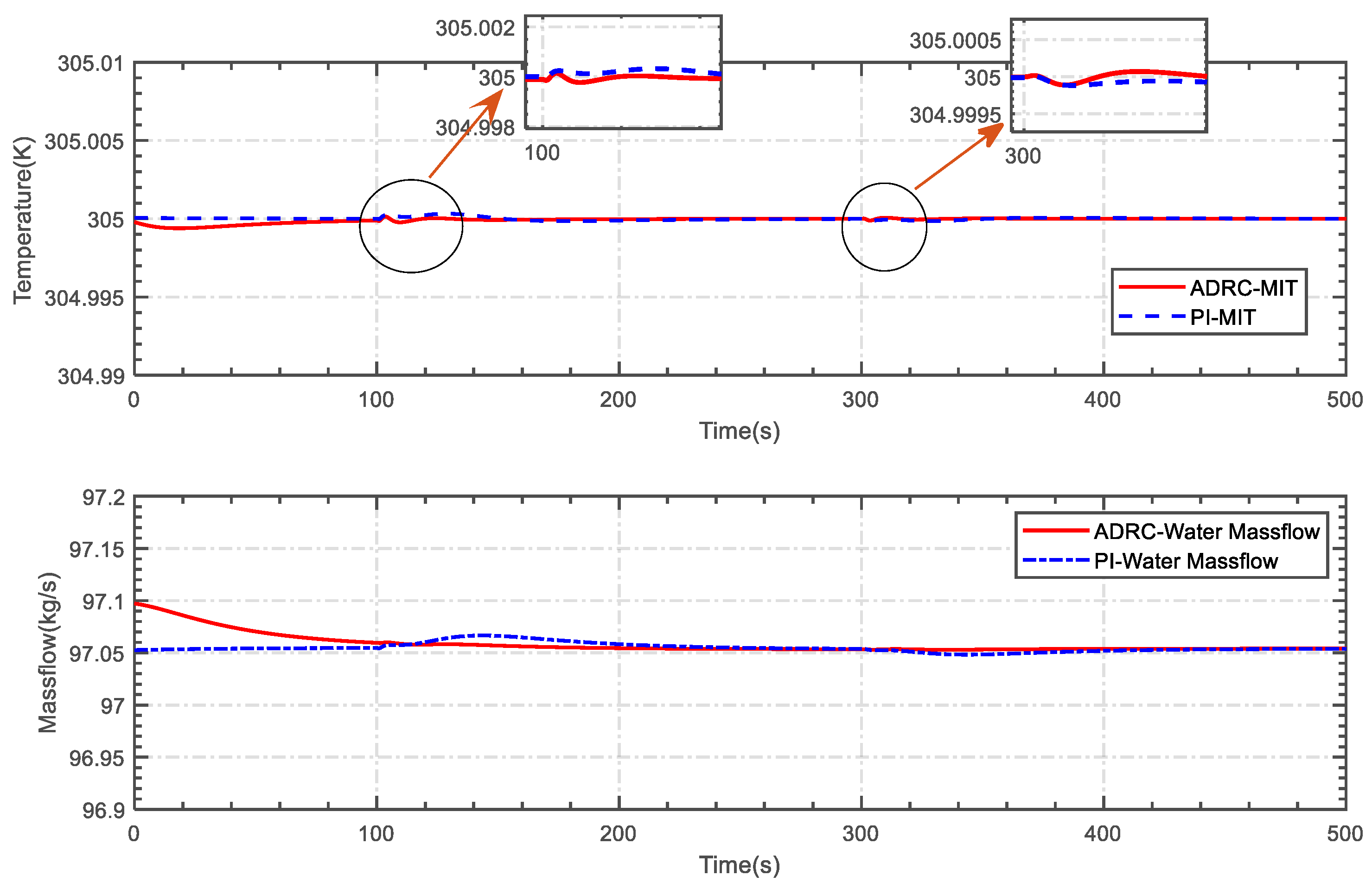
5.1. Case 1
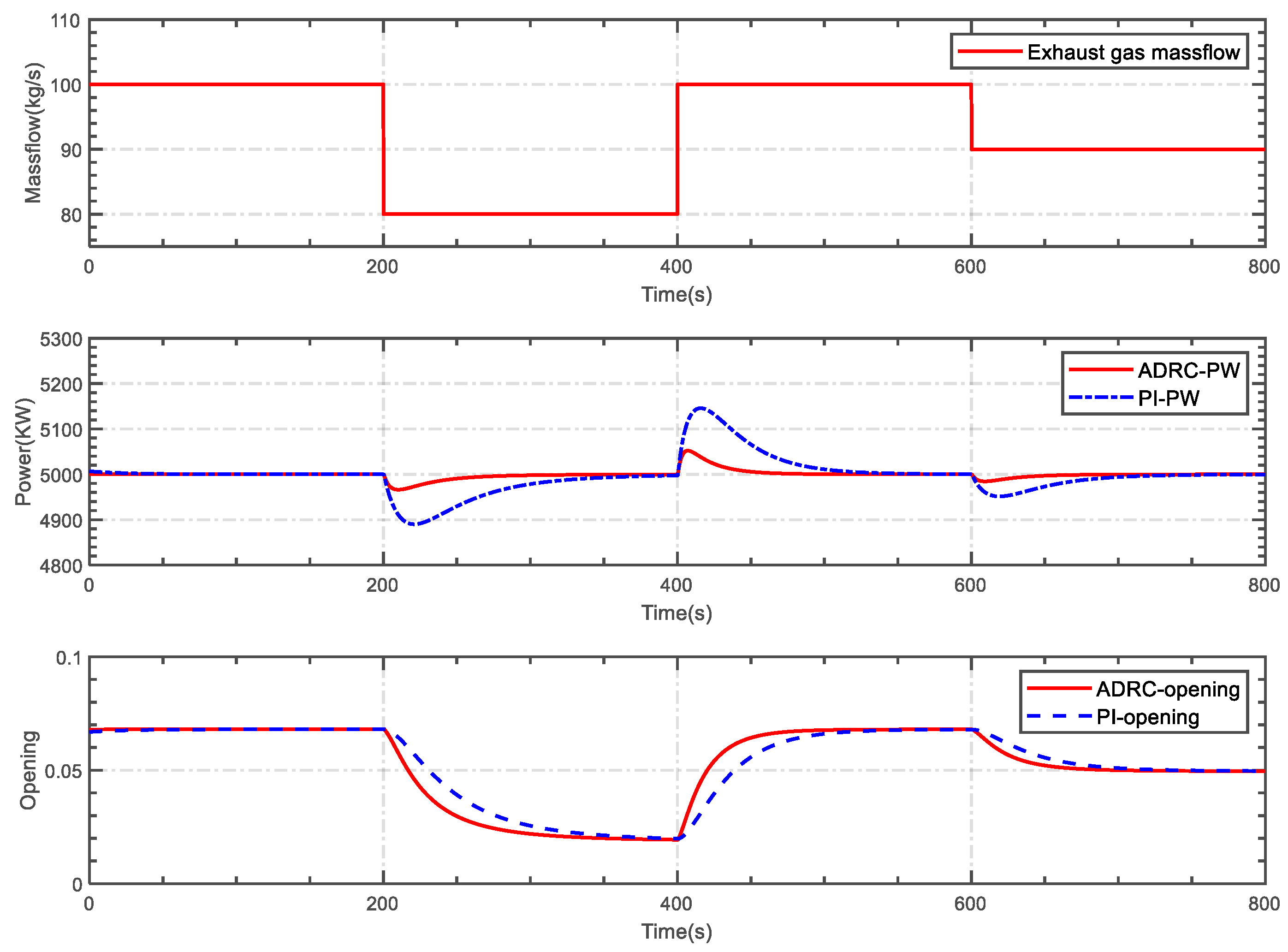
5.2. Case 2
5.3. Case 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| GT | gas turbine |
| HRHX | Heat Recovery Reat Exchanger |
| MC | main compressor |
| RC | re-compressor |
| G | generator |
| PCHE | printed circuit heat exchanger |
| S-CO2 | supercritical carbon dioxide |
| ORC | organic Rankine cycle |
| BCV | bypass valve controller |
| FCV | flow control valves |
| WHR | waste heat recovery |
| PI | Proportional–Integral |
| ADRC | Active Disturbance Rejection Control |
| ESO | Extended State Observer |
| Symbols | |
| heat transfer area, m2 | |
| hydraulic diameter, m | |
| mass flow rate, kg/s | |
| Nusselt number | |
| Prandtl number | |
| Darcy’s resistance | |
| Kinematic viscosity, cm2/s | |
| Reynolds number | |
| Pressure ratio | |
| efficiency | |
| convective heat transfer coefficient, W/(m2, K) | |
| Subscripts | |
| com | compressor |
| turb | turbine |
| in | inlet |
| out | outlet |
| h | hot-side fluid |
| c | cold-side fluid |
| w | wall |
References
- Moisseytsev, A.; Sienicki, J.J.; Lv, Q. Dry Air Cooler Modeling for Supercritical Carbon Dioxide Brayton Cycle Analysis; ANL-ART-50, 1342159; Argonne National Lab. (ANL): Argonne, IL, USA, 2016. [Google Scholar]
- Pasch, J.; Conboy, T.; Fleming, D.; Rochau, G. Supercritical CO2 Recompression Brayton Cycle: Completed Assembly Description; SAND2012-9546, 1057248; Sandia National Laboratories (SNL): Albuquerque, NM, USA, 2012. [Google Scholar]
- Utamura, M.; Hasuike, H.; Ogawa, K.; Yamamoto, T.; Fukushima, T.; Watanabe, T.; Himeno, T. Demonstration of Supercritical CO2 Closed Regenerative Brayton Cycle in a Bench Scale Experiment. In Proceedings of the Volume 3: Cycle Innovations; Education; Electric Power; Fans and Blowers; Industrial and Cogeneration; American Society of Mechanical Engineers: Copenhagen, Denmark, 2012; pp. 155–164. [Google Scholar]
- Ahn, Y.; Lee, J.; Kim, S.G.; Lee, J.I.; Cha, J.E.; Lee, S.-W. Design Consideration of Supercritical CO2 Power Cycle Integral Experiment Loop. Energy 2015, 86, 115–127. [Google Scholar] [CrossRef]
- Neises, T.; Turchi, C. A Comparison of Supercritical Carbon Dioxide Power Cycle Configurations with an Emphasis on CSP Applications. Energy Procedia 2014, 49, 1187–1196. [Google Scholar] [CrossRef]
- Olumayegun, O.; Wang, M. Dynamic Modelling and Control of Supercritical CO2 Power Cycle Using Waste Heat from Industrial Processes. Fuel 2019, 249, 89–102. [Google Scholar] [CrossRef]
- Neises, T.; Turchi, C. Supercritical Carbon Dioxide Power Cycle Design and Configuration Optimization to Minimize Levelized Cost of Energy of Molten Salt Power Towers Operating at 650 °C. Sol. Energy 2019, 181, 27–36. [Google Scholar] [CrossRef]
- Khan, M.N.; Zoghi, M.; Habibi, H.; Zanj, A.; Anqi, A.E. Waste Heat Recovery of Two Solar-Driven Supercritical CO2 Brayton Cycles: Exergoeconomic Analysis, Comparative Study, and Monthly Performance. Appl. Therm. Eng. 2022, 214, 118837. [Google Scholar] [CrossRef]
- Song, J.; Li, X.; Wang, K.; Markides, C.N. Parametric Optimisation of a Combined Supercritical CO2 (S-CO2) Cycle and Organic Rankine Cycle (ORC) System for Internal Combustion Engine (ICE) Waste-Heat Recovery. Energy Convers. Manag. 2020, 218, 112999. [Google Scholar] [CrossRef]
- Song, J.; Li, X.; Ren, X.; Gu, C. Performance Improvement of a Preheating Supercritical CO2 (S-CO2) Cycle Based System for Engine Waste Heat Recovery. Energy Convers. Manag. 2018, 161, 225–233. [Google Scholar] [CrossRef]
- Zare, V.; Mahmoudi, S.M.S.; Yari, M. An Exergoeconomic Investigation of Waste Heat Recovery from the Gas Turbine-Modular Helium Reactor (GT-MHR) Employing an Ammonia–Water Power/Cooling Cycle. Energy 2013, 61, 397–409. [Google Scholar] [CrossRef]
- Yoon, S.Y.; Kim, M.J.; Kim, I.S.; Kim, T.S. Comparison of Micro Gas Turbine Heat Recovery Systems Using ORC and Trans-Critical CO2 Cycle Focusing on off-Design Performance. Energy Procedia 2017, 129, 987–994. [Google Scholar] [CrossRef]
- Najjar, Y.S.H.; Abubaker, A.M.; El-Khalil, A.F.S. Novel Inlet Air Cooling with Gas Turbine Engines Using Cascaded Waste-Heat Recovery for Green Sustainable Energy. Energy 2015, 93, 770–785. [Google Scholar] [CrossRef]
- Nami, H.; Ertesvåg, I.S.; Agromayor, R.; Riboldi, L.; Nord, L.O. Gas Turbine Exhaust Gas Heat Recovery by Organic Rankine Cycles (ORC) for Offshore Combined Heat and Power Applications–Energy and Exergy Analysis. Energy 2018, 165, 1060–1071. [Google Scholar] [CrossRef]
- Cao, Y.; Mihardjo, L.W.W.; Dahari, M.; Tlili, I. Waste Heat from a Biomass Fueled Gas Turbine for Power Generation via an ORC or Compressor Inlet Cooling via an Absorption Refrigeration Cycle: A Thermoeconomic Comparison. Appl. Therm. Eng. 2021, 182, 116117. [Google Scholar] [CrossRef]
- Wang, S.; Liu, C.; Li, J.; Sun, Z.; Chen, X.; Wang, X. Exergoeconomic Analysis of a Novel Trigeneration System Containing Supercritical CO2 Brayton Cycle, Organic Rankine Cycle and Absorption Refrigeration Cycle for Gas Turbine Waste Heat Recovery. Energy Convers. Manag. 2020, 221, 113064. [Google Scholar] [CrossRef]
- Du, J.; Guo, J.; Zhang, Z.; Li, M.; Ren, F.; Liu, Y. A Triple Cascade Gas Turbine Waste Heat Recovery System Based on Supercritical CO2 Brayton Cycle: Thermal Analysis and Optimization. Energy Convers. Manag. X 2022, 16, 100297. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Liao, G.; Zhang, F.; Jiaqiang, E.; Tan, S. Design and Off-Design Performance Analysis of Supercritical Carbon Dioxide Brayton Cycles for Gas Turbine Waste Heat Recovery. Appl. Therm. Eng. 2023, 235, 121295. [Google Scholar] [CrossRef]
- Bonalumi, D.; Giuffrida, A.; Sicali, F. Techno-Economic Investigations of Supercritical CO2-Based Partial Heating Cycle as Bottoming System of a Small Gas Turbine. Energy 2022, 252, 124066. [Google Scholar] [CrossRef]
- Giuffrida, A.; Akramieh, E. Analysis of Partial Heating Supercritical CO2 Cycles Bottoming Small-Power Gas Turbine Units. Energy Convers. Manag. X 2023, 17, 100341. [Google Scholar] [CrossRef]
- Bonalumi, D.; Giuffrida, A.; Sicali, F. A Case Study of Cascade Supercritical CO2 Power Cycle for Waste Heat Recovery from a Small Gas Turbine. Energy Convers. Manag. X 2022, 14, 100212. [Google Scholar] [CrossRef]
- Cao, Y.; Zhan, J.; Cao, Q.; Si, F. Techno-Economic Analysis of Cascaded Supercritical Carbon Dioxide Combined Cycles for Exhaust Heat Recovery of Typical Gas Turbines. Energy Convers. Manag. 2022, 258, 115536. [Google Scholar] [CrossRef]
- Jin, Q.; Xia, S.; Xie, T.; Huang, J. Multi-Objective Optimization of Recompression S-CO2 Cycle for Gas Turbine Waste Heat Recovery. Appl. Therm. Eng. 2023, 229, 120601. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Bian, X.; Cai, J.; Tian, H.; Shu, G.; Li, X.; Qin, Z. Review of Dynamic Performance and Control Strategy of Supercritical CO2 Brayton Cycle. Energy AI 2021, 5, 100078. [Google Scholar] [CrossRef]
- Hu, H.; Guo, C.; Cai, H.; Jiang, Y.; Liang, S.; Guo, Y. Dynamic Characteristics of the Recuperator Thermal Performance in a S–CO2 Brayton Cycle. Energy 2021, 214, 119017. [Google Scholar] [CrossRef]
- Deng, T.; Li, X.; Wang, Q.; Ma, T. Dynamic Modelling and Transient Characteristics of Supercritical CO2 Recompression Brayton Cycle. Energy 2019, 180, 292–302. [Google Scholar] [CrossRef]
- Ma, T.; Li, M.-J.; Xu, J.-L.; Cao, F. Thermodynamic Analysis and Performance Prediction on Dynamic Response Characteristic of PCHE in 1000 MW S-CO2 Coal Fired Power Plant. Energy 2019, 175, 123–138. [Google Scholar] [CrossRef]
- Battisti, F.G.; Delsoto, G.S.; da Silva, A.K. Transient Analysis and Optimization of a Recuperative sCO2 Brayton Cycle Assisted by Heat and Mass Storage Systems. Energy 2018, 150, 979–991. [Google Scholar] [CrossRef]
- Luu, M.T.; Milani, D.; McNaughton, R.; Abbas, A. Advanced Control Strategies for Dynamic Operation of a Solar-Assisted Recompression Supercritical CO2 Brayton Power Cycle. Appl. Therm. Eng. 2018, 136, 682–700. [Google Scholar] [CrossRef]
- Zhang, F.; Feng, M.; Dai, H.; Wu, Z.; Liao, G. Off-Design and Control Performance Analysis of a Novel Supercritical Carbon Dioxide Power Cycle for Waste Heat Recovery. Appl. Therm. Eng. 2023, 235, 121393. [Google Scholar] [CrossRef]
- Dai, C.; Song, P.; Ma, C.; Zhang, K.; Zheng, W.; Chen, L.; Guo, X.; Lin, Y.; Qiu, Z. Research on Response Characteristics and Control Strategy of the Supercritical Carbon Dioxide Power Cycle. Processes 2021, 9, 1943. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Y.; Hong, G.; Li, J. Comparative Study of the Supercritical Carbon-Dioxide Recompression Brayton Cycle with Different Control Strategies. Prog. Nucl. Energy 2021, 137, 103770. [Google Scholar] [CrossRef]
- Ferrero, S. Modelica Dynamic Modeling of a Supercritical CO2 Loop for Solar and Nuclear Applications. Master′s Thesis, Politecnico di Torino, Torino, Italy, 2020. [Google Scholar]
- Jiang, Y. Design and Dynamic Modeling of Printed Circuit Heat Exchangers for Supercritical Carbon Dioxide Brayton Power Cycles. Appl. Energy 2018, 231, 1019–1032. [Google Scholar] [CrossRef]
- Carstens, N.A.; Hejzlar, P.; Driscoll, M.J. Control System Strategies and Dynamic Response for Supercritical CO2 Power Conversion Cycles. Cent. Adv. Nucl. Energy Syst. 2006. Available online: https://corpora.tika.apache.org/base/docs/govdocs1/418/418386.pdf (accessed on 1 February 2024).
- Moisseytsev, A.; Kulesza, K.P.; Sienicki, J.J. Control System Options and Strategies for Supercritical CO2 Cycles; ANL-GENIV-081, 958037; Argonne National Lab. (ANL): Argonne, IL, USA, 2009. [Google Scholar]
- Moisseytsev, A.; Sienicki, J.J. Dynamic Control Analysis of the AFR-100 SMR SFR with a Supercritical CO2 Cycle and Dry Air Cooling: Part I—Plant Control Optimization. In Proceedings of the 2018 26th International Conference on Nuclear Engineering, London, UK, 22–26 July 2018; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2018. [Google Scholar]
- Gao, Z. Active Disturbance Rejection Control: A Paradigm Shift in Feedback Control System Design. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; IEEE: Minneapolis, MN, USA, 2006; p. 7. [Google Scholar]
- Jin, H.; Song, J.; Lan, W.; Gao, Z. On the Characteristics of ADRC: A PID Interpretation. Sci. China Inf. Sci. 2020, 63, 209201. [Google Scholar] [CrossRef]



| Parameter | HRHX | Regenerator | Cooler |
|---|---|---|---|
| 173.01 | 269.12 | 153.78 | |
| 2808.60 | 3184.02 | 2729.16 | |
| 0.15 | 0.17 | 0.15 | |
| Number of modules | 9 | 14 | 8 |
| Component | Compression/Expansion Ratio [6,35] | Isentropic Efficiency [6] |
|---|---|---|
| Turbine | 0.9 | |
| Main compressor | 0.89 | |
| Re-compressor | 0.88 |
| Data Source | Reference [36] | Reference [33] | Literature [6] |
|---|---|---|---|
| Hot-side outlet temperature/K | 305.14 | 388.15 | 349.15 |
| Relative difference | 1.36% | 0.76% | 0.56% |
| Cool-side outlet temperature/K | 305.87 | 464.83 | 633.15 |
| Relative difference | 2.01% | 1.15% | 0.93% |
| State | m (kg/s) | Pressure (KPa) | T (K) |
|---|---|---|---|
| 1 | 80.40 | 24,975.33 | 632.72 |
| 2 | 80.40 | 8082.63 | 516.62 |
| 3 | 80.40 | 7982.91 | 358.28 |
| 4 | 53.98 | 7982.91 | 358.28 |
| 5 | 26.42 | 7982.91 | 358.28 |
| 6 | 53.98 | 7936.48 | 305.84 |
| 7 | 53.98 | 25,111.03 | 340.95 |
| 8 | 53.98 | 25,095.39 | 494.88 |
| 9 | 26.42 | 25,046.36 | 458.61 |
| 10 | 80.40 | 25,046.36 | 482.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, B.; Zhang, F.; Lee, K.Y.; Hu, H.; Wang, T.; Zhang, B. Dynamic Modeling and Control of Supercritical Carbon Dioxide Power Cycle for Gas Turbine Waste Heat Recovery. Energies 2024, 17, 1343. https://doi.org/10.3390/en17061343
Ma B, Zhang F, Lee KY, Hu H, Wang T, Zhang B. Dynamic Modeling and Control of Supercritical Carbon Dioxide Power Cycle for Gas Turbine Waste Heat Recovery. Energies. 2024; 17(6):1343. https://doi.org/10.3390/en17061343
Chicago/Turabian StyleMa, Bowen, Fan Zhang, Kwang Y. Lee, Hemin Hu, Tao Wang, and Bing Zhang. 2024. "Dynamic Modeling and Control of Supercritical Carbon Dioxide Power Cycle for Gas Turbine Waste Heat Recovery" Energies 17, no. 6: 1343. https://doi.org/10.3390/en17061343
APA StyleMa, B., Zhang, F., Lee, K. Y., Hu, H., Wang, T., & Zhang, B. (2024). Dynamic Modeling and Control of Supercritical Carbon Dioxide Power Cycle for Gas Turbine Waste Heat Recovery. Energies, 17(6), 1343. https://doi.org/10.3390/en17061343









