Abstract
This study addresses the critical gap in the literature regarding the energy efficiency of intermodal terminals in smart cities, mainly focusing on crane operations during train loading processes. Novelty’s contribution lies in developing a comprehensive simulation model in FlexSim, where quantitative analysis of crane energy consumption, factoring in container location in the storage yard, rehandling operations, and crane movement strategies were performed. Moreover, the analysis of hoist, trolley, and gantry movements was performed to evaluate their impact on overall container loading process energy efficiency. The findings reveal that the choice of train loading method significantly influences crane energy consumption, thereby affecting the operational costs, environmental footprint, and energy efficiency of the logistics hub in the form of an intermodal terminal. This research provides a methodology for assessing and enhancing the energy efficiency of intermodal terminals and highlights the broader implications for smart city sustainability goals, including reduced greenhouse gas emissions, lower operating costs, and improved transportation infrastructure. The outcomes of this research can possibly support smart city planners and logistics managers in making informed decisions to optimise intermodal terminal operations, contributing to urban areas’ sustainable development and economic resilience.
1. Introduction
The concept of a smart city is based on the utilisation of advanced information and communication technologies (ICT), large datasets, data analysis tools, and innovative solutions to improve the quality of life for residents, enhance the efficiency of municipal services, and promote sustainable urban development. The goals of the smart city concept are achieved by leveraging modern technologies such as the Internet of Things (IoT), artificial intelligence (AI), data analysis, and blockchain to develop intelligent solutions and services. ICT infrastructure plays a crucial role in realising this concept [1]. As a result, the smart city concept aims to integrate various resources such as transportation, education, health, energy, and public safety to maximise the efficiency of managing these resources. An essential element of this concept is also the pursuit of sustainable development through proper monitoring and management of energy consumption. From the perspective of freight transport, this concept envisions the use of modern technologies to create a more efficient, sustainable, and secure logistics system that contributes to improving the quality of life for residents. Freight transport in a smart city is crucial for the functioning of the entire urban logistics system. It encompasses the service of businesses and residents, who are both senders and receivers of goods, and efficient logistics within the city. From the perspective of freight transport, a smart city utilises advanced technologies such as supply chain management (SCM) systems to optimise logistics processes. Additionally, automation, data analysis, and real-time monitoring enable effective route planning, minimisation of delays, and optimisation of resource utilisation in the form of transportation means or storage space for goods. These systems, in turn, are supported by integrated logistics platforms that connect various supply chain elements, including storage, transportation, and data management. These platforms enable better planning and coordination of logistical activities [2]. Utilising these technologies enables effective planning of the city’s freight transport service to minimise the impact of freight transport on urban traffic [3].
Due to limitations on the movement of freight vehicles in cities, arising from their size, permissible total weight, and often emission levels, the efficient execution of freight services for senders and recipients in a smart city requires the use of facilities that will enable the deconsolidation of large cargo flows entering the city and the consolidation of cargoes sent from the city and its immediate surroundings. Examples of such facilities are Urban Consolidation Centres and intermodal terminals. Urban Consolidation Centres are facilities where large streams of goods arriving in the city are collected, grouped, and then distributed to their final destinations within the city. The issue of Urban Consolidation Centres is one of the most frequently addressed topics in the literature related to urban logistics [4]. This is because such facilities can potentially address the environmental and social challenges urban transportation systems pose [5]. The first publications addressing this issue date back to the early 1970s [6]. However, in practice, initiatives involving the construction of such facilities often do not come to fruition [7]. This results from a series of challenges that such concepts must face. Coordinating various suppliers, carriers, and recipients while dealing with diverse delivery requirements can lead to operational difficulties. Stakeholders, including businesses, transport companies, and local authorities, may resist such changes due to concerns about disruptions, costs, or favouring established practices [8].
Therefore, one of the solutions to the cargo logistics problem in a smart city can be intermodal terminals, which, as practice indicates, are often located inside cities at nodes and railway lines. Intermodal terminals also offer storage space, allowing for flexible management of deliveries and pickups. Moreover, with proper storage and transhipment infrastructure and information technology infrastructure, intermodal terminals often become central hubs where various transport operators can collaborate effectively, exchange information, and plan transportation [9].
In addition to the functions performed by intermodal terminals, a significant aspect favouring their use for smart city operations is the rapid development of containerisation. Since its inception in the mid-20th century, containerised transport has enabled a standardised method of freight transport, ensuring the safety and efficiency of goods transportation. In 2012, container throughput at ports worldwide was at the level of 662 million TEUs. 10 years later, it achieved the value of 866 million TEUs. The global container transport market is forecast to grow at a compound annual growth rate (CAGR) of over four percent between 2019 and 2027 [10]. The presented values clearly indicate that with the increase in intermodal transport, there will be a need for the development of both infrastructure and organisational aspects of container terminals, including those located in or near the city, to handle large volumes of cargo both inbound to and outbound from the city and its surroundings [11].
The use of intermodal terminals in urban logistics also aligns with the European Commission’s 2011 White Paper on Transport recommendations. According to the goals set forth in this document, it is anticipated that by 2030, 30% of road freight transport over distances exceeding 300 km should be shifted to other modes of transport, such as rail or water transport. By 2050, this percentage should exceed 50%. Therefore, the realisation of deliveries to and from the city via rail-road transport, with operations conducted in intermodal terminals, may become necessary soon [12].
The literature analyses conducted concerning the use of intermodal terminals for cargo handling in the city indicate that so far, there have been few publications on this subject. The application of a keyword query (“urban” OR “city”) AND (“intermodal terminal” OR “container terminal”) in the Web of Science database returned only 55 results. Most of these publications address the issue of work organisation in maritime terminals located in large ports, which are usually part of urban agglomerations [13,14].
Among the works on rail-road intermodal terminals located in the city or its vicinity, one can distinguish works concerning the rationalisation of their location [15,16], or studies examining and assessing the investment risk associated with the location of a terminal in a given city area [17]. Some publications investigate the issue of the impact of intermodal terminals on logistic processes in the city [18]. From the perspective of urban logistics, some publications focus on studying the impact of freight traffic serving intermodal terminals on city congestion as well as the impact of using intermodal terminals in cities to reduce air pollution [19,20].
Literature analysis shows that there is essentially a lack of publications on the energy efficiency of intermodal terminals handling cargo in the city. Indeed, in their work [21], the authors address the issue of the energy efficiency of a rail-road intermodal terminal, but they do not present the necessary calculations related to energy consumption. The authors of this work focus on developing a generic algorithm for scheduling crane operations, and the study of the energy efficiency of the intermodal terminal is merely reduced to identifying factors that influence energy consumption in the outbound container handling process.
Therefore, the aim of the article is to calculate and examine the crane energy consumption during the train loading in the intermodal terminal handling freight from the city. These studies were conducted on a simulation model developed in Flexsim in which the storage yard of the intermodal terminal, the loading front, and consequently the process of loading containers onto wagons were replicated. The energy efficiency of an intermodal train loading process is conditioned by the location of containers in the storage yard, the necessity of rehandling containers in the storage yard in order to pick up those designated for loading, as well as the crane operation strategy resulting from the distribution of coupling pins on container wagons (understood as the algorithm for allocation of containers to wagons and the order of their handling by the crane).
As a result of the conducted research, it was possible to answer the question of how the aforementioned factors affect crane energy consumption and consequently the energy efficiency of the entire process. The data for the crane energy consumption calculation was determined based on analyses conducted in work [22] for an RTG crane.
The remaining part of the article is organised as follows: A brief literature review on the optimisation of handling processes in intermodal terminals and related energy consumption by handling equipment is presented in Section 2. In Section 3, the article outlines the description of the research problem addressed. Section 4 conducts simulation experiments and presents the results of the calculations. Section 5 summarises the conducted research.
2. Literature Review
2.1. Intermodal Train Loading
In addition to providing various logistics services such as consolidation, deconsolidation, transportation, forwarding, and customs clearance, an intermodal terminal in a smart city primarily handles container transshipments in the truck-train relationship. Containers arriving at the terminal by rail are transferred to the yard. Some of them are then transported by truck directly to customers, while others undergo deconsolidation, allowing small batches of goods to be delivered to recipients in the city. The process of container dispatch is precisely the opposite. Some containers are delivered directly from senders, while others are formed in the terminal by consolidating smaller shipments sent from the city. The specificity of the intermodal terminal’s operation leads to a series of decision-making problems directly affecting cargo handling time in the terminal, transport, and transhipment cycle times, and consequently, the efficiency of process execution and the energy efficiency of the terminal. Among the fundamental decision-making problems determining the efficiency of the terminal, it is necessary to distinguish [23,24,25]: the distribution of containers in the storage yard, scheduling the work of yard cranes, and loading intermodal trains. The first of these problems involves determining the optimal location for container storage to prevent the need to move other containers to extract a specific one. Scheduling the work of yard cranes at the terminal involves allocating containers to cranes and determining the order in which the crane handles these containers. The loading of intermodal trains is directly related to these issues. The literature on maritime terminals devotes a significant amount of space to issues such as scheduling the work of cranes or arranging containers in the storage yard [26,27]. Unfortunately, the processes occurring in land terminals, although they may appear such as those in maritime terminals, have a different course in land terminals [24]. This is because deliveries to the terminal and shipments are characterised by high variability, mainly influenced by urgent containers that need handling [28]. One of the very first publications that advanced the understanding of the train loading problem by offering a substantial contribution by creating practical models that can be adapted to diverse, specific environments were the papers [29,30].
The issue of loading intermodal trains is a challenging one because, when planning the arrangement of containers on wagons, it is crucial to consider factors such as the configuration of coupling pins on wagons, the gross weights of loaded containers, and the associated permissible axle loads of the wagons, as well as the maximum filling of wagon capacity to minimise the train length and aerodynamic resistance. One of the studies extensively addresses the issue of loading intermodal trains [30]. In addition to the configuration of coupling pins on wagons, the authors also considered weight restrictions for wagons and various types and weights of containers, including the arrangement of their coupling corners and centre of mass. Later in work [31], they added uncertainty in the weight of containers and faults in the wagons. Similarly, the loading of a train was considered in the work [32].
In addition to the configuration of coupling pins on wagons and the proper distribution of the load on wagon axles resulting from the weight of containers, another factor influencing the strategy of intermodal train loading is the train’s aerodynamics, as considered in the publication [33]. According to the authors, the train’s aerodynamics significantly impact the train’s stability in motion and its energy consumption.
The planning of the intermodal train loading is directly related to the optimisation issues of container storage and movement in the yard. In [34], the authors formulated a MILP load planning model to maximise train utilisation while minimising reshuffling costs in the stacking area and unproductive crane movements as the train is loaded. Also, in [35], the authors considered the situation of train loading, where containers were sequentially loaded on the wagons to maximise the priority of containers to be loaded while minimising the number of rehandles in the yard. Similar issues were considered in [21,36].
The literature analysis in this area indicates a lack of publications that comprehensively consider all aspects of loading trains while simultaneously considering the location of containers in the storage yard.
2.2. Crane Energy Efficiency
In the inland terminals serving urban agglomerations and their surroundings, the typical equipment used includes RMG cranes, RTG cranes, or Reachstackers [37,38]. Various energy sources and power loading equipment are adapted to the specific location and operations performed at a given terminal. Many intermodal terminals use electricity supplied by the power grid. Loading machines, such as rail-mounted gantry cranes and sometimes rubber-tired gantry cranes, are connected to a constant power source, enabling efficient and continuous operation. Some loading machines in intermodal terminals are equipped with internal combustion engines, allowing them to be self-powered. This solution is particularly useful in locations where access to electricity may be limited. This type of power is typically used in Reachstackers and rubber-tired gantry cranes (RTG). In RTG cranes powered this way, a diesel engine drives a generator that produces the necessary electricity. The electricity is then rectified, and the DC power is distributed to all electric motors driving the hoist, trolley, and RTG crane’s gantry [39].
Contemporary technologies increasingly utilise electric batteries to power loading machines. These environmentally friendly solutions can be charged from both traditional and renewable sources, such as photovoltaic panels [40]. Some loading machines utilise hybrid power systems, combining various energy sources, such as a combustion engine and electric batteries. This allows for the optimal use of resources and reduces greenhouse gas emissions [39].
The choice of an appropriate power source depends on various factors, such as the type of machine, local infrastructure conditions, the availability of energy resources, and priorities related to ecology and sustainable development. The final choice often considers a combination of different technologies, ultimately aiming to optimise energy consumption and minimise the impact of loading equipment in terminals on the environment.
Technological progress in energy generation, storage, distribution, conversion, and consumption significantly influences the energy efficiency of an intermodal terminal [41]. In recent years, scientific publications addressing energy consumption by loading devices have increasingly focused on energy storage methods [42]. This energy can be recovered by the loading device, for example, during the lowering of a container by the gantry crane hoist. Research indicates that implementing an appropriate energy storage system on the crane can reduce fuel consumption, decrease the size of the combustion engine, and simultaneously extend its engine life [43]. These storage systems may include supercapacitors [44], batteries [45], and flywheel systems [46].
Equally crucial for improving the energy efficiency of an intermodal terminal is proper planning and coordinating the work of devices. Extensive studies have been conducted on reducing the energy consumption of equipment operations, especially in automated container terminals. Here, we mention just a few examples. In [47], the authors proposed an optimisation model that minimises the total number of operations performed on containers using machine learning techniques. In [48], the authors delved into the determinants impacting energy efficiency during container loading operations. Their research focused on addressing the challenge of reducing energy consumption in container handling and reshuffling processes. In one study [49], the authors examined the energy consumption patterns of diverse handling equipment within a rail-water intermodal container terminal. Their primary objective was to optimise overall operational efficiency by minimising processing times in the context of multi-device coordination, integrated scheduling, and constrained storage space. Some publications on optimising intermodal terminals’ energy efficiency are dedicated to AGV vehicles, their scheduling, and route planning [50,51,52,53].
A distinct group of publications related to terminal energy efficiency comprises works in which authors, alongside minimising energy consumption, also pay attention to air pollution. One of the publications that indicates the correlation between energy consumption, CO2 emissions, and the layout of an intermodal terminal is the study [54]. In the course of this investigation, an estimation was made regarding the energy utilisation and carbon dioxide (CO2) emissions within container terminals, considering the variations in their layouts. The computation of energy consumption involved the analysis of utility data, in conjunction with the assessment of fuel and electricity usage specific to each container-handling equipment present in the terminal. To gauge CO2 emissions, a methodology based on the movement characteristics—such as the frequency and distance covered by each container-handling equipment—was employed. Similar considerations were presented in [55,56,57].
For the purposes of the research conducted in this article, literature on crane energy efficiency was analysed to find data on crane energy consumption. Such data was presented in a paper [58]. Referring to data from the port of Rotterdam, the authors of [58] presented the values of instantaneous energy consumption by the STS crane. Unfortunately, due to the dimensions of the STS crane and the operations it performs, this data could not be used to calculate the energy consumption of the RTG crane at the land intermodal terminal. Further analysis of the literature revealed that an interesting approach to the analysis of the energy efficiency of an intermodal terminal was presented in [22]. The authors conducted a study examining energy consumption by RTG cranes in a maritime intermodal terminal over eight days. An energy analysis concerning the various motors of the crane has been carried out. The range of percentages of the total recoverable energy has been calculated depending on the workload of the specific day. The data on the instantaneous energy consumption of the RTG crane presented in this work were the starting point for the analyses carried out in our article.
The literature analysis on the optimisation of energy consumption by handling equipment indicates that publications mainly focus on maritime terminals. It is challenging to find publications that address this issue in land terminals located in or near cities, especially considering that transport and handling processes in land terminals differ from those in maritime terminals.
Therefore, this study aimed to analyse the energy efficiency of an intermodal terminal located in a city where the gantry crane is the primary handling equipment. The research focused on energy consumption during the loading of intermodal trains, as this process significantly determines the cycle time of the gantry crane, and minimising it is crucial for the energy efficiency of the intermodal terminal.
3. Problem Description
3.1. Basic Assumptions for Train Loading
The article addresses the issue of loading intermodal trains and its impact on the energy efficiency of a land intermodal terminal located in a city, particularly in the context of energy consumption by the gantry crane. Generally, a land-based intermodal terminal consists of freight tracks, a roadway for trucks and various handling machines, and a storage yard for containers. An example of the layout of the basic functional zones of the terminal is presented in Figure 1.
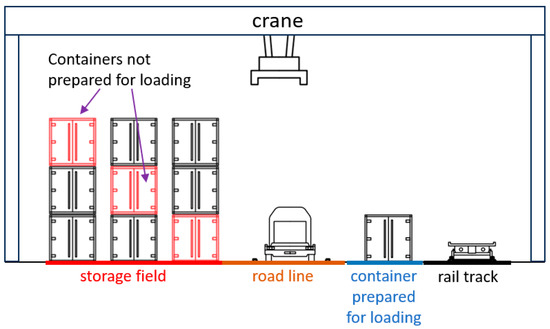
Figure 1.
An example of the intermodal terminal layout.
The practice of handling containers in an intermodal terminal indicates that it is reasonable to prepare containers in advance for loading onto trains. Containers prepared for loading onto trains are usually positioned along the loading track, minimising the train handling time at the terminal. Of course, these containers need to be retrieved from the storage yard. Depending on the stacking height of containers, retrieving containers from the storage yard may involve the need to move other containers. This means that to handle one container, the gantry crane will have to perform several cycles, affecting the crane’s working time and the amount of energy consumed. The article assumes that containers in the storage yard will be stacked in a maximum of three layers.
Again, the practice of loading intermodal trains suggests that despite preparing containers for train loading, some will still need to be loaded directly from the storage yard. This is justified by the uncertainty regarding the final list of containers leaving the terminal on a given train, as a previously planned container may be replaced by an unplanned one at the last moment. This issue has been considered in the simulation model presented later in the article.
In addition to the arrangement of containers in the terminal planned for loading, a significant influence on the time required for this loading process i the configuration of coupling pins on wagons. Container wagons are generally adapted for transporting containers of various sizes by allowing changes to the configuration of coupling pins that secure the container to the wagon (see Figure 2). Incorrect configuration of coupling pins on a particular wagon results in the inability to load the container and will require manual changes to the pin configuration. The article assumes that the pin configuration on all wagons allows for loading all planned containers without requiring manual pin configuration changes. Additionally, in the simulation studies, the loading of ISO 20’, 30’, and 40’ containers onto wagons with a capacity of 3 TEU (TEU—twenty-foot equivalent unit) was assumed.
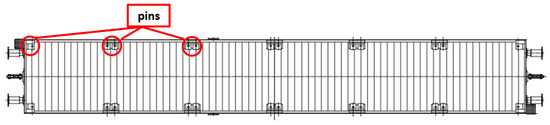
Figure 2.
Example of pin configuration of the wagon. (Own work based on [59]).
The factors mentioned above have been considered in further calculations and strongly influence the distances covered by the gantry crane gate, the trolley, and the hoist, resulting in energy consumption during the loading of intermodal trains.
3.2. Decision Model Assumptions
The decision problem of loading a train involves determining the allocation of containers to slots on wagons and the sequence in which containers are loaded onto the wagons. For the study, five strategies were developed based on which containers are loaded onto wagons in the appropriate order:
- L1—priority of the wagons—algorithm chooses the first slot on the first wagon in the head of a train and then searches for the first matching container starting from the head of the yard (search for a container that satisfies pin configuration constraints as well as the wagon boogie maximum payload constraints). Pin and boogie constraints are checked in every strategy.
- L2—priority of the containers—algorithm chooses the first container starting from the head of the yard and then searches for the first matching slot on the wagon starting from the head of the train.
- L3—shortest distance from the wagon to a container—algorithm chooses the first slot on the first wagon in the head of a train and then searches for the closest matching container.
- L4—shortest distance from the container to the wagon—algorithm chooses the first container starting from the head of the yard and then searches for the closest matching slot on the wagon.
- L5—shortest distance from the current container to the wagon and from the current wagon to the container (nearest neighbour algorithm). The algorithm chooses the first available container and then searches for the closest matching slot on the wagon. In the next step, the algorithm searches for the container closest to the slot from the previous step.
A proper approach to handling containers in the storage yard significantly impacts the working time of the gantry crane in an intermodal terminal. Monitoring the arrangement of containers in the storage yard allows for minimising the crane’s movements, thereby reducing energy consumption. Therefore, the article considered two strategies for handling containers retrieved for loading directly from the storage yard:
- S1—containers set aside to extract a specific container were rearranged to their original positions in the storage yard in each loading cycle of the gantry crane.
- S2—containers set aside to extract a specific container were not returned to their original positions by the gantry crane.
As mentioned earlier, the practice of loading containers onto trains suggests preparing these containers in advance along the loading track. The article considered two variants of preparing containers along the track:
- V1—containers prepared along the track were arranged sequentially from the beginning of the loading track, regardless of the location of a specific container in the storage yard.
- V2—containers placed along the track were positioned perpendicular to their initial position in the storage yard.
As a result of compiling strategies for the gantry crane’s operation, handling containers in the storage yard, and strategies for preparing them for loading along the track, 20 variants of handling trains and containers at the intermodal terminal were obtained. These variants were further subjected to simulation studies later in the article.
3.3. Basic Assumptions for Research Methodology
The choice of research methodology usually depends on the research problem’s objectives, available resources (time, financial, technological), and data. Combining several methods could also be practical and provide a more comprehensive picture of the solved problem.
In this case, a specific issue related to analysing the energy consumption of the container train loading process is examined. This problem requires estimating the energy consumption by the crane engines during all of its movements performed througout various methods of train loading. Therefore, conducting measurements in the actual process at the intermodal terminal could require developing and applying a mathematical model that estimates energy consumption during crane operations or utilising simulation modelling tools. In the first case, the research is expensive, time-consuming, and often impossible from the point of view of access to the actual terminal. Mathematical modelling involves applying certain simplifications and averages due to the loading process’s dynamics, variability, and randomness (which is not necessary in the case of simulation). Therefore, we decided to combine all three methods. A simulation model of the crane operation was developed. It includes mathematical formulas for estimating energy consumption based on actual measurements (taken from [22]).
The simulation model calculates the speeds and distances covered by specific elements of the gantry crane during the loading process, which were identified for each of the considered variants. This information determined the working time of the gantry crane gate, trolley, and hoist. The identified times in each variant were then used to calculate the energy consumption of these gantry crane components.
4. Simulation Research
Experiments were conducted using an original simulation model. The model was developed using the FlexSim 23.2.3 tool. It is an environment designed for building discrete simulation models and conducting simulation experiments. As it is a commercial and licensed tool, the research presented in this paper was carried out under a license owned by the Warsaw University of Technology, Faculty of Transport. The prepared model mapped the various elements of a container terminal using appropriately parameterised Flexsim library objects. All the processes regarding selecting, preparing, and loading containers onto the train were programmed in Process Flow and FlexScript modules (integral FlexSim modules). The research also considered several parameters and functions that enabled estimating crane energy consumption during individual intermodal train loading strategies.
4.1. Simulation Model and Assumptions
The simulation model consists of several essential elements and areas (see Figure 3):

Figure 3.
Container loading front. Screen captured from the simulation model in FlexSim.
- RTG gantry crane,
- container storage field, containing containers that wait for loading
- rail-road, on which the train with wagons is placed for loading,
- storage lane, on which containers are laid down in a specific sequence before the loading process
- containers.
The parameters of an RTG gantry crane that were used in simulation experiments are shown in Table 1. Crane serviced 20 ft (1C, TEU), 30 ft (1B), and 40 ft (1A) containers. For each type of container, the different weight categories have been assigned. It was assumed that the maximum permissible weights of individual container types do not exceed 23.2 t (20 ft), 25.4 t (30 ft), and 30.48 (40 ft). In the research conducted, it was assumed that the container’s weight would impact the lifting and lowering speed of the hoist. By analysing actual measurements from the publication [22], we noticed that the lifting speed of a 40 tonne container is limited to 26 m/min. In contrast, a container weighing approximately 2 tonnes achieves a lifting speed of around 52 m/min. Therefore, it was assumed that the container’s lifting speed (VHL) can be written as a linear function, depending on the weight of the lifted container (WC).

Table 1.
Crane parameters (own work).
We also assumed that the lifting and lowering speeds would be the same (VHL = VHD).
The container storage field is an area intended for storing containers. It has around 360 containers in capacity. The containers are stored over 485 m in two levels and three rows. At the beginning of the simulation, containers are randomly placed in the container storage field. There are always available containers needed to load the complete train among the stored containers.
The rail road (on which the train with wagons is placed for loading) is long enough to accommodate around 30 wagons. Each wagon has a total capacity of up to 3 TEU (60 ft). Therefore, the following container combinations can be created on a single wagon: 20 ft + 40 ft, 30 ft + 30 ft, 20 ft + 30 ft, and 20 ft + 20 ft + 20 ft.
4.2. Simulation Process
The operating logic of the simulation model can be briefly presented in the following several bullet points:
- Generating an initial stock of containers in the container storage field.
- Generating a set of wagons and assigning them types of containers.
- Checking the availability of containers at the storage field that are necessary for loading. If the availability condition is not met, random containers in the storage field are replaced with those for which there is demand.
- Carrying out the container preparation process (placing containers along the rail road).
- Carrying out the train loading process (container transportation between the storage line and wagons on the rail-road).
- Collecting characteristics and parameters and estimating the energy consumption.
- Checking if all wagons are loaded. If so, the simulation ends.
The container preparation process for loading occurs when containers are transferred from the container storage field to the storage line (located along the rail road). The purpose of this process is to shorten the overall train loading process. During preparation, there may be a need to conduct the reshuffling process. Reshuffling occurs when the container essential for retrieval (from the storage field) is at the bottom of the stack. In such a situation, containers stacked on top of it need to be lifted and moved to the nearest stack (stack with a height not exceeding the maximum crane’s lifting height). The process continues until there is a direct opportunity to lift the needed container. After the reshuffling, containers can be returned to the stack from which they were retrieved. This process will be referred to as additional reshuffling. Its execution is optional and can take place after completing the preparation process for each container.
4.3. Estimation of Energy Consumption
The primary objective of the research is to estimate the energy consumption of the train loading process for various scenarios of crane operation. Process characteristics are collected to calculate the energy consumption during simulation (see Table 2). The total energy consumed by the crane is the sum of the energy consumption by the drives of its structural elements as well as energy losses (ECL), namely:

Table 2.
Characteristics collected from the simulation.
Actual energy consumption measurements by the RTG crane, published in [22], have been considered. The publication’s authors conducted measurements for eight days of the container handling system’s operation. Varying workloads characterised the days, and the different weights had containers. The obtained results are summarised in Table 3. The publication presents the energy consumption values for the drives of the crane’s structural elements and the amounts of energy that can be recovered during crane operation.

Table 3.
Energy consumption results for the RTG crane [22].
Based on the data presented in Table 1, the energy consumption curve for the crane was plotted (Figure 4). Subsequently, the formula for the cumulative energy consumption function after a specified crane work time was determined (Equation (3)):

Figure 4.
Average energy consumption of the crane over time.
As a result of the simulation studies, estimated distances (LX, LY, LZ) and working times for individual structural elements of the crane (TX, TY, TZ) can be determined. Consequently, to estimate the total energy consumed by the crane, the relationship (2) can be utilised. According to [22], the energy consumed by the gantry (SGEC), hoist (SHEC), and trolley (STEC) constitutes approximately 31%, 62%, and 7% of the total energy consumed by the crane, respectively. It is assumed, therefore, that individual energy consumption can be described using the relationships (4)–(6):
The total time of hoist working (TZ) used in Formula (6) is divided into the time of hoist lifting loaded (TZUL) and hoist lifting empty (TZUE). The time TZUL depends on the hoist lifting speed (VHL), and the weight of the lifted container (WC). Thus, the weight of the containers influences the hoist energy consumption.
During the operation of the crane, energy recovery is also possible. According to the research results presented in [22] and Table 2, the percentage share of energy recovery from the gantry’s work (SGER) and hoist (SHER) reaches values of approximately 3.7% and 81.5%, respectively. In the case of the hoist’s operation, energy is recovered only during lowering with a load (TZDE) and without a load (TZDE). Therefore, the following relationships were adopted in the simulation studies to estimate the total amount of recovered energy (7), the amount of energy recovered during the gantry’s operation (8), and the hoist’s operation (9):
To summarise, the estimation of energy consumption in the simulation model is based on:
- basic stacker crane parameters (e.g., speed, lifting height) implemented in the model—see Table 1;
- distances between the places of collection and storage of containers, estimated by the simulation model at various stages of the simulation;
- operating times of individual engines of the crane’s structural elements (gantry, hoist, trolley), estimated in the model based on the distances covered and the parameters of the stacker crane (e.g., travel and lifting speed);
- individual data on energy consumption by stacker crane motors measured and presented by authors of publication [22]—see Table 3;
- functional dependencies (2)–(9) developed based on research from a previous publication [22].
4.4. Simulation Scenarios
In order to evaluate different approaches to the train loading process, 20 different simulation scenarios were formulated. Each scenario was characterised by one of the five analysed crane operation strategies, an additional reshuffling process, and the selected container preparation method. The data for each simulation scenario is presented in Table 4.

Table 4.
Simulation scenarios.
Reshuffling is a process in which containers placed on top of the container needed for retrieval must be moved to adjacent stacks to make the target container accessible. An example of this process is illustrated in Figure 5.
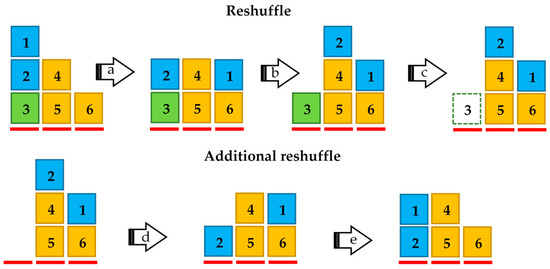
Figure 5.
Reshuffle (a, b, c) and additional reshuffle processes (d, e).
In order to retrieve container number 3, it is necessary to shift containers 1 and 2. In the subsequent stages of the process, container 1 is moved onto container number 6, and then container 2 onto container 4 (or onto 1). This sequence enables access to container number 3, which can be easily retrieved. The simulation model performs this reshuffling process (if necessary) during the containers’ loading preparation. After their completion, the containers are moved to the storage line, awaiting further loading stages. At this stage, the shifted containers (numbers 1 and 2) can either remain in their new locations for further processing or return to the stack from which they were initially taken (an additional reshuffle). The additional reshuffle process involves moving the containers previously relocated in the reshuffling process (container numbers 1 and 2 in Figure 5) back to the stack from which they were initially retrieved.
Both methods of preparing containers for loading, as analysed in the scenarios, are presented in Figure 6. They differ in the way containers are arranged in the storage line. In the first case (Figure 6a), containers taken from the storage field are placed sequentially along the rail road, starting from the beginning. In the second case (Figure 6b), containers taken from the storage field are transported to the storage line at the nearest available location relative to the pickup point.

Figure 6.
Container preparation methods—first method (a) and second one (b).
For the study, each of the analysed variants underwent ten simulation experiments. In each experiment, the distribution of containers stored in the storage field, as well as the distribution of pins and wagons in the serviced trains, was independently randomised. As a result, some quantities were estimated, such as: distances covered by individual structural elements of the crane (gantry, hoist, trolley), drive times (gantry, hoist, trolley), energy consumed by the crane’s drives (gantry, hoist, trolley), energy recovered during the crane’s drive operation (gantry, hoist), total train loading time, time for individual stages of the loading process (preparation, cleaning, loading), and energy consumed and recovered during these stages. The average values of these quantities were also calculated. The results are summarised in Table A1 in Appendix A.
4.5. Simulation Experiments and Results
In the area of conducted research, the most significant criteria for evaluation were considered to be the total energy consumption by the crane and the total loading time of the train. These criteria directly influence the cost of the train loading process and its efficiency. Therefore, in the first instance, the total amounts of consumed and recovered energy and the duration of the train loading process were compared for each scenario (Figure 7 and Table 5). The difference between the total operation time and the process time (Table 5) lies in the fact that in the former case, the time of operation for all drives of the container handling system is summed. In contrast, in the latter, the time between the start and end of the train loading process is considered (including the time for preparing containers for loading).

Figure 7.
Total energy consumption and recovery, total process time for each scenario.

Table 5.
Total average distance, total average time and energy consumption, and total average energy recovery for each scenario.
The total energy consumption in the analysed variants ranged from 80.21 kWh to 141.14 kWh. It means that the increase in energy consumption between the best scenario (Scenario 20) and the worst scenario (Scenario 8) was approximately 75.96%. A similar ranking of scenarios occurred when comparing the duration of the process (Table 6). In this case, the process time ranged from 4.98 h to 7.92 h, resulting in a 59.04% increase in the train loading time. For both criteria (energy consumption and time), the two best scenarios were Scenario 20 and Scenario 10. These scenarios used the fifth strategy for the crane’s operation and additional reshuffling procedures.

Table 6.
The scenario sequence complies with the energy consumption and process time criteria.
Simulation results obtained from all scenarios are presented in Figure 8. For all of them, with the increase in total energy consumption:

Figure 8.
Energy (a) and time (b) consumption share—scenarios sequence according to increasing total energy consumption.
- the percentage of gantry working time increases,
- the percentage of energy consumed by the gantry increases,
- the percentage of energy consumed by the hoist and trolley decreases,
- the percentage of energy recovered from total energy consumption decreases.
This indicates that energy consumed by the gantry has the most significant impact on overall energy consumption. The scenarios with more extended gantry operations (i.e., covering greater distances along the loading track) are more energy-intensive. Even though the hoist drives have the highest individual energy consumption, the share of energy consumed by the gantry is approximately 6.8 to 13 times greater than that of the hoist, accounting for 79% to 89% of the energy consumed by the crane (Figure 8a). The reduction in the share of energy consumed by the hoist (in relation to the total energy) also leads to a decrease in the amount of recovered energy (the majority of recovered energy comes from the hoist’s operation). The changes in the share of energy consumption and time during different operations in different scenarios are presented in Table 7.

Table 7.
Scenario sequence for the energy consumption and process time criteria.
For each type of crane operation strategy, the average values of various characteristics obtained from all simulation experiments were estimated (Table 8). Thus, it was possible to identify the best strategy. The results indicate that the best strategy in terms of energy consumption is Strategy No. 5. It had the shortest total distance covered by all structural elements of the crane (gantry, trolley, hoist) and the shortest train loading process time. Each subsequent (worse) strategy was characterised by an increase in the total distances covered, an increase in the loading process time, and an increase in the energy consumption by the gantry in relation to the hoist and trolley. It is also worth noting that the differences in the results obtained for the first three strategies (strategy No. 5, 1, and 2) are small. The increases in energy consumption between strategies No. 5 and 2 are only 2.28%, and the increase in loading time is 0.38%. Given that the average values are comparable, it can be assumed that they are equivalent in terms of their attractiveness and applicability. However, Strategies No. 4 and 3 proved to be significantly worse. In this case, the increase in energy consumption (compared to Strategy No. 5) was 27.22%, and the increase in the total time of the loading process was 21.56%.

Table 8.
Average values of characteristics for each crane operation strategy.
The analysis of the results indicates that the container preparation method can significantly impact the train loading time and the energy consumed during the process. The application of the second container preparation method in various scenarios (with the same crane operation strategy and additional reshuffling method—see Table 9) allowed for a reduction in the loading process time by an average of approximately 12% and a decrease in energy consumption by an average of about 14% (Table 9).

Table 9.
Average benefits from using the second container preparation method.
Additional reshuffling is a process that, in most cases, prolongs the train loading time and increases energy consumption. This is because it involves additional crane movements, returning to the location of container retrieval from the storage field, and performing additional operations on the relocated containers. This is reflected in almost all the analysed scenarios. An exception is Strategy 5 (Scenarios 10 and 20), for which the total loading time and overall energy consumption in variants with additional reshuffling were reduced. This is related to the specificity of this strategy. After loading a container onto the train, the crane searches for the next container to retrieve closest to that location. In the case of additional reshuffling, the gantry’s work cycle did not end at the place where the container was deposited but at the point of its retrieval. This disrupted the standard sequence of containers being retrieved for loading. In this case, the disruption led to positive results, shortening the distance covered by the gantry, the loading time, and the resulting energy consumption.
A comparison of the results for the best and worst scenarios showed potential benefits that a logistics hub could achieve. These benefits include, among others, a reduction in the intermodal train loading time by approximately 37% (2.94 h) and a decrease in electricity consumption by about 43% (60.49 kWh).
The reduction in loading time enables a 37% decrease in the crane’s engagement time. During this period, the crane can be used for other tasks in the storage yard or to prepare containers to load another train. It leads to an increase in the logistics hub’s efficiency and the number of trains and containers served daily. The hub’s handling potential (with one track) could be increased from 2 to 3 trains per day.
The reduction in energy consumption leads to financial savings. Assuming the cost of 1 kWh is approximately €0.57, annual savings can reach up to €75,023.17 (energy savings at 131.62 MWh, serving three trains per day, operating 20 days per month).
Another crucial aspect is the carbon footprint generated and the amount of CO2 emissions released into the environment. According to [60], the carbon intensity of electricity per kilowatt-hour in Poland is 633 g of CO2 equivalents per kilowatt-hour. Therefore, reducing energy consumption through proper train loading organisations can decrease CO2 emissions by approximately 27,771.74 kg of CO2 annually.
Based on simulation results from all scenarios, the shares of average energy consumption (Figure 9a) and time consumption (Figure 9b) were determined. Gantry has the largest share in energy consumption (85%), followed by hoists (9%), trolleys (4%), and containers picking up and picking off (2%). The shares of individual operation duration and motor work were as follows: gantry (71%), trolley (13%), hoist (7%), and containers picking up and picking off (9%).

Figure 9.
Shares of average energy (a) and time (b) consumption for all scenarios.
The values of energy consumption by individual stacker crane drives that we used for research came from the publication [22]. Therefore, we compared the results presented in Figure 9a with the shares of energy consumption by the RTG crane from that publication. In [22], hoist operations had the largest share of average energy consumption (61%), followed by gantry operations (31%), and finally, trolley operations, losses, and others (7%). Thus, these results are significantly different from those obtained from our research. It is related to the operating characteristics of the stacker crane at various types of intermodal terminals.
In marine terminals (such as those analysed in [22]), containers are taken from the ship and moved to the yard or train (or vice versa). There is a significant difference in height between the places of collecting and depositing the containers, even up to several dozen metres (40–60 m). Thus, hoist processes take a long time and consume up to 61% of energy. The gantry (31%) and trolley (7%) have a significantly smaller share of energy consumption.
In the case of land intermodal terminals, the differences in height between the places where containers are picked up and put away are significantly smaller. In such situations, the most common and time-consuming movements are those along the railroad (71%), followed by trolleys and hoists (Figure 9b). Regarding energy consumption, the gantry has the largest share, followed by the hoist and trolley (Figure 9a).
It can be noticed that the share of individual crane movements is related to the type of intermodal terminal. For this reason, the type of terminal will also determine crane energy consumption. The results of our research indicate that due to the enormous workload of the hoist, the unit hourly energy consumption by cranes in marine terminals is almost four times higher than in the case of land terminals. In marine terminals, overhead cranes’ average hourly energy consumption is approximately 69.8 kWh (see Table 3 and [22]), while in the land terminal, it is approximately 17.23 kWh.
5. Conclusions
The aim of the article was to calculate and examine the crane energy consumption during the train loading in the intermodal terminal handling freight from the smart city.
Based on the literature research, it was found that there is a lack of publications on the use of intermodal terminals for smart city freight handling. There is also a lack of publications on the study of the energy efficiency of such facilities. Therefore, taking into account the smart city’s requirement to minimise energy consumption of transport processes, our original contribution to the article was the analysis of the energy efficiency of the intermodal train loading process performed by a crane, including the location of containers in the storage yard, container rehandling in the storage yard, as well as the crane operation strategy. This made it possible to determine the energy consumption generated by hoist, trolley, and gantry moves. As a result of the conducted research, it was possible to answer the question of how the aforementioned factors affect crane energy consumption and consequently the energy efficiency of the entire process.
The research in the paper unequivocally demonstrated that selecting an intermodal train loading scenario impacts the crane’s working time and energy consumption. Consequently, choosing an appropriate method for intermodal train loading can determine the efficiency of the entire logistics hub, its operational costs, and its environmental and energy efficiency. Improving the energy efficiency of a logistic hub in the form of an intermodal terminal can bring many benefits to a smart city. It primarily means reduced energy consumption, contributing to the mitigation of greenhouse gas emissions, and thereby supporting sustainable development goals.
Furthermore, enhancing the energy efficiency of the logistic hub will also positively impact the overall transportation infrastructure in the smart city, facilitating a smoother and more sustainable flow of goods. It, in turn, will contribute to reducing traffic congestion, lowering emissions, and ultimately minimising external transportation costs.
The simulation model presented in the paper is a crucial tool for researching cranes’ energy consumption in intermodal terminals. However, analyses of its functionality have revealed certain limitations that require further development. Specifically, this involves the need to supplement the model with actual measurements of energy consumption by various crane engines (currently, mathematical formulas yielding approximate values are utilised). Additionally, it is essential to consider randomness and variability in the processes carried out in the model and the needs of its users. There are plans to develop and implement advanced optimisation algorithms (based on AI, neural networks, and machine learning) in the model, enabling productive and energy-efficient management of loading intermodal trains and handling the container storage yard. Working on these aspects is crucial for further refining the model and maximising the benefits of its application for smart cities’ needs.
The findings from this study have the potential to guide smart city planners and logistics managers towards strategic enhancements in intermodal terminal operations, fostering sustainable urban development, and bolstering the economic stability of city environments.
Author Contributions
Conceptualisation, M.K. and R.J.; methodology, M.K., N.C.-G. and R.J.; validation, M.K. and N.C.-G.; formal analysis, M.K. and R.J.; investigation, M.K.; resources, R.J.; data curation, M.K.; writing—original draft preparation, M.K., N.C.-G. and R.J.; writing—review, R.J.; visualisation, M.K.; supervision, M.K., R.J. and N.C.-G.; project administration, R.J. and N.C.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research is a result of a project funded by the National Science Centre, Poland (project no. 2022/04/Y/ST8/00134). Project title: Energy optimal urban logistics as a service (E-Laas). Project implemented as part of the call ERA-NET Cofund Urban Accessibility and Connectivity (EN-UAC China Call) organised by JPI Urban Europe and the National Natural Science Foundation of China (NSFC) funded from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 875022.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Simulation results—mean values from the results of all scenario replications.
Table A1.
Simulation results—mean values from the results of all scenario replications.
| Scenario | Type of Operation/Motor Usage | Distance [m] | Time of Operation [h] | Time Share [%] | Energy Consumption [kWh] | Energy Share [%] | Energy Recovery [kWh] | Energy Recovery Share [%] | Process Time [h] |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Gantry | 9561.43 | 4.024 | 72.56 | 87.75 | 86.24 | 3.25 | 3.7 | 0.000 |
| 1 | Trolley | 2834.32 | 0.679 | 12.51 | 3.35 | 3.37 | 0 | 0 | 0.000 |
| 1 | Hoist | 1108.62 | 0.373 | 6.86 | 8.17 | 8.21 | 8.11 | 99.36 | 0.000 |
| 1 | Picking up/Picking off/idle | 0 | 0.438 | 8.07 | 2.16 | 2.17 | 0 | 0 | 0.000 |
| 1 | Total | 13,504.37 | 5.514 | 100 | 101.43 | 100 | 11.36 | 11.35 | 5.719 |
| 2 | Gantry | 9383.35 | 3.949 | 71.5 | 86.1 | 85.52 | 3.19 | 3.7 | 0.000 |
| 2 | Trolley | 2873.81 | 0.688 | 13.02 | 3.4 | 3.55 | 0 | 0 | 0.000 |
| 2 | Hoist | 1132.48 | 0.381 | 7.18 | 8.34 | 8.67 | 8.33 | 99.79 | 0.000 |
| 2 | Picking up/Picking off/idle | 0 | 0.440 | 8.3 | 2.17 | 2.26 | 0 | 0 | 0.000 |
| 2 | Total | 13,389.64 | 5.458 | 100 | 100.01 | 100 | 11.51 | 11.82 | 5.659 |
| 3 | Gantry | 12,184.76 | 5.128 | 76.83 | 109.97 | 88.69 | 4.07 | 3.7 | 0.000 |
| 3 | Trolley | 2890.12 | 0.692 | 10.59 | 3.36 | 2.77 | 0 | 0 | 0.000 |
| 3 | Hoist | 1138.54 | 0.383 | 5.85 | 8.24 | 6.78 | 8.22 | 99.83 | 0.000 |
| 3 | Picking up/Picking off/idle | 0 | 0.440 | 6.74 | 2.14 | 1.76 | 0 | 0 | 0.000 |
| 3 | Total | 16,213.42 | 6.644 | 100 | 123.71 | 100 | 12.29 | 10.05 | 6.864 |
| 4 | Gantry | 11,567.47 | 4.868 | 76.03 | 104.88 | 88.26 | 3.88 | 3.7 | 0.000 |
| 4 | Trolley | 2909.58 | 0.697 | 10.89 | 3.39 | 2.86 | 0 | 0 | 0.000 |
| 4 | Hoist | 1151.69 | 0.387 | 6.05 | 8.37 | 7.05 | 8.32 | 99.38 | 0.000 |
| 4 | Picking up/Picking off/idle | 0 | 0.450 | 7.02 | 2.19 | 1.84 | 0 | 0 | 0.000 |
| 4 | Total | 15,628.74 | 6.402 | 100 | 118.82 | 100 | 12.2 | 10.27 | 6.615 |
| 5 | Gantry | 12,455.95 | 5.242 | 76.8 | 112.17 | 88.58 | 4.15 | 3.7 | 0.000 |
| 5 | Trolley | 2878.91 | 0.689 | 10.54 | 3.34 | 2.76 | 0 | 0 | 0.000 |
| 5 | Hoist | 1145.03 | 0.385 | 5.9 | 8.3 | 6.88 | 8.25 | 99.36 | 0.000 |
| 5 | Picking up/Picking off/idle | 0 | 0.442 | 6.77 | 2.15 | 1.78 | 0 | 0 | 0.000 |
| 5 | Total | 16,479.89 | 6.759 | 100 | 125.95 | 100 | 12.4 | 10.11 | 6.962 |
| 6 | Gantry | 9874.69 | 4.156 | 70.35 | 89.97 | 84.84 | 3.33 | 3.7 | 0.000 |
| 6 | Trolley | 3148.51 | 0.754 | 13.23 | 3.7 | 3.63 | 0 | 0 | 0.000 |
| 6 | Hoist | 1267.51 | 0.426 | 7.45 | 9.27 | 9.08 | 9.22 | 99.45 | 0.000 |
| 6 | Picking up/Picking off/idle | 0 | 0.511 | 8.96 | 2.51 | 2.46 | 0 | 0 | 0.000 |
| 6 | Total | 14,290.71 | 5.847 | 100 | 105.45 | 100 | 12.55 | 12.16 | 6.140 |
| 7 | Gantry | 9315.05 | 3.920 | 70.12 | 85.4 | 84.67 | 3.16 | 3.7 | 0.000 |
| 7 | Trolley | 3062.56 | 0.733 | 13.21 | 3.61 | 3.61 | 0 | 0 | 0.000 |
| 7 | Hoist | 1264.69 | 0.425 | 7.66 | 9.28 | 9.27 | 9.26 | 99.83 | 0.000 |
| 7 | Picking up/Picking off/idle | 0 | 0.500 | 9.01 | 2.46 | 2.46 | 0 | 0 | 0.000 |
| 7 | Total | 13,642.3 | 5.580 | 100 | 100.75 | 100 | 12.42 | 12.39 | 5.831 |
| 8 | Gantry | 14,148.45 | 5.955 | 77.65 | 126.04 | 89.1 | 4.66 | 3.7 | 0.000 |
| 8 | Trolley | 3084.46 | 0.739 | 9.8 | 3.54 | 2.55 | 0 | 0 | 0.000 |
| 8 | Hoist | 1275.88 | 0.429 | 5.7 | 9.11 | 6.57 | 9.09 | 99.86 | 0.000 |
| 8 | Picking up/Picking off/idle | 0 | 0.515 | 6.84 | 2.47 | 1.78 | 0 | 0 | 0.000 |
| 8 | Total | 18,508.8 | 7.638 | 100 | 141.14 | 100 | 13.76 | 9.86 | 7.923 |
| 9 | Gantry | 11,809.2 | 4.970 | 74.46 | 106.51 | 87.33 | 3.94 | 3.7 | 0.000 |
| 9 | Trolley | 3135.87 | 0.751 | 11.32 | 3.64 | 3 | 0 | 0 | 0.000 |
| 9 | Hoist | 1270.35 | 0.427 | 6.45 | 9.18 | 7.6 | 9.13 | 99.43 | 0.000 |
| 9 | Picking up/Picking off/idle | 0 | 0.515 | 7.77 | 2.5 | 2.06 | 0 | 0 | 0.000 |
| 9 | Total | 16,215.41 | 6.663 | 100 | 121.82 | 100 | 13.07 | 10.79 | 6.982 |
| 10 | Gantry | 7044.24 | 2.965 | 63.97 | 65.47 | 80.77 | 2.42 | 3.7 | 0.000 |
| 10 | Trolley | 3079.02 | 0.737 | 16.02 | 3.68 | 4.58 | 0 | 0 | 0.000 |
| 10 | Hoist | 1245.53 | 0.419 | 9.08 | 9.28 | 11.53 | 9.22 | 99.43 | 0.000 |
| 10 | Picking up/Picking off/idle | 0 | 0.504 | 10.94 | 2.52 | 3.13 | 0 | 0 | 0.000 |
| 10 | Total | 11,368.79 | 4.624 | 100 | 80.94 | 100 | 11.64 | 14.45 | 5.022 |
| 11 | Gantry | 7959.5 | 3.350 | 68.47 | 73.84 | 83.76 | 2.73 | 3.7 | 0.000 |
| 11 | Trolley | 2892.61 | 0.693 | 14.37 | 3.45 | 3.98 | 0 | 0 | 0.000 |
| 11 | Hoist | 1132.72 | 0.381 | 7.88 | 8.43 | 9.69 | 8.38 | 99.37 | 0.000 |
| 11 | Picking up/Picking off/idle | 0 | 0.448 | 9.28 | 2.24 | 2.57 | 0 | 0 | 0.000 |
| 11 | Total | 11,984.83 | 4.872 | 100 | 87.96 | 100 | 11.11 | 12.73 | 5.096 |
| 12 | Gantry | 7885.07 | 3.319 | 67.47 | 73.05 | 82.94 | 2.7 | 3.7 | 0.000 |
| 12 | Trolley | 2905.68 | 0.696 | 14.74 | 3.47 | 4.12 | 0 | 0 | 0.000 |
| 12 | Hoist | 1164.82 | 0.391 | 8.29 | 8.66 | 10.28 | 8.64 | 99.83 | 0.000 |
| 12 | Picking up/Picking off/idle | 0 | 0.449 | 9.5 | 2.24 | 2.66 | 0 | 0 | 0.000 |
| 12 | Total | 11,955.56 | 4.854 | 100 | 87.41 | 100 | 11.35 | 13.33 | 5.077 |
| 13 | Gantry | 10,427.73 | 4.389 | 74.34 | 95.17 | 87.29 | 3.52 | 3.7 | 0.000 |
| 13 | Trolley | 2869.03 | 0.687 | 11.75 | 3.37 | 3.12 | 0 | 0 | 0.000 |
| 13 | Hoist | 1124.87 | 0.378 | 6.46 | 8.22 | 7.61 | 8.21 | 99.83 | 0.000 |
| 13 | Picking up/Picking off/idle | 0 | 0.436 | 7.45 | 2.14 | 1.98 | 0 | 0 | 0.000 |
| 13 | Total | 14,421.63 | 5.890 | 100 | 108.9 | 100 | 11.73 | 10.83 | 6.125 |
| 14 | Gantry | 9937.25 | 4.182 | 72.62 | 90.86 | 86.28 | 3.36 | 3.7 | 0.000 |
| 14 | Trolley | 2953.69 | 0.707 | 12.53 | 3.48 | 3.38 | 0 | 0 | 0.000 |
| 14 | Hoist | 1151.04 | 0.387 | 6.85 | 8.44 | 8.19 | 8.39 | 99.35 | 0.000 |
| 14 | Picking up/Picking off/idle | 0 | 0.452 | 8 | 2.22 | 2.15 | 0 | 0 | 0.000 |
| 14 | Total | 14,041.98 | 5.728 | 100 | 104.99 | 100 | 11.75 | 11.33 | 5.963 |
| 15 | Gantry | 8162.84 | 3.436 | 68.71 | 75.49 | 83.88 | 2.79 | 3.7 | 0.000 |
| 15 | Trolley | 2939.12 | 0.704 | 14.2 | 3.5 | 3.92 | 0 | 0 | 0.000 |
| 15 | Hoist | 1158.39 | 0.389 | 7.86 | 8.59 | 9.65 | 8.53 | 99.39 | 0.000 |
| 15 | Picking up/Picking off/idle | 0 | 0.457 | 9.24 | 2.27 | 2.55 | 0 | 0 | 0.000 |
| 15 | Total | 12,260.34 | 4.986 | 100 | 89.84 | 100 | 11.32 | 12.69 | 5.303 |
| 16 | Gantry | 7929.61 | 3.337 | 65.67 | 73.21 | 81.75 | 2.71 | 3.7 | 0.000 |
| 16 | Trolley | 3136.25 | 0.751 | 15.26 | 3.73 | 4.33 | 0 | 0 | 0.000 |
| 16 | Hoist | 1278.09 | 0.430 | 8.73 | 9.48 | 10.99 | 9.43 | 99.43 | 0.000 |
| 16 | Picking up/Picking off/idle | 0 | 0.509 | 10.34 | 2.53 | 2.93 | 0 | 0 | 0.000 |
| 16 | Total | 12,343.95 | 5.027 | 100 | 88.94 | 100 | 12.14 | 13.96 | 5.328 |
| 17 | Gantry | 8893.32 | 3.743 | 67.95 | 81.53 | 83.28 | 3.02 | 3.7 | 0.000 |
| 17 | Trolley | 3166.66 | 0.758 | 14.18 | 3.74 | 3.95 | 0 | 0 | 0.000 |
| 17 | Hoist | 1292.05 | 0.435 | 8.13 | 9.5 | 10.05 | 9.48 | 99.85 | 0.000 |
| 17 | Picking up/Picking off/idle | 0 | 0.521 | 9.74 | 2.57 | 2.72 | 0 | 0 | 0.000 |
| 17 | Total | 13,352.03 | 5.457 | 100 | 97.34 | 100 | 12.5 | 13.12 | 5.757 |
| 18 | Gantry | 9930.75 | 4.180 | 71.13 | 90.56 | 85.28 | 3.35 | 3.7 | 0.000 |
| 18 | Trolley | 3079.6 | 0.737 | 12.84 | 3.62 | 3.49 | 0 | 0 | 0.000 |
| 18 | Hoist | 1255.15 | 0.422 | 7.36 | 9.17 | 8.87 | 9.15 | 99.81 | 0.000 |
| 18 | Picking up/Picking off/idle | 0 | 0.498 | 8.67 | 2.44 | 2.36 | 0 | 0 | 0.000 |
| 18 | Total | 14,265.51 | 5.837 | 100 | 105.78 | 100 | 12.5 | 12.01 | 6.123 |
| 19 | Gantry | 9355.43 | 3.937 | 69.59 | 85.61 | 84.37 | 3.17 | 3.7 | 0.000 |
| 19 | Trolley | 3148.74 | 0.754 | 13.58 | 3.71 | 3.73 | 0 | 0 | 0.000 |
| 19 | Hoist | 1267.41 | 0.426 | 7.69 | 9.31 | 9.39 | 9.25 | 99.38 | 0.000 |
| 19 | Picking up/Picking off/idle | 0 | 0.507 | 9.15 | 2.5 | 2.52 | 0 | 0 | 0.000 |
| 19 | Total | 13,771.59 | 5.625 | 100 | 101.12 | 100 | 12.42 | 12.45 | 5.919 |
| 20 | Gantry | 6931.09 | 2.917 | 63.07 | 64.46 | 80.19 | 2.39 | 3.7 | 0.000 |
| 20 | Trolley | 3153.06 | 0.755 | 16.47 | 3.77 | 4.74 | 0 | 0 | 0.000 |
| 20 | Hoist | 1263.16 | 0.425 | 9.27 | 9.42 | 11.85 | 9.37 | 99.4 | 0.000 |
| 20 | Picking up/Picking off/idle | 0 | 0.513 | 11.19 | 2.56 | 3.22 | 0 | 0 | 0.000 |
| 20 | Total | 11,347.31 | 4.610 | 100 | 80.21 | 100 | 11.75 | 14.75 | 4.982 |
References
- Gracias, J.S.; Parnell, G.S.; Specking, E.; Pohl, E.A.; Buchanan, R. Smart Cities—A Structured Literature Review. Smart Cities 2023, 6, 1719–1743. [Google Scholar] [CrossRef]
- Pečar, M.; Papa, G. Transportation problems and their potential solutions in smart cities. In Proceedings of the 2017 International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 18–20 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 195–199. [Google Scholar]
- Potdar, V.; Batool, S.; Krishna, A. Risks and challenges of adopting electric vehicles in smart cities. In Smart Cities: Development and Governance Frameworks; Springer: Cham, Switzerland, 2018; pp. 207–240. [Google Scholar]
- Lagorio, A.; Pinto, R.; Golini, R. Research in urban logistics: A systematic literature review. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 908–931. [Google Scholar] [CrossRef]
- Allen, J.; Browne, M.; Woodburn, A.; Leonardi, J. The role of urban consolidation centres in sustainable freight transport. Transp. Rev. 2012, 32, 473–490. [Google Scholar] [CrossRef]
- Paddeu, D.; Fancello, G.; Fadda, P. An experimental customer satisfaction index to evaluate the performance of city logistics services. Transport 2017, 32, 262–271. [Google Scholar] [CrossRef]
- Nordtømme, M.E.; Bjerkan, K.Y.; Sund, A.B. Barriers to urban freight policy implementation: The case of urban consolidation center in Oslo. Transp. Policy 2015, 44, 179–186. [Google Scholar] [CrossRef]
- Allen, J.; Browne, M.; Woodburn, A.; Leonardi, J. A review of urban consolidation centres in the supply chain based on a case study approach. Supply Chain Forum Int. J. 2014, 15, 100–112. [Google Scholar] [CrossRef]
- Gronalt, M.; Schultze, R.C.; Posset, M. Intermodal transport—Basics, structure, and planning approaches. In Sustainable Transportation and Smart Logistics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 123–149. [Google Scholar]
- Statista Container Shipping. Available online: https://www.statista.com/topics/1367/container-shipping/ (accessed on 23 December 2023).
- Škultéty, F.; Beňová, D.; Gnap, J. City logistics as an imperative smart city mechanism: Scrutiny of clustered EU27 capitals. Sustainability 2021, 13, 3641. [Google Scholar] [CrossRef]
- European Commission (EC). Roadmap to a Single European Transport Area—Towards a Competitive and Resource Efficient Transport System; White Paper; European Commission: Brussels, Belgium, 28 March 2011; Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52011DC0144&from=EN (accessed on 23 December 2023).
- Buchari, E.; Putranto, D.D.A.; Rahman, A. Analysis of model loading and unloading time of ships at Boom Baru Port, Palembang, Indonesia. MATEC Web Conf. 2017, 138, 07012. [Google Scholar] [CrossRef]
- Koo, P.H.; Lee, W.S.; Jang, A.D.W. Fleet sizing and vehicle routing for container transportation in a static environment. OR Spectr. 2004, 26, 193–209. [Google Scholar] [CrossRef]
- Martinov, S. Increasing the accuracy of evaluation in selecting a location for establishing an intermodal terminal. MATEC Web Conf. 2018, 234, 06004. [Google Scholar] [CrossRef]
- Lee, E. Spatial analysis for an intermodal terminal to support agricultural logistics: A case study in the upper great plains. Manag. Res. Rev. 2015, 38, 299–319. [Google Scholar] [CrossRef]
- Raicu, R.; Raicu, Ş.; Popa, M.; Costescu, D. On the evaluation of urban logistics intermodal terminal projects. Procedia-Soc. Behav. Sci. 2012, 39, 726–738. [Google Scholar] [CrossRef][Green Version]
- Görçün, Ö.F. Analysis of the Effects of Intermodal Terminals for the Solutions of Urban Logistics Problems in Istan-bul City. In Dynamics in Logistics: Proceedings of the 4th International Conference LDIC; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 685–691. [Google Scholar]
- Grubisic, N.; Krljan, T.; Maglić, L.; Vilke, S. The microsimulation model for assessing the impact of inbound traffic flows for container terminals located near city centers. Sustainability 2020, 12, 9478. [Google Scholar] [CrossRef]
- Brnjac, N.; Badanjak, D.; Babi, D. Reducing congestion in urban transport by using intermodal transport solutions. WIT Trans. Built Environ. 2007, 96, 45–52. [Google Scholar]
- Wang, L.; Zhu, X. Container Loading Optimization in Rail–Truck Intermodal Terminals Considering Energy Consumption. Sustainability 2019, 11, 2383. [Google Scholar] [CrossRef]
- Papaioannou, V.; Pietrosanti, S.; Holderbaum, W.; Becerra, V.M.; Mayer, R. Analysis of energy usage for RTG cranes. Energy 2017, 125, 337–344. [Google Scholar] [CrossRef]
- Jacyna, M.; Jachimowski, R.; Szczepański, E.; Izdebski, M. Road vehicle sequencing problem in a rail-road intermodal terminal–simulation research. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 135–1148. [Google Scholar]
- Boysen, N.; Fliedner, M.; Jaehn, F.; Pesch, E. A survey on container processing in railway yards. Transp. Sci. 2013, 47, 312–329. [Google Scholar] [CrossRef]
- Nehring, K.; Jachimowski, R. Modelling of container train handling in the land intermodal terminal. In Carpathian Logistics Congress 2019; Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie: Kraków, Poland, 2020. [Google Scholar]
- Steenken, D.; Voß, S.; Stahlbock, R. Container Terminal Operation and Operations Research—A Classification and Literature Review. OR Spectr. 2004, 26, 3–49. [Google Scholar]
- Stahlbock, R.; Voß, S. Operations research at container terminals: A literature update. OR Spectr 2008, 30, 1–52. [Google Scholar] [CrossRef]
- Heggen, H.; Braekers, K.; Caris, A. Optimising train load planning: Review and decision support for train planners. In Computational Logistics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 193–208. [Google Scholar]
- Corry, P.; Kozan, E. Optimised loading patterns for intermodal trains. OR Spectr. 2008, 30, 721–750. [Google Scholar] [CrossRef]
- Bruns, F.; Knust, S. Optimised load planning of trains in intermodal transportation. OR Spectr. 2012, 34, 511–533. [Google Scholar] [CrossRef]
- Bruns, F.; Goerigk, M.; Knust, S.; Schöbel, A. Robust load planning of trains in intermodal transportation. OR Spectr. 2014, 36, 631–668. [Google Scholar] [CrossRef]
- Heggen, H.; Braekers, K.; Caris, A. A multi-objective approach for intermodal train load planning. OR Spectr. 2018, 40, 341–366. [Google Scholar] [CrossRef]
- Li, C.; Burton, D.; Kost, M.; Sherida, J.; Thompson, M.C. Flow Topology of a Container Train Wagon Subjected to Varying Local Loading Configurations. J. Wind Eng. Ind. Aerodyn. 2017, 169, 12–29. [Google Scholar] [CrossRef]
- Ambrosino, D.; Siri, S. Models for train load planning problems in a container terminal. In Computer-based Modelling and Optimisation in Transportation; Springer: Berlin/Heidelberg, Germany, 2014; Volume 262, pp. 15–25. [Google Scholar]
- Ambrosino, D.; Caballini, C.; Siri, S. A mathematical model to evaluate different train loading and stacking policies in a container terminal. Marit. Econ. Logist. 2013, 15, 292–308. [Google Scholar] [CrossRef]
- Li, X.; Otto, A.; Pesch, E. Solving the single crane scheduling problem at rail transshipment yards. Discret. Appl. Math. 2019, 264, 134–147. [Google Scholar] [CrossRef]
- Jacyna, M.; Pyza, D.; Jachimowski, R. Intermodal Terminal Designing—Case Study; Warsaw University of Technology: Warsaw, Poland, 2019. [Google Scholar]
- Carboni, A.; Deflorio, F. Simulation of rail-road terminal operations and traffic control strategies in critical scenarios. Transp. Res. Procedia 2020, 45, 325–332. [Google Scholar] [CrossRef]
- Konecranes Rubber Tired Gantry Cranes. Available online: www.konecranes.com/port-equipment-services/container-handling-equipment/rubber-tired-gantry-cranes (accessed on 21 December 2023).
- Kalmar. Kalmar Hands over Its First Fully Electric Straddle Carrier. Available online: https://www.kalmarglobal.com/news--insights/press_releases/2023/kalmar-hands-over-its-first-fully/ (accessed on 21 December 2023).
- Parise, G.; Parise, L.; Malerba, A.; Pepe, F.M.; Honorati, A.; Chavdarian, P.B. Comprehensive peak-shaving solutions for port cranes. IEEE Trans. Ind. Appl. 2017, 53, 1799–1806. [Google Scholar] [CrossRef]
- Mahlia, T.M.I.; Saktisahdan, T.J.; Jannifar, A.; Hasan, M.H.; Matseelar, H.S.C. A review of available methods and development on energy storage; technology update. Renew. Sustain. Energy Rev. 2014, 33, 532–545. [Google Scholar] [CrossRef]
- Flynn, M.M.; McMullen, P.; Solis, O. High-speed flywheel and motor drive operation for energy recovery in a mobile gantry crane. In Proceedings of the APEC 07-Twenty-Second Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 25 February–1 March 2007; p. 11511157. [Google Scholar]
- Kim, S.; Sul, S. Control of rubber tyred gantry crane with energy storage based on supercapacitor. IEEE Trans. Power Electron. 2006, 21, 1420–1427. [Google Scholar] [CrossRef]
- Baalbergen, F.; Bauer, P.; Ferreira, J.A. Energy storage and power management for typical 4Q-load. IEEE Trans. Ind. Electron. 2009, 56, 1485–1498. [Google Scholar] [CrossRef]
- Pietrosanti, S.; Alasali, F.; Holderbaum, W. Power management system for RTG crane using fuzzy logic controller. Sustain. Energy Technol. Assess. 2020, 37, 100639. [Google Scholar] [CrossRef]
- Zhang, C.; Guan, H.; Yuan, Y.; Chen, W. Machine learning-driven algorithms for the container relocation problem. Transp. Res. Part B Methodol. 2020, 139, 102–131. [Google Scholar] [CrossRef]
- Li, Y.; Chu, F.; Zheng, F.; Liu, M. A bi-objective optimisation for integrated berth allocation and quay crane assignment with preventive maintenance activities. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2938–2955. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, X.; Ali, H. Multiple Equipment Integrated Scheduling and Storage Space Allocation in Rail-Water Intermodal Container Terminals Considering Energy Efficiency. Transp. Res. Rec. 2019, 2673, 199–209. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Zhou, Y.; Postolache, O. Adaptive auto-tuning mathematical approaches for integrated optimisation of automated container terminal. Math. Probl. Eng. 2019, 2019, 7641670. [Google Scholar] [CrossRef]
- Chen, X.; He, S.; Zhang, Y.; Tong, L.; Zhou, X. Yard crane and AGV scheduling in automated container terminal: A multi-robot task allocation framework. Transp. Res. Part C Emerg. Technol. 2020, 114, 241–271. [Google Scholar] [CrossRef]
- Jonker, T.; Duinkerken, M.B.; Yorke-Smith, S.; de Waal, A.; Negenborn, R.R. Coordinated optimisation of equipment operations in a container terminal. Flex. Serv. Manuf. J. 2021, 33, 281–311. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, L.; Xu, L. Multi-AGV dispatching and routing problem based on a three-stage decomposition method. Math. Biosci. Eng. 2020, 17, 5150–5172. [Google Scholar] [CrossRef]
- Budiyanto, M.A.; Huzaifi, M.H.; Sirait, S.J.; Prayoga, P.H.N. Evaluation of CO2 emissions and energy use with different container terminal layouts. Sci. Rep. 2021, 11, 5476. [Google Scholar] [CrossRef]
- Okşaş, O. Carbon emission strategies for container handling equipment using the activity-based method: A case study of Ambarlı container port in Turkiye. Mar. Policy 2023, 149, 105480. [Google Scholar] [CrossRef]
- Linder, A.J. CO2 restrictions and cargo throughput limitations at California ports: A closer look at AB 32 and port-to-port shipping. Public Work. Manag. Policy 2010, 14, 374–391. [Google Scholar] [CrossRef]
- Garg, A.; Shukla, P.R.; Kankal, B.; Mahapatra, D. CO2 emission in India: Trends and management at sectoral, sub-regional and plant levels. Carbon Manag. 2017, 8, 111–123. [Google Scholar] [CrossRef]
- Geerlings, H.; Heij, R.; van Duin, R. Opportunities for peak shaving the energy demand of ship-to-shore quay cranes at container terminals. J. Shipp. Trade 2018, 3, 3. [Google Scholar] [CrossRef]
- PKP Cargo. Rail Wagons Catalogue. Available online: www.pkpcargo.com/wp-content/uploads/2023/10/pkpcargo_katalogwagonow_3008_19.pdf/ (accessed on 28 December 2023).
- Ember—Yearly Electricity Data (2023); Ember—European Electricity Review (2022); Energy Institute—Statistical Review of World Energy (2023). Available online: https://ourworldindata.org/grapher/carbon-intensity-electricity (accessed on 30 December 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).