Abstract
The aim of this paper is to report on the state of the art of the literature on the most recent challenges in the energy domain that can be addressed through the use of quantum computing technology. More in detail, to the best of the authors’ knowledge, the scope of the literature review considered in this paper is specifically limited to forecasting, grid management (namely, scheduling, dispatching, stability, and reliability), battery production, solar cell production, green hydrogen and ammonia production, and carbon capture. These challenges have been identified as the most relevant business needs currently expressed by energy companies on their path towards a net-zero economy. A critical discussion of the most relevant methodological approaches and experimental setups is provided, together with an overview of future research directions. Overall, the key finding of the paper, based on the proposed literature review, is twofold: namely, (1) quantum computing has the potential to trigger significant transformation in the energy domain by drastically reducing CO2 emissions, especially those relative to battery production, solar cell production, green hydrogen and ammonia production, as well as point-source and direct-air carbon capture technology; and (2) quantum computing offers enhanced optimization capability relative to relevant challenges that concern forecasting solar and wind resources, as well as managing power demand, facility allocation, and ensuring reliability and stability in power grids.
1. Introduction
Quantum computers are devices that harness the distinct principles of quantum mechanics for computational tasks. However, this definition involves crucial nuances. Classical computers, like the ones used in producing this article, also integrate quantum mechanics by relying on semiconductor material properties inherently grounded in quantum principles. Nevertheless, classical computers engage solely in binary information processing, using variables set to either 0 or 1 to derive the desired outcome. By contrast, quantum computers store information in a fundamentally quantum manner, utilizing quantum bits or qubits as the basic units. Qubits exploit three unique quantum properties: superposition, interference, and entanglement.
Superposition in quantum physics refers to the capacity of quantum entities to inhabit states that blend apparently opposing realities. Unlike a classical coin, which can be either heads or tails, a quantum coin can simultaneously exist in a state that is both or in-between—depicting an infinite array of potential combinations involving heads and tails. As a result, qubits within a quantum computer are not limited to the binary states of 0 or 1 typical of classical bits but can occupy fascinating and valuable superposition states throughout computation.
Upon establishing superposition, the relevance of interference emerges. Upon measuring a qubit, leading to either 0 or 1, the likelihood of a particular result is ascertained by aggregating the different pathways depicted by superposition states. Contributions to a specific result from a given superposition state may be positive or negative, enabling constructive or destructive interference to enhance or diminish specific outcomes. Thus, a measurement producing a singular result may carry unique indications of numerous superimposed states.
Entanglement, famously termed by Einstein as a “spooky interaction at a distance,” stands as one of the most intriguing facets of quantum mechanics. It allows two distinct quantum systems to intertwine, converting their quantum state into a unified phenomenon rather than two separate ones. This complexity poses a challenge in breaking down quantum systems into smaller parts for reductionist analysis. While specifying the classical state of bits necessitates only pieces of information, specifically the 0/1 state of each bit, articulating the quantum state of qubits demands numbers due to the distinct quantum amplitudes for every potential configuration. This intricacy is intrinsic to the challenge of simulating quantum systems on classical computers, underscoring the disparity between the two domains.
Despite these notable characteristics, quantum computing poses challenges. Quantum states are inherently delicate, and the act of measuring a qubit, determining it as state 0 or 1, disrupts the superposition (leading to a “collapse”). Regrettably, measurement goes beyond intentional actions by experimenters, introducing inherent complexities.
Quantum computers may face critical issues due to interactions with the external environment, requiring the termination and restart of quantum operations. As a result, these computers typically require strict isolation and often need cooling to low temperatures to minimize external interference. Ongoing research focuses on developing technologies for quantum error correction. These advancements aim to protect vital quantum information by dispersing it across multiple qubits, enabling the identification and correction of accidental interactions before compromising quantum operations. The implementation of such technologies could pave the way for achieving “fault-tolerant” quantum computers. However, attaining fault-tolerant quantum computers involves substantial progress in engineering and fundamental scientific comprehension.
While classical computers excel at everyday, straightforward processing, the new machines are well-suited for intricate tasks such as quantum simulations in molecular chemistry, optimization, and prime factorization. Quantum computing could efficiently solve these specific problems much faster than even the most powerful supercomputer today. Furthermore, this new technology could tackle certain problems that have long been deemed unsolvable. For instance, factoring a 2048-bit prime number with today’s supercomputer takes about one trillion years. With quantum computing, this calculation could be completed in approximately one minute. Recent innovations suggest that the inaugural generation of fault-tolerant quantum computing could be operational by the conclusion of this decade, with some quantum computing companies proposing an even earlier timeline.
Various emerging quantum technologies extend beyond the scope of this discussion. In the realm of quantum computing, theoretical arguments propose potential enhancements in energy efficiency compared to traditional computing. However, the practical realization of these energy savings remains uncertain, given the substantial cooling and control hardware overheads necessary for practical systems [1]. Moreover, there are concepts for “quantum heat engines” that might store and process energy in unconventional ways, potentially surpassing the efficiencies achievable with classical engines. Nevertheless, these ideas are still in the early exploratory stages of theoretical and scientific development [2].
In the context of this paper, quantum computing specifically relates to information-processing technologies, excluding considerations of quantum sensing or communication.
In particular, the potential transformation brought about by quantum computing in the battle against climate change is noteworthy. It has the capacity to reshape the economics of decarbonization, emerging as a pivotal element in capping global warming at the designated 1.5 °C target.
Despite being in its early developmental stages—with projections suggesting the arrival of the initial fault-tolerant quantum computing generation in the latter half of this decade—there is a surge in breakthroughs, escalating investments, and a proliferation of startups. In this respect, some major tech firms have already produced so-called “noisy intermediate-scale quantum” (NISQ) machines. However, these machines lack the capability to execute the calculations expected from fully operational quantum computers.
At the 2021 United Nations Climate Change Conference (COP26), countries and corporations set ambitious emissions reduction targets. Meeting these goals would necessitate an extraordinary annual investment of $4 trillion by 2030, marking the most substantial capital reallocation in human history. However, even if fully achieved, these measures would only bring the temperature reduction to a range of 1.7 °C to 1.8 °C by 2050—falling short of the crucial 1.5 °C threshold to prevent catastrophic climate change.
Realizing the commitment to net-zero emissions, as undertaken by countries and certain industries, requires advancements in climate technology currently beyond reach. Existing supercomputers lack the capability to solve some of these complex problems. Quantum computing emerges as a potential game changer, with the capacity to contribute to the development of climate technologies capable of offsetting approximately 7 gigatons of additional CO2 impact annually by 2035. This has the potential to align with the 1.5 °C target.
Quantum computing’s impact extends to challenging and emissions-intensive sectors like agriculture and direct-air capture. It could also expedite advancements in large-scale technologies such as solar panels and batteries. Overall, this article explores potential breakthroughs enabled by quantum computing and attempts to quantify the expected impact of leveraging this technology, anticipated to be available in this decade.
Motivation and Paper Structure
Very few review papers focusing on energy applications of quantum computing exist in the literature. We grouped and listed them in Table 1.

Table 1.
Recent review papers focusing on energy applications of quantum computing.
Yet, to the best of the authors’ knowledge, we claim that this is the only survey paper to date that pinpoints the most relevant quantum computing applications that can serve as a pathway toward a net-zero economy, together with an up-to-date review of the most frequently used quantum computing frameworks.
As introduced above, quantum computing has, indeed, the potential to trigger significant transformations across various sectors, leading to profound effects on carbon reduction and elimination.
More in detail, in this paper, we review how this impact extends to addressing persistent sustainability challenges, namely:
- Improving forecasting performance to better manage the variability in solar and wind resources;
- Managing power demand in power grids;
- Ensuring reliability and stability in power systems;
- Enhancing electric vehicle batteries;
- Advancing renewable solar technology;
- Expediting the cost reduction of hydrogen for a feasible alternative to fossil fuels;
- Leveraging green ammonia as both a fuel and fertilizer;
- Improving the performance of point-source and direct-air carbon capture technology.
In alignment with the crucial decarbonization focal points discussed in McKinsey’s Climate Math Report [7], we believe that these can be pinpointed as the most relevant quantum computing applications that can serve as a pathway toward a net-zero economy. It can be estimated that, by 2035, the highlighted use cases could facilitate the elimination of over 7 gigatons of CO2 equivalent (CO2-eq) annually, surpassing the current trajectory. This translates to a cumulative reduction of more than 150 gigatons over the next 30 years.
In addition, we provide an up-to-date review of the most used quantum computing frameworks, which are being increasingly used to apply quantum computing to business problems and are thus being promoted even by large cloud providers, namely:
- Cirq;
- Forest;
- LIQUi|>;
- Ocean;
- ProjectQ;
- Qiskit;
- Quantum Development Kit;
- Quipper;
- Strawberry Fields;
- XACC.
The paper is structured as follows. Section 2 reviews the main quantum computing algorithms that are relevant to the rest of the discussion. Section 3 highlights, in turn, the quantum computing hardware that is relevant to the considered applications. Section 4 reports and discusses the potential quantum computing applications that address the sustainability challenges listed above. Section 5 discusses the impact of such applications in terms of reduction in CO2 emissions, also providing visual understanding in this respect. Section 6 specifically makes suggestions for research directions relative to designing, planning, and operating power systems. Section 7 reviews the most used quantum computing frameworks. Concluding remarks in Section 8 end the paper.
2. A Brief Review of the Quantum Computing Algorithms That Are Relevant to Energy Applications
A quantum computer does not possess any inherent enchantment making it universally quicker than its classical counterpart. The addition of two numbers might not be hastened by quantum computers any more swiftly than by classical ones. For many applications, quantum computing likely will not offer noticeable advantages. Yet, quantum computers can leverage distinct aspects of quantum mechanics—specifically, superposition, interference, and entanglement—to execute algorithms beyond classical machines’ capabilities. The so-called quantum speedup occurs when quantum mechanics provides algorithmic advantages, surpassing known classical alternatives in terms of speed. It is vital to note that a faster quantum device may not necessarily aim to reduce computation time. Instead, it could perform more calculations or address a larger problem within the same timeframe or invest more time in finding the optimal solution. Quantum circuits, which include arithmetic operations like addition, multiplication, and division, are crucial for implementing quantum algorithms in hardware.
In particular, quantum speedups manifest in various degrees. A polynomial quantum speedup implies that if a classical computer accomplishes a task of size in a specific time, a quantum computer will achieve faster results by a polynomial factor in . On the other hand, an exponential quantum speedup signifies that the performance improvement factor is exponential in . The field of quantum complexity theory is still evolving, and many aspects are still unknown. Furthermore, potential quantum speedups may be mitigated by enhancements in classical software. To gauge the speedup, one must compare it with the best-known classical approach.
The main quantum computing algorithms that are relevant to the energy applications discussed in the subsequent sections are the following:
- Quantum annealing. Quantum annealing involves algorithms aiming to utilize quantum processes for discovering low-energy solutions in optimization challenges. The quantum speedup from these techniques remains unclear. In the quantum annealing process, a quantum system initiates with a known easily created state. Gradually, it introduces an energy landscape encoding the optimization problem, imposing substantial energy penalties for constraint violations. According to the adiabatic theorem of quantum mechanics, the quantum computer’s final state becomes the minimum energy state, representing the optimal problem solution. Annealing-based quantum computers excel at finding minima within a vast yet finite problem space. Integrating quantum annealing with other mathematical programming paradigms enhances the ability to reach a global optimum on a larger problem scale. Demonstrations have indicated D-Wave’s speedup in comparison to classical solvers, including simulated annealing, on NP-hard graph problems [8,9].
- Grover’s algorithm. Grover’s algorithm focuses on finding items in a database, featuring a quantum speedup equal to the square root of the database size.
- Harrow–Hassidim–Lloyd (HHL) algorithm. The HHL is an algorithm extracting information from solutions to linear systems, significantly reducing the time required for systems of equations from scaling with to .
For the sake of completeness, there also exists Shor’s algorithm, which efficiently factors large numbers, potentially compromising cryptography systems like RSA. Yet, despite being noteworthy in the quantum computing landscape, it is not proposed for use in any of the references cited in this paper.
The above-mentioned approaches constitute quantum algorithms, but it is crucial to highlight that quantum algorithms are likely just one component of a quantum computing system. Calibration and control pose serious classical challenges that must be addressed to construct and manage quantum computers. Some proposed methods, especially in the near term, rely on “hybrid” quantum/classical algorithms, where a smaller quantum algorithm, more feasible in the near term, acts as a subroutine in a larger classical algorithm.
In discussing time frames for demonstrating quantum algorithms, we caution that even those identified as near-term possibilities are likely to be showcased only in research settings, validating quantum computing hardware and software. Significant deployment of quantum computing in commercial applications to address operational problems is unlikely in the next few years. Short-term quantum computing technologies, like annealing, may reach the demonstration phase sooner, although substantial hardware advancements might still be necessary for eventual deployment. Long-term possibilities, such as HHL, require considerable progress in quantum technology, possibly necessitating the development of fault-tolerant quantum computers.
3. A Primer on Quantum Computing Hardware
A qubit, a conceptual mathematical entity, mirrors the numerical values 0 and 1 themselves. Just as a classical bit can be represented through a reflective surface on an optical disk, a magnetic direction on a hard drive, or a pulse of radio waves on your Wi-Fi network, a qubit can be expressed through diverse quantum systems. Due to the absence of a general-purpose, large-scale quantum computer, there is no standardized qubit platform dominating the industry. Here, we briefly explore the major players in the quantum computing hardware domain. Additional details can be found in tutorial papers such as [10,11].
Among the notable technologies, there is a qubit family built with superconducting materials, frequently aluminum. Instances in this category comprise transmons, xmons, and fluxonium qubits [12]. Superconducting qubits constitute the focus of research at Google, IBM, and the deployed D-Wave System. These qubits encode quantum information in the arrangement of electromagnetic fields that are unique to superconducting materials displaying no resistance to electrical flow. Gigahertz-frequency microwave pulses manipulate the qubit states. However, maintaining superconductivity requires cooling the qubits to fractions of a degree above absolute zero, demanding extensive cooling and vacuum systems. While superconducting qubits operate swiftly, fabrication challenges impede consistent production, necessitating continuous recalibration. They also demonstrate relatively brief data stability lifetimes, with quantum information lost within milliseconds at best [13]. This occurrence is recognized as decoherence.
Instead, trapped-ion quantum computing, stemming from technologies in atomic physics and clocks, has drawn commercial interest from startups like IonQ. It utilizes ions (electrically charged single atoms) suspended above a surface, using radio-frequency electric fields. Quantum information is stored in the electrons’ state within the atom, manipulated using laser pulses. Trapped ions offer the advantage of identical properties for every qubit, as every atom of the same isotope and charge is identical. While trapped-ion qubits have longer lifetimes than superconducting qubits (in the order of seconds), they require more time for manipulation [14].
Beyond these qubit technologies, several alternatives with less current commercial attention exist. Photonic qubits, pursued by companies like PsiQuantum and Xanadu, store quantum information in individual photons, which are challenging to disturb [3]. However, this makes interactions between these qubits, necessary for computations, difficult to achieve. Semiconductor spin qubits, relying on semiconductor physics akin to current computer chips, hold the promise of rapid large-scale manufacturing, but control and computation technologies for these systems have not matured to the same level as superconductors and trapped ions. Lastly, topological quantum computing, a long-standing pursuit, envisions storing quantum information in a stable, long-range ordering that requires no error correction. Yet, constructing and performing calculations with topological qubits has proven elusive for researchers.
A critical challenge of quantum computing technology resides in coping with quantum errors. Quantum errors denote discrepancies or disruptions in quantum computations, stemming from factors like decoherence and quantum noise. These inaccuracies pose a threat to the dependability and precision of quantum information processing.
Quantum error correction (QEC) encompasses a range of techniques and algorithms crafted to alleviate the impact of quantum errors within quantum computing. Diverging from classical error correction, which relies on redundancy for error detection and correction, QEC utilizes quantum principles to safeguard quantum information without direct replication (as the no-cloning theorem prohibits copying). QEC entails dispersing logical information across entangled states of multiple physical qubits, employing syndrome measurements to identify errors without obliterating the quantum information. Specific quantum operations are then implemented for corrections, restoring the effects of errors and upholding the integrity of quantum computations amidst the intrinsic noise and errors in quantum systems.
4. Potential Applications of Quantum Computing in the Energy Domain
As anticipated in Section 1, quantum computing is expected to yield its major impact on the following sustainability challenges: (i) improving forecasting performance to better manage the variability in solar and wind resources; (ii) managing power demand in power grids; (iii) ensuring reliability and stability in power systems; (iv) enhancing electric vehicle batteries; (v) advancing renewable solar technology; (vi) expediting the cost reduction of hydrogen for a feasible alternative to fossil fuels; (vii) leveraging green ammonia as both a fuel and fertilizer; (viii) improving the performance of point-source and direct-air carbon capture technology. For each of them, we discuss the relevant problems as well as the solutions and benefits resulting from quantum computing in the next subsections.
4.1. Taking Advantage of Quantum Computing on Forecasting
Ensuring the reliable integration of renewable energy necessitates precise forecasting to manage the variability in solar and wind resources. Tools for predicting wind and solar generation blend weather observations, numerical weather prediction models, atmospheric processes, and statistical analysis. Presently, supercomputers tackle intricate fluid dynamic equations, and machine learning techniques, such as deep neural networks, provide supplementary computational support. Forecasting encounters challenges due to the system’s chaotic nature and imprecision in initial measurements, mandating predictions across various time horizons, spanning from weeks to minutes.
The potential economic gains from enhanced solar forecasting are significant, with estimates from the New England grid operator proposing savings in the tens of millions of dollars [15,16]. Quantum methodologies, particularly within the realm of quantum machine learning, present enticing possibilities for advancing solar forecasting—an area actively explored by both public and private sector entities [17,18].
In particular, the efficacy of quantum approaches in forecasting hinges on identifying critical areas where quantum computers can enhance computational performance. Quantum variational eigensolvers offer a potential solution, exhibiting scalability with the number of qubits for addressing nonlinear problems [18]. In the realm of solar and wind production forecasting, exploiting quantum capabilities for representing atmospheric phenomena could result in more accurate simulations in less time. Projects may involve constructing hybrid quantum/classical computers heavily reliant on existing methods. Hybrid methodologies, handling extensive data processing, prove suitable for intricate machine learning algorithms, where quantum computers manage computationally intensive functions, while classical methods address other facets of the process [19].
Also, the quantum approach to challenges in meteorological predictions is expected to be particularly profitable. Meteorological predictions involve intricate interactions guided by fluid physics laws and nonlinear partial differential equations of Navier–Stokes. Quantum computing has undergone initial investigations utilizing both the gate model [20,21] and annealing [22] for this purpose.
4.2. Taking Advantage of Quantum Computing on Scheduling and Dispatching in Power Grids
Grid operators face the task of managing power demand across diverse time scales, encompassing immediate daily operations, day-ahead planning, and long-term capital improvements. Balancing power supply optimization within constraints like transmission limits, safety, reliability, and environmental policies presents a complex optimization challenge. The inclusion of renewable resources, especially distributed ones like rooftop solar, adds intricacy by introducing individually controlled resources. Scheduling and dispatch activities must accommodate the stochastic nature of renewable resource availability and the growing intelligence of the grid, incorporating more sensors, storage, electric vehicle demand, and devices for demand control.
The inherent NP-hard nature of scheduling and dispatching problems renders exact solutions impractical for large systems. Current computational approaches rely on approximations and heuristics due to the complexities introduced by renewable resources. Quantum approaches, including quantum annealing and Quantum Approximate Optimization Algorithms (QAOA), exhibit promise. Quantum annealing directly encodes problems into the quantum system’s energy landscape [23], while QAOA integrates classical optimization with quantum states to discover optimal solutions [24]. The potential computational advantages of these quantum approaches over traditional heuristic methods necessitate further research for a comprehensive understanding of their effectiveness.
4.3. Taking Advantage of Quantum Computing on Power System Stability and Reliability
The power system operates within stringent constraints aimed at ensuring reliability and stability. These constraints are crucial for upholding the safety, dependability, and efficiency of the electrical power supply. Reliability, indicating the system’s consistent ability to meet demand, is a priority for organizations like NERC, aiming for a standard of one day of unforced outage per 10 years [25]. Voltage maintenance standards, such as ANSI’s requirement for a 5% variation from the nominal value of , further contribute to system reliability.
The robustness of the power system against disturbances is therefore particularly critical. Traditionally designed to withstand any contingency, signifying its capability to handle the failure of a single transmission line or generating asset, this requires excess power capacity for disconnected generation and rapid availability to prevent system collapse due to supply–demand imbalances.
In addition to establishing a new steady-state solution post-asset loss, the grid must endure transient disturbances, modeled through the electrical system’s normal modes. Any deviations from the equilibrium state should naturally damp out within short time scales—ranging from milliseconds to a few minutes. Excitations persisting or amplifying could pose risks to equipment.
Quantum computer scientists have identified algorithms applicable to electrical power problems concerned with system stability and reliability. Grover’s algorithm, a renowned quantum technique, provides a speedup in searching databases. Initially designed for searching marked items, its application can extend to various search problems using amplitude estimation. For example, quantum computers programmed to recognize unsafe contingencies could use amplitude estimation to identify scenarios leading to grid instabilities or blackouts [26].
Another promising quantum algorithm is HHL, known for its exponential speedup in solving linear systems of equations compared to classical algorithms. HHL’s proficiency in addressing linear systems suggests its potential applications in power system stability [27]. Areas like state estimation for determining the current power system state and anomaly detection, along with solving differential equations to evaluate system behavior during transient disturbances, demonstrate HHL’s relevance to power system reliability. However, HHL’s demanding nature, requiring numerous qubits and reliable low-error operations, makes it less likely for near-term use on available devices.
4.4. Taking Advantage of Quantum Computing on Battery Production
Batteries play a crucial role in achieving zero-carbon electrification, which is necessary to decrease CO2 emissions in transportation and secure grid-scale energy storage for intermittent sources like solar panels or wind. Batteries stand out as a pivotal technology globally, particularly in a world striving to reshape its energy sources and consumption patterns. Lithium-ion (Li-ion) batteries, in particular, play a vital role in energy transition, acting as a crucial facilitator for electric vehicles (EVs). Substantial resources from industry, academia, and governments have been dedicated to enhancing Li-ion technology, sparking creativity in the process. Notably, companies like Mercedes-Benz, in collaboration with the quantum computer firm PsiQuantum, are innovatively exploring computational methods to optimize battery chemistries. Enhancing the energy density of lithium-ion (Li-ion) batteries allows for cost-effective applications in electric vehicles and energy storage. In the last decade, innovation stagnated, with a 50% improvement in battery energy density from 2011 to 2016, followed by only a 25% increase from 2016 to 2020. The projected improvement is just 17% from 2020 to 2025.
Kim et al. in [28] indicate that quantum computing can revolutionize battery chemistry simulation, especially in terms of breakthroughs in understanding electrolyte complex formation, finding substitute materials for cathode/anode with identical properties, or eliminating the battery separator. Consequently, batteries with 50% higher energy density may be developed for heavy-goods electric vehicles, advancing their economic viability. Although the impact on passenger EVs might be limited, as they are expected to reach cost parity before the first quantum computers come online, potential cost savings for consumers remain.
Lithium-ion batteries consist of four essential components: a cathode, anode, electrolyte, and separator. Ensuring optimal performance in each of these constituents is vital for developing high-efficiency batteries designed for challenging applications like electric vehicles and energy storage systems. Mercedes-Benz R&D and PsiQuantum endeavored to improve Li-ion electrolytes, the substance facilitating the movement of positively charged ions between a battery’s cathode and anode [29].
Efficient and high-performance electrolyte optimization demands a thorough comprehension of the fundamental chemical processes. To tackle this, the researchers suggested a strategy involving the simulation of chemical reactions in liquid Li-ion electrolytes at the molecular level. Nevertheless, conventional computers encounter difficulties handling such intricate simulations due to their complexity. As an alternative, the researchers recommended employing quantum computers, capitalizing on the peculiarities of quantum mechanics to expedite specific calculations, including those pertaining to quantum chemistry. More in detail, an electrolyte, found within batteries, permits an electric charge flow between electrodes. For battery efficiency, the electrolyte needs high ionic conductivity, should not react with electrodes, and resist temperature changes. Depending on battery type, electrolytes may be liquid, gel, or dry polymer. Soluble salts, acids, and bases serve as electrolytes. In Li-ion batteries, lithium hexafluorophosphate (LiPF6) and ethylene carbonate (EC) are common electrolytes. Additives like fluoroethylene carbonate (FEC) enhance electrolytes. Researchers suggest simulations with these components. Placing salt in a solvent leads to ion dissociation (solvation). Researchers propose quantum chemical simulations to calculate solvation’s dissociation energy in two solvent environments—with and without additives. The aim is to identify the more suitable environment for dissociation. This study illustrates how researchers could understand Li-ion electrolytes, offering insights into optimizing electrolytes. Researchers claim quantum chemical simulations aid in designing superior electrolytes. The focus of the cited studies (namely, [28,29]) is not just on an electrolyte additive’s efficacy but mostly on understanding the costs and requirements of simulating quantum chemical reactions. Researchers view this as a step toward harnessing quantum computing for real-world problem-solving. Quantum computers, expected to enable accurate simulations, could provide new insights into challenging molecules.
Moreover, Ho et al. in [30] investigate how higher-density energy batteries can serve as a grid-scale storage solution, transforming the world’s grids. Reducing the cost of grid-scale storage by half could significantly boost the use of economically competitive solar power, especially in regions with challenging generation profiles. Modeling suggests that halving the cost of both solar panels and batteries might increase solar use by 60% in Europe by 2050, and even greater impacts are anticipated in regions without a high carbon price.
By combining the aforementioned use cases, improved batteries could contribute to an additional 1.2 gigaton reduction in carbon dioxide emissions by 2035.
4.5. Taking Advantage of Quantum Computing on Solar Cell Production
Solar cells, crucial for electricity in a net-zero economy, remain distant from their theoretical efficiency, despite cost reductions. Current crystalline silicon-based cells operate at around 20 percent efficiency. Perovskite crystal structures offer up to 40 percent theoretical efficiency, potentially surpassing silicon. However, challenges such as long-term stability issues and potential toxicity in some variations hinder mass production [31].
Claudino et al. claim in [32] that quantum computing emerges as a relevant solution, enabling precise simulations of perovskite structures with various base atoms and doping. This approach aims to identify solutions with higher efficiency, durability, and environmental safety. Achieving the theoretical efficiency increase could cut the levelized cost of electricity (LCOE) by 50 percent. Simulating the impact of quantum-enabled solar panels, especially cheaper and more efficient ones, reveals increased adoption in regions with lower carbon prices (e.g., China) and countries in Europe with high irradiance (Spain, Greece) or unfavorable conditions for wind energy (Hungary). The combination with inexpensive battery storage amplifies the positive effects.
This technology, if successful, could mitigate an additional 0.3 gigatons of CO2 emissions by 2035.
Instead, according to [33], in a partnership between Phasecraft, a quantum startup, and Google Quantum AI, researchers have developed a quantum computing algorithm that uncovers characteristics of electronic systems, potentially enhancing various eco-friendly technologies. This breakthrough marks significant progress in utilizing quantum computers to identify low-energy features of strongly correlated electronic systems, a challenge classical computers cannot tackle.
Such an innovative algorithm is the first capable of examining ground-state properties of the Fermi–Hubbard model on a quantum computer, offering valuable insights into the electronic and magnetic properties of materials.
The Fermi–Hubbard model, a key benchmark for near-term quantum computers, serves as a fundamental system with non-trivial correlations beyond classical methods. Unveiling the lowest-energy state of the Fermi–Hubbard model enables the calculation of crucial physical properties.
This approach has numerous potential advantages, including assisting in the design of new materials for more efficient batteries, solar cells, and high-temperature superconductors, surpassing the capabilities of even the most powerful supercomputers.
Quantum computing has been pushed to unprecedented levels, as researchers, employing a highly efficient algorithm and advanced error-mitigation techniques, conducted an experiment four times larger and with ten times more quantum gates than any previous record. This puts an emphasis on the actual scalability of the proposed algorithm, anticipating its adaptation to more powerful quantum computers with hardware advancements.
4.6. Taking Advantage of Quantum Computing on Green Hydrogen and Ammonia Production
Hydrogen is widely regarded as a potential substitute for fossil fuels in various sectors of the economy, particularly in industries requiring high temperatures where electrification is impractical or insufficient. This is especially true for applications like steelmaking or ethylene production, where hydrogen serves as a crucial feedstock.
Prior to the gas price spikes in 2022, green hydrogen was approximately 60 percent more costly than natural gas. However, advancements in electrolysis present an opportunity to significantly lower the production cost of hydrogen.
Polymer electrolyte membrane (PEM) electrolyzers, which split water to produce green hydrogen, have seen recent improvements but still encounter two major challenges.
- First, they lack optimal efficiency, and, although pulsing the electrical current has shown improved efficiency in laboratory settings, scaling this approach remains a challenge.
- Secondly, electrolyzers face issues with the delicate membranes that facilitate the passage of split hydrogen from the anode to the cathode, along with catalysts that expedite the overall process. The challenge lies in achieving effective interactions between catalysts and membranes, as enhancing catalyst efficiency often accelerates membrane wear. The understanding of these interactions is currently insufficient for the design of improved membranes and catalysts.
According to [34], quantum computing offers a solution by modeling the energy state of pulse electrolysis to optimize catalyst usage, thereby increasing efficiency. Additionally, quantum computing can simulate the chemical composition of catalysts and membranes, ensuring the most efficient interactions. This could potentially elevate the efficiency of the electrolysis process to 100 percent, resulting in a 35 percent reduction in hydrogen production costs. When coupled with the discovery of more affordable solar cells through quantum computing (as discussed earlier), the overall cost of hydrogen could be slashed by 60 percent.
The increased utilization of hydrogen resulting from these advancements has the potential to curtail CO2 emissions by an additional 0.9 gigatons by the year 2035.
Ammonia, on the other hand, primarily recognized as a fertilizer, holds the potential to serve as a fuel, positioning it as a promising decarbonization solution for the global shipping industry. Currently constituting 2 percent of total global final energy consumption, ammonia is conventionally produced through the energy-intensive Haber–Bosch process using natural gas. While there are alternative methods for generating green ammonia, they generally involve similar processes, such as utilizing green hydrogen as a feedstock or capturing and storing carbon dioxide emissions from the process.
One innovative approach is nitrogenase bioelectrocatalysis, mirroring the natural nitrogen fixation process in plants. In this method, nitrogen gas from the air is transformed into ammonia through the catalyzation of nitrogenase enzymes. Notably, this bioelectrocatalysis can be conducted at room temperature and at a 1 bar pressure, in stark contrast to the Haber–Bosch process, which operates at 500 °C under high pressure, consuming substantial energy in the form of natural gas.
Despite advancements in replicating nitrogen fixation artificially, challenges like enzyme stability, oxygen sensitivity, and low rates of ammonia production by nitrogenase hinder scalability. Quantum computing, according to the approaches proposed in [34,35], offers a solution by simulating processes to enhance enzyme stability, protect against oxygen sensitivity, and improve ammonia production rates by nitrogenase. This simulation could lead to a significant 67 percent reduction in costs compared to current green ammonia production through electrolysis, making green ammonia more economical than traditionally produced ammonia. Such cost efficiency not only mitigates the CO2 impact of ammonia production for agricultural use but also accelerates the breakeven for ammonia in shipping, a key decarbonization option, by ten years.
Leveraging quantum computing to enable cost-effective green ammonia as a shipping fuel ultimately has the potential to reduce an additional 0.3 gigatons of CO2 emissions by 2035.
4.7. Taking Advantage of Quantum Computing on Carbon Capture
Achieving net zero necessitates a focus on carbon capture, with both point-source and direct methods benefitting from the potential of quantum computing.
Point-source capture involves directly capturing CO2 emissions from industrial sites like cement or steel blast furnaces. However, the majority of CO2 capture remains economically unfeasible due to its high energy intensity. A potential remedy lies in the use of innovative solvents, such as water-lean and multiphase solvents, offering lower energy requirements. Yet, predicting the molecular properties of these materials poses challenges. Quantum computing offers a solution by facilitating a more precise modeling of molecular structures, enabling the design of new, efficient solvents. This advancement could potentially reduce the process cost by 30 to 50 percent.
This quantum-assisted approach holds considerable potential for decarbonizing industrial processes, potentially yielding an additional decarbonization impact of up to 1.5 gigatons annually, including cement.
Direct-air capture, involving the extraction of CO2 from the atmosphere, is crucial for achieving net zero. However, this method is currently costly and even more energy-intensive than point-source capture. Adsorbents, particularly novel ones like metal–organic frameworks (MOFs), show promise in significantly reducing energy requirements and infrastructure capital costs. MOFs, acting as immense sponges with vast surface areas, can absorb and release CO2 at lower temperature changes compared to conventional technology.
Quantum computing plays a pivotal role in advancing research on novel adsorbents like MOFs [36,37,38], addressing challenges arising from sensitivity to oxidation, water, and degradation caused by CO2. Novel adsorbents with enhanced adsorption rates could bring down technology costs to $100 per ton of CO2-eq captured, a critical threshold for adoption, especially considering the expectations of corporate climate leaders like Microsoft, who anticipate paying $100 per ton for premium carbon removals in the long term. This breakthrough could lead to an additional reduction of 0.7 gigatons of CO2 annually by 2035.
5. Discussion on the Impact of Quantum Computing on the Considered Application Scenarios
In this paper, we considered the following applications of quantum computing: (i) improving forecasting performance to better manage the variability in solar and wind resources; (ii) managing power demand in power grids; (iii) ensuring reliability and stability in power systems; (iv) enhancing electric vehicle batteries; (v) advancing renewable solar technology; (vi) expediting the cost reduction of hydrogen for a feasible alternative to fossil fuels; (vii) leveraging green ammonia as both a fuel and fertilizer; and (viii) improving the performance of point-source and direct-air carbon capture technology.
In summary, relative to challenges (i)–(iii), researchers and engineers in the power system domain have yet to convincingly exhibit the quantum advantage. This is primarily due to the current state of quantum hardware in the NISQ era, characterized by noise and limited resources. Despite these challenges, their valuable research efforts pave the way for further advancements in the field.
The prospect of a significant deployment of quantum computing to tackle operational power system issues in the near future seems unlikely, given the early stage of quantum computing development. However, some projections about the availability timeline of various quantum computing technologies for grid problem-solving can be formulated. For instance, quantum annealing technology is anticipated to be accessible in the short term for addressing power systems optimization problems. On the other hand, technologies like variational quantum algorithms (such as variational quantum linear solvers and, notably, QAOA) appear to necessitate further technological advancements before practical deployment. Lastly, deep quantum circuits, exemplified by the HHL algorithm, requiring fault-tolerant quantum computers, seem distant from the demonstration phase.
Instead, as regards challenges (iv)–(viii), the implementation of cutting-edge quantum technology stands as a transformative force in the quest to curb carbon emissions. By harnessing the unique capabilities of quantum computing, these advancements not only represent a technological leap but also hold the key to substantial reductions in gigatons of CO2 emissions. Table 2, for the sake of clarity, reports the description as well as the expected benefits for challenges (iv)–(viii). Illustrated in the accompanying chart in Figure 1, we provide a visual representation of the substantial reductions in carbon dioxide emissions by 2035, achieved through the adoption of the implemented technologies.

Table 2.
Description and expected benefits for challenges (v)–(viii).
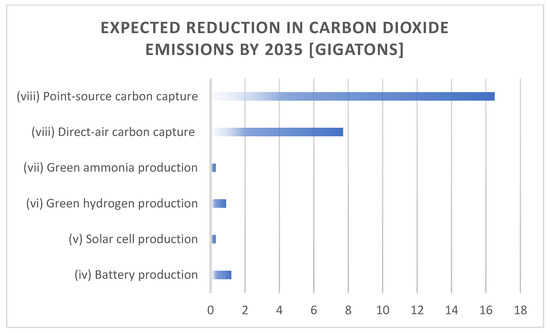
Figure 1.
Impact of quantum-computing-driven innovation in terms of reduction in CO2 emissions for challenges (iv)–(viii).
The current decarbonization pace, as of 2023, is estimated to be removing 2 gigatons of CO2 per year through the carbon dioxide removal technologies available [39]. Therefore, quantum computing offers the potential to remove and sequester carbon dioxide at +122%, with respect to the current rate.
6. Suggestions for Research Directions Relative to Designing, Planning, and Operating Power Systems
In this Section, we focus on pinpointing some of the problems discussed in the literature where mathematical optimization is used for strategic energy system design and planning, still without quantum computing, and, in this respect, we briefly highlight research directions where quantum computing may be particularly helpful despite its relatively low technology readiness level.
In particular, challenges such as facility location allocation for energy systems infrastructure development, unit commitment in electric power systems operations, and heat exchanger network synthesis, all of which are part of energy systems optimization, are addressed using classical algorithms on conventional CPU-based computers and quantum algorithms on quantum computing hardware.
Strategic energy system design and planning involve crucial aspects like facility location and allocation, as noted in [40,41]. Some optimization problems in energy infrastructure development can be framed as facility location/allocation issues. There has been extensive research on these models, leading to the development of various algorithms [40,42,43]. For instance, one common problem is determining the best location for wind farms, considering grid constraints. Deciding where to place solar, wind, or hydro power facilities can also involve minimizing opening and transportation costs while meeting demand and resource constraints. The quadratic assignment problem is a key challenge in this area. Hub-based electricity storage network design, for example, can be modeled as a quadratic assignment problem. Biofuel supply chain optimization also often employs quadratic programming. This problem’s complexity has led to numerous formulations and solution methods [44]. In power grid optimization, the goal is to assign n power plants to n regions to minimize interplant transportation costs. The problem involves two matrices, and , where is the cost of moving one unit of energy from to , and is the energy units to be transported from to . Each assignment variable indicates whether plant is assigned to location . The assignment constraints ensure only one facility per location. For simplicity, demand and resource constraints are not considered here. The Koopmans Beckmann formulation of this problem is given by
The D-Wave annealers used in [8,9] are explicitly built for optimization and sampling problems; therefore, optimization problems tend to run faster on them than on classical computers.
Another very relevant optimization problem in the operation of power systems is that of unit commitment (UC). The UC problem is typically framed as a large-scale mixed integer nonlinear problem, which is challenging to solve due to the nonlinear cost function and the combinatorial nature of feasible solutions. It has been established that UC is NP-hard and NP-complete, making it impossible to devise an algorithm with polynomial computation time for its solution. Various techniques have been proposed to address the UC problem, including deterministic approaches, meta-heuristic methods, and combinatorial strategies. Efficient optimization techniques are crucial when integrating high levels of renewable energy sources into power systems. As the number of energy sources increases, the UC problem becomes more challenging, necessitating the development of effective methodologies to address it. Unit commitment aims to minimize the total operational cost while meeting system and generator constraints over a specified time horizon. System power balance, spinning reserves, and generation power limits are among the constraints in unit commitment. Given a set of units , the power generated by each unit to meet a given load requirement is represented by , while the fuel cost ci of the committed unit is typically expressed as a quadratic polynomial with coefficients , , and . The UC problem for a single time period is mathematically formulated as a mixed-integer quadratic programming problem, where the binary variable indicates whether unit is online. The generated power limits for each unit are constrained by lower bound and upper bound .
Only an unconstrained quadratic optimization problem can be mapped onto the D-wave system; therefore, the mixed-integer quadratic programming problem in (2) cannot be directly solved on a quantum computing system. The UC problem must be reformulated into a quadratic unconstrained binary optimization model, which can be achieved by discretizing the problem space. Then, it too can be embedded on a D-wave quantum processor, similarly as for the previous problem.
Last but not least, to prevent excessive energy consumption in industrial plants, it is essential to integrate processes energetically. Heat exchanger network synthesis (HENS) is a systematic approach to managing energy costs in a process. The costs of heating and cooling are regulated by hot and cold utilities and the heat exchangers in a network. Improving heat transfer in heat exchanger devices through various techniques can also help reduce these costs and ensure efficient energy conversion. In a process, a cold stream can be heated by either a hot utility or a hot stream, while a hot stream can be cooled by a cold utility or another cold stream. HENS is an NP-hard problem for which there is no exact polynomial-time computational algorithm. Several metaheuristic techniques capable of handling complex problems within a feasible computational time have been proposed [45,46]. Sequential synthesis and simultaneous synthesis are two well-known groups of methods for addressing the HENS problem. Sequential synthesis involves decomposing a problem into three subproblems: minimum utility cost, minimum number of matches, and minimum cost network problems. These subproblems can be addressed more easily than the original single-task problem. The minimum number of matches problem involves determining the minimum cost of matches that meet the heat supply and demand for a heat exchanger network. This simple HENS subproblem with only one temperature interval is NP-hard in the strong sense. For a heat exchanger network with m sources and n sinks and a single temperature interval, there is a heat supply at each source and a heat demand at each sink . The cost for each possible match between a source and a sink is denoted by . The variables represent the total heat exchanged between source and sink , while the existence of a heat match between them is indicated by a binary variable . This matching problem can be formulated as in (3), where the first two constraints represent energy balance, and the third one is a logical constraint.
This problem was actually solved on D-Wave’s 2000Q quantum processor [47], with considerable benefit with respect to a solution based on classical computers.
More in general, to the best of the authors’ knowledge, the practical implementation of quantum computing in power systems involves several challenges. First, it is crucial to develop quantum algorithms tailored to specific optimization problems in power systems. Researchers are currently working on adapting existing classical algorithms or devising new quantum approaches to improve computational efficiency.
Moreover, quantum hardware, such as qubits and quantum gates, faces challenges like decoherence and error rates, as mentioned earlier. Overcoming these obstacles requires advancements in error-correction techniques and the development of more stable quantum processors.
Collaborations between quantum computing experts and energy domain specialists are vital to identify practical applications, define problem constraints, and integrate quantum solutions into existing energy infrastructure. As the field progresses, hybrid approaches combining classical and quantum computing may emerge as transitional solutions to address real-world challenges in the energy sector.
7. Main Frameworks to Explore Quantum Computing
With the surging interest in quantum computing, an expanding array of development libraries and tools emerges for this domain. Diverse development environments and simulators cater to major languages like Python, C/C++, and Java, among others. Prominent quantum computing research centers predominantly favor Python as the language for constructing quantum circuits. Python’s appeal lies in its flexibility and high-level nature, enabling programmers to focus on problem-solving without excessive concern for formalities. Python is dynamically typed and interpreted, streamlining the learning curve and garnering substantial support from the quantum computing community.
The schematic diagram in Figure 2 illustrates the quantum computing stack, encompassing quantum algorithms and applications at the highest level and the physical realizations of quantum computers at the lowest level. Intermediary components, such as control, readout, and quantum error correction modules, connect these layers. Quantum programming languages facilitate interaction with the stack’s summit, involving low-level instructions for gates and qubits. Due to the impracticality of manual programming, quantum computers interface with higher-level quantum programming languages within development libraries.
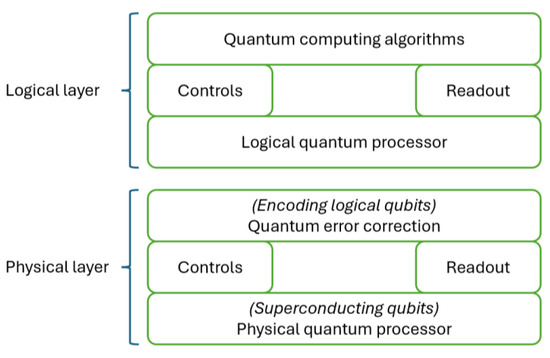
Figure 2.
Quantum computing stack, representing a system view of a quantum information processor. It is divided into a physical and a logical layer. The physical layer consists of a physical quantum processor having both input and output lines controlled by the quantum error correction processor, thus providing the actual error correction. The quantum error correction processor is in turn controlled by the logical layer, which defines the encoded qubits and performs the logical operations for the desired quantum algorithm selected on top of the stack.
Cloud quantum computers enable the execution of algorithms on authentic quantum hardware. Development libraries facilitate this functionality. For pre-execution code testing on a quantum computer, most frameworks offer a simulator running on classical computing systems. This simulation can operate either locally or in the cloud. As it operates on a classical machine, it lacks the ability to process genuine quantum states. Nevertheless, it proves beneficial for validating code syntax and flow.
A multitude of quantum programming languages is now accessible, encompassing both functional and imperative languages. Functional options include Qiskit, LIQUi|>, Q#, and Quipper. Imperative languages for quantum computing programming comprise Cirq, Scaffold, and ProjectQ. Below, we list their main characteristics.
- Cirq. Since 2018, Google’s quantum computing development library has been Cirq. It empowers developers to construct and implement quantum circuits using standard unary, binary, and ternary operators. Python serves as the host language for Cirq, and the entire library can be accessed at [48].
- ∘
- Pros. Developed by Google, Cirq is known for its emphasis on providing low-level control over quantum circuits. It integrates well with TensorFlow Quantum for machine learning applications.
- ∘
- Cons. It may be less user-friendly for those new to quantum computing. It primarily targets researchers and developers comfortable with lower-level quantum operations.
- Qiskit. The Quantum Information Science Kit, or Qiskit, stands as IBM’s quantum computing development library. It offers a versatile framework for quantum computer programming. Comprising four core modules across the quantum computing stack, the Qiskit development library includes, as follows:
- ∘
- Qiskit Terra: serving as the foundation, Terra provides essential elements for composing quantum programs at the circuit and pulse level, optimizing them for specific physical quantum processors.
- ∘
- Qiskit Aer: this module supplies a C++ simulator framework and tools for constructing noise models, facilitating realistic simulations of errors during execution on real devices.
- ∘
- Qiskit Ignis: focused on understanding and mitigating noise in quantum circuits and devices, Ignis provides a framework for these purposes.
- ∘
- Qiskit Aqua: Aqua houses a library of cross-domain quantum algorithms, forming the basis for near-term quantum computing applications.
The entire Qiskit library can be accessed at [49].- ∘
- Pros. Developed by IBM, Qiskit is well supported, with a large community. It is the best choice for beginners and offers a comprehensive set of tools for quantum computing, including simulators and access to real quantum hardware.
- ∘
- Cons. The rapid evolution of the platform may result in occasional compatibility issues.
- Forest. Forest, Rigetti’s development library, aligns with the Python-based trend of its predecessors. It encompasses a set of tools for efficient quantum programming. Users compose quantum programs in pyQuil, where low-level instructions are translated into Quil (Quantum Instruction Language) and transmitted to the quantum computer. The term “Forest” encompasses the complete collection of programming tools in this toolchain, including Quil, pyQuil, and additional components like Grove—a compilation of quantum algorithms coded in pyQuil. The entire library is accessible at [50].
- ∘
- Pros. Rigetti’s quantum virtual machine allows for a fast simulation of quantum circuits, which can be useful for testing and debugging. Forest includes a variety of tools and libraries for quantum computing, such as pyQuil, which is a Python library for quantum programming, and offers cloud access to their quantum processors, allowing users to run their quantum programs on real quantum hardware.
- ∘
- Cons. Forest is designed specifically for Rigetti’s quantum processors; therefore, it may not be as versatile as other quantum programming languages that can work with multiple quantum hardware platforms. The documentation for Forest may not be as extensive as other quantum programming languages, making it more challenging for beginners to learn. Forest may not have as large of a community or as many resources available as other quantum programming languages, which can make it more difficult to find help or support.
- Quantum Development Kit (QDK) [51]. The QDK, developed by Microsoft in 2018, stands out as a quantum computing development library. In contrast to prior Python-based languages, it introduced Q#, a distinct language tailored for crafting quantum programs. Q# diverges from Python-based libraries like Qiskit and pyQuil in various aspects. Explicit type declarations become necessary in Q#, and curly braces replace the indentation convention in Python. Executing programs with QDK demands three separate files: (i) a .qs file housing quantum operations (equivalent to Python functions), (ii) a .cs driver file where quantum operations execute within the main program, and (iii) a .csproj file outlining project specifics and including metadata on computer architecture and package references.
- ∘
- Pros. Integrated with Visual Studio, Q# is designed for quantum development within the Microsoft ecosystem. It provides a high-level quantum-focused language along with classical host programs.
- ∘
- Cons. It has limited support for quantum hardware compared to simulators, and it is primarily suited for Microsoft Quantum Development Kit users.
- LIQUi|> [52]. LIQUi|> or Liquid represents a quantum computing software architecture and tool suite encompassing a programming language, optimization, and scheduling algorithms, along with quantum simulators. This framework facilitates the translation of a quantum algorithm, presented as a high-level program, into the low-level machine instructions essential for a quantum device. Developed by the Quantum Architectures and Computation Group (QuArC) at Microsoft Research, LIQUi|> plays a crucial role in advancing quantum computing technologies. Delving into LIQUi|>‘s specifics, it serves as a comprehensive software platform crafted by QuArC to support the development and comprehension of quantum protocols, algorithms, error correction methodologies, and quantum devices. LIQUi|> boasts the capability to simulate Hamiltonians, quantum circuits, quantum stabilizer circuits, and quantum noise models. Operating in Client, Service, and Cloud modes, it empowers users to express circuits using a high-level functional language (F#). The system allows for the simulation of circuit data structures, enabling seamless integration with other components for tasks like circuit optimization, quantum error correction, gate replacement, export, or rendering. The modular architecture of LIQUi|> ensures flexibility, allowing for easy extensions as needed.
- ∘
- Pros. LIQUi|> provides a high-level programming model that abstracts away many of the low-level details of quantum computing, making it easier for developers to write and understand quantum algorithms. LIQUi|> is designed to integrate seamlessly with classical programming languages like C#, F#, and Python, allowing developers to leverage their existing skills and tools. LIQUi|> includes built-in support for quantum error correction, which is essential for building reliable quantum algorithms. LIQUi|> uses strong typing to help prevent common programming errors, making it easier to write correct quantum code. LIQUi|> is actively developed by Microsoft Research, which means it is likely to continue to improve and evolve over time.
- ∘
- Cons. LIQUi|> currently only supports a limited set of quantum hardware, including Microsoft’s Quantum Development Kit and the Quantum Development Kit for Azure. This means that developers may not be able to run their algorithms on all available quantum hardware. LIQUi|> is a relatively new language; therefore, it may not have as large of a community or as many resources available as more established languages like Qiskit or Cirq. LIQUi|>‘s documentation is still relatively sparse, which can make it difficult for developers to learn how to use the language effectively.
- Quipper [53]. Quipper is a quantum programming language that stands out for its versatility, enabling the programming of a diverse range of non-trivial quantum algorithms. Impressively, it can generate quantum gate representations involving trillions of gates. Designed for a model of computation where a classical computer controls a quantum device, Quipper avoids reliance on any specific quantum hardware model. Its effectiveness and user-friendly nature have been demonstrated through practical applications. Importantly, Quipper serves as a gateway to leveraging formal methods for the analysis of quantum algorithms, contributing to the advancement of quantum computation beyond theoretical exercises.
- ∘
- Pros. Developed by Microsoft Research and the University of Edinburgh, Quipper is a functional programming language that supports both classical and quantum computation. It is designed for expressing quantum algorithms at a high level.
- ∘
- Cons. It may not be as widely adopted as other languages, and the learning curve might be steeper for those unfamiliar with functional programming concepts.
- In addition to the aforementioned libraries, other noteworthy ones include, as follows [54]:
- ∘
- ProjectQ, a Python library incorporating a high-performance C++ quantum computer simulator;
- ∘
- Strawberry Fields, a Python library centered around continuous-variable quantum computing;
- ∘
- Ocean, a Python library facilitating quantum annealing on D-Wave quantum computers;
- ∘
- XACC, an independent hardware-agnostic quantum programming framework.
8. Conclusions
This paper provides an extensive literature review specifically limited to recent trends in energy applications of quantum computing. In particular, the contexts around which most of the business needs of energy suppliers and utility companies currently revolve in this respect are the following: improving forecasting performance to better manage the variability in solar and wind resources; managing power demand in power grids; ensuring reliability and stability in power systems; enhancing electric vehicle batteries; advancing renewable solar technology; expediting the cost reduction of hydrogen for a feasible alternative to fossil fuels; leveraging green ammonia as both a fuel and fertilizer; and improving the performance of point-source and direct-air carbon capture technology.
The key finding of this paper, based on the proposed literature review, is twofold, namely, as follows:
- Quantum computing has the potential to trigger significant transformation in the energy domain by drastically reducing CO2 emissions.
- Quantum computing offers enhanced optimization capability relative to relevant challenges that concern forecasting solar and wind resources, as well as managing power demand, facility allocation, and ensuring reliability and stability in power grids.
Quantum computing is definitely expected to be a game changer with respect to the above-mentioned application scenarios, yielding benefits that range from optimizing grid management to significantly increasing decarbonization. However, future work in terms of research and innovation will be primarily aimed at overcoming the current state of quantum technology in the NISQ era, which is characterized by noise and limited resources and thus still prevents the engineering and industrializing of any prototyped technology.
Funding
This research received no external funding.
Data Availability Statement
No new data were created.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Choi, C.Q. Quantum Computers Exponentially Faster at Untangling Insights. IEEE Spectrum. 2022. Available online: https://spectrum.ieee.org/quantum-computing (accessed on 3 January 2024).
- Niedenzu, W.; Mukherjee, V.; Ghosh, A. Quantum engine efficiency bound beyond the second law of thermodynamics. Nat. Commun. 2018, 9, 165. [Google Scholar] [CrossRef]
- Franklin, D.; Chong, F.T. Challenges in reliable quantum computing. In Nano, Quantum and Molecular Computing; Springer: New York, NY, USA, 2004; pp. 247–266. [Google Scholar] [CrossRef]
- Giani, A.; Eldredge, G. How Quantum Computing Can Tackle Climate and Energy Challenges. Available online: https://eos.org/features/how-quantum-computing-can-tackle-climate-and-energy-challenges (accessed on 17 January 2024).
- Paudel, H.P.; Syamlal, M.; Crawford, S.E.; Lee, Y.L.; Shugayev, R.A.; Lu, P.; Ohodnicki, P.R.; Mollot, D.; Duan, Y. Quantum computing and simulations for energy applications: Review and perspective. ACS Eng. Au 2022, 2, 151–196. [Google Scholar] [CrossRef]
- Golestan, S.; Habibi, M.R.; Mousazadeh Mousavi, S.Y.; Guerrero, J.M.; Vasquez, J.C. Quantum computation in power systems: An overview of recent advances. Energy Rep. 2023, 9, 584–596. [Google Scholar] [CrossRef]
- Climate Math: What a 1.5-Degree Pathway Would Take, McKinsey. Available online: https://www.mckinsey.com/~/media/mckinsey/business%20functions/sustainability/our%20insights/climate%20math%20what%20a%201%20point%205%20degree%20pathway%20would%20take/climate-math-what-a-1-point-5-degree-pathway-would-take-final.pdf (accessed on 17 January 2024).
- Djidjev, H.N.; Chapuis, G.; Hahn, G.; Rizk, G. Efficient combinatorial optimization using quantum annealing. arXiv 2016, arXiv:1801.08653. [Google Scholar]
- Ajagekar, A.; Humble, T.; You, F. Quantum computing based hybrid solution strategies for large-scale discrete-continuous optimization problems. Comput. Chem. Eng. 2020, 132, 106630. [Google Scholar] [CrossRef]
- Humble, T.S.; Thapliyal, H.; Munoz-Coreas, E.; Mohiyaddin, F.A.; Bennink, R.S. Quantum computing circuits and devices. IEEE Des. Test. 2019, 36, 69–94. [Google Scholar] [CrossRef]
- Giani, A.; Eldredge, Z. Quantum Computing Opportunities in Renewable Energy. SN Comput. Sci. 2021, 2, 393. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting quibits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Kjaergaard, M.; Schwartz, M.; Braumuller, J.; Krantz, P.; Wang, J.I.J.; Gustavsson, S.; Oliver, W.D. Superconducting qubits: Current state of play. Annu. Rev. Condens. Matter Phys. 2020, 11, 369–395. [Google Scholar] [CrossRef]
- Bruzewicz, C.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Kleissl, J. Solar Energy Forecasting Advances and Impacts on Grid Integration. Available online: https://www.energy.gov/sites/default/files/2019/10/f67/1%20Solar-Forecasting-2-Annual-Review_Kleissl_1.pdf (accessed on 17 January 2024).
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Hamann, H.F. A Multi-Scale, Multi-Model, Machine-Learning Solar Forecasting Technology; U.S. Department of Energy: Washington, DC, USA, 2017. [CrossRef]
- Marquis, M.; Benjamin, S.; James, E.; Lantz, K.; Molling, C. A Public-Private-Academic Partnership to Advance Solar Power Forecasting; U.S. Department of Energy: Washington, DC, USA, 2015. [CrossRef]
- Suchara, M.; Alexeev, Y.; Chong, F.; Finkel, H.; Hoffmann, H.; Larson, J.; Osborn, J.; Smith, G. Hybrid quantum-classical computing architectures. In Proceedings of the 3rd International Workshop on Post-Moore Era Supercomputing, Dallas, TX, USA, 11 November 2018. [Google Scholar]
- Gaitan, F. Finding flows of a navier-Stokes fluid through quantum computing. NPI Quant. Inf. 2019, 6, 61. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Sreenivasan, K. Quantum computation of fluid dynamics. Pramana–J. Phys. 2020, 123. [Google Scholar] [CrossRef]
- Ray, N.; Banerjee, T.; Nadiga, B.; Karra, S. Towards solving Navier-Stokes equation on quantum computers. arXiv 2019, arXiv:1904.09033. [Google Scholar]
- Vereno, D.; Khodaei, A.; Neureiter, C.; Lehnhoff, S. Quantum–classical co-simulation for smart grids: A proof-of-concept study on feasibility and obstacles. Energy Inform. 2023, 6 (Suppl. S1), 25. [Google Scholar] [CrossRef]
- Jing, H.; Wang, Y.; Li, Y. Data-driven quantum approximate optimization algorithm for power systems. Commun. Eng. 2023, 2, 12. [Google Scholar] [CrossRef]
- NERC. Planning Resource Adequacy Analysis, Assessment and Documentation; NERC: Atlanta, GA, USA, 2021. [Google Scholar]
- Habibi, M.R.; Golestan, S.; Soltanmanesh, A.; Guerrero, J.M.; Vasquez, J.C. Power and Energy Applications Based on Quantum Computing: The Possible Potentials of Grover’s Algorithm. Electronics 2022, 11, 2919. [Google Scholar] [CrossRef]
- Gao, F.; Wu, G.; Guo, S.; Dai, W.; Shuang, F. Solving DC Power Flow Problems Using Quantum and Hybrid algorithms. arXiv 2022, arXiv:2201.04848. [Google Scholar] [CrossRef]
- Kim, I.H.; Liu, Y.H.; Pallister, S.; Pol, W.; Roberts, S.; Lee, E. Fault-tolerant resource estimate for quantum chemical simulations: Case study on Li-ion battery electrolyte molecules. Phys. Rev. Res. 2022, 4, 023019. [Google Scholar] [CrossRef]
- Rice, J.E.; Gujarati, T.P.; Motta, M.; Takeshita, T.Y.; Lee, E.; Latone, J.A.; Garcia, J.M. Quantum computation of dominant products in lithium–sulfur batteries. J. Chem. Phys. 2021, 154, 134115. [Google Scholar] [CrossRef]
- Ho, A.; McClean, J.; Ping Ong, S. Promise and Challenges of Quantum Computing for Energy Storage. Joule 2018, 2, 810–813. [Google Scholar] [CrossRef]
- Almosni, S.; Delamarre, A.; Jehl, Z.; Suchet, D.; Cojocaru, L.; Giteau, M.; Behaghel, B.; Julian, A.; Ibrahim, C.; Tatry, L.; et al. Material challenges for solar cells in the twenty-first century: Directions in emerging technologies. Sci. Technol. Adv. Mater. 2018, 19, 336–369. [Google Scholar] [CrossRef]
- Claudino, D.; Peng, B.; Kowalski, K.; Humble, T.S. Modeling Singlet Fission on a Quantum Computer. J. Phys. Chem. Lett. 2023, 14, 5511–5516. [Google Scholar] [CrossRef]
- Choubisa, H.; Abed, J.; Mendoza, D.; Matsumura, H.; Sugimura, M.; Yao, Z.; Wang, Z.; Sutherland, B.R.; Aspuru-Guzik, A.; Sargent, E.H. Accelerated chemical space search using a quantum-inspired cluster expansion approach. Matter 2022, 6, 605–625. [Google Scholar] [CrossRef]
- González-Cabaleiro, R.; Thompson, J.A.; Vilà-Nadal, L. Looking for Options to Sustainably Fixate Nitrogen. Are Molecular Metal Oxides Catalysts a Viable Avenue? Front. Chem. 2021, 9, 742565. [Google Scholar] [CrossRef]
- Clary, J.M.; Jones, E.B.; Vigil-Fowler, D.; Chang, C.; Graf, P. Exploring the scaling limitations of the variational quantum eigensolver with the bond dissociation of hydride diatomic molecules. Int. J. Quantum Chem. 2023, 123, e27097. [Google Scholar] [CrossRef]
- Yamabayashi, T.; Atzori, M.; Tesi, L.; Cosquer, G.; Santanni, F.; Boulon, M.E.; Morra, E.; Benci, S.; Torre, R.; Chiesa, M.; et al. Scaling Up Electronic Spin Qubits into a Three-Dimensional Metal-Organic Framework. J. Am. Chem. Soc. 2018, 140, 12090–12101. [Google Scholar] [CrossRef] [PubMed]
- Greene-Diniz, G.; Manrique, D.Z.; Sennane, W.; Magnin, Y.; Shishenina, E.; Cordier, P.; Llewellyn, P.; Krompiec, M.; Rančić, M.J.; Ramo, D.M. Modelling carbon capture on metal-organic frameworks with quantum computing. EPJ Quantum Technol. 2022, 9, 37. [Google Scholar] [CrossRef]
- Dahale, G.R. Quantum simulations for carbon capture of metal-organic frameworks. In Proceedings of the 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 17–22 September 2023. [Google Scholar]
- Ho, D.T. Carbon dioxide removal is not a current climate solution—We need to change the narrative. Nature 2023, 616, 7955. [Google Scholar] [CrossRef]
- Hörsch, J.; Hofmann, F.; Schlachtberger, D.; Brown, T. PyPSA-Eur: An open optimisation model of the European transmission system. Energy Strategy Rev. 2018, 22, 207–215. [Google Scholar] [CrossRef]
- Gaete-Morales, C.; Gallego-Schmid, A.; Stamford, L.; Azapagic, A. A novel framework for development and optimisation of future electricity scenarios with high penetration of renewables and storage. Appl. Energy 2019, 250, 1657–1672. [Google Scholar] [CrossRef]
- Bordin, C.; Tomasgard, A. SMACS MODEL, a stochastic multihorizon approach for charging sites management, operations, design, and expansion under limited capacity conditions. J. Energy Storage 2019, 26, 100824. [Google Scholar] [CrossRef]
- Bordin, C.; Mishra, S.; Palu, I. A multihorizon approach for the reliability oriented network restructuring problem, considering learning effects, construction time, and cables maintenance costs. Renew. Energy 2021, 168, 878–895. [Google Scholar] [CrossRef]
- Loiola, E.M.; de Abreu, N.M.M.; Boaventura-Netto, P.O.; Hahn, P.; Querido, T. A survey for the quadratic assignment problem. Eur. J. Oper. Res. 2007, 176, 657–690. [Google Scholar] [CrossRef]
- Ponce-Ortega, J.M.; Hernández-Pérez, L.G. Metaheuristic Optimization Programs. In Optimization of Process Flowsheets through Metaheuristic Techniques; Springer: Berlin/Heidelberg, Germany, 2019; pp. 27–51. [Google Scholar]
- Toimil, D.; Gómez, A. Review of metaheuristics applied to heat exchanger network design. Int. Trans. Oper. Res. 2017, 24, 7–26. [Google Scholar] [CrossRef]
- Ajagekar, A.; You, F. Quantum computing for energy systems optimization: Challenges and opportunities. Energy 2019, 179, 76–89. [Google Scholar] [CrossRef]
- Cirq. Available online: https://github.com/quantumlib/Cirq (accessed on 17 January 2024).
- Qiskit. Available online: https://github.com/Qiskit (accessed on 17 January 2024).
- Forest. Available online: https://github.com/rigetti/pyquil (accessed on 17 January 2024).
- Quantum Development Kit. Available online: https://learn.microsoft.com/en-us/azure/quantum/overview-what-is-qsharp-and-qdk (accessed on 17 January 2024).
- Liquid. Available online: https://stationq.github.io/Liquid/ (accessed on 17 January 2024).
- Quipper. Available online: https://github.com/thephoeron/quipper-language (accessed on 17 January 2024).
- Ernst, A. An Overview of Quantum Computing Frameworks. Available online: https://www.ginkgo-analytics.com/an-overview-of-quantum-computing-frameworks/ (accessed on 17 January 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).