A New Method of Reducing the Inrush Current and Improving the Starting Performance of a Line-Start Permanent-Magnet Synchronous Motor

Abstract

This paper presents a new method of reducing the inrush current and improving the starting performance of a line-start permanent-magnet synchronous motor (LSPMSM). The novelty of the proposed method relies on the selection of the time instant of the connection of the stator winding to the grid, for which the smallest values of the amplitudes of inrush currents are obtained. To confirm the effectiveness of the developed method of limiting the inrush current, simulations and experimental studies were carried out. The algorithm and dedicated computer code developed by the authors for the analysis of transient coupled phenomena in the LSPMSM were used to study the impact of the time instant of connection of the winding to the grid on the motor start-up process. The algorithm was based on a field model of coupled electromagnetic and thermal phenomena in the studied motor. To verify the developed model of the phenomena and the proposed method, experimental research was carried out on a purpose-built computerised test stand. Good concordance between the results of the experiments and simulations confirmed the high reliability of the proposed model, as well as the effectiveness of the developed approach in limiting the inrush current and improving the starting performance of LSPMSMs.

1. Introduction

Modern permanent-magnet synchronous motors that are adapted for direct starting (LSPMSM) are characterised by a higher power density, higher power factor, and higher efficiency than those of induction machines of the same size [1,2]. For these reasons, LSPMSMs are increasingly used in constant-speed electric drives, particularly pump and fan drives in the mining [3,4] industry. The use of this type of motor instead of squirrel-cage induction motors leads to measurable economic and environmental benefits. An unquestionable advantage of the LSPMSM is the lack of a need for expensive power electronics that are necessary for the frequency start-up of other types of permanent-magnet synchronous motors [5,6].

A direct start of an LSPMSM is performed by connecting the motor stator windings directly to the power grid [3,7]. The disadvantage of LSPMSMs is their very large inrush currents [8,9]. Their values can exceed the rated current by many times. Similarly to asynchronous machines, the inrush currents of an LSPMSM increase together with the load torque and the moment of inertia of the rotating masses of the powertrain system. Large values of the inrush current lead to increased power losses in the windings and an increase in the temperature of the motor components [8]. Therefore, frequently repeated start-ups, especially at high-load moments of inertia, can lead to an excessive increase in the temperature of an LSPMSM’s components, especially the permanent magnets [8,10]. Unfortunately, as the temperature increases, the resistance of the machine’s excitation magnets to their partial irreversible demagnetisation under the influence of the magnetic field generated by the currents in the stator windings decreases [10,11,12]. It should be noted that the partial demagnetisation of magnets leads to irreversible deterioration of motor performance. The problem of the partial demagnetisation of magnets and the possibility of irreversible deterioration of the performance of LSPMSMs have been analysed in detail in [8,13,14], among others. Furthermore, large inrush currents and accompanying voltage drops in the power supply network can make it difficult to start a motor (and even to fail synchronization) and can cause interference with the operation of other electric consumers that are supplied by the same network [15].

For the reasons mentioned above, in order to reduce the negative impact of the inrush current on performance and motor operation, as well as on the behaviour of other mains-powered equipment, the authors attempted to develop a new method for limiting the inrush current in an LSPMSM. The concept of the method is described in Section 2. The structure of an LSPMSM’s magnetic circuit, as well as the problems of self-starting and rotor synchronization, are discussed first to better explain the essence of the problem being solved and justify the advisability of undertaking this research. On the basis of the literature research that was carried out, it is indicated how the improvement of the motor’s starting parameters and the limitation of the starting current were sought.

The results of the computational experiments carried out to confirm the effectiveness of the developed inrush-current-limiting method are presented and discussed in Section 3. The calculations were carried out using an algorithm and computer code developed by the authors to analyse the coupled electromagnetic and thermal phenomena in an LSPMSM. In the next section, the results of the experiments on a dedicated test bench confirming the results of the calculations are presented. The conclusions resulting from the conducted research are given in Section 5.

2. Issues of the LSPMSM Start-Up Process

In order to achieve the starting capabilities of an LSPMSM, a cage winding is placed in its rotor. In the rotor core, in addition to the squirrel-cage winding, there are also permanent magnets arranged within the pole pitch, usually in V, U, or W shapes [16,17,18]. Direct starting involves connecting the stator windings directly to the power grid. During this process, inrush currents with an amplitude many times greater than the amplitude of the rated current can occur in the stator windings, as in squirrel-cage asynchronous machines. When the voltage source (grid) is connected to the winding, the asynchronous torque produced by the cage winding accelerates the rotor to a speed close to the rotational speed of the stator field, and then the synchronous torque pulls the rotor to fall into synchronism [3,19,20]. Synchronisation of the rotor occurs under the action of the so-called pull-in torque. This torque has a source in the magnetic interaction between the stator currents and the field excited by the permanent magnets placed in the rotor. The value of the pull-in torque is determined by the winding currents, permanent magnet flux, and relative position stator and rotor field axes. Therefore, the pull-in torque will pulsate with a frequency corresponding to the slip between the rotor speed and synchronous speed and will have a close-to-constant value at the synchronous speed of the rotor.

When starting an LSPMSM, in addition to the asynchronous torque driving the rotor and the pull-in torque, braking torque is also generated. Its sources are the currents in the stator winding induced by the magnetic field created by the permanent magnets rotating with the rotor [19,21,22]. It should be noted that the value of the braking torque decreases when the rotor speed increases. Nevertheless, too high of a value of the braking torque at the beginning of the motor start-up process can lead to failed synchronization. Therefore, in order to avoid unsuccessful synchronisation, it is necessary to design the motor so that over the entire range of rotor speed variations during the start-up process, a sufficiently large excess of the resultant starting torque over the load torque is ensured [23]. The desired course and value of the asynchronous, pull-in, and braking torques are obtained through the appropriate selection of the geometry and material of the magnetic circuit, including, among other things, the material of the permanent magnets, the shape and dimensions of the rotor slots, and the resistivity of the cage winding [3,4,19,23,24]. Obtaining good starting characteristics for an LSPMSM is very complicated because the known design methods of improving one of the figures of merit usually lead to the deterioration of the others.

For example, in [24], in order to increase the value of the starting torque and decrease the inrush current at the initial stage of the starting process, an increase in the resistance of the cage winding bars was proposed. Unfortunately, increasing the resistance of the winding decreased the asynchronous torque at rotor speeds close to the synchronous speed, leading to a deterioration of the motor’s synchronisation properties [3]. On the other hand, in [23], the desired shape of the starting torque characteristics was pursued by changing the shape of the cage winding, and in [1,25], in order to increase the starting torque and the pull-in torque, the use of a double-cage winding in the rotor was proposed. It was found that by appropriately selecting both the shape and position of the bars of the double-cage winding, it was possible to obtain a sufficiently large value of the asynchronous torque over the entire range of speed changes during start-up. The disadvantage of this solution was that the space in the rotor for permanent magnets was significantly reduced, leading to deterioration of the motor performance at synchronous speed. The effects of both the shape and dimensions of permanent magnets on the starting and rated parameters of the motors were studied in [17]. It was found, among other things, that increasing the flux of permanent magnets and, thus, improving the rated parameters led to a deterioration of the motor starting performance by, among other things, increasing the braking torque [3].

An effective way to minimise the influence of the braking torque on the starting process and to improve the synchronisation properties of a motor is to use a pole-change winding that is known from asynchronous machines in the stator [3,13,16]. The motor start-up is carried out with a smaller number of poles, and after obtaining a speed slightly above the rated speed (corresponding to a higher number of poles) of the motor, the winding is switched to a larger number of poles—for example, from 2 to 4. Synchronisation takes place from “above”, that is, when the rotor speed is higher than the synchronous speed. The results of research on the effect of the rotor speed at which the windings are reconnected on the starting process were presented in [13]. The drawback of the discussed approach was the large number of coil group leads from the machine and the complex switching equipment required to reconnect the structure of the phase windings under load. In consequence, the cost of the drive system was increased while its reliability was decreased.

Summarising the above considerations, it can be said that when designing LSPMSMs, the steady-state performance (efficiency, power factor, and synchronous torque) must be met together with the requirements regarding the start-up process (starting torque, pull-in torque, and braking torque) [1,2,3,15,16,26] while ensuring that the magnets are resistant to partial demagnetisation. This is because, as mentioned in the introduction, the magnets’ resistance to demagnetisation decreases with increasing starting current and magnet temperature.

It should be highlighted that, in the studies discussed above, no attempts were made to minimise the inrush current as a compromise solution. The inrush current obtained in the design calculations was treated as the resultant quantity for which the desired starting and rated parameters of the motor were obtained [19,21]. It should be noted that the method of reducing the inrush current by reducing the supply voltage is not suitable for LSPMSMs. This is because lowering the voltage causes a decrease in the asynchronous starting torque, which can lead to stalling of the motor due to the braking torque generated during starting.

Some studies, such as [26], presented the concept of minimising the inrush current by decreasing the main magnetic flux at motor start-up and then increasing it in steady-state operation. To change the main magnetic flux, a special arrangement was proposed to move the magnets in the rotor in the radial direction. Despite the promising results, it seems that the practical implementation of this idea can be difficult and expensive.

An additional strong motivation for conducting research on limiting the inrush current stems from the fact that minimising the inrush current leads to a reduction in the electrical power drawn from the grid during the start-up process, which decreases power losses in the windings and reduces the increase in the temperature of machine components. This, in turn, leads to a reduction in the risk of the partial demagnetisation of magnets. In addition, by limiting the inrush current and the associated voltage drops in the power grid, motor starting is less likely to interfere with the operation of other electrical equipment powered from the same grid.

For the above reasons, the authors proposed a different approach to the problem of inrush current limitation. The study assumes that commercially available LSPMSMs meet compromise requirements for the starting and rated parameters, and the developed method is intended to enable the minimisation of the starting current for already manufactured motors.

The proposed method of limiting the inrush current is based on the well-known fact that the current waveform and amplitude after switching on at time t = 0 of the voltage u = U_msin(ωt + α_ph) with respect to the real inductor depend on the resistance R, inductance L of the circuit, and the phase angle α_ph, where U_m and ω are the maximum value and the voltage pulsation, respectively. Minimising the inrush current by finding the optimal value of α_ph for a simple RL circuit describing a real inductor when R, L, and ω are known is a trivial task. The question is if the optimal value of α_ph can be determined for a complex three-phase system, such as the winding of an LSPMSM. The transient state accompanying the connection of the three-phase motor winding to the power grid is similar in terms of phenomena, except that different amplitudes and different shapes of the current waveforms in the individual phase windings are obtained due to the phase shifts between supply voltages (resulting in different values of the phase voltages at t = 0). Another major difference from a simple RL circuit is the fact that, once the rotor starts moving, the current waveforms are also affected by the voltages in the phase windings induced by the flux generated by the rotating permanent magnets. In a symmetrical machine, after the steady-state starting process, the phase currents have the same amplitude, and their waveforms are shifted by 120°.

Considering the impact of α_ph on the amplitude and current waveform in each phase and taking into account the electromechanical phenomena in LSPMSMs, the following question arises: Is it possible to determine such an angle α_ph for which the lowest possible inrush current is obtained for a given load moment and inertia of the rotating masses of the powertrain system?

To answer this question and verify the effectiveness of the proposed method of limiting the inrush current based on selecting the optimal value of angle α_ph, a detailed simulation study of the LSPMSM start-up process was carried out. The authors’ software was used for this purpose, and the scope of the study and the obtained calculation results are presented in Section 3.

3. FEA of the LSPMSM Start-Up Process

In this study, the authors used an algorithm and computer code that they developed for the analysis of coupled phenomena in an LSPMSM to study the influence of the angle α_ph on the start-up process [8,24]. The algorithm was based on a two-dimensional field model of coupled electromagnetic and thermal phenomena in a motor. The algorithm and computer code have already been presented in detail in other works, such as in [8,19]. Therefore, this article is limited only to the characterisation of their main features and capabilities. The model of phenomena included equations describing the distribution of the magnetic field and thermal fields, the voltage equations of the electrical circuits of the stator and rotor, and the equations of the dynamics of the moving elements of the drive system. It took the nonlinearity of the magnetic circuit, the effect of temperature on the resistivity of current-carrying materials, the magnetic flux produced by permanent magnets, and the process of partial demagnetisation of permanent magnets into account [19]. The algorithm and code for the analysis of transient coupled phenomena used the finite element method in conjunction with the time discretization technique to solve the discrete model equations. Both the algorithm and code were experimentally verified, and the comparison of the computational and experimental results confirmed the high reliability of the representation of the phenomena occurring in an LSPMSM [8].

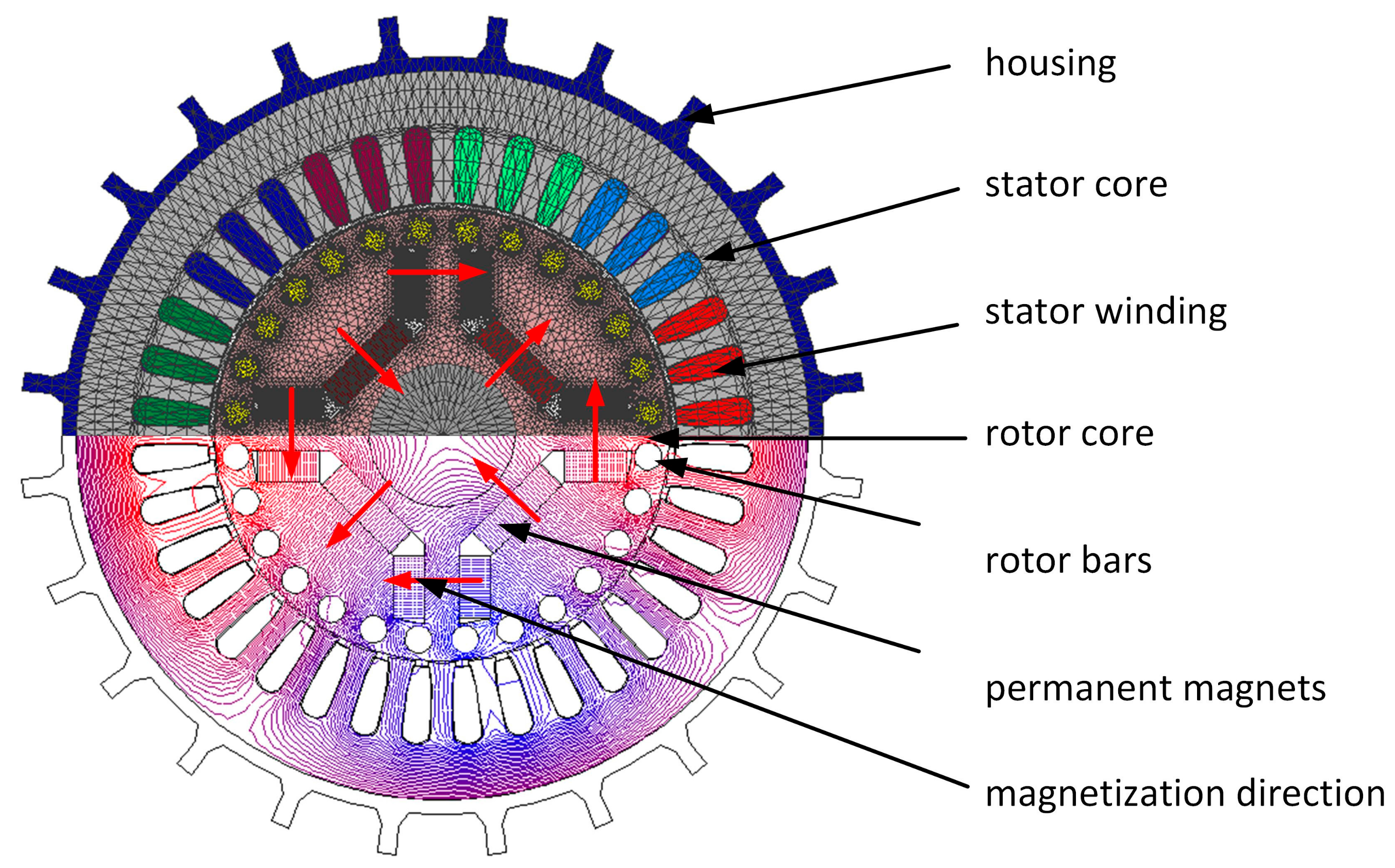
The starting process of an LSPMSM with the rated parameters shown in

Table 1. Rated parameters of the studied LSPMSM.

UN [V]	IN [A]	PN [kW]	fN [Hz]	nN [rpm]	ηN [-]	cosφN [-]
400	6.9	3.8	50	1500	0.89	0.94

was studied. The structure of the motor is shown in Figure 1. It was assumed that the stator phase windings were connected in a star arrangement.

It was assumed that the considered LSPMSM was powered by a three-phase symmetrical voltage system described by the following equations.

$$u_a={\sqrt{2}U}_{N}sin\left(\omega t+{\alpha }_{ph}\right)$$

(1a)

$$u_b={\sqrt{2}U}_{N}sin\left(\omega t+\frac{2}{3}\pi +{\alpha }_{ph}\right)$$

(1b)

$$u_c={\sqrt{2}U}_{N}sin\left(\omega t+\frac{4}{3}\pi +{\alpha }_{ph}\right)$$

(1c)

where u_a, u_b, and u_c are line-to-line supply voltages, ω = 2πf is the pulsation, $U$_N is the rated voltage of the motor, and f is the supply voltage frequency.

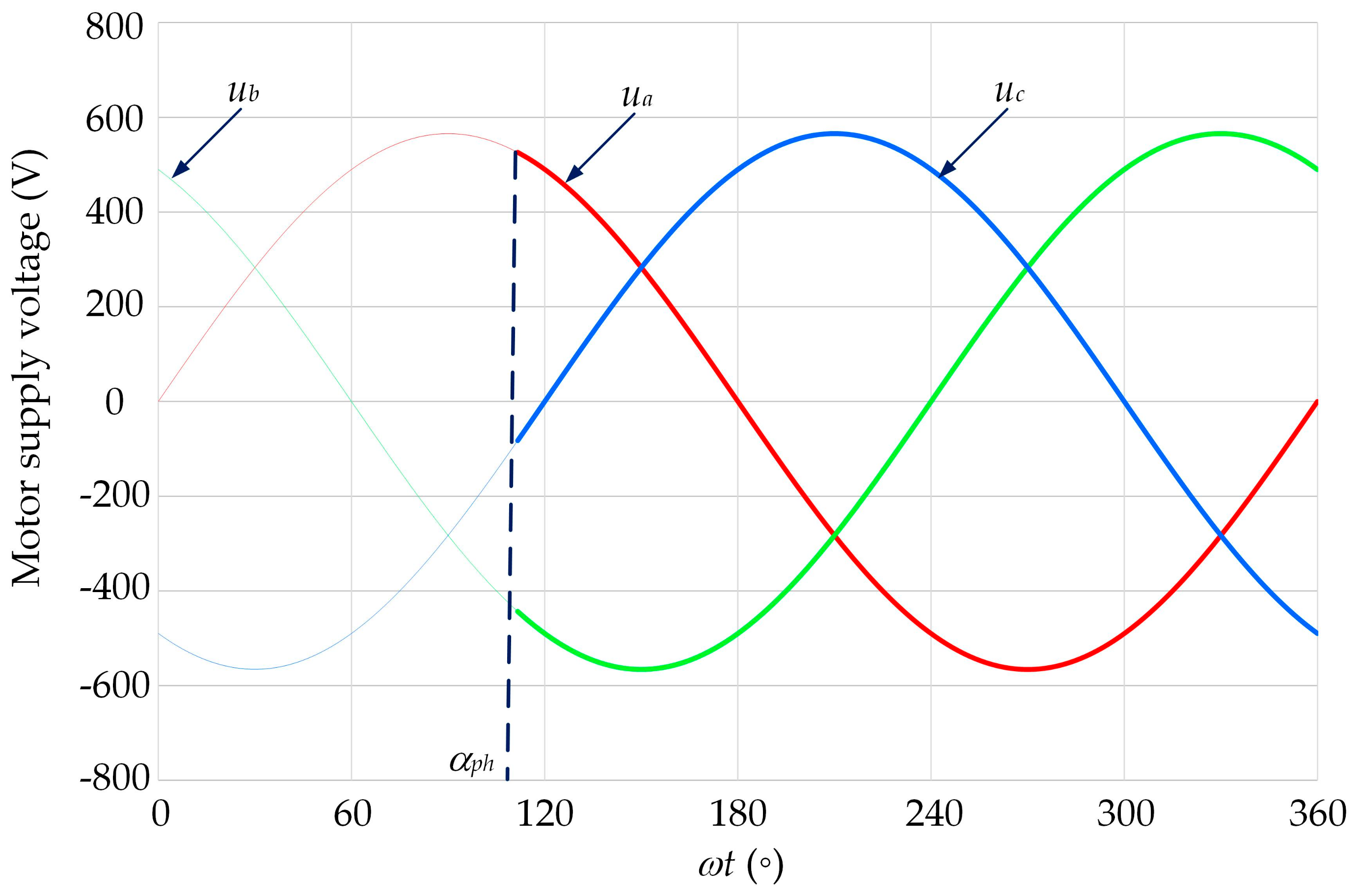
The waveforms of the line voltages are illustrated in Figure 2. It was assumed that the switching on of the voltage to the motor winding occurred at time t = 0. Thus, the points of intersection of the vertical dashed line with the voltage waveforms determined the values of the supply voltages at the time of switching on the motor (Figure 2).

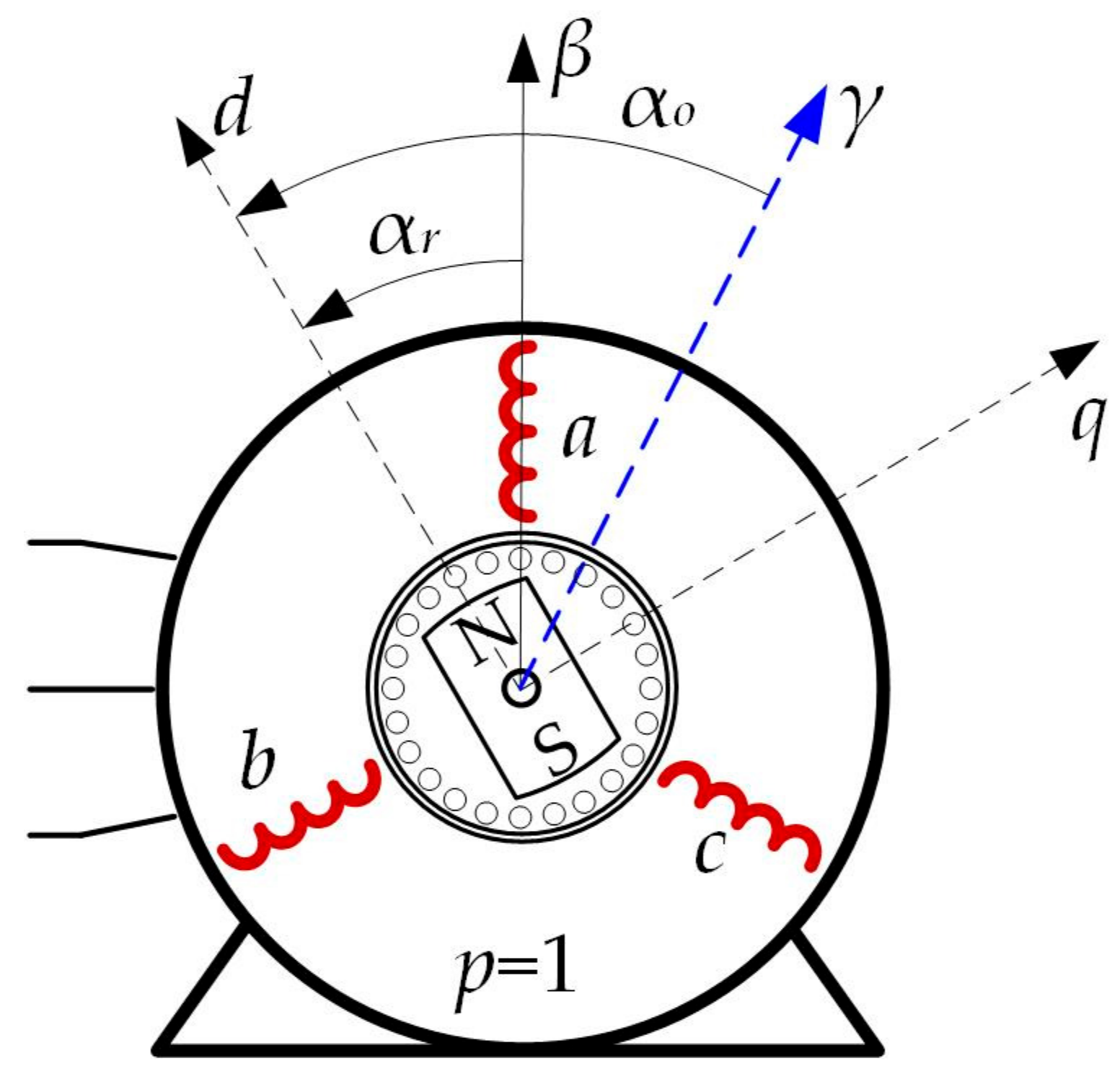
Simulation studies of the effects of the phase angle α_ph on the start-up process and the amplitude of the starting current were carried out in stages. First, a polar coordinate system was adopted in the motor with the reference axis β coinciding with the axis of the phase winding a. The introduced designations are illustrated in Figure 3, with the number p of pairs of poles in the machine being assumed to be equal to 1 for simplicity in the figure. In the tests, in order to easily compare the results, it was assumed that before the calculations, the rotor was set in such an angular position that the magnetic d-axis of the rotor coincided with the reference β-axis. The desired settings of the magnetic d-axis of the rotor on the β-axis were obtained by implementing the rotor positioning procedure. This procedure involved the stator winding producing a magnetic field distribution whose axis coincided with the reference direction β. This field distribution was obtained when the stator windings were supplied with a DC current with values derived from a symmetric three-phase current system for the time instant at which the current in phase a had its maximum value, i.e., for ωt = π/2.

$$I_a={\sqrt{2}I}_{N}sin\left(\omega t\right)$$

(2a)

$$I_b={\sqrt{2}I}_{N}sin\left(\omega t+\frac{2}{3}\pi \right)$$

(2b)

$$I_c=\sqrt{2}{I}_{N}sin\left(\omega t+\frac{4}{3}\pi \right)$$

(2c)

where I_a, I_b, and I_c are currents in phases a, b, and c, respectively, and I_N is the rated current of the motor.

When the stator windings were supplied with the currents resulting from Equations (2a)–(2c), electromagnetic torque was created in the motor. It caused the rotor to rotate to a position for which the rotor’s magnetic axis d coincided with the phase winding axis a, i.e., the rotor rotated to a position for which the angle α_r = 0 (Figure 3).

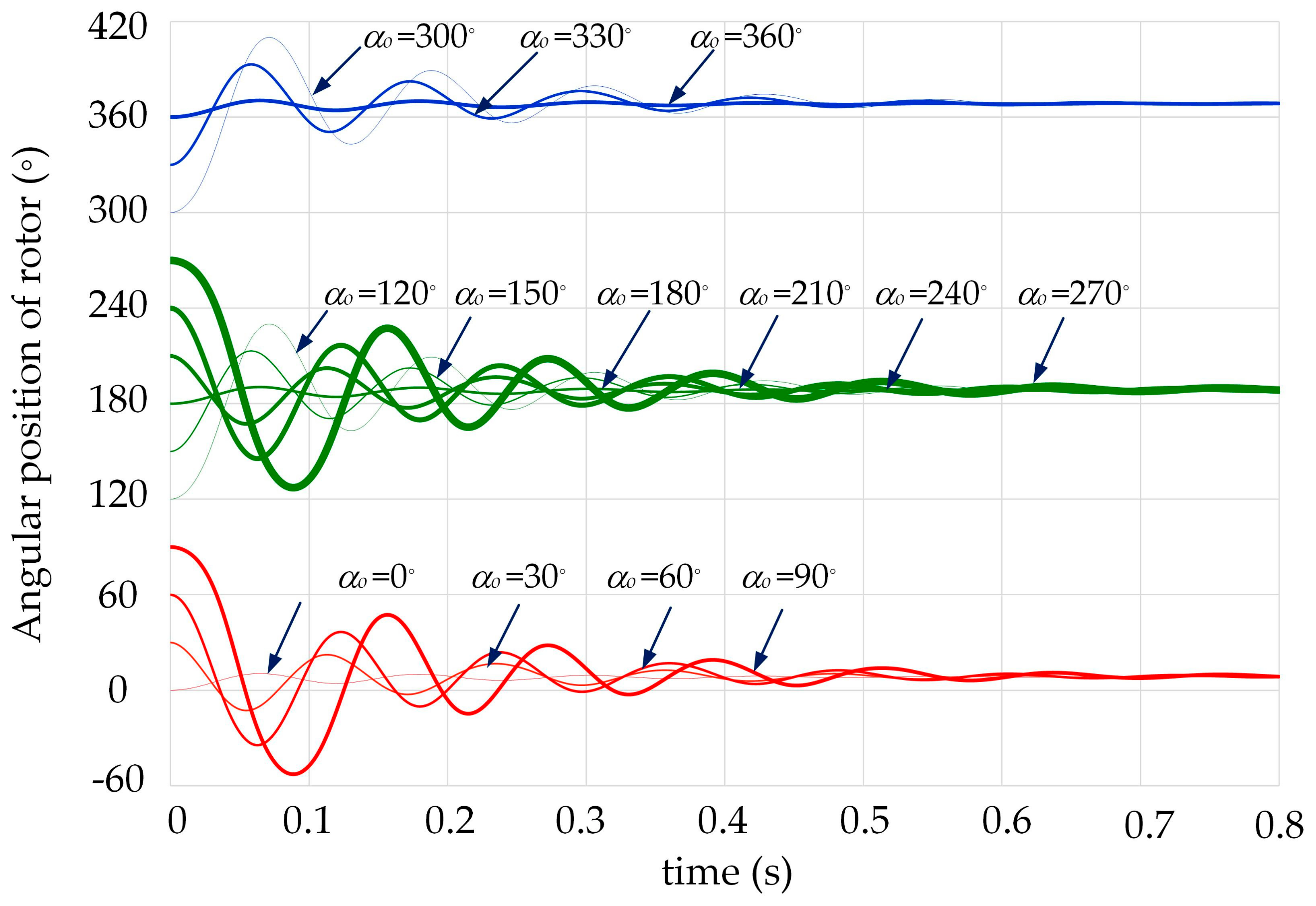
The rotor positioning procedure was implemented under the assumption that the motor load torque was equal to zero. To verify the correctness of the operation of the rotor positioning procedure, the calculations assumed different initial rotor positions α_o with a step of 30°, with the angle α_o being calculated from an arbitrary reference direction, which is denoted by γ in Figure 3. The resulting waveforms of the angular position of the rotor are shown in Figure 4. The initial values of the angle α_o were on the axis of ordinates for time t = 0. From the obtained waveforms, it can be seen that when the motor windings were supplied with DC voltage, the angular position of the rotor changed from the initial position α_o to the final position, for which the rotor field d-axis coincided with the β-axis. At the same time, the oscillations in the rotor’s angular position waveforms disappeared after a time of about 0.8 s. Given that the number of pole pairs in the motor was p = 2, a twice-repeated distribution of the magnetic field along the circumference of the stator could be distinguished in the machine, and thus, two β-axes were angularly displaced from each other by an angle of 360°/p = 180°. Therefore, in Figure 4, two rotor positions for which the rotor d-axis coincided with the β-axis can be distinguished. For the initial positions α_o of the rotor that were greater than 270°, the fixed angular positions of the rotor after supplying the windings with DC current took values greater than 360°. The final position of the rotor obtained for these conditions due to the full rotation of the rotor coincided with the angular position of the rotor obtained for angles α_o that were smaller than 120°. Further, it was assumed that the angular position of the rotor for which the d-axis coincided with the β-axis was α_o = 8.21°.

After aligning the d-axis of the rotor with the reference β-axis, we proceeded to analyse the effects of the value of the angle α_ph on the course of the starting process and the amplitude of the starting current. Since it followed from the considerations presented in Section 1 that LSPMSMs are most often used to drive pumps and fans, it was assumed that the motor was loaded with a fan with mechanical characteristics described by the relation

$$T_L=sign\left(n\right)0.6e^{0.002318\left|n\right|}$$

(3)

where T_L is the load torque and n is the rotational speed of the rotor. The mechanical characteristics of the fan are shown in Figure 5. At the rated rotational speed n_N of the rotor, the load torque was T_L(n_N) = 19.4 Nm. The total moment of inertia of the rotating masses in the drive system consisting of the motor and the fan was assumed to be J = 0.0083 kg·m².

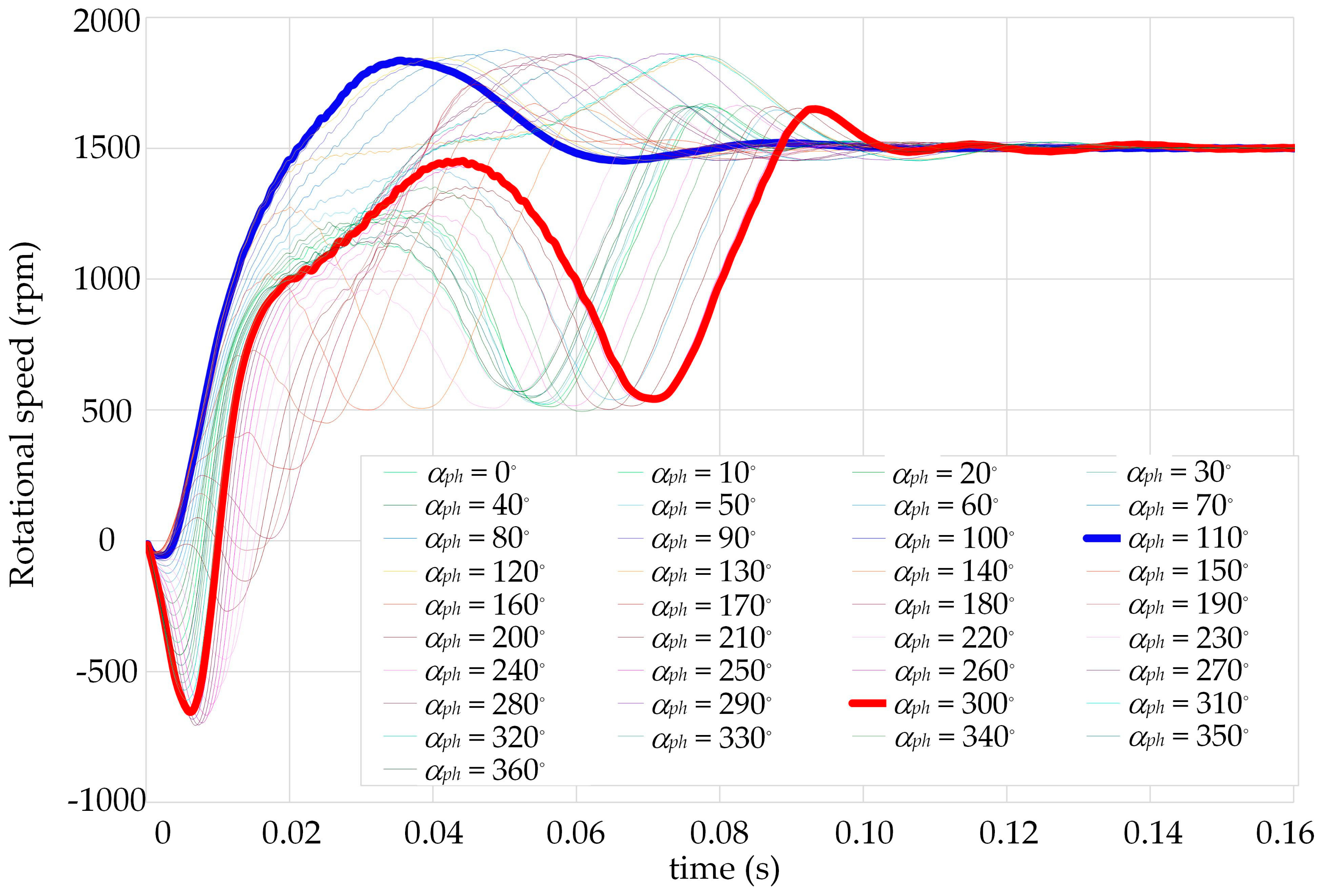
Furthermore, it was assumed that the motor was connected at time t = 0 to a three-phase grid with a voltage described by Equations (1a)–(1c), with U_N = 400 V and f = 50 Hz. The calculations of the starting process were repeated for the phase angle α_ph while varying every 10° in the range from 0° to 360°. The velocity waveforms obtained as a result of the calculations are shown in Figure 6. For all analysed angles α_ph, the start-ups proceeded correctly, i.e., the rotor fell into synchronism. It can be seen in the figure that the angle α_ph had a strong influence on the speed waveform during the start-up.

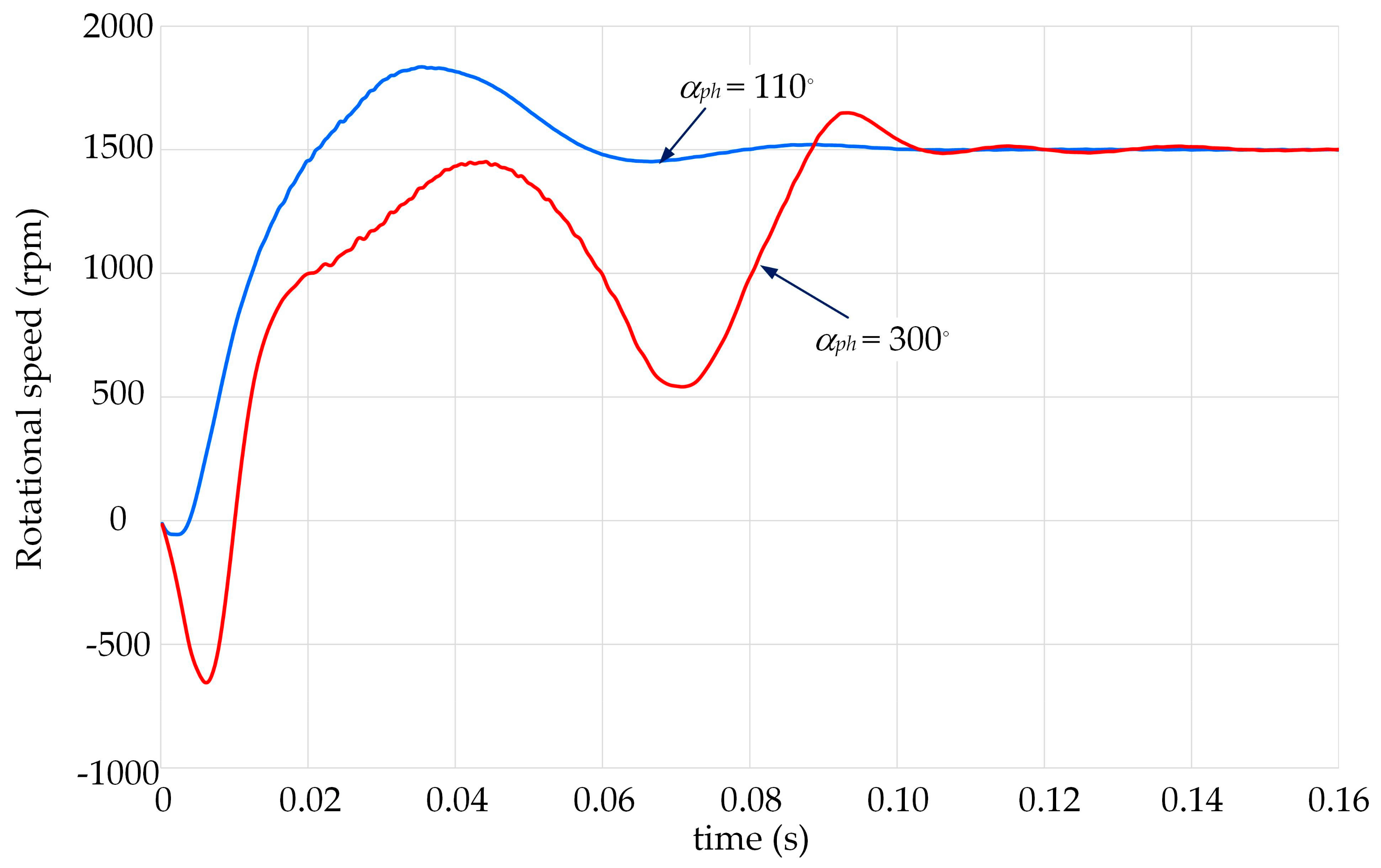
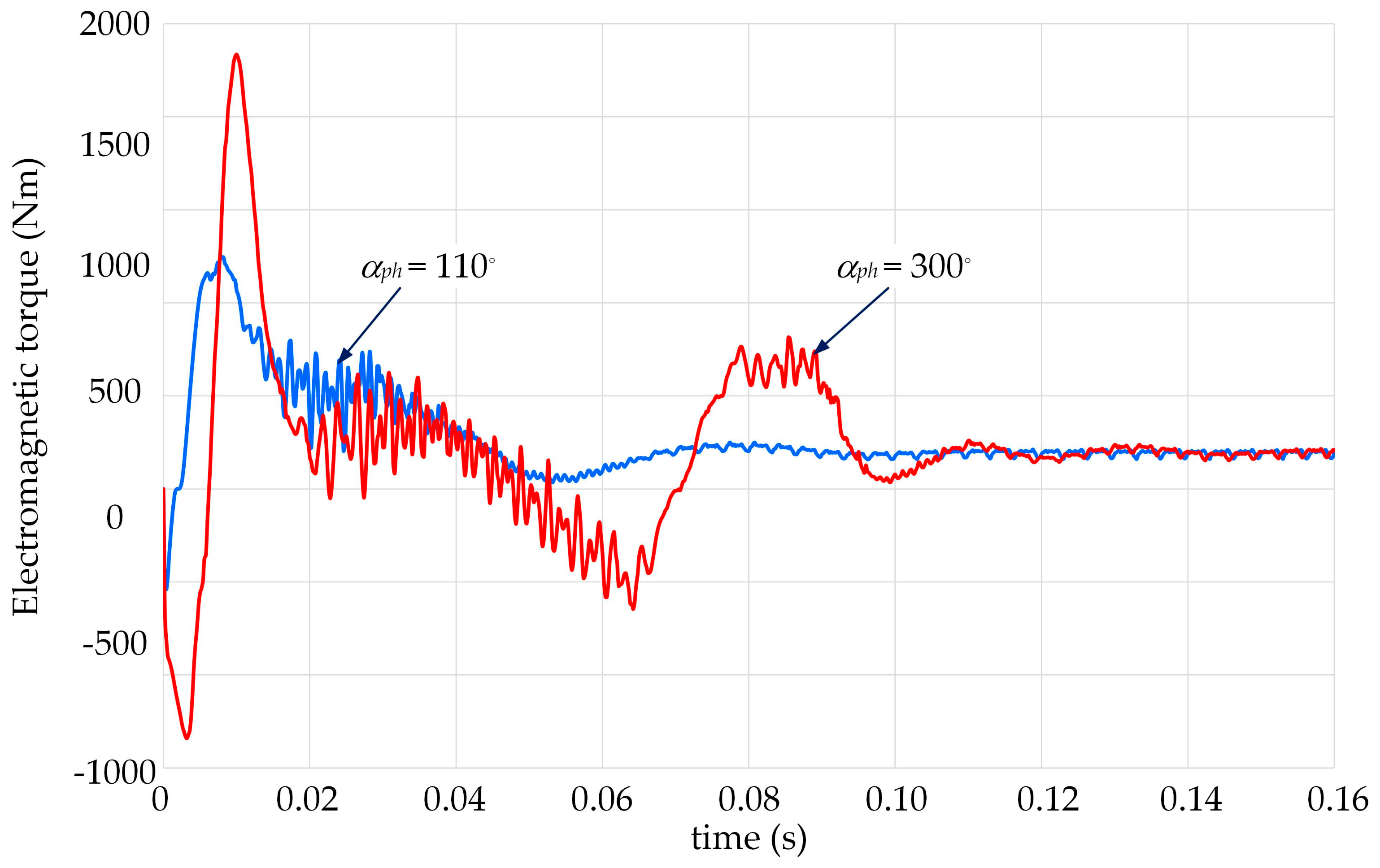
The bold lines in Figure 6 highlight the rotor speed waveforms obtained for angles α_ph equal to 110° and 300°, for which, respectively, the rotor fell into synchronism the fastest, and the start-up took the longest. The speed waveforms extracted from Figure 6 for angles of 110° and 300° are summarised in Figure 7, while the corresponding velocity waveforms of the electromagnetic torque and electrical power drawn from the grid, respectively, are shown in Figure 8 and Figure 9. From the comparison of the electromagnetic torque waveforms, it can be seen that for α_ph = 110°, except for the initial start-up phase, the electromagnetic torque was positive, and its waveform was established faster. Moreover, its amplitude was almost twice as small as the maximum torque value obtained for α_ph = 300°. The instantaneous values of the electromagnetic torque were up to approximately 9.7 times higher than the rated torque of the motor. The pulsations visible in the torque waveforms were caused by the slots located in the stator and rotor cores.

It can be noted in Figure 9 that the instantaneous power drawn from the grid at start-up could reach values as high as 8.7 times the rated power of the motor. At the same time, during start-up, the power consumed by the motor for α_ph = 300°, except in three narrow time intervals, was greater than the power consumed for the switching angle α_ph = 110°.

In order to compare the energy intensity of the analysed starts, the total electrical energy consumed by the motor from the grid over 0.16 s was calculated. It amounted to 1508.4 Ws and 1004.6 Ws for angles of 300° and 110°, respectively. The ratio of these energies was about 1.5. Figure 10 summarises the energy loss waveforms in the stator and rotor windings and in the core during start-up. The total loss energy at 0.16 s for angles of 300° and 110° was 986.64 Ws and 302.37 Ws, respectively. Thus, the selection of the voltage switching angle had a great impact on the energy consumption from the grid, on the energy losses during start-up, and, therefore, on the cost of motor operation. In the analysed operating states, the energy–loss ratio was about 3.26.

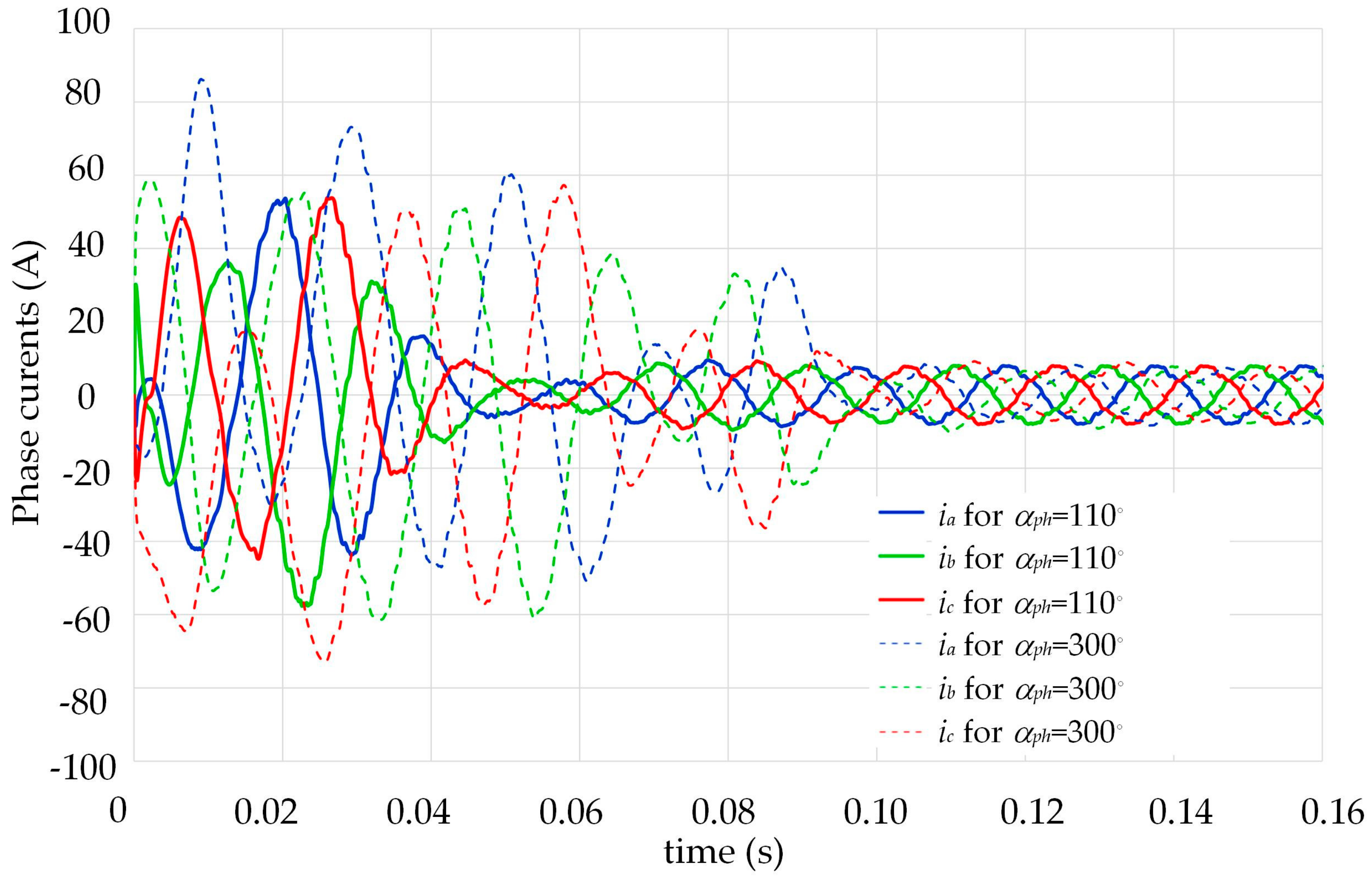
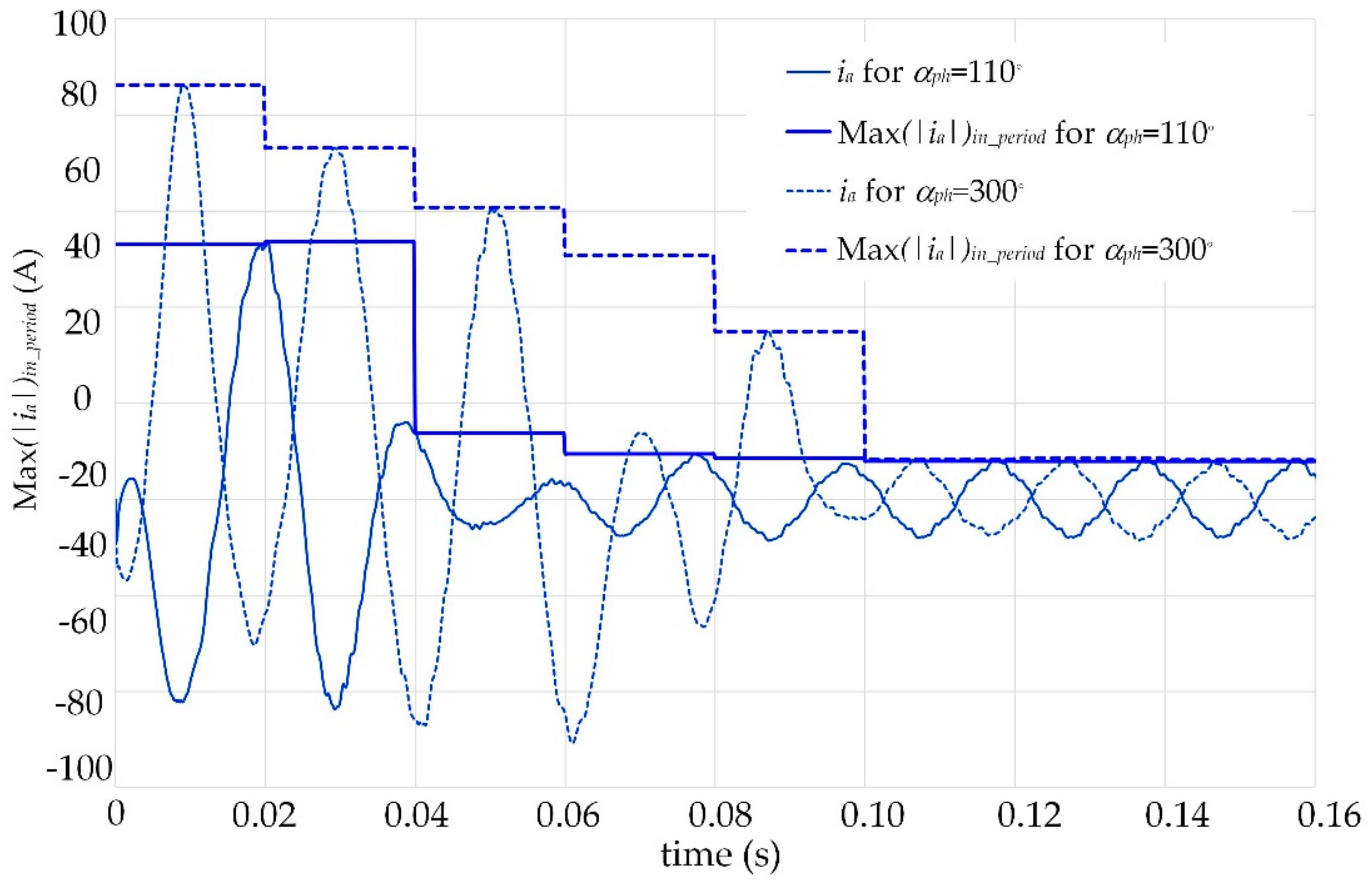
The waveforms obtained during motor start-up are shown in Figure 11. From the comparison of the waveforms, it can be seen that for the start-up carried out for the angle α_ph = 110°, they stabilised after a time of about 0.1 s, and for the angle α_ph = 300°, they stabilised after a time of approximately 0.14 s. In addition, for the angle α_ph = 300°, larger current amplitudes were observed. As discussed in the introduction, due to the higher current values and longer start-up time, the power losses in the motor’s windings increased, which led to an increase in the temperature of the motor components, including the permanent magnets. As a result, the risk of partial irreversible demagnetisation of the permanent magnets increased. In addition, due to increases in voltage drops in the power grid, large inrush currents can more strongly affect/disturb other equipment supplied by the same power grid. To facilitate the comparison of current amplitudes in individual phase windings during motor start-up, a parameter was introduced to determine the value of the maximum current in successive periods of the supply voltage. For example, for phase a and current i_a, this parameter is expressed by Max(|i_a|)_{in_period}, and it takes a value equal to the maximum value of the current in subsequent periods of the supply voltage. 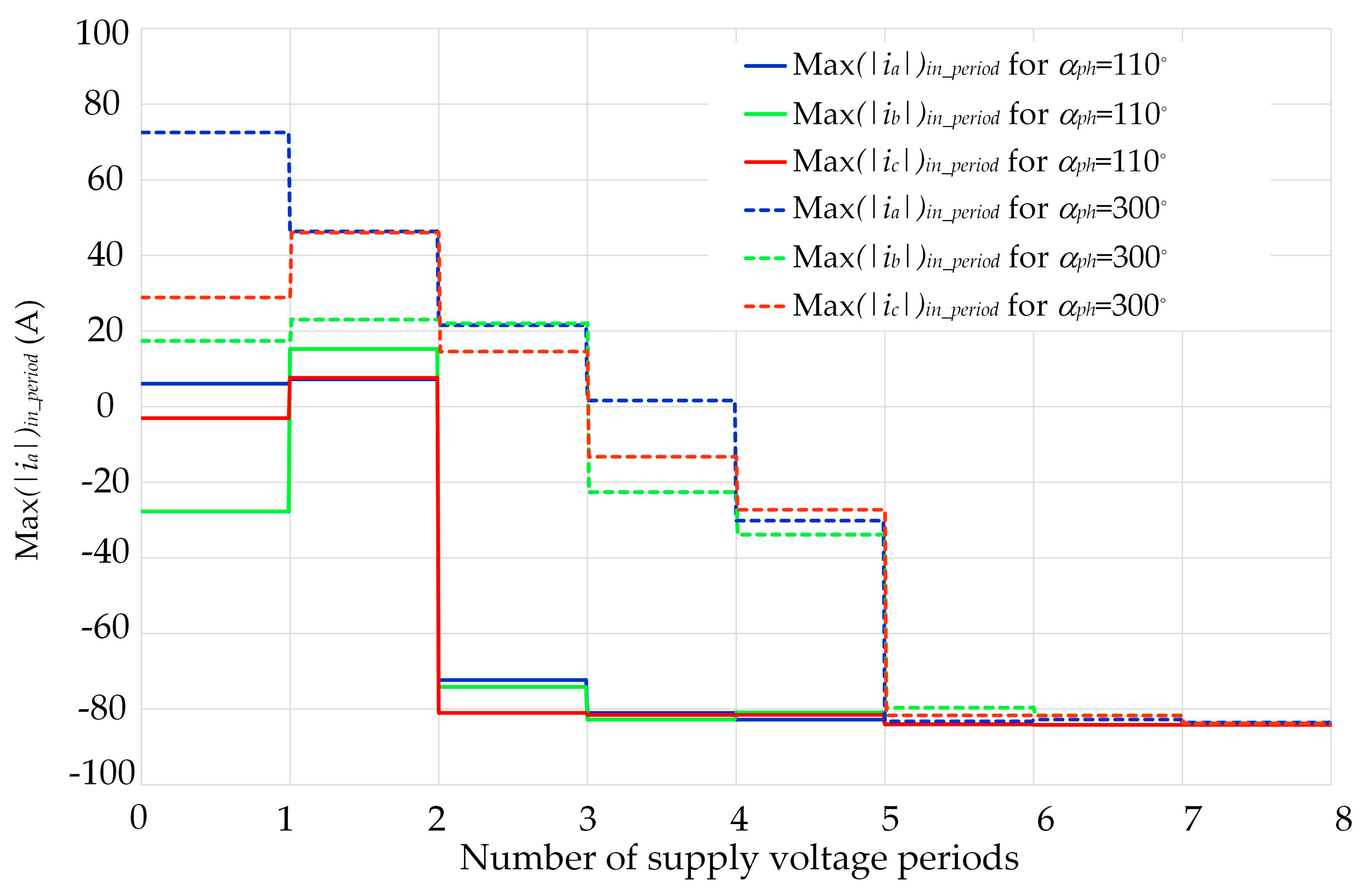Example waveforms of this parameter for current i_a determined during the start-ups conducted for angles equal to 300° and 110° are shown in Figure 12. A comparison of the maximum currents in all phases depending on the number of consecutive periods of the supply voltage is provided in Figure 13.

The obtained waveforms confirmed that the maximum current values at successive periods of the supply voltage strongly depended on the angle of voltage switching. The ratio of the maximum values of phase currents at start-up made for α_ph angles of 300° and 110° was about 1.5. Moreover, the current waveforms for α_ph = 110° were established after five periods of supply voltage, and for the α_ph = 300° angle, they were established only after seven periods. Thus, the start-up time was able to be reduced by about 28%.

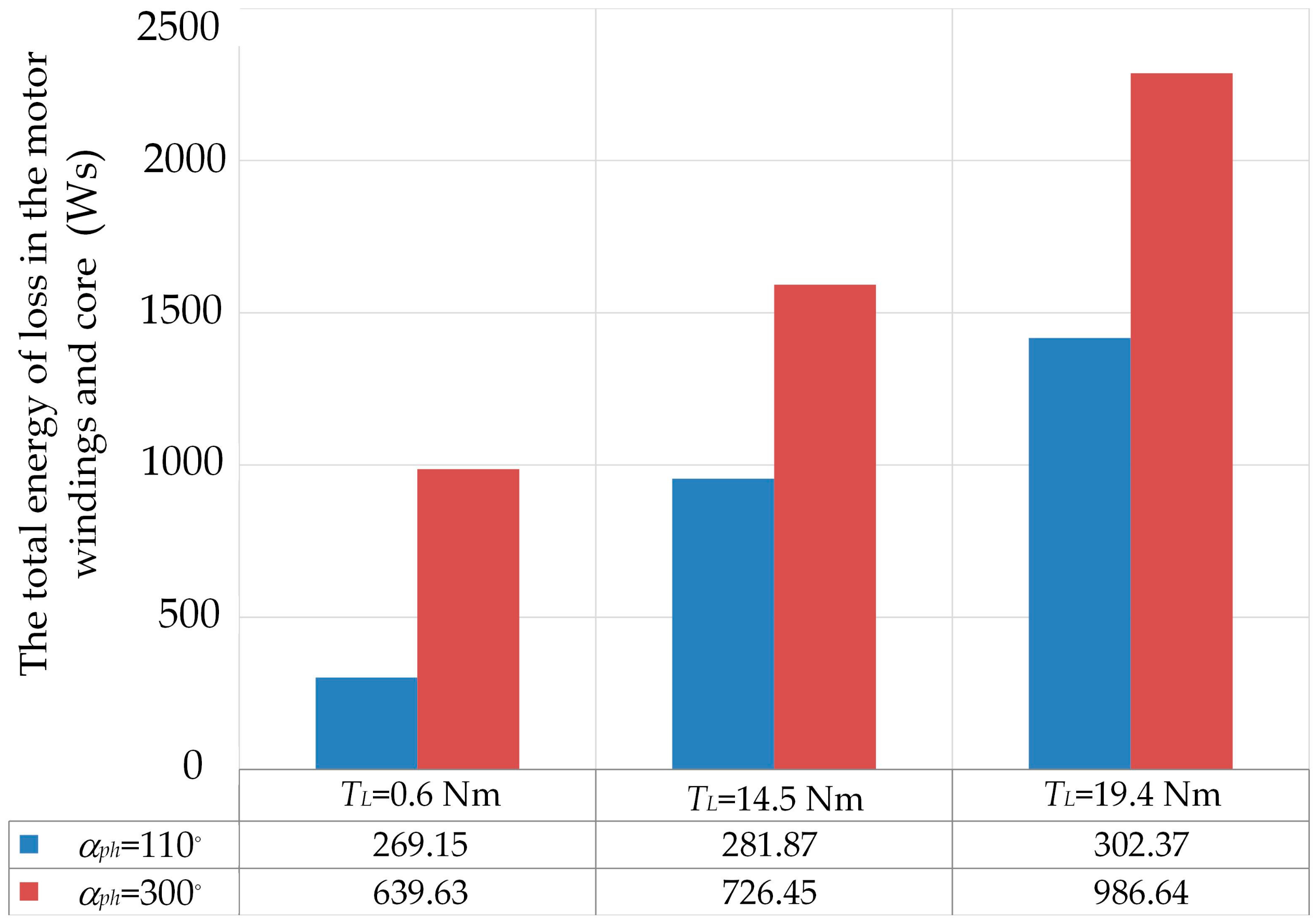
In further studies, in order to determine the effect of the load torque while maintaining the moment of inertia J = 0.0083 kg·m² on the energy losses during start-up, we analysed the start-up of the motor: (a) at an idle load torque of T_L = 0.6 Nm, (b) loaded with a fan with mechanical characteristics described by the relation T_L = sign(n)0.6e^0.002123|n|, and (c) loaded with a fan with mechanical characteristics resulting from relation (3). In the case of (b), the load torque at the rated motor speed was 15.4 Nm, while in the case of (c), it was 19.4 Nm. The calculated total energies during the motor start-up process are compared in Figure 14. It should be noted that energy was given off in the form of the integration of power losses in the stator and rotor windings, as well as in the core of the machine. When the motor was loaded with a torque of 19.4 Nm, the total energy losses during the start-up of the motor for an angle of α_ph = 300° were approximately 3.26 times higher than the energy losses for an angle of α_p = 110°. On the other hand, the effect of the load torque change on the energy losses at an angle of α_ph = 110° was small and did not exceed 12.3%.

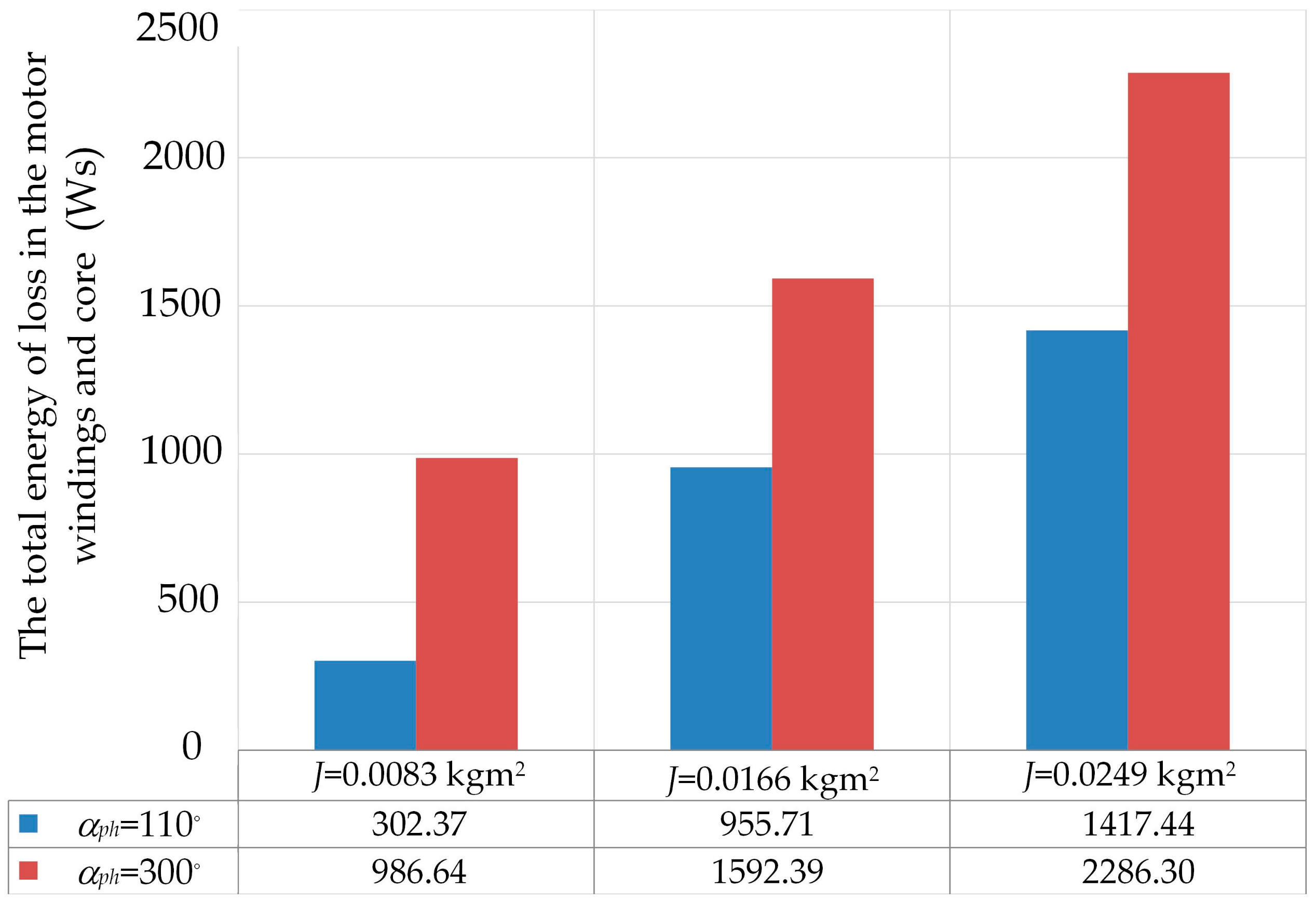
Next, similar studies were performed to evaluate the impact of the moment of inertia on energy losses during the motor start-up process. The effect of the moment of inertia of the rotating masses J on the total energy of losses in the winding and core during the start-up of a motor loaded with a fan that had mechanical characteristics described by relation (3) is shown in Figure 15.

A comparison of the loss energy confirmed that the moment of inertia had a significant effect on the motor losses during the start-up. An increase in the moment of inertia made it more difficult to start the motor and resulted in an increase in the current amplitude and a longer starting time. Nevertheless, finding the proper time instant for switching on the motor still led to a significant reduction in losses during the start-up process.

4. Experimental Studies of the LSPMSM Start-Up Process

The purpose of this study was to confirm the findings reported in Section 3 regarding the effect of the angle α_ph on the waveform and amplitude of the inrush current of an LSPMSM. A prototype motor with the parameters summarised in Table 1 was used for this research. Due to the lack of a fan with the parameters described in Equation (3), the experimental studies were carried out for a motor loaded with a magnetorheological brake [27,28,29], which produced a load torque of 19.4 Nm. The developed computerised test stand is shown in Figure 16.

The test bed consisted of (1) the LSPMSM prototype being tested, (2) an MT100-type torque transducer, (3) a water-cooled magnetorheological fluid (MRF) brake, (4) an electronic contactor, and (5) a measurement system equipped with data acquisition cards and a dedicated Virtual Instrument developed in the National Instrument LabVIEW environment. The electronic contactor (4) is switched by a control signal generated by a microprocessor-based control system that was developed (6). The control system measured the line-to-line grid voltage u_a and determined the time t_o at which the voltage crossed zero (on the positive slope). The control system allowed one to specify the delay Δt of the signal switching on the electronic contactor counting from time t_o. For the constant frequency of the grid, the delay time Δt corresponded to the switching angle α_ph = ωΔt. Before each test of the motor start-up process, the rotor positioning procedure described in Section 3 was performed. A series of measurements for different values of the delay parameter Δt with a step corresponding to 10° for α_ph were performed, and the results were studied in order to evaluate the impact on the motor start-up process. Focussing only on the evaluation of the start-up time, two values of the delay parameter Δt corresponding to the shortest and longest start-up times of the motor were selected for further studies. The load characteristics of the motor in its numerical model were adopted to represent the inertia and load torque of the MRF, and simulations of the start-up were carried out.

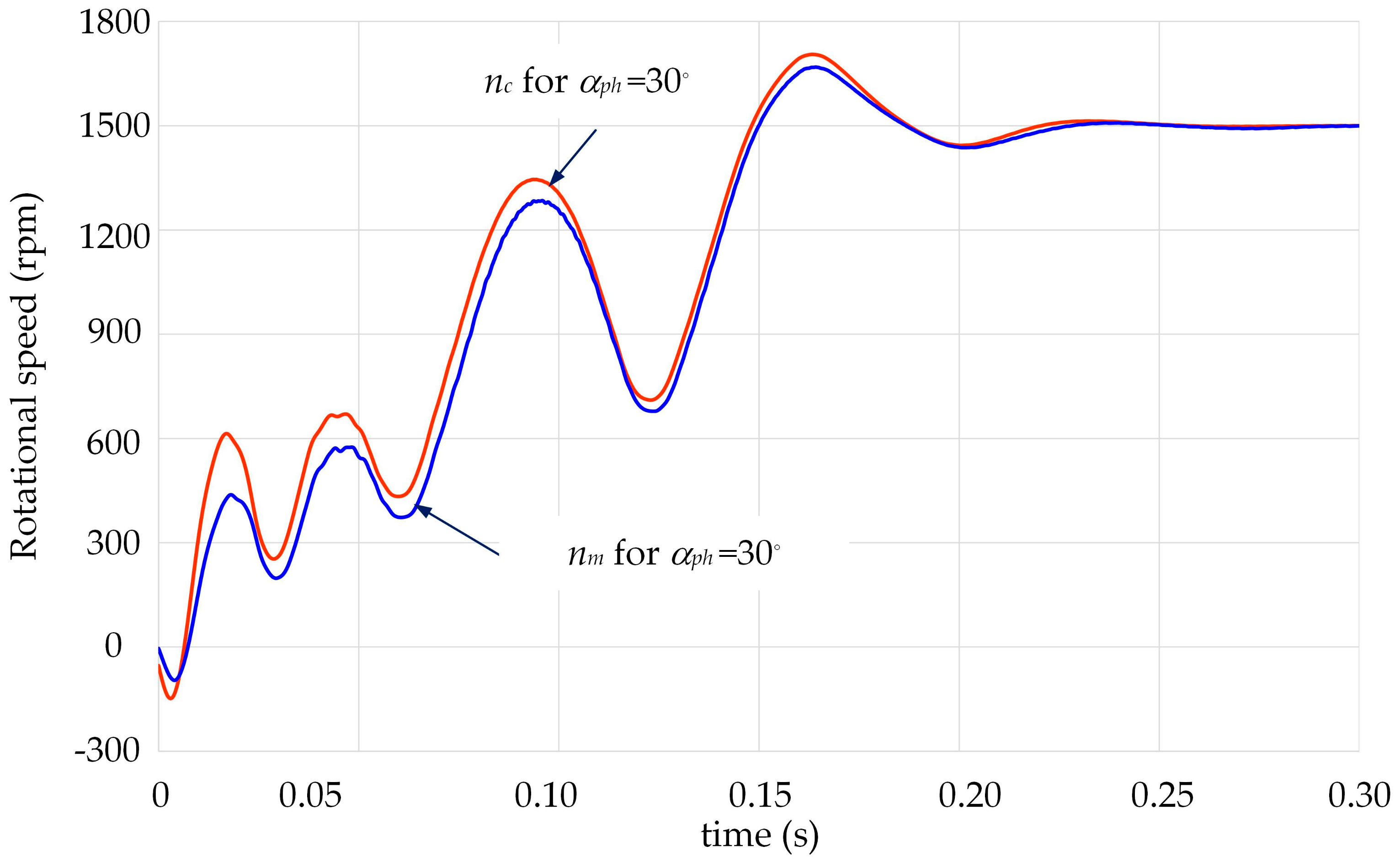
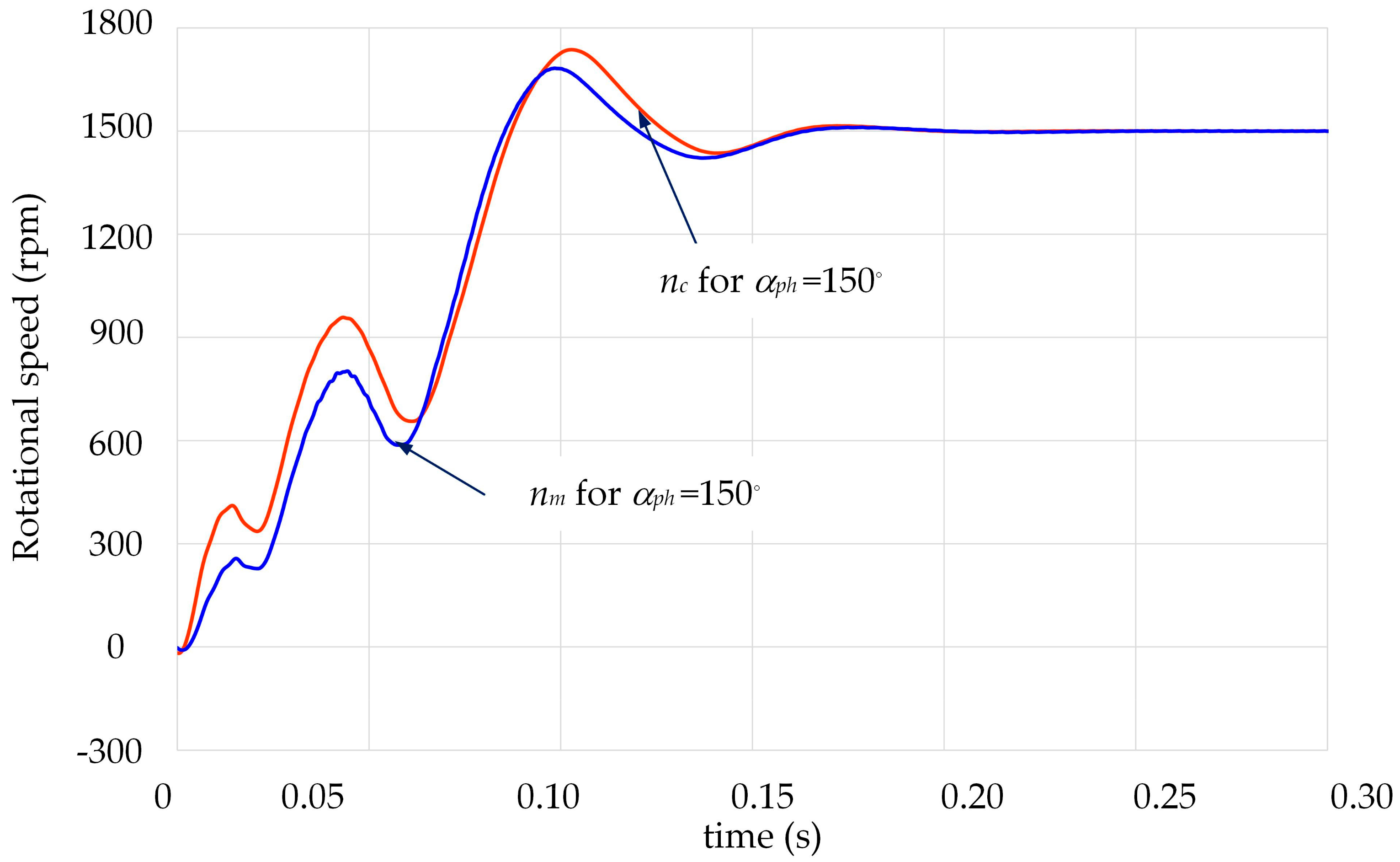
Selected results of the experimental tests for values of angle α_ph that were equal to 30° and 150°—corresponding to shortest and longest start-up times of the motor—are shown in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. The figures also include the results of simulations carried out for the same conditions as those set on the test bench. For the above-mentioned values of angle α_ph, the shortest and longest starting times were obtained in simulation studies of the start-up process of a motor loaded with a constant torque of 19.5 Nm. 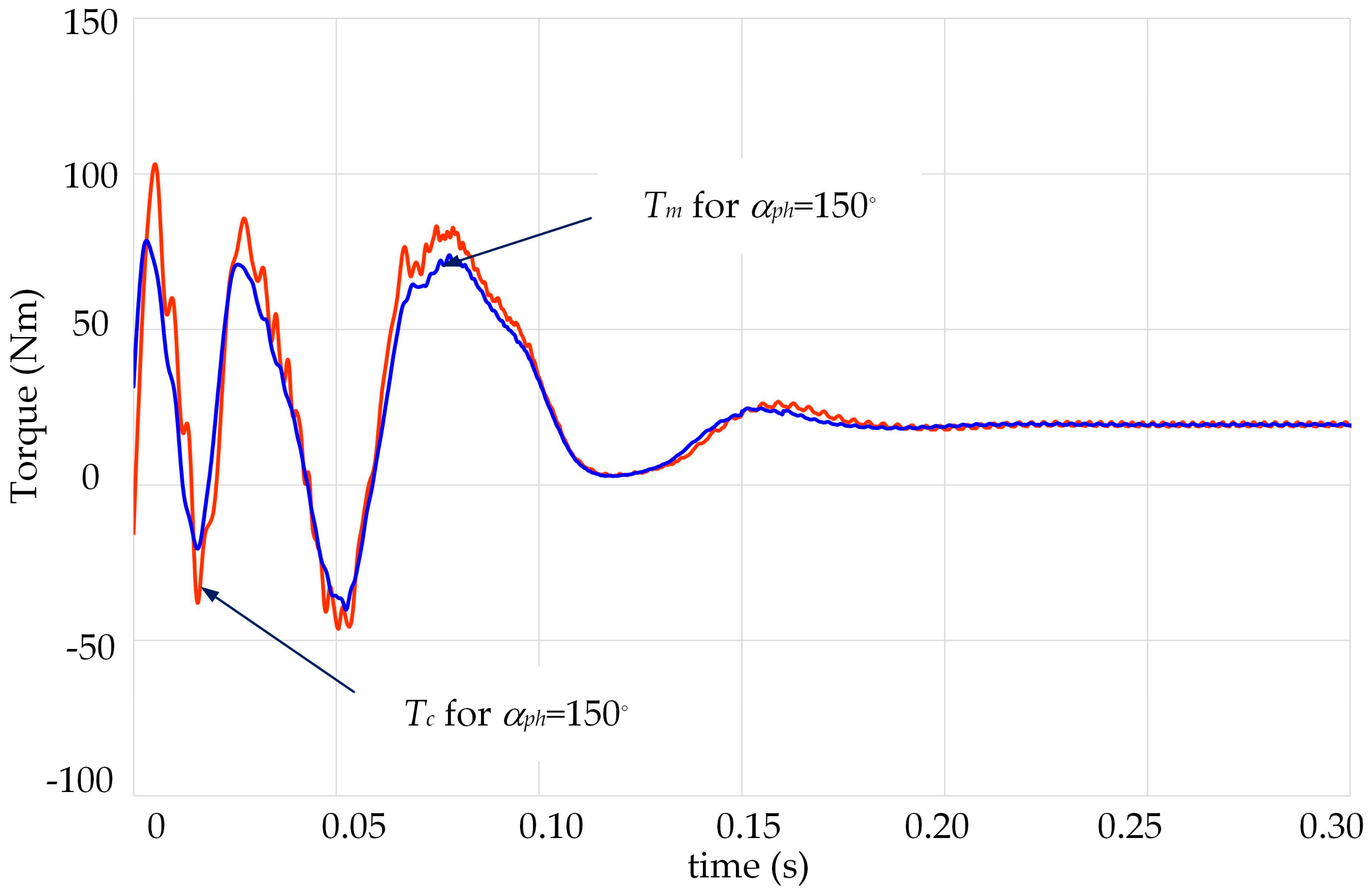Figure 17 and Figure 18 show that these times lasted approximately 0.2 and 0.3 s, respectively. Example waveforms of the measured shaft torque T_m and the calculated electromagnetic torque T_c acting on the motor rotor obtained for α_ph = 150° are compared in Figure 19.

The waveforms of the phase currents that were measured and calculated for values of angle α_ph that were equal to 30° and 150° are shown in Figure 20 and Figure 21, respectively. The effects of the switching angle α_ph could be observed in both the start-up time (i.e., the time calculated from the moment that the voltage was switched on until the current waveforms reached steady-state amplitudes) and the shape of the phase current waveforms. On the other hand, it was observed that the effect of the angle α_ph on the maximum value of the phase currents when starting a motor loaded with constant torque was small. The analysis of the phase current waveforms showed that the maximum current values for angles of 150° and 30° in the measurements were 64.61 A and 65.55 A, and in the calculations, they were 68.54 A and 69.61 A, respectively. Thus, the maximum current value decreased with respect to the maximum current value obtained for the angle of 150° by only about 1.5%.

A comparison of the effects of the angle α_ph on the maximum current value during the start-up process of a motor loaded with constant torque and a motor loaded with a fan (see Section 3) showed that the developed method of reducing the inrush current was effective only for loads with a strong dependence of the load torque on the shaft speed, as these were mechanical characteristics of the fan. However, it should be noted that when the motor was loaded with constant torque, despite the lack of a visible effect of the switching angle on the value of the inrush current, a much shorter start-up time was obtained for an optimal angle α_ph. As a result, less energy was lost in the motor, and the motor drew less energy from the grid during the start-up process.

The good agreement between the simulations and experimental results confirmed the high reliability of the calculations that were carried out and the algorithm and software used for the analysis of transient coupled phenomena in LSPMSMs.

5. Conclusions

This article presents a new method of minimizing the inrush current of an LSPMSM, which involves selecting the time instant at which all three voltages supplying the stator winding are switched in such a way that the smallest values of the amplitudes of the phase currents are obtained. In order to implement the proposed method and define the time instant of the connection of the winding to the supply voltage, as discussed above, the phase angle α_ph was introduced. α_ph = ωt_d, or more precisely, the delay time t_d of switching on the voltage was calculated from the time when the line voltage u_a crossed zero on the positive slope (Figure 2). It should be noted that before switching on the voltage at the moment for which the angle has an optimal value, i.e., a value that minimises the inrush currents, the rotor should be aligned in an angular position for which the phase axis a coincides with the magnetic axis of the rotor d. For this purpose, a rotor alignment procedure was proposed. The calculation results presented in Section 3 confirm the effectiveness of the developed method of inrush current reduction when the motor is loaded with a fan-type load.

Based on the experimental studies that were carried out, it can be concluded that the good agreement between the calculation results and the measurement results confirmed the suitability of the authors’ algorithm and software for the analysis of transient coupled phenomena in an LSPMSM and indicated the high reliability of the results of the simulation studies that were carried out. Based on the experiments, it should also be highlighted that in the case of an LSPMSM with a driving load and a constant value of the load torque with respect to the rotor speed, the proposed method is less effective than for loads that show a high dependence of the load torque on the speed (such as the fan-type characteristics studied in Section 3). In the case of loads with a constant value of the torque with respect to the speed, the proposed method allows one only to reduce the inrush current’s impact by reducing the start-up time.

It should be noted that due to the complex interaction during the start-up of the rotating field generated by the stator winding with the field generated by the permanent magnets in the rotor, the phase angle of voltage switching must be selected individually for the mechanical characteristics of the load and the moment of inertia of the rotating masses of a particular powertrain system. For this purpose, one can use the algorithm presented in Section 3 or select this angle experimentally by realizing a series of start-ups with preset values of α_ph.

The studies that were conducted confirm that limiting the start-up current reduces the electrical energy drawn from the grid during start-up, thus decreasing power losses in the windings. As a result, this leads to a reduction in the increase in temperature of the machine’s components, thus reducing the risk of the partial demagnetisation of the magnets. Moreover, by limiting the inrush current and associated voltage drops in the power grid, motor starting is less likely to interfere with the operation of other electrical equipment supplied by the same grid.