Effect of Soil Properties and Powertrain Configuration on the Energy Consumption of Wheeled Electric Agricultural Robots
Abstract
1. Introduction
2. Modeling of Tire Soil–Interaction and Agricultural Machinery: State of the Art
2.1. Tire–Soil Interaction Models
2.2. Simulation of Agricultural Machinery
2.3. Research Gap
3. Materials and Methods
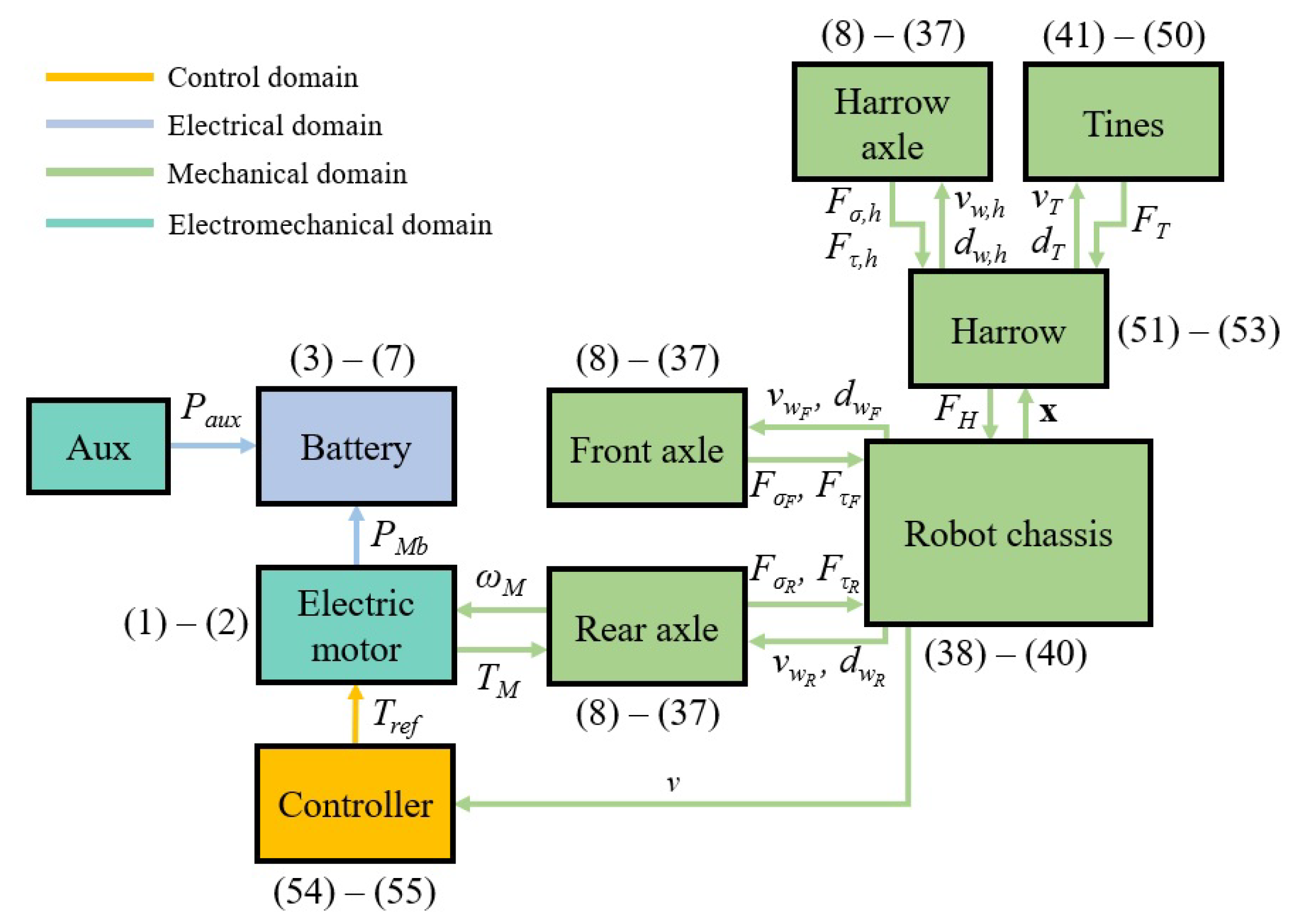
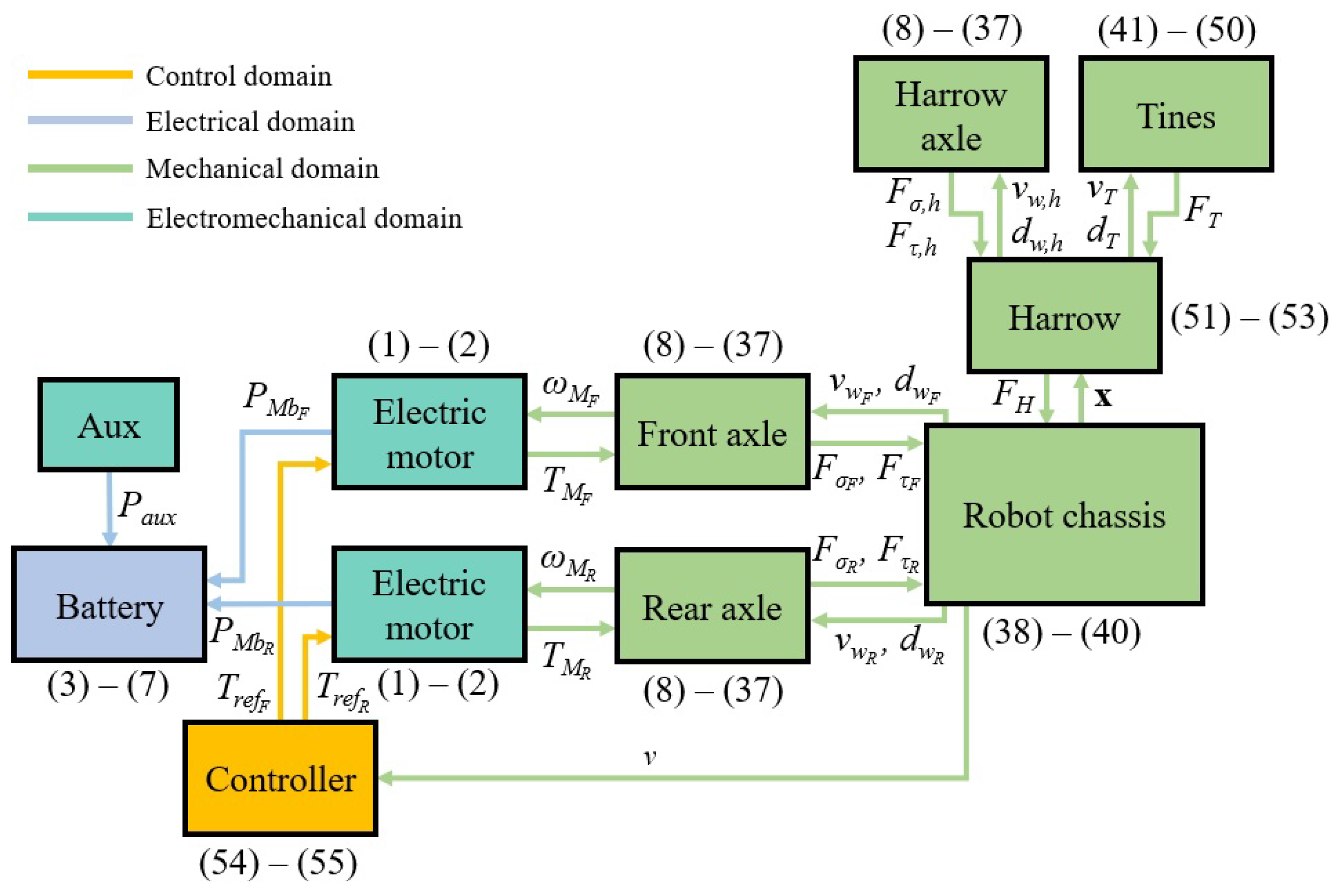
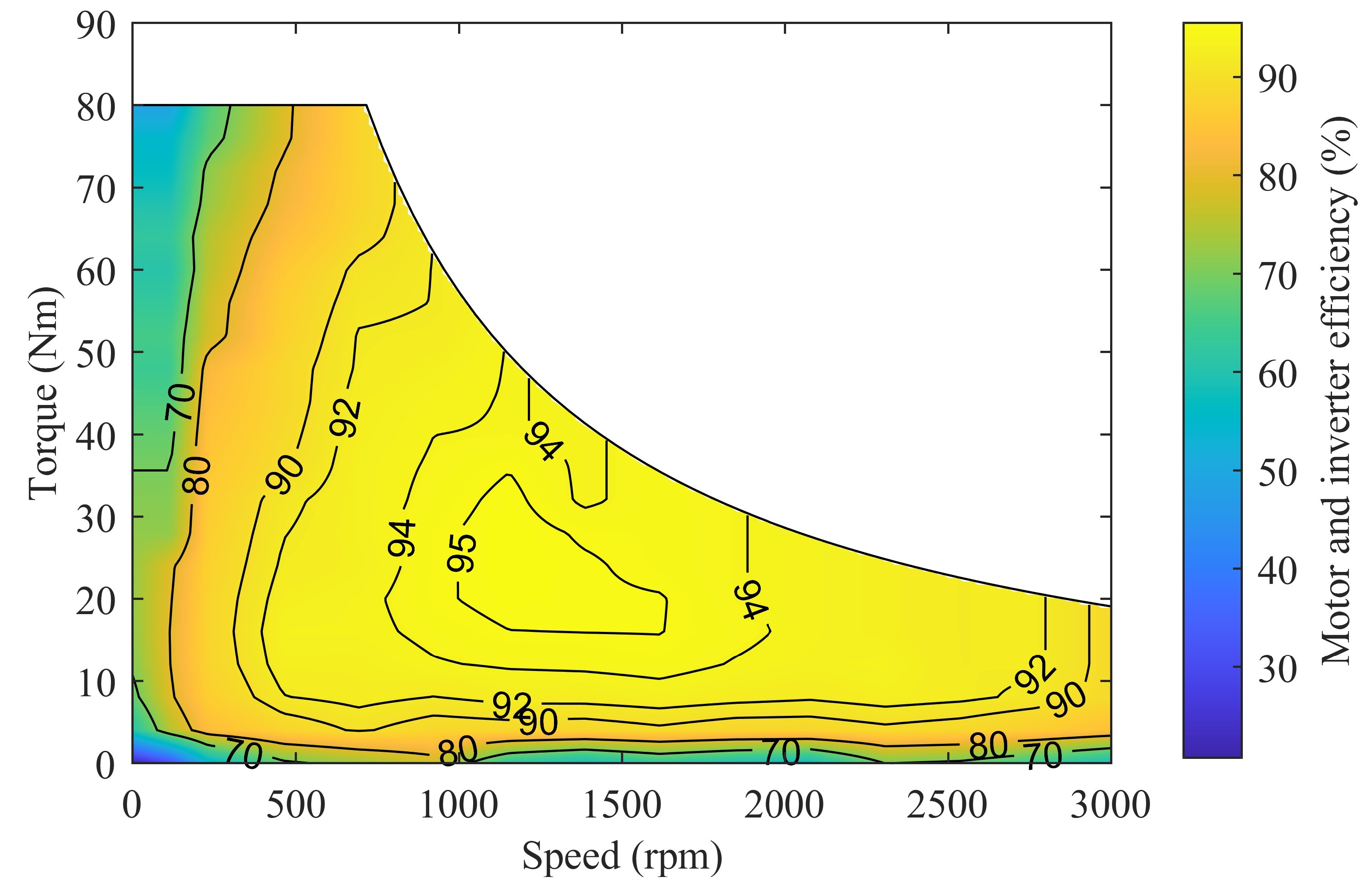
3.1. Powertrain Model
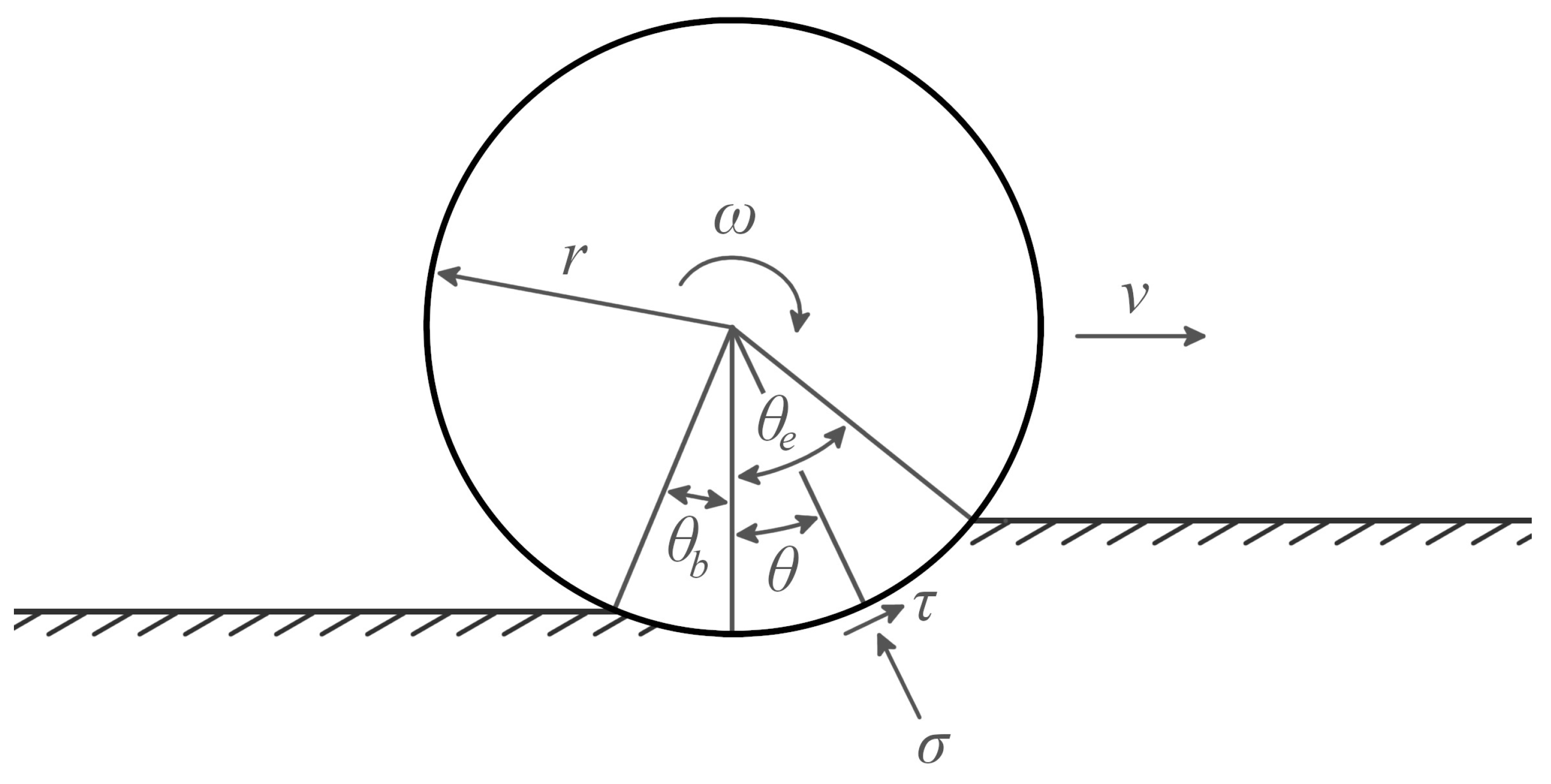
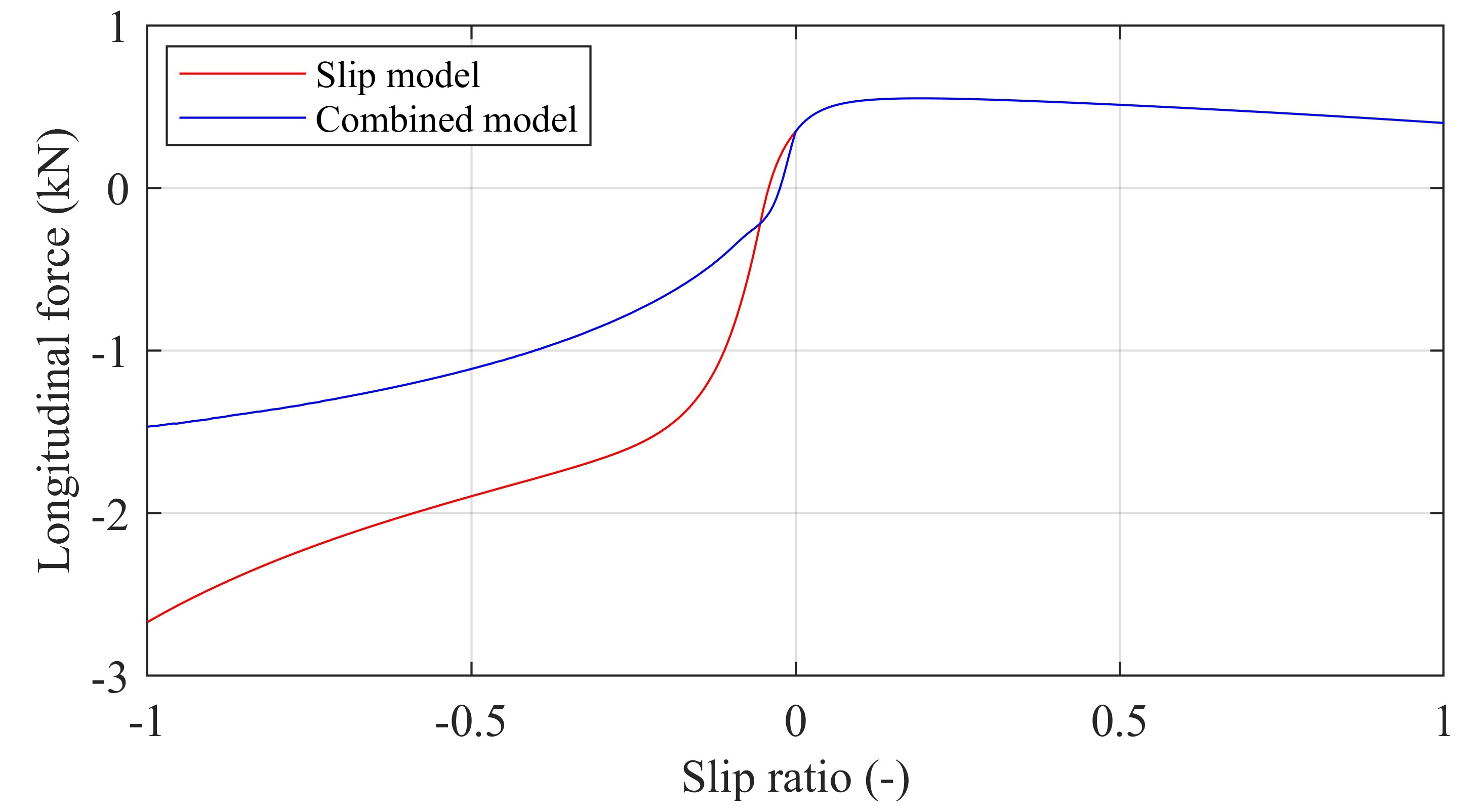
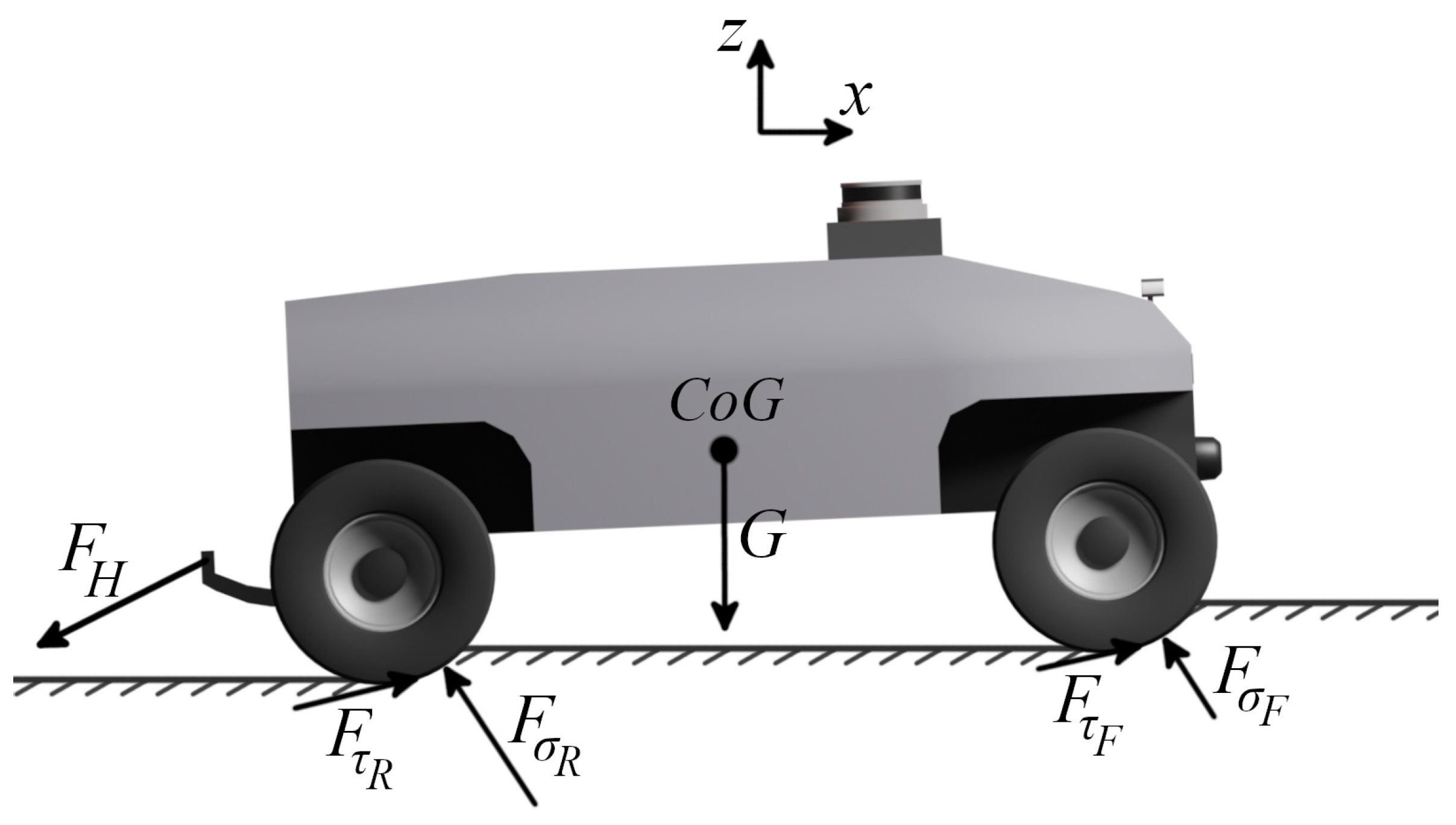
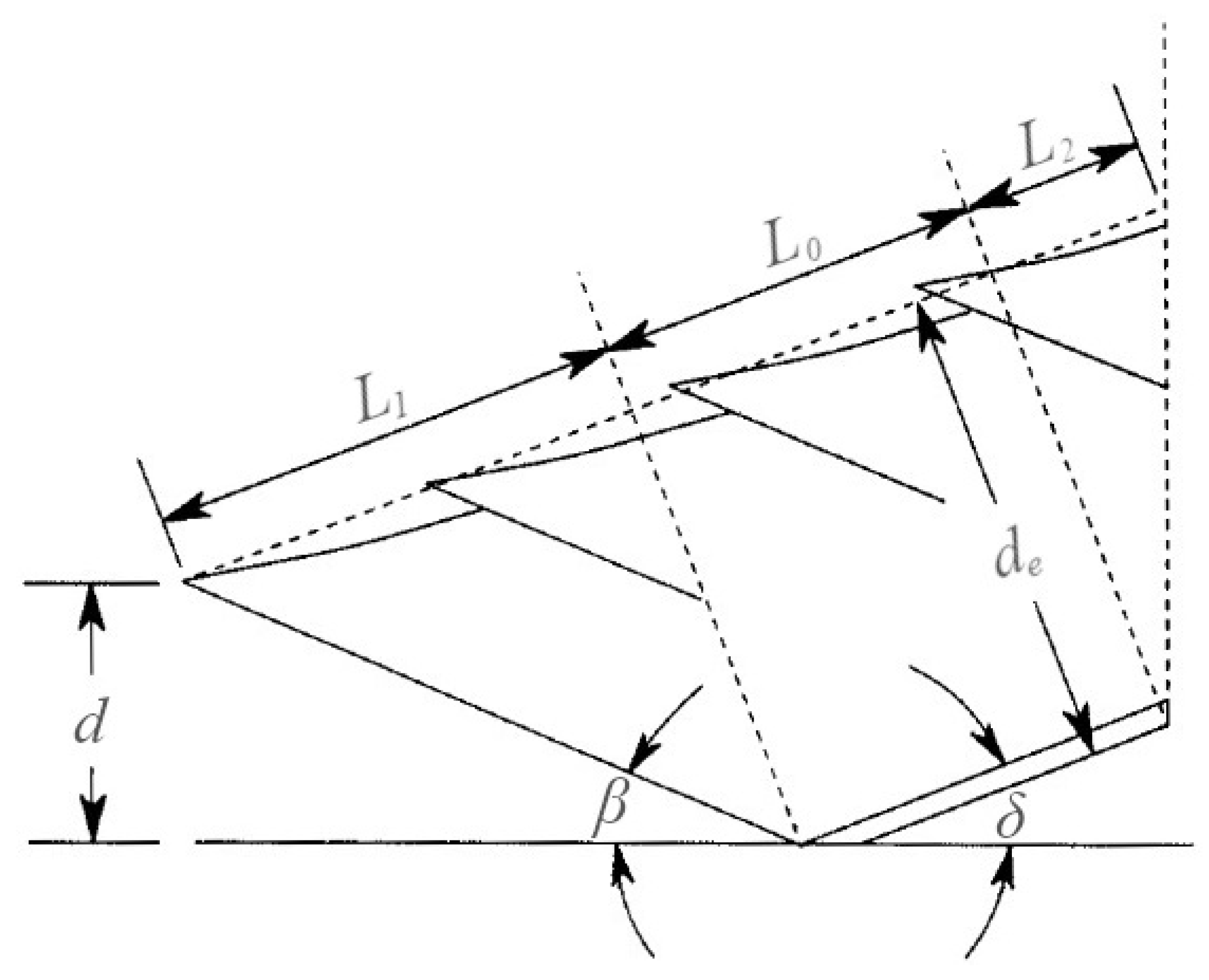
3.2. Tire–Soil Interaction Model
3.3. Robot Equations of Motion and Harrow Dynamics
3.4. Simulation Parameters
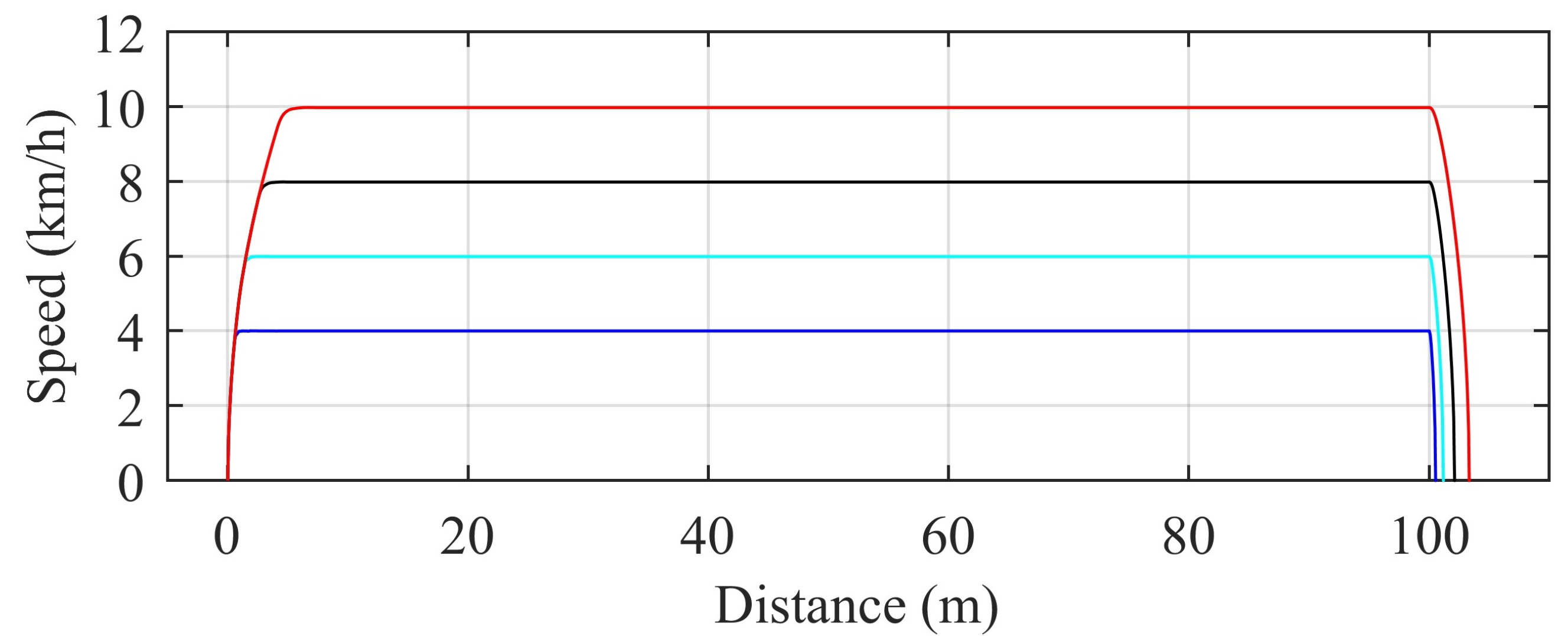
3.5. Control
4. Results and Discussion
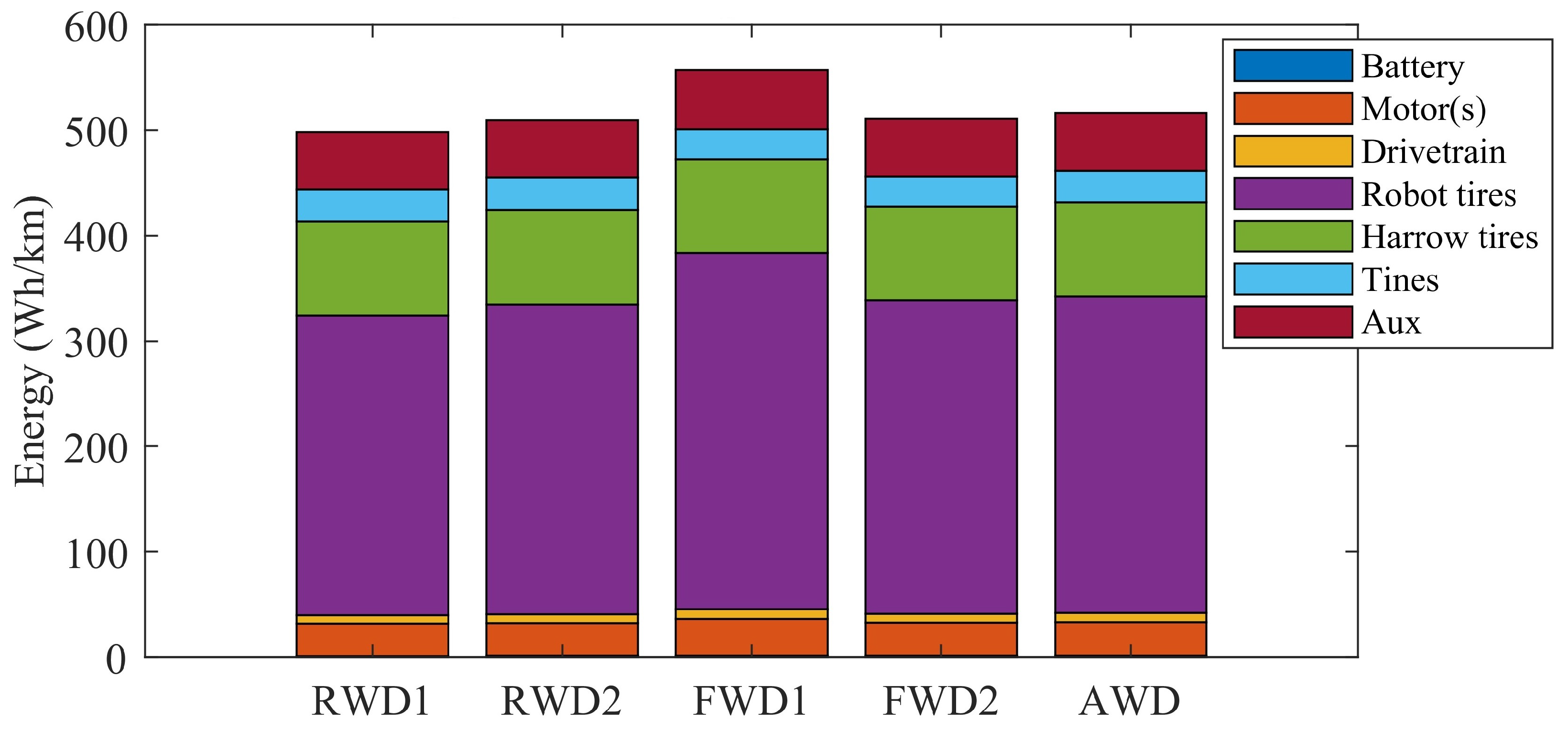
4.1. Success Matrices and Energy Consumption Variation
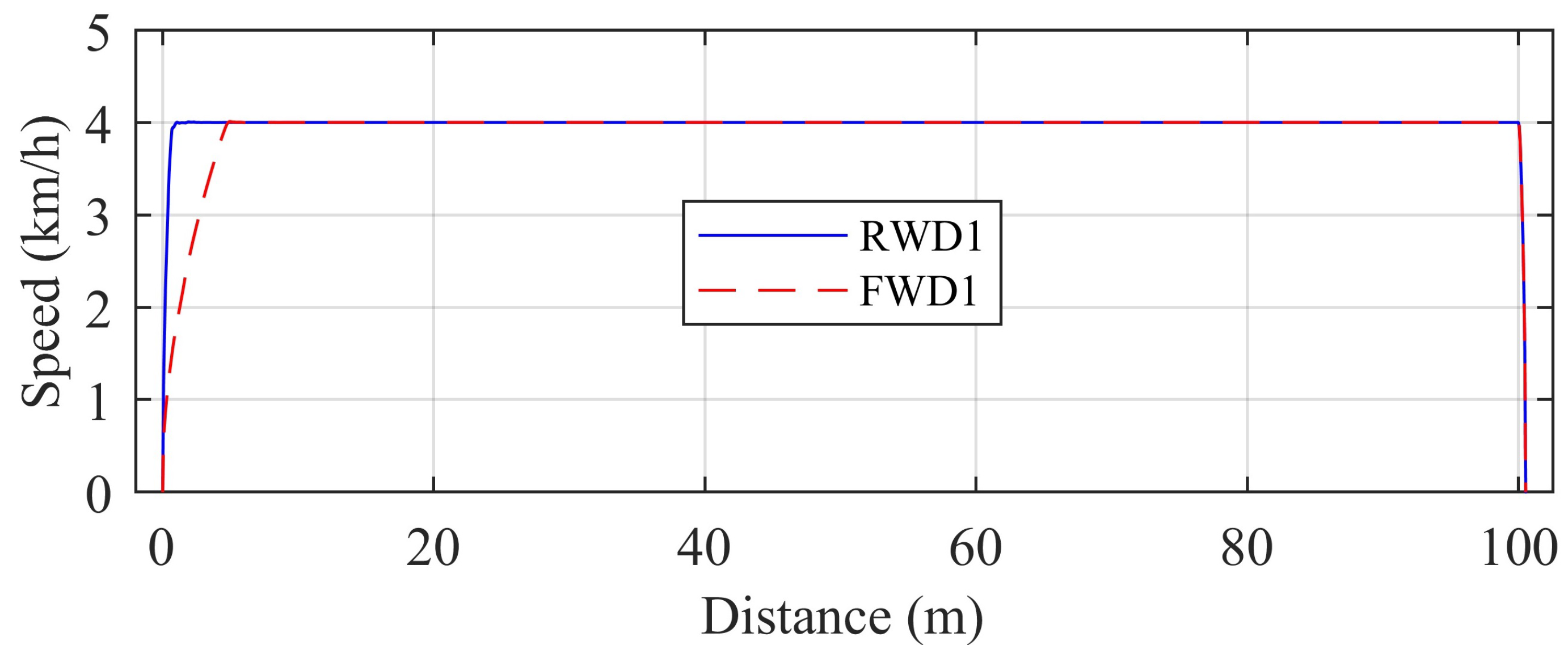
4.2. Performance Comparison with a Light Workload
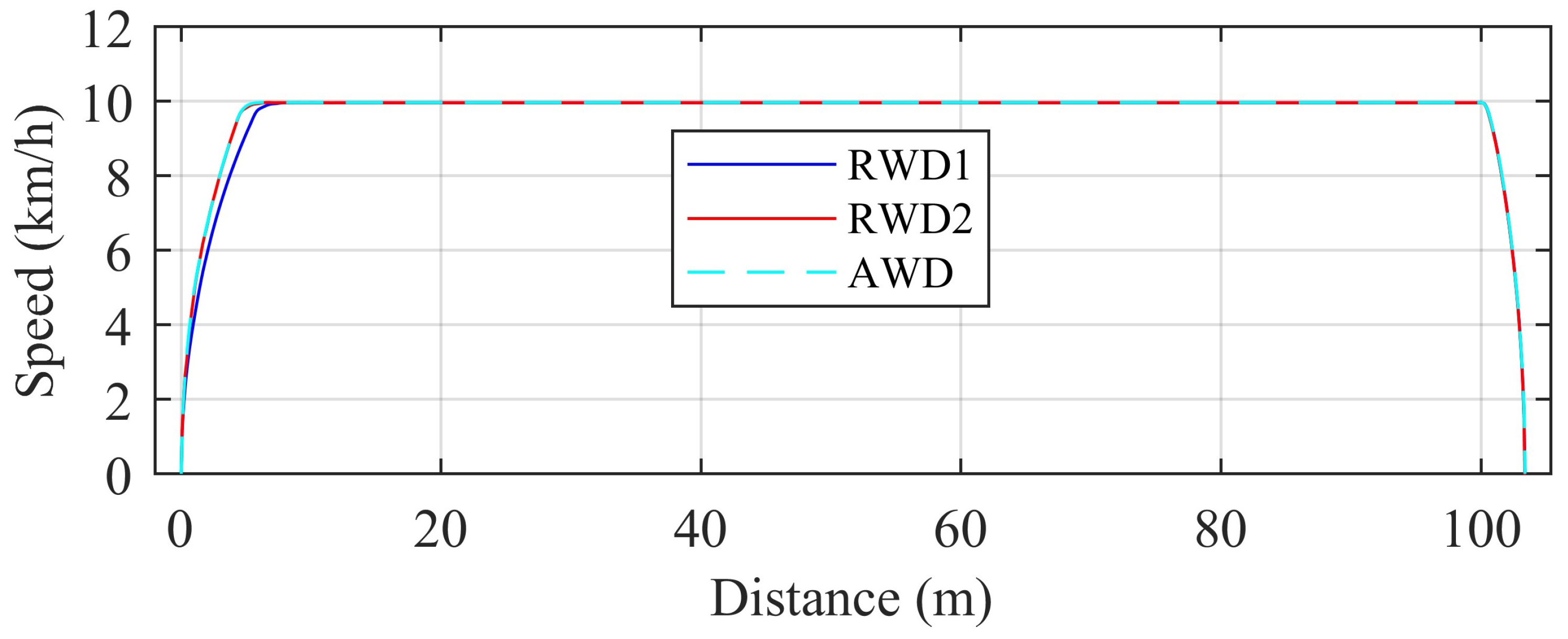
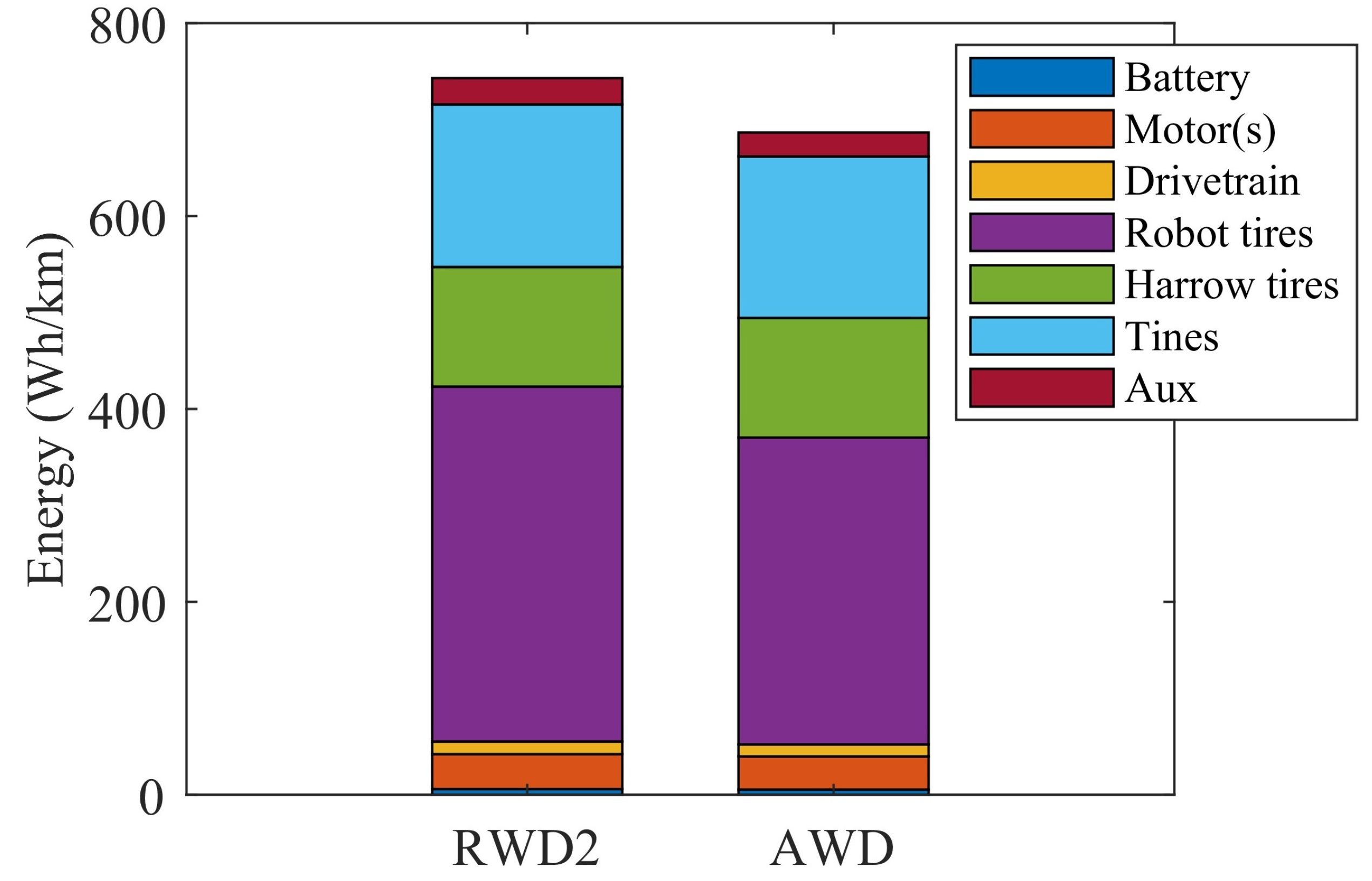
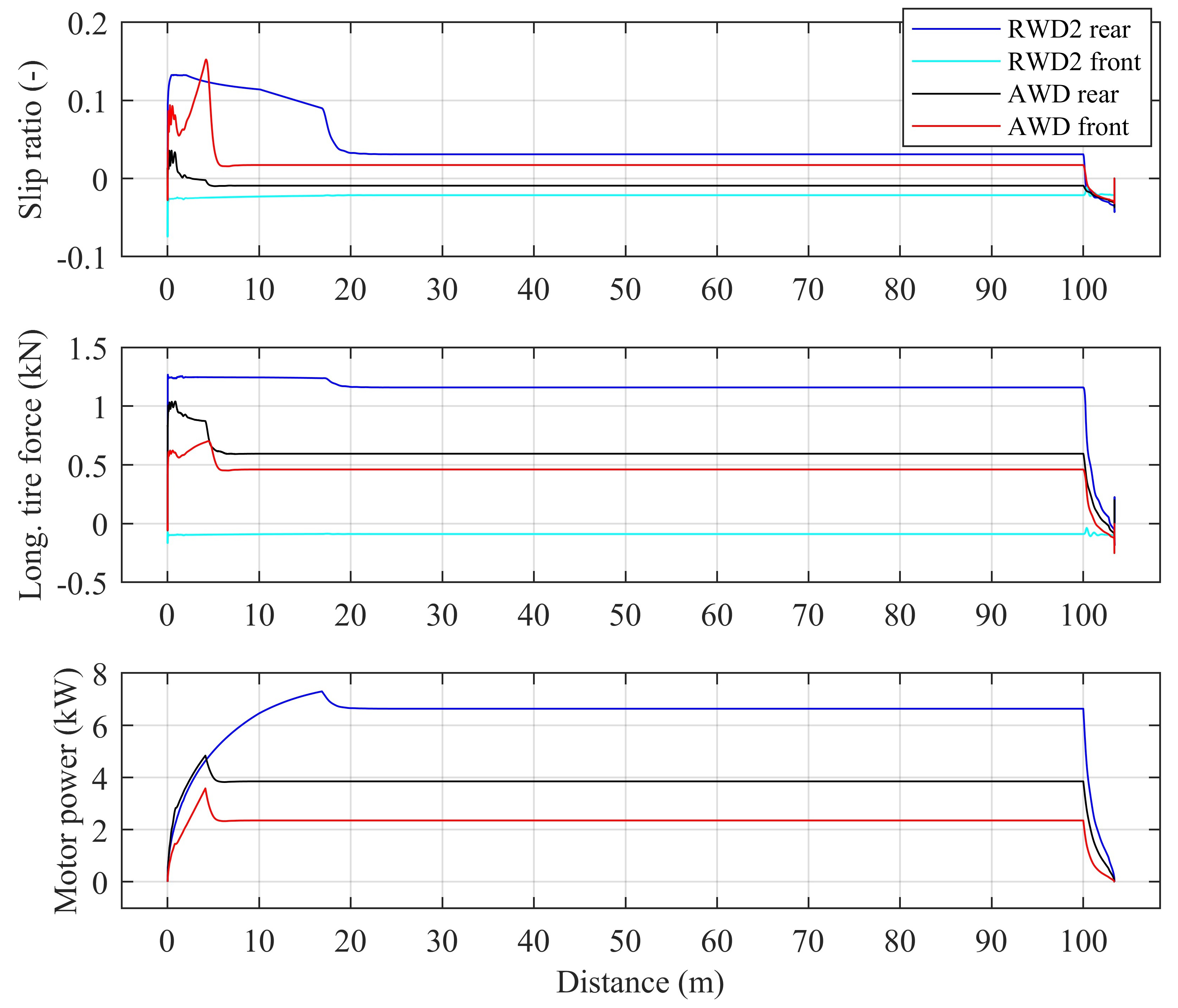
4.3. Comparison of RWD and AWD
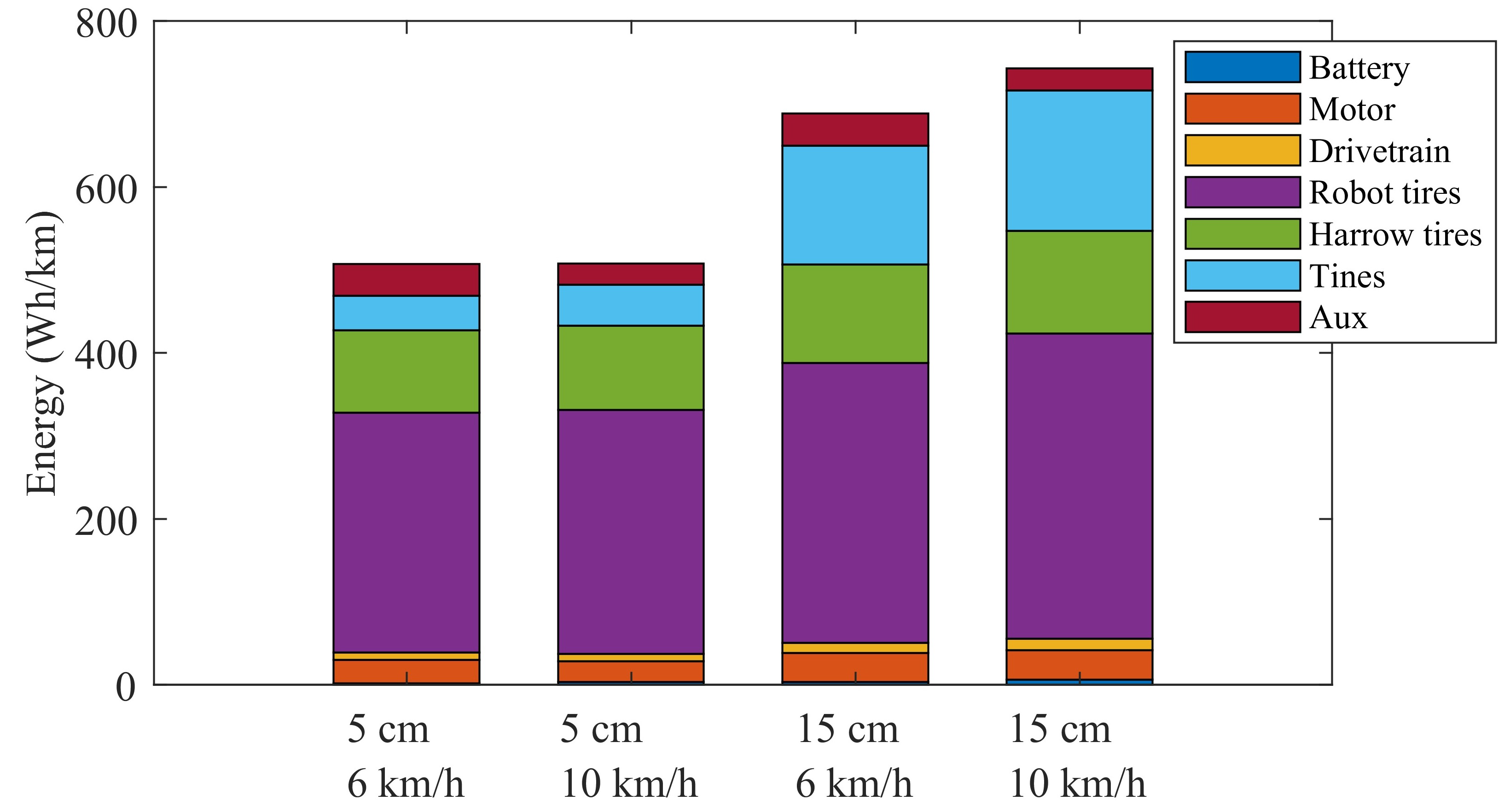
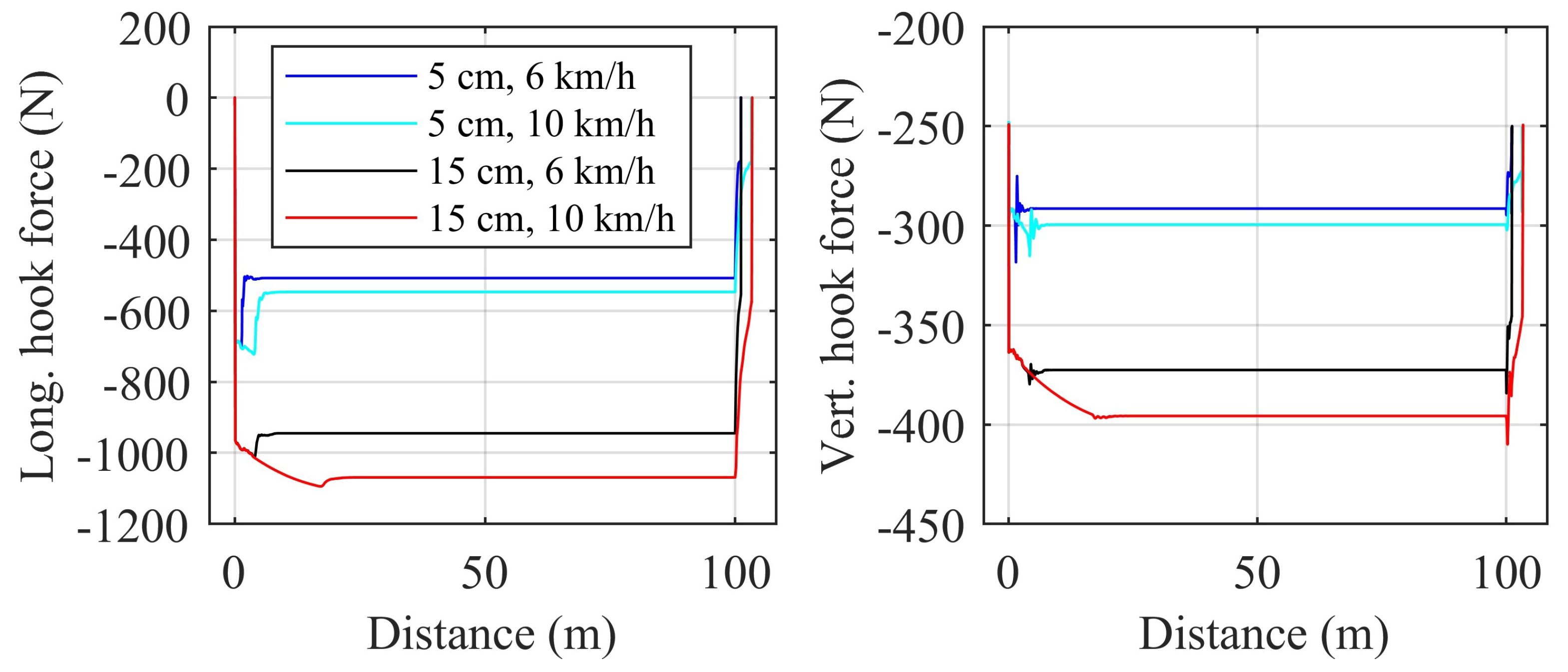
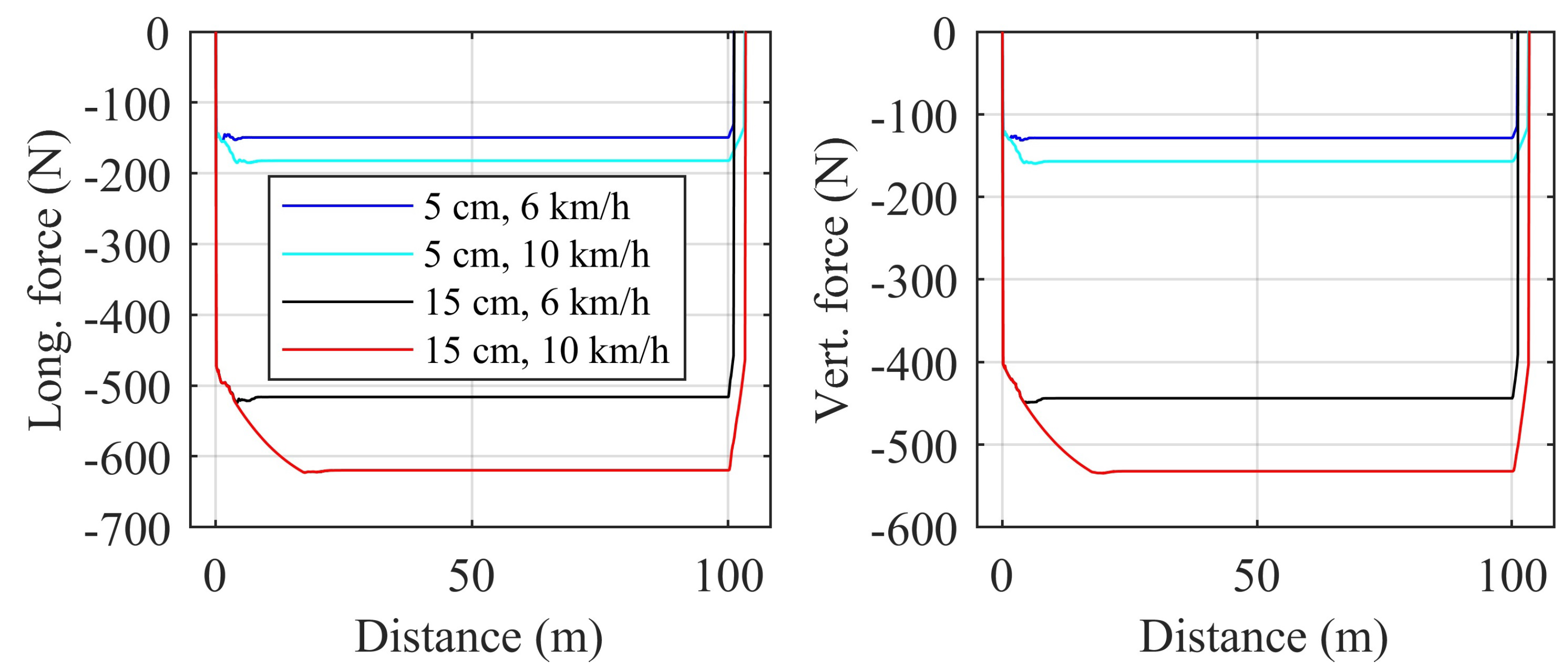
4.4. Effect of Operation Cycle on Energy Consumption
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ATV | All-terrain vehicle |
| AWD | All-wheel drive |
| CoG | Center of gravity |
| DEM | Discrete element method |
| FEM | Finite element method |
| FWD | Front-wheel drive |
| GHG | Greenhouse gas |
| ICE | Internal combustion engine |
| NMC | Nickel manganese cobalt |
| PV | Photovoltaic |
| RWD | Rear-wheel drive |
| SOC | State of charge |
| SOD | State of discharge |
| SPH | Smoothed particle hydrodynamics |
| TC | Traction control |
References
- United Nations, Department of Economic and Social Affairs, Population Division. World Population Prospects 2022. Available online: https://population.un.org/wpp/Graphs/DemographicProfiles/Line/900 (accessed on 1 January 2024).
- Ghobadpour, A.; Monsalve, G.; Cardenas, A.; Mousazadeh, H. Off-Road Electric Vehicles and Autonomous Robots in Agricultural Sector: Trends, Challenges, and Opportunities. Vehicles 2022, 4, 843–864. [Google Scholar] [CrossRef]
- Tubiello, F.; Salvatore, M.; Ferrara, A.; House, J.; Federici, S.; Rossi, S.; Biancalani, R.; Condor Golec, R.; Jacobs, H.; Flammini, A.; et al. The Contribution of Agriculture, Forestry and other Land Use activities to Global Warming, 1990–2012. Glob. Chang. Biol. 2015, 21, 2655–2660. [Google Scholar] [CrossRef] [PubMed]
- Climate Change and Agriculture in the EU. Available online: https://agriculture.ec.europa.eu/sustainability/environmental-sustainability/climate-change_en (accessed on 10 November 2023).
- Gerber, P.J.; Steinfeld, H.; Henderson, B.; Mottet, A.; Opio, C.; Dijkman, J.; Falcucci, A.; Tempio, G. Tackling Climate Change through Livestock: A Global Assessment of Emissions and Mitigation Opportunities; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2013. [Google Scholar]
- Lovarelli, D.; Bacenetti, J. Exhaust gases emissions from agricultural tractors: State of the art and future perspectives for machinery operator. Biosyst. Eng. 2019, 186, 204–213. [Google Scholar] [CrossRef]
- Ragazou, K.; Garefalakis, A.; Zafeiriou, E.; Passas, I. Agriculture 5.0: A New Strategic Management Mode for a Cut Cost and an Energy Efficient Agriculture Sector. Energies 2022, 15, 3113. [Google Scholar] [CrossRef]
- Hernandez-Escobedo, Q.; Muñoz-Rodríguez, D.; Vargas-Casillas, A.; Juárez Lopez, J.M.; Aparicio-Martínez, P.; Martínez-Jiménez, M.P.; Perea-Moreno, A.J. Renewable Energies in the Agricultural Sector: A Perspective Analysis of the Last Three Years. Energies 2022, 16, 345. [Google Scholar] [CrossRef]
- Lajunen, A.; Kivekäs, K.; Freyermuth, V.; Vijayagopal, R.; Kim, N. Simulation of Alternative Powertrains in Agricultural Tractors. In Proceedings of the 36th International Electric Vehicle Symposium and Exhibition (EVS36), Sacramento, CA, USA, 11–14 June 2023. [Google Scholar]
- Lagnelöv, O.; Larsson, G.; Nilsson, D.; Larsolle, A.; Hansson, P.A. Performance comparison of charging systems for autonomous electric field tractors using dynamic simulation. Biosyst. Eng. 2020, 194, 121–137. [Google Scholar] [CrossRef]
- Malik, A.; Kohli, S. Electric tractors: Survey of challenges and opportunities in India. Mater. Today Proc. 2020, 28, 2318–2324. [Google Scholar] [CrossRef]
- Engström, J.; Lagnelöv, O. An Autonomous Electric Powered Tractor—Simulation of All Operations on a Swedish Dairy Farm. J. Agric. Sci. Technol. 2018, 8, 182–187. [Google Scholar] [CrossRef]
- Lagnelöv, O.; Dhillon, S.; Larsson, G.; Nilsson, D.; Larsolle, A.; Hansson, P.A. Cost analysis of autonomous battery electric field tractors in agriculture. Biosyst. Eng. 2021, 204, 358–376. [Google Scholar] [CrossRef]
- Lagnelöv, O.; Larsson, G.; Larsolle, A.; Hansson, P.A. Life cycle assessment of autonomous electric field tractors in Swedish agriculture. Sustainability 2021, 13, 11285. [Google Scholar] [CrossRef]
- Olkkonen, V.; Lind, A.; Rosenberg, E.; Kvalbein, L. Electrification of the agricultural sector in Norway in an effort to phase out fossil fuel consumption. Energy 2023, 276, 127543. [Google Scholar] [CrossRef]
- Farokhi Soofi, A.; Manshadi, S.D.; Saucedo, A. Farm electrification: A road-map to decarbonize the agriculture sector. Electr. J. 2022, 35, 107076. [Google Scholar] [CrossRef]
- Beltrami, D.; Iora, P.; Tribioli, L.; Uberti, S. Electrification of Compact Off-Highway Vehicles—Overview of the Current State of the Art and Trends. Energies 2021, 14, 5565. [Google Scholar] [CrossRef]
- Thakur, A.; Venu, S.; Gurusamy, M. An extensive review on agricultural robots with a focus on their perception systems. Comput. Electron. Agric. 2023, 212, 108146. [Google Scholar] [CrossRef]
- Schneider, A.; Klabunde, F.; Buck, L.; Ohlhoff, M.; Reis, L.; Olvermann, M.; Kauffeld, S.; Engel, B.; Glatzel, G.; Schröder, B.; et al. Drawing transformation pathways for making use of joint effects of food and energy production with biodiversity agriphotovoltaics and electrified agricultural machinery. J. Environ. Manag. 2023, 335, 153811–153823. [Google Scholar] [CrossRef] [PubMed]
- Gorjian, S.; Ebadi, H.; Trommsdorff, M.; Sharon, H.; Demant, M.; Schindele, S. The advent of modern solar-powered electric agricultural machinery: A solution for sustainable farm operations. J. Clean. Prod. 2023, 292, 126030. [Google Scholar] [CrossRef]
- Roshanianfard, A.; Noguchi, N.; Okamoto, H.; Ishii, K. A review of autonomous agricultural vehicles (The experience of Hokkaido University). J. Terramech. 2020, 91, 155–183. [Google Scholar] [CrossRef]
- Keller, T.; Sandin, M.; Colombi, T.; Horn, R.; Or, D. Historical increase in agricultural machinery weights enhanced soil stress levels and adversely affected soil functioning. Soil Tillage Res. 2019, 194, 104293. [Google Scholar] [CrossRef]
- Lagnelöv, O.; Larsson, G.; Larsolle, A.; Hansson, P.A. Impact of lowered vehicle weight of electric autonomous tractors in a systems perspective. Smart Agric. Technol. 2023, 4, 100156. [Google Scholar] [CrossRef]
- Dasch, J.M.; Gorsich, D.J. TARDEC Story: Sixty-Five Years of Innovation, 1946–2010; Army Tank Automotive Research, Development and Engineering Center (TARDEC): Detroit, MI, USA, 2012. [Google Scholar]
- Taheri, S.; Sandu, C.; Taheri, S.; Pinto, E.; Gorsich, D. A technical survey on Terramechanics models for tire-terrain interaction used in modeling and simulation of wheeled vehicles. J. Terramech. 2015, 57, 1–22. [Google Scholar] [CrossRef]
- Rula, A.A.; Nuttall, C.J. An Analysis of Ground Mobility Models (ANAMOB); U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1971. [Google Scholar]
- Turnage, G.W. Prediction of in-Sand Tire and Wheeled Vehicle Drawbar Performance; Technical Report; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1984. [Google Scholar]
- Wismer, R.D.; Luth, H.J. Off-road traction prediction for wheeled vehicles. J. Terramech. 1973, 10, 49–61. [Google Scholar] [CrossRef]
- Brixius, W.W. Traction prediction equations for bias ply tires. Am. Soc. Agric. Eng. 1987, 8, 87–1622. [Google Scholar]
- Hegazy, S.; Sandu, C. Experimental investigation of vehicle mobility using a novel wheel mobility number. J. Terramech. 2013, 50, 303–310. [Google Scholar] [CrossRef]
- Schreiber, M.; Kutzbach, H. Influence of soil and tire parameters on traction. Res. Agric. Eng. 2008, 54, 43–49. [Google Scholar] [CrossRef]
- Wong, J.Y.; Reece, A.R. Prediction of rigid wheel performance based on analysis of soil-wheel stresses, part I. Performance of driven rigid wheels. J. Terramech. 1967, 4, 81–98. [Google Scholar] [CrossRef]
- Wong, J.Y.; Reece, A.R. Prediction of rigid wheel performance based on analysis of soil-wheel stresses, part II. Performance of towed rigid wheels. J. Terramech. 1967, 4, 7–25. [Google Scholar] [CrossRef]
- Bekker, M.G. Theory of Land Locomotion; The University of Michigan Press: Ann Arbor, MI, USA, 1956. [Google Scholar]
- Bekker, M.G. Off-the-Road Locomotion; The University of Michigan Press: Ann Arbor, MI, USA, 1960. [Google Scholar]
- Sandu, C.; Sandu, A.; Li, L. Stochastic modeling of terrain profiles and soil parameters. SAE Trans. 2005, 114, 211–220. [Google Scholar]
- Mao, S.; Han, R. Nonlinear complementarity equations for modeling tire-soil interaction-An incremental Bekker approach. J. Sound Vib. 2008, 312, 380–398. [Google Scholar] [CrossRef]
- Senatore, C.; Sandu, C. Off-road tire modeling and the multi-pass effect for vehicle dynamics simulation. J. Terramech. 2011, 48, 265–276. [Google Scholar] [CrossRef]
- Senatore, C.; Sandu, C. Torque distribution influence on tractive efficiency and mobility of off-road wheeled vehicles. J. Terramech. 2011, 48, 372–383. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, Z. Semi-empirical model for elastic tyre trafficability and methods for the rapid determination of its related parameters. Biosyst. Eng. 2018, 174, 204–218. [Google Scholar] [CrossRef]
- Jiang, Q.; Cao, M.; Wang, Y.; Wang, J. Quantification of the soil stiffness constants using physical properties of paddy soils in Yangtze Delta Plain, China. Biosyst. Eng. 2020, 200, 89–100. [Google Scholar] [CrossRef]
- Holtz, D.; Singh, A.; Megiveron, M. Tire-soil modeling for vehicle reollover over sloped compressible terrains. In Proceedings of the ASME 2014 International Design Engineering Technical Conferences & Computer and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar]
- Krenn, R.; Gibbesch, A. Soft Soil Contact Modeling Technique for Multi-Body System Simulation. In Trends in Computational Contact Mechanics; Zavarise, G., Wriggers, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 135–155. [Google Scholar]
- Krenn, R.; Hirzinger, G. Simulation of rover locomotion on sandy terrain-modeling, verification and validation. In Proceedings of the 10th Workshop on ASTRA, Noordwijk, The Netherlands, 18–20 October 2008. [Google Scholar]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An Open Source Multi-physics Dynamics Engine. In Higher Performance Computing in Science and Engineering—Lecture Notes in Computer Science; Kozubek, T., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 19–49. [Google Scholar]
- Serban, R.; Taylor, M.; Negrut, D.; Tasora, A. Chrono::Vehicle: Template-based ground vehicle modelling and simulation. Int. J. Veh. Perform. 2018, 5, 18–39. [Google Scholar] [CrossRef]
- Serban, R.; Taves, J.; Zhou, Z. Real-Time Simulation of Ground Vehicles on Deformable Terrain. J. Comput. Nonlinear Dyn. 2023, 18, 081007. [Google Scholar] [CrossRef]
- Young, A.; Taves, J.; Elmquist, A.; Benatti, S.; Tasora, A.; Serban, R.; Negrut, D. Enabling Artificial Intelligence Studies in Off-Road Mobility Through Physics-Based Simulation of Multiagent Scenarios. J. Comput. Nonlinear Dyn. 2022, 17, 051001. [Google Scholar] [CrossRef]
- Benatti, S.; Young, A.; Elmquist, A.; Taves, J.; Tasora, A.; Serban, R.; Negrut, D. End-to-end learning for off-road terrain navigation using the Chrono open-source simulation platform. Multibody Syst. Dyn. 2022, 54, 399–414. [Google Scholar] [CrossRef]
- Harnisch, C.; Lach, B.; Jakobs, R.; Troulis, M. A new tyre–soil interaction model for vehicle simulation on deformable ground. Int. J. Veh. Mech. Mobil. 2005, 43, 384–394. [Google Scholar] [CrossRef]
- Karpman, E.; Kövecses, J.; Teichmann, M. Terramechanics models augmented by machine learning representations. J. Terramech. 2023, 107, 75–89. [Google Scholar] [CrossRef]
- Gipser, M. FTire—The tire simulation model for all applications related to vehicle dynamics. Int. J. Veh. Mech. Mobil. 2007, 45, 139–151. [Google Scholar] [CrossRef]
- Roşca, R.; Cârlescu, P.; Ţenu, I. A semi-empirical traction prediction model for an agricultural tyre, based on the super ellipse shape of the contact surface. Soil Tillage Res. 2014, 141, 10–18. [Google Scholar] [CrossRef]
- Pavlov, C.; Johnson, A. A terramechanics model for high slip angle and skid with prediction of wheel-soil interaction geometry. J. Terramech. 2024, 111, 9–19. [Google Scholar] [CrossRef]
- Jasoliya, D.; Untaroiu, A.; Untaroiu, C. A review of soil modeling for numerical simulations of soil-tire/agricultural tools interaction. J. Terramech. 2024, 111, 41–64. [Google Scholar] [CrossRef]
- Yong, R.N.; Fattah, E.A.; Boonsinsuk, P. Analysis and prediction of tyre-soil interaction and performance using finite elements. J. Terramech. 1978, 15, 43–63. [Google Scholar] [CrossRef]
- Nakashima, H.; Oida, A. Algorithm and implementation of soil–tire contact analysis code based on dynamic FE–DE method. J. Terramech. 2004, 41, 127–137. [Google Scholar] [CrossRef]
- Fervers, C.W. Improved FEM simulation model for tire–soil interaction. J. Terramech. 2004, 41, 87–100. [Google Scholar] [CrossRef]
- Recuero, A.; Serban, R.; Peterson, H.; Sugiyama, P.; Jayakumar, P.; Negrut, D. A high-fidelity approach for vehicle mobility simulation: Nonlinear finite element tires operating on granular material. J. Terramech. 2017, 72, 39–54. [Google Scholar] [CrossRef]
- Li, H.; Schindler, C. Analysis of soil compaction and tire mobility with finite element method. Proc. Inst. Mech. Eng. Part K J. Multibody Dyn. 2013, 227, 275–291. [Google Scholar] [CrossRef]
- Zhao, C.; Zang, M. Analysis of rigid tire traction performance on a sandy soil by 3D finite element–discrete element method. J. Terramech. 2014, 55, 29–37. [Google Scholar] [CrossRef]
- Michael, M.; Vogel, F.; Peters, B. DEM–FEM coupling simulations of the interactions between a tire tread and granular terrain. Comput. Methods Appl. Mech. Eng. 2015, 289, 227–248. [Google Scholar] [CrossRef]
- Serban, R.; Negrut, D.; Recuero, A.; Jayakumar, P. An integrated framework for high-performance, high-fidelity simulation of ground vehicle-tyre-terrain interaction. Int. J. Veh. Perform. 2019, 5, 233–259. [Google Scholar] [CrossRef]
- Xia, K.; Yang, Y. Three-dimensional finite element modeling of tire/ground interaction. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 498–516. [Google Scholar] [CrossRef]
- Chou, C.; Zhu, F.; Skelton, P.; Wagner, C.; Yang, K. Numerical simulations of tyre/soil interaction using geomaterial properties characterised with a new calibration method. Int. J. Veh. Saf. 2012, 5, 287–306. [Google Scholar] [CrossRef]
- Suvanjumrat, C.; Rugsaj, R. The dynamic finite element model of non-pneumatic tire under comfortable riding evaluation. Int. J. GEOMATE 2020, 19, 62–68. [Google Scholar] [CrossRef]
- Melanz, D.; Jayakumar, P.; Negrut, D. Experimental validation of a differential variational inequality-based approach for handling friction and contact in vehicle/granular-terrain interaction. J. Terramech. 2016, 65, 1–13. [Google Scholar] [CrossRef]
- Hu, W.; Zhou, Z.; Chandler, S.; Apostolopoulos, D.; Kamrin, K.; Serban, R.; Negrut, D. Traction control design for off-road mobility using an SPH-DAE cosimulation framework. Multibody Syst. Dyn. 2022, 55, 165–188. [Google Scholar] [CrossRef]
- Osinenko, P.V.; Geissler, M.; Herlitzius, T. A method of optimal traction control for farm tractors with feedback of drive torque. Biosyst. Eng. 2015, 129, 20–33. [Google Scholar] [CrossRef]
- Shao, X.; Zheng, B.; Luo, Z.; Song, Z. Establishment and Validation of a Structural Dynamics Model with Power Take-Off Driveline for Agricultural Tractors. Agriculture 2022, 12, 1297. [Google Scholar] [CrossRef]
- Birkmann, C.; Fedde, T.; Frerichs, L. Drivetrain, Chassis and Tire-Soil Contact Influence on Power Shift Operations in Standard Tractors. Landtechnik 2018, 73, 146–160. [Google Scholar]
- Li, B.; Sun, D.; Hu, M.; Zhou, X.; Wang, D.; Xia, Y.; You, Y. Automatic gear-shifting strategy for fuel saving by tractors based on real-time identification of draught force characteristics. Biosyst. Eng. 2020, 193, 46–61. [Google Scholar] [CrossRef]
- Sim, K.; Lee, H.; Yoon, J.W.; Choi, C.; Hwan, S.H. Effectiveness evaluation of hydro-pneumatic and semi-active cab suspension for the improvement of ride comfort of agricultural tractors. J. Terramech. 2017, 69, 23–32. [Google Scholar] [CrossRef]
- Zahidi, Y.; El Moufid, M.; Benhadou, S.; Medromi, H. An Assessment of Low-Cost Tractor Motorization with Main Farming Implements. World Electr. Veh. J. 2020, 11, 74. [Google Scholar] [CrossRef]
- Rossi, C.; Pontara, D.; Falcomer, C.; Bertoldi, M.; Mandrioli, R. A Hybrid–Electric Driveline for Agricultural Tractors Based on an e-CVT Power-Split Transmission. Energies 2021, 14, 6912. [Google Scholar] [CrossRef]
- Zhu, Z.; Lai, L.; Sun, X.; Chen, L.; Cai, Y. Design and Analysis of a Novel Mechanic- Electronic-Hydraulic Powertrain System for Agriculture Tractors. IEEE Access 2021, 9, 153811–153823. [Google Scholar] [CrossRef]
- Regazzi, N.; Maraldi, M.; Molari, G. A theoretical study of the parameters affecting the power delivery efficiency of an agricultural tractor. Biosyst. Eng. 2019, 186, 214–227. [Google Scholar] [CrossRef]
- Majdoubi, R.; Masmoudi, L.; Elharif, A. Coupled nonlinear controller for vehicle trajectory tracking in a deformable soil: Application to a four-wheeled mobile agricultural robot. J. Terramech. 2023, 110, 47–68. [Google Scholar] [CrossRef]
- Malavazi, F.B.P.; Guyonneau, R.; Fasquel, J.B.; Lagrange, S.; Mercier, F. LiDAR-only based navigation algorithm for an autonomous agricultural robot. Comput. Electron. Agric. 2018, 154, 71–79. [Google Scholar] [CrossRef]
- American Society of Agricultural Engineers (ASAE). Agricultural Machinery MANAGEMENT Data (ASAE D497.4); American Society of Agricultural Engineers (ASAE): St. Joseph, MI, USA, 2000. [Google Scholar]
- Söhne, W. Some Basic Considerations of Soil Mechanics as Applied to Agricultural Engineering; National Institute of Agricultural Engineering: Silsoe, UK, 1956. [Google Scholar]
- Battiato, A.; Diserens, E.; Sartori, L. Traction performance simulation for mechanical front wheel drive tractors: Towards a practical computer tool. J. Agric. Eng. 2013, 44, 338–343. [Google Scholar] [CrossRef]
- Kivekäs, K.; Lajunen, A.; Baldi, F.; Vepsäläinen, J.; Tammi, K. Reducing the energy consumption of electric buses with design choices and predictive driving. IEEE Trans. Veh. Technol. 2019, 68, 11409–11419. [Google Scholar] [CrossRef]
- Janosi, Z.; Hanamoto, B. Analytical determination of drawbar pull as a function of slip for tracked vehicles in deformable soils. In Proceedings of the 1st International Conference on Terrain-Vehicle Systems, Turin, Italy, 1961. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2001; p. 20. [Google Scholar]
- J670_202206; SAE Vehicle Dynamics Standards Committee. Vehicle Dynamics Terminology. Society of Automotive Engineers: Warrendale, PA, USA, 2022.
- Liang, D.; Gao, H.; Deng, Z.; Tao, J. Wheel slip-sinkage and its prediction model of lunar rover. J. Cent. South Univ. Technol. 2010, 17, 129–135. [Google Scholar]
- Holm, I.C. Multi-pass behaviour of pneumatic tires. J. Terramech. 1969, 6, 47–71. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Goering, C.E.; Rohrbach, R.P.; Buckmaster, D.R. Soil Tillage. In Engineering Principles of Agricultural Machines, 2nd ed.; ASABE: St. Joseph, MI, USA, 2006; pp. 169–229. [Google Scholar]
- Taiwan Golden Bee Co., Ltd. Blade Service Manual; Taiwan Golden Bee Co., Ltd.: Taiwan City, Taiwan.
- Argonne National Laboratory Vehicle & Mobility Systems Department. Autonomie. Available online: https://vms.taps.anl.gov/tools/autonomie/ (accessed on 10 November 2023).
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thévenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Wong, J.Y. Terramechanics and Off-Road Vehicle Engineering: Terrain Behaviour, Off-road Vehicle Performance and Design, 2nd ed.; Elsevier: Oxford, UK, 2010; pp. 86–125. [Google Scholar]
- Perozzi, D.; Mattetti, M.; Molari, G.; Sereni, E. Methodology to analyse farm tractor idling time. Biosyst. Eng. 2016, 148, 81–89. [Google Scholar] [CrossRef]
- Troncon, D.; Alberti, L. Case of Study of the Electrification of a Tractor: Electric Motor Performance Requirements and Design. Energies 2020, 13, 2197. [Google Scholar] [CrossRef]
- Lajunen, A. Simulation of energy efficiency and performance of electrified powertrains in agricultural tractors. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference (VPPC), Merced, CA, USA, 1–4 November 2022. [Google Scholar]








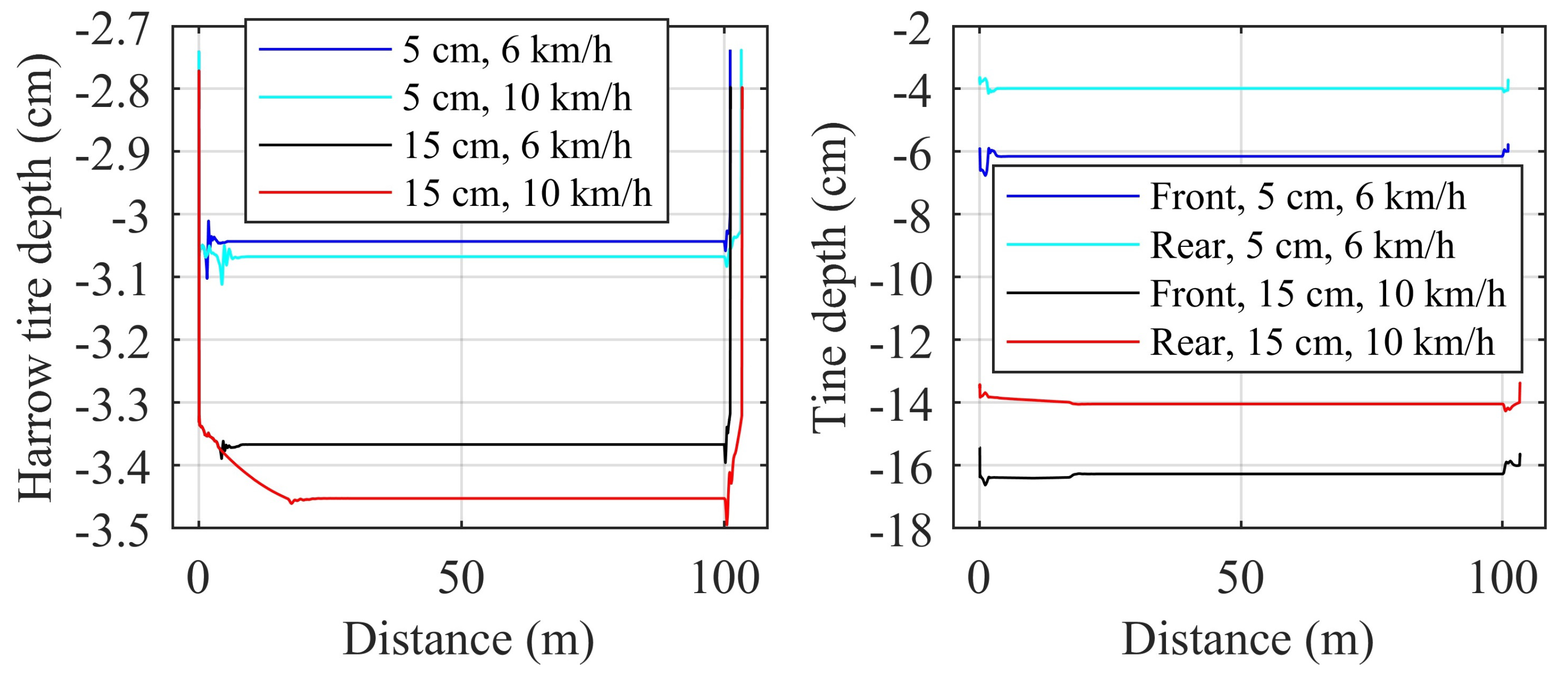
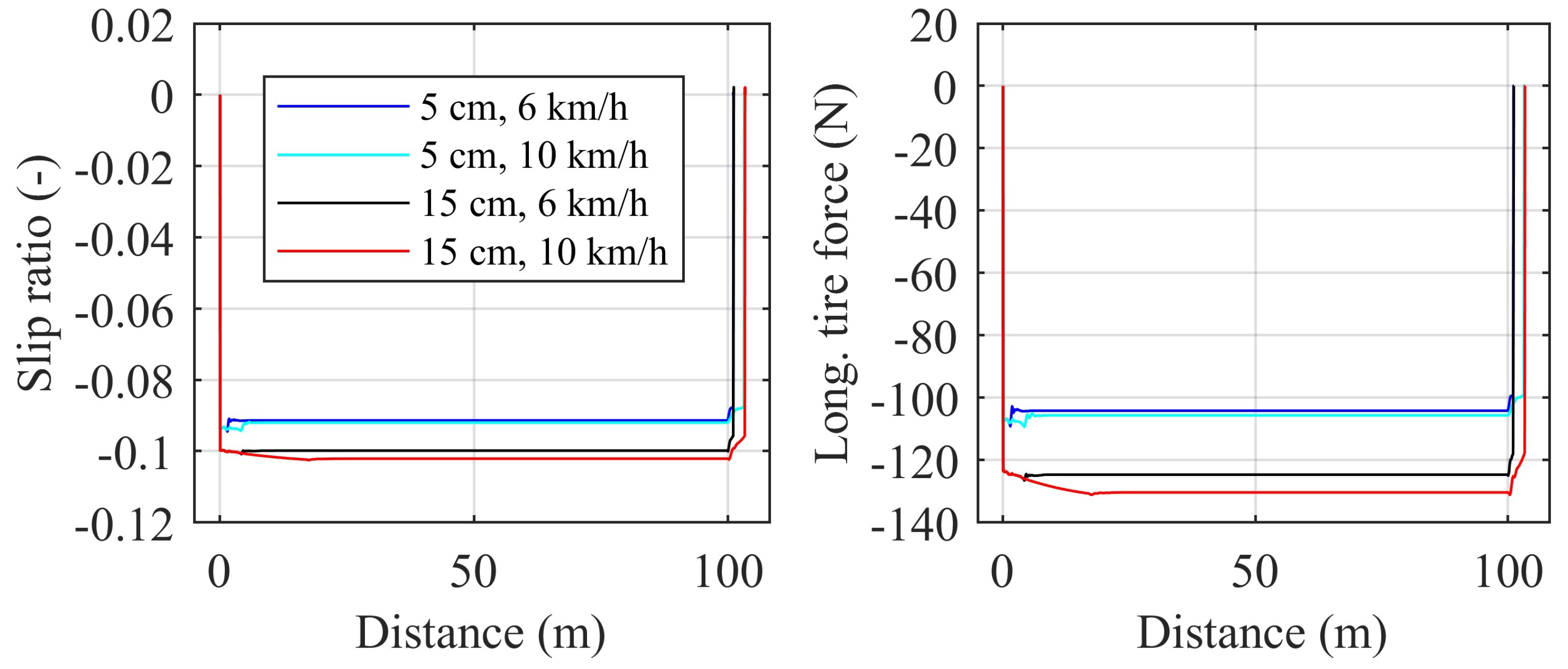
| Parameter | Value |
|---|---|
| Wheelbase (m) | 1.29 |
| Track width (m) | 1.20 |
| AWD curb weight (kg) | 520 |
| RWD/FWD curb weight (kg) | 490 |
| AWD EM max. power (kW) | 6 |
| AWD EM max. torque (Nm) | 80 |
| RWD/FWD EM max. power (kW) | 12 |
| RWD/FWD EM max. torque (Nm) | 160 |
| EM max. speed (rpm) | 3000 |
| Final drive ratio (-) | 17.95 |
| Final drive efficiency (%) | 98 |
| Battery capacity (Ah) | 360 |
| Battery energy capacity (kWh) | 17.3 |
| Battery nominal voltage (V) | 48.1 |
| Tire diameter (m) | 0.635 |
| Tire width (m) | 0.203 |
| Aux. device power demand (W) | 200 |
| RWD1 | RWD2 | FWD1 | FWD2 | AWD | |
|---|---|---|---|---|---|
| Front weight fraction (%) | 40 | 30 | 60 | 70 | 50 |
| Rear weight fraction (%) | 60 | 70 | 40 | 30 | 50 |
| Parameter | Value |
|---|---|
| Length (m) | 2.0 |
| Width (m) | 1.30 |
| Mass (kg) | 200 |
| Number of tine rows (-) | 2 |
| Number of tines per row (-) | 5 |
| Tine length (m) | 0.25 |
| Tine width (m) | 0.02 |
| Tine angle (deg) | 25 |
| Tire diameter (m) | 0.584 |
| Tire width (m) | 0.178 |
| Parameter | Sandy Loam | Clayey Loam |
|---|---|---|
| Cohesive modulus (-) | 24.45 | 4.43 |
| Frictional modulus (-) | 96.34 | 87.60 |
| Cohesion c (Pa) | 3300 | 6100 |
| Friction angle (deg) | 33.7 | 26.6 |
| Shear deformation modulus k (m) | 0.0076 | 0.0037 |
| Density (kg/m3) | 1549 | 1664 |
| Moisture content (%) | 49 | 52 |
| 0.4 | 0.2 | 0.8 | 0.6 | 0.1178 | 0.1672 | 0.0348 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kivekäs, K.; Lajunen, A. Effect of Soil Properties and Powertrain Configuration on the Energy Consumption of Wheeled Electric Agricultural Robots. Energies 2024, 17, 966. https://doi.org/10.3390/en17040966
Kivekäs K, Lajunen A. Effect of Soil Properties and Powertrain Configuration on the Energy Consumption of Wheeled Electric Agricultural Robots. Energies. 2024; 17(4):966. https://doi.org/10.3390/en17040966
Chicago/Turabian StyleKivekäs, Klaus, and Antti Lajunen. 2024. "Effect of Soil Properties and Powertrain Configuration on the Energy Consumption of Wheeled Electric Agricultural Robots" Energies 17, no. 4: 966. https://doi.org/10.3390/en17040966
APA StyleKivekäs, K., & Lajunen, A. (2024). Effect of Soil Properties and Powertrain Configuration on the Energy Consumption of Wheeled Electric Agricultural Robots. Energies, 17(4), 966. https://doi.org/10.3390/en17040966






