Review of Heat Transfer Characteristics of Natural Gas Hydrate
Abstract
1. Introduction
2. Heat Transfer Measurement Methods
2.1. Heat Flow Density and Specific Heat Capacity Measurement
2.2. Effective Thermal Conductivity Measurement
2.3. Improvement in Measurement Method for Thermal Conductivity of Natural Gas Hydrate
3. Study of Heat Transfer Characteristics of Gas Hydrate
3.1. Effect of Porous Media Material on Heat Transfer Characteristics of Hydrate
3.2. Effect of Porosity of Porous Media on Heat Transfer Characteristics of Hydrate
3.3. Effect of Particle Size of Porous Media on Heat Transfer Characteristics
3.4. Effect of Hydrate Saturation and Water Saturation on Heat Transfer Characteristics
3.5. Effect of the Hydrate Dissociation Process on Heat Transfer
3.6. Effect of Environmental Heat Conduction on Hydrate Dissociation Process
4. Predictive Model for ETC
5. Study of Heat Transfer Mechanism of Hydrate
5.1. Methods for Studying Heat Transfer Mechanisms on a Molecular Scale
5.2. Host Molecular Heat Transfer Mechanism
5.3. Guest Molecular Heat Transfer Mechanism
6. Development and Discussion of Heat Transfer in a Multi-phase Complex System
7. Conclusions
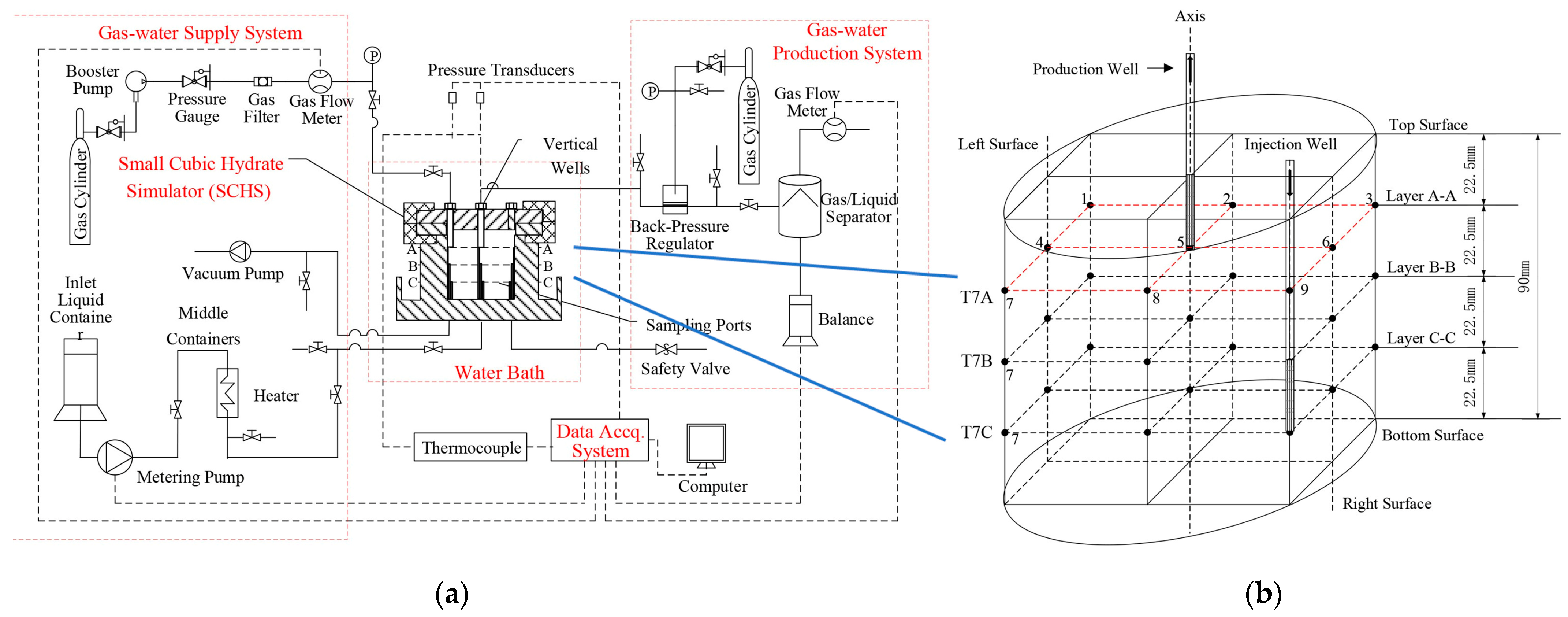
- (a)
- The heat transfer measurement methods of natural gas hydrate mainly include heat flux measurement and ETC measurement. The heat flux measurement method realizes the visualization of the heat transfer process by measuring the temperature changes at different positions and qualitatively analyzes the heat transfer path of the system; the ETC measurement method obtains the ETC of the system by calculating the temperature response between the measuring points and quantitatively analyzes the heat transfer characteristics of the system.
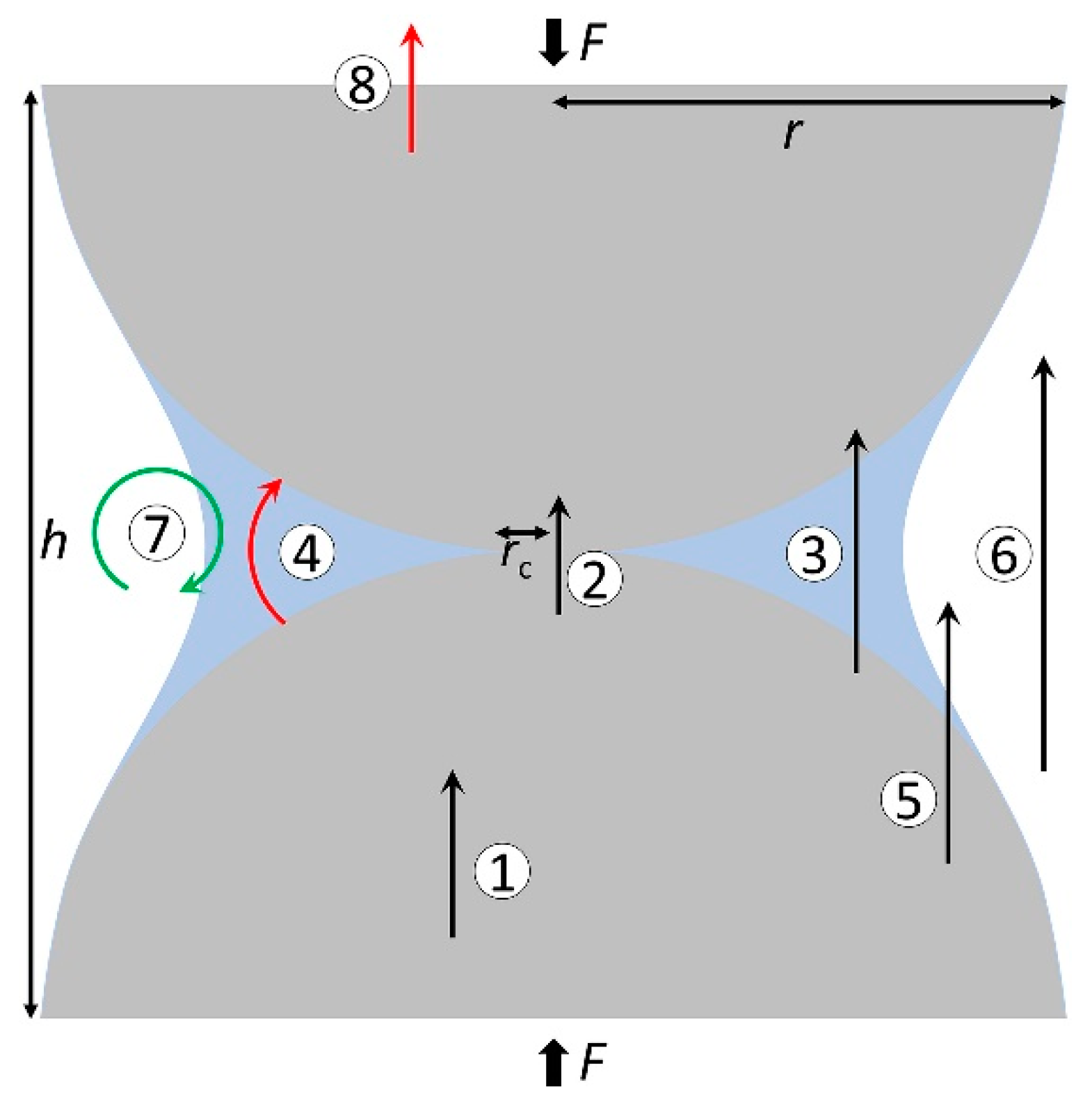
- (b)
- The phase change in the hydrate in the process of hydrate decomposition causes the change in heat conduction and heat convection. The effective heat transfer of hydrate plays an important role in the control of the hydrate decomposition rate.
- (c)
- The natural gas hydrate reservoir is a multi-component complex sediment system. The thermal conductivity of these components is different, and the decomposition of the hydrate itself and the environmental heat transfer of the reservoir in which the hydrate is located have an impact on the natural gas hydrate and the reservoir. Therefore, the heat transfer characteristics of natural gas hydrate reservoirs are not only related to the material of porous media, pore structure, and particle size distribution, but also to the water content of the system, hydrate saturation and distribution, hydrate decomposition, and reservoir heat conduction.
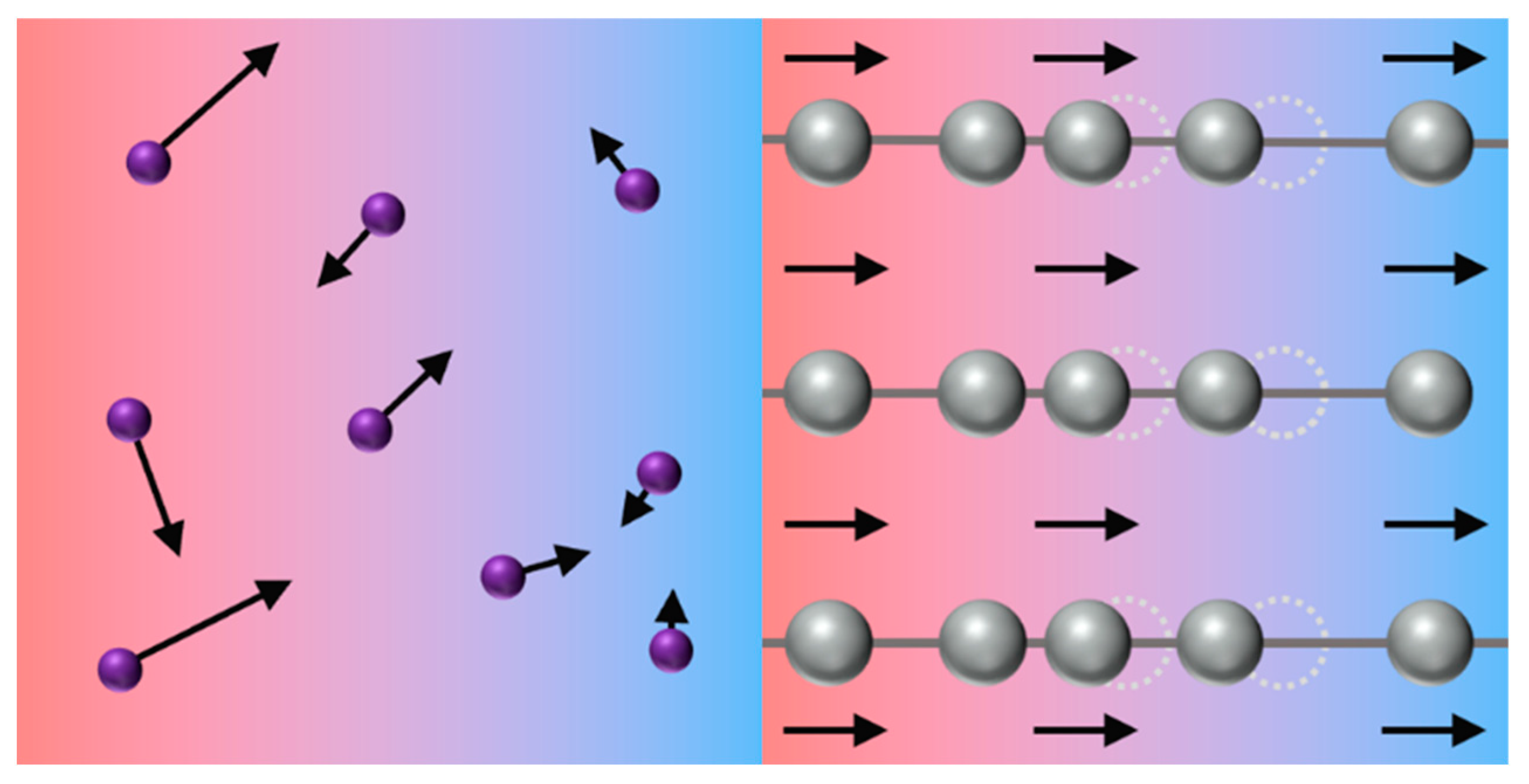
- (d)
- The study of the heat transfer mechanism of natural gas hydrates found that the interaction between host molecules is dominant in the process of heat transfer. The vibration of the hydrate cage lattice will diffuse heat. The local vibration of guest molecules affects the vibration of host water molecules. The coupling vibration of guest molecules determines the transfer intensity of heat energy. Therefore, the enhancement in the interaction between host and guest molecules will help to improve the thermal conductivity of hydrates.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ETC | Effective thermal conductivity |
| AI | Artificial intelligence |
| EMD | Equilibrium molecular dynamics simulation |
| NEMD | Non-equilibrium molecular dynamics simulation |
| HCACF | Heat current autocorrelation function |
| PDOS | Projected density of state |
| VCCF | Velocity cross-correlation function |
References
- Sloan, E.D. Natural-Gas Hydrates. J. Pet. Technol. 1991, 43, 1414–1417. [Google Scholar] [CrossRef]
- Sloan, E.D. Gas hydrates: Review of physical/chemical properties. Energy Fuels 1998, 12, 191–196. [Google Scholar] [CrossRef]
- Kvenvolden, K.A. Methane hydrate in the global organic carbon cycle. Terra Nova 2002, 14, 302–306. [Google Scholar] [CrossRef]
- Argentino, C.; Conti, S.; Fioroni, C.; Fontana, D. Evidences for Paleo-Gas Hydrate Occurrence: What We Can Infer for the Miocene of the Northern Apennines (Italy). Geosciences 2019, 9, 134. [Google Scholar] [CrossRef]
- Yin, Z.; Linga, P. Methane hydrates: A future clean energy resource. Chin. J. Chem. Eng. 2019, 27, 2026–2036. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Zhang, X.; Liu, J.-W.; Lee, Y.; Li, X.-S. Natural gas hydrate resources and hydrate technologies: A review and analysis of the associated energy and global warming challenges. Energy Environ. Sci. 2021, 14, 5611–5668. [Google Scholar] [CrossRef]
- Hassanpouryouzband, A.; Joonaki, E.; Farahani, M.V.; Takeya, S.; Ruppel, C.; Yang, J.H.; English, N.J.; Schicks, J.M.; Edlmann, K.; Mehrabian, H.; et al. Gas hydrates in sustainable chemistry. Chem. Soc. Rev. 2020, 49, 5225–5309. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.W.; Lu, C.; Wang, P.K.; Liang, Q.Y. Hydrate phase transition and seepage mechanism during natural gas hydrate production tests in the South China Sea: A review and prospect. Geol. China 2022, 49, 749–769. [Google Scholar] [CrossRef]
- Song, Y.C.; Cheng, C.X.; Zhao, J.F.; Zhu, Z.H.; Liu, W.G.; Yang, M.J.; Xue, K.H. Evaluation of gas production from methane hydrates using depressurization, thermal stimulation and combined methods. Appl. Energy 2015, 145, 265–277. [Google Scholar] [CrossRef]
- Guangjin, C.; Changyu, S.; Qinglan, M. Gas Hydrate Science and Technology; Chemical Industry Press: Beijing, China, 2008. [Google Scholar]
- Zeng, H.; Zhang, Y.; Zhang, L.; Chen, Z.; Li, X. Study on Hydrate Production Behaviors by Depressurization Combined with Brine Injection in the Excess-Water Hydrate Reservoir. Entropy 2022, 24, 765. [Google Scholar] [CrossRef]
- Vasheghani Farahani, M.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Development of a coupled geophysical–geothermal scheme for quantification of hydrates in gas hydrate-bearing permafrost sediments. Phys. Chem. Chem. Phys. 2021, 23, 24249–24264. [Google Scholar] [CrossRef]
- Vasheghani Farahani, M.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Insights into the climate-driven evolution of gas hydrate-bearing permafrost sediments: Implications for prediction of environmental impacts and security of energy in cold regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef] [PubMed]
- Ruppel, C. Permafrost-Associated Gas Hydrate: Is It Really Approximately 1% of the Global System? J. Chem. Eng. Data 2015, 60, 429–436. [Google Scholar] [CrossRef]
- Liu, W.; Fan, A.W.; Huang, X.M. Heat and Mass Transfer Theory and Application of Porous Media; Science Press: Beijing, China, 2006. [Google Scholar]
- Li, X.Y.; Li, X.S.; Wang, Y.; Li, G.; Zhang, Y.; Hu, H.Q.; Wan, K.; Zeng, H.P. Influence of Particle Size on the Heat and Mass Transfer Characteristics of Methane Hydrate Formation and Decomposition in Porous Media. Energy Fuels 2021, 35, 2153–2164. [Google Scholar] [CrossRef]
- Liu, S.; Liu, S.; Ren, T. Ultrasonic tomography based temperature distribution measurement method. Measurement 2016, 94, 671–679. [Google Scholar] [CrossRef]
- Jia, Y.; Chernyshev, V.; Skliar, M. Ultrasound measurements of segmental temperature distribution in solids: Method and its high-temperature validation. Ultrasonics 2016, 66, 91–102. [Google Scholar] [CrossRef]
- Jia, Y.L.; Skliar, M. Noninvasive Ultrasound Measurements of Temperature Distribution and Heat Fluxes in Solids. Energy Fuels 2016, 30, 4363–4371. [Google Scholar] [CrossRef]
- Sumi, C.; Kuwabara, J. Determination of thermal conductivity distribution from internal temperature distribution measurements. Rev. Sci. Instrum. 2006, 77, 064904. [Google Scholar] [CrossRef]
- Stoll, R.D.; Bryan, G.M. Physical properties of sediments containing gas hydrates. J. Geophys. Res. Solid Earth 1979, 84, 1629–1634. [Google Scholar] [CrossRef]
- Handa, Y.P. Compositions, enthalpies of dissociation, and heat capacities in the range 85 to 270 K for clathrate hydrates of methane, ethane, and propane, and enthalpy of dissociation of isobutane hydrate, as determined by a heat-flow calorimeter. J. Chem. Thermodyn. 1986, 18, 915–921. [Google Scholar] [CrossRef]
- Dai, S.; Cha, J.H.; Rosenbaum, E.J.; Zhang, W.; Seol, Y. Thermal conductivity measurements in unsaturated hydrate-bearing sediments. Geophys. Res. Lett. 2015, 42, 6295–6305. [Google Scholar] [CrossRef]
- Wan, L.H.; Liang, D.Q.; Guan, J.A. The Present Situation of Studies on Thermal Conduction of Gas Hydrate. Adv. NR Energy 2014, 2, 385–389. [Google Scholar]
- Sun, S.C.; Zhao, J.R.; Zhao, J.; Hao, Y.C.; Yang, J. The effective thermal conductivity of methane hydrate-bearing seasand. J. Chem. Thermodyn. 2019, 132, 423–431. [Google Scholar] [CrossRef]
- Tavman, I.H. Effective thermal conductivity of granular porous materials. Int. Commun. Heat Mass Transf. 1996, 23, 169–176. [Google Scholar] [CrossRef]
- Wei, G.; Wang, L.; Xu, C.; Du, X.; Yang, Y. Thermal conductivity investigations of granular and powdered silica aerogels at different temperatures and pressures. Energy Build. 2016, 118, 226–231. [Google Scholar] [CrossRef]
- Von Herzen, R.; Maxwell, A.E. The measurement of thermal conductivity of deep-sea sediments by a needle-probe method. J. Geophys. Res. 1959, 64, 1557–1563. [Google Scholar] [CrossRef]
- Waite, W.F.; de Martin, B.J.; Kirby, S.H.; Pinkston, J.; Ruppel, C.D. Thermal conductivity measurements in porous mixtures of methane hydrate and quartz sand. Geophys. Res. Lett. 2002, 29, 82-1–82-4. [Google Scholar] [CrossRef]
- Li, D.L.; Du, J.W.; He, S.; Liang, D.Q.; Zhao, X.Y.; Yang, X.Y. Measurement and modeling of the effective thermal conductivity for porous methane hydrate samples. Sci. China-Chem. 2012, 55, 373–379. [Google Scholar] [CrossRef]
- Shi, L. Experimental Study on Thermal Conductivity of Gas Hydrate; Guangzhou Institute of Energy Conversion: Guangzhou, China, 2002. [Google Scholar]
- Yang, L.; Zhao, J.F.; Liu, W.G.; Yang, M.J.; Song, Y.C. Experimental study on the effective thermal conductivity of hydrate-bearing sediments. Energy 2015, 79, 203–211. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, B.; Yang, L.; Cheng, C.; Song, Y. A novel apparatus for in situ measurement of thermal conductivity of hydrate-bearing sediments. Rev. Sci. Instrum. 2015, 86, 085110. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Y.; Li, X.S.; Zhang, Y.; Chen, Z.Y. Experimental study of methane hydrate dissociation in porous media with different thermal conductivities. Int. J. Heat Mass Transf. 2019, 144, 118528. [Google Scholar] [CrossRef]
- Wang, B.; Fan, Z.; Lv, P.F.; Zhao, J.F.; Song, Y.C. Measurement of effective thermal conductivity of hydrate-bearing sediments and evaluation of existing prediction models. Int. J. Heat Mass Transf. 2017, 110, 142–150. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, J.F.; Wang, B.; Liu, W.G.; Yang, M.J.; Song, Y.C. Effective thermal conductivity of methane hydrate-bearing sediments: Experiments and correlations. Fuel 2016, 179, 87–96. [Google Scholar] [CrossRef]
- Zhao, J.F.; Wang, J.Q.; Liu, W.G.; Song, Y.C. Analysis of heat transfer effects on gas production from methane hydrate by thermal stimulation. Int. J. Heat Mass Transf. 2015, 87, 145–150. [Google Scholar] [CrossRef]
- Cortes, D.D.; Martin, A.I.; Yun, T.S.; Francisca, F.M.; Santamarina, J.C.; Ruppel, C. Thermal conductivity of hydrate-bearing sediments. J. Geophys. Res.-Solid Earth 2009, 114, B11103. [Google Scholar] [CrossRef]
- Priest, J.A.; Best, A.I.; Clayton, C.R.I. A laboratory investigation into the seismic velocities of methane gas hydrate-bearing sand. J. Geophys. Res. Solid Earth 2005, 110, B04102. [Google Scholar] [CrossRef]
- Priest, J.A.; Rees, E.V.L.; Clayton, C.R.I. Influence of gas hydrate morphology on the seismic velocities of sands. J. Geophys. Res. Solid Earth 2009, 114, B11205. [Google Scholar] [CrossRef]
- Best, A.I.; Priest, J.A.; Clayton, C.R.I.; Rees, E.V.L. The effect of methane hydrate morphology and water saturation on seismic wave attenuation in sand under shallow sub-seafloor conditions. Earth Planet. Sci. Lett. 2013, 368, 78–87. [Google Scholar] [CrossRef]
- Tupsakhare, S.S.; Kattekola, S.; Castaldi, M.J. An Application of the Results from the Large-Scale Thermal Stimulation Method of Methane Hydrate Dissociation to the Field Tests. Ind. Eng. Chem. Res. 2017, 56, 4588–4599. [Google Scholar] [CrossRef]
- Wei, R.P.; Shi, K.J.; Guo, X.W.; Wang, T.; Lv, X.; Li, Q.P.; Zhang, Y.; Zhao, J.F.; Yang, L. Evolving thermal conductivity upon formation and decomposition of hydrate in natural marine sediments. Fuel 2021, 302, 121141. [Google Scholar] [CrossRef]
- Wu, D.D.; Li, S.X.; Guo, Y.; Liu, L.; Wang, Z.Q. A novel model of effective thermal conductivity for gas hydrate-bearing sediments integrating the hydrate saturation and pore morphology evolution. Fuel 2022, 324, 124825. [Google Scholar] [CrossRef]
- Li, D.L.; Liang, D.Q. Experimental study on the effective thermal conductivity of methane hydrate-bearing sand. Int. J. Heat Mass Transf. 2016, 92, 8–14. [Google Scholar] [CrossRef]
- Vasheghani Farahani, M.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Heat Transfer in Unfrozen and Frozen Porous Media: Experimental Measurement and Pore-Scale Modeling. Water Resour. Res. 2020, 56, e2020WR027885. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Carslaw, H.S. Conduction of Heat in Solids. J. Eng. Mater. Technol. Trans. Asme 1986, 108–378. [Google Scholar]
- Nasirian, A.; Cortes, D.D.; Dai, S. The physical nature of thermal conduction in dry granular media. Geotech. Lett. 2015, 5, 1–5. [Google Scholar] [CrossRef]
- Batchelor, G.K.; Obrien, R.W. Thermal or Electrical-Conduction through a Granular Material. Proc. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci. 1977, 355, 313–333. [Google Scholar]
- Midttomme, K.; Roaldset, E. The effect of grain size on thermal conductivity of quartz sands and silts. Pet. Geosci. 1998, 4, 165–172. [Google Scholar] [CrossRef]
- Zhan, L.; Wang, Y.; Li, X.S. Experimental study on characteristics of methane hydrate formation and dissociation in porous medium with different particle sizes using depressurization. Fuel 2018, 230, 37–44. [Google Scholar] [CrossRef]
- Ahn, J.; Jung, J. Effects of Fine Particles on Thermal Conductivity of Mixed Silica Sands. Appl. Sci. 2017, 7, 650. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, L.; Feng, J.C.; Li, X.S. Influence of the Particle Size of Sandy Sediments on Heat and Mass Transfer Characteristics during Methane Hydrate Dissociation by Thermal Stimulation. Energies 2019, 12, 4227. [Google Scholar] [CrossRef]
- Singh, D.N.; Devid, K. Generalized relationships for estimating soil thermal resistivity. Exp. Therm. Fluid Sci. 2000, 22, 133–143. [Google Scholar] [CrossRef]
- Wei, R.P.; Xia, Y.Q.; Qu, A.X.; Lv, X.; Fan, Q.; Zhang, L.X.; Zhang, Y.; Zhao, J.F.; Yang, L. Dependence of thermal conductivity on the phase transition of gas hydrate in clay sediments. Fuel 2022, 317, 123565. [Google Scholar] [CrossRef]
- He, J.; Li, X.S.; Chen, Z.Y.; You, C.Y.; Yan, K.F.; Xia, Z.M.; Li, Q.P. Effect of hydrate distribution on effective thermal conductivity changes during hydrate formation in hydrate-bearing quartz sands. Int. J. Heat Mass Transf. 2021, 174, 121289. [Google Scholar] [CrossRef]
- Li, X.Y.; Feng, J.C.; Li, X.S.; Wang, Y.; Hu, H.Q. Experimental study of methane hydrate formation and decomposition in the porous medium with different thermal conductivities and grain sizes. Appl. Energy 2022, 305, 117852. [Google Scholar] [CrossRef]
- Henninges, J.; Huenges, E.; Burkhardt, H. In situ thermal conductivity of gas-hydrate-bearing sediments of the Mallik 5L-38 well. J. Geophys. Res. Solid Earth 2005, 110, B11206. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Chen, Z.; Li, Q.; Xia, Z.; Zhang, Y.; Wang, Y.; You, C. Effective thermal conductivity changes of the hydrate-bearing quartz sands in depressurization and soaking. J. Nat. Gas Sci. Eng. 2021, 89, 103878. [Google Scholar] [CrossRef]
- Kamath, V.A.; Holder, G.D.; Angert, P.F. 3 Phase Interfacial Heat-Transfer during the Dissociation of Propane Hydrates. Chem. Eng. Sci. 1984, 39, 1435–1442. [Google Scholar] [CrossRef]
- Kamath, V.A.; Holder, G.D. Dissociation Heat-Transfer Characteristics of Methane Hydrates. Aiche J. 1987, 33, 347–350. [Google Scholar] [CrossRef]
- Zhao, J.F.; Cheng, C.X.; Song, Y.C.; Liu, W.G.; Liu, Y.; Xue, K.H.; Zhu, Z.H.; Yang, Z.; Wang, D.Y.; Yang, M.J. Heat Transfer Analysis of Methane Hydrate Sediment Dissociation in a Closed Reactor by a Thermal Method. Energies 2012, 5, 1292–1308. [Google Scholar] [CrossRef]
- Pooladi-Darvish, M.; Hong, H. Effect of conductive and convective heat flow on gas production from natural hydrates by depressurization. In Advances in the Study of Gas Hydrates; Springer: Boston, MA, USA, 2004; pp. 43–65. [Google Scholar]
- Kou, X.; Wang, Y.; Li, X.S.; Zhang, Y.; Chen, Z.Y. Influence of heat conduction and heat convection on hydrate dissociation by depressurization in a pilot-scale hydrate simulator. Appl. Energy 2019, 251, 113405. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Liu, G.; Yang, H.; Huang, H. Numerical Simulations of Decomposition of Hydrate Particles in Flowing Water Considering the Coupling of Intrinsic Kinetics with Mass and Heat Transfer Rates. ACS Omega 2021, 6, 23355–23367. [Google Scholar] [CrossRef]
- Hao, Y.M.; Li, X.Z.; Li, S.X.; Lu, G.Z.; Liu, Y.Y.; Wei, X.L. Heat conduction and thermal convection on thermal front movement during natural gas hydrate thermal stimulation exploitation. Oil Gas Sci. Technol.-Rev. D Ifp Energ. Nouv. 2018, 73, 40. [Google Scholar] [CrossRef]
- Krivchikov, A.I.; Romantsova, O.O.; Korolyuk, O.A. The effect of proton ordering on the thermal conductivity of clathrate tetrahydrofuran hydrate. Low Temp. Phys. 2008, 34, 648–654. [Google Scholar] [CrossRef]
- Li, G.; Li, B.; Li, X.S.; Zhang, Y.; Wang, Y. Experimental and Numerical Studies on Gas Production from Methane Hydrate in Porous Media by Depressurization in Pilot-Scale Hydrate Simulator. Energy Fuels 2012, 26, 6300–6310. [Google Scholar] [CrossRef]
- Li, B.; Liang, Y.P.; Li, X.S.; Wu, H.J. Numerical analysis of methane hydrate decomposition experiments by depressurization around freezing point in porous media. Fuel 2015, 159, 925–934. [Google Scholar] [CrossRef]
- Wan, Q.C.; Si, H.; Li, B.; Li, G. Heat transfer analysis of methane hydrate dissociation by depressurization and thermal stimulation. Int. J. Heat Mass Transf. 2018, 127, 206–217. [Google Scholar] [CrossRef]
- Oyama, H.; Konno, Y.; Masuda, Y.; Narita, H. Dependence of Depressurization-Induced Dissociation of Methane Hydrate Bearing Laboratory Cores on Heat Transfer. Energy Fuels 2009, 23, 4995–5002. [Google Scholar] [CrossRef]
- Cheng, C.X.; Zhao, J.F.; Yang, M.J.; Liu, W.G.; Wang, B.; Song, Y.C. Evaluation of Gas Production from Methane Hydrate Sediments with Heat Transfer from Over-Underburden Layers. Energy Fuels 2015, 29, 1028–1039. [Google Scholar] [CrossRef]
- Rocha, L.A.O.; Neagu, M.; Bejan, A.; Cherry, R.S. Convection with phase change during gas formation from methane hydrates via depressurization of porous layers. J. Porous Media 2001, 4, 283–295. [Google Scholar] [CrossRef]
- Shahbazi, A.; Pooladi-Darvish, M. Behavior of depressurization in type III hydrate reservoirs. In Proceedings of the Canadian Unconventional Resources and International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010; OnePetro: Richardson, TX, USA, 2010. [Google Scholar]
- Sloan Jr, E.D.; Koh, C.A. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Sun, X.; Mohanty, K.K. Kinetic simulation of methane hydrate formation and dissociation in porous media. Chem. Eng. Sci. 2006, 61, 3476–3495. [Google Scholar] [CrossRef]
- Sun, X.; Mohanty, K. Simulation of hydrate reservoir, SPE 93015. In Proceedings of the Presentations of SPE Reservoir Symposium, Woodlands, TX, USA, 31 January–2 February 2005; pp. 3–5. [Google Scholar]
- Yan, K.F.; Li, X.S.; Chen, Z.Y.; Xia, Z.M.; Xu, C.G.; Zhang, Z.Q. Molecular Dynamics Simulation of the Crystal Nucleation and Growth Behavior of Methane Hydrate in the Presence of the Surface and Nanopores of Porous Sediment. Langmuir 2016, 32, 7975–7984. [Google Scholar] [CrossRef]
- Walsh, M.R.; Koh, C.A.; Sloan, E.D.; Sum, A.K.; Wu, D.T. Microsecond Simulations of Spontaneous Methane Hydrate Nucleation and Growth. Science 2009, 326, 1095–1098. [Google Scholar] [CrossRef]
- Fang, B.; Moultos, O.A.; Lu, T.; Sun, J.X.; Liu, Z.C.; Ning, F.L.; Vlugt, T.J.H. Effects of nanobubbles on methane hydrate dissociation: A molecular simulation study. Fuel 2023, 345, 128230. [Google Scholar] [CrossRef]
- English, N.J.; Tse, J.S.; Carey, D.J. Mechanisms for thermal conduction in various polymorphs of methane hydrate. Phys. Rev. B 2009, 80, 134306. [Google Scholar] [CrossRef]
- Yang, P.Z. Investigation of Gas Thermal Conductivity in Nanopore by Molecular Dynamics; Chongqing University: Chongqing, China, 2017. [Google Scholar]
- Tretiakov, K.V.; Scandolo, S. Thermal conductivity of solid argon at high pressure and high temperature: A molecular dynamics study. J. Chem. Phys. 2004, 121, 11177–11182. [Google Scholar] [CrossRef]
- Liu, M.; Xu, Z. Phonon heat conduction and quantum correction of methane hydrate. CIESC J. 2020, 71, 1424–1431. [Google Scholar]
- Manley, M.E.; May, A.F.; Winn, B.L.; Abernathy, D.L.; Sahul, R.; Hermann, R.P. Phason-Dominated Thermal Transport in Fresnoite. Phys. Rev. Lett. 2022, 129, 255901. [Google Scholar] [CrossRef]
- English, N.J.; Tse, J.S. Mechanisms for thermal conduction in methane hydrate. Phys. Rev. Lett. 2009, 103, 015901. [Google Scholar] [CrossRef]
- Sutton, S.R.; Eiser, J.R. The effect of fear-arousing communications on cigarette smoking: An expectancy-value approach. J. Behav. Med. 1984, 7, 13–33. [Google Scholar] [CrossRef]
- English, N.J.; Tse, J.S. Guest and host contributions towards thermal conduction in various polymorphs of methane hydrate. Comput. Mater. Sci. 2010, 49, S176–S180. [Google Scholar] [CrossRef]
- Zhou, Y.; Morshedifard, A.; Lee, J.; Qomi, M.J.A. The contribution of propagons and diffusons in heat transport through calcium-silicate-hydrates. Appl. Phys. Lett. 2017, 110, 043104. [Google Scholar] [CrossRef]
- English, N.J.; Gorman, P.D.; MacElroy, J.M. Mechanisms for thermal conduction in hydrogen hydrate. J. Chem. Phys. 2012, 136, 044501. [Google Scholar] [CrossRef]
- Li, Q.; Liu, C. The mechanism of heat transport in methane si hydrate under high pressure based on molecular dynamics simulation. J. Eng. Thermophys. 2015, 36, 714–719. [Google Scholar]
- Yuan, C.Y.; Zhang, Z.Y.; Zhu, J.; Zhao, J.F.; Yang, L.; Zhang, L.X.; Song, Y.C.; Tang, D.W. Ultralow thermal conductivity in tetrahydrofuran clathrate hydrate. Appl. Phys. Lett. 2021, 119, 133902. [Google Scholar] [CrossRef]
- Wan, L.; Liang, D.; Wu, N.; Guan, J. Molecular dynamics simulation on influence of guest molecule number on methane hydrate thermal performance. J. Chem. Ind. Eng. 2012, 63, 382–386. [Google Scholar]
- Andersson, P.; Ross, R.G. Effect of guest molecule size on the thermal conductivity and heat capacity of clathrate hydrates. J. Phys. C Solid State Phys. 1983, 16, 1423. [Google Scholar] [CrossRef]
- Zakrzewski, M.; White, M.A. Thermal conductivities of a clathrate with and without guest molecules. Phys. Rev. B 1992, 45, 2809–2817. [Google Scholar] [CrossRef]
- Ross, R.G.; Andersson, P.; Bäckström, G. Unusual PT dependence of thermal conductivity for a clathrate hydrate. Nature 1981, 290, 322–323. [Google Scholar] [CrossRef]
- Inoue, R.; Tanaka, H.; Nakanishi, K. Molecular dynamics simulation study of the anomalous thermal conductivity of clathrate hydrates. J. Chem. Phys. 1996, 104, 9569–9577. [Google Scholar] [CrossRef]
- Tse, J.S.; Klug, D.D.; Zhao, J.Y.; Sturhahn, W.; Alp, E.E.; Baumert, J.; Gutt, C.; Johnson, M.R.; Press, W. Anharmonic motions of Kr in the clathrate hydrate. Nat. Mater. 2005, 4, 917–921. [Google Scholar] [CrossRef]
- Wang, Z.L.; Yuan, K.P.; Tang, D.W. Thermal Transport in Methane Hydrate by Molecular Dynamics and Phonon Inelastic Scattering. Chin. Phys. Lett. 2015, 32, 104401. [Google Scholar] [CrossRef]
- Rosenbaum, E.J.; English, N.J.; Johnson, J.K.; Shaw, D.W.; Warzinski, R.P. Thermal conductivity of methane hydrate from experiment and molecular simulation. J. Phys. Chem. B 2007, 111, 13194–13205. [Google Scholar] [CrossRef]
- Li, X.; Wei, R.; Li, Q.; Pang, W.; Chen, G.; Sun, C. Application of infrared thermal imaging technique in in-situ temperature field measurement of hydrate-bearing sediment under thermal stimulation. Energy 2023, 265, 126321. [Google Scholar] [CrossRef]
- Shen, J.R.; Ireland, P.T.; Wang, Z.; Jones, T.V. Transient liquid crystal heat transfer measurement technology. J. Eng. Thermophys. 1993, 2, 193–196. [Google Scholar]
- Xu, Y.; Rao, Y. Measurement Accuracy and Application of Liquid Crystal Thermography Technique in Turbulent Flow Heat Transfer. J. Shanghai Jiaotong Univ. 2013, 47, 1185–1190+1197. [Google Scholar]
- Zhang, Z.W.; Jiang, R.; Zhu, Y.J.; Guo, W.M.; Zhao, J.; Chen, Y.; Li, Y.L.; Ding, B.Y. Measurement of Thermal Conductivity of Zr-Based Bulk Metallic Glass by Laser Flash Method. Mater. China 2023, 42, 181–184. [Google Scholar]
- Xu, Y.R. Development of Near-Field Raman Thermometry for Studying the Thermophysical Property of Carbon-Based Low-Dimensional Materials; Wuhan University: Wuhan, China, 2019. [Google Scholar]
- Duan, Z.; Tan, X.; Sun, Q.; Yan, X. Experimental study on the influence of water content and salt content on thermal conductivity of silty clay. Prog. Geophys. 2021, 36, 1834–1841. [Google Scholar]
- Xu, H.; Jiao, Z.; Zhang, Z.; Huffman, M.; Wang, Q. Prediction of methane hydrate formation conditions in salt water using machine learning algorithms. Comput. Chem. Eng. 2021, 151, 107358. [Google Scholar] [CrossRef]
- Li, Z.; Xia, J.; Liu, Z.; Lei, G.; Lee, K.; Ning, F. Missing Sonic Logs Generation for Gas Hydrate-Bearing Sediments via Hybrid Networks Combining Deep Learning with Rock Physics Modeling. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Luo, K.; Shen, Y.; Li, J.; An, Q. Pressure-Induced Stability of Methane Hydrate from Machine Learning Force Field Simulations. J. Phys. Chem. C 2023, 127, 7071–7077. [Google Scholar] [CrossRef]
- Zhang, N.; Yu, X.; Pradhan, A.; Puppala, A.J. Effects of Particle Size and Fines Content on Thermal Conductivity of Quartz Sands. Transp. Res. Rec. 2015, 2510, 36–43. [Google Scholar] [CrossRef]
- Park, S., II; Hartley, J.G. Measurement of the effective thermal conductivities of molding sands at high temperatures. KSME J. 1996, 10, 480–488. [Google Scholar] [CrossRef]
- Kiyohashi, H.; Sasaki, S.; Masuda, H. Effective thermal conductivity of silica sand as a filling material for crevices around radioactive-waste canisters. High Temp. High Press. 2004, 35, 179–192. [Google Scholar] [CrossRef]
- Michot, A.; Smith, D.; Degot, S.; Gault, C. Thermal Conductivity and Specific Heat of Kaolinite: Evolution with Thermal Treatment. J. Eur. Ceram. Soc. 2008, 28, 2639–2644. [Google Scholar] [CrossRef]
- Goto, S.; Yamano, M.; Morita, S.; Kanamatsu, T.; Hachikubo, A.; Kataoka, S.; Tanahashi, M.; Matsumoto, R. Physical and thermal properties of mud-dominant sediment from the Joetsu Basin in the eastern margin of the Japan Sea. Mar. Geophys. Res. 2017, 38, 393–407. [Google Scholar] [CrossRef]
- Muraoka, M.; Ohtake, M.; Susuki, N.; Yamamoto, Y.; Suzuki, K.; Tsuji, T. Thermal properties of methane hydrate-bearing sediments and surrounding mud recovered from Nankai Trough wells. J. Geophys. Res. Solid Earth 2014, 119, 8021–8033. [Google Scholar] [CrossRef]
- Moqsud, M.A.; Hayashi, S.; Du, Y.J.; Suetsugu, D. Technology, accessment of thermal properties of mud of the Ariske sea, Japan. Daffodil Int. Univ. J. Sci. 2007, 2, 1. [Google Scholar]
- Ramires, M.L.V.; Fareleira, J.M.N.A.; Nieto de Castro, C.A.; Dix, M.; Wakeham, W.A. The thermal conductivity of toluene and water. Int. J. Thermophys. 1993, 14, 1119–1130. [Google Scholar] [CrossRef]
- Waite, W.F.; Gilbert, L.Y.; Winters, W.J.; Mason, D.H. Estimating thermal diffusivity and specific heat from needle probe thermal conductivity data. Rev. Sci. Instrum. 2006, 77, 044904. [Google Scholar] [CrossRef]
- Caldwell, D.R. Thermal conductivity of sea water. Deep Sea Res. Oceanogr. Abstr. 1974, 21, 131–137. [Google Scholar] [CrossRef]
- Kannuluik, W.; Carman, E. The Temperature Dependence of the Thermal Conductivity of Air. Aust. J. Chem. 1951, 4, 305–314. [Google Scholar] [CrossRef]
- Prasad, R.C.; Mani, N.; Venart, J.E.S. Thermal conductivity of methane. Int. J. Thermophys. 1984, 5, 265–279. [Google Scholar] [CrossRef]
- Prasad, R.C.; Wang, G.; Venart, J.E.S. The thermal conductivity of propane. Int. J. Thermophys. 1989, 10, 1013–1027. [Google Scholar] [CrossRef]
- Jamieson, D.T.; Tudhope, J.S. Physical properties of sea water solutions: Thermal conductivity. Desalination 1970, 8, 393–401. [Google Scholar] [CrossRef]
- Akhmedova-Azizova, L.A.; Abdulagatov, I.M. Thermal Conductivity of Aqueous CaCl2 Solutions at High Temperatures and High Pressures. J. Solut. Chem. 2014, 43, 421–444. [Google Scholar] [CrossRef]
- Waite, W.F.; Pinkston, J.; Kirby, S.H. Preliminary Laboratory Thermal Conductivity Measurements in Pure Methane Hydrate and Methane Hydrate-Sediment Mixtures: A Progress Report. In Proceedings of the Fourth International Conference on Gas Hydrates, Yokohama, Japan, 19–23 May 2002; pp. 728–733. [Google Scholar]
- Waite, W.; Gilbert, L.; Winters, W.; Mason, D. Thermal Property Measurements in Tetrahydrofuran (THF) Hydrate between −25 and +4 °C, and Their Application to Methane Hydrate. AGU Fall Meet. Abstr. 2004, 2004, OS41C-0489. [Google Scholar]
- Huang, D.Z.; Fan, S.S. Thermal conductivity of methane hydrate formed from sodium dodecyl sulfate solution. J. Chem. Eng. Data 2004, 49, 1479–1482. [Google Scholar] [CrossRef]
- Huang, D.Z.; Fan, S.S.; Liang, D.Q.; Feng, Z.P. Measurements of gas hydrate composition and its thermal conductivity. Chin. J. Geophys. Chin. Ed. 2005, 48, 1125–1131. [Google Scholar]

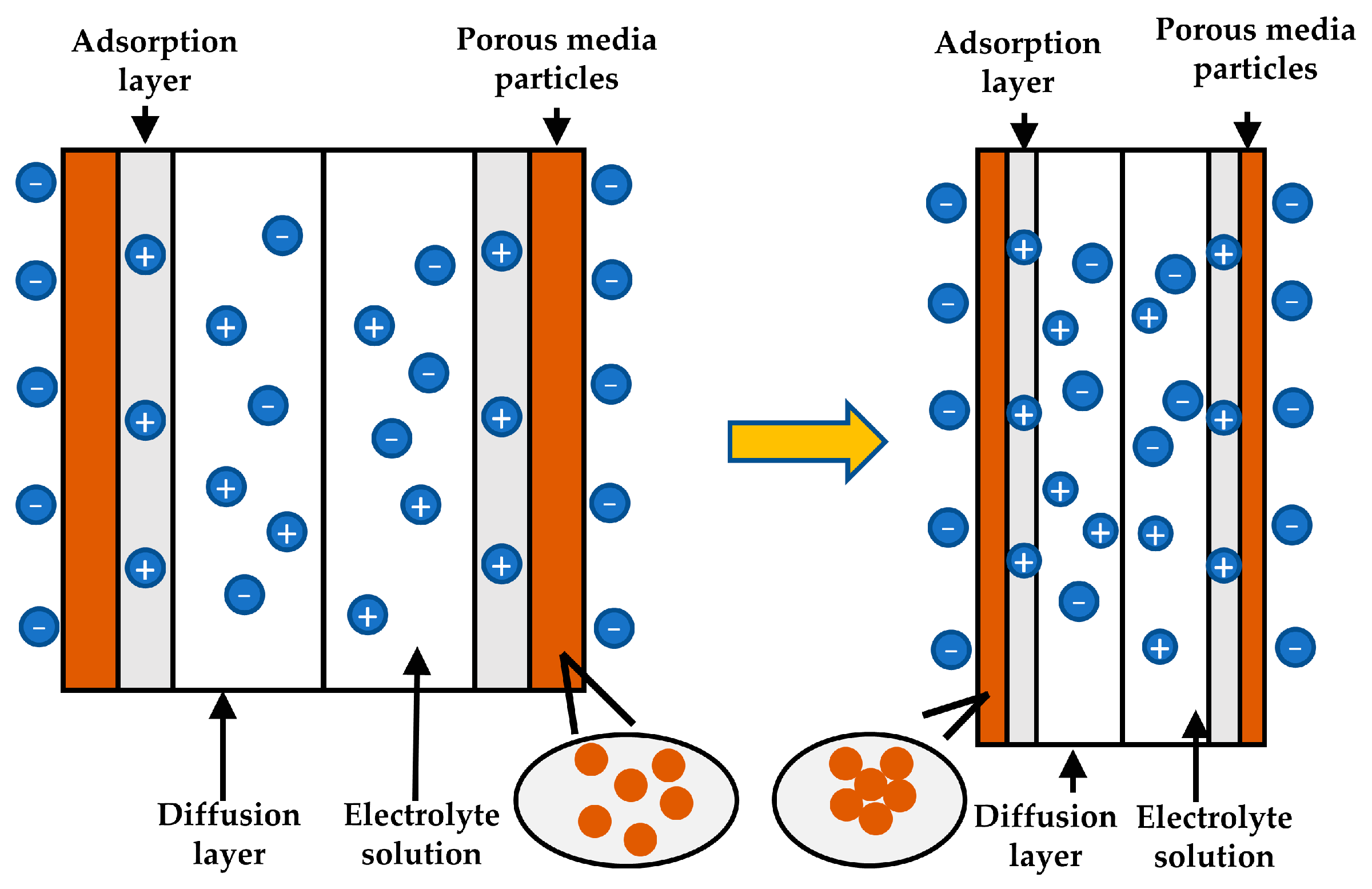
| Method | Diagram | Formula | Literatures |
|---|---|---|---|
| Hot wire | 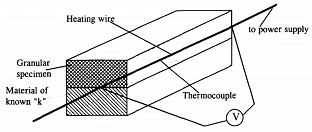 | From ref. [26] Copyright (1996), with permission from Elsevier. | |
| Hot strip | 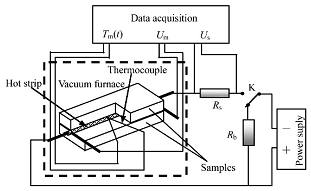 | From ref. [27] Copyright (2016), with permission from Elsevier. | |
| Probe | 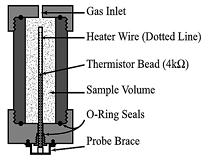 | From ref. [29] Copyright 2002 by the American Geophysical Union. | |
| TPHS | 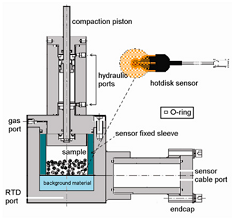 | From ref. [30] Copyright © 2011, Science China Press and Springer-Verlag Berlin Heidelberg. |
| Category | Porous Media Materials | Normal Particle Size |
|---|---|---|
| Natural sediments | Silicon dioxide | 25–58 μm |
| Grit | 1.0–2.0 mm | |
| Montmorillonite | 0.5–25 μm | |
| Clay | 0.25–0.425 mm | |
| Artificial sediments | Silica sand | 300–450 μm |
| Activated carbon | 2.19 nm | |
| Quartz sand | 13–27 nm | |
| Glass bead | 0.105–1.397 mm | |
| Silica gel | 0.105–0.150 mm |
| Model | Formula |
|---|---|
| Parallel model | |
| Continuous model | |
| Discrete model | |
| Square root model |
| Porous Media | Particle Size/μm | Porosity/% | Thermal Conductivity /(W·m−1K−1) | Studies |
|---|---|---|---|---|
| Quartz sand | 20–63 | 41 | 0.45 | [50] |
| Quartz sand | 200–500 | 38 | 0.83 | [50] |
| Quartz sand | 600–830 | 35 | 1.03 | [50] |
| Quartz sand | 362 | 42 | 0.275 | [110] |
| Silica sand | 431 | 41 | 0.35 | [111] |
| Silica sand | 330 | 37 | 0.73 | [52] |
| Silica sand | 840 | 37 | 0.55 | [52] |
| Silica sand | 74 | 40.5 | 0.174 | [112] |
| Silica sand | 150 | 40.5 | 0.234 | [112] |
| Silica sand | 420 | 42.5 | 0.245 | [112] |
| Silica sand | 590 | 37.5 | 0.267 | [112] |
| Silica sand | 1680 | 39.0 | 0.402 | [112] |
| Kaolin (300 °C) | - | 40.0 | 0.2 | [113] |
| Sea mud (Joetsu Basin, eastern Japan Sea) | - | 70 | 0.90 | [114] |
| Sea mud (Nankai Trough, Japan) | 8.9 | 36 | 1.05 | [115] |
| Sea mud (Ariake Sea, Japan) (undried) | - | - | 0.7 | [116] |
| Sea mud (Ariake Sea, Japan) (undried) | - | - | 0.09 | [116] |
| Gas/Liquid | Temperature/K | Thermal Conductivity/(W·m−1K−1) | Studies |
|---|---|---|---|
| Water | 298.78 | 0.609 | [117] |
| Ice | 263.15 | 2.28 | [118] |
| Sea water | 273.15 | 0.581 | [119] |
| Air | 273.15 | 0.024 | [120] |
| Methane | 260.05 | 0.086 | [121] |
| Methane (gas) | 300.06 | 0.114 | [121] |
| Propane (liquid) | 261.72 | 0.123 | [122] |
| Propane (gas) | 300.35 | 0.018 | [122] |
| NaCl solution | 298.15 | 0.594 | [123] |
| NaCl solution | 298.15 | 0.583 | [123] |
| NaCl solution | 298.15 | 0.574 | [123] |
| CaCl2 solution | 293.15 | 0.55 | [124] |
| CaCl2 solution | 293.15 | 0.602 | [124] |
| Porous Media | Guest Molecules | Particle Size/μm | Porosity/% | Thermal Conductivity /(W·m−1K−1) | Studies |
|---|---|---|---|---|---|
| Quartz sand | CH4 | 50 | 39 | 0.421 | [16] |
| Quartz sand | CH4 | 100 | 32 | 1.15 | [125] |
| Quartz sand | CH4 | 150 | 40 | 0.457 | [16] |
| Quartz sand | THF | 125–250 | 42.4 | 2.58 | [126] |
| Quartz sand | CH4 | 300–125 | 47 | 0.999–1.024 | [127] |
| Quartz sand | CH4 + C2H6 + C3H8 + THF | 300–125 | 47 | 1.238–1.294 | [128] |
| Quartz sand | THF | 300–125 | 47 | 1.879–1.967 | [127] |
| Quartz sand | CH4 | 250–425 | 41 | 1.568–1.493 | [45] |
| Quartz sand | CH4 | 250–425 | 44 | 1.32–1.5 | [45] |
| Quartz sand | THF | 250–500 | 40.5 | 2.65 | [126] |
| Quartz sand | CH4 | 500 | 40.5 | 0.470 | [16] |
| Quartz sand | THF | 500–1000 | 40.5 | 2.66 | [126] |
| Quartz sand | CH4 | 1150 | 42.5 | 0.46 | [16] |
| Silica sand | THF | 430 | 37.5 | 0.725 | [32] |
| Silica sand | THF | 800 | 39.0 | 0.7 | [32] |
| Silica sand | THF | 1190 | 40.0 | 0.675 | [32] |
| Silica sand | THF | 2000 | 40.5 | 0.66 | [32] |
| Silica sand | THF | 4330 | 42.5 | 0.649 | [32] |
| Sea mud (Nankai Trough, Japan) | CH4 | 87 | 46.7 | 1.51 | [115] |
| Sea mud (Nankai Trough, Japan) | CH4 | 140 | 46.7 | 1.65 | [115] |
| Sea mud (Nankai Trough, Japan) | CH4 | 215 | 41.0 | 1.55 | [115] |
| Sea mud (northern South China Sea) | THF | <60 (90%) + 60–140 (10%) | 42.5 | 0.61 | [43] |
| Sea mud (offshore Qingdao, China) | CH4 | 63–250 (22%) + 250–500 (78%) | 40 | 1.134–1.270 | [25] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, M.; Yan, K.; Li, X.; Chen, Z.; Wang, Y.; Feng, J.; Chen, C. Review of Heat Transfer Characteristics of Natural Gas Hydrate. Energies 2024, 17, 717. https://doi.org/10.3390/en17030717
Mao M, Yan K, Li X, Chen Z, Wang Y, Feng J, Chen C. Review of Heat Transfer Characteristics of Natural Gas Hydrate. Energies. 2024; 17(3):717. https://doi.org/10.3390/en17030717
Chicago/Turabian StyleMao, Minghang, Kefeng Yan, Xiaosen Li, Zhaoyang Chen, Yi Wang, Jingchun Feng, and Chang Chen. 2024. "Review of Heat Transfer Characteristics of Natural Gas Hydrate" Energies 17, no. 3: 717. https://doi.org/10.3390/en17030717
APA StyleMao, M., Yan, K., Li, X., Chen, Z., Wang, Y., Feng, J., & Chen, C. (2024). Review of Heat Transfer Characteristics of Natural Gas Hydrate. Energies, 17(3), 717. https://doi.org/10.3390/en17030717









