Forest Stand Growth Forecasting in the Context of Changes in the Insolation of Building Roofs
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
- Step 1
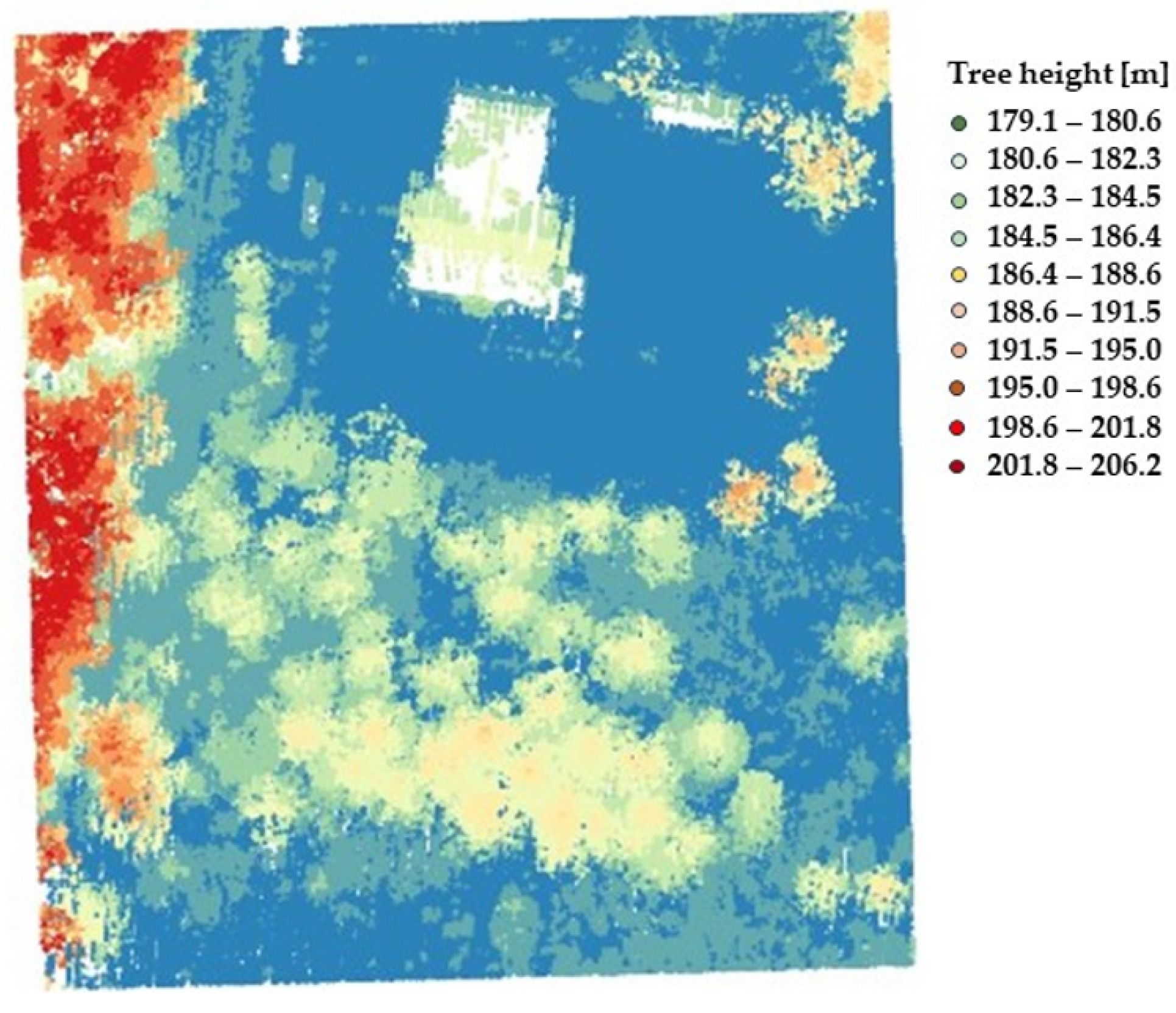
- DSM generation: a DSM of the area around the building was generated as a TIN model.
- Step 2
- Digital terrain model (DTM) acquisition: a DTM of the area around the building to provide a reference surface for the tree height measurements was downloaded from geoportal.gov.pl.
- Step 2
- Calculating the Canopy Height Models (CHM) for e1 and e2 epochs: this can be carried out by simply differencing DSM and DTM in both epochs.
- Step 4
- Individual tree tops identification: to identify individual tree tops in the CHM, the Local Maximum Function was used.
- Step 5
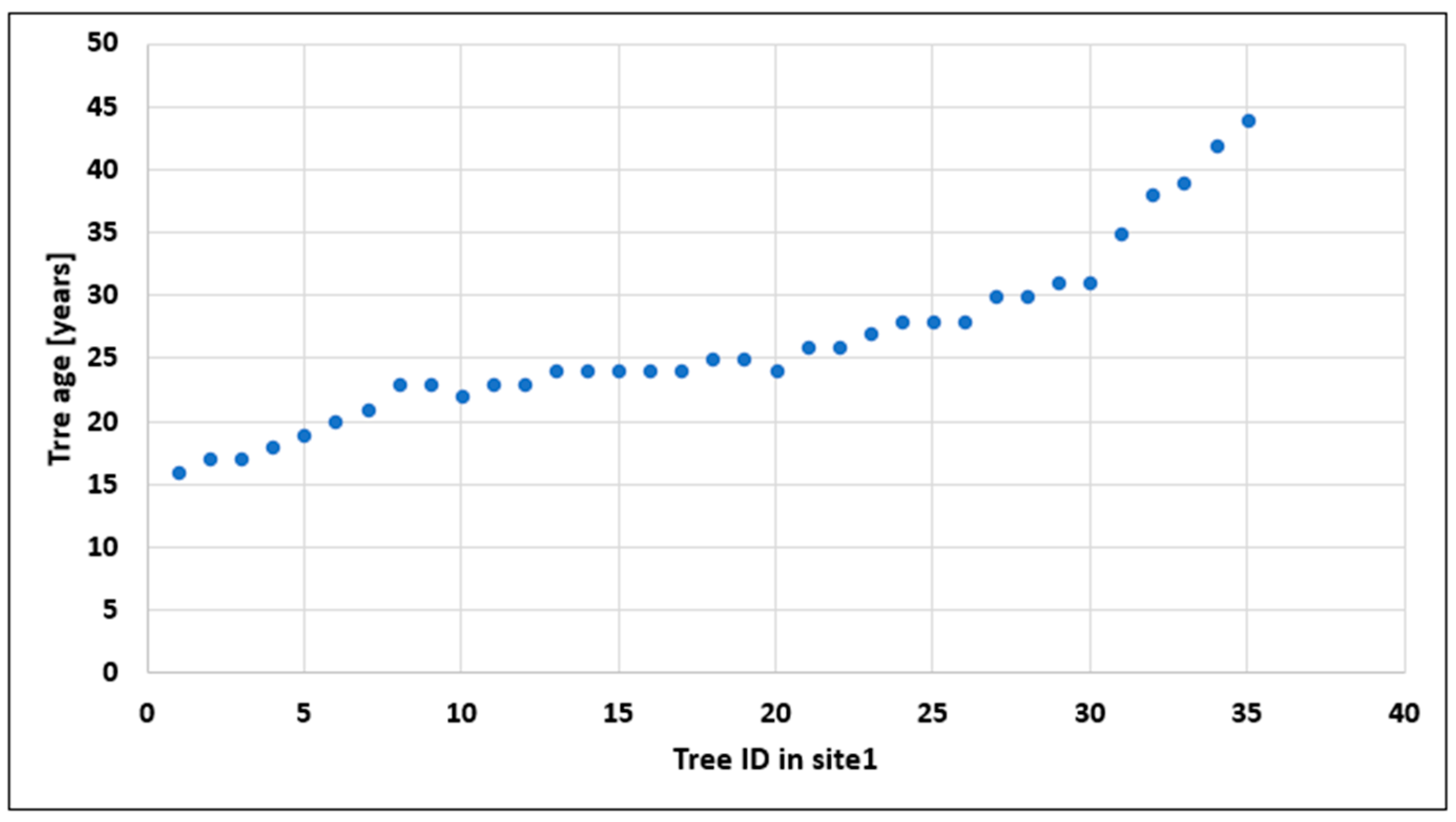
- Calculating tree growth: the growth of each tree was calculated by comparing the heights of tree tops between two epochs.
- Step 6
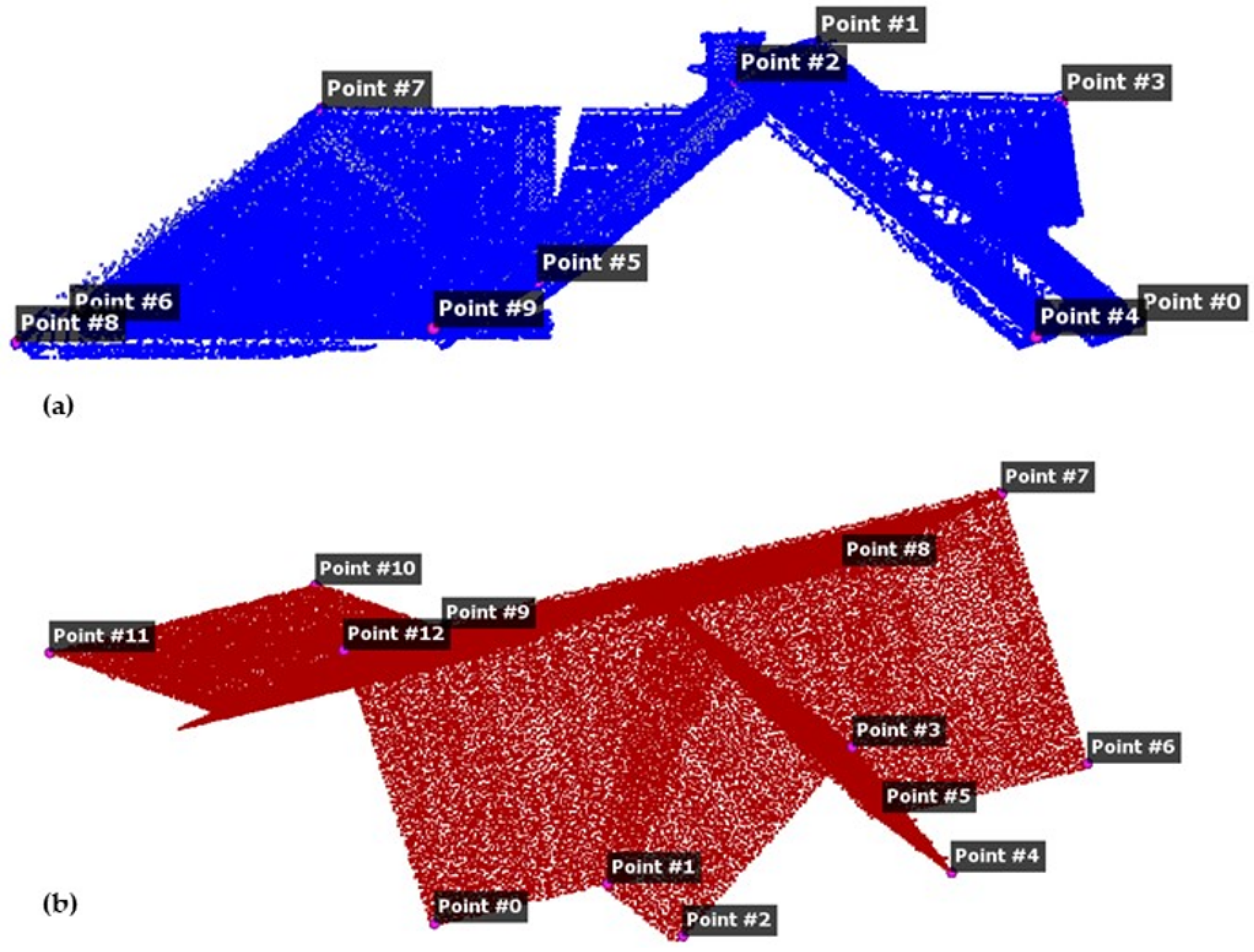
- Verification of the methodology used in steps 3 to 5: direct and indirect measurements on the point cloud were used for this verification.
- Step 7
- Future growth prediction: statistical models to predict the future growth validated by actual tree growth obtained in step 5 were used.

- Open access journals: there are several open access journals that publish research on tree growth models.
- Research repositories: many research institutions and universities have repositories where researchers can publish their work.
- Government agencies: government agencies such as the United States Forest Service and the Canadian Forest Service often publish research on tree growth models [27].
- Commercial software: commercial software providers such as Sim4Tree v. 4.2, Heureka v. 2.21.3, and Forest Vegetation Simulator (FVS v 2023.07.28) provide access to their tree growth models.
- Scientific conferences: attending scientific conferences such as the International Union of Forest Research Organizations (IUFRO) and the International Society of Arboriculture (ISA) can also provide opportunities to learn about tree growth models [28].
2.2. Equipment and Access to the Data
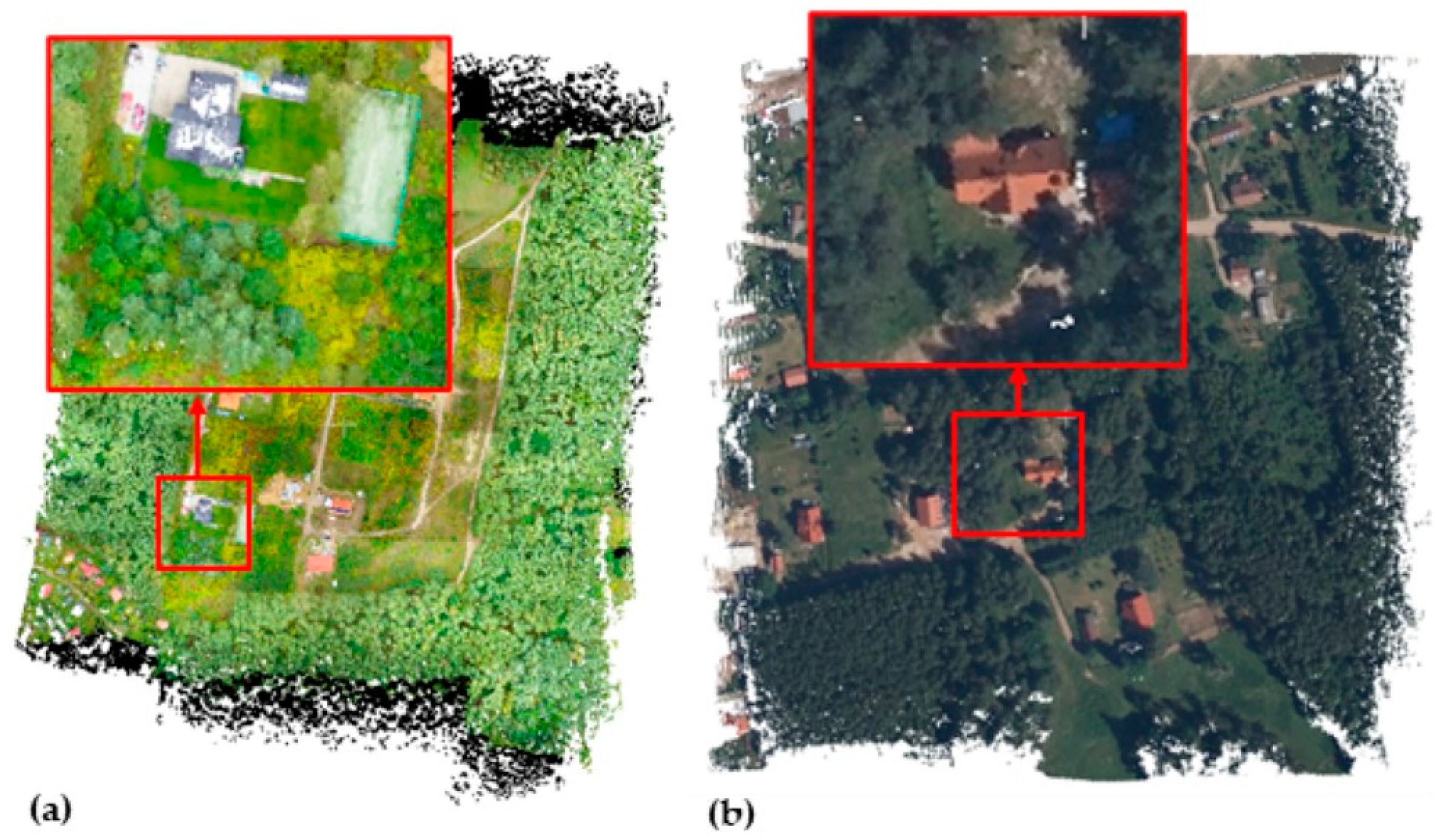
2.2.1. ALS Point Cloud–e1 Epoch
2.2.2. UAV with LiDAR Sensors–e2 Epoch
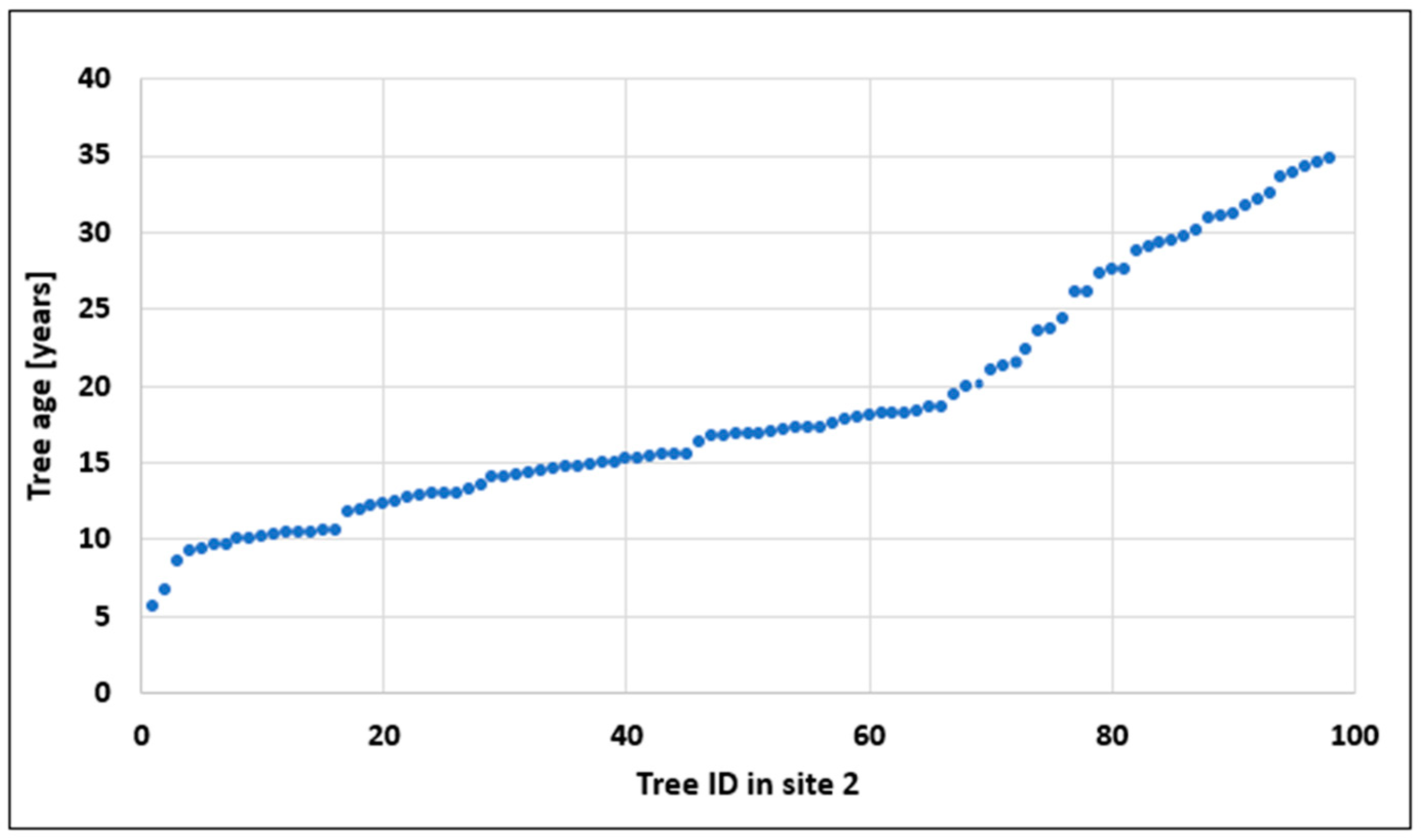
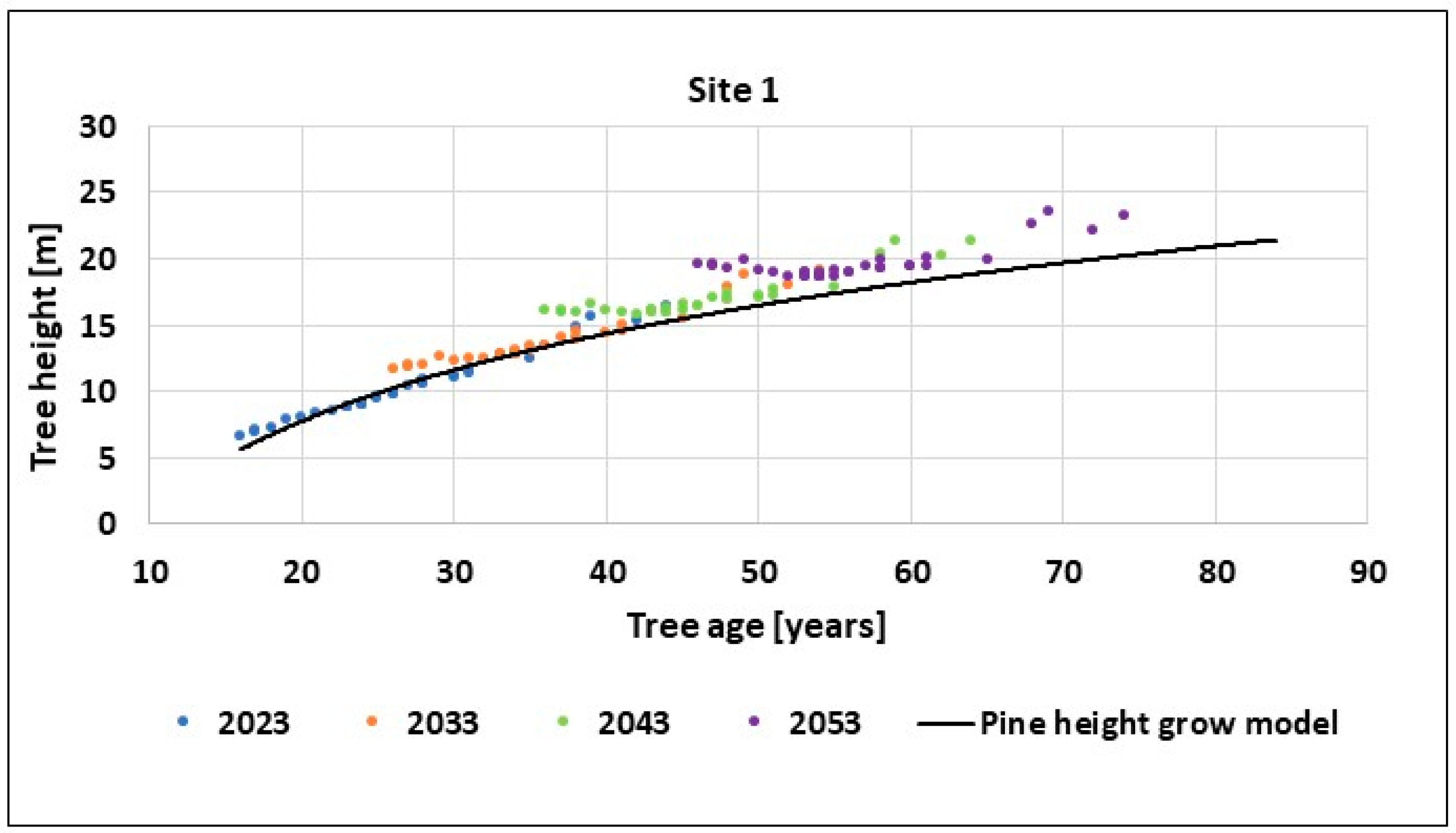
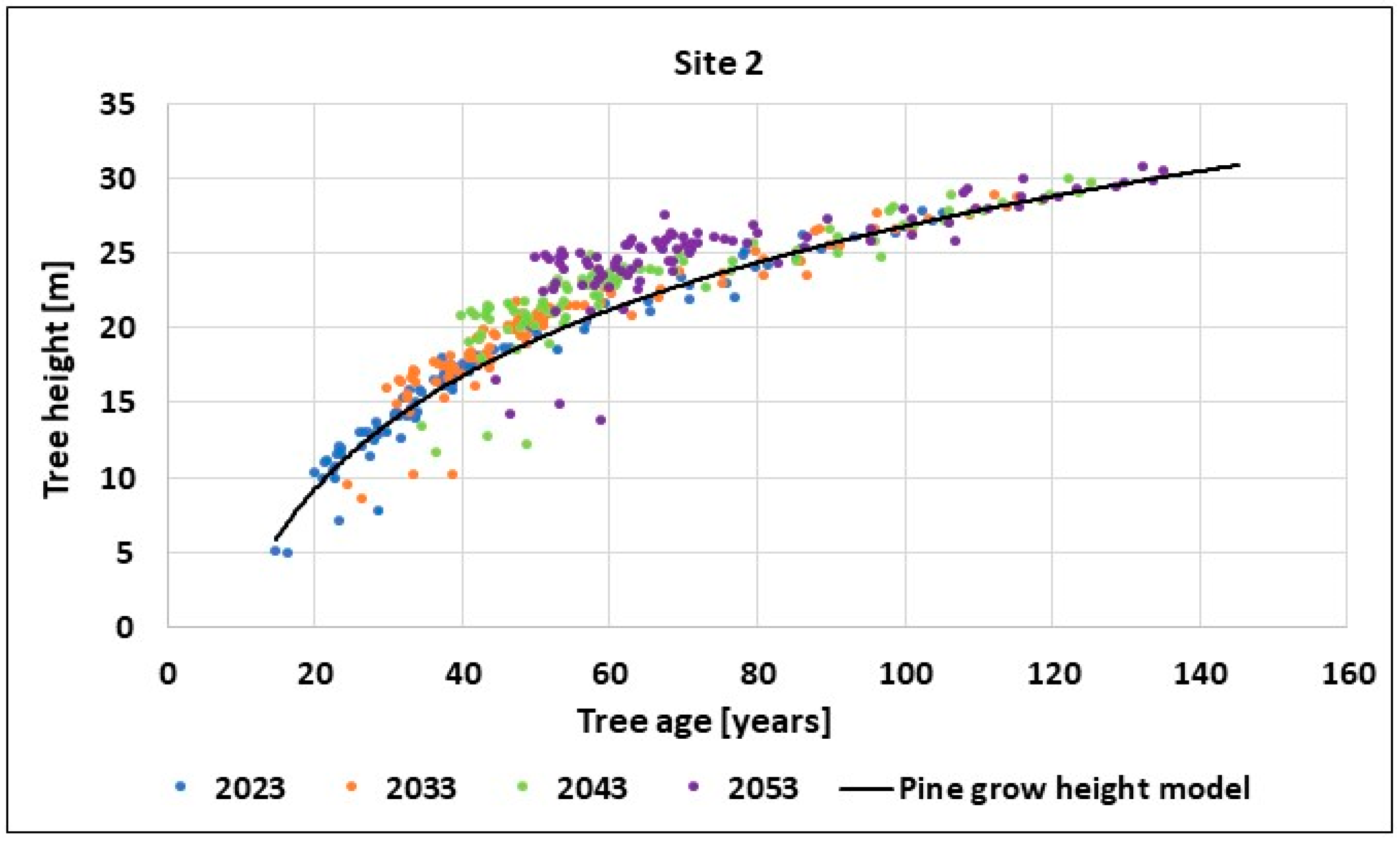
3. Results
3.1. Data Processing
3.2. Total Insolation Calculation SEPtree+
- n—the number of PVPCs;
- ∑mi—the sum of minutes in one day when the PVPC is in sunlight.
4. Discussion
5. Conclusions
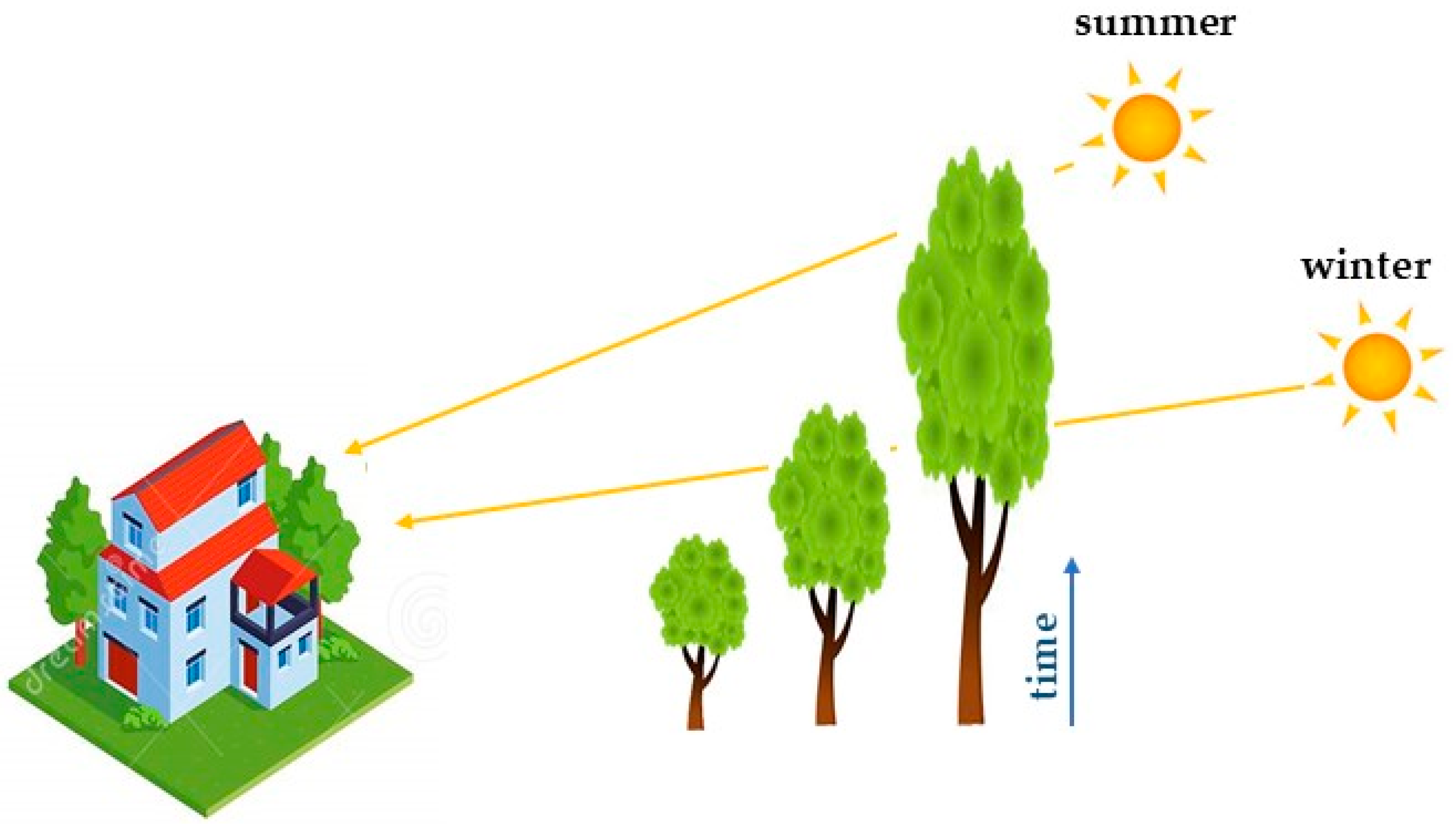
- Curtains in the form of trees affect the insolation of the objects where the PV system is planned to be installed. Therefore, the impact of tree growth on the surroundings of the facility should be taken into account.
- To determine the impact of tree stand growth on the facility’s insolation, at least two measurement epochs should be available so that tree growth over time can be calculated and future growth can be predicted. The other way is to use the locally applicable tree growth tables of a specific species to calculate the tree growth in subsequent years in the future.
- Calculated tree increments in individual years constitute the source of input data for the developed SEP-tree+ tool, which can be used to predict the solar insolation of buildings in the future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALS | airborne laser scanning |
| ULS | unmanned aerial vehicle with laser scanning |
| LiDAR | Light Detection and Ranging |
| PV | Photovoltaic |
| DSM | digital surface model |
| DTM | digital terrain model |
| CHM | Canopy Height Models |
| IUFRO | Forest Research Organizations |
| SEPtree+ | Sun Exposition based on Tree Growth Planner |
| LMF | Local Maximum Function |
| TDC | Tree Density Calculator |
| TIN | Triangular Irregular Network |
| PVGIS | Photovoltaic Geographical Information System |
| ZS | zonal statistics |
| FMP | Forest Management Plan |
| PCM | point cloud measurement |
| PVPC | the centers of potential photovoltaic panels |
| TMTPI | total minutes of insolation of total panels |
References
- Aslani, M.; Seipel, S. Rooftop segmentation and optimization of photovoltaic panel layouts in digital surface models. Comput. Environ. Urban Syst. 2023, 105, 102026. [Google Scholar] [CrossRef]
- Zukowski, M.; Kosior-Kazberuk, M.; Blaszczynski, T. Energy and Environmental Performance of Solar Thermal Collectors and PV Panel System in Renovated Historical Building. Energies 2021, 14, 7158. [Google Scholar] [CrossRef]
- Freitas, S.; Reinhart, C.; Brito, M. Minimizing storage needs for large scale photovoltaics in the urban environment. Sol. Energy 2018, 159, 375–389. [Google Scholar] [CrossRef]
- Trzmiel, G.; Głuchy, D.; Kurz, D. The impact of shading on the exploitation of photovoltaic installations. Renew. Energy 2022, 153, 480–498. [Google Scholar] [CrossRef]
- Sung, S.H.; Jiang, R.; Huang, X.; Xie, C. Panels v. Trees: Broadening the Pathways of Engineering Education Through Integration With Social Studies. Sci. Scope 2022, 45, 24–33. [Google Scholar] [CrossRef]
- Sugihara, K.; Shen, Z. Automatic Generation of 3D Building Models with Efficient Solar Photovoltaic Generation. Int. Rev. Spat. Plan. Sustain. Dev. 2017, 5, 4–14. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zöld, A.; Seprödi-Egeresi, M. Photovoltaic Arrays on Flat Roofs—An Aspect of Yearly Energy Production. Adv. Mater. Res. 2014, 899, 222–227. [Google Scholar] [CrossRef]
- Błaszczak-Bąk, W.; Janicka, J.; Kozakiewicz, T.; Chudzikiewicz, K.; Bąk, G. Methodology of Calculating the Number of Trees Based on Als Data for Forestry Applications for the Area of Samławki Forest District. Remote Sens. 2022, 14, 16. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.S.; Longo, M.; Clark, D.B. Tropical tree size–frequency distributions from airborne lidar. Ecol. Appl. 2020, 30, e02154. [Google Scholar] [CrossRef]
- Frontiers Production Office. Erratum: Solar Energy Potential Assessment on Rooftops and Facades in Large Built Environments Based on LiDAR Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 2020, 6, 30; Erratum in Front. Built Environ. 2018, 4, 14. [Google Scholar]
- Bouguerra, S.; Yaiche, M.R.; Gassab, O.; Sangwongwanich, A.; Blaabjerg, F. The Impact of PV Panel Positioning and Degradation on the PV Inverter Lifetime and Reliability. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3114–3126. [Google Scholar] [CrossRef]
- Libra, M.; Mrázek, D.; Tyukhov, I.; Severová, L.; Poulek, V.; Mach, J.; Šubrt, T.; Beránek, V.; Svoboda, R.; Sedláček, J. Reduced Real Lifetime of PV Panels–Economic Consequences. Sol. Energy 2023, 259, 229–234. [Google Scholar] [CrossRef]
- Baig, S. Evaluating the Tree Shading Effect on Solar PV Panels to Maximize the Energy Production Using LIDAR Data. Master’s Thesis, Itä-Suomen yliopisto, Kuopio, Finland, 2023. [Google Scholar]
- Dereli, Z.; Yücedağ, C.; Pearce, J.M. Simple and low-cost method of planning for tree growth and lifetime effects on solar photovoltaic systems performance. Sol. Energy 2013, 95, 300–307. [Google Scholar] [CrossRef][Green Version]
- Yancho, J.M.M.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Plowright, A. Fine-Scale Spatial and Spectral Clustering of UAV-Acquired Digital Aerial Photogrammetric (DAP) Point Clouds for Individual Tree Crown Detection and Segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4131–4148. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Iqbal, I.A.; Osborn, J.; Stone, C.; Lucieer, A. A Comparison of Als and Dense Photogrammetric Point Clouds for Individual Tree Detection in Radiata Pine Plantations. Remote Sens. 2021, 13, 3536. [Google Scholar] [CrossRef]
- Corte, A.P.D.; Rex, F.E.; de Almeida, D.R.A.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Zambrano, A.M.A.; da Cunha Neto, E.M.; Veras, H.F.P.; et al. Measuring Individual Tree Diameter and Height Using Gatoreye High-Density UAV-Lidar in an Integrated Crop-Livestock-Forest System. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth, and Yield; Springer: Berlin, Germany, 2009; Volume 684. [Google Scholar]
- Vidal, C.; Alberdi, I.; Hernández, L.; Redmond, J. National Forest Inventories: Assessment of Wood Availability and Use; Springer Science + Business Media: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Da Luz, N.B.; Garrastazu, M.C.; Rosot, M.A.D.; Maran, J.C.; De Oliveira, Y.M.M.; Franciscon, L.; Cardoso, D.J.; De Freitas, J.V. Brazilian National Forest Inventory—A Landscape Scale Approach to Monitoring and Assessing Forested Landscapes. Pesqui. Florest. Bras. 2018, 38, 1–14. [Google Scholar] [CrossRef]
- Altrell, D. Multipurpose National Forest Inventory in Mongolia, 2014–2017-a Tool to Support Sustainable Forest Management. Geogr. Environ. Sustain. 2019, 12, 167–183. [Google Scholar] [CrossRef]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E. National forest inventories. Pathways for Common Reporting. Eur. Sci. Found. 2010, 1, 541–553. [Google Scholar]
- Szymkiewicz, B. Tables of Holdings Measurement and Growth of Timber Stock; Polskie Wydawnictwo Rolne i Leśne: Warsaw, Poland, 1983; pp. 28–29. [Google Scholar]
- Bruchwald, A. MDI−1 growth model for pine. Las Pol. 1985, 9, 10−15. [Google Scholar]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
- Hawkins, B.J. A Tribute: Robert John van Den Driessche, Tree Physiologist, 1933–2018. Can. J. For. Res. 2018, 48, v–vii. [Google Scholar] [CrossRef]
- Ford-Robertson, F.C. International Union of Forest Research Organizations. Nature 1961, 192, 614–615. [Google Scholar] [CrossRef]
- Crabbé, A.H.; Cahy, T.; Somers, B.; Verbeke, L.P.; Van Coillie, F. Tree Density Calculator Software (Version x.x) [Software]. 2020. Available online: https://bitbucket.org/kul-reseco/localmaxfilter (accessed on 17 October 2023).








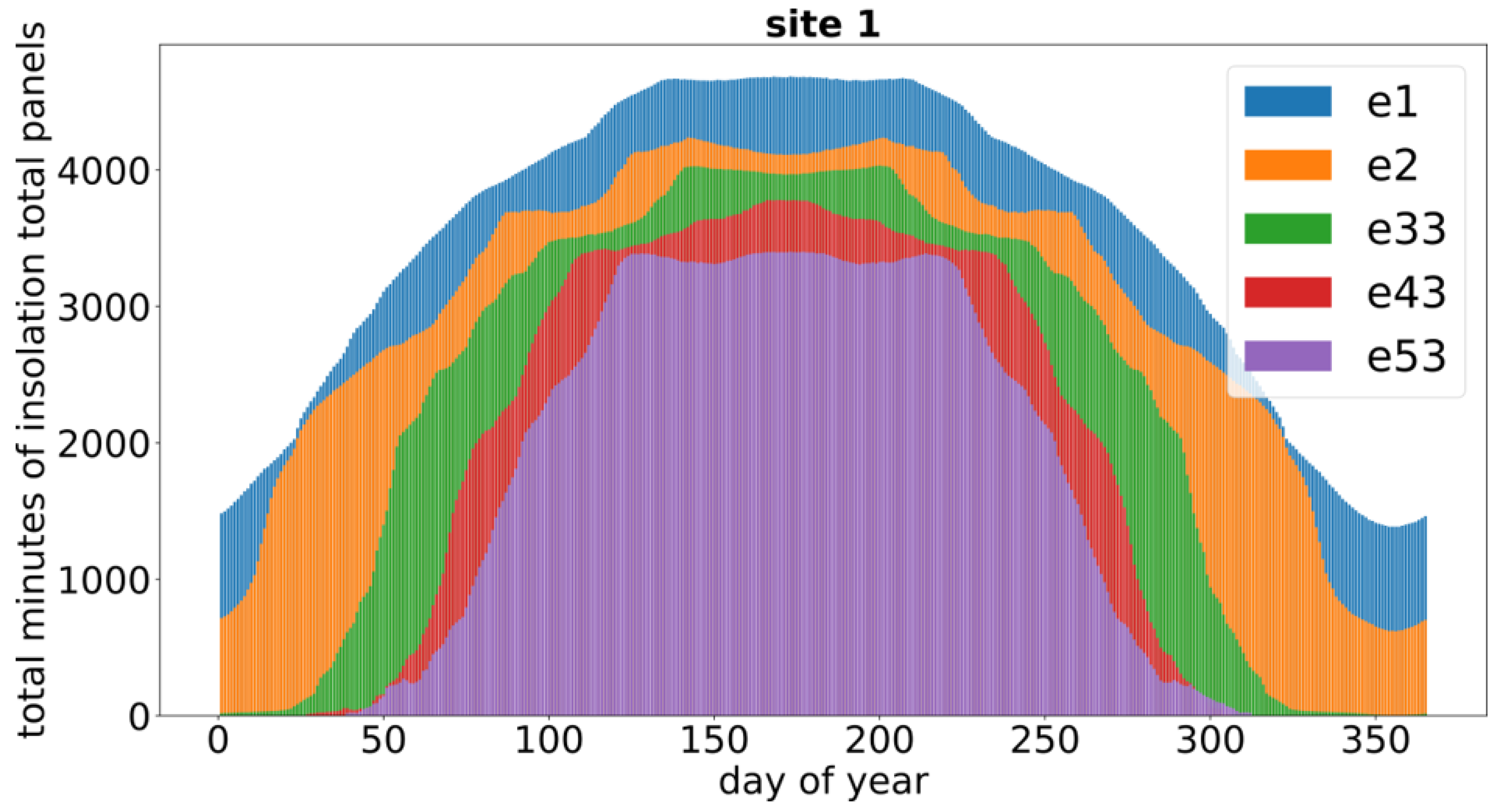
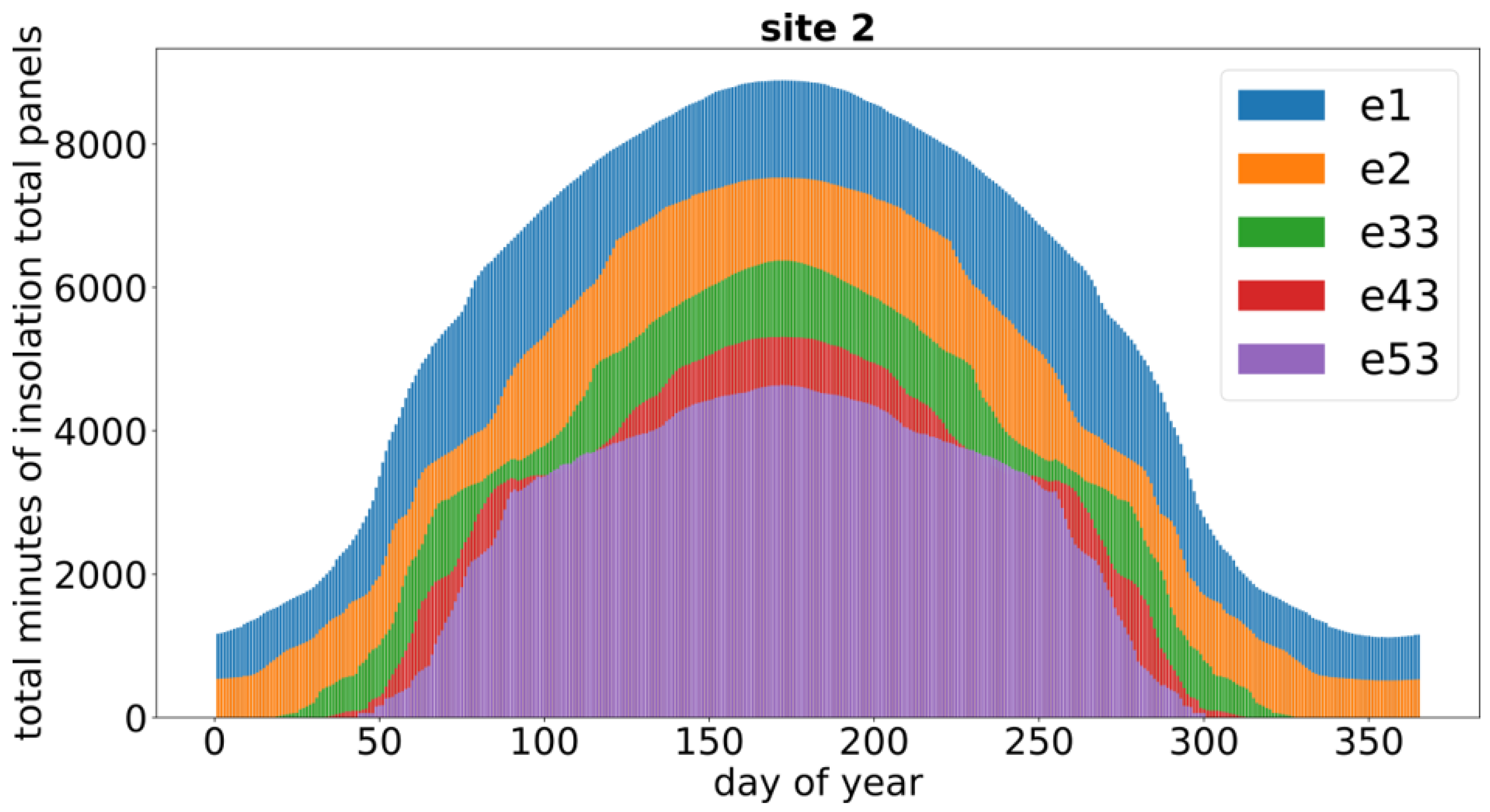

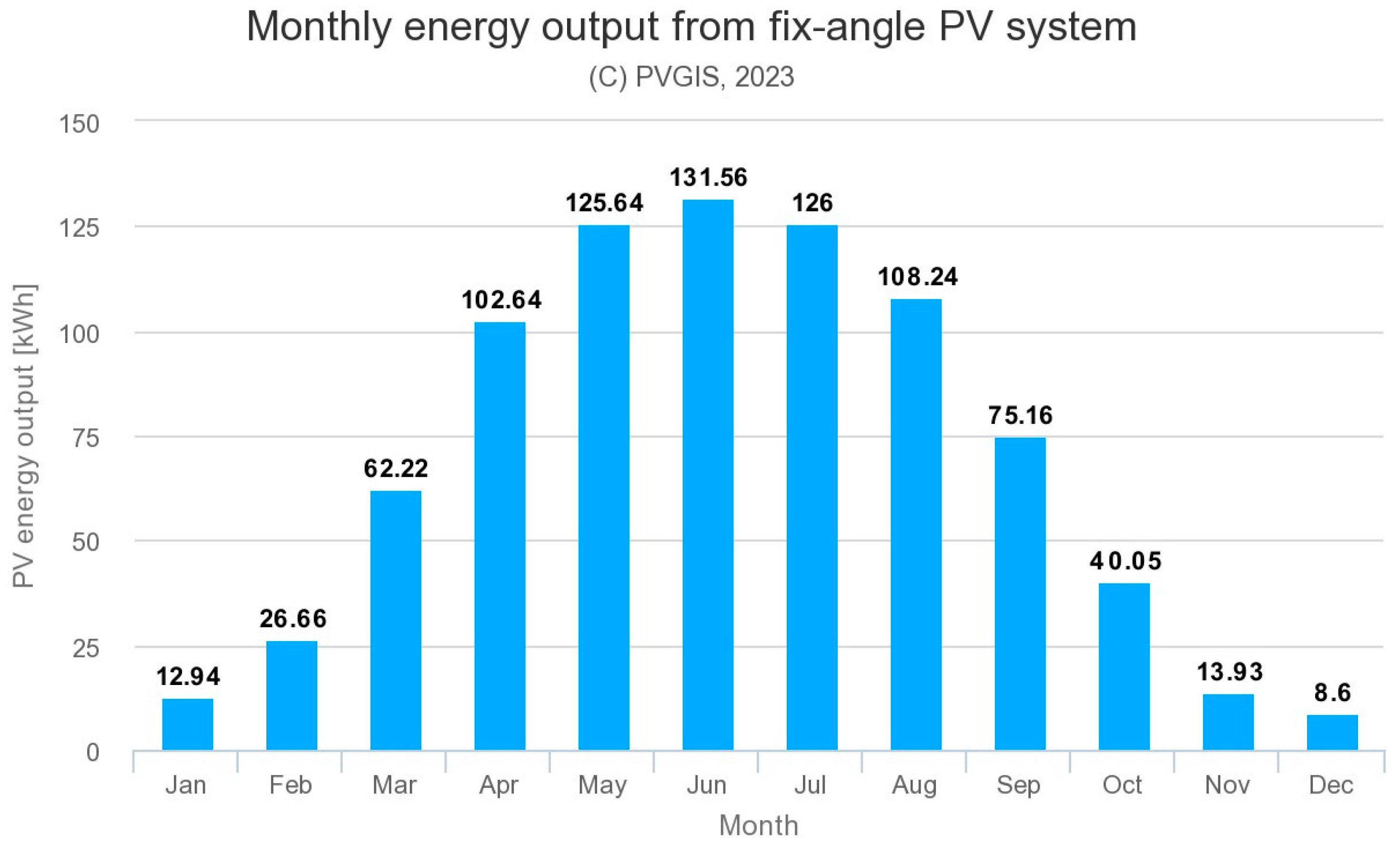
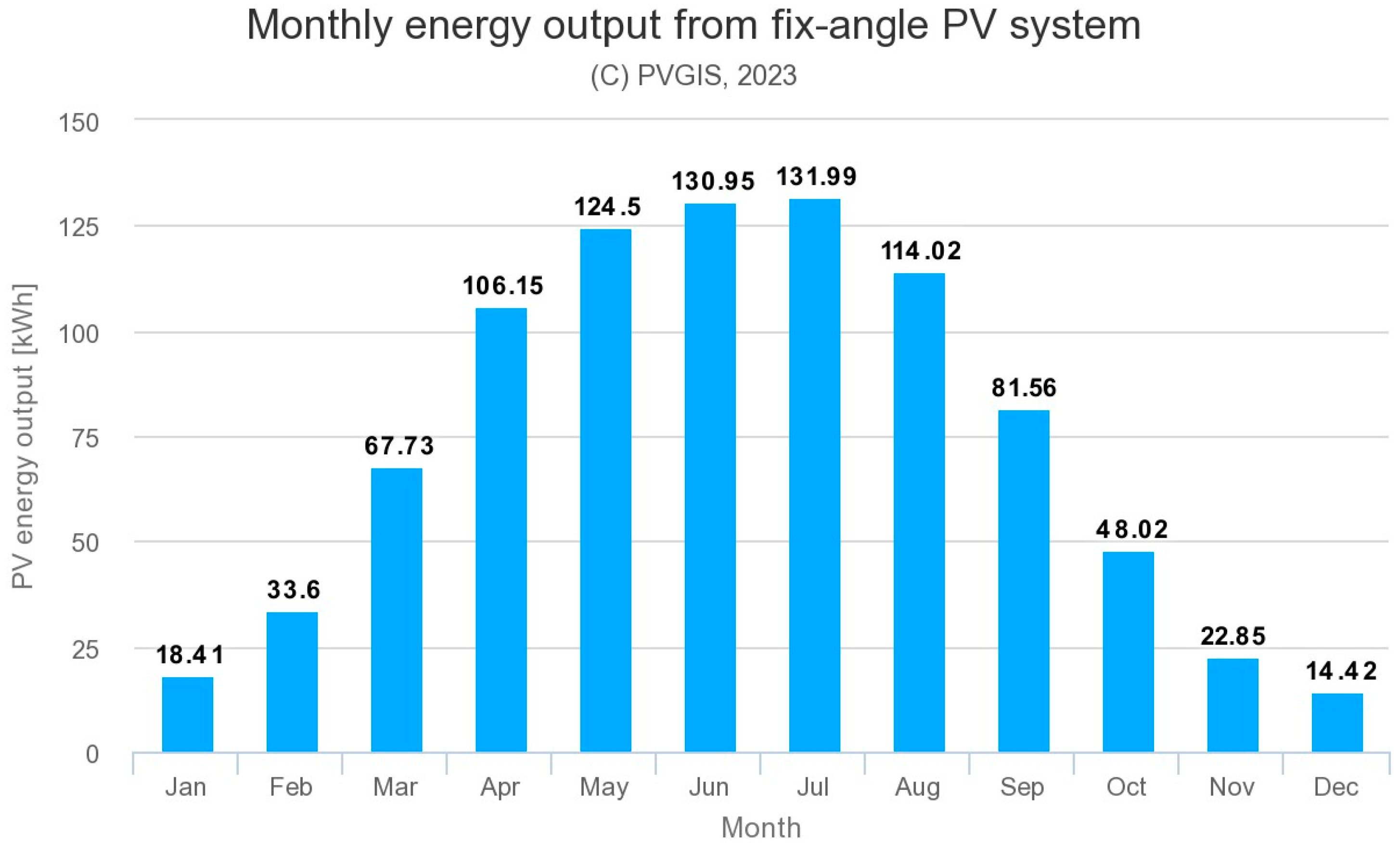
| Tree ID | Tree Growth between Epochs e1 and e2 [m] | ||
|---|---|---|---|
| LMF | ZS | PCM | |
| 1 | X | 4.11 | 4.18 |
| 2 | X | 3.19 | 2.65 |
| 3 | 4.78 | 4.56 | 4.56 |
| 4 | 4.58 | 4.68 | 4.75 |
| 5 | 5.75 | 5.75 | 5.8 |
| 6 | 11.11 | 11.31 | 10.93 |
| 7 | 3.44 | 3.23 | 3.13 |
| 8 | 4.87 | 4.88 | 4.84 |
| 9 | 5.81 | 5.78 | 5.77 |
| 10 | 4.16 | 4.17 | 4.16 |
| 11 | 6.54 | 6.53 | 6.53 |
| 12 | 7.46 | 7.59 | 7.69 |
| 13 | 6.18 | 6.23 | 6.23 |
| 14 | 7.58 | 7.5 | 7.5 |
| 15 | 7.07 | 7.15 | 7.14 |
| 16 | 6.1 | 6.04 | 5.97 |
| 17 | 7.35 | 7.34 | 7.33 |
| Novelty | Application | Advantage |
|---|---|---|
| the predicted growth of trees |
|
|
| SEPtree+ tool |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelc-Mieczkowska, R.; Błaszczak-Bąk, W.; Janicka, J.; Kozakiewicz, T. Forest Stand Growth Forecasting in the Context of Changes in the Insolation of Building Roofs. Energies 2024, 17, 594. https://doi.org/10.3390/en17030594
Pelc-Mieczkowska R, Błaszczak-Bąk W, Janicka J, Kozakiewicz T. Forest Stand Growth Forecasting in the Context of Changes in the Insolation of Building Roofs. Energies. 2024; 17(3):594. https://doi.org/10.3390/en17030594
Chicago/Turabian StylePelc-Mieczkowska, Renata, Wioleta Błaszczak-Bąk, Joanna Janicka, and Tomasz Kozakiewicz. 2024. "Forest Stand Growth Forecasting in the Context of Changes in the Insolation of Building Roofs" Energies 17, no. 3: 594. https://doi.org/10.3390/en17030594
APA StylePelc-Mieczkowska, R., Błaszczak-Bąk, W., Janicka, J., & Kozakiewicz, T. (2024). Forest Stand Growth Forecasting in the Context of Changes in the Insolation of Building Roofs. Energies, 17(3), 594. https://doi.org/10.3390/en17030594






