Experimental Insights into the Fermentation of Pyro-Syngas to Ethanol in a Semi-Batch and Continuous Stirred Bioreactor with Mathematical Modelling and Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemical Composition of Rice Straw
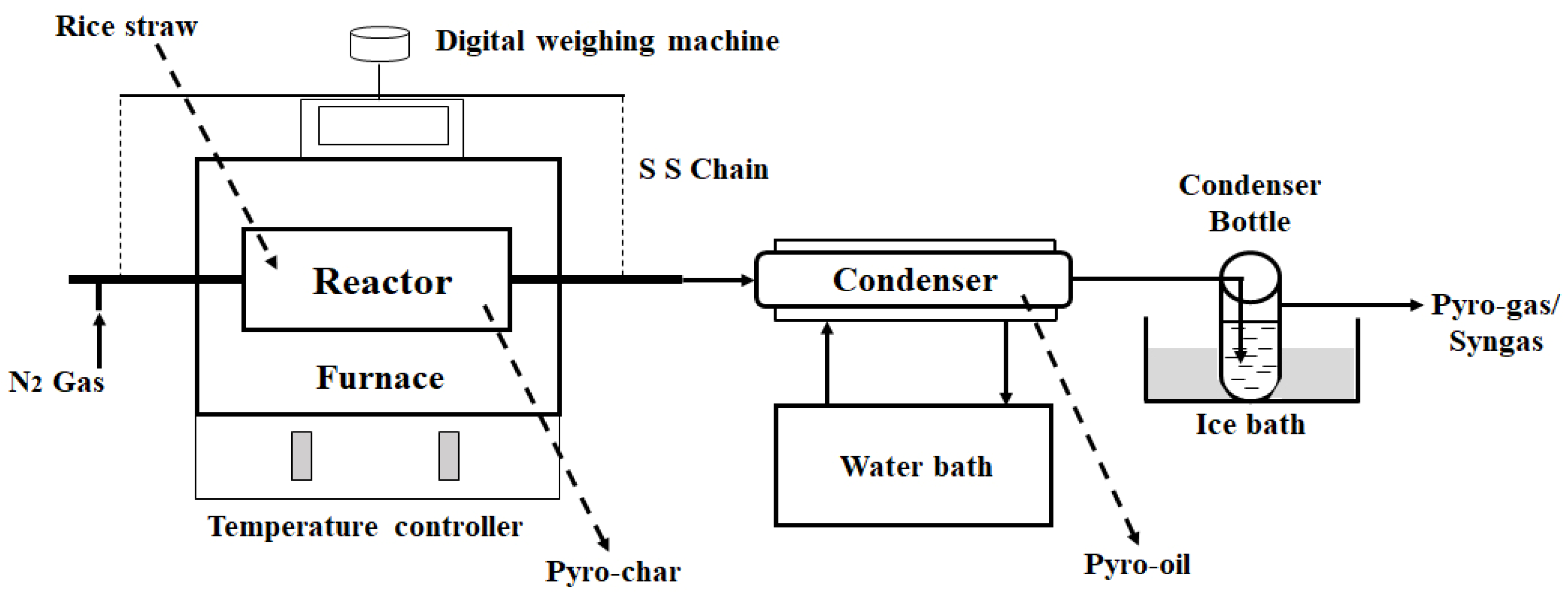
2.2. Pyrolysis of Rice Straw
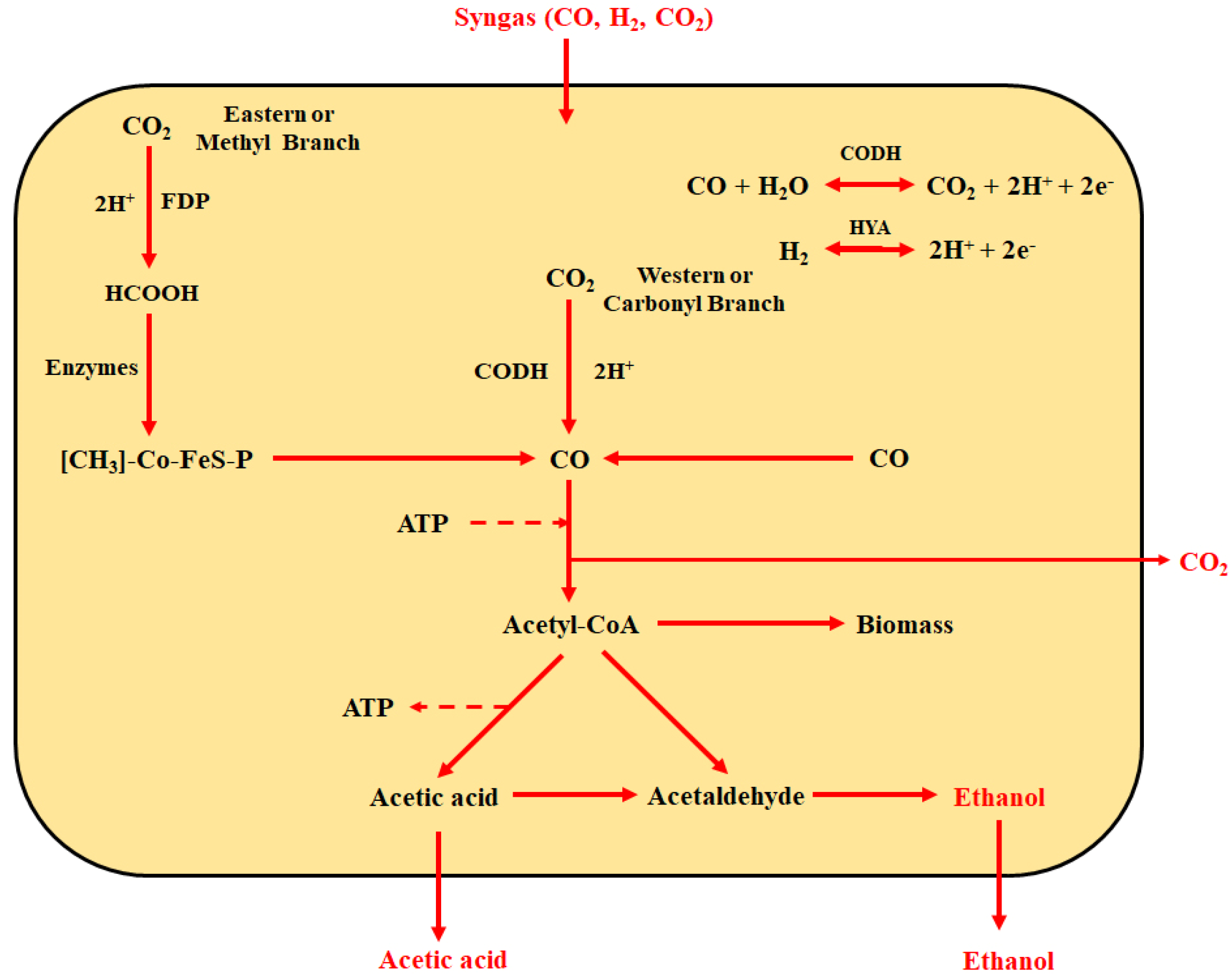
2.3. Pyro-Syngas Fermentation
2.3.1. Microorganism
2.3.2. Preparation of Modified Clostridial Medium for Growth
2.3.3. Pre-Adaptation of UACJUChE1 to Simulated Pyro-Syngas and Maintenance of Stock Culture
2.3.4. Batch Experiments for Determination of Growth Kinetics of UACJUChE1
Experiments for Growth Kinetics on CO
Experiments for Growth Kinetics on CO2 and H2
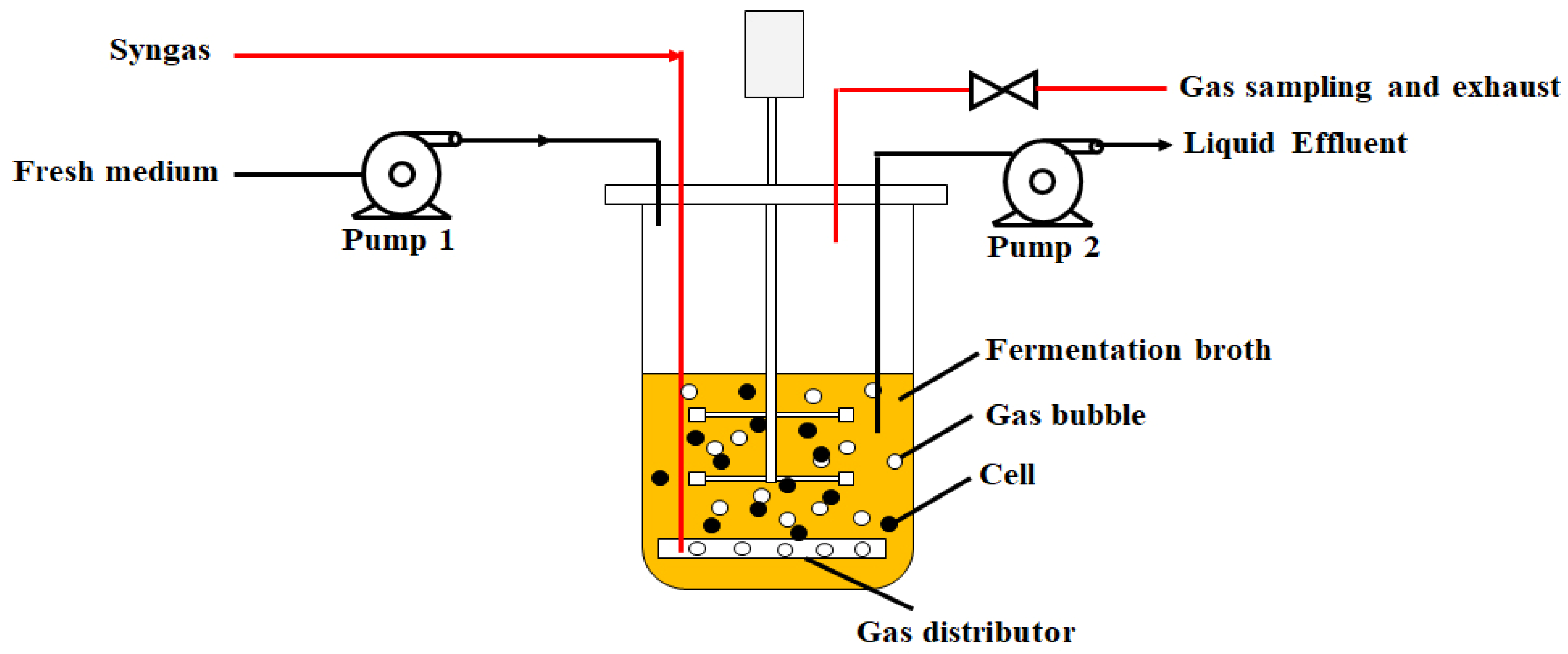
2.3.5. Stirred Tank Bioreactor for Pyro-Syngas Fermentation
Determination of Effect of Stirring Speed and Gas Velocity on O2 Mass Transfer Coefficient
Strategy of Operation of the Bioreactor in Semi-Batch and Continuous Modes
- Start-up
- Operation of the bioreactor
3. Theoretical Analysis
3.1. Growth Kinetics
3.1.1. Kinetics of Growth on CO
3.1.2. Kinetics of Growth on CO2–H2 Mixture
3.2. Mathematical Model
- Biomass growth on carbon monoxide
- Biomass growth on carbon dioxide and hydrogen
- Ethanol production fromcarbon monoxide
- Ethanol production from carbon dioxide and hydrogen
- Conversion of acetate into ethanol in the presence of CO
- Conversion of acetic acid into ethanol in the presence of H2
- Mole Balance Equations
- Semi-batch Reactor
- Gas Phase
- Liquid Phase
- Continuous Reactor
3.3. Optimization of Ethanol Concentration in Semi-Batch and Continuous Bioreactors
3.3.1. Semi-Batch Bioreactor
3.3.2. Continuous Bioreactor
4. Results and Discussion
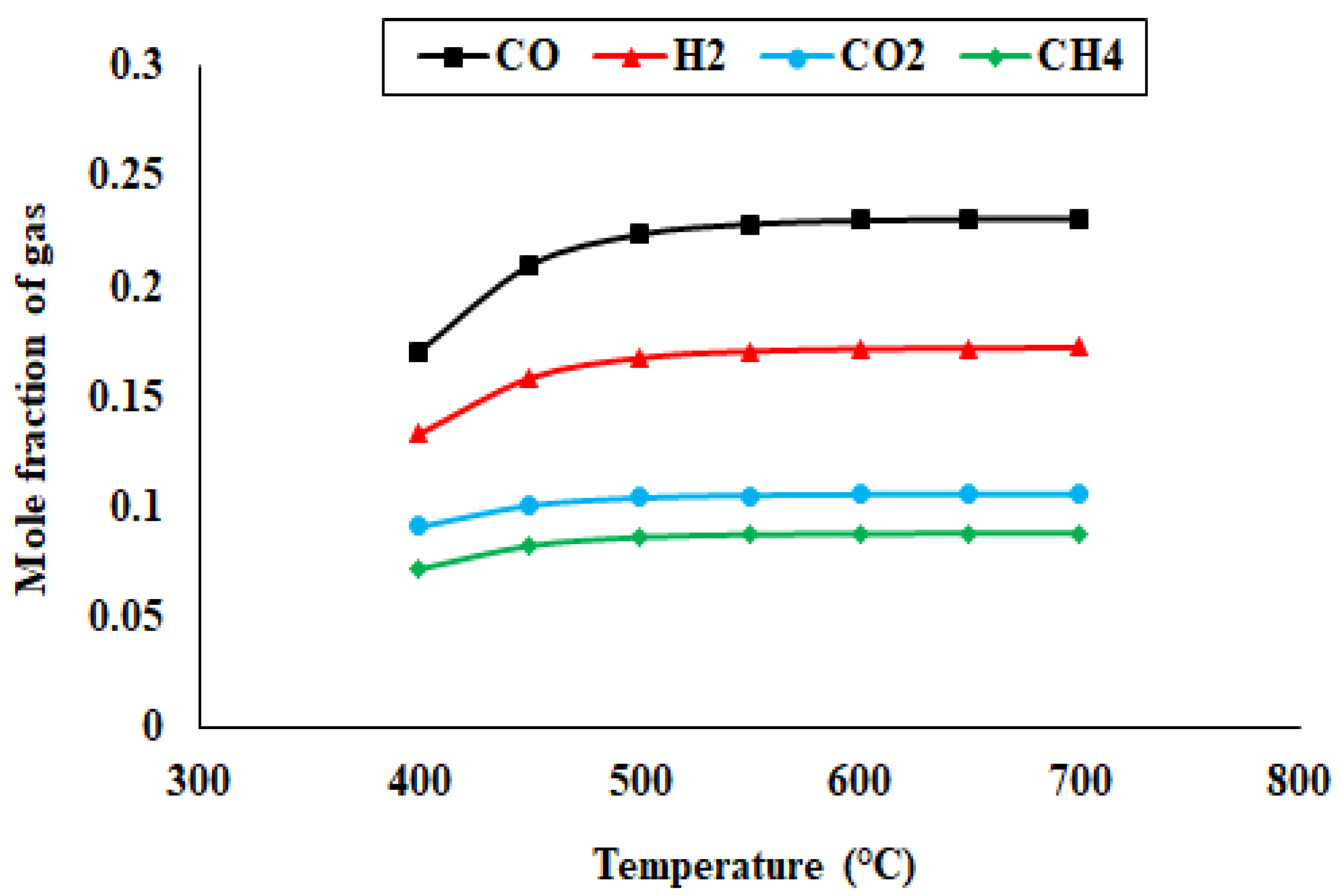
4.1. Composition and Volumetric Flow Rates of Pyro-Syngas
4.2. Values of Parameters
4.2.1. for Different Gases
4.2.2. Model Parameters
4.2.3. Significance of Model Parameters and Their Comparison with Similar Studies
4.3. Performance of the Bioreactor in Semi-Batch and Continuous Modes
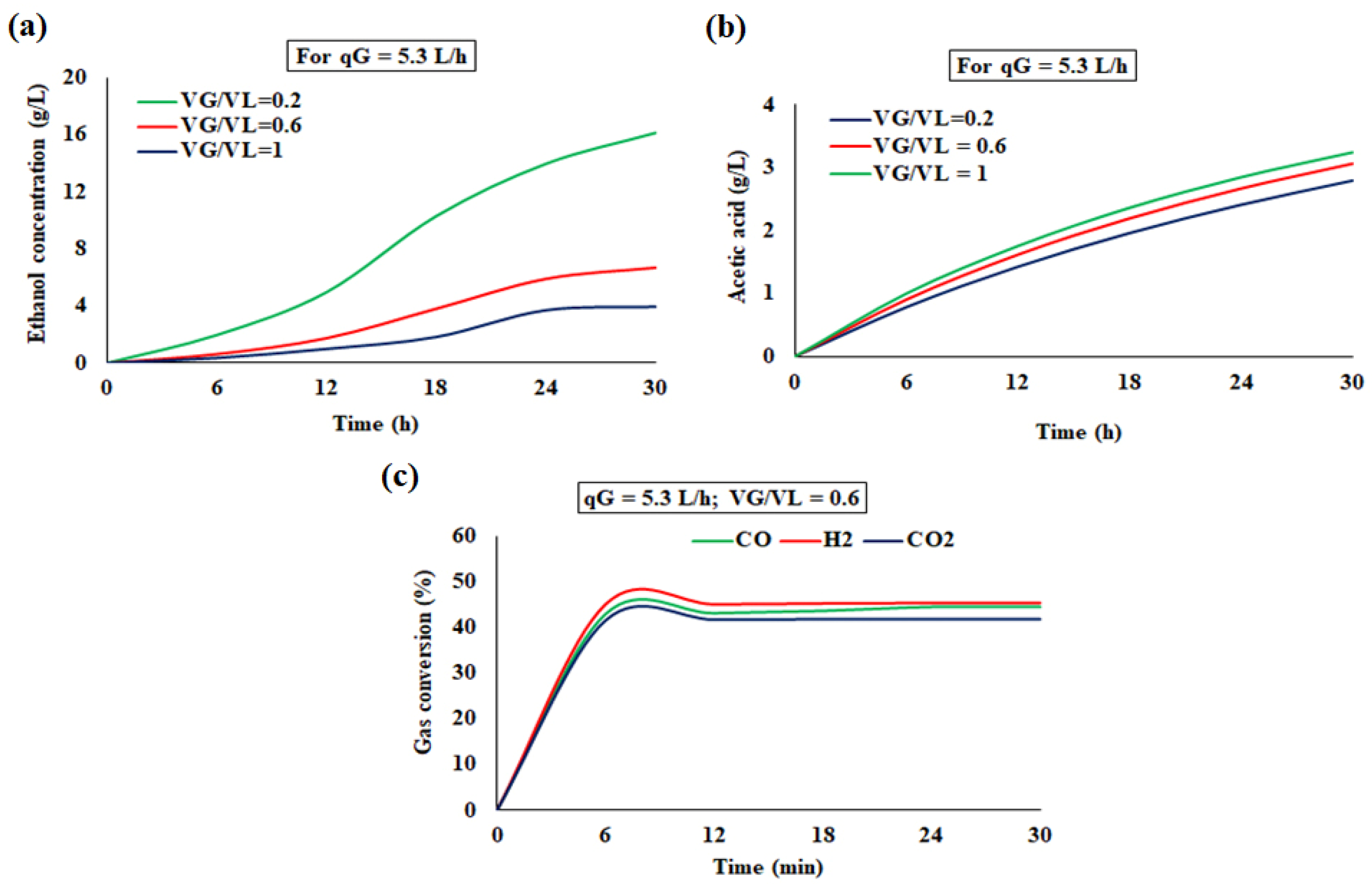
4.3.1. Bioreactor Dynamics in the Semi-Batch Mode
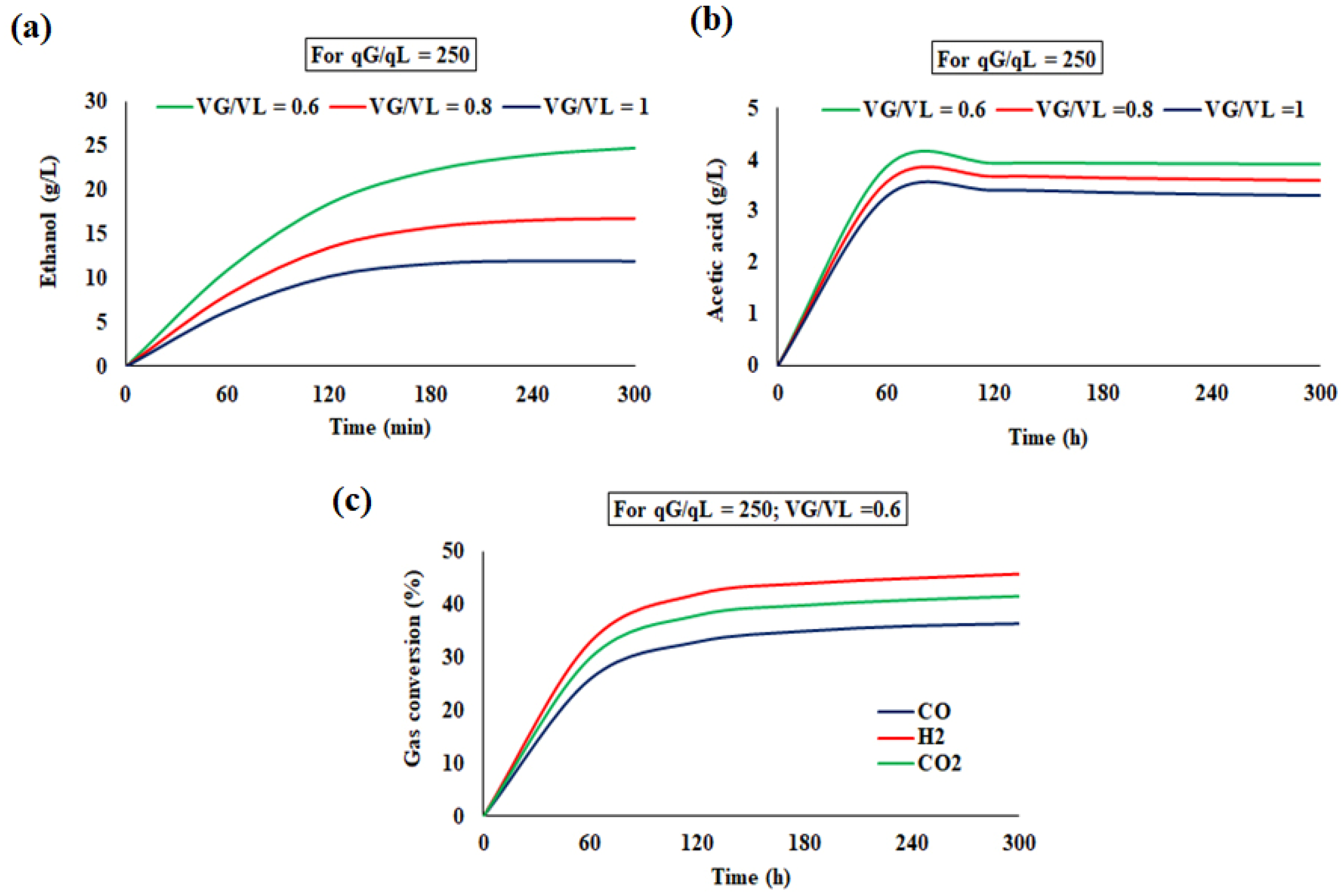
4.3.2. Bioreactor Dynamics in the Continuous Mode
Simulated Profile for the Continuous Reactor
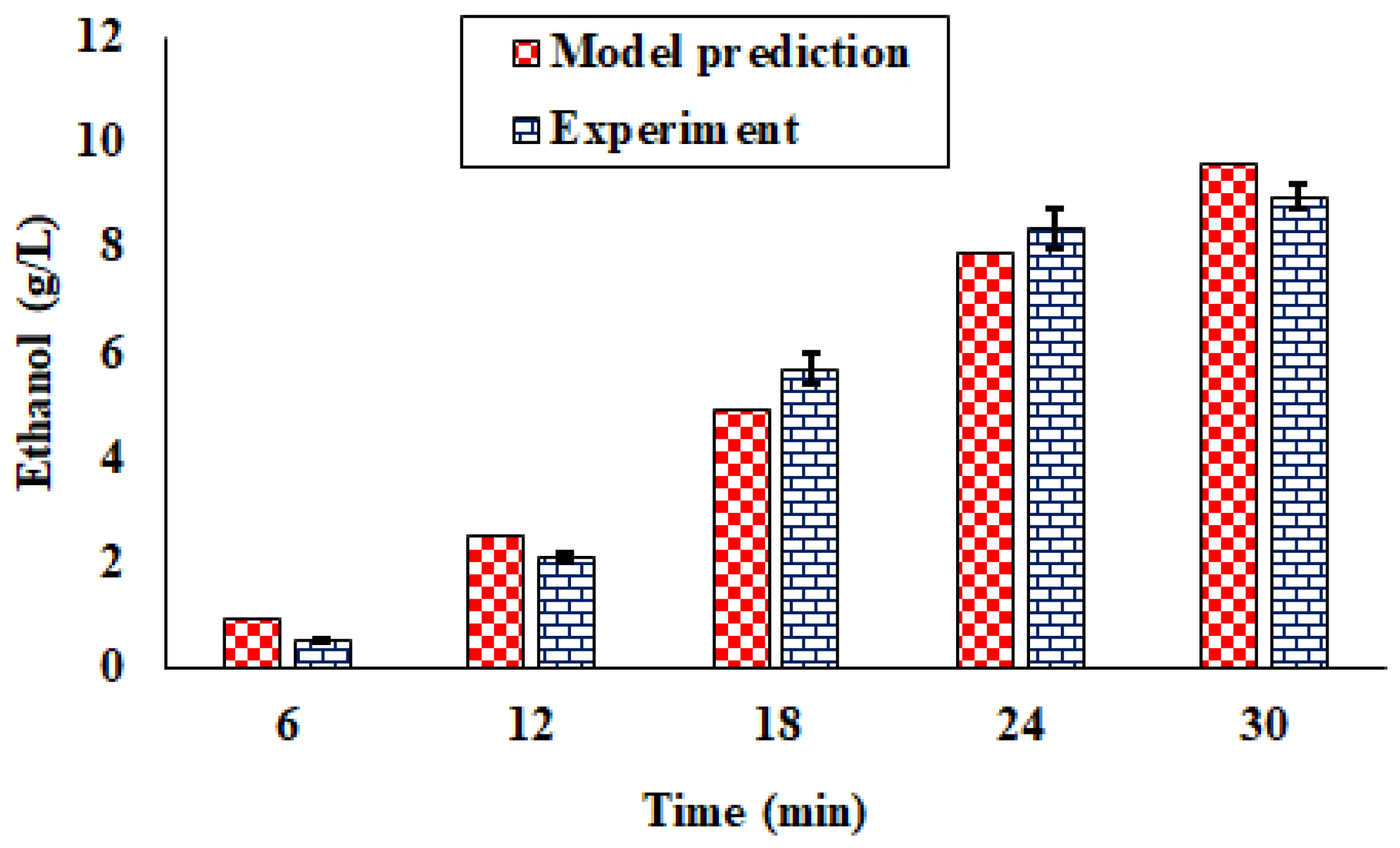
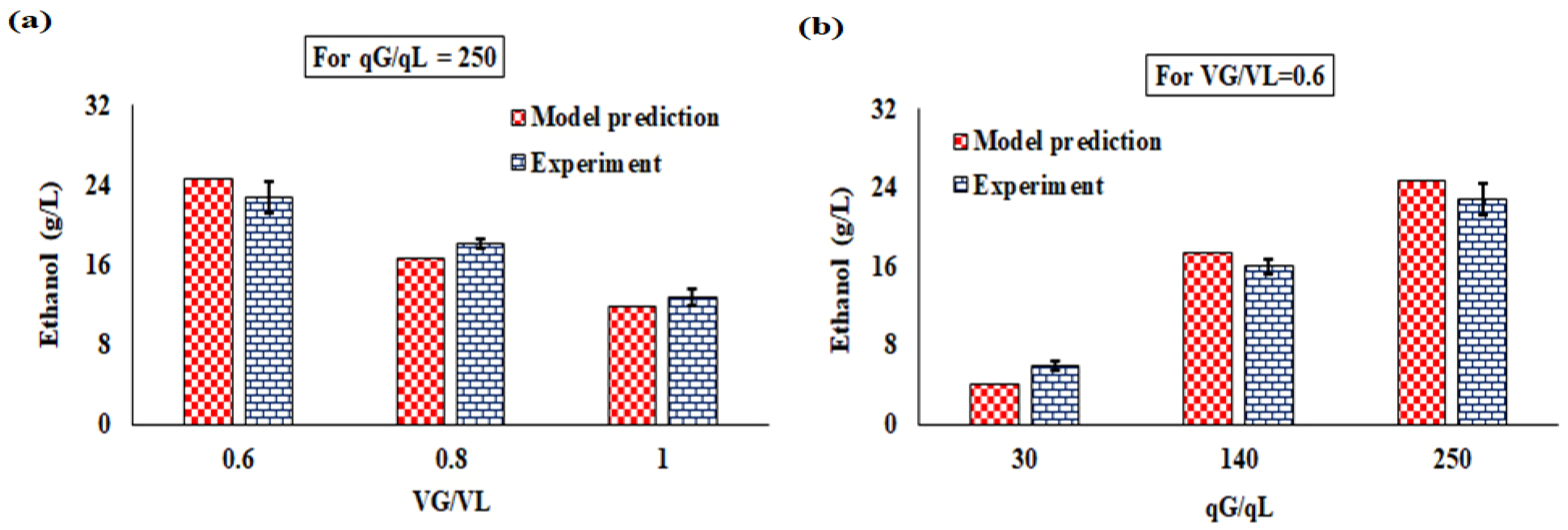
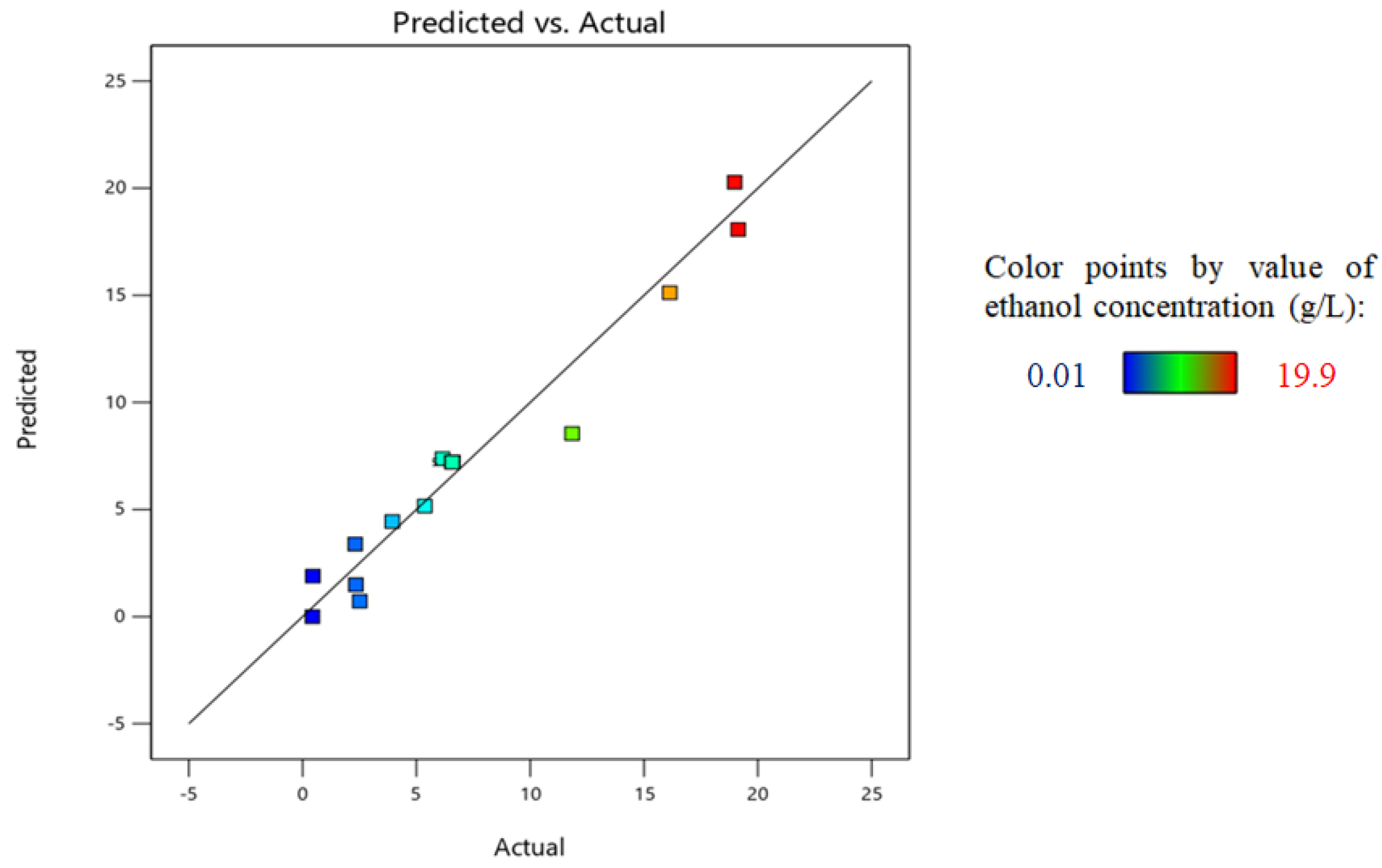
4.4. Comparison of Simulated and Experimental Results
4.4.1. Semi-Batch Operation
4.4.2. Continuous Operation
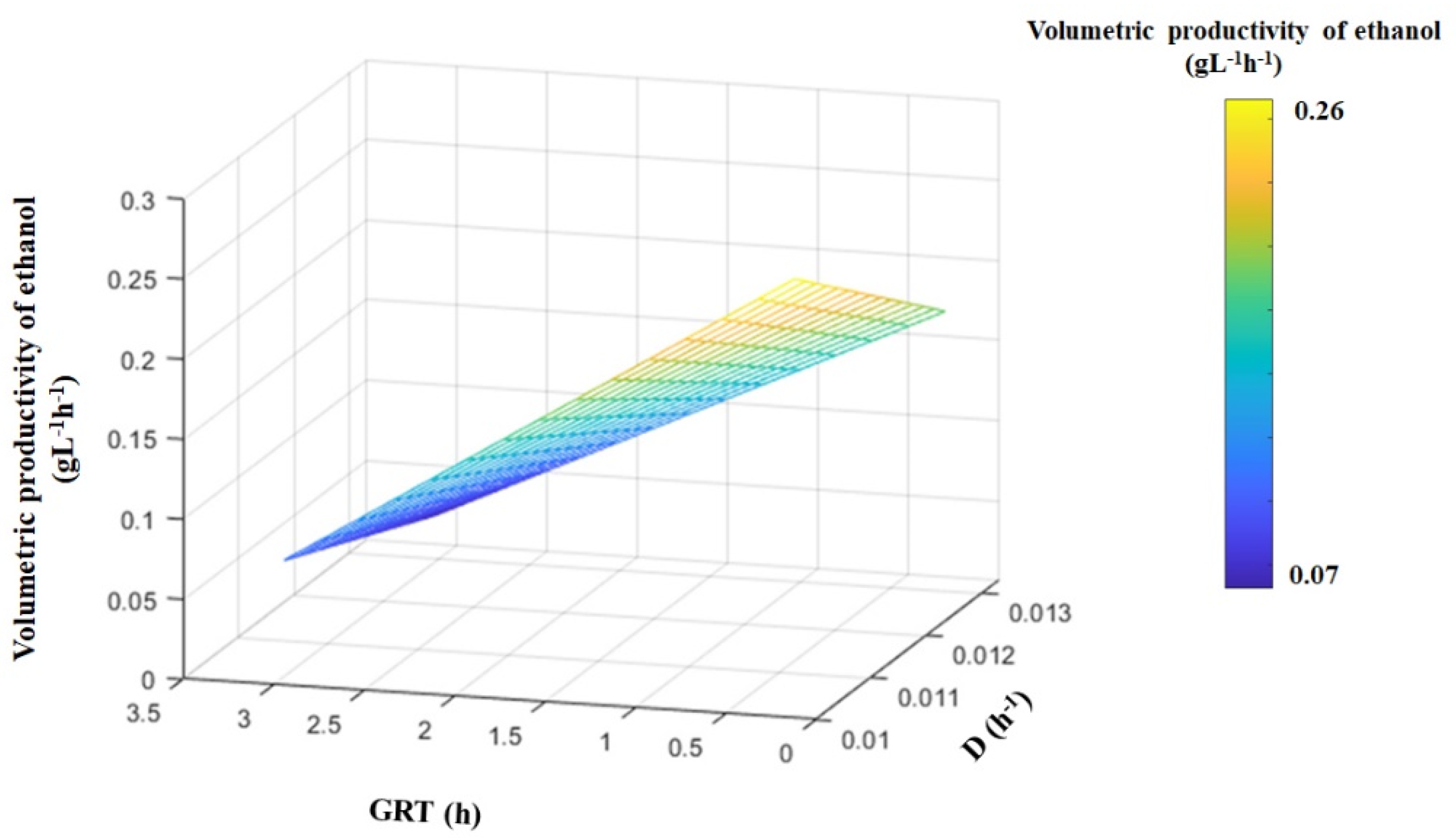
4.5. Effect of Gas Residence Time (GRT) and Dilution Factor (D) on the Volumetric Productivity of Ethanol
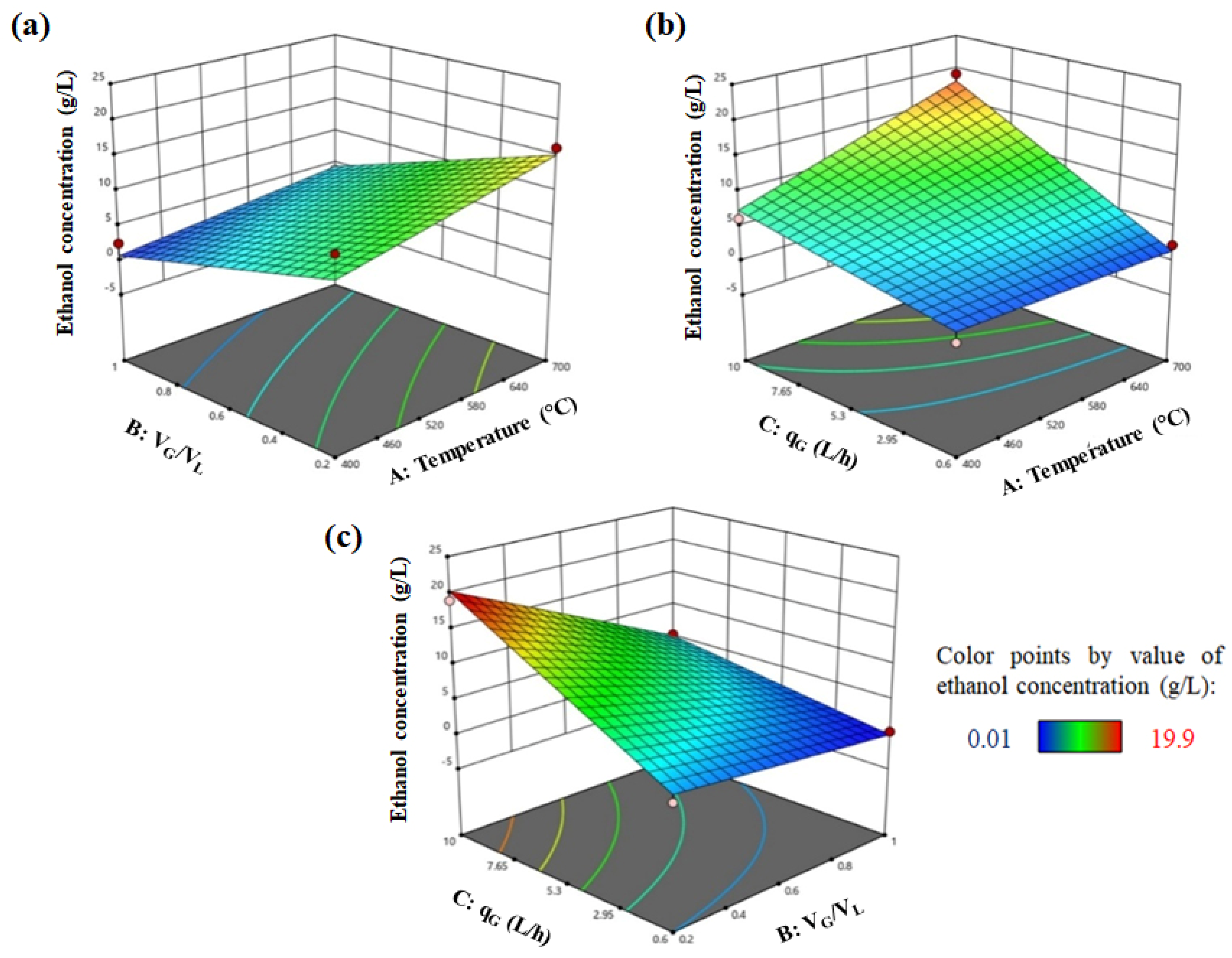
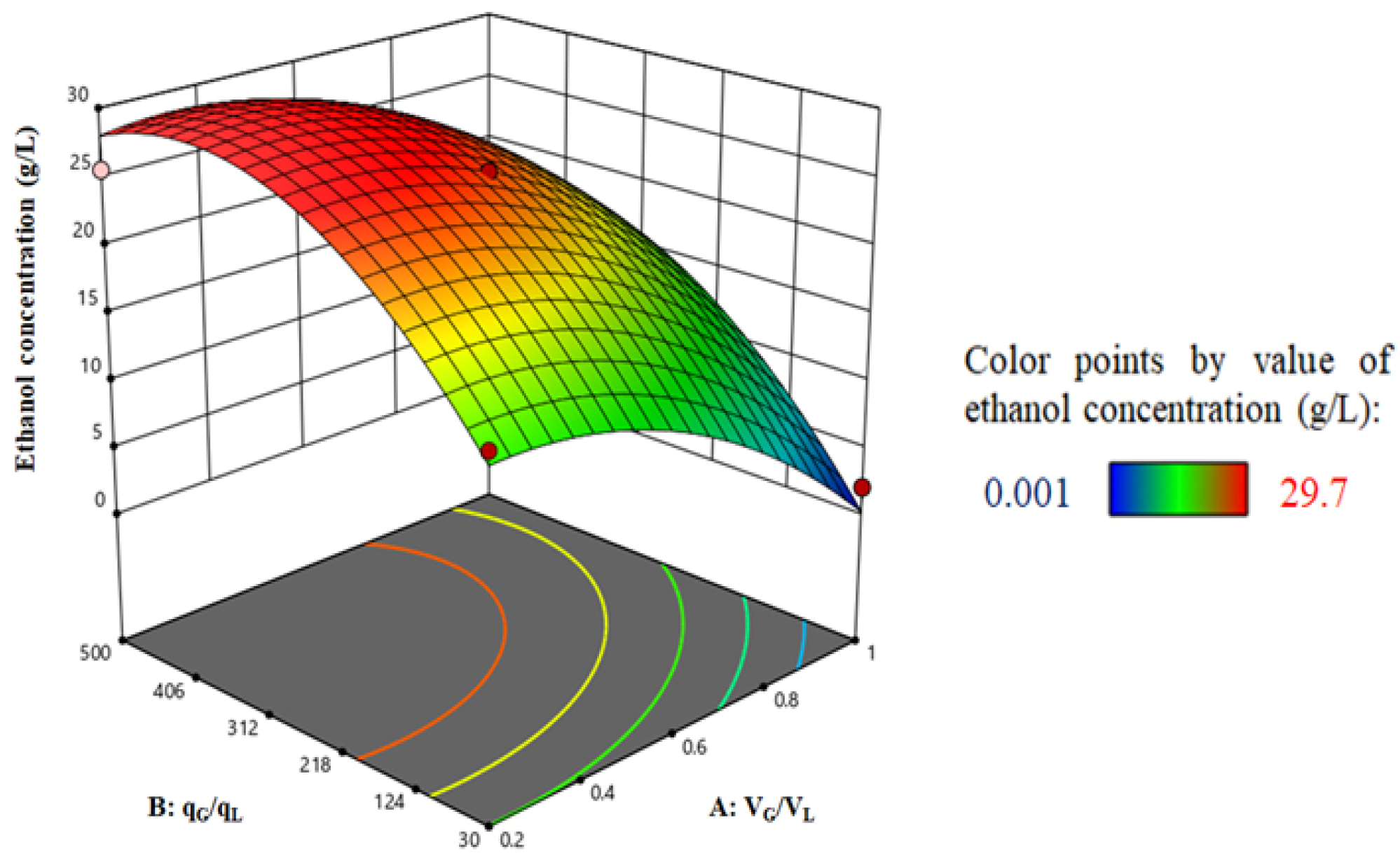
4.6. Optimization Results for Semi-Batch and Continuous Bioreactors
4.6.1. Semi-Batch Bioreactor
4.6.2. Syngas Fermentation in the Continuous Bioreactor
4.7. Comparison of Semi-Batch and Continuous Operation of a Pyro-Syngas Fermenter
4.8. Comparison with Similar Studies and Uniqueness
4.9. Challenges, Model Critique, and Future Scope
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chowdhury, R.; Ghosh, S.; Debnath, B.; Manna, D. Indian agro-wastes for 2G biorefineries: Strategic decision on conversion processes. In Sustainable Energy Technology and Policies: A Transformational Journey; Springer: Singapore, 2018; Volume 1, pp. 353–373. [Google Scholar]
- Kaur, M.; Malik, D.P.; Malhi, G.S.; Sardana, V.; Bolan, N.S.; Lal, R.; Siddique, K.H. Rice residue management in the Indo-Gangetic Plains for climate and food security. A review. Agron. Sustain. Dev. 2022, 42, 92. [Google Scholar] [CrossRef]
- Hassan, M.K.; Chowdhury, R.; Ghosh, S.; Manna, D.; Pappinen, A.; Kuittinen, S. Energy and environmental impact assessment of Indian rice straw for the production of second-generation bioethanol. Sustain. Energy Technol. Assess. 2021, 47, 101546. [Google Scholar] [CrossRef]
- Chowdhury, R.; Ghosh, S.; Manna, D.; Das, S.; Dutta, S.; Kleinsteuber, S.; Strauber, H.; Hassan, M.K.; Kuittinen, S.; Pappinen, A. Hybridization of sugar-carboxylate-syngas platforms for the production of bio-alcohols from lignocellulosic biomass (LCB)–A state-of-the-art review and recommendations. Energy Convers. Manag. 2019, 200, 112111. [Google Scholar] [CrossRef]
- Pacheco, M.; Moura, P.; Silva, C. A Systematic Review of Syngas Bioconversion to Value-Added Products from 2012 to 2022. Energies 2023, 16, 3241. [Google Scholar] [CrossRef]
- Faraji, M.; Saidi, M. Experimental and simulation study of peanut shell-derived activated carbon and syngas production via integrated pyrolysis-gasification technique. Process Saf. Environ. Prot. 2023, 171, 874–887. [Google Scholar] [CrossRef]
- Li, N.; Pan, Y.; Yan, Z.; Liu, Q.; Yan, Y.; Liu, Z. Cornstalk pyrolysis for syngas in a two-stage electromagnetic induction reactor. Fuel 2023, 336, 127124. [Google Scholar] [CrossRef]
- Chen, D.; Zhuang, X.; Gan, Z.; Cen, K.; Ba, Y.; Jia, D. Co-pyrolysis of light bio-oil leached bamboo and heavy bio-oil: Effects of mass ratio, pyrolysis temperature, and residence time on the biochar. Chem. Eng. J. 2022, 437, 135253. [Google Scholar] [CrossRef]
- Li, X.; Liu, P.; Huang, S.; Wu, S.; Li, Y.; Wu, Y.; Lei, T. Study on the mechanism of syngas production from catalytic pyrolysis of biomass tar by Ni–Fe catalyst in CO2 atmosphere. Fuel 2023, 335, 126705. [Google Scholar] [CrossRef]
- Esquivel-Elizondo, S.; Delgado, A.G.; Rittmann, B.E.; Krajmalnik-Brown, R. The effects of CO2 and H2 on CO metabolism by pure and mixed microbial cultures. Biotechnol. Biofuels 2017, 10, 220. [Google Scholar] [CrossRef]
- Kennes, D.; Abubackar, H.N.; Diaz, M.; Veiga, M.C.; Kennes, C. Bioethanol production from biomass: Carbohydrate vs syngas fermentation. J. Chem. Technol. Biotechnol. 2016, 91, 304–317. [Google Scholar] [CrossRef]
- Diender, M. Exploration of Microbial Systems as Biocatalysts for Conversion of Synthesis Gas to Bio-Based Chemicals. Ph.D. Dissertation, Wageningen University and Research, Wageningen, The Netherlands, 2019. Available online: https://research.wur.nl/en/publications/exploration-of-microbial-systems-as-biocatalysts-for-conversion-o (accessed on 12 October 2023).
- Siebler, F.; Lapin, A.; Takors, R. Synergistically applying 1-D modeling and CFD for designing industrial scale bubble column syngas bioreactors. Eng. Life Sci. 2020, 20, 239–251. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Gomez, J.A.; Höffner, K.; Barton, P.I.; Henson, M.A. Metabolic modeling of synthesis gas fermentation in bubble column reactors. Biotechnol. Biofuels 2015, 8, 89. [Google Scholar] [CrossRef] [PubMed]
- Vandecasteele, J. Experimental and Modelling Study of Pure-Culture Syngas Fermentation for Biofuels Production. Master’s Thesis, Universiteit Gent, Gent, Belgium, 2016. Volume 356. Available online: https://lib.ugent.be/catalog/rug01:002275054 (accessed on 10 October 2023).
- Almeida Benalcázar, E.; Noorman, H.; MacielFilho, R.; Posada, J.A. Modeling ethanol production through gas fermentation: A biothermodynamics and mass transfer-based hybrid model for microbial growth in a large-scale bubble column bioreactor. Biotechnol. Biofuels 2020, 13, 59. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Mohamed, A.R.; Najafpour, G.D.; Younesi, H.; Uzir, M.H. Kinetic studies on fermentative production of biofuel from synthesis gas using Clostridium ljungdahlii. Sci. World J. 2014, 2014, 910590. [Google Scholar] [CrossRef] [PubMed]
- Puiman, L.; Almeida Benalcázar, E.; Picioreanu, C.; Noorman, H.J.; Haringa, C. Downscaling Industrial-Scale Syngas Fermentation to Simulate Frequent and Irregular Dissolved Gas Concentration Shocks. Bioengineering 2023, 10, 518. [Google Scholar] [CrossRef] [PubMed]
- De Medeiros, E.M.; Posada, J.A.; Noorman, H.; Filho, R.M. Dynamic modeling of syngas fermentation in a continuous stirred-tank reactor: Multi-response parameter estimation and process optimization. Biotechnol. Bioeng. 2019, 116, 2473–2487. [Google Scholar] [CrossRef] [PubMed]
- Ruggiero, G.; Lanzillo, F.; Raganati, F.; Russo, M.E.; Salatino, P.; Marzocchella, A. Bioreactor modelling for syngas fermentation: Kinetic characterization. Food Bioprod. Process. 2022, 134, 1–18. [Google Scholar] [CrossRef]
- Sluiter, A.; Hames, B.; Ruiz, R.; Scarlata, C.; Sluiter, J.; Templeton, D.; Crocker, D.L.A.P. Determination of structural carbohydrates and lignin in biomass. Lab. Anal. Proced. 2008, 1617, 1–16. [Google Scholar]
- Chowdhury, R.; Sarkar, A. Reaction kinetics and product distribution of slow pyrolysis of Indian textile wastes. Int. J. Chem. React. Eng. 2012, 10, A67. [Google Scholar] [CrossRef]
- Sarkar, A.; Chowdhury, R. Co-pyrolysis of paper waste and mustard press cake in a semi-batch pyrolyzer—Optimization and bio-oil characterization. Int. J. Green Energy 2016, 13, 373–382. [Google Scholar] [CrossRef]
- Ghosh, S.; Pathak, S.; Manna, D.; Chowdhury, R. Acidogenic mixed consortium isolated from soil of agricultural field: Acid production behaviour and growth kinetics under the influence of pretreatment hydrolysate of rice straw (RS). Indian Chem. Eng. 2021, 63, 206–218. [Google Scholar] [CrossRef]
- Gill, N.K.; Appleton, M.; Baganz, F.; Lye, G.J. Quantification of power consumption and oxygen transfer characteristics of a stirred miniature bioreactor for predictive fermentation scale-up. Biotechnol. Bioeng. 2008, 100, 1144–1155. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Wang, Q.; Soklun, H.; Qu, G.; Xia, T.; Guo, X.; Lia, H.; Zhu, L. A green strategy for simultaneous Cu (II)-EDTA decomplexation and Cu precipitation from water by bicarbonate-activated hydrogen peroxide/chemical precipitation. Chem. Eng. J. 2019, 370, 1298–1309. [Google Scholar] [CrossRef]
- Abubackar, H.N.; Veiga, M.C.; Kennes, C. Biological conversion of carbon monoxide: Rich syngas or waste gases to bioethanol. Biofuels Bioprod. Biorefining 2011, 5, 93–114. [Google Scholar] [CrossRef]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Phillips, J.R.; Clausen, E.C.; Gaddy, J.L. Synthesis gas as substrate for the biological production of fuels and chemicals. Appl. Biochem. Biotechnol. 1994, 45, 145–157. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mohamed, A.R.; Najafpour, G.; Younesi, H.; Uzir, M.H. Clostridium ljungdahlii for production of biofuel from synthesis gas. Energy Sources Part A Recovery Util. Environ. Eff. 2016, 38, 427–434. [Google Scholar]
- Fox, J.D.; Kerby, R.L.; Roberts, G.P.; Ludden, P.W. Characterization of the CO-induced, CO-tolerant hydrogenase from Rhodospirillum rubrum and the gene encoding the large subunit of the enzyme. J. Bacteriol. 1996, 178, 1515–1524. [Google Scholar] [CrossRef] [PubMed]
- Rajagopalan, S.; Datar, R.P.; Lewis, R.S. Formation of ethanol from carbon monoxide via a new microbial catalyst. Biomass Bioenergy 2002, 23, 487–493. [Google Scholar] [CrossRef]
- Ranzi, E.; Cuoci, A.; Faravelli, T.; Frassoldati, A.; Migliavacca, G.; Pierucci, S.; Sommariva, S. Chemical kinetics of biomass pyrolysis. Energy Fuels 2008, 22, 4292–4300. [Google Scholar] [CrossRef]
- Pati, S.; De, S.; Chowdhury, R. Exploring the hybrid route of bio-ethanol production via biomass co-gasification and syngas fermentation from wheat straw and sugarcane bagasse: Model development and multi-objective optimization. J. Clean. Prod. 2023, 395, 136441. [Google Scholar] [CrossRef]
- Pati, S.; De, S.; Chowdhury, R. Integrated techno-economic, investment risk and life cycle analysis of Indian lignocellulosic biomass valorisation via co-gasification and syngas fermentation. J. Clean. Prod. 2023, 423, 138744. [Google Scholar] [CrossRef]

| Component | Cellulose | Hemicellulose | Lignin |
|---|---|---|---|
| % (w/w) | 38.31 ± 1.67 | 21.09 ± 0.92 | ±0.59 |
| SL No. | T (°C) | VG/VL | qG (L/h) | CO:CO2:H2:CH4:N2 | VG (L) | VL (L) |
|---|---|---|---|---|---|---|
| 1 | 550 | 0.6 | 5.3 | 22.8:10.5:17.1:8.7:21.7 | 1.125 | 1.875 |
| 2 | 550 | 0.6 | 5.3 | 22.8:10.5:17.1:8.7:21.7 | 1.125 | 1.875 |
| 3 | 400 | 0.6 | 10 | 17.0:9.1:13.3:7.1:27.0 | 1.125 | 1.875 |
| 4 | 700 | 1 | 5.3 | 23.1:10.6:17.2:8.8:21.5 | 1.5 | 1.5 |
| 5 | 400 | 1 | 5.3 | 17.0:9.1:13.3:7.1:27.0 | 1.5 | 1.5 |
| 6 | 550 | 0.2 | 10 | 22.8:10.5:17.1:8.7:21.7 | 0.5 | 2.5 |
| 7 | 700 | 0.2 | 5.3 | 23.1:10.6:17.2:8.8:21.5 | 0.5 | 2.5 |
| 8 | 400 | 0.2 | 5.3 | 17.0:9.1:13.3:7.1:27.0 | 0.5 | 2.5 |
| 9 | 550 | 1 | 10 | 22.8:10.5:17.1:8.7:21.7 | 1.5 | 1.5 |
| 10 | 700 | 0.6 | 0.6 | 23.1:10.6:17.2:8.8:21.5 | 1.125 | 1.875 |
| 11 | 700 | 0.6 | 10 | 23.1:10.6:17.2:8.8:21.5 | 1.125 | 1.875 |
| 12 | 550 | 0.2 | 0.6 | 22.8:10.5:17.1:8.7:21.7 | 0.5 | 2.5 |
| 13 | 550 | 1 | 0.6 | 22.8:10.5:17.1:8.7:21.7 | 1.5 | 1.5 |
| 14 | 550 | 0.6 | 5.3 | 22.8:10.5:17.1:8.7:21.7 | 1.125 | 1.875 |
| 15 | 550 | 0.6 | 5.3 | 22.8:10.5:17.1:8.7:21.7 | 1.125 | 1.875 |
| 16 | 550 | 0.6 | 5.3 | 22.8:10.5:17.1:8.7:21.7 | 1.125 | 1.875 |
| 17 | 400 | 0.6 | 0.6 | 17.0:9.1:13.3:7.1:27.0 | 1.125 | 1.875 |
| SL No. | VG/VL | qG/qL | VG (L) | VL (L) | qG (L/h) | qL (L/h) |
|---|---|---|---|---|---|---|
| 1 | 1 | 500 | 1.5 | 1.5 | 10 | 0.02 |
| 2 | 1 | 30 | 1.5 | 1.5 | 0.6 | 0.02 |
| 3 | 0.6 | 265 | 1.125 | 1.875 | 5.3 | 0.02 |
| 4 | 0.6 | 265 | 1.125 | 1.875 | 5.3 | 0.02 |
| 5 | 0.6 | 265 | 1.125 | 1.875 | 5.3 | 0.02 |
| 6 | 0.2 | 30 | 0.5 | 2.5 | 0.6 | 0.02 |
| 7 | 0.6 | 265 | 1.125 | 1.875 | 5.3 | 0.02 |
| 8 | 0.2 | 500 | 0.5 | 2.5 | 10 | 0.02 |
| 9 | 0.6 | 265 | 1.125 | 1.875 | 5.3 | 0.02 |
| 10 | 0.6 | 597.3 | 1.125 | 1.875 | 11.94 | 0.02 |
| 11 | 0.03 | 265 | 0.1 | 2.9 | 5.3 | 0.02 |
| 12 | 0.6 | 0 | 1.125 | 1.875 | 0 | 0.02 |
| 13 | 1.16 | 265 | 1.62 | 1.38 | 5.3 | 0.02 |
| Process | Specific Growth or Product Generation Rate (µ) |
|---|---|
| (i) Biomass growth on CO | |
| (ii) Biomass growth on CO2 and H2 | |
| (iii) Ethanol production from CO | |
| (iv) Ethanol production from CO2 and H2 | |
| (v) Conversion of acetate into ethanol using CO as electron donor | |
| (vi) Conversion of acetate into ethanol using H2 as electron donor |
| Input Variables | Unit | Coded Variable Level | Model Response | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| Temperature (A) | °C | 400 | 550 | 700 | Ethanol concentration (g/L) after 30 h operation |
| VG/VL (B) | 0.2 | 0.6 | 1 | ||
| qG (C) | L/h | 0.6 | 5.3 | 10 | |
| Input Variables | Unit | Coded Variable Level | Model Response | ||
|---|---|---|---|---|---|
| −1 | 0 | 1 | |||
| VG/VL (A) | - | 0.2 | 0.6 | 1 | Ethanol concentration (g/L) after 300 h operation |
| qG/qL (B) | - | 30 | 265 | 500 | |
| Temperature | Yield of Pyro-Products | ||
|---|---|---|---|
| °C | Pyro-Char | Pyro-Oil | Pyro-Syngas |
| 400 | 41.39 ± 1.97 | 27.01 ± 1.12 | 31.60 ± 1.01 |
| 450 | 37.98 ± 1.32 | 27.33 ± 1.01 | 34.69 ± 1.29 |
| 500 | 34.91 ± 1.89 | 28.02 ± 1.39 | 37.07 ± 1.33 |
| 550 | 30.09 ± 1.08 | 27.07 ± 1.02 | 42.84 ± 1.40 |
| 600 | 28.51 ± 0.52 | 25.37 ± 0.72 | 46.12 ± 2.11 |
| 650 | 25.34 ± 0.32 | 23.98 ± 0.15 | 50.68 ± 2.39 |
| 700 | 23.32 ± 0.33 | 22.09 ± 0.17 | 54.59 ± 2.42 |
| Process | Yield Coefficients (mol/mol) |
|---|---|
| (i) Biomass growth on CO | , , |
| (ii) Biomass growth on CO2 and H2 | , , |
| (iii) Ethanol production from CO | , |
| (iv) Ethanol production from CO2 and H2 | , |
| (v) Conversion of acetate into ethanol using CO as electron donor | , , , |
| (vi) Conversion of acetate into ethanol using H2 as electron donor | , |
| Symbol | Significance | Unit | Source | |
|---|---|---|---|---|
| Product of mass transfer coefficient (mh−1) and specific surface area (m2/m3) of CO in the bioreactor | 23.5–100.7 | h−1 | Determined | |
| Product of mass transfer coefficient (mh−1) and specific surface area (m2/m3) of CO2 in the bioreactor | 27–116.7 | h−1 | Determined | |
| Product of mass transfer coefficient (mh−1) and specific surface area (m2/m3) of H2 in the bioreactor | 20–87.4 | h−1 | Determined | |
| Henry’s law constant of CO | 0.0008 | mol/L/atm | [28] | |
| Henry’s law constant of CO2 | 0.00066 | mol/L/atm | [28] | |
| Henry’s law constant of H2 | 0.025 | mol/L/atm | [28] | |
| Maximum specific growth rate on CO | 0.192 | h−1 | Determined | |
| Maximum specific growth rate on CO2 and H2 | 0.045 | h−1 | Determined | |
| Maximum specific production rate of ethanol from CO | 0.20 | h−1 | [15] | |
| Maximum specific production rate of ethanol from CO2 and H2 | 0.0001 | h−1 | [15] | |
| Maximum specific production rate of ethanol through conversion of acetate using CO as electron donor | 0.20 | h−1 | [15] | |
| Maximum specific production rate of ethanol through conversion of acetate using H2 as electron donor | 0.20 | h−1 | [15] | |
| Saturation constant for CO for growth | 0.000078 | mol/L | [15] | |
| Saturation constant for H2 for growth | 0.00022 | mol/L | [15] | |
| Saturation constant for CO2 for growth | 0.00022 | mol/L | [15] | |
| Saturation constant of acetic acid for ethanol production from CO/CO2 and H2 | 0.0005 | mol/L | [15] | |
| Saturation constant of acetic acid for ethanol production from acetate | 0.0005 | mol/L | [15] | |
| Inhibition constant of CO for growth on CO | 0.002 | mol/L | [15] | |
| Inhibition constant of CO for growth on CO2 and H2 | 7 × 10−9 | mol/L | [15] | |
| Inhibition constant of acetic acid for growth on CO/CO2 and H2 | 0.0104 | mol/L | [15] |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 534.72 | 6 | 89.12 | 34.53 | <0.0001 | significant |
| A-Temperature | 53.05 | 1 | 53.05 | 20.55 | 0.0011 | |
| B-VG/VL | 171.22 | 1 | 171.22 | 66.34 | <0.0001 | |
| C-qG | 243.21 | 1 | 243.21 | 94.23 | <0.0001 | |
| AB | 2.04 | 1 | 2.04 | 0.7923 | 0.3943 | |
| AC | 30.80 | 1 | 30.80 | 11.93 | 0.0062 | |
| BC | 34.40 | 1 | 34.40 | 13.33 | 0.0045 | |
| Residual | 25.81 | 10 | 2.58 | |||
| Lack of Fit | 25.81 | 6 | 4.30 | |||
| Pure Error | 0.0000 | 4 | 0.0000 | |||
| Cor Total | 560.53 | 16 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 1142.09 | 5 | 228.42 | 63.15 | <0.0001 | significant |
| A-VG/VL | 329.07 | 1 | 329.07 | 90.97 | <0.0001 | |
| B-qG/qL | 453.60 | 1 | 453.60 | 125.40 | <0.0001 | |
| AB | 3.67 | 1 | 3.67 | 1.01 | 0.3475 | |
| A2 | 116.09 | 1 | 116.09 | 32.09 | 0.0008 | |
| B2 | 280.71 | 1 | 280.71 | 77.61 | <0.0001 | |
| Residual | 25.32 | 7 | 3.62 | |||
| Lack of Fit | 25.32 | 3 | 8.44 | |||
| Pure Error | 0.0000 | 4 | 0.0000 | |||
| Cor Total | 1167.41 | 12 |
| Feed Gas Composition | Mode of Operation | Microorganism Used | Maximum Ethanol Concentration (g/L) | Reference |
|---|---|---|---|---|
| CO:CO2:H2:N2 32:8:32:28 | Batch | Clostridium ljungdahlii | 0.778 | [15] |
| H2:CO 75:25 | Continuous | Clostridium ljungdahlii | 1.304 | [16] |
| CO:CO2:H2:inert 55:10:20:15 | Continuous | Clostridium ljungdahlii | 45.0 | [19] |
| 100% CO | Batch | Clostridium carboxidivorans | 0.4 | [20] |
| 100% CO | Continuous | Clostridium carboxidivorans | 5.6 | [20] |
| CO:CO2:H2:CH4: N2 17.0:9.1:13.3:7.1:27.0; 22.8:10.5:17.1:8.7:21.7; 23.1:10.6:17.2:8.8:21.5 | Semi-batch | Clostridial consortium, UACJUChE1 | 13.1 | Present study |
| CO:CO2:H2:CH4: N2 23.1:10.6:17.2:8.8:21.5 | Continuous | Clostridial consortium, UACJUChE1 | 29.4 | Present study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manna, D.; Chowdhury, R.; Calay, R.K.; Mustafa, M.Y. Experimental Insights into the Fermentation of Pyro-Syngas to Ethanol in a Semi-Batch and Continuous Stirred Bioreactor with Mathematical Modelling and Optimization. Energies 2024, 17, 562. https://doi.org/10.3390/en17030562
Manna D, Chowdhury R, Calay RK, Mustafa MY. Experimental Insights into the Fermentation of Pyro-Syngas to Ethanol in a Semi-Batch and Continuous Stirred Bioreactor with Mathematical Modelling and Optimization. Energies. 2024; 17(3):562. https://doi.org/10.3390/en17030562
Chicago/Turabian StyleManna, Dinabandhu, Ranjana Chowdhury, Rajnish K. Calay, and Mohamad Y. Mustafa. 2024. "Experimental Insights into the Fermentation of Pyro-Syngas to Ethanol in a Semi-Batch and Continuous Stirred Bioreactor with Mathematical Modelling and Optimization" Energies 17, no. 3: 562. https://doi.org/10.3390/en17030562
APA StyleManna, D., Chowdhury, R., Calay, R. K., & Mustafa, M. Y. (2024). Experimental Insights into the Fermentation of Pyro-Syngas to Ethanol in a Semi-Batch and Continuous Stirred Bioreactor with Mathematical Modelling and Optimization. Energies, 17(3), 562. https://doi.org/10.3390/en17030562









