Abstract
Economic Dispatch Problems (EDP) refer to the process of determining the power output of generation units such that the electricity demand of the system is satisfied at a minimum cost while technical and operational constraints of the system are satisfied. This procedure is vital in the efficient energy management of electricity networks since it can ensure the reliable and efficient operation of power systems. As power systems transition from conventional to modern ones, new components and constraints are introduced to power systems, making the EDP increasingly complex. This highlights the importance of developing advanced optimization techniques that can efficiently handle these new complexities to ensure optimal operation and cost-effectiveness of power systems. This review paper provides a comprehensive exploration of the EDP, encompassing its mathematical formulation and the examination of commonly used problem formulation techniques, including single and multi-objective optimization methods. It also explores the progression of paradigms in economic dispatch, tracing the journey from traditional methods to contemporary strategies in power system management. The paper categorizes the commonly utilized techniques for solving EDP into four groups: conventional mathematical approaches, uncertainty modelling methods, artificial intelligence-driven techniques, and hybrid algorithms. It identifies critical research gaps, a predominant focus on single-case studies that limit the generalizability of findings, and the challenge of comparing research due to arbitrary system choices and formulation variations. The present paper calls for the implementation of standardized evaluation criteria and the inclusion of a diverse range of case studies to enhance the practicality of optimization techniques in the field.
1. Introduction
Power grids, involving conventional thermal power plants that run on fossil fuels, play a vital role in energy generation. They are responsible for producing a significant proportion of the electricity energy mix. This is despite the fact that several alternative energy sources such as renewable energies are available to power system operators. Two main characteristics of thermal power plants, namely, reliability and affordability, cause thermal plants to hold a prominent position among other sources of electricity in electricity generation.
According to the U.S. Energy Information Administration (EIA) [1], fossil fuels have been the largest sources of energy for electricity generation from 1950 to 2021. Table 1, depicts the contribution of various energy sources in billions of kilowatt hours (kWh), thereby showcasing the significant role of fossil fuels in meeting the electricity demand in the United States. Natural gas and coal were shown to constitute about 38% and 22% of the total generation, respectively, and were reported as the two largest sources of electricity generation in the U.S. in 2021. Additionally, thermal plants powered by fossil fuels have generated about 60% of the total electricity generation in 2022 [1]. The data of US energy sources in 2022 [1], have been utilized to create Figure 1, illustrating the distribution of these energy sources.

Table 1.
Comparison of Energy Generation Sources.
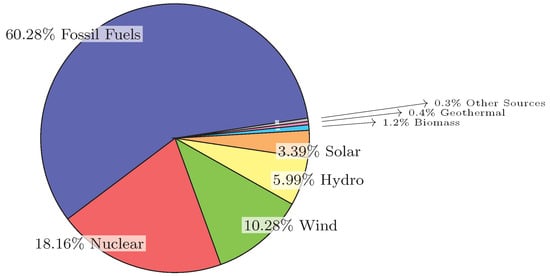
Figure 1.
Composition of electricity generation by different sources in percentages.
Population and urbanization growth, along with the growth of industries, have contributed to continuous increments in electricity consumption. The scarcity of fossil fuels and the adverse environmental impacts of thermal power plants are the major driving forces with respect to efficiently managing the power network and obtaining the optimal power generation schedule for the power system. It is noteworthy that power networks are vast in size and include multiple generators and transmission networks that span huge geographical areas. Hence, the management of the electricity grid is a complex task that involves several challenges [2]. One of the major challenges that power system operators face when managing the electricity grid is maintaining the balance between electricity demand and generation. It is a technically difficult task to store electricity on a large scale; therefore, it is highly significant to retain the supply and demand equilibrium in the power networks.
Moreover, in order to have an economically feasible power system, the network must meet the electricity demand while minimizing the operation cost. The economic challenge stems from the fact that the generation cost varies from one generator to another one. This is because the cost of generated electricity at a specific generator is affected by several factors such as local fuel cost, the availability of the generator, and the plant’s maintenance cost [3]. Hence, to efficiently run the power system, it is vital to address the above-mentioned techno-economic constraints while operating electricity grids.
The EDP refers to the process of calculating the output power of each available generator to meet the total network demand while minimizing operation costs and/or generators’ carbon dioxide emissions [4]. Essentially, the EDP involves identifying the most efficient scheduling of generators while considering various economic and technical limitations associated with both the committed generators and the power grid. The primary concept in the EDP is to prioritize the generators with the lowest marginal costs for operation, and the marginal cost of the overall system is determined by the generator with the highest cost.
Economic dispatch offers several advantages, including lower operating costs, increased efficiency, and reduced emissions. By optimizing the output of each generator, economic dispatch can help to minimize the overall cost of electricity production. Additionally, it can help to maximize the efficiency of the power system and reduce its negative environmental impact by utilizing the most cost-effective and least-polluting generators first.
The assistance of economic dispatch greatly facilitates the optimization of electricity network operation, thereby making it an essential tool for achieving efficient operation of the power grid. System operators can reap a multitude of benefits from economic dispatch, including economic, technical, health, and climate advantages [5]. By enhancing system efficiency and reducing greenhouse gas emissions, economic dispatch can have a positive impact on health and the climate. Additionally, it can lead to increased reliability and more effective utilization of power sources for the electricity grid. Therefore, it is of utmost importance to define and solve the EDP precisely.
The EDP has been a persistent issue in the literature since 1920, thereby leading to extensive research in this area [6].
While numerous review papers on the economic dispatch problem (EDP) exist in the literature, most tend to focus narrowly on specific aspects. For instance, several existing reviews focus exclusively on narrow categories of optimization techniques or specific theoretical approaches [7,8,9,10]. Others limit their scope to particular optimization strategies or theoretical frameworks, with each addressing only a fragment of the broader EDP landscape [11]. Additionally, certain reviews target specific types of power systems [12,13]. In contrast, the present research provides a comprehensive examination of the EDP, thus tracing its evolution from traditional to modern power systems. We systematically categorize research studies based on the type of problem formulation and subsequently analyze the array of methods used for solving the EDP, thereby encompassing a wide range of approaches from conventional to advanced techniques. This approach provides an extensive, in-depth overview of the EDP, thereby offering researchers in the field a holistic and detailed perspective of the subject matter. Furthermore, this paper makes a significant contribution by focusing exclusively on publications from 2018 to 2023, thereby providing a current and relevant perspective on economic dispatch. This approach ensures that it serves as an authoritative guide for future research, thus highlighting recent trends and fostering new explorations and developments in the field:
- We conduct a critical analysis of the existing literature that assesses the performance, advantages, and drawbacks of the algorithms used in prior research studies.
- We establish the current state of the art by providing an up-to-date and innovative classification of EDP formulations, objective functions, and optimization algorithms.
- We synthesize the existing literature to offer a useful starting point for future research work in the field of the EDP.
- We identify gaps in the existing literature and highlight areas that require further investigation.
The paper is structured as follows: Section 2 outlines the research methodology employed to conduct the present review. Section 3 discusses the evolution of paradigms in economic dispatch, thus detailing the shift from conventional techniques to modern strategies in power system management. Section 4 and Section 5 classify the EDP formulation and optimization techniques, respectively. Section 6 discusses the findings in detail. Finally, Section 7 summarizes the conclusions of the paper.
2. Research Methodology
The present research employs a systematic literature review that utilizes Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines. The PRISMA guidelines involve four primary steps. First, the research scope is identified by the researcher. Next, proper keywords are selected by the researcher to search databases for the most relevant studies. The third step is focused on eligibility analysis, while the fourth step deals with data analysis [14].
The scope of the research in this review paper is the formulation and optimization of economic dispatch. The Scopus database was selected for the literature search, articles that were considered irrelevant were excluded, and those that were relevant underwent a full-text review. The formulation and optimization techniques utilized in each article were carefully recorded, along with their contributions to the field. The backward referencing approach was also employed to identify additional related papers. The fourth step of the PRISMA guidelines was completed by classifying the collected papers based on their problem formulation and optimization techniques employed.
The database was searched using the keywords “Optimization”, “Economic Dispatch”, “Virtual Power Plants”, and “Multi Energy Systems” with a search of article titles, abstracts, and keywords, thereby resulting in 5070 articles retrieved. Economic dispatch has been extensively researched in the power systems literature due to its long-standing relevance, but the emergence of smart grids has renewed interest in this topic. To ensure a focus on contemporary research, this review paper restricted the publication years to 2018–2023. This was to exclude studies that revolve around traditional power systems, thus resulting in a selection of 4481 documents. Additionally, research studies with irrelevant keywords such as heat and hydrogen storage, reactive power, thermoelectric power systems, forecasting, economic and social effects, digital storage, model predictive control, economics, cogeneration plants, electric load flow, and commerce were excluded to ensure a focused approach on the main topic of interest. Papers written in non-English languages were also excluded. As a result, 889 relevant documents were obtained. Furthermore, nonrelevant subject areas such as social science, business management and accounting, medicine, art and humanities, and others were excluded. This resulted in a total of 288 documents. Subsequently, these articles underwent screening based on their abstract and title. As a result, 175 papers were further evaluated through a full article assessment and included in this comprehensive review.
3. Evolving Paradigms in Economic Dispatch: From Conventional Techniques to Modern Power System Strategies
In this section, we discuss the evolution of economic dispatch, thereby tracing its progression from established conventional power systems to innovative contemporary models. We begin with an analysis of the traditional economic dispatch, thereby detailing the foundational principles and strategies employed in earlier power system optimization. The focus then shifts to the application of economic dispatch in the realm of virtual power plants (VPPs), thereby emphasizing the transformative role of these technologies in introducing decentralization and advanced management techniques to the field. Finally, the discussion extends to the utilization of economic dispatch within multienergy systems (MESs), thus underscoring the significance of integrating various energy sources to optimize efficiency and promote environmental sustainability. Each subsection presents a distinct, yet interconnected aspect of the ongoing progression in economic dispatch strategies.
3.1. Foundations of Economic Dispatch in Conventional Power Systems
Economic dispatch problems (EDPs) represent a fundamental optimization challenge within traditional power systems. The principal aim of the EDP is to optimize the cost-efficiency of electricity generation, thereby concurrently ensuring adherence to the plethora of constraints associated with power system operations. Achieving this objective requires the formulation of the EDP as an optimization problem that incorporates an objective function and a set of constraints.
The EDP in its most fundamental form is commonly known as the classic EDP. The primary objective of this problem is to minimize the generation cost of electricity in a power system, with the cost function typically defined as a quadratic equation. The optimization problem involves constraints related to the generation load balance, power loss, and generation limits for each power plant. The conventional mathematical formulation of the EDP is represented by the following equation [15]:
The total generation cost in Equation (1) is represented by , with the cost coefficients for the ith generator denoted by , , and . The electricity demand and loss are denoted by and , respectively. The output limits for the ith generator are shown as and .
The classical economic dispatch formulation often falls short in real-world scenarios, especially as traditional power systems, once dominated by fossil fuels and thermal generators, have evolved. Modern power networks now incorporate a variety of renewable energy sources, thereby altering system components and necessitating new approaches in economic dispatch problem solving. These changes have spurred advancements in the EDP, with studies proposing innovative objective functions and formulations. Building on this, the next section explores the EDP within VPPs, thereby showcasing advanced solutions for these modern, complex power systems.
3.2. VPP-Based Economic Dispatch
In contrast to traditional power systems, which predominantly consist of conventional thermal generators, contemporary power systems are increasingly inclusive of renewable energy sources dispersed throughout the network. While these renewables offer considerable environmental and economic advantages, their integration into the power system presents a myriad of challenges [16]. These challenges encompass aspects such as grid stability, variable energy output, and demand–supply management. This complex landscape has been a driving force behind the inception of the concept of virtual power plants (VPPs). A virtual power plant (VPP) is comprised of a heterogeneous array of distributed energy resources (DERs) that are controlled in a centralized manner [17]. VPPs represent a strategic response to these challenges, thereby providing an innovative framework for the efficient and effective integration of diverse energy resources into the power grid. This innovative approach reflects the transition from classic power systems to VPPs, thereby signaling a shift towards more decentralized and flexible energy management [18,19,20].
This transformation has led to a notable shift in the economic dispatch problem (EDP), thereby resulting in a significant deviation from traditional EDP approaches. The integration of diverse renewable energy sources within virtual power plants (VPPs) presents unique challenges, thus driving this change. These complexities require redefining traditional EDP strategies to effectively manage the variable and intermittent nature of renewables, thereby ensuring efficient and reliable energy management in a sustainable power generation landscape [21].
The formulation of the EDP for VPPs can be categorized into two distinct approaches: centralized and distributed. In the centralized approach for EDP formulation in VPPs, control and decision making are centralized at one point. All distributed energy resources (DERs) within the VPP network transmit real-time data, including energy generation and constraints, to this central controller. The controller processes this data to solve the EDP, thereby aiming to maximize the overall system efficiency. The formulated dispatch strategy is then communicated back to the DERs for execution. This approach involves the aggregation of data and operational commands from various distributed energy resources (DERs) within the VPP network to a central control unit [22].
This approach facilitates harmonized operations across the network, thereby potentially enhancing the overall system efficiency. However, it necessitates a substantial communication infrastructure due to the continuous exchange of extensive data between the main controller and DERs dispersed over a vast network. Another challenge is maintaining the privacy of DERs owners, as sensitive operational data are transmitted to the central operator. Additionally, the centralized processing model introduces the risk of a single-point failure, which could potentially lead to a systemic collapse [23].
In contrast to the centralized paradigm, the distributed approach to economic dispatch in VPPs represents a fundamentally different strategy. In this methodology, DERs are each equipped with individual intelligence, thereby enabling autonomous decision making. Each DER utilizes real-time data and specific constraints to achieve the most locally optimal operation for its subproblem. This objective is accomplished through communication and information exchange with neighboring units, thereby ensuring a coordinated approach while maintaining individual operational autonomy [24].
The theoretical foundation and practical applications of the distributed approach in VPPs have been explored in recent research [25,26,27,28,29,30,31,32,33,34,35,36]. These studies provide valuable insights into the intricacies of implementing such systems, addressing key challenges such as communication technology requirements, system resilience, and the complex interplay between local and global objectives. Such coordination necessitates advanced communication and control technologies. However, unlike centralized systems, this approach is not prone to single-point failures, as each DER can operate independently, enhancing the system’s overall resilience. While the distributed approach offers these advantages, it faces the complexity of balancing local and global objectives, requiring sophisticated optimization algorithms [37]. A summarized overview of these key research works, including their methodologies, findings, and contributions, is presented in Table 2 for a comprehensive comparative analysis.

Table 2.
Comprehensive summary of distributed EDPs in VPPs.
3.3. MES-Based Economic Dispatch
Building upon the advancements presented in VPPs, the concept of multienergy systems (MESs), also known as integrated energy systems, emerges as an even more integrative approach in modern energy management. These systems integrate a diverse array of energy carriers, such as electricity, heat, and gas, into a unified framework, thus resulting in a significant advancement in creating a more efficient energy system [40,41]. In this context, the EDP for MESs plays a crucial role in optimizing the allocation of various energy resources, thereby ensuring the most efficient use of the integrated energy mix. The literature reveals extensive research on economic dispatch planning—EDP—for MESs, with 78 papers meeting our search criteria described in Section 2. In the following paragraphs, we will briefly discuss the key and most influential papers among these, particularly focusing on those which have garnered 80 or more citations. This approach allows us to highlight the most significant contributions and emerging trends in the realm of the EDP for MESs, thereby emphasizing studies that have had a substantial impact and recognition in the field.
The concept of economic emission dispatch for an MES comprising combined heat and power has been explored in [42]. This study introduces a two-stage technique to address EDP challenges within this system. Initially, a novel metaheuristic algorithm, the Dominance-Based Evolutionary Algorithm (-DEA), was employed to tackle the multiobjective problem. Subsequently, fuzzy C-Means (FCM) clustering was applied to the Pareto optimal solutions, followed by the use of a gray relation projection (GRP) on these clusters to identify the most balanced compromise solutions. This proposed methodology was tested across three distinct case studies of varying complexity, wherein the results underscore its effectiveness and efficiency.
The optimal scheduling of a comprehensive regional integrated system in Tianjin, China was examined in [43]. This system encompasses a variety of components, including combined cooling, heating, and power (CCHP), thermal energy storage, electric energy storage, electric boilers, wind turbines, and photovoltaic systems. The study considered constraints like energy balance and external network transmission power, with the primary goal of minimizing the system’s total cost. This included energy transaction costs, operational expenses, energy storage costs, and environmental impact costs. To solve this EDP, the fruit fly optimization algorithm was employed. The study explored three different operational modes: “Following Power Load”, “Following Heat Load”, and an “Optimal Scheduling” mode—which integrates both power and heat loads. The findings indicate that the optimal scheduling solution significantly outperformed the scenarios focusing solely on either heat or power load.
The study in [44] investigated the impact of various storage technologies, including lithium-ion, vanadium redox, ice, and phase change material thermal storage, on multienergy systems (MESs). Utilizing mixed integer quadratic programming, it conducted a sensitivity analysis for optimal dispatch problems (ODPs) in MESs and also determined the optimal dispatch strategy using the in-house developed simulation tool known as ©E-OPT. This methodology was applied to two distinct case studies: the first connected to the national electricity network and the second operating in island mode. The case studies catered to electricity and peak cooling demands of 1600 kWe and 3000 kWc, respectively. The results indicate that the island mode, particularly due to higher fuel prices, benefits significantly from incorporating energy storage technologies, thereby achieving a 23% reduction in CO emissions.
In [45], a novel multiplayer harmony search (MPHS) algorithm was developed to address nonconvex, nonlinear, large-scale EDPs for combined heat and power (CHP) systems. The core principle of the proposed MPHS method involves improvising harmonies through the collective experiences of multiple players to achieve the optimal solution for the CHPED. This approach was tested on two case studies: a 24-unit case study and an 84-unit case study, thus representing a large-scale scenario. The results demonstrate significant cost savings amounting to over 17 million dollars annually and exhibited superior performance compared to other algorithms such as the gravitational search algorithm, improved group search optimization, cuckoo optimization algorithm, crisscross optimization algorithm, and improved PSO.
4. Economic Dispatch Problem (EDP) Formulation
The optimization techniques used for EDPs can be classified into two distinct groups depending on the type of their objective function—single- vs multiobjective optimization—as illustrated in Figure 2. This section presents an overview of these two categories and the objective functions used in the field of the EDP. Additionally, the research studies carried out from each perspective are briefly discussed in the following subsections.
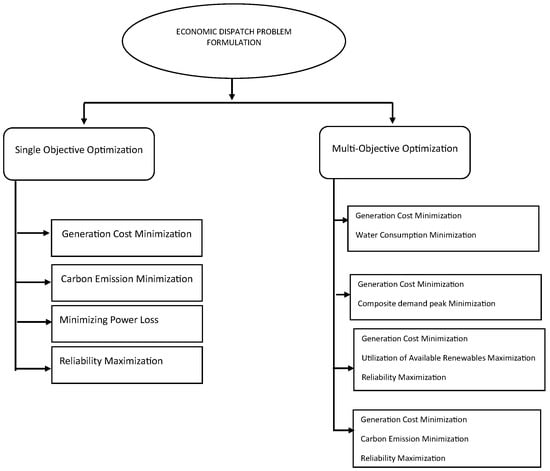
Figure 2.
Classification of EDP Formulation.
4.1. Single Objective Optimization
Single-objective optimization is a category of optimization problems in which a single objective function is optimized. The fundamental aim of single-objective optimization is to determine the optimal solution that minimizes or maximizes the objective function while complying with certain constraints.
This type of optimization is extensively utilized to solve the EDP. While the classical EDP is primarily focused on minimizing the generation cost, power system operators may have other objectives of interest in practical scenarios. In the academic literature, the most commonly investigated objectives for the EDP encompass minimizing the cost of generating electricity and reducing emissions, as well as maximizing the reliability and profitability of power systems. The subsequent paragraphs explore research studies carried out on single-objective optimization for the EDP.
In the context of EDP, various costs must be minimized, including the generation cost, fuel costs, start-up costs, and transmission costs. Numerous research studies considered formulating the EDP as a single optimization problem by developing models that capture the various costs involved [46,47,48,49,50,51].
In addition to the costs mentioned earlier, carbon emission trading costs are also becoming an increasingly important factor in EDP. Carbon emission trading costs represent the financial implications of a power plant’s carbon footprint and thus must be included in the objective function of the cost minimization problem. By incorporating carbon emission trading costs, power companies can accurately estimate the financial burden of their carbon footprint and take proactive measures to reduce it. A number of research studies have examined the inclusion of carbon emission trading costs in the objective function of the EDP [52,53,54,55]. However, other research methodologies involve integrating emission constraints into the optimization problem and managing the trade-offs between minimizing emissions and costs [56,57,58]. This approach strives to identify the optimal dispatch solution that satisfies electricity demand while minimizing the environmental impact of power generation.
Another critical objective function in economic dispatch is the maximization of power system reliability. Ensuring an uninterrupted and consistent supply of electricity to consumers is a crucial aspect of power system operations. To achieve this goal, power companies must design and operate their systems in a manner that can withstand unforeseen disturbances and events, such as equipment failures, natural disasters, and demand fluctuations [59]. Several research studies have addressed the significance of the objective function in maximizing power system reliability in economic dispatch. This objective is accomplished by integrating constraints related to power loss into the optimization problem while solving the EDP [60,61,62,63,64]. Table 3 presents a comprehensive summary of single objective function approaches in EDPs.

Table 3.
Comprehensive summary of single objective function approaches in EDPs.
4.2. Multiobjective Optimization
In addition to the commonly used single-objective functions in the EDP, there are also research studies that explore the integration of multiple objectives into the optimization problem. In the EDP, the multiobjective optimization problem involves considering two or more objectives simultaneously. One category of the multiobjective EDP is the environmental EDP, which aims to minimize both generation-related costs and environmental-related costs as objectives. Specifically, this involves minimizing fuel costs and emission costs. The literature contains a significant number of papers that address this type of problem [65,66,67,68,69,70,71].
Researchers have employed different combinations of single objectives to solve the EDP. For instance, a multiobjective optimization approach was developed to conduct economic dispatch for a hybrid microgrid system in Sweden [72]. The objective was to minimize operating costs and emissions while maximizing system reliability.
Similarly, the EDP was solved for a microgrid that includes electric vehicles, renewable energies, and transferable electricity load [73]. The problem was formulated as a multiobjective optimization that aims to minimize costs, maximize the utilization of available renewable energies, and enhance microgrid security by reducing power fluctuations caused by interactions between the microgrid and the main grid.
In addition to the studies discussed above, researchers have also investigated multiobjective EDPs in other contexts. For example, a multiobjective EDP was presented where a test system consisting of renewable energy sources and energy storage systems was considered in previous research [74]. The study aimed to determine the optimum scheduling of the test system by simultaneously minimizing two objective functions: the generation cost and the composite demand peak. To solve the problem, the authors employed a multiobjective optimization approach that generated a set of Pareto optimal solutions representing the trade-offs between the two objectives.
Another example of the multiobjective EDP was where a dynamic system consisting of wind power and energy storage systems was considered in previous research [75]. The study aimed to solve the EDP by employing a multiobjective optimization approach that took into account the trade-offs between two objectives: the operational cost and the water consumption in the power production process. The objective was to minimize the total generation cost while simultaneously optimizing water consumption. The research constructed a multiobjective optimization that generated a set of Pareto optimal solutions representing the trade-offs between the two objectives. Table 4 depicts a comprehensive summary of the multiobjective function approaches in EDPs.

Table 4.
Overview of multiobjective function strategies in EDPs.
5. EDP Optimization Techniques
Various optimization techniques have been used in the literature for solving economic dispatch problems. These techniques can be divided into four categories based on the mathematical algorithm used for finding a solution: conventional, probabilistic, artificial intelligence (AI), and hybrid. This classification is demonstrated in Figure 3. The conventional techniques include Newton’s method, the lambda iteration algorithm, the interior point method (IPM), and quadratic programming (QP). The uncertainty modeling methods involve stochastic, chance constraints programming (CCP), and robust optimization. AI methods include artificial neural networks (ANNs), deep learning (DL), reinforcement learning (RL), fuzzy logic, and metaheuristic algorithms. Hybrid techniques combine two or more of the aforementioned methods to enhance their performance. This section presents a review of the most commonly used techniques in each category for solving economic dispatch problems.
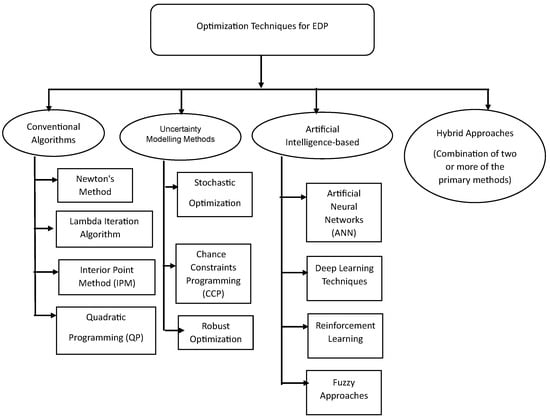
Figure 3.
Classification of EDP formulation.
5.1. Conventional Mathematical Methods
The conventional optimization algorithms for solving EDPs were commonly employed in early studies, where the problem formulation of the system was designed to be simple and only included the generation cost as the objective function, with the power balance, generation limits, and transmission loss as constraints. The subsequent paragraphs discuss the early studies that employed classical optimization techniques to provide effective solutions for the EDP.
5.1.1. Newton’s Method
This method is one of the well-known classic optimization methods, which is an iterative technique. This method employs the second derivative of the objective function and updates an initial probable solution in several iterations in order to find the root of the derivatives of the objective function that are associated with the optimal solution of the problem [76]. This algorithm has been widely used in the context of the EDP [77,78,79,80,81,82,83].
Although Newton’s method is a prevalent optimization algorithm, it presents certain drawbacks when utilized for solving EDPs. To begin with, the method can become computationally expensive and time-consuming when handling large-scale systems. Secondly, the computation and inversion of the Hessian matrix required by the method may lead to numerical instability and accuracy issues. Another limitation of Newton’s method is its susceptibility to converging towards local optima instead of the global optimum, especially if the initial solution is insufficiently proximate to the true solution. Consequently, while Newton’s method may be effective for certain EDPs, it may not always represent the most efficient or dependable method.
Given the limitations of Newton’s method, recent studies have sought to address these issues by combining the method with other optimization techniques [84] or developing revised variants of Newton’s method [85,86]. Alternatively, the problem formulation may be approximated in a manner that renders Newton’s method suitable for solving the problem [87,88].
5.1.2. Lambda Iteration Algorithm
This technique, also referred to as the Lagrange multiplier method, is an approach that is usually utilized for solving optimization problems. The technique entails the introduction of a series of Lagrange multipliers, which act as coefficients that enable the constraints to be integrated into the objective function [89]. The technique then optimizes the augmented function, which encompasses both the original objective function and the added constraints represented by the Lagrange multipliers.
The lambda optimization technique has extensive applications in various fields, including, but not limited to, economic dispatch. While some research studies employed the conventional lambda iteration algorithm to solve classic economic dispatch problems [90,91,92,93], more contemporary investigations have developed advanced variants of the method that are better suited to handle real-world systems [94,95,96,97,98,99]. This approach is adopted to obtain the optimal dispatch while accounting for prohibited operating zones and effectively mitigating the oscillatory behavior that is commonly observed in the conventional lambda iteration method. Furthermore, the literature documents several research studies that have integrated the lambda iteration method with other optimization techniques to mitigate its limitations. The present study classifies these research efforts as hybrid methods and presents them in Section 5.
The lambda iteration technique exhibits several advantages over Newton’s method in optimization problems. Firstly, it is generally more robust and less sensitive to the initial guess, thereby resulting in a higher probability of convergence to the global optimum as opposed to local optima. Additionally, as it does not necessitate the computation and inversion of the Hessian matrix, it is less computationally expensive and does not encounter accuracy issues as is the case with Newton’s method. While the lambda iteration technique has advantages over Newton’s algorithm, it may not be able to obtain the global optimum solution in the presence of nonsmooth or nonconvex objective functions or constraints.
5.1.3. Interior Point Method (IPM)
The interior point method (IPM) was initially developed in 1984 [100]. This technique consists of an iterative process where an interior point is identified, which is a feasible point located inside the feasible region defined by the constraints, and then gradually moved towards the optimal solution [101]. In the literature, some research studies have utilized the IPM and its variations for solving the EDP [69,102,103,104].
In comparison to other traditional optimization techniques, IPMs are known for their ability to handle a wide range of constraints. However, these methods are vulnerable to the issue of yielding infeasible solutions, especially when solving nonlinear objective functions, if the step size is not carefully selected. This is because the selection of the step size in the interior point method can greatly affect the convergence and feasibility of the solution [105]. Therefore, careful consideration of the step size is crucial in ensuring the effectiveness of the interior point method when solving nonlinear optimization problems.
5.1.4. Quadratic Programming (QP)
Quadratic programming is a nonlinear programming method that was developed in the 1940s [106]. It is usually utilized to solve an optimization problem where the objective function is quadratic and subject to linear constraints. In the scope of the EDP, QP is applied to minimize the cost of the power generation when subject to various constraints such as generator output limits, transmission line limits, and demand requirements.
This optimization algorithm has demonstrated its effectiveness in solving the EDP with a quadratic cost function and linear constraints. The efficacy of QP in solving EDPs has motivated many researchers to utilize this technique [107,108,109]. It is noteworthy that QP is a more versatile and robust than other conventional optimization techniques. This is attributed to its ability to handle nonconvex functions and linear constraints. Nonetheless, QP requires the optimization problem to be formulated in a specific format consisting of a quadratic objective function and linear constraints. This may limit its feasibility when applied to real-world power systems, which often involve complex nonlinear constraints.
As elaborated previously, traditional optimization techniques have their own strengths and limitations. Additionally, these techniques are limited to solving the simplest form of the EDP. However, in practical power systems, EDPs are much more complex and involve additional constraints beyond those found in classic EDP formulations, such as valve-point effects and prohibited operating zones for generators.
Such constraints result in a highly nonlinear and discontinuous feasible region, which poses significant challenges to optimization. Conventional solution methods, such as linear programming, Lagrange relaxation, nonlinear programming, quadratic programming, dynamic programming, and the interior point method, may encounter difficulties due to their strict requirements for continuity, convexity, the differentiability of the objective functions, and sensitivity to initial values of the optimized variables. Hence, it is crucial to employ more advanced techniques to obtain optimal solutions for EDPs in real-world scenarios.
5.2. Uncertainty Modelling Methods
Modern power systems are distinguished by the extensive integration of renewable energy sources, such as wind power and photovoltaic systems, which introduce significant uncertainties due to the volatile nature of their primary sources. Additionally, the electricity load of the system exhibits intermittent behavior, thereby resulting in the incorporation of several probabilistic variables in the economic dispatch problem for modern power systems.
Uncertainty modeling methods involve accounting for uncertain and variable inputs and parameters to identify a solution that performs optimally across a range of possible scenarios. Hence, these techniques have garnered considerable attention as a means of solving the EDP for modern power systems.
Uncertainty modeling method algorithms applied to solve the EDP can be categorized into three groups, namely, stochastic optimization, chance constraints optimization, and robust optimization. This subsection presents a discussion of some of the commonly employed uncertainty modelling techniques for solving the EDP. Additionally, recent research studies that employ these techniques for solving EDP are also discussed. This will provide insights into the effectiveness of different uncertainty modeling methods and their potential for solving complex EDPs in modern power systems.
5.2.1. Stochastic Optimization
Stochastic optimization is a class of optimization methods that are well suited for stochastic problems, where the objective function and/or constraints incorporate random variables. These algorithms aim to determine the optimal solution for stochastic problems by representing the intermittencies in the problem formulation with established distributions [110].
A stochastic optimization approach for the multiobjective EDP aiming to minimize operation cost and maximize renewable energy penetration was presented [111]. To represent the uncertainties associated with renewable energy sources, all possible dynamic scenarios were generated, and a scenario reduction technique was employed to mitigate the computational complexity. The feasibility of the developed stochastic method was evaluated by applying it to IEEE 118-bus and IEEE 30-bus test systems. The results show that the proposed stochastic optimization algorithm enables a high level of renewable energy penetration compared to deterministic techniques.
Some previously presented approaches [111,112] have proposed a multistage stochastic optimization algorithm for minimizing the total cost in power systems. The algorithm employs a scenario tree to account for the uncertainty of renewable energy reserves and the feasible output of each generation unit. Subsequently, stochastic dual dynamic programming (SDDP) is employed to obtain the most optimal solution. The effectiveness of the proposed approach has been verified by applying it to an IEEE 118-bus power system, and the results demonstrate its effectiveness.
A study [113] proposed the use of a nested sparse grid-based stochastic collocation method for solving the EDP in the presence of renewable energy sources. The method approximates the random variables in the system using finite-order expansion. Two IEEE test systems of different sizes (1009- and 39-bus) were used to evaluate the proposed method. The results indicate that the method is effective in finding the optimal solution regardless of the size of the system.
5.2.2. Chance Constraint Programming (CCP)
CCP is an uncertainty modeling technique employed to tackle optimization problems that have constraints with a possibility of being violated [114]. These types of problems are common in the field of renewable energy, where the availability of energy sources can be uncertain. These models differ from conventional optimization problems, which face challenges when solving problems where the inequality functions are not distinctly presented in the problem formulation. Furthermore, they aim to find solutions that satisfy the constraints with a certain degree of confidence [115].
Several studies reported in the literature utilized the CCP to solve EDPs [116,117]. The objective of such studies is to find the optimal solution for an electricity–gas power system’s EDP by minimizing the cost of carbon emissions trading and the risk associated with renewable energy output [54]. The problem formulation considers various risks, such as transmission line overload risk and the loss of load risk. To obtain the optimal dispatch for the case study, a CCP method was employed. The results obtained from [54] demonstrate the effectiveness of the utilized method.
In contrast to the approach that utilizes the conventional CCP [54], a novel CCP-based method was introduced [118] for solving the EDP. This method addresses the limitation of the conventional CCP in managing the fast increase in the integration rate of renewable sources. Besides minimizing the generation cost, the proposed approach utilizes curtailment strategies to determine the generation and curtailment plan sequentially. The effectiveness of this method was evaluated by comparing it with a scenario-based algorithm, and its superior performance was validated.
5.2.3. Robust Optimization
The origins of the development of robustness optimization can be traced back to the 1950s [119]. This method is a type of optimization that aims to identify a solution that is not only optimal but also resilient to variations and uncertainties in the input parameters. It involves the consideration of worst-case scenarios in the decision-making process and the formulation of constraints to ensure that the system remains within a feasible region under all possible variations [120]. The suitability of robust optimization for solving the EDP in modern power systems with a large-scale integration of renewable energies is attributed to its inherent characteristics. These properties of robust optimization make it a viable technique for addressing the EDP in contemporary power systems that feature the extensive integration of renewable energy sources.
A novel self-adaptive step size robust optimization method for an efficient solution of EDP involving flexible electricity resources was developed [121]. This study accounted for the uncertainties associated with load and renewable energy resources, as well as practical constraints related to power line congestion. The proposed approach solved multiple subproblems in parallel, thereby ensuring information security.
In a similar manner, distributional robust optimization was employed to address the uncertainties arising from the integration of wind power into the electricity grid in an EDP [122]. The proposed approach generated the worst-case probability distribution using a data-driven generative adversarial network. Furthermore, the level of robustness of the technique can be adjusted by modifying the number of auxiliary data.
As elaborated in this section, the approaches consider the stochastic nature and variability of input parameters, including load demand and renewable energy generation, thereby rendering them more effective when addressing the requirements of modern power systems in contrast to the classical optimization techniques expounded in Section 4.
This characteristic of uncertainty modeling methods results in a more robust and flexible solution that can adapt to changing conditions and minimize the likelihood of violating operational constraints. Additionally, despite conventional mathematical algorithms, uncertainty modeling techniques can incorporate risk management and mitigation strategies, which can help improve the economic and environmental performance of power systems.
Despite the aforementioned advantages of uncertainty modeling techniques, their computational complexity, limited accuracy, and scalability remain significant challenges, especially when handling large-scale complex power systems with numerous variables and constraints. To overcome these limitations, researchers have developed and implemented AI techniques for solving the EDP. The succeeding subsection elaborates on the commonly utilized AI-driven techniques in the domain of the EDP.
5.3. AI-Based Techniques
These optimization techniques refer to a category of optimization algorithms that employ AI principles to optimize a system or process. Such optimization techniques are designed to learn from data, identify patterns, and make intelligent decisions to achieve optimal outcomes for a given system or process [123].
AI optimization techniques have been developed and employed by researchers in the field of economic dispatch to overcome the shortcomings of conventional and uncertainty modeling methods, which include not only limited scalability and computational complexity but also limited accuracy, the inability to handle nonlinear and nonconvex problems, and sensitivity to initialization and local optima. The most frequently used AI-based optimization methods for solving the EDP encompass a variety of algorithms, including artificial neural networks (ANNs), support vector machines (SVMs), reinforcement learning (RL), deep learning (DL), fuzzy logic (FL), and metaheuristic algorithms, which have been developed and employed by researchers in the field of economic dispatch. These methods are discussed in the subsequent subsection.
5.3.1. Artificial Neural Networks (ANNs)
Artificial neural networks (ANNs) are a type of AI-based algorithm that take inspiration from the structure and functioning of the human brain. ANN models are composed of interconnected nodes or neurons that perform mathematical operations to process information [124]. The basic architecture of an ANN typically consists of an input layer, one or more hidden layers, and an output layer. Input data are fed into the ANN via the input layer, and the learning process occurs in the hidden layers, where activation functions are applied to the input data to produce the output. The final output data are provided by the output layer [125].
In the domain of economic dispatch, ANN models can be trained using historical data to learn the mapping between input variables, such as the generators’ output, renewable energy availability, the electricity load profile, and the optimal dispatch solution, which are set as output neurons.
ANN-based optimization techniques offer several advantages when solving EDPs. They are able to handle nonlinear and complex relationships among input and output variables, thereby making them highly accurate in predicting optimal solutions. ANN models can also adapt to changing conditions and update the solution for online scheduling, thereby providing a flexible and robust approach to economic dispatch. In addition, these models can be trained using historical data, which simplifies the optimization process and reduces the need for detailed system information. Such advantages have encouraged researchers to use them for solving economic dispatch problems. Various types of neural networks are available, each with distinct architectures and activation functions. Artificial neural networks (ANNs) [126,127,128,129], convolutional neural networks (CNNs) [130,131,132], recurrent neural networks (RNNs) [133,134,135], and Hopfield neural networks (HNNs) [136,137,138] are commonly employed in economic dispatch applications.
5.3.2. Deep Learning Techniques
Another class of AI-based algorithms is deep learning (DL). This technique belongs to the group of machine learning algorithms and employs neural networks consisting of multiple layers to extract high-level features from large and complex datasets [139]. DL-based methods excel in optimization tasks by effectively modeling complex and nonlinear relationships among input and output variables. Hence, they have been broadly used in the EDP [140,141,142,143].
In a study, a DL-based optimization algorithm was employed to solve a security-constrained EDP in a smart grid scenario where the clearing frequency is continuously increasing [144]. The proposed method provides a fast solution for the EDP by initially identifying the active constraints of the problem using DL. A transfer learning approach is then used to fine-tune the parameters of the DL model. The results of the experiments conducted on two IEEE test systems validated the efficiency of the proposed technique in terms of computational efficiency [144].
While the aforementioned research study applied DL techniques to provide efficient solutions for a security-constrained EDP, another study [145] utilized DL for a multiregion EDP considering interconnected tie lines. The proposed DL-based method employs a hierarchical structure and utilizes historical data sets for performing the optimization task online. The effectiveness of the proposed method was demonstrated through its application to a large-scale IEEE test system [145].
5.3.3. Reinforcement Learning (RL)
These techniques involve an agent learning to make decisions in an environment by maximizing a reward signal. This learning procedure occurs through trial and error and can be mathematically formulated as a Markov decision process (MDP) [146].
Researchers have employed reinforcement learning techniques in economic dispatch tasks [147,148]. This is due to the fact that RL is proficient in managing the stochastic nature of variables and is capable of learning optimal decisions through trial and error in intricate and dynamic environments. Additionally, RL can improve its performance over time through continuous learning and adaptation to changing conditions, thereby making it a promising optimization technique for EDPs.
A research study [149] proposed a novel optimization framework for an EDP in a smart grid environment by employing the DL technique. The approach involves three main steps. The first step utilizes DL to determine the optimal output of the generators. In the second step, an improved consequent algorithm, is applied to the optimal outputs obtained from step one to achieve an efficient solution for the EDP. Finally, the proposed method’s efficiency was evaluated by applying it to two different test systems.
While some studies assumed that the cost function of the generations is known [149], other studies [150] have applied a DL technique for an EDP in a smart grid where the objective functions of the generation units are not mathematically formulated. To address this issue, a novel DR-based algorithm has been developed. The proposed algorithm consists of two methods: state action value function approximation and distributed optimization based on multiplier splitting. This approach effectively handles the lack of prior knowledge of the system. The proposed DL-based model was evaluated by applying it to several case studies, thereby demonstrating its effectiveness [150].
5.3.4. Fuzzy Approaches
Fuzzy logic is a widely recognized method for performing reasoning and decision-making tasks when dealing with uncertain or imprecise input information. This technique employs a fuzzifier that can handle a high level of tolerance for uncertainties and imprecision. Fuzzy optimization allows for the incorporation of imprecise or uncertain data, which is common in real-world energy systems [151]. This technique is based on fuzzy set theory, which uses membership functions to represent uncertain data. Several fuzzy techniques have been developed, as exemplified in [152,153]. The basic stages of the fuzzy process are illustrated in Figure 4.
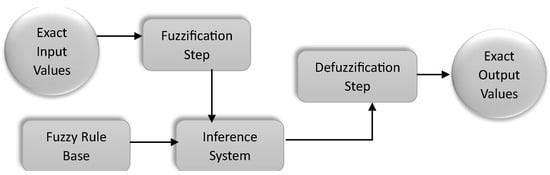
Figure 4.
Illustration of the Basic Fuzzy Logic Process.
In economic dispatch, Fuzzy optimization is a popular technique that has been used to improve the efficiency of the dispatch process by incorporating the uncertainties associated with load forecasting, fuel prices, and other factors [154,155,156]. An EDP that involves uncertainties in wind generation and electricity loads was considered in a research study [157]. These uncertainties ere modeled using the Dubois possibility and probability consistency principle. Fuzzy second extension theory was then utilized to obtain the optimal output of each generator. To validate the effectiveness of the proposed technique, the model was applied to an IEEE 30-bus system.
In a similar manner, another research study [73], employed fuzzy optimization techniques to obtain the optimal solution for a multiobjective EDP in a microgrid. The study considered the influence of the charging–discharging behavior of electric vehicles and demand-side response resources on the economic operation of a photovoltaic grid-connected microgrid system. Four distinct scenarios were examined, with each corresponding to a specific charging behavior of electric vehicles and transferable load. The results obtained from the study demonstrated that an orderly electric vehicle charging behavior, coupled with the participation of transferable load in the electricity market, led to the most efficient solution for the EDP.
Building upon the foundation of fuzzy optimization in the EDP, the Adaptive Neuro-Fuzzy Inference System (ANFIS) emerges as a groundbreaking approach [158]. The ANFIS extends the capabilities of traditional fuzzy logic by integrating neural network learning, thereby offering enhanced adaptability and precision in handling the multifaceted challenges of economic dispatch.
EDPs for modern power systems operate in a dynamic environment, which is characterized by several variables such as electricity load, fuel prices, and renewable energy sources, all of which are prone to sudden fluctuations. Such rapid changes necessitate a system capable of quick adaptation. While traditional fuzzy systems may lack the required responsiveness, the ANFIS stands out for its ability to learn and adapt to new patterns and conditions over time, thereby significantly enhancing decision-making accuracy [159,160,161]. Furthermore, a major challenge in fuzzy systems is parameter tuning, which involves manually adjusting algorithm parameters and membership functions. This process is time-consuming and does not always guarantee optimal results. However, the ANFIS effectively addresses this issue by automating the tuning process through its learning mechanism, thereby continuously optimizing these parameters to achieve enhanced performance [162]. While fuzzy approaches excel in managing uncertainty, they often lack precision in complex scenarios with multiple conflicting objectives. The ANFIS, equipped with advanced learning capabilities, enhances the precision of solutions while still effectively managing uncertainties [163]. As power systems grow in size and complexity, the efficiency and scalability of traditional fuzzy systems often prove to be insufficient. In contrast, the ANFIS, enhanced by its neural network components, is more adept at efficiently handling larger and more complex systems. Additionally, the ANFIS’s adaptive learning feature helps to avoid overfitting to specific scenarios or datasets, thereby providing superior generalization across a variety of EDP scenarios.
Based on the aforementioned advantages of the ANFIS over traditional fuzzy systems for the EDP in modern power systems, this algorithm has garnered significant attention from researchers in the field. Numerous studies have employed the ANFIS to address the EDP in power system optimization, thereby demonstrating its superior performance and adaptability [164,165,166,167]. This widespread adoption of the ANFIS in academic and practical research underscores its effectiveness and potential in advancing energy management solutions.
5.3.5. Metaheuristic Algorithms
Metaheuristic is a class of optimization techniques in AI that is commonly used in the literature for solving complex problems like economic dispatch. These techniques employ an efficient search strategy for exploring the vast solution space in order to obtain an optimal solution [168]. These algorithms are typically engineered to tackle complex and multi-dimensional problems, such as the EDP in power systems, by systematically exploring a wide range of potential solutions through iterative search processes [169].
Metaheuristic optimization techniques are advantageous for solving EDPs due to their ability to efficiently explore complex and nonlinear search spaces. Additionally, these techniques are capable of handling constraints and uncertainties and can provide near-optimal or optimal solutions within a reasonable time frame.
Metaheuristic algorithms (MAs) can be classified into four distinct categories, which include evolutionary algorithms (EAs), swarm intelligence (SI) methods, approaches based on natural phenomena, and algorithms inspired by human behavior [170]. Over a few decades, numerous MAs have been developed, among which genetic algorithm (GA) [129,171,172,173,174,175], particle swarm optimization (PSO) [176,177,178,179,180,181], ant colony optimization (ACO) [182,183,184,185], and artificial bee colony (ABC) [186,187,188,189,190,191] and their variants have been extensively applied to solve the EDP. The main feature of these nature-inspired algorithms is their reliance on searching the space of potential solutions to find optimal or near-optimal outcomes. This search is carried out iteratively, and in each iteration, the search space is narrowed down based on the calculated cost function of each potential solution within the space. Moreover, they aim to balance exploration and exploitation in each search iteration to ensure that existing solutions are refined, and new feasible solutions are discovered.
Although MAs are powerful tools for solving complex optimization problems such as economic dispatch, their usage comes with certain drawbacks. A significant limitation of MAs is their inability to ensure the discovery of the global optimum, particularly when the search space is extensive and the problem exhibits high nonlinearity. Moreover, these algorithms often necessitate substantial parameter optimization and could be extremely vulnerable to initial conditions, which can result in suboptimal solutions.
5.4. Hybrid Algorithms
In the context of economic dispatch, research studies have explored the development of hybrid optimization algorithms to identify optimal solutions. These research efforts propose combining hybrid metaheuristic algorithms like GA [192], PSO and its variants [193,194,195,196,197], ant lion optimization algorithm [198], slap swarm [199], crow search algorithm [200], and firefly [201], along with traditional optimization techniques such as Lambda iteration algorithm [202], with AI-based techniques such as neural networks, fuzzy systems, and DL. This is due to the primary limitation of AI-based techniques, which require parameter tuning. As discussed earlier, choosing the best parameters for these approaches is a challenging task for researchers, as they significantly impact the performance of these techniques. Hybrid optimization algorithms have shown the ability to mitigate this drawback of AI-based techniques when applied to EDPs. The utilization of optimization algorithms in conjunction with AI-based methods allows for fine-tuning the parameters, thereby resulting in more efficient solutions.
From another perspective, researchers have combined metaheuristic algorithms to achieve more efficient optimization techniques, thus resulting in hybrid approaches. This integration aims to mitigate the disadvantages of individual metaheuristic algorithms discussed previously. Some of these hybrid techniques, utilized for solving the EDP, include the PSO-bat algorithm [203,204], PSO-ACO [205], PSO-ant lion optimization [206], PSO-Imperialist competitive algorithm [207], and slab-simulated annealing algorithm [208].
6. Discussion
The optimization of the EDP is a fundamental task in power systems, which can result in considerable economic and environmental impacts. The primary objective of economic dispatch is to minimize the cost of power generation, which is subject to power demand and system constraints. Due to the rising demand for energy and the integration of renewable sources, the EDP has become more complex. Consequently, discovering precise and efficient solutions to this problem is essential for researchers, policymakers, and power system operators. Effective economic dispatch can lead to substantial cost savings, reduce greenhouse gas emissions, and enhance the stability and reliability of the power grid.
The objective of this review paper is to provide an up-to-date overview of the latest advancements in problem formulation and optimization techniques used for solving EDPs, with a particular focus on conventional techniques, uncertainty modelling methods, AI-based techniques, and hybrid methodologies. This section highlights the key findings of the review and discusses their potential implications for future research and practical applications in the field of energy management.
Conventional optimization techniques, including Newton’s method, the lambda iteration algorithm, the interior point method (IPM), and quadratic programming (QP), were widely used in early studies of economic dispatch due to their ability to handle the classic EDP. These techniques are known for their accuracy in obtaining optimal solutions, easy implementation, and well-established theoretical foundations. However, they may not be suitable for complex and nonlinear problems and can suffer from high computational costs, especially for large-scale power systems. Additionally, they assume perfect knowledge of input data, which may not reflect real-world uncertainties and variations in the power system.
Uncertainty modeling approaches such as robust optimization, chance constraint programming, and stochastic optimization have also been discussed in the literature as potential solutions to the EDPs. These techniques consider the uncertainties and variations in the input parameters and constraints of the optimization problem to provide solutions that are robust and dependable. The robust optimization approach aims to find a solution that is feasible under the worst-case scenario, whereas the CCP method incorporates uncertainty constraints to ensure that the probability of satisfying constraints is above a predefined threshold. Stochastic optimization methods utilize probability distributions to model the uncertain parameters and generate solutions that are optimally average over the distribution.
AI-based algorithms such as ANN, Fuzzy, RL, DL, and metaheuristic algorithms are frequently employed as optimization techniques for the EDP. These techniques are recognized for their capability to handle nonlinear and complex problems. Furthermore, they have been demonstrated to reduce computational complexity and enhance efficiency when compared to classical or uncertainty modeling methods. However, their performance is significantly impacted by model parameters, thereby necessitating careful parameter tuning to achieve optimal results.
All of the aforementioned optimization techniques possess distinct advantages and disadvantages, and there is no definitive guidance for selecting the appropriate optimization technique. To leverage the benefits of multiple approaches while overcoming their limitations, researchers have proposed hybrid models that integrate two or more primary models. For example, some studies have combined AI-based techniques with metaheuristic techniques to enhance the optimization technique. Furthermore, metaheuristic techniques can be combined to achieve better performance when applied to the EDP. After examining the research studies discussed in this paper, two primary limitations were identified. These limitations are briefly summarized in the following paragraph.
After analyzing the existing literature, it was observed that the majority of research studies focus on the evaluation of optimization approaches using a single case study. Nonetheless, it is of great importance to evaluate the optimization method performance by applying it to diverse case studies. This is due to the fact that an optimization technique that performs well on smaller or medium-sized systems (in terms of the number of buses in the power system or the number of constraints of the problem) may fail when applied to larger-scale systems that represent real-world scenarios. Therefore, it is advisable for researchers to include a diverse range of case studies with varying sizes and conditions to improve the practicality and feasibility of their optimization techniques.
The choice of the system to be investigated is arbitrary, and researchers can choose any system with any combination of constraints. The problem formulation can vary significantly according to the components of the power system. That is to say, different components in microgrids will result in different formats of the objective function and constraints. Furthermore, due to varying perspectives among system operators, the objective function and constraints used in solving EDPs can differ significantly from one researcher to another. As a result, comparing research studies in this field can be challenging.
7. Conclusions
This review comprehensively analyzes a broad range of optimization algorithms in the context of EDPs, with a dual categorization framework. Initially, we discuss the evolution of economic dispatch, thus charting its development from classic, established power systems to cutting-edge, modern frameworks. Following this, the optimization techniques are classified into four distinct categories—conventional mathematical models, uncertainty-based, AI-based, and hybrid techniques—based on the algorithms utilized by each technique.
Our analysis begins by examining the finer details of problem formulations in EDPs, thereby highlighting the significant effect these classifications have on the selection of optimization algorithms. The efficiency and computational complexity inherent in each optimization technique category are thoroughly assessed. It is observed that the simpler the formulation of the EDP, the more straightforward the optimization algorithms employed. In the context of single objective optimization, there is a tendency towards straightforward implementation, often seen in conventional methods. However, in multiobjective optimization, more sophisticated approaches, such as AI-based and uncertainty modeling methods, are utilized. Although these advanced algorithms are efficient in dealing with complex problems, they also carry the drawback of higher computational requirements. An additional key finding from this review is the noticeable performance superiority of hybrid models. These models combine various optimization techniques, thereby efficiently utilizing the strengths of each to achieve enhanced efficiency and robustness.
For future research endeavors, it is recommended to conduct a comprehensive assessment of the efficacy of optimization techniques for EDPs across varied case studies, including power systems of various sizes and complexities. This approach will facilitate a comprehensive assessment of the scalability and practical relevance of these optimization techniques in real-world scenarios, thereby enhancing our insight into their performance under various circumstances. Additionally, the development of a standardized framework for EDP problem formulation is of great importance. Such a framework would facilitate meaningful comparisons and benchmarking across studies, accommodating the diversity in power system components and operational objectives. Collectively, these efforts will significantly contribute to advancing efficient and universally applicable optimization solutions in energy management.
Author Contributions
Conceptualization, F.M. and A.A.; methodology, F.M.; validation, F.M. and A.A.; formal analysis, F.M.; investigation, F.M. and A.A.; resources, F.M. and A.A.; data curation, F.M.; writing—original draft preparation, F.M.; writing—review and editing, A.A.; visualization, F.M.; supervision, A.A.; project administration, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the American University of Sharjah through providing a Graduate Research Assistantship (GTA) to the first author, which was provided by the Office of Research and Graduate Studies as part of the support to the PhD Program in Engineering Systems Management. The work in this paper was also supported, in part, by the Open Access Program from the American University of Sharjah.
Conflicts of Interest
The authors declare no conflict of interest. This paper represents the opinions of the author(s) and does not mean to represent the position or opinions of the American University of Sharjah.
Abbreviations
The following abbreviations are used in this manuscript:
| EDPs | Economic Dispatch Problems |
| EIA | Energy Information Administration |
| kWh | Kilowatt Hours |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| AI | Artificial Intelligence |
| IPM | Interior Point Method |
| QP | Quadratic Programming |
| CCP | Chance Constraints Programming |
| ANNs | Artificial Neural Networks |
| DL | Deep Learning |
| RL | Reinforcement Learning |
| SVMs | Support Vector Machines |
| FL | Fuzzy Logic |
| CNNs | Convolutional Neural Networks |
| RNNs | Recurrent Neural Networks |
| HNNs | Hopfield Neural Networks |
| MDP | Markov Decision Process |
| MAs | Metaheuristic Algorithms |
| EAs | Evolutionary Algorithms |
| SI | Swarm Intelligence |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithm |
| ABC | Artificial Bee Colony |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
References
- U.S. Energy Information Administration. How Much Carbon Dioxide Is Produced When Different Fuels Are Burned? Available online: https://www.eia.gov/tools/faqs/faq.php?id=427&t=3 (accessed on 15 May 2023).
- Liu, Y.; Yang, C.; Jiang, L.; Xie, S.; Zhang, Y. Intelligent Edge Computing for IoT-Based Energy Management in Smart Cities. IEEE Netw. 2019, 33, 111–117. [Google Scholar] [CrossRef]
- Durvasulu, V.; Hansen, T.M. Market-based generator cost functions for power system test cases. IET Cyber-Phys. Syst. Theory Appl. 2018, 3, 194–205. [Google Scholar] [CrossRef]
- Kunya, A.B.; Abubakar, A.S.; Yusuf, S.S. Review of economic dispatch in multi-area power system: State-of-the-art and future prospective. Electr. Power Syst. Res. 2023, 217, 109089. [Google Scholar] [CrossRef]
- Qu, B.; Zhu, Y.; Jiao, Y.; Wu, M.; Suganthan, P.; Liang, J. A survey on multi-objective evolutionary algorithms for the solution of the environmental/economic dispatch problems. Swarm Evol. Comput. 2018, 38, 1–11. [Google Scholar] [CrossRef]
- Happ, H.H. Optimal power dispatch—A comprehensive survey. IEEE Trans. Power Appar. Syst. 1977, PAS-96, 841–854. [Google Scholar] [CrossRef]
- Lolla, P.R.; Rangu, S.K.; Dhenuvakonda, K.R.; Singh, A.R. A comprehensive review of soft computing algorithms for optimal generation scheduling. Int. J. Energy Res. 2021, 45, 1170–1189. [Google Scholar] [CrossRef]
- Riaz, M.; Ahmad, S.; Hussain, I.; Naeem, M.; Mihet-Popa, L. Probabilistic Optimization Techniques in Smart Power System. Energies 2022, 15, 825. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Liu, P.; Sun, Q.; Wu, Z.; Lu, X. Application of two-stage robust optimization theory in power system scheduling under uncertainties: A review and perspective. Energy 2022, 251, 123942. [Google Scholar] [CrossRef]
- Moreno-Castro, J.; Ocaña Guevara, V.S.; León Viltre, L.T.; Gallego Landera, Y.; Cuaresma Zevallos, O.; Aybar-Mejía, M. Microgrid Management Strategies for Economic Dispatch of Electricity Using Model Predictive Control Techniques: A Review. Energies 2023, 16, 5935. [Google Scholar] [CrossRef]
- Gajanan, L.S.; Kirar, M.; Paliwal, P.; Rajak, N. A State-of-the-Art Review on Modern Artificial Intelligence based Techniques for Economic Load Dispatch. In Proceedings of the 2023 IEEE Renewable Energy and Sustainable E-Mobility Conference (RESEM), Bhopal, India, 17–18 May 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Li, L.; Pei, J.; Shen, Q. A Review of Research on Dynamic and Static Economic Dispatching of Hybrid Wind–Thermal Power Microgrids. Energies 2023, 16, 3985. [Google Scholar] [CrossRef]
- Alsagri, A.S.; Alrobaian, A.A. Optimization of Combined Heat and Power Systems by Meta-Heuristic Algorithms: An Overview. Energies 2022, 15, 5977. [Google Scholar] [CrossRef]
- Page, M.; McKenzie, J.; Bossuyt, P.; Boutron, I.; Hoffmann, T.; Mulrow, C.; Shamseer, L.; Tetzlaff, J.; Akl, E.; Brennan, S.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Al Farsi, F.N.; Albadi, M.H.; Hosseinzadeh, N.; Al Badi, A.H. Economic Dispatch in power systems. In Proceedings of the 2015 IEEE 8th GCC Conference & Exhibition, Muscat, Oman, 1–4 February 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Ang, T.Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strategy Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Zhang, H.; Zhao, Y.; Shi, J.; Ding, H. A Review on Virtual Power Plant Concept, Application and Challenges. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 4328–4333. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Z.; Ju, P.; Wu, H. A Distributed Two-Stage Economic Dispatch for Virtual Power Plant Based on an Improved Exact Diffusion Algorithm. Front. Energy Res. 2021, 9, 734801. [Google Scholar] [CrossRef]
- Oladimeji, O.; Ortega, A.; Sigrist, L.; Rouco, L.; Sánchez-Martin, P.; Lobato, E. Optimal Participation of Heterogeneous, RES-based Virtual Power Plants in Energy Markets. arXiv 2021, arXiv:2112.02200. [Google Scholar] [CrossRef]
- Iria, J.; Coelho, A.; Soares, F. Network-secure bidding strategy for aggregators under uncertainty. Sustain. Energy Grids Netw. 2022, 30, 100666. [Google Scholar] [CrossRef]
- Naval, N.; Yusta, J.M. Virtual power plant models and electricity markets—A review. Renew. Sustain. Energy Rev. 2021, 149, 111393. [Google Scholar] [CrossRef]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Núñez-Mata, O. Energy Management Systems for Microgrids: Main Existing Trends in Centralized Control Architectures. Energies 2020, 13, 547. [Google Scholar] [CrossRef]
- Gao, H.; Jin, T.; Feng, C.; Li, C.; Chen, Q.; Kang, C. Review of virtual power plant operations: Resource coordination and multidimensional interaction. Appl. Energy 2024, 357, 122284. [Google Scholar] [CrossRef]
- Qiu, H.; Vinod, A.; Lu, S.; Gooi, H.B.; Pan, G.; Zhang, S.; Veerasamy, V. Decentralized mixed-integer optimization for robust integrated electricity and heat scheduling. Appl. Energy 2023, 350, 121693. [Google Scholar] [CrossRef]
- Wasti, S.; Ubiratan, P.; Afshar, S.; Disfani, V. Distributed Dynamic Economic Dispatch using Alternating Direction Method of Multipliers. arXiv 2020, arXiv:2005.09819. [Google Scholar]
- Li, P.; Liu, Y.; Xin, H.; Jiang, X. A Robust Distributed Economic Dispatch Strategy of Virtual Power Plant under Cyber-Attacks. IEEE Trans. Ind. Inform. 2018, 14, 4343–4352. [Google Scholar] [CrossRef]
- Lu, Q.; Yang, Y.; Zhu, Y.; Xu, T.; Wu, W.; Chen, J. Distributed Economic Dispatch for Active Distribution Networks with Virtual Power Plants. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 328–333. [Google Scholar] [CrossRef]
- Lin, L.; Guan, X.; Peng, Y.; Wang, N.; Maharjan, S.; Ohtsuki, T. Deep Reinforcement Learning for Economic Dispatch of Virtual Power Plant in Internet of Energy. IEEE Internet Things J. 2020, 7, 6288–6301. [Google Scholar] [CrossRef]
- Ye, H.; Huang, H.; He, Y.; Xu, M.; Yang, Y.; Qiao, Y. Optimal Scheduling Method of Virtual Power Plant Based on Model Predictive Control. In Proceedings of the 2023 3rd International Conference on Energy, Power and Electrical Engineering (EPEE), Wuhan, China, 15–17 September 2023; pp. 1439–1443. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Wang, Y.; Zhu, J.; Gooi, H.B.; Xin, H. Distributed Real-Time Multi-Objective Control of a Virtual Power Plant in DC Distribution Systems. IEEE Trans. Power Deliv. 2022, 37, 1876–1887. [Google Scholar] [CrossRef]
- Cao, C.; Xie, J.; Yue, D.; Huang, C.; Wang, J.; Xu, S.; Chen, X. Distributed Economic Dispatch of Virtual Power Plant under a Non-Ideal Communication Network. Energies 2017, 10, 235. [Google Scholar] [CrossRef]
- Xie, J.; Cao, C. Non-Convex Economic Dispatch of a Virtual Power Plant via a Distributed Randomized Gradient-Free Algorithm. Energies 2017, 10, 1051. [Google Scholar] [CrossRef]
- Wu, X.; Xiong, H.; Li, S.; Gan, S.; Hou, C.; Ding, Z. Improved Light Robust Optimization Strategy for Virtual Power Plant Operations with Fluctuating Demand. IEEE Access 2023, 11, 53195–53206. [Google Scholar] [CrossRef]
- Naughton, J.; Wang, H.; Cantoni, M.; Mancarella, P. Co-Optimizing Virtual Power Plant Services Under Uncertainty: A Robust Scheduling and Receding Horizon Dispatch Approach. IEEE Trans. Power Syst. 2021, 36, 3960–3972. [Google Scholar] [CrossRef]
- Hadayeghparast, S.; SoltaniNejad Farsangi, A.; Shayanfar, H. Day-ahead stochastic multi-objective economic/emission operational scheduling of a large scale virtual power plant. Energy 2019, 172, 630–646. [Google Scholar] [CrossRef]
- Yi, Z.; Xu, Y.; Gu, W.; Wu, W. A Multi-Time-Scale Economic Scheduling Strategy for Virtual Power Plant Based on Deferrable Loads Aggregation and Disaggregation. IEEE Trans. Sustain. Energy 2020, 11, 1332–1346. [Google Scholar] [CrossRef]
- Setiawan, E.A. Concept and Controllability of Virtual Power Plant; Kassel University Press GmbH: Kassel, Germany, 2007. [Google Scholar]
- Open Energy Information. Main Page. 2017. Available online: http://en.openei.org/wiki/Main_Page (accessed on 12 February 2017).
- NREL. Home Page. 2017. Available online: http://www.nrel.gov/midc (accessed on 14 February 2017).
- Liu, J.; Song, C.; Tao, R.; Wang, X. Cooperative Operation for Integrated Multi-Energy System Considering Transmission Losses. IEEE Access 2020, 8, 96934–96945. [Google Scholar] [CrossRef]
- Byeon, G.; Van Hentenryck, P. Unit Commitment With Gas Network Awareness. IEEE Trans. Power Syst. 2020, 35, 1327–1339. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Zhao, D.; Li, G.; Chen, C. A two-stage approach for combined heat and power economic emission dispatch: Combining multi-objective optimization with integrated decision making. Energy 2018, 162, 237–254. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Huang, Y.; Yang, J.; Ma, Y.; Yu, H.; Zeng, M.; Zhang, F.; Zhang, Y. Operation optimization of regional integrated energy system based on the modeling of electricity-thermal-natural gas network. Appl. Energy 2019, 251, 113410. [Google Scholar] [CrossRef]
- Mazzoni, S.; Ooi, S.; Nastasi, B.; Romagnoli, A. Energy storage technologies as techno-economic parameters for master-planning and optimal dispatch in smart multi energy systems. Appl. Energy 2019, 254, 113682. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Asadi, S.; Geem, Z.W. Large-scale combined heat and power economic dispatch using a novel multi-player harmony search method. Appl. Therm. Eng. 2019, 154, 493–504. [Google Scholar] [CrossRef]
- Daniela, L.; Chaturvedi, K.; Kolhe, M.L. Dynamic economic load dispatch using Levenberg Marquardt algorithm. In Proceedings of the 4th International Symposium on Hydrogen Energy, Renewable Energy and Materials, HEREM, Energy Procedia, Bangkok, Thailand, 13–14 June 2018; pp. 95–103. [Google Scholar]
- Santra, D.; Mukherjee, A.; Sarker, K.; Mondal, S. Dynamic economic dispatch using hybrid metaheuristics. J. Electr. Syst. Inf. Technol. 2020, 7, 3. [Google Scholar] [CrossRef]
- Younes, Z.; Alhamrouni, I.; Mekhilef, S.; Reyasudin, M. A memory-based gravitational search algorithm for solving economic dispatch problem in micro-grid. Ain Shams Eng. J. 2021, 12, 1985–1994. [Google Scholar] [CrossRef]
- Pan, S.; Jian, J.; Yang, L. A hybrid MILP and IPM approach for dynamic economic dispatch with valve-point effects. Int. J. Electr. Power Energy Syst. 2018, 97, 290–298. [Google Scholar] [CrossRef]
- Bhattacharjee, V.; Khan, I. A non-linear convex cost model for economic dispatch in microgrids. Appl. Energy 2018, 222, 637–648. [Google Scholar] [CrossRef]
- Aydin, E.; Purlu, M.; Turkay, B.E. Economic Dispatch of Multi-Microgrid Systems by Using Particle Swarm Optimization. In Proceedings of the 2021 13th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 25–27 November 2021; pp. 268–272. [Google Scholar] [CrossRef]
- Zhang, R.; Yan, K.; Li, G.; Jiang, T.; Li, X.; Chen, H. Privacy-preserving decentralized power system economic dispatch considering carbon capture power plants and carbon emission trading scheme via over-relaxed ADMM. Int. J. Electr. Power Energy Syst. 2020, 121, 106094. [Google Scholar] [CrossRef]
- Nagarajan, K.; Rajagopalan, A.; Angalaeswari, S.; Natrayan, L.; Mammo, W.D. Combined Economic Emission Dispatch of Microgrid with the Incorporation of Renewable Energy Sources Using Improved Mayfly Optimization Algorithm. Comput. Intell. Neurosci. 2022, 2022, 6461690. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Wu, G.; Shen, X.; Ma, Y.; Gou, J.; Xu, W.; Liu, J. Low-carbon economic dispatch of electricity-gas systems. Energy 2021, 226, 120267. [Google Scholar] [CrossRef]
- Akbari-Dibavar, A.; Mohammadi-Ivatloo, B.; Zare, K.; Khalili, T.; Bidram, A. Economic-Emission Dispatch Problem in Power Systems with Carbon Capture Power Plants. IEEE Trans. Ind. Appl. 2021, 57, 3341–3351. [Google Scholar] [CrossRef]
- Joshi, P.M.; Verma, H. An improved TLBO based economic dispatch of power generation through distributed energy resources considering environmental constraints. Sustain. Energy Grids Netw. 2019, 18, 100207. [Google Scholar] [CrossRef]
- He, L.; Lu, Z.; Zhang, J.; Geng, L.; Cai, Y.; Li, X. Economic dispatch of multi-area integrated electricity and natural gas systems considering emission and hourly spinning reserve constraints. Int. J. Electr. Power Energy Syst. 2021, 132, 107177. [Google Scholar] [CrossRef]
- Palit, D.; Chakraborty, N. Optimal bidding in emission constrained economic dispatch. Int. J. Environ. Sci. Technol. 2019, 16, 7953–7972. [Google Scholar] [CrossRef]
- Ghiasi, M.; Ghadimi, N.; Ahmadinia, E. An analytical methodology for reliability assessment and failure analysis in distributed power system. SN Appl. Sci. 2019, 1, 44. [Google Scholar] [CrossRef]
- Garcia, M.; Baldick, R. Approximating Economic Dispatch by Linearizing Transmission Losses. IEEE Trans. Power Syst. 2020, 35, 1009–1022. [Google Scholar] [CrossRef]
- Pan, S.; Jian, J.; Chen, H.; Yang, L. A full mixed-integer linear programming formulation for economic dispatch with valve-point effects, transmission loss and prohibited operating zones. Electr. Power Syst. Res. 2020, 180, 106061. [Google Scholar] [CrossRef]
- Chen, X.; Tang, G. Solving static and dynamic multi-area economic dispatch problems using an improved competitive swarm optimization algorithm. Energy 2022, 238, 122035. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K.K.K. Dynamic programming for scalable just-in-time economic dispatch with non-convex constraints and anytime participation. Int. J. Electr. Power Energy Syst. 2020, 123, 106217. [Google Scholar] [CrossRef]
- Hamdi, M.; Idomghar, L.; Chaoui, M.; Kachouri, A. An improved adaptive differential evolution optimizer for non-convex Economic Dispatch Problems. Appl. Soft Comput. 2019, 85, 105868. [Google Scholar] [CrossRef]
- Xu, D.; Xiao, J.; Wang, X. Environmental economic dispatch of power system based on multi-objective improved hybrid leapfrog algorithm. In Proceedings of the 2022 2nd International Conference on Electrical Engineering and Control Science (IC2ECS), Nanjing, China, 16–18 December 2022; pp. 504–510. [Google Scholar] [CrossRef]
- Carrillo-Galvez, A.; Flores-Bazán, F.; López Parra, E. On the solution of the Environmental/Economic Dispatch problem using Lagrangian duality. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 619–623. [Google Scholar] [CrossRef]
- Omar, A.I.; Ali, Z.M.; Al-Gabalawy, M.; Abdel Aleem, S.H.E.; Al-Dhaifallah, M. Multi-Objective Environmental Economic Dispatch of an Electricity System Considering Integrated Natural Gas Units and Variable Renewable Energy Sources. Mathematics 2020, 8, 1100. [Google Scholar] [CrossRef]
- Zhang, L.; Khishe, M.; Mohammadi, M.; Mohammed, A.H. Environmental economic dispatch optimization using niching penalized chimp algorithm. Energy 2022, 261, 125259. [Google Scholar] [CrossRef]
- Carrillo-Galvez, A.; Flores-Bazán, F.; López, E. A duality theory approach to the environmental/economic dispatch problem. Electr. Power Syst. Res. 2020, 184, 106285. [Google Scholar] [CrossRef]
- Dashtdar, M.; Flah, A.; Hosseinimoghadam, S.M.S.; Reddy, C.R.; Kotb, H.; AboRas, K.M.; Jasińska, E.; Jasiński, M. Solving the environmental/economic dispatch problem using the hybrid FA-GA multi-objective algorithm. Energy Rep. 2022, 8, 13766–13779. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Z.; Dai, C.; Xu, X.; Xiong, Z.; Su, Q. Multiobjective Grey Prediction Evolution Algorithm for Environmental/Economic Dispatch Problem. IEEE Access 2020, 8, 84162–84176. [Google Scholar] [CrossRef]
- Azaza, M.; Wallin, F. Multi objective particle swarm optimization of hybrid micro-grid system: A case study in Sweden. Energy 2017, 123, 108–118. [Google Scholar] [CrossRef]
- Hou, H.; Xue, M.; Xu, Y.; Xiao, Z.; Deng, X.; Xu, T.; Liu, P.; Cui, R. Multi-objective economic dispatch of a microgrid considering electric vehicle and transferable load. Appl. Energy 2020, 262, 114489. [Google Scholar] [CrossRef]
- Alamri, A.; AlOwaifeer, M.; Sakis Meliopoulos, A.P. Multi-Objective Unit Commitment Economic Dispatch for Power Systems Reliability Assessment. In Proceedings of the 2020 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Liege, Belgium, 18–21 August 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Azizivahed, A.; Karandeh, R.; Cecchi, V.; Naderi, E.; Li, L.; Zhang, J. Multi-Area Dynamic Economic Dispatch Considering Water Consumption Minimization, Wind Generation, and Energy Storage System. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Alvarado, F.L. Penalty Factors From Newton’s Method. IEEE Trans. Power Appar. Syst. 1978, PAS-97, 2031–2040. [Google Scholar] [CrossRef]
- Han, S. A Globally Convergent Method for Nonlinear Programming; Technical Report 75-257; Department of Computer Science, Cornell University: Ithaca, NY, USA, 1975. [Google Scholar]
- Ferrero, R.W.; Shahidehpour, S.M. Dynamic Economic Dispatch in Deregulated Systems. Electr. Power Syst. Res. 1997, 19, 433–439. [Google Scholar] [CrossRef]
- Chen, J.F.; Chen, S.D. Multi objective power dispatch with line flow constraints using the fast Newton-Raphson method. IEEE Trans. Energy Convers. 1997, 12, 86–93. [Google Scholar] [CrossRef]
- Barcelo, W.; Rastgoufard, P. Control area performance improvement by extended security constrained economic dispatch. IEEE Trans. Power Syst. 1997, 12, 120–128. [Google Scholar] [CrossRef]
- Lin, C.; Chen, S.; Huang, C.L. A direct Newton-Raphson economic dispatch. IEEE Trans. Power Syst. 1992, 7, 1149–1154. [Google Scholar] [CrossRef]
- Chen, S.D.; Chen, J.F. A direct Newton–Raphson economic emission dispatch. Int. J. Electr. Power Energy Syst. 2003, 25, 411–417. [Google Scholar] [CrossRef]
- Ramanathan, R. Fast economic dispatch based on the penalty factors from Newton’s method. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 1624–1629. [Google Scholar] [CrossRef]
- Xu, T.; Wu, W.; Zheng, W.; Sun, H.; Wang, L. Fully Distributed Quasi-Newton Multi-Area Dynamic Economic Dispatch Method for Active Distribution Networks. IEEE Trans. Power Syst. 2018, 33, 4253–4263. [Google Scholar] [CrossRef]
- Qin, J.; Wan, Y.; Yu, X.; Kang, Y. A Newton Method-Based Distributed Algorithm for Multi-Area Economic Dispatch. IEEE Trans. Power Syst. 2020, 35, 986–996. [Google Scholar] [CrossRef]
- da Costa, G. Modified Newton method for reactive dispatching. Int. J. Electr. Power Energy Syst. 2002, 24, 815–819. [Google Scholar] [CrossRef]
- Chaiamarit, K.; Nuchprayoon, S. Economic dispatch solution considering demand and wind speed uncertainties based on Newton’s method. In Proceedings of the 2013 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 8–11 December 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Abouheaf, M.I.; Lee, W.J.; Lewis, F.L. Dynamic formulation and approximation methods to solve economic dispatch problems. IET Gener. Transm. Distrib. 2013, 7, 866–873. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Zhan, J.P.; Wu, Q.H.; Guo, C.X.; Zhou, X.X. Fast λ-Iteration Method for Economic Dispatch with Prohibited Operating Zones. IEEE Trans. Power Syst. 2014, 29, 990–991. [Google Scholar] [CrossRef]
- Muda, H.; Othman, A.; Julai, N. Economic Dispatch Strategy for Solar Hybrid System using Lambda Iteration Method. J. Telecommun. Electron. Comput. Eng. JTEC 2017, 9, 85–89. [Google Scholar]
- Adhinarayanan, T.; Sydulu, M. Efficient Lambda Logic Based Optimization Procedure to Solve the Large Scale Generator Constrained Economic Dispatch Problem. J. Electr. Eng. Technol. 2009, 4, 301–309. [Google Scholar] [CrossRef]
- Hemamalini, S.; Simon, S.P. Dynamic economic dispatch using Maclaurin series based Lagrangian method. Energy Convers. Manag. 2010, 51, 2212–2219. [Google Scholar] [CrossRef]
- Ananduta, W.; Ocampo-Martinez, C.; Nedić, A. A Distributed Augmented Lagrangian Method Over Stochastic Networks for Economic Dispatch of Large-Scale Energy Systems. IEEE Trans. Sustain. Energy 2021, 12, 1927–1934. [Google Scholar] [CrossRef]
- Tang, C.; Xu, J.; Tan, Y.; Sun, Y.; Zhang, B. Lagrangian Relaxation with Incremental Proximal Method for Economic Dispatch with Large Numbers of Wind Power Scenarios. IEEE Trans. Power Syst. 2019, 34, 2685–2695. [Google Scholar] [CrossRef]
- Shao, S.; Gao, F.; Wu, J. A Novel Lagrangian Relaxation Method for Distributed Multi-Area Economic Dispatch. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Denver, CO, USA, 17–21 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Zuo, Y. Research on time-varying economic dispatch of smart grid based on Lagrangian pairing. E3S Web Conf. 2023, 375, 03010. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y. A lagrange relaxation-based alternating iterative algorithm for non-convex combined heat and power dispatch problem. Electr. Power Syst. Res. 2019, 177, 105982. [Google Scholar] [CrossRef]
- Qader, M. Power management in a hydrothermal system considering maintenance using Lagrangian relaxation and augmented Lagrangian methods. Alex. Eng. J. 2022, 61, 8177–8188. [Google Scholar] [CrossRef]
- Gondzio, J. Interior point methods 25 years later. Eur. J. Oper. Res. 2012, 218, 587–601. [Google Scholar] [CrossRef]
- Potra, F.A.; Wright, S.J. Interior-point methods. J. Comput. Appl. Math. 2000, 124, 281–302. [Google Scholar] [CrossRef]
- Li, B.; Yin, L.; Wang, Y.; Ma, Y. Robust Economic Optimal Dispatch Method of Wind Power System considering AC Power Flow Constraints. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 1578–1584. [Google Scholar] [CrossRef]
- Pinheiro, R.B.; Balbo, A.R.; Cabana, T.G.; Nepomuceno, L. Solving Nonsmooth and Discontinuous Optimal Power Flow problems via interior-point p-penalty approach. Comput. Oper. Res. 2022, 138, 105607. [Google Scholar] [CrossRef]
- El-Sayed, W.T.; El-Saadany, E.F.; Zeineldin, H.H.; Al-Sumaiti, A.S. Fast initialization methods for the nonconvex economic dispatch problem. Energy 2020, 201, 117635. [Google Scholar] [CrossRef]
- Xihui, Y.; Quintana, V. Improving an interior-point-based OPF by dynamic adjustments of step sizes and tolerances. IEEE Trans. Power Syst. 1999, 14, 709–717. [Google Scholar] [CrossRef]
- Wright, S.J. Continuous Optimization (Nonlinear and Linear Programming). In The Princeton Companion to Applied Mathematics; Higham, N.J., Dennis, M.R., Glendinning, P., Martin, P.A., Santosa, F., Tanner, J., Eds.; Princeton University Press: Princeton, NJ, USA, 2015; pp. 281–293. [Google Scholar]
- McLarty, D.; Panossian, N.; Jabbari, F.; Traverso, A. Dynamic economic dispatch using complementary quadratic programming. Energy 2019, 166, 755–764. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, Y.; Liu, J.; Miao, X.; Zhang, X.; Zhu, Z.; Wang, Z. Economic Dispatch of Micro-grid Based on Sequential Quadratic Programming-Model and Formulation. E3S Web Conf. 2019, 136, 01010. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. A Sequential Quadratic Programming Model for the Economic–Environmental Dispatch in MT-HVDC. In Proceedings of the 2019 IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Manizales, Colombia, 30–31 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hlalele, T.G.; Naidoo, R.M.; Bansal, R.C.; Zhang, J. Multi-objective stochastic economic dispatch with maximal renewable penetration under renewable obligation. Appl. Energy 2020, 270, 115120. [Google Scholar] [CrossRef]
- Lu, R.; Ding, T.; Qin, B.; Ma, J.; Fang, X.; Dong, Z. Multi-Stage Stochastic Programming to Joint Economic Dispatch for Energy and Reserve with Uncertain Renewable Energy. IEEE Trans. Sustain. Energy 2020, 11, 1140–1151. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, M.; Lu, W.; Deng, Z. Stochastic Optimization of Economic Dispatch with Wind and Photovoltaic Energy Using the Nested Sparse Grid-Based Stochastic Collocation Method. IEEE Access 2019, 7, 91827–91837. [Google Scholar] [CrossRef]
- Van Ackooij, W.; Zorgati, R.; Henrion, R.; Möller, A. Chance constrained programming and its applications to energy management. In Stochastic Optimization-Seeing the Optimal for the Uncertain; IntechOpen: London, UK, 2011. [Google Scholar]
- Peng, S. Chance Constrained Problem and Its Applications. Ph.D. Thesis, Université Paris Saclay, Paris, France, Xi’an Jiaotong University, Xi’an, China, 2019. [Google Scholar]
- Wu, C.; Kargarian, A.; Jeon, H.W. Data-Driven Nonparametric Joint Chance Constraints for Economic Dispatch with Renewable Generation. IEEE Trans. Ind. Appl. 2021, 57, 6537–6546. [Google Scholar] [CrossRef]
- Qi, N.; Pinson, P.; Almassalkhi, M.R.; Cheng, L.; Zhuang, Y. Chance-Constrained Generic Energy Storage Operations under Decision-Dependent Uncertainty. arXiv 2023, arXiv:2201.06407. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, W.; Wang, B.; Li, M. Chance-Constrained Economic Dispatch Considering Curtailment Strategy of Renewable Energy. IEEE Trans. Power Syst. 2021, 36, 5792–5802. [Google Scholar] [CrossRef]
- Hedman, K.; Korad, A.; Zhang, M.; Dominguez-Garcia, A.; Jiang, X. The Application of Robust Optimization in Power Systems; Technical Report; Power Systems Engineering Research Center (PSERC): Chandigarh, India, 2014. [Google Scholar]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and applications of robust optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Y.; Sun, H.; Khan, I. A distributed robust optimization approach for the economic dispatch of flexible resources. Int. J. Electr. Power Energy Syst. 2021, 124, 106360. [Google Scholar] [CrossRef]
- Zhao, B.; Qian, T.; Tang, W.; Liang, Q. A data-enhanced distributionally robust optimization method for economic dispatch of integrated electricity and natural gas systems with wind uncertainty. Energy 2022, 243, 123113. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. [Google Scholar] [CrossRef]
- Kim, K.G. Book Review: Deep Learning. Healthc. Inform. Res. 2016, 22, 351–354. [Google Scholar] [CrossRef]
- Arora, V.; Mahla, S.K.; Leekha, R.S.; Dhir, A.; Lee, K.H.; Ko, H. Intervention of Artificial Neural Network with an Improved Activation Function to Predict the Performance and Emission Characteristics of a Biogas Powered Dual Fuel Engine. Electronics 2021, 10, 584. [Google Scholar] [CrossRef]
- Liu, H.; Shen, X.; Guo, Q.; Sun, H. A data-driven approach towards fast economic dispatch in electricity–gas coupled systems based on artificial neural network. Appl. Energy 2021, 286, 116480. [Google Scholar] [CrossRef]
- Mehmood, K.; Cheema, K.M.; Tahir, M.F.; Tariq, A.R.; Milyani, A.H.; Elavarasan, R.M.; Shaheen, S.; Raju, K. Short term power dispatch using neural network based ensemble classifier. J. Energy Storage 2021, 33, 102101. [Google Scholar] [CrossRef]
- Nangia, U.; Jain, N.; Rastogi, P.; Malik, R.; Jain, P. Artificial Neural Network algorithms for the optimum solution of Economic load dispatch problem. In Proceedings of the 2021 International Conference on Communication, Control and Information Sciences (ICCISc), Idukki, India, 16–18 June 2021; Volume 1, pp. 1–6. [Google Scholar] [CrossRef]
- Kalakova, A.; Nunna, H.S.V.S.K.; Jamwal, P.K.; Doolla, S. A Novel Genetic Algorithm Based Dynamic Economic Dispatch with Short-Term Load Forecasting. IEEE Trans. Ind. Appl. 2021, 57, 2972–2982. [Google Scholar] [CrossRef]
- Hasan, F.; Kargarian, A. Topology-Aware Learning Assisted Branch and Ramp Constraints Screening for Dynamic Economic Dispatch. IEEE Trans. Power Syst. 2022, 37, 3495–3505. [Google Scholar] [CrossRef]
- Gaikwad, P.S. Using Graph Convolutional Network and Message Passing Neural Networks for Solving Unit Commitment and Economic Dispatch in a Day Ahead Energy Trading Market Based on ERCOT Nodal Model. Ph.D. Thesis, The University of Texas, Arlington, TX, USA, 2020. [Google Scholar]
- King, E.; Drgoňa, J.; Tuor, A.; Abhyankar, S.; Bakker, C.; Bhattacharya, A.; Vrabie, D. Koopman-based Differentiable Predictive Control for the Dynamics-Aware Economic Dispatch Problem. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 2194–2201. [Google Scholar] [CrossRef]
- Wang, J.; He, X.; Huang, J.; Chen, G. Recurrent Neural Network for Nonconvex Economic Emission Dispatch. J. Mod. Power Syst. Clean Energy 2021, 9, 46–55. [Google Scholar] [CrossRef]
- Kearns, J.; Briere, C. Integration of Real-Time Building Data into Economic Dispatch of Dynamically Electrified Building Steam Systems; Medley Thermal LLC: Somerville, MA, USA, 2020. [Google Scholar]
- Lyu, Z.; Wang, Y.; Wang, J.; Zhang, L.; Shen, J.; Wang, X. Short-term electricity price forecasting G-LSTM model and economic dispatch for distribution system. IOP Conf. Ser. Earth Environ. Sci. 2020, 467, 012186. [Google Scholar] [CrossRef]
- Tsegaye, S.; Shewarega, F.; Bekele, G. Hopfield Neural Network-based Security Constrained Economic Dispatch of Renewable Energy Systems. EAI Endorsed Trans. Energy Web 2021, 8, 168224. [Google Scholar] [CrossRef]
- Duong, T.L.; Nguyen, P.D.; Phan, V.D.; Vo, D.N.; Nguyen, T.T. Optimal Load Dispatch in Competitive Electricity Market by Using Different Models of Hopfield Lagrange Network. Energies 2019, 12, 2932. [Google Scholar] [CrossRef]
- Tsegaye, S.; Shewarega, F.; Bekele, G. Artificial Intelligence Based Security Constrained Economic Dispatch of Ethiopian Renewable Energy Systems: A Comparative Study. In Advances of Science and Technology; Berihun, M.L., Ed.; Springer: Cham, Switzerland, 2022; pp. 522–542. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Shlezinger, N.; Eldar, Y.C.; Boyd, S.P. Model-Based Deep Learning: On the Intersection of Deep Learning and Optimization. IEEE Access 2022, 10, 115384–115398. [Google Scholar] [CrossRef]
- Xu, B.; Guo, F.; Zhang, W.A.; Li, G.; Wen, C. E2 DNet: An Ensembling Deep Neural Network for Solving Nonconvex Economic Dispatch in Smart Grid. IEEE Trans. Ind. Inform. 2022, 18, 3066–3076. [Google Scholar] [CrossRef]
- Xu, Y.; Song, Y.; Deng, Y.; Liu, Z.; Guo, X.; Zhao, D. Low-carbon economic dispatch of integrated energy system considering the uncertainty of energy efficiency. Energy Rep. 2023, 9, 1003–1010. [Google Scholar] [CrossRef]
- Yin, L.; Gao, Q.; Zhao, L.; Wang, T. Expandable deep learning for real-time economic generation dispatch and control of three-state energies based future smart grids. Energy 2020, 191, 116561. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Z.; Yu, J.; Xie, K.; Jin, L. Fast Economic Dispatch in Smart Grids Using Deep Learning: An Active Constraint Screening Approach. IEEE Internet Things J. 2020, 7, 11030–11040. [Google Scholar] [CrossRef]
- Tang, H.; Lv, K.; Bak-Jensen, B.; Chen, W. Deep neural network-based hierarchical learning method for dispatch control of multi-regional power grid. Neural Comput. Appl. 2022, 34, 5063–5079. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; A Bradford Book: Cambridge, MA, USA, 2018. [Google Scholar]
- Bora, T.C.; Mariani, V.C.; dos Santos Coelho, L. Multi-objective optimization of the environmental-economic dispatch with reinforcement learning based on non-dominated sorting genetic algorithm. Appl. Therm. Eng. 2019, 146, 688–700. [Google Scholar] [CrossRef]
- Fang, D.; Guan, X.; Hu, B.; Peng, Y.; Chen, M.; Hwang, K. Deep Reinforcement Learning for Scenario-Based Robust Economic Dispatch Strategy in Internet of Energy. IEEE Internet Things J. 2021, 8, 9654–9663. [Google Scholar] [CrossRef]
- Fu, Y.; Guo, X.; Mi, Y.; Yuan, M.; Ge, X.; Su, X.; Li, Z. The distributed economic dispatch of smart grid based on deep reinforcement learning. IET Gener. Transm. Distrib. 2021, 15, 2645–2658. [Google Scholar] [CrossRef]
- Dai, P.; Yu, W.; Wen, G.; Baldi, S. Distributed Reinforcement Learning Algorithm for Dynamic Economic Dispatch with Unknown Generation Cost Functions. IEEE Trans. Ind. Inform. 2020, 16, 2258–2267. [Google Scholar] [CrossRef]
- Lodwick, W.A.; Untiedt, E.A. Fuzzy Optimization. In Granular, Fuzzy, and Soft Computing; Lin, T.Y., Liau, C.J., Kacprzyk, J., Eds.; Springer: New York, NY, USA, 2023; pp. 755–791. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. In Readings in Fuzzy Sets for Intelligent Systems; Dubois, D., Prade, H., Yager, R.R., Eds.; Morgan Kaufmann: Burlington, MA, USA, 1993; pp. 387–403. [Google Scholar] [CrossRef]
- Izquierdo, S.; Izquierdo, L.R. Mamdani fuzzy systems for modelling and simulation: A critical assessment. SSRN 2017. [Google Scholar] [CrossRef]
- Ma, Y.W.; Deng, F.C.; Song, X.T.; Piao, C.H. A Fuzzy Random Scheduling Model of Islanded Microgrid Considering Dual Uncertainty of EV. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020; pp. 230–235. [Google Scholar] [CrossRef]
- Al-Sakkaf, S.; Kassas, M.; Khalid, M.; Abido, M.A. An Energy Management System for Residential Autonomous DC Microgrid Using Optimized Fuzzy Logic Controller Considering Economic Dispatch. Energies 2019, 12, 1457. [Google Scholar] [CrossRef]
- Madadi, S.; Mohammadi-Ivatloo, B.; Tohidi, S. Decentralized optimal multi-area generation scheduling considering renewable resources mix and dynamic tie line rating. J. Clean. Prod. 2019, 223, 883–896. [Google Scholar] [CrossRef]
- Zhao, K. Fuzzy Modelling of Power System Economic Dispatch Incorporating Load and Wind Generation Uncertainties. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), Shanghai, China, 24–25 October 2019. [Google Scholar]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Pourdaryaei, A.; Mohammadi, M.; Karimi, M.; Mokhlis, H.; Illias, H.A.; Kaboli, S.H.A.; Ahmad, S. Recent Development in Electricity Price Forecasting Based on Computational Intelligence Techniques in Deregulated Power Market. Energies 2021, 14, 6104. [Google Scholar] [CrossRef]
- Xing, Y.; Lien, F.S.; Melek, W.; Yee, E. A Multi-Hour Ahead Wind Power Forecasting System Based on a WRF-TOPSIS-ANFIS Model. Energies 2022, 15, 5472. [Google Scholar] [CrossRef]
- Lara-Cerecedo, L.O.; Hinojosa, J.F.; Pitalúa-Díaz, N.; Matsumoto, Y.; González-Angeles, A. Prediction of the Electricity Generation of a 60-kW Photovoltaic System with Intelligent Models ANFIS and Optimized ANFIS-PSO. Energies 2023, 16, 6050. [Google Scholar] [CrossRef]
- Pournazarian, B.; Sangrody, R.; Saeedian, M.; Gomis-Bellmunt, O.; Pouresmaeil, E. Enhancing Microgrid Small-Signal Stability and Reactive Power Sharing Using ANFIS-Tuned Virtual Inductances. IEEE Access 2021, 9, 104915–104926. [Google Scholar] [CrossRef]
- Shihabudheen, K.V.; Raju, S.K.; Pillai, G.N. Control for Grid-Connected DFIG-based Wind Energy System Using Adaptive Neuro-Fuzzy Technique. Int. Trans. Electr. Energy Syst. 2018, 28, e2526. [Google Scholar] [CrossRef]
- Reddy, P.D.P. Particle Swarm Optimization Algorithm with ANFIS for Economic Load Dispatch. Int. J. Res. Appl. Sci. Eng. Technol. 2018, 6, 1125–1130. [Google Scholar] [CrossRef]
- Roy, K.; Mandal, K.K.; Mandal, A.C. Smart energy management for optimal economic operation in grid-connected hybrid power system. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 1–21. [Google Scholar] [CrossRef]
- Roy, P.; Liao, Y.; He, J. Economic Dispatch for Grid-Connected Wind Power with Battery-Supercapacitor Hybrid Energy Storage System. IEEE Trans. Ind. Appl. 2023, 59, 1118–1128. [Google Scholar] [CrossRef]
- Ulutas, A.; Altas, I.H.; Onen, A.; Ustun, T.S. Neuro-Fuzzy-Based Model Predictive Energy Management for Grid Connected Microgrids. Electronics 2020, 9, 900. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Chapter 10—Metaheuristic Algorithms: A Comprehensive Review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Sangaiah, A.K., Sheng, M., Zhang, Z., Eds.; Intelligent Data-Centric Systems; Academic Press: Cambridge, MA, USA, 2018; pp. 185–231. [Google Scholar] [CrossRef]
- Bianchi, L.; Dorigo, M.; Gambardella, L.; Gutin, G.; Karapetyan, D.; Sartori, E.; Schaerf, A. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Dahou, A.; Abualigah, L.; Yu, L.; Alshinwan, M.; Khasawneh, A.M.; Lu, S. Advanced metaheuristic optimization techniques in applications of deep neural networks: A review. Neural Comput. Appl. 2021, 33, 14079–14099. [Google Scholar] [CrossRef]
- Zou, D.; Li, S.; Kong, X.; Ouyang, H.; Li, Z. Solving the combined heat and power economic dispatch problems by an improved genetic algorithm and a new constraint handling strategy. Appl. Energy 2019, 237, 646–670. [Google Scholar] [CrossRef]
- Yeh, W.C.; He, M.F.; Huang, C.L.; Tan, S.Y.; Zhang, X.; Huang, Y.; Li, L. New genetic algorithm for economic dispatch of stand-alone three-modular microgrid in DongAo Island. Appl. Energy 2020, 263, 114508. [Google Scholar] [CrossRef]
- Ponciroli, R.; Stauff, N.E.; Ramsey, J.; Ganda, F.; Vilim, R.B. An Improved Genetic Algorithm Approach to the Unit Commitment/Economic Dispatch Problem. IEEE Trans. Power Syst. 2020, 35, 4005–4013. [Google Scholar] [CrossRef]
- Pulluri, H.; Vyshnavi, M.; Shraddha, P.; Sai Priya, B.; Sri Hari, T.; Preeti. Genetic Algorithm with Multi-Parent Crossover Solution for Economic Dispatch with Valve Point Loading Effects. In Innovations in Electrical and Electronics Engineering; Saini, H.S., Srinivas, T., Vinod Kumar, D.M., Chandragupta Mauryan, K.S., Eds.; Springer: Singapore, 2020; pp. 429–438. [Google Scholar]
- Kumar Dey, S.; Prasad Dash, D.; Basu, M. Application of NSGA-II for environmental constraint economic dispatch of thermal-wind-solar power system. Renew. Energy Focus 2022, 43, 239–245. [Google Scholar] [CrossRef]
- Xin, J.; Yu, L.; Wang, J.; Li, N. A diversity-based parallel particle swarm optimization for nonconvex economic dispatch problem. Trans. Inst. Meas. Control 2023, 45, 452–465. [Google Scholar] [CrossRef]
- Ju, Y. Application of Improved Particle Swarm Optimization Algorithm in Power Economic Dispatch System. In Cyber Security Intelligence and Analytics; Xu, Z., Alrabaee, S., Loyola-González, O., Cahyani, N.D.W., Ab Rahman, N.H., Eds.; Springer: Cham, Switzerland, 2023; pp. 216–226. [Google Scholar]
- Singh, A.; Khamparia, A. Solution to Economic Dispatch Problem Using Modified PSO Algorithm. In Proceedings of Second Doctoral Symposium on Computational Intelligence; Gupta, D., Khanna, A., Kansal, V., Fortino, G., Hassanien, A.E., Eds.; Springer: Singapore, 2022; pp. 889–897. [Google Scholar]
- Marhatang, M.; Djalal, M.R. Optimal Economic Dispatch Using Particle Swarm Optimization in Sulselrabar System. IAES Int. J. Artif. Intell. 2022, 11, 221–228. [Google Scholar] [CrossRef]
- Salim, N.A.; Iqmal Bin Amin, M.A.; Mohamad, H.; Yasin, Z.M. Particle Swarm Optimization to Solve Economic Dispatch Considering Different Iterations of Loss Coefficient. In Proceedings of the 2022 IEEE International Conference on Power and Energy (PECon), Langkawi, Malaysia, 5–6 December 2022; pp. 454–459. [Google Scholar] [CrossRef]
- Xin-gang, Z.; Ji, L.; Jin, M.; Ying, Z. An improved quantum particle swarm optimization algorithm for environmental economic dispatch. Expert Syst. Appl. 2020, 152, 113370. [Google Scholar] [CrossRef]
- Kumar, A.; Thakur, M.; Mittal, G. Planning optimal power dispatch schedule using constrained ant colony optimization. Appl. Soft Comput. 2022, 115, 108132. [Google Scholar] [CrossRef]
- Vasovala, P. Application of Ant Colony Optimization Technique in Economic Load Dispatch of IEEE-26 Bus System with Valve Point Loading. Int. J. Res. Appl. Sci. Eng. Technol. 2021, 9, 51–58. [Google Scholar] [CrossRef]
- Srivastava, A.; Singh, S. Implementation of Ant Colony Optimization in Economic Load Dispatch Problem. In Proceedings of the 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020; pp. 1018–1024. [Google Scholar] [CrossRef]
- Al-Amyal, F.; Al-attabi, K.J.; Al-khayyat, A. Multistage Ant Colony Algorithm for Economic Emission Dispatch Problem. In Proceedings of the 2019 International IEEE Conference and Workshop in Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 20–21 November 2019; pp. 161–166. [Google Scholar] [CrossRef]
- Rabiee, A.; Jamadi, M.; Mohammadi-Ivatloo, B.; Ahmadian, A. Optimal Non-Convex Combined Heat and Power Economic Dispatch via Improved Artificial Bee Colony Algorithm. Processes 2020, 8, 1036. [Google Scholar] [CrossRef]
- Haripuddin; Suyuti, A.; Said, S.M.; Syam Akil, Y. Dynamic Economic Dispatch for 150 kV Sulselbar Power Generation Systems Using Artificial Bee Colony Algorithm. In Proceedings of the 2019 International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 24–25 July 2019; pp. 817–822. [Google Scholar] [CrossRef]
- ul Hassan, T.; Alquthami, T.; Butt, S.E.; Tahir, M.F.; Mehmood, K. Short-term optimal scheduling of hydro-thermal power plants using artificial bee colony algorithm. Energy Rep. 2020, 6, 984–992. [Google Scholar] [CrossRef]
- Afandi, A.N.; Wibawa, A.P.; Patmantara, S.; Fujita, G.; Hani, S.; Sulistyowati, Y. Economic Assessment of Power Grid Development Using Artificial Bee Colony Algorithm. Period. Polytech. Electr. Eng. Comput. Sci. 2022, 66, 72–79. [Google Scholar] [CrossRef]
- Habib, H.U.R.; Subramaniam, U.; Waqar, A.; Farhan, B.S.; Kotb, K.M.; Wang, S. Energy Cost Optimization of Hybrid Renewables Based V2G Microgrid Considering Multi Objective Function by Using Artificial Bee Colony Optimization. IEEE Access 2020, 8, 62076–62093. [Google Scholar] [CrossRef]
- Ettappan, M.; Vimala, V.; Ramesh, S.; Kesavan, V.T. Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using Artificial Bee Colony Algorithm. Microprocess. Microsystems 2020, 76, 103085. [Google Scholar] [CrossRef]
- Zheng, C.; Eskandari, M.; Li, M.; Sun, Z. GA-Reinforced Deep Neural Network for Net Electric Load Forecasting in Microgrids with Renewable Energy Resources for Scheduling Battery Energy Storage Systems. Algorithms 2022, 15, 338. [Google Scholar] [CrossRef]
- Masoumi, A.; Ghassem-Zadeh, S.; Hosseini, S.H.; Ghavidel, B.Z. Application of neural network and weighted improved PSO for uncertainty modeling and optimal allocating of renewable energies along with battery energy storage. Appl. Soft Comput. 2020, 88, 105979. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Bardhan, A.; Kardani, N.; Samui, P.; Hu, J.W.; Ramzy, A. Novel application of adaptive swarm intelligence techniques coupled with adaptive network-based fuzzy inference system in predicting photovoltaic power. Renew. Sustain. Energy Rev. 2021, 148, 111315. [Google Scholar] [CrossRef]
- Azeem, F.; Ahmad, A.; Gondal, T.M.; Arshad, J.; Rehman, A.U.; Eldin, E.M.T.; Shafiq, M.; Hamam, H. Load Management and Optimal Sizing of Special-Purpose Microgrids Using Two Stage PSO-Fuzzy Based Hybrid Approach. Energies 2022, 15, 6465. [Google Scholar] [CrossRef]
- Rohiem, N.H.; Soeprijanto, A.; Putra, D.F.U.; Syai’in, M.; Sulistiawati, I.B.; Zahoor, M.; Shah, L.A. Resolving Economic Dispatch with Uncertainty Effect in Microgrids Using Hybrid Incremental Particle Swarm Optimization and Deep Learning Method: Resolving Economic Dispatch with Uncertainty Effect in Microgrids. Proc. Pak. Acad. Sci. Phys. Comput. Sci. 2021, 58, 119–129. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Z.; Xu, W.; Zhu, F.; Lyu, X.; Fu, M. Bi-Objective Dispatch of Multi-Energy Virtual Power Plant: Deep-Learning-Based Prediction and Particle Swarm Optimization. Appl. Sci. 2019, 9, 292. [Google Scholar] [CrossRef]
- Roy, K.; Mandal, K.K.; Mandal, A.C. Ant-Lion Optimizer algorithm and recurrent neural network for energy management of micro grid connected system. Energy 2019, 167, 402–416. [Google Scholar] [CrossRef]
- Mahmoud, K.; Abdel-Nasser, M.; Mustafa, E.; Ali, Z.M. Improved Salp–Swarm Optimizer and Accurate Forecasting Model for Dynamic Economic Dispatch in Sustainable Power Systems. Sustainability 2020, 12, 576. [Google Scholar] [CrossRef]
- Ramachandran, M.; Mirjalili, S.; Malli Ramalingam, M.; Charles Gnanakkan, C.A.R.; Parvathysankar, D.S.; Sundaram, A. A ranking-based fuzzy adaptive hybrid crow search algorithm for combined heat and power economic dispatch. Expert Syst. Appl. 2022, 197, 116625. [Google Scholar] [CrossRef]
- Abdullah, M.N.; Abdullah, N.; Aswan, N.F.; Jumaat, S.A.; Radzi, N.H.M.; Nor, A.F.M. Combined economic-emission load dispatch solution using firefly algorithm and fuzzy approach. Indones. J. Electr. Eng. Comput. Sci. 2019, 16, 127–135. [Google Scholar] [CrossRef]
- Adipala, P.; Paiton, P.; Labuan, P.; Indramayu, P.; Rembang, P.; Pacitan, P. A hybrid method of ann-bp and lambda iteration for anomalous short-term economic dispatch of hydrothermal power systems. J. Eng. Sci. Technol. 2020, 15, 4061–4074. [Google Scholar]
- Ellahi, M.; Abbas, G.; Satrya, G.B.; Usman, M.R.; Gu, J. A Modified Hybrid Particle Swarm Optimization with Bat Algorithm Parameter Inspired Acceleration Coefficients for Solving Eco-Friendly and Economic Dispatch Problems. IEEE Access 2021, 9, 82169–82187. [Google Scholar] [CrossRef]
- Ellahi, M.; Abbas, G. A Hybrid Metaheuristic Approach for the Solution of Renewables-Incorporated Economic Dispatch Problems. IEEE Access 2020, 8, 127608–127621. [Google Scholar] [CrossRef]
- Suyono, H.; Subekti, E.; Purnomo, H.; Nurwati, T.; Hasanah, R.N. Economic Dispatch of 500 kV Java-Bali Power System using Hybrid Particle Swarm-Ant Colony Optimization Method. In Proceedings of the 2020 12th International Conference on Electrical Engineering (ICEENG), Cairo, Egypt, 7–9 July 2020; pp. 5–10. [Google Scholar] [CrossRef]
- Merah, H.; Gacem, A.; Benattous, D.; Labbi, Y.; Malik, O.P. Solving Economic Dispatch Problem Using a New Hybrid PSO-ALO Algorithm. In Proceedings of the 2020 1st International Conference on Communications, Control Systems and Signal Processing (CCSSP), El Oued, Algeria, 16–17 May 2020; pp. 487–492. [Google Scholar] [CrossRef]
- Chen, J.; Imani Marrani, H. An Efficient New Hybrid ICA-PSO Approach for Solving Large Scale Non-convex Multi Area Economic Dispatch Problems. J. Electr. Eng. Technol. 2020, 15, 1127–1145. [Google Scholar] [CrossRef]
- Dihem, A.; Salhi, A.; Naimi, D.; Bensalem, A. Economic Dispatch Solution Using Hybrid Salp Swarm Algorithm and Simulated Annealing Approach. J. Telecommun. Electron. Comput. Eng. JTEC 2020, 12, 57–63. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).