Wing Sails: Numerical Analysis of High-Performance Propulsion Systems for a Racing Yacht
Abstract
1. Introduction
1.1. High-Performance Wing Sail State of the Art
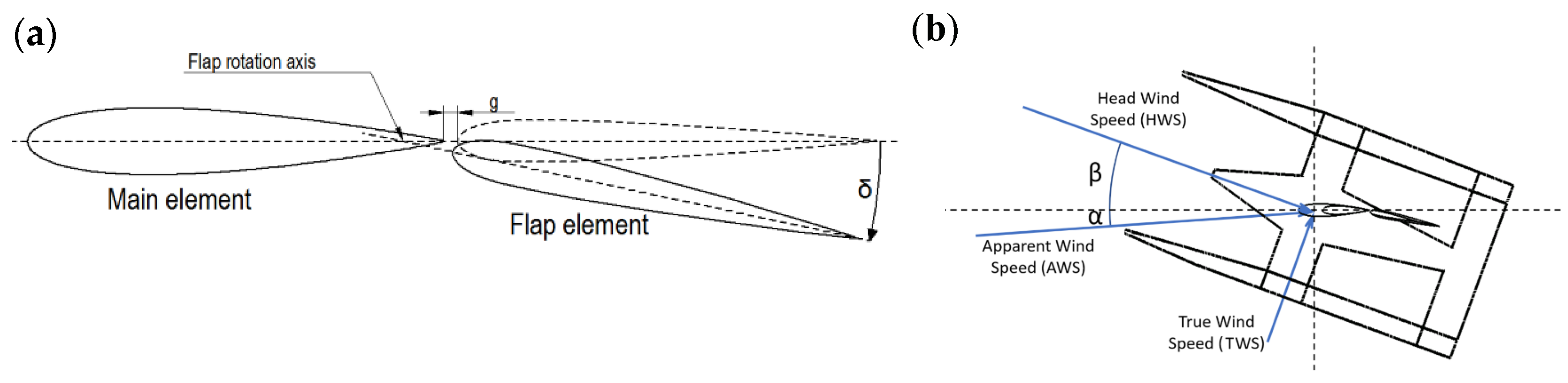
1.2. Wing Sail Operation and Basic Notations
2. Numerical Methods
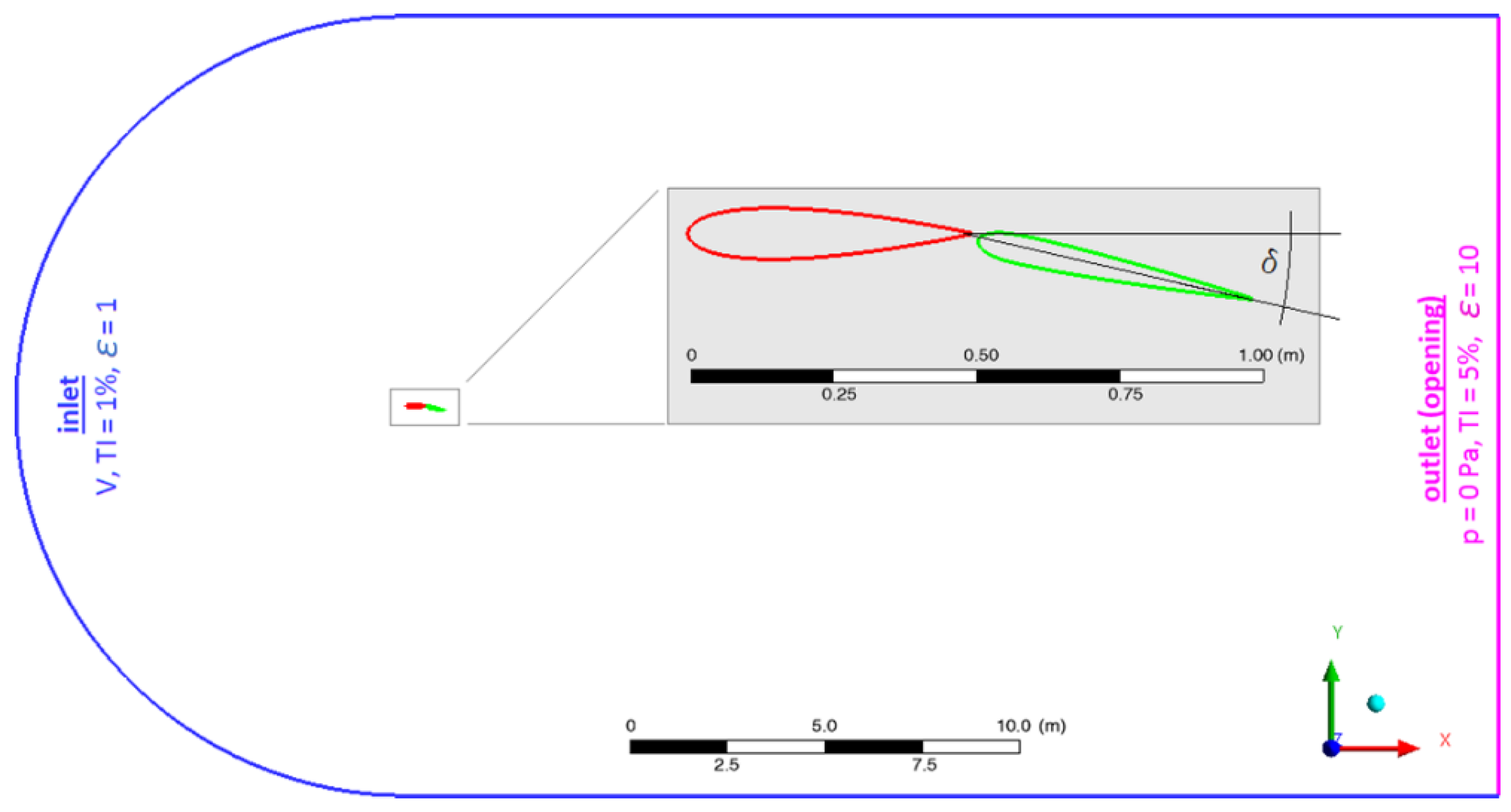
2.1. Two-Dimensional Simulation
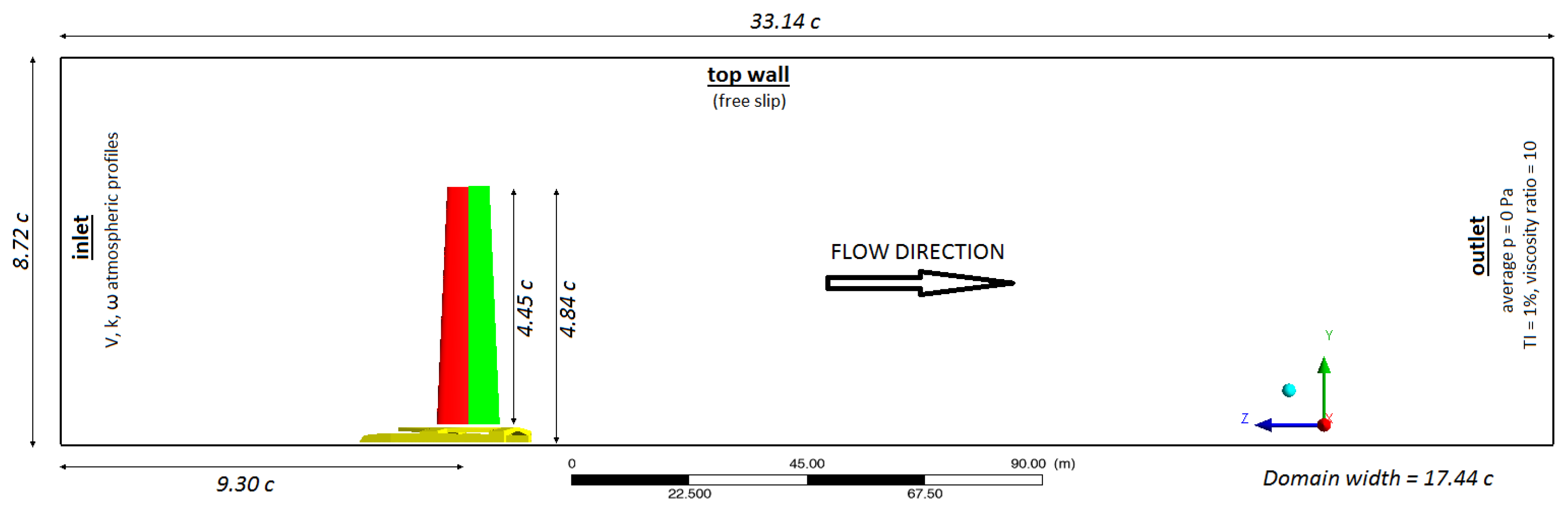
2.2. Three-Dimensional Simulation
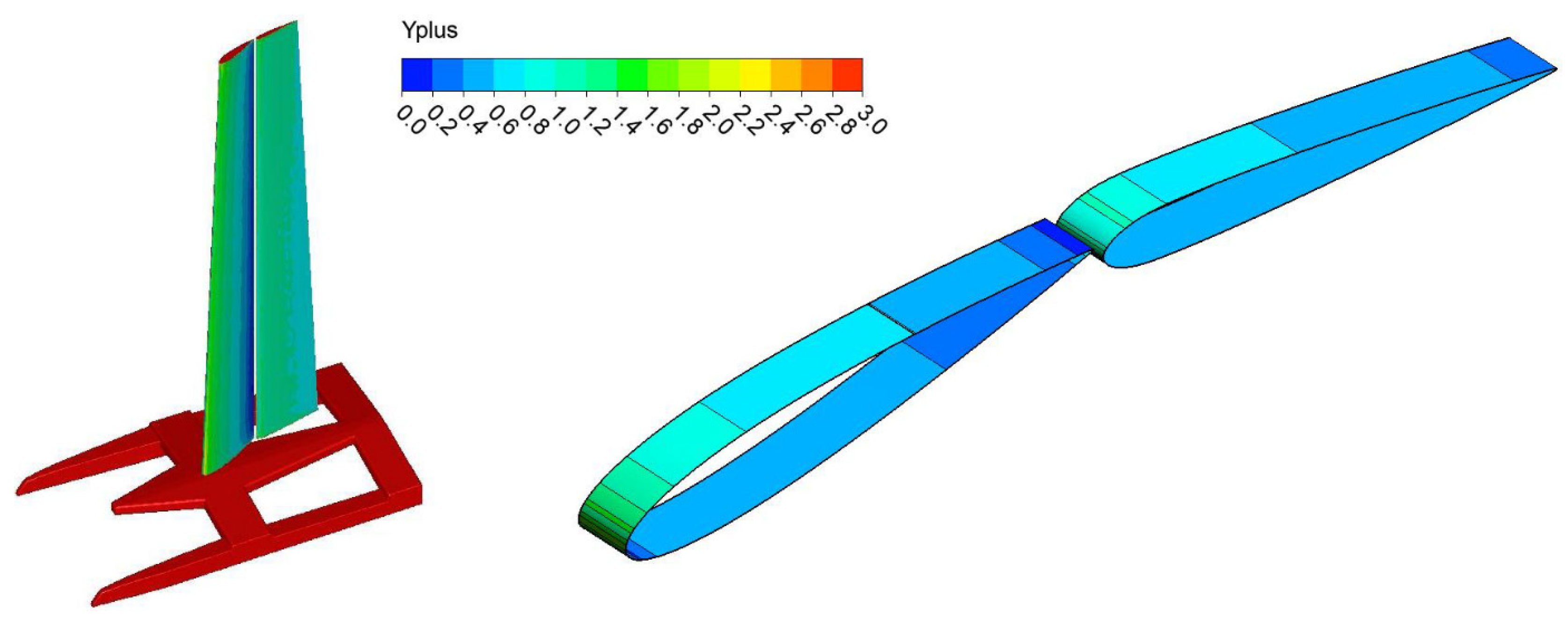
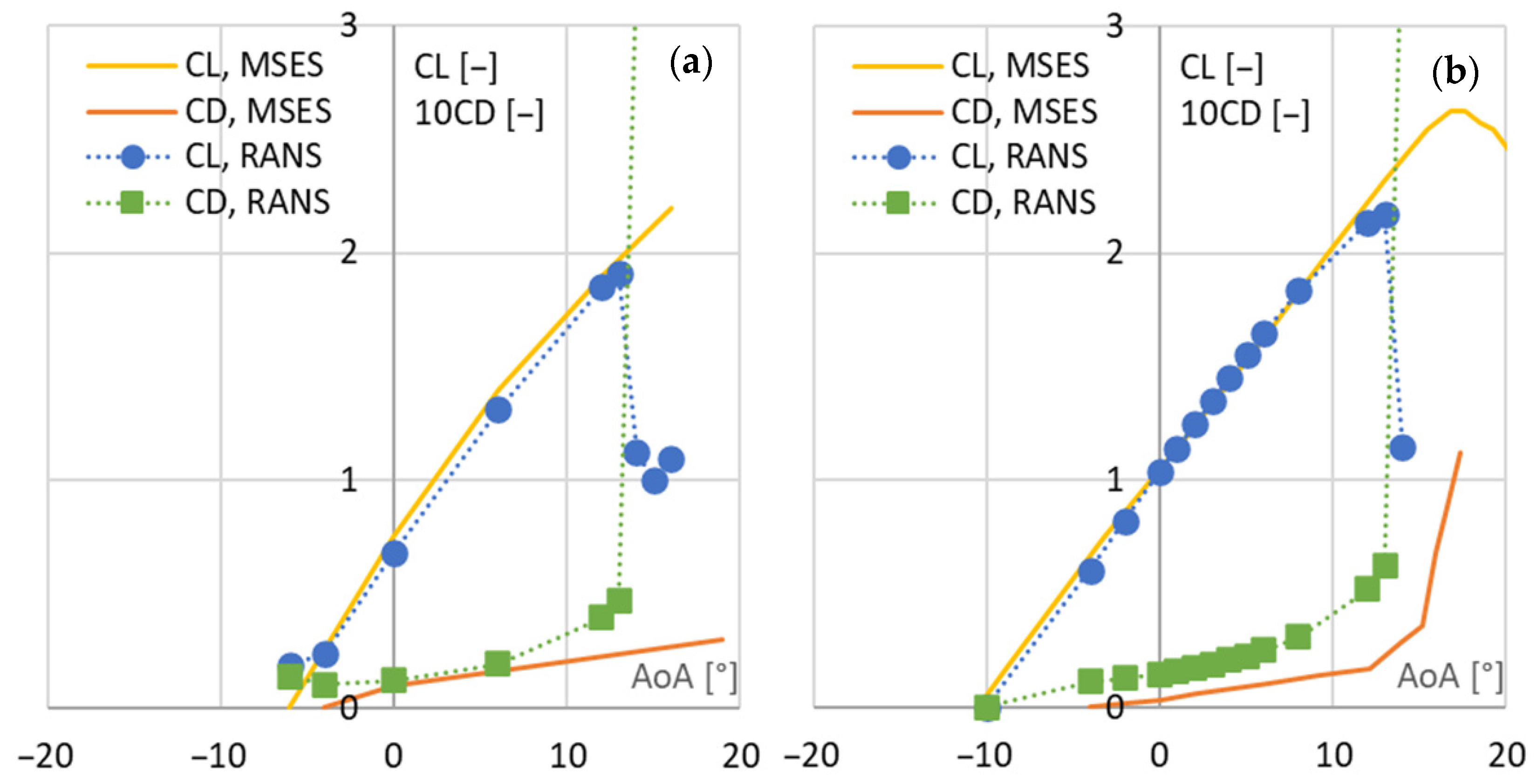
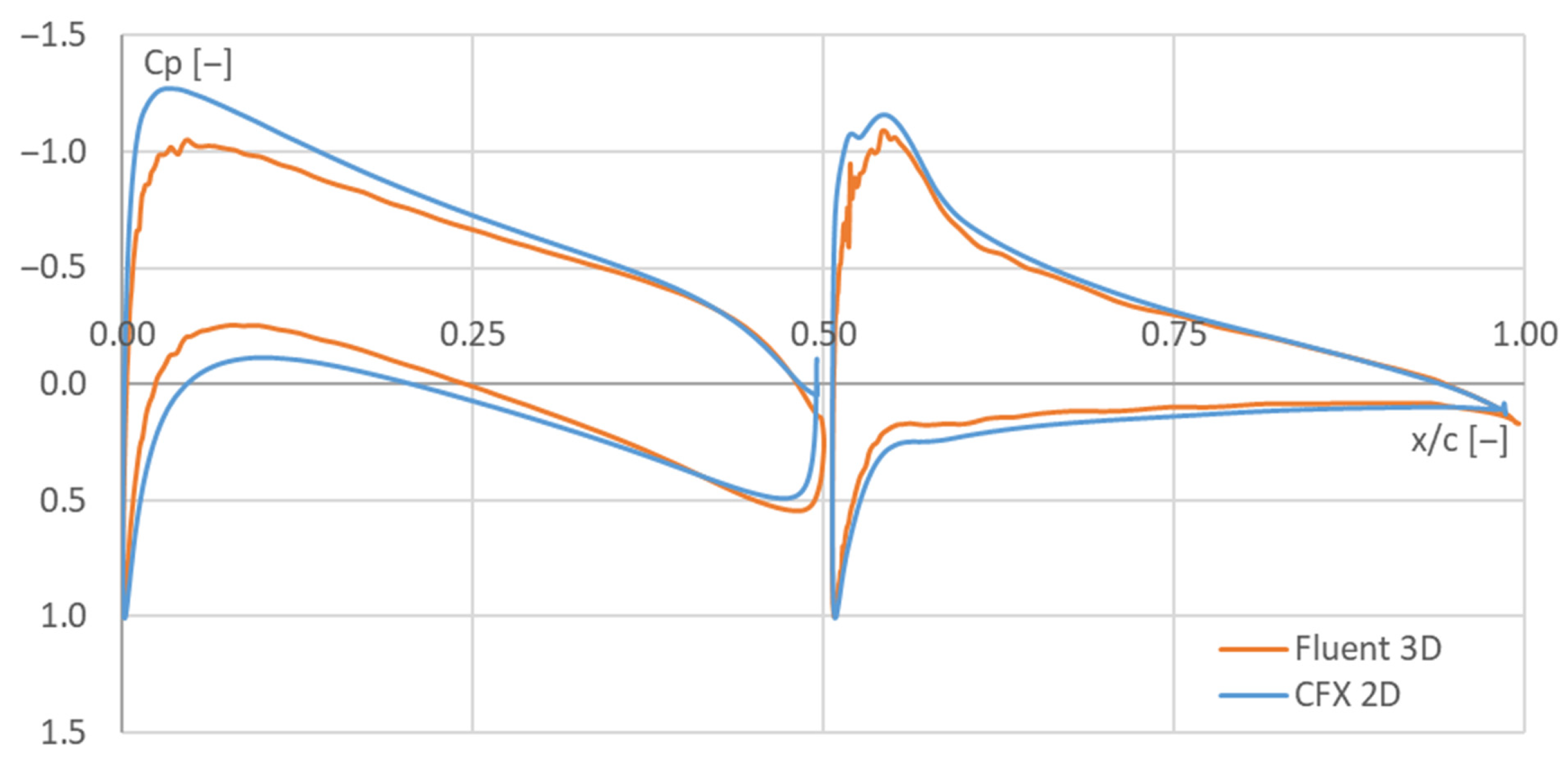
2.3. Model Verification
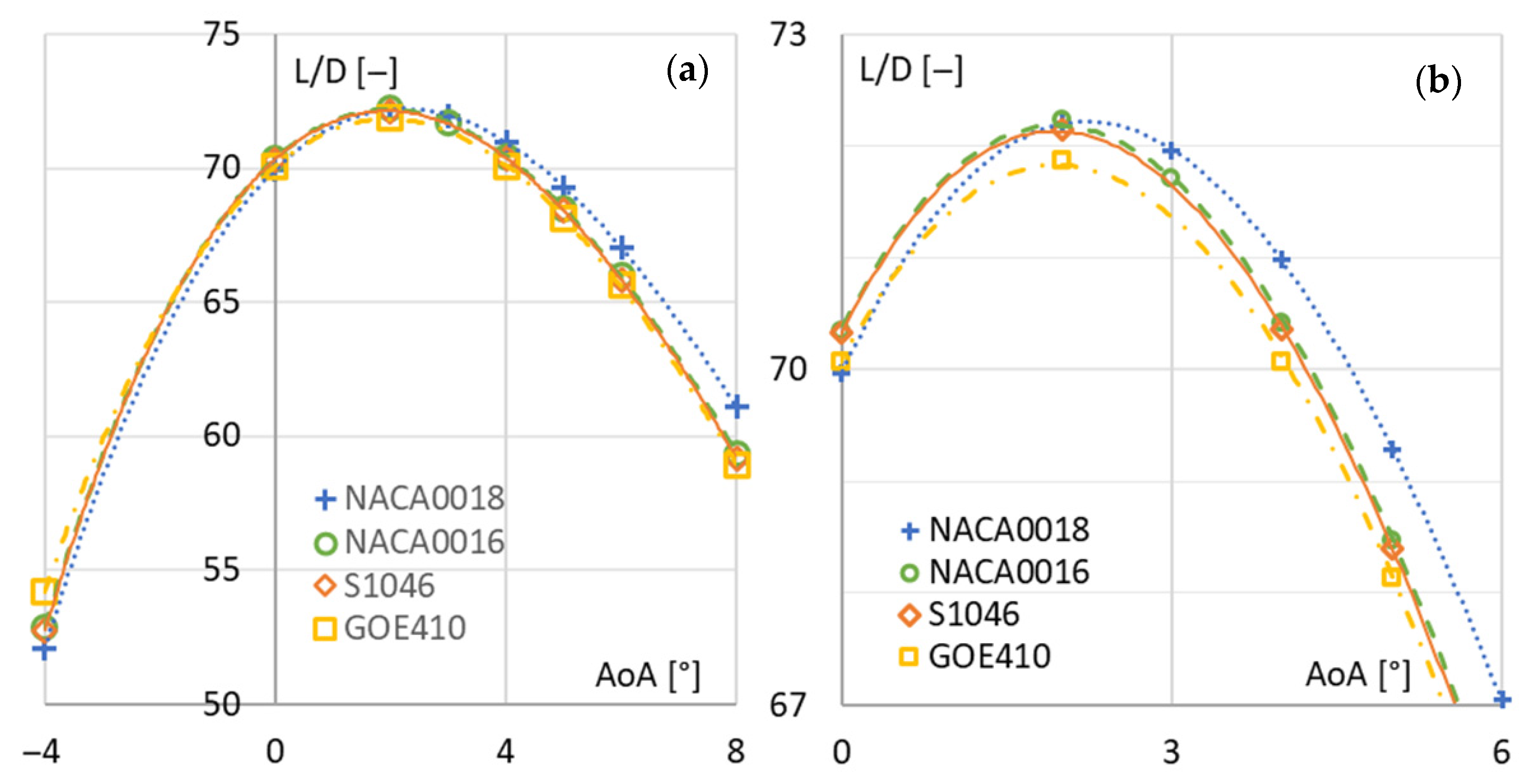
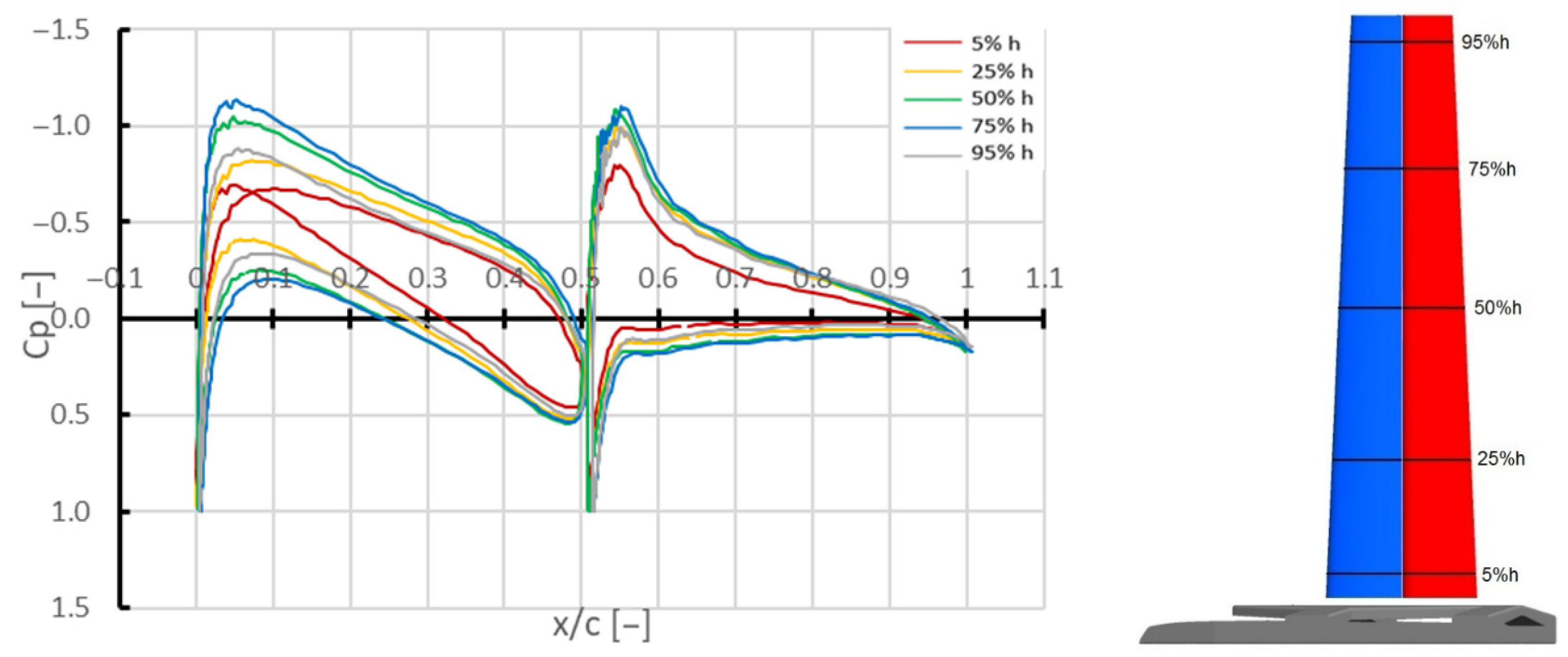
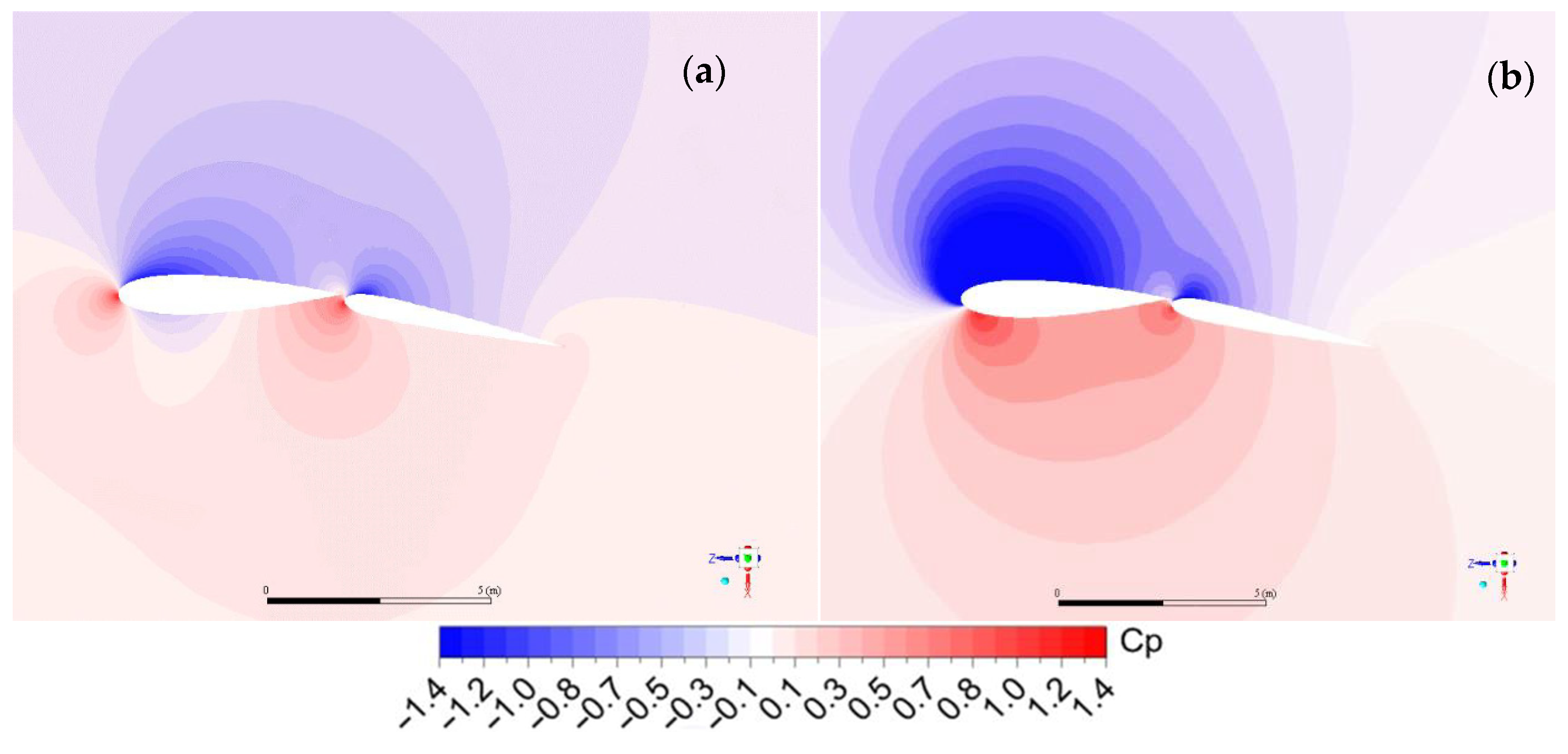
3. Results and Discussion
3.1. Wing Sail Performance—Comparative Study and Analysis
3.2. Flow around a 3D Wing Sail System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- America’s Cup Race Management. America’s Cup “72” Class Rule; ACRM, 2010. Available online: https://web.archive.org/web/20131001060304/http://noticeboard.americascup.com/governing-documents/ac72-class-rule/ (accessed on 1 November 2023).
- Associated Press. Kiwis Reach Record Speed in AC 72-Foot Catamaran; NBC Universal Media, 2013. Available online: https://www.nbcbayarea.com/news/sports/kiwis-reach-record-speed-in-ac-72-foot-catamaran/1949645/ (accessed on 1 November 2023).
- Marchaj, C.A. Sail Performance: Techniques to Maximise Sail Power; Adlard Coles Nautical: London, UK, 2003. [Google Scholar]
- Larsson, L.; Eliasson, R.; Orych, M. Principles of Yacht Design; A&C Black: London, UK, 2014. [Google Scholar]
- Lee, H.J.Y.; Lee, D.-J.; Choi, S. Surrogate model based design optimization of multiple wing sails considering flow interaction effect. Ocean. Eng. 2016, 121, 422–436. [Google Scholar] [CrossRef]
- Oxford Essential Dictionary of the, U.S. Military; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Ariffin, N.I.B.; Hannan, M.A. Wingsail technology as a sustainable alternative to fossil fuel. IOP Conf. Ser. Mater. Sci. Eng. 2020, 788, 012062. [Google Scholar] [CrossRef]
- Silva, M.F.; Friebe, A.; Malheiro, B.; Guedes, P.; Ferreira, P.; Waller, M. Rigid wing sailboats: A state of the art survey. Ocean Eng. 2019, 187, 106150. [Google Scholar] [CrossRef]
- Sail-World Australia. America’s Cup-Oracle Team USA Emerges Victorious. 2013. Available online: https://www.sail-world.com/Australia/Americas-Cup-Oracle-Team-USA-emerges-victorious/-115062 (accessed on 7 January 2024).
- Chapin, V.; Gourdain, N.; Verdin, N.; Fiumara, A.; Senter, J. Aerodynamic study of a two-elements wingsail for high performance multihull yachts. In Proceedings of the 5th High Performance Yacht Design Conference, Auckland, New Zealand, 10–12 March 2015. [Google Scholar]
- Fiumara, A.; Gourdain, N.; Chapin, V.; Senter, J.; Bury, Y. Numerical and experimental analysis of the flow around a two-element wingsail at Reynolds number 0.53 × 106. Int. J. Heat Fluid Flow 2016, 62, 538–551. [Google Scholar] [CrossRef]
- Fiumara, A.; Gourdain, N.; Chapin, V.; Senter, J. Aerodynamic Analysis around a C-Class Catamaran in Gust Conditions using LES and Unsteady RANS Approaches. In Proceedings of the International Conference on Innovation in High Performance Sailing Yachts INNOVSAIL, Lorient, France, 28–30 June 2017. [Google Scholar]
- Fiumara, A.; Gourdain, N.; Chapin, V.; Senter, J. Aerodynamic analysis of a C-class-like catamaran in simplified unsteady wind conditions using LES and URANS modeling. J. Wind. Eng. Ind. Aerodyn. 2018, 180, 262–275. [Google Scholar] [CrossRef]
- Bordogna, G.; Keuning, J.A.; Huijsmans, R.H.M.; Belloli, M. Wind-tunnel experiments on the aerodynamic interaction between two rigid sails used for wind-assisted propulsion. Int. Shipbuild. Prog. 2018, 65, 93–125. [Google Scholar] [CrossRef]
- Khaware, A.; Gupta, V.K.; Punekar, H.; Sharkey, P. Numerical Simulation of Ship Motion and Life Boat Launch using Overset Mesh. In Proceedings of the 11th International Workshop on Ship and Marine Hydrodynamic, Hamburg, Germany, 21–24 September 2019. [Google Scholar]
- ANSYS. ANSYS Fluent 18.2 Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Grassi, C.; Foresta, M.; Lombardi, G.; Katz, J. Study of rigid sail aerodynamics. Int. J. Small Craft Technol. 2013, 155, 13–24. [Google Scholar]
- Foresta, M.; Grassi, C.; Katz, J.; Lombardi, G. Lift and Drag Measurements of Tandem, Symmetric Airfoils. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Fiumara, A.; Gourdain, N.; Chapin, V.; Senter, J. Comparison of wind tunnel and freestream conditions on the numerical predictions of the flow in a two elements wingsail. In Proceedings of the AAAF 50th Applied Aerodynamics Conference (AERO 2015), Toulouse, France, 30 March–1 April 2015. [Google Scholar]
- Collie, S.; Fallow, B.; Hutchins, N.Y.H. Aerodynamic design development of AC72 wings. In Proceedings of the 5th High Performance Yacht Design Conference 2015 (HPYD 5), Auckland, New Zealand, 10–12 March 2015. [Google Scholar]
- Dane, R.; Mathew, N.; McBride, I. Rigid Wing Sail. USA Patent 9937987, 2 November 2016. [Google Scholar]
- Fiumara, A.; Gourdain, N.; Chapin, V.; Senter, J. Aerodynamic analysis of 3D multi-elements wings: An application to wingsails of flying boats. In Proceedings of the Royal Aeronautical Society 2016 Applied Aerodynamic Conference, Bristol, UK, 19–21 July 2016. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Li, C.; Wang, H.; Sun, P. Numerical Investigation of a Two-Element Wingsail for Ship Auxiliary Propulsion. J. Mar. Sci. Eng. 2020, 8, 333. [Google Scholar] [CrossRef]
- Honarmand, M.; Djavareshkian, M.H.; Feshalami, B.F.; Esmaeilifar, E. Numerical Simulation of a Pitching Airfoil Under Dynamic Stall of Low Reynolds Number Flow. J. Aerosp. Technol. Manag. 2019, 11, e4819. [Google Scholar] [CrossRef]
- Götten, F.; Finger, F.; Havermann, M.; Braun, C. A highly automated method for simulating airfoil characteristics at low Reynolds number using a RANS-transition approach. In Proceedings of the Deutscher Luft-und Raumfahrtkongress—DLRK 2019, Darmstadt, Germany, 29 September–1 October 2019. [Google Scholar]
- Esmaeilifar, E.; Djavareshkian, M.H.; Feshalami, B.F.; Esmaeili, A. Hydrodynamic simulation of an oscillating hydrofoil near free surface in critical unsteady parameter. Ocean Eng. 2017, 141, 227–236. [Google Scholar] [CrossRef]
- Ferrari, J.A. Influence of Pitch Axis Location on the Flight Characteristics of a NACA 0012 Airfoil in Dynamic Stall. Master’s Thesis, Rensselaer Polytechnic Institute, Troy, Turkey, 2012. [Google Scholar]
- Murad, J. Defining Turbulent Boundary Conditions. SimScale, 6 November 2020. Available online: https://www.simscale.com/forum/t/defining-turbulent-boundary-conditions/80895 (accessed on 1 November 2023).
- Viola, I.M.; Flay, R.G.J. Sail aerodynamics: Understanding pressure distributions on upwind sails. Exp. Therm. Fluid Sci. 2011, 35, 1497–1504. [Google Scholar] [CrossRef]
- Lipian, M.; Dobrev, I.; Massouh, F.; Jozwik, K. Small wind turbine augmentation: Numerical investigations of shrouded- and twin-rotor wind turbines. Energy 2020, 201, 117588. [Google Scholar] [CrossRef]
- Sobczak, K.; Obidowski, D.; Reorowicz, P.; Marchewka, E. Numerical Investigations of the Savonius Turbine with Deformable Blades. Energies 2020, 13, 3717. [Google Scholar] [CrossRef]
- Bradshaw, P.; Huang, G.P. The Law of the Wall in Turbulent Flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 1995, 451, 165–188. [Google Scholar]
- Drela, M. A User’s Guide to MSES 3.05; MIT Department of Aeronautics and Astronautics: Cambridge, MA, USA, 2007. [Google Scholar]
- Duraisamy, K.; Spalart, P.R.; Rumsey, C.L. Status, Emerging Ideas and Future Directions of Turbulence Modeling Research in Aeronautics; NASA: Hampton, VA, USA, 2017.
- Hoerner, S.F. Fluid-Dynamic Drag; Hoerner Fluid Dynamics: Bakersfield, CA, USA, 1965; p. 455. [Google Scholar]
- Wilkinson, N.; Kensington, A. Battle of the boats—How technology won the America’s Cup. In IPENZ Centenary Lecture Series; IPENZ: New Plymouth, New Zealand, 2014. [Google Scholar]
- Hagemeister, N.; Flay, R.G.J. Velocity Prediction of Wing-Sailed Hydrofoiling Catamarans. J. Sail. Technol. 2019, 4, 66–83. [Google Scholar] [CrossRef]
- Sailonline NavSim, A.B. Archived Races. 31 May 2021. Available online: http://www.sailonline.org/races/all/archive/ (accessed on 1 November 2023).
- Blakeley, A.W.; Flay, R.; Richards, P.J. Design and Optimisation of Multi-Element Wing Sails for Multihull Yachts. In Proceedings of the 18th Australasian Fluid Mechanics Conference, Launceston, Australia, 3–7 December 2012. [Google Scholar]
- Blakeley, A.W.; Flay, R.; Furukawa, H.; Richards, P.J. Evaluation of Multi-Element Wing Sail Aerodynamics from Two-Dimensional Wind Tunnel Investigations. In Proceedings of the 5th High Performance Yacht Design Conference, Auckland, New Zealand, 10–12 March 2015. [Google Scholar]









| 2D | 3D | |
|---|---|---|
| Solver | ANSYS CFX 18.2 | ANSYS Fluent 18.2 |
| Tested aerofoils—mainsail | NACA 0016, NACA 0018, GOE 410, S1046 | NACA 0018 |
| Tested aerofoils—flap | Custom (max. thickness of 0.1 c at 0.15 c from the leading edge) | |
| Total chord length | 1 m | 8.6 m |
| Reynolds number Re | Approx. 3 × 106 | Approx. 7 × 106–25 × 106 |
| Angle of attack α | −5–10° | −6–9° |
| Flap deflection angle δ | 0°, 4°, 8°, 12°, 16° | 12° |
| Dynamic viscosity µ | 1.831 × 10−5 kg∙m−1∙s−1 |
| Density ρ | 1.185 kg∙m−3 |
| Molar Mass | 28.96 kg∙mol−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawecki, B.; Kulak, M.; Lipian, M. Wing Sails: Numerical Analysis of High-Performance Propulsion Systems for a Racing Yacht. Energies 2024, 17, 549. https://doi.org/10.3390/en17030549
Kawecki B, Kulak M, Lipian M. Wing Sails: Numerical Analysis of High-Performance Propulsion Systems for a Racing Yacht. Energies. 2024; 17(3):549. https://doi.org/10.3390/en17030549
Chicago/Turabian StyleKawecki, Bartosz, Michal Kulak, and Michal Lipian. 2024. "Wing Sails: Numerical Analysis of High-Performance Propulsion Systems for a Racing Yacht" Energies 17, no. 3: 549. https://doi.org/10.3390/en17030549
APA StyleKawecki, B., Kulak, M., & Lipian, M. (2024). Wing Sails: Numerical Analysis of High-Performance Propulsion Systems for a Racing Yacht. Energies, 17(3), 549. https://doi.org/10.3390/en17030549








