Research on Voltage Compensation Methods and Optimization Algorithm for Insulated Core Transformer High-Voltage Power Supply

Abstract

The insulated core transformer (ICT) power supply is widely employed in electron beam accelerators (EBAs) due to its high power, heightened efficiency, and stable operation. However, the segmented-core structure of the ICT power supply increases magnetic leakage, which leads to it adversely affecting the consistency of the output voltages in the rectifier stages. Currently, numerous studies focus on stage voltage compensation, including turns compensation, capacitor compensation, dummy primary winding compensation, and full-parameter compensation. This paper presents a unified simulation model and an improved gradient-based genetic algorithm, which can also optimize the parameters of the four compensation methods. Based on this, the performance of the power supply using the four compensation methods under different ICT energy levels and power supply requirements is studied, and the selection suggestions are given. This work fills the gap in the performance comparison and application research of various compensation methods.

1. Introduction

Electron beams are widely applied in material modification [1], environmental protections [2,3], electron microscopy [4,5], and so on [6]. The ICT power supply, renowned for its high efficiency (>85%), robust power output, and reliability, has emerged as a preferred option for supplying energy to the electron beam [7,8].

The general structure of a three-phase ICT (insulated core transformer), as depicted in Figure 1, comprises two yokes, three magnetic core columns, one set of primary wingdings (p), and multiple sets of secondary windings (1#, 2# … s# ... N#) [9]. With dummy primary winding (DPW) compensation, a set of dummy primary wingdings (d) of the same size as the primary wingdings are added to the top of the core. The primary cores and primary wingdings are situated in the lowest layer. The secondary cores, secondary wingdings, and the rectifier circuits comprise the rectifier disk. Lastly, the N stages are stacked from bottom to top. By connecting the DC outputs of the stages in series, the power supply can achieve a high output voltage, which is then used to supply power to the electron accelerator. Compared to conventional transformers, the ICT exhibits a significant distinction: its magnetic cores are segmented by insulating sheets with a high dielectric capability. This segmentation leads to a considerable amount of magnetic flux leakage, resulting in two unfavorable consequences: (1) a reduction in the induced voltage of the secondary windings; and (2) an increase in leakage inductance and output impedance [10]. The voltage doubling rectifier circuit converts the three-phase AC output from the secondary windings into DC. Due to the withstand voltage limitation of the rectifier circuit and insulation materials [11], the stage output voltage must not exceed the rated value. Significant voltage fluctuations between stages can result in underutilization of the rectifier disks, leading to a decrease in the overall output voltage.

To reduce the stage output voltage nonuniformity, several methods have been suggested by researchers. Van de Graaff proposes the I-shaped magnetic core [11,12] to reduce magnetic flux leakage. However, this approach entails complex manufacturing processes and high costs [13]. The turns compensation method increases the turns of the secondary windings according to the magnetic flux leakage distribution of each stage [13]. The capacitor compensation method [14,15] employs parallel capacitors across the secondary windings, and the additional excitation flux generated by the capacitive current is used to compensate the flux leakage. However, when the number of ICT layers is large, these two methods are difficult to ensure the high stage voltage consistency from load to full load. The full-parameter compensation method, proposed by the Huazhong University of Science and Technology (HUST) [16], integrates turns compensation and capacitor compensation to achieve a high voltage consistency. Additionally, the DPW compensation adds a set of dummy primary wingdings to induce additional flux to compensate for the magnetic leakage.

With the exception of the I-shaped magnetic core method, the other four compensation methods are commonly utilized in engineering due to their ease of fabrication using regular cores and a simpler adjustment of winding turns or compensation capacitance values. However, there is a lack of analysis and comparison of their performance and application range. On the other hand, for the parameter optimization of these compensation methods, researchers have proposed the artificial iterative method (IM) [16], genetic algorithm (GA) [17], particle swarm optimization (PSO) [8,18], and other methods. However, these methods are difficult to satisfy the optimization of all compensation methods simultaneously. Therefore, this paper innovatively proposes a unified calculation model and an improved gradient-based genetic algorithm, which can be applied to the four compensation methods. At the same time, the calculation of the number of turns or the compensation capacitance value for the traditional turns compensation, traditional capacitor compensation, and dummy primary compensation methods is improved from a formula to an iterative algorithm optimization. Furthermore, based on the unified simulation model and algorithm, the performance of different compensation methods for different voltage levels of ICT applications was compared. Finally, through comparison, this paper gives the use scenarios and selection recommendations of different compensation methods, which fills the research gap and contributes to the design optimization of an ICT.

2. Compensation Methods

The following is a brief review of the four compensation methods.

2.1. Turns Compensation Method

The traditional turns compensation method is based on the law that the induced voltage of the secondary winding is proportional to the number of turns. If the mutual inductances between the primary winding and each secondary winding M_ps are equal, each secondary winding can output the same no-load voltage $U_s^n$. According to this principle, secondary winding turns n_s can be calculated by (1) [16].

$$n_s=\frac{U_s^n}{U_p^n}\frac{{L_p}^{\left(1\right)}}{{M_{ps}}^{\left(1\right)}}{n}_{p}k$$

(1)

$U_p^n$ is the input voltage of the primary winding under no-load conditions, whose unit is V. The superscript “n” stands for the no-load case. M_ps⁽¹⁾ = M_ps/(n_s*n_p) is the single-turn mutual inductance [19] from the primary winding to the s# secondary winding, whose units are H; L_p⁽¹⁾ = L_p/n_p² is the single-turn self-inductance of the primary winding, whose units are H. The mutual inductance matrix of single-turn wingdings on the same phase M⁽¹⁾ can fully describe the terminal voltage–current properties of the transformer. Its value can be obtained via finite-element method (FEM) simulation or be measured [20]. The k is the unified compensation coefficient and used to compensate the voltage drop of rectifier diodes, and its value is 1.1~1.4.

The traditional turns compensation method ensures the second winding output voltages under no-load conditions $U_s^n$ are equal. However, when the power supply is loaded, the voltages of the secondary windings located far from the primary winding decrease to a greater extent. Therefore, it is difficult to keep the output voltages consistent [16]. Different from this, the improved turns compensation method (ITC) takes the n_s calculated by Equation (1) as the initial value, while the voltage nonuniformity at no-load and full-load conditions and the load adjustment rate are taken as the optimization objectives, and finally, the optimal secondary winding turns are solved by the optimization algorithm. This method can improve the load-carrying capacity of the power supply.

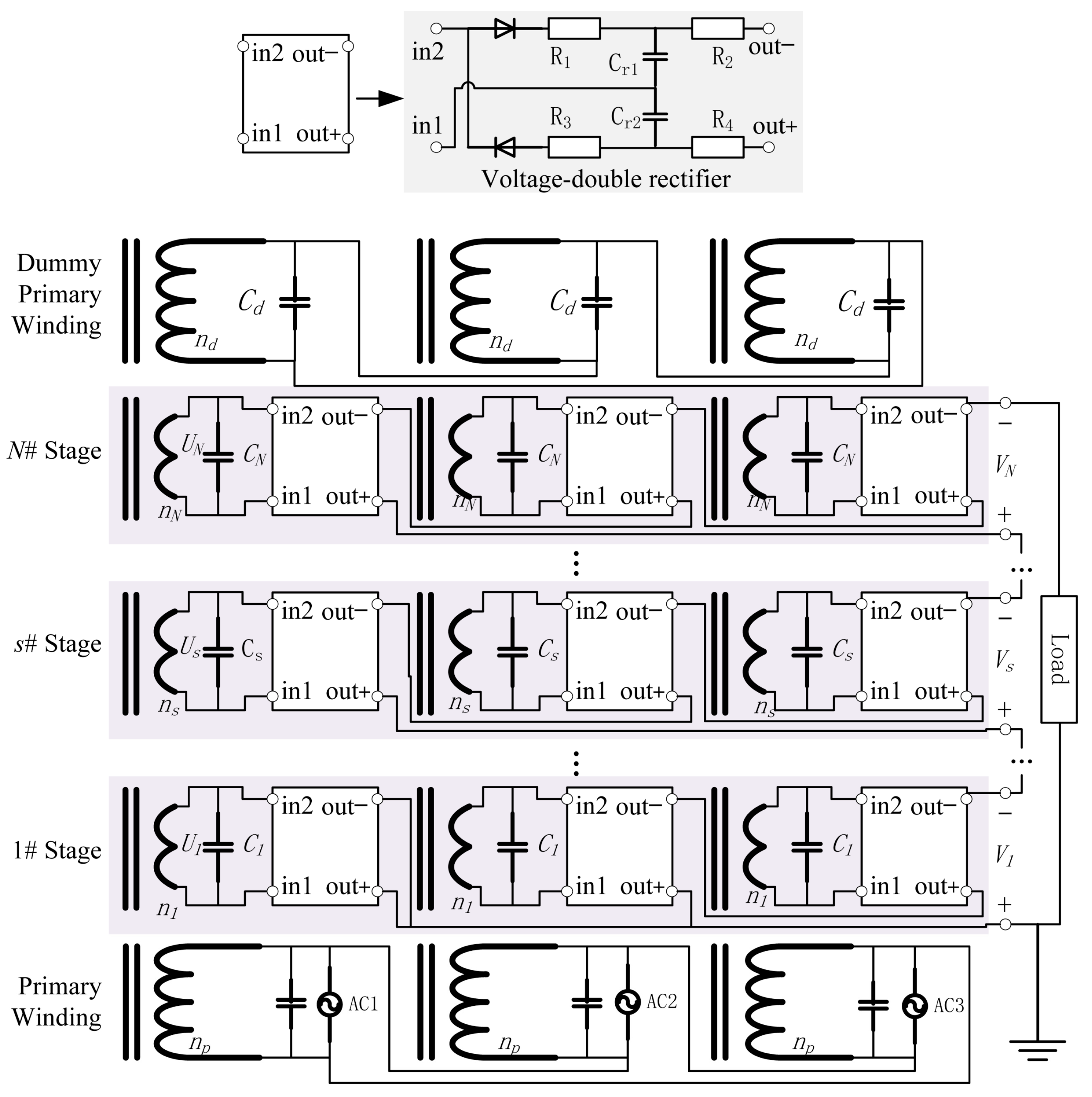
2.2. Dummy Primary Winding Compensation Method (DPWC)

The dummy primary winding (DPW) technique is employed in the accelerator from the manufacturer Wosik. The DWP is connected in parallel with a resonant capacitor C_d. With an aim to curtail expenses, the DPWs are usually exactly the same as the primary windings. In order to generate the same magnetic flux as the real primary winding, the voltage $U_d^n$ of the DWP at no load is designed to be equal to the input voltage $U_p^n$ of the primary winding. The current of the DWP also approximates that of the primary winding. Hence, neglecting the winding’s resistance, the value of C_d should be Equation (2), whose unit is F.

$$C_d=1/({\omega }^2{n}_p^2({L^{(1)}}_p+{M^{(1)}}_{pd}))$$

(2)

ω is the angular frequency of 100π rad/s.

In this case, the magnetic flux of the s# secondary winding is affected by both the primary winding and the DWP, so its turns n_s calculation should be Equation (3).

$$n_s=\frac{U_s}{U_p}\frac{{L_p}^{\left(1\right)}+{M_{pd}}^{\left(1\right)}}{{M_{ps}}^{\left(1\right)}+{M_{ds}}^{\left(1\right)}}{n}_{p}k$$

(3)

Just like the traditional turns compensation, when the power supply is loaded, the output voltages of the secondary windings in the middle section will decrease more. Similarly, n_s (s = 1…N) can be set as the variables for optimization in the DWPC, and the result of Equation (3) can be used as the initial value for optimization.

2.3. Capacitor Compensation Method

The traditional capacitor compensation method was applied in the Cross ICT of KSI [21] and the planar ICT [13] of the Chinese Academy of Sciences. The capacitive current of the compensation capacitor induces magnetic flux to compensate for the magnetic flux drop by the insulation gap. Based on this compensation principle, C_s is (4) [21], whose unit is F.

$$C_s=l_g/\left({n_s}^2{\omega }^2{\mu }_0{S}_{core}\right)$$

(4)

l_g is the height of the insulation gap, whose unit is m. S_core is the cross-sectional area of the magnetic core, whose unit is m². μ₀ is the permeability of the insulation sheet. The traditional capacitor compensation also experiences significant fluctuations in stage voltage uniformity from a no-load to a full-load condition [16]. Recognizing the ease of adjusting capacitance C_s by combining capacitors with varying parameter specifications, an improved capacitor compensation method (ICC) is introduced. C_s (s = 1…N) are set as the optimization variables, achieving optimal voltage uniformity through an optimization algorithm.

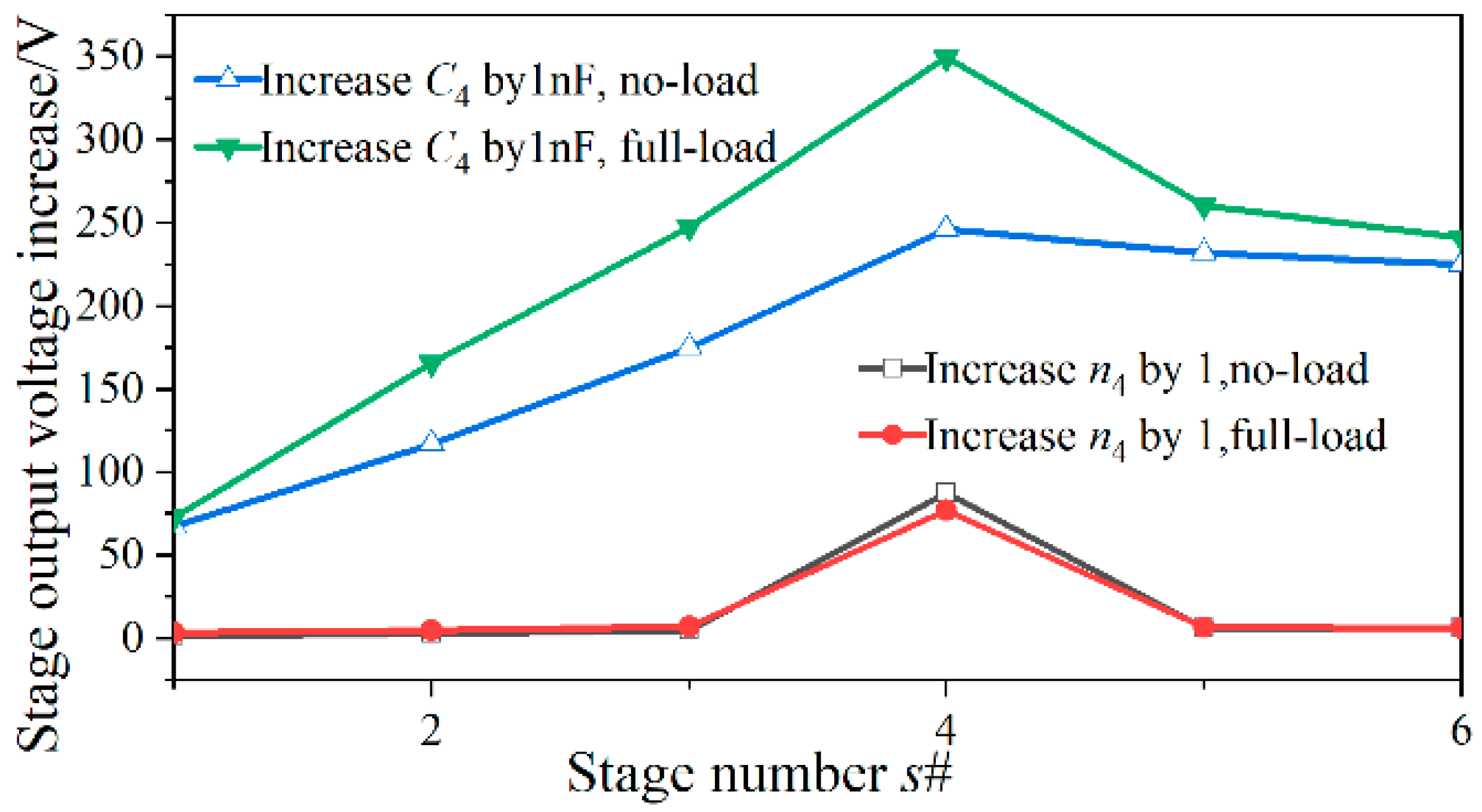
2.4. Full-Parameter Compensation Method

The full-parameter compensation method (FPC) [16] combines both turns compensation and capacitor compensation methods. In this approach, n_s and C_s are optimized so that each stage can achieve a similar output voltage and load regulation. For instance, in a study conducted by [17], a genetic algorithm was utilized to simultaneously optimize n_s and C_s, resulting in significant improvement in the performance of a six-layer three-phase ICT. Figure 2 displays a photograph of the rectifier stage in the HUST-ICT [17].

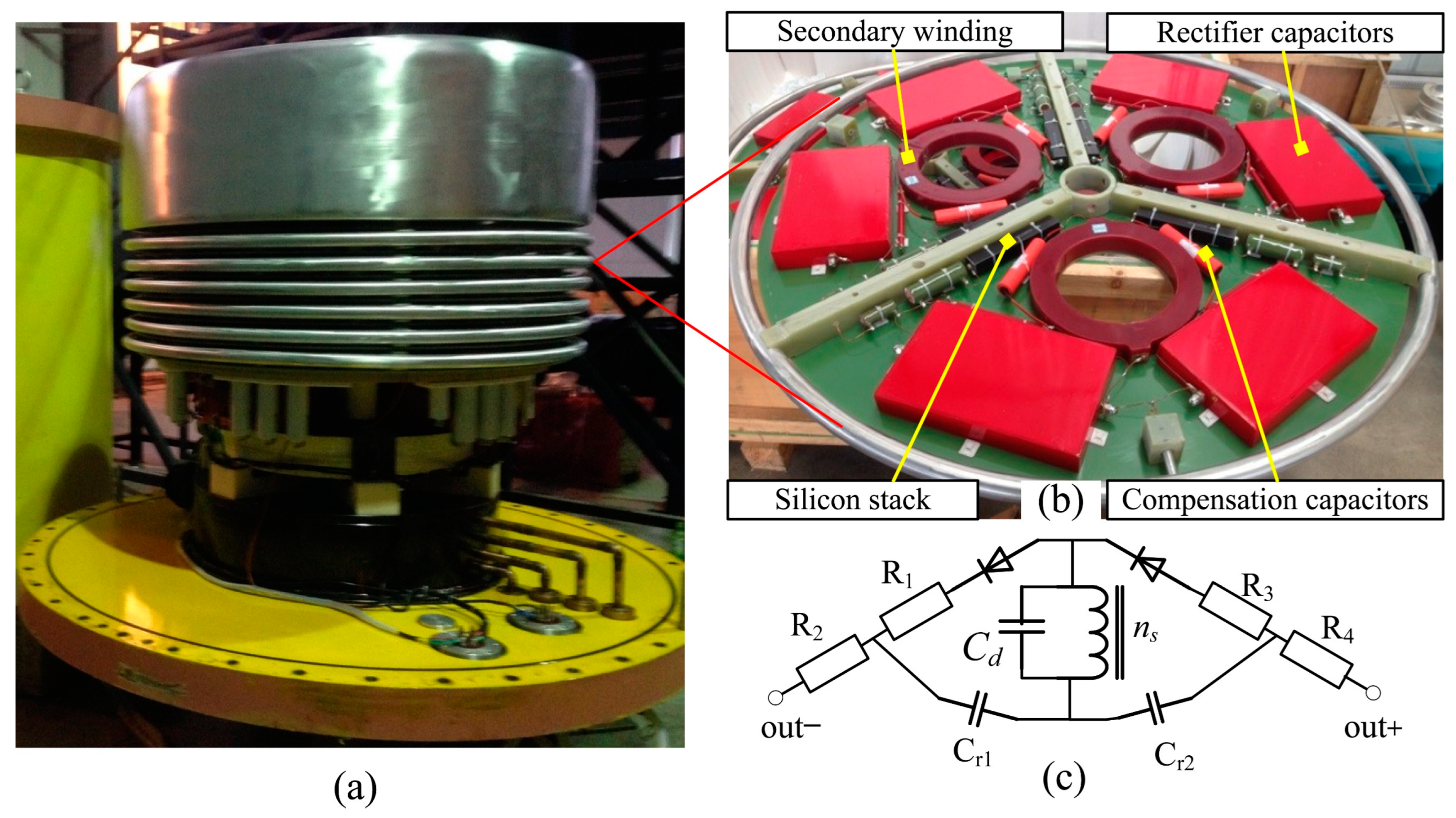
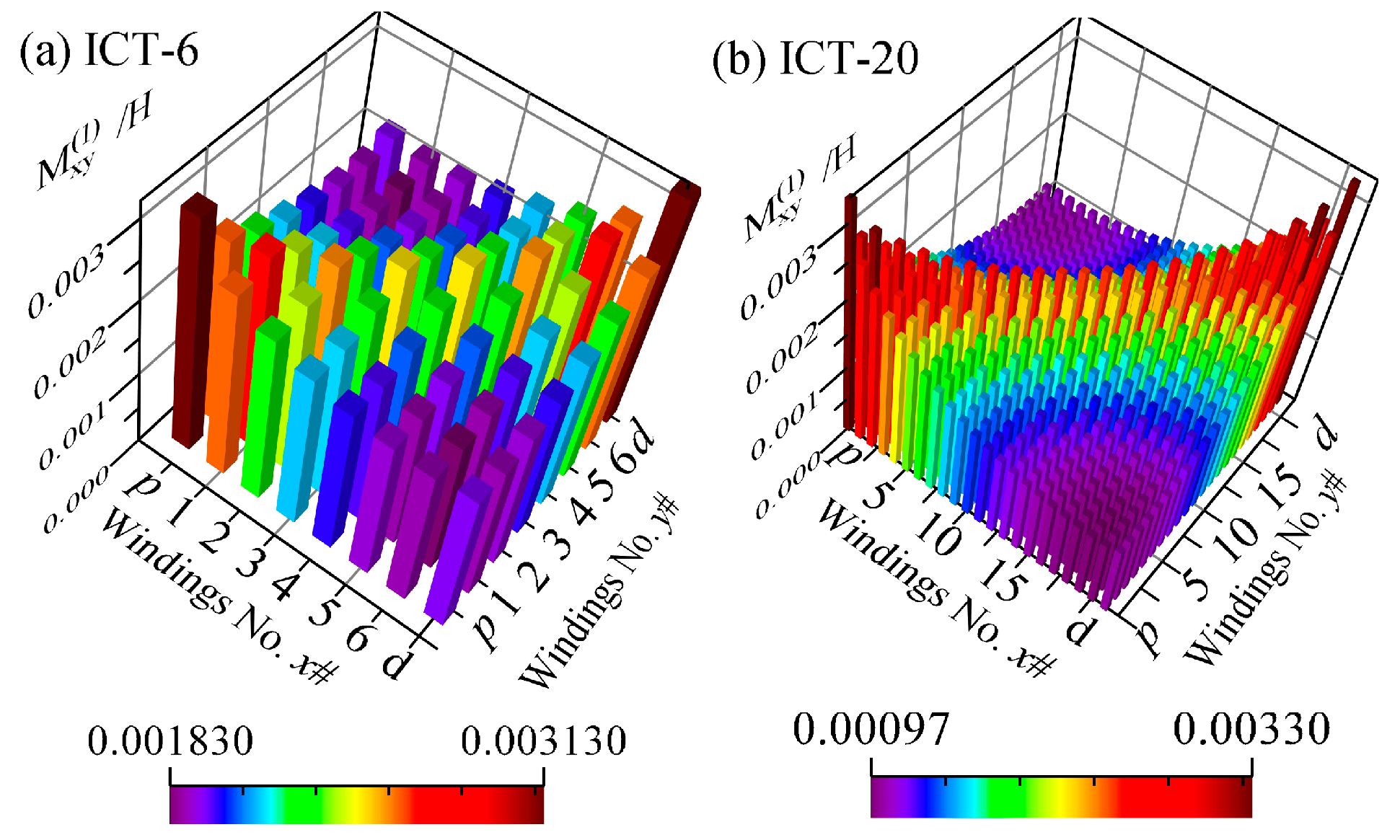
3. Unified Circuit Model and Simulation Method

To facilitate the implementation of the optimization algorithm for the four compensation methods, a unified circuit simulation model (Figure 3) is presented. This model serves as a comprehensive circuit diagram that describes all four compensation methods, including a mutual inductance matrix, compensation capacitors, and voltage multiplier rectifier circuits [22]. As depicted in

Table 1. The variables and constraints of different compensation methods.

	Constraints	Variables
ITC	nd = 0, Cd = 0, Cs = 0	ns
DPWC	nd = np, Cd is from Equation (2), Cs = 0	ns
ICC	nd = 0, Cd = 0, ns is from Equation (1)	Cs
FPC	nd = 0, Cd = 0	Cs, ns

, by setting different variables and constraints, the performance of the power supply can be calculated under various compensation parameters for different compensation methods. Here, n_d = 0 represents the absence of the DWP, while C_s = 0 indicates no parallel compensation capacitors. Setting these parameters to zero does not affect the model or equation-solving process.

At no load, after the power supply reaches a steady state, the input current of the rectifier tends to zero and the current waveform of the secondary wingdings becomes sinusoidal. In such cases, the output voltages and currents of the windings satisfy the transformer Equation (5).

$$U=j\omega MI+RI\approx j\omega MI$$

(5)

in which $U={\left[{\dot{U}}_p,{\dot{U}}_1\cdots {\dot{U}}_N,{\dot{U}}_d\right]}^{\mathrm{T}}$, $I={\left[{\dot{I}}_p,{\dot{I}}_1\cdots {\dot{I}}_N,{\dot{I}}_d\right]}^{\mathrm{T}}$ are the column vector of the voltages and currents of the wingdings, and R is the resistance matrix of the windings, which can be neglected because the resistance of the windings is much smaller than the impedance of the capacitors.

When the secondary windings and DWP are connected in parallel with the compensation capacitors, the voltages and currents of these windings satisfy the Ohm’s law:

$${\dot{U}}_x={\dot{I}}_x/(j\omega C_x) x = 1\dots N, d$$

(6)

By combining Equations (5) and (6), we can obtain $U_s^n$ and $I_s^n$. When there are no compensation capacitors, $I_s^n$ = 0. Then, the stage output voltage $V_s^n$ after the rectifier is calculated by the formula $V_s^n=2\sqrt{2}{U}_s^n$.

Under the full-load condition, the current waveform becomes complex due to the nonlinearity of the rectifier circuit. In such cases, the voltages and currents can be calculated by a numerical method such as MATLAB/Simulink software 2016b [23]. This simulation methodology has undergone experimental validation, demonstrating that the maximum difference between the simulation results and actual experimental data in HUST-ICT is below 0.4%, with a root-mean-square error of 0.14% [16].

The $V_s^n$ and $V_s^l$ are transformed into normalized values by ${\eta }_s=V_s/V_{\max }$. V_max = max ($V_1^n$, $V_2^n$…$V_N^n$, $V_1^l$, $V_2^l$…$V_N^l$). Then, the voltage nonuniformity δⁿ and δ^l are calculated by Equation (7).

$$\delta =\frac{1}{N}{\displaystyle \sum _{s=1}^N\frac{\left(V_{\max }-V_s\right)}{V_{\max }}}=1-\frac{1}{N}{\displaystyle \sum _{s=1}^N{\eta }_s}$$

(7)

Load regulation S_L indicates the alteration in the output voltage from no load to full load, whilst the input voltage of the primary winding remains constant. This value is related to the short-circuit impedance of the transformer. The smaller the value, the greater the output current and the stronger the load-carrying capacity. It is calculated by (8).

$$S_L=({\displaystyle \sum _{s=1}^N{V}_s^n}-{\displaystyle \sum _{s=1}^N{V}_s^l})/{\displaystyle \sum _{s=1}^N{V}_s^n}$$

(8)

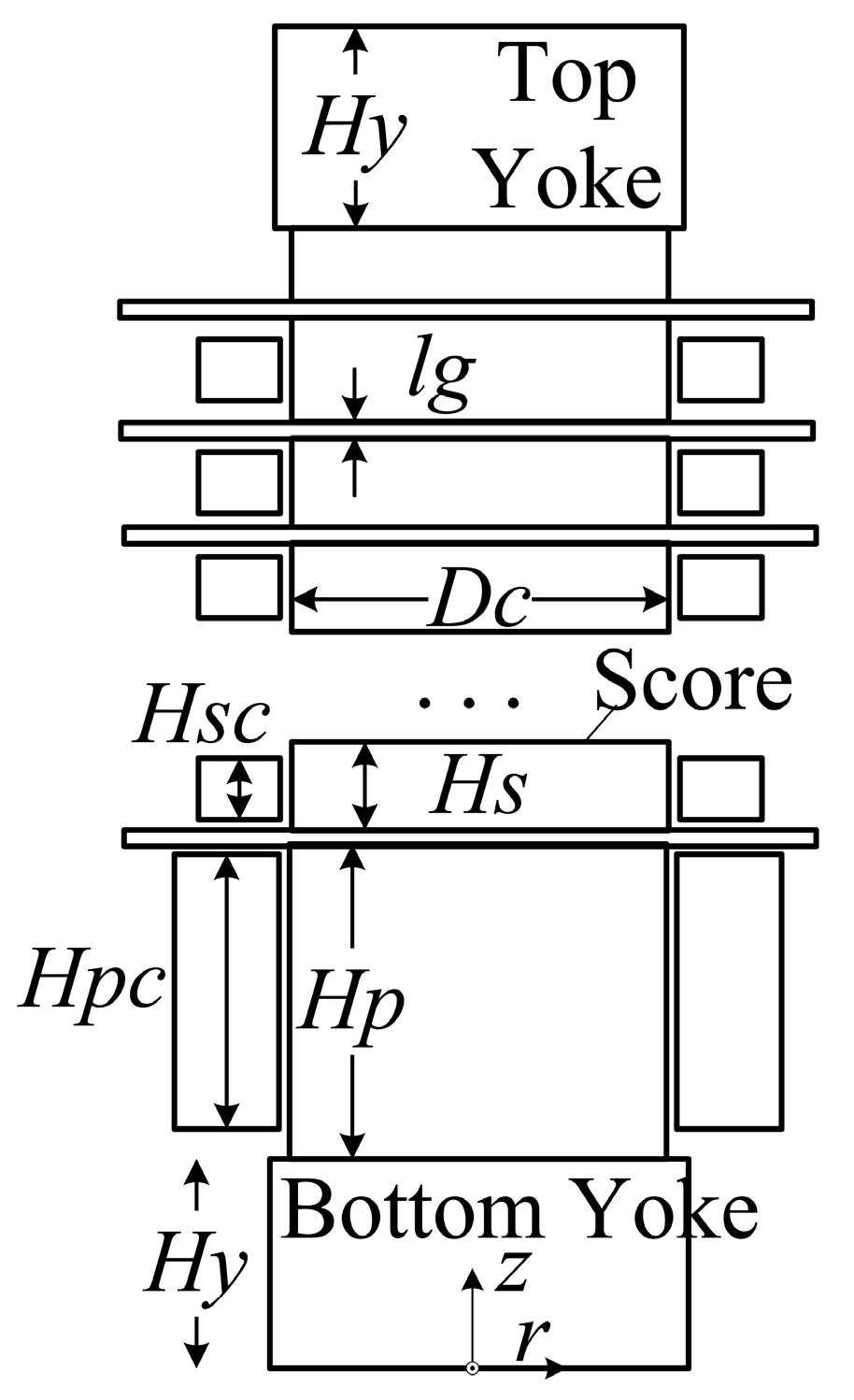
4. Parameters of ICT for Two Energy Levels

ICT high-voltage power supplies are commonly employed in accelerators with the highest beam energies below or around 1000 keV [6]. This article aims to compare the performances of four compensation methods and different optimization algorithms on ICTs with different voltage levels. Taking into account the differences in stage number N, magnetic flux leakage distribution, and application fields of ICTs with different output voltages, this article focuses on two specific examples: three-phase ICTs with output voltages of 350 kV and 1100 kV. Both are designed with a rated stage output voltage of 60 kV. The primary structural dimensions of these ICTs are presented in

Table 2. The dimensional parameters of two typical ICT structures.

	ICT-6	ICT-20
N	6	20
Dc/mm	178	250
Score/mm2	2.3 × 104	4.9 × 104
np, nd	92	32
lg/mm	2	2
Hs/mm	45.6	38
Hp/mm	125	170
Hsc/mm	31.5	27.5
Hpc/mm	155	190
Yoke diameter/mm	660	960
Hy/mm	100	120

and Figure 4, while the main parameters of ICT-6 remain the same as the HUST-IC [16].

Based on the structural dimensions, we established four FEM simulation models to calculate the mutual inductance matrix of single-turn wingdings M⁽¹⁾ for ICT-6, ICT-6 with DPW, ICT-20, and ICT-20 with DPW.

The M⁽¹⁾ 3D bar charts of ICT-6 with DPW and ICT-20 with DPW are shown in Figure 5a and Figure 5b, respectively, both of which exhibit saddle-shaped curves. In Figure 5b, the maximum value of M⁽¹⁾ is the self-inductance coefficient of the primary wingding or DWP, which is 0.0033 H. And the minimum value is M⁽¹⁾_dp, which is 9.6 × 10⁻⁴ H. In fact, the simulation of M⁽¹⁾ without DPW is basically the same as the ICT with DPW, as shown in Figure 5, exhibiting only a marginal difference of 1 × 10⁻⁵ due to slightly shorter magnetic circuits. The error between the mutual inductance matrix obtained via the FEM simulation and the actual prototype test results is less than 2.5% [16]. Therefore, the FEM result can be fully utilized to study and compare the effects of various compensation methods.

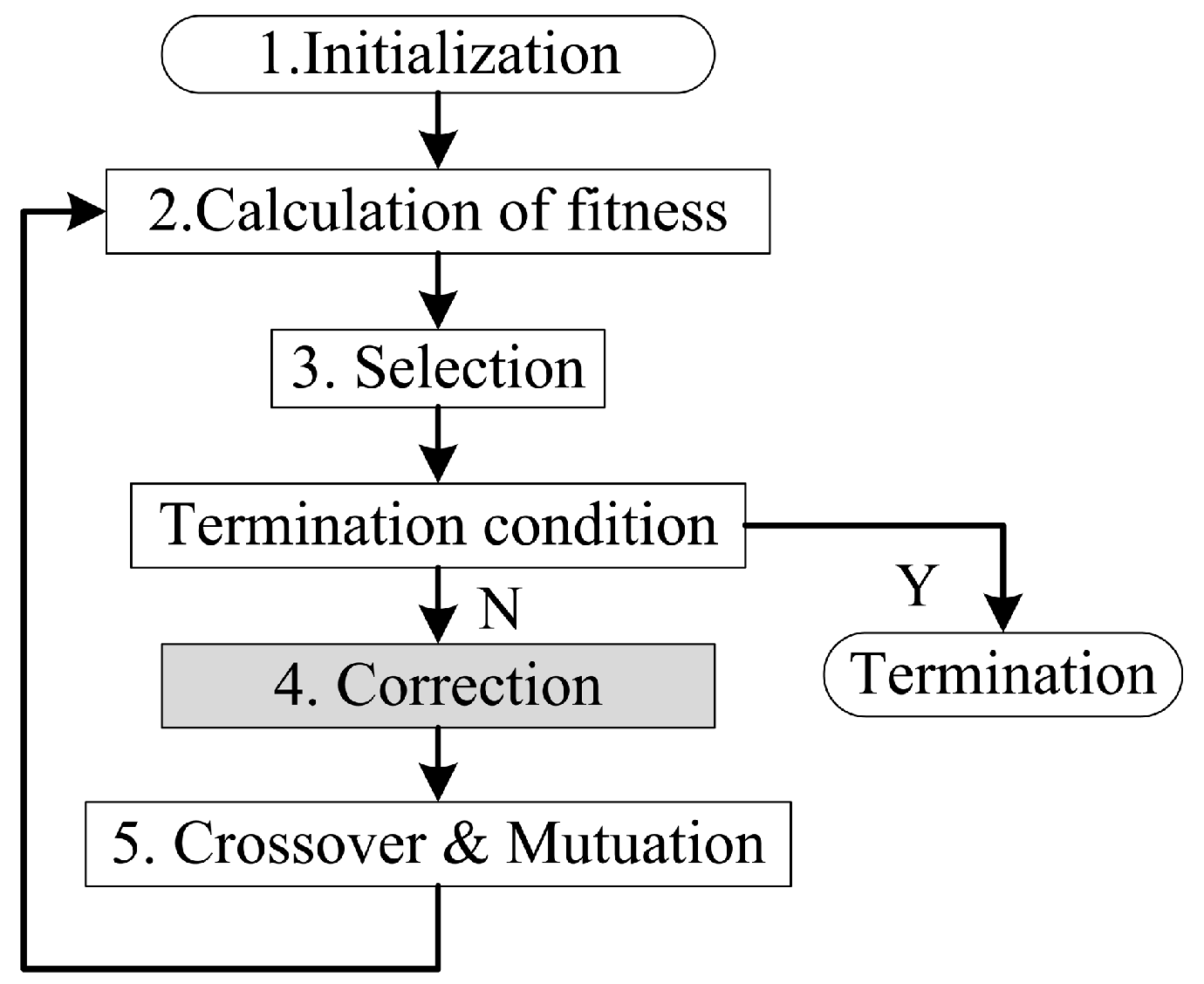
5. Optimization Algorithm

The essence of the compensation optimization is to find a set of compensation parameters (n_s or C_s) that can produce the optimal value for δⁿ, δ^l, and S_L. This is a classic nonlinear, multi-variable, multi-objective optimization issue. For ICTs with more stages, there are more compensation parameters. Optimization algorithms such as GA and PSO can suffer from slow convergence and optimization difficulties, and it may prematurely converge to a local optimal solution [24].

Using stage 4# of ICT-6 as a case study, the relationship between the compensation parameters and output voltage is investigated, as shown in Figure 6. It can be observed that an increase in C₄ leads to an increase in all stage output voltages. This is because the excitation current generated by C₄ also passes through the other secondary windings. On the other hand, an increase in n₄ only affects V₄, exhibiting an ideal positive correlation. Therefore, using the IM method to optimize the turns parameters will have a faster convergence, higher efficiency, and more precise optimization results. The compensation parameter changes in the other stages also have a similar compensation effect.

Based on these characteristics, an improved gradient-based genetic algorithm (IGGA) was proposed to optimize the compensation parameters, which combines the IM and canonical GA. It improves the search efficiency and convergence speed of the algorithm by analyzing and utilizing the gradient information to guide the evolutionary direction of the GA [25]. At the same time, after adding the gradient correction disturbance, the global convergence is improved [26]. Its calculation flow is shown in Figure 7, and its steps are briefly introduced as follows.

Step 1: A set of candidate solutions, {n₁, n₂, n₃, … n_N, C₁, C₂, …, C_N}, is created during initialization in the same way as in ref. [17].

Step 2: Calculation of fitness, which is constructed with δⁿ, δ^l, S_L.

$$f=W_{\delta }\times \max ({\delta }_n,{\delta }_l)+W_{SL}{S}_L$$

(9)

W_δ is the weight coefficient of the voltage nonuniformity and its value is set as 1. W_SL is the weight coefficient of S_L and its value is set as 0.1.

Step 3: Reserve the excellent candidate solutions and discard others in the selection.

Step 4: A set of fresh solutions (${C_s}^{\prime }$, ${n_s}^{\prime }$) are generated by correcting the solution in accordance with Equations (10) and (11).

$${C_s}^{\prime }=C_s+k_c(1-{\eta }_s^m)C_{\max }$$

(10)

$${n_s}^{\prime }=k_n(1-{\eta }_s^m)n_s$$

(11)

C_max denotes the maximum value of the specified solution space for the capacitor. k_c and k_n are the relaxation factors for the capacitance and turns, respectively. ${\eta }_s^m=\max ({\eta }_s^n,{\eta }_s^l)$

Step 5: A new generation of progeny populations is generated by crossover and mutation operations.

The whole process of the IGGA is implemented in the MATLAB/Simulink module with code. When the crossover rate and mutuation rate are both set to 0, the IGGA will regress to the IM. When relaxation factors k_c and k_n are set to 0, the IGGA will regress to the canonical GA. We utilized the IM, GA, and IGGA to optimize the four compensation methods. The convergence curves of their fitness functions are depicted in Figure 8. During the calculation, the number of populations is set to 10 times the number of stage numbers N.

Figure 8a,b show that when using the GA to optimize the ITC and DPWC, the convergence has not ended at the 50th generation, and the best fitness value is also poor. However, when the IM and IGGA are used, convergence can be achieved before 30 generations. From Figure 8c,d, it can be seen that when using the IM to optimize the ICC and FPC, the convergence speed is faster, but the best fitness value is poor and it only converges to the local optimum. Among all four compensation methods, the IGGA achieves the global optimum with the fastest convergence speed. Therefore, it is a universal algorithm for optimal ICT design. It can be seen from the comparison of the final convergence values that the minimum fitness can be obtained by optimizing the FPC method via the IGGA.

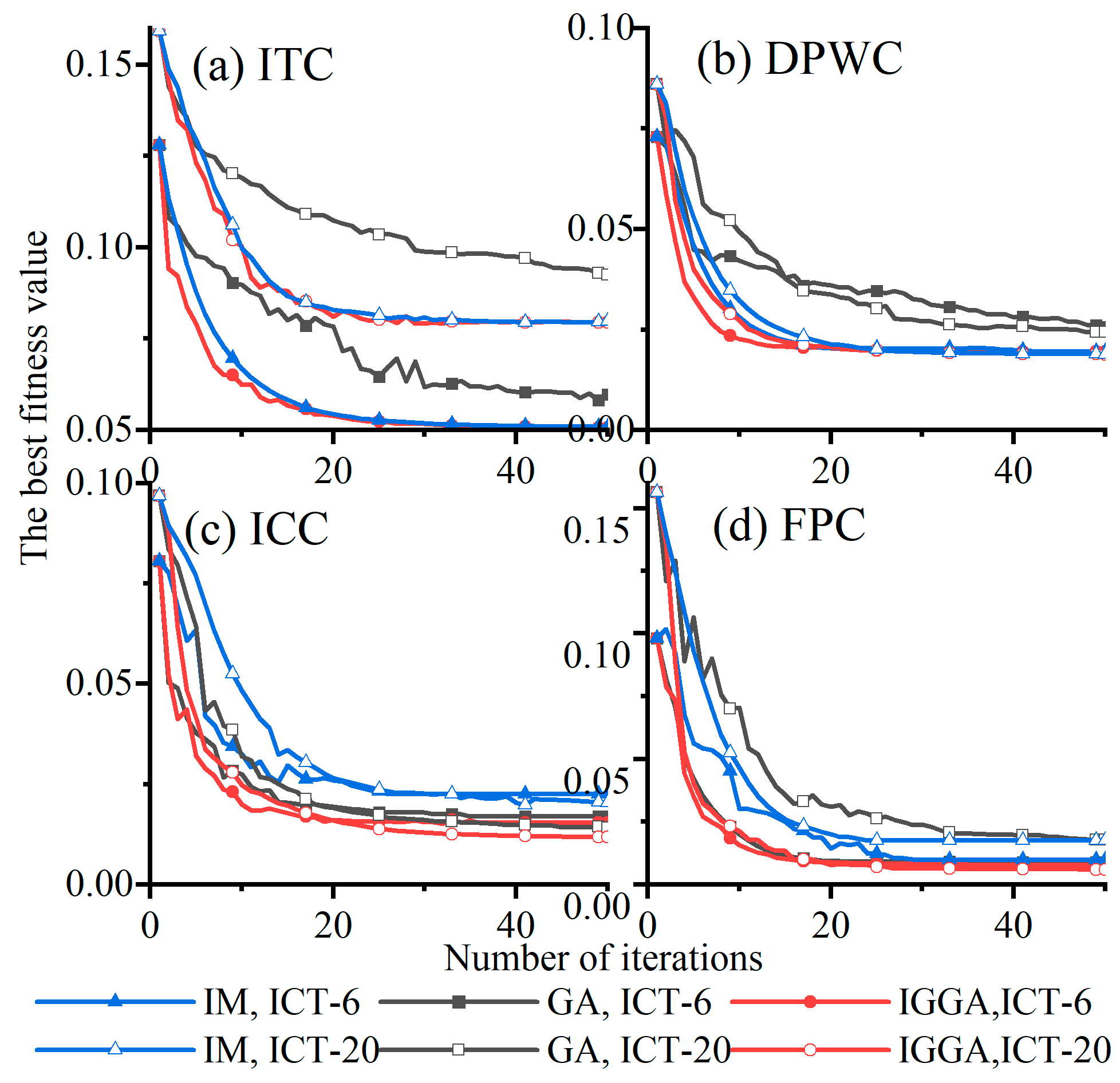
6. Comparison of Optimization Results

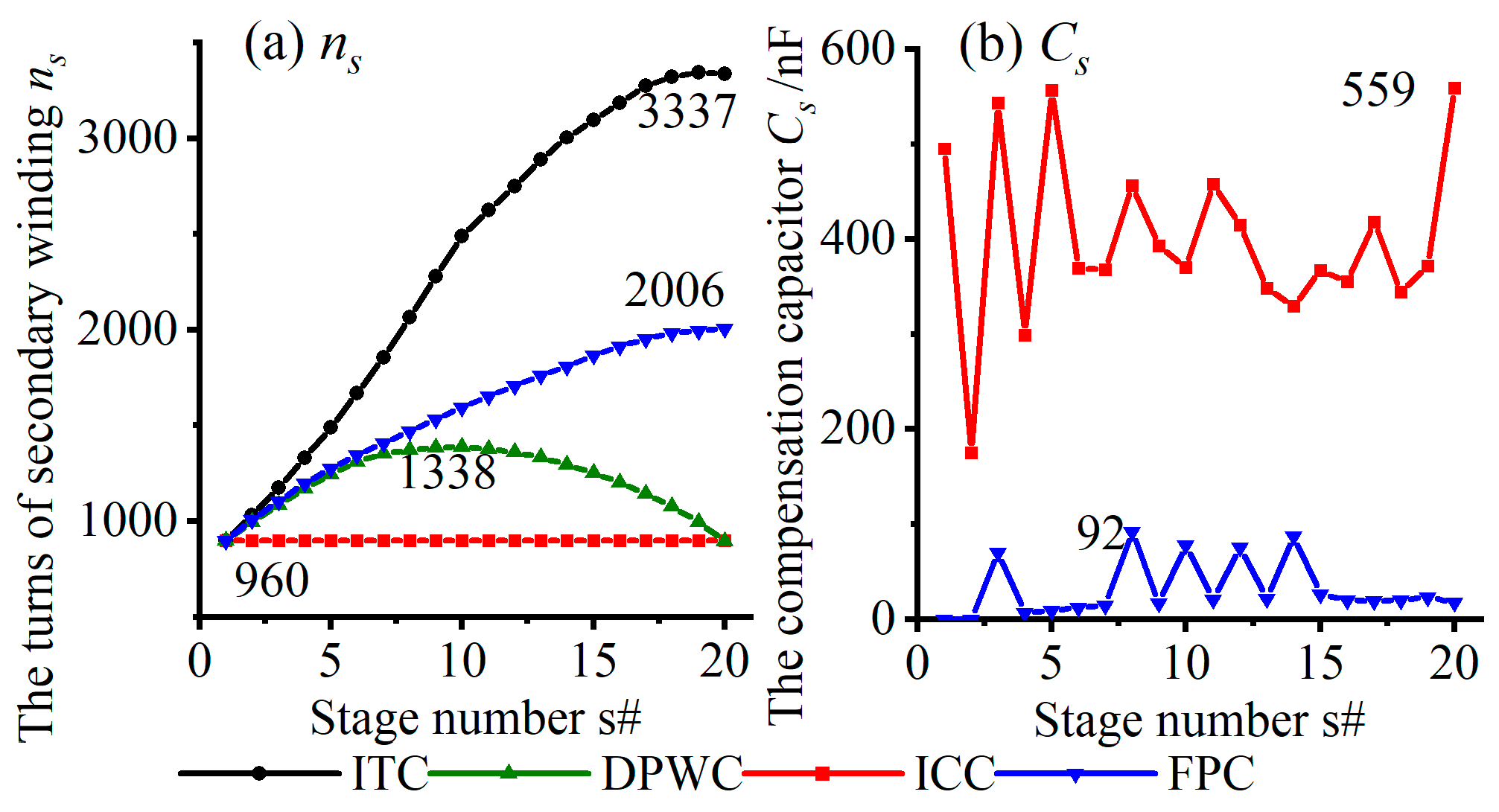
6.1. Optimal Compensation Parameters

Figure 9 and Figure 10 illustrate the optimization results of the four compensation methods for two design models, ICT-6 and ICT-20, using the IGGA. It can be observed that the ITC method requires the largest number of secondary turns (n_s), with n_s increasing as the stage number (s) increases. For instance, in ICT-6, n₁ = 2736 and n₆ = 4783, while in ICT-20, n₁ = 700 and n₆ = 3337. In the case of the DPWC, the distributions of n_s follow an inverted U-shaped pattern. In the case of the ICC, n_s remains constant in each layer. However, there is no clear relationship between the C_s and s. Lastly, in the FPC method, n_s also increases slightly with the s, but at a slower rate compared to the ITC method.

As shown in Figure 8 and Figure 9, the compensation parameters vary among different methods. Therefore, it is crucial to choose the suitable compensation method based on the specific requirements and characteristics of the ICT power supply design.

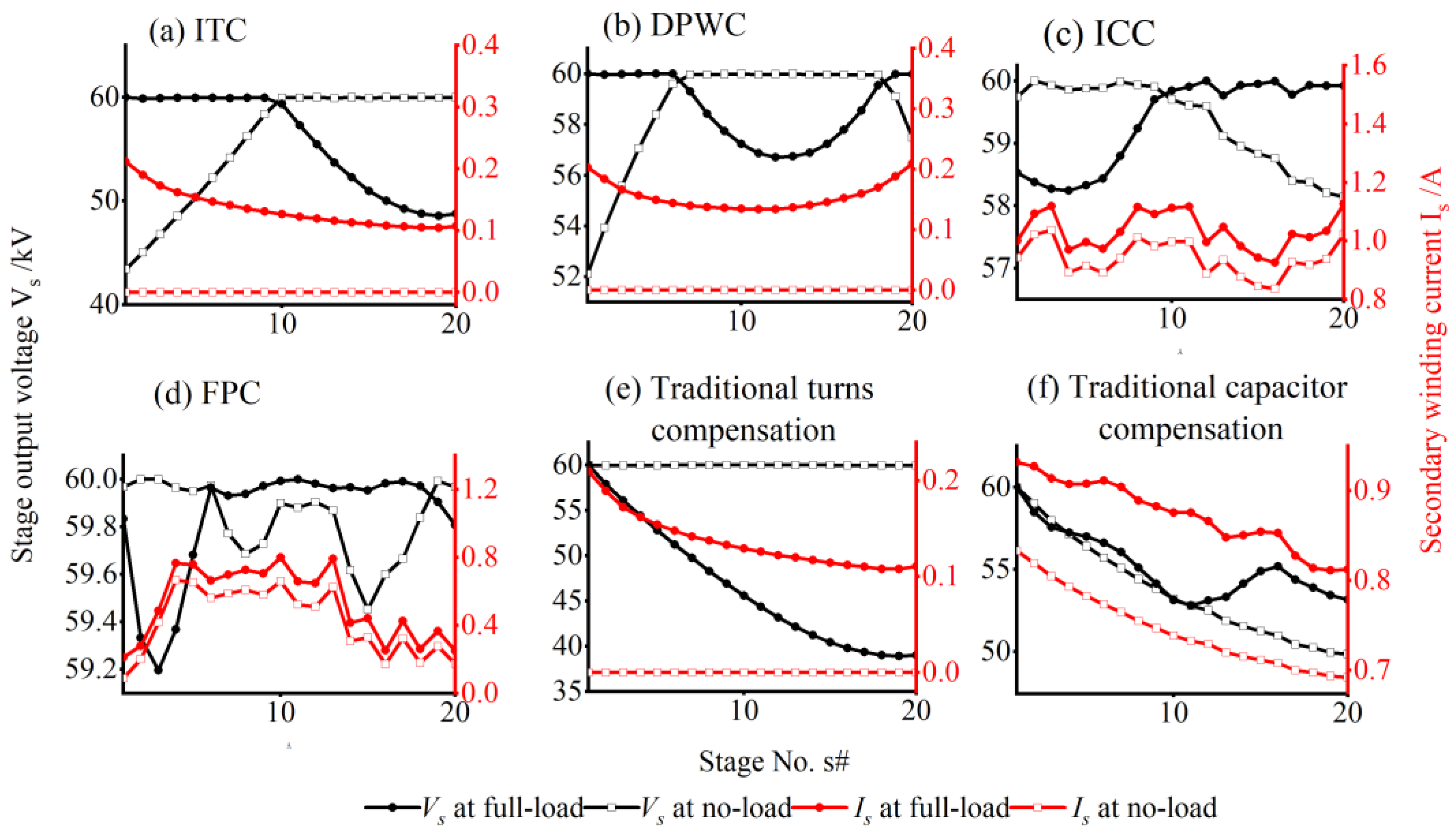
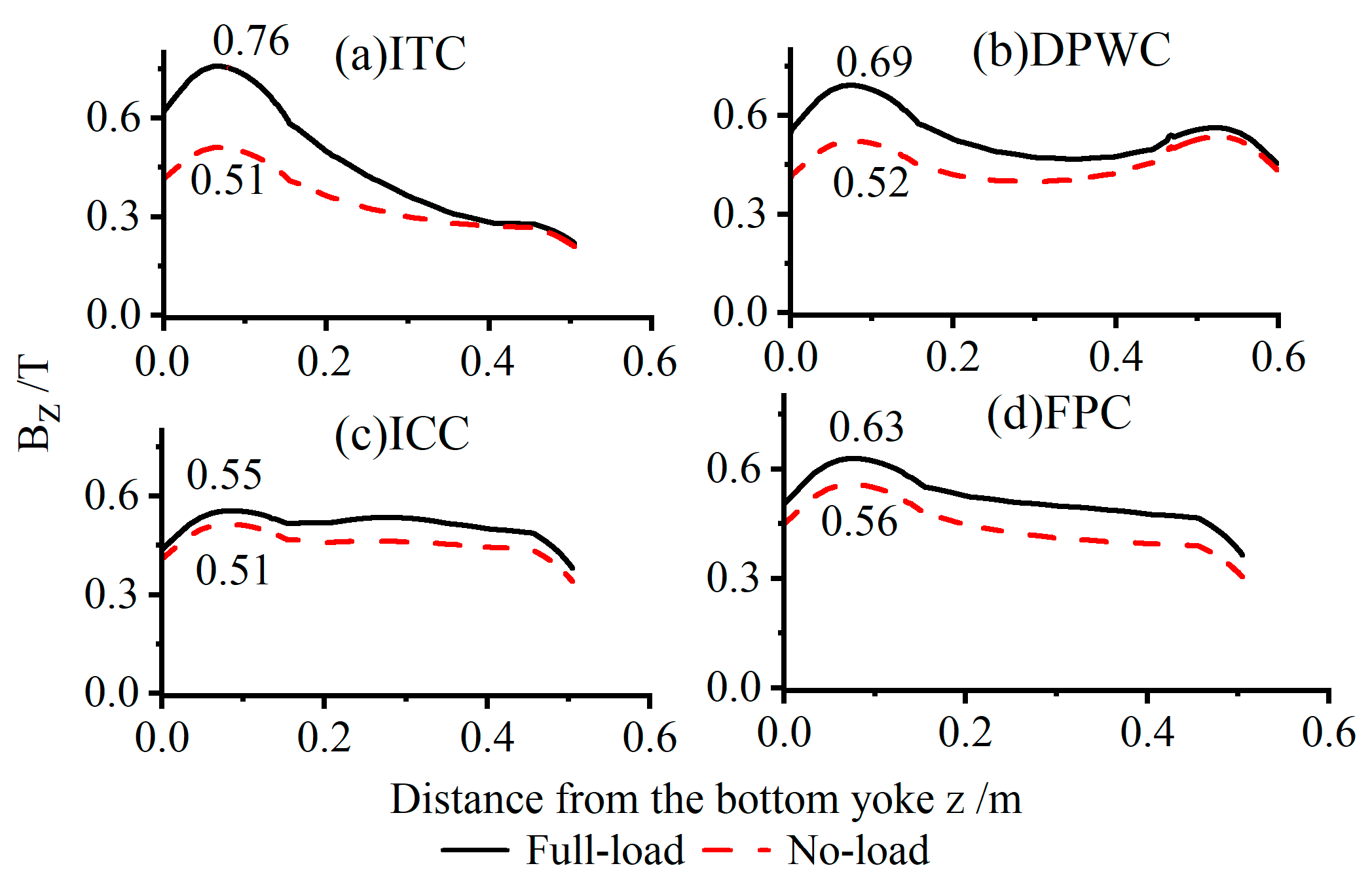
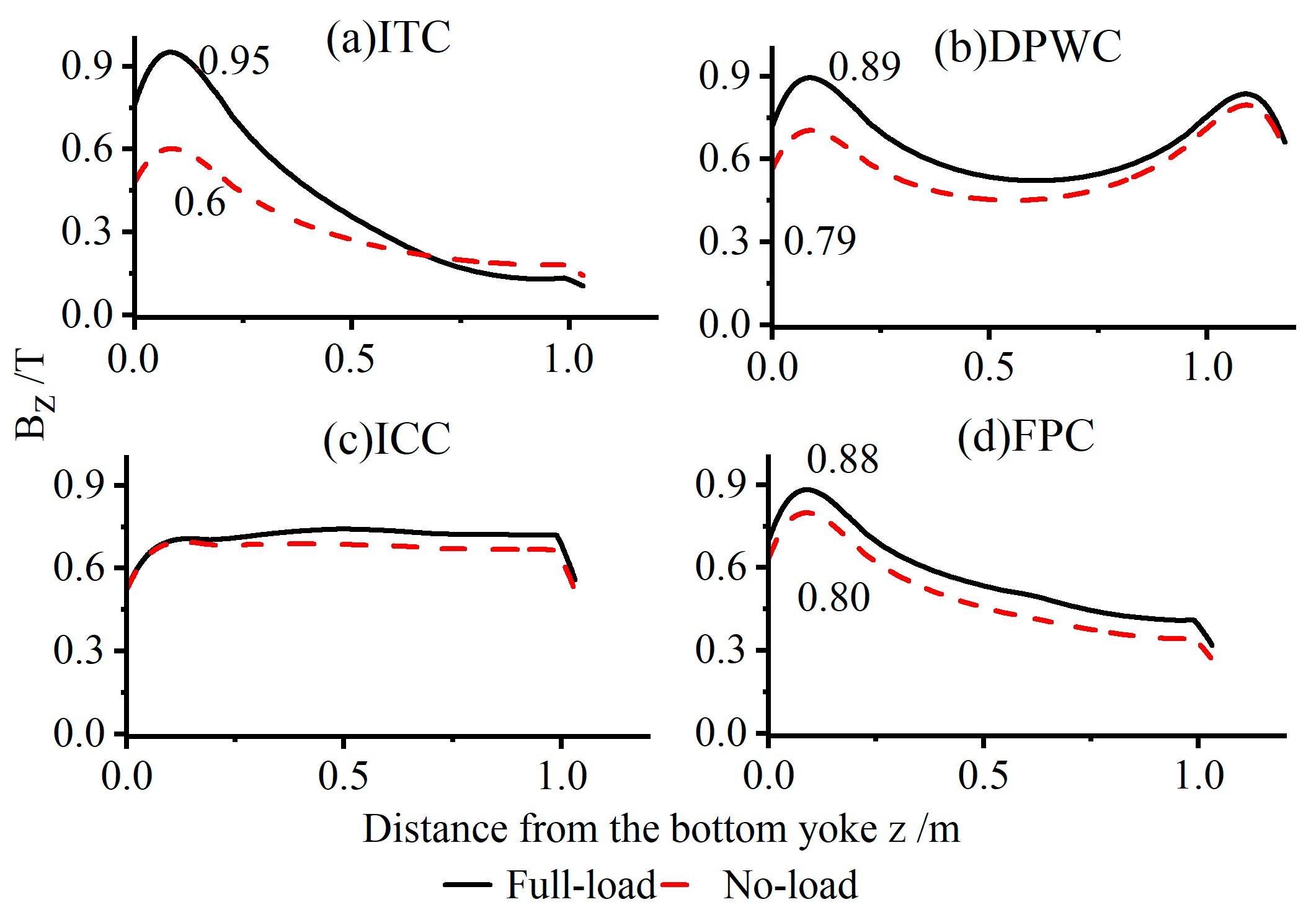
6.2. Optimized ICT Performance

Based on the optimal compensation parameters in Figure 9 and Figure 10, the distributions of the stage output voltages vs. and the winding currents I_s are calculated, as shown in Figure 11 and Figure 12. From Figure 11 and Figure 12a regarding the ITC, the vs. of ICT-6 and ICT-20 exhibit the same distribution rule. At full load, the vs. of the secondary wingdings near the primary wingdings (s < N/2) is around a rated voltage of 60 kV. However, for the other half of the secondary wingdings (s ≥ N/2), the vs. decreases with the increasing s. At no load, the distribution of vs. is exactly the opposite. From Figure 11 and Figure 12b regarding the DPWC, at full load, the vs. at both ends of the cores are around 60 kV, while the middle section sinks; conversely, at no load, the opposite pattern occurs. The I_s of the full load for the ITC and DWPC are low, and the I_s of the no load is 0.

Furthermore, in Figure 11 and Figure 12c,d, it can be observed that both the ICC and FPC methods exhibit a remarkably uniform stage output voltage distribution close to 60 kV. The current distributions are similar to the compensation capacitance distribution in Figure 9 and Figure 10b. Moreover, their values of I_s are larger than the other two methods. Comparing between Figure 11c,d and Figure 12c,d, it can be seen that the maximum I_s in ICT-20 are more than three times those in ICT-6. The reason is that ICT-20 has fewer secondary wingding turns and a larger compensation capacitance, so the currents are larger.

Comparing Figure 11e and Figure 12e with Figure 11a and Figure 12a, Figure 11f and Figure 12f with Figure 11c and Figure 12c, it can be seen that the uniformities of the improved compensation method are greatly improved compared with the traditional methods.

Finally, the statistical data of the optimized ICT performance presented in

Table 3. Comparison of (δ_l and δ_n) and load regulation rate (S_L) with different compensation methods.

		ITC	DPW	ICC	FPC
ICT-6	δn	4.32%	1.64%	1.53%	0.52%
	δl	4.32%	1.65%	1.53%	0.52%
	SL	32.81%	24.4%	7.48%	11.38%
ICT-20	δn	7.74%	2.20%	1.30%	0.51%
	δl	7.71%	2.18%	1.07%	0.43%
	SL	36.43%	21.1%	2.70%	12.16%

reveal that the sorting of δ_n and δ_l for different methods is as follows: ITC > DPWC > ICC > FPC. The sorting of S_L is ITC > DPWC > FPC > ICC. Additionally, with regard to the FPC method, the performance of ICT-6 and ICT-20 remains unchanged despite an increase in the number of stages.

After conducting FEM simulations based on the optimal compensation parameters and winding currents I_s, the magnetic field B_z curves along the z-axis on the magnetic core are obtained. By comparing Figure 13 and Figure 14, it is observed that the magnetic field curves of the two ICTs are similar, except that the magnetic field peak value of ICT-20 is slightly larger than that of ICT-6. Moreover, the ranking of the magnetic field peak values for different compensation methods is as follows: ITC > DPW > FPC > ICC. It can be inferred that the power margin of the ICT source increases as the magnetic field peak value decreases at a full load. Furthermore, the ICC has the best uniformity in magnetic field distribution, followed by the DPW. The more balanced the magnetic field distribution, the more balanced the permeability utilization will be, and the heat generation of the magnetic core is also distributed more evenly [27], thus enhancing the power supply’s carrying capacity.

6.3. Recommendations on the Selection of Compensation Methods

Based on the results of the compensation optimization, characteristics, and processing complexity discussed earlier, we can infer and analyze the suitable scenarios for different compensation methods.

(1)

The ITC does not require compensation capacitors; it only needs windings of different turns, resulting in a simple engineering implementation. However, this method exhibits poor voltage uniformity (ICT-20: 7.7%) and S_L (ICT-20: 36.43%). These values indicate the high internal resistance of the power supply and limited load capacity, resulting in a low output voltage and small output current. Therefore, the method is recommended for an ICT with a lower voltage level and smaller output current.

(2)

The DPWC increases the complexity of engineering implementation more than the ITC by adding a set of DPWs and also increases the overall height of the device. Moreover, the axial magnetic field distribution is more uniform, and the peak value is smaller. Yet, it can slightly decrease δ and S_L. Hence, it is recommended to use the DPWC in situations requiring a higher ICT output voltage and larger output current (greater than the ITC).

(3)

The characteristic of the ICC is that all the secondary windings have the same number of turns, and only different values of compensating capacitors need to be paralleled, making it relatively easy to implement. After undergoing this method, the winding current I_s becomes larger, the magnetic field peak becomes smaller and distributed more evenly, with a low load regulation rate and robust load-carrying capacity. Therefore, it is recommended to use the ICC method in situations requiring a higher output current (greater than 200 mA). This method is applicable to ICTs of all voltage levels.

(4)

The advantage of the FPC lies in its excellent nonuniformity and relatively good load regulation suitable for ICTs with various voltage levels. Furthermore, this method is particularly suitable on some occasions where the voltage level is very high, or where the voltage distribution is required to be very uniform due to the small insulation design margin.

7. Conclusions

In this paper, a unified simulation model and an improved gradient-based genetic algorithm are proposed for four used ICT stage output voltage compensation methods (improved turns compensation, improved capacitor compensation, dummy primary winding compensation, and full-parameter compensation), which can optimize the compensation parameters quickly and efficiently. Using this model and algorithm, we optimize the parameters of the ICT at different voltage levels using the four compensation methods and comprehensively compare and analyze the effectiveness. We then summarize the compensation effect and provide suggestions for the use of the compensation methods. The unified model and optimization algorithm presented in this paper provide an effective tool for designing and analyzing a conventional ICT, and also have a certain reference value for the design of other types of ICTs such as ferrite and multi-winding transformers. Furthermore, the selection suggestions of this study fill in the blank of related research and provide a valuable reference for how to choose compensation methods in an ICT power supply design.