Abstract
Ice slurry is a phase-changing material composed of liquid water, ice crystals, and a freezing point depressant. It is finer and more uniform compared to ice cubes or flake ices and is used in many industries, such as food preservation, comfortable cooling, medical protective cooling, sport cooling, instrument cooling, firefighting, and artificial snowmaking, due to its high energy storage density. Ice slurry with high concentration can be used for cleaning equipment as its friction is several times greater than that of water at the same flow rate. This paper describes in detail the developments of ice slurry, including production methods, concentration measurement approaches, flow and heat transfer characteristics, as well as its applications in various industries. Problems to be solved or improved are also discussed, providing suggestions for better developments and applications in industrial environments.
1. Introduction
Ice slurry is a phase-changing mixture composed of pure water and ice crystal, which has a freezing point depressant. The freezing point depressant, which is an additive, is used to lower the crystallization temperature of water. As ice crystals cannot be produced from pure water without such an additive, its presence ensures that the water solution does not form large ice blocks. The four most commonly used freezing point depressants in industry are sodium chloride (salt), ethanol, ethylene glycol, and propylene glycol; see Table 1. Figure 1 shows ice slurry in a bucket, which is fine and uniform and different from ice cubes or flake ice. This mixture offers a high energy storage density due to its latent heat (about 334 kJ/kg), which makes it either a heat exchange medium of a cold carrier or an energy storage medium of a cold storage system. With the development of methods to produce ice slurry, applications have been extended. The original purpose of ice slurry was for food preservation, which can date back many millennia. Due to the intensification of global greenhouse effects and the requirements for energy conservation and emission reduction, ice slurry has been used more frequently as the secondary refrigerant in air conditioning systems. As the price and demand of electricity are different throughout a day, ice slurry can be produced and stored during off-peak periods, when the electricity is cheaper. The thermal energy storage can then be released through the melting of the ice slurry during the daytime peak, when the price of electricity is 2–3 times higher than that at off-peak. Ice slurry can also be used in office buildings for comfortable cooling, which can be seen in many developed countries, especially in Japan [1,2]. To date, the application range of ice slurry has been extended to the mining industry, pipeline pigging, medical applications, artificial snow production, and firefighting [1,3,4,5].

Table 1.
Most commonly used freezing point depressants in industry.

Figure 1.
Ice slurry—mixture of pure water, ice crystal, and freezing point depressant.
The fraction of ice crystal in the slurry is key in determining whether ice slurry is a Newtonian or a non-Newtonian fluid (critical fraction). The flow and heat transfer characteristics of a non-Newtonian fluid are more complicated than those of a Newtonian fluid. The literature mainly focuses on specific aspects, including the production methods, storage modes, fraction measurement approaches, flow rheological behaviors, and heat transfer characteristics [6,7,8,9,10,11]. Among the available literature on flow and heat transfer characteristics of ice slurry, most studies consider ice slurry with low ice concentration, which is mainly used in building cooling, secondary refrigerant of air conditioning systems, and medical surgery [1]. Ice slurry with a higher fraction is usually used for pipeline pigging [3]. The fluid properties can make the slurry flow through various topologies, and the solid properties can produce friction with the internal surface of the pipeline and then remove the stains. If the ice slurry generates a blockage of the pipeline, it will melt after some time. Compared to traditional cleaning methods, ice slurry pigging is faster, cleans better with less water, and is a pollution-free effluent.
There is literature already available on ice slurry, but studies are usually not comprehensive or detailed. This paper provides a state-of-the-art review of the development and application of ice slurry. The second section introduces production methods, the third section discusses ice fraction measurement approaches, the fourth section deals with flow behavior, the fifth section discusses heat transfer characteristics, the sixth section introduces the application of ice slurry, and the last section provides the conclusions from this work.
2. Ice Slurry Production Methods
Ice slurry production methods are important in the entire ice slurry application process as they relate to energy consumption. For energy conservation and emission reduction, production methods with high generation at low energy consumption should be adopted. From the invention of ice-making systems until now, there have been mainly five production methods of ice slurry: surface-scraping, supercooling, vacuum-based, fluidized bed, and direct contact method, which are shown in Table 2. The definition, benefits/merits, and drawbacks of these production methods are described below.

Table 2.
Comparison of ice slurry production methods.
2.1. Surface-Scraping Method
Figure 2 shows the schematic diagram of ice slurry production by surface-scraping. The surface-scraping method [12,13,14] involves water with a freezing point depressant that is kept in cooling mode between the ice-making machine and the ice-storing tank. When the temperature of the cooling water becomes lower than that of its crystallization point, a thin layer of ice appears on the surface of the tube wall in the generator, which is scraped off by the scraper inside the generator and pumped into the ice-storing tank. The operating performance of the surface-scraping method is relatively stable, and the ice crystals generated are relatively fine. However, its production efficiency is low, energy consumption is large, and the scraper is prone to wear due to long operating hours. The surface-scraping approach is currently one of the most widely used and mature methods for the dynamic production of ice slurry.
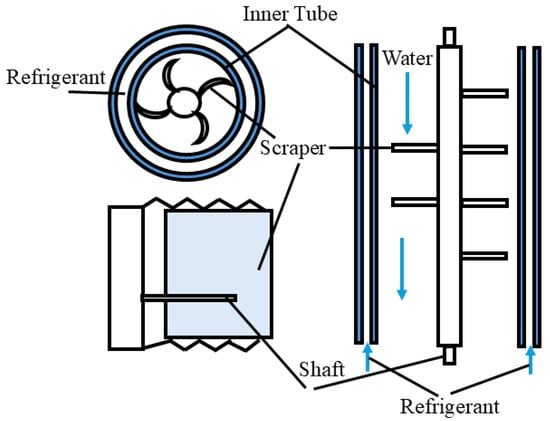
Figure 2.
Schematic diagram of ice slurry production by surface-scraping method [12,13,14].
2.2. Supercooling Method
The supercooling method [15,16,17], as the name suggests, is a method that cools the water flowing through a super cooler to a temperature below the freezing point of water and maintains the supercooling state until it is removed through ultrasonic stimulation to produce a mixture of water and ice crystals, which can be seen in Figure 3. This method has many advantages, such as high heat transfer efficiency, a simple production system, technical maturity, and mass production. However, the supercooling degree of the water is difficult to control, and an ice blockage can easily form in the super cooler, which prevents the system from achieving continuous ice slurry generation. The supercooled brine method is a more promising and energy-efficient technology to generate ice slurry than the surface-scraping generator (higher evaporation temperature of the evaporator within the refrigeration system) and due to the absence of moving components [18].
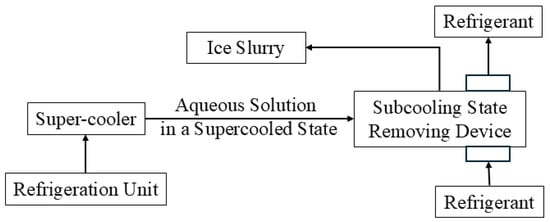
Figure 3.
Flow chart of ice slurry production by the supercooling method [15,16,17].
2.3. Vacuum Method
The vacuum method [19,20] does not require any refrigerant or cold carrier. When an aqueous solution is suddenly injected into a vacuum environment, some of the aqueous solution is evaporated quickly as its current temperature is much higher than the saturation temperature corresponding to the vacuum pressure, and some of the aqueous solution is cooled quickly to form ice crystals [21], see Figure 4. Compared to other ice slurry production methods, the vacuum method utilizes self-evaporation to generate ice slurry without refrigerant or cold carrier. This reduces the loss caused by the heat exchangers and enhances the heat transfer performance. The vacuum method is also safe and environment-friendly. However, the crystallization kinetics theory is the core of the process, and it is difficult to understand and achieve accurately. Furthermore, the ice slurry production needs high requirements, for instance, air tightness and strength of equipment.
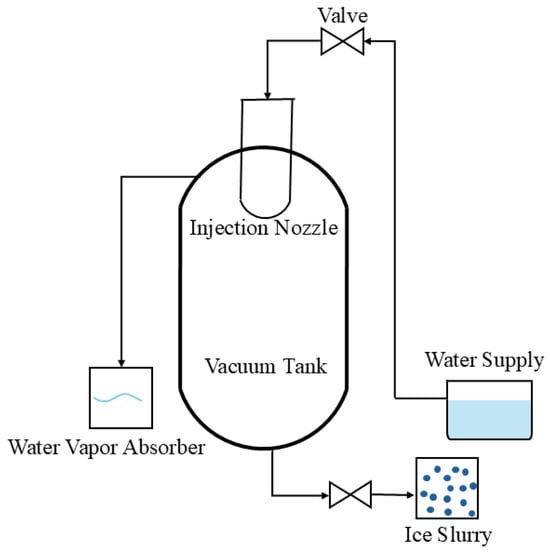
Figure 4.
Schematic diagram of ice slurry production by vacuum method [19,20].
2.4. Fluidized Bed Method
Figure 5 shows the schematic diagram of ice slurry production from the fluidized bed method. For this approach [22,23], the liquid enters the equipment from the bottom and flows to the top, while the refrigerant is injected at the top and flows down to the bottom. Both exchange heat through tube walls and form countercurrent heat transfer. Small stainless steel balls of different diameters are added to the fluidized bed to prevent the walls from freezing as they strike the wall. This helps to form fine ice crystals and also improves the efficiency of the heat exchange. Finally, the ice slurry flows out from the upper outlet, and the cooled aqueous solution, containing the stainless balls, returns to the equipment for another cycle of ice production. The strengths of the fluidized bed method include simple design of the tube shells, high efficiency of heat exchange, and low price for the device. However, the production process of the entire system is difficult to control, and the refrigerant consumption is large. The fluidized bed method is still currently under research.
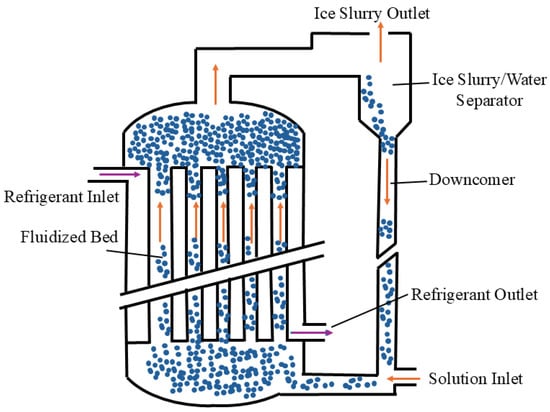
Figure 5.
Schematic diagram of ice slurry production by fluidized bed method [22,23].
2.5. Direct Contact Method
For the direct contact method [24,25], the aqueous solution is in direct contact with the refrigerant to exchange heat before the aqueous solution is cooled to generate ice slurry; see Figure 6. Compared to indirect contact methods, the direct contact method reduces the thermal resistance between the aqueous solution and the refrigerant and also improves the efficiency of the heat transfer. The equipment size of the direct contact method is smaller due to the lack of an evaporation coil. Low device cost, low energy consumption, and low operation and maintenance costs form the main advantages of the direct contact method. However, large refrigerant consumption, ice blockage around the nozzle, and hard separation of the refrigerant and the aqueous solution are the main causes for restricting the development of the direct contact method for ice slurry production. Ice-making devices based on the direct contact method are being actively researched.
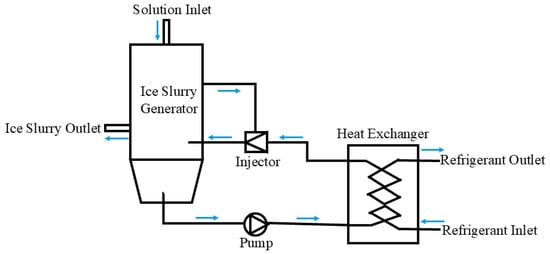
Figure 6.
Schematic diagram of ice slurry production by direct contact method [24,25].
2.6. Deicing Method
When the evaporation temperature of the refrigeration system is lower than 0 °C, an ice layer will appear on the surface of the evaporator. This ice layer increases the thermal resistance of heat transfer and increases the air flow resistance for forced circulation evaporators, which will affect the heat exchange efficiency. Therefore, independently of the cooling method used, deicing should be applied to remove any ice formed on the cold surfaces. When using this approach, the formed ice layer is removed periodically using electrohydrodynamic (EHD), low-frequency oscillation, ultrasonic vibration methods, a hot gas reverse cycle, an electric heater, or other methods that can be used to limit ice formation, for instance, desiccant dehumidifiers or controlling strategies [26].
3. Measurement Methods of Ice Slurry Concentration
An ice slurry is a mixture of a solid-fluid, two-phase material, where the solid phase is in the form of ice crystals. The concentration of ice crystals in the ice slurry changes with heat exchange. Hence, the measurement of ice crystal concentration is essential in an entire ice slurry application process, especially before and during use. This section introduces the different ice slurry concentration measurement methods before and during use, as per Figure 7.
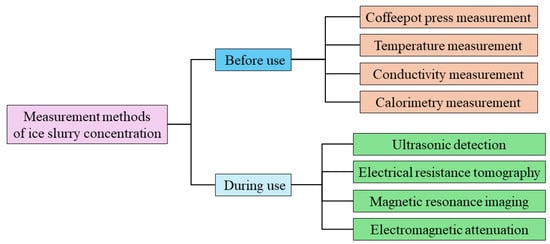
Figure 7.
Measurement methods of ice slurry concentration.
3.1. Measurement Prior Use
The ice slurry concentration can be measured before being used. Commonly used methods are the coffeepot press measurement, the temperature measurement, the conductivity measurement, and the calorimetry measurement. The mechanisms, strengths, and drawbacks of these methods are described below.
3.1.1. Coffeepot Press Measurement
Before ice slurry is being used, the coffeepot approach can be used to measure its concentration [27]. In this process, the ice slurry to be measured is put into a coffee pot, which is emptied into a filter. The remaining ice crystal volume in the filter is then divided by the initial volume of the ice slurry, giving the concentration (volume fraction) of the ice slurry. The coffeepot press measurement is relatively easy to perform and is suitable for engineering applications. However, the measured value is usually higher than the actual value due to the gaps between the ice crystals. The coffee pot press measurement is still the most used method because of its simplicity.
3.1.2. Temperature Measurement
Temperature is a very important parameter to determine the formation and melting of ice crystals. For a certain volume of saltwater, the more ice crystals due to cooling, the less the pure water. This means that the salinity of the remaining brine solution becomes higher. Different salinity corresponds to different freezing points. Based on the relationship between the saltwater freezing point and its salinity, the concentration of the ice slurry can be calculated under different temperatures [28,29].
where CA of the CA(T0) formulation is the initial additive concentration of the carrier fluid at the freezing point T0, and CA of CA(Tm) is the additive concentration of the carrier fluid at the ice slurry temperature Tm. A detailed derivation of this method is provided in [30]. This approach is accurate if the ice slurry is uniform and balanced, but it can be difficult to keep the ambient temperature constant, hence difficult to ensure the accuracy of the measured value.
3.1.3. Conductivity Measurement
The conductivity measurement method [31] uses conductivity to calculate the concentration of ice slurry. Taking saltwater as an example, the total quality of the ice slurry is the sum of the quality of pure water, salt, and ice crystals. The relationship between the concentration and salinity of ice slurry can be obtained through the derivation of expressions of salinity and ice fraction [31].
where φ is the concentration of ice slurry, C is the initial salt concentration of the carrier fluid before ice crystals form, and Ci is the salt concentration of the carrier fluid in the ice slurry.
The corresponding salinity is obtained through the conductivity, and the concentration of ice slurry is obtained based on the relationship of concentration and salinity. A detailed derivation of this method is provided in [31]. This method is simple and easy to operate. However, its accuracy depends on the uniformity of the brine of the ice slurry. Because the density of ice is less than that of water, without continuous stirring, ice crystals tend to float and accumulate, which causes the salinity in the accumulated ice slurry to be different from that in other places. The inhomogeneity of salinity in the slurry will affect the reliability of the measured conductivity.
3.1.4. Calorimetry Measurement
Calorimetry [32] is a method for measuring the heat involved in various processes, such as chemical reactions and phase transitions. The equation is as follows:
where Q is the heat energy transferred in a calorimetry experiment, m is the mass of the substance being studied, c is the specific heat capacity of the substance, and ΔT is the temperature difference of the whole process. For such a process, an ice slurry sample is heated to melt completely in the calorimeter. The total input heat is then measured and the ice crystal fraction estimated based on the heat balance theory.
Calorimetry is accurate and easy to operate, showing no more than ±1.3% error. This approach is currently seen as the ‘gold standard’ in the ice slurry concentration measurement across the industry.
3.2. Measurement During Use
The ice slurry concentration changes when used, for instance in the food industry, pipeline pigging, and fluid processing industries. A non-invasive method is required for concentration measurement [33]. For the food industry, ice slurry can be used to reduce the length of a cleaning cycle [34]. For pipeline pigging, when high concentration ice slurry flows to remove sediment, a non-invasive method is also required to measure the solid fraction of the ice slurry. Non-invasive approaches mainly include ultrasonic detection, electrical resistance tomography, magnetic resonance imaging, and electromagnetic attenuation. Compared with intrusive detection, non-intrusive methods do not affect ice crystal movements, and the carrier fluid flows and ensures the synchronization of the concentration and velocity measurement.
3.2.1. Ultrasonic Detection
There are different ultrasonic concentration meters that can be used for ice slurry. Ultrasonic signals are sent from the transmitter and pass across the ice slurry. In this process, some of the ultrasonic signals are scattered at the interface of the ice particles, some are absorbed by the ice particles, and the rest is received by the receiver. Therefore, for a specific frequency of ultrasonic signals, the higher the number of ice particles, the higher the ultrasonic signal attenuation, which means that fewer signals are received by the receiver.
Shire et al. [33] used such ultrasound signals to detect the concentration of ice slurry within pipelines. Figure 8 shows the specific rig they used. Their results showed that ultrasonic signals obtained through tested products and ice slurry are different. The speed of sound through the ice slurry is indeed higher than through other fluids tested, but its signal attenuation is also larger than that of other fluids. Note that signals obtained from ultrasonic experiments are reproducible and reliable under static and dynamic flow conditions, which shows that the mixture or the interface between products and ice slurry under static and dynamic flow conditions can be detected using this non-invasive method.
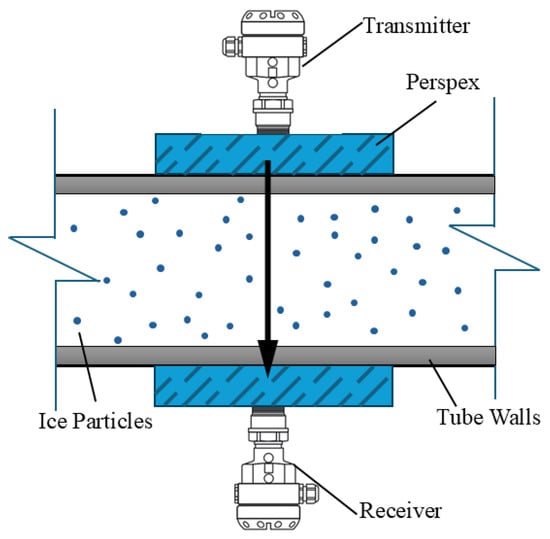
Figure 8.
Set-up of ultrasonic signal [33].
Evans et al. [27] continued to investigate the survival distance of high-concentration ice slurry as a plunger entity in steel pipes through the ultrasound method from Shire et al. [33] and obtained that the survival distance increases with concentration of ice slurry.
3.2.2. Electrical Resistance Tomography
Electrical resistance tomography (ERT) is also a non-intrusive method used for detecting the solid fraction of ice slurry. The electrical conductivity distribution inside the object is reconstructed by the change in resistance as the current passes through the object, and the concentration distribution of the solid particles can be derived from the data processing procedure [35,36,37,38,39,40,41,42]. The detailed schematic of ERT in the ice slurry flow is shown in Figure 9 [43]. The ERT technique has excellent time resolution, which is suitable for time-dependent multiphase flow measurement and is also cheap. It can also be used to identify the flow regimes under different operating conditions. However, a continuous electrical contact with the liquid flowing in a pipe is necessary, and the conductivity of the liquid must be smaller than that of the electrode of the transducer, which means that the conductivity of the liquid phase must be detected before using the ERT to measure the concentration of the solid phase.
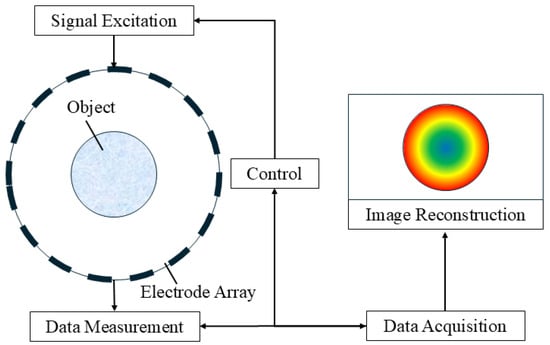
Figure 9.
Principle of electrical resistance tomography [43].
3.2.3. Magnetic Resonance Imaging
Magnetic resonance imaging (MRI) has been originally used as a diagnostic technique in medical applications. It uses the nuclear magnetic resonance phenomenon of certain nuclei in human tissue to reconstruct the image of certain aspects of the human body after the radiofrequency (RF) signal obtained is processed through a computer. Figure 10 shows the process of nucleus change during an MRI. It can also be used as a non-invasive technique to measure the concentration of ice slurry in a pipeline system.
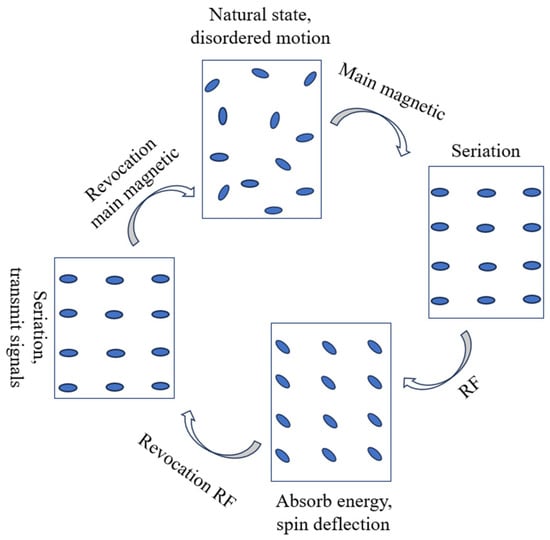
Figure 10.
Process of nucleus change during MRI.
To date, several researchers have used this approach to investigate the concentrations and velocity within solid-liquid two-phase flows [44,45,46,47,48]. The MRI technique has many advantages, such as local concentration measurement of solid phase, estimation of the velocity field, and microstructure measurement of multiphase flow in complicated systems. However, it is difficult to operate, and the equipment is expensive due to the targeted design. Therefore, only little research has been completed on MRI thus far.
3.2.4. Electromagnetic Attenuation
Electromagnetic attenuation (EM) occurs when an electromagnetic wave propagates through an object due to the scattered and absorbed wave energy from part particles. Electromagnetic attenuation in ice, water, and brine varies highly with wave frequency [49]. As a non-invasive measurement, electromagnetic attenuation has been utilized to investigate the concentration of particles. Hales et al. [50] measured the ice fraction by the electromagnetic waves with a frequency of 2.5 GHz. The results showed that the electromagnetic waves are absorbed rapidly by the water molecules, but there is little loss in intensity through the ice due to key differences in the atomic structures of the materials. The ice fraction measured can be approximated to ±1.2% by a VNA spectrum analyzer, then through mathematical processing and analysis, which rivals the error in calorimetry, ±1.2%. Moreover, Hales et al. [51] investigated the influence of salinity and temperature on electromagnetic wave attenuation in brine and derived a method for calculating varying salinity in ice slurry, which was successful in eliminating some error caused by uncontrollable changes in brine salinity.
4. Flow Characteristics of Ice Slurry
As a fluid medium with an uncertain flow state, the flow characteristics of ice slurry form the research focus of many researchers. Ice slurry does not belong to a traditional solid-liquid, two-phase mixture due to the phase change of the solid phase. Here, the solid phase refers to ice crystals, and the crystal fraction in the ice slurry is changing. In addition, the flow characteristics of ice slurry with a high solid fraction are different from those of ice slurry with a lower solid fraction. Note that a critical solid fraction can be considered for ice slurries to distinguish between Newtonian and non-Newtonian fluids, but this critical value provided in the literature is different and based on experimental settings and conditions. The flow characteristics of ice slurry are thus very complex. This section mainly introduces flow patterns, rheological behavior, and pressure drop in ice slurry.
4.1. Flow Patterns
Due to the presence of ice crystals, the flow state of ice slurry is not constant, and some relevant literature describes these flow patterns. Tian et al. [52] divided the flow patterns of ice slurry into three and named them suspension flow, moving-bed flow, and stationary-bed flow, as shown in Figure 11a. Firstly, the suspension flow shows that ice crystals are completely suspended when they flow in the ice slurry at a high flow rate. Here, the suspension flow can be subdivided into a homogeneous flow with ice crystals distributing uniformly across the entire section and a heterogeneous flow with ice crystals distributed nonuniformly throughout the cross section. Secondly, the moving-bed flow pattern occurs at lower flow velocity and is divided into two layers. The upper layer is a moving-bed layer, which is formed due to the accumulation of ice crystals moving upward and can be propelled by the carrier fluid. The lower layer is a heterogeneous flow layer. The moving-bed layer has the maximum packing fraction of ice crystals, and those ice crystals tend to agglomerate, which increases the risk of ice blockage. Thirdly, compared to the moving-bed flow rate, the flow velocity of the stationary-bed flow is much lower, which makes the carrier liquid not able to drive part crystals of the moving-bed layer and result in the formation of the stationary-bed layer at the top of the pipe. For the stationary-bed flow, the cross section of the pipe is divided into three layers: the suspended layer, the moving-bed layer, and the stationary-bed layer.
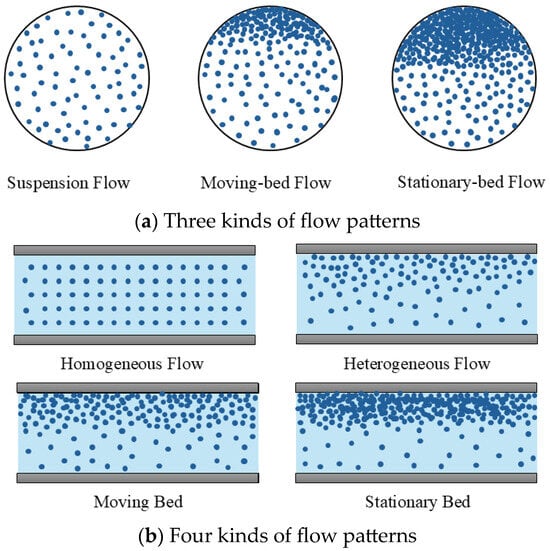
Figure 11.
Flow patterns of ice slurry [29,52].
Wang et al. [29] also described the flow patterns of ice slurry in a horizontal pipe, which are shown in Figure 11b. Four flow patterns are seen: the homogeneous flow, the heterogeneous flow, the moving bed flow, and the stationary bed flow. The heterogeneous flow has a higher particle concentration at the top of the pipe compared to the homogeneous flow. Based on the above analysis, the flow velocity and particle concentration are two key parameters in the ice slurry flow, especially the flow velocity. The velocity that turns the suspension flow into the moving bed flow is called the critical velocity. The flow above the critical velocity produces safe transportation. Therefore, during some operations, both the moving bed and the stationary bed flows should be avoided.
4.2. Rheological Behavior
Rheology mainly investigates the deformation and flow of physical materials under conditions of stress, strain, temperature, humidity, radiation, and time. It applies to substances with complex structures, and its research object is mainly fluids. As a special fluid with phase change, the flow rheology of ice slurry is more complicated than that of ordinary fluids without phase change. The particle fraction is a key parameter to distinguish between Newtonian and non-Newtonian fluids, but as mentioned previously, this critical value can be different based on experimental conditions [53,54,55,56,57,58]. Ayel et al. [59] established an ice mass fraction range of 6–15% from the definition of Newtonian fluids and non-Newtonian fluids by summarizing previous researchers’ work results. Based on this reference, ice slurry with an ice mass fraction over 15% is defined as a non-Newtonian fluid. When the ice slurry behaves as a Newtonian fluid, its shear stress is:
Here, τ, μs, and ω are the shear stress, shear viscosity, and shear rate, respectively.
Table 3 summarizes relevant viscosity formulas of ice slurry for different types of fluids. Ice slurry with a lower solid fraction is similar to a suspension, where the viscosity originates from Einstein’s model, based on a flow of low concentration spherical particles. This model does not consider the particle diameter and the interaction between the particles, and its expression is [60]:
where μs, μcf, and Cs are the shear viscosity of the ice slurry, shear viscosity of the carrier fluid, and solid concentration of the ice slurry, respectively.
Based on the above viscosity model, Thomas [61] proposed a new formula, taking into account the interaction between the particles. The specific viscosity expression is then:
Thomas’ correlation, which is one of the best-known and widely used correlations, is initially proposed to quantify the shear viscosity of ice slurry as a Newtonian fluid, but it can also be used to investigate the non-Newtonian behavior of ice slurry. For this condition to be applicable, the solid fraction of the ice slurry should not be more than 0.625 and the range of particle diameters should be within 0.099–435 μm. The fact that Thomas’ correlation could predict the shear viscosity of ice slurry with more than 15% solid fraction was experimentally verified by Hansen et al. [62]. Ismail and Radwan [63], however, developed another correlation, which is:
This correlation suggests that the shear viscosity of the ice slurry will approach infinity as the solid concentration of the ice slurry is close to 0.5897. From the above shear viscosity correlations, it can be established that the shear viscosity of the ice slurry increases with particle concentration, but the particle concentration has an upper limit value, over which the ice slurry flow possibly produces aggregation or ice blockage.
When ice slurry is used for ice pigging, its concentration is very high, in which case it is completely a non-Newtonian fluid. According to the different constitutive equations, non-Newtonian fluids can be divided into three categories: time-independent, time-dependent, and viscoelastic. The time-independent non-Newtonian fluid is also called the generalized Newtonian fluid, which includes mushy fluids, suspensions, and plastic melts in nature. Based on the above definitions, ice slurry with high concentration is considered a generalized Newtonian fluid. Such generalized Newtonian fluids are mainly divided into plastic fluids and pseudoplastic fluids. Chhabra and Richardson [64] established that there are four rheological models suitable for ice slurry as a non-Newtonian fluid: the Power law model, the Bingham model, the Herschel-Bulkley model and the Casson model. Their corresponding correlations are, respectively [64]:
where τs and ω are the shear stress of the ice slurry and the shear rate, respectively, kp and khb are the rheological coefficients, np and nhb are the rheological indexes, μb and μc are the plastic viscosities, and τb, τhb, and τc are the yield stresses.
The rheological parameters are different depending on the rheological models. These parameters can be determined from experiments and existing semi- or empirical formulas. Kumano et al. [65,66] measured the pressure drop of ice slurry flow and applied the power law model to describe the ice slurry rheological behavior. The Bingham model was employed to depict its rheological behavior in a horizontal pipe [67,68]. Illan and Viedma [69,70] adopted the Herschel-Buckley model to research the rheology of ice slurry experimentally, and the corresponding rheological parameters were obtained through dimensional analysis. Doetsch [71] used the Casson model to describe the ice slurry rheology and obtain the model’s parameters through experiments. Monteiro and Bansal [72] investigated the pressure drop characteristics and rheological modeling of ice slurry flow in pipes and established that the Bingham model, Herschel-Buckley model, and Casson model can all simulate the flow behavior of ice slurry, but only the Herschel-Buckley model can predict the experimental trend as it considers the size of ice crystals. Illan and Viedma [70] obtained the constitutive equation conforming to the Herschel-Buckley model by fitting, giving the following rheological parameters:
where Cs, d, and D are the concentration of the ice slurry, the diameter of the ice particles, and the diameter of the pipe, respectively. From the above correlations, the shear stress τhb is a function of the concentration of ice slurry and ratio of the diameter of the ice particle to the diameter of the pipe, and the rheological coefficient and index are only related to the ratio of the diameter of the ice particles to the diameter of the pipe.

Table 3.
Viscosity formulas of ice slurry for different types of fluid.
Table 3.
Viscosity formulas of ice slurry for different types of fluid.
| Viscosity Formula | Solid Fraction | Fluid Type | Description | References |
|---|---|---|---|---|
| <15% | Newtonian | No consideration of particle diameter and interaction between particles | [60] | |
| <62.5% | Newtonian/ non-Newtonian | Particle diameters: 0.099–435 μm; Interaction between particles considered | [61] | |
| <58.97% | Newtonian/ non-Newtonian | Shear viscosity increases with particle concentration | [63] | |
| >15% | non-Newtonian | Power law model | [65,66] | |
| >15% | non-Newtonian | Bingham model | [67,68] | |
| >15% | non-Newtonian | Herschel-Bulkley model | [69,70] | |
| >15% | non-Newtonian | Casson model | [71] |
4.3. Pressure Drop
The pressure drop of ice slurry within a pumpable fluid is also an important research topic, which directly affects the energy consumption of relevant equipment. Ice slurry can bring efficiency improvements in cooling systems as it reduces the pumping energy consumption and lowers the required temperature difference of the heat exchanger due to its phase-change properties [1,2,47,52]. To achieve the same cold energy, the amount of chilled water needed is much higher than the amount of ice slurry. Although the pumping energy consumption of ice slurry is higher than that of chilled water for each run, the number of times ice slurry is pumped is far less than the number of times chilled water is, due to the large latent heat of ice slurry.
Many studies have investigated the pressure drop of ice slurry flowing in various equipment, including pipes, heat exchangers, pumps, fittings, and valves. Pressure drop calculation of ice slurry can adopt the Darcy-Weisbach equation, which is one of the most widely applied correlations to predict the pressure drop and is defined as [73]:
where f, Leq, D, ρs, νs, ms, and vs are the friction factors, the geometric length of the straight pipe (or the equivalent length of the fitting), the diameter of the pipe, the density, the mean flow velocity, and the mass and volume of the ice slurry, respectively.
The correlation for the friction factor of ice slurry is not immediate for different flow states. Friction factors of ice slurry with lower concentration, as for a Newtonian fluid, include the friction factors of laminar and turbulent flows. The corresponding correlations for horizontal flows are as follows [74,75]:
where Re is the pipe Reynolds number of the Newtonian fluid, and it is defined in Equation (19), in which μs is defined in Equation (6).
When ice slurry behaves as a non-Newtonian fluid, its friction factor is also different. There are four suitable rheological models: the Power law model, Bingham model, Herschel-Bulkley model, and Casson model, which were introduced previously in Section 4.2 and are shown in Table 4. For the Power law fluid, friction factors for laminar and turbulent flows can be respectively estimated using Equations (17) and (20) [74,76,77].
where Re is the pipe Reynolds number of the Power law fluid, defined as per Equation (21).

Table 4.
Four rheological models of ice slurry.
For the Bingham fluid, the friction factors for laminar and turbulent flows can be calculated using Equations (22) and (23) [64,67,68], respectively.
where Re and He are the pipe Reynolds number and the Hedstrom number of the Bingham fluid, respectively, which are defined through Equations (24) and (25).
The friction factors for laminar and turbulent flows when considering the Herschel-Bulkley fluid can be predicted using Equations (20) and (26) [69,70], respectively.
with Re and He the pipe Reynolds number and the Hedstrom number of the Herschel-Bulkley fluid, respectively, which are defined through Equations (27) and (28).
The friction factors for the Casson fluid can be predicted using Equations (31) and (32) [71] for laminar and turbulent flows, respectively.
where Re and Ca are the pipe Reynolds number and the Casson number of the Casson fluid, defined in Equations (33) and (34).
Researchers investigated the pressure drop of ice slurry through experiments, analytical theory, and numerical simulations. Shire et al. [78] analyzed the relationship between pressure drop, flow rate, and ice fraction in a straight pipe (with and without an orifice). The results showed that the behavioral trend of the measured pressure drop of the thick ice slurry (solid fraction > 40%) is in agreement with the trend observed by other researchers for the ice slurry with lower solid fractions; the pressure drop of constant diameter pipes increases both with ice fraction and flow rate; the pressure drop ratio of ice slurries to water decreases with the flow rate; the pressure drop ratio of the ice slurry with 40% content through an orifice is lower than that of water, which is thought to result from the particles in the slurry preventing or reducing the development and effects of turbulence in the flow, or is caused by the localized melting and refreezing of ice crystals at the orifice.
Shire et al. [79] also investigated the relationship between the pressure drop of a heat exchanger and the flow rate and ice fraction. The pressure drops were found to be greater than those with water only and rose with the increase of ice fraction and flow velocity. Apart from these, the pressure differential required to drive the ice slurry through the plate heat exchanger is found to be less than might have been anticipated from studying models for viscosity. In addition, the pressure drop of the ice slurry has a square relationship with flow rate and an exponential relationship with ice fraction.
Bellas et al. [80] investigated the pressure drop of ice slurry with mean ice fractions between 5 and 20% and established that the pressure drops increase with increasing flow rate and ice fraction, which is in line with the results of other researchers for ice crystals up to 0.6 mm in diameter.
Gupta [81] obtained different results through experimental investigations with ice fractions between 0 and 20%. The authors showed that the pressure drops keep constant when the solid fraction is below 20% and increase rapidly when the solid fraction exceeds 20%.
Kalaiselvam et al. [82] investigated the pressure drop characteristics of ice slurry in tube-fin heat exchangers through numerical simulations. The authors developed a user-defined function (UDF) incorporating the phase change source term, and the latent heat term was considered. Fernandez-Seara et al. [83] investigated the pressure drop characteristics of a terminal fan coil unit with ice slurry as coolant and established that the pressure drop is a function of the flow rate, ice concentration, and Reynolds number and that the transition from laminar to turbulent flow occurs between Reynolds numbers of 2100 and 2200.
Wang et al. [84] carried out experimental investigations on heterogeneous ice slurry flow in horizontal pipes with circular, rectangular, and slit rectangular cross-sections and showed that ice concentration and flow velocity have a great effect on the rheological behavior of heterogeneous ice slurry. The effect is manifested in two aspects. First, the ice slurry flow displays an obvious asymmetry along the pipe axis with the flow velocity decreasing, and secondly, the heterogeneous phenomenon of ice slurry is weaker with the decrease of ice concentration and pipe diameter.
Singh and Kachhwaha [85] experimentally validated a thermohydraulic model for predicting the pressure drop of chilled water and ice slurry (10% ice fraction) in a plate heat exchanger and showed that the pressure drop of the ice slurry increases exponentially with flow velocity and concentration. They also highlighted that the freezing point depressant highly influences the pressure drop at lower flow velocity. The discrepancy limit of the thermohydraulic model predicting the pressure drop of the chilled water and ice slurry is within ±15%, compared to experimental data.
Mi et al. [86] investigated experimentally and theoretically the flow characteristics of ice slurry (0–20% solid fraction) produced by supercooling without freezing point depressant in a plate heat exchanger and found that the pressure drops increase with the flow velocity, but a low ice concentration has little effect. The pressure drops of ice slurry were shown to vary with the Reynolds number for different ice concentrations. A density reduction and a viscosity increase of the slurry with increasing ice concentration reduced the Reynolds number.
Monteiro and Bansal [72] explored the pressure drop and rheological modeling of ice slurry flowing in a horizontal pipe and found that the pressure drop is a function of flow velocity.
Although the results obtained by many researchers are not entirely consistent, based on the above analysis, the change trend of pressure drop in ice slurry is almost identical. The generally accepted result is that the pressure drop of ice slurry increases with flow rate and ice concentration. The specific change law of the pressure drop is also obviously different due to its phase change and the required concentration for different applications.
5. Heat Transfer Characteristics of Ice Slurry
As a fluid medium with phase change, the heat transfer characteristics of ice slurry are also more complicated than those of normal fluids. Its heat transfer performance with different concentrations in an equipment determines its melting rate. Therefore, the heat transfer characteristics of ice slurry are also a focus for many researchers. This section mainly introduces the heat transfer coefficient and melting calculation of ice slurry.
5.1. Heat Transfer Coefficient
The heat transfer coefficient reflects the efficiency of the heat transfer at the solid-fluid interface. For ice slurry applications, the fluid and solid, respectively, refer to the ice slurry and equipment. The heat transfer coefficient of the ice slurry flowing in different equipment is different and is difficult to determine due to its multiphase nature and the ice particle melting. Since the equipment applying the ice slurry mainly includes a heat exchanger and a pipe, this section mainly introduces the heat transfer coefficient formulas of these two types; see also Table 5.

Table 5.
Heat transfer models of ice slurry.
The heat transfer coefficient formula of a tubular heat exchanger is provided by Equation (35) [87].
where Uo is the overall heat transfer coefficient, hs is the heat transfer coefficient between the pipe wall and the ice slurry, hl is the heat transfer coefficient between the laboratory (ambient) air and the pipe wall, A is the area of the heat transfer, kw is the thermal conductivity of the pipe wall, and D and L are the diameter and length of the pipe, respectively.
The heat transfer coefficient for a plate heat exchanger can be obtained from Equation (36) [88].
where ew is the wall thickness of the plate heat exchanger.
The heat transfer coefficient can also be obtained by the Nusselt number (Nu). This dimensionless parameter is the ratio of convective heat to conducted heat across the boundary in the heat transfer of a fluid surface, which describes the intensity of convective heat transfer. Its expression is as follows:
where h and k are the convective heat transfer coefficient and thermal conductivity of the fluid, respectively, and L is the characteristic length of the system.
Vicente et al. [89] carried out an experimental investigation on the heat transfer of spirally corrugated tubes in turbulent flow and established Nu formulas under smooth and corrugated tubes, respectively; see Equations (38) and (39).
where Pr and α refer to the Prandtl number and severity index of the corrugated tube.
Based on the research results from Vicente, Illan, and Viedma [69,70], they went on to study the heat transfer characteristics of ice slurry in pipelines and obtained Nu formulas of ice slurry under smooth and corrugated pipes; see Equations (40) and (42).
C in Equation (40) is the ice mass fraction, and Reref and Prref should be calculated using reference fluid properties (corresponding to the carrier fluid at 0 °C).
Other researchers have also established empirical formulas of Nu and heat transfer coefficient for ice slurry, for instance Christensen and Kauffeld [55], Jensen et al. [57], Meewisse and Ferreira [90], and Harada et al. [91]. However, these formulas are only useful in relatively limited conditions. It is difficult to propose a general formula suitable for all applications of ice slurry due to the phase change involved. Therefore, the application ranges of these empirical formulas should be clear before adopting them. Besides, more investigation regarding the heat transfer coefficient of ice slurry should be carried out, and more accurate and extensively applicable formulas should be proposed, which could provide valuable reference for engineering applications.
5.2. Variation Rules of Heat Transfer Coefficient
Due to the unconventional solid-liquid two-phase mixture, the heat transfer characteristics of ice slurry are also more complicated than for normal fluids. The heat transfer coefficient is mainly determined by specific factors, including ice concentration, total volume of ice slurry, material type of the pipe, diameter of the pipe, flow rate of the fluid, ambient temperature, and so on. The heat transfer coefficient values of ice slurry can be significantly different depending on the application, with larger values for high ice concentration than for ice slurry with low ice concentration.
Many researchers have investigated the heat transfer coefficient of ice slurry [92,93,94,95]. Mokrani et al. [96] studied experimentally the effects of chaotic advection on heat transfer and showed that the heat transfer efficiency of a chaotic coil is 28% more than that of a helical coil at a very low Reynolds number, which makes the chaotic coil more suitable for ice slurry flow.
Bellas et al. [80] studied the heat transfer characteristics of ice slurry for ice fractions between 5 and 20% in a plate heat exchanger. They showed that the heat transfer capacity of the plate heat exchanger increases by more than 30% when ice slurry is used instead of a single-phase liquid flow. The overall heat transfer coefficient of the plate heat exchanger increases with the flow velocity of the ice slurry, but it displays no significant changes at a low ice fraction (5–20%).
Egolf et al. [97] carried out an investigation on the thermodynamics and heat transfer of ice slurry in a horizontal circular pipe and showed that the heat transfer coefficient of ice slurry flow increases with the Reynolds number and ice concentration at ice fractions less than 30%.
Bedecarrats et al. [98] studied the thermal and hydrodynamic characteristics of ice slurry in a corrugated tube heat exchanger. The authors established that the ice concentration has a greater influence on the heat transfer coefficient in a laminar flow with an ice fraction less than 30%.
Haruki and Horibe [99] investigated the correlation between the heat transfer characteristics of ice slurry and some parameters, including the ice packing factor, mean flow velocity, input heat flux, and coil radius in a helical-coiled pipe. They showed that the flow resistance of ice slurry is influenced by the interaction between the buoyant and centrifugal force due to a secondary flow. However, its heat transfer coefficient is influenced by the latent heat of the ice particles.
Fernandez-Seara and Diz [100] studied experimentally the thermo-hydraulic characteristics of ice slurry in an offset strip-fin plate heat exchanger. They concluded that flow instabilities of ice slurry appear at a very low flow velocity under isothermal conditions due to the ice blockage of some channels of the heat exchanger. However, a stable flow is achieved when heat exchanges are present. They also established that the heat transfer rate and overall heat transfer coefficient of ice slurry have a slight increase with ice concentration.
Leiper et al. [101] studied the thermal efficiency of ice slurry produced by crushing ice blocks. They created a method for calculating the enthalpy of brine ice slurry, which was used as the basis of a model predicting the resultant slurry properties from the mixing of ice water and salt. Leiper et al. [102] carried on this research by comparing two ice slurry production methods. The first one was the mixing of crushed ice in a solution with a freezing point depressant (FPD), and the second one was to consider a scraped surface ice maker with FPD solution feedstock. Nearly a 20% energy saving through comminution was obtained, as the crushing method has higher heat transfer performance than the scraping-surface method.
Quarini et al. [103] developed an analytical model based on transient heat transfer within solids to predict the thermal performance and longevity of an ice pig in a pipe. The model predicted the heat transfer reasonably well, but the effects of penetration, which may occur through the ice pig, were not accounted for.
Brooks et al. [104] evaluated four materials (nylon, polytetrafluoroethylene, silicon rubber, and aluminum) that could be used to improve the heat transfer performance of a helical coiled heat exchanger design for ice slurry flow. The results showed that the aluminum pipe has a high conductivity, which made it difficult to control the ice slurry production rate, but the nylon and polytetrafluoroethylene materials offer a higher ice slurry production rate due to their lower heat conductivity.
Yang et al. [105] proposed a better theoretical model compared to conventional prediction models to determine the thermal conductivity of ice slurry, considering the influence of the latent heat of ice crystal melting. Experimental and predicted results were consistent, and the minimum and maximum relative error were 0.05 and 8.96%, respectively.
Gao et al. [106] studied the heat transfer and flow characteristics of the aqueous graphene nanofluid ice slurry in a horizontal circular pipe based on the Euler-Euler model, considering coupled interphase heat and mass transfer. They showed that the asymmetry of the fluid temperature distribution is dampened with ice packing factor, the temperature of the pipe bottom decreases with ice concentration, and the heat transfer capacity of the nanofluid with high concentration is higher than that of the nanofluid with low concentration.
Cai et al. [107] researched the hydraulic and heat transfer properties of ice slurry in a helical-coiled tube based on the Eulerian-Eulerian model and found that the ice melting rate near the inner wall is higher than that near the outer wall due to the secondary flow and local heat transfer coefficient of ice slurry, which rises linearly with the Reynolds number. Cai et al. [108] went on to investigate numerically the influence of a pulsating flow on the heat and mass transfer of ice slurry. They established that a pulsating flow could enhance the heat transfer of ice slurry and that the heat transfer coefficient of ice slurry increases with pulsating frequency, relative amplitude of velocity, cycle-averaged velocity, ice particle size, and ice concentration.
Suzuki et al. [109] studied the cooling performance of ice slurry in a square duct through a thermally immersed boundary-lattice Boltzmann method. They found that the Nusselt number increases with the Reynolds number and ice packing factor.
Based on the above literature on heat transfer characteristics of ice slurry, it can be established that the heat transfer coefficient of ice slurry increases with ice concentration. This is due to the phase change of the ice slurry with large latent heat. However, studies on the heat transfer characteristics of ice slurry should continue due to its numerous current and potential future applications.
6. Applications
Ice slurry has been used for a long time. Its initial use was for preserving food and extending its lifetime. Then, ice slurry has been used for comfortable cooling, including building cooling, district cooling, kitchen cooling, and mining cooling. It has also been used in medical protective cooling, including cardiac arrest, kidney and heart surgery, spinal cord and brain protection, organ transplantation recovery, etc. Ice slurry has also been used for pipeline pigging, sport cooling, artificial snowmaking, firefighting, etc. This section mainly introduces detailed applications of ice slurry, as also illustrated in Figure 12.
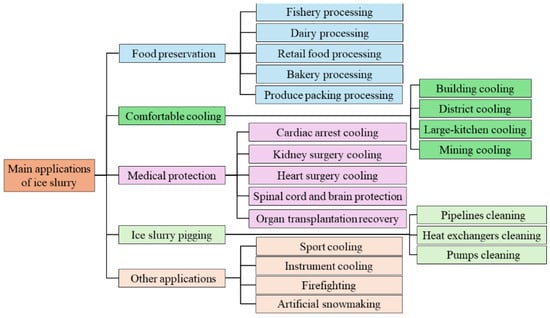
Figure 12.
Main applications of ice slurry.
6.1. Food Preservation
6.1.1. Fishery Processing
Food quality and safety have always been an important issue in human life [110,111]. Fish is one of the most commonly eaten foods; hence, its freshness and quality are essential. Compared to conventional ice cubse or flake ice, ice slurry has a larger, more uniform contact surface with fish. The melting rate and cooling rate of ice slurry are higher than those of ice cubes or flake ice, which can make the fish cool rapidly, slow the growth of bacteria, and obtain better freshness. Therefore, ice slurry is an excellent medium for fish cooling. Comparative tests between ice slurry and flake ice have been carried out [112,113,114]. Wang et al. [115] compared the cooling performance of ice slurry and flake ice on fish and showed that the ice slurry had a better performance than flake ice in preserving the freshness and quality of the fish. Paul [116] investigated the cooling rate of ice slurry and flake ice on plaice, and the results showed that the time required for the flake ice to cool the plaice down to 2 °C is more than three times slower than that for ice slurry. Annamalai et al. [117] carried out an investigation on the quality change of croaker fish stored in ice slurry and flake ice. The authors established that the shelf life of the croaker fish could be up to 15 days when using ice slurry to preserve instead of using flake ice. There are currently numerous ice slurry plants built for freshening fish in many countries, such as Iceland, Japan, and Norway. The application of ice slurry is increasing for cooling, storage, and transportation of fish onboard fishing vessels and barges, and some literature [118,119] reported that many fish species, such as tuna, yellowtail, cod, hake, mackerel, mussel, shrimp, and sardine, are successfully cooled and transported with ice slurry. The use of ice slurry in the fishing industry is thus being increasingly improved with the development of ice slurry production and storage technology, which brings great convenience to the fishing industry.
6.1.2. Dairy and Retail Food Processing
The production of dairy products requires rigorous processing. Gladis [120] introduced the application of ice slurry for a cheddar cheese plant with a daily production of 90,720 kg. Throughout the production process, the cooling times required during the processing were different. Considering all processes, the total peak cooling demand could be up to 396 kW, lasting only 1 h during the day, and the cooling demand range of the remaining 23 h was 56–148 kW. A dynamic ice slurry system was built to lower the total peak cooling demand, which comprised an ice generator with a 106 kWh capacity and a storage tank with a 24.6 volume and a 763 kWh capacitor. The dynamic ice slurry production system could meet a very large cooling load of the cheese plant in a short time by melting stored ice slurry quickly due to the phase change of the ice slurry with a large latent heat.
Moreover, former large retail stores adopted conventional centralized refrigeration systems that required a lot of refrigerants. Such systems faced the risk of refrigerant leakage due to numerous joints and long-distance pipeline transportation. Later on, ice slurry was applied in retail food stores as a secondary refrigerant, which significantly cut down the refrigerant usage in the primary system due to the phase change of ice slurry with a high latent heat. Several investigations have been carried out on the application of ice slurry as a secondary refrigerant in Europe and Japan [121,122]. Lueders [123] proposed an innovative cooling system for retail food stores. This system included two ice slurry loops and separate storage tanks for the ice slurry. The first loop was used to accommodate the building cooling and condensing requirements using a chilled liquid solution from the bottom of the tank. The second loop was used to satisfy the cooling demand of the medium and food display cabinets using ice slurry with an ice fraction of 15%. It was estimated that this ice slurry cooling system would have an 89% and 3.5% increase in the cost investment and energy consumption, respectively, but it would also have a 49% saving in electricity cost and a 4.4-year payback period by shifting 80% of peak period energy consumption to off peak period. Davies and Lowes [124] proposed a high-efficiency refrigeration system that was similar to the above-mentioned system.
6.1.3. Bakery Processing
The taste of baked food is largely determined by the processing of the dough, especially the temperature. Kauffeld et al. [125] reported that ice slurry could be used to cool the dough, replacing flake ice and CO2. Flake ice needs to be weighed manually and applied directly as the ingredient to keep the dough at the optimum temperature, which is not convenient to operate. CO2 can cool the dough, but it causes drawbacks, such as high operating costs and greenhouse gas emissions. The use of ice slurry in an automated system for bakery processing could cool the dough and save labor and operation time while improving the efficiency of dough processing and being innocuous to the environment. The application of ice slurry for dough products, including white bread, sweet bread, and baguettes, can be found in North, Central, and South America. Kauffeld et al. [125] also reported that the ice crystals of ice slurry can be easily mixed with the dough, which keeps the dough temperature even, removes the need to knead it excessively, and obtains better dough quality. Furthermore, the use of ice slurry could produce a homogenous size of alveolus inside the bread, while the use of crushed or flake ice could make the dough sticky, affect the gluten quality, and lead to a bad appearance of the crumbs.
6.1.4. Packing Processing
Produce should be preserved in a low-temperature environment to maintain their freshness once harvested. Ice slurry is a good and effective post-harvest cooling medium for various farm products, such as Chinese leaf, spinach, tomato, potato, asparagus, broccoli, carrot, grape, banana, apple, cantaloupe, etc. Kauffeld et al. [125] reported some typical cases. For example, once harvested, the broccoli was packed in waxed cartons and was frozen rapidly using ice slurry, which could prevent wilting, inhibit enzymatic degradation and microorganism growth, and reduce ethylene production. A conventional method to maintain freshness is to manually add a certain amount of ice to the top of each carton, but this approach is not suitable for large-scale operations, uses significant labor, and causes uneven cooling of the produce due to an uneven distribution of ice. However, the use of an automatic pallet icing chamber design including a stainless-steel enclosure can improve the icing efficiency. The stainless-steel enclosure can handle a pallet of 48 cases for each icing operation, which only requires one worker to put the pallet into the chamber. When the locally positioned icing switch is turned on, two front doors are closed automatically. A circulating pump will then transport the ice slurry from the storage tank to the top of the enclosure. The ice slurry located at the top is then distributed to four vertical slots built on the side walls, and the ice slurry flows through the hand openings and fills up the voids throughout all cartons within 90 s. Finally, the pallet can be moved out of the chamber after the ice particles are tightly packed with the produce. The combination of ice slurry and automation technology is thus highly convenient for produce preservation.
6.2. Comfortable Cooling
6.2.1. Building Cooling
Ice slurry-based cooling systems are being used in many countries. Wang and Kusumoto [126] reported that the number of ice slurry cooling systems installed was the largest in Japan, compared to other countries. Rivet [127] explained that Japan had about over 400 ice slurry cooling systems, whereas Europe only had probably 150 before 2009. As well known, conventional air conditioning systems for building cooling often consume lots of energy and cannot meet the demands at peak-electricity periods. However, ice slurry can be produced in off-peak electricity periods and be stored in a tank. During the daytime, the ice slurry can be used as a second refrigerant and applied in air conditioning systems to relieve the pressure of electricity consumption.
In the USA, heating, ventilation, air-conditioning, and cooling (HVAC) accounts for the largest proportion of energy consumption of commercial buildings, and about half of this proportion is used for cooling. With the development of the technology production of ice slurry, storage, and operation, countries increasingly begin to consider ice slurry cooling systems. The use of ice slurry cooling systems for building cooling can therefore reduce energy consumption, greenhouse gas emissions, and power pressure.
6.2.2. District and Large Kitchen Cooling
A district cooling system refers to a system in which one or more energy stations built centrally produce lots of cold energy. This cold energy is then transported to each building of the district with the required cooling loads through the regional pipeline network. The use of a district cooling system can save space, improve the efficiency of the cold energy distribution and reduce environmental pollution. Compared to conventional chilled water as a cooling medium in district cooling systems, ice slurry can provide more cold energy in the same volume and save on operating costs due to the phase change with high latent heat. Kauffeld et al. [125] reported an example on the application of ice slurry in a district cooling system. This example was a five-year demonstration program where the ice slurry produced by a central plant was supplied to multiple buildings on the Argonne campus. Figure 13 shows the working process. The left part is the ice slurry production and storage; the right part shows the buildings required to cool; and the bottom part displays the transportation pipeline and the heat exchanger. The ice slurry from the storage tank (left side) is circularly pumped to each building in the right part until the cooling load required for each building is met.
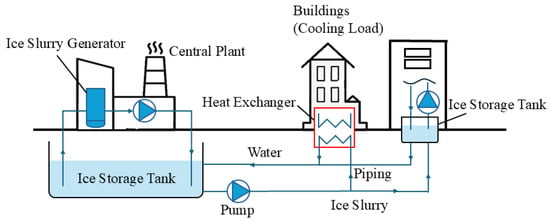
Figure 13.
Working process of the ice slurry applied in the district cooling system [125].
Yoo et al. [128] investigated the flow properties of ice slurry in a test building. They showed that the solid fraction of ice slurry could be up to 16% at a higher flow rate, and no blockage occurred during the transport process. Chung et al. [129] investigated the feasibility of using ice slurry for a district cooling system in Korea and showed that the system could provide an increasingly cooling load compared to an ice-based cooling system. The above examples show that ice slurry can provide high benefits and potential in district cooling systems.
A large kitchen is also a place requiring much cooling load. Compingt et al. [130] introduced several ice slurry cooling systems installed in large European institutional kitchens. One of the largest ice slurry cooling systems in the industry was installed in a hospital kitchen in Germany, named ‘Klinikum Stuttgart’. This kitchen was built in 2007 and could produce more than 6000 daily meals. The generated ice slurry is transported to each part requiring a cooling load, such as re-cooled vessels, refrigerated rooms, portioning stations, and about 130 cooled tray transport trolleys made of stainless steel, which ensure reliable cooling transport and gentle regeneration of food. Compared with conventional blast cooling, ice slurry cooling chills the food faster, provides longer shelf life, and reduces waste, manual handling, and dishwashing, and therefore greatly reduces labor costs, energy consumption, and produces better and fresher food for consumers.
6.2.3. Mining Cooling
Coal is a conventional and important resource with large reserves and distribution worldwide. It is widely used in steel, electric power, chemical industry, and other industries. However, most of the coal lies 1000 m underground, resulting in hard mining. The high surroundings temperatures are, however, not suitable for miners or mining machines, and a cooling system needs to be in place. Some literature [131,132] reported that the deeper the mine, the bigger the machines, and the larger the rock surface, the higher the temperature in the tunnels and the higher pumping costs of chilled water. With the development of the mining industry, the depth of mines has now exceeded 3000 m, with temperatures over 50 °C. Compared to a traditional chilled water system for mine cooling, an ice slurry cooling system could produce the same cold demand at a lower flow velocity and reduce the mining equipment and operation costs. Sheer [133] experimentally investigated the pneumatic conveying of large ice particles by mine shaft pipelines and verified the feasibility for ice particles to be transported underground for mining cooling. Ophir and Koren [134] reported an ice slurry plant made of four ice slurry units at Western Deep Level Gold Mine, in South Africa. Each ice slurry unit, including a large vapor compressor, worked at 4000 m underground. During the mining cooling process, the vertical and horizontal conveying were achieved by gravity and with a pneumatic pumping system, respectively. Chen et al. [135] numerically investigated the thermodynamic performance of a proposed split-type vapor compression refrigerator (SVCR) for controlling the heat hazards in deep mines. They highlighted that when the depth of the mine was not more than 1250 m, a SVCR system for cooling a mine is better. Otherwise, an ice slurry system is more adapted.
6.3. Medical Protective Cooling
6.3.1. Cardiac Arrest Cooling
The heart provides sufficient blood to other organs and tissues, takes away the metabolic waste, and maintains the normal function of cells. The use of ice slurry for cooling blood and organs gives paramedics more time to save patients when a cardiac arrest occurs. Kauffeld et al. [125] described a first medical protective cooling example carried out by Argonne and the University of Chicago (UC) for a cardiac arrest outside a hospital. Ice slurry was transported to the lungs without contacting the blood and cooled the blood circulating in the brain and heart, which reduced the oxygen-deficient damage, as the cooling of ice slurry slowed the metabolism of the cells. After the melting of the ice slurry in the lungs, the residual saline solution could be removed from the body through a suction tube. Ice slurry in cardiac arrest cooling can therefore increase the survival rate of patients with heart disease.
6.3.2. Kidney Surgery Cooling
Cooling is needed to relieve the oxygen-deficient pressure of the kidney during a kidney surgery. Conventional kidney surgery would make a long incision in the abdomen, and the renal artery and vein are clamped to reduce the amount of blood lost during surgery. In this case, the kidney is surrounded by ice blocks through a manual operation to reduce the ischemia damage of the kidney and prolong clamping time by more than 30 min. With the development of medical technology, minimally invasive laparoscopic kidney surgery gradually replaced the traditional open-cavity kidney surgery as it reduced psychological fear and postoperative recovery time. Ice slurry cooling then replaced ice blocks cooling, as the channels to cool the kidney got smaller for a minimally invasive surgery. Researchers [136,137] investigated ice slurry cooling technology for laparoscopic kidney surgery. More investigations on the application of ice slurry in cooling both animal and human kidneys can be found in the literature; see [138,139,140], for instance.
6.3.3. Other Medical Protective Cooling
In addition to the kidney medical applications described above, ice slurry is also used in heart surgery cooling, spinal cord and brain protection, and organ transplantation recovery. Otake et al. [141] reported that the arrhythmia and myocardial necrosis in pigs with acute myocardial infarction could be attenuated by cold saline. Kauffeld et al. [125] described that Argonne engineers and UC surgeons investigated heart muscle protection, spinal cord and brain neurological protection, and organ transplantation recovery with ice slurry. Ice slurry cooling can protect the heart from reperfusion damage caused by the balloon angioplasty opening a blocked artery and can protect the spinal cord and brain from ischemia, reperfusion injury, and neurological damage. Furthermore, ice slurry can improve the survival ability of transplanted organs by rapid cooling.
6.4. Ice Slurry Pigging
Ice slurry can also be used as a cleaning medium. Quarini et al. [142] discussed in detail ice slurry with high concentration as a pigging medium. Some literature [143,144] reported the discoloration in potable water distribution systems and public awareness of drinking water safety. The internal surface of a pipeline indeed produces impurities, sediments, and will rust when used for a long time. Therefore, pipeline cleaning is very important for water quality and pipeline preservation.
Traditional methods used for pipeline cleaning mainly include chemical and physical approaches. Chemical cleaning [145,146] refers to the addition of chemicals to clean a pipeline. Common chemical methods include acid and alkali cleaning, which are often adopted together. However, the chemical reactions when applying chemical cleaning will corrode the pipeline and pollute the environment after long-term use. Physical cleaning utilizes the physical force to clean a pipeline wall, usually through high-pressure water jet washing, pig cleaning, and gas-water pulse cleaning. High-pressure water jet cleaning [147,148] uses water in a high-pressure and high-speed state, which is not suitable for the cleaning of long pipelines with small diameters and consumes large quantities of water. Pig cleaning [149] uses a pig launched into a pipeline. The pressure difference generated by the pipeline conveying medium is used as power to push the pig along the pipeline and scrap sediments from the wall surface. This approach is suitable for pipelines of constant diameter. Gas-water pulse flushing [150] uses high-pressure gas that is driven into the pipeline at a certain frequency to form an intermittent airflow. The expansion and compression of the gas are used to form a turbulent flow that increases the shear stress at the walls. However, this method needs a large amount of water and does not generate a better cleaning than with pigging.
Ice slurry with a high mass fraction has both fluid and solid properties. Compared to traditional cleaning methods, ice slurry pigging has several advantages. Quarini [151] reported that the fluid properties could adapt the ice slurry to a variety of topological pipe structures, and the solid properties allow ice slurry to produce much greater friction than water, which makes the ice slurry clean pipelines in a shorter time, provides better cleaning effects, uses less water, and generates pollution-free effluents.
Ice slurry with a high mass fraction can clean equipment, such as pipelines, pumps, and heat exchangers [152,153]. Figure 14 and Figure 15 show typical examples of results obtained when cleaning equipment parts with ice slurry.

Figure 14.
Centrifugal pump cleaning.

Figure 15.
Pipelines cleaning.
6.5. Other Applications
Ice slurry offers a large potential in many industrial applications. In addition to those described previously, ice slurry can also be applied to sport cooling, instrument cooling, firefighting, artificial snowmaking, and so on [154,155,156]. Those applications are not discussed here, though. Currently, with the improvement of the technology for producing and storing, ice slurry use has made significant progress. It is expected that its use will form a more efficient alternative to traditional systems in many aspects in the near future.
7. Conclusions
Ice slurry has a long history of development and application. This review has mainly introduced the production methods, concentration measurement approaches, flow characteristics, heat transfer properties, and has described different applications of ice slurry. This can be summarized as follows:
- The production methods of ice slurry mainly include surface-scraping, supercooling, vacuum, fluidized bed, and direct contact methods. Among them, the surface-scraping method is still the most widely used approach due to its mature technology. Other methods are still under development and are not ready for full commercialization yet.
- The concentration of ice crystals in ice slurry is changing due to the heat exchange. The measurement of ice crystal concentration is divided into two steps: prior and current use. For the prior use, the common methods are the coffeepot press measurement, temperature measurement, conductivity measurement, and calorimetry measurement. For ice slurry flowing in pipelines, non-invasive approaches are adopted to measure its concentration, including ultrasonic detection, electrical resistance tomography, magnetic resonance imaging, and electromagnetic attenuation, which do not affect the ice crystal movements and carrier fluid flows and ensure the synchronization of the concentration and velocity measurement compared to intrusive detection.
- The flow characteristics of ice slurry are more complex than those of normal Newtonian fluids. There are four rheological models suitable for ice slurry as a non-Newtonian fluid: the Power law model, the Bingham model, the Herschel-Bulkley model, and the Casson model. Based on numerous studies on the rheological behavior and the pressure drop change of ice slurry, a generally accepted result is that the pressure drop of ice slurry increases with flow rate and ice concentration.
- Likewise, the heat transfer characteristics of ice slurry are also more complex than those of normal Newtonian fluids. Based on previous studies on the heat transfer property of ice slurry, the generally accepted conclusion is that the heat transfer coefficient of ice slurry increases with ice concentration, which is due to the phase change with a large latent heat.
- To date, ice slurry has been used in many industries, such as food preservation, comfortable cooling, medical protective cooling, pipeline cleaning, sport cooling, instrument cooling, firefighting, artificial snowmaking, etc. Most of these applications utilize its cooling. Pipeline pigging applications use the friction between the ice slurry with high concentration and the inner wall of the pipe, where the friction from the ice slurry is several times greater than that of water at the same flow rate.
Though the special properties of ice slurry make it an important alternative in many aspects, there are nevertheless technical problems to resolve to move forward. Those include:
- A better production method that is efficient, reliable, energy-saving, mass-production, and fully commercial.
- A better storage method that can control the growth of ice crystals in the ice slurry, prevent ice slurry from clumping, and ensure its smoothness and uniformity.
- A better concentration measurement method that is nonintrusive, accurate, easily operated, and cheap.
- A clearer relationship between rheological and heat transfer characteristics, including flow rate, ice concentration, ice volume, diameter, length, material, and shape of the equipment, through experiments and numerical simulations.
If the above problems are solved or improved, the application of ice slurry will improve and will become extensive and energy-saving. This would be in line with the current sustainable development targets setup worldwide.
Author Contributions
Conceptualization, H.S., P.G.V., and J.Z.; methodology, H.S.; formal analysis, H.S.; data curation, J.Z.; writing—original draft preparation, H.S.; writing—review and editing, P.G.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data related to this research are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bellas, I.; Tassou, S.A. Present and future applications of ice slurries. Int. J. Refrig. Rev. Int. Du Froid 2005, 28, 115–121. [Google Scholar] [CrossRef]
- Kuriyama, T.; Sawahata, Y. Slurry ice transportation and cold distribution system. In Proceedings of the Information Booklet for the Technical Tour of the Fourth Workshop of IIR Ice Slurry, Working Party, Kyoto, Japan, 13 November 2001; pp. 1–6. [Google Scholar]
- Evans, T.S. Technical Aspects of Pipeline Pigging with Flowing Ice Slurries; University of Bristol: Bristol, UK, 2007. [Google Scholar]
- Tabuchi, S.; Horie, S.; Kawanami, S.; Inoue, D.; Morizane, S.; Inoue, J.; Nagano, C.; Sakurai, M.; Serizawa, R.; Hamada, K. Efficacy of ice slurry and carbohydrate–electrolyte solutions for firefighters. J. Occup. Health 2021, 63, e12263. [Google Scholar] [CrossRef] [PubMed]
- Tuchayi, S.M.; Wang, Y.; Khodorova, A.; Pence, I.J.; Evans, C.L.; Anderson, R.R.; Lerner, E.A.; Woolf, C.J.; Garibyan, L. Cryoneurolysis with injectable ice slurry modulates mechanical skin pain. J. Investig. Dermatol. 2023, 143, 134–141. [Google Scholar] [CrossRef] [PubMed]
- Honke, M.; Safarik, M.; Herzog, R. R718 turbo chillers and vacuum ice generation—Two applications of a new generation of high speed, high capacity R718 centrifugal compressors. In Proceedings of the 24th IIR International Congress of Refrigeration, Yokohama, Japan, 16–22 August 2015; pp. 16–22. [Google Scholar]
- Kauffeld, M. Heat transfer and pressure drop with ice slurry. In Proceedings of the Fourth IIR Gustav Lorentzen Conference on Natural Working Fluids, West Lafayette, IN, USA, 25–28 July 2000. [Google Scholar]
- Kauffeld, M.; Ernst, G. Influence of the wall surface roughness on the supercooling degree of water flowing inside a heat exchanger. In Proceedings of the 11th IIR Conference on Phase Change Materials and Slurries for Refrigeration and Air Conditioning, Karlsruhe, Germany, 18–20 May 2016. [Google Scholar]
- Langlois, V.; Gautherin, W.; Laurent, J.; Royon, L.; Fournaison, L.; Delahaye, A.; Jia, X. Ultrasonic determination of the particle concentration in model suspensions and ice slurry. Int. J. Refrig. 2011, 34, 1972–1979. [Google Scholar] [CrossRef]
- Norgaard, E.; Albrecht, S. Ice concentrators. In Proceedings of the Fourth IIR Ice slurry Workshop, Osaka, Japan, 12–13 November 2001. [Google Scholar]
- Nørgaard, E.; Sørensen, T.; Hansen, T.; Kauffeld, M. Performance of components of ice slurry systems: Pumps, plate heat exchangers, and fittings. Int. J. Refrig. 2005, 28, 83–91. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Zhuang, K.; Fu, R.; Lin, S.; Li, X. Performance study and efficiency improvement of ice slurry production by scraped-surface method. Appl. Sci. 2018, 9, 74. [Google Scholar] [CrossRef]
- Rayhan, F.A.; Pamitran, A.S. Performance of Ice Slurry Generator with Mechanical Scraper Using R-22 and R-290. Int. J. Technol. 2017, 8, 1191–1196. [Google Scholar] [CrossRef]
- Yamada, M.; Fukusako, S.; Kawabe, H. A quantitative evaluation of the production performance of ice slurry by the oscillatory moving cooled wall method. Int. J. Refrig. 2002, 25, 199–207. [Google Scholar] [CrossRef]
- Bédécarrats, J.-P.; David, T.; Castaing-Lasvignottes, J. Ice slurry production using supercooling phenomenon. Int. J. Refrig. 2010, 33, 196–204. [Google Scholar] [CrossRef]
- Brooks, S. Supercooling Brine in a Helical Coiled Heat Exchanger for Ice Slurry Production: Experiments Supercooling Brine in Heat Exchangers to Generate Ice Slurry Hygienically and Efficiently; University of Bristol: Bristol, UK, 2019. [Google Scholar]
- Shi, X.J.; Zhang, P. A comparative study of different methods for the generation of tetra-n-butyl ammonium bromide clathrate hydrate slurry in a cold storage air-conditioning system. Appl. Energy 2013, 112, 1393–1402. [Google Scholar] [CrossRef]
- Kauffeld, M.; Gund, S. Ice slurry–History, current technologies and future developments. Int. J. Refrig. 2019, 99, 264–271. [Google Scholar] [CrossRef]
- Liu, X.; Zhuang, K.Y.; Lin, S.; Zhang, Z.; Li, X.L. Determination of Supercooling Degree, Nucleation and Growth Rates, and Particle Size for Ice Slurry Crystallization in Vacuum. Crystals 2017, 7, 128. [Google Scholar] [CrossRef]
- Shin, H.T.; Lee, Y.P.; Jurng, J. Spherical-shaped ice particle production by spraying water in a vacuum chamber. Appl. Therm. Eng. 2000, 20, 439–454. [Google Scholar] [CrossRef]
- Hongfen, C.; Wenzhuang, Z.; Weisan, H.; Xuelai, Z. Vacuum ice-making technology and characteristic analysis. J. Mol. Liq. 2022, 360, 119360. [Google Scholar] [CrossRef]
- Meewisse, J.W. Fluidized Bed Ice Slurry Generator for Enhanced Secondary Cooling Systems; Technische Universiteit Delft: Delft, The Netherlands, 2002. [Google Scholar]
- Zhengbiao, P.; Zhulin, Y.; Liang, K.; Jie, C. Ice slurry formation in a cocurrent liquid-liquid flow. Chin. J. Chem. Eng. 2008, 16, 552–557. [Google Scholar]
- Thongwik, S.; Vorayos, N.; Kiatsiriroat, T.; Nuntaphan, A. Thermal analysis of slurry ice production system using direct contact heat transfer of carbon dioxide and water mixture. Int. Commun. Heat Mass Transf. 2008, 35, 756–761. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Su, L.; Dong, K.J.; Liu, T.Q. Experimental study of ice slurry production system using direct contact heat transfer of RC318 and water in a horizontal pipe. Energy Procedia 2019, 158, 4495–4501. [Google Scholar] [CrossRef]
- Amer, M.; Wang, C. Review of defrosting methods. Renew. Sustain. Energy Rev. 2017, 73, 53–74. [Google Scholar] [CrossRef]
- Evans, T.S.; Quarini, G.L.; Shire, G.S.F. Investigation into the transportation and melting of thick ice slurries in pipes. Int. J. Refrig. 2008, 31, 145–151. [Google Scholar] [CrossRef]
- Melinder, Å. Thermophysical Properties of Aqueous Solutions Used as Secondary Working Fluids. Ph.D. Thesis, Kungliga Tekniska Högskolan, Stockholm, Sweden, 2007. [Google Scholar]
- Wang, J.H.; Wang, S.G.; Zhang, T.F.; Battaglia, F. Mathematical and experimental investigation on pressure drop of heterogeneous ice slurry flow in horizontal pipes. Int. J. Heat Mass Transf. 2017, 108, 2381–2392. [Google Scholar] [CrossRef]
- Hägg, C. Ice Slurry as Secondary Fluid in Refrigeration Systems: Fundamentals and Applications in Supermarkets. Ph.D. Thesis, Kungliga Tekniska Högskolan, Stockholm, Sweden, 2005. [Google Scholar]
- Rui, W. Experimental Study on Pigging Effect of Ice Slurry; China University of Petroleum: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Ferguson, H.F.; Frurip, D.J.; Pastor, A.J.; Peerey, L.M.; Whiting, L.F. A review of analytical applications of calorimetry. Thermochim. Acta 2000, 363, 1–21. [Google Scholar] [CrossRef]
- Shire, S.; Quarini, I.; Ayala, R.S. Ultrasonic detection of slurry ice flows. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2005, 219, 217–225. [Google Scholar] [CrossRef]
- Quarini, G.L. Pigging with pumpable ice-update. Food Link News 2003, 45, 10–11. [Google Scholar]
- Albion, K.J.; Briens, L.; Briens, C.; Berruti, F. Multiphase Flow Measurement Techniques for Slurry Transport. Int. J. Chem. React. Eng. 2011, 9, 1–50. [Google Scholar] [CrossRef]
- Dickin, F.; Wang, M. Electrical resistance tomography for process applications. Meas. Sci. Technol. 1996, 7, 247–260. [Google Scholar] [CrossRef]
- Fangary, Y.S.; Williams, R.A.; Neil, W.A.; Bond, J.; Faulks, I. Application of electrical resistance tomography to detect deposition in hydraulic conveying systems. Powder Technol. 1998, 95, 61–66. [Google Scholar] [CrossRef]
- Giguère, R.; Fradette, L.; Mignon, D.; Tanguy, P.A. Characterization of slurry flow regime transitions by ERT. Chem. Eng. Res. Des. 2008, 86, 989–996. [Google Scholar] [CrossRef]
- Lucas, G.; Cory, J.; Waterfall, R.; Loh, W.; Dickin, F. Measurement of the solids volume fraction and velocity distributions in solids–liquid flows using dual-plane electrical resistance tomography. Flow Meas. Instrum. 1999, 10, 249–258. [Google Scholar] [CrossRef]
- Norman, J.T.; Bonnecaze, R.T. Measurement of solids distribution in suspension flows using electrical resistance tomography. Can. J. Chem. Eng. 2005, 83, 24–36. [Google Scholar] [CrossRef]
- Wang, M.; Jones, T.F.; Williams, R.A. Visualization of asymmetric solids distribution in horizontal swirling flows using electrical resistance tomography. Chem. Eng. Res. Des. 2003, 81, 854–861. [Google Scholar] [CrossRef]
- Zhang, J.G.; Mab, F.C. Application of Electrical Resistance Tomography to Ice-water Two-phase Flow Parameters Measurement. Key Eng. Mater. 2013, 562–565, 686–690. [Google Scholar] [CrossRef]
- Aw, S.R.; Rahim, R.A.; Rahiman, M.H.F.; Yunus, F.R.M.; Goh, C.L. Electrical resistance tomography: A review of the application of conducting vessel walls. Powder Technol. 2014, 254, 256–264. [Google Scholar] [CrossRef]
- Edelhoff, D.; Walczak, L.; Henning, S.; Weichert, F.; Suter, D. High-resolution MRI velocimetry compared with numerical simulations. J. Magn. Reson. 2013, 235, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Graham, L.J.W.; Pullum, L. An investigation of complex hybrid suspension flows by magnetic resonance imaging. Can. J. Chem. Eng. 2002, 80, 200–207. [Google Scholar] [CrossRef]
- Powell, R.L. Experimental techniques for multiphase flows. Phys. Fluids 2008, 20, 040605. [Google Scholar] [CrossRef]
- Pullum, L.; Graham, L.; Rudman, M.; Hamilton, R. High concentration suspension pumping. Miner. Eng. 2006, 19, 471–477. [Google Scholar] [CrossRef]
- Sederman, A.J.; Johns, M.L.; Bramley, A.S.; Alexander, P.; Gladden, L.F. Magnetic resonance imaging of liquid flow and pore structure within packed beds. Chem. Eng. Sci. 1997, 52, 2239–2250. [Google Scholar] [CrossRef]
- Ray, P.S. Broadband complex refractive indices of ice and water. Appl. Opt. 1972, 11, 1836–1844. [Google Scholar] [CrossRef]
- Hales, A.; Quarini, G.; Hilton, G.; Ash, D.; Lucas, E.; McBryde, D.; Yun, X. Ice fraction measurement of ice slurries through electromagnetic attenuation. Int. J. Refrig. 2014, 47, 98–104. [Google Scholar] [CrossRef]
- Hales, A.; Quarini, G.; Hilton, G.; Jones, L.; Lucas, E.; McBryde, D.; Yun, X. The effect of salinity and temperature on electromagnetic wave attenuation in brine. Int. J. Refrig. 2015, 51, 161–168. [Google Scholar] [CrossRef]
- Tian, Q.Q.; He, G.G.; Wang, H.; Cai, D.H. Simulation on transportation safety of ice slurry in ice cooling system of buildings. Energy Build. 2014, 72, 262–270. [Google Scholar] [CrossRef]
- Bel, O. Contribution à l’étude du Comportement Thermohydraulique d’un Mélange Diphasique: Lecoulis de Glace. Etude Théorique et Expérimentale. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 1996. [Google Scholar]
- Lakhdar, M.A.B.; Lallemand, A. Comportement Thermohydraulique d’un Fluide Frigoporteur Diphasique: Le Coulis de Glace. Etude Théorique et Expérimentale. Ph.D. Thesis, INSA Lyon, Villeurbanne, France, 1998. [Google Scholar]
- Christensen, K.G.; Kauffeld, M. Heat transfer measurements with ice slurry. In Proceedings of the Heat Transfer Issues in Natural Refrigerants, IIR/IIF, College Park, MD, USA, 31 December 1997; pp. 127–141. [Google Scholar]
- Doetsch, C. Pressure drop and flow pattern of ice slurries. In Proceedings of the 3rd Workshop on Ice Slurries of the IIR, Lucerne, Switzerland, 1 January 2001; pp. 53–54. [Google Scholar]
- Jensen, E.N.; Christensen, K.G.; Hansen, T.M.; Schneider, P.; Kauffeld, M. Pressure drop and heat transfer with ice slurry. In Proceedings of the Conférence IIR-Gustav Lorentzen sur les fluides actifs naturels à Purdue, West Lafayette, IN, USA, 25 July 2000; pp. 572–580. [Google Scholar]
- Royon, L. Qu’est-ce que le coulis de glace stabilisée: Fluides et lubrifiants. Rev. Générale Du Froid 1998, 88, 57–60. [Google Scholar]
- Ayel, V.; Lottin, O.; Peerhossaini, H. Rheology, flow behaviour and heat transfer of ice slurries: A review of the state of the art. Int. J. Refrig. 2003, 26, 95–107. [Google Scholar] [CrossRef]
- Einstein, A. A new determination of molecular dimensions. Annln. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Thomas, D.G. Transport characteristics of suspension: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles. J. Colloid Sci. 1965, 20, 267–277. [Google Scholar] [CrossRef]
- Hansen, T.M.; Kauffeld, M.; Grosser, K.; Zimmermann, R. Viscosity of ice slurry. In Proceedings of the Second Workshop on Ice Slurries of the International Institute of Refrigeration, Paris, France, 25–26 May 2000; p. 8. [Google Scholar]
- Ismail, K.A.R.; Radwan, M.M. Modeling of ice crystal growth in laminar falling films for the production of pumpable ice slurries. Energy Convers. Manag. 2003, 44, 65–84. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Kumano, H.; Hirata, T.; Shirakawa, M.; Shouji, R.; Hagiwara, Y. Flow characteristics of ice slurry in narrow tubes. Int. J. Refrig. 2010, 33, 1513–1522. [Google Scholar] [CrossRef]
- Kumano, H.; Yamanada, Y.; Makino, Y.; Asaoka, T. Effect of initial aqueous solution concentration on rheological behavior of ice slurry. Int. J. Refrig. 2016, 68, 218–225. [Google Scholar] [CrossRef]
- Niezgoda-Żelasko, B.; Zalewski, W. Momentum transfer of ice slurry flows in tubes, experimental investigations. Int. J. Refrig. 2006, 29, 418–428. [Google Scholar] [CrossRef]
- Niezgoda-Żelasko, B.; Żelasko, J. Generalized non-Newtonian flow of ice-slurry. Chem. Eng. Process. Process Intensif. 2007, 46, 895–904. [Google Scholar] [CrossRef]
- Illán, F.; Viedma, A. Experimental study on pressure drop and heat transfer in pipelines for brine based ice slurry. Part I: Operational parameters correlations. Int. J. Refrig. 2009, 32, 1015–1023. [Google Scholar] [CrossRef]
- Illán, F.; Viedma, A. Experimental study on pressure drop and heat transfer in pipelines for brine based ice slurry Part II: Dimensional analysis and rheological model. Int. J. Refrig. 2009, 32, 1024–1031. [Google Scholar] [CrossRef]
- Doetsch, C. Pressure drop calculation of ice slurries using the Casson model. In Proceedings of the 5th Workshop on Ice Slurries, IIF/IIR, Stockholm, Sweden, 30–31 May 2002; pp. 15–21. [Google Scholar]
- Monteiro, A.C.S.; Bansal, P.K. Pressure drop characteristics and rheological modeling of ice slurry flow in pipes. Int. J. Refrig. 2010, 33, 1523–1532. [Google Scholar] [CrossRef]
- Brown, G.O. The history of the Darcy-Weisbach equation for pipe flow resistance. In Environmental and Water Resources History; ASCE: Reston, VA, USA, 2002; pp. 34–43. [Google Scholar]
- Grozdek, M.; Khodabandeh, R.; Lundqvist, P. Experimental investigation of ice slurry flow pressure drop in horizontal tubes. Exp. Therm. Fluid Sci. 2009, 33, 357–370. [Google Scholar] [CrossRef]
- Kumano, H.; Mizui, A.; Higashi, N. Flow characteristics of ice slurry in a horizontal tube during solidification. Int. J. Refrig. 2018, 85, 184–190. [Google Scholar] [CrossRef]
- Dodge, D.; Metzner, A. Turbulent flow of non—Newtonian systems. AIChE J. 1959, 5, 189–204. [Google Scholar] [CrossRef]
- Hanks, R.W.; Ricks, B.L. Transitional and turbulent pipeflow of pseudoplastic fluids. J. Hydronautics 1975, 9, 39–44. [Google Scholar] [CrossRef]
- Shire, G.S.F.; Quarini, G.L.; Rhys, T.D.L.; Evans, T.S. The anomalous pressure drop behaviour of ice slurries flowing through constrictions. Int. J. Multiph. Flow 2008, 34, 510–515. [Google Scholar] [CrossRef][Green Version]
- Shire, G.S.F.; Quarini, G.L.; Evans, T.S. Pressure drop of flowing ice slurries in industrial heat exchangers. Appl. Therm. Eng. 2009, 29, 1500–1506. [Google Scholar] [CrossRef][Green Version]
- Bellas, J.; Chaer, I.; Tassou, S.A. Heat transfer and pressure drop of ice slurries in plate heat exchangers. Appl. Therm. Eng. 2002, 22, 721–732. [Google Scholar] [CrossRef]
- Gupta, R.P. Effect of a New Friction-Reducing Additive on Sunwell Ice Slurry Characteristics; National Research Council of Canada: Ottawa, ON, Canada, 1990. [Google Scholar]
- Kalaiselvam, S.; Karthik, P.; Prakash, S.R. Numerical investigation of heat transfer and pressure drop characteristics of tube–fin heat exchangers in ice slurry HVAC system. Appl. Therm. Eng. 2009, 29, 1831–1839. [Google Scholar] [CrossRef]
- Fernández-Seara, J.; Diz, R.; Uhía, F.J.; Dopazo, J.A. Experimental analysis on pressure drop and heat transfer of a terminal fan-coil unit with ice slurry as cooling medium. Int. J. Refrig. 2010, 33, 1095–1104. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhang, T.F.; Wang, S.G. Heterogeneous ice slurry flow and concentration distribution in horizontal pipes. Int. J. Heat Fluid Flow 2013, 44, 425–434. [Google Scholar] [CrossRef]
- Singh, R.; Kachhwaha, S.S. Heat Transfer and Pressure Drop Analysis of Chilled Water and Ice Slurry in a Plate Heat Exchanger. J. Therm. Sci. Eng. Appl. 2016, 8, 011020. [Google Scholar] [CrossRef]
- Mi, S.; Cai, L.L.; Ma, K.B.; Liu, Z.Q. Investigation on flow and heat transfer characteristics of ice slurry without additives in a plate heat exchanger. Int. J. Heat Mass Transf. 2018, 127, 11–20. [Google Scholar] [CrossRef]
- Farajollahi, B.; Etemad, S.G.; Hojjat, M. Heat transfer of nanofluids in a shell and tube heat exchanger. Int. J. Heat Mass Transf. 2010, 53, 12–17. [Google Scholar] [CrossRef]
- Wang, J.H.; Battaglia, F.; Wang, S.G.; Zhang, T.F.; Ma, Z.J. Flow and heat transfer characteristics of ice slurry in typical components of cooling systems: A review. Int. J. Heat Mass Transf. 2019, 141, 922–939. [Google Scholar] [CrossRef]
- Vicente, P.G.; García, A.; Viedma, A. Experimental investigation on heat transfer and frictional characteristics of spirally corrugated tubes in turbulent flow at different Prandtl numbers. Int. J. Heat Mass Transf. 2004, 47, 671–681. [Google Scholar] [CrossRef]
- Meewisse, J.; Infante-Ferreira, C. Optimal properties of ice slurries in secondary cooling systems. In Proceedings of the 4 th–IIR-Gustaw Lorentzen Conference on Natural Working Fluids, Purdue University, West Lafayette, IN, USA; 2000; pp. 513–520. [Google Scholar]
- Harada, E.; Toda, M.; Kuriyama, M.; Konno, H. Heat-Transfer between Wall and Solid-Water Suspension Flow in Horizontal Pipes. J. Chem. Eng. Jpn. 1985, 18, 33–38. [Google Scholar] [CrossRef]
- Kawanami, T.; Yamada, M.; Fukusako, S. Melting characteristics of fine particle ice slurry at the return bend of flow path. In Proceedings of the Third Workshop on Ice Slurries of the International Institute of Refrigeration, Lucerne, Switzerland; 2001; pp. 16–18. [Google Scholar]
- Knodel, B.D.; France, D.M.; Choi, U.S.; Wambsganss, M.W. Heat transfer and pressure drop in ice-water slurries. Appl. Therm. Eng. 2000, 20, 671–685. [Google Scholar] [CrossRef]
- Stamatiou, E.; Kawaji, M.; Lee, B.; Goldstein, V. Experimental investigation of ice-slurry flow and heat transfer in a plate-type heat exchanger. In Proceedings of the 3rd IIR Workshop on Ice Slurries, Lucerne, Switzerland, 16–18 May 2001; pp. 16–18. [Google Scholar]
- Zhao, J.; Liu, Y.; Zhang, E.; Chen, P.J.S.e.t.d.f. Experiment study on cooling coil performance with ice slurry as working fluid. In Proceedings of the International Symposium on Air Conditioning in High Rise Buildings, Shanghai, China, 9–12 September 1997; pp. 495–499. [Google Scholar]
- Mokrani, A.; Castelain, C.; Peerhossaini, H. The effects of chaotic advection on heat transfer. Int. J. Heat Mass Transf. 1997, 40, 3089–3104. [Google Scholar] [CrossRef]
- Egolf, P.W.; Kitanovski, A.; Ata-Caesar, D.; Stamatiou, E.; Kawaji, M.; Bedecarrats, J.P.; Strub, F. Thermodynamics and heat transfer of ice slurries. Int. J. Refrig. 2005, 28, 51–59. [Google Scholar] [CrossRef]
- Bédécarrats, J.-P.; Strub, F.; Peuvrel, C. Thermal and hydrodynamic considerations of ice slurry in heat exchangers. Int. J. Refrig. 2009, 32, 1791–1800. [Google Scholar] [CrossRef]
- Haruki, N.; Horibe, A. Flow and heat transfer characteristics of ice slurries in a helically-coiled pipe. Int. J. Refrig. 2013, 36, 1285–1293. [Google Scholar] [CrossRef]
- Fernández-Seara, J.; Diz, R. Thermo-hydraulic behavior of ice slurry in an offset strip-fin plate heat exchanger. Int. J. Refrig. 2014, 41, 171–180. [Google Scholar] [CrossRef]
- Leiper, A.N.; Ash, D.G.; McBryde, D.J.; Quarini, G.L. Improving the thermal efficiency of ice slurry production through comminution. Int. J. Refrig. 2012, 35, 1931–1939. [Google Scholar] [CrossRef]
- Leiper, A.N.; Hammond, E.C.; Ash, D.G.; McBryde, D.J.; Quarini, G.L. Energy conservation in ice slurry applications. Appl. Therm. Eng. 2013, 51, 1255–1262. [Google Scholar] [CrossRef]
- Quarini, G.; Aislie, E.; Ash, D.; Leiper, A.; McBryde, D.; Herbert, M.; Deans, T. Transient thermal performance of ice slurries pumped through pipes. Appl. Therm. Eng. 2013, 50, 743–748. [Google Scholar] [CrossRef]
- Brooks, S.; Tierney, M.; Quarini, G. Experimental investigation of different materials for use in ice slurry generation. Int. J. Refrig. 2021, 129, 97–108. [Google Scholar] [CrossRef]
- Yang, S.W.; Liang, K.F.; Wang, L.; Liu, J.; Li, Y.C.; Chen, C.S.; Yuan, Y. Experimental study on effects of particle melting and micro-convection on measurement of thermal conductivity of ice slurry. Int. Commun. Heat Mass Transf. 2022, 136, 106178. [Google Scholar] [CrossRef]
- Gao, Y.G.; Ning, Y.L.; Xu, M.H.; Wu, C.Z.; Mujumdar, A.S.; Sasmito, A.P. Numerical investigation of aqueous graphene nanofluid ice slurry passing through a horizontal circular pipe: Heat transfer and fluid flow characteristics. Int. Commun. Heat Mass Transf. 2022, 134, 106022. [Google Scholar] [CrossRef]
- Cai, L.; Mi, S.; Luo, C.; Liu, Z. Numerical investigation of hydraulic and heat transfer characteristics of two-phase ice slurry in helically coiled tubes. Energy Build. 2022, 256, 111773. [Google Scholar] [CrossRef]
- Cai, L.; Mi, S.; Luo, C.; Liu, Z. Numerical investigation on heat and mass transfer characteristics of ice slurry in pulsating flow. Int. J. Heat Mass Transf. 2022, 189, 122722. [Google Scholar] [CrossRef]
- Suzuki, K.; Kuroiwa, T.; Asaoka, T.; Yoshino, M. Particle-resolved simulations of ice slurry flows in a square duct by the thermal immersed boundary–lattice Boltzmann method. Comput. Fluids 2021, 228, 105064. [Google Scholar] [CrossRef]
- Kishore, A.; Aravind, S.M.; Kumar, P.; Singh, A.; Kumari, K.; Kumar, N. Innovative Packaging Strategies for Freshness and Safety of Food Products: A Review. Packag. Technol. Sci. 2024, 37, 399–427. [Google Scholar] [CrossRef]
- Ssubi, J.A.; Mukisa, I.M.; Muyanja, C.K. Knowledge, attitudes and practices of fresh Nile perch value chain handlers towards food safety requirements in Uganda. Heliyon 2024, 10, e31432. [Google Scholar] [CrossRef]
- Lydon, K.A.; Farrell-Evans, M.; Jones, J.L. Evaluation of Ice Slurries as a Control for Postharvest Growth of Vibrio spp. in Oysters and Potential for Filth Contamination. J. Food Prot. 2015, 78, 1375–1379. [Google Scholar] [CrossRef]
- Rey, M.S.; Miranda, J.M.; Aubourg, S.; Barros-Velázquez, J. Improved microbial and sensory quality of clams (Venerupis rhomboideus), oysters (Ostrea edulis) and mussels (Mytilus galloprovincialis) by refrigeration in a slurry ice packaging system. Int. J. Food Sci. Technol. 2012, 47, 861–869. [Google Scholar] [CrossRef]
- Rodríguez, Ó.; Barros-Velázquez, J.; Piñeiro, C.; Gallardo, J.M.; Aubourg, S.P. Effects of storage in slurry ice on the microbial, chemical and sensory quality and on the shelf life of farmed turbot (Psetta maxima). Food Chem. 2006, 95, 270–278. [Google Scholar] [CrossRef]
- Wang, M.; Hansen, T.; Kauffeld, M.; Christensen, K.; Goldstein, V. Application of ice slurry technology in fishery. In Proceedings of the 20th International Congress of Refrigeration, IIF/IIR, Sydney, Australia, 19–24 September 1999; pp. 569–573. [Google Scholar]
- Paul, J. Innovative Applications of Pumpable Ice Slurry; Institute of Refrigeration: London, UK, 2002. [Google Scholar]
- Annamalai, J.; Lakshmi, N.M.; Sivam, V.; Rao, R.C.N. A Comparative Study on the Quality Changes of Croaker (Johnius dussumieri) Fish Stored in Slurry Ice and Flake Ice. J. Aquat. Food Prod. Technol. 2018, 27, 508–517. [Google Scholar] [CrossRef]
- Piñeiro, C.; Barros-Velázquez, J.; Aubourg, S.P. Effects of newer slurry ice systems on the quality of aquatic food products: A comparative review versus flake-ice chilling methods. Trends Food Sci. Technol. 2004, 15, 575–582. [Google Scholar] [CrossRef]
- Wang, M.J.; Goldstein, V. Ice slurry: Advanced fish chilling and preservation technology. In Proceedings of the American Fisheries Society Symposium, Quebec, QC, Canada, 11–12 August 2003; pp. 379–386. [Google Scholar]
- Gladis, S. Ice slurry thermal energy storage for cheese process cooling. ASHRAE Trans. 1997, 103, 725–729. [Google Scholar]
- Hansen, T.M.; Kauffeld, M.; Sari, O.; Egolf, P.W.; Pasche, F. Research, development and applications of ice slurry in Europe. In Proceedings of the Fourth Workshop on Ice Slurries of the International Institute of Refrigeration, Osaka, Japan, 1 January 2001; pp. 1–12. [Google Scholar]
- Tassou, S.; Chaer, I.; Bellas, J.; Terzis, G. Comparison of the performance of ice slurry and traditional primary and secondary refrigerants in refrigerated food display cabinet cooling coil. In Proceedings of the Fourth Workshop on Ice Slurries, Osaka, Japan, 12–13 November 2001; pp. 87–95. [Google Scholar]
- Lueders, D. Application of ice slurry/TES technology to supermarkets using ammonia refrigeration. In Proceedings of the 21st Annual Meeting of the International Meeting of Ammonia Refrigeration, Dallas, TX, USA, 21–24 March 1999; pp. 301–326. [Google Scholar]
- Davies, T.W.; Lowes, A.L. A high efficiency refrigeration system. In Proceedings of the IIR conference New Technologies in Commercial Refrigeration, Paris, France, Urbana, IL, USA, 22–23 July 2002; pp. 93–100. [Google Scholar]
- Kauffeld, M.; Wang, M.J.; Goldstein, V.; Kasza, K.E. Ice Slurry Applications. Int. J. Refrig. 2010, 33, 1491–1505. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.J.; Kusumoto, N. Ice slurry based thermal storage in multifunctional buildings. Heat Mass Transf. 2001, 37, 597–604. [Google Scholar] [CrossRef]
- Rivet, P. Overview of PCM applications around the worls—Regional overview Europe. In Proceedings of the 8 th IIR Conference on Phase Change Materials and Slurries for Refrigeration and Air Conditioning, Karlsruhe, Germany, 3–5 June 2009; pp. 3–5. [Google Scholar]
- Yoo, H.; Lee, S.H.; Lee, Y.P. A Field Application Case of the Direct Ice Slurry Transporting System for District Cooling. Int. J. Air Cond. Refrig. 2012, 18, 43–53. [Google Scholar] [CrossRef]
- Chung, J.D.; Lee, Y.P.; Yoo, H.; Lee, J.H.; Lee, C.J.; Moon, S.J. Feasibility Study for Ice-Slurry to District Cooling System in Korea. In Proceedings of the Volume 1: Heat Transfer in Energy Systems; Thermophysical Properties; Theory and Fundamental Research in Heat Transfer, Minneapolis, MN, USA, 14–19 July 2013; p. 001. [Google Scholar]
- Compingt, A.; Blanc, P.; Quidort, A. Slurry for refrigeration industrial kitchen application. In Proceedings of the 8th IIR Conference on Phase Change Material and Slurries for Refrigeration and Air Conditioning, Karlsruhe, Germany, 3–5 June 2009. [Google Scholar]
- Hager, M.; Kaemper, T. The hydraulic transport of ice for mine-cooling. Powder Handl. Process. 1991, 3, 317–325. [Google Scholar]
- Sheer, T.; Correia, R.; Chaplain, E.; Hemp, R. Research into the use of ice for cooling deep mines. In Proceedings of the Third International Mine Ventilation Congress, Harrogate, UK, 13–19 June 1984; pp. 277–282. [Google Scholar]
- Sheer, T.J. Pneumatic Conveying of Ice Particles through Mine-Shaft Pipelines. Powder Technol. 1995, 85, 203–219. [Google Scholar] [CrossRef]
- Ophir, A.; Koren, A. Vacuum freezing vapor compression process (VFVC) for mine cooling. In Proceedings of the 20th International Congress of Refrigeration, IIF/IIR, Sydey, Australia, 19–24 September 1999; p. 508. [Google Scholar]
- Chen, W.; Liang, S.; Liu, J. Proposed split-type vapor compression refrigerator for heat hazard control in deep mines. Appl. Therm. Eng. 2016, 105, 425–435. [Google Scholar] [CrossRef]
- Kasza, K.; Chang, F.; Oras, J.; Fisher, B.; Shalhav, A.; Oriveto, M.; Mills, R. Modelling of kidney cooling using ice slurry during laparoscopic surgery. In Proceedings of the Bioengineering Conference, Amelia Island, FL, USA, 21–25 June 2006. [Google Scholar]
- Laven, B.A.; Kasza, K.E.; Rapp, D.E.; Orvieto, M.A.; Lyon, M.B.; Oras, J.J.; Beiser, D.G.; Vanden Hoek, T.L.; Son, H.; Shalhav, A.L. A pilot study of ice-slurry application for inducing laparoscopic renal hypothermia. BJU Int. 2007, 99, 166–170. [Google Scholar] [CrossRef]
- Colli, J.L.; Dorsey, P.; Grossman, L.; Lee, B.R. Retrograde renal cooling to minimize ischemia. Int. Braz. J. Urol. 2013, 39, 37–45. [Google Scholar] [CrossRef][Green Version]
- Summers, E.; Cervantes, T.; Batzer, R.; Simpson, C.; Lewis, R.; Stark, J. Renal Cooling Device for Use in Minimally Invasive Surgery. J. Med. Devices 2012, 6, 021007. [Google Scholar] [CrossRef]
- Tyritzis, S.I.; Kyroudi, A.; Liatsikos, E.; Manousakas, T.; Karayannacos, P.; Kostomitsopoulos, N.; Zervas, A.; Pavlakis, K.; Stolzenburg, J.U.; Constantinides, C. Comparison of prolonged warm and cold ischemia on the solitary kidney during partial nephrectomy in a rabbit model. World J. Urol. 2007, 25, 635–640. [Google Scholar] [CrossRef] [PubMed]
- Otake, H.; Shite, J.; Paredes, O.L.; Shinke, T.; Yoshikawa, R.; Tanino, Y.; Watanabe, S.; Ozawa, T.; Matsumoto, D.; Ogasawara, D.; et al. Catheter-based transcoronary myocardial hypothermia attenuates arrhythmia and myocardial necrosis in pigs with acute myocardial infarction. J. Am. Coll. Cardiol. 2007, 49, 250–260. [Google Scholar] [CrossRef]
- Quarini, G.; Ainslie, E.; Herbert, M.; Deans, T.; Ash, D.; Rhys, D.; Haskins, N.; Norton, G.; Andrews, S.; Smith, M. Investigation and development of an innovative pigging technique for the water-supply industry. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2010, 224, 79–89. [Google Scholar] [CrossRef]
- Vreeburg, J.H.; Boxall, J.B. Discolouration in potable water distribution systems: A review. Water Res. 2007, 41, 519–529. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Lv, J.; Zhang, Y.; Ye, B. Public Awareness of Drinking Water Safety and Contamination Accidents: A Case Study in Hainan Province, China. Water 2018, 10, 446. [Google Scholar] [CrossRef]
- Meroufel, A.A. Corrosion Control during Acid Cleaning of Heat Exchangers. In Corrosion and Fouling Control in Desalination Industry; Saji, V.S., Meroufel, A.A., Sorour, A.A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 209–224. [Google Scholar]
- Tait, W.S. Corrosion prevention and control of chemical processing equipment. In Handbook of Environmental Degradation of Materials; Kutz, M., Ed.; William Andrew Publishing: Norwich, NY, USA, 2005; pp. 565–581. [Google Scholar]
- Burfoot, D.; Middleton, K. Effects of operating conditions of high pressure washing on the removal of biofilms from stainless steel surfaces. J. Food Eng. 2009, 90, 350–357. [Google Scholar] [CrossRef]
- Mucchetti, G.; Bonvini, B.; Francolino, S.; Neviani, E.; Carminati, D. Effect of washing with a high pressure water spray on removal of Listeria innocua from Gorgonzola cheese rind. Food Control. 2008, 19, 521–525. [Google Scholar] [CrossRef]
- Quarini, J.; Shire, S. A review of fluid-driven pipeline pigs and their applications. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2007, 221, 1–10. [Google Scholar] [CrossRef]
- Yang, K.; Wu, C.; Yuan, Y.; Yu, J. Application of Virtual Instrument Technique in Data Acquisition of Gas-Water Pulse Pipe Cleaning Experiment. In Proceedings of the 2nd International Congress on Computer Applications and Computational Science, Bali, Indonesia, 15–17 November 2011; Gaol, F.L., Nguyen, Q.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 465–470. [Google Scholar]
- Quarini, J. Ice-pigging to reduce and remove fouling and to achieve clean-in-place. Appl. Therm. Eng. 2002, 22, 747–753. [Google Scholar] [CrossRef]
- Hales, A.J.; Quarini, G.; Ash, D. The use of ice pigging technology to clean shell and tube exchangers. In Proceedings of the 13th UK Heat Transfer Conference (UKHTC2013), London, UK, 2–3 September 2013. [Google Scholar]
- Shire, G.S.F. The Behaviour of Ice Pigging Slurries; University of Bristol: Bristol, UK, 2006. [Google Scholar]
- Davies, T.W. Slurry ice as a heat transfer fluid with a large number of application domains. Int. J. Refrig. 2005, 28, 108–114. [Google Scholar] [CrossRef]
- Morris, N.B.; Coombs, G.; Jay, O. Ice Slurry Ingestion Leads to a Lower Net Heat Loss during Exercise in the Heat. Med. Sci. Sports Exerc. 2016, 48, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Stevens, C.J.; Dascombe, B.; Boyko, A.; Sculley, D.; Callister, R. Ice slurry ingestion during cycling improves Olympic distance triathlon performance in the heat. J. Sports Sci. 2013, 31, 1271–1279. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).