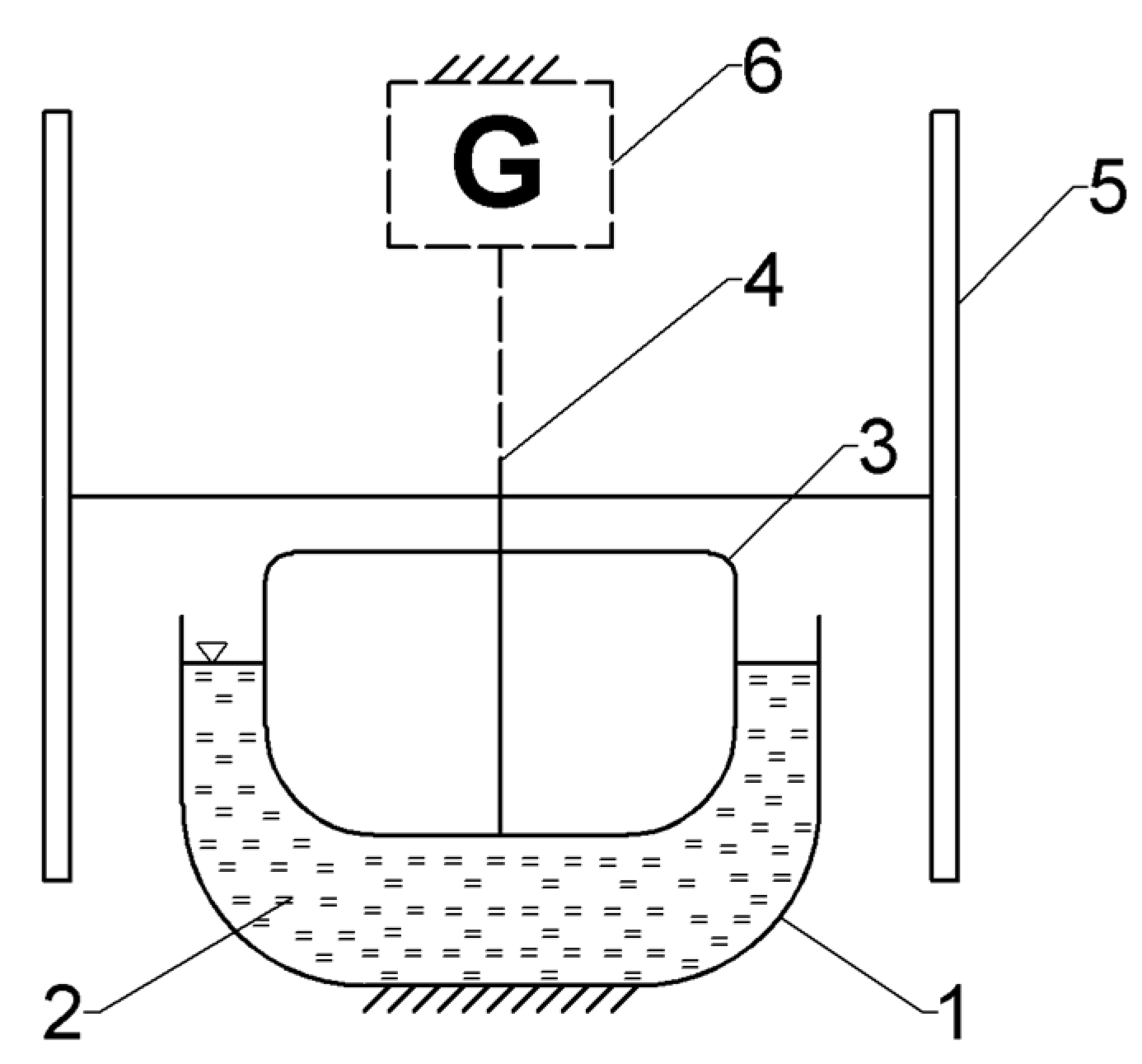
Figure 1.
Configuration of bowl-shaped floating straight-blade VAWT (according to [
31]): 1—foundation box, 2—water, 3—floating bowl-shaped shell, 4—shaft, 5—blades, 6—electricity generator.
Figure 1.
Configuration of bowl-shaped floating straight-blade VAWT (according to [
31]): 1—foundation box, 2—water, 3—floating bowl-shaped shell, 4—shaft, 5—blades, 6—electricity generator.
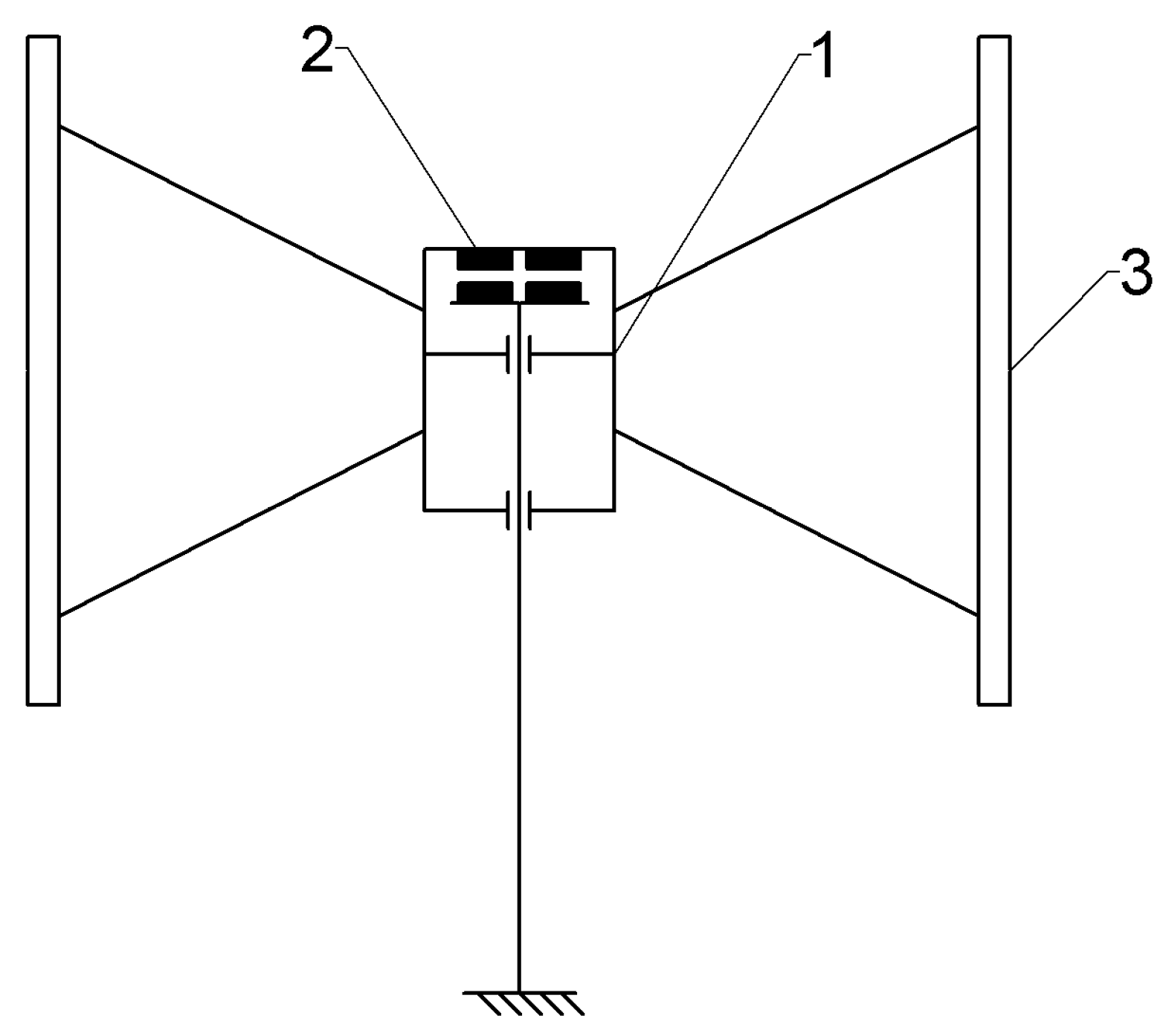
Figure 2.
Diagram of a levitating VAWT wind turbine installed on frictionless magnetic bearings (configuration of magnets, blades, rotors, stators and a shaft) (according to [
36]): 1—shaft, 2—magnetic bearing, 3—rotor magnets, 4—stator coils, 5—blades, 6—support struts.
Figure 2.
Diagram of a levitating VAWT wind turbine installed on frictionless magnetic bearings (configuration of magnets, blades, rotors, stators and a shaft) (according to [
36]): 1—shaft, 2—magnetic bearing, 3—rotor magnets, 4—stator coils, 5—blades, 6—support struts.
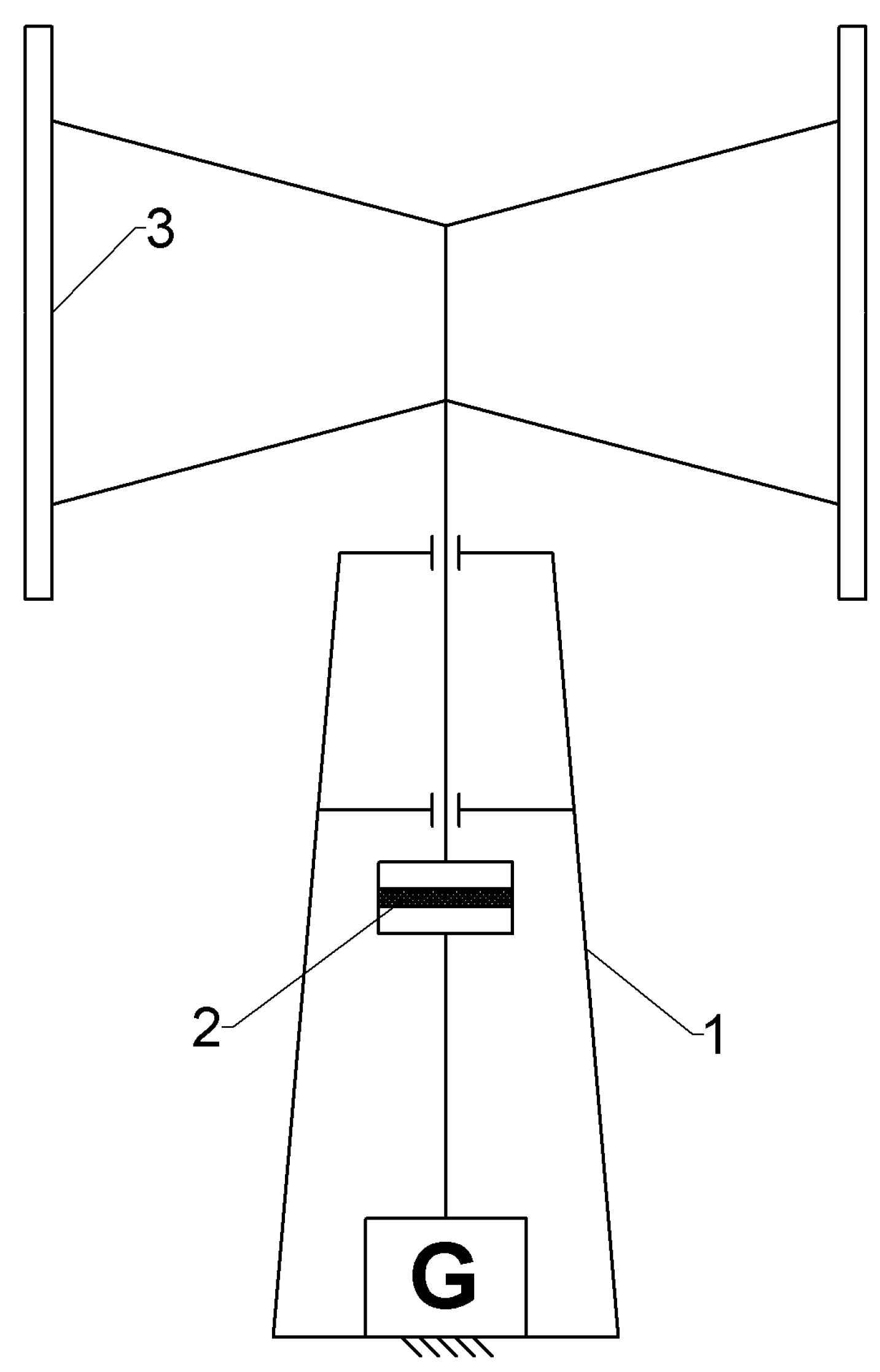
Figure 3.
Bearing of a wind turbine using the magnetic bearing relief based on permanent magnets (according to [
40]): 1—body, 2—magnetic bearing, 3—blades.
Figure 3.
Bearing of a wind turbine using the magnetic bearing relief based on permanent magnets (according to [
40]): 1—body, 2—magnetic bearing, 3—blades.
Figure 4.
Scheme diagram of the wind turbine with a friction clutch (according to [
41]): 1—turbine tower, 2—friction clutch, 3—blades.
Figure 4.
Scheme diagram of the wind turbine with a friction clutch (according to [
41]): 1—turbine tower, 2—friction clutch, 3—blades.
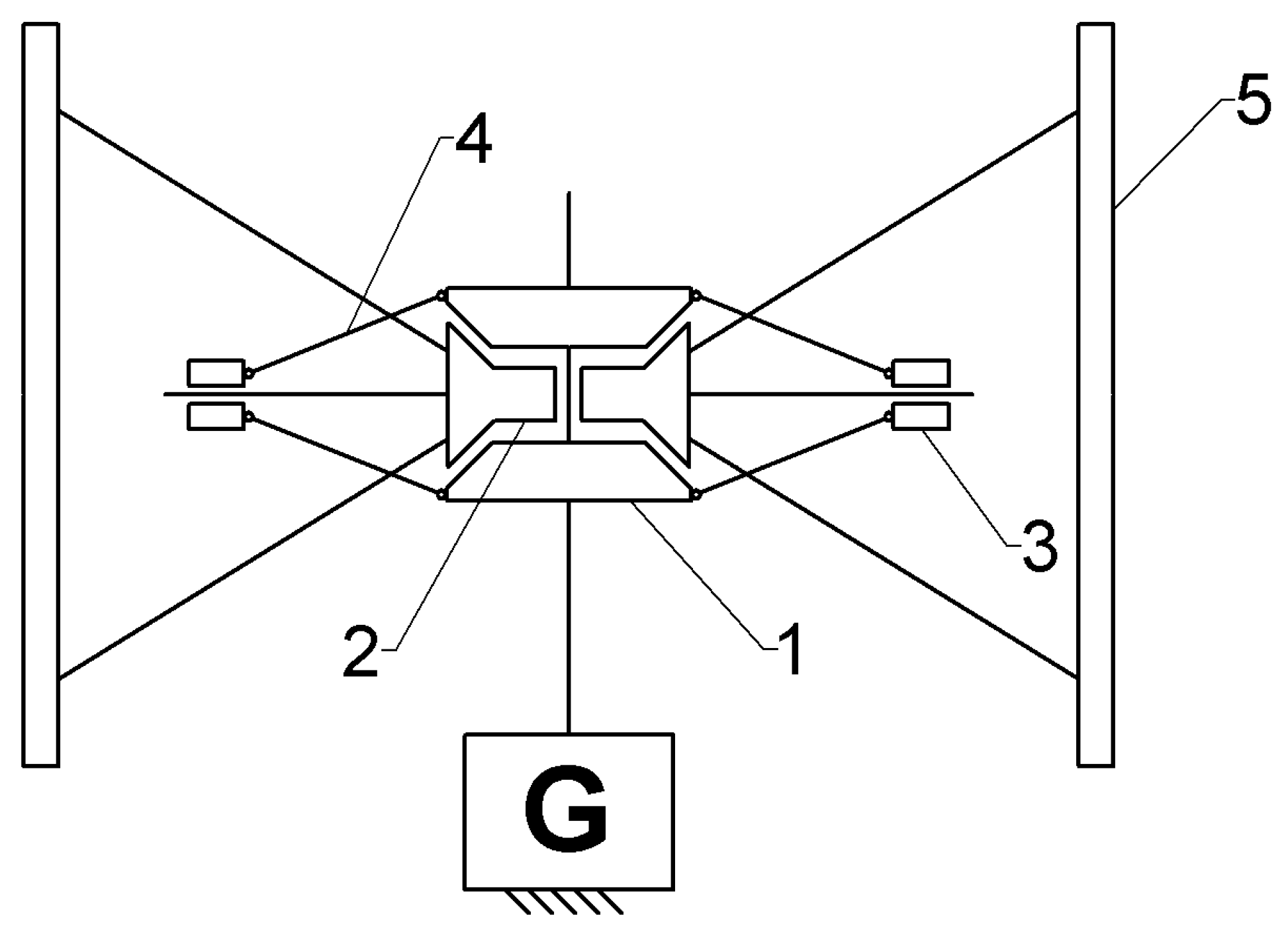
Figure 5.
Diagram of a wind turbine with a generator starting mechanism (according to [
42]): 1—clamping components, 2—friction disc, 3—inertial sliders, 4—arm, 5—blades.
Figure 5.
Diagram of a wind turbine with a generator starting mechanism (according to [
42]): 1—clamping components, 2—friction disc, 3—inertial sliders, 4—arm, 5—blades.
Figure 6.
Diagram of a wind turbine with a drive transmission mechanism using the rollers (according to [
43]): 1—clutch seat, 2—roller, 3—large tooth gear, 4—small tooth gear, 5—blades.
Figure 6.
Diagram of a wind turbine with a drive transmission mechanism using the rollers (according to [
43]): 1—clutch seat, 2—roller, 3—large tooth gear, 4—small tooth gear, 5—blades.
Figure 7.
Bearing of a wind turbine using the plain bearings (according to [
46]): 1—body, 2—sliding surface, 3—base, 4—lubricating oil.
Figure 7.
Bearing of a wind turbine using the plain bearings (according to [
46]): 1—body, 2—sliding surface, 3—base, 4—lubricating oil.
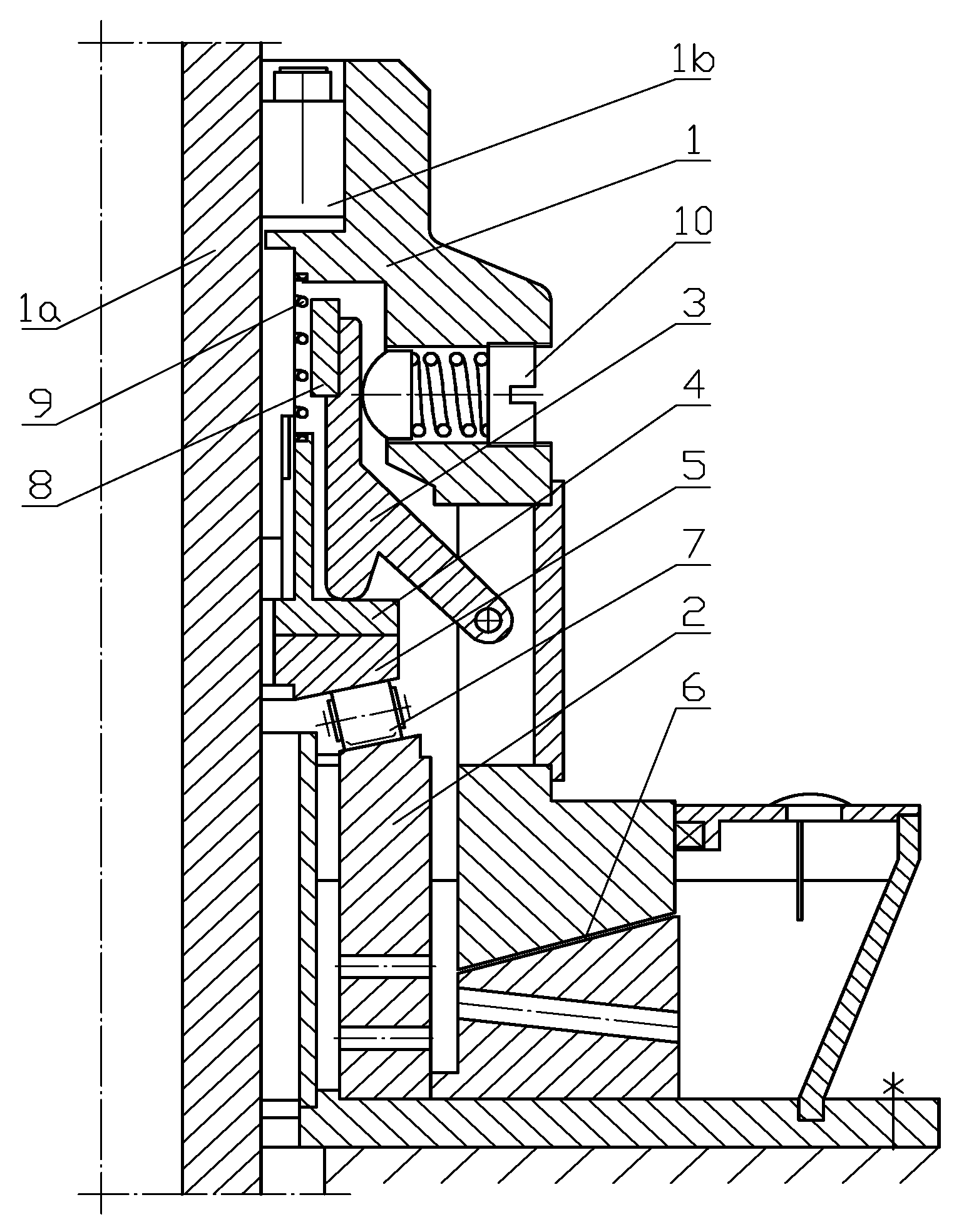
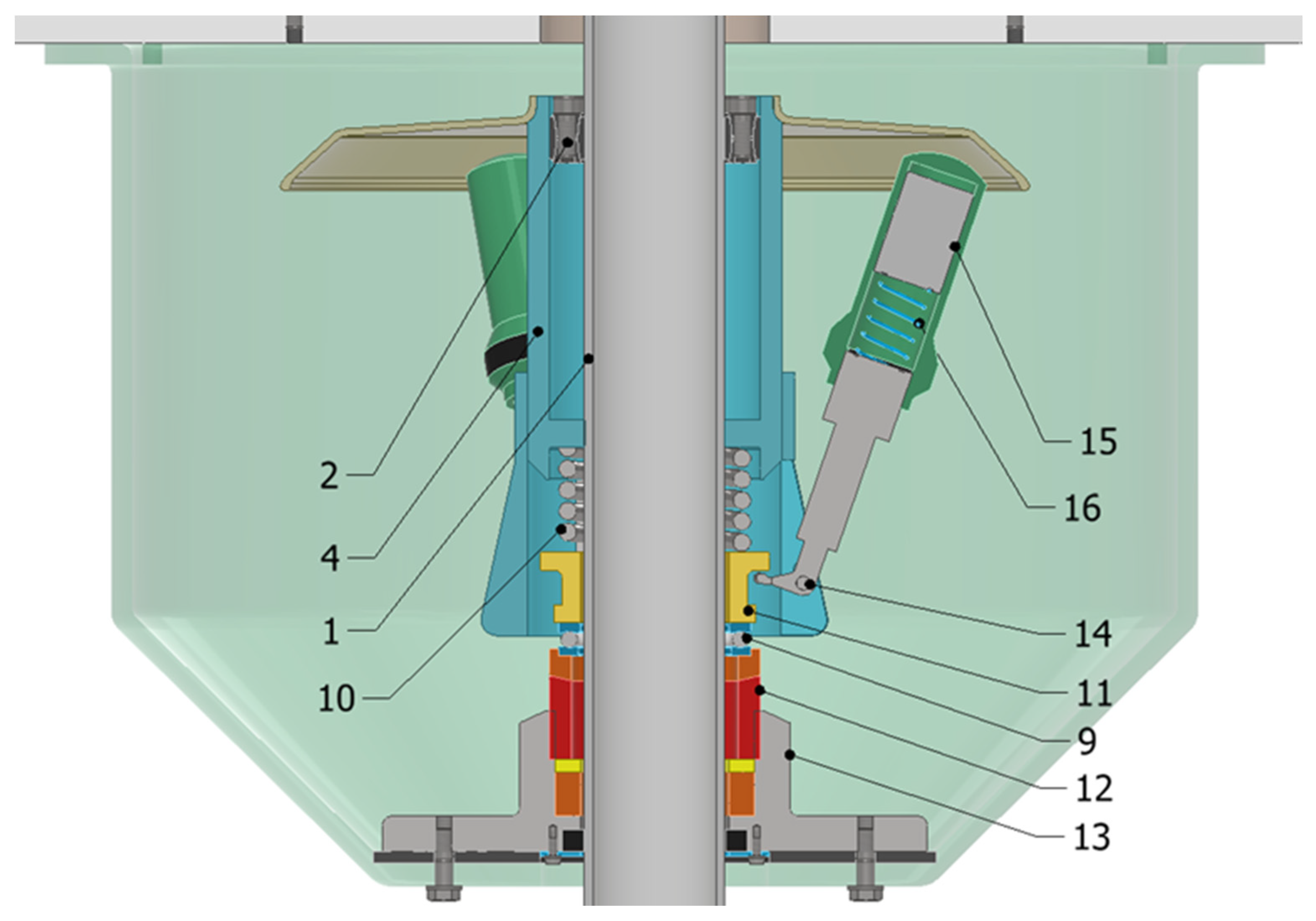
Figure 8.
Hybrid bearing with a conical-shaped journal where: 1—upper plain bearing enclosure, 1a—turbine main shaft, 1b—expansion rings, 2—base, 3—lever, 4—intermediate element, 5—rolling bearing raceway, 6—plain bearing, 7—rolling bearing, 8—inertial weight, 9—spring, 10—adjusting screw.
Figure 8.
Hybrid bearing with a conical-shaped journal where: 1—upper plain bearing enclosure, 1a—turbine main shaft, 1b—expansion rings, 2—base, 3—lever, 4—intermediate element, 5—rolling bearing raceway, 6—plain bearing, 7—rolling bearing, 8—inertial weight, 9—spring, 10—adjusting screw.
Figure 9.
Three-dimensional model of the hybrid bearing with a conical journal.
Figure 9.
Three-dimensional model of the hybrid bearing with a conical journal.
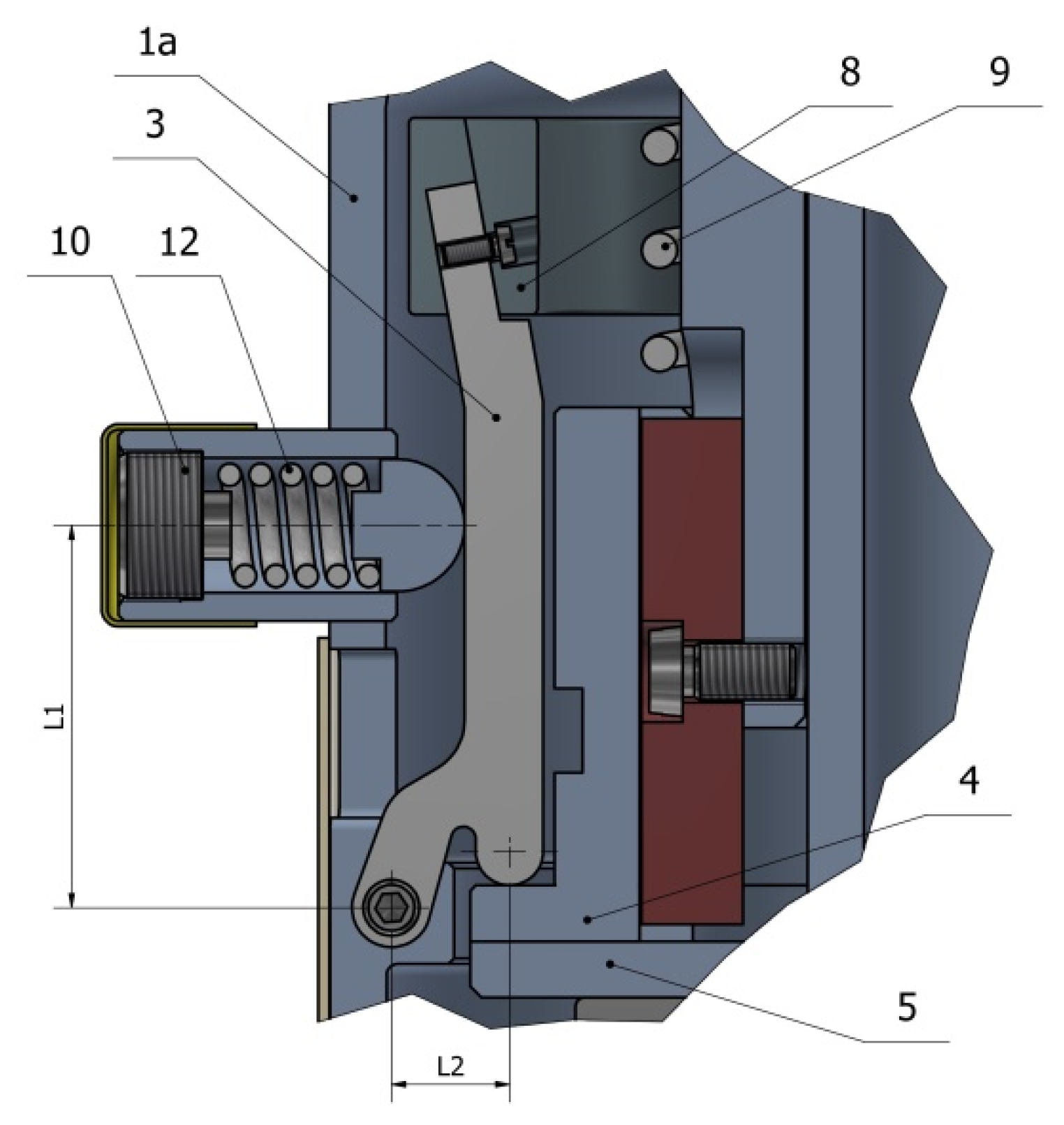
Figure 10.
Lever of the wind turbine bearing load switching mechanism: 1a—main shaft of the turbine, 3—lever, 4—intermediate element, 5—rolling bearing raceway, 8—inertial weight, 9—spring, 10—adjusting screw, 12—pressuring spring.
Figure 10.
Lever of the wind turbine bearing load switching mechanism: 1a—main shaft of the turbine, 3—lever, 4—intermediate element, 5—rolling bearing raceway, 8—inertial weight, 9—spring, 10—adjusting screw, 12—pressuring spring.
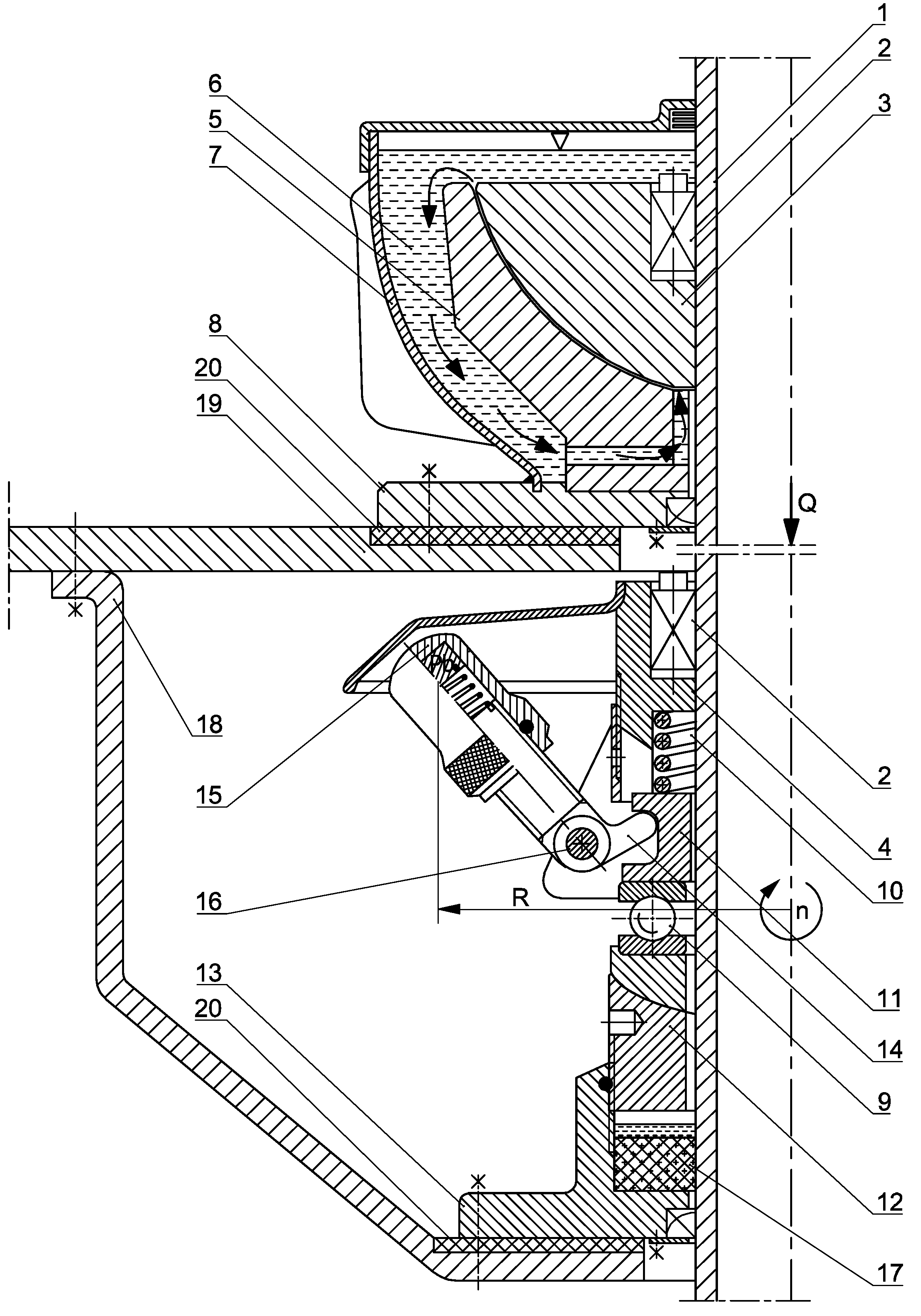
Figure 11.
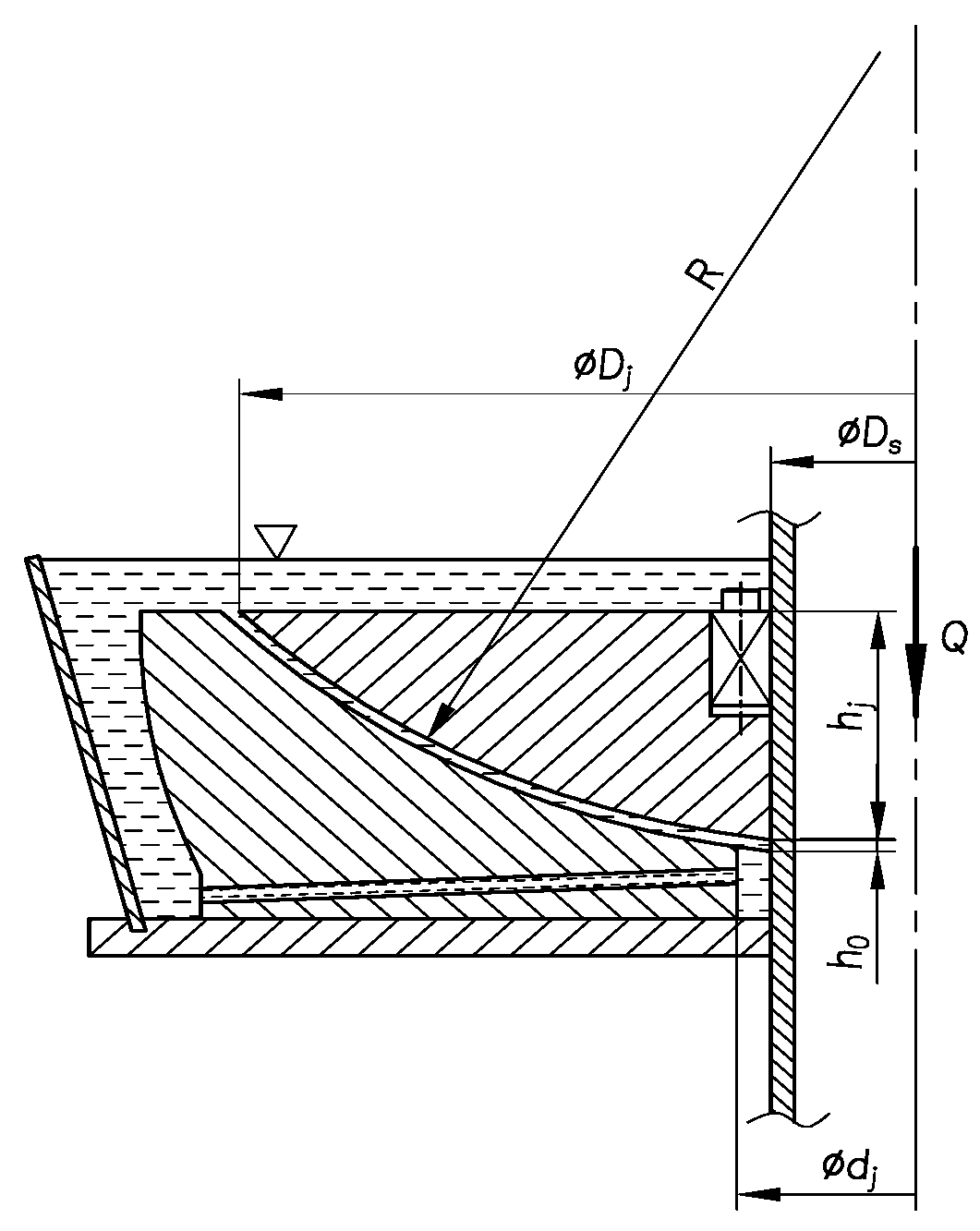
Hybrid bearing with a spherical-shaped journal: 1—tubular shaft, 2—expansion ring, 3—spherical journal of the plain bearing, 4—support sleeve, 5—plain bearing shell, 6—lubricating liquid, 7—enclosure, 8—base of the plain bearing, 9—thrust roller bearing, 10—compression spring 11—sliding sleeve, 12—adjusting sleeve, 13—base, 14—inertial weight lever, 15—inertial weight, 16—inertial lever axis, 17—self-lubricating bearing, 18—console, 19—building ceiling, 20—damping pad, Q—longitudinal load on the shaft, R—radius of rotation, n—rotational speed of the wind turbine shaft.
Figure 11.
Hybrid bearing with a spherical-shaped journal: 1—tubular shaft, 2—expansion ring, 3—spherical journal of the plain bearing, 4—support sleeve, 5—plain bearing shell, 6—lubricating liquid, 7—enclosure, 8—base of the plain bearing, 9—thrust roller bearing, 10—compression spring 11—sliding sleeve, 12—adjusting sleeve, 13—base, 14—inertial weight lever, 15—inertial weight, 16—inertial lever axis, 17—self-lubricating bearing, 18—console, 19—building ceiling, 20—damping pad, Q—longitudinal load on the shaft, R—radius of rotation, n—rotational speed of the wind turbine shaft.
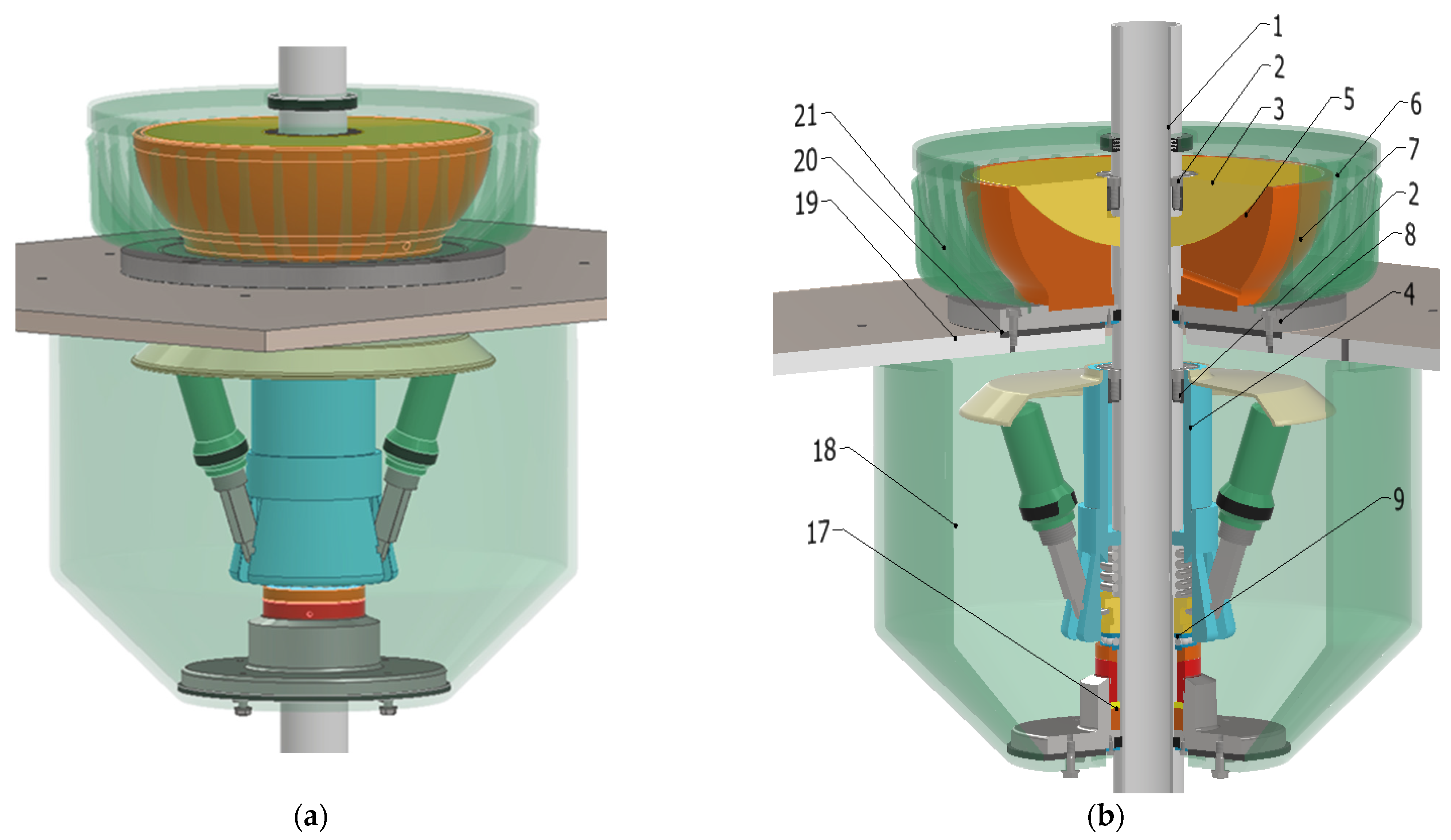
Figure 12.
Three-dimensional model of a hybrid bearing with a spherical journal (a)—view, (b)—cross-section: 1—tubular shaft, 2—expansion ring, 3—spherical journal of the plain bearing, 4—support bushing, 5—pan, 6—lubricating liquid, 7—enclosure, 8—plain bearing base, 9—trust roller bearing, 17—self-lubricating bearing, 18—console, 19—building ceiling, 20—damping pad, 21—vertical ribs.
Figure 12.
Three-dimensional model of a hybrid bearing with a spherical journal (a)—view, (b)—cross-section: 1—tubular shaft, 2—expansion ring, 3—spherical journal of the plain bearing, 4—support bushing, 5—pan, 6—lubricating liquid, 7—enclosure, 8—plain bearing base, 9—trust roller bearing, 17—self-lubricating bearing, 18—console, 19—building ceiling, 20—damping pad, 21—vertical ribs.
Figure 13.
Design form of the automatic bearing load switching mechanism: 1—tubular shaft, 2—expansion ring, 4—supporting bushing, 9—trust roller bearing, 10—pressure spring, 11—moving bushing, 12—adjusting bushing, 13—base, 14—inertial weight lever, 15—inertial weight, 16—pressure spring.
Figure 13.
Design form of the automatic bearing load switching mechanism: 1—tubular shaft, 2—expansion ring, 4—supporting bushing, 9—trust roller bearing, 10—pressure spring, 11—moving bushing, 12—adjusting bushing, 13—base, 14—inertial weight lever, 15—inertial weight, 16—pressure spring.
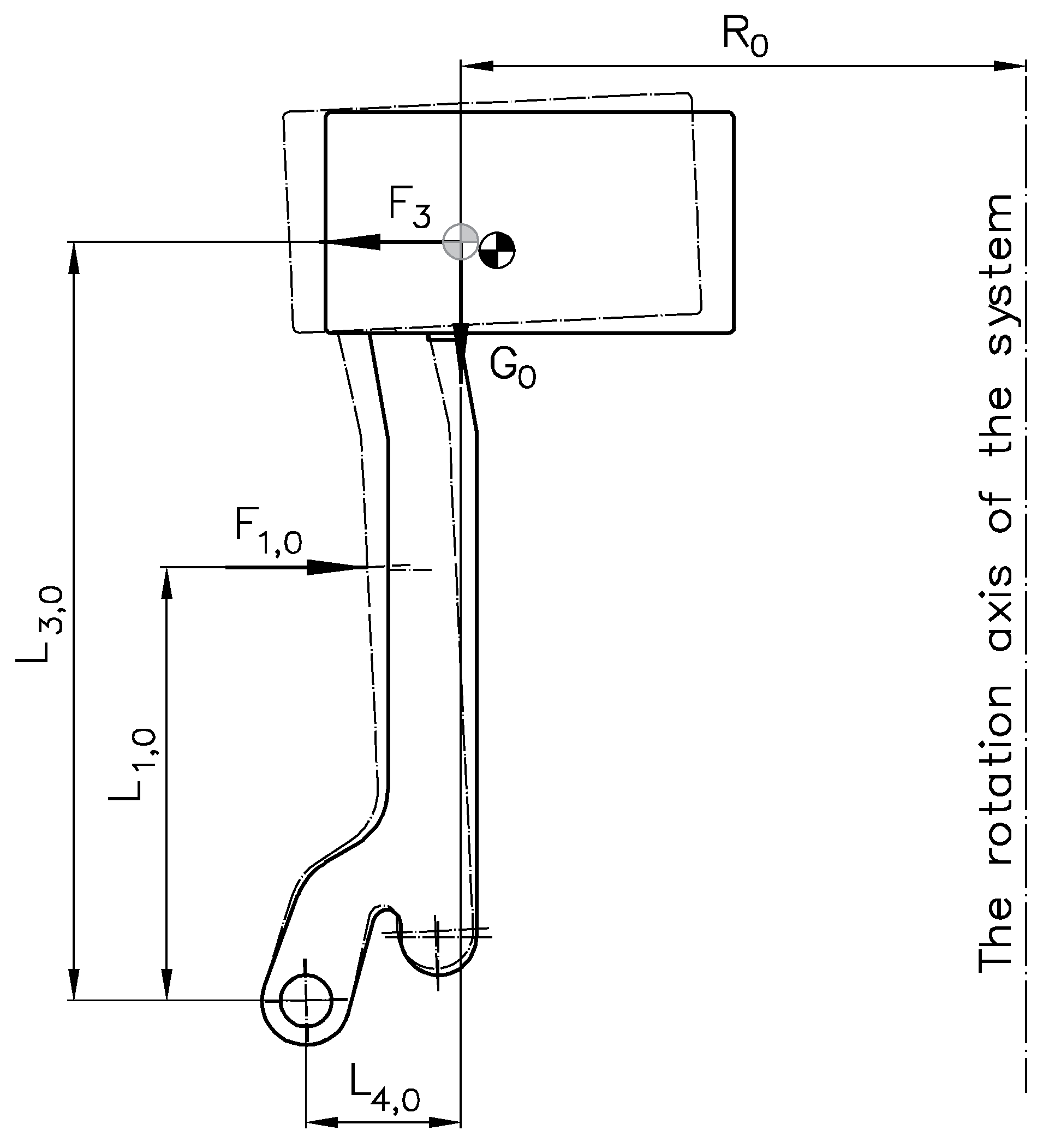
Figure 14.
Load diagram of the lever of the bearing load switching mechanism in the case of a standstill wind turbine: G0—weight of the lever and inertial weight, F1—force in the pressure spring, F2—reaction of the intermediate element.
Figure 14.
Load diagram of the lever of the bearing load switching mechanism in the case of a standstill wind turbine: G0—weight of the lever and inertial weight, F1—force in the pressure spring, F2—reaction of the intermediate element.
Figure 15.
The system of forces acting on the lever after relieving the rolling bearing.
Figure 15.
The system of forces acting on the lever after relieving the rolling bearing.
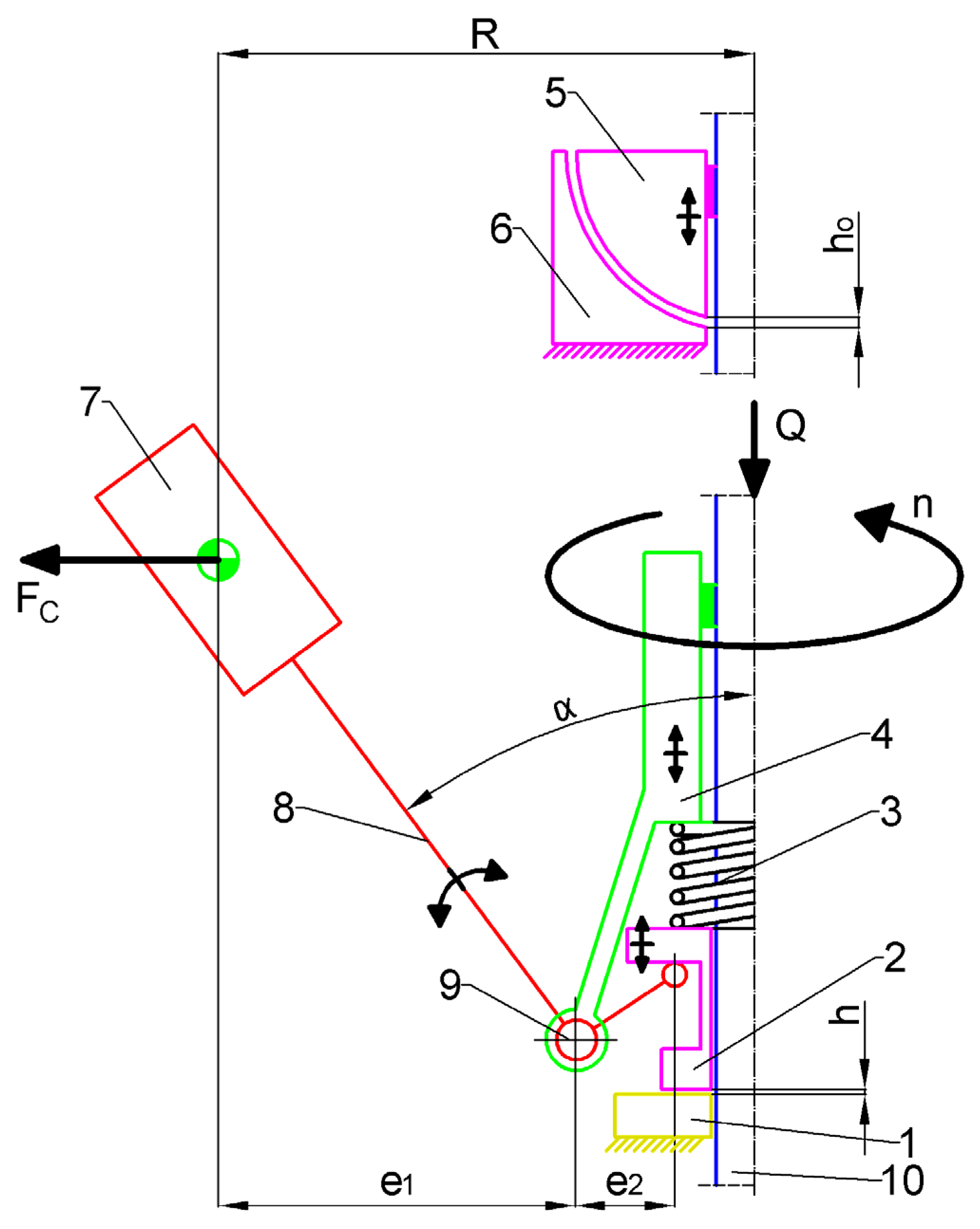
Figure 16.
Kinematic diagram of the mechanism for automatically switching the load to the bearings, where: 1—fixed raceway of the thrust roller bearing, 2—sliding sleeve, 3—compressing spring, 4—supporting sleeve, 5—ball journal of the plain bearing, 6—bushing, 7—inertial mass, 8—lever of the switching mechanism, 9—axis of rotation of the lever of the load switching mechanism, 10—tubular shaft, Q—axial load, FC—centrifugal force of the inertial mass, R—radius of action of the inertial mass, e1—arm of action of the inertial mass lever, e2—operating arm of the mechanism switching lever, α—initial angle of inertial mass lever deflection, n—rotational speed of the hybrid bearing, h0—height of the lubrication gap of the plain bearing, h—height of the gap above the thrust rolling bearing.
Figure 16.
Kinematic diagram of the mechanism for automatically switching the load to the bearings, where: 1—fixed raceway of the thrust roller bearing, 2—sliding sleeve, 3—compressing spring, 4—supporting sleeve, 5—ball journal of the plain bearing, 6—bushing, 7—inertial mass, 8—lever of the switching mechanism, 9—axis of rotation of the lever of the load switching mechanism, 10—tubular shaft, Q—axial load, FC—centrifugal force of the inertial mass, R—radius of action of the inertial mass, e1—arm of action of the inertial mass lever, e2—operating arm of the mechanism switching lever, α—initial angle of inertial mass lever deflection, n—rotational speed of the hybrid bearing, h0—height of the lubrication gap of the plain bearing, h—height of the gap above the thrust rolling bearing.
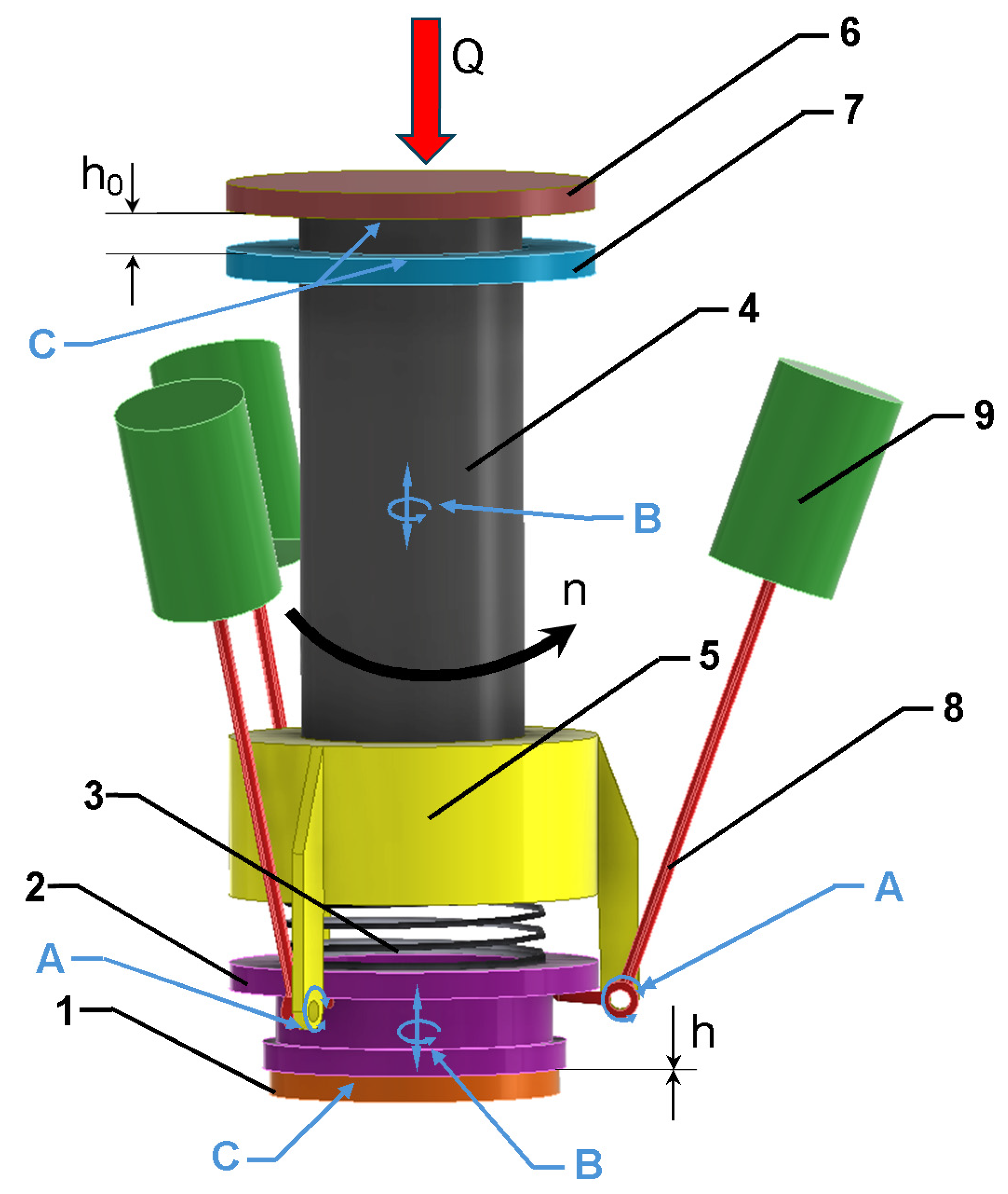
Figure 17.
A solid model used to simulate the operation of the automatic mechanism for switching the load to bearings, where: 1—fixed raceway of a thrust roller bearing, 2—sliding sleeve, 3—compressing spring, 4—tubular shaft, 5—supporting sleeve, 6—ball journal of a plain bearing, 7—bushing, 8—switching mechanism lever, 9—inertial mass, A—swivel connection, B—swivel and slide connection, C—3D contact connection.
Figure 17.
A solid model used to simulate the operation of the automatic mechanism for switching the load to bearings, where: 1—fixed raceway of a thrust roller bearing, 2—sliding sleeve, 3—compressing spring, 4—tubular shaft, 5—supporting sleeve, 6—ball journal of a plain bearing, 7—bushing, 8—switching mechanism lever, 9—inertial mass, A—swivel connection, B—swivel and slide connection, C—3D contact connection.
Figure 18.
Assumed design of a plain bearing with a spherical journal.
Figure 18.
Assumed design of a plain bearing with a spherical journal.
Figure 19.
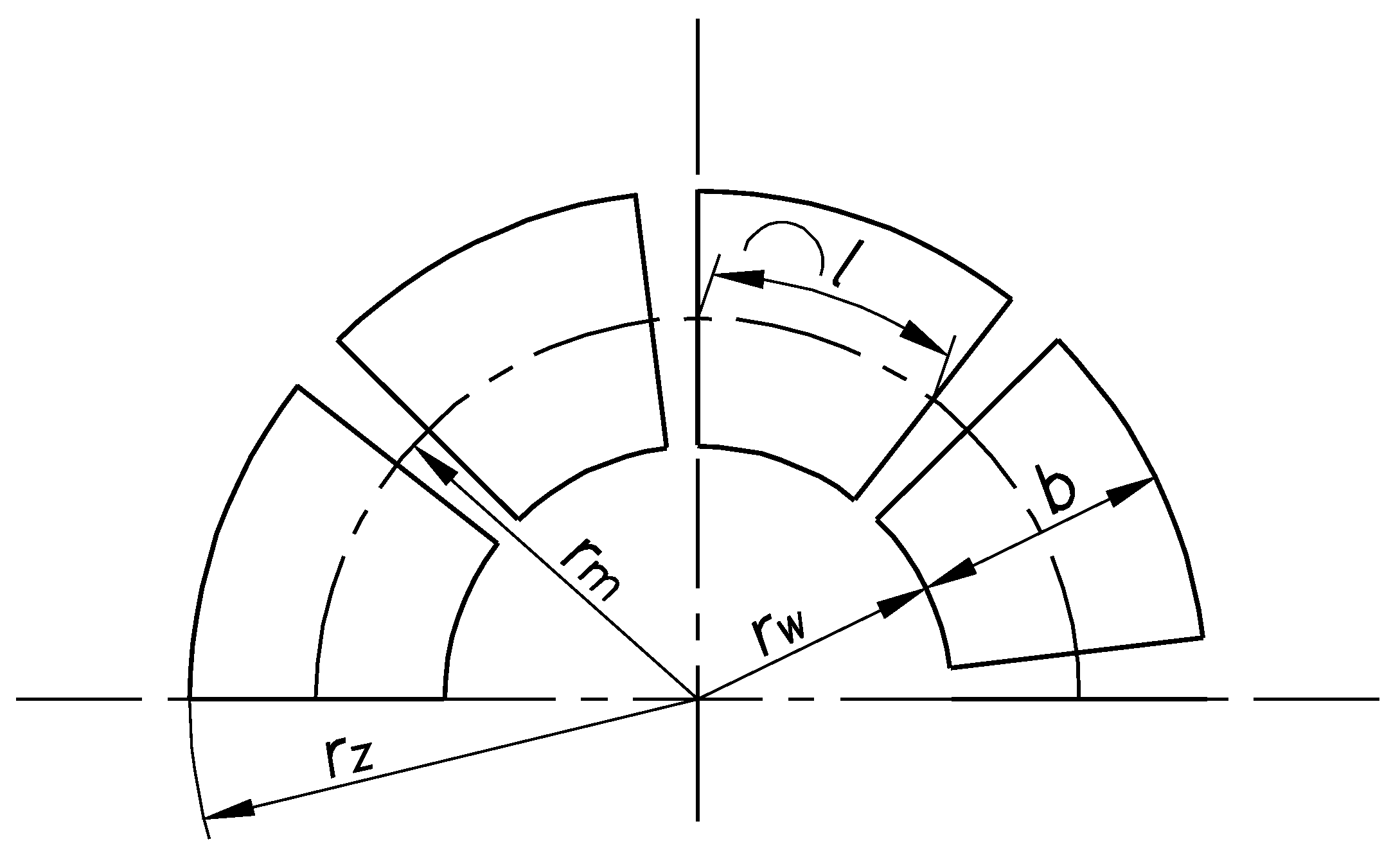
Schematic diagram of an equivalent segment bearing.
Figure 19.
Schematic diagram of an equivalent segment bearing.
Figure 20.
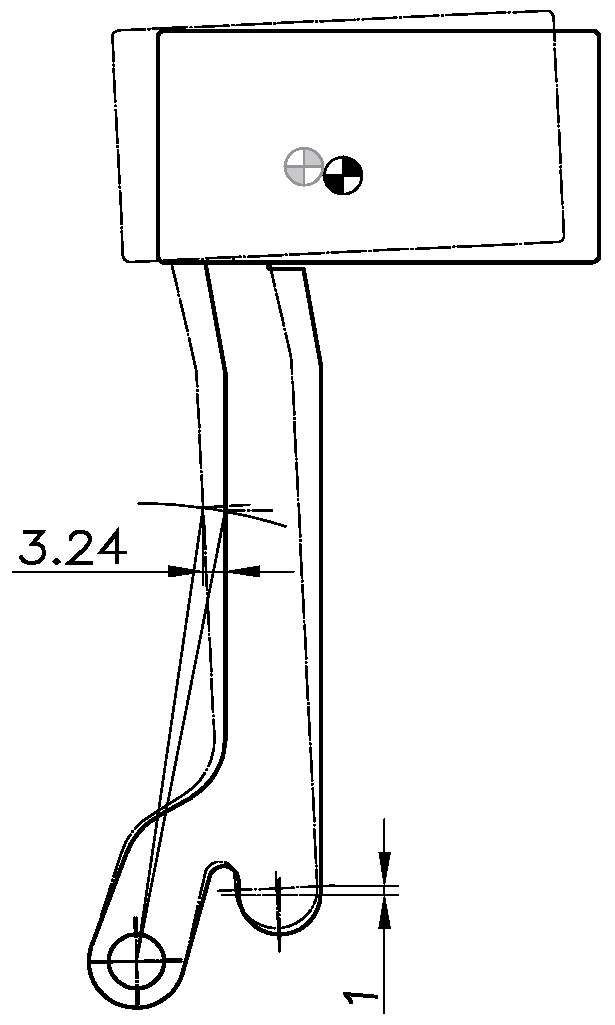
Rotation of the lever to create a lubrication gap of 1 mm between the lever and the intermediate element.
Figure 20.
Rotation of the lever to create a lubrication gap of 1 mm between the lever and the intermediate element.
Figure 21.
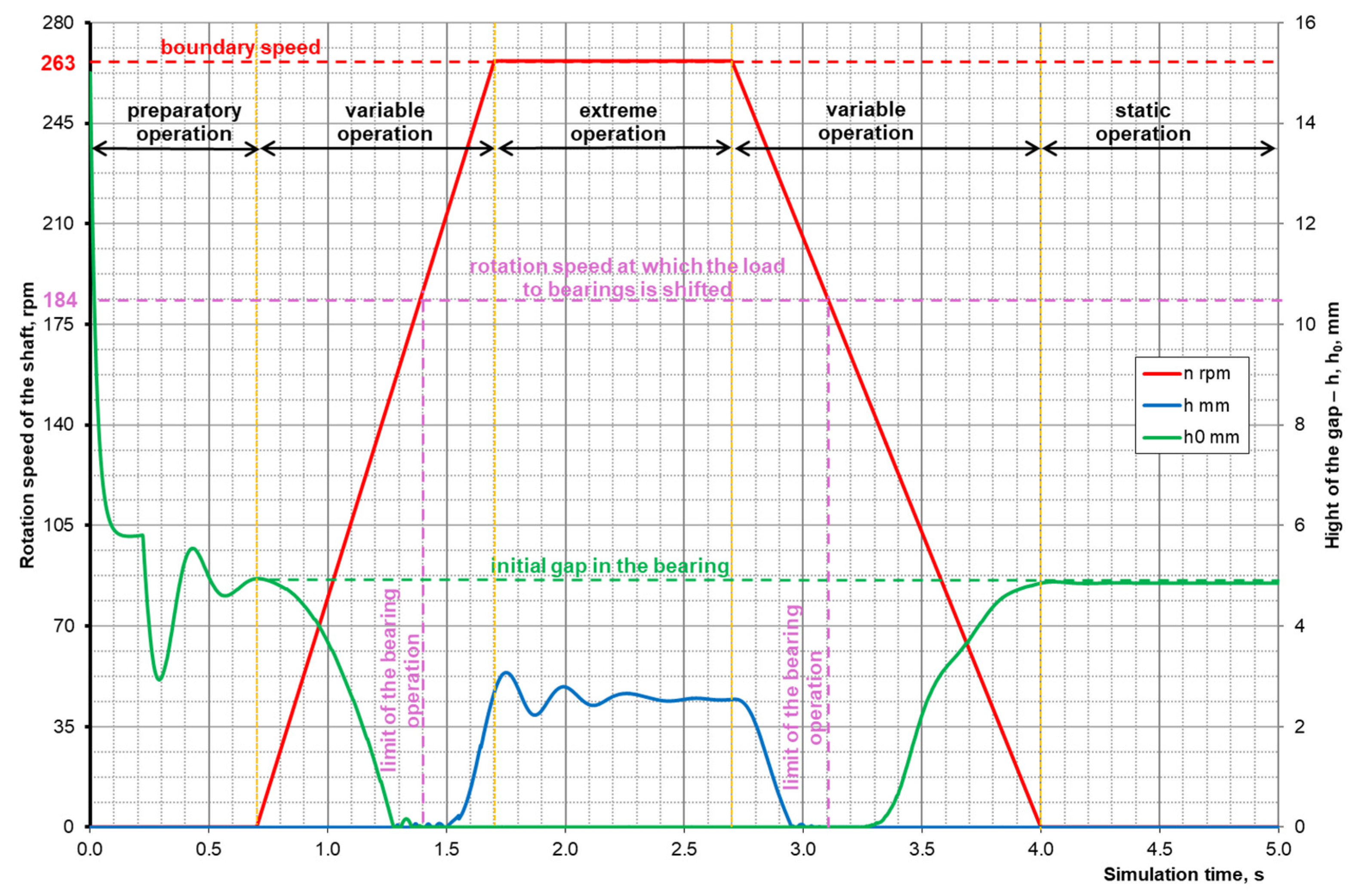
Simulation of operation of the mechanism for automatically shifting the load to bearings.
Figure 21.
Simulation of operation of the mechanism for automatically shifting the load to bearings.
Figure 22.
Dependence of the shaft rotation speed n0 on the load-bearing capacity index K and on the height of the lubrication gap h0.
Figure 22.
Dependence of the shaft rotation speed n0 on the load-bearing capacity index K and on the height of the lubrication gap h0.
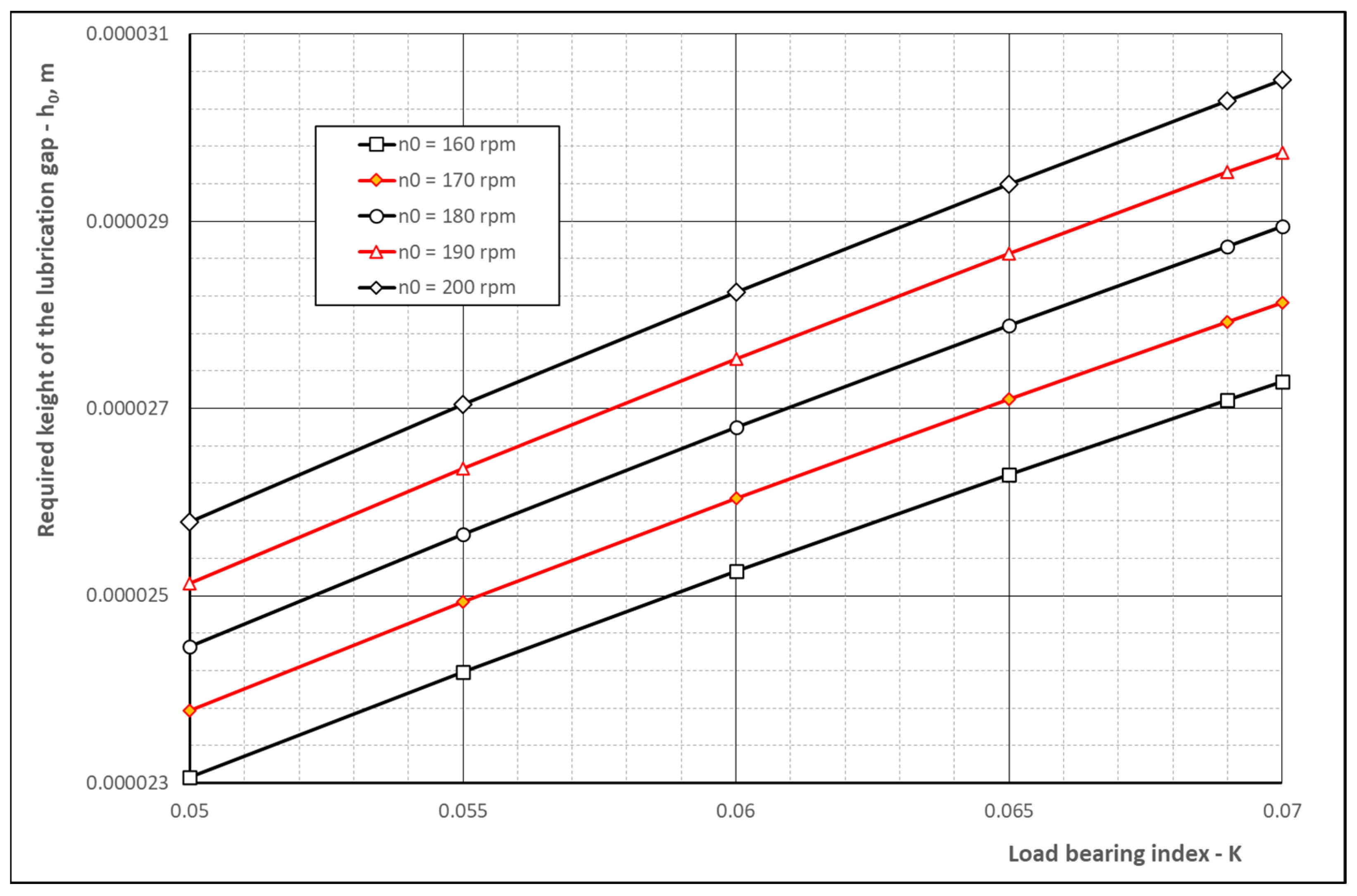
Figure 23.
Dependence of the required height of the lubrication gap h0 on the load bearing index K for the selected values of shaft rotation speed n0.
Figure 23.
Dependence of the required height of the lubrication gap h0 on the load bearing index K for the selected values of shaft rotation speed n0.
Table 1.
Technical parameters of vertical-axis wind turbines (VAWTs) [
13,
14].
Table 1.
Technical parameters of vertical-axis wind turbines (VAWTs) [
13,
14].
| Parameter | Value |
|---|
| Turbine model | ECOROTE 0.3 KW | ECOROTE 1 KW | ECOROTE 1.5 KW | ECOROTE 2.8 KW | JFVC 3 KW | JFVC 5 KW | JFVC 10 KW |
| Rotor diameter, m | 1 | 1 | 2.2 | 2.2 | 3.2 | 3.2 | 4 |
| Height of the blades, m | 1.2 | 2.17 | 1.5 | 3 | 1.8 | 1.8 | 3.6 |
| Starting wind speed, m·s−1 | 2 | 2 | 1.5 | 1.25 | 2.5 | 2.5 | 3 |
| Rated wind speed, m·s−1 | 10 | 10 | 10 | 12 | 12 | 12 | 12 |
| Limit wind speed, m·s−1 | 25 | 25 | 25 | 25 | 40 | 40 | 40 |
| rpmmax | 536 | 550 | 250 | 250 | 50 | 50 | 50 |
| Total weight, kg | 48 | 52 | 155 | 185 | 235 | 288 | 400 |
| Rated power, W | 300 | 1000 | 1500 | 2800 | 3000 | 5000 | 10,000 |
| Max power, W | 600 | 1252 | 2000 | 3670 | 3500 | 6000 | 11,000 |
| Turbine type | Vertical |
| Drive transmission | Generator on a joint turbine axle |
| Blades | Aluminium | Composite |
| Noise level acc. to PN-EN 61400-11 Standard [15] | Does not exceed 46 dB at a distance of 60 m at wind speed 8 m·s−1 |
| Anticorrosion protection | Yes |
| Conformity with the standards | CE, IEC 61400-2 [16], 61400-11 |
Table 2.
Determination of force F1 in the pressing spring in the case when the turbine shaft is standstill.
Table 2.
Determination of force F1 in the pressing spring in the case when the turbine shaft is standstill.
| Parameter | Symbol | Value |
|---|
| Mass of the shaft | m | 200 kg |
| Mass of the lever | m0 | 1.92 kg |
| Lever geometric features (see Figure 14) | L1 | 68 mm |
| L2 | 21 mm |
| L3 | 119 mm |
| L4 | 32 mm |
| L5 | 4 mm |
| Force in the pressing spring | F1 | 201.7 N |
Table 3.
Determination of boundary rotation speed n0 at which total load is taken over by the plain bearings.
Table 3.
Determination of boundary rotation speed n0 at which total load is taken over by the plain bearings.
| Parameter | Symbol | Value |
|---|
| Force in the pressing spring | F1,0 | 278 N |
| Mass of the lever | m0 | 1.92 kg |
| Lever geometric features (see Figure 15) | L1,0 | 68 mm |
| L3,0 | 21 mm |
| L4,0 | 119 mm |
| R0 | 32 mm |
| Boundary angular speed | ω0 | 30.76 s−1 |
| Boundary rotation speed | n0 | 293.7 rpm |
Table 4.
Parameters of the automatic mechanism for switching the load to bearings.
Table 4.
Parameters of the automatic mechanism for switching the load to bearings.
| Parameter | Value |
|---|
| Simulation time (t) | 5 s |
| Load to the shaft (Q) | 2020 N |
| Gravity acceleration (g) | 9.81 m·s−2 |
| Preparatory lubrication gap height (h0) | 15 mm |
| Inertial mass (9) | 1.543 kg |
| Mass moment of inertia of inertial masses (α = 0°) | 29,377 kg·mm2 |
| Compressing spring stiffness (3) | 400 N·mm−1 |
| Compressing spring damping effect (3) | 10 N·s·mm−1 |
| 3D contact connection stiffness (C) | 1000 kN·mm−1 |
| 3D contact joint damping (C) | 10 N·s·mm−1 |
Table 5.
Technical parameters of the equivalent segment bearing.
Table 5.
Technical parameters of the equivalent segment bearing.
| Parameter | Symbol | Value |
|---|
| Axial load | Q | 2020 N |
| Internal radius | rw | 50 mm |
| External radius | rz | 95.81 mm |
| Average radius | rm | 72.90 mm |
| Segment width | b, l | 45.81 |
| Average pressure in an equivalent plain bearing | | 0.120 MPa |