Neutronics Analysis on High-Temperature Gas-Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method
Abstract
1. Introduction
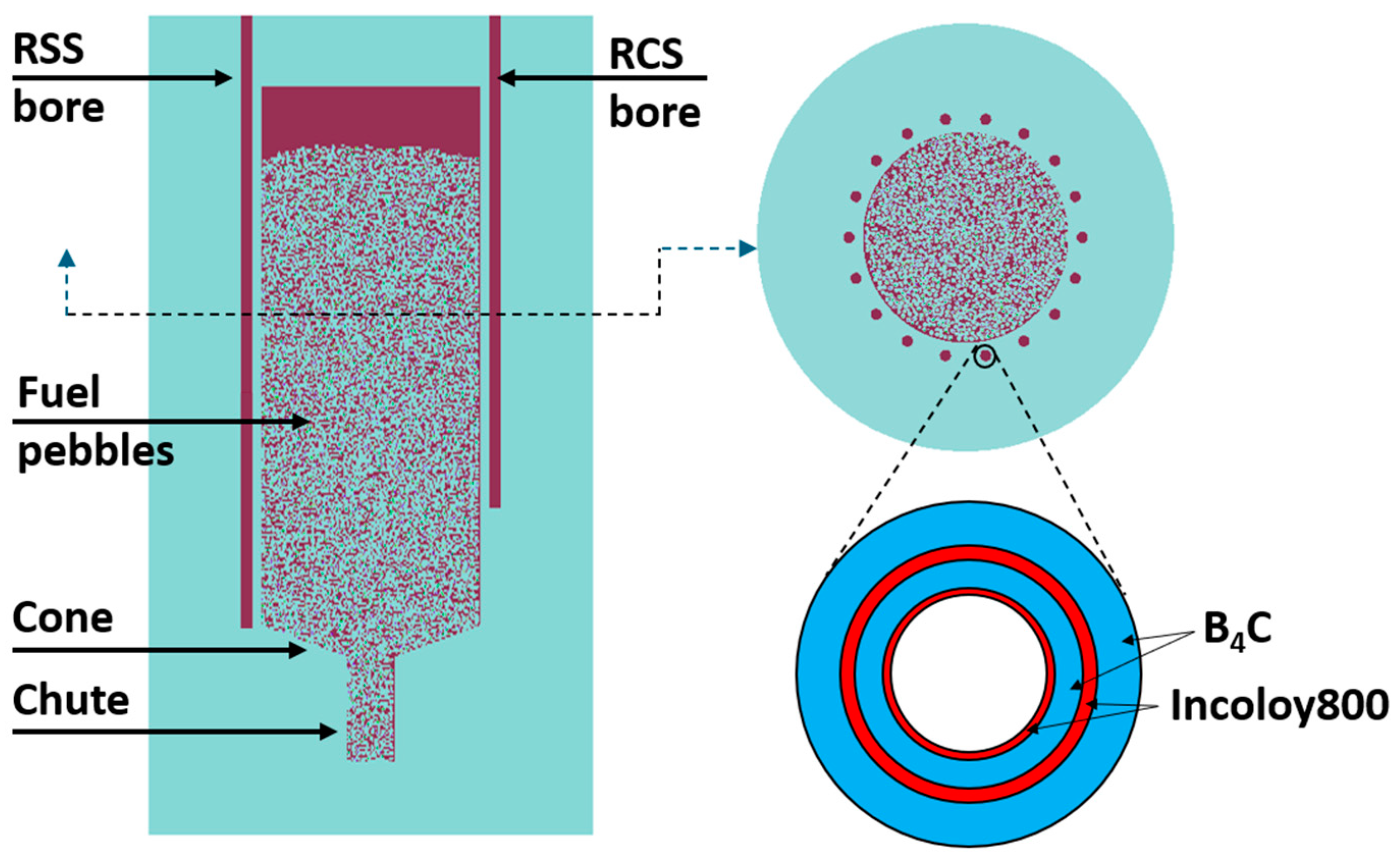
2. Overview of the Xe-100 Reactor
2.1. Xe-100 Reactor
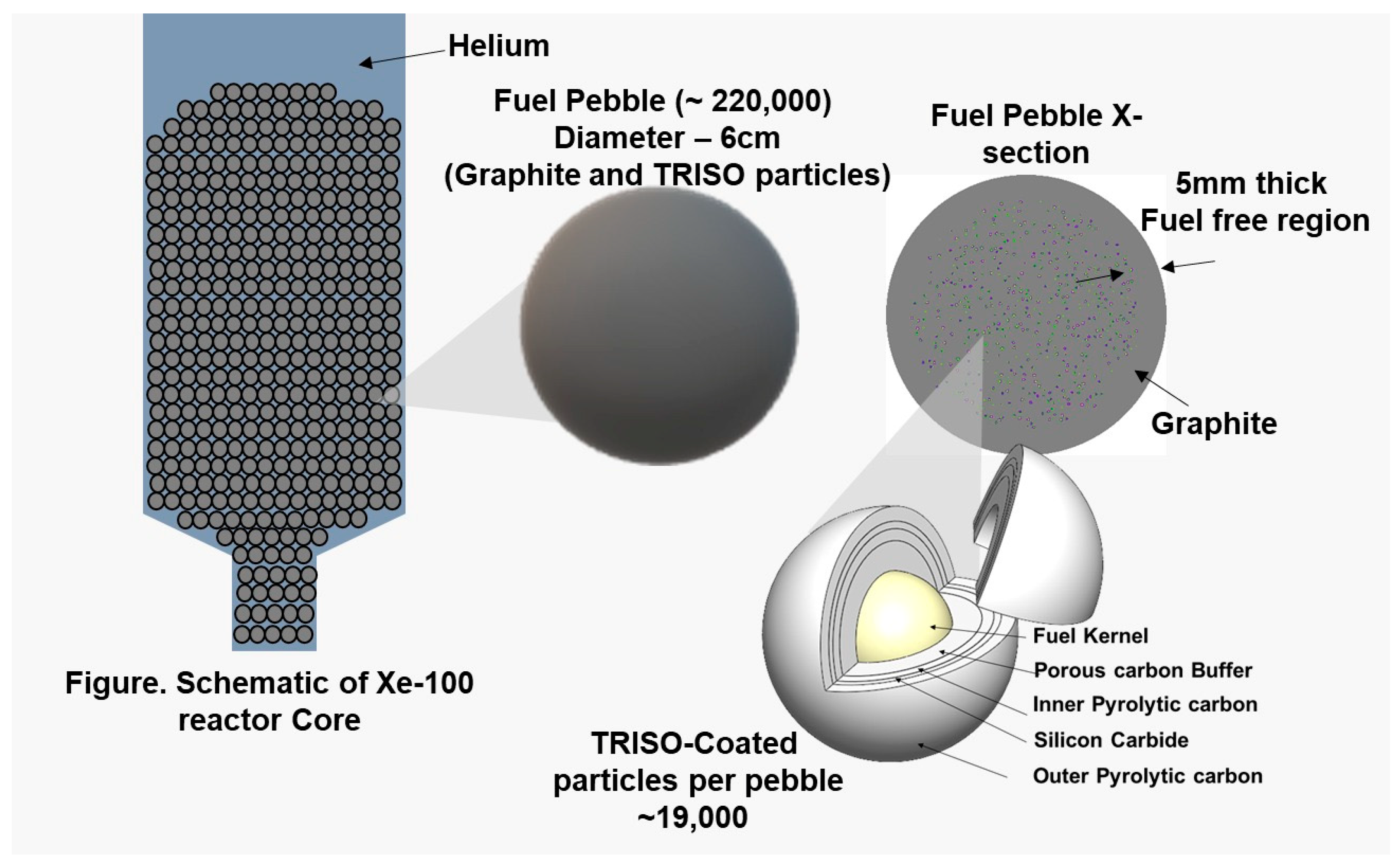
2.2. Fuel Characteristics
2.3. Equilibrium State of HTG-PBR
3. Computational Modelling Approaches
3.1. MCM for Neutronics Simulations
3.2. DEM for Pebble Movement
3.3. Fuel Depletion Model
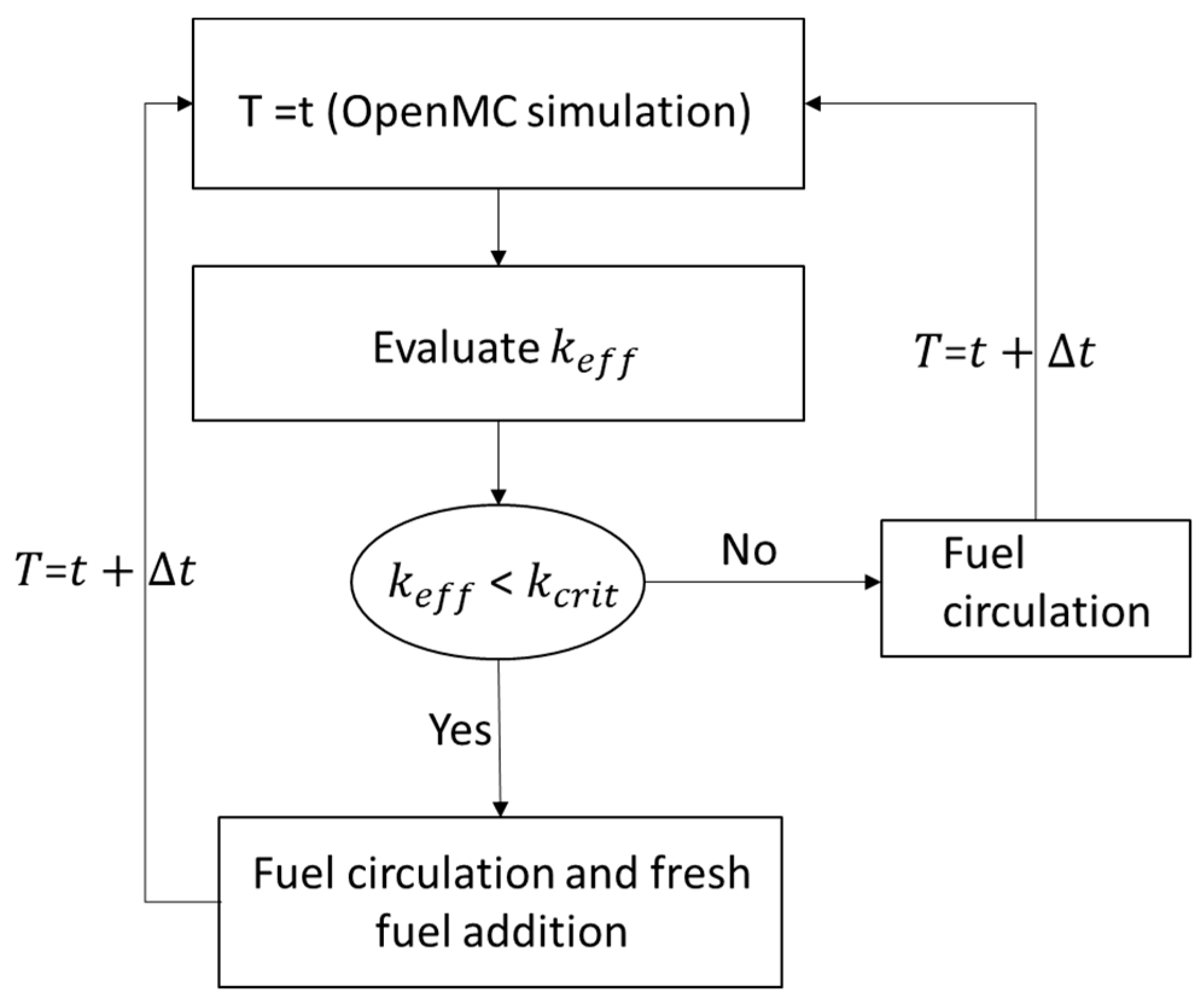
3.4. Equilibrium Core Search Process
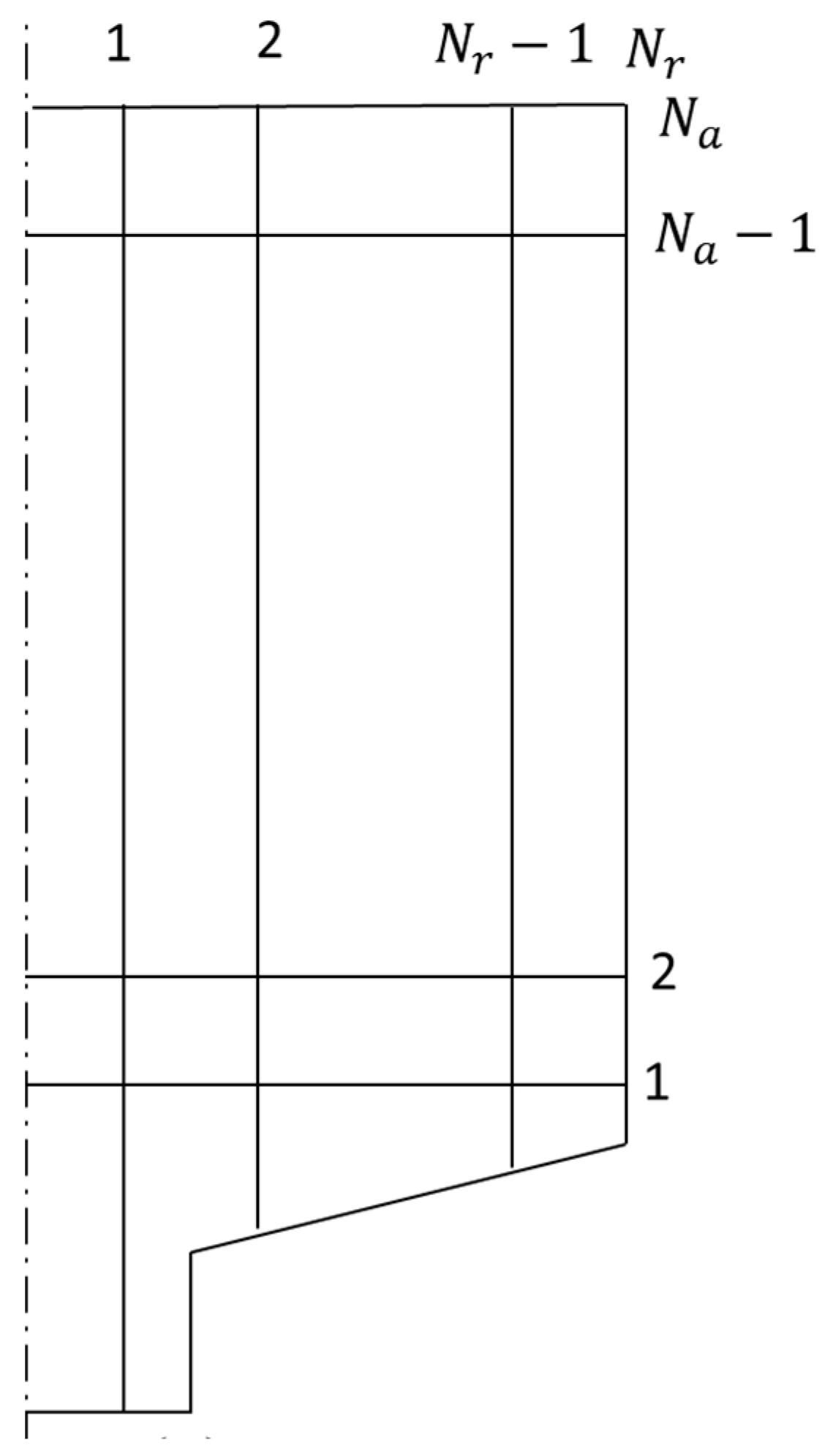
3.4.1. Pebble Grouping
3.4.2. Fuel Circulation Modeling
3.4.3. Fresh Fuel Loading Modeling
4. Results and Discussion
4.1. MCM Verification—Single Pebble Neutronics
4.2. DEM Validation—Pebble Bed Packing
4.3. Static Xe-100 Reactor Core Analysis
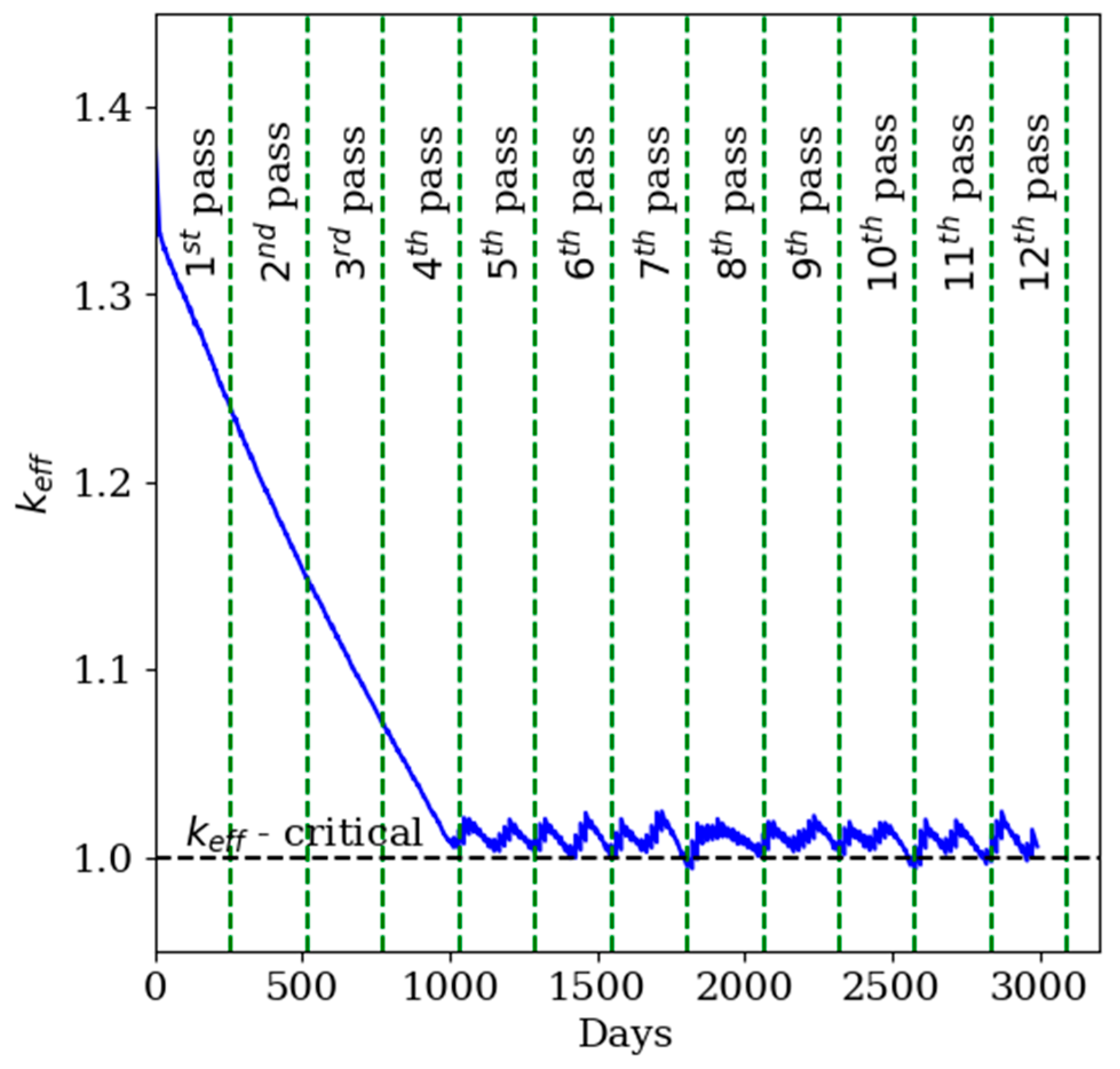
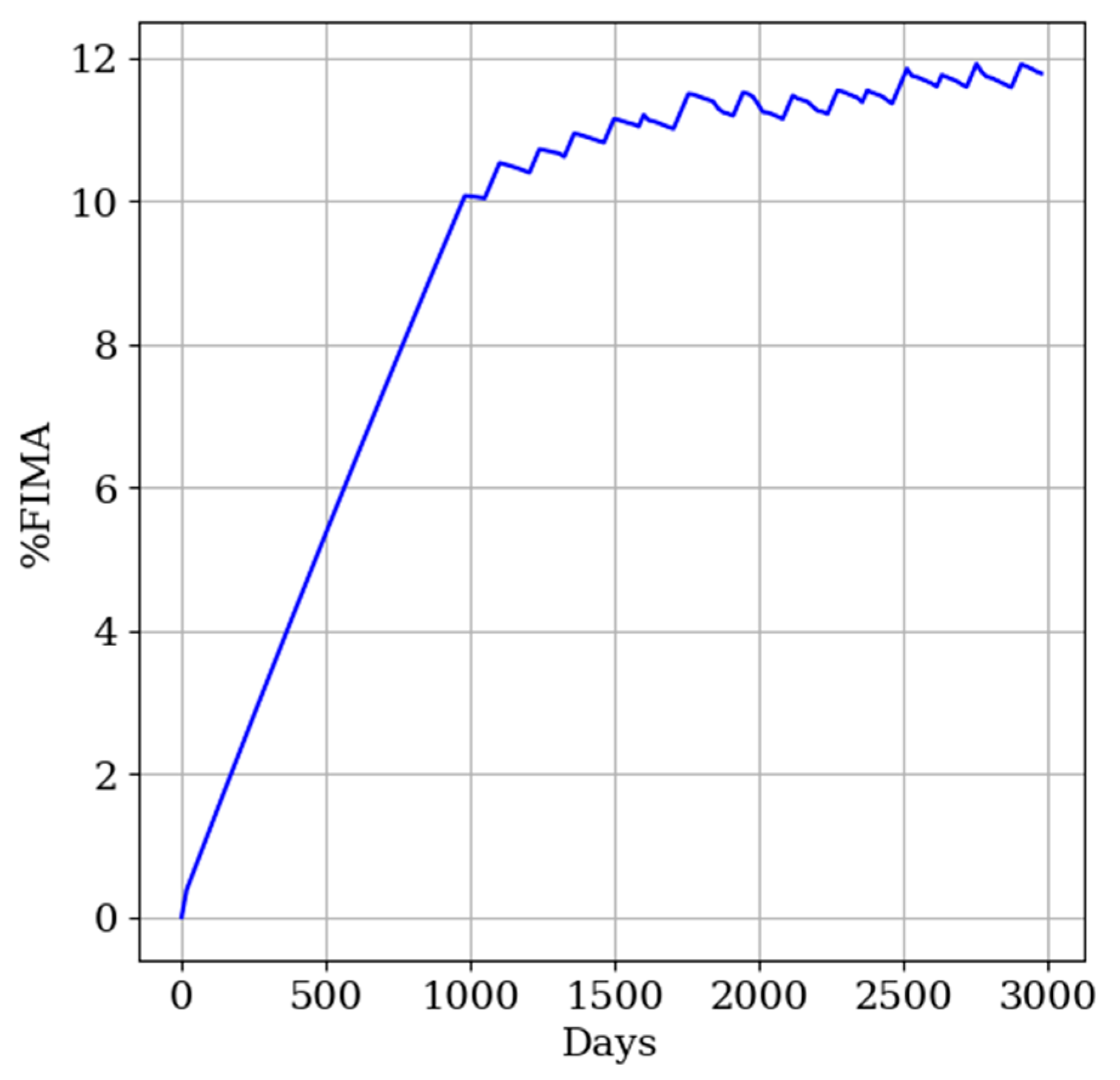
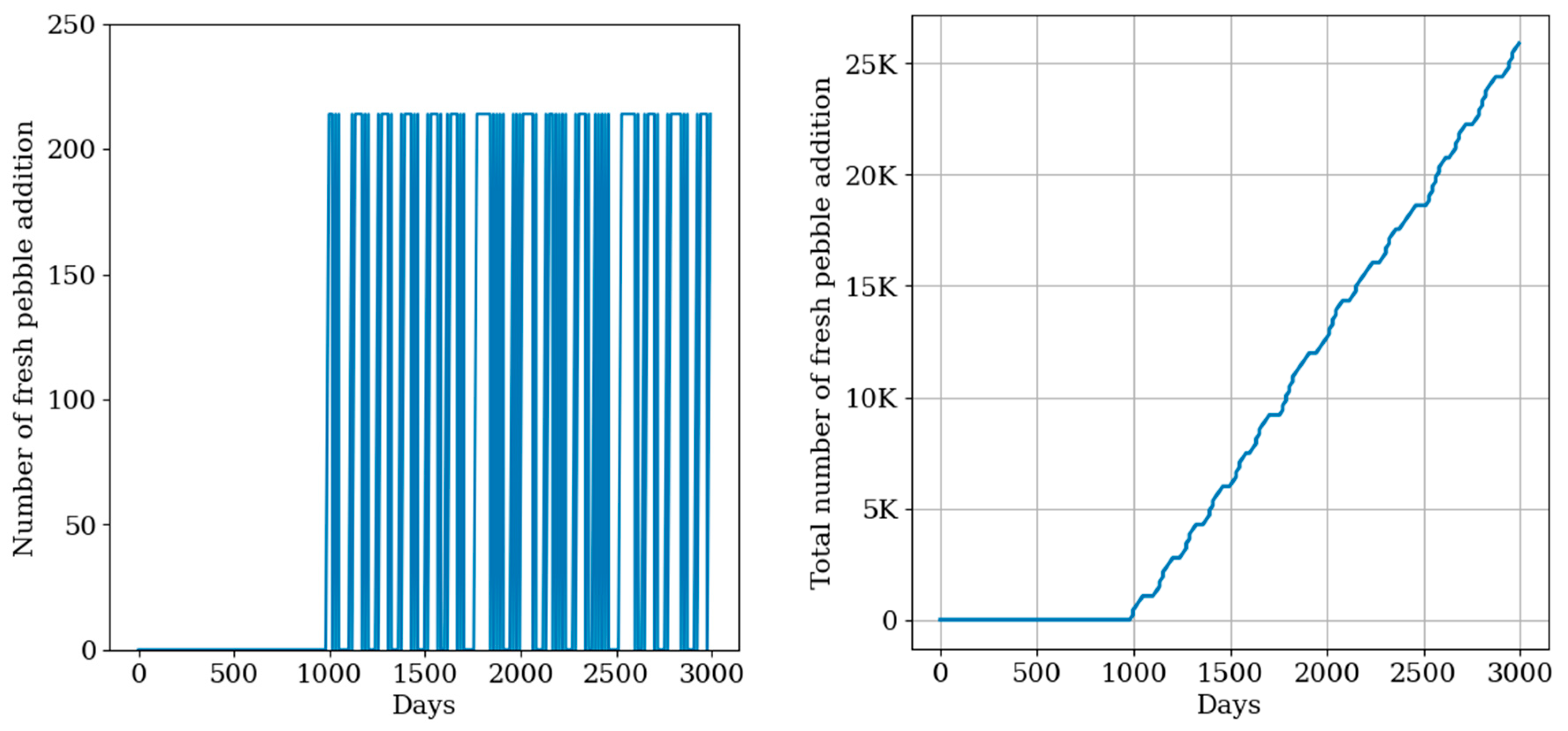
4.4. Equilibrium for the Xe-100 Reactor with Pebble Circulation and Loading
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bouchard, J.; Bennett, R. Generation IV advanced nuclear energy systems. Nucl. Plant J. 2008, 26, 42–45. [Google Scholar]
- Mulder, E.J.; Boyes, W.A. Neutronics characteristics of a 165 MWth Xe-100 reactor. Nucl. Eng. Des. 2020, 357, 110415. [Google Scholar] [CrossRef]
- Lu, C.; Wu, Z. A New Method to Efficiently Estimate the Equilibrium State of Pebble Bed Reactors. Nucl. Technol. 2022, 208, 1577–1590. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, J.; She, D.; Forget, B. Modelling of the HTR-PM Pebble-bed Reactor using OpenMC. Trans. Am. Nucl. Soc. 2020, 22, 9–12. [Google Scholar]
- OECD. Nuclear Development; OECD Nuclear Engery Agency: Paris, France, 2022. [Google Scholar] [CrossRef]
- Mulder, E.J.; Van Staden, M. The Coupled Neutronics and Thermo-Fluid Dynamics Design Characteristics of the Xe-100 200 MWth Reactor; Transactions of the American Nuclear Society: La Grange Park, IL, USA, 2016. [Google Scholar]
- Teuchert, E.; Hansen, U.; Haas, K.A. VSOP-Computer Code System for Reactor Physics and Fuel Cycle Simulation (Juel—1649); Kernforschungsanlage Juelich GmbH, NTRL: Jülich, Germany, 1980. [Google Scholar]
- Terry, W.K.; Gougar, H.D.; Ougouag, A.M. Direct deterministic method for neutronics analysis and computation of asymptotic burnup distribution in a recirculating pebble-bed reactor. Ann. Nucl. Energy 2002, 29, 1345–1364. [Google Scholar] [CrossRef]
- Lu, C.; Hiscox, B.D.; Terrani, K.A.; Brown, N.R. Fully ceramic microencapsulated fuel in prismatic high temperature gas-cooled reactors: Analysis of reactor performance and safety characteristics. Ann. Nucl. Energy 2018, 114, 277–287. [Google Scholar] [CrossRef]
- Setiadipura, T.; Obara, T. Annals of Nuclear Energy Development of Monte Carlo-based pebble bed reactor fuel management code. Ann. Nucl. Energy 2014, 71, 313–321. [Google Scholar] [CrossRef]
- Werner, C.J.; Bull, J.S.; Solomon, C.J.; Brown, F.B.; McKinney, G.W.; Rising, M.E.; Dixon, D.A.; Martz, R.L.; Hughes, H.G.; Cox, L.J.; et al. MCNP Version 6.2 Release Notes (No. LA-UR-18-20808); Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 2018. [Google Scholar]
- Fratoni, M.; Greenspan, E. Equilibrium core composition search methodologies for pebble bed reactors. Nucl. Sci. Eng. 2010, 166, 1–16. [Google Scholar] [CrossRef]
- Wu, S.-C.; Sheu, R.-J.; Peir, J.-J.; Liang, J.-H. Burnup Computation for HTR-10 Using Layer-to-Layer Movement. In International Conference on Nuclear Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 55836. [Google Scholar]
- Stewart, R.; Balestra, P.; Reger, D.; Merzari, E.; Strydom, G. High-fidelity simulations of the run-in process for a pebble-bed reactor. Ann. Nucl. Energy 2024, 195, 110193. [Google Scholar] [CrossRef]
- Robert, Y.; Siaraferas, T.; Fratoni, M. Hyper-fidelity depletion with discrete motion for pebble bed reactors. Sci. Rep. 2023, 13, 12711. [Google Scholar] [CrossRef]
- Nedderman, R.M.; Tuzun, U. A kinematic model for the flow of granular materials. Powder Technol. 1979, 22, 243–253. [Google Scholar] [CrossRef]
- Mullins, W.W. Stochastic theory of particle flow under gravity. J. Appl. Phys. 1972, 43, 665–678. [Google Scholar] [CrossRef]
- Caram, H.; Hong, D.C. Random-walk approach to granular flows. Phys. Rev. Lett. 1991, 67, 828–831. [Google Scholar] [CrossRef]
- Bazant, M.Z. The spot model for random-packing dynamics. Mech. Mater. 2006, 38, 717–731. [Google Scholar] [CrossRef]
- Thornton, C. On the relationship between the modulus of particulate media and surface energy of the constituent particles. J. Phys. D Appl. Phys. 1993, 26, 1587–1591. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Yang, X.T.; Tang, Z.W.; Wang, W.J.; Tu, J.Y.; Liu, Z.Y.; Li, J. Experimental and numerical validation of a two-region-designed pebble bed reactor with dynamic core. Nucl. Eng. Des. 2012, 246, 277–285. [Google Scholar] [CrossRef]
- Reger, D.; Merzari, E.; Balestra, P.; Stewart, R.; Strydom, G. Discrete element simulation of Pebble Bed Reactors on graphics processing units. Ann. Nucl. Energy 2023, 190, 109896. [Google Scholar] [CrossRef]
- Reger, D.; Merzari, E.; Balestra, P.; Schunert, S.; Hassan, Y.; King, S. Direct Numerical Simulation and Large Eddy Simulation of a 67-Pebble-Bed Experiment. Nucl. Technol. 2024, 210, 1258–1278. [Google Scholar] [CrossRef]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Chrono, D.N. An open source multi-physics dynamics engine. In High Performance Computing in Science and Engineering: Second International Conference; Kozubek, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Romano, P.K.; Horelik, N.E.; Herman, B.R.; Nelson, A.G.; Forget, B.; Smith, K. OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 2015, 82, 90–97. [Google Scholar] [CrossRef]
- Kloss, C.; Goniva, C.; Hager, A.; Amberger, S.; Pirker, S. Models, algorithms and validation for opensource DEM and CFD–DEM. Prog. Comput. Fluid Dyn. Int. J. 2012, 12, 140–152. [Google Scholar] [CrossRef]
- Kadak, A.C.; Bazant, M.Z. Pebble Flow Experiments For Pebble Bed Reactors. In Proceedings of the 2nd International Topical Meeting on High Temperature Reactor Technology, Beijing, China, 22–24 September 2004. [Google Scholar]
- Olivier, L.D.; Mulder, E.J.; Wang, Z. Mechanistic source terms for the Xe-100 reactor XSTERM Code Development Approach. In Proceedings of the International Topical Meeting on High Temperature Reactor Technology (HTR 2016), Las Vegas, NV, USA, 6–10 November 2016; Volume 18587. [Google Scholar]
- Kondratiev, V.V.; Sysoev, I.A.; Kolosov, A.D.; Galishnikova, V.V.; Gladkikh, V.A.; Karlina, A.I.; Karlina, Y.I. Development and Testing of the Thermoelectric Thermal Energy Conversion Device in the Conditions of Existing Aluminum Production. Materials 2022, 15, 8526. [Google Scholar] [CrossRef] [PubMed]
- Colak, Ü.; Seker, V. Monte Carlo criticality calculations for a pebble bed reactor with MCNP. Nucl. Sci. Eng. 2005, 149, 131–137. [Google Scholar] [CrossRef]
- Romano, P.K.; Josey, C.J.; Johnson, A.E.; Liang, J. Depletion capabilities in the OpenMC Monte Carlo particle transport code. Ann. Nucl. Energy 2020, 152, 107989. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software, Simcenter STAR-CCM+ User Guide, Version 2021.1. Adaptive Mesh Refinement for Overset Meshes, Siemens. 2021; pp. 3067–3070. Available online: https://plm.sw.siemens.com/en-US/simcenter/fluids-thermal-simulation/star-ccm/ (accessed on 24 April 2021).
- Cetnar, J. General solution of Bateman equations for nuclear transmutations. Ann. Nucl. Energy 2006, 33, 640–645. [Google Scholar] [CrossRef]
- Josey, C.; Forget, B.; Smith, K. High order methods for the integration of the Bateman equations and other problems of the form of y’ = F(y, t)y. J. Comput. Phys. 2017, 350, 296–313. [Google Scholar] [CrossRef]
- Harp, J.M.; Demkowicz, P.A.; Winston, P.L.; Sterbentz, J.W. An analysis of nuclear fuel burnup in the AGR-1 TRISO fuel experiment using gamma spectrometry, mass spectrometry, and computational simulation techniques. Nucl. Eng. Des. 2014, 278, 395–405. [Google Scholar] [CrossRef]
- Raflis, H.; Ilham, M.; Su’ud, Z.; Waris, A.; Irwanto, D. Comparative Study on Fuel Assembly of Modular Gas-cooled Fast Reactor using MCNP and OpenMC Code. J. Phys. Conf. Ser. 2021, 1772, 012031. [Google Scholar] [CrossRef]
- Leppänen, J.; Pusa, M.; Viitanen, T.; Valtavirta, V.; Kaltiaisenaho, T. The Serpent Monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 2015, 82, 142–150. [Google Scholar] [CrossRef]


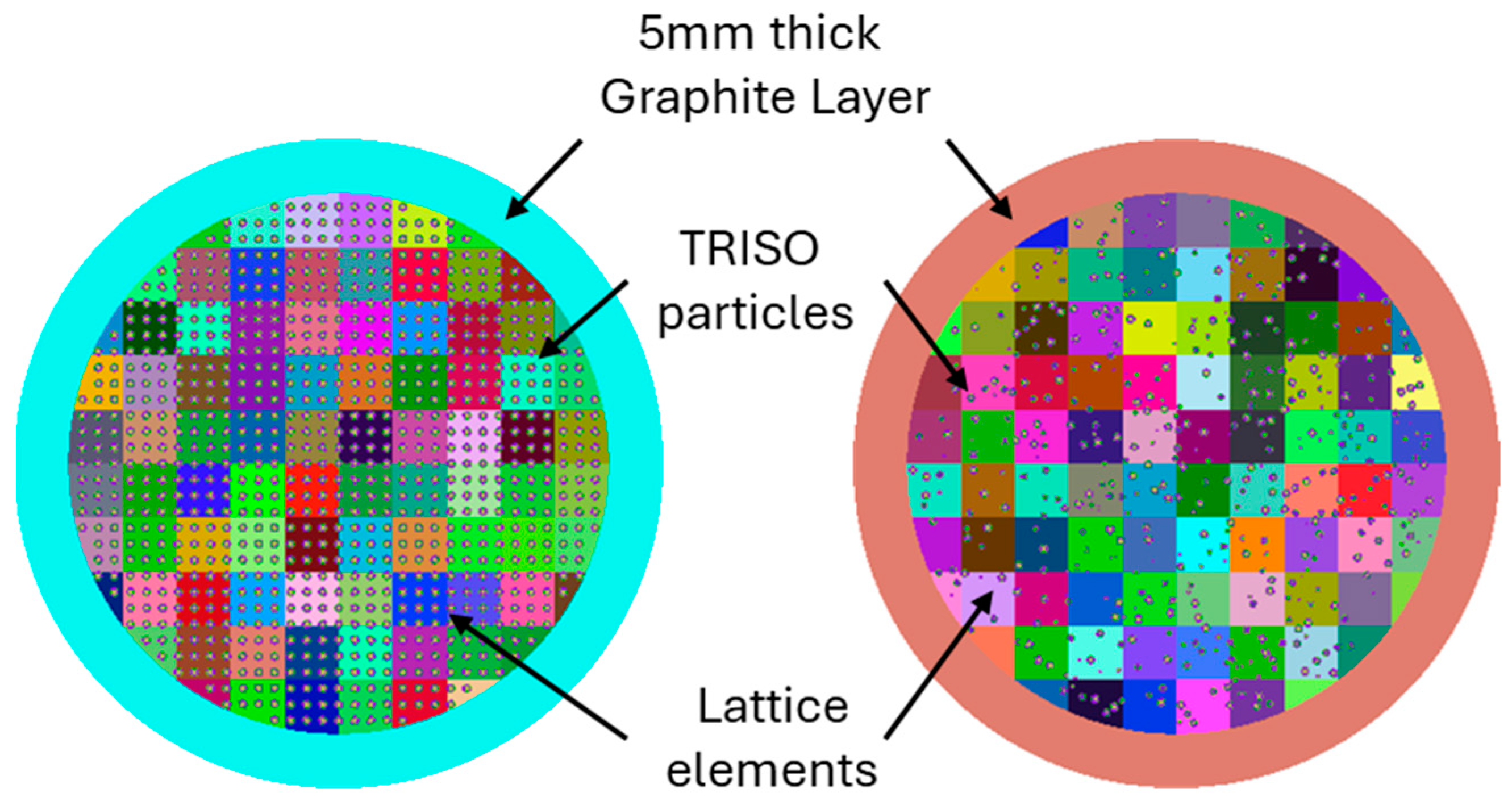

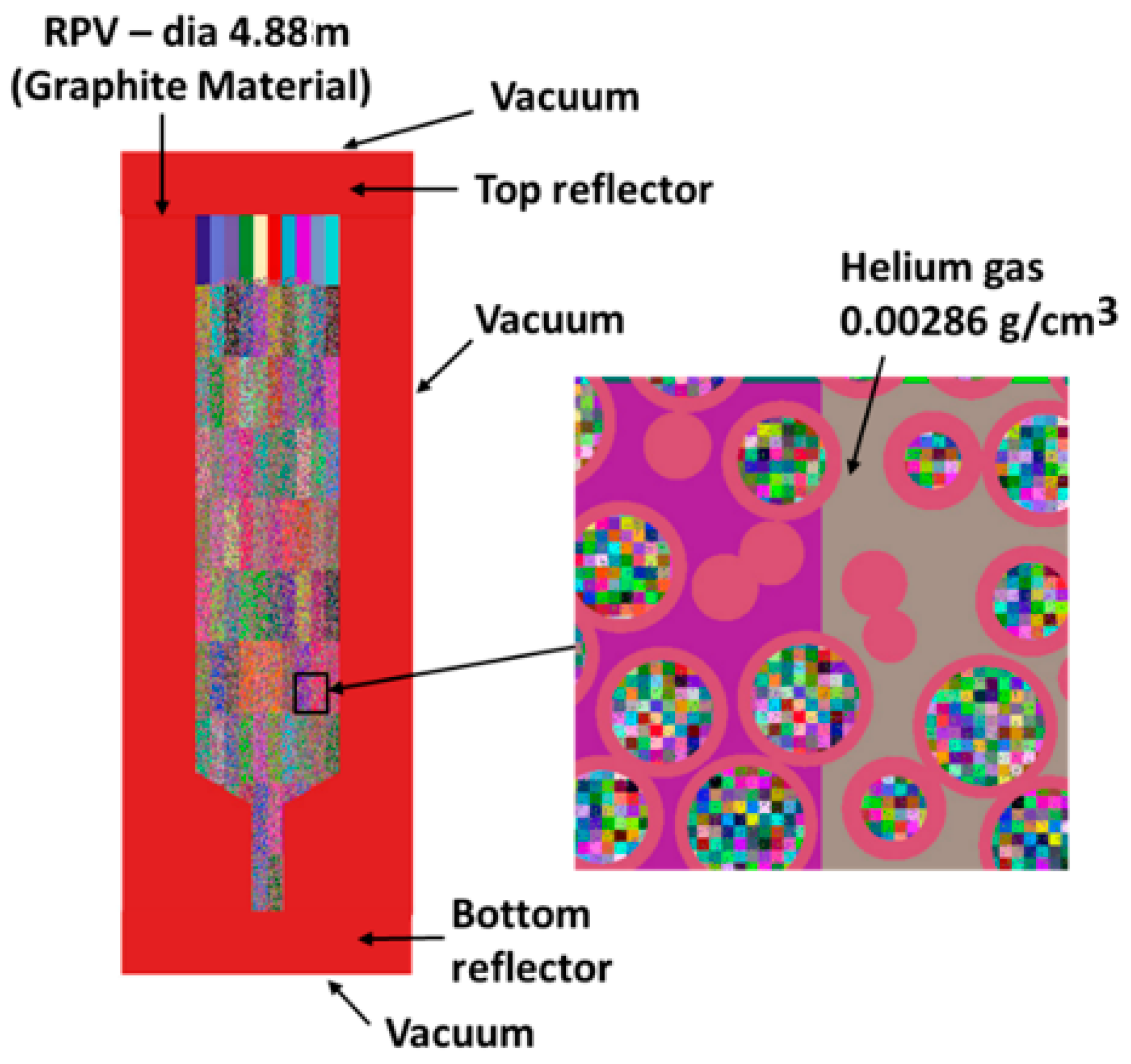

| Material | Density (g/cm3) | Composition (Atomic Fraction) | Dimension (μm) |
|---|---|---|---|
| UCO Fuel Kernel | 10.9 | 235U: 0.05232 238U: 0.28101 16O: 0.49982 17O: 0.00019 C: 0.16667 | 425 (diameter) |
| Carbon Buffer | 1.0 | C: 1.0 | 100 (thickness) |
| Inner PyC | 1.9 | C: 1.0 | 40 (thickness) |
| SiC | 3.2 | C: 0.5 Si: 0.5 | 35 (thickness) |
| Outer PyC | 1.9 | C: 1.0 | 40 (thickness) |
| Pebble Model | Code | k∞ (White B.C.) | k∞ (Mirror B.C.) | Diff. in k∞ |
|---|---|---|---|---|
| Uniform | MCNP | 1.60743 ± 0.00008 | 1.61471 ± 0.00004 | −0.00728 |
| OpenMC | 1.60818 ± 0.00011 | 1.61560 ± 0.00012 | −0.00750 | |
| Deviation | −0.00067 | −0.00089 | - | |
| Random | MCNP | 1.61017 ± 0.00007 | 1.61723 ± 0.00006 | −0.00706 |
| OpenMC | 1.61025 ± 0.00011 | 1.61739 ± 0.00012 | −0.00714 | |
| Deviation | 0.00008 | 0.00016 | - |
| Pebble Model | Code | k∞ (White B.C.) | k∞ (Mirror B.C.) | Diff. in k∞ |
|---|---|---|---|---|
| Uniform | MCNP | 1.50820 ± 0.00007 | 1.51774 ± 0.00007 | −0.00954 |
| OpenMC | 1.50789 ± 0.00012 | 1.51757 ± 0.00012 | −0.00968 | |
| Deviation | 0.00031 | 0.00017 | - | |
| Random | MCNP | 1.51203 ± 0.00008 | 1.52111 ± 0.00006 | −0.00908 |
| OpenMC | 1.51071 ± 0.00012 | 1.51980 ± 0.00012 | −0.00909 | |
| Deviation | −0.00132 | −0.00131 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehta, K.S.; Goddard, B.; Wu, Z. Neutronics Analysis on High-Temperature Gas-Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method. Energies 2024, 17, 5188. https://doi.org/10.3390/en17205188
Mehta KS, Goddard B, Wu Z. Neutronics Analysis on High-Temperature Gas-Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method. Energies. 2024; 17(20):5188. https://doi.org/10.3390/en17205188
Chicago/Turabian StyleMehta, Kashminder S., Braden Goddard, and Zeyun Wu. 2024. "Neutronics Analysis on High-Temperature Gas-Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method" Energies 17, no. 20: 5188. https://doi.org/10.3390/en17205188
APA StyleMehta, K. S., Goddard, B., & Wu, Z. (2024). Neutronics Analysis on High-Temperature Gas-Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method. Energies, 17(20), 5188. https://doi.org/10.3390/en17205188






