Applications of Machine Learning Technologies for Feedstock Yield Estimation of Ethanol Production
Abstract
1. Introduction
2. First- and Second-Generation Ethanol Production
3. Machine Learning Technologies for Feedstock Estimation of Ethanol
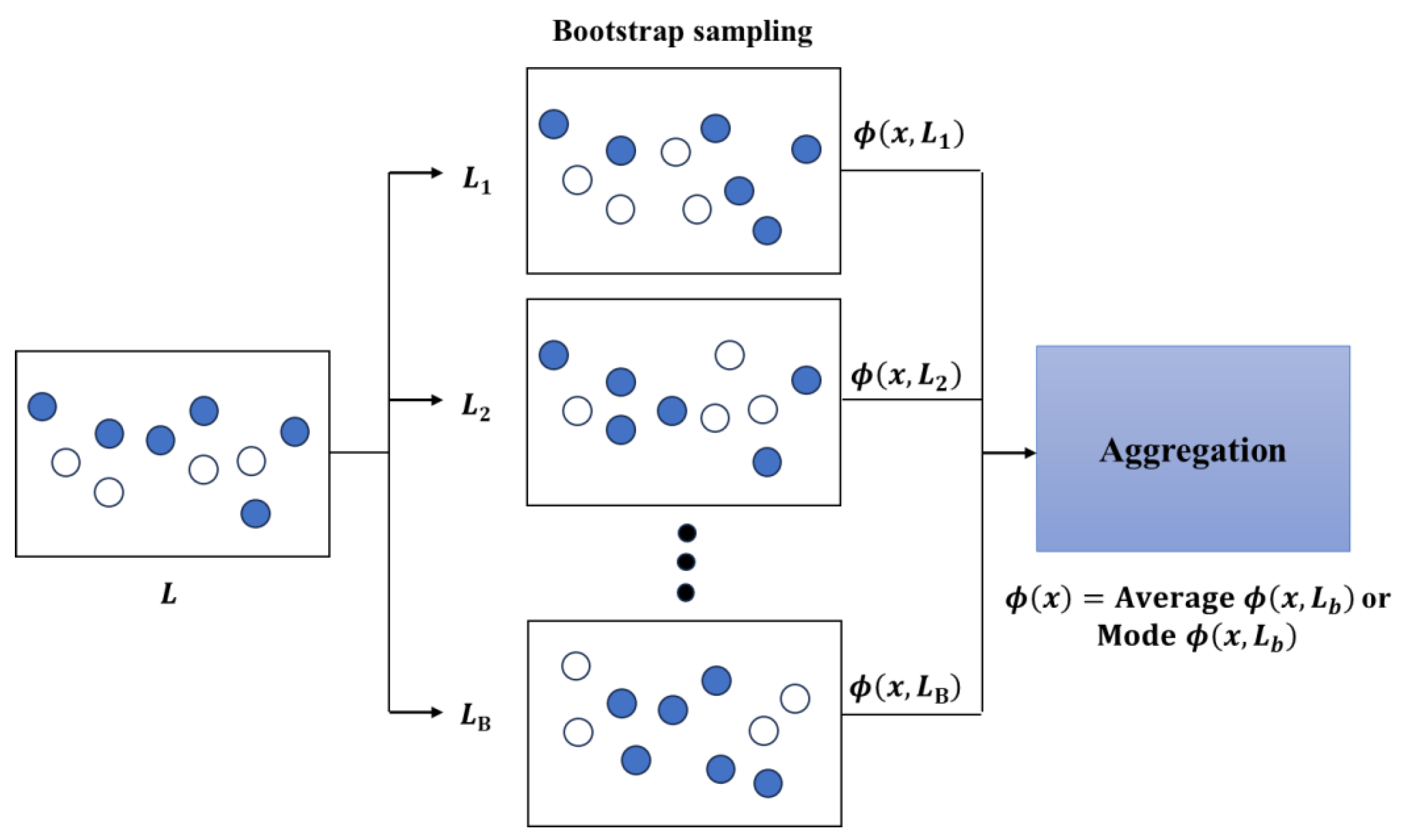
3.1. Regression Model-Based Estimation
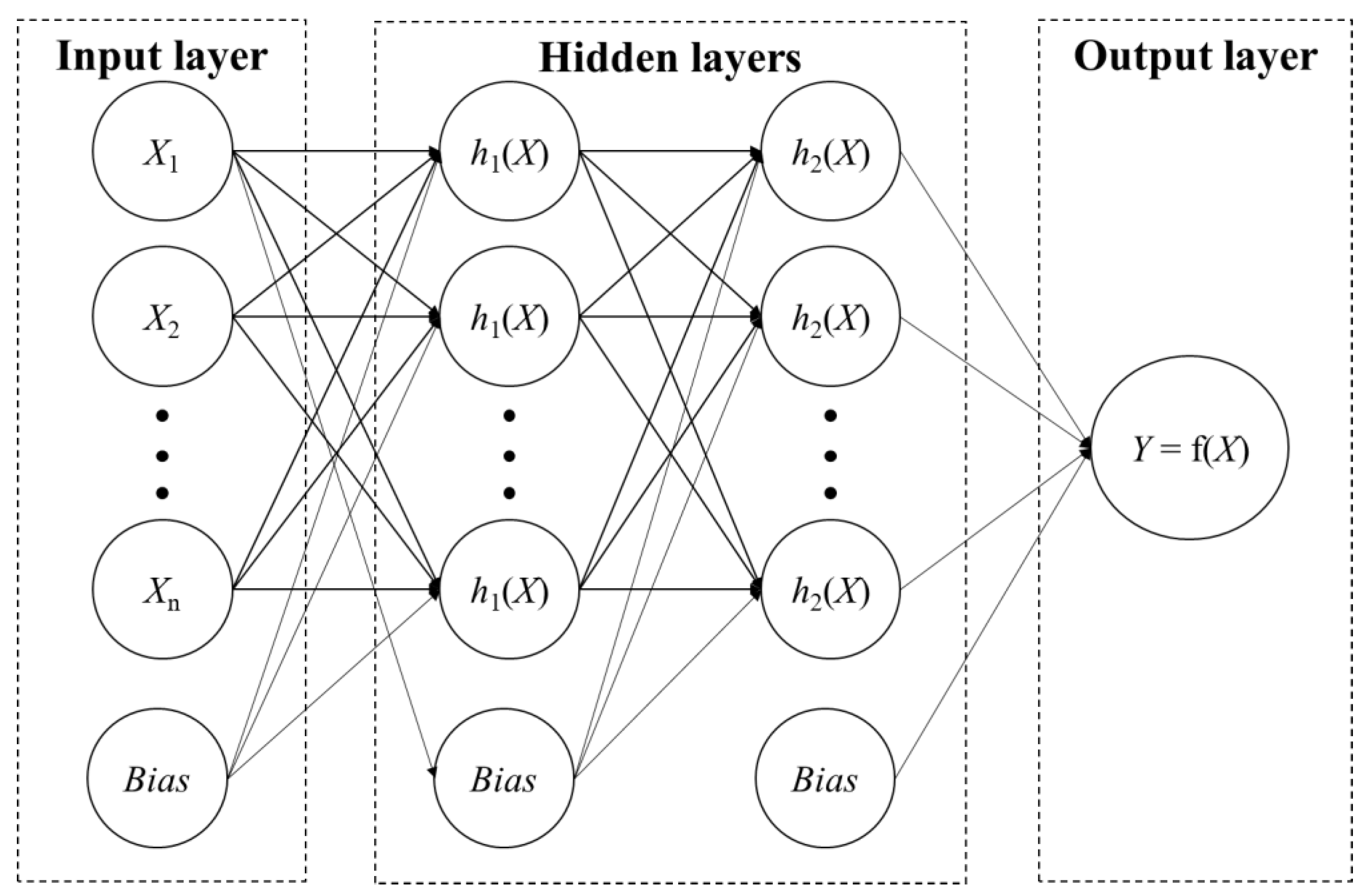
3.2. Neural Network-Based Estimation
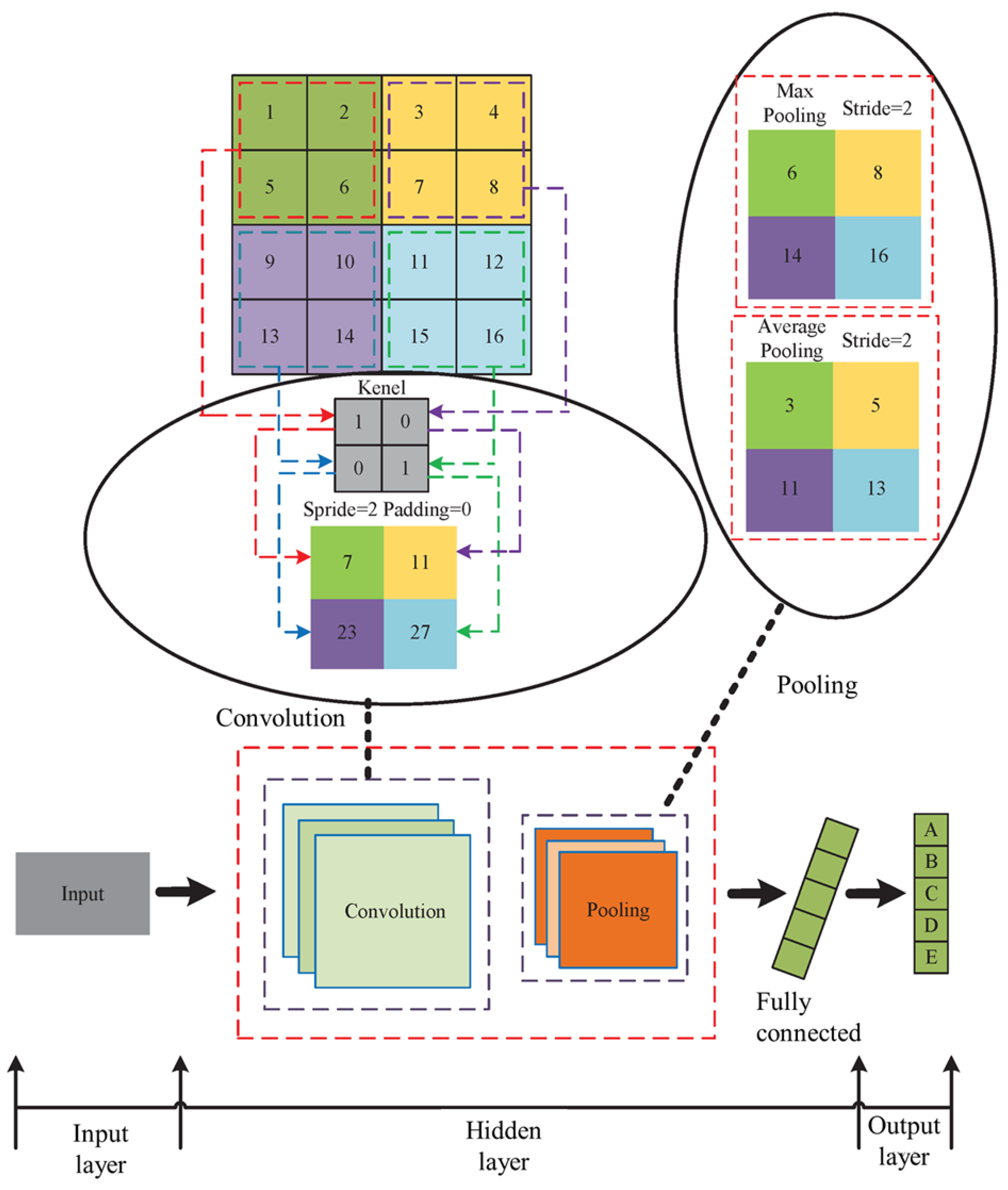
3.3. Image Data-Based Estimation
3.4. Machine Learning Techniques Applied to Other Operations of Biofuel Production
3.5. Discussion
4. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tse, T.J.; Wiens, D.J.; Reaney, M.J.T. Production of Bioethanol-A Review of Factors Affecting Ethanol Yield. Fermentation 2021, 7, 268. [Google Scholar] [CrossRef]
- Robak, K.; Balcerek, M. Review of Second Generation Bioethanol Production from Residual Biomass. Food Technol. Biotechnol. 2018, 56, 174–187. [Google Scholar] [CrossRef] [PubMed]
- Renewable Fuels Association. Annual Ethanol Production. Available online: https://ethanolrfa.org/markets-and-statistics/annual-ethanol-production (accessed on 6 July 2024).
- Renewable Fuels Association. Ethanol Industry Outlook. 2019. Available online: https://d35t1syewk4d42.cloudfront.net/file/18/RFA_outlook_2019_newlogo.pdf (accessed on 6 July 2024).
- Renewable Fuels Association. Ethanol Industry Outlook. 2020. Available online: https://d35t1syewk4d42.cloudfront.net/file/21/2020-Outlook-Final-for-Website.pdf (accessed on 6 July 2024).
- Zheng, J.L.; Zhu, Y.H.; Su, H.Y.; Sun, G.T.; Kang, F.R.; Zhu, M.Q. Life cycle assessment and techno-economic analysis of fuel ethanol production via bio-oil fermentation based on a centralized-distribution model. Renew. Sustain. Energy Rev. 2022, 167, 112714. [Google Scholar] [CrossRef]
- Li, H.; Li, S. Optimization of continuous solid-state distillation process for cost-effective bioethanol production. Energies 2020, 13, 854. [Google Scholar] [CrossRef]
- Dickson, R.; Liu, J.J. A strategy for advanced biofuel production and emission utilization from macroalgal biorefinery using superstructure optimization. Energy 2021, 221, 119883. [Google Scholar] [CrossRef]
- Khan, S.; Naushad, M.; Iqbal, J.; Bathula, C.; Ala’a, H. Challenges and perspectives on innovative technologies for biofuel production and sustainable environmental management. Fuel 2022, 325, 124845. [Google Scholar] [CrossRef]
- Yazdanparast, R.; Jolai, F.; Pishvaee, M.S.; Keramati, A. A resilient drop-in biofuel supply chain integrated with existing petroleum infrastructure: Toward more sustainable transport fuel solutions. Renew. Energy 2022, 184, 799–819. [Google Scholar] [CrossRef]
- Ambaye, T.G.; Vaccari, M.; Bonilla-Petriciolet, A.; Prasad, S.; van Hullebusch, E.D.; Rtimi, S. Emerging technologies for biofuel production: A critical review on recent progress, challenges and perspectives. J. Environ. Manag. 2021, 290, 112627. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Garg, N.; Tyagi, A.K. Viable feedstock options and technological challenges for ethanol production in India. Curr. Sci. 2016, 111, 815–822. [Google Scholar] [CrossRef]
- Vohra, M.; Manwar, J.; Manmode, R.; Padgilwar, S.; Patil, S. Bioethanol production: Feedstock and current technologies. J. Environ. Chem. Eng. 2014, 2, 573–584. [Google Scholar] [CrossRef]
- Slade, R.; Bauen, A.; Shah, N. The commercial performance of cellulosic ethanol supply-chains in Europe. Biotechnol. Biofuels 2009, 2, 573–584. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, S. Hybrid simulation framework for the production management of an ethanol biorefinery. Renew. Sustain. Energy Rev. 2022, 155, 111911. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Green, C.H.M.; Jeong, J. Multivariate polynomial regression modeling of total dissolved-solids in rangeland stormwater runoff in the Colorado River Basin. Environ. Model. Softw. 2022, 157, 105523. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised learning. In Machine Learning Techniques for Multimedia: Case Studies on Organization and Retrieval; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Renewable Fuels Association. Ethanol Industry Outlook. 2024. Available online: https://d35t1syewk4d42.cloudfront.net/file/2666/RFA_Outlook_2024_full_final_low.pdf (accessed on 6 July 2024).
- Malik, K.; Sharma, P.; Yang, Y.L.; Zhang, P.; Zhang, L.H.; Xing, X.H.; Yue, J.W.; Song, Z.Z.; Nan, L.; Su, Y.J.; et al. Lignocellulosic biomass for bioethanol: Insight into the advanced pretreatment and fermentation approaches. Ind. Crop. Prod. 2022, 188, 115569. [Google Scholar] [CrossRef]
- Dias, M.O.S.; Ensinas, A.V.; Nebra, S.A.; Maciel, R.; Rossell, C.E.V.; Maciel, M.R.W. Production of bioethanol and other bio-based materials from sugarcane bagasse: Integration to conventional bioethanol production process. Chem. Eng. Res. Des. 2009, 87, 1206–1216. [Google Scholar] [CrossRef]
- An, H.J.; Wilhelm, W.E.; Searcy, S.W. Biofuel and petroleum-based fuel supply chain research: A literature review. Biomass Bioenergy 2011, 35, 3763–3774. [Google Scholar] [CrossRef]
- Zabed, H.; Sahu, J.N.; Suely, A.; Boyce, A.N.; Faruq, G. Bioethanol production from renewable sources: Current perspectives and technological progress. Renew. Sust. Energy Rev. 2017, 71, 475–501. [Google Scholar] [CrossRef]
- McAloon, A.; Taylor, F.; Yee, W.; Ibsen, K.; Wooley, R. Determining the Cost of Producing Ethanol from Corn Starch and Lignocellulosic Feedstocks; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2000.
- Slewinski, T.L. Non-structural carbohydrate partitioning in grass stems: A target to increase yield stability, stress tolerance, and biofuel production. J. Exp. Bot. 2012, 63, 4647–4670. [Google Scholar] [CrossRef] [PubMed]
- Bothast, R.J.; Schlicher, M.A. Biotechnological processes for conversion of corn into ethanol. Appl. Microbiol. Biotechnol. 2005, 67, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Aditiya, H.B.; Mahlia, T.M.I.; Chong, W.T.; Nur, H.; Sebayang, A.H. Second generation bioethanol production: A critical review. Renew. Sustain. Energy Rev. 2016, 66, 631–653. [Google Scholar] [CrossRef]
- Bai, Y.; Luo, L.; van der Voet, E. Life cycle assessment of switchgrass-derived ethanol as transport fuel. Int. J. Life Cycle Assess. 2010, 15, 468–477. [Google Scholar] [CrossRef]
- Balat, M.; Balat, H.; Öz, C. Progress in bioethanol processing. Prog. Energy Combust. Sci. 2008, 34, 551–573. [Google Scholar] [CrossRef]
- Larnaudie, V.; Ferrari, M.D.; Lareo, C. Switchgrass as an alternative biomass for ethanol production in a biorefinery: Perspectives on technology, economics and environmental sustainability. Renew. Sustain. Energy Rev. 2022, 158, 112115. [Google Scholar] [CrossRef]
- Dos Santos, L.V.; de Barros Grassi, M.C.; Gallardo, J.C.M.; Pirolla, R.A.S.; Calderón, L.L.; de Carvalho-Netto, O.V.; Parreiras, L.S.; Camargo, E.L.O.; Drezza, A.L.; Missawa, S.K. Second-generation ethanol: The need is becoming a reality. Ind. Biotechnol. 2016, 12, 40–57. [Google Scholar] [CrossRef]
- Limayem, A.; Ricke, S.C. Lignocellulosic biomass for bioethanol production: Current perspectives, potential issues and future prospects. Prog. Energy Combust. Sci. 2012, 38, 449–467. [Google Scholar] [CrossRef]
- Horn, S.J.; Vaaje-Kolstad, G.; Westereng, B.; Eijsink, V.G.H. Novel enzymes for the degradation of cellulose. Biotechnol. Biofuels 2012, 5, 45. [Google Scholar] [CrossRef]
- Keshwani, D.R.; Cheng, J.J. Switchgrass for bioethanol and other value-added applications: A review. Bioresour. Technol. 2009, 100, 1515–1523. [Google Scholar] [CrossRef] [PubMed]
- Dias, M.O.S.; Cunha, M.P.; Maciel, R.; Bonomi, A.; Jesus, C.D.F.; Rossell, C.E.V. Simulation of integrated first and second generation bioethanol production from sugarcane: Comparison between different biomass pretreatment methods. J. Ind. Microbiol. Biotechnol. 2011, 38, 955–966. [Google Scholar] [CrossRef] [PubMed]
- Palacios-Bereche, R.; Mosqueira-Salazar, K.J.; Modesto, M.; Ensinas, A.V.; Nebra, S.A.; Serra, L.M.; Lozano, M.A. Exergetic analysis of the integrated first- and second-generation ethanol production from sugarcane. Energy 2013, 62, 46–61. [Google Scholar] [CrossRef]
- Ahamed, T.; Tian, L.; Zhang, Y.; Ting, K.C. A review of remote sensing methods for biomass feedstock production. Biomass Bioenergy 2011, 35, 2455–2469. [Google Scholar] [CrossRef]
- Dimov, D.; Uhl, J.H.; Löw, F.; Seboka, G.N. Sugarcane yield estimation through remote sensing time series and phenology metrics. Smart Agric. Technol. 2022, 2, 100046. [Google Scholar] [CrossRef]
- Shahhosseini, M.; Hu, G.P.; Archontoulis, S.V. Forecasting Corn Yield with Machine Learning Ensembles. Front. Plant Sci. 2020, 11, 1120. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S. Performance Estimation Modeling via Machine Learning of an Agrophotovoltaic System in South Korea. Energies 2021, 14, 6724. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L.Z. Crop Yield Prediction Using Deep Neural Networks. Front. Plant Sci. 2019, 10, 621. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.C.; Roth, H.R.; Gao, M.C.; Lu, L.; Xu, Z.Y.; Nogues, I.; Yao, J.H.; Mollura, D.; Summers, R.M. Deep Convolutional Neural Networks for Computer-Aided Detection: CNN Architectures, Dataset Characteristics and Transfer Learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef]
- Shastry, A.; Sanjay, H.; Bhanusree, E. Prediction of crop yield using regression techniques. Int. J. Soft Comput. 2017, 12, 96–102. [Google Scholar]
- Ansarifar, J.; Wang, L.Z.; Archontoulis, S.V. An interaction regression model for crop yield prediction. Sci. Rep. 2021, 11, 17754. [Google Scholar] [CrossRef] [PubMed]
- Johann, A.L.; de Araújo, A.G.; Delalibera, H.C.; Hirakawa, A.R. Soil moisture modeling based on stochastic behavior of forces on a no-till chisel opener. Comput. Electron. Agric. 2016, 121, 420–428. [Google Scholar] [CrossRef]
- Kim, S.; Seo, J.; Kim, S. Machine Learning Technologies in the Supply Chain Management Research of Biodiesel: A Review. Energies 2024, 17, 1316. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Wang, L.; Yang, G.; Li, Z.; Xu, F. An efficient nonlinear interval uncertain optimization method using Legendre polynomial chaos expansion. Appl. Soft Comput. 2021, 108, 107454. [Google Scholar] [CrossRef]
- Bertsimas, D.; Van Parys, B. Sparse hierarchical regression with polynomials. Mach. Learn. 2020, 109, 973–997. [Google Scholar] [CrossRef]
- Dette, H.; Melas, V.B.; Pepelyshev, A. Optimal designs for estimating individual coefficients in polynomial regression—A functional approach. J. Stat. Plan. Inference 2004, 118, 201–219. [Google Scholar] [CrossRef][Green Version]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J.A. LASSO regression. Br. J. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- Dong, X.B.; Yu, Z.W.; Cao, W.M.; Shi, Y.F.; Ma, Q.L. A survey on ensemble learning. Front. Comput. Sci. 2020, 14, 241–258. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; An, K.Y.A. An integrated multi-modeling framework to estimate potential rice and energy production under an agrivoltaic system. Comput. Electron. Agric. 2023, 213, 108157. [Google Scholar] [CrossRef]
- Sakamoto, T. Incorporating environmental variables into a MODIS-based crop yield estimation method for United States corn and soybeans through the use of a random forest regression algorithm. ISPRS J. Photogramm. Remote Sens. 2020, 160, 208–228. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, S.; Athaiya, A. Activation functions in neural networks. Towards Data Sci. 2017, 6, 310–316. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Apicella, A.; Donnarumma, F.; Isgrò, F.; Prevete, R. A survey on modern trainable activation functions. Neural Netw. 2021, 138, 14–32. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, H.; Zhong, R.H.; Xu, J.F.; Xu, J.L.; Huang, J.F.; Wang, S.W.; Ying, Y.B.; Lin, T. A deep learning approach to conflating heterogeneous geospatial data for corn yield estimation: A case study of the US Corn Belt at the county level. Glob. Chang. Biol. 2020, 26, 1754–1766. [Google Scholar] [CrossRef]
- Kuwata, K.; Shibasaki, R. Estimating Crop Yields with Deep Learning and Remotely Sensed Data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 858–861. [Google Scholar]
- Sun, J.; Lai, Z.L.; Di, L.P.; Sun, Z.H.; Tao, J.B.; Shen, Y.L. Multilevel Deep Learning Network for County-Level Corn Yield Estimation in the US Corn Belt. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5048–5060. [Google Scholar] [CrossRef]
- García-Martínez, H.; Flores-Magdaleno, H.; Ascencio-Hernández, R.; Khalil-Gardezi, A.; Tijerina-Chávez, L.; Mancilla-Villa, O.R.; Vázquez-Peña, M.A. Corn Grain Yield Estimation from Vegetation Indices, Canopy Cover, Plant Density, and a Neural Network Using Multispectral and RGB Images Acquired with Unmanned Aerial Vehicles. Agriculture 2020, 10, 277. [Google Scholar] [CrossRef]
- Albelwi, S.; Mahmood, A. A Framework for Designing the Architectures of Deep Convolutional Neural Networks. Entropy 2017, 19, 242. [Google Scholar] [CrossRef]
- Krichen, M. Convolutional Neural Networks: A Survey. Computers 2023, 12, 151. [Google Scholar] [CrossRef]
- Li, Z.W.; Liu, F.; Yang, W.J.; Peng, S.H.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef]
- Kim, Y.; On, Y.; So, J.; Kim, S.; Kim, S. A Decision Support Software Application for the Design of Agrophotovoltaic Systems in Republic of Korea. Sustainability 2023, 15, 8830. [Google Scholar] [CrossRef]
- Yang, W.; Nigon, T.; Hao, Z.Y.; Paiao, G.D.; Fernández, F.G.; Mulla, D.; Yang, C. Estimation of corn yield based on hyperspectral imagery and convolutional neural network. Comput. Electron. Agric. 2021, 184, 106092. [Google Scholar] [CrossRef]
- Khaki, S.; Pham, H.; Han, Y.; Kuhl, A.; Kent, W.; Wang, L.Z. DeepCorn: A semi-supervised deep learning method for high-throughput image-based corn kernel counting and yield estimation. Knowl. Based Syst. 2021, 218, 106874. [Google Scholar] [CrossRef]
- Horikawa, Y.; Imai, T.; Takada, R.; Watanabe, T.; Takabe, K.; Kobayashi, Y.; Sugiyama, J. Chemometric Analysis with Near-Infrared Spectroscopy for Chemically Pretreated Erianthus toward Efficient Bioethanol Production. Appl. Biochem. Biotechnol. 2012, 166, 711–721. [Google Scholar] [CrossRef]
- Magaña, C.; Núñez-Sánchez, N.; Fernández-Cabanás, V.M.; García, P.; Serrano, A.; Pérez-Marín, D.; Pemán, J.M.; Alcalde, E. Direct prediction of bioethanol yield in sugar beet pulp using Near Infrared Spectroscopy. Bioresour. Technol. 2011, 102, 9542–9549. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, K.; Tachibana, S.; Konishi, M. Modeling growth and fermentation inhibition during bioethanol production using component profiles obtained by performing comprehensive targeted and non-targeted analyses. Bioresour. Technol. 2019, 281, 260–268. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Weng, C.; Huang, H.Q.; Achal, V.; Wang, D.C. Optimization of Bioethanol Production Using Whole Plant of Water Hyacinth as Substrate in Simultaneous Saccharification and Fermentation Process. Front. Microbiol. 2016, 6, 1411. [Google Scholar] [CrossRef]
- Shenbagamuthuraman, V.; Kasianantham, N. Microwave irradiation pretreated fermentation of bioethanol production from Chlorella vulgaris Biomasses: Comparative analysis of response surface methodology and artificial neural network techniques. Bioresour. Technol. 2023, 390, 129867. [Google Scholar] [CrossRef] [PubMed]
- Dave, N.; Varadavenkatesan, T.; Selvaraj, R.; Vinayagam, R. Modelling of fermentative bioethanol production from indigenous Ulva prolifera biomass by Saccharomyces cerevisiae NFCCI1248 using an integrated ANN-GA approach. Sci. Total Environ. 2021, 791, 148429. [Google Scholar] [CrossRef] [PubMed]
- Mondal, P.; Sadhukhan, A.K.; Ganguly, A.; Gupta, P. Optimization of process parameters for bio-enzymatic and enzymatic saccharification of waste broken rice for ethanol production using response surface methodology and artificial neural network-genetic algorithm. 3 Biotech 2021, 11, 28. [Google Scholar] [CrossRef]
- Concu, R.; Cordeiro, M.N.D.S.; Munteanu, C.R.; González-Díaz, H. PTML Model of Enzyme Subclasses for Mining the Proteome of Biofuel Producing Microorganisms. J. Proteome Res. 2019, 18, 2735–2746. [Google Scholar] [CrossRef]
- Konishi, M. Bioethanol production estimated from volatile compositions in hydrolysates of lignocellulosic biomass by deep learning. J. Biosci. Bioeng. 2020, 129, 723–729. [Google Scholar] [CrossRef]
- Fernández, M.C.; Pantano, M.N.; Rodriguez, L.; Scaglia, G. State estimation and nonlinear tracking control simulation approach. Application to a bioethanol production system. Bioprocess Biosyst. Eng. 2021, 44, 1755–1768. [Google Scholar] [CrossRef]
- Ostos-Garrido, F.J.; de Castro, A.I.; Torres-Sánchez, J.; Pistón, F.; Peña, J.M. High-Throughput Phenotyping of Bioethanol Potential in Cereals Using UAV-Based Multi-Spectral Imagery. Front. Plant Sci. 2019, 10, 948. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Cho, J.; Park, S.; Jarrín Perez, F.X.; Kiniry, J.R. Simulated biomass, climate change impacts, and nitrogen management to achieve switchgrass biofuel production at diverse sites in US. Agronomy 2020, 10, 503. [Google Scholar] [CrossRef]
- Chen, Y.; Ale, S.; Rajan, N. Spatial variability of biofuel production potential and hydrologic fluxes of land use change from cotton (Gossypium hirsutum L.) to Alamo switchgrass (Panicum virgatum L.) in the Texas High Plains. BioEnergy Res. 2016, 9, 1126–1141. [Google Scholar] [CrossRef]
- Hussain, J. Deep Learning Black Box Problem; University of Michigan Dearborn: Dearborn, MI, USA, 2019. [Google Scholar]
- Eitel, F.; Schulz, M.A.; Seiler, M.; Walter, H.; Ritter, K. Promises and pitfalls of deep neural networks in neuroimaging-based psychiatric research. Exp. Neurol. 2021, 339, 113608. [Google Scholar] [CrossRef]
- Coşgun, A.; Günay, M.E.; Yıldırım, R. Machine learning for algal biofuels: A critical review and perspective for the future. Green Chem. 2023, 25, 3354–3373. [Google Scholar] [CrossRef]

| Variables | Description | Unit |
|---|---|---|
| Plant population | The number of plants per acre. | plants/acre |
| Planting progress | The weekly cumulative percentage of corn planted within each state. | % |
| Minimum air temperature | Daily minimum air temperature. | °C |
| Maximum air temperature | Daily maximum air temperature. | °C |
| Precipitation | Daily total precipitation. | mm |
| Shortwave radiation | The amount of incoming solar radiation. | W/ |
| Water vapor pressure | The pressure exerted by water vapor in the atmosphere. | Pa |
| Snow water equivalent | The amount of water contained in the snowpack. | kg/ |
| Day length | The duration of daylight each day. | Sec |
| Soil | 180 soil feature variables considering soil organic matter, sand content, soil pH, soil bulk density, field capacity, and hydraulic conductivity. | N/A |
| Yield | Annual corn yield data. | bu/acre |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, H.; Kim, S. Applications of Machine Learning Technologies for Feedstock Yield Estimation of Ethanol Production. Energies 2024, 17, 5191. https://doi.org/10.3390/en17205191
Lim H, Kim S. Applications of Machine Learning Technologies for Feedstock Yield Estimation of Ethanol Production. Energies. 2024; 17(20):5191. https://doi.org/10.3390/en17205191
Chicago/Turabian StyleLim, Hyeongjun, and Sojung Kim. 2024. "Applications of Machine Learning Technologies for Feedstock Yield Estimation of Ethanol Production" Energies 17, no. 20: 5191. https://doi.org/10.3390/en17205191
APA StyleLim, H., & Kim, S. (2024). Applications of Machine Learning Technologies for Feedstock Yield Estimation of Ethanol Production. Energies, 17(20), 5191. https://doi.org/10.3390/en17205191








