Research on the Influence of Moisture in the Solid Insulation Impregnated with an Innovative Bio-Oil on AC Conductivity Used in the Power Transformers
Abstract
1. Introduction
2. DC and AC Conductivity of Pressboard-Insulating Oil-Water Composites–Theoretical Foundations
2.1. Classical Models of Polarization and Associated Conductivity
2.2. DC and AC Conductivity Considering the Quantum Mechanical Phenomenon of Electron Tunneling
3. Materials and Methods
4. Study of DC and AC Conductivity of the Pressboard-Bio Insulating Oil-Moisture Composite
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Graczkowski, A. Dielectric response of cellulose impregnated with different insulating liquids. Przegląd Elektrotech. 2010, 86, 223–225. [Google Scholar]
- Wei, Y.; Han, W.; Li, G.; Liang, X.; Gu, Z.; Hu, K. Aging Characteristics of Transformer Oil-Impregnated Insulation Paper Based on Trap Parameters. Polymers 2021, 13, 1364. [Google Scholar] [CrossRef] [PubMed]
- Qi, B.; Dai, Q.; Li, C.; Zeng, Z.; Fu, M.; Zhuo, R. The Mechanism and Diagnosis of Insulation Deterioration Caused by Moisture Ingress into Oil-Impregnated Paper Bushing. Energies 2018, 11, 1496. [Google Scholar] [CrossRef]
- Lundgaard, L.E.; Hansen, W.; Linhjell, D.; Painter, T.J. Aging of Oil-Impregnated Paper in Power Transformers. IEEE Trans. Power Deliv. 2004, 19, 230–239. [Google Scholar] [CrossRef]
- Oommen, T.V.; Prevost, T.A. Cellulose insulation in oil-filled power transformers: Part II—Maintaining insulation integrity and life. IEEE Electr. Insul. Mag. 2006, 22, 5–14. [Google Scholar] [CrossRef]
- Fabre, J.; Pichon, A. Deteriorating Processes and Products of Paper in Oil Application to Transformers. In Proceedings of the International Conference on Large High Voltage Electric Systems, Paris, France, 15–25 June 1960; p. 137. [Google Scholar]
- Liu, J.; Zhang, H.; Geng, C.; Fan, X.; Zhang, Y. Aging Assessment Model of Transformer Insulation Based on Furfural Indicator under Different Oil/Pressboard Ratios and Oil Change. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1061–1069. [Google Scholar] [CrossRef]
- Prevost, T.A.; Oommen, T.V. Cellulose insulation in oil-filled power transformers: Part I—History and development. IEEE Electr. Insul. Mag. 2006, 22, 28–35. [Google Scholar] [CrossRef]
- Gielniak, J.; Graczkowski, A.; Moranda, H.; Przybylek, P.; Walczak, K.; Nadolny, Z.; Moscicka-Grzesiak, H.; Feser, K.; Gubanski, S. Moisture in cellulose insulation of power transformers—Statistics. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 982–987. [Google Scholar] [CrossRef]
- Raetzke, S.; Koch, M.; Krueger, M.; Talib, A. Condition assessment of instrument transformers using Dielectric Response Analysis. Elektrotech. Inftech. 2013. [Google Scholar] [CrossRef]
- Lelekakis, N.; Martin, D.; Guo, W.; Wijaya, J.; Lee, M. A field study of two online dry-out methods for power transformers. IEEE Electr. Insul. Mag. 2012, 28, 32–39. [Google Scholar] [CrossRef]
- Martin, D.; Perkasa, C.; Lelekakis, N. Measuring paper water content of transformers: A new approach using cellulose isotherms in nonequilibrium conditions. IEEE Trans. Power Deliv. 2013, 28, 1433–1439. [Google Scholar] [CrossRef]
- Subocz, J. Przewodnictwo i Relaksacja Dielektryczna Warstowywch Układów Izolacyjnych; Wydawnictwo Uczelniane, Ed.; Uczelniane Zachodniopomorskiego Uniwersytetu Technologicznego w Szczecinie: Szczecin, Poland, 2012; ISBN 8376631136/9788376631134. [Google Scholar]
- Martínez, M.; Pleite, J. Improvement of RVM test interpretation using a Debye equivalent circuit. Energies 2020, 13, 323. [Google Scholar] [CrossRef]
- Islam, M.M.; Lee, G.; Hettiwatte, S.N. A review of condition monitoring techniques and diagnostic tests for lifetime estimation of power transformers. Electr. Eng. 2018, 100, 581–605. [Google Scholar] [CrossRef]
- Fofana, I.; Hadjadj, Y. Electrical-Based Diagnostic Techniques for Assessing Insulation Condition in Aged Transformers. Energies 2016, 9, 679. [Google Scholar] [CrossRef]
- Sarkar, S.; Sharma, T.; Baral, A.; Chatterjee, B.; Dey, D.; Chakravorti, S. An expert system approach for transformer insulation diagnosis combining conventional diagnostic tests and PDC, RVM data. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 882–891. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, J.; Zhang, Y.; Ma, Y.; Shen, Y.; Zhen, X.; Chen, Z. Effectiveness Analysis and Temperature Effect Mechanism on Chemical and Electrical-Based Transformer Insulation Diagnostic Parameters Obtained from PDC Data. Energies 2018, 11, 146. [Google Scholar] [CrossRef]
- Mishra, D.; Haque, N.; Baral, A.; Chakravorti, S. Assessment of interfacial charge accumulation in oil-paper interface in transformer insulation from polarization-depolarization current measurements. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1665–1673. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Zheng, H.; Wang, K. Feasibility of a universal approach for temperature correction in frequency domain spectroscopy of transformer insulation. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 1766–1773. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Zhang, Y.; Zhang, C.; Wang, Z. Aging evaluation and moisture prediction of oil-immersed cellulose insulation in field transformer using frequency domain spectroscopy and aging kinetics model. Cellulose 2020, 27, 7175–7189. [Google Scholar] [CrossRef]
- Yang, L.; Chen, J.; Gao, J.; Zheng, H.; Li, Y. Accelerating frequency domain dielectric spectroscopy measurements on insulation of transformers through system identification. IET Sci. Meas. Technol. 2018, 12, 247–254. [Google Scholar] [CrossRef]
- Żukowski, P.; Kołtunowicz, T.N.; Kierczyński, K.; Subocz, J.; Szrot, M.; Gutten, M.; Sebok, M.; Jurcik, J. An analysis of AC conductivity in moist oil-impregnated insulation pressboard. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2156–2164. [Google Scholar] [CrossRef]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 1984; Volume 45, ISBN 978-3-662-02405-8. [Google Scholar]
- Żukowski, P.; Kierczyński, K.; Kołtunowicz, T.N.; Rogalski, P.; Subocz, J. Application of elements of quantum mechanics in analysing AC conductivity and determining the dimensions of water nanodrops in the composite of cellulose and mineral oil. Cellulose 2019, 26, 2969–2985. [Google Scholar] [CrossRef]
- NYTRO® BIO 300X—THE NEW BIO-BASED ALTERNATIVE from NYNAS, Transform. Technol. Mag. 2020, 46–51. Available online: https://www.powersystems.technology/community-hub/in-focus/nytro-bio-300x-the-new-bio-based-alternative-from-nynas.html (accessed on 2 September 2024).
- Wolmarans Carl, P.; Abrahams, R.; Pahlavanpour, B. Biodegradable electroinsulating fluids based on low viscosity hydrocarbons. Energetyka 2021, 9, 649–652. [Google Scholar]
- Wolmarans, C.; Gamil, A.; Al-Abadi, A.; Milone, M.; Jornaan, J.; Hellberg, R. Type Testing of 80 MVA Power Transformer with a new Bio-based, Biodegradable and Low Viscosity Insulating liquid. In Proceedings of the Conference: CIGRE Session, Paris, France, 28 August–2 September 2022; p. 11125. [Google Scholar]
- Koch, M.; Tenbohlen, S.; Krüger, M.; Kraetge, A. A Comparative Test and Consequent Improvements on Dielectric Response Methods. In Proceedings of the 15th International Symposium on High Voltage Engineering, Ljubljana, Slovenia, 27–31 August 2007. [Google Scholar]
- Mamunya, Y.P.; Davydenko, V.V.; Pissis, P.; Lebedev, E.V. Electrical and thermal conductivity of polymers filled with metal powders. Eur. Polym. J. 2002, 38, 1887–1897. [Google Scholar] [CrossRef]
- ISO/TS 80004-2:2015; Nanotechnologies—Vocabulary—Part 2: Nano-Objects. ISO: Geneva, Switzerland, 2015. Available online: https://www.iso.org/standard/54440.html (accessed on 3 December 2021).
- The European Commission. Commission Recommendation of 18 October 2011 on the definition of nanomaterial. Off. J. Eur. Union 2011, 38–40. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2011:275:0038:0040:EN:PDF (accessed on 1 September 2024).
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials, 2nd ed.; Clarendon Press: Oxford, UK; New York, NY, USA, 1979; ISBN 9780198512882. [Google Scholar]
- Jonscher, A.K. Dielectric Relaxation in Solids; Chelsea Dielectrics Press: London, UK, 1983. [Google Scholar]
- Chelkowski, A. Fizyka Dielektryków; Wydaw. Naukowe PWN: Warszawa, Poland, 1993; ISBN 830111245X. [Google Scholar]
- Waygood, A. An Introduction to Electrical Science, 2nd ed.; Routledge: New York, NY, USA, 2019. [Google Scholar]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Żukowski, P.; Kołtunowicz, T.; Partyka, J.; Węgierek, P.; Komarov, F.F.; Mironov, A.M.; Butkievith, N.; Freik, D. Dielectric properties and model of hopping conductivity of GaAs irradiated by H+ ions. Vacuum 2007, 81, 1137–1140. [Google Scholar] [CrossRef]
- Available online: https://weidmann-electrical.com/insulation-technology/transformerboard/cellulose-based/ (accessed on 5 September 2024).
- Fofana, I.; Wasserberg, V.; Borsi, H.; Gockenbach, E. Retrofilling conditions of high-voltage transformers. IEEE Electr. Insul. Mag. 2001, 17, 17–30. [Google Scholar] [CrossRef]
- Ekanayake, C.; Gubanski, S.M.; Graczkowski, A.; Walczak, K. Frequency Response of Oil Impregnated Pressboard and Paper Samples for Estimating Moisture in Transformer Insulation. IEEE Trans. Power Deliv. 2006, 21, 1309–1317. [Google Scholar] [CrossRef]
- Walczak, K.; Graczkowski, A.; Gielniak, J.; Morańda, H.; Mościcka-Grzesiak, H.; Ekanayake, C.; Gubański, S. Dielectric frequency response of cellulose samples with various degree of moisture content and aging. Prz. Elektrotech. 2006, 1, 264–267. [Google Scholar]
- Zhang, J.; Zhang, B.; Fan, M.; Wang, L.; Ding, G.; Tian, Y.; Chen, Q. Effects of external radiation heat flux on combustion characteristics of pure and oil-impregnated transformer insulating paperboard. Process Saf. Prog. 2018, 37, 362–368. [Google Scholar] [CrossRef]
- Kouassi, K.; Fofana, I.; Cissé, L.; Hadjadj, Y.; Yapi, K.; Diby, K. Impact of Low Molecular Weight Acids on Oil Impregnated Paper Insulation Degradation. Energies 2018, 11, 1465. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Zhang, Y.; Lai, B.; Jiao, J. Analysis of low-frequency polarisation behaviour for oil-paper insulation using logarithmic-derivative spectroscopy. High Volt. 2021, 6, 460–469. [Google Scholar] [CrossRef]
- ASTM D1533-20; Standard Test Method for Water in Insulating Liquids by Coulometric Karl Fischer Titration. ASTM International: West Conshohocken, PA, USA, 2020. Available online: https://www.astm.org/d1533-20.html (accessed on 2 September 2024).
- Rowlinson, J.S.; Widom, B. Molecular Theory of Capillarity; Clarendon Press: Oxford, UK, 1982. [Google Scholar]
- DIRANA—The Fastest Way of Moisture Determination of Power- and Instrument Transformers and Condition Assessment of Rotating Machines. Omicron 2018, L2894. Available online: https://pdf.directindustry.com/pdf/omicron-electronics/dirana-fastest-way-moisture-determination-power-instrument-transformers-condition-assessment-rotating-machines/13971-42092.html (accessed on 3 September 2024).
- Żukowski, P.; Kołtunowicz, T.N.; Kierczyński, K.; Rogalski, P.; Subocz, J.; Szrot, M.; Gutten, M.; Sebok, M.; Korenciak, D. Dielectric losses in the composite cellulose–mineral oil–water nanoparticles: Theoretical assumptions. Cellulose 2016, 23, 1609–1616. [Google Scholar] [CrossRef][Green Version]
- Zukowski, P.; Rogalski, P.; Koltunowicz, T.N.; Kierczynski, K.; Subocz, J.; Zenker, M. Cellulose Ester Insulation of Power Transformers: Researching the Influence of Moisture on the Phase Shift Angle and Admittance. Energies 2020, 13, 5511. [Google Scholar] [CrossRef]
- Zukowski, P.; Rogalski, P.; Koltunowicz, T.N.; Kierczynski, K.; Bondariev, V. Precise measurements of the temperature-frequency dependence of the conductivity of cellulose—Insulating oil—Water nanoparticles composite. Energies 2020, 14, 32. [Google Scholar] [CrossRef]
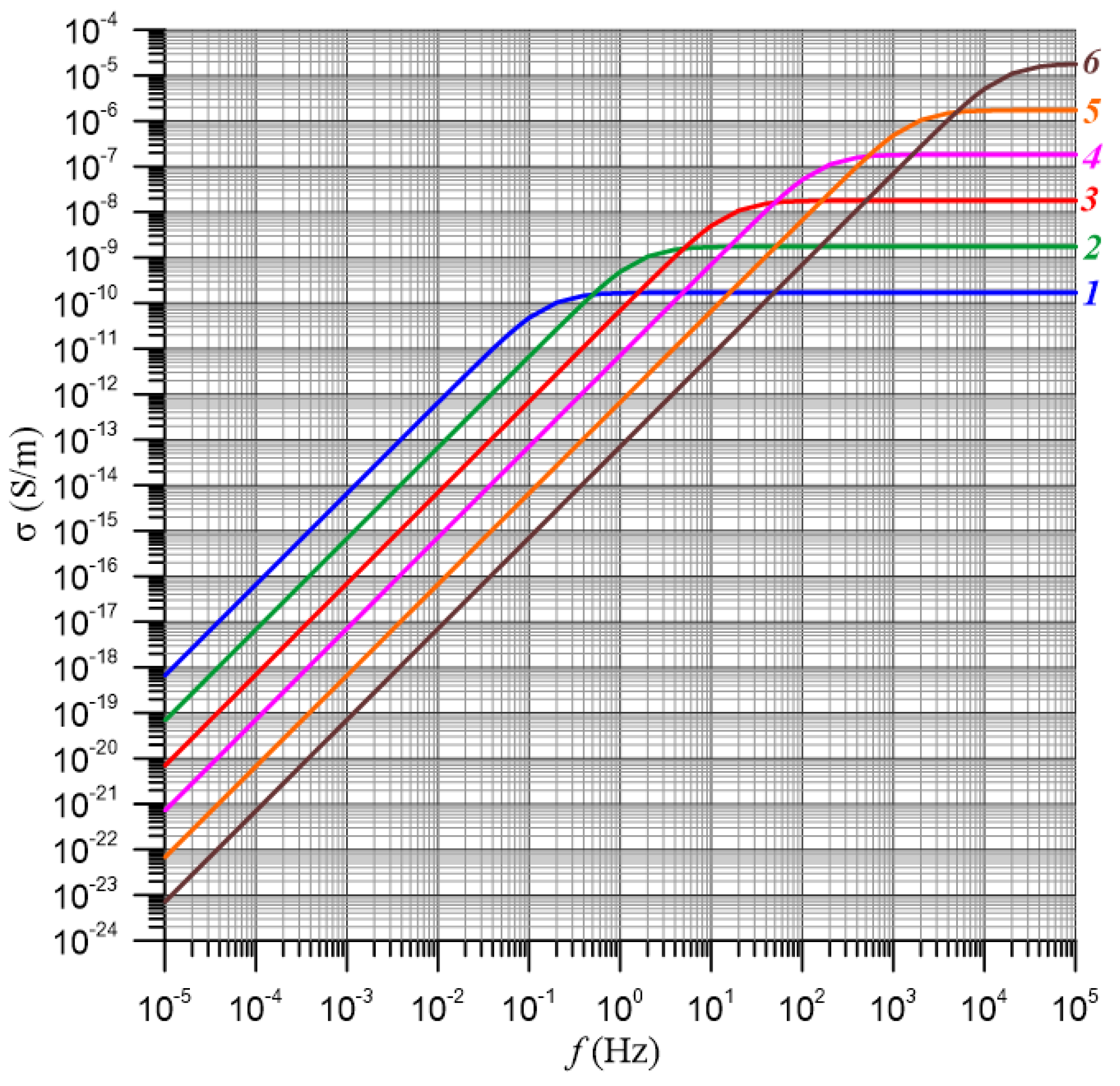
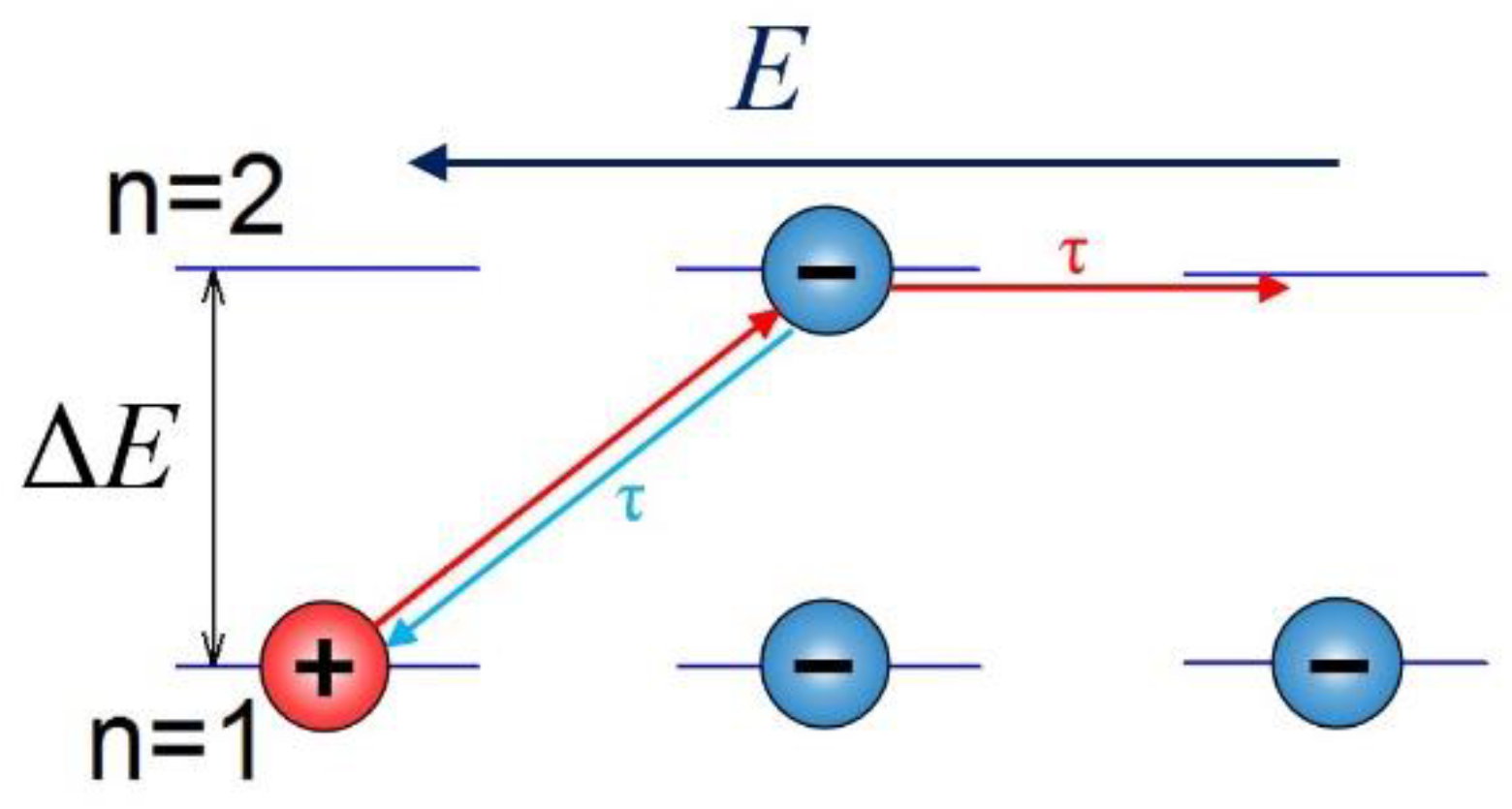
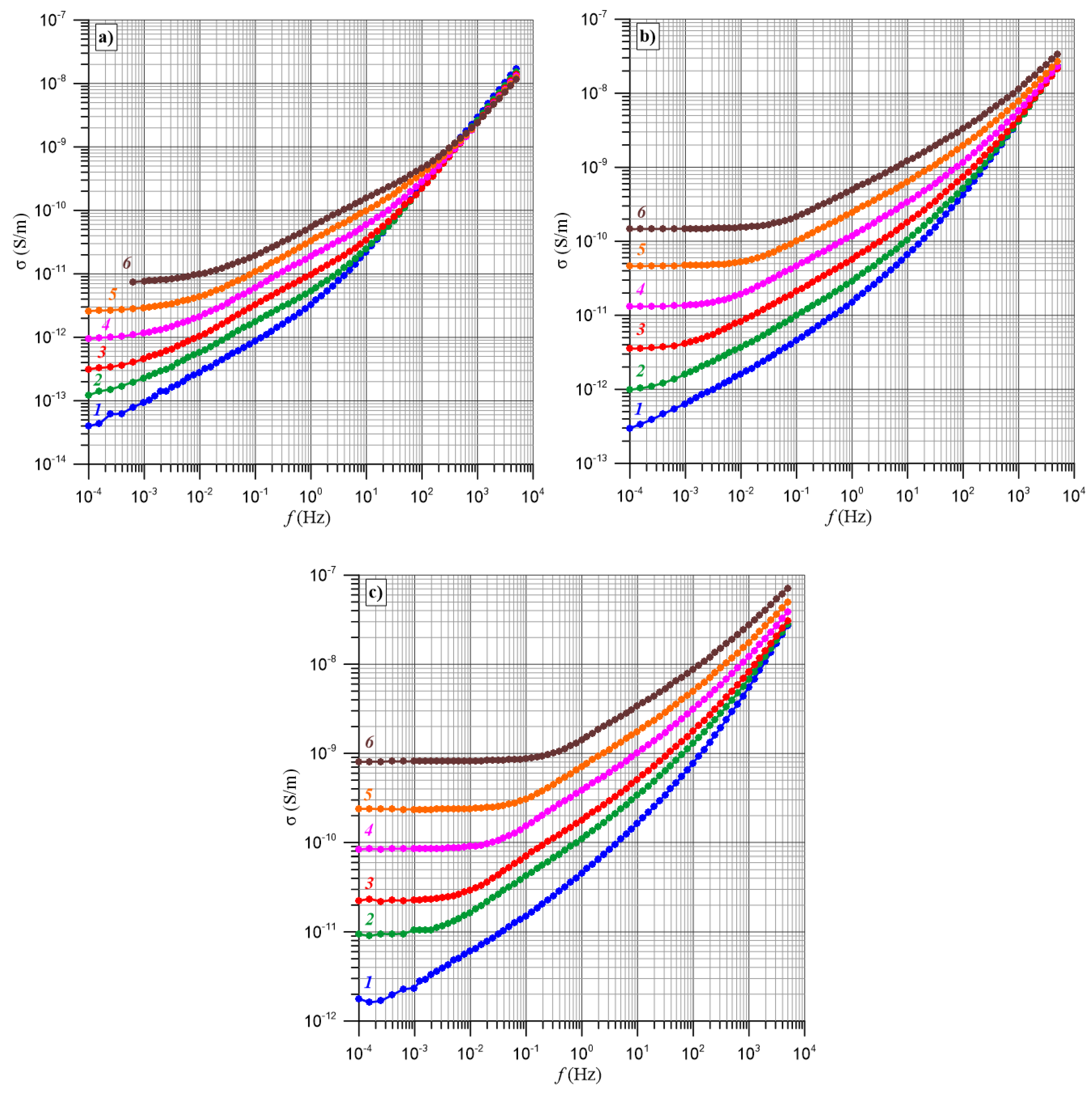


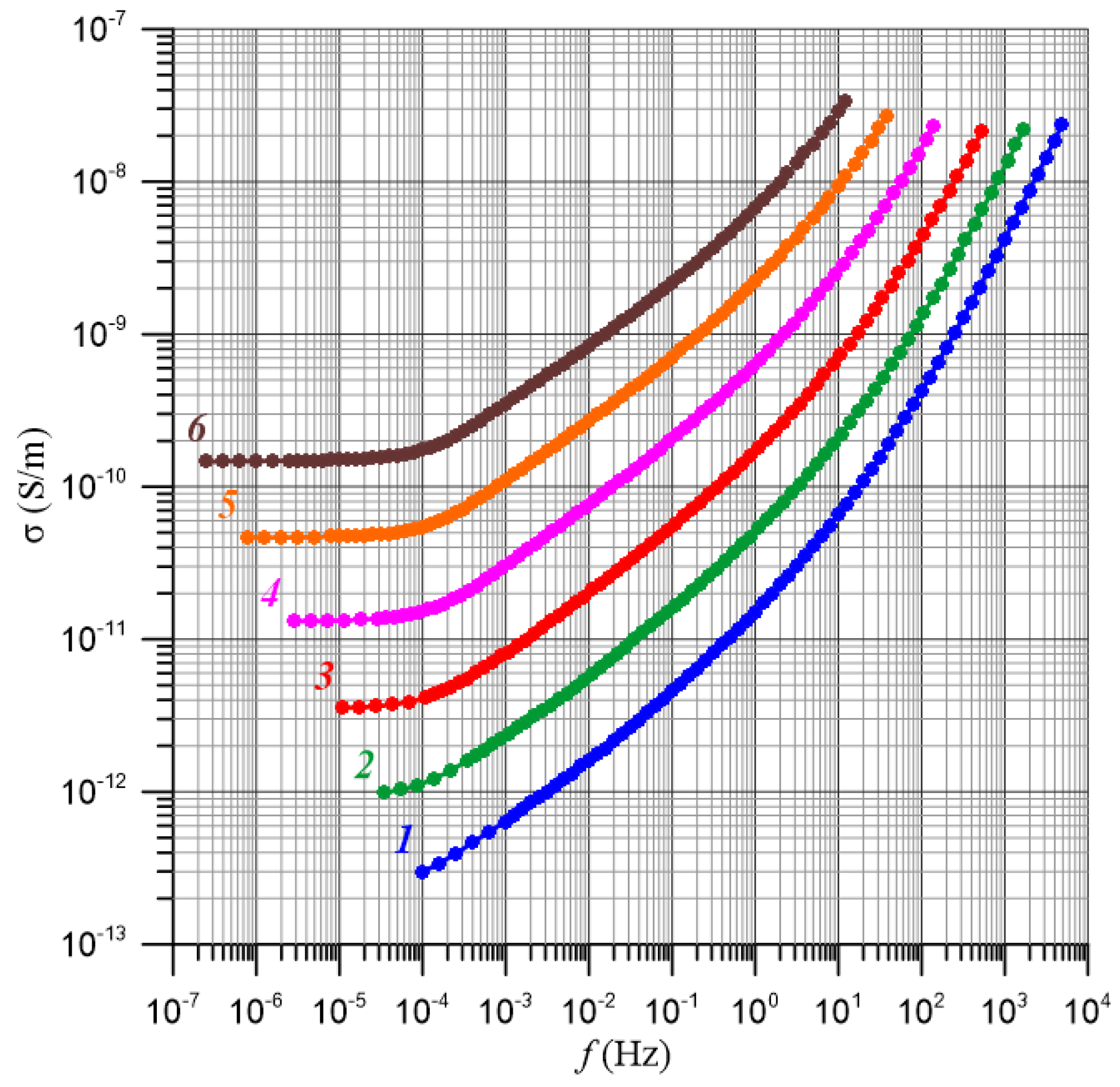

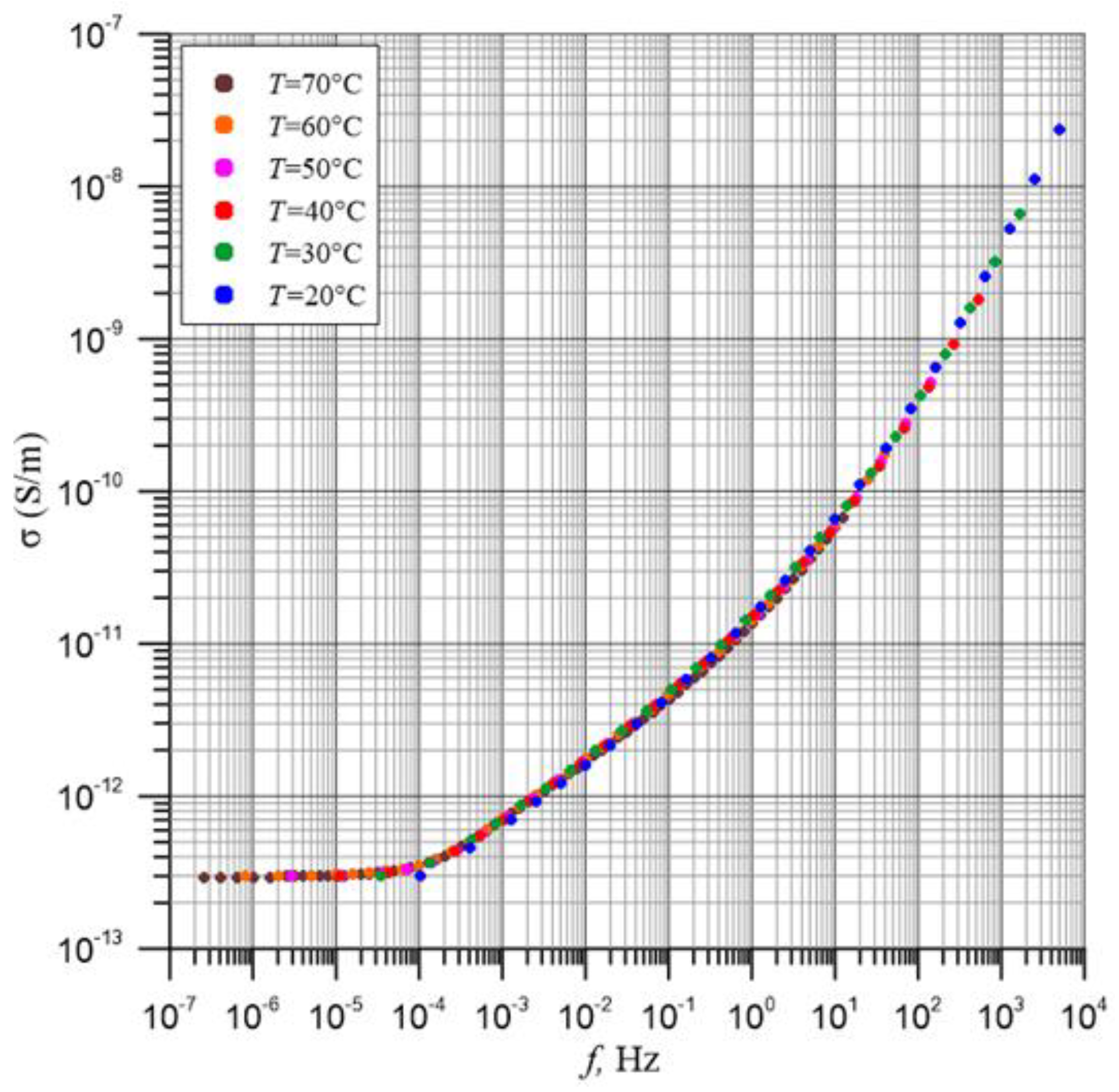
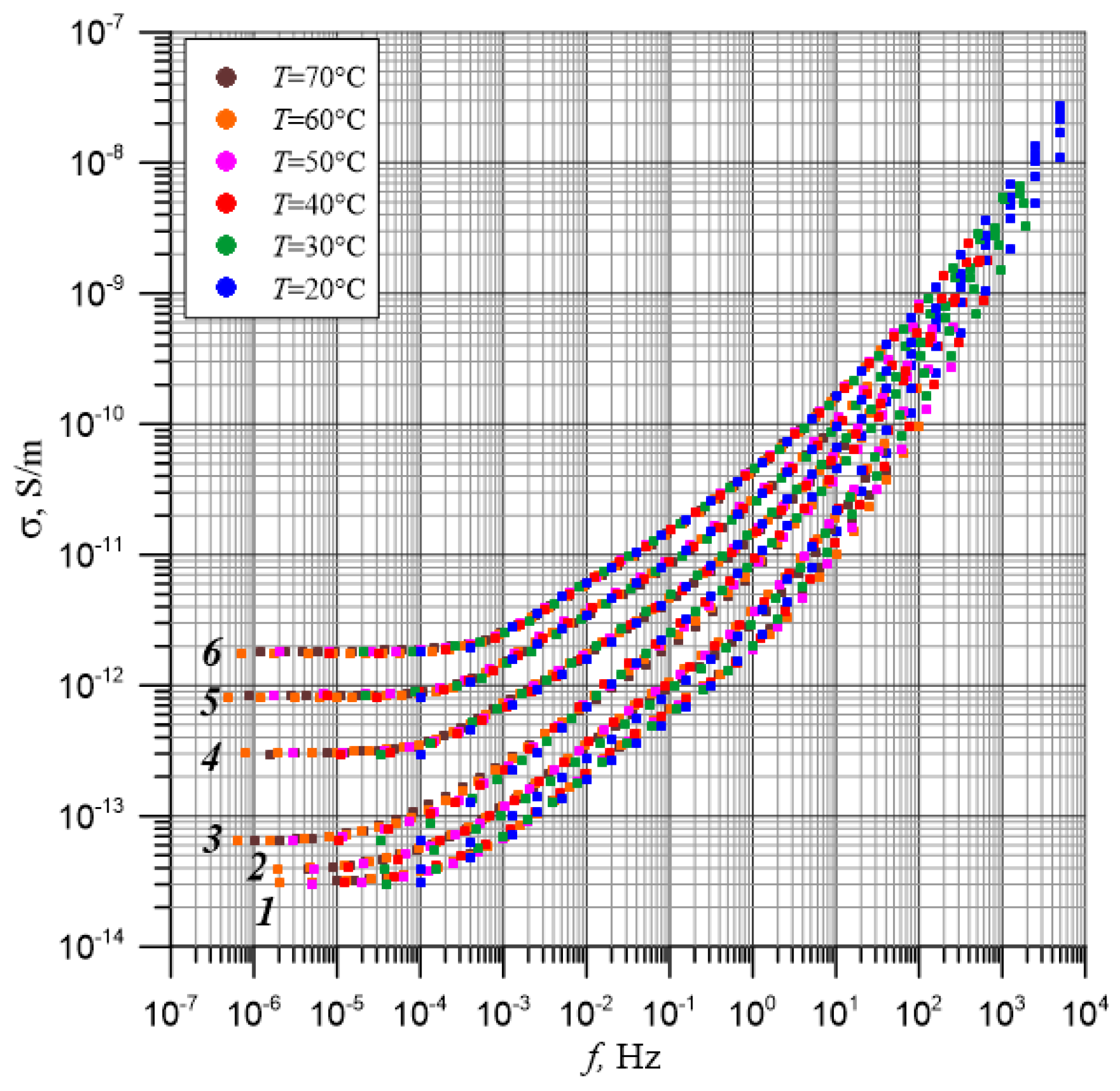
| No | σ, S/m | ΔEi(τ) | f, Hz | ΔEi(σ) | ||
|---|---|---|---|---|---|---|
| 1 | 1.00 · 10−12 | 1.015 | 0.9980 | 1.00 · 10−4 | 1.110 | 0.9998 |
| 2 | 1.28 · 10−12 | 1.021 | 0.9975 | 2.15 · 10−4 | 1.101 | 0.9995 |
| 3 | 1.64 · 10−12 | 1.026 | 0.9972 | 4.64 · 10−4 | 1.097 | 0.9995 |
| 4 | 2.09 · 10−12 | 1.040 | 0.9973 | 1.00 · 10−3 | 1.100 | 0.9997 |
| 5 | 2.67 · 10−12 | 1.052 | 0.9974 | 2.15 · 10−3 | 1.099 | 0.9998 |
| 6 | 3.42 · 10−12 | 1.061 | 0.9974 | 4.64 · 10−3 | 1.098 | 0.9998 |
| 7 | 4.37 · 10−12 | 1.070 | 0.9976 | 1.00 · 10−2 | 1.096 | 0.9998 |
| 8 | 5.59 · 10−12 | 1.077 | 0.9978 | 2.15 · 10−2 | 1.091 | 0.9999 |
| 9 | 7.15 · 10−12 | 1.080 | 0.9979 | 4.64 · 10−2 | 1.083 | 0.9998 |
| 10 | 9.15 · 10−12 | 1.082 | 0.9982 | 1.00 · 10−1 | 1.077 | 0.9998 |
| 11 | 1.17 · 10−11 | 1.084 | 0.9983 | 2.15 · 10−1 | 1.073 | 0.9998 |
| 12 | 1.50 · 10−11 | 1.085 | 0.9983 | 4.64 · 10−1 | 1.069 | 0.9998 |
| 13 | 1.91 · 10−11 | 1.085 | 0.9985 | 1.00 · 100 | 1.067 | 0.9998 |
| 14 | 2.45 · 10−11 | 1.085 | 0.9987 | 2.15 · 100 | 1.065 | 0.9997 |
| 15 | 3.13 · 10−11 | 1.084 | 0.9988 | 4.64 · 100 | 1.065 | 0.9996 |
| 16 | 4.00 · 10−11 | 1.083 | 0.9988 | 1.00 · 101 | 1.067 | 0.9996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zukowski, P.; Kierczynski, K.; Rogalski, P.; Okal, P.; Zenker, M.; Pajak, R.; Szrot, M.; Molenda, P.; Koltunowicz, T.N. Research on the Influence of Moisture in the Solid Insulation Impregnated with an Innovative Bio-Oil on AC Conductivity Used in the Power Transformers. Energies 2024, 17, 5164. https://doi.org/10.3390/en17205164
Zukowski P, Kierczynski K, Rogalski P, Okal P, Zenker M, Pajak R, Szrot M, Molenda P, Koltunowicz TN. Research on the Influence of Moisture in the Solid Insulation Impregnated with an Innovative Bio-Oil on AC Conductivity Used in the Power Transformers. Energies. 2024; 17(20):5164. https://doi.org/10.3390/en17205164
Chicago/Turabian StyleZukowski, Pawel, Konrad Kierczynski, Przemyslaw Rogalski, Pawel Okal, Marek Zenker, Rafal Pajak, Marek Szrot, Pawel Molenda, and Tomasz N. Koltunowicz. 2024. "Research on the Influence of Moisture in the Solid Insulation Impregnated with an Innovative Bio-Oil on AC Conductivity Used in the Power Transformers" Energies 17, no. 20: 5164. https://doi.org/10.3390/en17205164
APA StyleZukowski, P., Kierczynski, K., Rogalski, P., Okal, P., Zenker, M., Pajak, R., Szrot, M., Molenda, P., & Koltunowicz, T. N. (2024). Research on the Influence of Moisture in the Solid Insulation Impregnated with an Innovative Bio-Oil on AC Conductivity Used in the Power Transformers. Energies, 17(20), 5164. https://doi.org/10.3390/en17205164








