Photovoltaic Power Intermittency Mitigating with Battery Storage Using Improved WEEC Generic Models

Abstract

The growing integration of renewable energy sources, such as photovoltaic and wind systems, into energy grids has underscored the need for reliable control mechanisms to mitigate the inherent intermittency of these sources. According to the Brazilian grid operator (ONS), there have been cascading disconnections in renewable energy distributed systems (REDs) in recent years, highlighting the need for robust control models. This article addresses this issue by presenting the validation of an active power ramp rate control (PRRC) function for a PV plant coupled with a Battery Energy Storage System (BESS) using WECC generic models. The proposed model underwent rigorous validation over an extended analysis period, demonstrating good accuracy using the Root Mean Squared Error (RMSE) and an R-squared (R²) metrics for the active power injected at the Point of Connection (POI), PV active power, and BESS State of Charge (SOC), providing valuable insights for medium and long-term analyses. The ramp rate control module was implemented within the plant power controller (PPC), leveraging second-generation Renewable Energy Systems (RES) models developed by the Western Electricity Coordination Council (WECC) as a foundational framework. We conducted simulations using the Anatem software, comparing the results with real-world data collected at 100 ms to 1000 ms intervals from a PV plant equipped with a BESS in Brazil. The proposed model underwent rigorous validation over an extended analysis period, with the presented results based on two days of measurements. The positive sequence model used to represent this control demonstrated good accuracy, as confirmed by metrics such as the Root Mean Squared Error (RMSE) and R-squared (R²). Furthermore, the article underscores the critical role of accurately accounting for the power sampling rate when calculating the ramp rate.

1. Introduction

Over the past two decades, numerous countries have integrated renewable energy power plants—such as photovoltaic (PV) and wind—into their energy sources. These sources offer significant environmental benefits compared to those that rely on fossil fuels. In recent years, installation costs have dropped considerably, and the efficiency of solar panels and electrical energy conversion systems has increased.

However, PV-generated power is highly intermittent and often non-dispatchable due to the randomness of solar irradiation. Rapid fluctuations in output power can be caused by passing clouds, which affect system dynamics through frequency or voltage fluctuations. This effect is especially true in weak or small isolated power systems on islands where PVs have greater penetration [1]. Moreover, weather events such as storms can briefly reduce solar generation from maximum generated power to negligible levels.

According to the Brazilian grid operator (ONS), there have been cascading disconnections in renewable energy distributed systems (REDs) in the years 2021 to 2024 [2], where one of the identified reasons is due to models not responding adequately. This highlights a significant scientific problem: the need for robust and accurate control mechanisms to manage the intermittency and fluctuations inherent in renewable energy sources like photovoltaic (PV) systems.

On the other hand, Battery Energy Storage Systems (BESS) have become increasingly popular in countries with high renewable energy usage. They help reduce power intermittency and bring flexibility and new services to the electrical system. However, implementing BESS necessitates sophisticated communication systems [3].

To maintain a reliable and secure power grid, regulating the rate at which energy generators introduce active power at the Point of Interconnection (POI) is necessary. This effect is especially important for balancing instantaneous generation and consumption. Some grid codes mandate this control mechanism to prevent sudden fluctuations in power supply that could lead to system instability and disruption. This means that the generation variation between two instances of time must be limited, and the energy generator may be penalized or have part of its generation cut if it does not meet the established criteria. Ramp restrictions for active power output also limit large frequency variations and Area Frequency Control Error (FRCE), which ensures that frequency quality parameters and FRCE for control areas are met [4].

Table 1. Ramping rate limits of different national grid codes. Source: Author, adapted from [5,6,7].

Country (TSO *)	Installed Capacity	Ramp Rate Rule
Puerto Rico (PREPA)	-	10%/min
Ireland (EirGrid)	-	30 MW/min
Hawaii (HECO)	-	2 MW/min
	-	1 MW/2 s
Germany (German TSOs)	-	10%/min
Denmark (Energinet)	-	20%/min
	-	60 MW/min
India (POSOCO)	-	10%/min
China (National Standard and SGCC enterprise Grid Code)	Installed capacity < 30 MW	3 MW/min
		10 MW/10 min
	Installed capacity < 200 MW	10%/min
		33.3%/10 min
	Installed capacity > 200 MW	15 MW/min
		50 MW/10 min

* TSO: Transmission System Operators.

specifies the power ramp rate limits in various grid codes across different countries. These limits vary depending on the country and can be expressed as a percentage of the installed solar and wind power capacity or as megawatt restrictions. Additionally, considering the duration of the power ramp rate limit period is crucial; some restrictions are instantaneous and calculated in seconds, while others span several minutes.

Network operators use computer simulations to predict the behavior of their network in failure incidents or extreme events. These simulations rely on accurate models of the network and the generating systems that dominate its behavior. For this reason, power plant operators provide models of their power plants. In many countries, generator owners must provide adjusted simulation models in specified formats before connecting their generating unit to the grid.

In 2010, the Renewable Energy Modeling Task Force (REMTF) of the Western Electricity Coordinating Council (WECC) initiated the development of generic models for wind and photovoltaic systems. In 2014, WECC released the second generation of these models, known as the WECC RES 2nd generation models, encompassing wind, photovoltaics, battery energy storage systems, and other renewable technologies. These models were designed to be modular, allowing for future advancements and seamless integration of emerging technologies, and they are extensively utilized in commercial simulation programs [8,9,10,11].

The WECC RES models use positive-sequence power flow and dynamic models that provide a good representation of recovery dynamics using integration time steps of a one-quarter cycle. This approach does not allow for a detailed representation of very fast controls and responses to imbalanced disturbances. It is recommended for electromechanical transient studies with simulation rates of up to 30 s, as well as mid-term simulations [12]. However, it is important to acknowledge that, like any model, these models have inherent limitations, as discussed in [13].

Some studies have been conducted based on the 2nd generation WECC RES models. The research on WECC models found that most applications were performed on wind farm models, with few articles applying BESS using the generic models. Only six articles addressed the application of BESS with WECC generic models in the last five years. In [14], the authors developed a generic model for inertia-based fast frequency response in wind turbines and other RES, increasing the range of the generic RES dynamic model’s applicability. In [15], WECC models for photovoltaic and energy storage systems were validated using the ANATEM software, emphasizing their role in power system stability. In [16], the authors used an optimization method to determine the appropriate parameters of the WECC models to represent a real energy storage system, using key parameter identification algorithms and an improved particle swarm optimization approach. [17] compared frequency control methods for large-scale power systems, focusing on battery integration. [18] modeled renewable energy sources in the OpenIPSL Modelica library, providing insights into system dynamics. These studies collectively underscore the significance of accurate modeling and control in enhancing the reliability and stability of renewable energy systems. In [19], the WECC Type 3 model of wind turbines was verified by the Spanish operational procedure PO 12.3. The results showed the effect of the transformer input current, which influences the accuracy of the behavior of the generic turbine model of wind energy when the validation criterion is applied at the low voltage measurement point. It was also verified that the WECC model complies with Spanish network procedures. In [20], a modal analysis of a photovoltaic plant connected to networks with different short-circuit capacities was carried out. The study verified the effects of the system impedance on the eigenvalues magnitude and phase of the voltage control transfer function. In [21], offshore wind turbine generator models considering detailed switching were implemented in the real-time simulator Opal-RT. The wind turbine model was validated against the WECC generic wind turbine model.

The active power ramp rate control (PRRC) model for PV with BESS has been analyzed using various models and simulation platforms. The paper [22] proposes a PRRC method to minimize power fluctuations in wind/PV hybrid output and regulate the battery State of Charge (SOC). A new real-time power allocation method based on BESS is presented using MATLAB software/SIMULINK. In [23], a PRRC of a BESS associated with a PV is proposed through adaptive moving average control and adaptive state of charge control. The results are experimentally verified in a field test using an energy storage system battery controlled via the Eclipse VOLTTRON platform. [24] investigate the impact of large-scale PV penetration on power systems using IEEE 9-bus, 39-bus, and 118-bus test systems, and show that BESS integration improves system stability and transient response. [25] compares hybrid renewable energy systems with and without BESS, using the HOMER program (version 3.14.0) and MATLAB/SIMULINK for statistical analysis, concluding that BESS inclusion improves energy quality and system efficiency. Ref. [26] propose a multimodal energy management model for PV systems, which regulates voltage, frequency, and reactive power compensation, using a real-time OPAL-RT simulator and historical demand data with a long short-term memory (LSTM) neural network.

Additionally, Ref. [27] presents a detailed methodology for BESS sizing in PV plants, evaluating a one-year mission profile of solar irradiance and ambient temperature from Goiânia, Brazil. Ref. [28] experimentally validate a new power smoothing method for grid-connected PV systems using supercapacitors, demonstrating the method’s effectiveness in mitigating power fluctuations through exhaustive laboratory experiments under different cloudiness events. Finally, in the paper [29], a methodology is presented to adjust and determine the time constant of a filtering or PRRC. This approach leads to a better reduction in PV power fluctuations through the analysis of irradiance variability from day to day, seeking to reduce the operation of unnecessary battery banks.

Furthermore, the economic analysis of energy storage systems is essential to evaluate the feasibility and long-term benefits of these systems. This analysis depends on various factors, such as the SOC control strategy, services provided by the BESS, and their respective remuneration according to the country, cycle degradation, and calendar aging. Currently, Brazil does not remunerate services associated with BESS and does not have a grid code limiting the power ramps of RES. The paper [30] presents an approach that integrates energy storage systems with wind turbines, utilizing daily optimization models and intra-day scheduling. These models consider the degradation of storage devices due to charging and discharging, providing a more accurate assessment of the economic benefits of different design schemes. Case studies involving a 10 MW wind farm demonstrate the proposed method’s effectiveness, highlighting the hybrid energy storage system’s ability to improve power generation stability and maximize economic benefits. Complementing this approach, [31] proposes a four-step iterative methodology for sizing photovoltaic plants coupled with battery energy storage systems. The research addresses optimizing BESS size, considering cycle degradation and calendar aging, to ensure compliance with grid codes and minimize replacement costs over the project’s lifespan. The case study, conducted on a 16.3 MW PV plant, demonstrates that LiFePO4 (LFP) batteries are more economical and efficient in terms of replacement and total cost over time than LiNiMnCoO2 (NMC) batteries.

Some methods for calculating the power ramp rate are outlined in the literature [5,32], differing in the sampling period and respective power value, as illustrated in Figure 1. Method (i) ($R{R}_i=(P_2-P_1)/(T_2-T_1)$, where $T_2-T_1=60 \mathrm{s}$) involves calculating the ramp rate by taking the difference between the power generated at two endpoints within a 1 min interval. Method (ii) ($R{R}_{ii}=(P_4-P_3)/(T_4-T_3)$) involves calculating the ramp rate by taking the difference between the minimum and maximum values of power generated over a specified time interval. Method (iii) ($R{R}_{iii}=(P_6-P_5)/1 \mathrm{s}$) involves calculating the ramp rate by taking the difference in power within 1 s. Each method should be used depending on the methodology adopted by the Grid Code.

The methods mentioned above can be mathematically translated by considering the power time series P(t) in kW, recorded with a given sampling period Δt (s), where the ramp rate (RR) can be defined as the difference between two consecutive power samples in the sampling period Δt, normalized to a time base in minutes, as indicated in (1).

$$R{R}_{\mathrm{k}\mathrm{W}/\mathrm{m}\mathrm{i}\mathrm{n}}(t)={\displaystyle \frac{P\left(t\right)-P(t-∆t)}{∆t}}\times 60 (\mathrm{k}\mathrm{W}/\mathrm{m}\mathrm{i}\mathrm{n})$$

(1)

It is worth noting that the WECC RES 2nd generation models do not have PRRC functionality for a PV plant associated with a BESS, and no articles were found presenting this function in the WECC RES models. This paper contributes by applying and validating an active power ramp rate control for a PV plant coupled with a BESS, leveraging 2nd generation WECC RES models as a foundational framework, using the Anatem software version 12.4 [33] developed by the Electrical Energy Research Center (CEPEL).

In this context, the primary objective of this study is to address the significant scientific problem of managing the intermittency and fluctuations inherent in renewable energy sources like PV systems. By developing and validating a PRRC function for PV plants coupled with BESS, this research aims to improve the reliability and stability of these systems. The validated model can be used to assess network requirements, equipment performance, and compliance with criteria, providing valuable insights for future implementations. Specific goals include analyzing the impact of PRRC on frequency in off-grid or on-grid industrial systems, developing optimal state of charge (SOC) control strategies for BESS, and determining optimal BESS sizing for different operational scenarios.

Results were compared with real-world data collected from a PV plant associated with a BESS in Brazil. Anatem is a tool for analyzing electromechanical stability in large-scale power systems, especially in the context of the Brazilian electrical system. It allows dynamic time-domain simulations, focusing on the nonlinear analysis of electromechanical transients. It is widely used by the Brazilian electrical sector entities, such as the National Electric System Operator (ONS) and the Energy Research Company (EPE).

The model underwent rigorous validation using one year of data, but the results were based on two days of measurements. The accuracy of the control module was confirmed through metrics such as the Root Mean Squared Error (RMSE) and R-squared (R²). This model enables the evaluation of network requirements, equipment performance, and compliance with criteria, providing valuable insights for medium and long-term analyses.

In addition, this paper also highlights the importance of correctly considering the power sampling rate when calculating the ramp rate, as it can produce different results, impacting compliance with grid codes and BESS sizing. The calculation implemented in the real plant controller was identified, and the correct implementation of the calculation was made in the developed model.

This paper is organized as follows: Section 2 describes the methodology followed in the research, including the ramp control module implemented in the PPC and the electrical system analyzed. Section 3 discusses the ramp rate calculation techniques, and the active power sampling period for ramp calculation is analyzed to identify the real control implemented in the plant. The model is then tested and validated in the Anatem software, and the simulated results are compared with real measured data in Section 4. Finally, the conclusions are presented in Section 5.

2. Proposed Methodology

The WECC RES 2nd generation PV, Wind, and BESS models consist of seven modular blocks that can be combined to represent specific renewable energy plant models [11,12,34]. These modules provide a comprehensive framework for modeling and analyzing renewable energy systems, facilitating accurate representation and control of various renewable sources and their integration into the electrical grid. This gap underscores the need for a robust PRRC function integrated with WECC models to enhance the flexibility and reliability of renewable energy systems, ensuring better compliance with grid codes and improving overall system stability.

However, it is worth highlighting that they do not include PRRC functionality for a PV with a BESS plant. The research on WECC models found that most applications were conducted on wind farm models, with few articles applying BESS using the generic models. Only six articles addressed the application of BESS with WECC generic models in the last five years. This gap underscores the need for a robust PRRC function integrated with WECC models to enhance the flexibility and reliability of renewable energy systems, ensuring better compliance with grid codes and improving overall system stability.

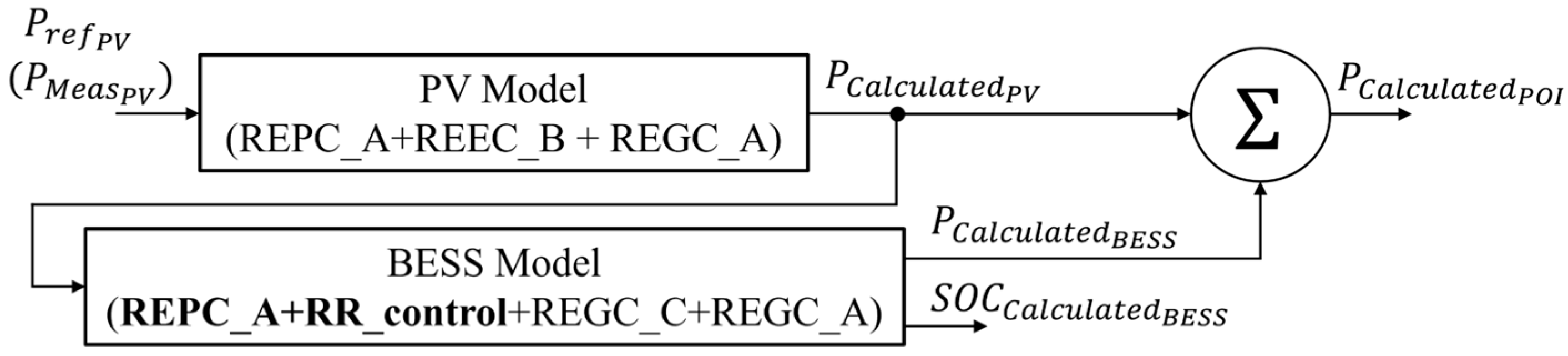
The block diagram of the PV and BESS models can be found in Figure 2 and Figure 3, respectively. The models comprise three main functional blocks:

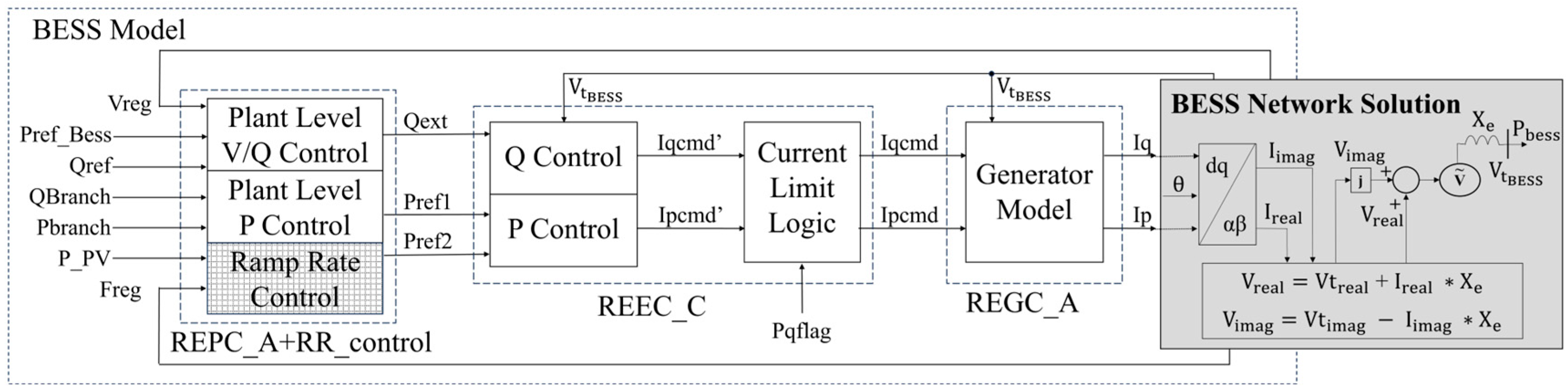
• REPC (Renewable Energy Plant Control) Module: The REPC module represents a PPC and establishes the control scheme for a conglomerate of renewable sources. It incorporates control functions for active and reactive power, voltage control, and frequency control for active power control.
• REEC (Renewable Energy Electric Control) Module: The REEC module represents the electrical controls of the electrical converters. It is connected in a closed-loop configuration with the REGC module, enabling it to adjust active and reactive power based on the output voltage and power from the REGC module. The REEC_B module is used for PV systems, while the REEC_C module is used for BESS models. The difference is that the REEC_C module is adapted to manage the charging and discharging of batteries, aiding in voltage stability and providing frequency support when necessary.
• REGC (Renewable Energy Generator Control) Module: This module represents the current injection model for renewable sources such as photovoltaic systems, batteries, and wind turbines. It accurately models the behavior of these sources regarding current injection into the electrical grid.

The generation controllers (REGC_A), electrical converters (REEC_B and REEC_C), and plant controller (REPC_A) models were used to represent the PV and BESS models in the tests and analyses, with their parameters sourced from references [9,11,24]. These parameters do not represent the performance of any particular inverter but have exhibited suitable responses. Some parameters were modified as indicated in Table I of reference [11]. The parameters for the ramp rate control can be found in the tables in the appendix.

In this context, this paper focuses on implementing active power ramp rate control in the plant controller for a PV with a BESS plant, utilizing the 2nd generation WECC models as a basis. The models were implemented in CEPEL’s Anatem software using the user-defined control modeling feature (CDU), allowing users to customize control loops’ representation for power generation units and equipment models.

2.1. Power Ramp Rate Control Function at REPC Module

The BESS’s power plant controller (PPC) now includes the ramp rate control function. To enhance the BESS REPC_A Controller model, a dedicated ramp rate control module (RR_Control) was developed to extend and improve the existing REPC_A model. The block diagram model of the ramp control implemented in RR_Control is illustrated in Figure 4.

The RR_Control module receives power generation data from one or more photovoltaic systems ($P_{PV-TOT}$) and transmits control signals based on the ramp rate to the BESS converter (REEC Model). The output of the ramp rate block is the ramp-controlled power at the POI ($P_{POI-RR}$). It is essential to highlight the necessity of performing power base correction for ramp control when working with per unit (p.u.) values, requiring the conversion between the power demand requested by the PV for ramp control and the adequate power to be commanded to the BESS.

The Ramp rate block utilizes the Rate LM block [33] to restrict the output within a maximum permitted variation. In minor disturbances, the output should mirror the input signal. In the case of input signals with substantial variation, the block will store the difference between the input and the restricted output and increment the output until this difference reaches zero. When analyzing an input curve and an output curve constrained by the ramp rate, illustrated in Figure 5, Equations (2)–(5) demonstrate the output curve constrained by the ramp rate.

$$R\left(t\right)={\displaystyle \frac{P_{input}\left(t\right)-P_{input}\left(t-∆t\right)}{∆t}}$$

(2)

$$if R\left(t\right)>R{R}_{max}, then P_{output}\left(t\right)=P_{output}\left(t-∆t\right)+R{R}_{max}∆t$$

(3)

$$if R{R}_{min}\le R\left(t\right)\le R{R}_{max}, then P_{output}\left(t\right)=P_{input}\left(t\right)$$

(4)

$$if R\left(t\right)<R{R}_{min}, then P_{output}\left(t\right)=P_{output}\left(t-∆t\right)+R{R}_{min}∆t$$

(5)

The maximum and minimum ramp rates can be adjusted through the parameters ${RR}_{max}$ and ${RR}_{min}$ given in pu/s. Therefore, it was necessary to conduct the conversion considering the sampling period from minute to s and the power base as the maximum power of the UFV-AR PV, as in Equation (6).

$$R{R}_{\left(\mathit{max}ormin\right)}={\displaystyle \frac{{RR}_{\left(\mathit{max}ormin\right)(\mathrm{k}\mathrm{W}/\mathrm{m}\mathrm{i}\mathrm{n})}}{60\mathrm{s}}}\times {\displaystyle \frac{1}{{P_{base}}_{\mathrm{k}\mathrm{W}}}} (\mathrm{p}\mathrm{u}/\mathrm{s})$$

(6)

The proportional-integral (PI) controller considers the power error of the BESS as input data. Therefore, it is necessary to subtract the dispatched powers from the PV and BESS from the required power at the POI at a given instant t. The parameters $kpg$ and $kig$ were adjusted to minimize the error concerning the POI power measured curve. Factors $F_{SOCmax}$ and $F_{SOCmin}$ are utilized to freeze the integrator of the PID controller when the battery reaches its maximum or minimum state of charge (SOC) limits. These factors have a value of one when the limits have not been reached and zero when the maximum or minimum SOC limit is reached. In other words, when the battery is fully charged, the control allows only discharge operation, and when the battery is discharged, the control enables only charging operation. The calculated power reference is commanded to the REEC_C converter module through the variables $P_{ordBESS}$ and $P_{refBESS}$, as indicated in Figure 4.

When the Ramp flag parameter is set to 1, the ramp control function is selected to send commands to the BESS. Conversely, when set to 0, the control (frequency or power factor) from the REPC_A module is chosen. The time constants $Tp$, $Tpk$, and $Tlag$ were utilized to represent any intentional phase lead or lag/delay in the communication process between the plant controller and the BESS or measurement delays of instruments or signal processing delays, typically adjusted between 0.1 ms and 20 ms. These adjustments are indicated in

Table A1. Ramp Rate Model Parameters.

Description	Symbol	Value
Active power up-ramp rate limit in the POI, p.u./s.	${RR}_{max}$	100 kW/min (*)	0.001515
		150 kW/min (**)	0.00227
Active power down-ramp rate limit in the POI, p.u./s.	${RR}_{min}$	100 kW/min (*)	−0.001515
		150 kW/min (**)	−0.00227
Maximum SOC, p.u.	${SOC}_{max}$	0.9
Minimum SOC, p.u.	${SOC}_{min}$	0.2
BESS rated charging or discharging time as sec.	T	1288.4
BESS lag time constant, sec.	$T_{p_K}$	0.02
Freeze lag time constant, sec.	$T_p$	0.0001
Ramp rate controller lag time constant, sec.	$T_{lag}$	0.02
Ramp Rate controller proportional gain, p.u.	$K_{p_G}$	0.01
Ramp Rate controller integral gain, p.u.	$K_{i_G}$	0.7
Ramp Rate response disable (=0) or enable (=1)	$ramp\_flag$	1

* 100 kW/min → 0.10 MW/min → ((0.1/1.1)/60) = 0.001515 pu/s ** 150 kW/min → 0.15 MW/min → ((0.15/1.1)/60) = 0.002273 pu/s.

—Appendix A.

The battery charge and discharge model are located in the REEC_C Electrical Control, and the block diagram can be seen in Figure 6. The charge and discharge time (T), as shown in Equation (7), depends on the BESS power converter ($P_{converter}$) in kW, BESS Ampere-Hour Capacity ($E_{BESS}$) in kWh, and BESS charge/discharge C-rate. The C-rate measures the rate at which a battery is charged or discharged relative to its maximum capacity. The simple integrator block, with the time constant T, represents the charging and discharging process. The level of charge in the battery is proportional to stored energy. Energy is the time integral of power since power is specified in units of watts = joules (energy) per second. Thus, by integrating the power coming out of (or going into when charging) the device, we obtain a representation of the state of charge.

$$T={\displaystyle \frac{E_{BESS}\left(\mathrm{k}\mathrm{w}/\mathrm{h}\right)}{{C-rate\ast P}_{converter}\left(\mathrm{k}\mathrm{w}\right)}}\times 3600 (\mathrm{s})$$

(7)

Figure 7 presents a flowchart containing the proposed methodology for implementing and validating the ramp rate control incorporated into the WECC 2nd generation model, creating the improved WECC generic model for PV and BESS.

2.2. System Test and Initialization

The data for this work was obtained from the supervisory system (SCADA) of the UFV-AR PV plant located in Northeast Brazil. The PV plant has a power capacity of 1100 kW and is associated with a Lithium-Ion BESS. The BESS has a converter power of 950 kW, a storage capacity of 340 kWh, and a BESS charge/discharge C-rate of one. The BESS is designed to control the generation ramps at the connection point and reduce the intermittency of the photovoltaic plant in the system.

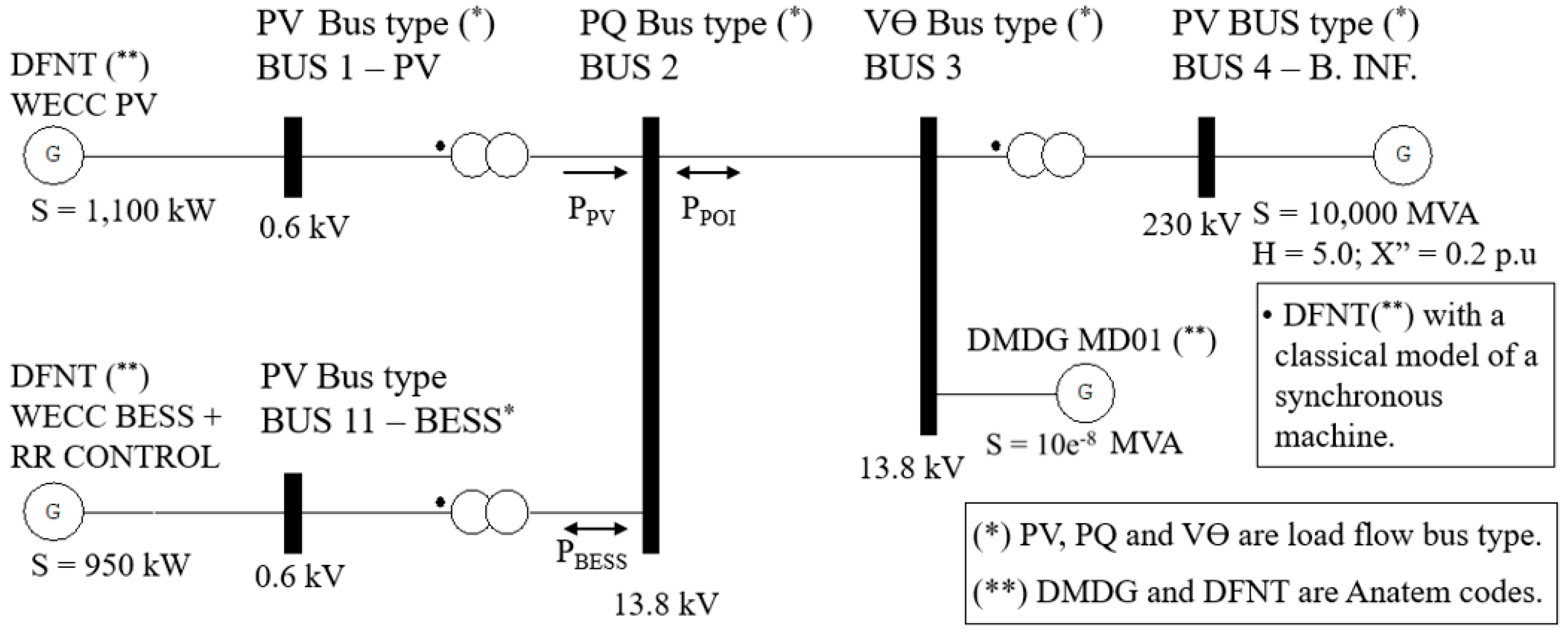
For validation, an equivalent system connected to an infinite bus was adopted, as presented in Figure 8. The electrical system contains five buses, with buses 1 and 11 at a rated voltage of 0.6 kV, buses 2 and 3 at 13.8 kV, and bus 4 at 230 kV. Transformers (1-2), (11-2), and (3-4) and lines 2-3 have a reactance of X = 0.0001 pu (0.01%). Bus 2 is the Point of Interconnection (POI) according to the UFV-AR PV system, where ($P_{POI}=P_{PV}+P_{BESS}$).

Buses 1, 4, and 11 were modeled as generation buses (P-V), bus 3 as a reference bus (V-θ) with a generator with practically zero power, and bar 2 as a load bus (P-Q bus). The PV and BESS are connected to buses 1 and 11, respectively. A synchronous machine with a much higher capacity than the plant is connected to bus 4 and is represented as an infinite bar in the transmission system. The buses were associated with the dynamic model through Anatem codes. This model was adopted due to the possibility of creating a controlled voltage or frequency source through specified input curves at bus 4 for other analyses, such as model responses due to system disturbances. More details can be found in [35].

The initial voltage and frequency of bus 4 is V = 1.0 pu and f = 1.0 pu. An integration step of 10 ms was used in the simulation. In Anatem software, PV and BESS were associated with the models indicated in Section 2.

Two metrics were used to verify the simulation error compared to the experimental data. These metrics are the Root Mean Squared Error (RMSE) [36] and the R-squared (R²) [37]. RMSE and R² are important in evaluating model performance as they complement each other. RMSE measures the magnitude of absolute errors between observed values and predicted values and provides a measure of model accuracy. On the other hand, R² indicates the proportion of variability explained by the model and provides a measure of the model’s goodness of fit. By considering both RMSE and R², we can obtain a more comprehensive view of model performance. A low RMSE value indicates good model accuracy, while a high R² value indicates a good model fit to the data. Therefore, it is essential to consider both RMSE and R² when evaluating whether the model fits the observed data.

3. Identification of the PRRC Technique Used in UFV-AR PV

The UFV-AR PPC has other control functionalities in addition to controlling active power ramps, such as frequency control and some BESS SOC control functionalities. Turning off all SOC controls was necessary to correctly identify the ramp control technique, keeping only the active power ramp control on. The ramp control can be adjusted with ramps between 1%/min and 20%/min, representing a ramp control at the POI of 11 kW/min and 220 kW/min at the PV power base (1100 kW).

The ramp calculation technique is impacted by several variables, such as the sampling period of the active power measurement and whether a filter was used on the measured input signal (for example, a moving average or pass filter). The active power data from the PV, POI, and BESS were monitored at different intervals ranging from 100 ms to 1 s. The BESS SOC data were measured from 100 ms to 15 s. The information was loaded into a Python program to align all the active power and SOC measurements on the same time stamp, which performed an interpolation. Various filters and parameter variations were tested, and it was concluded that the UFV-AR controller did not use any filter on the measured or acquired signal or that the acquired signal was already filtered.

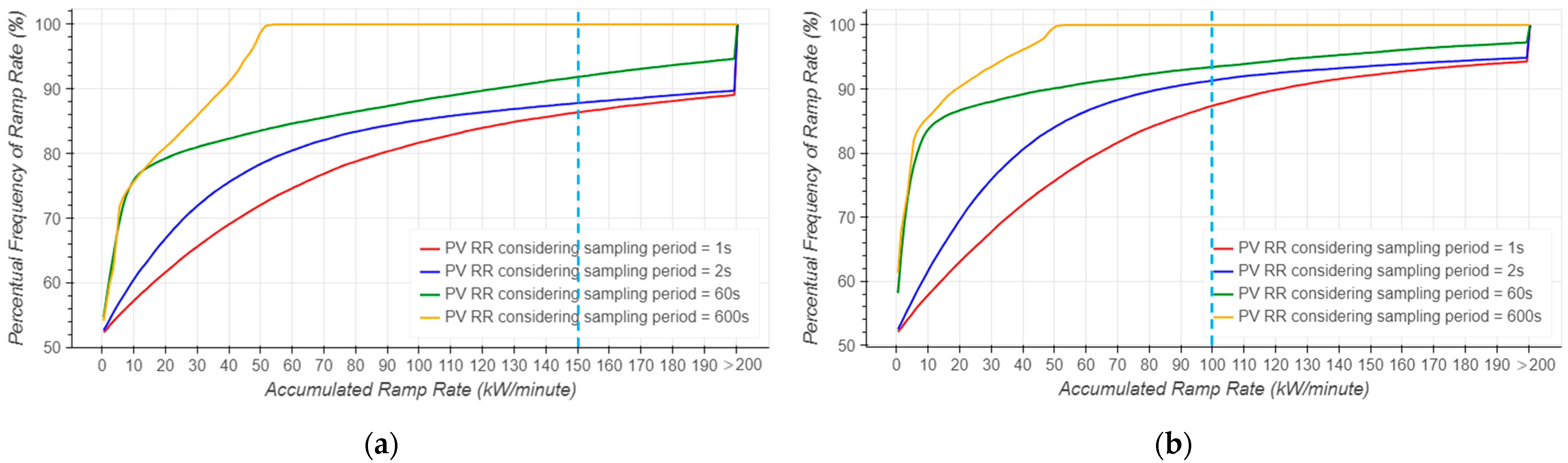
The RR calculation was analyzed using different time intervals (∆t = 1 s, 2 s, 60 s, 600 s), normalized to a minute basis according to Equation (1). The model underwent rigorous validation over an extended analysis period, with two days of measurements presented in the results of this paper. On one day, the control was set to a ramp rate of 150 kW/minute; another day, the ramp rate was set to 100 kW/minute.

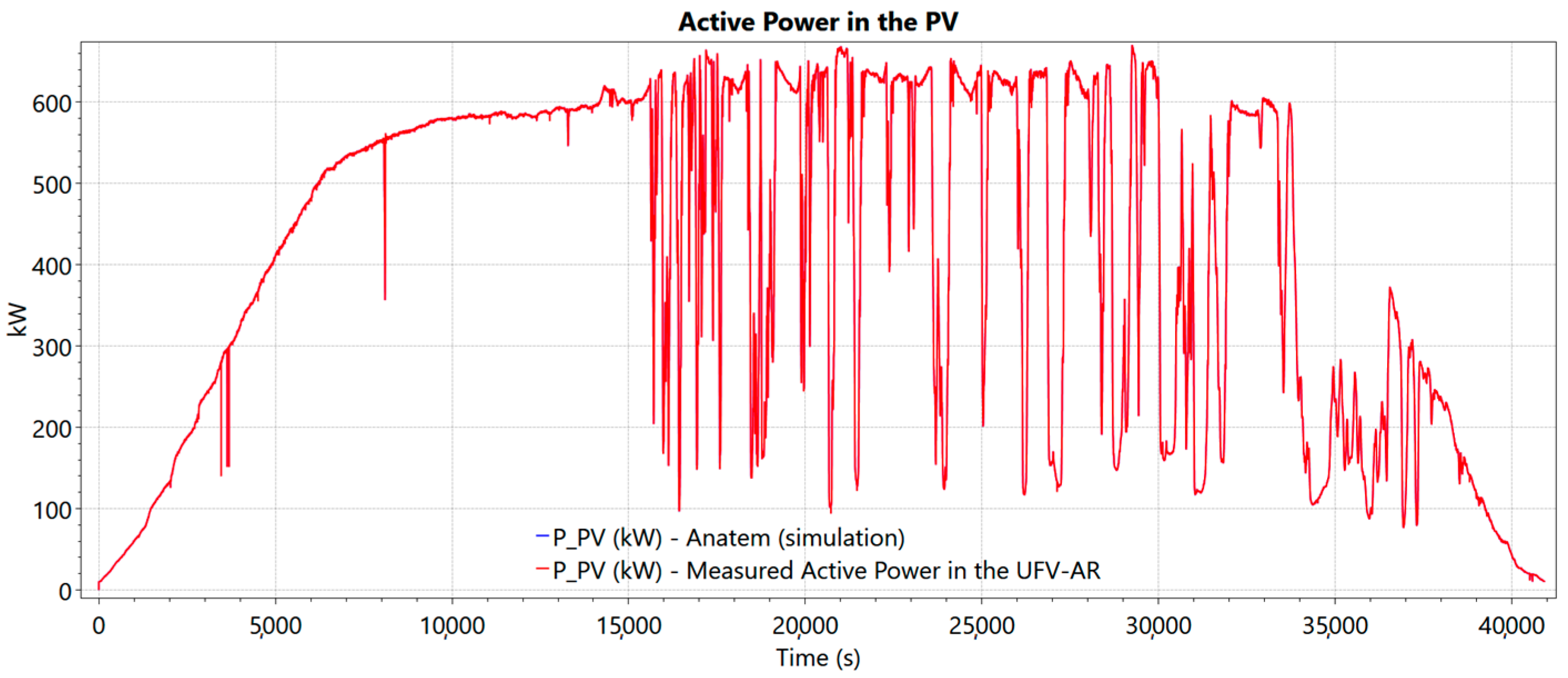
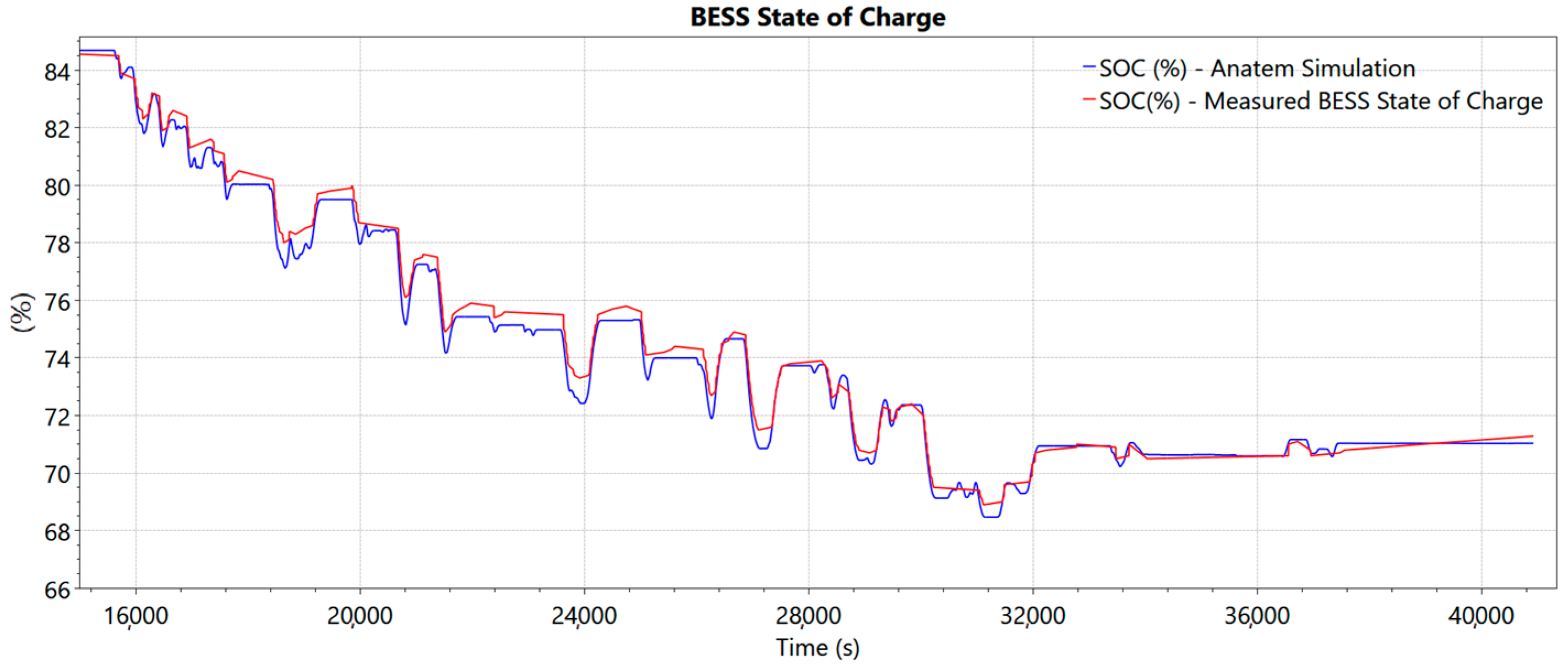
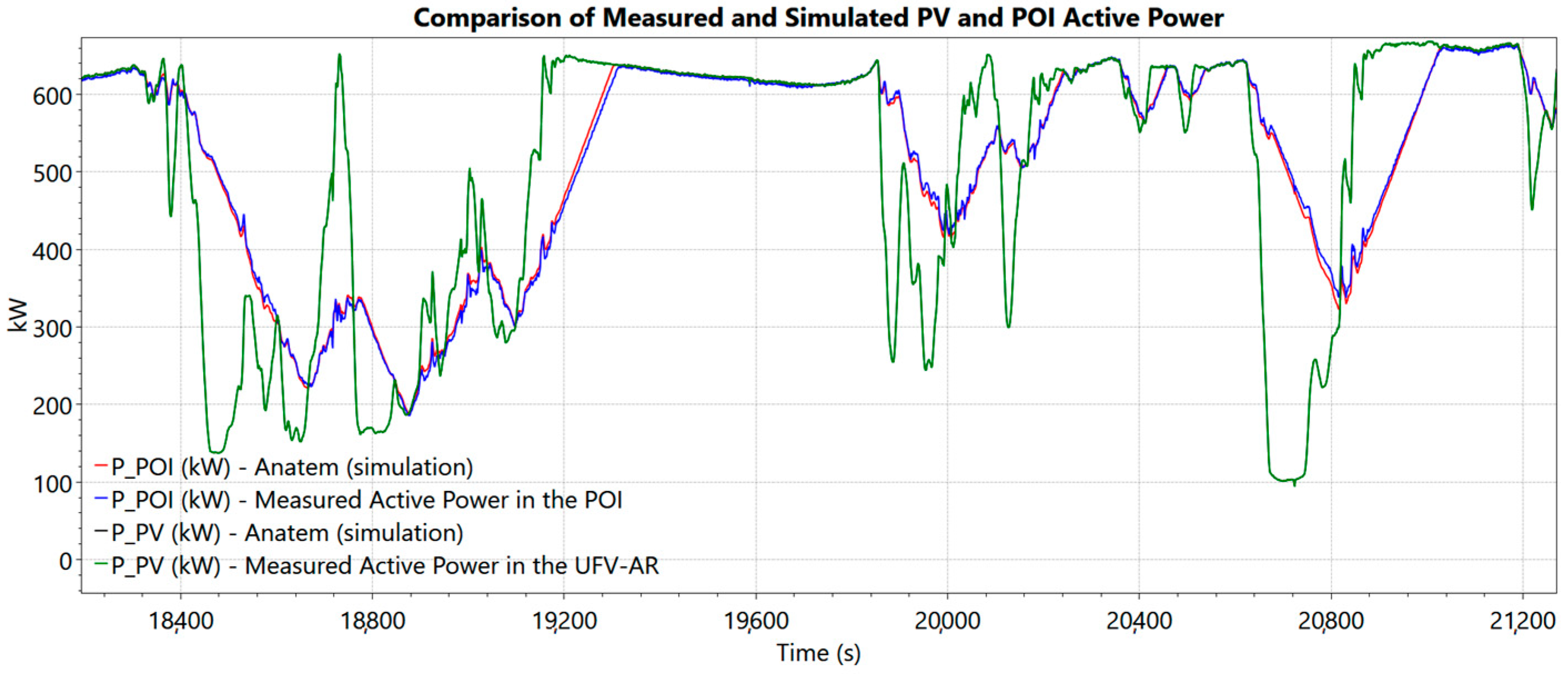
Figure 9a,b illustrate the power generated by the photovoltaic system, the output power at the connection point controlled by BESS for the adjusted RR, the BESS SOC. Figure 10a,b show the calculated accumulated RR histogram of the PV power in absolute values for Day 1 and Day 2, and Figure 11a,b show the calculated accumulated RR histogram of the POI for Day 1 and Day 2. After analyzing the RR histograms in the POI of Day 1 and Day 2, it was found that the correct calculation for meeting the ramps was ∆t = 60 s, where the RR service was 99.6% and 99.3%, respectively. When considering the histogram of the power generated only by PV, the RR service was 92% in Day 1 and 95.7% in Day 2, both with ∆t = 60 s.

This indicates that the service to the ramps depends on the power generated by PV, which fluctuates with the weather behavior during the day. Interestingly, in Day 2, the service of the ramps only by PV is higher than in Day 1, even though a more restrictive RR criterion is observed. The difference between the analysis of PV power and POI is due to the role of BESS in controlling RR. It was found that the SOC was reduced by 10% in the case of Day 1, and 13% in the case of Day 2.

Based on the analysis, it has been found that there is a significant variation in the ramp rate calculation depending on the period used (∆t), mainly when smaller periods are used. A higher ramp rate may be observed if the signal fluctuates quickly in small moments. However, this will not represent the average used per minute.

This analysis highlights the importance of grid codes specifying the measurement and calculation method for ramp rate, ensuring that plant controllers are correctly programmed to comply with these requirements.

4. Simulation Results and Validation of the Power Ramp Rate Control Model

To validate the photovoltaic model associated with the BESS, we considered the models mentioned in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 with a sampling period of ∆t = 60 s, as identified in Section 3. Figure 12 shows the combination of these models, where the measured power of the PV is used as an input signal to the reference power of the PV model in REPC_A. The PV model then provides the calculated active power of the PV. The calculated active power (output) of the PV is then used as the input signal of the BESS’s PPC (REPC_A+RR Control). The outputs of the BESS model are the active power calculated by the BESS to maintain the ramps under a specific value specified in the POI and the BESS SOC within its minimum and maximum limits. The sum of the power calculated by the BESS and the power calculated by the PV is controlled by ramps at the POI.

The measurements from Day 2 are presented in Figure 9b, Figure 10b and Figure 11b were used to present the results, with RR control set to 100 kW/min. The measured PV active power curve is the input data for the model developed in the Anatem software, with the following comparisons being carried out in the following figures:

• Figure 13—Measured PV power × PV power calculated by Anatem for Day 2;
• Figure 14—Measured POI power × POI power calculated by Anatem for Day 2;
• Figure 15—Measured BESS SOC × BESS SOC calculated by Anatem for Day 2.

Figure 15 presents the BESS SOC, where minor errors in simulated SOC control compared to the actual measured SOC can be observed. The detailed analysis found that the SOC data sampling performed by SCADA receives updates more slowly than the power measurement of the PV plants and BESS, which are read directly by the instrument transformers. Additionally, part of the discrepancy is due to the simplified model used for the SOC, represented by the transfer function 1/(T.s). These minor instantaneous errors may be correlated to controller delays or additional control schedules beyond the ramp control, presenting some unexpected behavior.

Table 2. Analysis of errors in the model response for the days 1 and 2.

Description of Variables	Day 1 (RR = 150 kW/min)		Day 2 (RR = 100 kW/min)
	RMSE	R2	RMSE	R2
$P_{PV}$ (PV Active Power)	0.000583	0.999992	0.000654	0.999990
$P_{POI}$ (POI Active Power)	0.004485	0.999485	0.005190	0.999307
$SOC$ (BESS State of Charge)	0.002672	0.994861	0.002828	0.997843

shows the errors calculated for two simulation days, and the results suggest that the model fits the data very well. It is also revealed that the model can explain almost all the variation observed in the values of the variables.

Figure 16 represents the ramp control in more detail, between 19,800 s and 21,200 s, where it can be observed that the Anatem model adheres excellently to real data in the POI output power and the calculated SOC for one-day simulation.

5. Conclusions

This work presented the development and validation of a new power ramp rate control module for a photovoltaic plant associated with a battery energy storage system, using second-generation Renewable Energy Systems models developed by the Western Electricity Coordination Council (WECC) as a foundational framework. This study addresses the significant scientific problem of managing the intermittency and fluctuations inherent in renewable energy sources. The accurate modeling and control provided by the PRRC function can significantly enhance the reliability and stability of PV systems, preventing undesirable disconnections. Future research will explore the impact of PRRC on frequency in off-grid or on-grid industrial systems, develop optimal SOC control strategies, and determine optimal BESS sizing.

The ramp rate control functionality was implemented in the BESS plant controller (PPC), specifically in the REPC_A module, with the addition of the ramp rate control module (RR_Control). The simulation results, compared with real data collected from a PV plant equipped with BESS in Brazil, demonstrated the accuracy of the developed model. The root mean square error (RMSE) and coefficient of determination (R²) metrics confirmed the accuracy of the implemented ramp rate control. The study also highlighted the importance of correctly considering the power sampling rate when calculating the ramp rate, as different sampling periods can produce distinct results.

The model underwent thorough validation over an extended analysis period, with two days of measurements reported in the article. The results demonstrate that the developed ramp rate control effectively reduces the intermittency of photovoltaic power generation, ensuring adherence to grid criteria and providing valuable insights for medium and long-term analyses. The incorporation of ramp rate control in REPC_A and the RR_Control module represents a significant advancement in renewable energy integration, offering a reliable solution for managing power fluctuations in photovoltaic plants paired with energy storage systems.

Furthermore, the analysis revealed that the correct consideration of the power sampling rate is crucial for the accuracy of ramp rate control, directly impacting compliance with grid codes and the sizing of the BESS. Identifying the ramp rate calculation technique used in the UFV-AR plant was also an essential step in ensuring the accuracy of the developed model.

In summary, this work validates the effectiveness of ramp rate control in PV plants with BESS using improved WECC models. The study’s main contributions include developing and validating the ramp rate control model, parameter adjustment techniques, and utilizing the Anatem software. By comparing simulation results with real-world data from a PV plant equipped with BESS in Brazil, the model’s accuracy was confirmed through metrics such as RMSE and R². Additionally, the analysis emphasized the critical role of power sampling rates in calculating ramp rates, impacting compliance with grid codes and BESS sizing. Overall, this research provides a robust foundation for future implementations and studies on managing intermittency in renewable energy generation.