1. Introduction
With the development of technology and industry, the integration of various electronic components is constantly improving. A typical example is the development of microelectronic components and micromachining techniques, which, in turn, has led to a significant increase in the number of transistors contained in each generation of electronic component chips [
1]. Moore’s Law states that the number of transistors in electronic component chips will continue to double almost every 2 years. This increase in transistors has boosted the processing power of electronic chips but has also exacerbated heat dissipation and power consumption issues [
2]. Over the past few decades, the heat generation of electronic components has risen to very high levels [
3]. In order to ensure the normal use of the chip, it is necessary to remove the heat generated by it in time [
4]. Therefore, urgent solutions are needed to address the heat dissipation problem of high-heat-flux components such as electronic chips. A substantial amount of research has been conducted on thermal management components for electronics, including studies on the actual working conditions and the effects of various cooling media. Faraji et al. [
5] investigated the inclined rectangular enclosure filled with Nano-enhanced Phase Change Material (NePCM), and the results indicated that the introduction of metallic nanoparticles had a positive effect on reducing the temperature of the heat source. Faraji et al. [
6] further analyzed the thermal and dynamic fluid flow for various enclosure inclinations (0°, 45°, and 90°) and Rayleigh numbers (Ra = 10
3–10
6), and established a quantitative analysis of the relationship between the inclination angle and the Rayleigh number on the heat transfer efficiency. Under this background, microchannel heat sinks (MCHSs) are increasingly being adopted.
Due to the high requirements for structural precision and strength in MCHSs, chemical etching and diffusion welding processes are often used in industry for the fabrication of MCHSs. Chemical etching significantly affects the surface formation quality of the workpiece [
7], and the undulation formed by etching can impact the heat transfer performance and fluidity of the MCHS. Compared to connection methods such as electron beam welding and laser welding, diffusion welding has unique advantages such as fewer fusion welding defects, a smaller heat-affected zone, and minimal thermal deformation [
8,
9,
10]. Shevchenko et al. [
11] studied the strength of welded joints of 304 stainless steel under laser action, and Djeloud et al. [
12] studied the residual stress during the welding of austenitic stainless steel. Ren et al. [
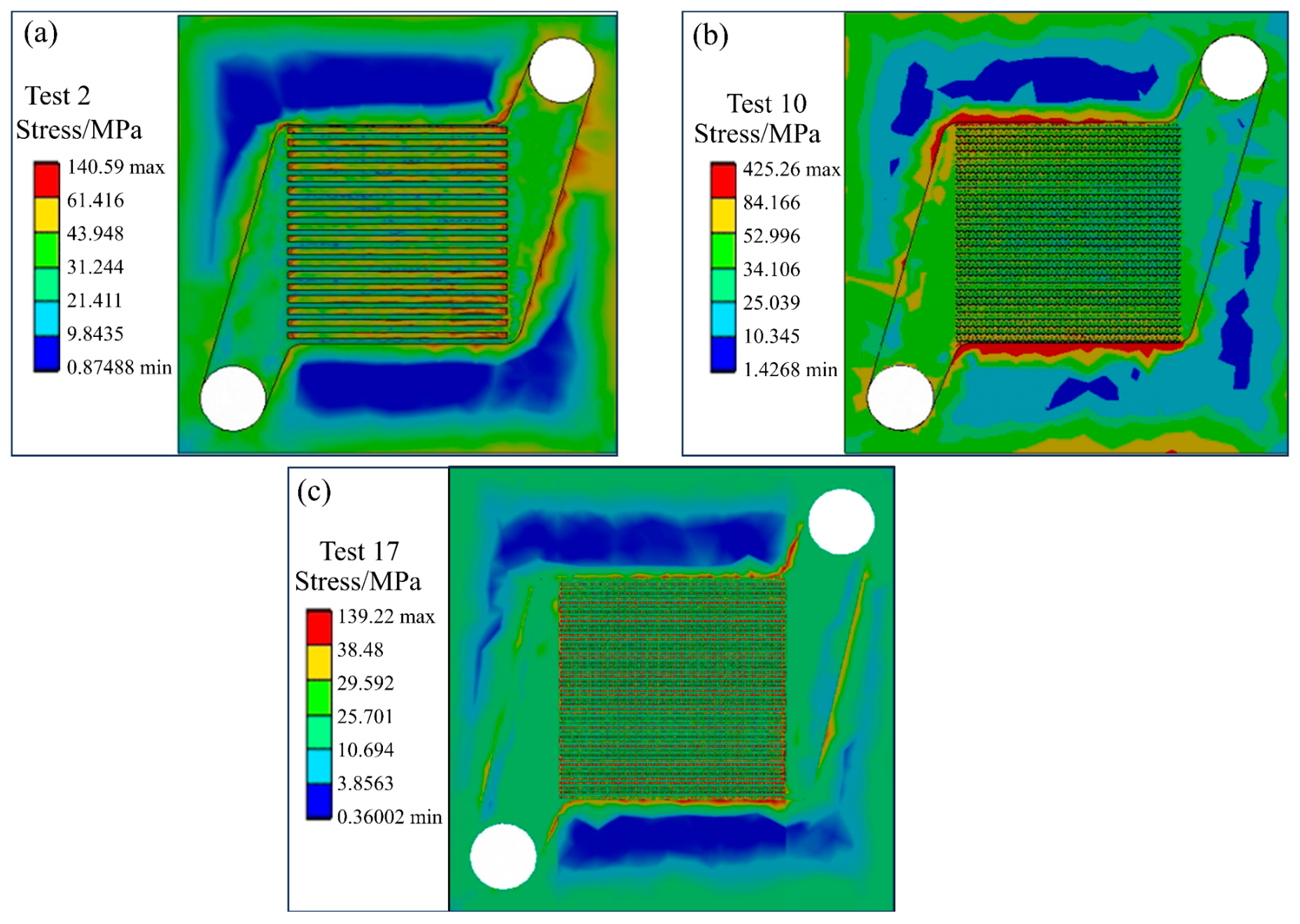
13] investigated the influence of surface roughness on diffusion welding by using the Gleeble 3500 thermal simulation testing machine. The result showed that small surface roughness was beneficial for the bonding process. Therefore, in the fabrication of high-precision MCHSs, the existence of surface roughness and residual stress on the machined surface has a significant impact on the overall performance and structural strength of the MCHS [
14,
15,
16].
In addition, the extremely small channel dimensions of MCHSs can significantly enhance their cooling performance, but, at this small scale, fluid flow is affected by scale effects. Therefore, it is necessary to study the impact of traditional theories on fluid flow at small scales. Tiselj et al. [
17] and Gao et al. [
18] studied the flow state of fluids on the basis of the microscale, and the basic fluid dynamics and traditional heat dissipation laws were basically applicable to the microchannels with a microchannel height greater than 0.4 mm. Li et al. [
19] also confirmed that the continuum hypothesis theory was applicable to MCHSs. The overall performance of the MCHS mainly depends on the following three key metrics: the heat dissipation capacity, cooling uniformity, and pressure drop [
20,
21,
22,
23]. To optimize the MCHS performance, researchers are exploring ways to improve its structure [
24]. Experimental and numerical research has been conducted on the heat dissipation and fluid flow performance of MCHSs. Wu et al. [
25] measured the friction factor in the trapezoidal MCHS and confirmed the results. Naphon et al. [
26] investigated the effects of various factors on the performance of the MCHS through experiments. The research findings suggest that surface roughness significantly impacts the performance of the MCHS, with a higher surface area and surface roughness leading to an increased heat transfer rate. Ghasemi et al. [
27] utilized the Response Surface Methodology (RSM) to study the complex multi-factorial influences of channel dimensions and nanofluids. The results indicated that reducing the channel size while maintaining a certain number of channels can improve the overall heat transfer performance. Researchers Tran et al. [
28] and Hasan et al. [
29] performed numerical studies on the performance of MCHSs with different cross-sectional shapes. They found that the round microchannel has the best hydraulic performance. Ma et al. [
30] studied the flow heat transfer characteristics of sawtooth microchannels, and the results showed that sawtooth microchannels could improve the heat transfer performance of MCHSs while increasing the pressure drop. Haertel et al. [
31] studied the cross-section shape of the microchannel and designed a branch structure through topology optimization, which improved the performance of the traditional microchannel by 7%. Zeng et al. [
32] proposed a novel optimization-inspired half-wave fin pattern, achieving a 10.5% reduction in pumping power compared to conventional fin structures at a heat flux of 50 W/cm
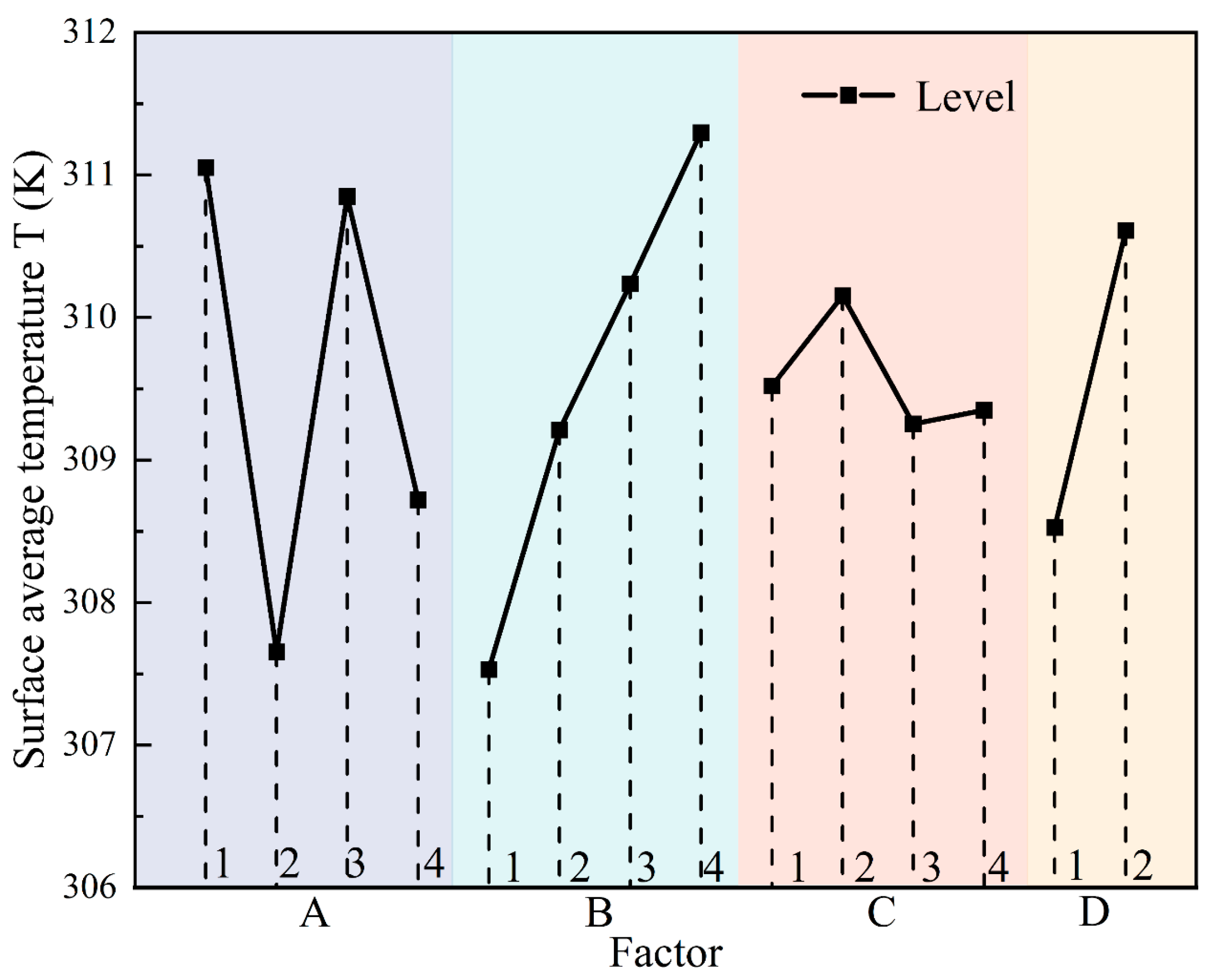
2. In view of the many factors such as the wall shape, aspect ratio, surface roughness, and many other factors, relevant scholars have carried out research on multi-objective optimization. Zou et al. [
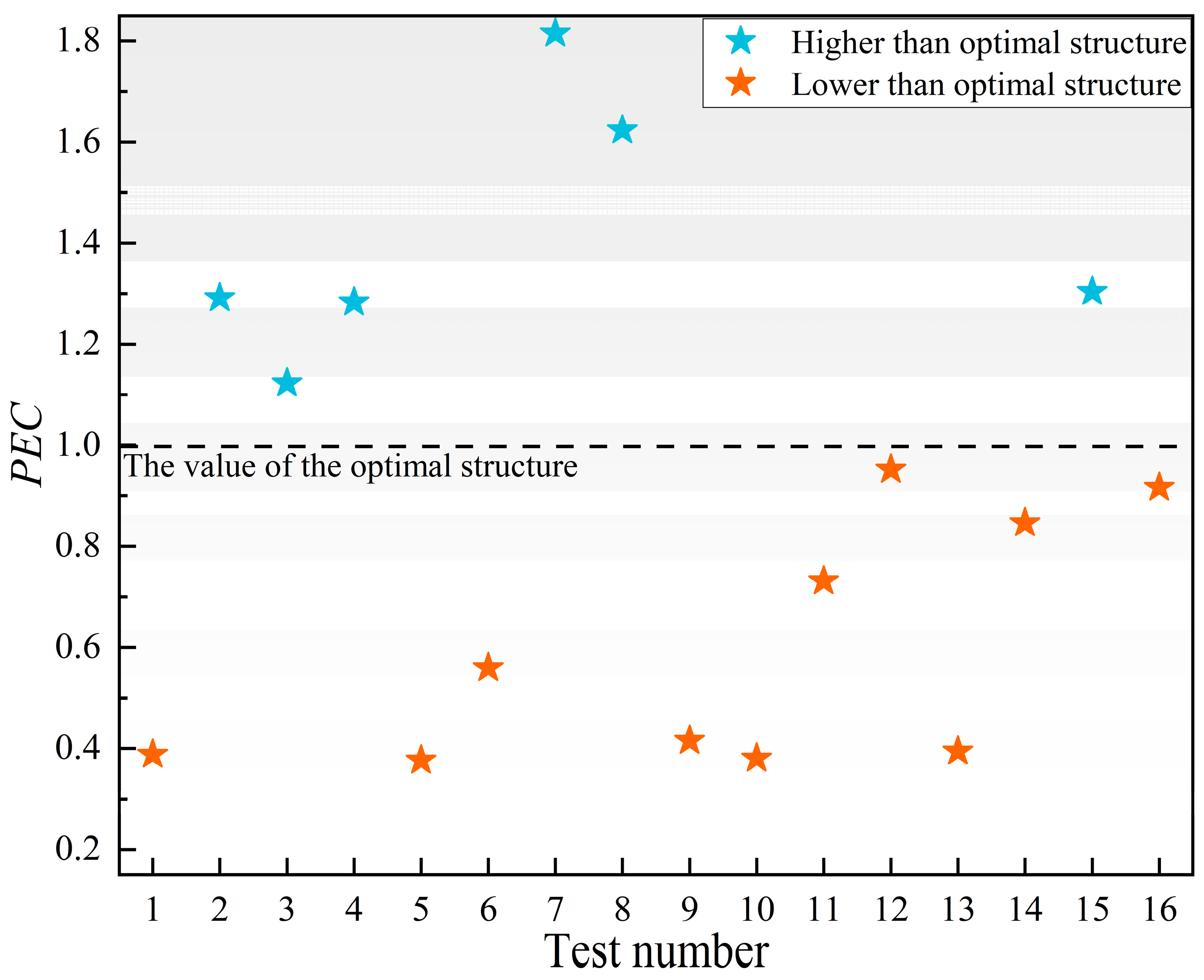
33] performed the multi-objective optimization of the heat sink to evaluate its pressure drop and temperature. Their optimized structure had a performance evaluation criterion (
PEC) of up to 1.67 compared to the conventional rectangular MCHS.
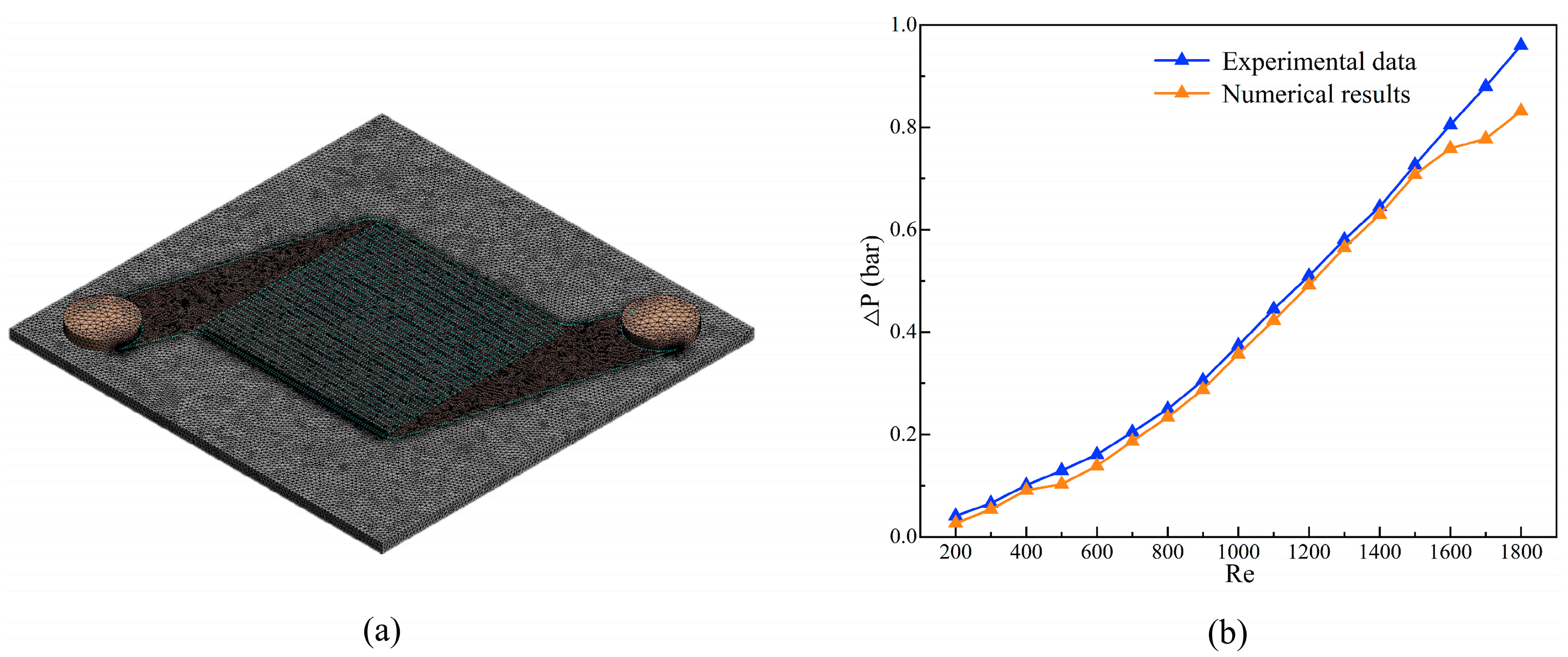
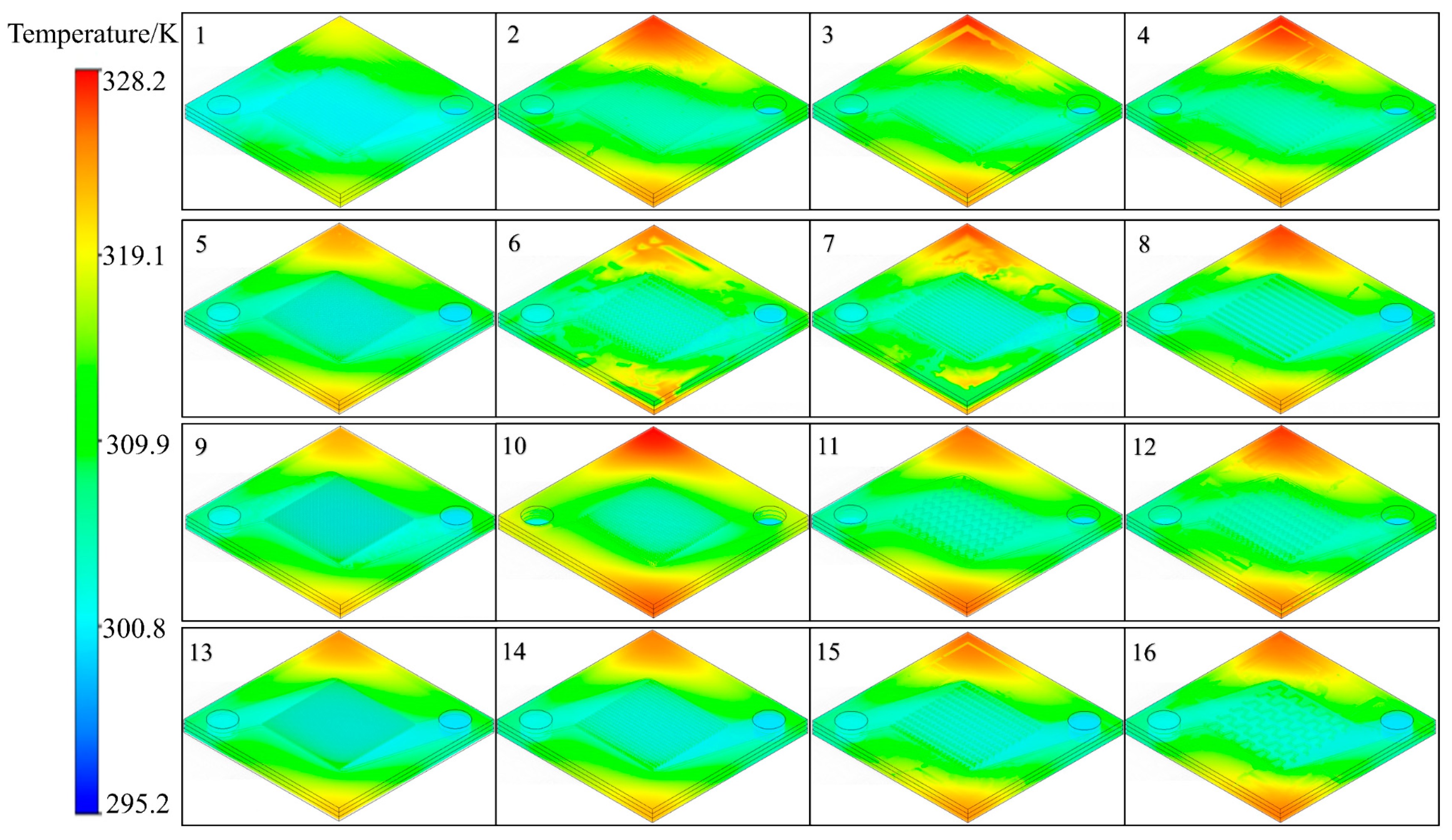
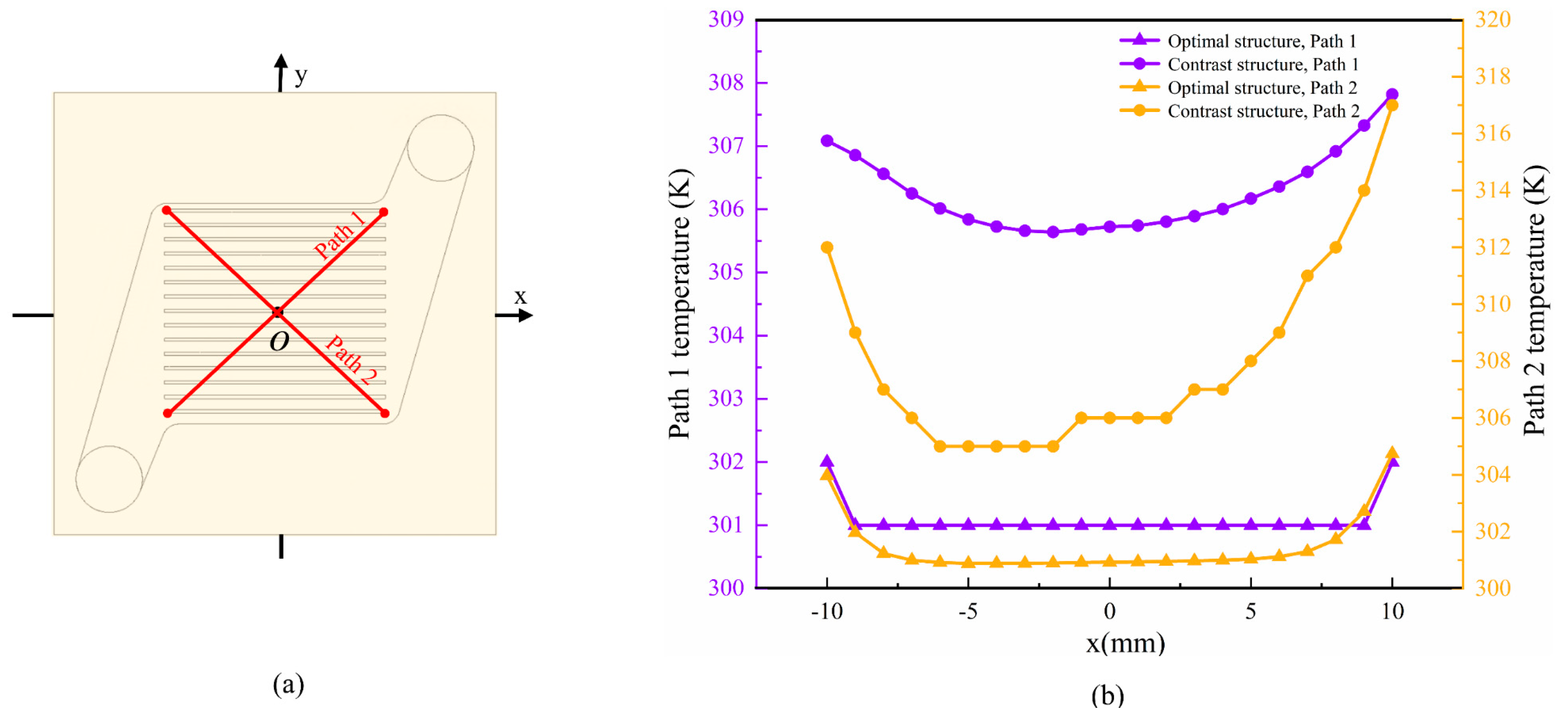
As can be seen from the above, optimizing the structure of the MCHS is an important means to improve its heat dissipation capacity, but how to maintain good fluidity is a problem that needs attention. In addition, it is necessary to study the thermal stress distribution in order to ensure that the high-precision MCHS has sufficient structural strength. In this study, a laminated MCHS was designed, and the influence of different microchannel structures on the heat transfer and stress distribution of the MCHS was studied. Taking the average surface temperature of the heat source as the evaluation metric, a four-factor orthogonal experiment was established with the shape, width, distribution density, and surface undulation of the microchannel as factors. The optimal structural combination was obtained by CFD numerical simulation using ANSYS Fluent v13.0 software. Furthermore, the thermal and mechanical coupling simulation was carried out with unidirectional coupling, and the thermal stress simulation of the structure before and after optimization was carried out to proofread the structural strength of the MCHS. Finally, analyzing the cooling uniformity, fluidity, and PEC of the optimized microchannel structure is crucial for understanding how different structural designs impact the microchannel’s performance.
2. Description of MCHS
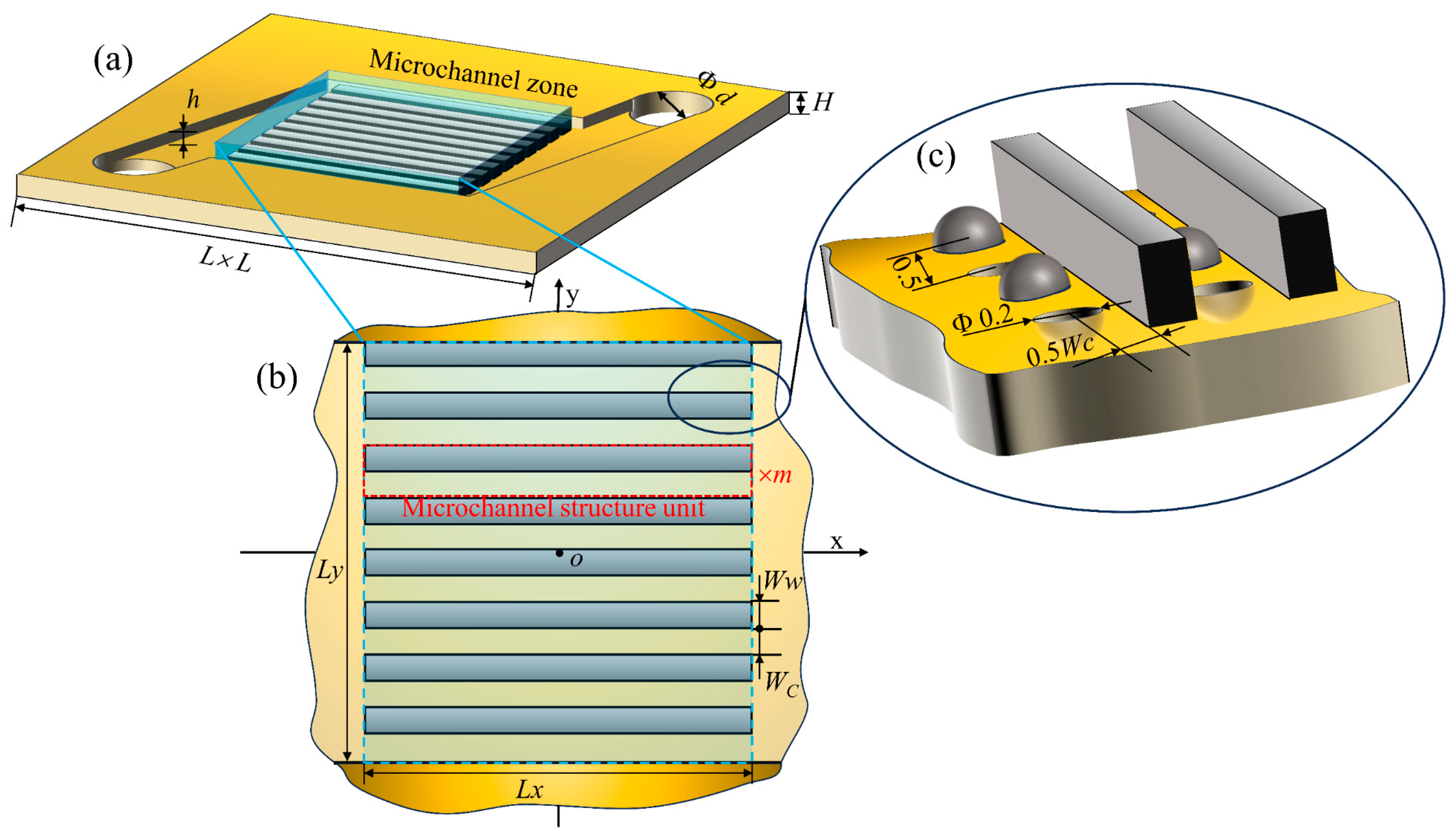
In this research, a new laminated microchannel heat sink (MCHS) was designed, as shown in
Figure 1, which is composed of several 304 stainless steel metal plates of three types superimposed, namely, the upper cover, the lower cover, and the microchannel layer. The three types of metal plates were processed from the same specifications of sheet-like raw materials (side length,
L = 80 mm; height,
H = 2 mm). In this MCHS, high-precision microchannels were prepared in the microchannel layer by the chemical etching process, and several metal plates were superposed into a whole by the diffusion welding process. The size diagram of the microchannel layer is shown in
Figure 2.
The unique feature of this design is that the three types of metal plates can be arbitrarily stacked in
n layers until the desired thickness or performance requirements are achieved. This greatly saves the cost of the MCHS preparation and reduces the waste of raw materials, while reserving the possibility for subsequent customization. In order to simplify the analysis process and obtain the general conclusion, a piece of each type of thin plate was taken from the laminated structure used in this paper. Specifically, the through-hole diameter of the upper cover and the lower cover is
d = 12 mm, which consistent with that of the microchannel layer, as shown in
Figure 2a; the height of the fluid domain in the microchannel layer is
h = 1 mm, and a microchannel zone was designed in the center of the layer, as shown in
Figure 2b; the length and width of the microchannel zone are
Lx = 20 mm and
Ly = 40 mm, respectively, and are composed of
m microchannel structural units arranged periodically; each microchannel structural unit is composed of a sidewall with a width of
Ww and a microchannel with a width of
Wc. In addition, in order to further explore the influence of microchannel machining roughness on the overall performance, this study designed surface undulation, as shown in
Figure 2c. The microchannel is periodically arranged with protruding or concave hemispheres, wherein the diameter of the hemispheres is 0.2 mm, the distance between the spherical center is 0.5 mm, and the distance between the spherical center and the sidewall is 0.5
Wc.
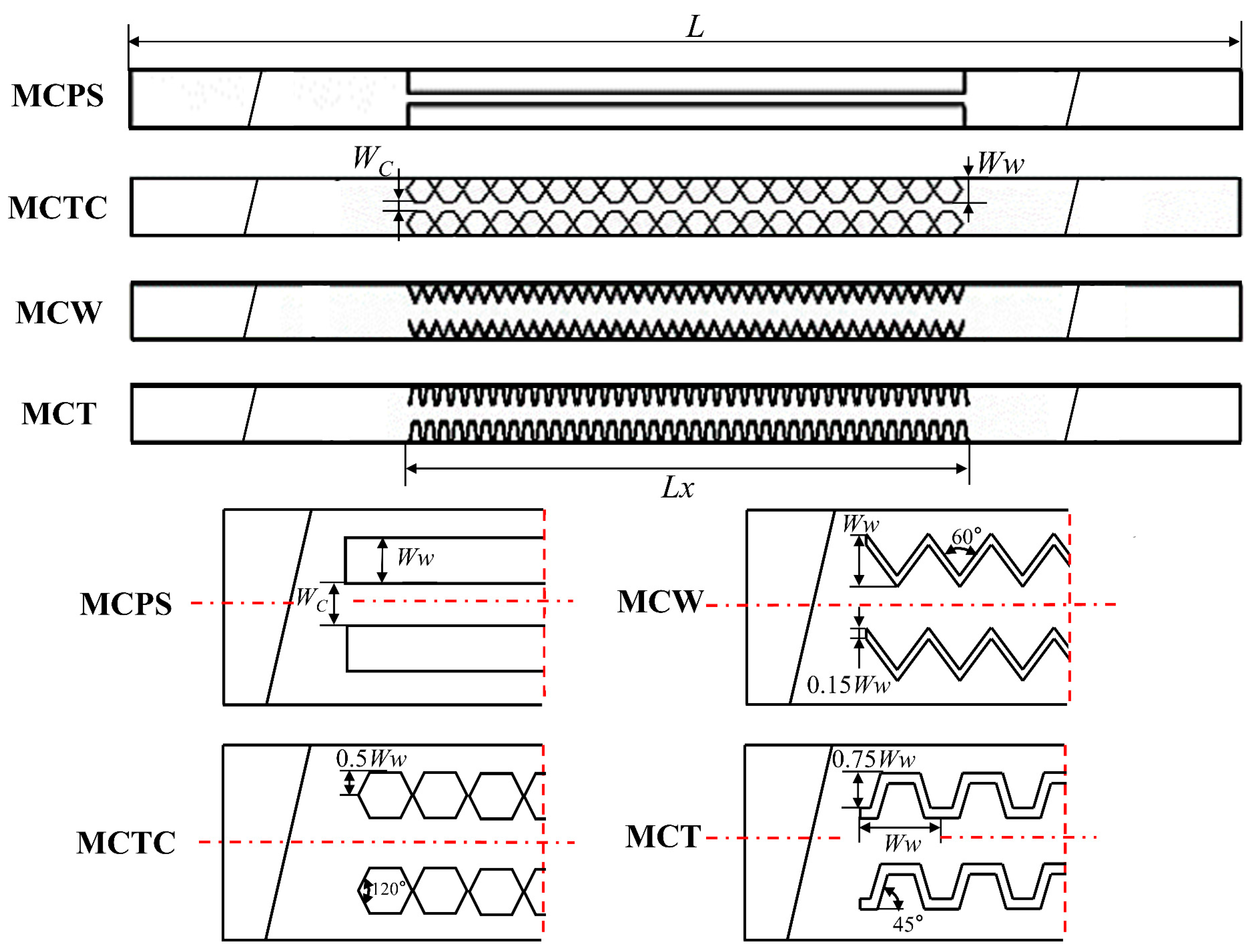
Finally, considering the difficulty of processing and the relatively mature existing design schemes, four microchannel structures were designed in this study, namely, the parallel straight microchannel (MCPS), triangular cavity microchannel (MCTC), wavy microchannel (MCW), and trapezoidal microchannel (MCT). Microchannels with different structures were compared and analyzed to explore the mechanism of their influence on the heat transfer performance and the structural strength of the MCHS. The four types of microchannel structures and their detailed parameters are shown in
Figure 3. The geometric parameters described above are shown in
Table 1. In this MCHS, the metal plate is 304 stainless steel and the cooling medium is deionized water. Their physical properties are listed in
Table 2.