Study on Leakage and Diffusion Behavior of Liquid CO2 Vessel in CCES
Abstract
1. Introduction
2. Physical Model and Governing Equations
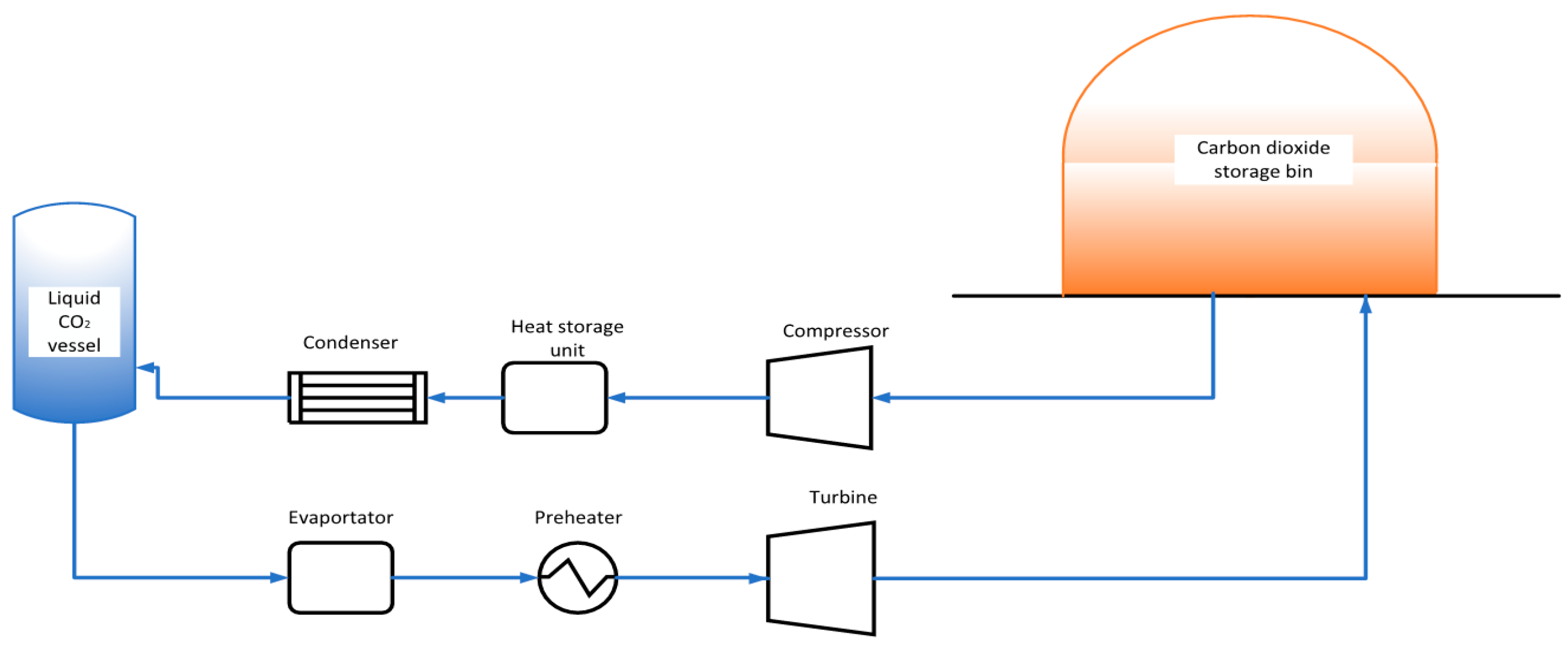
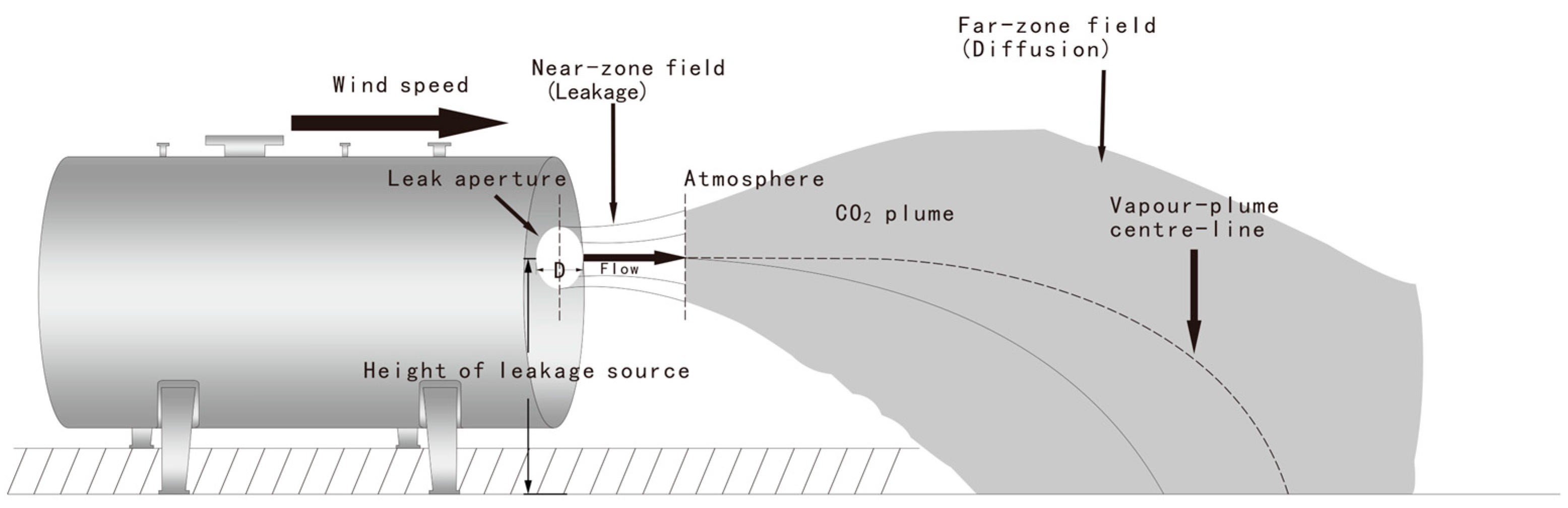
2.1. Physical Model
2.2. Flow Equations
- (1)
- Continuity equation:=
- (2)
- Equation of motion
- (3)
- Energy equation
- (4)
- Equation of state
2.3. Diffusion Equations
3. Results and Discussion
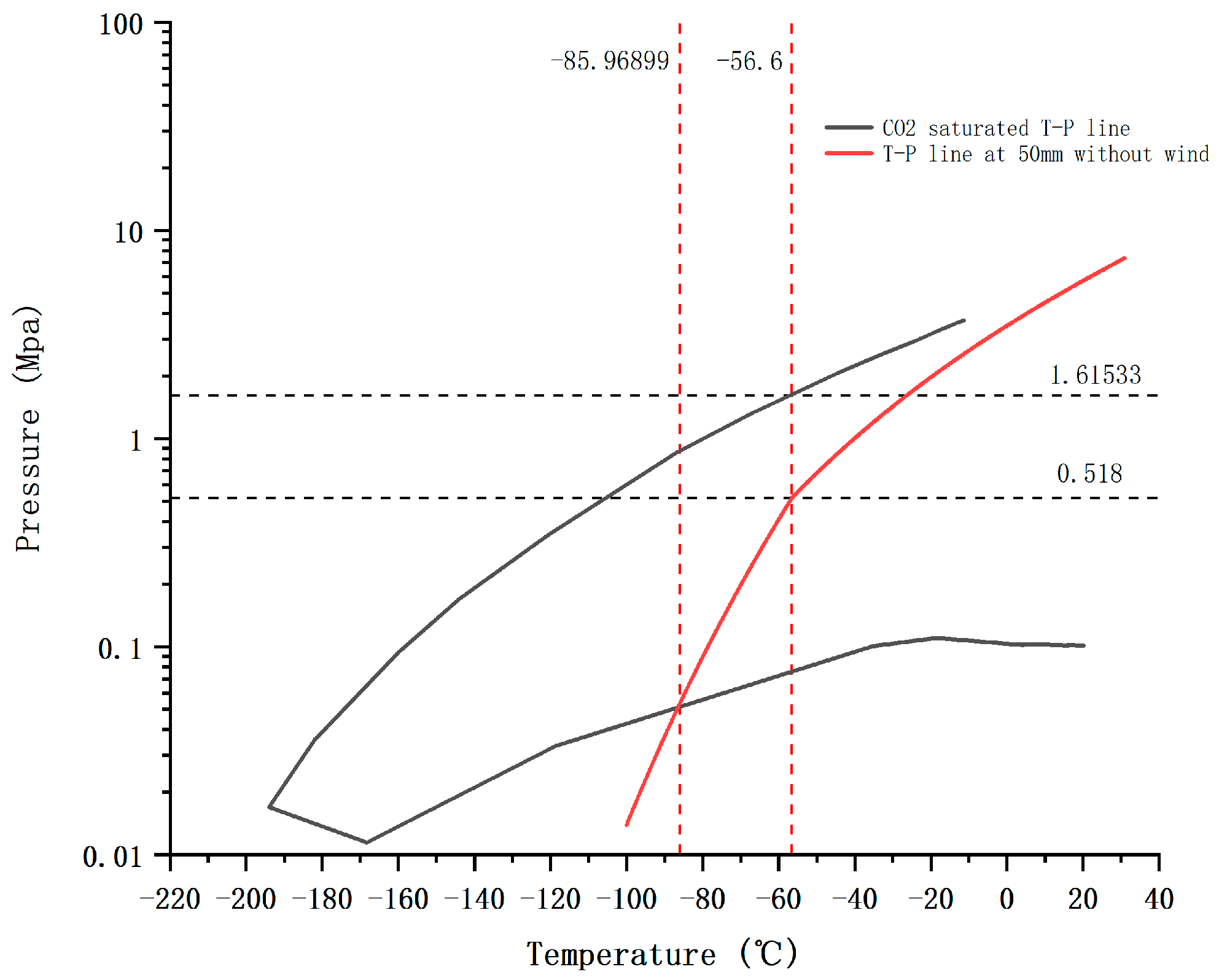
3.1. Leakage Behavior in the Near-Zone Field
3.2. Diffusion Behavior in Far-Zone Field
3.2.1. Wind Speed
3.2.2. Leakage Aperture
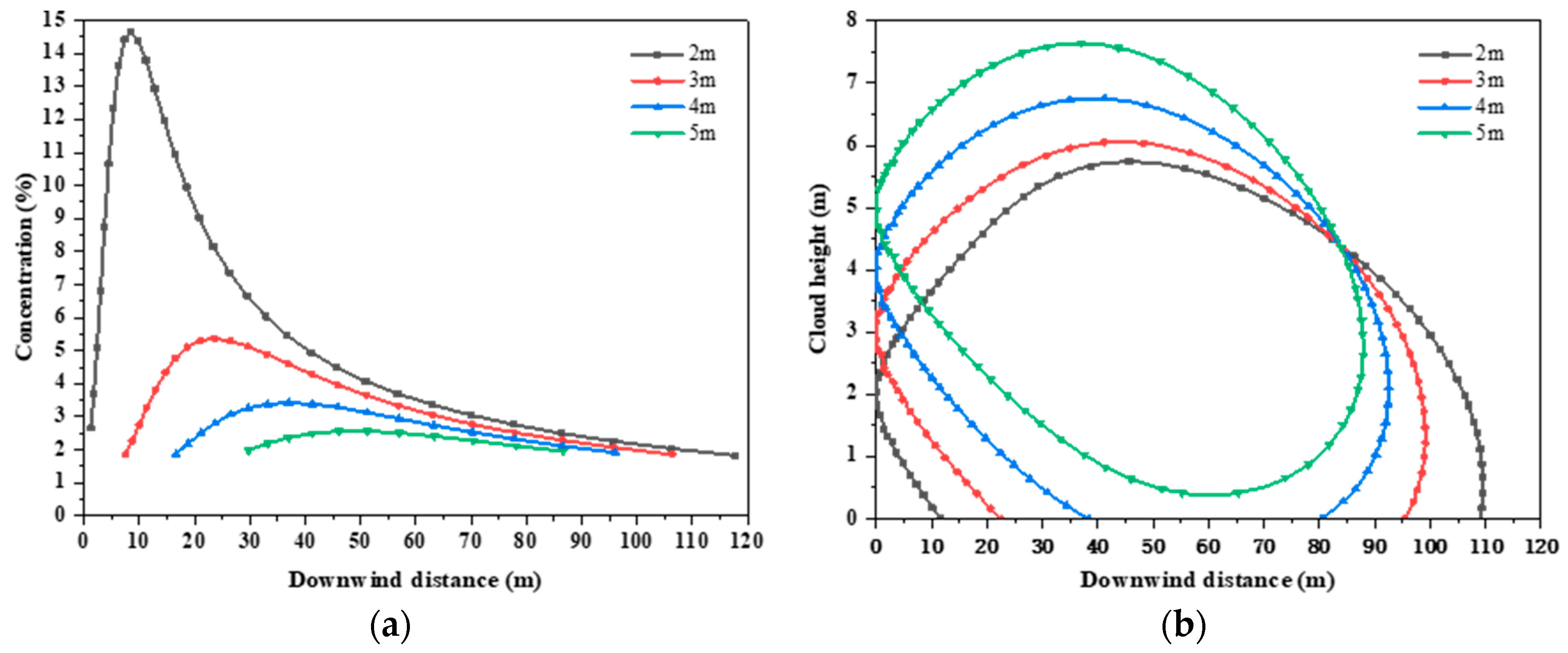
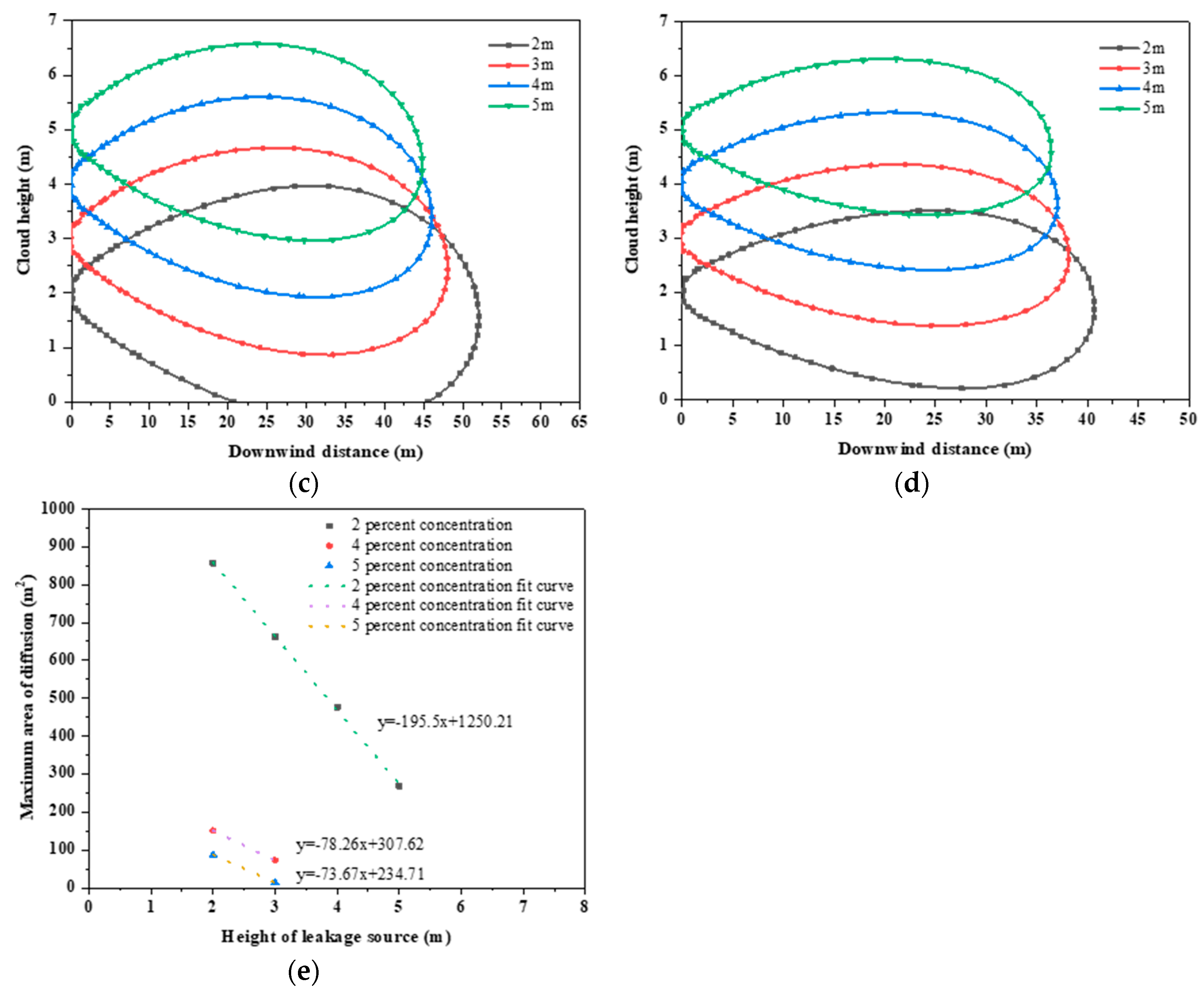
3.2.3. Leakage Source Height
4. Conclusions
- (1)
- Based on the choking flow theory, transonic flow occurs in the near-zone of the leak. The low-temperature zone of a 50 mm leak aperture can reach 0.74 m downwind, and does not really change with wind speed. In the leakage direction, the maximum damage zone of high-speed flow can reach 7.70 m;
- (2)
- In the far-zone of the leak, diffusion behavior is key. The wind speed is linearly inversely proportional to the maximum diffusion area of the cloud. The high-concentration zones were concentrated at the downwind distance from 6.97 to 8.02 m, and the minimum concentration could reach up to 5.39%;
- (3)
- Leakage aperture has a significant effect on the diffusion of a carbon dioxide cloud. When the leakage aperture is less than 50 mm, the maximum diffusion area of the cloud is directly proportional to three times the leakage aperture. The high-concentration area is concentrated in the downwind direction at a distance of 8.02~8.46 m, and the lowest concentration reaches up to 5.85%. when the wind speed is 3 m/s, and the leakage height is 2 m, the diffusion area of the cloud is directly proportional to three times the leakage aperture with a 50 mm aperture;
- (4)
- In the average breathable zone of 1.5 m, there is a linear inverse relationship between the height of the leak and the maximum dispersion area. At a height of 2 m or 3 m, the maximum concentration is above 4%, which can render a person unconscious within a few minutes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, J.; Yue, Y.; Zhang, J.; Yang, J.; Li, X.; Song, Y.; Zhang, Z. Research status and development prospect of carbon dioxide energy storage technology. Energy Storage Sci. Technol. 2022, 11, 3285–3296. [Google Scholar]
- Xu, W.; Zhao, P.; Gou, F.; Wu, W.; Liu, A.; Wang, J. A combined heating and power system based on compressed carbon dioxide energy storage with carbon capture: Exploring the technical potential. Energy Convers. Manag. 2022, 260, 1–16. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, Z.; Yan, L.; Wang, J.; Yao, S. Experiment and numerical investigation on flow characteristics and near-field structure of dense phase CO2 pipeline leakage. Process Saf. Environ. Prot. 2024, 182, 327–344. [Google Scholar] [CrossRef]
- Yin, B.; Gao, X.; Zhang, X.; Yang, S. Report of an acute carbon dioxide poisoning incident. Gems Health 2010, 1, 248. [Google Scholar]
- He, J.; Xiao, Y.; Huang, L.; Li, A.; Chen, Y.; Ma, Y.; Li, W.; Liu, D.; Zhan, Y. Application of leakage pre-warning system for hazardous chemical storage vessel based on YOLOv3-prePReLU algorithm. J. Loss Prev. Process Ind. 2022, 80, 104905. [Google Scholar] [CrossRef]
- Frith, S.; Hu, J. A suspended cloud of death over Cameroon. Gems Health 1993, 12, 31–35. [Google Scholar]
- Zhao, C. The Numerical Simulation on Liquid Phase Leakage and Dispersion Process of LNG Vessel. Dalian Univ. Technol. 2018, 6, 101. [Google Scholar]
- Zhu, G.; Cao, Q.; Wang, M.; Yu, J.; Yan, X.; Yu, S.; Liu, C. Risk analysis of diffusion of supercritical CO2 pipeline leakage. J. Saf. Environ. 2022, 22, 1486–1494. [Google Scholar]
- Ha, Y.-C.; Seo, J.-K.; Hwang, J.-H.X.; Ryu, S.-H. Method for Preventing Asphyxiation Accidents by a CO2 Extinguishing System on a Ship. Fire Sci. Eng. 2015, 29, 57–64. [Google Scholar] [CrossRef][Green Version]
- Gu, S.; Li, Y.; Lin, T.; Wang, C.; Hu, Q.; Zhang, D.; Xiao, Y.; Wang, J.; Stefan, I. An experimental study on the flow characteristics during the leakage of high pressure CO2 pipelines. Process Saf. Environ. Protection 2019, 125, 92–101. [Google Scholar] [CrossRef]
- Chen, B.; Cui, W.; Guo, H.; Xiao, H. Influence of wind speed on leakage and diffusion characteristics of supercritical-dense phase carbon dioxide. Sci. Technol. Eng. 2019, 19, 144–149. [Google Scholar]
- Wang, C.; Li, Y.; Lin, T.; Gu, S.; Hu, Q.; Zhang, D.; Xiao, Y.; Wang, J. Experimental study on dispersion behavior during the leakage of high pressure CO2 pipelines. Exp. Therm. Fluid Sci. 2019, 105, 77–84. [Google Scholar] [CrossRef]
- Yu, S.; Yan, X.; He, Y.; Yu, J.; Chen, S. Study on the leakage morphology and temperature variations in the soil zone during large-scale buried CO2 pipeline leakage. Energy 2024, 288, 129674. [Google Scholar] [CrossRef]
- Liu, Z.; Xiu, Z.; Zhao, Y.; Li, M.; Li, P.; Cai, P.; Liang, Y. Experimental study on the leakage temperature field of buried CO2 pipelines. Environ. Sci. Pollut. Res. Int. 2023, 30, 70288–70302. [Google Scholar] [CrossRef]
- Chen, L.; Yan, X.; Hu, Y.; Yang, K.; Yu, S.; Yu, J.; Chen, S. Depressurization and heat transfer during leakage of supercritical CO2 from a pipeline. Greenh. Gases Sci. Technol. 2022, 12, 616–628. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Tong, X.; Gong, J. Risk probability evaluation for the effect of obstacle on CO2 leakage and dispersion indoors based on uncertainty theory. J. Loss Prev. Process Ind. 2022, 74, 104652. [Google Scholar] [CrossRef]
- Mao, N.; Wang, Z.; Chao, Z.; Xuan, T. Qualitative and quantitative investigation on concentration of indoor dense gas caused by leakage and diffusion. Environ. Prog. Sustain. Energy 2019, 38, 424–434. [Google Scholar] [CrossRef]
- Hu, Y.; Yan, X.; Chen, L.; Yu, S.; Liu, C.; Yu, J. Leakage hazard distance of supercritical CO2 pipelines through experimental and numerical studies. Int. J. Greenh. Gas Control 2022, 119, 103730. [Google Scholar] [CrossRef]
- Kang, L.; Zhou, X.; Ran, T.; He, T.; Fang, Y.; Lin, S. Investigation of flow characteristics in small-scale highly pressurized leaked CO2 jet plume from pipeline. Int. J. Therm. Sci. 2019, 141, 160–170. [Google Scholar]
- Tian, G.; Yuan, Z.; Huang, Y.; Wang, J.; Wang, Y.; Zeng, C.; Huang, J. Experimental study of accidental release behavior of high-pressurized CO2 vessel. Process Saf. Environ. Prot. 2021, 145, 83–93. [Google Scholar] [CrossRef]
- Lu, Z.; Yan, L.; Xiao, C.; Yao, J. Numerical study of the transient behaviour of high pressure CO2 pipeline leakage. J. Saf. Environ. 2021, 21, 758–763. [Google Scholar]
- Wareing, C.J.; Fairweather, M.; Falle, S.A.; Woolley, R.M. Validation of a model of gas and dense phase CO2 jet releases for carbon capture and storage application. Int. J. Greenh. Gas Control. 2014, 20, 20254–20271. [Google Scholar] [CrossRef]
- Liu, F. Study on the Leakage and Diffusion Behavior of Supercritical Pressure CO2 from Pipelines. Master’s Thesis, Tsinghua University, Beijing, China, 2016. [Google Scholar]
- Marko, G.; Marco, P.; Giacomo, A.; Alessandro, T.; Romain, L. Comparison of UDM and CFD simulations of a time varying release of LPG in geometrical complex environment. J. Loss Prev. Process Ind. 2017, 44, 56–68. [Google Scholar]
- Shi, B.; Nie, S.; Sun, J. Research on the leakage risk of hydrogen pipelines based on dynamic Bayesian model. J. Saf. Environ. 2022, 22, 909–918. [Google Scholar]
- Bariha, N.; Mishra, M.I.; Srivastava, C.V. Fire and explosion hazard analysis during surface transport of liquefied petroleum gas (LPG): A case study of LPG truck vesseler accident in Kannur, Kerala, India. J. Loss Prev. Process Ind. 2016, 40, 449–460. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, M.; Huang, X.; Chen, J. Scenario analysis of road transport accidents involving flammable and explosive hazardous chemicals. China Saf. Sci. J. 2019, 29, 172–176. [Google Scholar]
- Sun, B.; Zhang, H.; Lü, S.; Chen, W. Numerical Simulation of Validation and Influence Factors of Explosion Accident Caused from LPG Vessel Leakage. Trans. Beijing Inst. Technol. 2021, 41, 137–142. [Google Scholar]
- Brzezinska, D.; Markowski, S.A. Experimental investigation and CFD modelling of the internal car park environment in case of accidental LPG release. Process Saf. Environ. Prot. 2016, 110, 5–14. [Google Scholar] [CrossRef]
- Zhao, G. An easy method to design gas/vapor relief system with rupture disk. J. Loss Prev. Process Ind. 2015, 35, 321–328. [Google Scholar] [CrossRef]





| Wind speed (m/s) | 1 | 3 | 5 | 7 | 9 |
| Height of leakage source (m) | 2 | ||||
| Leakage aperture (mm) | 20 | ||||
| Atmospheric Stability Scale | F | ||||
| High level of concern (m) | 1.5 | ||||
| Wind Speed (m/s) | 2% Concentration Area | 4% Concentration Area | 5% Concentration Area | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | |
| 1 | 36.32 | 3.3 | 78.46 | 18.25 | 2.69 | 12.04 | 14.78 | 2.56 | 4.47 |
| 3 | 33.23 | 3.29 | 68.2 | 16.76 | 2.68 | 9.91 | 13.72 | 2.55 | 3.38 |
| 5 | 30.45 | 3.27 | 58.39 | 15.56 | 2.66 | 8.24 | 12.87 | 2.54 | 2.52 |
| 7 | 27.98 | 3.24 | 50.01 | 14.60 | 2.65 | 6.94 | 12.17 | 2.53 | 1.84 |
| 9 | 25.74 | 3.21 | 42.90 | 13.78 | 2.63 | 5.87 | 11.58 | 2.51 | 1.27 |
| Leakage Aperture (mm) | Height of Leakage Source (m) | Wind Speed (m/s) | Atmospheric Stability Scale | High Level of Concern (m) |
|---|---|---|---|---|
| 10 | 2 | 3 | F | 1.5 |
| 20 | 2 | 3 | F | 1.5 |
| 30 | 2 | 3 | F | 1.5 |
| 40 | 2 | 3 | F | 1.5 |
| 50 | 2 | 3 | F | 1.5 |
| Leakage Aperture (mm) | 2% Concentration Area | 4% Concentration Area | 5% Concentration Area | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | |
| 10 | 14.16 | 2.62 | 6.92 | 8.23 | 2.34 | - | 6.84 | 2.28 | - |
| 20 | 33.23 | 3.29 | 68.20 | 16.76 | 2.68 | 9.91 | 13.72 | 2.55 | 3.38 |
| 30 | 57.29 | 4.06 | 216.04 | 26.73 | 3.04 | 36.66 | 21.27 | 2.83 | 19.87 |
| 40 | 83.91 | 4.87 | 480.06 | 38.39 | 3.46 | 81.3 | 29.89 | 3.14 | 45.84 |
| 50 | 111.66 | 5.63 | 878.29 | 51.04 | 3.97 | 146.75 | 39.46 | 3.50 | 83.46 |
| Height of Leakage Source (m) | Leakage Aperture (mm) | Wind Speed (m/s) | Atmospheric Stability Scale | High Level of Concern (m) |
|---|---|---|---|---|
| 2 | 50 | 1 | F | 1.5 |
| 3 | 50 | 1 | F | 1.5 |
| 4 | 50 | 1 | F | 1.5 |
| 5 | 50 | 1 | F | 1.5 |
| Height of Leakage Source (m) | 2% Concentration Area | 4% Concentration Area | 5% Concentration Area | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | Downwind (m) | Height (m) | Maximum Area Overlooking (m2) | |
| 2 | 109.53 | 5.74 | 857.35 | 52.04 | 3.97 | 151.1 | 40.67 | 3.51 | 87.37 |
| 3 | 99.12 | 6.06 | 662.49 | 48.06 | 4.67 | 72.84 | 38.15 | 4.36 | 13.7 |
| 4 | 92.5 | 6.75 | 476.2 | 46.05 | 5.61 | - | 37.03 | 5.33 | - |
| 5 | 87.90 | 7.64 | 267.78 | 44.83 | 6.58 | - | 36.43 | 6.31 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Wang, J.; Wu, S.; Liu, X.; Zhu, B.; Fan, Y. Study on Leakage and Diffusion Behavior of Liquid CO2 Vessel in CCES. Energies 2024, 17, 3613. https://doi.org/10.3390/en17153613
Gao L, Wang J, Wu S, Liu X, Zhu B, Fan Y. Study on Leakage and Diffusion Behavior of Liquid CO2 Vessel in CCES. Energies. 2024; 17(15):3613. https://doi.org/10.3390/en17153613
Chicago/Turabian StyleGao, Lin, Jinlong Wang, Song Wu, Xuan Liu, Binfei Zhu, and Yuguang Fan. 2024. "Study on Leakage and Diffusion Behavior of Liquid CO2 Vessel in CCES" Energies 17, no. 15: 3613. https://doi.org/10.3390/en17153613
APA StyleGao, L., Wang, J., Wu, S., Liu, X., Zhu, B., & Fan, Y. (2024). Study on Leakage and Diffusion Behavior of Liquid CO2 Vessel in CCES. Energies, 17(15), 3613. https://doi.org/10.3390/en17153613





