Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach
Abstract
1. Introduction
2. Background
2.1. Machine Learning Algorithms
2.2. Cointegration Theory
3. Wind Turbine SCADA Data
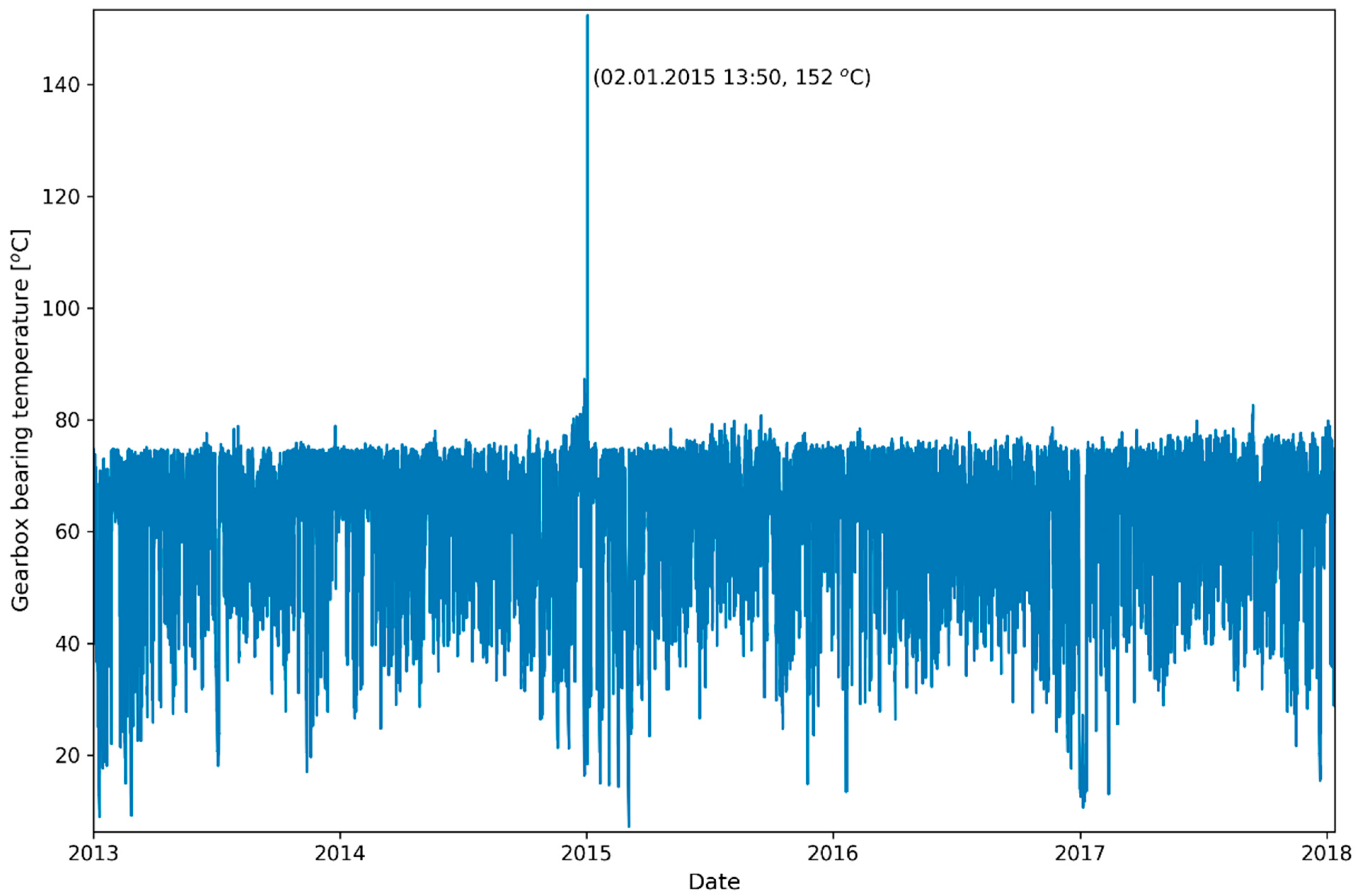
3.1. Data Description
3.2. Data Preprocessing
4. Condition Monitoring and Fault Detection Using ML Methods
4.1. Training ML-Based Normal Behaviour Models of the Gearbox Bearing Temperature
- MLP: number of hidden layers and neurons within a layer, and learning rate;
- RF: number of estimators;
- XGBoost: number of estimators, maximum depth of a tree, and learning rate.
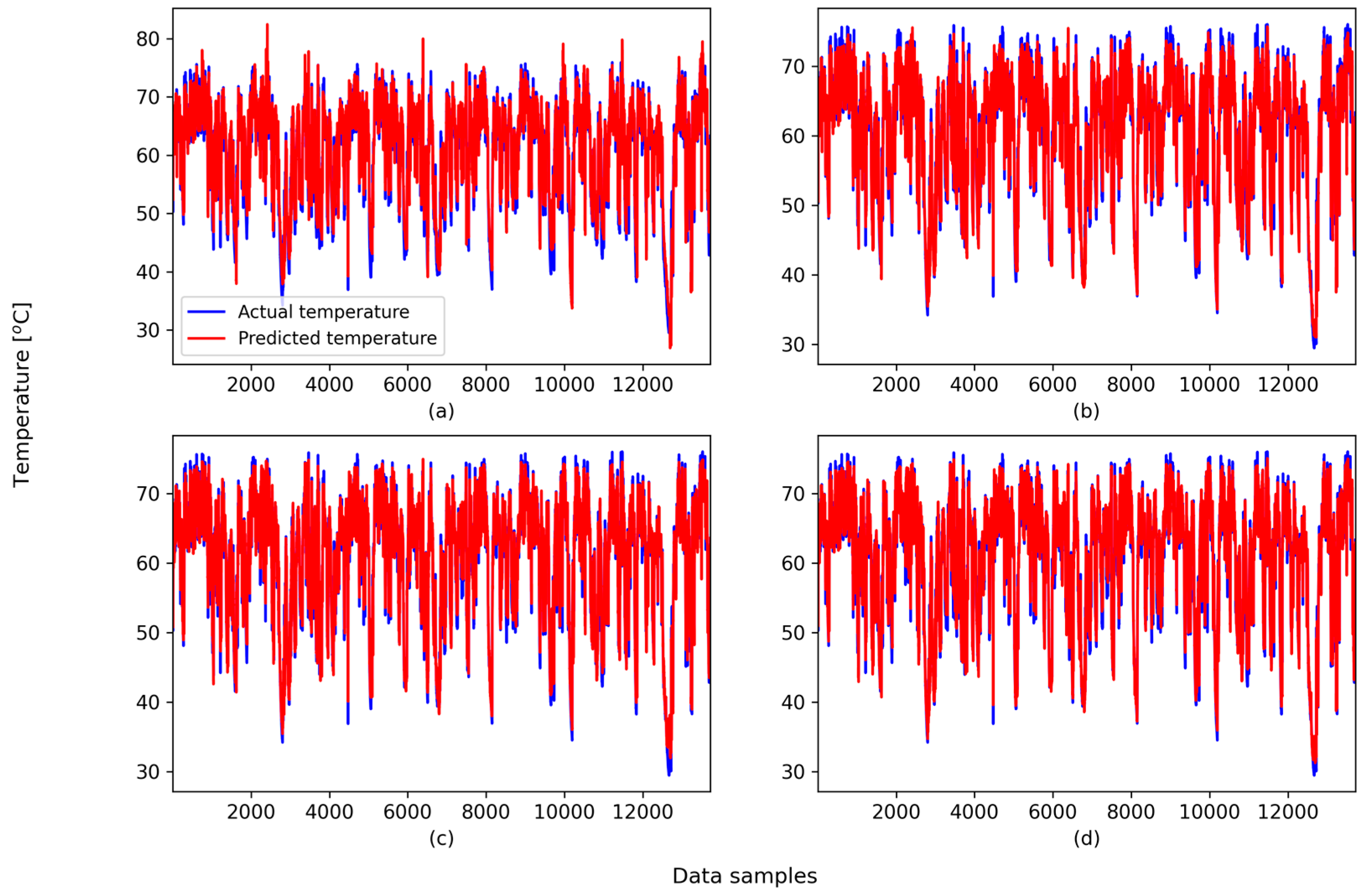
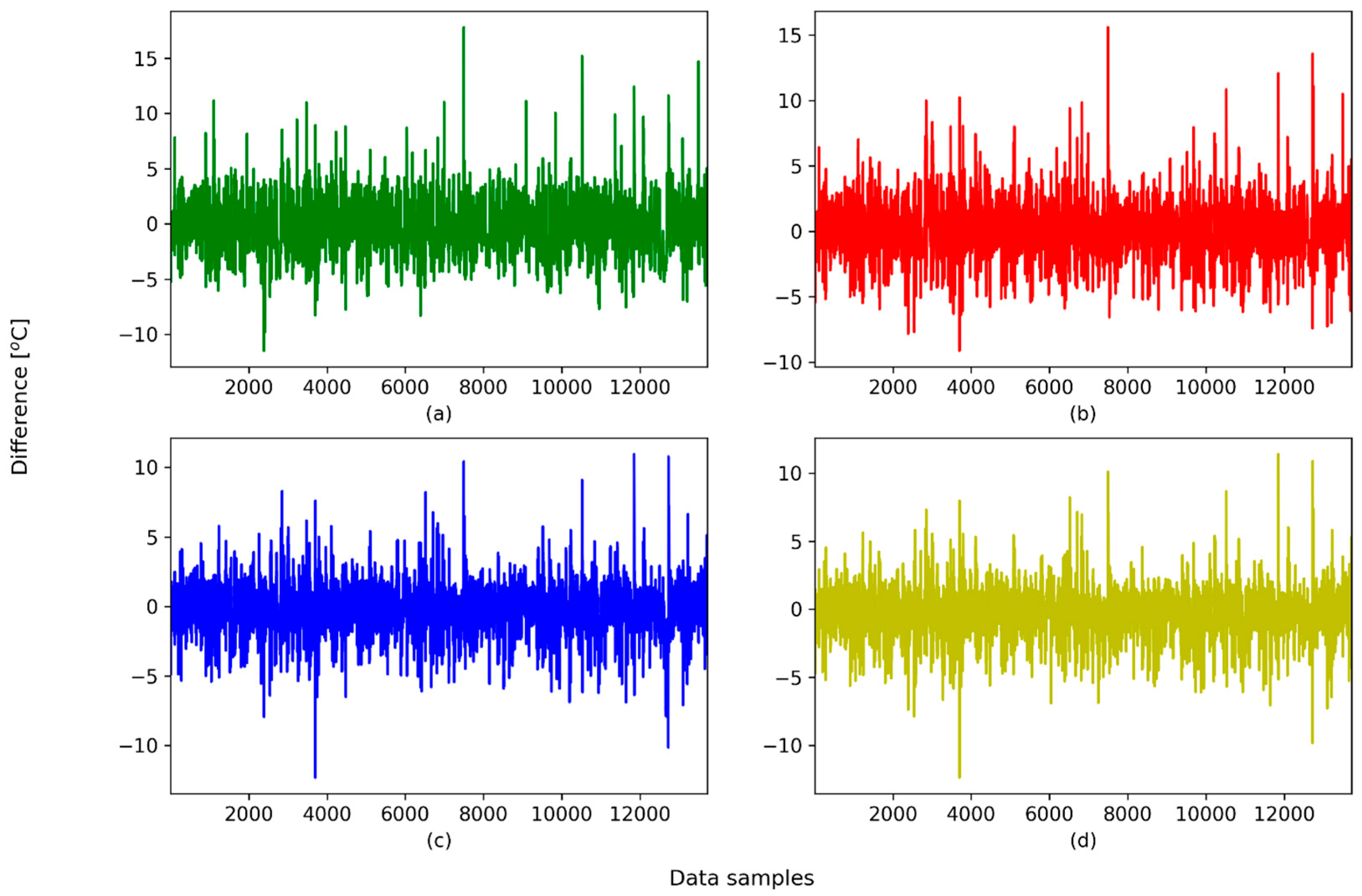
4.2. Testing the XGBoost Model for the Prediction of the Gearbox Failure
4.3. Testing the RF Model for the Prediction of the Gearbox Failure
4.4. Discussion
5. Condition Monitoring and Fault Detection Using Cointegration Analysis
5.1. Training the Cointegration-Based Monitoring Model
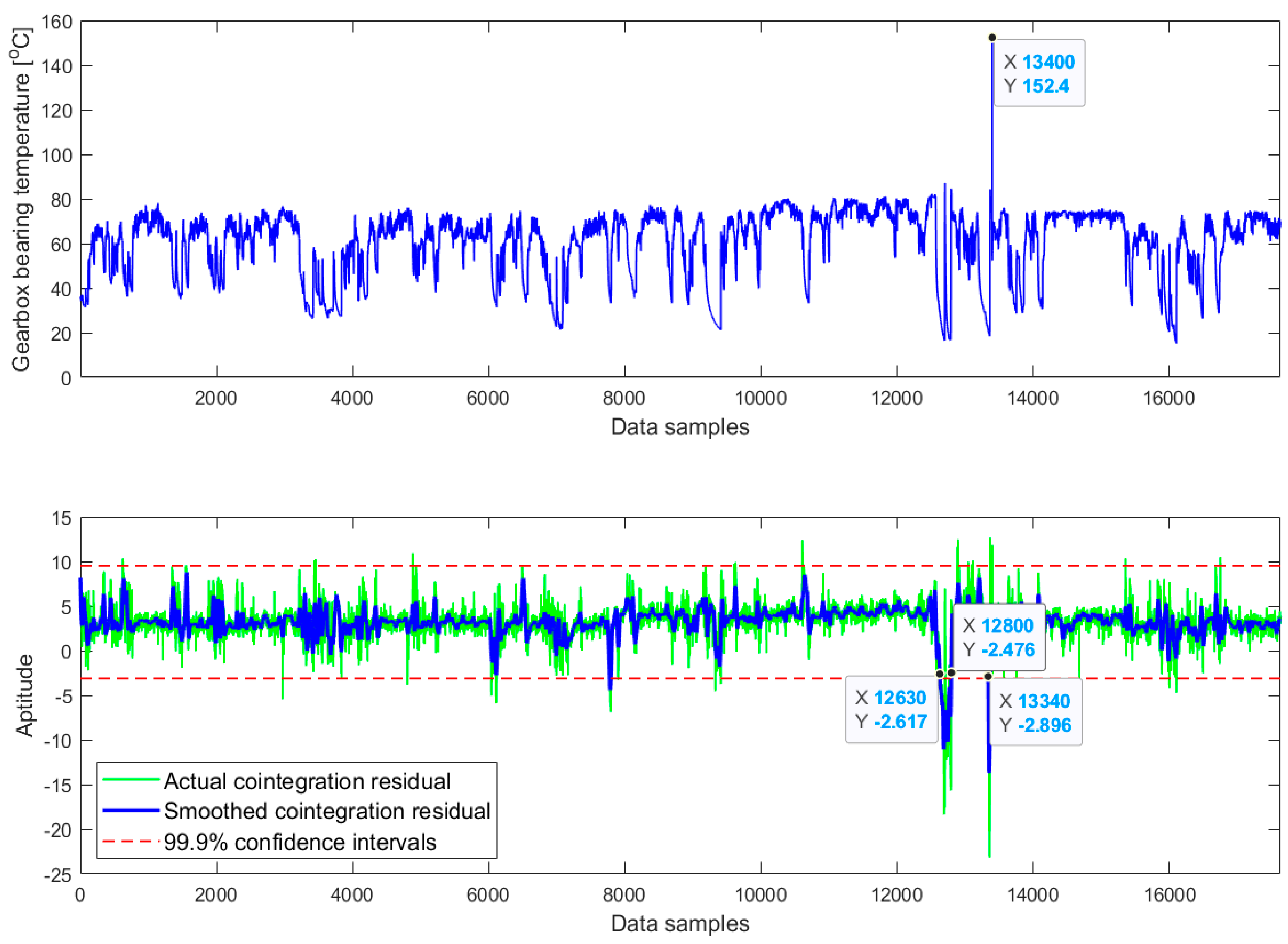
5.2. Testing the Cointegration-Based Monitoring Model for the Prediction of the Gearbox Failure
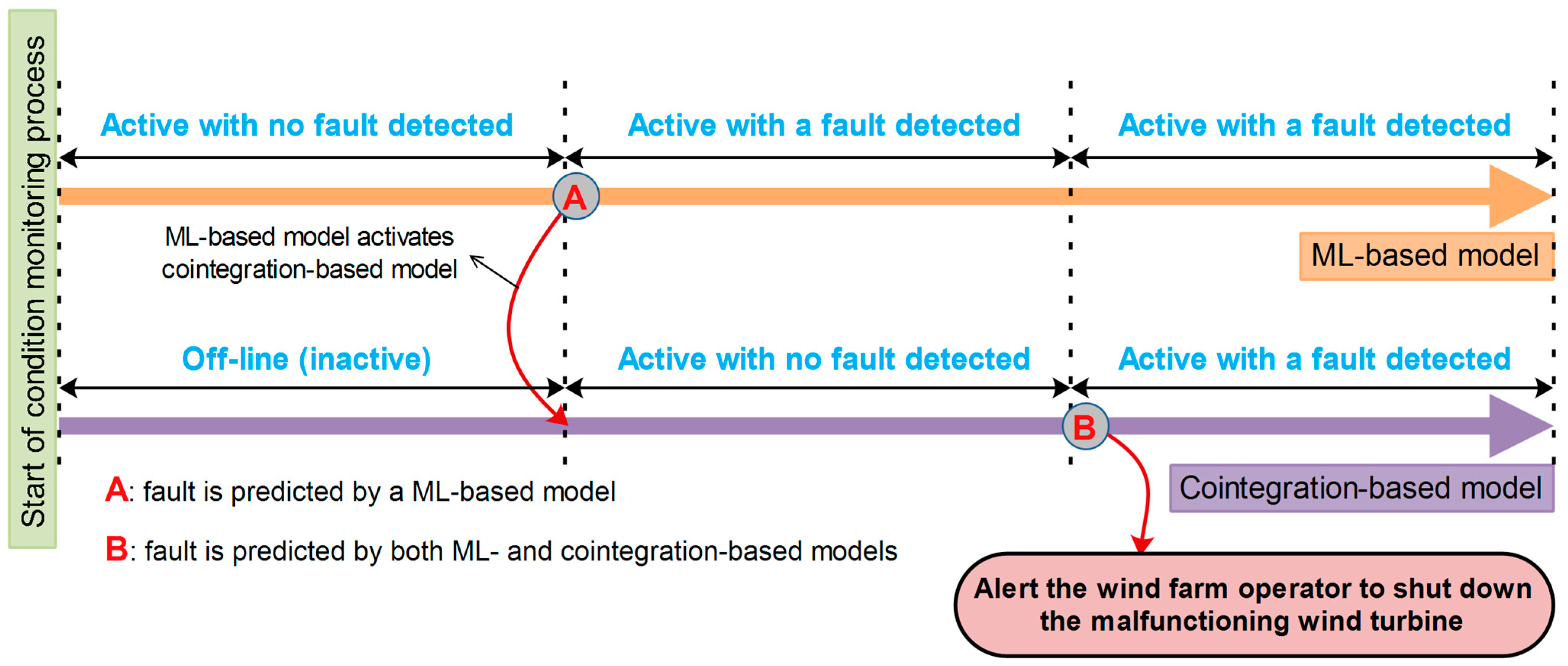
6. A Proposal for the Combination of ML and Cointegration for Wind Turbine Monitoring
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature/Abbreviation
| ANN | Artificial Neural Network |
| AI | Artificial Intelligence |
| CNN | Convolutional Neural Network |
| DNN | Deep Neural Network |
| DT | Decision Tree |
| GBT | Gradient Boosting Tree |
| LR | Linear Regression |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MSE | Mean-Squared Error |
| OLS | Ordinary Least Squares |
| O&M | Operation and Maintenance |
| RF | Random Forest |
| SCADA | Supervisory Control and Data Acquisition |
| SVM | Support Vector Machine |
References
- Global Wind Energy Council. Global Wind Report: Annual Market Update 2024. Available online: https://gwec.net/global-wind-report-2024/ (accessed on 16 April 2024).
- Gao, Z.; Liu, X. An overview on fault diagnosis, prognosis and resilient control for wind turbine systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Khan, P.W.; Byun, Y.C. A review of machine learning techniques for wind turbine’s fault detection, diagnosis, and prognosis. Int. J. Green Energy 2024, 21, 771–786. [Google Scholar] [CrossRef]
- Murgia, A.; Verbeke, R.; Tsiporkova, E.; Terzi, L.; Astolfi, D. Discussion on the suitability of SCADA-based condition monitoring for wind turbine fault diagnosis through temperature data analysis. Energies 2023, 16, 620. [Google Scholar] [CrossRef]
- Morrison, R.; Liu, X.; Lin, Z. Anomaly detection in wind turbine SCADA data for power curve cleaning. Renew. Energy 2022, 184, 473–486. [Google Scholar] [CrossRef]
- Pozo, F.; Vidal, Y.; Salgado, Ó. Wind turbine condition monitoring strategy through multiway PCA and multivariate inference. Energies 2018, 11, 749. [Google Scholar] [CrossRef]
- Chen, P.; Lin, Z.; Xie, Z.; Qu, C. Real-time yaw-misalignment calibration and field-test verification of wind turbine via machine learning methods. Mech. Syst. Signal Process. 2024, 208, 110972. [Google Scholar] [CrossRef]
- Castellani, F.; Astolfi, D.; Sdringola, P.; Proietti, S.; Terzi, L. Analyzing wind turbine directional behavior: SCADA data mining techniques for efficiency and power assessment. Appl. Energy 2017, 185, 1076–1086. [Google Scholar] [CrossRef]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Chandrasekhar, K.; Stevanovic, N.; Cross, E.J.; Dervilis, N.; Worden, K. Damage detection in operational wind turbine blades using a new approach based on machine learning. Renew. Energy 2021, 168, 1249–1264. [Google Scholar] [CrossRef]
- Santolamazza, A.; Dadi, D.; Introna, V. A data-mining approach for wind turbine fault detection based on SCADA data analysis using artificial neural networks. Energies 2021, 14, 1845. [Google Scholar] [CrossRef]
- Bangalore, P.; Letzgus, S.; Karlsson, D.; Patriksson, M. An artificial neural network-based condition monitoring method for wind turbines, with application to the monitoring of the gearbox. Wind Energy 2017, 20, 1421–1438. [Google Scholar] [CrossRef]
- Cui, Y.; Bangalore, P.; Tjernberg, L.B. A fault detection framework using recurrent neural networks for condition monitoring of wind turbines. Wind Energy 2021, 24, 1249–1262. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, P.; Yang, X.; Hu, A.; Su, H. Fault detection of wind turbine based on SCADA data analysis using CNN and LSTM with attention mechanism. Measurement 2021, 175, 109094. [Google Scholar] [CrossRef]
- Ulmer, M.; Jarlskog, E.; Pizza, G.; Manninen, J.; Goren Huber, L. Early fault detection based on wind turbine SCADA data using convolutional neural networks. PHM Soc. Eur. Conf. 2020, 5, 9. [Google Scholar] [CrossRef]
- Teng, W.; Cheng, H.; Ding, X.; Liu, Y.; Ma, Z.; Mu, H. DNN-based approach for fault detection in a direct drive wind turbine. IET Renew. Power Gener. 2018, 12, 1164–1171. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Hu, W.; Yan, X. Anomaly detection and fault analysis of wind turbine components based on deep learning network. Renew. Energy 2018, 127, 825–834. [Google Scholar] [CrossRef]
- Sun, S.; Wang, T.; Yang, H.; Chu, F. Condition monitoring of wind turbine blades based on self-supervised health representation learning: A conducive technique to effective and reliable utilization of wind energy. Appl. Energy 2022, 313, 118882. [Google Scholar] [CrossRef]
- Ren, H.; Liu, W.; Shan, M.; Wang, X. A new wind turbine health condition monitoring method based on VMD-MPE and feature-based transfer learning. Measurement 2019, 148, 106906. [Google Scholar] [CrossRef]
- Zhan, J.; Wu, C.; Ma, X.; Yang, C.; Miao, Q.; Wang, S. Abnormal vibration detection of wind turbine based on temporal convolution network and multivariate coefficient of variation. Mech. Syst. Signal Process. 2022, 174, 109082. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, B.; Deng, L.; Liu, X. A hybrid attention improved ResNet based fault diagnosis method of wind turbines gearbox. Measurement 2021, 179, 109491. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Wang, X.; Shaheer, M.A. A novel hierarchical hyper-parameter search algorithm based on greedy strategy for wind turbine fault diagnosis. Expert Syst. Appl. 2022, 202, 117473. [Google Scholar] [CrossRef]
- Perez-Sanjines, F.; Peeters, C.; Verstraeten, T.; Antoni, J.; Nowé, A.; Helsen, J. Fleet-based early fault detection of wind turbine gearboxes using physics-informed deep learning based on cyclic spectral coherence. Mech. Syst. Signal Process. 2023, 185, 109760. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, Y.; Wang, Q. Fault detection in wind turbine generators using a meta-learning-based convolutional neural network. Mech. Syst. Signal Process. 2023, 200, 110528. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Wu, X.; Liu, G. Failure mode classification of IGBT modules under power cycling tests based on data-driven machine learning framework. IEEE Trans. Power Electron. 2023, 38, 16130–16141. [Google Scholar] [CrossRef]
- Ma, G.; Xu, S.; Jiang, B.; Cheng, C.; Yang, X.; Shen, Y.; Yang, T.; Huang, Y.; Ding, H.; Yuan, Y. Real-time personalized health status prediction of lithium-ion batteries using deep transfer learning. Energy Environ. Sci. 2022, 15, 4083–4094. [Google Scholar] [CrossRef]
- Attia, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.H.; Chen, M.H.; Cheong, B.; Perkins, N.; Yang, Z.; et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 2020, 578, 397–402. [Google Scholar] [CrossRef]
- Yampikulsakul, N.; Byon, E.; Huang, S.; Sheng, S.; You, M. Condition monitoring of wind power system with nonparametric regression analysis. IEEE Trans. Energy Convers. 2014, 29, 288–299. [Google Scholar]
- Letzgus, S. Change-point detection in wind turbine SCADA data for robust condition monitoring with normal behaviour models. Wind Energy Sci. 2020, 5, 1375–1397. [Google Scholar] [CrossRef]
- Dao, P.B. Condition monitoring and fault diagnosis of wind turbines based on structural break detection in SCADA data. Renew. Energy 2022, 185, 641–654. [Google Scholar] [CrossRef]
- Bilendo, F.; Lu, N.; Badihi, H.; Meyer, A.; Cali, Ü.; Cambron, P. Multitarget normal behavior model based on heterogeneous stacked regressions and change-point detection for wind turbine condition monitoring. IEEE Trans. Ind. Inform. 2024, 20, 5171–5181. [Google Scholar] [CrossRef]
- Dao, P.B. A CUSUM-based approach for condition monitoring and fault diagnosis of wind turbines. Energies 2021, 14, 3236. [Google Scholar] [CrossRef]
- Latiffianti, E.; Sheng, S.; Ding, Y. Wind turbine gearbox failure detection through cumulative sum of multivariate time series data. Front. Energy Res. 2022, 10, 904622. [Google Scholar] [CrossRef]
- Dao, P.B. On Wilcoxon rank sum test for condition monitoring and fault detection of wind turbines. Appl. Energy 2022, 318, 119209. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Cointegration and error-correction: Representation, estimation and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Johansen, S. Statistical analysis of cointegration vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Cross, E.J.; Worden, K.; Chen, Q. Cointegration: A novel approach for the removal of environmental trends in structural health monitoring data. Proc. R. Soc. A 2011, 467, 2712–2732. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Cointegration approach for temperature effect compensation in Lamb wave based damage detection. Smart Mater. Struct. 2013, 22, 095002. [Google Scholar] [CrossRef]
- Tabrizi, A.A.; Al-Bugharbee, H.; Trendafilova, I.; Garibaldi, L. A cointegration-based monitoring method for rolling bearings working in time-varying operational conditions. Meccanica 2017, 52, 1201–1217. [Google Scholar] [CrossRef]
- Salvetti, M.; Sbarufatti, C.; Cross, E.J.; Corbetta, M.; Worden, K.; Giglio, M. On the performance of a cointegration-based approach for novelty detection in realistic fatigue crack growth scenarios. Mech. Syst. Signal Process. 2019, 123, 84–101. [Google Scholar] [CrossRef]
- He, H.; Wang, W.; Zhang, X. Frequency modification of continuous beam bridge based on co-integration analysis considering the effect of temperature and humidity. Struct. Health Monit. 2019, 18, 376–389. [Google Scholar] [CrossRef]
- Tomé, E.S.; Pimentel, M.; Figueiras, J. Damage detection under environmental and operational effects using cointegration analysis—Application to experimental data from a cable-stayed bridge. Mech. Syst. Signal Process. 2020, 135, 106386. [Google Scholar] [CrossRef]
- Turrisi, S.; Cigada, A.; Zappa, E. A cointegration-based approach for automatic anomalies detection in large-scale structures. Mech. Syst. Signal Process. 2022, 166, 108483. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J. Cointegration and how it works for structural health monitoring. Measurement 2023, 209, 112503. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J.; Barszcz, T.; Uhl, T. Condition monitoring and fault detection in wind turbines based on cointegration analysis of SCADA data. Renew. Energy 2018, 116, 107–122. [Google Scholar] [CrossRef]
- Dao, P.B.; Staszewski, W.J.; Uhl, T. Operational condition monitoring of wind turbines using cointegration method. In Advances in Condition Monitoring of Machinery in Non-Stationary Operations, Applied Condition Monitoring; Timofiejczuk, A., Chaari, F., Zimroz, R., Bartelmus, W., Haddar, M., Eds.; Chapter 21; Springer: Cham, Switzerland, 2018; Volume 9, pp. 223–233. [Google Scholar]
- Dao, P.B. Condition monitoring of wind turbines based on cointegration analysis of gearbox and generator temperature data. Diagnostyka 2018, 19, 63–71. [Google Scholar] [CrossRef]
- Sun, X.; Xue, D.; Li, R.; Li, X.; Cui, L.; Zhang, X.; Wu, W. Research on condition monitoring of key components in wind turbine based on cointegration analysis. IOP Conf. Ser. Mater. Sci. Eng. 2019, 575, 012015. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, C.; Duan, H.; Ma, Y.; Li, J.; Cui, L. Realization of condition monitoring of gear box of wind turbine based on cointegration analysis. In Advances in Asset Management and Condition Monitoring; Smart Innovation, Systems and Technologies; Ball, A., Gelman, L., Rao, B., Eds.; Springer: Cham, Switzerland, 2020; Volume 166, pp. 281–291. [Google Scholar]
- Zhang, C.; Zhao, G.; Wu, Y. Wind turbine condition monitoring based on SCADA data co-integration analysis. In Mechanisms and Machine Science, Proceedings of the IncoME-VI and TEPEN 2021, Tianjin, China, 20–23 October 2021; Zhang, H., Feng, G., Wang, H., Gu, F., Sinha, J.K., Eds.; Springer: Cham, Switzerland, 2023; Volume 117, pp. 97–103. [Google Scholar]
- Qadri, B.A.; Ulriksen, M.D.; Damkilde, L.; Tcherniak, D. Cointegration for detecting structural blade damage in an operating wind turbine: An experimental study. In Dynamics of Civil Structures, Proceedings of the 37th IMAC, A Conference and Exposition on Structural Dynamics 2019, Orlando, FL, USA, 28–31 January 2019; Pakzad, S., Ed.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2020; Volume 2, pp. 173–180. [Google Scholar]
- Xu, M.; Li, J.; Wang, S.; Yang, N.; Hao, H. Damage detection of wind turbine blades by Bayesian multivariate cointegration. Ocean Eng. 2022, 258, 111603. [Google Scholar] [CrossRef]
- Dao, P.B. On cointegration analysis for condition monitoring and fault detection of wind turbines using SCADA data. Energies 2023, 16, 2352. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Y.; Wang, P. A hierarchical modeling strategy for condition monitoring and fault diagnosis of wind turbine using SCADA data. Measurement 2024, 227, 114325. [Google Scholar] [CrossRef]
- Kuai, H.; Civera, M.; Coletta, G.; Chiaia, B.; Surace, C. Cointegration strategy for damage assessment of offshore platforms subject to wind and wave forces. Ocean Eng. 2024, 304, 117692. [Google Scholar] [CrossRef]
- Zolna, K.; Dao, P.B.; Staszewski, W.J.; Barszcz, T. Nonlinear cointegration approach for condition monitoring of wind turbines. Math. Probl. Eng. 2015, 2015, 978156. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Artigao, E.; Martín-Martínez, S.; Honrubia-Escribano, A.; Gómez-Lázaro, E. Wind turbine reliability: A comprehensive review towards effective condition monitoring development. Appl. Energy 2018, 228, 1569–1583. [Google Scholar] [CrossRef]
- Jin, X.; Xu, Z.; Qiao, W. Condition monitoring of wind turbine generators using SCADA data analysis. IEEE Trans. Sustain. Energy 2021, 12, 202–210. [Google Scholar] [CrossRef]
- Meyer, A. Multi-target normal behaviour models for wind farm condition monitoring. Appl. Energy 2021, 300, 117342. [Google Scholar] [CrossRef]
- Castellani, F.; Natili, F.; Astolfi, D.; Vidal, Y. Wind turbine gearbox condition monitoring through the sequential analysis of industrial SCADA and vibration data. Energy Rep. 2024, 12, 750–761. [Google Scholar] [CrossRef]
- Dao, P.B.; Barszcz, T.; Staszewski, W.J. Anomaly detection of wind turbines based on stationarity analysis of SCADA data. Renew. Energy 2024, 232, 121076. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2017; 572p. [Google Scholar]
- Zivot, E.; Wang, J. Modeling Financial Time Series with S-PLUS, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- LeSage, J.P. Econometrics Toolbox. Available online: https://www.spatial-econometrics.com (accessed on 27 August 2024).
- ENGIE OpenData. SCADA Datasets of La Houte Bourne Wind Farm. Available online: https://opendata-renewables.engie.com/explore/index (accessed on 18 September 2023).
- Scikit-Learn. Machine Learning in Python. Available online: https://scikit-learn.org/stable/ (accessed on 16 May 2024).
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Luo, J.; Ying, K.; Bai, J. Savitzky–Golay smoothing and differentiation filter for even number data. Signal Process. 2005, 85, 1429–1434. [Google Scholar] [CrossRef]
- Bilendo, F.; Meyer, A.; Badihi, H.; Lu, N.; Cambron, P.; Jiang, B. Applications and modeling techniques of wind turbine power curve for wind farms—A review. Energies 2023, 16, 180. [Google Scholar] [CrossRef]

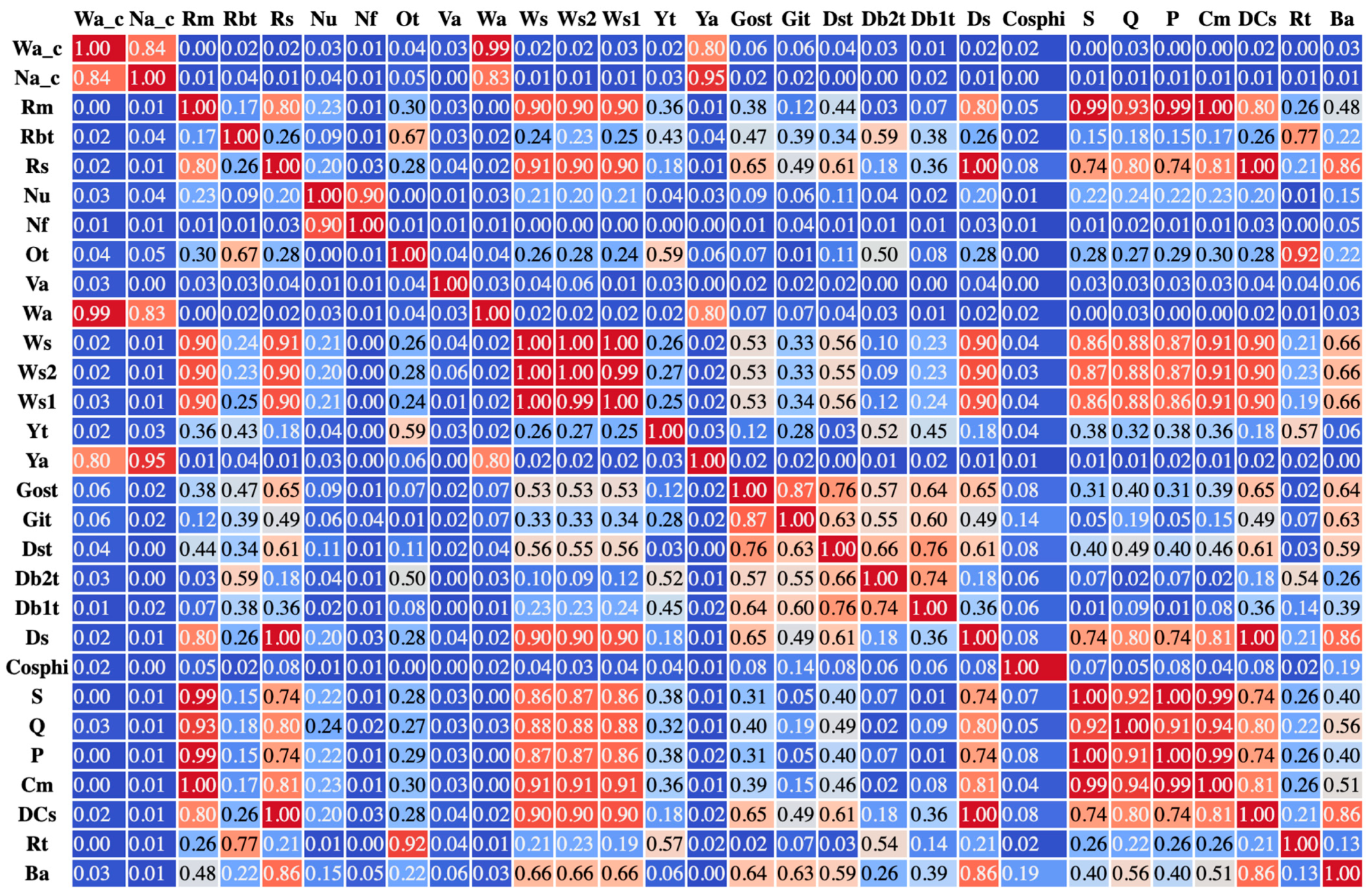




| No. | Parameters | Abbreviation | Units | Pearson Corr. Coefficient (min–max) |
|---|---|---|---|---|
| 1 | Absolute wind direction corrected | Wa_c | deg | 0.00–0.99 |
| 2 | Torque | Rm | Nm | 0.00–1.00 |
| 3 | Rotor bearing temperature | Rbt | °C | 0.00–0.77 |
| 4 | Grid voltage | Nu | V | 0.00–0.90 |
| 5 | Outdoor temperature | Ot | °C | 0.00–0.92 |
| 6 | Vane position | Va | deg | 0.00–0.06 |
| 7 | Nacelle temperature | Yt | °C | 0.00–0.59 |
| 8 | Gearbox oil sump temperature | Gost | °C | 0.01–0.87 |
| 9 | Generator bearing temperature 1 | Db1t | °C | 0.00–0.76 |
| 10 | Generator bearing temperature 2 | Db2t | °C | 0.00–0.74 |
| 11 | Power factor | Cosphi | [-] | 0.00–0.19 |
| 12 | Pitch angle | Ba | deg | 0.00–0.86 |
| Method | Training Time | R2 Score | MSE | MAE | Max. Error |
|---|---|---|---|---|---|
| LR | 0.058 [s] | 0.953 | 4.402 | 1.478 | 22.194 |
| MLP | 7.431 [s] | 0.973 | 2.566 | 1.105 | 19.998 |
| RF | 96.585 [s] | 0.998 | 0.206 | 0.302 | 6.923 |
| XGBoost | 0.302 [s] | 0.986 | 1.333 | 0.819 | 10.690 |
| Method | Inference Time | R2 Score | MSE | MAE | Max. Error |
|---|---|---|---|---|---|
| LR | 0.001 [s] | 0.954 | 3.866 | 1.417 | 17.771 |
| MLP | 0.010 [s] | 0.971 | 2.447 | 1.094 | 15.578 |
| RF | 0.303 [s] | 0.975 | 2.134 | 1.030 | 12.358 |
| XGBoost | 0.007 [s] | 0.977 | 1.978 | 0.991 | 12.376 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knes, P.; Dao, P.B. Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach. Energies 2024, 17, 5055. https://doi.org/10.3390/en17205055
Knes P, Dao PB. Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach. Energies. 2024; 17(20):5055. https://doi.org/10.3390/en17205055
Chicago/Turabian StyleKnes, Paweł, and Phong B. Dao. 2024. "Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach" Energies 17, no. 20: 5055. https://doi.org/10.3390/en17205055
APA StyleKnes, P., & Dao, P. B. (2024). Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach. Energies, 17(20), 5055. https://doi.org/10.3390/en17205055







