Underground Hydrogen Storage Safety: Experimental Study of Hydrogen Diffusion through Caprocks
Abstract
1. Introduction
| Formation | Depth | Porosity | Hydr. Conduct./Permeability | Dry/Wet | Pressure and Temperature | Method | Gas Used | Values | |
|---|---|---|---|---|---|---|---|---|---|
| [37] | Boom clay | 200 ÷ 300 m | 36 ÷ 43% | - | Saturated | T: 25 °C p: up to 5 bar | In- and through-diffusion tests | H2 | 4.2 × 10−12 m2/s to 1.6 × 10−10 m2/s |
| [38] | Callovo-Oxfordian clay | 430 ÷ 550 m | 23% | K = 10 × 10−22 m2 | Saturated | T: 30 to 80 °C p: 10 ÷ 50 bar | Through-diffusion method Helium leak detection using mass spectrometry | He | 2 × 10−12 m2/s |
| [24] | Callovo-Oxfordian clay | ~500 m | 13 ÷ 15% | K ~ 10 × 10−22 m2 | Dry | T: Ambient p: 1.5 ÷ 4 bar | Water vapor sorption isotherm [39] | Water vapor | 1 × 10−8 m2/s |
| [22] (data reported on [23,40]) | Boom clay | 200 ÷ 300 m | 31 ÷ 45% | Saturated | T: 25 °C p: ambient | In-diffusion and through-diffusion experiments [38] | H2 | 3.0 × 10−11 m2/s | |
| [21] | Boom clay | 200 ÷ 300 m | 31 ÷ 45% | Saturated | T: 25 °C | In diffusion and through-diffusion experiments [38] | H2 | 5 × 10−12 m2/s to 4 × 10−10 m2/s | |
| [36] | Callovo-Oxfordian clay | 430 ÷ 550 m | - | - | Dry | T: 90 and 120 °C p: 0.45 bar | Through diffusion | H2 | 1.4 × 10−7 m2/s |
| [40] | Callovo-Oxfordian clay | 430 ÷ 550 m | - | - | Wet | - | - | H2 | 1.1 × 10−11 m2/s |
| [41] | Boom clay | 200 ÷ 300 m | 37% | 3.3 × 10−12 m/s | Saturated | T: 21 ± 2 °C p ~10 bar | Through diffusion | Ne, Ar | Ne: 5.1 × 10−10 m2/s Ar: 2 ± 0.1 10−10 m2/s |
| Opalinus clay | ~300 m | 12% | 1.8 × 10−13 m/s | Saturated | T: 21 ± 2 °C p ~10 bar | Through diffusion | He | He: 5.4 × 10−10 m2/s | |
| [23] | Opalinus clay | ~300 m | 17 ÷ 19% | 3 × 10−12 m/s | Water content: 7% | T: 15 ÷ 16 °C p: 1.5 bar | Gas circulation module and a water sampling module [15] | Mixture of H2 (5%) He (5%), Ne (5%), and Ar (85%) | H2: 8.12 × 10−11 m2/s Ne: 6.39 × 10−11 m2/s He: 11.53 × 10−11 m2/s |
| [42] | Synthetic Na-montmorillonites | - | 7 ÷ 12% | Dry | T: 26.85 °C; p: up to 60 bar | Thermogravimetric (TGA) | H2 | 9.9 × 10−8 m2/s | |
| [23] | Boom clay | 200 ÷ 300 m | - | 1.5 ÷ 8 × 10−12 m/s | Saturated | T: ambient (21 °C) p: 10 bar | Double through-diffusion test [43] | Mixture of H2 (5%) and Ar (95%) | 2.64 × 10−10 m2/s |
| [35] | Marcellus shale | 2395.7 m | - | - | Dry | T: 60 °C p: up to 100 bar | Thermogravimetric (TGA) | CH4, C2H6 | 0.63 mg/g (CH4 at 5 bar) 2.99 mg/g (CH4 at 103.2 bar) |
| [26] | Caprock samples (late Neogene) | - | 28 ÷ 35% | Saturated | T: 20° ÷ 22 °C p: 40 bar | Binary diffusion setup [44] | H2 | 8 × 10−11 m2/s (fresh) 1.1 × 10−8 m2/s (long-stored) 1.8 × 10−10 m2/s (re-saturated) |
2. Materials and Methods
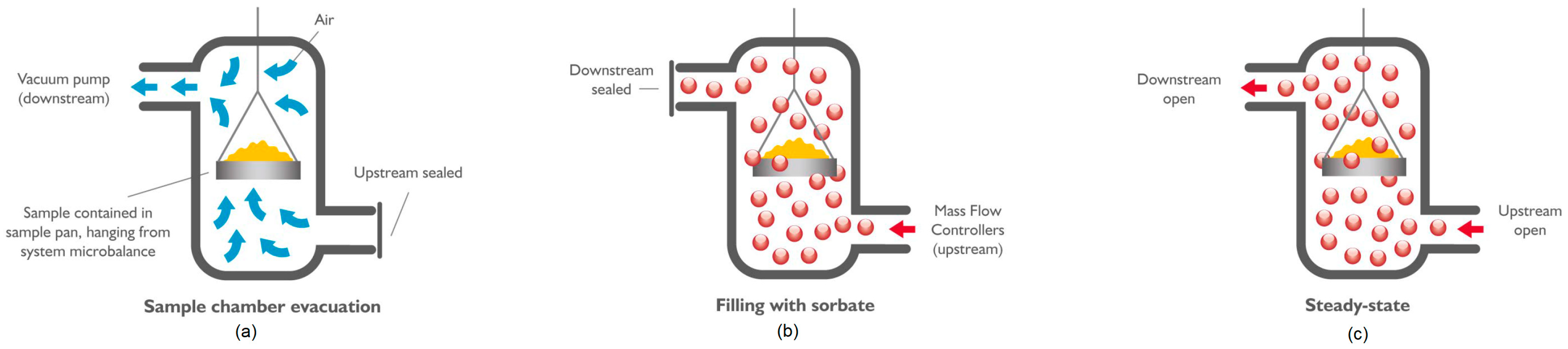
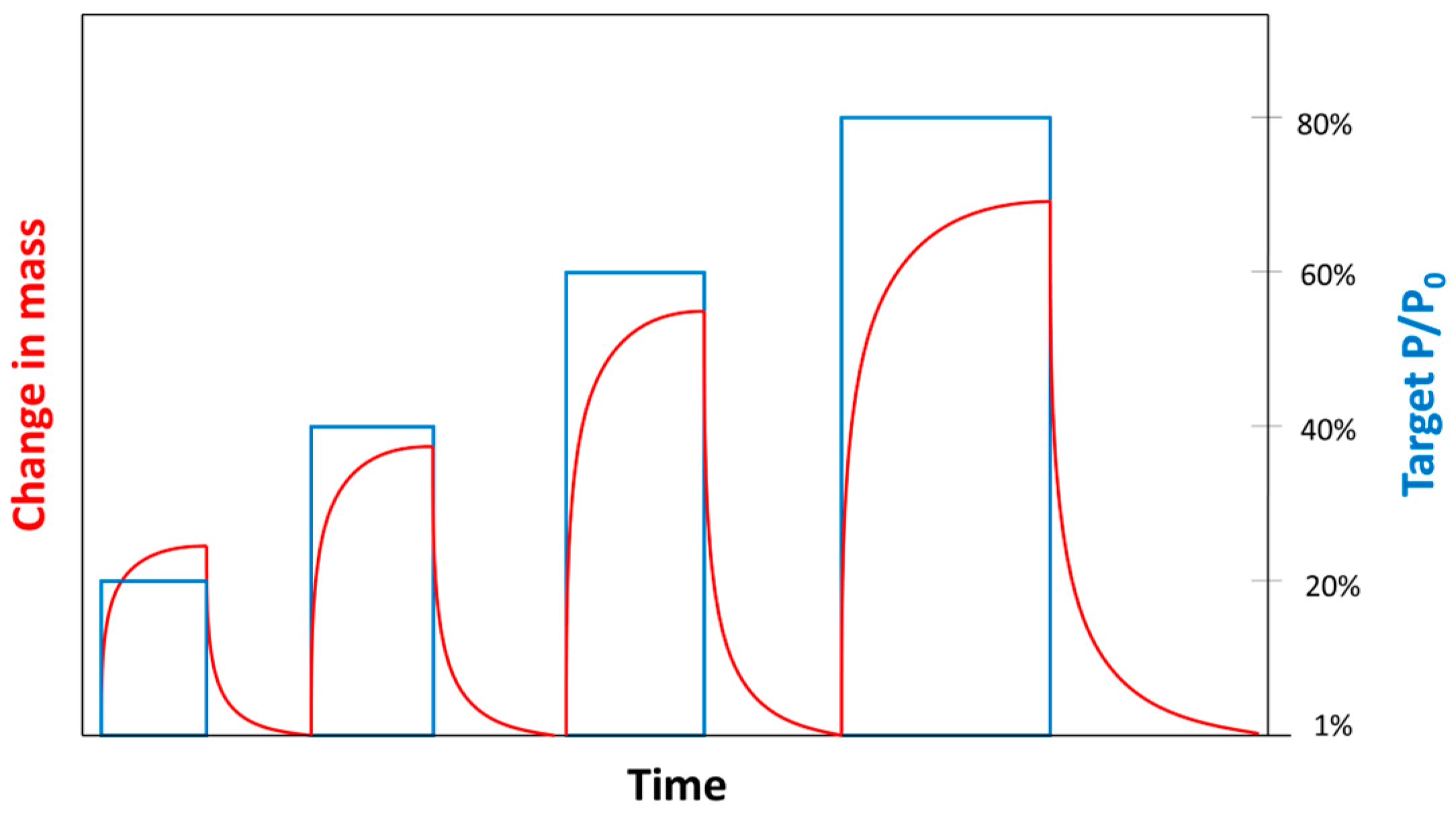
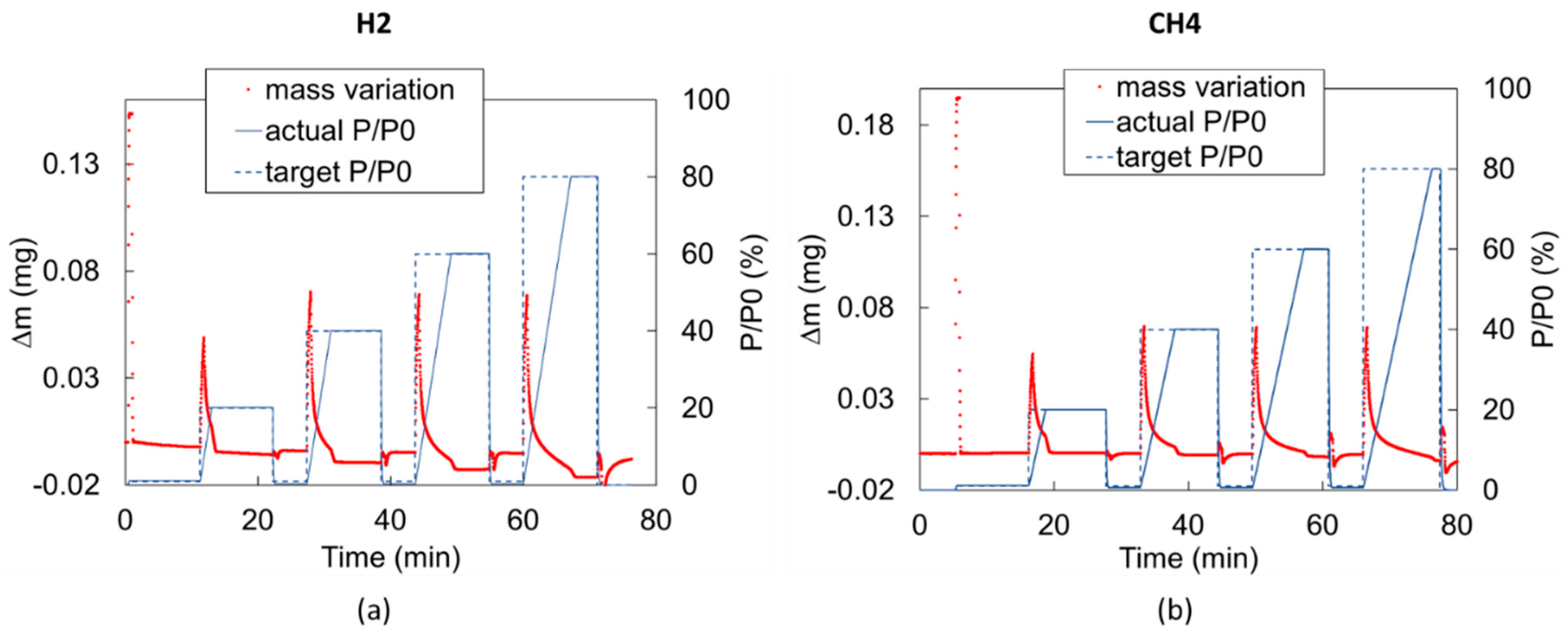
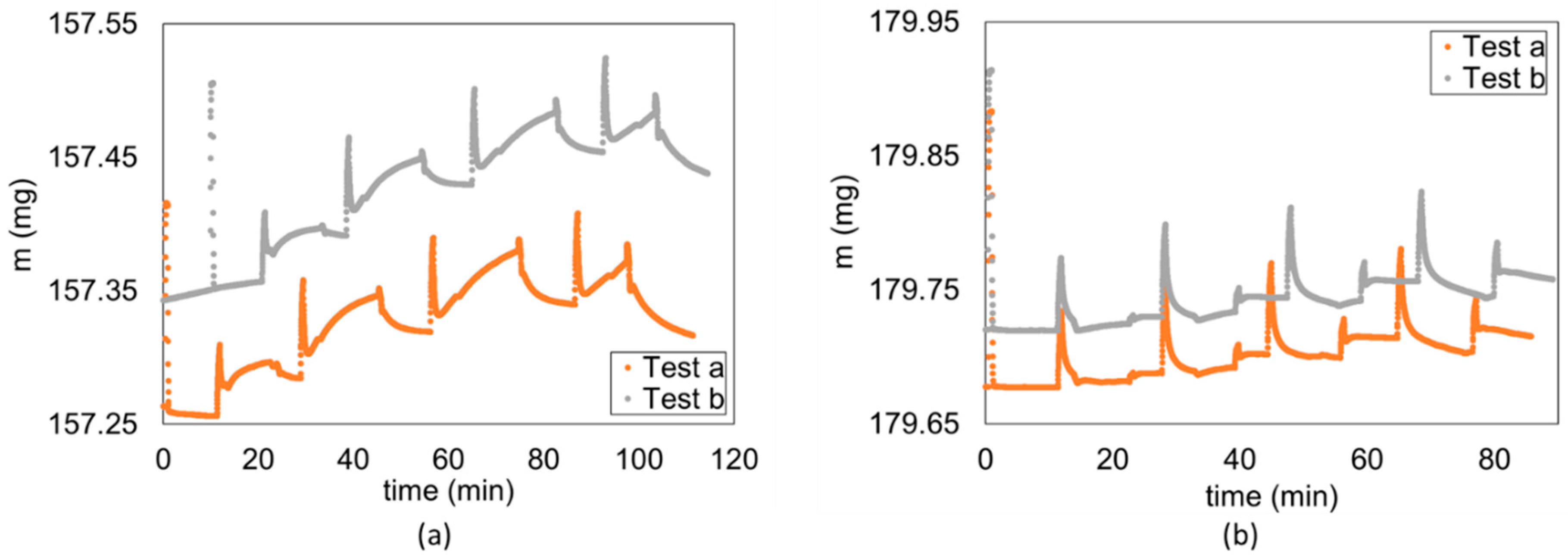
2.1. Experiment Description
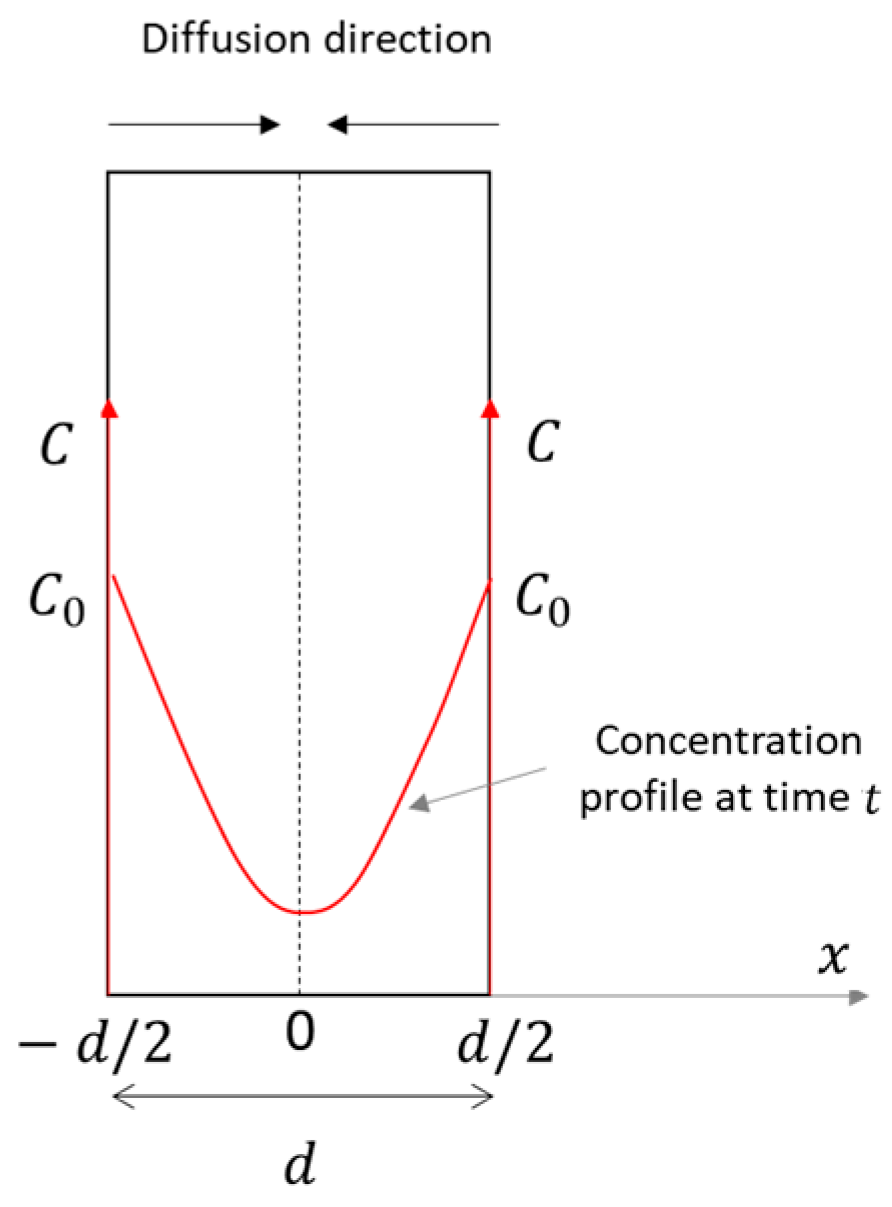
2.2. Theoretical Background
- a thin plane geometry, with a constant thickness ();
- double-side exposure;
- diffusion only across the sample, i.e., in a single direction () (Figure 4);
- a constant and uniform source concentration (), equal on both sides;
- constant diffusion;
- isothermal conditions.
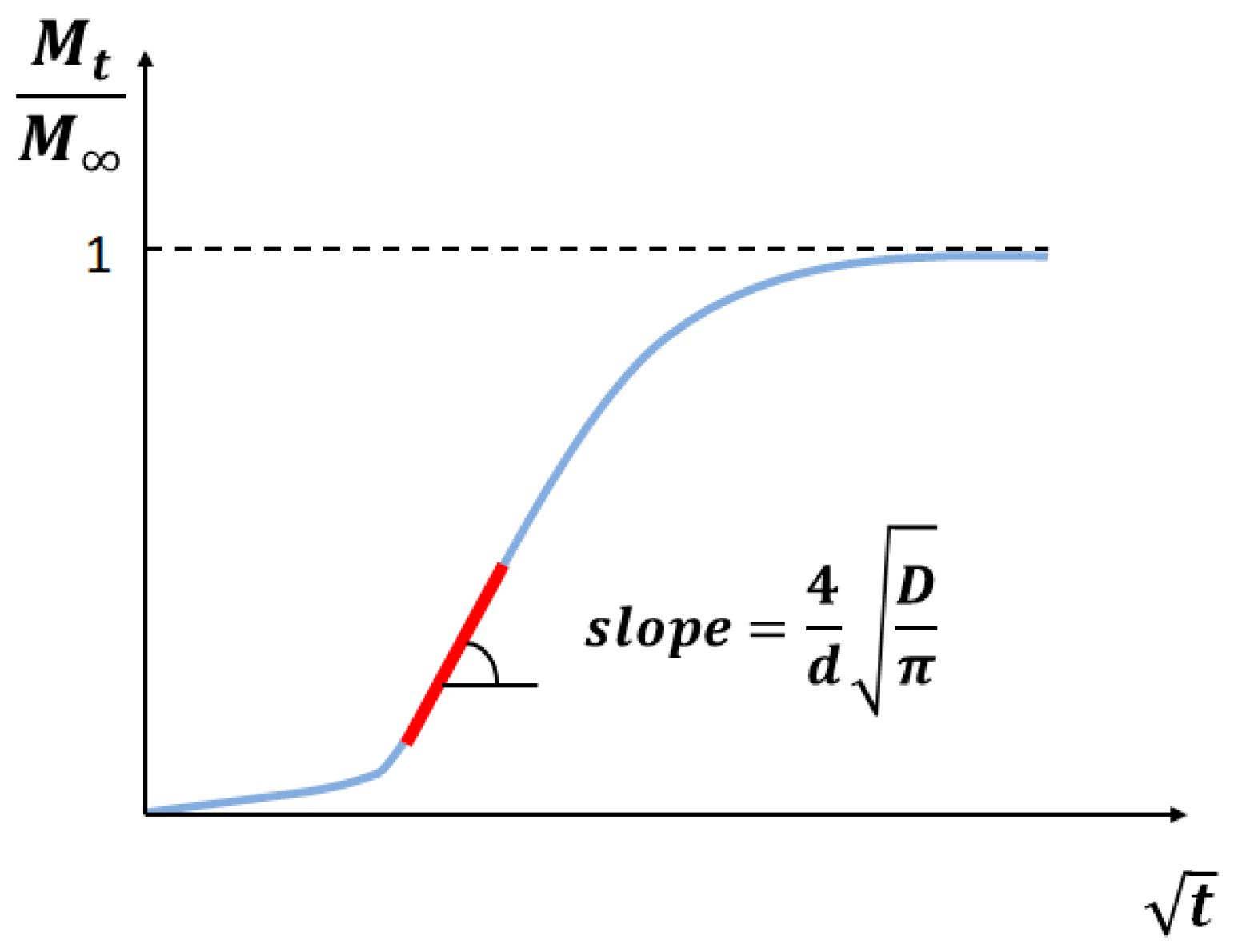
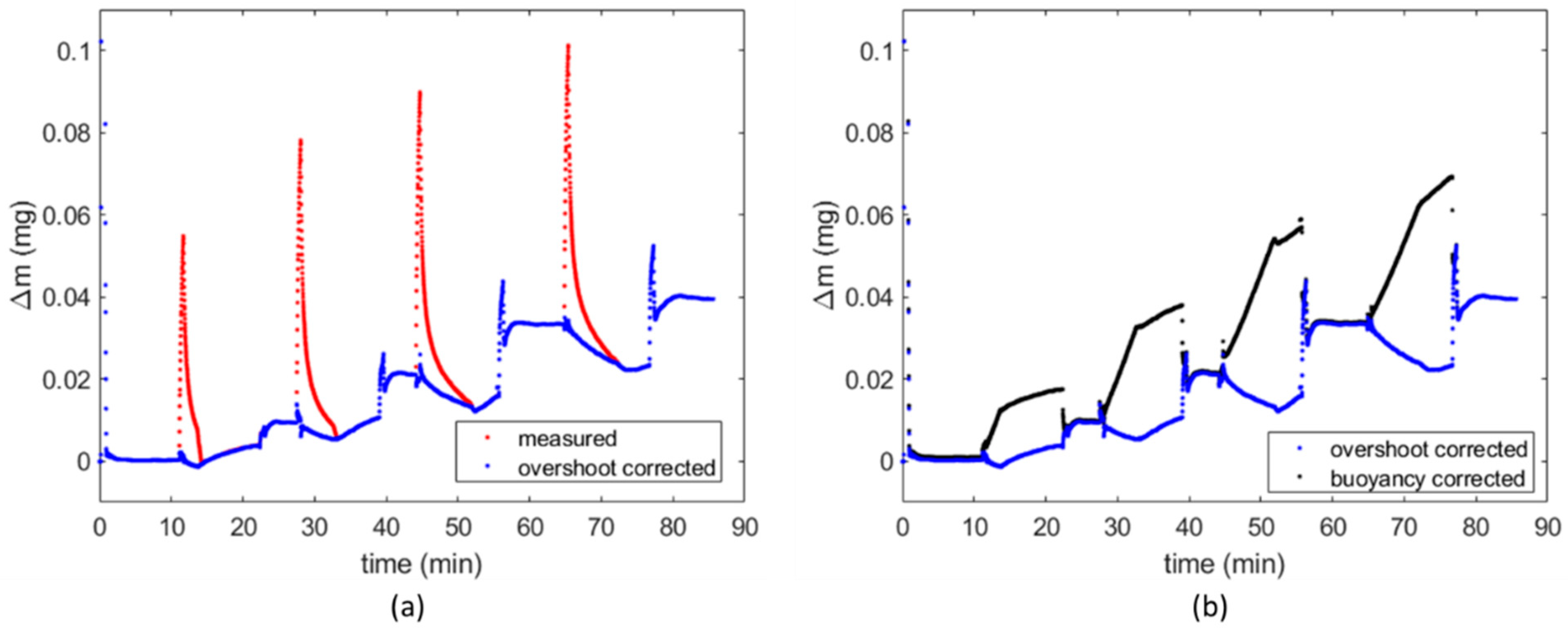
2.3. Data Processing
2.4. Caprock Samples and Mineralogic Analysis
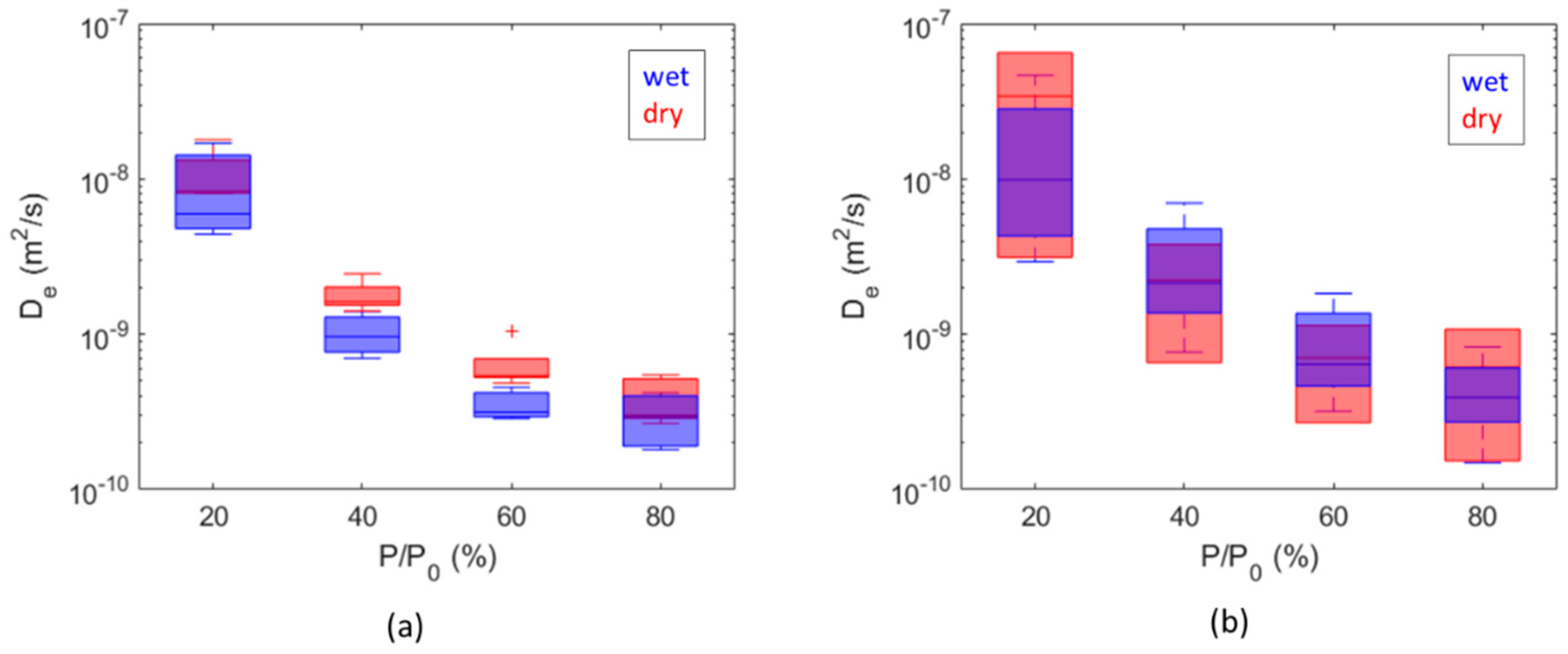
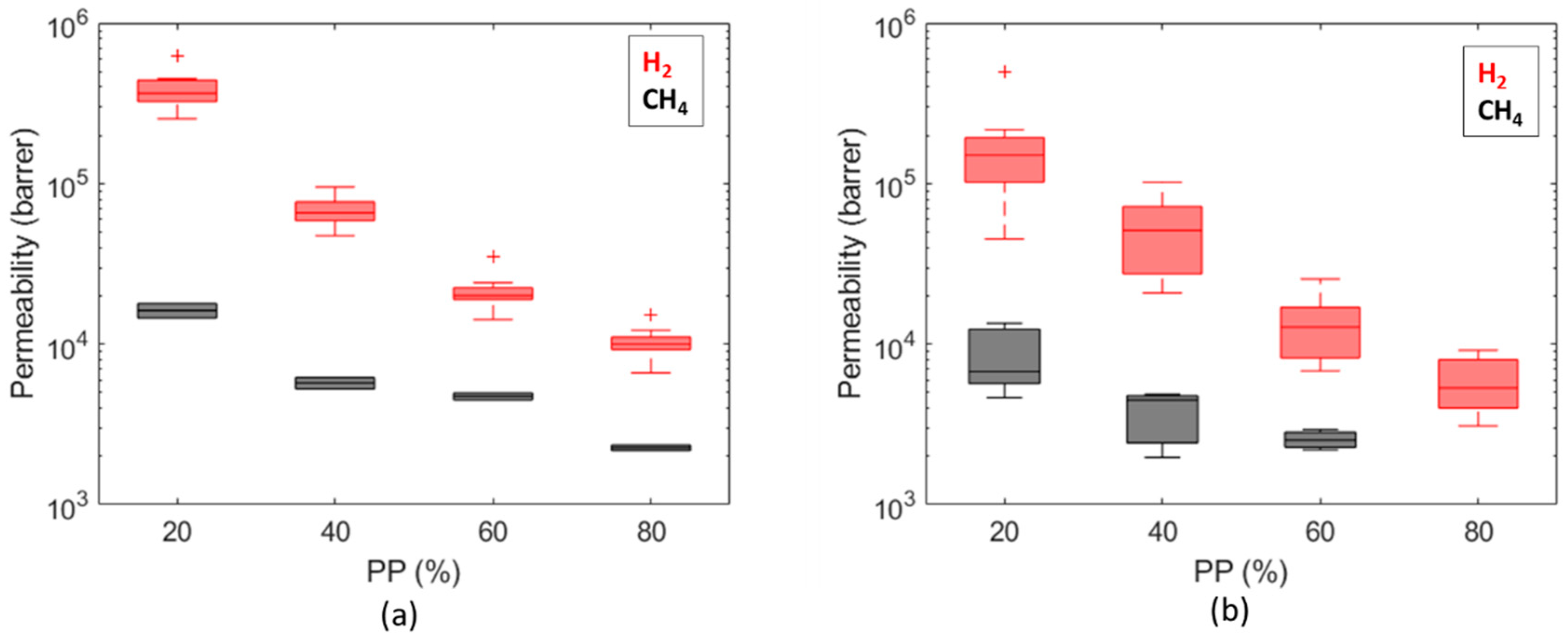
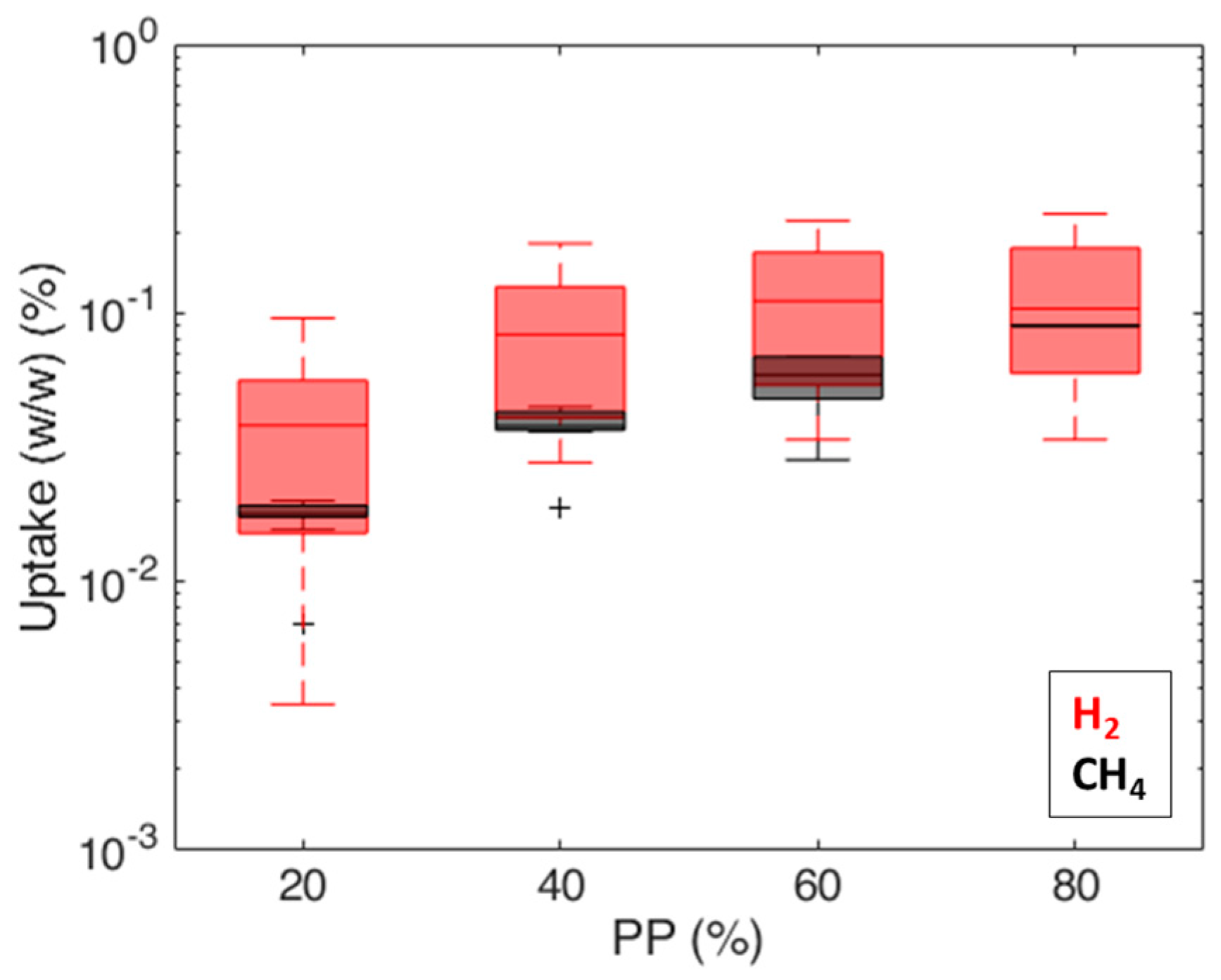
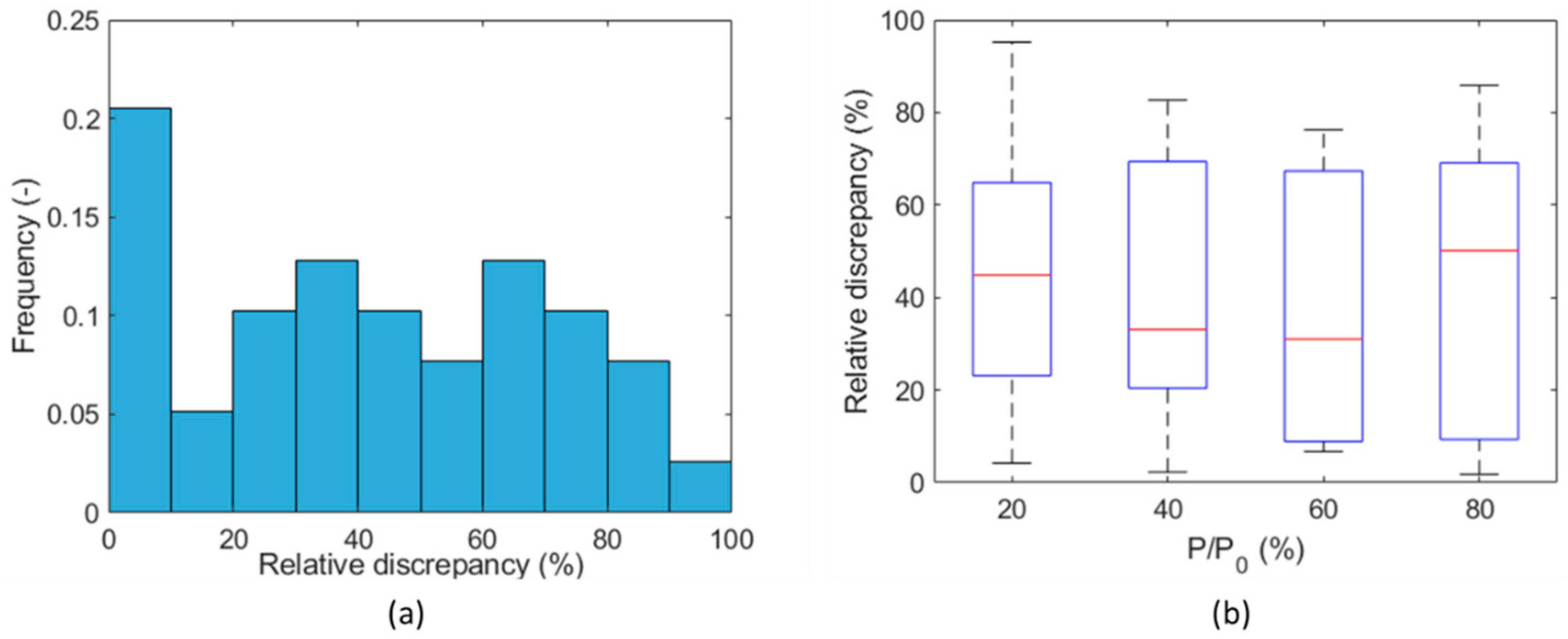
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Calibration of the microbalance:
- Introduce an empty sample pan into the DVS;
- Set the incubator temperature (45 °C) and impose the vacuum;
- Wait until the mass measurement stabilizes (this is reached when the mass variation in time is below the threshold of ); the stabilization of the mass measurement could take up to 2 h;
- Record the mass of the empty pan reached after stabilization.
- Measurement of the initial mass:
- Introduce the sample;
- Dry the sample (optional): the preheater temperature is increased up to 400 °C and then decreased again to 45 °C;
- Impose the vacuum (Figure 2a);
- Wait until the mass stabilizes.
- Sorption step:
- Desorption step:
- The chamber is evacuated;
- The mass is measured every 1 s until the equilibrium mass is reached().
References
- Bünger, U.; Landinger, H.; Pschorr-Schoberer, E.; Schmidt, P.; Weindorf, W.; Jöhrens, J.; Lambrecht, U.; Naumann, K.; Lischke, A. Power to Gas in Transport—Status Quo and Perspectives for Development; Federal Ministry of Transport and Digital Infrastructure (BMVI): Berlin, Germany, 2021.
- Langmi, H.W.; Engelbrecht, N.; Modisha, P.M.; Bessarabov, D. Hydrogen storage. In Electrochemical Power Sources: Fundamentals, Systems, and Applications; Elsevier: Amsterdam, The Netherlands, 2022; pp. 455–486. [Google Scholar] [CrossRef]
- Rhodes, R. Explosive Lessons in Hydrogen Safety. Apple Knowl. Serv. ASK Mag. NASA 2011, 41, 46–50. [Google Scholar]
- Benetatos, C.; Bocchini, S.; Carpignano, A.; Chiodoni, A.; Cocuzza, M.; Deangeli, C.; Eid, C.; Ferrero, D.; Gerboni, R.; Giglio, G.; et al. How underground systems can contribute to meet the challenges of energy transition. GEAM Geoing. Ambient. Mineraria 2021, 58, 65–80. [Google Scholar] [CrossRef]
- Zivar, D.; Kumar, S.; Foroozesh, J. Underground hydrogen storage: A comprehensive review. Int. J. Hydrogen Energy 2021, 46, 23436–23462. [Google Scholar] [CrossRef]
- Al-Shafi, M.; Massarweh, O.; Abushaikha, A.S.; Bicer, Y. A review on underground gas storage systems: Natural gas, hydrogen and carbon sequestration. Energy Rep. 2023, 9, 6251–6266. [Google Scholar] [CrossRef]
- Benetatos, C.; Rocca, V.; Verga, F.; Adinolfi, L.; Marzano, F. Deformation behavior of a regional shale formation from integrated laboratory and well data analysis: Insights for underground fluid storage in northern Italy. Geoenergy Sci. Eng. 2023, 229, 212109. [Google Scholar] [CrossRef]
- Benetatos, C.; Catania, F.; Giglio, G.; Pirri, C.F.; Raeli, A.; Scaltrito, L.; Serazio, C.; Verga, F. Workflow for the Validation of Geomechanical Simulations through Seabed Monitoring for Offshore Underground Activities. J. Mar. Sci. Eng. 2023, 11, 1387. [Google Scholar] [CrossRef]
- Vasile, N.S.; Bellini, R.; Bassani, I.; Vizzarro, A.; Azim, A.A.; Coti, C.; Barbieri, D.; Scapolo, M.; Viberti, D.; Verga, F.; et al. Innovative high pressure/high temperature, multi-sensing bioreactors system for microbial risk assessment in underground hydrogen storage. Int. J. Hydrogen Energy 2024, 51, 41–50. [Google Scholar] [CrossRef]
- Haddad, P.G.; Ranchou-Peyruse, M.; Guignard, M.; Mura, J.; Casteran, F.; Ronjon-Magand, L.; Sénéchal, P.; Isaure, M.P.; Moonen, P.; Hoareau, G.; et al. Geological storage of hydrogen in deep aquifers—An experimental multidisciplinary study. Energy Environ. Sci. 2022, 15, 3400–3415. [Google Scholar] [CrossRef]
- Bassani, I.; Bellini, R.; Vizzarro, A.; Coti, C.; Pozzovivo, V.; Barbieri, D.; Pirri, C.F.; Verga, F.; Menin, B. Biogeochemical characterization of four depleted gas reservoirs for conversion into underground hydrogen storage. Environ. Microbiol. 2023, 25, 3683–3702. [Google Scholar] [CrossRef]
- Luboń, K.; Tarkowski, R. Influence of capillary threshold pressure and injection well location on the dynamic CO2 and H2 storage capacity for the deep geological structure. Int. J. Hydrogen Energy 2021, 46, 30048–30060. [Google Scholar] [CrossRef]
- Shi, Z.; Jessen, K.; Tsotsis, T.T. Impacts of the subsurface storage of natural gas and hydrogen mixtures. Int. J. Hydrogen Energy 2020, 45, 8757–8773. [Google Scholar] [CrossRef]
- Hemme, C.; Van Berk, W. Hydrogeochemical Modeling to Identify Potential Risks of Underground Hydrogen Storage in Depleted Gas Fields. Appl. Sci. 2018, 8, 2282. [Google Scholar] [CrossRef]
- Vinsot, A.; Appelo, C.A.J.; Lundy, M.; Wechner, S.; Lettry, Y.; Lerouge, C.; Fernandez, A.M.; Labat, M.; Tournassat, C.; De Canniere, P.; et al. In situ diffusion test of hydrogen gas in the Opalinus Clay. Geol. Soc. Lond. Spec. Publ. 2014, 400, 563–578. [Google Scholar] [CrossRef]
- Wise, D.L.; Houghton, G. The diffusion coefficients of ten slightly soluble gases in water at 10–60 °C. Chem. Eng. Sci. 1966, 21, 999–1010. [Google Scholar] [CrossRef]
- Engineering Toolbox. Solubility of Gases in Water. 2008. Available online: https://www.engineeringtoolbox.com/gases-solubility-water-d_1148.html (accessed on 22 April 2021).
- Boving, T.B.; Grathwohl, P. Tracer diffusion coefficients in sedimentary rocks: Correlation to porosity and hydraulic conductivity. J. Contam. Hydrol. 2001, 53, 85–100. [Google Scholar] [CrossRef]
- Shukla, R.; Ranjith, P.; Haque, A.; Choi, X. A review of studies on CO2 sequestration and caprock integrity. Fuel 2010, 89, 2651–2664. [Google Scholar] [CrossRef]
- Liu, J.; Wang, S.; Javadpour, F.; Feng, Q.; Cha, L. Hydrogen Diffusion in Clay Slit: Implications for the Geological Storage. Energy Fuels 2022, 36, 7651–7660. [Google Scholar] [CrossRef]
- Aertsens, M. Re-Evaluation of the Experimental Data of the MEGAS Experiment on GasMigration through Boom-Clay. SCK CEN, Mol, Belgium, SCK CEN-ER-100. 2009. Available online: http://hdl.handle.net/10038/1182 (accessed on 22 April 2021).
- Krooss, B.M. Evaluation of Database on Gas Migration through Clayey Host Rocks; Belgian National Agency for Radioactive Waste and Enriched Fissile Material (ONDRAF-NIRAS): Aachen, Germany, 2008. [Google Scholar]
- Jacops, E.; Wouters, K.; Volckaert, G.; Moors, H.; Maes, N.; Bruggeman, C.; Swennen, R.; Littke, R. Measuring the effective diffusion coefficient of dissolved hydrogen in saturated Boom Clay. Appl. Geochem. 2015, 61, 175–184. [Google Scholar] [CrossRef]
- Boulin, P.F.; Angulo-Jaramillo, R.; Daian, J.-F.; Talandier, J.; Berne, P. Pore gas connectivity analysis in Callovo-Oxfordian argillite. Appl. Clay Sci. 2008, 42, 276–283. [Google Scholar] [CrossRef]
- Panfilov, M. Underground and pipeline hydrogen storage. In Compendium of Hydrogen Energy; Elsevier: Amsterdam, The Netherlands, 2016; pp. 91–115. [Google Scholar] [CrossRef]
- Michelsen, J.; Hagemann, B.; Ganzer, L.; Hujer, W. Measurement of Hydrogen Diffusion through Caprock Samples. In Proceedings of the Sixth International Conference on Fault and Top Seals, Vienna, Austria, 26–28 September 2022; European Association of Geoscientists & Engineers: Vienna, Austria, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Roberts, R.C. Molecular diffusion of Gases. In American Institute of Physics Handbook; Gray, D.E., Ed.; Mc-Graw Hill Book Company: New York, NY, USA, 1972; pp. 2249–2252. [Google Scholar]
- Pandey, G.N.; Tek, M.R. Diffusion of Fluids Through Porous Media with Implications in Petroleum Geology. Aapg Bull. 1974, 58, 291–303. [Google Scholar] [CrossRef]
- Schloemer, S.; Krooss, B.M. Molecular transport of methane, ethane and nitrogen and the influence of diffusion on the chemical and isotopic composition of natural gas accumulations. Geofluids 2004, 4, 81–108. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, S. Estimation of Pressure-Dependent Diffusive Permeability of Coal Using Methane Diffusion Coefficient: Laboratory Measurements and Modeling. Energy Fuels 2016, 30, 8968–8976. [Google Scholar] [CrossRef]
- Crank, J.; Park, G.S. (Eds.) Diffusion in Polymers, 3rd ed.; Academic Press: London, UK, 1977. [Google Scholar]
- Wang, Y.; Tsotsis, T.T.; Jessen, K. Competitive Sorption of Methane/Ethane Mixtures on Shale: Measurements and Modeling. Ind. Eng. Chem. Res. 2015, 54, 12187–12195. [Google Scholar] [CrossRef]
- Zhang, T.; Ellis, G.S.; Ruppel, S.C.; Milliken, K.; Yang, R. Effect of organic-matter type and thermal maturity on methane adsorption in shale-gas systems. Org. Geochem. 2012, 47, 120–131. [Google Scholar] [CrossRef]
- Weniger, P.; Kalkreuth, W.; Busch, A.; Krooss, B.M. High-pressure methane and carbon dioxide sorption on coal and shale samples from the Paraná Basin, Brazil. Int. J. Coal Geol. 2010, 84, 190–205. [Google Scholar] [CrossRef]
- Dasani, D.; Wang, Y.; Tsotsis, T.T.; Jessen, K. Laboratory-Scale Investigation of Sorption Kinetics of Methane/Ethane Mixtures in Shale. Ind. Eng. Chem. Res. 2017, 56, 9953–9963. [Google Scholar] [CrossRef]
- Didier, M.; Leone, L.; Greneche, J.-M.; Giffaut, E.; Charlet, L. Adsorption of Hydrogen Gas and Redox Processes in Clays. Environ. Sci. Technol. 2012, 46, 3574–3579. [Google Scholar] [CrossRef]
- Volckaert, G.; Ortiz, L.; De Cannière, P.; Put, M.; Horseman, S.T.; Harrington, J.F.; Fioravante, V.; Impey, M. MEGAS Modelling and Experiments on Gas Migration in Repository Host Rocks; Publications Office of the EU: Luxembourg, 1994; Available online: http://bookshop.europa.eu/en/megas-pbCGNA16235/?CatalogCategoryID=DjYKABstgekAAAEjwpEY4e5L (accessed on 6 March 2023).
- Rebour, V.; Billiotte, J.; Deveughele, M.; Jambon, A.; Le Guen, C. Molecular diffusion in water-saturated rocks: A new experimental method. J. Contam. Hydrol. 1997, 28, 71–93. [Google Scholar] [CrossRef]
- Beaudoing, G. Sorption and desorption bench of water vapour and vapour transfer through unsaturated materials. In Proceedings of the 4th International Symposium on Moisture and Creep Effects on Paper, Board and Containers, Grenoble, France, 18–19 March 1999. [Google Scholar]
- Bardelli, F.; Mondelli, C.; Didier, M.; Vitillo, J.G.; Cavicchia, D.R.; Robinet, J.C.; Leone, L.; Charlet, L. Hydrogen uptake and diffusion in Callovo-Oxfordian clay rock for nuclear waste disposal technology. Appl. Geochem. 2014, 49, 168–177. [Google Scholar] [CrossRef]
- Grade, A.; Govaerts, J.; Volckaert, G.; Mazurek, M. Determination of Diffusion Coefficients of Dissolved Gases in Boom Clay and Opalinus Clay; Campus Groep T., KU Leuven: Leuven, Belgium, 2013. [Google Scholar]
- Mondelli, C.; Bardelli, F.; Vitillo, J.G.; Didier, M.; Brendle, J.; Cavicchia, D.R.; Robinet, J.C.; Charlet, L. Hydrogen adsorption and diffusion in synthetic Na-montmorillonites at high pressures and temperature. Int. J. Hydrogen Energy 2015, 40, 2698–2709. [Google Scholar] [CrossRef]
- Shackelford, C.D. Laboratory diffusion testing for waste disposal—A review. J. Contam. Hydrol. 1991, 7, 177–217. [Google Scholar] [CrossRef]
- Wicke, E.; Kallenbach, R. Die Oberflächendiffusion von Kohlendioxyd in aktiven Kohlen. Kolloid Z. 1941, 97, 135–151. [Google Scholar] [CrossRef]
- Surface Measurement Systems. DVS Vacuum, Technical Sheet. 2022. Available online: https://www.surfacemeasurementsystems.com/products/dynamic-vapor-sorption-instruments/competitive-sorption-analyzer/dvs-vacuum/ (accessed on 6 March 2023).
- Karimi, M. Diffusion in Polymer Solids and Solutions. In Mass Transfer in Chemical Engineering Processes; Marko, J., Ed.; InTech: London, UK, 2011. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- DVS Advanced Analysis Suite v7.0—User Manual; Surface Measurement Systems: Allentown, PA, USA, 2012.
- Stannett, V. The transport of gases in synthetic polymeric membranes—An historic perspective. J. Membr. Sci. 1978, 3, 97–115. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Gajda, D.; Lutyński, M. Hydrogen Permeability of Epoxy Composites as Liners in Lined Rock Caverns—Experimental Study. Appl. Sci. 2021, 11, 3885. [Google Scholar] [CrossRef]
- Derkowski, A.; Ziemianski, P. Similarity and dissimilarity of factors controlling methane and hydrogen gas adsorption in geologic formations. In Proceedings of the 2022 Goldschmidt Conference, Honolulu, HI, USA, 10–15 July 2022. [Google Scholar] [CrossRef]
- Truche, L.; Joubert, G.; Dargent, M.; Martz, P.; Cathelineau, M.; Rigaudier, T.; Quirt, D. Clay minerals trap hydrogen in the Earth’s crust: Evidence from the Cigar Lake uranium deposit, Athabasca. Earth Planet. Sci. Lett. 2018, 493, 186–197. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, J.; Jin, Z.; Sun, Q.; Zou, R.; Meng, Q.; Liu, K.; Su, Y.; Zhang, Q. High-pressure hydrogen adsorption in clay minerals: Insights on natural hydrogen exploration. Fuel 2023, 344, 127919. [Google Scholar] [CrossRef]
- Li, W.; Pang, X.; Snape, C.; Zhang, B.; Zheng, D.; Zhang, X. Molecular Simulation Study on Methane Adsorption Capacity and Mechanism in Clay Minerals: Effect of Clay Type, Pressure, and Water Saturation in Shales. Energy Fuels 2019, 33, 765–778. [Google Scholar] [CrossRef]
- Kuila, U.; Prasad, M. Surface Area and Pore-Size Distribution in Clays and Shales. In All Days; SPE: Denver, CO, USA, 2011; p. SPE-146869-MS. [Google Scholar] [CrossRef]
- Ismail, A.F.; Khulbe, K.C.; Matsuura, T. Gas Separation Membranes: Polymeric and Inorganic; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Ziemiański, P.P.; Derkowski, A. Structural and textural control of high-pressure hydrogen adsorption on expandable and non-expandable clay minerals in geologic conditions. Int. J. Hydrogen Energy 2022, 47, 28794–28805. [Google Scholar] [CrossRef]
- Jacops, E.; Volckaert, G.; Maes, N.; Weetjens, E.; Govaerts, J. Determination of gas diffusion coefficients in saturated porous media: He and CH4 diffusion in Boom Clay. Appl. Clay Sci. 2013, 83–84, 217–223. [Google Scholar] [CrossRef]
- Ho, T.A.; Dang, S.T.; Dasgupta, N.; Choudhary, A.; Rai, C.S.; Wang, Y. Nuclear magnetic resonance and molecular simulation study of H2 and CH4 adsorption onto shale and sandstone for hydrogen geological storage. Int. J. Hydrogen Energy 2024, 51, 158–166. [Google Scholar] [CrossRef]
- Reitenbach, V.; Ganzer, L.; Albrecht, D.; Hagemann, B. Influence of added hydrogen on underground gas storage: A review of key issues. Environ. Earth Sci. 2015, 73, 6927–6937. [Google Scholar] [CrossRef]



| Gas | Solubility in Water (g/kg) | Diffusivity in Water (×10−9 m2/s) | Diffusivity in Air (×10−6 m2/s) | |||
|---|---|---|---|---|---|---|
| @ 20 °C, 1 atm | @ 60 °C, 1 atm | @ 20 °C, 1 atm | @ 60 °C, 1 atm | @ 20 °C, 1 atm | @ 100 °C, 1 atm | |
| CH4 | 0.023 | 0.007 | 1.62 | 6.7 | 0.21 | 0.321 |
| H2 | 0.0016 | 0.0012 | 4.58 | 13.1 | 0.756 | 1.1536 |
| Mineral | Composition (wt %) | Formula | ||
|---|---|---|---|---|
| Caprock1 | Caprock2 | |||
| Tectosilicates | quartz | 24 ÷ 25.4 | 16.7 ÷ 20.3 | SiO2 |
| plagioclase (albite, anorthite) | 7.2 ÷ 9.1 | 4.0 ÷ 7.1 | (Na,Ca)(Si,Al)4O8 | |
| K-feldspar | 9.3 ÷ 9.7 | 5.5 ÷ 8.6 | KAlSi3O8 | |
| Carbonates | calcite | 32.5 ÷ 33.8 | 24.9 ÷ 35.9 | CaCO3 |
| dolomite | 7.4 ÷ 8.1 | 16.2 ÷ 20.5 | CaMg(CO3)2 | |
| siderite | 0 | 0.4 ÷ 0.6 | FeCO3 | |
| Phyllosilicates | illite | 6.2 ÷ 10.9 | 6.1 ÷ 24.9 | (K,H3O)(Al,Mg,Fe)2(Si,Al)4O10[(OH)2,(H2O)] |
| chlorite | 3.5 ÷ 3.8 | 1.9 ÷ 2.5 | (Mg, Fe)3(Si, Al)4O10(OH)2•(Mg, Fe)3(OH)6 | |
| kaolinite | 2.6 ÷ 3.1 | 2.1 ÷ 3.7 | Al2Si2O5(OH)4 | |
| Additional minerals | pyrite | 0 | 0.2 ÷ 0.4 | FeS2 |
| halite | 1.1 ÷ 2.4 | 0.0 ÷ 0.2 | NaCl | |
| Sample ID | Core Sample ID | Wet/Dry | Width (mm) | Mass (mg) | Density (kg/m3) | Tested to Gas |
|---|---|---|---|---|---|---|
| Flake1_3 | Caprock1 | wet | 2 | 141.8 | 1773 | H2 |
| Flake1_4 | Caprock1 | dry | 2.66 | 200.7 | 1676 | H2 |
| Flake1_5 | Caprock1 | wet | 1.6 | 157.3 | 2091 | H2 |
| Flake1_6 | Caprock1 | dry | 2.1 | 172.6 | 1612 | H2 |
| Flake1_7 | Caprock1 | dry | 1.9 | 187.7 | 1764 | H2 |
| Flake1_10 | Caprock1 | wet | 2.36 | 179.7 | 1523 | CH4 |
| Flake2_1 | Caprock2 (bottom) | wet | 1.55 | 198 | 2276 | H2 |
| Flake2_2 | Caprock2 (bottom) | wet | 1.5 | 215 | 1869 | H2 |
| Flake2_3 | Caprock2 (top) | dry | 1.5 | 144.6 | 1928 | H2 |
| Flake2_4 | Caprock2 (top) | wet | 1.84 | 160.6 | 2108 | H2 |
| Flake2_5 | Caprock2 (top) | wet | 1.83 | 211.6 | 2290 | H2 |
| Flake2_6 | Caprock2 (top) | wet | 2.06 | 203.2 | 1970 | CH4 |
| Flake2_7 | Caprock2 (top) | wet | 1.86 | 193.5 | 2081 | CH4 |
| Flake2_8 | Caprock2 (bottom) | wet | 1.4 | 195.9 | 1727 | CH4 |
| Flake2_9 | Caprock2 (bottom) | wet | 1.75 | 235.97 | 1751 | CH4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salina Borello, E.; Bocchini, S.; Chiodoni, A.; Coti, C.; Fontana, M.; Panini, F.; Peter, C.; Pirri, C.F.; Tawil, M.; Mantegazzi, A.; et al. Underground Hydrogen Storage Safety: Experimental Study of Hydrogen Diffusion through Caprocks. Energies 2024, 17, 394. https://doi.org/10.3390/en17020394
Salina Borello E, Bocchini S, Chiodoni A, Coti C, Fontana M, Panini F, Peter C, Pirri CF, Tawil M, Mantegazzi A, et al. Underground Hydrogen Storage Safety: Experimental Study of Hydrogen Diffusion through Caprocks. Energies. 2024; 17(2):394. https://doi.org/10.3390/en17020394
Chicago/Turabian StyleSalina Borello, Eloisa, Sergio Bocchini, Angelica Chiodoni, Christian Coti, Marco Fontana, Filippo Panini, Costanzo Peter, Candido Fabrizio Pirri, Michel Tawil, Andrea Mantegazzi, and et al. 2024. "Underground Hydrogen Storage Safety: Experimental Study of Hydrogen Diffusion through Caprocks" Energies 17, no. 2: 394. https://doi.org/10.3390/en17020394
APA StyleSalina Borello, E., Bocchini, S., Chiodoni, A., Coti, C., Fontana, M., Panini, F., Peter, C., Pirri, C. F., Tawil, M., Mantegazzi, A., Marzano, F., Pozzovivo, V., Verga, F., & Viberti, D. (2024). Underground Hydrogen Storage Safety: Experimental Study of Hydrogen Diffusion through Caprocks. Energies, 17(2), 394. https://doi.org/10.3390/en17020394








