Wind Power Bidding Based on an Ensemble Differential Evolution Algorithm with a Problem-Specific Constraint-Handling Technique

Abstract

The intermittent nature of wind power generation induces great challenges for power bidding in the electricity market. The deployment of battery energy storage can improve flexibility for power bidding. This paper investigates an optimal power bidding strategy for a wind–storage hybrid power plant in the day-ahead electricity market. To handle the challenges of the uncertainties of wind power generation and electricity prices, the optimal bidding problem is formulated as a risk-aware scenario-based stochastic programming, in which a number of scenarios are generated using a copula-based approach to represent the uncertainties. These scenarios consider the temporal correlation of wind power generation and electricity prices between consecutive time intervals. In the stochastic programming, a more practical but nonlinear battery operation cost function is considered, which leads to a nonlinear constrained optimization problem. To solve the nonlinear constrained optimization problem, an ensemble differential evolution (EDE) algorithm is proposed, which makes use of the merits of an ensemble of mutant operators to generate mutant vectors. Moreover, a problem-specific constraint-handling technique is developed. To validate the effectiveness of the proposed EDE algorithm, it is compared with state-of-the-art DE-based algorithms for constrained optimization problems, including a constrained composite DE (C²oDE) algorithm and a novel DE (NDE) algorithm. The experimental results demonstrate that the EDE algorithm is much more reliable and much faster in finding a better bidding strategy against benchmarking algorithms. More precisely, the average values of the success rate are 0.893, 0.667, and 0.96 for C²oDE, NDE, and EDE, respectively. Compared to C²oDE and NDE, the average value of the mean number of function evaluations to succeed with EDE is reduced by 76% and 59%, respectively.

1. Introduction

Renewable energies, e.g., wind power and solar power, are essential in order to achieve carbon neutrality by the middle of the century, and the installation of renewable generation has been increasing rapidly all around the world [1]. The intermittent nature of renewable resources, however, makes it a great challenge for renewable energy producers to bid in the electricity market [2,3]. In the deregulated electricity market, renewable energy producers must buy or sell the imbalance between the day-ahead bid and the real generation in the balancing market, which can lead to a great loss of profit [4].

The intermittent nature of renewable resources, i.e., solar radiation and wind speed, introduce uncertainty to renewable power generation. To handle the challenge of uncertainty, forecasting is a widely used technique, which can provide a forecasting value or a forecasting interval [5,6]. Lee et al. [7] developed a wind power and electricity price probabilistic forecasting model, based on which an advanced offer curve was further built in the day-ahead electricity market.

To incorporate the uncertainty of renewable generation and electricity prices in the power bidding strategy, stochastic programming including scenario-based stochastic optimization [8], robust optimization [9], and chance-constrained optimization [10] have been applied for the development of an optimal bidding strategy. Maneesha et al. [11] developed a two-stage stochastic joint bidding framework for a wind power plant and pumped storage plant. A robust bidding model in the day-ahead electricity market was proposed by [12], in which a Gaussian mixture model was used to deal with the uncertainties of renewable generation, while the information-gap decision theory was applied to deal with the uncertainty of prices. Hosseini et al. [13] developed an auxiliary classifier Wasserstein generative adversarial network-based wind scenario generation method to capture its uncertainty in day-ahead wind power bidding. In [14], the Beta and Weibull probability distribution function are used to generate scenarios of solar and wind power, respectively, and forward-reduction-based algorithms are used for scenario reduction. Among these stochastic programming methods, robust optimization is conservative while chance-constrained optimization is difficult to solve. Scenario-based stochastic optimization is easy to implement and provides a practical framework to yield efficient solutions for time-sequential decision problems [15]. Such properties of scenario-based stochastic optimization make it a competitive approach for renewable power bidding. However, scenario-based stochastic optimization has to make a trade-off between modeling accuracy and computation complexity whereby a large number of scenarios will better capture the uncertainty while increasing the computation complexity. Renewable generation and electricity prices illustrate a high temporal correlation. Nevertheless, the temporal correlation is seldom considered in the scenario-based stochastic optimization of the renewable power bidding strategy.

In addition to stochastic programming, game-theory based approaches [16] and deep reinforcement learning-based methods [17] have also been developed. In [18], a deep reinforcement learning approach was proposed for the self-dispatch of a wind–storage integrated system in the real-time electricity market, in which the integrated system could learn the bidding strategy and charging policy from historical data and whose predictions of wind power generation were unnecessary.

To control the financial risk of bidding offers due to renewable generation uncertainty, risk management approaches, e.g., conditional value at risk (CVaR), are widely considered. Ghavidel et al. [19] developed a risk-constrained bidding strategy for the joint operation of wind power and compressed-air energy storage based on CvaR. In [20], a novel risk management method based on second-order stochastic dominance constraints was proposed for wind power bidding.

To further weaken the impact of renewable generation uncertainty on power bidding, the utility-scale deployment of battery energy storage has been used to improve the flexibility of renewable energy systems for a more reliable and efficient integration into power systems [21]. In [22], a robust model predictive control was developed for the optimal power bidding of a wind farm in combination with energy storage. Nitsch et al. [23] investigated the bidding strategy for battery energy storage on the day-ahead and automatic frequency restoration reserve markets. The above studies rarely consider the nonlinearity of the battery degradation cost that highly depends on the operation regime of the battery, e.g., temperature, charging/discharging frequency, depth of discharge (DoD), and state of charge (SoC). Improper operation can greatly shorten the life span of battery devices. The studies in [24] illustrate that it is valuable to consider the nonlinearity of the battery degradation function for the optimal operation of battery devices. Renewable power bidding problems are often formulated as mixed integer linear programming, which can be easily solved by commercial solvers. The consideration of the nonlinearity of the battery degradation function will lead to nonlinear programming and will require an efficient heuristic optimization method, e.g., evolutionary algorithms (EAs) [25]. EAs are widely applied in engineering to solve complex nonlinear and nonconvex optimization problems [26,27]. However, to obtain satisfying optimization performance, proper EAs should be designed to handle the challenges of being trapped in local optimal constraints and large-scale decision making.

To summarize, the uncertainty of renewable generation induces great challenges for power bidding in the spot electricity market. Scenario-based stochastic programming is an efficient method for handling the challenges of uncertainty; however, previous studies seldom consider the temporal correlation of renewable generation and electricity prices in generating scenarios. Risk management approaches can be used to control the financial risk of bidding strategies. The utilization of battery energy storage can improve the flexibility of renewable energy systems for power bidding, while the operation cost of the battery is rarely discussed.

Considering the above concerns, this paper investigates the optimal power bidding strategy for a wind–storage hybrid power plant in the Nord Pool Electricity market, which is Europe’s leading market offering day-ahead and intra-day markets to consumers. Plenty of studies on power bidding are based on the Nord Pool Electricity market [28,29]. The novelty and main contributions of this research are summarized as follows:

(1)

A risk-aware scenario-based bidding strategy considering battery operation costs is developed. To account for the temporal correlation of wind power generation and electricity prices, a number of scenarios are generated using a copula-based approach. Moreover, the conditional value at risk (CVaR) is applied to control the financial risk of bidding strategy. More importantly, a more practical but nonlinear battery operation cost function is considered to derive an appropriate battery operation regime.

(2)

The power bidding strategy is formulated as a constrained nonlinear stochastic programming. To solve the constrained nonlinear optimization problem, an ensemble differential evolution (EDE) algorithm is proposed, in which an ensemble of mutant operators is used to generate mutant vectors for the better exploration of the decision space. In addition, a problem-specific constraint-handling approach is developed to handle the constraint in the bidding problem.

(3)

To validate the effectiveness of the proposed EDE algorithm in finding the optimal bidding strategy, the proposed EDE algorithm is compared with state-of-the-art DE-based algorithms for constrained optimization problems. The experimental results illustrate that the proposed EDE algorithm is much more reliable and much faster in finding a better bidding strategy.

The remainder of this paper is organized as follows. The methods and materials for the development and validation of the optimal wind power bidding strategy are illustrated in Section 2. The experimental results are provided in Section 3, and the conclusions and discussions are given in Section 4.

2. Methods and Materials

In this section, the bidding problem for a wind–storage power plant will firstly be introduced in Section 2.1, which is followed by the introduction of battery operation costs due to battery degradation in Section 2.2. The formulation of risk-aware bidding optimization problems considering the bidding revenue and battery operation costs is presented in Section 2.3, while the EDE-based optimization algorithm is given in Section 2.4. At the end of this section, the materials for the experimental study will be introduced.

2.1. Power Bidding in the Electricity Market

The revenue of a wind power producer in a short-term electricity market is composed of three parts: power trading in the day-ahead market, in the intra-day market, and in the balancing market. In this paper, power trading in the intra-day market is not considered; hence, the revenue for a trading day is given by (1):

$$R={\displaystyle \sum _{t=1}^{N_t}{\pi }_{d,t}\cdot P_{d,t}\cdot \Delta t+{\pi }_{r,t}\cdot \left(P_{W,t}-P_{B,t}-P_{d,t}\right)\cdot \Delta t}$$

(1)

where ${\pi }_{d,t}$ and ${\pi }_{r,t}$ denote the electricity price at time period t in the day-ahead market and the balancing market, respectively. The variables $P_{d,t}$ and $P_{W,t}$ denote the power committed by the wind power producer in the day-ahead market and the actual wind power generated by the wind farm, respectively. The variable $P_{B,t}$ represents the charging power (if $P_{B,t}>0$) or the discharging power (if $P_{B,t}<0$) of the battery energy storage system, and $\Delta t$ denotes the duration of time interval t. The variable N_t denotes the number of time interval in a trading day. In the Nord Pool market, N_t = 24 and Δt = 1 h.

In the balancing market, if the actual power offered by the hybrid power plant is greater than the committed volume, then the down-regulation price is activated; otherwise, the up-regulation price is activated. The revenue, considering the up- and down-regulation prices, is:

$$R={\displaystyle \sum _{t=1}^{N_t}{\pi }_{d,t}\cdot P_{d,t}\cdot \Delta t+\left\{\begin{array}{c}{\pi }_{down,t}\cdot \left(P_{W,t}-P_{B,t}-P_{d,t}\right)\cdot \Delta t, \mathrm{if} P_{W,t}-P_{B,t}\ge P_{d,t}\\ {\pi }_{up,t}\cdot \left(P_{W,t}-P_{B,t}-P_{d,t}\right)\cdot \Delta t,\hspace{1em}\mathrm{if} P_{W,t}-P_{B,t}<P_{d,t}\end{array}\right.}$$

(2)

where ${\pi }_{up,t}$ and ${\pi }_{down,t}$ denote the up-regulation price and down-regulation price, respectively, satisfying ${\pi }_{down,t}\le {\pi }_{d,t}\le {\pi }_{up,t}$.

Let us define

$${\lambda }_{down,t}=\frac{{\pi }_{down,t}}{{\pi }_{d,t}}$$

(3)

and

$${\lambda }_{up,t}=\frac{{\pi }_{up,t}}{{\pi }_{d,t}}$$

(4)

Then, the bidding revenue becomes

$$R={\displaystyle \sum _{t=1}^{N_t}{\pi }_{d,t}\cdot P_{d,t}\cdot \Delta t+\left\{\begin{array}{c}{\lambda }_{down,t}\cdot {\pi }_{d,t}\cdot \left(P_{W,t}-P_{B,t}-P_{d,t}\right)\cdot \Delta t, \mathrm{if} P_{W,t}-P_{B,t}\ge P_{d,t}\\ {\lambda }_{up,t}\cdot {\pi }_{d,t}\cdot \left(P_{W,t}-P_{B,t}-P_{d,t}\right)\cdot \Delta t,\hspace{1em}\mathrm{if} P_{W,t}-P_{B,t}<P_{d,t}\end{array}\right.}$$

(5)

2.2. Battery Energy Storage System’s Operational Costs

The operational costs of a battery energy system are caused by battery degradation. DoD is the critical factor determining the battery cycle life, if it operates under certain conditions on temperature and SoC, as illustrated in [30]. This paper considers the battery cycle life as a function of DoD in (6) [31], which defines the battery life span in terms of the number of charging/discharging cycles.

$$L\left(d_B\right)={\alpha }_0\cdot d_B{}^{-{\alpha }_1}\cdot \exp \left(-{\alpha }_2\cdot d_B\right)$$

(6)

where L denotes the battery cycle life and d_B denotes the DoD. The parameters α₀, α₁, and α₂ are positive coefficients.

A charging event or a discharging event induces battery capacity degradation in (7), and such degradation leads to the degradation cost in (8).

$$\Delta E_B\left(d_B\right)=\frac{E_{B,r}}{2L\left(d_B\right)}$$

(7)

$$\Delta C_B\left(d_B\right)=\frac{C_B\cdot E_{B,r}}{2L\left(d_B\right)}$$

(8)

where $E_{B,r}$ and $C_B$ denote the rated capacity and capital cost of the battery energy storage system, respectively.

In the power bidding problem, there can be several charging and discharging events for a given operation regime $\left\{P_{B,t}\left|{}_{t=1}^{N_t}\right.\right\}$. A charging or discharging event can be identified by checking the power flow direction. A charging or discharging event sustaining k intervals from t + 1 to t + k, $\left\{P_{B,t^{\prime }}\left|{}_{t^{\prime }=t+1}^{t+k}\right.\right\}$, satisfies the condition in (9), whereby the power flow direction should not change.

$$\left\{\begin{array}{l}{P}_{B,t^{\prime }}\cdot P_{B,t^{\prime }+1}>0,\mathrm{for} t^{\prime }=t+1,\dots ,t+k-1\\ P_{B,t^{\prime }}\cdot P_{B,t^{\prime }+1}<=0,\mathrm{for} t^{\prime }=t+k\end{array}\right.$$

(9)

The DoD for the charging/discharging event is given by (10):

$$d_{B,t^{\prime }\left|{}_{t^{\prime }=t+1}^{t+k}\right.}=\left\{\begin{array}{c}\frac{{\displaystyle \sum _{t^{\prime }=t+1}^{t+k}{\eta }_{B,c}\cdot P_{B,t^{\prime }}\cdot \Delta t}}{E_{B,t}},\mathrm{if} P_{B,t^{\prime }}>0\\ \frac{-{\displaystyle \sum _{t^{\prime }=t+1}^{t+k}{P}_{B,t^{\prime }}\cdot \Delta t}}{{\eta }_{B,d}\cdot E_{B,t}}, \mathrm{if} P_{B,t^{\prime }}<0\end{array}\right.$$

(10)

where ${\eta }_{B,c}$ and ${\eta }_{B,d}$ denote the charging efficiency and discharging efficiency, respectively. The variable $E_{B,t}$ describes the battery capacity at the end of time interval t (or at the beginning of time interval t + 1), and the change of $E_{B,t}$ between two consecutive events is determined by (7).

Supposing that there are M charging/discharging events for the given operation regime $\left\{P_{B,t}\left|{}_{t=1}^{N_t}\right.\right\}$ and each event sustains k_m time intervals from t_m + 1 to t_m + k_m, the operational cost for such an operation regime is as follows:

$$C={\displaystyle \sum _{m=1}^M\frac{C_B\cdot E_{B,r}}{2L\left(d_{B,t^{\prime }\left|{}_{t^{\prime }=t_m+1}^{t_m+k}\right.}\right)}}$$

(11)

To maximize the battery lifespan, its operation also satisfies following conditions:

$$P_{B,\min }\le P_{B,t}\le P_{B,\max }$$

(12)

$$So{C}_{B,\min }\le So{C}_{B,t}\le So{C}_{B,\max }$$

(13)

where P_B,min < 0 and P_B,max > 0 denote the minimum discharging power and maximum charging power, respectively. The variable SoC_B,t represents the level of energy stored in the battery at the end of time interval t, and its dynamic is defined by (14):

$$So{C}_{B,t+1}=So{C}_{B,t}+\left\{\begin{array}{c}\frac{{\eta }_{B,c}\cdot P_{B,t+1}\cdot \Delta t}{E_{B,t}}, \mathrm{if} P_{B,t+1}\ge 0\\ \frac{P_{B,t+1}\cdot \Delta t}{{\eta }_{B,d}\cdot E_{B,t}}, \mathrm{if} P_{B,t+1}<0\end{array}\right.$$

(14)

2.3. Risk-Aware Bidding Optimization Problem

If we consider the revenue of bidding in the electricity market and the operational cost of the battery energy storage system, then the net income, I, of the wind power producer can be derived as follows:

$$I=R-C$$

(15)

The wind power producer determines the bidding offer, $\left\{P_{d,t}\left|{}_{t=1}^{N_t}\right.\right\}$, and the operation regime of the battery energy storage system, $\left\{P_{B,t}\left|{}_{t=1}^{N_t}\right.\right\}$, to maximize the net income. However, the above bidding problem is subject to uncertainty from wind power generation, the day-ahead electricity price, and the imbalance price.

The objective of the power bidding problem is formulated in (16) and is subject to the constraints in (12) and (13), which maximizes the expected net income, E(I), considering the risk.

$$\max \left(1-\tau \right)\cdot E\left(I\right)+\tau \cdot CVa{R}_{\beta }\left(I\right)$$

(16)

The CVaR is defined as follows:

$$CVa{R}_{\beta }\left(I\right)=E\left(I\left|I\le Va{R}_{\beta }\left(I\right)\right.\right)$$

(17)

$$Va{R}_{\beta }\left(I\right)=\max \left\{i\left|F_I\left(i\right)\le 1-\beta \right.\right\}$$

(18)

where τ is a weight parameter between the expected net come and CVaR, and the parameter β denotes the confidence level. The function $F_I\left(i\right)$ denotes the cumulative function of net income I.

The uncertainty in the bidding revenue comes from $P_{W,t}$, ${\pi }_{d,t}$, ${\lambda }_{down,t}$, and ${\lambda }_{up,t}$. Note that if ${\lambda }_{down,t}\ne 1$, then ${\lambda }_{up,t}=1$ and vice versa. Let us define ${\lambda }_t={\lambda }_{down,t}+{\lambda }_{up,t}-1$. It is easy to derive that if ${\lambda }_t\le 1$, then ${\lambda }_{up,t}=1$ and ${\lambda }_{down,t}={\lambda }_t$ and that if ${\lambda }_t>1$, then ${\lambda }_{down,t}=1$ and ${\lambda }_{up,t}={\lambda }_t$. Hence, only an uncertainty associated with $P_{W,t}$, ${\pi }_{d,t}$, and ${\lambda }_t$ should be considered.

Assuming that the random variables $P_{W,t}$, ${\pi }_{d,t}$, and ${\lambda }_t$ are mutually independent (cross-variable independent) as in [32], a number of scenarios generated from their distributions can be used to represent their uncertainties. The distribution of the day-ahead electricity price and wind generation can be obtained through probabilistic forecasting techniques [33,34]. The imbalance price illustrates high volatility and is difficult to forecast. The frequency distribution of the historical data of ${\lambda }_t$ is considered to represent its probabilistic density function [32]. To consider the temporal correlation for each variable, e.g., the correlation between $P_{W,t}$ and $P_{W,t+1}$, a copula-based strategy is used to generate scenarios [15]. If we suppose that there are N_s scenarios and that each scenario yields a net income I_s with given $\left\{P_{d,t}\left|{}_{t=1}^{N_t}\right.\right\}$ and $\left\{P_{B,t}\left|{}_{t=1}^{N_t}\right.\right\}$, then

$$E(I)=\frac{1}{N_s}{\displaystyle \sum _{s=1}^{N_s}{I}_s}$$

(19)

$$CVa{R}_{\beta }(I)=\frac{1}{\beta \cdot N_s}{\displaystyle \sum _{s^{\prime }=1}^{\beta \cdot N_s}{I}_{s^{\prime }}}$$

(20)

where $I_{s^{\prime }}$ denotes the values of the net income in an ascending order of I_s.

2.4. Optimization Algorithm

The objective function in (16) is nonlinear and nonconvex on the decision variables. To solve the optimization problem, an ensemble DE (EDE) algorithm along with a problem-specific constraint-handling technique is proposed.

2.4.1. Ensemble Differential Evolution Algorithm

A standard DE algorithm is composed of four stages, namely, initialization, mutation, crossover, and selection [35]. In the proposed EDE algorithm, an ensemble of mutation operators is adopted to generate mutant vectors. The flowchart of the proposed EDE algorithm is shown in Figure 1, and the details of the algorithm are discussed below.

For notation simplicity in the explanation of the optimization algorithm, let us define the decision vector as $\overrightarrow{x}=\left(P_{d,1},\dots ,P_{d,N_t},P_{B,1},\dots ,P_{B,N_t}\right)$ and the objective function as $f\left(\overrightarrow{x}\right)$.

In the initialization stage, a population of N_p candidate solutions are randomly initialized in the decision space, i.e., $\left\{{\overrightarrow{x}}_1,{\overrightarrow{x}}_2\dots ,{\overrightarrow{x}}_{N_p}\right\}$.

In the mutation stage, an ensemble of mutant operators is adopted to generate mutant vectors, which takes advantage of different mutant operators for a better exploration of the decision space. In the EDE algorithm, the population is divided into three sub-groups, and in each sub-group, a particular mutant operator is applied. However, all the sub-groups share the population for the selection of individuals to form differential vectors. The following three mutant operators, namely, DE/rand/1 in (21), DE/current-to-best/1 in (22), and DE/current-to-random/1 in (23), are considered:

$${\overrightarrow{v}}_i^g={\overrightarrow{x}}_{r_1}^g+F_i^g\cdot \left({\overrightarrow{x}}_{r_2}^g-{\overrightarrow{x}}_{r_3}^g\right) \mathrm{for} i=1,\dots ,\frac{N_p}{3}$$

(21)

$${\overrightarrow{v}}_i^g={\overrightarrow{x}}_i^g+F_{1,i}^g\cdot \left({\overrightarrow{x}}_{best}^g-{\overrightarrow{x}}_i^g\right)+F_{2,i}^g\cdot \left({\overrightarrow{x}}_{r_1}^g-{\overrightarrow{x}}_{r_2}^g\right) \mathrm{for} i=\frac{N_p}{3}+1,\dots ,\frac{2N_p}{3}$$

(22)

$${\overrightarrow{v}}_i^g={\overrightarrow{x}}_i^g+r\cdot \left({\overrightarrow{x}}_{r_1}^g-{\overrightarrow{x}}_i^g\right)+F_i^g\cdot \left({\overrightarrow{x}}_{r_2}^g-{\overrightarrow{x}}_{r_3}^g\right) \mathrm{for} i=\frac{2N_p}{3}+1,\dots ,N_p$$

(23)

where ${\overrightarrow{x}}_{r_1}^g$, ${\overrightarrow{x}}_{r_2}^g$, and ${\overrightarrow{x}}_{r_3}^g$ are three mutually distinct individuals randomly selected from the population. The subscript i and the superscript g denote the ith individual in the population and the gth generation in the evolution process, respectively. The variable F denotes the mutant factor, and r is a random number uniformly generated from [0, 1].

The DE/rand/1 mutant operator is the most frequent one, while DE/current-to-best/1 can speed up the convergence, and DE/current-to-random/1 promotes diversity [36]. Hence, the ensemble of the above mutant operators is expected to improve the optimization performance.

In the crossover stage, the widely deployed binomial crossover in (24) is used:

$$u_{i,j}^g=\left\{\begin{array}{c}{v}_{i,j}^g, \mathrm{if} r_j<C{R}_i^g \mathrm{or} j=j_{rand}\\ x_{i,j}^g, \mathrm{otherwise} \end{array}\right.$$

(24)

where j denotes the jth element in a vector, CR is the crossover rate, and j_rand is an integer uniformly selected from [1, 2N_t].

In this paper, a problem-specific constraint-handling technique will be proposed, and the individuals are selected based on the objective function value, as in (25):

$${\overrightarrow{x}}_i^{g+1}=\left\{\begin{array}{c}{\overrightarrow{u}}_i^g, \mathrm{if} f\left({\overrightarrow{u}}_i^g\right)\ge f\left({\overrightarrow{x}}_i^g\right)\\ {\overrightarrow{x}}_i^g, \mathrm{otherwise} \end{array}\right.$$

(25)

The mutation factor and crossover rate are critical for DE algorithms, and they are set as follows [37]:

$$F_i^{g+1}=\left\{\begin{array}{c}{F}_l+r_1\cdot F_u, \mathrm{if} r_2<{\xi }_1\\ F_i^g, \mathrm{otherwise} \end{array}\right.$$

(26)

$$C{R}_i^{g+1}=\left\{\begin{array}{c}{r}_3, \mathrm{if} r_4<{\xi }_2\\ C{R}_i^g, \mathrm{otherwise} \end{array}\right.$$

(27)

where F_l and F_u are the lower and upper bounds of F, respectively; ξ₁ and ξ₂ are the control parameters; and r₁, r₂, r₃, and r₄ are random numbers uniformly selected from [0, 1].

2.4.2. Constraint-Handling Technique

The generally considered constraint-handling techniques for EA-based constrained optimization problems include the feasibility rule, penalty method, stochastic ranking method, ε-constraint method, and multi-objective method [38]. In this paper, a problem-specific constraint-handling technique is proposed.

There are two kinds of constraints, namely, the boundary constraint in (12) and the inequality constraint in (13). If a component $v_{i,j}^g$ of a mutant vector ${\overrightarrow{v}}_i^g$ violates its boundary [L_j, U_j], the component will be reset as follows [39]:

$$v_{i,j}^g=\left\{\begin{array}{c}\min \left\{U_j,2L_j-v_{i,j}^g\right\}, \mathrm{if} v_{i,j}^g<L_j\\ \max \left\{L_j,2U_j-v_{i,j}^g\right\}, \mathrm{if} v_{i,j}^g>U_j\end{array}\right.$$

(28)

The problem-specific constraint-handling technique deals with the SoC constraint in (13), which is a function of the decision variables, $\left\{P_{B,t}\left|{}_{t=1}^{N_t}\right.\right\}$. For a charging event $\left\{P_{B,t^{\prime }}\left|{}_{t^{\prime }=t+1}^{t+k}\right.\right\}$, if $So{C}_{t+k}>So{c}_{\max }$, then the charging event will be reset by (29):

$$P_{B,t^{\prime }}=\frac{So{C}_{\max }-So{C}_t}{d_{B,t^{\prime }\left|{}_{t+1}^{t+k}\right.}}\cdot P_{B,t^{\prime }}$$

(29)

For a discharging event $\left\{P_{B,t^{\prime }}\left|{}_{t^{\prime }=t+1}^{t+k}\right.\right\}$, if $So{C}_{t+k}<So{c}_{\min }$, then the discharging event will be reset following (30):

$$P_{B,t^{\prime }}=\frac{So{C}_t-So{C}_{\min }}{d_{B,t^{\prime }\left|{}_{t+1}^{t+k}\right.}}\cdot P_{B,t^{\prime }}$$

(30)

The proposed constraint-handling technique maintains the power flow directions and power ratio between time intervals learned from the EDE algorithm, which is valuable for speeding up the convergence.

The framework of the proposed EDE algorithm is summarized in Algorithm 1.

Algorithm 1: Ensemble differential evolution

Input: Np: the population size; [Fl, Fu]: the boundary of mutation factor; ξ1, ξ2: control parameters for mutation factor and crossover rate; max_FES: maximum number of function evaluations; Initialization: Set g = 1; /* the number of generation */ Randomly generate an initial population from the decision space, i.e., $\left\{{\overrightarrow{x}}_1^g,{\overrightarrow{x}}_2^g,\dots ,{\overrightarrow{x}}_{N_p}^g\right\}$; Randomly initialize the mutation factor from [Fl, Fu]; Randomly initialize the crossover rate from [0, 1]; for i = 1 : Np do  if ${\overrightarrow{x}}_i^g$ violates the constraints then   $\mathrm{reset} {\overrightarrow{x}}_i^g$ as per the proposed constraint handling technique;  Evaluate the objective function, $f\left({\overrightarrow{x}}_i^g\right)$; end Select the best individual ${\overrightarrow{x}}_{best}^g$ from the population; Set FES = Np; /*FES denotes the number of function evaluations */ Population Evolution: for i = 1 : Np do  if $1\le i\le \frac{N_p}{3}$ then    generate mutant vector ${\overrightarrow{v}}_i^g$ following DE/rand/1 strategy;  if $\frac{N_p}{3}<i\le \frac{2N_p}{3}$ then   generate mutant vector ${\overrightarrow{v}}_i^g$ following DE/current-to-best/1 strategy;   if $\frac{2N_p}{3}<i\le N_p$ then   generate mutant vector ${\overrightarrow{v}}_i^g$ following DE/current-to-random/1 strategy;  if ${\overrightarrow{v}}_i^g$ violates the constraints then    reset ${\overrightarrow{v}}_i^g$ as per the proposed constraint handling technique;  Apply the crossover operation to generate trial vector ${\overrightarrow{u}}_i^g$;  Evaluate the objective function, $f\left({\overrightarrow{u}}_i^g\right)$;  Apply the selection operation; end Select the best individual ${\overrightarrow{x}}_{best}^g$ from the population; Update mutation factor; Update crossover rate; Set FES = FES + Np; Set g = g + 1; Stop Criterion: If FES > max_FES then stop the algorithm and output best individual ${\overrightarrow{x}}_{best}^g$ in the population; Else repeat the “Population Evolution” process.

2.5. Experimental Materials

The day-ahead electricity price, imbalance price, and power generation of a wind power plant in 2019 from the Nord pool electricity market, https://www.nordpoolgroup.com/ (accessed on 1 June 2021), are used for the development of copula models and for the derivation of the distribution of λ_t. The standard deviations of the forecasting errors of the day-ahead electricity price and wind power generation are assumed to be 10%. For each bidding day, 1000 independent scenarios will be generated to represent their uncertainties. Figure 2 illustrates the day-ahead electricity price, imbalance price, and wind power generation for this case study.

The rated capacity of the battery energy storage system is 78 MWh with a charging/discharging efficiency of 0.98. The P_max and P_min are assumed to be 26 MW and −26 MW, respectively, and SoC_min and SoC_max are assumed to be 0.1 and 0.9, respectively.

The setting of the parameters of the EDE algorithm is as follows: N_p = 180, max_EFS = 5.4 × 10⁵, F_l = 0.1, F_u = 0.9, and ξ₁ = ξ₂ = 0.1. The values of τ and β in the objective function are set as follows: τ = 0.2 and β = 0.1.

To validate the effectiveness of the proposed optimization algorithm in optimal power bidding, this paper compares the performance of the proposed optimization algorithm against state-of-the-art DE algorithms for constrained optimization problems, i.e., C²oDE [36] and NDE [40]. The C²oDE also deploys a variety of mutant operators to generate trail vectors. However, the proposed EDE algorithm is different form C²oDE in following ways: (i) in C²oDE, three trail vectors are generated for each individual by applying different mutant operators, while only the best trail vector is compared with the target individual for selection; (ii) the C²oDE integrates an ε-constraint method and the feasibility rule to handle the constraints. The proposed EDE is also different from the composite DE algorithms [24] in candidate selection and the constraint-handling technique. In NDE, a novel mutant operator is developed, and the feasibility rule is applied for constraint handling.

3. Results

To illustrate the robustness of optimization algorithms in finding the optimal strategy, 25 independent runs are performed for each optimization algorithm on each bidding day. This paper evaluates the optimization performance from the feasible rate (FR), success rate (SR), optimization accuracy, and convergence speed [41]. A solution is feasible if it satisfies the constraints. If at least one feasible solution is found in a run, it is called a feasible run. Similarly, if a feasible solution satisfying the successful condition is found in a run, it is called a successful run. In this study, the successful condition is defined as $f\left(\overrightarrow{x}\right)\ge 0.999f\left({\overrightarrow{x}}^{*}\right)$, where ${\overrightarrow{x}}^{*}$ denotes the best-known solution by all the algorithms. The best solution and the number of function evaluations (FEs) needed to find a successful solution are recorded for each run. The FR and SR define the ratio of feasible runs and successful runs with respect to total runs, respectively.

The best, mean, median, worst, and standard deviation (Std.) of the objective values of the best solutions over 25 runs as well as the FR are reported in

Table 1. Feasible rate (FR) and optimization accuracy over 25 independent runs.

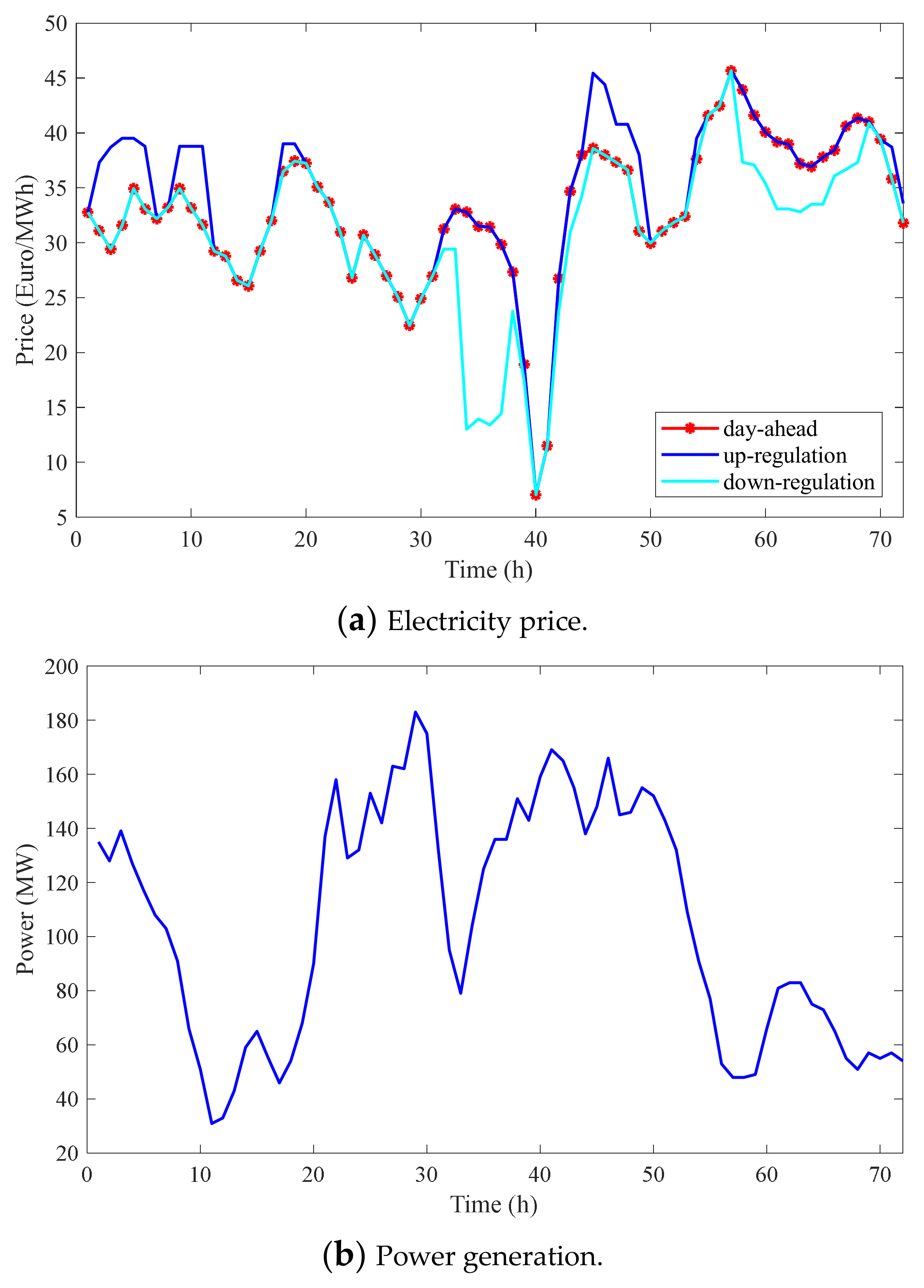
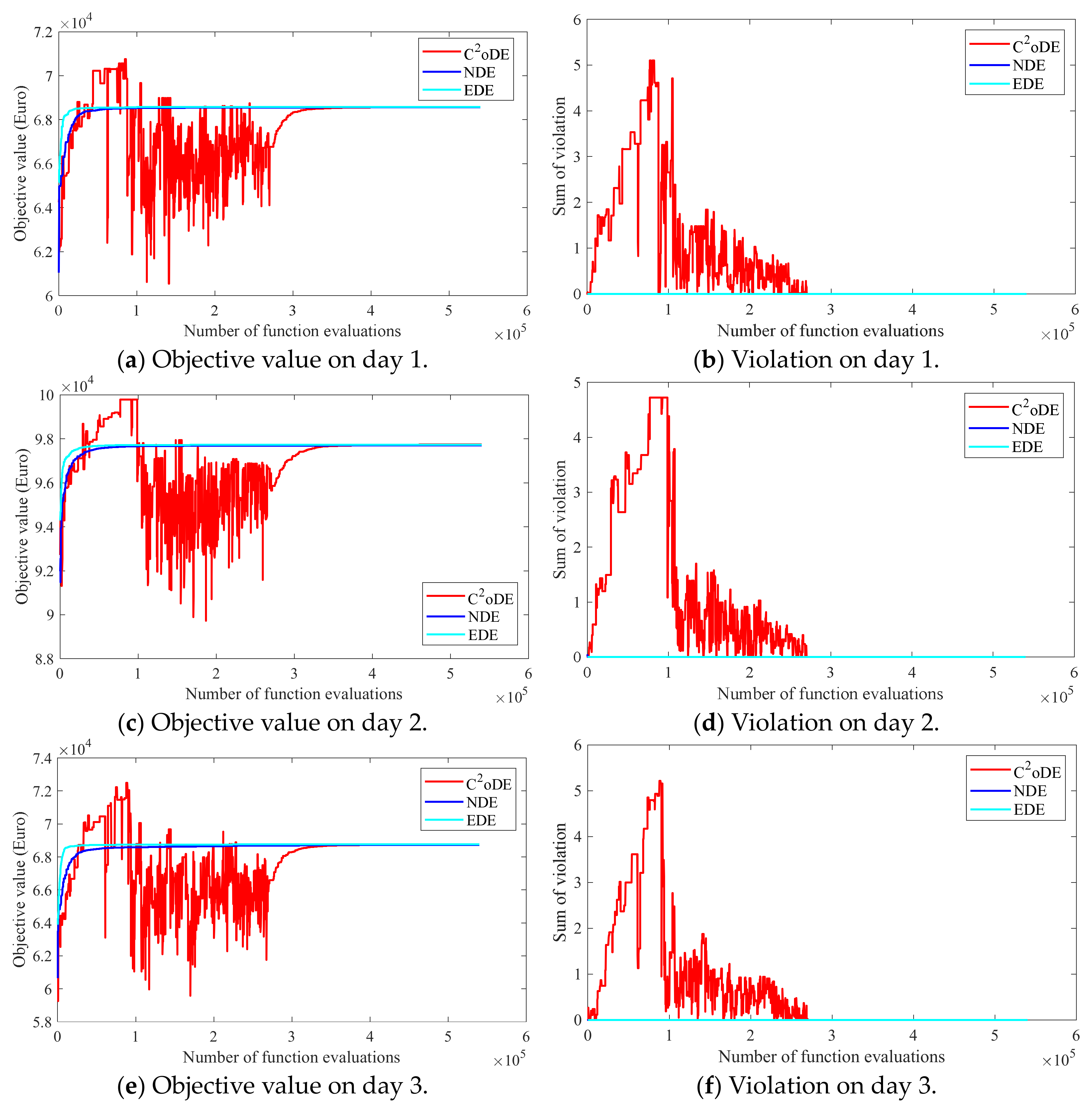
Bidding Day	Algorithm	FR	Best	Mean	Median	Worst	Std.
Day 1	C2oDE [36]	1	6.8595 × 104	6.8577 × 104	6.8574 × 104	6.8561 × 104	1.0116 × 101
	NDE [40]	1	6.8594 × 104	6.8571 × 104	6.8573 × 104	6.8551 × 104	1.2398 × 101
	EDE	1	6.8606 × 104	6.8583 × 104	6.8581 × 104	6.8572 × 104	8.6052 × 100
Day 2	C2oDE [36]	1	9.7789 × 104	9.7747 × 104	9.7751 × 104	9.7686 × 104	3.1887 × 101
	NDE [40]	1	9.7778 × 104	9.7699 × 104	9.7704 × 104	9.7539 × 104	5.4927 × 101
	EDE	1	9.7763 × 104	9.7730 × 104	9.7727 × 104	9.7709 × 104	1.4013 × 101
Day 3	C2oDE [36]	1	6.8804 × 104	6.8754 × 104	6.8746 × 104	6.8717 × 104	2.3752 × 101
	NDE [40]	1	6.8778 × 104	6.8728 × 104	6.8728 × 104	6.8690 × 104	2.2401 × 101
	EDE	1	6.8807 × 104	6.8766 × 104	6.8763 × 104	6.8720 × 104	2.5149 × 101

. From Table 1, the proposed EDE algorithm outperforms the benchmarking algorithms in terms of objective values on day 1 and day 3, while on day 2, C²oDE performs better than the proposed EDE algorithm in terms of the best, mean, and median values. These results illustrate that the proposed EDE algorithm is competitive in terms of optimization accuracy with state-of-the-art optimization algorithms.

Table 2. Success rate (SR) and number of FEs needed to succeed over 25 independent runs.

Bidding Day	Algorithm	SR	Best	Mean	Median	Worst	Std.
Day 1	C2oDE [36]	1	334,980	366,660	359,820	414,360	17,550
	NDE [40]	1	97,020	169,236	153,540	287,640	49,104
	EDE	1	32,040	45,900	45,540	63,900	7596
Day 2	C2oDE [36]	0.96	339,840	376,398	364,500	449,100	29,250
	NDE [40]	0.72	63,000	243,414	228,240	540,000	125,064
	EDE	1	32,400	78,840	69,300	171,900	31,482
Day 3	C2oDE [36]	0.72	353,700	427,086	409,860	510,840	55,476
	NDE [40]	0.28	140,940	271,008	251,100	407,700	86,454
	EDE	0.88	58,680	156,078	111,960	335,160	91,746

presents the best, mean, median, worst, and standard deviation of the number of FEs needed to succeed over the successful runs as well as the SR. It is observable that the proposed EDE algorithm provides a much higher SR than the benchmarking algorithms and can find successful solutions with a much faster speed. More precisely, the average values of SR on the three days are 0.893, 0.667, and 0.96 for C²oDE, NDE, and EDE, respectively. Compared to C²oDE and NDE, the average value of the mean number of FEs needed to succeed on the three days with EDE is reduced by 76% and 59%, respectively.

To better present the search process, Figure 3 illustrates the evolution of the best solution in a successful run (the run with the median number of FEs needed to succeed). These figures clearly demonstrate the powerful capacity of the proposed EDE algorithm in finding optimal solutions against the state-of-the-art algorithms for constrained optimization.

To summarize, the proposed EDE algorithm generally outperforms the benchmarking algorithms in finding optimal solutions, while it provides a much higher SR at a much faster speed. That is to say, the proposed EDE algorithm is much more reliable and faster in finding better solutions.

4. Conclusions and Discussions

In this paper, the optimal power bidding strategy for a wind–storage hybrid power plant is studied. The challenge for power bidding mainly lies in the uncertainties of wind generation and electricity prices. To handle this challenge, the power bidding problem is formulated as a risk-aware scenario-based stochastic programming, in which a number of scenarios are generated using a copula-based approach to represent the uncertainties. The copula-based generation of scenarios considers the temporal correlation of wind generation and electricity prices between consecutive time intervals. Moreover, this paper considers a more practical but nonlinear degradation function of the battery to derive a more appropriate battery operation regime, which leads to a nonlinear constrained optimization problem.

To solve the nonlinear constrained optimization problem, an EDE algorithm is proposed, which deploys an ensemble of mutant operators to generate mutant vectors. The EDE algorithm makes use of the merits of each mutant operator to improve the optimization performance. In addition, a problem-specific constraint-handling technique is developed. The proposed EDE algorithm is compared with state-of-the-art DE-based algorithms for constrained optimization problems, including C²oDE and NDE. The experimental results illustrate that the proposed EDE algorithm is much more reliable and much faster in finding a better solution. More precisely, the average values of SR on the three days are 0.893, 0.667, and 0.96 for C²oDE, NDE, and EDE, respectively. Compared to C²oDE and NDE, the average value of the mean number of FEs needed to succeed on the three days with EDE is reduced by 76% and 59%, respectively.

The numerical results demonstrate the efficiency of the developed bidding strategy considering battery degradation costs. However, to further verify its effectiveness, experiments on real wind–storage power plants are required.