Abstract
This paper extends the literature on the relationship between oil price shocks and financial markets by examining the effect of supply and demand oil shocks on emerging energy markets, stocks of emerging markets, and gold and exploring the impact of unpredictable oil events on the degree of connectedness among these markets. We show that the effect of supply oil price disturbances drives volatility spillovers in emerging markets with prominent medium- and long-term effects, unlike demand oil price unanticipated changes, particularly during turbulent periods such as the 2008 subprime crisis, the COVID-19 pandemic, and the 2015 oil price crash. These volatility spillover effects are influenced by a marked relationship between supply oil disturbances and emerging energy markets. We also expose that the COVID-19 pandemic volatility spillover consequences in emerging markets are unprecedented compared to the 2008 financial crisis. This can be attributed to the different nature of the related oil price disturbances and financial crises. Overall, the findings highlight the role of crude oil supply shocks as drivers not only of volatility dynamics in energy and equity emerging markets but also of financial connectedness patterns in these economies.
1. Introduction
As commodities have become strategic investment instruments in recent years, their effect on financial markets, examined mainly through the analysis of volatility spillovers, has received special interest in numerous works in the financial literature [1,2,3,4,5,6]. This considers the implications that this type of study has for investors and regulatory organizations in terms of portfolio optimization, optimal asset allocation, risk management strategies, and policy designs [1,2,3]. Currently, this type of study is becoming more imperative as a consequence of recurring booms and crises experienced by commodity and stock markets, the increasing globalization of economies, the steady financial market liberalization, and the accelerated expansion of cutting-edge communication technologies [3]. In addition, commodities have become an interesting diversification, hedging, and safe-haven instrument in the design of strategies by investors, a phenomenon known in the literature as commodity financialization [4,5]. This interest appears to have increased during turbulent periods [6,7], which has given rise to an increasing relationship between commodities and equity markets in the recent past [7].
Considering that oil has become one of the most tactical commodities globally, the effect of oil prices on financial markets has received notable attention within the volatility spillovers research strand. This takes into account the consequences that crude oil price fluctuations can have for the global economic trade and stability of crude oil exporting and importing countries [8]. In this line, the literature has documented that oil has become a driving factor behind geopolitical risks, macroeconomic trends, consumer sentiment, and corporate profitability. Moreover, there is evidence that oil market developments can have considerable effects on the world economy and financial markets [9,10,11]. The growing number of works in this research line has documented that demand and supply oil shocks have heterogeneous effects on financial markets. In consequence, since the seminal work of Kilian [12], a rapidly growing number of papers have been dedicated to examining whether oil price effects on financial markets were mainly driven by supply or demand factors by distinguishing between oil supply and demand disturbances [11]. However, most of these works have focused on the study of oil price unanticipated changes in developed stock markets [13,14,15], with a smaller number of works dedicated to studying other financial markets, including bond markets [11,16], precious metals [17], and energy markets [18,19].
The existing empirical evidence on the relationship between oil price disturbances and emerging markets is rather limited. Therefore, this work is mainly motivated by the absence of a significant number of papers focused on the analysis of the effects of supply and demand oil shocks in this type of market. Accordingly, the first contribution of this work is to examine the volatility spillovers among supply and demand oil shocks, energy and stocks of emerging markets, and gold. This topic has special relevance, considering the particularities in terms of complexity and fragility that characterize emerging markets, where understanding volatility spillover dynamics could be convenient for regulatory entities to preserve financial stability [20]. Moreover, previous studies have suggested the presence of specific connectedness patterns during turbulent periods, such as financial crises and market crashes [21,22,23]. These patterns imply interruptions or reversals in volatility spillover effects in the case of commodities, where volatility spillover dynamics appear to be time and event-dependent during these intervals [24,25]. In consequence, the second contribution of this work is the analysis of volatility spillover dynamics during the COVID-19 pandemic in emerging markets and their comparison with previous turbulent episodes.
In addition, our work contributes to the volatility spillover research strand in a third way, extending the literature related to the relationship between oil shocks and energy markets. Previous works have documented mixed conclusions about this relationship. However, the study of this interrelation employing supply and demand oil shocks rather than lumping them together has proven to generate clearer results [19]. Then, the examination of volatility spillovers among oil supply and demand shocks and emerging energy markets is pertinent to build on the financial literature. Moreover, gold is included in the analyzed system, taking into account that this is the most recognized “safe haven” precious metal [26], which makes this asset an appealing alternative to devising the optimal portfolio and dynamic hedging strategies in periods of turbulence generated by oil disturbances [27,28].
Finally, a fourth contribution of this work is the volatility spillover analysis employing time domain and frequency domain methods, which constitutes a topic to be explored in emerging markets. Although some works have employed time-domain approaches to study spillovers in this type of market, frequency-domain frameworks have not been extensively utilized. However, these types of models are more relevant to the present context as they allow for the examination of connectedness in the short, medium, and long terms, offering deeper insights into volatility spillover dynamics [3].
To sum up, the motivation for this work lies in the following reasons. First, the empirical evidence on the relationship between oil price disturbances and emerging markets is limited. Hence, our study contributes to the literature, providing new insights about this interrelation. This topic is of special interest to academics and practitioners, considering the particularities in terms of complexity and fragility that characterize emerging markets [20]. Second, although related works have found evidence of specific connectedness patterns during turbulent periods, such as financial crises and market crashes [21,22,23], the analysis of volatility spillover dynamics during the COVID-19 pandemic in emerging markets, and their comparison with previous turbulent episodes constitutes a field to be explored. Third, mixed conclusions about the relationship between oil shocks and energy markets have been documented. However, the study of this interrelation employing supply and demand oil shocks separately has generated clearer results [19]. Therefore, our application presents new evidence concerning this discussion with special emphasis on emerging markets. Finally, volatility spillovers in emerging markets employing time domain and frequency domain methods have not been widely explored. Hence, our exercise is relevant given that this type of analysis could shed light on volatility connectedness dynamics in this type of economy.
The remainder of this paper is organized as follows. In Section 2, we provide a review of the past literature. In Section 3, the employed methodology is presented. The empirical results and discussion are presented in Section 4, and Section 5 provides the conclusions and the policy and practical implications emanating from this study.
2. Related Works
2.1. Oil Shocks and Financial Markets
The influence of oil disturbances on financial markets has been extensively studied in the financial literature, given the relevance of oil prices in the financial and economic stability of global economies. This relationship can be explained based on the theory of equity valuation, which postulates that an increase in oil prices leads to decreasing aggregate stock prices, estimated as the summation of the discounted figures of expected cash flows at different periods since the movements in the oil price are likely to generate opposite influence on real output [3]. In recent years, the study of this topic has become more relevant, considering the transformation of oil from a basic commodity to an international commodity [8].
In this regard, there is a growing number of works in this research strand, mainly dedicated to examining the effects of oil prices on stock markets. For instance, Creti et al. [29] highlight the importance of the analysis of oil shocks through the dynamic conditional correlation method (DCC-GARCH), suggesting that oil is the commodity with the closest relationship with stock markets. Bazak and Pavlova [30] conducted a study about the financialization of commodities through a Diag-BEKK model, where they state that the propagation of risk between the WTI crude oil futures market and the stock market is more significant after extreme events such as those that occurred on September 11, 2001. Huang et al. [31] also confirm that volatility in the crude oil market is transmitted to the stock market, and Sharif et al. [32] argue that the U.S. stock market may be driven by oil prices in the short term.
However, it has been documented that not all sectors are affected by oil price disturbances in the same magnitude or manner. Some sectors are considerably affected, while others are slightly affected or not affected at all [33,34]. Moreover, since the seminal work of Kilian [13], different works have concluded that demand and supply oil shocks have heterogeneous effects on financial markets and sectors. In consequence, an increasing number of papers have been dedicated to examining whether oil price effects on financial markets are mainly driven by supply or demand factors by distinguishing between oil supply and demand shocks [11]. This is the case of energy markets, where previous studies have generated mixed conclusions about the spillover effects between oil disturbances and this type of market. In this regard, the study of this relationship employing supply and demand oil shocks rather than lumping them together has proven to generate clearer results [19]. For instance, Du and He [35] confirm the existence of risk spillovers between the oil and stock markets and point out the importance of disturbances in one market as a tool to predict shocks in the other. Mokni [36] reports that stock returns react variably to oil disturbances. In particular, there is a greater reaction to changes in oil demand, and for oil-exporting countries, demand unanticipated changes generally have a positive impact on stock returns.
Another relationship that should be taken into consideration is that between oil and precious metals, particularly gold. Through different studies, the predominance of this metal as a representative commodity to analyze volatility spillovers among precious metals and other markets is observed [37]. This, considering that gold is the most recognized “safe haven” precious metal [26], makes this asset an appealing alternative to devising optimal portfolios and dynamic hedging strategies in periods of turbulence generated by oil shocks [27,28,38]. Moreover, gold and oil are two of the most traded commodities; therefore, investors tend to diversify their portfolios with these materials alternately or in combination [39]. The existence of linkages between crude oil and gold prices is consistently confirmed through empirical analyses, along with the long-term equilibrium between these markets [40]. For instance, Tiwari et al. [3] found that titanium, platinum, gold, and silver are net volatility contributors. On the contrary, steel, crude oil, equities, and palladium are volatility receivers.
However, most of the previous studies related to volatility spillovers among oil shocks, energy, stocks, and gold are mainly focused on developed markets, with a reduced number of contributions focused on particular emerging markets such as China or BRIC countries. For instance, Luo and Ji [41] note that volatility in the US crude oil market spills over China’s agricultural markets. Wu et al. [42] confirm the impact of crude oil price volatility on China’s commodity markets through the construction of static dependence networks, noticing the crucial role of oil price as a component connector. From this scenario, the study of volatility spillovers among crude oil disturbances and different financial emerging market surges is an interesting field to be explored. This considers the particularities in terms of complexity and fragility that characterize these markets, where understanding volatility spillover dynamics could be convenient for regulatory entities to preserve financial stability [20].
Moreover, previous studies have suggested the presence of specific connectedness patterns during turbulent periods, such as financial crises and market crashes, which imply interruptions or reversals in volatility spillover effects in the case of commodities [21,22,23], suggesting that connectedness dynamics appear to be time and event dependent during these intervals [24,25]. This phenomenon is also supported by Ready [43], Benk and Gillman [44] and Elgammal et al. [45], who confirm that price fluctuations have a more significant impact on financial markets in times of extreme emergencies. Given that volatility spillovers are exacerbated by high-magnitude situations that threaten economic and market stability, such as the COVID-19 pandemic, the study of volatility spillovers in emerging markets becomes more relevant to analyzing the peculiarities and special features of volatility connectedness in turbulent periods for this type of fragile economy (It is worth noting that despite emerging energy markets presenting common features, there are marked economic and social differences among them to be considered. The particular characteristics and issues of specific emerging energy markets are studied in different documents, including the works of Poudyal et al. [46], Pokhrel et al. [47], Lin et al. [48], Sha and Sharma [49], and Santos et al. [50]).
2.2. Econometric Approaches
A topic of great relevance to recent economic research is the detailed study of common movements and volatility contagion effects between markets and assets. Starting from the pioneering work of Engle et al. [51], numerous studies have examined volatility spillover patterns across different variables. Specifically, multivariate specifications from the GARCH family have captured a large part of the work in this research area. Within the GARCH models family, a considerable number of approaches have been presented in the literature to model volatility transmission. Initially, the BEKK model, proposed by Engle and Kroner [52], received great acceptance due to its appropriate correlation matrix structure [18,53]. As a result, this model has been employed to analyze volatility linkages in different scenarios, which include stocks [54] and commodity markets [55,56].
Subsequently, the DCC model [57] emerged as a widely adopted multivariate volatility approach as a consequence of its simplicity and ease of interpretation [58]. This method ensures “the positive definiteness of the conditional covariance matrices and the ability to parsimoniously describe time-varying conditional correlations and covariances in a way” ([58], p. 69). Therefore, the DCC model has been employed for volatility analysis in commodities [59,60,61] and stock markets for developed and emerging countries [62,63,64].
Despite the advantages of DCC and BEKK models to conduct volatility transmission exercises in different settings, these approaches present notable limitations. De Almeida et al. [65] state that the BEKK model may generate erroneous conditional relations forecasts. Furthermore, the DCC model may present shortcomings, as discussed by Li [23], since it fails to capture the dynamic patterns of volatility spillovers and the net effect of bidirectional volatility relationships.
To address these shortcomings, Diebold and Yilmaz [66,67,68] developed a volatility spillover analysis framework based on the forecast error variance decompositions from vector autoregressions. This proposal presents substantial advantages for the study of volatility spillovers in financial markets. Particularly, the results obtained from this approach allow us to study volatility spillovers from a dynamic perspective. Moreover, net, directional, and total volatility spillovers can be examined, allowing for the identification of individual and systemic spillover effects [69]. In addition, this method is simple and intuitive [66] and can be employed to measure spillovers at various levels, including assets, firms, sectors, markets, and countries [68].
Considering the advantages offered by this framework, it has been widely employed to analyze volatility spillovers in a variety of markets or sectors, including energy markets [70,71,72], stock markets [73], and financial and economic sectors [74,75]. Moreover, different extensions have been developed to model and capture additional volatility spillover features. In this regard, Baruník and Krehlik [76] developed an approach to examining volatility connectedness at different frequencies employing the Fourier transformation on the Diebold and Yilmaz [67] method [77]. This model examines the total and directional spillovers among financial markets at short-, intermediate-, and long-term frequencies, which are crucial for market agents to quantify the extent, direction, and intensity of spillovers at different terms [78].
As a result, this innovative approach has been employed to analyze volatility spillovers among multiple markets and assets, such as traditional [16,77] and renewable [79,80,81] energy markets, cryptocurrencies [82], and developed stock markets [83,84]. However, the analysis of volatility spillovers in emerging markets through this framework is limited and constitutes a topic to be explored, given the peculiarities of this type of economy.
3. Materials and Methods
In this section, the methodology employed to develop our exercise is presented. Hence, the time domain method proposed by Diebold and Yilmaz [67] is described. Next, we introduce the volatility spillover approach in the frequency domain (the short-term, medium-term, and long-term) developed by Baruník and Krehlik [76]. These methods are based on the generalized forecast error variance decomposition (GFEVD) and the GFEVD spectral representations of the vector autoregressive (VAR) model, respectively.
3.1. Volatility Estimation
Since volatility spillovers are analyzed in this exercise, in the first stage, volatility is estimated to subsequently be employed as input in the posterior steps. Volatility estimation is based on the monthly estimated variance of the asset at time t ( [67,85], which is computed as follows:
where is the maximum price of asset at time , and corresponds to its minimum price. Then, this measure is annualized according to Equation (2).
Once volatility is calculated, the descriptive statistics for the analyzed variables are computed and analyzed.
3.2. Diebold–Yilmaz (DY) Spillover Model
The K-variable VAR (p) model can be conceived as
where defines the vector of the employed variables at time , and denotes the coefficient matrices. The error vector is independent and identically distributed, and white noise has a covariance matrix Σ. When the VAR model is stable, Equation (3) can be reexpressed as the infinite-order moving average ), formed according to the following equation:
where is a matrix of infinite lag polynomials. Based on the generalized VAR framework, the H-step-ahead GFEVD can be expressed as
where is a coefficient matrix of the polynomial at lag , and . defines the contribution of the model’s variable to the forecast error variance of the factor at horizon . To totalize one as the sum of the elements in each GFEVD row, each entry is standardized by the sum of the rows according to Equation (6):
is the pairwise spillover from to at horizon , which is used to measure the spillover effect from market to . Furthermore, the total spillover is denoted as the share of variance in the forecasts, which is contributed by errors other than own errors. The pairwise spillover can be aggregated into the total spillover in the form of the following equation:
where is the trace operator. The total spillover in all markets demonstrates the overall spillover. In addition, the DY model has two metrics to define the directional spillover. The directional spillover to variable from the other variables in the system is defined as
The directional spillover from variable to others of the VAR model is represented by Equation (9):
From Equations (8) and (9), the net directional spillover of variable can be obtained as follows:
3.3. Baruník and Krehlik (BK) Model
This model employs the Fourier transform to convert the Diebold and Yilmaz spillover results into the method based on frequency dynamics. The generalized causation spectrum over frequencies is denoted according to Equation (11):
where is the Fourier transform of the impulse response . It should be emphasized that is the component of the jth variable’s spectrum at the ω frequency due to shocks in the variable. can be weighted by the frequency share of the variable variance to obtain the generalized decomposition of variance in the frequency dynamics. This weighting function can be expressed as
It exhibits the power of the variable at a given frequency, which amounts to a constant value of through frequencies. When the impulse Fourier transform is a complex number, the weighted complex numbers’ square coefficients are the generalized factor spectrum and, hence, the real number. Formally, we build the frequency band .
Then, the GFEVD under the frequency band is defined according to Equation (13):
The total spillover (frequency connectedness) can be defined on the frequency band according to the following expression:
where Tr{.} is the trace operator, and is the summation of all factors of the matrix.
From Equation (14), the “from others” frequency directional spillovers measure can be estimated following Equation (15).
In addition, the “to others” frequency directional spillovers measure is given by the following expression.
Finally, from Equations (15) and (16), the net directional spillover of variable on the frequency band is represented by Equation (17).
4. Results and Discussion
In this section, the main results obtained from the employed methodology are presented. First, the data and the descriptive statistics of the utilized variables are analyzed. Posteriorly, the time and the frequency domain volatility spillovers for the utilized system are exhibited and examined.
4.1. Data and Descriptive Statistics
The main objective of the developed exercise is to analyze the volatility spillover dynamics among supply and demand oil shocks, gold, and energy and stocks of emerging markets. In consequence, monthly prices for the MSCI emerging markets index, the MSCI emerging markets energy index, and gold were retrieved from Bloomberg. For oil supply and demand shocks, the decomposed oil supply and oil inventory demand shocks constructed by Baumeister and Hamilton [86] were downloaded from the personal website of Professor Christiane Baumeister at “https://sites.google.com/site/cjsbaumeister/research (accessed on 14 August 2023)”. All the price series have been transformed to log returns as a way to circumvent the problem of non-stationarity or unit roots of the time series [87] to posteriorly be used as inputs to estimate volatility, as described in the methodology section. The analyzed period comprises 246 observations ranging from October 2002 to March 2023. Table 1 shows the main features of the employed data.

Table 1.
Oil shocks, energy, and stock measures.
Table 2 exhibits the descriptive statistics estimated from the employed variables. As can be observed, well-known returns stylized facts are evidenced in the utilized indices. The stock index mean is around 17.5, with a maximum (minimum) annualized volatility of 119.8 (4.76). Similar results are observed for gold, which has an average volatility of around 15.99, with a maximum (minimum) of around 64.5 (5.5). As expected, the energy index volatility is higher, reaching a mean of around 22.7 with maximum and minimum values of around 156.1 and 5.8, respectively. The three employed assets exhibit positive skewness and excess kurtosis coefficients, which implies that the utilized data do not fit a normal distribution.

Table 2.
Descriptive statistics.
To complement the presented features, Figure 1 depicts the gold, the stocks, and energy indices volatilities. Moreover, the supply and demand oil shocks historical data are shown. In the graph, it is possible to observe a continuously changing behavior in the employed variables over the analyzed sample. However, it can be noted that gold and the energy and stocks of emerging market volatilities reached their highest peaks around the 2008 subprime financial crisis and the COVID-19 pandemic. In addition, it is noted that the volatility values exhibited by these variables were considerably higher during the 2008 crisis compared to the second turmoil event. On the contrary, the supply and demand oil shocks time series maintain a relatively stable behavior during the subprime crisis to posteriorly exhibit their lowest values throughout the COVID-19 pandemic. These findings suggest that the subprime crisis and the COVID-19 pandemic have different effects on the analyzed variables.
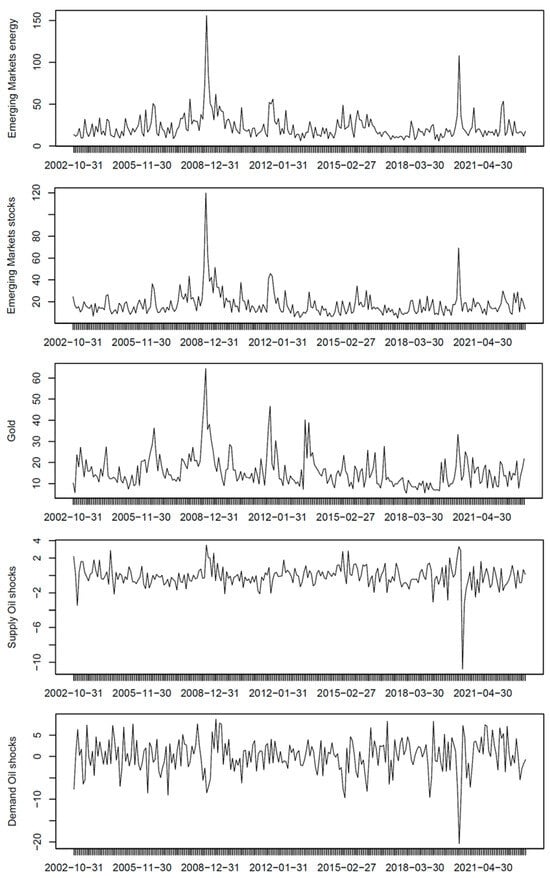
Figure 1.
Emerging market stocks and energy indices volatility, gold, and oil shocks.
4.2. Time-Domain Analysis
In this section, a static analysis of the total sample was developed to obtain general insights about the volatility spillover dynamics between the employed variables. In this regard, we selected four and ten as the order of the VAR model and the number of days ahead for the forecast errors, respectively, as proposed by Diebold and Yilmaz [67]. In Table 3, each entry ij (row i and column j) shows the estimated contribution to the forecast error variance of asset i volatility coming from shocks in asset j. The “from others” column reports the gross directional spillovers from the other assets to the asset in the corresponding row. Meanwhile, the “to others” row totalizes the contribution of each asset (column) to the other assets in the table. In addition, the “Net” row represents the net directional returns (volatility) spillovers, estimated by subtracting the “to others” from the “from others” measure. The Overall Connectedness Measure (OCM) proposed by Diebold and Yilmaz [67] can be found in the lower right corner of the table.

Table 3.
Volatility spillovers.
As can be observed, the OCM indicates that spillovers account for 42.41% of the total sample’s variance in volatility forecast error. Moreover, from a static perspective, gold, energy, and stocks of emerging markets indices are net transmitters of disturbances to the system, whereas the supply and demand oil shocks measures are net receivers of shocks from the system. In this regard, gold and the emerging markets energy index present high net spillover measures in the analyzed system. When analyzing the gross directional spillovers, it is possible to observe that the emerging markets energy and stock indices exhibit the highest effects on the other variables. However, in the case of the stock index, this effect is mitigated by the impact that this market receives from the system, resulting in a negative net spillover measure.
Numerous studies in the financial literature highlight the changing behavior of volatility spillovers over different intervals. In consequence, in Figure 1, the OCM is analyzed from a dynamic perspective to understand the changing patterns of volatility connectedness among the studied variables. This exercise was developed using a rolling window length of 54 observations and 3 months ahead forecast errors [88]. As can be observed, the OCM does not exhibit stable behavior. On the contrary, this measure is fluctuating continuously in a range between 30 and 50. The OCM’s highest peaks were reached during the subprime crisis and the COVID-19 pandemic, when this index showed values over 60 and 70, respectively. This confirms that volatility spillovers increase during turbulent periods, as previous studies suggest [21,22,23]. However, it should be mentioned that Figure 2 shows a higher increase in volatility spillovers during the COVID-19 pandemic compared to the 2008 financial crisis, suggesting that the impact of the 2020 crisis is unprecedented [77]. Finally, it is evidenced that the high levels of connectedness reached during both financial crises were maintained during the following years.
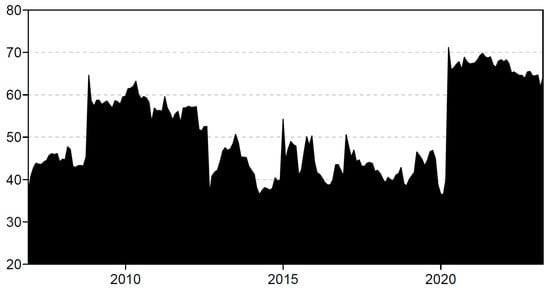
Figure 2.
Volatility spillovers OCM.
4.3. Frequency-Domain Analysis
To obtain further insights into the volatility spillover dynamics among the employed variables, the Baruník and Krehlik [76] approach is utilized to examine spillovers in the short, medium, and long terms. In this exercise, a rolling window length of 54 observations and 13 months ahead forecast errors [88] were employed. Moreover, the intervals from 1 to 6 months, 6 to 12 months, and 12 months onwards were defined as short, medium, and long terms, respectively [89]. Table 4 (Panel A) presents the volatility spillovers among gold, emerging markets energy and stock indices, and supply and demand oil shocks in the short (Panel A), medium (Panel B), and long terms (Panel C). In addition, Figure 3 depicts these results through network representations.

Table 4.
Volatility spillovers at different frequencies.
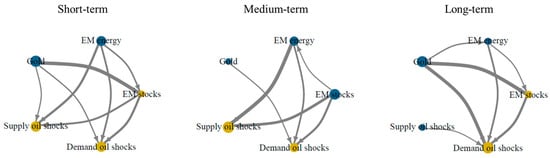
Figure 3.
Network representation of volatility spillovers at different frequencies. This figure represents the volatility spillovers in the analyzed system. Blue nodes correspond to assets that are net transmitters of shocks to the system, and yellow nodes depict indices that are net receivers of shocks from the system. The thickness of the line represents the strength of the association between two variables.
Table 4 exhibits that the share of frequency of 1 to 6 months (short term) has the highest contribution to the total volatility connectedness, which is 43.5%. It should be mentioned that the connectedness degree is lower in the medium term and reaches its lowest value in the long term, with OCM values around 21% and 9%, respectively. Moreover, it is evidenced that the emerging markets energy index and gold are net transmitters of disturbances to the system at all frequencies. However, the emerging markets energy index presents higher transmission effects to the system in the short and medium terms. Meanwhile, the net spillovers from gold to the system are prominent in the short term, reaching a value over 10% versus the same measure in the medium and long terms, which are below 3%. In addition, it is worth noting that supply and demand oil disturbances are net receivers of shocks from the system at all the analyzed frequencies. Nonetheless, when moving from short to long terms, the net spillover indices for these variables become less negative, approaching zero, which could suggest that the effects from these variables on the system need longer periods to be reflected. In the case of the stock index, the net spillover effects are less clear. This variable acts as a net transmitter of unanticipated changes to the system only in the medium term; meanwhile, it is a net receiver of shocks from the system in the short and long terms. All in all, our results suggest that the medium-term effects are predominant for this index, considering the magnitude of the estimated net spillovers.
These findings are confirmed by Figure 3, where volatility spillovers among the employed measures are represented as networks. Coherently, in the short term, it is possible to observe a larger number of linkages between the network nodes compared to the medium and long terms, confirming a greater degree of connectedness between the system variables, as previously suggested. Likewise, it is possible to observe that the nodes corresponding to the emerging markets energy index and gold are blue at all frequencies, confirming their role as net transmitters of volatility to the system. This can be explained by the high degree of interference and the notable repercussions that volatility in these markets can have on the other variables in the system. On the contrary, in the case of the demand and supply oil shock nodes, the yellow color suggests that these variables act as net receivers of shocks from the system at most of the analyzed frequencies. Interestingly, in the long term, the supply oil shock node presents a blue color, which suggests that these shocks act as net transmitters of shocks to the system at this time horizon. This indicates that the effects of supply oil shocks on the system require long periods to be reflected, as Table 4 evidences.
As mentioned before, volatility spillovers are dynamic and changing over time. In this sense, it is pertinent to examine the volatility spillovers from a dynamic perspective. Figure 4 shows the OCM in the short, medium, and long terms, as previously defined, using a rolling window of 54 observations [88]. As can be seen, the estimated OCM follows a continuously changing behavior with three outstanding peaks. The first is related to the subprime financial crisis when long-term effects are prominent and persistent over time. The second peak, reached in 2015, can be explained by the oil crisis, which started after an oil price crash over 50% at the end of 2014, with long-term dominant effects. The third peak, around the COVID-19 pandemic, is mainly characterized by short-term effects with some medium- and long-term effects.
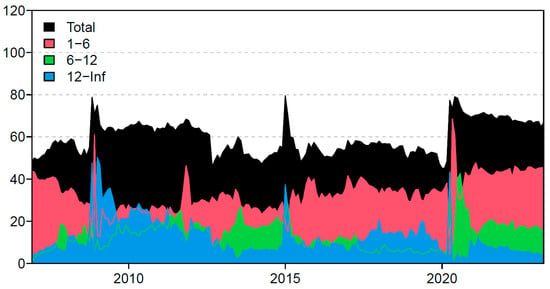
Figure 4.
Dynamic volatility OCM at different frequencies.
These results are noteworthy, considering that they provide evidence about the different impacts of financial crises according to their nature [90]. While the 2009 financial crisis originated in the financial sector to posteriorly spread to the rest of the economy, the COVID-19 pandemic crisis emerged from a shock that affected real production sectors and the prices of energy inputs, triggering shifts in global oil demand and supply [9,64,72,91]. On the other hand, the 2015 oil price crash attributed to a large negative flow demand shock associated with an unexpectedly slowing global economy [92]. Furthermore, it is evidenced that stocks and emerging energy markets are considerably affected during intervals with substantial oil disturbances. Specifically, there are particular patterns in the degree of connectedness and changes in the frequency of spillovers during these episodes.
In consequence, net volatility spillovers for each asset and index were estimated in the short, medium, and long terms. As depicted in Figure 5, the emerging markets energy index presents similar patterns to the supply oil shocks measure. Both net volatility spillover series exhibited increases during the 2008 and 2020 financial crises and the 2015 oil price crash. This is not the case with the demand oil shocks variable, which acts as a net receiver of disturbances from the system for most of the analyzed period. This is reasonable considering that it has been suggested that unanticipated changes in the oil supply play a more relevant role than demand shocks in price oil fluctuations [86]. In this line, it could be expected that the emerging markets energy index is affected by drastic changes in oil prices, mainly driven by supply oil shocks. Moreover, it should be mentioned that medium- and long-term effects are predominant when supply oil disturbances are net transmitters of shocks to the system; meanwhile, short-term effects are prominent during these intervals for the energy index, except for the mentioned financial crisis and the 2015 oil price crash. The above suggests that the effects of energy markets induced by the oil supply unanticipated changes are enduring over time in emerging markets.
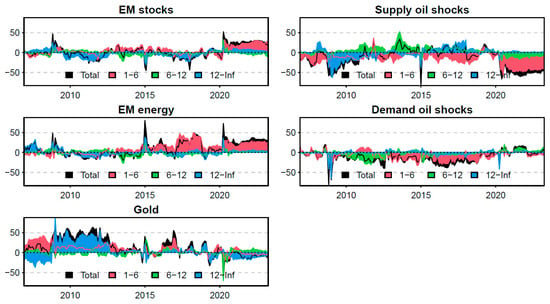
Figure 5.
Net volatility spillovers at different frequencies.
In addition, the net spillovers for these variables reached higher values during the 2015 and the COVID-19 pandemic compared to the subprime crisis, which confirms that volatility spillover effects are different, depending on the nature and origin of turbulent periods. Finally, Figure 5 suggests that the stock index is a net transmitter of shocks to the system during the 2008 subprime crisis and the COVID-19 pandemic, with long- and short-term dominant effects, respectively. Conversely, gold acted as a net transmitter of shocks to the system, with mixed long- and short-term effects, until the 2020 pandemic, when this asset became a net receiver of disturbances from the system.
5. Conclusions, Recommendations, Policy Insights, Limitations, and Future Works
This paper aims to shed light on the time- and frequency-domain dynamics of volatility spillovers among supply and demand oil shocks, energy, and stocks of emerging markets, and gold. In this line, the analysis is developed in two stages. First, the time-domain volatility spillovers for the analyzed system are explored employing the Diebold and Yilmaz [67] framework. In the second stage, the frequency-domain volatility spillovers are examined in short, medium, and long terms.
The main conclusions obtained from the developed exercise can be summarized as follows. First, volatility connectedness among supply and demand oil shocks, energy and stocks of emerging markets, and gold does not maintain a stable behavior. On the contrary, changing patterns are evidenced over the analyzed interval. Particularly, the OCM increases considerably during turbulent periods, as previous studies suggest [21,22,23]. Second, our results evidence that the impact of the COVID-19 pandemic on emerging markets is unprecedented, as concluded by previous studies in different contexts [77]. This proves that volatility spillovers exhibited higher increases during the COVID-19 pandemic compared to the 2008 financial crisis and the 2015 oil price crash. Moreover, it is evidenced that the high levels of connectedness reached during turbulent periods are maintained during the following years.
Third, when examining the frequency-domain spillovers, our results suggest that in the analyzed system, the share of frequency from 1 to 6 months (short term) has the highest contribution to the total volatility connectedness, followed by the medium- and the long-term effect contributions. Fourth, it is observed that the OCM estimated at different frequencies follows a continuously changing behavior with three outstanding peaks. The first is related to the subprime financial crisis when long-term effects are prominent and persistent over time. The second peak, reached in 2015, started after an oil price crash of over 50% at the end of 2014, with long-term dominant effects, and the third peak, explained by the COVID-19 pandemic, is mainly characterized by short-term effects with some medium- and long-term effects. These results are noteworthy, considering that they provide new evidence about the different impacts of financial crises according to their nature [90]. This is because the 2008 financial crisis originated in the financial sector and posteriorly spread to the rest of the economy. Meanwhile, the COVID-19 pandemic crisis emerged from a shock that affected real production sectors and the prices of energy inputs, triggering shifts in global oil demand and supply [9,64,72,91]. On the other hand, the 2015 oil price crash is attributed to a large negative flow demand shock associated with an unexpectedly slowing global economy [92]. Fifth, the volatility spillover dynamics in emerging markets are clearly related to oil price disturbances. Particularly, in our study, it is evidenced that stocks and emerging energy markets are considerably affected during intervals with prominent supply oil shocks. Sixth, it is exhibited that the emerging markets energy index presents similar patterns to those observed in the supply oil shocks variable. As a result, both net volatility spillover measures increased during the 2008 subprime crisis, the COVID-19 pandemic, and the 2015 oil price crash. This is not the case for the demand oil shocks variable, which acts as a net receiver of disturbances from the system for most of the analyzed period. It is reasonable to suggest that supply oil shocks play a more relevant role than demand unanticipated changes in price oil fluctuations [86]. In this line, it is reasonable to expect that the energy index is affected by drastic changes in oil prices, mainly driven by supply oil shocks. This finding is remarkable, considering that it provides new evidence about the impact of supply oil shocks on emerging energy markets. Moreover, it is suggested that the effects of energy markets induced by supply oil shocks are enduring over time in emerging markets.
The obtained conclusions have interesting implications for investors and regulatory organizations. In the case of investors, our study provides prominent insights about the volatility spillover dynamics among demand and supply oil shocks, gold, and energy and stocks of emerging markets. These insights can be useful to design hedging and investment strategies at different time horizons. In addition, our results can be employed to anticipate turbulent periods in emerging markets derived from supply oil shocks, which is relevant to implementing adequate financial risk management strategies. In addition, regulatory organizations can benefit from our exercise. On the one side, our findings could be used to guide decisions about financial and economic policies to protect emerging markets against the short- and long-term impacts of supply and demand oil shocks. Furthermore, the understanding of volatility spillovers can be useful to anticipate turbulent periods in emerging markets, which is of special interest, considering the fragility and instability of this type of economy.
The aforementioned implications gain special interest in the current context as a result of the reduction in the production of more than two million barrels introduced by Abdulaziz bin Salman, Saudi Minister of Energy, at the end of 2023. Given that a sudden cut in oil production can be seen as a supply oil shock, the obtained results suggest that its effects can be reflected in emerging energy and stock markets in the long term. This shows that oil supply shocks act as net transmitters of shocks to the studied system in this time horizon. In particular, according to our findings, the effects of the supply oil shock could take around a year to be reflected in the mentioned markets. In the case of emerging energy markets, a greater effect would be expected, considering the close relationship between oil supply shocks and this type of market, which increases when notable shocks occur. In the case of the stock market, a considerable negative effect would also be expected, given that oil supply shocks act as net transmitters of volatility to this market in the long term. In the case of gold, no considerable direct effects would be expected. However, gold volatility could increase, given the eventual detriment of the stock market.
The developed application presents limitations that do not compromise the relevance of the obtained results and can be addressed in future works. First, it could be interesting to analyze the volatility spillover dynamics for the studied system with data at different periodicities, such as daily or monthly. This confirms that new insights about volatility spillover effects in emerging markets can be derived from this exercise. Second, the developed implementation employs representative indices to capture the energy and stocks of emerging market behavior in aggregate. However, it could be pertinent to explore differences in volatility spillover dynamics according to the peculiarities of these sectors in specific emerging countries, considering the marked differences that characterize these economies. Third, the obtained findings are limited to examining volatility connectedness effects for energy and stocks of emerging markets. However, this application could be extended to examine these effects in other economic sectors, including the interrelation with developed markets. The aforementioned limitations can be addressed in future works to obtain new findings about volatility spillover dynamics in emerging markets.
Author Contributions
J.M.-M., conceptualization, methodology, software, writing; A.A.-O., conceptualization, writing—reviewing and editing; N.G., methodology, reviewing, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Universidad del Rosario, School of Management, the Gabriel Vegalara educational fund, and the Colombian Department of Science, Technology, and Innovation [COLCIENCIAS-757 call].
Data Availability Statement
The datasets generated during and/or analyzed during the current study are not publicly available due to Bloomberg property rights but are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Arouri, M.E.H.; Lahiani, A.; Nguyen, D.K. World gold prices and stock returns in China: Insights for hedging and diversification strategies. Econ. Model. 2015, 44, 273–282. [Google Scholar] [CrossRef]
- Basher, S.A.; Sadorsky, P. Hedging emerging market stock prices with oil, gold, VIX, and bonds: A comparison between DCC, ADCC and GO-GARCH. Energy Econ. 2016, 54, 235–247. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Mishra, B.R.; Solarin, S.A. Analysing the spillovers between crude oil prices, stock prices and metal prices: The importance of frequency domain in USA. Energy J. 2021, 220, 119732. [Google Scholar] [CrossRef]
- Ding, S.; Cui, T.; Zheng, D.; Du, M. The effects of commodity financialization on commodity market volatility. Resour. Policy 2021, 73, 102220. [Google Scholar] [CrossRef]
- Natoli, F. Financialization of commodities before and after the great financial crisis. J. Econ. Surv. 2021, 35, 488–511. [Google Scholar] [CrossRef]
- Ji, Q.; Zhang, D.; Zhao, Y. Searching for safe-haven assets during the COVID-19 pandemic. Int. Rev. Financ. Anal. 2020, 71, 101526. [Google Scholar] [CrossRef]
- Urom, C.; Ndubuisi, G.; Del Lo, G.; Yuni, D. Global commodity and equity markets spillovers to Africa during the COVID-19 pandemic. Emerg. Mark. Rev. 2023, 55, 100948. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J. Crude oil price shocks, volatility spillovers, and global systemic financial risk transmission mechanisms: Evidence from the stock and foreign exchange markets. Resour. Policy 2023, 85, 103875. [Google Scholar] [CrossRef]
- Sadorsky, P. Oil price shocks and stock market activity. Energy Econ. 1999, 21, 449–469. [Google Scholar] [CrossRef]
- Hamilton, J.D. Understanding crude oil prices. Energy J. 2009, 30, 179–206. [Google Scholar] [CrossRef]
- Demirer, R.; Ferrer, R.; Shahzad, S.J.H. Oil price shocks, global financial markets and their connectedness. Energy Econ. 2020, 88, 104771. [Google Scholar] [CrossRef]
- Kilian, L. Not all oil price shocks are alike: Disentangling demand and supply shocks in the crude oil market. Am. Econ. Rev. 2009, 99, 1053–1069. [Google Scholar] [CrossRef]
- Kilian, L.; Park, C. The impact of oil price shocks on the US stock market. Int. Econ. Rev. 2009, 50, 1267–1287. [Google Scholar] [CrossRef]
- Kang, W.; Ratti, R.A.; Yoon, K.H. Time-varying effect of oil market shocks on the stock market. J. Bank. Financ. 2015, 61, S150–S163. [Google Scholar] [CrossRef]
- Basher, S.A.; Haug, A.A.; Sadorsky, P. The impact of oil-market shocks on stock returns in major oil-exporting countries. J. Int. Money Financ. 2018, 86, 264–280. [Google Scholar] [CrossRef]
- Umar, Z.; Aharon, D.Y.; Esparcia, C.; AlWahedi, W. Spillovers between sovereign yield curve components and oil price shocks. Energy Econ. 2022, 109, 105963. [Google Scholar] [CrossRef]
- Umar, Z.; Jareño, F.; Escribano, A. Oil price shocks and the return and volatility spillover between industrial and precious metals. Energy Econ. 2021, 99, 105291. [Google Scholar] [CrossRef]
- Karali, B.; Ramirez, O.A. Macro determinants of volatility and volatility spillover in energy markets. Energy Econ. 2014, 46, 413–421. [Google Scholar] [CrossRef]
- Naeem, M.A.; Peng, Z.; Suleman, M.T.; Nepal, R.; Shahzad, S.J.H. Time and frequency connectedness among oil shocks, electricity and clean energy markets. Energy Econ. 2020, 91, 104914. [Google Scholar] [CrossRef]
- Chen, J.; Yang, L. A bibliometric review of volatility spillovers in financial markets: Knowledge bases and research fronts. Emerg. Mark. Financ. Trade 2021, 57, 1358–1379. [Google Scholar] [CrossRef]
- Goodell, J.W. COVID-19 and finance: Agendas for future research. Financ. Res. Lett. 2020, 35, 101512. [Google Scholar] [CrossRef] [PubMed]
- Laborda, R.; Olmo, J. Volatility spillover between economic sectors in financial crisis prediction: Evidence spanning the great financial crisis and COVID-19 pandemic. Res. Int. Bus. Financ. 2021, 57, 101402. [Google Scholar] [CrossRef]
- Li, W. COVID-19 and asymmetric volatility spillovers across global stock markets. N. Am. J. Econ. Financ. 2021, 58, 101474. [Google Scholar] [CrossRef]
- Antonakakis, N.; Kizys, R. Dynamic spillovers between commodity and currency markets. Int. Rev. Financ. Anal. 2015, 41, 303–319. [Google Scholar] [CrossRef]
- Liu, P.; Power, G.J.; Vedenov, D. Fair-weather Friends? Sector-specific volatility connectedness and transmission. Int. Rev. Econ. Financ. 2021, 76, 712–736. [Google Scholar] [CrossRef]
- Bouoiyour, J.; Selmi, R.; Wohar, M.E. Measuring the response of gold prices to uncertainty: An analysis beyond the mean. Econ. Model. 2018, 75, 105–116. [Google Scholar] [CrossRef]
- Chang, C.L.; McAleer, M.; Wang, Y. Testing Co-Volatility spillovers for natural gas spot, futures and ETF spot using dynamic conditional covariances. Energy J. 2018, 151, 984–997. [Google Scholar] [CrossRef]
- Bonato, M.; Gupta, R.; Lau, C.K.M.; Wang, S. Moments-based spillovers across gold and oil markets. Energy Econ. 2020, 89, 104799. [Google Scholar] [CrossRef]
- Creti, A.; Joëts, M.; Mignon, V. On the links between stock and commodity markets’ volatility. Energy Econ. 2013, 37, 16–28. [Google Scholar] [CrossRef]
- Basak, S.; Pavlova, A. A model of financialization of commodities. J. Financ. 2016, 71, 1511–1556. [Google Scholar] [CrossRef]
- Huang, S.; An, H.; Lucey, B. How do dynamic responses of exchange rates to oil price shocks co-move? From a time-varying perspective. Energy Econ. 2020, 86, 104641. [Google Scholar] [CrossRef]
- Sharif, A.; Aloui, C.; Yarovaya, L. COVID-19 pandemic, oil prices, stock market, geopolitical risk and policy uncertainty nexus in the US economy: Fresh evidence from the wavelet-based approach. Int. Rev. Financ. Anal. 2020, 70, 101496. [Google Scholar] [CrossRef]
- Phan, D.H.B.; Sharma, S.S.; Narayan, P.K. Oil price and stock returns of consumers and producers of crude oil. J. Int. Financ. Mark. Inst. Money 2015, 34, 245–262. [Google Scholar] [CrossRef]
- Mugaloglu, E.; Polat, A.Y.; Tekin, H.; Dogan, A. Oil price shocks during the COVID-19 pandemic: Evidence from United Kingdom energy stocks. Energy Res. Lett. 2021, 2. [Google Scholar] [CrossRef]
- Du, L.; He, Y. Extreme risk spillovers between crude oil and stock markets. Energy Econ. 2015, 51, 455–465. [Google Scholar] [CrossRef]
- Mokni, K. Time-varying effect of oil price shocks on the stock market returns: Evidence from oil-importing and oil-exporting countries. Energy Rep. 2020, 6, 605–619. [Google Scholar] [CrossRef]
- Yaya, O.S.; Tumala, M.M.; Udomboso, C.G. Volatility persistence and returns spillovers between oil and gold prices: Analysis before and after the global financial crisis. Resour. Policy 2016, 49, 273–281. [Google Scholar] [CrossRef]
- Ewing, B.T.; Malik, F. Volatility transmission between gold and oil futures under structural breaks. Int. Rev. Econ. Financ. 2013, 25, 113–121. [Google Scholar] [CrossRef]
- Sari, R.; Hammoudeh, S.; Soytas, U. Dynamics of oil price, precious metal prices, and exchange rate. Energy Econ. 2010, 32, 351–362. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wei, Y.M. The crude oil market and the gold market: Evidence for cointegration, causality and price discovery. Resour. Policy 2010, 35, 168–177. [Google Scholar] [CrossRef]
- Luo, J.; Ji, Q. High-frequency volatility connectedness between the US crude oil market and China’s agricultural commodity markets. Energy Econ. 2018, 76, 424–438. [Google Scholar] [CrossRef]
- Wu, F.; Zhao, W.L.; Ji, Q.; Zhang, D. Dependency, centrality and dynamic networks for international commodity futures prices. Int. Rev. Econ. Financ. 2020, 67, 118–132. [Google Scholar] [CrossRef]
- Ready, R.C. Oil prices and the stock market. Rev. Financ. 2018, 22, 155–176. [Google Scholar] [CrossRef]
- Benk, S.; Gillman, M. Granger predictability of oil prices after the Great Recession. J. Int. Money Financ. 2020, 101, 102100. [Google Scholar] [CrossRef]
- Elgammal, M.M.; Ahmed, W.M.; Alshami, A. Price and volatility spillovers between global equity, gold, and energy markets prior to and during the COVID-19 pandemic. Resour. Policy 2021, 74, 102334. [Google Scholar] [CrossRef] [PubMed]
- Poudyal, R.; Loskot, P.; Nepal, R.; Parajuli, R.; Khadka, S.K. Mitigating the current energy crisis in Nepal with renewable energy sources. Renew. Sust. Energ. Rev. 2019, 116, 109388. [Google Scholar] [CrossRef]
- Pokhrel, B.; Bhattarai, N.; Poudyal, R.; Gautam, R.; Paudyal, K.N. Grid parameters analysis of 11 kV radial feeder on residential areas based on forecasted emerging load: A case study of Tarkeshwor Municipality, Nepal. J. Eng. Issues Solut. 2023, 2, 120–137. Available online: https://www.researchgate.net/profile/Rupesh-Gautam-8/publication/371335628_Grid_parameters_analysis_of_11_kV_radial_feeder_on_residential_areas_based_on_forecasted_emerging_load_A_case_study_of_Tarkeshwor_Municipality_Nepal/links/647f50afb3dfd73b7769752a/Grid-parameters-analysis-of-11-kV-radial-feeder-on-residential-areas-based-on-forecasted-emerging-load-A-case-study-of-Tarkeshwor-Municipality-Nepal.pdf (accessed on 2 January 2024). [CrossRef]
- Lin, J.; Kahrl, F.; Yuan, J.; Liu, X.; Zhang, W. Challenges and strategies for electricity market transition in China. Energy Policy 2019, 133, 110899. [Google Scholar] [CrossRef]
- Sha, Y.; Sharma, S.S. Research on pandemics special issue of the journal emerging markets finance and trade. Emerg. Mark. Financ. Trade 2020, 56, 2133–2137. [Google Scholar] [CrossRef]
- Santos, A.Q.O.; da Silva, A.R.; Ledesma, J.J.G.; de Almeida, A.B.; Cavallari, M.R.; Junior, O.H.A. Electricity Market in Brazil: A Critical Review on the Ongoing Reform. Energies 2021, 14, 2873. [Google Scholar] [CrossRef]
- Engle, R.F.; Ito, T.; Lin, W.L. Meteor showers or heat waves? Heteroskedastic intra-daily volatility in the foreign exchange market. Econometrica 1990, 58, 525–542. [Google Scholar] [CrossRef]
- Engle, R.F.; Kroner, K.F. Multivariate simultaneous generalized ARCH. Econom. Theory 1995, 11, 122–150. [Google Scholar] [CrossRef]
- Liu, X.; An, H.; Huang, S.; Wen, S. The evolution of spillover effects between oil and stock markets across multi-scales using a wavelet-based GARCH–BEKK model. Phys. A Stat. Mech. Appl. 2017, 465, 374–383. [Google Scholar] [CrossRef]
- Cardona, L.; Gutiérrez, M.; Agudelo, D.A. Volatility transmission between US and Latin American stock markets: Testing the decoupling hypothesis. Res. Int. Bus. Financ. 2017, 39, 115–127. [Google Scholar] [CrossRef]
- Jin, X.; Lin, S.X.; Tamvakis, M. Volatility transmission and volatility impulse response functions in crude oil markets. Energy Econ. 2012, 34, 2125–2134. [Google Scholar] [CrossRef]
- Thenmozhi, M.; Maurya, S. Crude oil volatility transmission across food commodity markets: A multivariate BEKK-GARCH approach. J. Emerg. Mark. Financ. 2020, 20, 131–164. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Fiszeder, P.; Fałdziński, M.; Molnár, P. Range-based DCC models for covariance and value-at-risk forecasting. J. Empir. Financ. 2019, 54, 58–76. [Google Scholar] [CrossRef]
- Yu, L.; Li, J.; Tang, L. Dynamic volatility spillover effect analysis between carbon market and crude oil market: A DCC-ICSS approach. Int. J. Glob. Energy Issues 2015, 38, 242–256. [Google Scholar] [CrossRef]
- Tsuji, C. Return transmission and asymmetric volatility spillovers between oil futures and oil equities: New DCC-MEGARCH analyses. Econ. Model. 2018, 74, 167–185. [Google Scholar] [CrossRef]
- Hou, Y.; Li, S.; Wen, F. Time-varying volatility spillover between Chinese fuel oil and stock index futures markets based on a DCC-GARCH model with a semi-nonparametric approach. Energy Econ. 2019, 83, 119–143. [Google Scholar] [CrossRef]
- Fallahi, F.; Hghighat, J.; Sanoubar, N.; Jahangiri, K. Study of correlation between volatility of stock, exchange and gold coin markets in Iran with DCC-GARCH model. Econ. Res. 2014, 14, 123–147. [Google Scholar]
- Shehzad, K.; Liu, X.; Tiwari, A.; Arif, M.; Rauf, A. Analysing time difference and volatility linkages between China and the United States during financial crises and stable period using VARX-DCC-MEGARCH model. Int. J. Financ. Econ. 2021, 26, 814–833. [Google Scholar] [CrossRef]
- Molina-Muñoz, J.; Mora–Valencia, A.; Perote, J.; Rodríguez-Raga, S. Volatility transmission dynamics between energy and financial indices of emerging markets: A comparison between the subprime crisis and the COVID-19 pandemic. Int. J. Emerg. Mark. 2023. [Google Scholar] [CrossRef]
- De Almeida, D.; Hotta, L.K.; Ruiz, E. MGARCH models: Trade-off between feasibility and flexibility. Int. J. Forecast. 2018, 34, 45–63. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Measuring financial asset return and volatility spillovers, with application to global equity markets. Econ. J. 2009, 119, 158–171. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yılmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Gamba-Santamaria, S.; Gomez-Gonzalez, J.E.; Hurtado-Guarin, J.L.; Melo-Velandia, L.F. Stock market volatility spillovers: Evidence for Latin America. Financ. Res. Lett. 2017, 20, 207–216. [Google Scholar] [CrossRef]
- Awartani, B.; Maghyereh, A.I. Dynamic spillovers between oil and stock markets in the Gulf Cooperation Council Countries. Energy Econ. 2013, 36, 28–42. [Google Scholar] [CrossRef]
- Zhang, D. Oil shocks and stock markets revisited: Measuring connectedness from a global perspective. Energy Econ. 2017, 62, 323–333. [Google Scholar] [CrossRef]
- Corbet, S.; Goodell, J.W.; Günay, S. Co-movements and spillovers of oil and renewable firms under extreme conditions: New evidence from negative WTI prices during COVID-19. Energy Econ. 2020, 92, 104978. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Cunado, J.; Gupta, R.; Wohar, M.E. Volatility spillovers across global asset classes: Evidence from time and frequency domains. Q. Rev. Econ. Financ. 2018, 70, 194–202. [Google Scholar] [CrossRef]
- Baruník, J.; Kočenda, E.; Vácha, L. Asymmetric connectedness on the US stock market: Bad and good volatility spillovers. J. Financ. Mark. 2016, 27, 55–78. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Trans-Atlantic equity volatility connectedness: US and European financial institutions, 2004–2014. J. Financ. Econ. 2015, 14, 81–127. [Google Scholar]
- Baruník, J.; Křehlík, T. Measuring the frequency dynamics of financial connectedness and systemic risk. J. Financ. Econ. 2018, 16, 271–296. [Google Scholar] [CrossRef]
- Zhang, W.; Hamori, S. Crude oil market and stock markets during the COVID-19 pandemic: Evidence from the US, Japan, and Germany. Int. Rev. Financ. Anal. 2021, 74, 101702. [Google Scholar] [CrossRef]
- Mensi, W.; Al-Yahyaee, K.H.; Al-Jarrah, I.M.W.; Vo, X.V.; Kang, S.H. Does volatility connectedness across major cryptocurrencies behave the same at different frequencies? A portfolio risk analysis. Int. Rev. Econ. Financ. 2021, 76, 96–113. [Google Scholar] [CrossRef]
- Ferrer, R.; Shahzad, S.J.H.; López, R.; Jareño, F. Time and frequency dynamics of connectedness between renewable energy stocks and crude oil prices. Energy Econ. 2018, 76, 1–20. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Ugolini, A.; Aiube, F.A.L. Network connectedness of green bonds and asset classes. Energy Econ. 2020, 86, 104629. [Google Scholar] [CrossRef]
- Ferrer, R.; Shahzad, S.J.H.; Soriano, P. Are green bonds a different asset class? Evidence from time-frequency connectedness analysis. J. Clean. Prod. 2021, 292, 125988. [Google Scholar] [CrossRef]
- Kumar, A.; Iqbal, N.; Mitra, S.K.; Kristoufek, L.; Bouri, E. Connectedness among major cryptocurrencies in standard times and during the COVID-19 outbreak. J. Int. Financ. Mark. Inst. Money 2022, 77, 101523. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, Y.; Wang, Q.; Liu, Y. International stock market risk contagion during the COVID-19 pandemic. Financ. Res. Lett. 2022, 45, 102145. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, P.; Huang, L. Time-frequency volatility spillovers between major international financial markets during the COVID-19 pandemic. Financ. Res. Lett. 2022, 46, 102244. [Google Scholar] [CrossRef] [PubMed]
- Parkinson, M. The extreme value method for estimating the variance of the rate of return. J. Bus. 1980, 53, 61–65. [Google Scholar] [CrossRef]
- Baumeister, C.; Hamilton, J.D. Structural interpretation of vector autoregressions with incomplete identification: Revisiting the role of oil supply and demand shocks. Am. Econ. Rev. 2019, 109, 1873–1910. [Google Scholar] [CrossRef]
- Yaya, O.S.; Ogbonna, A.E.; Adesina, O.A.; Alobaloke, K.A.; Vo, X.V. Time-variation between metal commodities and oil, and the impact of oil shocks: GARCH-MIDAS and DCC-MIDAS analyses. Resour. Policy 2022, 79, 103036. [Google Scholar] [CrossRef]
- He, F.; Wang, Z.; Yin, L. Asymmetric volatility spillovers between international economic policy uncertainty and the US stock market. N. Am. J. Econ. Financ. 2020, 51, 101084. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Yan, X.X. The impact of US economic policy uncertainty on WTI crude oil returns in different time and frequency domains. Int. Rev. Econ. Financ. 2020, 69, 750–768. [Google Scholar] [CrossRef]
- Hanif, W.; Teplova, T.; Rodina, V.; Alomari, M.; Mensi, W. Volatility spillovers and frequency dependence between oil price shocks and green stock markets. Resour. Policy 2023, 85, 103860. [Google Scholar] [CrossRef]
- Basher, S.A.; Sadorsky, P. Oil price risk and emerging stock markets. Glob. Financ. J. 2006, 17, 224–251. [Google Scholar] [CrossRef]
- Baumeister, C.; Kilian, L. Understanding the Decline in the Price of Oil since June 2014. J. Assoc. Environ. Resour. Econ. 2016, 3, 131–158. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).