Impacts of Electric Vehicle Charging Station with Photovoltaic System and Battery Energy Storage System on Power Quality in Microgrid

Abstract

The expected increase in electric vehicles necessitates an expansion in charging stations. However, this increase could introduce issues to the power grid, such as the deterioration of voltage stability and an increase in microgrid loading. To address these issues, innovative solutions are imperative. One potential solution is the implementation of charging control mechanisms. This paper analyzes the impact of a residential charging station on a low voltage microgrid from the power quality point of view using a one-year operation simulation. Thirty-seven charging station scenarios with different locations within the network were examined, including instances with no charging control and various combinations involving charging control, photovoltaic power plant, and battery energy storage system. The simulation results of the charging station without charging control show a decrease in some power quality indicators, such as exceeding voltage change thresholds after charging station connection and increasing power losses. On the contrary, the scenarios implementing charging control and local resources effectively mitigate the adverse effects of charging stations on the microgrid.

1. Introduction

The transportation sector stands as a major contributor to climate change, primarily reliant on diminishing fossil fuels like petrol and diesel. Given the imminent scarcity of these resources, electric vehicles have significant interest due to their potential to reduce both fuel consumption and emissions as mentioned in [1]. The European Union (EU) has set goals to curtail greenhouse gas emissions by a minimum of 55% by 2030, relative to 1990 levels, with a specific target of reducing emissions from the transportation sector by 90%. In line with these objectives, the EU Council has endorsed a preliminary approach to a proposal for a regulation that establishes infrastructure for alternative fuels. The primary objective of this proposal [2] is to establish an accessible network of charging stations. This will increase the number of charging stations across the EU, including Slovakia. However, the increasing number of charging stations may introduce issues to the electrical grid to which they are connected. These issues can be related to voltage stability, control, and the potential degradation of power quality. The severity of these adverse impacts primarily depends on the power consumption of the charging stations and the existing conditions of the power grid. To prevent any disruptions in the operation of the power grid, it is important to conduct an analysis of the impact of charging stations. The influences of an electric vehicle charging station are shown in the referenced publications [3,4].

A large number of simultaneously charging electric vehicles can produce pronounced power peaks, particularly during periods of high consumption. This can cause significant issues, including voltage fluctuations, instantaneous load peaks, and increased power losses. The effective implementation of charging control mechanisms can be a pivotal strategy to address these issues. An analogous approach is delineated in the reference [5]. In the paper [6], a review of different control strategies related to the control of microgrids with electric vehicle charging stations is presented. The paper also discusses the importance of the utilization of control mechanisms, renewable energy resources (RES), and storage systems to mitigate the undesirable effects of charging station integration into the microgrids.

This study investigates the influence of the presented residential charging station operation with the PV power plant, the BESS, and charging control mechanisms on the CIGRE Residential Low Voltage Distribution Network (CIGRE RLVDN) microgrid. The CIGRE RLVDN microgrid has also been utilized in prior research by other authors [7,8,9]. In the study presented in reference [7], the authors introduce a novel strategy for optimizing demand load shifting as a part of day-ahead energy management. Subsequently, they applied and tested this strategy on the CIGRE RLVDN. Another study [8] demonstrates methods to mitigate voltage sags within the CIGRE RLVDN. Additionally, in reference [9], an evaluation of harmonic distortion in the CIGRE RLVDN is provided, considering five distinct scenarios of photovoltaic penetration.

The main contribution of this study resides in the comprehensive analysis of the presented charging station system for six distinctive charging station operational scenarios. The charging station operation scenarios encompass various cases of charging station operation configurations, including the operation with no charging control and variable combinations of operations with the charging control, the PV power plant, and the BESS. Furthermore, the investigation assesses the impact of operating the charging station at three different nodes of the microgrid to see how the location of its connection affects voltage fluctuations. Moreover, to the best of the authors’ knowledge, there is no existing study that has conducted such an experimental testing of a residential charging station operation with a charging control mechanism and complementary power sources in order to evaluate its impact on the power quality of the low voltage microgrid in such a comprehensive way as is presented in this study.

The rest of this paper is organized as follows: Section 2 discusses the materials and methods used within this paper. Section 3 presents the results of the charging station operation analysis and its impact on the microgrid. Discussion of the results is presented in Section 4, and Section 5 concludes the paper.

2. Materials and Methods

2.1. Computing Program and Electrical Grid

The evaluation and analysis of the impact of electric vehicle charging station connection to the microgrid is performed using the open-source computation program Pandapower. This program is used for power system modeling, analysis, and optimization. Pandapower comprises two distinct libraries: Pandas, utilized for data analysis, and Pypower solver, employed for power flow computations. The simulation model within Pandapower was constructed using the Python programming language [10]. To conduct the simulations, the microgrid system depicted in Figure 1 was utilized. This microgrid is based on the topological structure derived from the CIGRE Residential Low Voltage Distribution Network (RLVDN) [11,12]. This specific grid configuration has been pre-defined and parameterized within the Pandapower library.

The simulated microgrid system is connected to an external grid (EG1) with a short circuit power of 100 MVA via a distribution transformer (T1) characterized by a transformation ratio of 20/0.4 kV and a rated apparent power of 500 kVA. The microgrid consists of 19 nodes, from which a single node N1 operates at the nominal voltage level of EG1 (20 kV). The remaining nodes (N2–N19) within the microgrid operate at a voltage level of 400 V. The combined length of the low-voltage lines (L1–L17) amounts to 5.7 km, and their capacitance is neglected.

The microgrid contains six distinct loads (C1–C6), each representing groups of residential customers. These consumers are characterized as constant power loads with a total installed power of 383.8 kW. All loads are considered to have a power factor of 0.95, which has an inductive character. The installed power capacities and representative load profiles (RLP) of individual residential customers are described in

Table 1. The installed powers of customers.

	S (kVA)	P (kW)	Q (kvar)	RLP
C1	200	190	62.45	RLP 2
C2	15	14.25	4.68	RLP 1
C3	52	49.4	16.24	RLP 3
C4	55	52.25	17.17	RLP 1
C5	35	33.25	10.93	RLP 2
C6	47	44.65	14.68	RLP 3

. A detailed description of each RLP is provided in the subsequent sections of this text.

Additionally, a single residential charging station was gradually connected to specific nodes within the microgrid, specifically nodes N3, N6, and N11. The selection of these locations was random, with the sole criterion being that charging stations would be positioned near the external grid, in the middle of the radial network, and far from the supplying external grid. Subsequently, two residential charging stations were gradually connected to the microgrid. This process involved the selection of various node combinations (N3 and N6, N3 and N11, and N6 and N11) where the charging stations were connected. For each of these selected nodes and node combinations, six distinct charging station operation scenarios (S1–S6) were implemented and subsequently analyzed.

2.2. Microgrid Operation Scenarios

The simulations were conducted over a period of one year, including a total of 8760 h. Throughout this simulated year, the consumption in the microgrid varied on an hourly basis. All customers in the microgrid were set to a constant power factor of 0.95 throughout the simulation period.

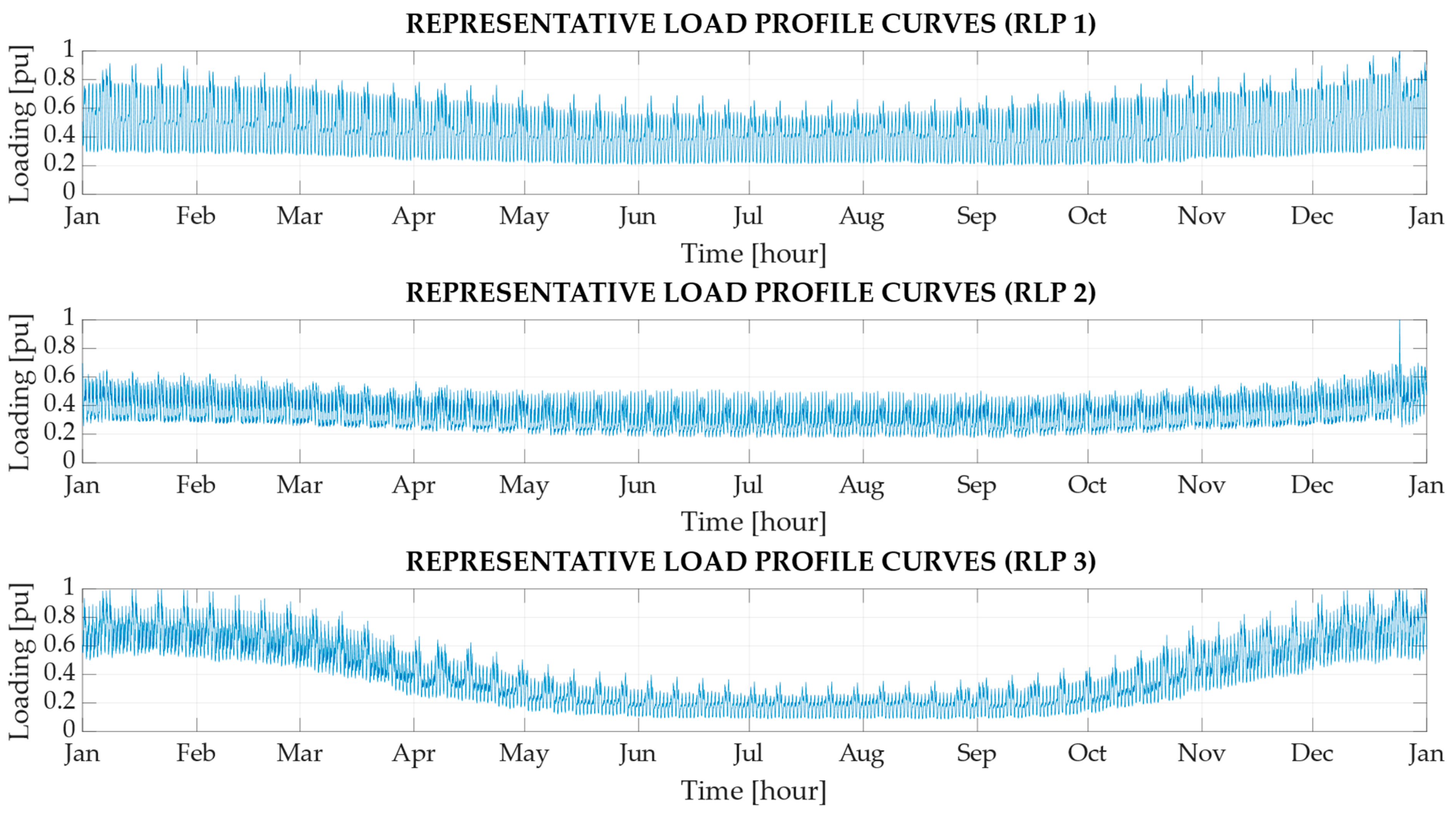
For variable consumption, RLPs shown in Figure 2 were employed. These RLPs were obtained from the Slovak distribution system operator [13]. Three different types of RLPs were utilized in the simulations, each representing a specific tariff and heating arrangement:

• RLP 1: this profile corresponds to a single rate tariff, involving electric water heating and the absence of electric heating.
• RLP 2: this profile corresponds to a double rate tariff, involving accumulation electric heating and electric water heating.
• RLP 3: this profile corresponds to a double rate tariff, involving direct electric heating and electric water heating.

These RLPs are used to generate varying load profiles and reflect the diverse consumption scenarios in the microgrid.

Figure 2 shows the representative load profile (RLP) curves illustrating the consumed powers for typical types of consumers in Slovakia. These power values are expressed in per-unit terms relative to the installed capacity of individual consumers. In the simulated microgrid, a total of six consumers are present. The installed powers of individual consumers are multiplied by the pu values of RLPs for the simulated period. This multiplication is performed based on Table 1, where each RLP is assigned to specific consumers. Consequently, the collective energy consumption of all microgrid consumers amounts to 1.26 GWh. This energy consumption exhibits a constant power factor of 0.95, which has an inductive character.

The consumption of the charging station (CS) is subject to variations over time, driven by electric vehicle (EV) charging demands. Power profiles are generated using the CS model outlined in [14]. The operation of the CS is modified based on six distinct scenarios, as detailed below:

• S1: the CS operates without charging control.
• S2: the CS operates with charging control.
• S3: the CS operates with charging control and a photovoltaic power plant + supplying excess energy to the grid.
• S4: the CS operates with charging control and a photovoltaic power plant + without supplying excess energy to the grid.
• S5: the CS operates with charging control, a photovoltaic power plant, and a battery storage system + supplying excess energy to the grid.
• S6: the CS operates with charging control, a photovoltaic power plant, and a battery storage system + without supplying excess energy to the grid.

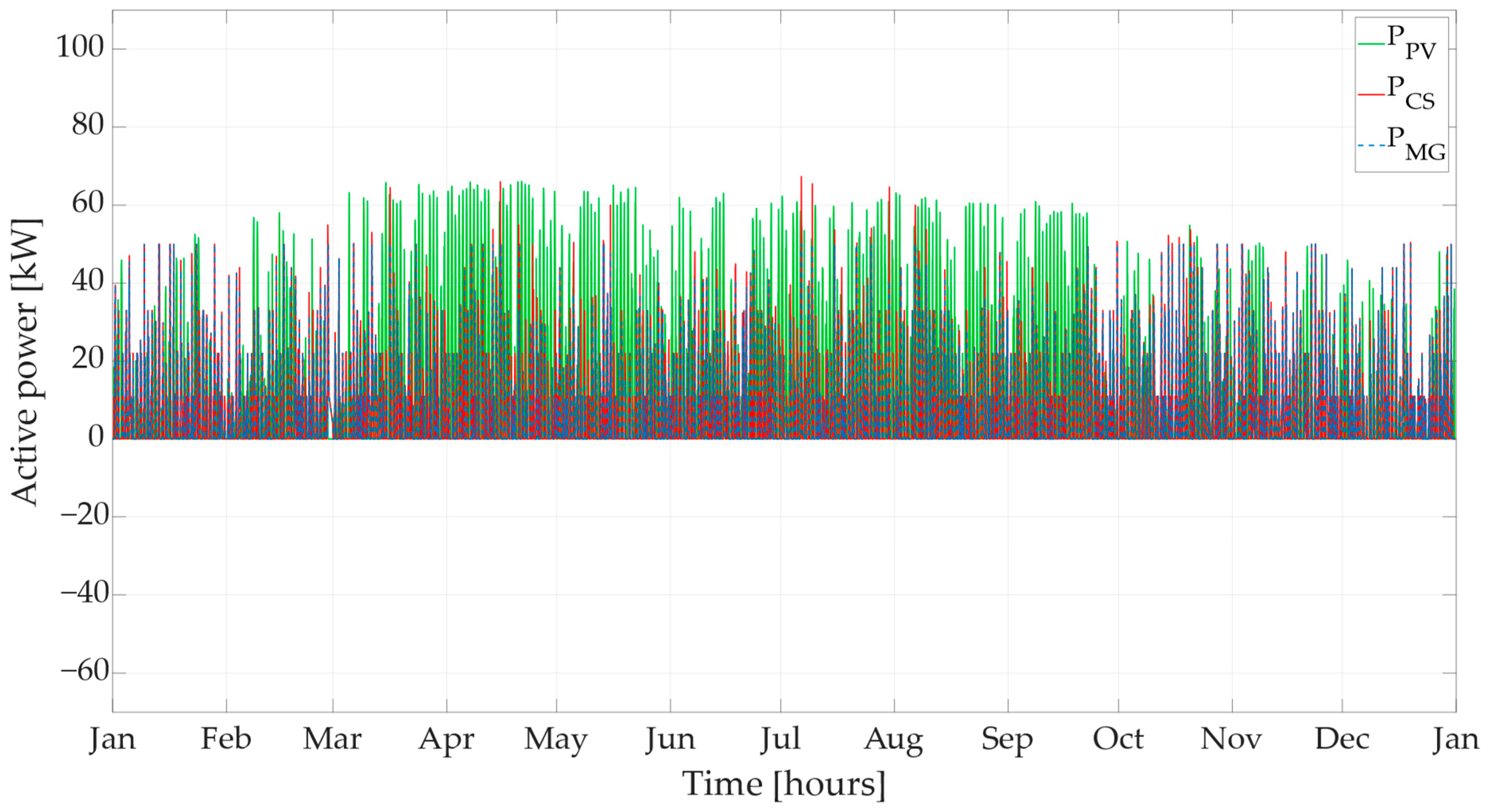
The detailed descriptions of all the charging station scenarios are provided in the subsequent sections of this text. Figure 3 illustrates the active power curves depicting the power exchange between the charging station and the microgrid across all scenarios. The active power of the charging station can assume either positive values, indicating consumption from the grid, or negative values, indicating supply to the grid. Throughout the charging station’s operation, it is assumed that power factor correction is in place, resulting in a constant power factor of one throughout the entire operational duration.

A total of 37 distinct scenarios were analyzed for the microgrid’s operation. Initially, in the baseline scenario, the charging station remained unconnected to the microgrid, and power consumption was solely generated by individual consumers following the RLP curves. This served as the reference scenario for comparison. Subsequently, 36 additional scenarios were evaluated, each involving the connection of the charging station to the microgrid. The set of 37 analyzed scenarios comprised one baseline scenario and 36 additional scenarios. These additional scenarios were derived from the combinations of CS scenarios (S1–S6) and the location of a single charging station at three nodes (N3, N6, and N11), resulting in 18 scenarios. Additionally, scenarios involving the location of two charging stations at three node combinations (N3 and N6, N3 and N11, and N6 and N11) were considered, adding 18 more scenarios to the analysis. To illustrate, the charging station was first connected to node N3, and all six charging station operation scenarios (S1–S6) were computed accordingly. This procedure was then replicated for the other selected nodes and node combinations within the microgrid. This systematic approach enabled a comprehensive assessment of the charging station’s impact on the microgrid, contingent upon its specific connection point within the network.

In these 36 scenarios, the power consumption patterns of individual consumers were maintained at the same levels as observed in the initial microgrid scenario, where the charging station was not yet integrated. The gradual connection of the charging station to selected nodes within the microgrid, as depicted in Figure 1, was executed.

2.3. Charging Station System

The charging station system interconnected with the simulated microgrid system is represented by a residential charging station integrated with a photovoltaic (PV) power plant and a battery energy storage system (BESS). PV power plant together with the BESS is used to provide power for the charging of EVs connected to the CS and thereby decrease the burden placed on the microgrid system represented by bus voltage fluctuations. The BESS is also used to maximize the use of the PV power plant. The charging station is designed to accommodate up to 30 EVs simultaneously. Therefore, CS consists of 30 level 2 charging stands, each with a maximal charging power of 11 kW. To represent the realistic operation of the residential charging station, the occupancy model presented in [14] based on the historical charging data [15] was utilized. PV power plant output is calculated based on the historical data from the publicly accessible online application PVGIS [16]. The parameters of the PV power plant and the BESS are stated in

Table 2. Charging station system parameters.

Charging Station	PV Power Plant	BESS
30 × 11 kW	80 kWp	150 kWh

.

The residential charging station model is based on the models presented in [17,18], in which the charging station model consisted only of a residential charging station and a PV power plant. Therefore, to ensure the optimal charging of EVs connected to the charging station and the optimal utilization of power from the PV power plant, the BESS is added to the system, and a charging control mechanism is utilized. The presented charging control mechanism is based on the control mechanism defined in [17], which was also used in our previous studies [14,18]. The control mechanism is used to minimize the difference between the charging power of EVs and the available power from the PV and the BESS. The control mechanism utilized in this paper solves the following optimization problem:

$$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e} {\gamma }_1·{\left[P_{uPV,t}^{ }-{\sum }_{i=1}^I·u_{EV,i}^t-u_{BES}^t\right]}^2-{{\gamma }_2·P}_{uPV,t}^{ }-{\gamma }_3·{\sum }_{i=1}^I·u_{EV,i}^t,$$

(1)

such that

$$0\le u_{EV,i}^t\le u_{EV}^{+},$$

(2)

$$u_{BES}^{-}\le u_{BES}^t\le u_{BES}^{+},$$

(3)

$$0\le P_{uPV,t}\le P_{PV,t},$$

(4)

where $\left\{{\gamma }_1, {\gamma }_{2,}{ \gamma }_3\right\}\in \mathbb{R}$ are weighting parameters, $P_{uPV,t}^{ } \left(\mathrm{k}\mathrm{W}\right)$ is the power drawn from the PVA at time step $t$, $u_{EV,i}^t \left(\mathrm{k}\mathrm{W}\right)$ is the charging rate of $i^{th}$ EV connected to the CS at time step $t$, $u_{EV,i}^{+}$ is the maximum charging rate, $u_{BES}^t \left(\mathrm{k}\mathrm{W}\right)$ is the charging/discharging rate of the BESS at time step $t$, $u_{BES}^{-} \left(\mathrm{k}\mathrm{W}\right)$ and $u_{BES}^{+} (\mathrm{k}\mathrm{W}$) are the maximal discharging and charging rates of the BESS, and $P_{PV,t} \left(\mathrm{k}\mathrm{W}\right)$ is the available power from the PVA.

Charging station operation is simulated for six different operational scenarios as was mentioned in Section 2.2. The priority of each power source in the microgrid used for a residential charging station is determined based on the weighting parameters for each scenario, with the policy that the use of the PV power source for EV charging is of the highest importance. For a better evaluation of the simulation results and their impacts on the microgrid operation, the same charging station occupancy data obtained using the occupancy model proposed in [14] were used for all scenarios, and the approximately same annual charging station consumption rate (64 MWh) was maintained for all scenarios using the energy control mechanism.

2.3.1. Charging Station Operation without Charging Control (S1)

The first scenario of charging station operation represents the operation of a residential charging station without the charging control mechanism, a PV power plant, and the BESS. In this scenario, the charging station is entirely dependent on the power drawn from the microgrid to facilitate the charging of EVs. During this process, the EVs are charged with the maximum charging power from the beginning to the end of the charging cycle. The charging station’s power consumption profile during this operational scenario is illustrated in Figure 3 (S1). An important observation in this scenario is that the depicted consumption curve shows multiple instances of significant power consumption peaks. This behavior requires attention as these power peaks present the potential to introduce operational problems for the microgrid operation.

2.3.2. Charging Station Operation with Charging Control (S2)

The second operational scenario of the charging station represents the operation of a residential charging station with a charging control mechanism. However, similar to the previous scenario, the charging station is still without a PV power plant and the BESS. Similarly, to the previous operational strategy, the charging station is again entirely dependent on the power drawn from the microgrid to support the charging of EVs. In contrast to the previous charging station operational scenario, in this scenario, the charging control mechanism is used to mitigate the occurrence of power peaks observed in the charging station power consumption. The charging control mechanism is used to control and redistribute the available power from the microgrid, thereby limiting the maximum power drawn, as illustrated in Figure 3 (S2).

This implementation provides several benefits, mainly centered on the potential to mitigate adverse effects resulting from significant power peaks in the charging station’s power consumption profile. By efficiently managing the rate of power extraction and its controlled redistribution, the charging station operation acquires a more synchronized and harmonious role within the microgrid system. This operational improvement can reduce the operational burden on the stability and the overall functionality of the microgrid.

2.3.3. Charging Station Operation with Charging Control, the PV Power Plant, and Distribution of Excess Energy to the Microgrid (S3)

In the third operational scenario, the charging station integrates a charging control mechanism together with a PV power plant. The PV power plant is used as a primary power source for the residential charging station, with power from the microgrid only being used when the PV power plant output is insufficient. In this operating configuration, the excess energy produced by the PV power plant is supplied to the microgrid.

Figure 4 illustrates the power exchange between the charging station system and the microgrid as well as the production of the PV power plant where the positive values signify the power consumption and production, while negative values represent the power supply to the microgrid system. In Figure 4, the power produced by the PV power plant is represented by the green curve, the red curve illustrates the charging station’s power consumption, and the power exchange between the charging station system and the microgrid is depicted by the blue curve. The power curve of power exchange between the charging station system and the microgrid is also illustrated in Figure 3 for a better comparison between different operation scenarios. Similarly, as in the previous scenario, controlled charging sets a limit for the power drawn from the microgrid to 50 kW as shown in Figure 4 (S3).

The utilization of the PV power plant decreases the dependence of the charging station on the power supply from the microgrid, consequently reducing the amount of power drawn from the microgrid. The combined implementation of controlled charging with PV power plant contributes to mitigating negative impacts resulting from variable energy consumption on the operation of the microgrid. On the other hand, this operation poses a potential problem for the microgrid because the charging station, by the character of its consumption, is unable to use the full potential of the PV plant, and thus, a significant part of the power from the PV plant remains unused and is sent to the microgrid.

2.3.4. Charging Station Operation with Charging Control and the PV Power Plant, without Distribution of Excess Energy to the Microgrid (S4)

The fourth scenario of charging station operation presents the same configuration of the charging station system as in Section 2.3.4 for the third operational scenario. In contrast to the previous scenario, this scenario does not consider the supply of the excess power from the PV power plant to the microgrid. Power curves for this scenario are illustrated in Figure 5, and power drawn from the microgrid is also shown in Figure 5 (S4) for comparison of power demand with other scenarios.

The main objective of this scenario is to analyze the impact of the charging station system on the microgrid, isolating and excluding the impact resulting from the supply of excess power from the PV power plant to the microgrid. By excluding the contribution of excess power, this scenario enables a more accurate evaluation of the charging station system’s effects on the microgrid stability.

2.3.5. Charging Station Operation with Charging Control, the PV Power Plant, the BESS, and Distribution of Excess Energy to the Microgrid (S5)

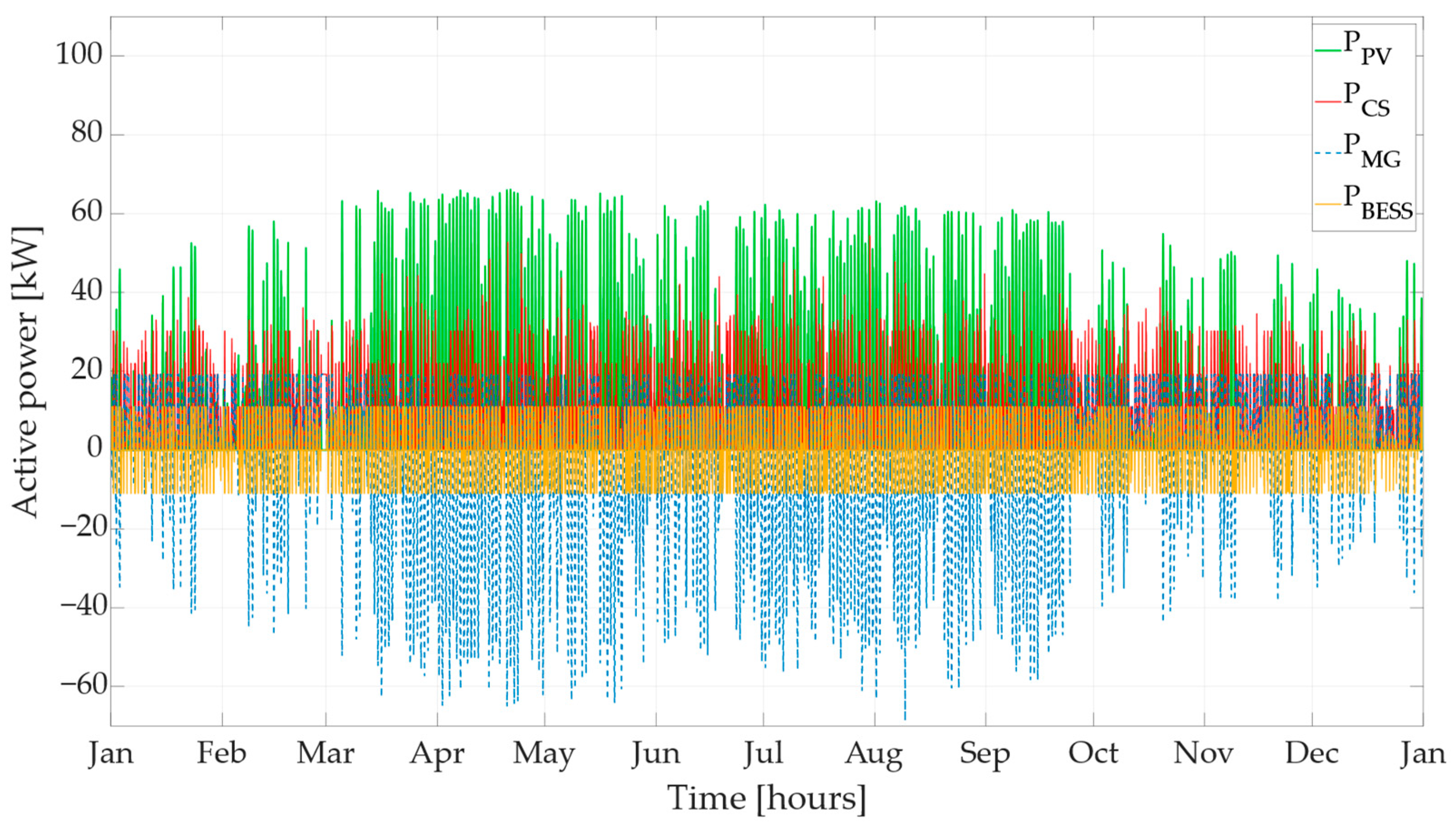
In the fifth charging station operational scenario, the charging station system consists of the residential charging station, the PV power plant, and the BESS. The charging station also contains the charging control mechanism that ensures the optimal charging of EVs and manages the efficient power allocation between EVs and the BESS. Similarly, to the previous two scenarios, the PV power plant serves as the primary power source for the EVs and the BESS within the charging station system. The BESS is charged solely from the PV power plant, thereby maximizing the use of this renewable power supply. When the PV power plant’s output is insufficient or the charging station’s power demand exceeds capacity, the BESS is used as a supplementary power source together with the microgrid to provide power for the charging of EVs. The surplus power generated by the PV power plant is supplied to the microgrid as in scenario S3.

Figure 6 depicts the power curves of PV power plant output (green curve), charging station consumption (red curve), power exchange between the charging station system and the microgrid (blue curve), and power exchange of the BESS. Positive values indicate power consumption (EVs and BESS) and production in order to visualize the utilization of available resources, whereas negative values signify power supply to the microgrid and power transfer from the BESS to the charging station. The power curve depicting the power exchange between the charging station and the microgrid can be also seen in Figure 6 (S5) for a better visualization of different scenarios.

By integrating the PV power plant and the BESS into the charging station system, in combination with the charging control mechanism, several advantageous outcomes emerge. The main one is the increased ability to utilize the power from the PV power plant, which leads to a significant reduction in both the power drawn from the microgrid and the excess power from the PV power plant supplied to the microgrid. The charging control mechanism introduces a new power draw limit (19.33 kW) as can be seen in Figure 6 (S5), further limiting the negative impacts associated with the charging station demand. However, similar to scenario S3, the prospect of excessive power from the PV power plant supplied to the microgrid poses a potential challenge to the microgrid stability.

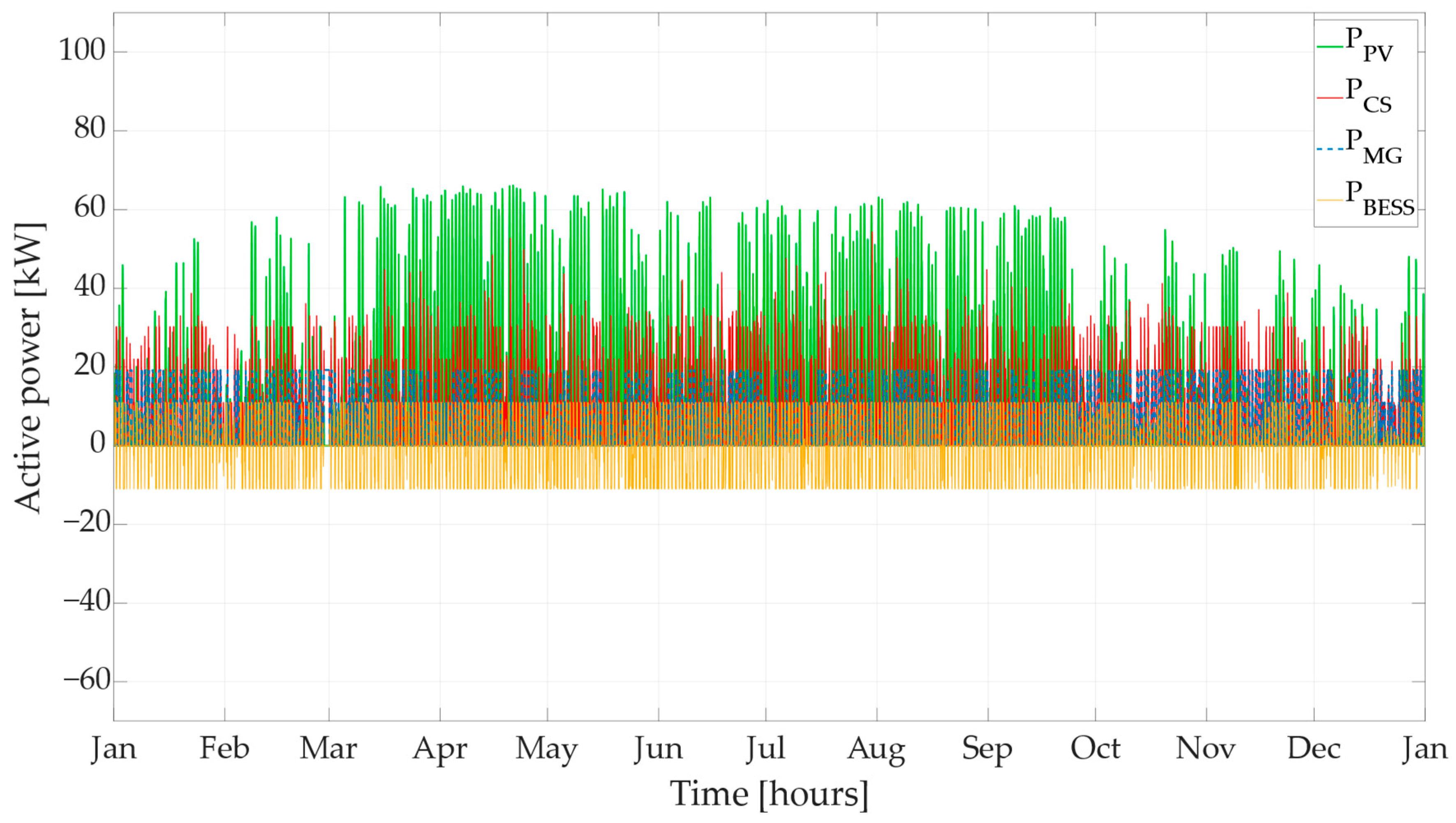
2.3.6. Charging Station Operation with Charging Control, the PV Power Plant, and the BESS, and without Distribution of Excess Energy to the Microgrid (S6)

The final (sixth) operational scenario involves the operation of a charging station system with a charging control mechanism, the PV power plant, and the BESS as presented in the previous section. However, the excess power from the PV power plant is not supplied to the microgrid in this scenario. Consistent with scenario S4, this operation configuration analyzes the impact of the charging station system on the microgrid, isolating and excluding the impact resulting from the supply of excess power from the PV power plant to the microgrid. Figure 7 illustrates the power curves of individual elements of the simulated system for this scenario.

3. Results

3.1. Impacts of the Single Charging Station on Voltage at the Nodes

3.1.1. Statistical Analysis of Voltage at the Selected Nodes

The statistical analysis of voltage data for the nodes where the charging station was gradually connected is presented in

Table 3. Statistical analysis of voltage at node N3.

N3
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (V)	397.25	397.19	397.19	397.27	397.2	397.27	397.23
Median (V)	397.34	397.27	397.27	397.34	397.28	397.34	397.31
Dispersion	0.86	0.91	0.91	0.96	0.92	0.92	0.89
Max (V)	398.86	398.86	398.86	398.86	398.86	398.86	398.86
Min (V)	392.37	392.26	392.26	392.26	392.26	392.29	392.29

,

Table 4. Statistical analysis of voltage at node N6.

N6
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (V)	393.33	392.99	392.94	393.44	393.02	393.45	393.16
Median (V)	393.71	393.21	393.2	393.65	393.32	393.73	393.5
Dispersion	6.37	7.51	7.5	8.74	7.5	7.82	7.03
Max (V)	397.51	397.51	397.51	399.07	397.51	399.07	397.51
Min (V)	382.26	381.64	381.64	381.64	381.64	381.79	381.79

and

Table 5. Statistical analysis of voltage at node N11.

N11
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (V)	390.04	389.08	389.09	390.3	389.28	390.32	389.63
Median (V)	390.63	389.51	389.51	390.51	389.75	390.7	390.13
Dispersion	14.60	19.64	19.54	25.96	19.45	21.33	17.26
Max (V)	396.32	396.32	396.32	401.44	396.32	401.44	396.32
Min (V)	373.46	371.91	371.92	371.92	371.92	372.29	372.29

. These specific nodes in which CS was connected are N3, N6, and N11. It is worth noting that results for node N3 are presented solely for the scenario in which the charging station was connected to this node. Subsequently, the charging station was disconnected from node N3. A similar approach was followed for nodes N6 and N11.

Table 3, Table 4 and Table 5 show that both the mean and median voltage values decrease as the distance from the distribution transformer increases. Across all scenarios, the mean and median voltage values exhibit approximate equivalency. While the connection of the charging station to the microgrid does induce a moderate increase in voltage dispersion, these alterations remain relatively small. The variations between the maximal and minimal voltage values are negligible, suggesting that these peaks are primarily attributed to the load fluctuations within the microgrid in all scenarios. This observation holds true for all nodes under examination.

The lowest recorded minimal voltage values across all scenarios were identified at node N16. Consequently,

Table 6. Maximal and minimal voltage values at node N16 with single charging station.

N16
	Scenario	S	S1	S2	S3	S4	S5	S6
N3	Min (pu)	0.917	0.917	0.917	0.917	0.917	0.917	0.917
	Max (pu)	0.991	0.991	0.991	0.991	0.991	0.991	0.991
N6	Min (pu)	0.917	0.916	0.916	0.916	0.916	0.916	0.916
	Max (pu)	0.991	0.991	0.991	0.992	0.991	0.991	0.991
N11	Min (pu)	0.917	0.915	0.915	0.915	0.915	0.916	0.916
	Max (pu)	0.991	0.991	0.991	0.992	0.991	0.991	0.991

presents these nodes’ maximum and minimum voltage values in pu. The same process was applied to determine these values as previously in the statistical analysis. The charging station was gradually connected and disconnected to nodes N3, N6, and N11.

Based on the results obtained from node N16, where the lowest voltage value was recorded, it can be concluded that the presence of the charging station throughout the year in all scenarios did not result in a breach of the acceptable voltage threshold of ±10%, following the technical standard EN 50160 [19]. In the context of both maximal and minimal annual voltage values, the impact of the charging station was negligible.

The subsequent sections of this article will present percentage changes in voltage for each hour of the year following the integration of the charging station across all scenarios.

3.1.2. Percentage Changes in Voltage after Connecting the Single Charging Station

In all charging station scenarios, a comparative analysis of voltages was conducted in relation to the scenario in which no charging station was present. For each charging station scenario, the percentage change in voltage was computed for each hour of the year. It is important to note that the maximum acceptable threshold for percentage voltage change following the connection of the charging station is ±3% [20]. These changes were calculated using the following equation:

$$∆V=\frac{V_{\mathrm{S}\mathrm{h}}-V_{\mathrm{W}\mathrm{h}}}{V_{\mathrm{W}\mathrm{h}}}·100,$$

(5)

where ∆V is the percentage change in voltage, V_Sh is the voltage at a specific hour after the connection of the charging station, and V_Wh is the voltage at the same hour in the absence of a charging station.

Table 7. Percentage voltage changes with single charging station.

Scenario	S1		S2		S3		S4		S5		S6
Voltage Change	+	−	+	−	+	−	+	−	+	−	+	−
N3 (%)	0	−0.23	0	−0.11	0.14	−0.11	0	−0.11	0.14	−0.04	0	−0.04
N6 (%)	0	−1.44	0	−0.72	0.9	−0.72	0	−0.72	0.9	−0.28	0	−0.28
N11 (%)	0	−3.57	0	−1.82	2.19	−1.82	0	−1.82	2.18	−0.7	0	−0.7

provides an overview of the maximal percentage voltage changes observed for each charging station scenario. Table 7 shows both positive and negative voltage changes for all modeled scenarios. Positive changes correspond to voltage increases attributed to the presence of the charging station’s photovoltaic power plant, while negative changes signify voltage reductions resulting from the consumption of the charging station.

The most substantial changes, both positive and negative, were observed at node N11 when the charging station was connected to this particular node. Notably, in scenario S1, a maximal negative change of −3.57%, exceeding the acceptable threshold, was observed at N11, due to the power consumption of the charging station. In scenarios S3 and S5, there were maximal positive changes of 2.19% and 2.18%, both do not exceed the acceptable threshold at node N11. The connection of the charging station to nodes N6 and N3 did not result in voltage changes exceeding acceptable levels, both in the positive and negative directions. As indicated by Table 7, it is evident that the impact of the charging station can be mitigated through strategic placement and the implementation of charging control. The magnitude of voltage change tends to decrease as the distance from the distribution transformer diminishes. The utilization of charging control leads to a reduction in maximal voltage change caused by the charging station’s consumption, with a decrease of 1.75% when comparing scenarios S1 and S2. Using only a PV power plant does not affect the maximal negative voltage change at node N11 when compared to scenario S2. However, the combination of the PV power plant and the BESS in scenarios S5 and S6 results in a further decrease in negative voltage change of 1.12% compared to that of scenario S2. The charging station supplies surplus energy to the grid only in scenarios S3 and S5. In both scenarios, the acceptable threshold was not exceeded. There is only a slight difference between solely using a PV power plant and using a combination of a PV power plant and the BESS. The maximal positive percentage change decreased by about 0.1% when the BESS was used.

Figure 8 presents a summary of voltage changes at node N11 when the charging station was connected to this specific node across all scenarios.

Red lines in Figure 8 delineate the permissible threshold for percentage voltage change. Over the year, this threshold was exceeded one time. The implementation of a charging control mechanism eliminated any exceedances of the threshold for negative voltage changes.

3.2. Impact of Two Charging Stations on Voltage at the Nodes

An additional charging station with a capacity of 30 vehicles was introduced to the microgrid due to the possibility of increased demand if all residents adopt electric vehicles. Consequently, two identical charging stations were incrementally connected to selected nodes. The selection included three combinations of nodes:

• Nodes N3 and N6;
• Nodes N3 and N11;
• Nodes N6 and N11.

For each of these node combinations, simulations were conducted for all scenarios (S1–S6), and both charging stations operated under the same scenario. In the case where a single charging station was connected to the microgrid, the lowest voltage levels were recorded at node N16. As a result, the maximal and minimal voltage values are presented in

Table 8. Maximal and minimal voltage values at node N16 with two charging stations.

N16
Scenario		S	S1	S2	S3	S4	S5	S6
N3, N6	Min (pu)	0.917	0.915	0.915	0.915	0.915	0.915	0.916
	Max (pu)	0.991	0.991	0.991	0.993	0.991	0.993	0.991
N3, N11	Min (pu)	0.917	0.915	0.915	0.915	0.915	0.916	0.916
	Max (pu)	0.991	0.991	0.991	0.993	0.991	0.992	0.991
N6, N11	Min (pu)	0.917	0.914	0.914	0.914	0.914	0.915	0.915
	Max (pu)	0.991	0.991	0.991	0.999	0.991	0.999	0.991

for the scenario with two charging stations.

In the presence of two charging stations, the voltage at node N16 and all other nodes remains within the allowable limit of ±10%, in accordance with the technical standard EN 50160 [19].

Percentage Changes in Voltage after Connecting the Two Charging Stations

Table 9. Percentage voltage changes with two charging stations.

Scenario		S1		S2		S3		S4		S5		S6
Voltage Change		+	−	+	−	+	−	+	−	+	−	+	−
N3, N6	N3 (%)	0	−0.48	0	−0.24	0.29	−0.24	0	−0.24	0.29	−0.09	0	−0.09
	N6 (%)	0	−1.68	0	−0.84	1.05	−0.84	0	−0.84	1.04	−0.32	0	−0.32
N3, N11	N3 (%)	0	−0.5	0	−0.26	0.3	−0.26	0	−0.26	0.3	−0.1	0	−0.1
	N11 (%)	0	−3.82	0	−1.94	2.34	−1.94	0	−1.94	2.32	−0.74	0	−0.74
N6, N11	N6 (%)	0	−3.02	0	−1.51	1.79	−1.51	0	−1.51	1.78	−0.57	0	−0.57
	N11 (%)	0	−5.13	0	−2.59	3.08	−2.59	0	−2.59	3.06	−0.99	0	−0.99

presents the voltage changes at nodes where charging stations were directly connected, incorporating each node combination. The same display method is employed as in Table 7.

The most substantial changes, both positive and negative, were observed at node N11 when the charging stations were connected to nodes N6 and N11. The influence of implementing the charging control mechanism, the PV power plant, or the BESS on the percentage voltage changes has a similar effect, as discussed in the previous section, when only a single charging station was connected. Figure 9 illustrates the percentage voltage changes at node N11 when charging stations were connected to nodes N6 and N11.

Figure 9 clearly illustrates that the magnitude of percentage voltage changes increases in all scenarios, and the number of allowable threshold exceedances of ±3% also rises compared to the case with a single charging station.

Table 10. Number of allowable threshold exceedances.

Scenario		S1		S2		S3		S4		S5		S6
Direction		(+)	(−)	(+)	(−)	(+)	(−)	(+)	(−)	(+)	(−)	(+)	(−)
N6, N11	N6	0	1	0	0	0	0	0	0	0	0	0	0
	N11	0	30	0	0	10	0	0	0	3	0	0	0

provides a summary of the exceedances in each scenario with the node combination of N6 and N11.

Red lines in Figure 9 delineate the permissible threshold for percentage voltage change.

The highest number of threshold exceedances of ±3% was observed at node N11. Node N6 exceeded the threshold only in one case.

3.3. Impact of the Charging Station on Loading of Transformer and Lines in the Distribution System

This subsection presents an analysis of the loading placed on the distribution transformer and power lines within the microgrid. Initially, the loading was computed in the absence of the charging station. Subsequently, the analysis was repeated considering the presence of the charging station across all scenarios.

3.3.1. Impact of the Single Charging Station on Distribution Transformer Loading

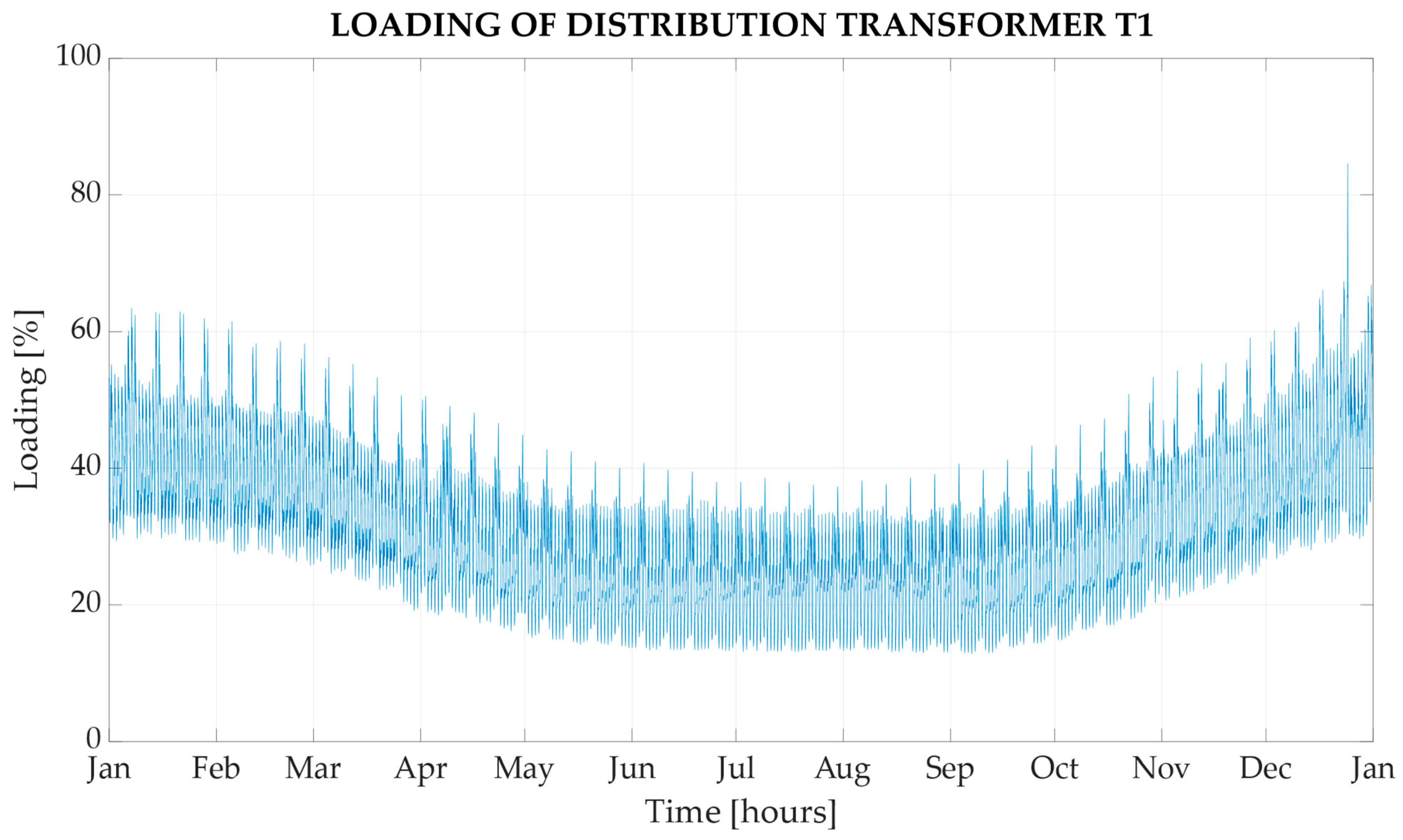
Figure 10 displays the percentage loading profile for distribution transformer T1 in the absence of the charging station.

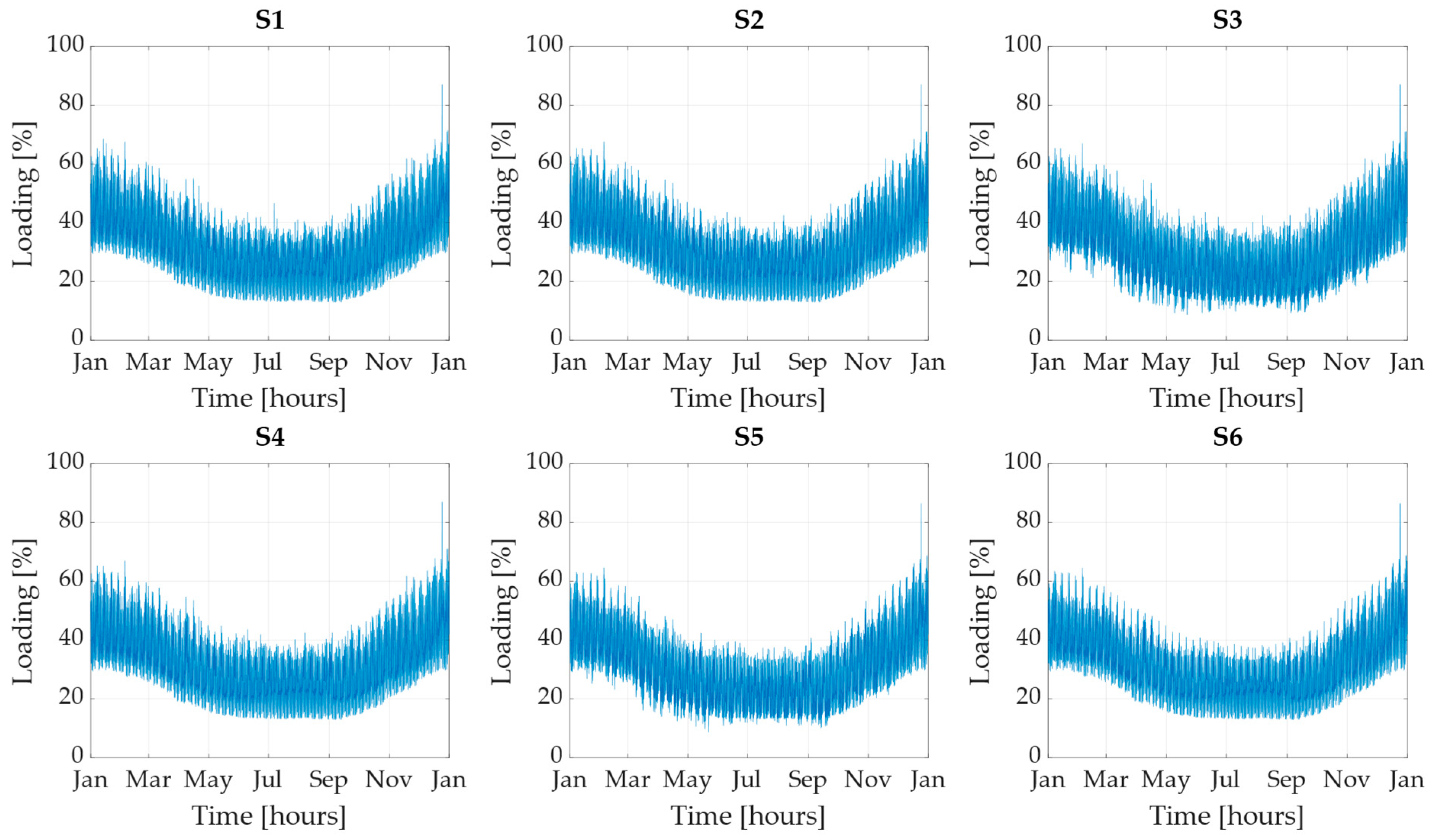
The percentage loading profile of the transformer closely mirrors the consumption patterns depicted by the RLP curves. Most loading levels fall within the range of up to 60%. The peak loading occurred on the 24th of December at 16:00. Figure 11 presents the loading curves for transformer T1, accounting for the presence of the charging station in the microgrid.

Figure 11 illustrates the percentage loading profiles of transformer T1 when the charging station was connected to node N11. These loading profiles remain unchanged regardless of whether the charging station was connected to nodes N3 or N6.

Table 11. Statistical analysis of transformer loading with single charging station.

N11
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (%)	30.9	32.4 (1.5)	32.4 (1.5)	30.5 (−0.4)	32.1 (1.2)	30.5 (−0.4)	31.6 (0.7)
Median (%)	29.9	31.7 (1.8)	31.7 (1.8)	30 (0.1)	31.2 (1.3)	29.7 (−0.2)	30.6 (0.7)
Max (%)	84.6	87 (2.4)	87 (2.4)	87 (2.4)	87 (2.4)	86.5 (1.9)	86.4 (1.8)
Min (%)	12.9	12.9 (0)	12.9 (0)	8.6 (−4.3)	12.9 (0)	8.6 (−4.3)	12.9 (0)
Max change (%)	-	22.3	10.8	10.8	10.8	4.1	4.1

provides an overview, encompassing the mean, median, minimal and maximal values, and maximal changes of transformer T1 loading, along with the percentage increases in these values, when compared to the scenario in which the charging station was absent from the microgrid. When the charging station’s connection point shifted from node N3 to other nodes, these values remained unchanged.

In Table 11, enclosed in brackets are the alterations, when compared to the scenario in which the charging station was absent. Importantly, it is observed that transformer T1 did not experience overloading in any of the scenarios. The maximum loading change, observed in scenario S1, amounts to 22.3%. In this particular case, this change did not lead to transformer overloading. However, if the charging station induced this change during peak loading, which reached 84.6%, it would result in transformer overloading. The maximal loading change was mitigated to 10.8% when employing charging control (S2) or combining a PV power plant with charging control (S3, S4). Furthermore, with the addition of the BESS to the aforementioned options, the maximal change decreased to 4.1%.

3.3.2. Impact of the Two Charging Stations on Loading of Distribution Transformer

Figure 12 displays the loading profile of distribution transformer T1 when charging stations were connected to nodes N6 and N11 across all scenarios.

The percentage loading profiles of transformer T1, as depicted in Figure 12, exhibit patterns closely resembling those observed when a single charging station was connected to the microgrid. However, the increase in loading due to the consumption of charging stations is more pronounced, as is the decrease in loading caused by the PV power plant. It is important to note that the transformer did not overload in any of the scenarios.

Table 12. Statistical analysis of transformer loading with two charging stations.

N6, N11
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (%)	30.9	33.9 (3)	33.9 (3)	30.4 (−0.5)	33.3 (2.4)	30.2 (−0.7)	32.2 (1.3)
Median (%)	29.9	33 (3.1)	33 (3.1)	30 (0.1)	32.2 (2.3)	29.7 (−0.2)	31.1 (−1.2)
Max (%)	84.6	89.3 (4.7)	89.3 (4.7)	89.3 (4.7)	89.3 (4.7)	88.2 (3.6)	88.2 (3.6)
Min (%)	12.9	12.9 (0)	12.9 (0)	5.9 (−7)	12.9 (0)	5.9 (−7)	12.9 (0)
Max change (%)	-	44.9	21.4	21.4	21.4	8.1	8.1

provides a statistical analysis of the transformer loading, both in scenarios without the presence of a charging station and in scenarios with the presence of two charging stations at nodes N6 and N11. The process used for Table 11 was also employed for Table 12.

The changes in the mean, median, and maximum and minimum values presented in Table 12 are relatively minor when compared to the scenario in which only a single charging station was connected to the microgrid (as shown in Table 11). The most substantial increase in loading, amounting to 44.9%, was observed in scenario S1. It is important to note that this increase, although notable, did not lead to transformer overload in this specific instance. However, such an increase could potentially overload the distribution transformer if it happened at a different time when the overall load from other sources within the microgrid is higher. Fortunately, the utilization of charging control mechanisms, PV power plants, and the BESS proves to be effective in mitigating the loading changes resulting from the charging stations.

3.3.3. Impact of the Single Charging Station on Power Lines Loading

The results derived from the analysis of transformer T1 loading suggest that the charging station is not anticipated to exert a substantial influence on the loading of the distribution lines. The highest impact on most of the lines is observed when the charging station is connected to the far end of the microgrid. As a result, during the simulations, the charging station was connected to node N11, and the power to the charging station was transmitted only through lines L1 to L9, with no effect on the other lines. The percentage change in loading is the same for all the aforementioned lines. Thus,

Table 13. Statistical analysis of line loading with single charging station.

L1
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (%)	12.3	13.4 (1.1)	13.4 (1.1)	12.1 (−0.2)	13.2 (0.9)	12.1 (−0.2)	12.8 (0.5)
Median (%)	11.5	12.8 (1.3)	12.8 (1.3)	11.6 (0.1)	12.5 (1)	11.4 (−0.1)	12.1 (0.6)
Max (%)	31.6	33.4 (1.8)	33.4 (1.8)	33.4 (1.8)	33.4 (1.8)	32.9 (1.3)	32.9 (1.3)
Min (%)	4.3	4.3 (0)	4.3 (0)	2.2 (−2.1)	4.3 (0)	2.2 (−2.1)	4.3 (0)
Max change (%)	-	16.2	7.8	7.8	7.8	3	3

presents a statistical analysis for the line with the highest loading in the scenario without the presence of the charging station, which is line L1.

Similar to the transformer, the changes in the mean, median, and maximal and minimal values of line loading induced by the presence of the charging station are negligible. The most substantial increase in loading for line L1 amounts to 16.2%. In the absence of the charging station, the maximal loading for line L1 stands at 31.6%, indicating that this line would not be overloaded in any case. Utilizing the charging control and a PV power plant reduces this change to 7.8%, while the inclusion of the BESS further diminishes it to 3%.

3.3.4. Impact of the Two Charging Stations on the Loading of Power Lines

The charging stations were connected to nodes N6 and N11 based on the results obtained from the preceding section, which suggested that these nodes would have the most pronounced impact on line loading. The results regarding line loading for this node combination are presented in

Table 14. Statistical analysis of line loading with two charging stations.

L1
Scenario	S	S1	S2	S3	S4	S5	S6
Mean (%)	12.3	14.5 (2.2)	14.5 (2.2)	12.7 (0.4)	14 (1.4)	12.2 (−0.1)	13.2 (0.9)
Median (%)	11.5	13.6 (2.1)	13.6 (2.1)	11.7 (0.2)	13 (1.5)	11.3 (−0.2)	12.4 (0.9)
Max (%)	31.6	45 (13.4)	40.4 (8.8)	40.4 (8.8)	40.4 (8.8)	34.2 (2.6)	34.2 (2.6)
Min (%)	4.3	4.3 (0)	4.3 (0)	2 (−2.3)	4.3 (0)	2.2 (−2.1)	4.3 (0)
Max change (%)	-	32.5	15.4	15.4	15.4	5.8	5.8

.

Comparable to the transformer, the variations in the mean, median, and minimum values, as presented in Table 14, are relatively minor when contrasted with those of the scenario in which only a single charging station was connected to the microgrid (Table 13). The maximum value of line loading in scenario S1 increased by 11.6% (Table 14) in comparison to that of the case with only a single charging station (Table 13). A maximal loading change of 32.5% in scenario S1 is not problematic because the line loading, driven by the consumption of other loads, remains low, with a maximal value of 31.6%.

3.4. Impact of the Single Charging Station on Power Losses in Lines

In this subsection, the power losses across all simulated scenarios are compared. These losses are depicted as the summation of active power losses in each line within the microgrid during the one year.

Table 15. Power losses in lines with single charging station.

Scenario	S	S1	S2	S3	S4	S5	S6
N3 (MWh/%)	16.75	16.76/0.04	16.76/0.04	16.75/0	16.76/0.04	16.75/0	16.76/0.04
N6 (MWh/%)	16.75	18.25/8.9	18.24/8.9	17.11/2.1	17.99/7.4	16.82/0.43	17.42/4
N11 (MWh/%)	16.75	19.7/17.6	19.69/17.5	17.83/6.4	19.18/14.5	17.11/2.1	18.03/7.6

displays the power losses for all scenarios in megawatts hours (MWh), with the percentage changes relative to the scenario where the charging station was not present.

Table 15 reveals a notable influence of the charging station’s placement on power losses. As the distance from the distribution transformer increases, power losses also escalate. When the charging station was connected to node N3, changes in losses, in comparison to those of the scenario without the presence of the charging station, were minimal. However, the highest losses were recorded when the charging station was connected to node N11. In scenario S1, losses increased by 17.6%. Charging control alone did not mitigate power losses. The combination of the charging control, the PV power plant, and the BESS demonstrated effectiveness in reducing these losses.

3.5. Impact of Two Charging Stations on Power Losses in Lines

Table 16. Power losses in lines with two charging stations.

Scenario	S	S1	S2	S3	S4	S5	S6
N3, N6 (MWh/%)	16.75	18.26/9	18.25/9	17.11/2.1	18/7.4	16.83/0.4	17.42/4
N3, N11 (MWh/%)	16.75	19.72/17.7	19.7/17.6	17.84/6.5	19.19/14.5	17.1/2.2	18.04/7.7
N6, N11 (MWh/%)	16.75	21.61/29	21.57/28.8	19.11/14	20.73/23.7	17.68/5.5	18.81/12.3

presents power losses for all scenarios, measured in MWh, when two charging stations are connected to the microgrid. The same format used in Table 15 is applied in Table 16.

The highest power losses occurred when the charging station was connected to nodes N6 and N11. In scenario S1, losses increased by 29%. However, the implementation of the charging control, the PV power plant, and the BESS effectively reduced these losses.

4. Discussion

The investigation focused on assessing the impacts of an electric vehicle charging station, coupled with a PV power plant and the BESS, on power quality in microgrid. The impacts were examined through power flow computations encompassing various scenarios. The results of power flow were analyzed, particularly focusing on voltages at distinct nodes, the loading of the distribution transformer and lines, and the power losses.

Voltage levels remain within the permissible threshold of ±10% as specified in the standard EN 50160 [19]. Nonetheless, the lowest recorded voltage value was 0.914 pu at node N16 when two charging stations were connected to the microgrid (at nodes N6 and N11) during scenario S1. This value is close to the allowable threshold of 0.9 pu. Hence, if the load conditions within the microgrid or the power consumption of the charging station increase, there is potential for the voltage to reach levels lower than 0.9 pu.

The technical specifications of the Slovak distribution company specify that the voltage change for connecting a new source (if its installed capacity is higher than 10.8 kW) should not exceed ±3% [20]. While the change for connecting a load is not explicitly defined, this article has considered it and applied a ±3% threshold for evaluation. When only one charging station was connected to the microgrid, it led to a single instance of threshold exceedance at node N11. However, the connection of a second charging station increased the number of these incidents to 30 at node N11 when charging stations were connected to nodes N6 and N11. This occurred in scenario S1 when the charging control, the PV power plant, and the BESS were not included. In other charging station scenarios, voltage changes did not exceed the −3% threshold. In the case when a PV power plant was included and surplus energy was supplied to the grid in scenario S3, the +3% threshold was exceeded by 10 times. When the BESS was also included, this number decreased to three. These exceedances could potentially pose issues, as the distribution company might reject the connection of charging stations.

Connecting one or two charging stations did not lead to the overloading of distribution transformer T1 or any of the lines. However, the loading level of the transformer and lines reached low values in the absence of charging stations. The mean value of transformer loading was 30.9%, and for lines, it was 12.3%. The maximum changes in loading caused by the charging station reached high values. For the transformer, it was 22.3% in the case of a single charging station and 44.9% for two stations. For the lines, it was 16.2% and 32.5%. If charging stations are potentially connected to a grid where the transformer and lines are already operating at higher loadings, these devices could be overloading. An effective charging control reduced loading changes for the transformer and line L1 by half in all cases. The inclusion of the BESS and PV power plants contributed to even further reductions in loading changes.

The presence of charging stations in the microgrid led to an increase in power losses in the lines. The extent of this increase was influenced by the specific charging station scenario. When a single charging station was connected, in scenario S1, annual losses increased by 17.6%, and in S2, by 17.5%. In S2, the implementation of charging control did not reduce losses significantly because the annual consumption of the charging station remained unchanged, and only the power peaks were mitigated. When two charging stations were connected, losses increased by 29% in scenario S1. This considerable increase in power losses could potentially result in higher charging costs due to increased distribution fees. The increase in charging prices could potentially slow down the development of electromobility, making electric vehicles more expensive for customers. To mitigate these losses and potentially reduce charging prices, the integration of PV power plants and the BESS proved to be effective measures.

5. Conclusions

The paper conducted an analysis of the impacts of an electric vehicle charging station on a low voltage microgrid. Thirty-seven charging station scenarios with different locations within the microgrid were examined. These scenarios encompassed a range of conditions, from those without any charging control to various combinations incorporating the charging control, photovoltaic power plants, and battery energy storage systems. Also, various indicators, including voltage at nodes, transformer and line loading, and power losses in lines during different charging station scenarios, were evaluated.

The simulation results of scenarios without charging control clearly indicate the deterioration of all studied quality indicators, such as a decrease in node voltages and an increase in power losses as well as power lines and transformer loading. However, only the voltage changes upon charging station connection exceeded the permitted values. But this is an important aspect as it can result in the dismissal of a charging station construction.

The Implementation of the charging control, the PV power plant, and the BESS in simulation scenarios effectively mitigates the impact of the charging station on the microgrid under examination. All quality indicators improved just by adding the charging control; however, the scenario with charging control together with the PV power plant and the BESS (scenarios S5 and S6) results in quality indicator values close to the ones present in the network without the charging station.

The presented study only focuses on the analysis of a low voltage microgrid with a residential charging station model. Since the character of operation and consumption in public charging stations is different than in residential charging stations, future research should focus on adding public charging station models to the evaluation of these qualitative indicators. Also, the impacts of reactive power and power electronic elements in charging stations should be studied in future studies.