Scaling Law of Flow and Heat Transfer Characteristics in Turbulent Radiative Rayleigh-Bénard Convection of Optically Thick Media †
Abstract
1. Introduction
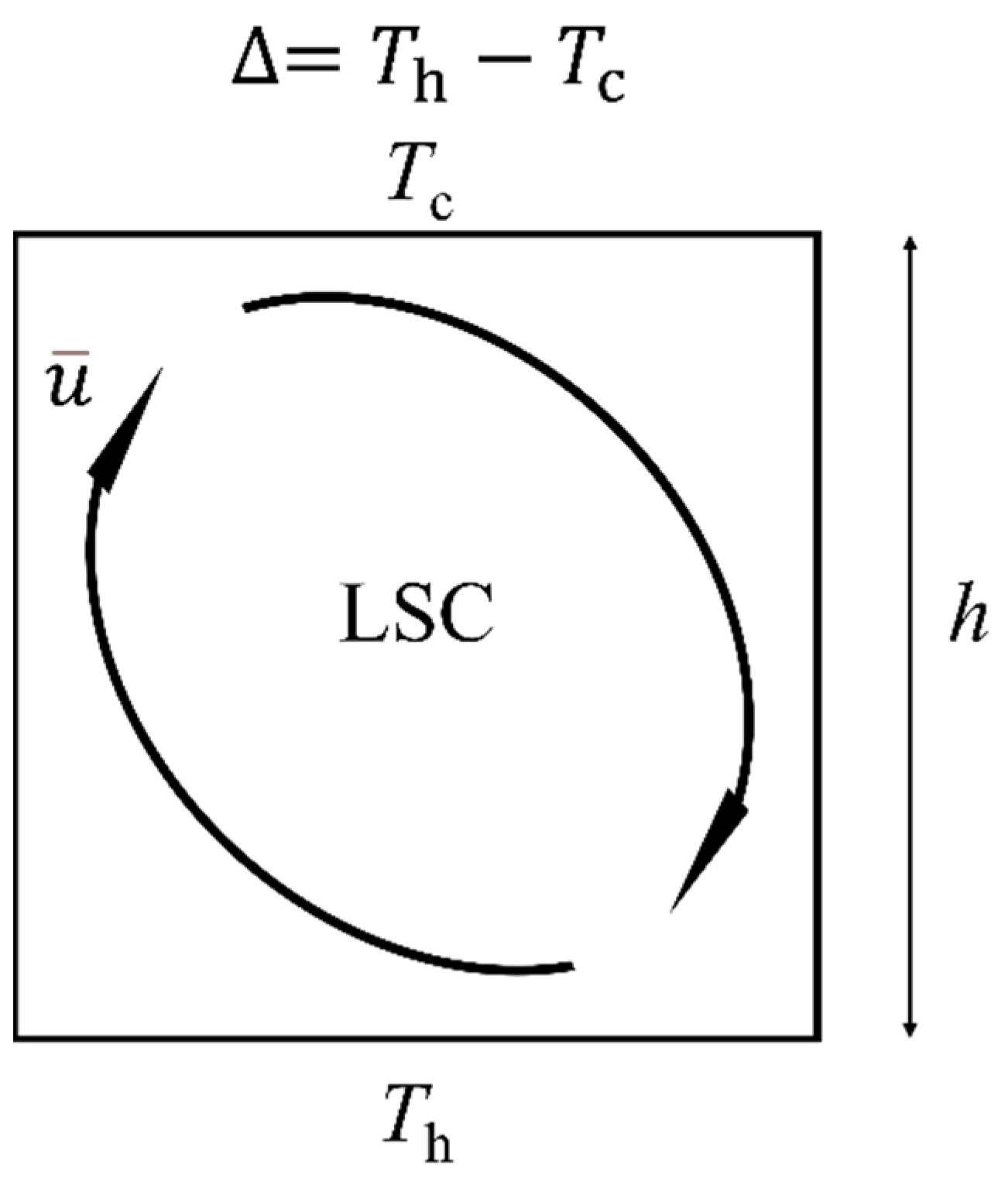
2. The Model
- An incompressible and optically thick fluid is considered;
- The Boussinessq approximation, as well as Rosseland diffusion approximation are invoked in this work;
- The flow is in a turbulent state and there exists a large-scale circulation (LSC);
- The kinetic BL is assumed to be of Prandtl-Blasius type.
3. Scaling Laws
- Regime I-a:, ,
- Regime I-b:, ,
- Regime II-a:, ,
- Regime II-b:, ,
- Regime III-a:, ,
- Regime III-b:, ,
- Regime IV-a:, ,
- Regime IV-b:, ,
4. Direct Numerical Simulations
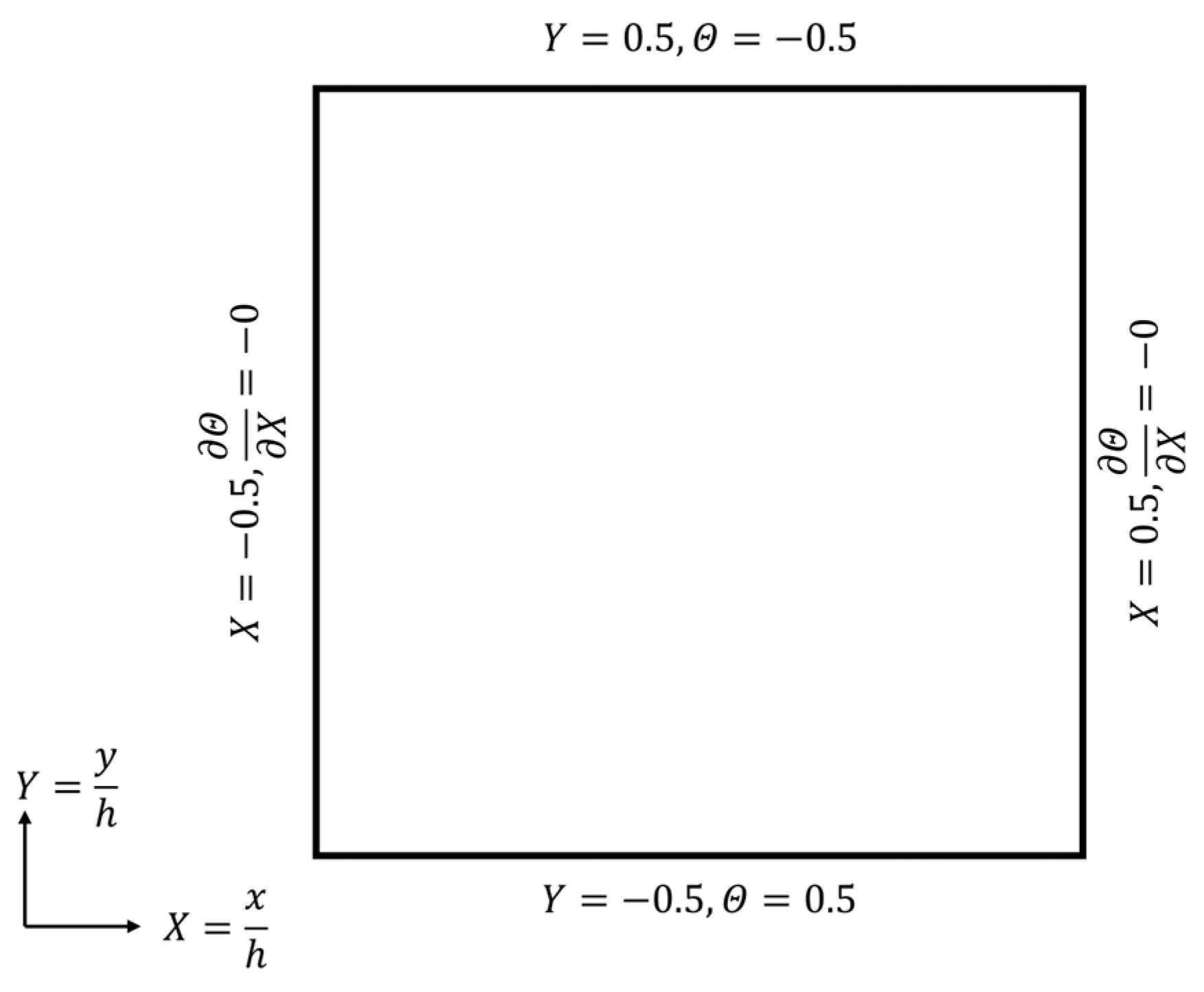
4.1. Numerical Model
4.2. Numerical Method and Validation
4.3. Effect of Radiation on Flow Structure
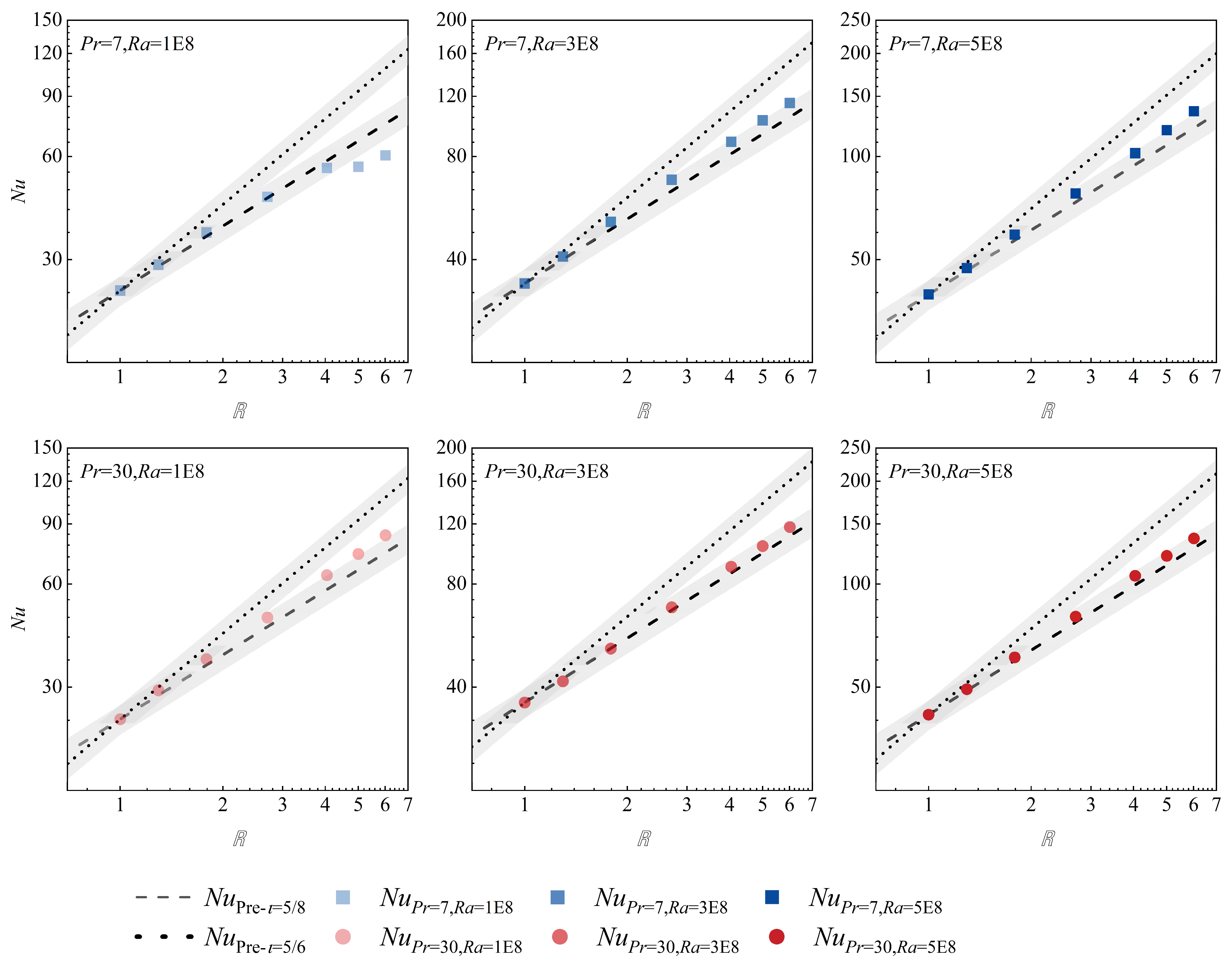
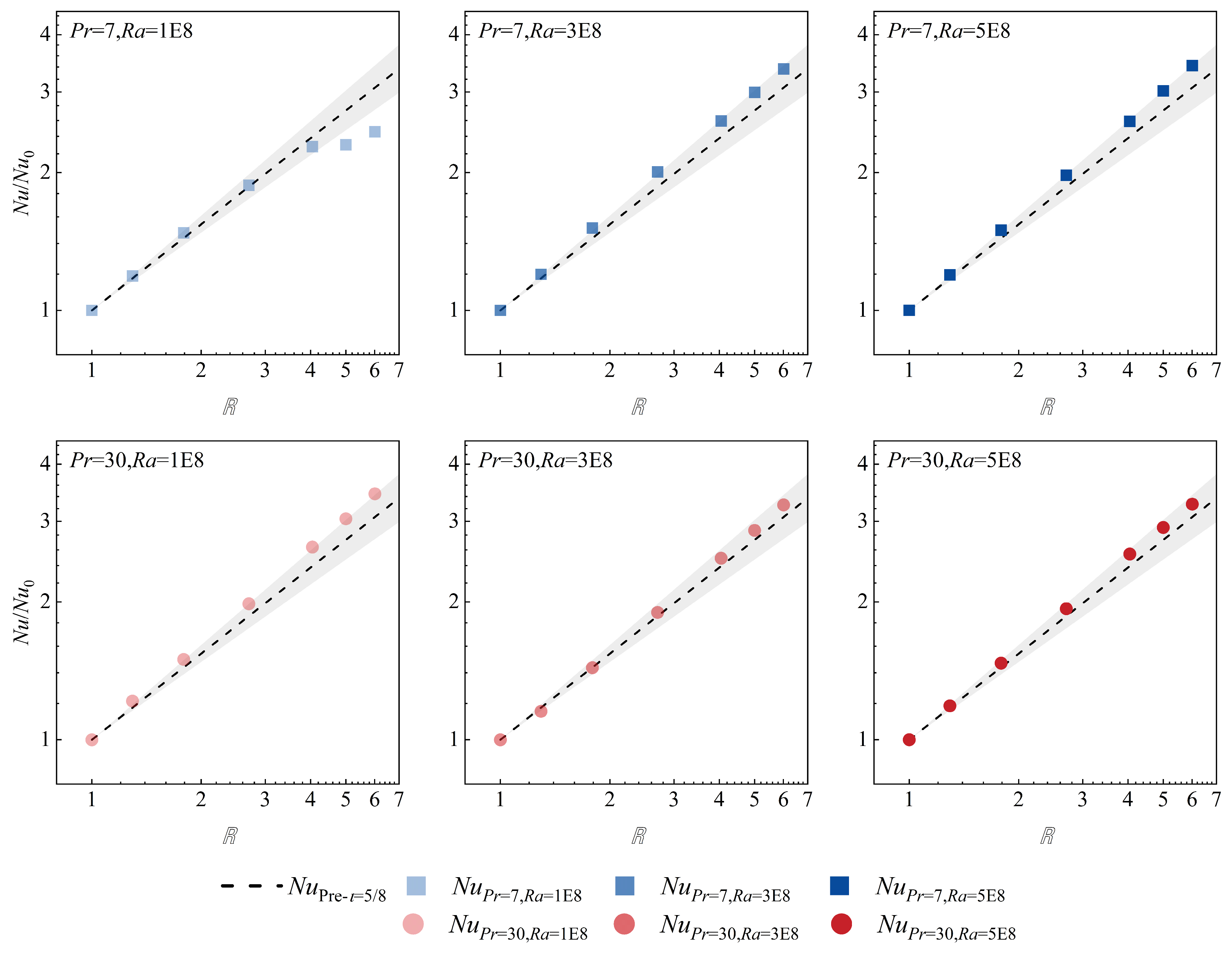
4.4. Comparisons between Scaling Law and DNS Results
5. Conclusions
- (1)
- Based on the turbulent dissipation theory and Rosseland approximation, the scaling laws in the four main regimes have been summarized within the scope of numerical simulation research presented in this paper (, , ), .
- (2)
- It has been found that due to the presence of thermal radiation, the Nu scaling law in the small Pr range of the GL model is more suitable for predicting the transport characteristics of optical thick media with large Pr. The deviation between the results of DNS and prediction model is approximately 10%.
- (3)
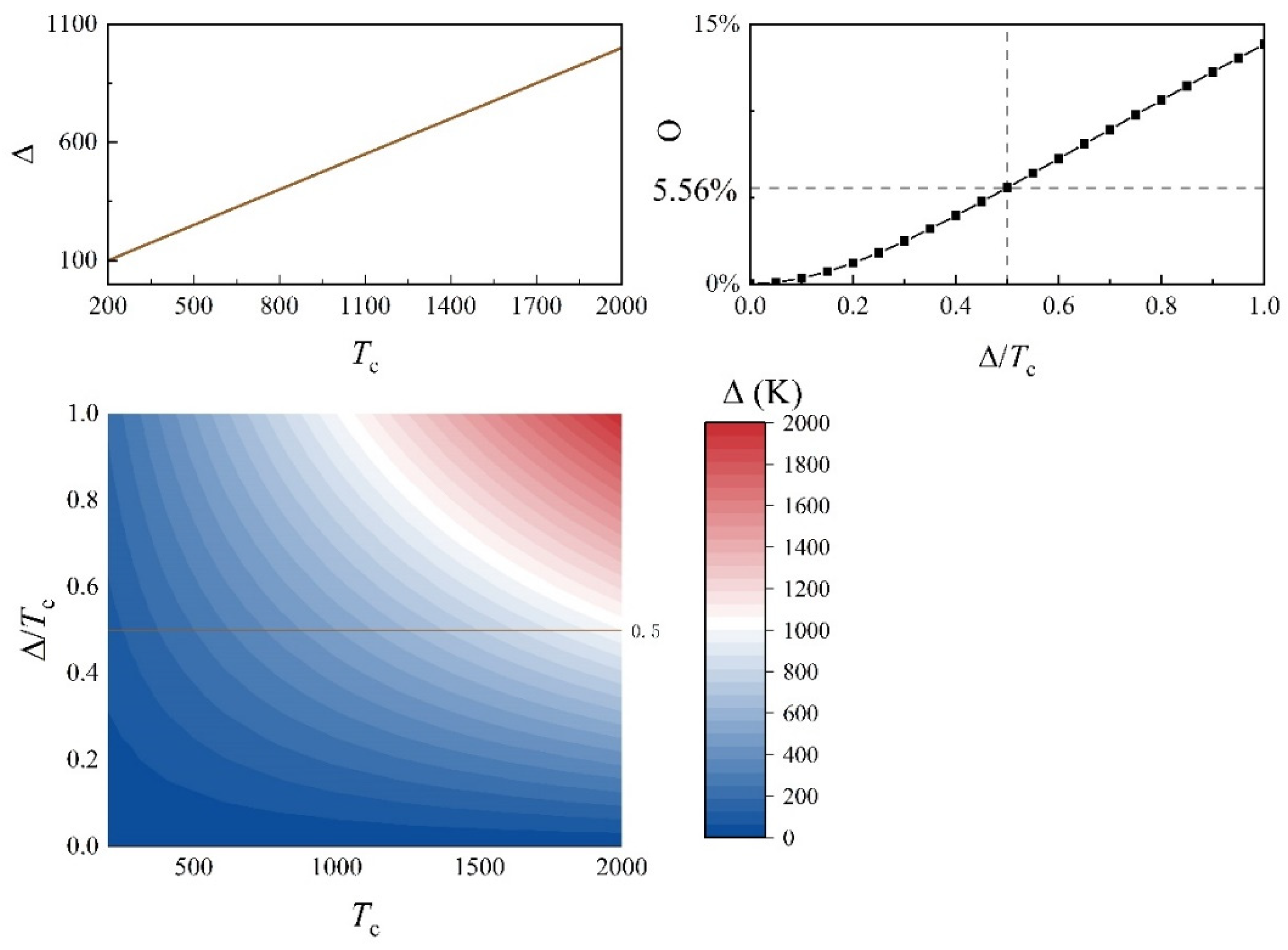
- The determination of reference temperature is discussed, and there is almost no difference between the arithmetic mean temperature and radiative mean temperature, especially within the scope of application of Boussinesq approximation.
- (4)
- The influence of thermal radiation results in a significant enhancement of heat transfer.
- (5)
- When , the LSC can been formed for weak radiation effect. The effect of radiation can stabilize flow, specifically manifested by a collapse of LSC as increases. However, the radiation effect weakens for larger Pr.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| g | gravitational acceleration | m·s−2 |
| h | length of the cavity | m |
| Ha | Hartmann number | - |
| I, Ib | radiation intensity, radiation intensity of black body | W·m−2 |
| Nu | Nusselt number | - |
| p, P | pressure, dimensionless pressure | kg∙m−1·s−1, - |
| Pl | Planck number | - |
| Pr | Prandtl number | - |
| qR | radiative heat flux | W·m−2 |
| Ra | Rayleigh number | - |
| Re | Reynold number | - |
| s | position vector | m |
| t | time | s |
| T | temperature | K |
| Tref | reference temperature | K |
| velocity | m·s−1 | |
| u | dimensionless velocity vector | - |
| uf | free-fall velocity | m·s−1 |
| the mean large-scale velocity | m·s−1 | |
| x, y, z | Cartesian coordinates | m |
| radiation parameter | - | |
| the average over any horizonal plane | - | |
| the volume average | - | |
| Δ | temperature difference | K |
| Greek symbols | ||
| β | thermal expansion coefficient | K−1 |
| βr | spectral extinction or attenuation coefficient | m−1 |
| Γ | aspect ratio | - |
| δ | the thickness of BL | m |
| ε | energy dissipation | - |
| εe | emissivity | - |
| θ | dimensionless temperature | - |
| κ | thermal diffusivity | m2∙s−1 |
| κa,λ | scattering coefficient | m−1 |
| λ | thermal conductivity | W·m−1·K−1 |
| σ | Stefan-Boltzmann constant | |
| σs,λ | absorption coefficient | m−1 |
| τ | dimensionless time | - |
| τr | optical thickness | - |
| ν | kinematic viscosity | m2·s−1 |
| Φ | scattering phase function | - |
| Ω, Ω’ | solid angle, incident solid angle | sr |
| Subscripts | ||
| h | hot plate | |
| c | cold plate | |
| u | kinetic related quantities | |
| T | thermal related quantities | |
| BL | contribution from BL | |
| bulk | contribution from bulk | |
| λ | spectrally dependent | |
References
- Arnaoutakis, G.E.; Katsaprakakis, D.A. Energy yield of spectral splitting concentrated solar power photovoltaic systems. Energies 2024, 17, 556. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, Z.; Lin, L.; Feng, Y. Molecular insights into thermal conductivity enhancement and interfacial heat transfer of molten salt/porous ceramic skeleton composite phase change materials. Int. J. Heat Mass Transf. 2024, 232, 125934. [Google Scholar] [CrossRef]
- Yuan, H.M.; Liu, S.T.; Li, T.H.; Yang, L.Y.; Li, D.H.; Bai, H.; Wang, X.D. Review on thermal properties with influence factors of solid-liquid organic phase-change micro/nanocapsules. Energies 2024, 17, 604. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. Numerical simulation for impact of Coulomb force on nanofluid heat transfer in a porous enclosure in presence of thermal radiation. Int. J. Heat Mass Transf. 2018, 118, 823–831. [Google Scholar] [CrossRef]
- Qasem, S.A.; Sivasankaran, S.; Siri, Z.; Mothman, W.A. Effect of thermal radiation on natural convection of a nanofluid in a square cavity with a solid body. Therm. Sci. 2021, 25, 1949–1961. [Google Scholar] [CrossRef]
- Alnaqi, A.A.; Aghakhani, S.; Pordanjani, A.H.; Bakhtiari, R.; Asadi, A.; Minh-Duc, T. Effects of magnetic field on the convective heat transfer rate and entropy generation of a nanofluid in an inclined square cavity equipped with a conductor fin: Considering the radiation effect. Int. J. Heat Mass Transf. 2019, 133, 256–267. [Google Scholar] [CrossRef]
- Roy, N.C.; Saha, L.K.; Siddiqa, S. Electrohydrodynamics and thermal radiation effects on natural convection flow in an enclosed domain. Int. Commun. Heat Mass Transf. 2021, 126, 105437. [Google Scholar] [CrossRef]
- Shah, F.; Asadullah; Ali, S.; Khan, S.U.; Akermi, M.; Nasr, S.; Hassani, R.; Jaballah, N.S. Thermal analysis for SWCNTs and MWCTs due to coaxially stretchable disks with applications of viscous dissipation and thermal radiation: Artificial neural network analysis. Int. Commun. Heat Mass Transf. 2024, 155, 107452. [Google Scholar] [CrossRef]
- Ali, M.Y.; Rahman, M.; Ali, M.M.; Ahmmed, S.F.; Haque, S. Data analysis of non-linear radiative electro-periodic MHD flow past a stretching sheet with activation energy impact. Int. Commun. Heat Mass Transf. 2024, 155, 107572. [Google Scholar]
- Kolsi, L.; Abidi, A.; Maatki, C.; Borjini, N.M.; Aissia, B.H. Combined radiation-natural convection in three-dimensional verticals cavities. Therm. Sci. 2011, 15, S327–S339. [Google Scholar] [CrossRef]
- Leporini, M.; Corvaro, F.; Marchetti, B.; Polonara, F.; Benucci, M. Experimental and numerical investigation of natural convection in tilted square cavity filled with air. Exp. Therm. Fluid Sci. 2018, 99, 572–583. [Google Scholar] [CrossRef]
- El Ayachi, R.; Raji, A.; Hasnaoui, M.; Bahlaoui, A. Combined effect of radiation and natural convection in a square cavity differentially heated with a periodic temperature. Numer. Heat Transf. Part A-Appl. 2008, 53, 1339–1356. [Google Scholar] [CrossRef]
- Wang, Y.; Sergent, A.; Saury, D.; Lemonnier, D.; Joubert, P. Numerical study of an unsteady confined thermal plume under the influence of gas radiation. Int. J. Therm. Sci. 2020, 156, 106474. [Google Scholar] [CrossRef]
- Martyushev, S.G.; Sheremet, M.A. Conjugate natural convection combined with surface thermal radiation in a three-dimensional enclosure with a heat source. Int. J. Heat Mass Transf. 2014, 73, 340–353. [Google Scholar] [CrossRef]
- Sivaraj, C.; Miroshnichenko, I.V.; Sheremet, M.A. Influence of thermal radiation on thermogravitational convection in a tilted chamber having heat-producing solid body. Int. Commun. Heat Mass Transf. 2020, 115, 104611. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Gibanov, N.S.; Sheremet, M.A. Numerical analysis of heat source surface emissivity impact on heat transfer performance in a rectangular enclosure at high Rayleigh numbers. Int. J. Comput. Methods Eng. Sci. Mech. 2020, 21, 205–214. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Toilibayev, A.A.; Sheremet, M.A. Simulation of thermal radiation and turbulent free convection in an enclosure with a glass wall and a local heater. Fluids 2021, 6, 91. [Google Scholar] [CrossRef]
- Qi, X.; Ma, W.; Liu, L. Effect of internal radiation on heat transfer during Ti:Sapphire crystal growth process by heat exchanger method. Int. J. Heat Mass Transf. 2021, 170, 121000. [Google Scholar] [CrossRef]
- Parsaee, S.; Payan, S.; Payan, A. Semi-transient thermal analysis from MHD-Participating fluid into a square cavity with variable optical thickness. Int. J. Therm. Sci. 2021, 169, 107072. [Google Scholar] [CrossRef]
- Gad, M.A.; Balaji, C. Effect of surface radiation on RBC in cavities heated from below. Int. Commun. Heat Mass Transf. 2010, 37, 1459–1464. [Google Scholar] [CrossRef]
- Soucasse, L.; Podvin, B.; Riviere, P.; Soufiani, A. Reduced-order modelling of radiative transfer effects on Rayleigh-Benard convection in a cubic cell. J. Fluid Mech. 2020, 898, A2. [Google Scholar] [CrossRef]
- Soucasse, L.; Podvin, B.; Riviere, P.; Soufiani, A. Low-order models for predicting radiative transfer effects on Rayleigh-Benard convection in a cubic cell at different Rayleigh numbers. J. Fluid Mech. 2021, 917, A5. [Google Scholar] [CrossRef]
- Song, J.J.; Li, P.X.; Chen, L.; Li, C.H.; Li, B.W.; Huang, L.Y. A review on Rayleigh-Benard convection influenced by the complicating factors. Int. Commun. Heat Mass Transf. 2023, 144, 106784. [Google Scholar] [CrossRef]
- Malkus, W.V.R. The Heat Transport and Spectrum of Thermal Turbulence. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1954, 225, 196–212. [Google Scholar]
- Heslot, F.; Castaing, B.; Libchaber, A. Transitions to turbulence in helium gas. Phys. Rev. A 1987, 36, 5870–5873. [Google Scholar] [CrossRef]
- Castaing, B.; Gunaratne, G.; Heslot, F.; Kadanoff, L.; Libchaber, A.; Thomae, S.; Wu, X.Z.; Zaleski, S.; Zanetti, G. Scaling of hard thermal turbulence in Rayleigh-Benard convection. J. Fluid Mech. 1989, 204, 1–30. [Google Scholar] [CrossRef]
- Sano, M.; Wu, X.Z.; Libchaber, A. Turbulence in helium-gas free-convection. Phys. Rev. A 1989, 40, 6421–6430. [Google Scholar] [CrossRef]
- Shraiman, B.I.; Siggia, E.D. Heat-transport in high-Rayleigh-number convection. Phys. Rev. A 1990, 42, 3650–3653. [Google Scholar] [CrossRef]
- Siggia, E.D. High Rayleigh number convection. Annu. Rev. Fluid Mech. 1994, 26, 137–168. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Scaling in thermal convection: A unifying theory. J. Fluid Mech. 2000, 407, 27–56. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 2001, 86, 3316–3319. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, S.; Lohse, D. Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 2002, 66, 016305. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, S.; Lohse, D. Fluctuations in turbulent Rayleigh-Benard convection: The role of plumes. Phys. Fluids 2004, 16, 4462–4472. [Google Scholar] [CrossRef]
- Chakraborty, S. On scaling laws in turbulent magnetohydrodynamic Rayleigh-Benard convection. Phys. D-Nonlinear Phenom. 2008, 237, 3233–3236. [Google Scholar] [CrossRef]
- Zuerner, T.; Liu, W.; Krasnov, D.; Schumacher, J. Heat and momentum transfer for magnetoconvection in a vertical external magnetic field. Phys. Rev. E 2016, 94, 043108. [Google Scholar] [CrossRef]
- Zurner, T. Refined mean field model of heat and momentum transfer in magnetoconvection. Phys. Fluids 2020, 32, 107101. [Google Scholar] [CrossRef]
- Yan, M.; Tobias, S.M.; Calkins, M.A. Scaling behaviour of small-scale dynamos driven by Rayleigh-Benard convection. J. Fluid Mech. 2021, 915, A15. [Google Scholar] [CrossRef]
- Urban, P.; Králík, T.; Hanzelka, P.; Musilova, V.; Vezník, T.; Schmoranzer, D.; Skrbek, L. Thermal radiation in Rayleigh-Benard convection experiments. Phys. Rev. E 2020, 101, 043106. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.Z.; Libchaber, A. Scaling relations in thermal turbulence—The aspect-ratio dependence. Phys. Rev. A 1992, 45, 842–845. [Google Scholar] [CrossRef]
- Li, P.X.; Luo, X.H.; Chen, L.; Song, J.J.; Li, B.W.; Karcher, C. Numerical research for the effect of magnetic field on convective transport process of molten salt in Rayleigh-Bénard system. Int. J. Therm. Sci. 2024, 195, 108605. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, X. Convective and radiative heat transfer in molten salts. Nucl. Technol. 2020, 206, 1721–1739. [Google Scholar] [CrossRef]
- Xie, M.; Zhu, Y.; Liu, Y.; Yuan, Y.; Tan, H. Measurement of spectral radiative characteristics of molten salt at high temperature using emission method. Appl. Therm. Eng. 2019, 149, 151–164. [Google Scholar] [CrossRef]
- Huang, M.; Wang, Y.; Bao, Y.; He, X. Heat transport and temperature boundary-layer profiles in closed turbulent Rayleigh–Bénard convection with slippery conducting surfaces. J. Fluid Mech. 2022, 943, A2. [Google Scholar] [CrossRef]
- Yang, J.L.; Zhang, Y.Z.; Jin, T.C.; Dong, Y.H.; Wang, B.F.; Zhou, Q. The Pr-dependence of the critical roughness height in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 2021, 911, A52. [Google Scholar] [CrossRef]
- Hossain, M.A.; Takhar, H.S. Thermal radiation effects on the natural convection flow over an isothermal horizontal plate. Heat Mass Transf. 1999, 35, 321–326. [Google Scholar] [CrossRef]
- Song, J.; Li, P.; Chen, L.; Zhao, Y.; Tian, F.; Li, B. Correlations for the transport characteristics of Radiative Rayleigh-Bénard convection in optically thick media. In Proceedings of the 21st International Conference on Sustainable Energy Technologies, Shanghai, China, 12–14 August 2024. [Google Scholar]

| Regime I | ||
| Regime II | ||
| Regime III | ||
| Regime IV |
| Grid Size | Nu | Error (%) |
|---|---|---|
| 128 × 128 | 39.17710 | - |
| 256 × 256 | 39.84992 | 1.72% |
| 384 × 384 | 40.03957 | 0.48% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Li, P.; Chen, L.; Zhao, Y.; Tian, F.; Li, B. Scaling Law of Flow and Heat Transfer Characteristics in Turbulent Radiative Rayleigh-Bénard Convection of Optically Thick Media. Energies 2024, 17, 5009. https://doi.org/10.3390/en17195009
Song J, Li P, Chen L, Zhao Y, Tian F, Li B. Scaling Law of Flow and Heat Transfer Characteristics in Turbulent Radiative Rayleigh-Bénard Convection of Optically Thick Media. Energies. 2024; 17(19):5009. https://doi.org/10.3390/en17195009
Chicago/Turabian StyleSong, Jiajun, Panxin Li, Lu Chen, Yuhang Zhao, Fengshi Tian, and Benwen Li. 2024. "Scaling Law of Flow and Heat Transfer Characteristics in Turbulent Radiative Rayleigh-Bénard Convection of Optically Thick Media" Energies 17, no. 19: 5009. https://doi.org/10.3390/en17195009
APA StyleSong, J., Li, P., Chen, L., Zhao, Y., Tian, F., & Li, B. (2024). Scaling Law of Flow and Heat Transfer Characteristics in Turbulent Radiative Rayleigh-Bénard Convection of Optically Thick Media. Energies, 17(19), 5009. https://doi.org/10.3390/en17195009






