On the Different Fair Allocations of Economic Benefits for Energy Communities
Abstract
1. Introduction
1.1. Literature Review
1.2. Objective and Novelty
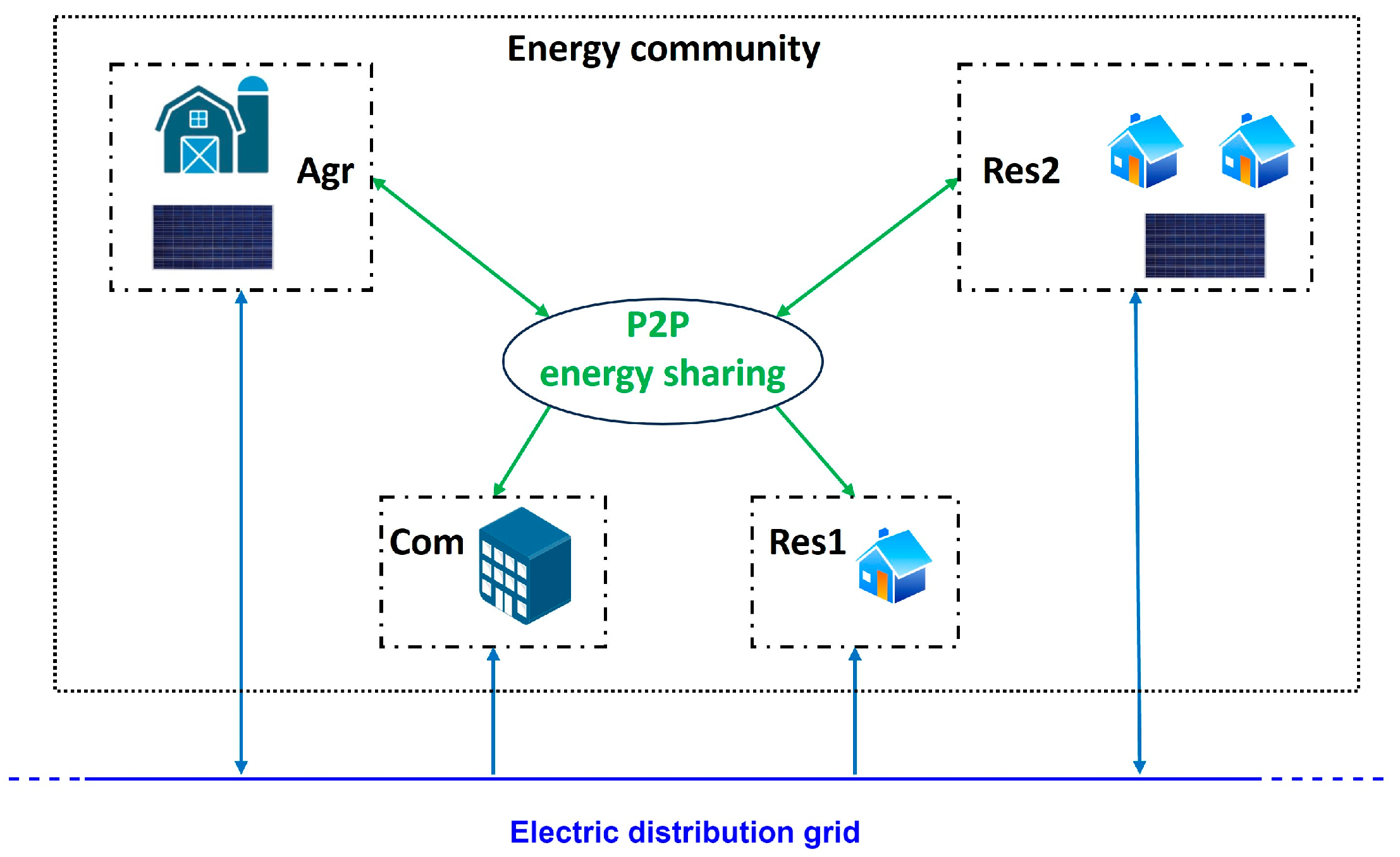
2. Materials and Methods
2.1. Cooperative Optimization Model of the EC
2.2. Social Welfare and Nash Bargaining Optimization Approaches
2.3. Shapley Value and Nucleolus Allocation Criteria
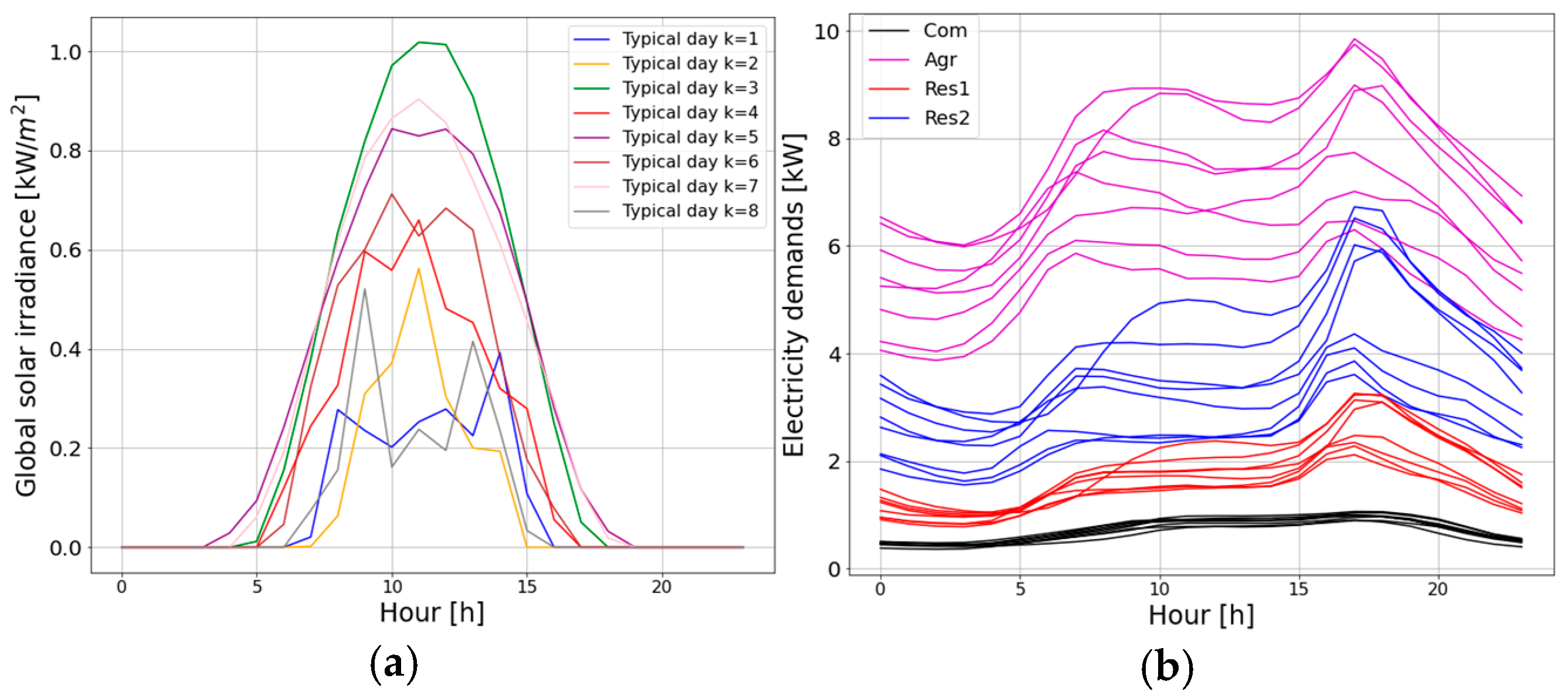
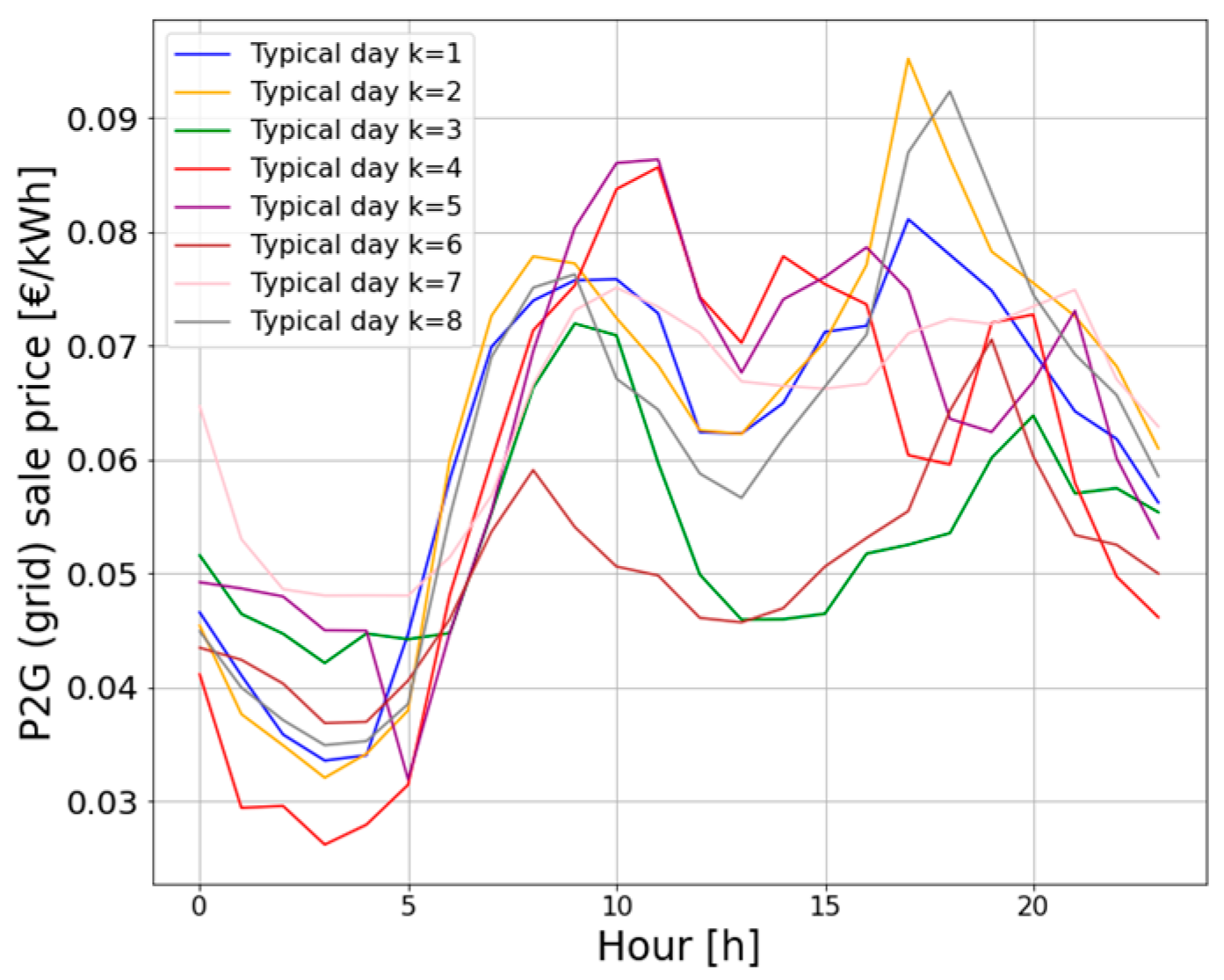
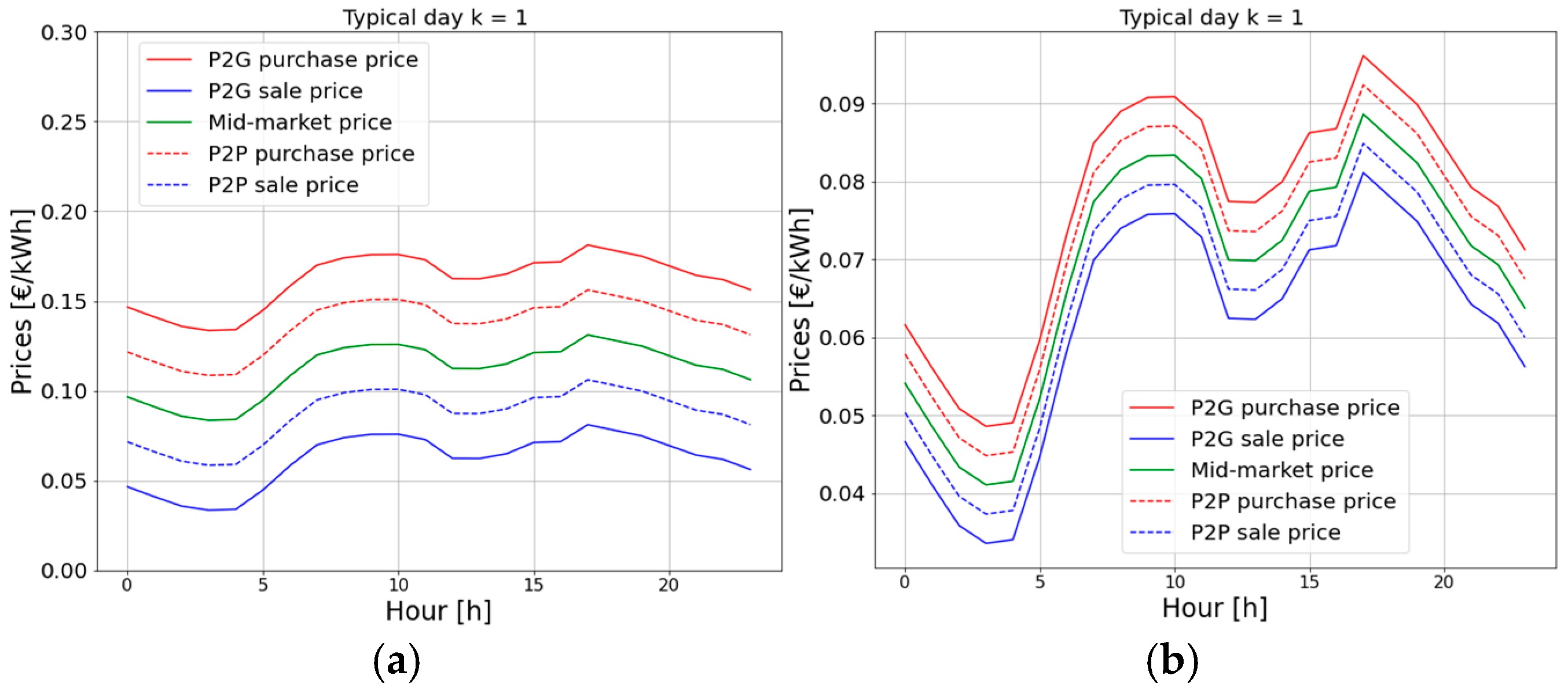
2.4. Input Data
3. Results and Discussion
3.1. Social Welfare and Nash Bargaining
3.2. Shapley Value and Nucleolus
3.3. Critical Remarks
- The cooperative operation of users, with the possibility of exchanging energy with the electric distribution grid (i.e., realizing P2G energy flows) and sharing energy within the EC (i.e., realizing P2P energy flows), is always profitable compared to the “disagreement” case, where each user operates individually by exchanging energy only with the grid (Table 1).
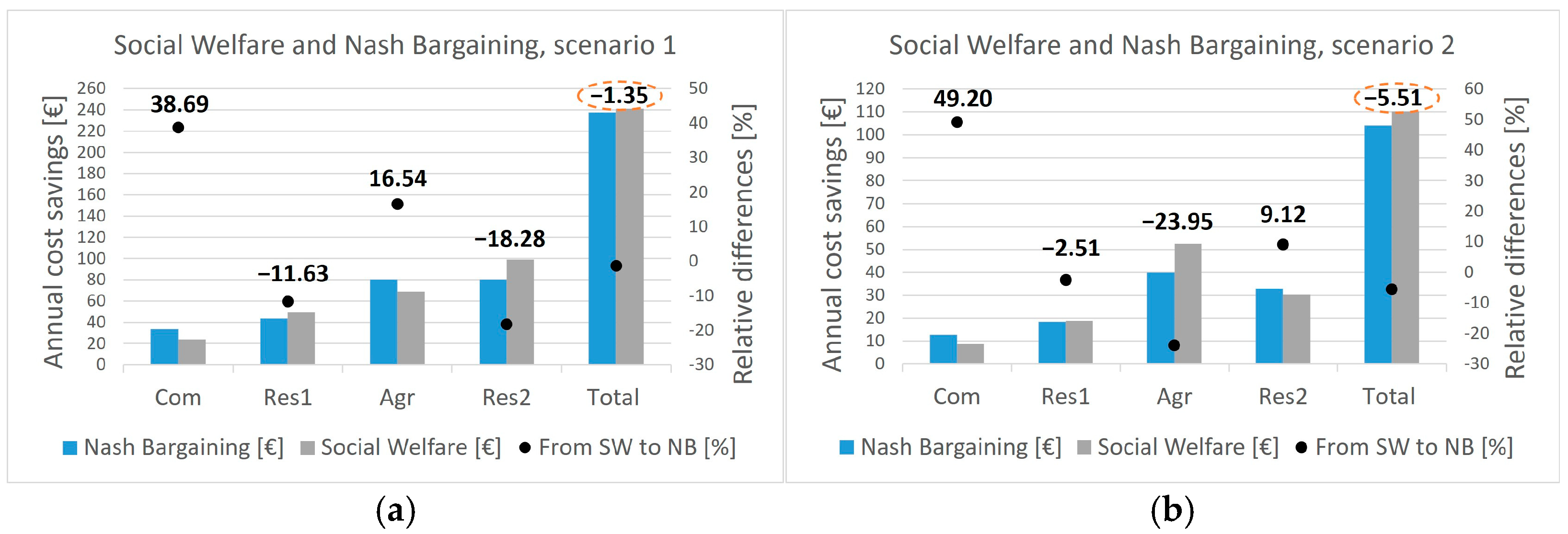
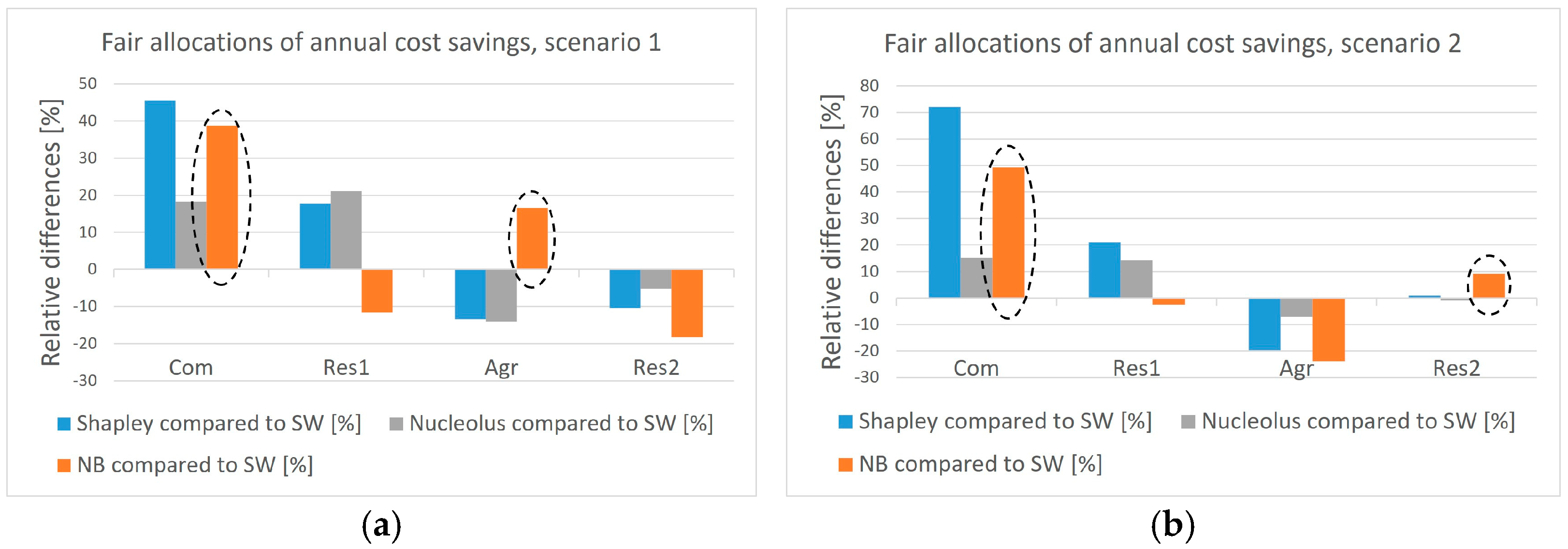
- The NB optimization approach provides a distribution of the optimal annual cost savings that satisfies the notion of “proportional fairness”, rewarding both the consumer with the lowest electricity demand (Com) and the PV prosumers (Agr and Res2) that contribute to the P2P energy sharing (Figure 5, Figure 6 and Figure 7). Compared to the base optimal SW solution (i.e., without re-distribution using Shapley value or Nucleolus), the optimal NB one allocates 39% (49%) and 17% (9%) higher annual cost savings to consumer Com and prosumer Agr (Com and Res2) in scenario 1 (2), respectively, with a POF (i.e., the reduction in the optimal total cost savings of the EC compared to those of the SW solution) of 1.4% (5.5%), in exchange for a distribution of the optimal annual cost savings that could be perceived as fair by both consumers and prosumers of the EC. The low POF sheds light on the low “price” to be paid (i.e., a small part of the total annual cost savings of the EC) to switch from a SW solution to an NB solution, which, being “proportional fair”, can satisfy both consumers with low electricity demands and prosumers contributing to the P2P energy sharing (and not only prosumers, as in the base SW solution, which is also unfair since prosumers have higher electricity demands and higher shares in the annual costs of the EC than consumers, Table 1). Thus, the main difference between the SW and NB solutions does not lie in the optimal total annual cost savings of the EC, but in how the optimal individual annual cost savings are distributed among the different EC members.
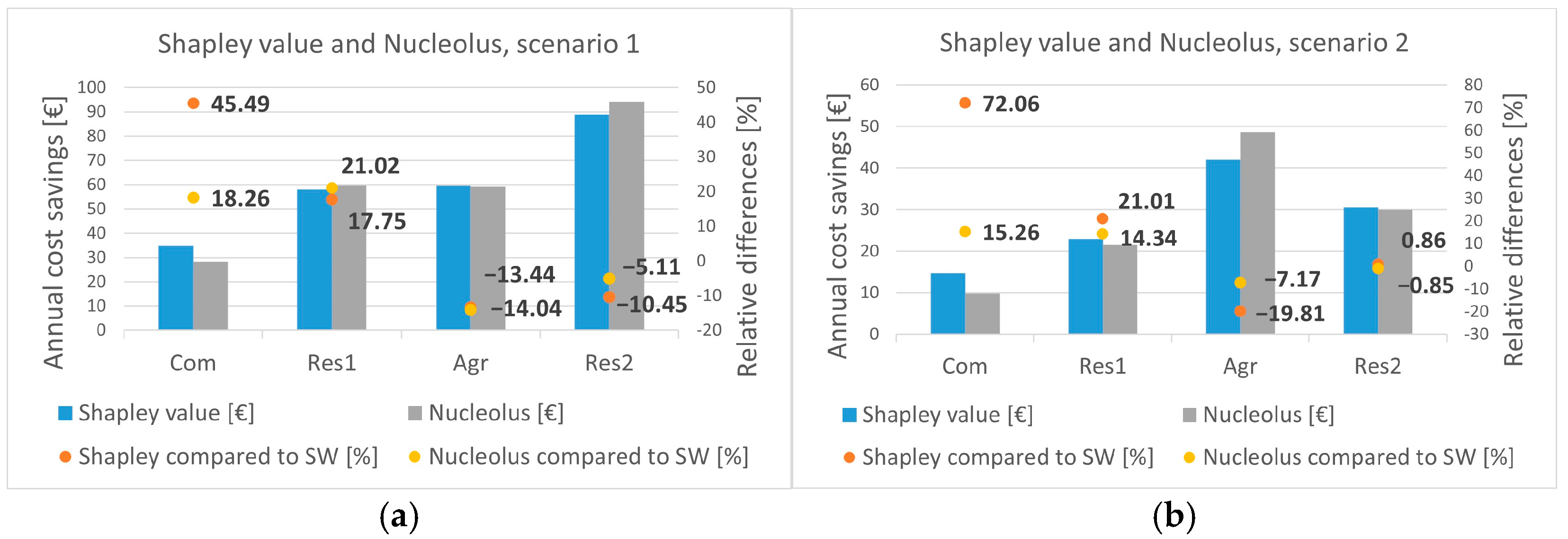
- The Shapley value criterion provides a re-distribution of the optimal total annual cost savings, found by SW, which is consistent with the notion of “individual fairness”, rewarding the users with the lowest electricity consumption more (Com and Res1 consumers) because the electricity demand of some users (Agr and Res2 prosumers) strongly influences the annual operational cost of the EC. Compared to the base optimal SW solution, Shapley value allocates 45% (72%) and 18% (21%) higher annual cost savings to Com and Res1 consumers with the lowest electricity demand in scenario 1 (2) (Figure 9). However, while Shapley value allocation might be appreciated by the most virtuous EC members with low electricity consumption, it could lead to unstable coalitions willing to leave the EC (see Figure 10).
- The Nucleolus criterion, also applied to re-distribute the optimal total annual cost savings of the EC found by SW, provides an alternative solution to the Shapley value allocation. Similar to the Shapley value, the Nucleolus re-distributes higher annual cost savings to Com and Res1 consumers compared to the base optimal SW solution (i.e., 18% and 21% higher in scenario 1, 15% and 14% higher in scenario 2, respectively). Moreover, the Nucleolus allocation embodies the notion of “collective fairness”, which ensures that all user coalitions are satisfied with the allocation of the total annual cost savings, resulting in a stable EC without objective reasons for coalitions to leave the EC. To avoid the instability problem raised by some coalitions in the Shapley value allocation, Nucleolus increases the annual cost savings of Res1 and Res2 in scenario 1 and Agr in scenario 2 compared to Shapley value just enough to persuade them to stay in the EC. For example, in scenario 1, the annual cost savings of Res1 and Res2 increase by 21% (18% with Shapley value) and decrease by 5% (10% with Shapley value), respectively, compared to the base optimal SW solution. However, the homogeneous distribution of annual cost savings by Nucleolus could be perceived as less “individually fair” compared to that of the Shapley value.
4. Conclusions
- The Shapley value and Nucleolus criteria can effectively reward users with low electricity consumption (i.e., Com and Res1 consumers in the considered case study). The Shapley value re-distributes 45–72% and 18–21%, respectively, while the Nucleolus re-distributes 15–18% and 14–21%, respectively, higher annual cost savings to Com and Res1 consumers compared to the base SW optimization. However, the Shapley value carries a risk of instability, as it could incentivize some coalitions to leave the EC due to perceived inequities associated with the lower benefits within the EC than in the case where the coalitions act independently. On the other hand, the Nucleolus criterion provides a more stable allocation, ensuring that all user coalitions are satisfied and want to stay in the EC, even though this allocation could be seen as less “individually fair” compared to the Shapley value (i.e., due to the smaller variations in the optimal annual cost savings with respect to the base SW solution).
- The NB approach rewards both the user with the lowest electricity consumption (i.e., Com) and PV prosumers (i.e., Agr and Res2) who contribute to the P2P energy sharing. Compared to the base SW optimization, NB distributes 39–49% higher annual cost savings to Com consumer and 9–17% higher savings to Agr and Res2 prosumers, albeit with an acceptable Price of Fairness (POF, i.e., the reduction in the optimal total benefit compared to the base SW solution) of 1.4% (scenario 1) and 5.5% (scenario 2).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| Agr | Agricultural |
| Com | Commercial |
| EC | Energy Community |
| MILP | Mixed-Integer Linear Programming |
| NB | Nash Bargaining |
| PBDR | Price-Based Demand Response |
| POF | Price of Fairness |
| PV | Photovoltaic |
| P2G | Peer-to-Grid |
| P2P | Peer-to-Peer |
| RES | Renewable Energy Sources |
| Res | Residential |
| RTP | Real-Time Pricing |
| SW | Social Welfare |
| Symbols | |
| Excess of coalition S | |
| N | Number of members of the EC |
| Coalition of users within the EC | |
| / | Cost of member i in the cooperative/disagreement case for typical day k, € |
| / | Profit of prosumer j in the cooperative/disagreement case for typical day k, € |
| Cost saving of member i for typical day k, € | |
| Profit increase in prosumer j for typical day k, € | |
| Annual incremental economic benefit of member i, € | |
| Value of coalition S, € | |
| Weight of typical day k | |
| Subscripts and superscripts | |
| c | Consumer |
| dis | Disagreement case |
| exp | Export to the grid |
| i | Member of the EC |
| imp | Import from the grid |
| incr | Incremental |
| j | Prosumer |
| k | Typical day of the year |
| max | Maximum |
| shift | Shifted electricity demand |
| t | Hour of typical day |
| tr | Mid-market rate price |
| tr,b | P2P purchase |
| tr,s | P2P sale |
| −/+ | Purchase/sale |
References
- Melnyk, A.; Cox, H.; Ghorbani, A.; Hoppe, T. Value dynamics in energy democracy: An exploration of community energy initiatives. Energy Res. Soc. Sci. 2023, 102, 103163. [Google Scholar] [CrossRef]
- de São José, D.; Faria, P.; Vale, Z. Smart energy community: A systematic review with metanalysis. Energy Strategy Rev. 2021, 36, 100678. [Google Scholar] [CrossRef]
- Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources (Recast). Available online: https://eur-lex.europa.eu/eli/dir/2018/2001/oj (accessed on 11 May 2022).
- Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU (Recast). Available online: https://eur-lex.europa.eu/eli/dir/2019/944 (accessed on 11 May 2022).
- Gianaroli, F.; Preziosi, M.; Ricci, M.; Sdringola, P.; Ancona, M.A.; Melino, F. Exploring the academic landscape of energy communities in Europe: A systematic literature review. J. Clean. Prod. 2024, 451, 141932. [Google Scholar] [CrossRef]
- EU. European Commission’s Communication, ‘Fit for 55’: Delivering the EU’s 2030 Climate Target on the Way to Climate Neutrality (COM(2021) 550 Final). Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX%3A52021DC0550 (accessed on 11 May 2022).
- D’Adamo, I.; Gastaldi, M.; Koh, S.L.; Vigiano, A. Lighting the future of sustainable cities with energy communities: An economic analysis for incentive policy. Cities 2024, 147, 104828. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, P.; Wu, D.; Liu, Z.; Liu, X.; Zhang, S.; Yang, X.; Ge, H. Multi-objective optimization design and multi-attribute decision-making method of a distributed energy system based on nearly zero-energy community load forecasting. Energy 2022, 239, 122124. [Google Scholar] [CrossRef]
- Marchetti, B.; Vitali, M.; Biancini, G. Renewable Energy Proliferation and the New Local Energy Community Paradigm: Analysis of a Case Study in Italy. Energies 2024, 17, 1599. [Google Scholar] [CrossRef]
- Chang, H.-C.; Ghaddar, B.; Nathwani, J. Shared community energy storage allocation and optimization. Appl. Energy 2022, 318, 119160. [Google Scholar] [CrossRef]
- Cutore, E.; Volpe, R.; Sgroi, R.; Fichera, A. Energy management and sustainability assessment of renewable energy communities: The Italian context. Energy Convers. Manag. 2023, 278, 116713. [Google Scholar] [CrossRef]
- Lazzari, F.; Mor, G.; Cipriano, J.; Solsona, F.; Chemisana, D.; Guericke, D. Optimizing planning and operation of renewable energy communities with genetic algorithms. Appl. Energy 2023, 338, 120906. [Google Scholar] [CrossRef]
- Barone, G.; Buonomano, A.; Cipolla, G.; Forzano, C.; Giuzio, G.; Russo, G. Designing aggregation criteria for end-users integration in energy communities: Energy and economic optimisation based on hybrid neural networks models. Appl. Energy 2024, 371, 123543. [Google Scholar] [CrossRef]
- Belloni, E.; Fioriti, D.; Poli, D. Optimal design of renewable energy communities (RECs) in Italy: Influence of composition, market signals, buildings, location, and incentives. Electr. Power Syst. Res. 2024, 235, 110895. [Google Scholar] [CrossRef]
- Dal Cin, E.; Carraro, G.; Volpato, G.; Lazzaretto, A.; Danieli, P. A multi-criteria approach to optimize the design-operation of Energy Communities considering economic-environmental objectives and demand side management. Energy Convers. Manag. 2022, 263, 115677. [Google Scholar] [CrossRef]
- Stegen, T.; Glavic, M.; Cornélusse, B.; Giannitrapani, A.; Paoletti, S. Sizing distributed energy resources in a renewable energy community with a grid-aware internal market structure. Electr. Power Syst. Res. 2024, 234, 110797. [Google Scholar] [CrossRef]
- Li, N.; Okur, Ö. Economic analysis of energy communities: Investment options and cost allocation. Appl. Energy 2023, 336, 120706. [Google Scholar] [CrossRef]
- Volpato, G.; Carraro, G.; Cont, M.; Danieli, P.; Rech, S.; Lazzaretto, A. General guidelines for the optimal economic aggregation of prosumers in energy communities. Energy 2022, 258, 124800. [Google Scholar] [CrossRef]
- Casalicchio, V.; Manzolini, G.; Prina, M.G.; Moser, D. From investment optimization to fair benefit distribution in renewable energy community modelling. Appl. Energy 2022, 310, 118447. [Google Scholar] [CrossRef]
- Zheng, S.; Jin, X.; Huang, G.; Lai, A.C. Coordination of commercial prosumers with distributed demand-side flexibility in energy sharing and management system. Energy 2022, 248, 123634. [Google Scholar] [CrossRef]
- Fina, B. Energy community incurred grid cost redistribution mechanisms considering different objectives and aspects of fairness. Energy Rep. 2024, 11, 6238–6254. [Google Scholar] [CrossRef]
- Li, N.; Hakvoort, R.A.; Lukszo, Z. Cost allocation in integrated community energy systems—A review. Renew. Sustain. Energy Rev. 2021, 144, 111001. [Google Scholar] [CrossRef]
- Pedrero, R.A.; Pisciella, P.; del Granado, P.C. Fair investment strategies in large energy communities: A scalable Shapley value approach. Energy 2024, 295, 131033. [Google Scholar] [CrossRef]
- van Bommel, N.; Höffken, J.I. Energy justice within, between and beyond European community energy initiatives: A review. Energy Res. Soc. Sci. 2021, 79, 102157. [Google Scholar] [CrossRef]
- Luo, C.; Zhou, X.; Lev, B. Core, shapley value, nucleolus and nash bargaining solution: A Survey of recent developments and applications in operations management. Omega 2022, 110, 102638. [Google Scholar] [CrossRef]
- Cappellaro, F.; D’Agosta, G.; De Sabbata, P.; Barroco, F.; Carani, C.; Borghetti, A.; Lambertini, L.; Nucci, C.A. Implementing energy transition and SDGs targets throughout energy community schemes. J. Urban Ecol. 2022, 8, juac023. [Google Scholar] [CrossRef]
- Bandeiras, F.; Gomes, Á.; Gomes, M.; Coelho, P. Application and challenges of coalitional game theory in power systems for sustainable energy trading communities. Energies 2023, 16, 8115. [Google Scholar] [CrossRef]
- Zatti, M.; Moncecchi, M.; Gabba, M.; Chiesa, A.; Bovera, F.; Merlo, M. Energy communities design optimization in the Italian framework. Appl. Sci. 2021, 11, 5218. [Google Scholar] [CrossRef]
- Nguyen, H.K.; Mohsenian-Rad, H.; Khodaei, A.; Han, Z. Decentralized reactive power compensation using nash bargaining solution. IEEE Trans. Smart Grid 2015, 8, 1679–1688. [Google Scholar] [CrossRef]
- Chiş, A.; Koivunen, V. Coalitional game-based cost optimization of energy portfolio in smart grid communities. IEEE Trans. Smart Grid 2017, 10, 1960–1970. [Google Scholar] [CrossRef]
- Bossu, A.; Durillon, B.; Davigny, A.; Barry, H.; Robyns, B.; Belaïd, F.; Saudemont, C. Coalitional game-based gain generation and distribution for collective self-consumption in an energy community. Math. Comput. Simul. 2024, 225, 129–147. [Google Scholar] [CrossRef]
- Han, L.; Morstyn, T.; McCulloch, M. Incentivizing prosumer coalitions with energy management using cooperative game theory. IEEE Trans. Power Syst. 2018, 34, 303–313. [Google Scholar] [CrossRef]
- Nash, J.F., Jr. The bargaining problem. Econom. J. Econom. Soc. 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Vespermann, N.; Hamacher, T.; Kazempour, J. Access economy for storage in energy communities. IEEE Trans. Power Syst. 2020, 36, 2234–2250. [Google Scholar] [CrossRef]
- Volpato, G.; Carraro, G. Different allocation mechanisms to distribute the total profits of the Italian Renewable Energy Community. In Proceedings of the ECOS 2023—The 36th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Las Palmas de Gran Canaria, Spain, 25–30 June 2023. [Google Scholar]
- Cremers, S.; Robu, V.; Hofman, D.; Naber, T.; Zheng, K.; Norbu, S. Efficient methods for approximating the Shapley value for asset sharing in energy communities. In Proceedings of the Thirteenth ACM International Conference on Future Energy Systems, Virtual, 28 June–1 July 2022; pp. 320–324. [Google Scholar]
- Siqin, Z.; Niu, D.; Li, M.; Gao, T.; Lu, Y.; Xu, X. Distributionally robust dispatching of multi-community integrated energy system considering energy sharing and profit allocation. Appl. Energy 2022, 321, 119202. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, G.; Spanos, C.J. Optimal sharing and fair cost allocation of community energy storage. IEEE Trans. Smart Grid 2021, 12, 4185–4194. [Google Scholar] [CrossRef]
- Fioriti, D.; Frangioni, A.; Poli, D. Optimal sizing of energy communities with fair revenue sharing and exit clauses: Value, role and business model of aggregators and users. Appl. Energy 2021, 299, 117328. [Google Scholar] [CrossRef]
- Limmer, S. Empirical Study of Stability and Fairness of Schemes for Benefit Distribution in Local Energy Communities. Energies 2023, 16, 1756. [Google Scholar] [CrossRef]
- Fischer, R.; Toffolo, A. Is total system cost minimization fair to all the actors of an energy system? Not according to game theory. Energy 2022, 239, 122253. [Google Scholar] [CrossRef]
- Ding, J.; Gao, C.; Song, M.; Yan, X.; Chen, T. Optimal operation of multi-agent electricity-heat-hydrogen sharing in integrated energy system based on Nash bargaining. Int. J. Electr. Power Energy Syst. 2023, 148, 108930. [Google Scholar] [CrossRef]
- Li, L.; Cao, X.; Zhang, S. Shared energy storage system for prosumers in a community: Investment decision, economic operation, and benefits allocation under a cost-effective way. J. Energy Storage 2022, 50, 104710. [Google Scholar] [CrossRef]
- Devi, N.N.; Thokchom, S.; Singh, T.D.; Panda, G.; Naayagi, R.T. Multi-stage bargaining of smart grid energy trading based on cooperative game theory. Energies 2023, 16, 4278. [Google Scholar] [CrossRef]
- Lund, P.D.; Lindgren, J.; Mikkola, J.; Salpakari, J. Review of energy system flexibility measures to enable high levels of variable renewable electricity. Renew. Sustain. Energy Rev. 2015, 45, 785–807. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Z.; Wang, D.; Ma, T. Peer-to-peer energy sharing with demand-side management for fair revenue distribution and stable grid interaction in the photovoltaic community. J. Clean. Prod. 2023, 383, 135271. [Google Scholar] [CrossRef]
- Tushar, W.; Saha, T.K.; Yuen, C.; Liddell, P.; Bean, R.; Poor, H.V. Peer-to-peer energy trading with sustainable user participation: A game theoretic approach. IEEE Access 2018, 6, 62932–62943. [Google Scholar] [CrossRef]
- Hoffmann, M.; Kotzur, L.; Stolten, D.; Robinius, M. A review on time series aggregation methods for energy system models. Energies 2020, 13, 641. [Google Scholar] [CrossRef]
- Zatti, M.; Gabba, M.; Freschini, M.; Rossi, M.; Gambarotta, A.; Morini, M.; Martelli, E. k-MILP: A novel clustering approach to select typical and extreme days for multi-energy systems design optimization. Energy 2019, 181, 1051–1063. [Google Scholar] [CrossRef]
- Volpato, G.; Bregolin, E.; Dal Cin, E.; Carraro, G.; Danieli, P.; Lazzaretto, A. Unsupervised and supervised machine learning techniques for timeseries aggregation in the design and operation optimization of multi-energy systems. In Proceedings of the ECOS 2024—The 37th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Rhodes, Greece, 30 June–5 July 2024. [Google Scholar]
- Ceglia, F.; Esposito, P.; Faraudello, A.; Marrasso, E.; Rossi, P.; Sasso, M. An energy, environmental, management and economic analysis of energy efficient system towards renewable energy community: The case study of multi-purpose energy community. J. Clean. Prod. 2022, 369, 133269. [Google Scholar] [CrossRef]
- Reis, I.F.; Gonçalves, I.; Lopes, M.A.; Antunes, C.H. A multi-agent system approach to exploit demand-side flexibility in an energy community. Util. Policy 2020, 67, 101114. [Google Scholar] [CrossRef]
- Reis, I.F.; Gonçalves, I.; Lopes, M.A.; Antunes, C.H. Assessing the influence of different goals in energy communities’ self-sufficiency—An optimized multiagent approach. Energies 2021, 14, 989. [Google Scholar] [CrossRef]
- Fan, S.; Ai, Q.; Piao, L. Bargaining-based cooperative energy trading for distribution company and demand response. Appl. Energy 2018, 226, 469–482. [Google Scholar] [CrossRef]
- Yaacoub, E.; Dawy, Z. A game theoretical formulation for proportional fairness in LTE uplink scheduling. In Proceedings of the 2009 IEEE Wireless Communications and Networking Conference, Budapest, Hungary, 5–8 April 2009; pp. 1–5. [Google Scholar]
- Yaïche, H.; Mazumdar, R.R.; Rosenberg, C. A game theoretic framework for bandwidth allocation and pricing in broadband networks. IEEE/ACM Trans. Netw. 2000, 8, 667–678. [Google Scholar] [CrossRef]
- Kelly, F.P.; Maulloo, A.K.; Tan, D.K.H. Rate control for communication networks: Shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 1998, 49, 237–252. [Google Scholar] [CrossRef]
- Kelly, F. Charging and rate control for elastic traffic. Eur. Trans. Telecommun. 1997, 8, 33–37. [Google Scholar] [CrossRef]
- Song, G.; Li, Y. Cross-layer optimization for OFDM wireless networks-part I: Theoretical framework. IEEE Trans. Wirel. Commun. 2005, 4, 614–624. [Google Scholar] [CrossRef]
- Bertsimas, D.; Farias, V.F.; Trichakis, N. The price of fairness. Oper. Res. 2011, 59, 17–31. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Cai, C.; Xue, L.; Ma, Y.; Shen, H.; Chen, X.; Liu, L. Research on the optimization method of integrated energy system operation with multi-subject game. Energy 2022, 245, 123305. [Google Scholar] [CrossRef]
- Danish Energy Agency. Energy Transport—Technology Descriptions and Projections for Long-Term Energy System Planning. Available online: https://ens.dk/sites/ens.dk/files/Analyser/technology_data_for_energy_transport.pdf (accessed on 8 February 2023).
- PVGIS. Photovoltaic Geographical Information System (PVGIS). Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 11 May 2022).
- Energinet. EnergiDataService. Available online: https://www.energidataservice.dk/tso-electricity/Elspotprices (accessed on 8 February 2023).
- GME. Gestore Mercati Energetici. Available online: https://www.mercatoelettrico.org/en/default.aspx (accessed on 11 May 2022).
- Bynum, M.L.; Hackebeil, G.A.; Hart, W.E.; Laird, C.D.; Nicholson, B.L.; Siirola, J.D.; Watson, J.-P.; Woodruff, D.L. Pyomo-Optimization Modeling in Python; Springer: Berlin/Heidelberg, Germany, 2021; Volume 67. [Google Scholar]
- Hart, W.E.; Watson, J.-P.; Woodruff, D.L. Pyomo: Modeling and solving mathematical programs in Python. Math. Program. Comput. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- Gurobi Optimization. Available online: https://www.gurobi.com/ (accessed on 11 May 2022).

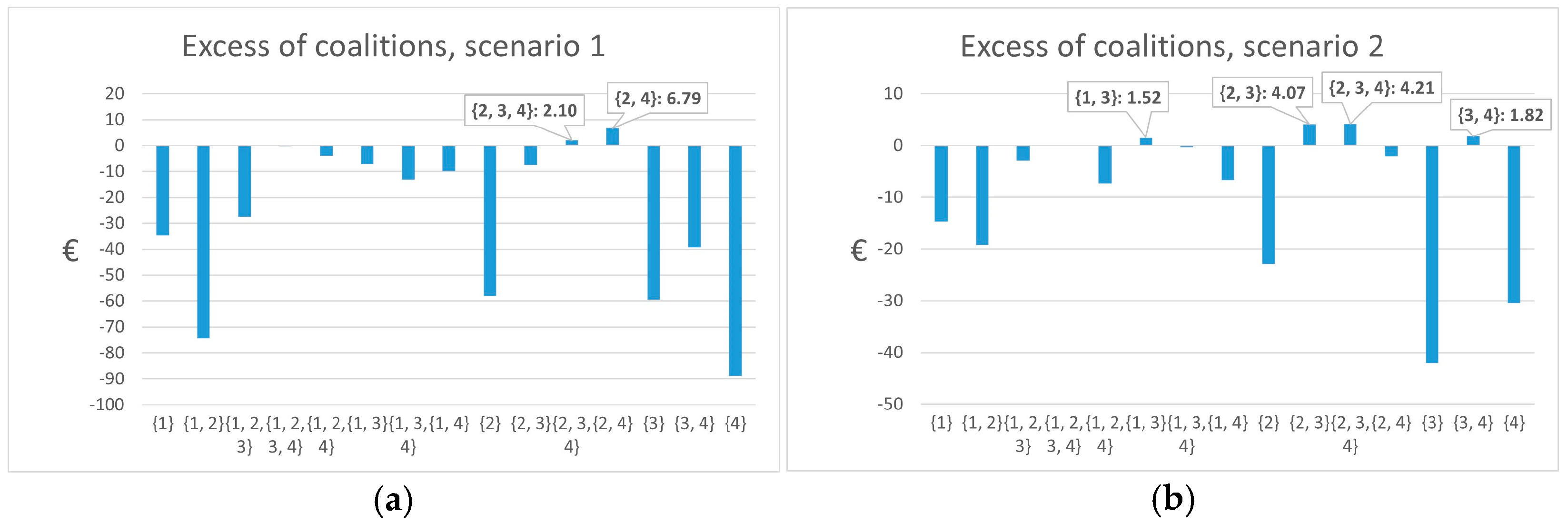
| (a) | |||
| Annual Costs [€], Scenario 1 with Grid Tariff Equal to 0.1 €/kWh | |||
| Member | Disagreement Case | Nash Bargaining | Social Welfare |
| Com | −1000.52 | −967.18 | −976.65 |
| Res1 | −2285.05 | −2241.50 | −2235.77 |
| Agr | −6153.55 | −6073.26 | −6084.82 |
| Res2 | −2751.90 | −2671.60 | −2652.69 |
| Total | −12,191.02 | −11,953.54 | −11,949.94 |
| (b) | |||
| Annual Costs [€], Scenario 2 with Grid Tariff Equal to 0.015 €/kWh | |||
| Member | Disagreement Case | Nash Bargaining | Social Welfare |
| Com | −476.17 | −463.40 | −467.61 |
| Res1 | −1085.24 | −1066.80 | −1066.33 |
| Agr | −2794.09 | −2754.18 | −2741.61 |
| Res2 | −1178.48 | −1145.49 | −1148.24 |
| Total | −5533.98 | −5429.86 | −5423.79 |
| Annual Cost Savings of Coalitions [€], Scenario 1 with Grid Tariff Equal to 0.1 €/kWh | ||||
|---|---|---|---|---|
| {1}: 0 | {1,2}: 18.46 | {1,2,3}: 124.65 | {1,2,3,4}: 241.08 | {1,2,4}: 177.6 |
| {1,3}: 87.17 | {1,3,4}: 169.95 | {1,4}: 113.68 | {2}: 0 | {2,3}: 110.04 |
| {2,3,4}: 208.45 | {2,4}: 153.65 | {3}: 0 | {3,4}: 109.02 | {4}: 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volpato, G.; Carraro, G.; Dal Cin, E.; Rech, S. On the Different Fair Allocations of Economic Benefits for Energy Communities. Energies 2024, 17, 4788. https://doi.org/10.3390/en17194788
Volpato G, Carraro G, Dal Cin E, Rech S. On the Different Fair Allocations of Economic Benefits for Energy Communities. Energies. 2024; 17(19):4788. https://doi.org/10.3390/en17194788
Chicago/Turabian StyleVolpato, Gabriele, Gianluca Carraro, Enrico Dal Cin, and Sergio Rech. 2024. "On the Different Fair Allocations of Economic Benefits for Energy Communities" Energies 17, no. 19: 4788. https://doi.org/10.3390/en17194788
APA StyleVolpato, G., Carraro, G., Dal Cin, E., & Rech, S. (2024). On the Different Fair Allocations of Economic Benefits for Energy Communities. Energies, 17(19), 4788. https://doi.org/10.3390/en17194788








