Abstract
In the context of energy conversion from renewable sources to distribution grids (insulated or not), a converter is often required to transfer energy from a low voltage source towards three-phase grids. This paper presents the HW design, the simulation results, and the conversion performance of a CSI converter intended to interface low-voltage renewable sources to three-phase grids. The main focus of this paper is to obtain the best performance in terms of voltage increase towards the output stage while maximizing the conversion efficiency. In comparison with the currently used energy conversion systems for small photovoltaic systems, hereafter some solutions were adopted to level and maximize the energy flow from the source to the DC-link and improve the quality of current supplied in terms of harmonic distortion. The proposed system is composed of two conversion stages: the first, voltage-to-current, the second current-to-current via a three-phase CSI bridge modulated with the SVM technique. The stages are not completely decoupled from an electrical point of view; therefore, in order to mitigate the effects of these interactions, synchronization strategies have been adopted.
Keywords:
current source inverter; CSI; renewable; photovoltaic; PV; space vector modulation; SVM; switched inductors 1. Introduction
Formulating a precise definition of “energy transition compatible with sustainable development”, not just from a strictly environmental point of view, is not an easy task. In fact, the concept of “energy transition” acquires a complexity often defined as “multidimensional” because it depends on numerous factors, such as geographical, environmental, social, and economic factors []. However, it is possible to give a definition of this process in a generic and commonly acceptable way as the “gradual change of society and the economy towards sustainable actions from an environmental, social and governance point of view”. The UN has addressed this topic numerous times since the 1980s (i.e., in the Brundtland Commission) and has universally described and structured the problems underlying the concept of sustainable development; see “UN Agenda 2030” []. The problems that need to be addressed to carry out a gradual transition are numerous, not all of them are easily solvable, and some of them have not yet even been outlined in their particular characteristics; for example, the criteria for the objective measurement of sustainability in the industrial sector, and even fewer in the civil and domestic spheres have been defined. A precise definition of the parameters with which to arrive at an objectively comparable model is still missing [,].
In Europe, the ESG European Institute Commission is an organization whose objective is to define and suggest the criteria for sustainable development from an economic and financial point of view; however, this is a difficult task due to the difficulty of building a taxonomy of all categories involved in these processes. If, on the one hand, it is clear that it is necessary to address the problem from a global point of view, on the other hand, it must be taken into account that the scenario is extremely heterogeneous given that the social, economic, and cultural conditions are extremely different. In Europe, there is an intense debate on how to address these problems and, above all, with what speed to boost the transformations that imply the removal of the dependence of energy production on fossil fuels. As mentioned, sustainable development cannot only be framed in an ecological context but also must consider important social and governance aspects. If we made the mistake of considering only one of these areas, there could be serious consequences and negative repercussions on the others [].
However, aside from these general considerations that we consider as a point of reference for our actions, one of the tasks of technicians and researchers is certainly to try to remove the obstacles that can make it difficult to adopt systems useful for the sustainable development process. Some important areas in which research is engaged studying innovative solutions that facilitate the transition at least from a technical and technological point of view are: the improvement of the energy efficiency of production from renewable sources; the reduction of costs of the equipment and its installation; the ease of use; the security; the duration and reduction of the environmental impact; the compatibility with other conversion systems connected to the same grid; and the increase of the life cycle [].
Through the interactions with companies producing PV systems and with users and potential users, some needs of a technical nature have emerged that have pushed us to identify solutions that can satisfy the requests. Many of these technical aspects concern the quality of the output voltage of DC/AC converters from photovoltaic sources that connect both to the electrical grid and to isolated grids. In particular, some specifications concern the stability in frequency and voltage amplitude on isolated grids [], whereas on prevalent power grids, problems have been highlighted regarding the current ripple affecting the output filters. This circumstance often makes it difficult to design this stage respecting the limits of both conducted and radiated electromagnetic compatibility and therefore following the rules dictated by the standards as well as in the specifications imposed by the operator of the electricity line.
From a more general point of view, further problems are highlighted, very often unintentionally overlooked by both conversion system manufacturers and users. One of these is the high harmonic content, both at high frequency and at frequencies lower than 50 Hz, introduced into electrical grids and that often propagates, causing unpredictable effects []. Dangerous interactions with other conversion systems can occur, generating potential situations of latent instability; they can be triggered by particular events such as the disconnection or connection of a branch of the electricity grid, or the onset of a fault [,].
A further requirement has been reported that concerns the voltage supplied by the panels and strings of photovoltaic panels. In particular, it is frequently considered useful to have conversion systems capable of operating on relatively low DC voltages, for example, around 100 V, in order to create very low voltage strings made up of several elements in parallel, each composed of no more than one pair of panels in series that can achieve a peak voltage rating of 120 V.
The main guidelines to follow for the design of a conversion system that meets the mentioned needs can be summarized as follows:
- Possibility of connection to isolated grids and a distribution grid;
- Connection to a very low voltage photovoltaic system, not exceeding 120 V;
- Drastic scaling of reactive elements;
- Improved performance in terms of harmonic content injected in the grid;
- Improvement of the overall reliability of the conversion system;
- Less susceptibility of the control system to grid disturbances, with particular regard to phenomena known as “harmonic stability” and greater robustness in terms of ability to contribute to grid.
Following the indicated criteria, a critical analysis is carried out aimed at identifying the most suitable conversion topology, considering and comparing both classic and less conventional configurations. From the studies reported in the bibliography, but also from the experience gained in the design of CSI converters, some important differences, among all types, emerge with strong evidence. The main aim of this work is therefore to identify a conversion configuration that is able to meet the requirements just listed. The main challenge is to be able to obtain a high step-up capacity, avoiding the use of a transformer and without compromising the overall efficiency.
Structure of Paper
The structure of this document shows the logical path that was followed to identify a conversion topology suitable for the imposed specifications.
The design solutions present in the literature based on both voltage source converters (below VSI) and CSI were considered by evaluating their respective characteristics and performances, as well as their adequacy with respect to the specifications set on the maximum voltage of the photovoltaic system and on their ability to interface with both a standard distribution grid or an insulated grid.
Section 2 reports the considerations that led to the choice of a CSI conversion bridge, and Section 3 describes the modulation technique used in the CSI bridge and the implementation method.
Section 4 considers a possible promising conversion solution, for the DC/DC conversion stage, in terms of voltage step-up capacity. In order to verify its performance and establish its ability to respond to the established specifications, some simulations were carried out that allowed it to be characterized. The data provided by these simulations suggested introducing some modifications to the DC/DC stage that allowed us to significantly improve its step-up capacity and to eliminate the fourth leg of the CSI bridge. The same section describes the modulation technique adopted for this stage and the related synchronization technique with the CSI bridge.
Finally, Section 5 reports the data relating to the simulation of the entire model, without controls of the output voltage (in the case of an isolated network) or the output current (in the case of connection to the distribution network); in this case, the module and the phase of the CSI reference current were set to constant values. Similarly, the model is not equipped with current control of the DC/DC stage since the duty cycle has been set at a constant value.
2. Issues and Advantages of Conversion Systems Based on CSI
Figure 1 shows the most commonly adopted conversion lines based on VSI inverters (Figure 1a) and CSI inverters (Figure 1b), both designed to allow the controlled transfer of electrical energy from a low voltage photovoltaic source to a electric grid. For each conversion line, a simplified conceptual diagram has been drawn, with the respective functional explanatory diagram at the bottom, in order to highlight the functions performed by the individual conversion elements and their characteristic circuits.
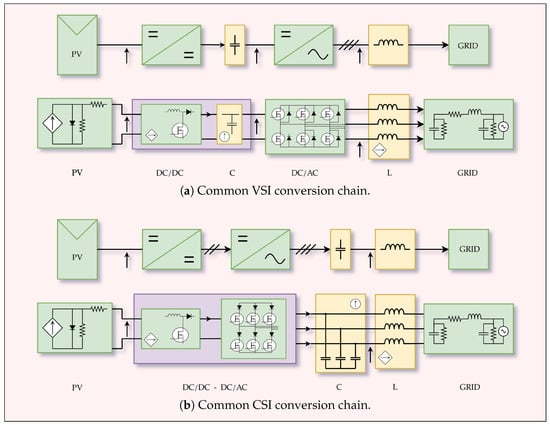
Figure 1.
General diagram of a conversion chain with VSI converter and CSI converter both connected to a power grid.
An important issue of PV conversion systems concerns their stability. As is well known, the tendency to instability is related to the impedance of the electric grid and its articulation. This feature is taken into account through the stability index [,,], which is strictly dependent on the overall impedance present on the connection node. As a result, grid stability is particularly critical for weak grids, microgrids, or isolated grids. From a strictly electrotechnical point of view, Figure 1a allows some important considerations to be made: The first is the need to insert highly inductive elements to connect the VSI inverter with the grid, given that both the VSI bridge and the grid could be considered as voltage generators. This fact has consequences for the difficulty in designing a current control system with sufficient dynamic performance to guarantee the control of the stability of the grid voltage []; furthermore, in this section, it is often necessary to use a transformer to reach sufficiently high voltage levels, introducing further factors that can influence the control dynamics []. The second remark concerns the DC/DC conversion section, which must be completed by a capacitive reactive element so that the inverter can be powered by voltage. The presence of a capacitance of a sufficiently high value does not allow high dynamic performance to be obtained in the DC-link voltage control, compromises the dynamic capability of the MPPT control [,], and introduces sub-synchronous resonances []. The choice of this capacitive element is critical, as it must be made on the basis of a difficult compromise given that, on the one hand, low value of the capacity reduces the settling time during environmental disturbances and allows the performance of the MPPT to be improved; on the other, the inverter current control requires strong stability of the DC-link voltage and therefore a high value of capacity. As a consequence of these conflicting needs, the design of the whole conversion line is particularly difficult to manage [].
Considering the CSI inverter based conversion line shown in Figure 1b, the following considerations can be made:
- The first is that the CSI can be considered, from a strictly electrotechnical point of view, a current generator; as such, it presents two interesting characteristics, which are the ability to have a more stiff control current compared to the VSI and, therefore, to require the presence of reactive elements of much more limited value on the connection to the grid, (C) and (L). This fosters the design of control systems for the current fed into the grid;
- The second is that the inverter requires a current power supply, so the DC/DC converter has no capacity (C), so it is clear that many of the problems related to the control of VSI-based conversion lines, which have been mentioned above, are greatly reduced in the case of CSI. Numerous comparative studies have been done by researchers on these two different types of conversion [,,,], from which interesting evaluations have emerged that suggest the convenience of adopting one or the other based on specific applications. In particular, in regard to the solution shown in Figure 1b, notable advantages have been highlighted in the implementation and design of the control of the current feeding the grid; furthermore, the stability of the DC-link and the performance of the MPPT are significantly improved. An obvious drawback is the higher losses due to the currents recirculating in the DC-link inductor and in the bridge. The capacity value is lower, even if the DC-link inductor is particularly bulky and requires very careful design to limit conduction losses. Similar to what happens for passive elements, switching losses are better in power devices, but conduction losses are worse.
- The third consideration, perhaps the most relevant, is that the CSI inverter has natural boost characteristics and, therefore, if the DC/DC converter is designed to support these characteristics, it is possible to avoid transformers and also to limit the size of the necessary reactive elements, both on the DC-link and on the grid connection.
Further observations can be made on the reliability of the two systems, remembering that the CSI has an intrinsically short circuit capability and shows greater general reliability. Based on all these considerations, the type chosen is the one based on the CSI converter, i.e., the one shown in Figure 1b. On this conversion line, it is now necessary to identify the types of the two DC/DC and DC/AC conversion stages and carry out a first rough sizing of the passive elements, keeping in mind that the sizing of the latter will have to be refined on the basis of the required dynamic performance of regulation systems.
3. CSI Bridge
In order to better introduce the common problem of the CSI topology and outline the solution, the CSI operation and the adopted modulation technique is reported below. The CSI bridge adopted in this project is based on a classic scheme; it is made up of three branches composed of power devices with diodes in series for blocking the currents during the switching phases.
The generic scheme is the one shown in Figure 2a. Figure 2b is rather trivial and is common to all CSI bridges; it represents the current base vectors that can be generated depending on the states of the devices. At the center of the diagram are the three free-wheeling states that do not circulate current in the capacitor bank.
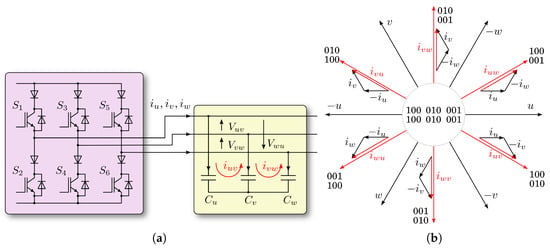
Figure 2.
CSI, main current vectors and related switch states. (a) CSI bridge and output reactive stage; (b) Vector diagram and related CSI status.
3.1. CSI Modulation Strategy
Less trivial, however, is the strategy that can be implemented to obtain a certain current value at the output of the bridge, or to pursue a certain voltage value, set as a reference. The scientific literature is full of more or less sophisticated solutions on this subject.
In the proposed implementation, the following criteria were followed to design the switching strategy for this project:
- Reduce the complexity of the calculation algorithms given that the entire modulation and control system will have to be implemented on a single microcontroller (Texas Instruments, C2000™ 32-bit MCU F28379D, Dallas, TX, USA). Programming is performed using Simulink Embedded Coder® Support Package (Matlab® release R2024a, from Mathworks Inc., update 3). which offers important advantages for rapid prototyping, software portability, and the production of standardized code for embedded systems. The Simulink® (Matlab® release R2024a, from Mathworks Inc., update 3) models, described below, were programmed according to criteria for the automatic production of code on a microcontroller; therefore, the functions for managing code under interrupt and the discretization of some variables were implemented;
- Modulation with vector current references, therefore of SVM type;
- Use of techniques aimed at the optimal exploitation of the devices, therefore symmetrical modulation in the respective quadrants.
Based on these indications, hereafter we can describe the various elements and the performed functions. Calling the reference current, it is broken down into its module and phase components , .
The entire time interval during which the first active state of the bridge is activated is calculated with the expression , where is the relative switching frequency with asymmetric modulation, and is the value of the reference current anomaly with respect to the first basis vector of the sector in which the reference current is located (see Figure 3). The entire time interval during which the second active state of the bridge is activated is calculated with the expression . The entire time interval during which the bridge must be in one of the states producing zero current on the three-phase system is given by the difference .
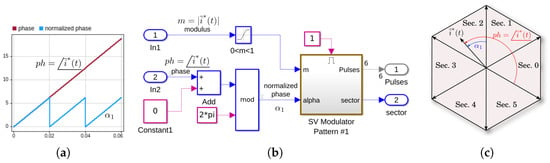
Figure 3.
Normalized phase computation. (a) Phase and normalized phase ; (b) Implemented Simulink® stage; (c) Vector diagram with reference current and phases.
The sector in which the reference current lies is obtained from the phase value, which is calculated with the aid of a look-up table that implements the function . This type of implementation, see Figure 4, was chosen to make the microcontroller code more efficient.

Figure 4.
Modulation times computation.
The subsequent functions transform , , and into the corresponding time intervals. In particular, Figure 5a shows the code that calculates the sequences with which the states of the bridge follow one another in any of the sectors. In this case, although the ramp used to generate the time base has a sawtooth shape, the switching strategy is symmetrical; however, it is relatively easy to swap to asymmetric switching by modifying the code reported in . The model reported in generates the numbering. Figure 5b shows the temporal diagram of the switching sequences and the spatial representation of the bridge states in sector 0, chosen as an example. The numbering, together with the sector number, are the input variables for a 3D matrix in which the states of the six bridge devices are stored. The device states are shown in Table A1 in Appendix A.
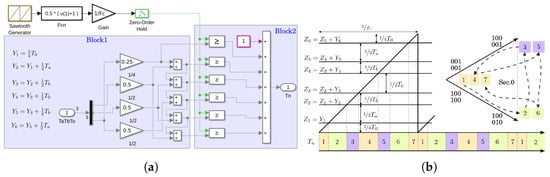
Figure 5.
SVM timing generation. (a) Simulink® block diagram; (b) implemented function and space sequence for sector 0.
3.2. Dead Time Implementation
Of course, there are numerous methods for implementing dead times in a CSI bridge modulator. In this project, it was chosen to avoid the use of indexed tables or matrices, preferring a direct calculation technique also based on the measurement of the state of the bridge in real time. Referring to the diagram in Figure 6, some areas have been highlighted in order to make the identification of functions clearer. The introduction of the dead time is done by delaying the falling edge of all six device control signals by an amount equal to , where is the smallest calculation period with which the microcontroller interrupt routines are managed. The delay is introduced by the sections indicated with and . The value of is a project parameter and can depend on numerous factors, including the choice of the type of power devices. An exception has been introduced in this simple procedure, which consists of delaying the control signals of devices when there is a sector change and when the state of the devices is in current free-wheeling. The detection of the free-wheeling state is carried out by the code of , and the further delay is introduced by the elements present in . This correction, although introducing a small distortion in the current control, is necessary to avoid too-short switching intervals near the transition between one sector and the adjacent one. Intervals of this type may not be adequately managed by the drivers and may have unpredictable consequences on the real state of the devices. It was therefore preferred to implement a more robust solution rather than a perfectly linear SVM modulation technique.
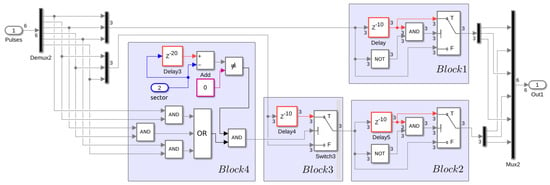
Figure 6.
Dead times.
4. Key Considerations on the DC/DC Conversion Stage Structure and Control
On the basis of the foregoing, it is necessary to identify a conversion topology for the DC/DC voltage/current stage, capable of supporting and delivering a sufficiently stable current considering the voltage present on the input terminals of the CSI bridge.
4.1. DC/DC Stage Topology Selection for Low Voltage PV Source
For simplicity, let us assume, in this phase, that the converter is connected to an ideal power grid. The CSI converter naturally presents a DC/AC operation if observed from the load towards the DC-link; the voltage present on the latter is extremely variable and is governed by the three-phase voltage on the terminals connected to the grid and by the CSI switching state that occurs at a given moment (see Figure 7).
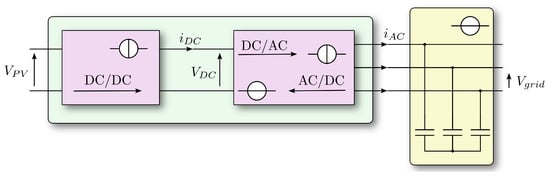
Figure 7.
Basic block diagram of the two active cascaded stages.
The value of this voltage can vary from zero when the bridge is in the current recirculation state to the peak line-to-line value of the grid when the bridge switches in correspondence with one of the maximum line-to-line grid voltage. IN addition, depending on the variability of the load and any reactive currents, it may occur that the voltage control system on the grid node injects a current such as to discharge the voltage on the bank of capacitors connected to the grid node; when this occurs, the switching state of the CSI reports a negative voltage on the DC-link. For the choice of DC/DC stage type most suitable for this project, the following general specifications were taken into consideration: no transformer, no interleaved type, no mutual coupling between inductors, and high step-up capacity. The choice fell on the typology known as “switched-inductors” [,,,,], which seems to meet all the requests mentioned.
4.2. General Topology of Proposed System and Validation of DC/DC Converter Stage
In order to validate the choice, some simulations in Matlab-Simulink® were carried out. Figure 8 shows the basic scheme on which the simulations were performed. Figure 8b represents the real scheme adopted in the simulation in which the CSI bridge in Figure 8a was replaced by a variable voltage generator in order to reduce calculation times. This simplification does not affects the results we want to achieve since, in this case, we only want to characterize the DC/DC stage. The aim is to determine the ability of the “switched-inductors” to generate current both as a function of the duty-cycle, with which the S device is controlled, and as a function of the DC-link voltage set by the CSI bridge. The overall simulation consists of sixteen distinct simulations in which the VPV voltage is kept constant at a value of 80 V. Each of them was performed with different VDC voltage values between 100 V and 400 V. The resulting data are shown in Figure 9. Each simulation was carried out for a total time interval of 140 ms. During this interval, the duty-cycle, which we briefly indicate further down with the symbol DS, was adjusted according to the curve shown in Figure 9b. The curves in Figure 9a show the current of inductors IL1,2 and IL2 that can be transferred from the DC/DC stage to the CSI according to the following expression:
where represent the local mean value of current. With these data, the following considerations can be made:
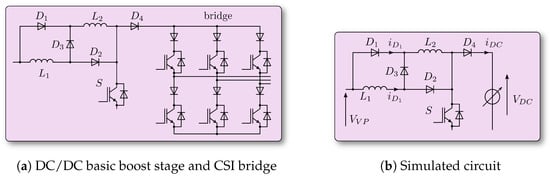
Figure 8.
Basic schematic diagrams used for the simulations.
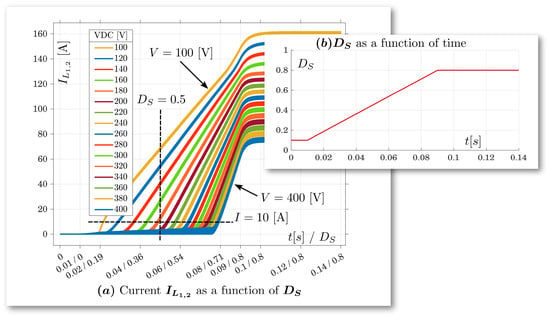
Figure 9.
Characteristic curves of the switched-inductor currents parameterized for different values of the DC link voltage.
- The circuit configuration of Figure 8 is capable of supplying a minimum value of current only by exceeding a certain DS for each value of the VDC voltage. In order to have a more detailed reference, Table 1 shows the DS value necessary to supply a minimum current of 10 A towards the CSI bridge for different values of the DC-link voltage.
 Table 1. Required DS to get a current of 10 A in the inductors for different DC-link voltage values and corresponding IDC current supplied to CSI bridge.
Table 1. Required DS to get a current of 10 A in the inductors for different DC-link voltage values and corresponding IDC current supplied to CSI bridge. - Beyond this value, the current increases quite linearly up to the maximum DS value, equal to 0.8, which was set in the simulations.
- In Figure 4b, it is worth noting the maximum current values IL1,2 that can be obtained with DS equal to 0.5. This current ranges from 10 A, for a VDC equal to 220 V, to over 80 A for a VDC equal to 100 V. Beyond this limit, it is not possible to obtain current values higher than the minimum limit of 10 A without increasing the DS value.
Considering these data, the DC/DC stage based on switched inductors appears to be an excellent candidate to meet the specifications because of its ability to generate the required current, for its voltage boost capabilities and, last but not least, for its circuital simplicity.
It is worth observing that the curves in Figure 9 have completely general features and therefore represent a useful general characterization of the “switched-inductors” circuit.
4.3. Converter Topology and Layout Issues
Modulation techniques for CSI converters were, and still are, studied extensively by the scientific community [,,,]. The main objectives of this research can be summarized in the following points:
- Reduce the harmonic content of the voltage generated by the CSI;
- Reduce switching losses;
- Improve dynamic performance;
- Improve the exploitation of switching devices and balance switching and conduction losses.
The main objectives of the choice of the modulation technique is the containment of the harmonic distortion of current supplied in the grid and the optimization of the performance in terms of overall efficiency. This involves making suitable technological choices, such as the selection of power components, making the most of their performance, also by increasing the switching frequency, and adopting modulation techniques that allow the THD value to be reduced. As is known, one of the most significant drawbacks of the CSI converter, compared to the VSI, is the outstanding conduction losses. The designer can act on various fronts in order to mitigate these losses. The first is certainly to use devices that have a low RON value; another important design aspect concerns the choice of the topology of the conversion system and as a direct consequence the layout design, which must also take into account the losses due to conduction of the tracks of the printed circuit and, as already mentioned, the reduction of parasitic inductances. The choice of switching devices will be discussed later in the text; here, it is appropriate to describe the method used in selecting the circuit topology. Many CSI configurations, especially those dedicated to conversion systems for photovoltaic systems, adopt the so-called fourth leg that supports the three legs of the bridge. This additional electrical branch was introduced to reduce common mode variations and earth leakage current [,] and also with the purpose of recirculating the free-wheeling current along a path with a single power device instead of through two devices of any one of the bridge branches []. This solution, although effective in some cases, seems to be less suitable for photovoltaic applications, as it requires the use of additional reactive elements to prevent the recirculating current from passing through the photovoltaic modules. A different circuit configuration solution, quite simple and widely described by [,], involves the recirculation of the current exactly at the ends terminals of the switched inductors, as shown in Figure 10, through the S7 device, which must be activated during free-wheeling intervals. This solution also has another important advantage because it allows one to design a printed circuit characterized by minimum paths of the recirculation current. It is also worth remembering that switching a current in a CSI inverter, unlike what happens in a VSI inverter, implies a serious commitment in studying the layout of the converter: it is particularly important to reduce parasitic inductances to the minimum possible present in electrical meshes in which strong current variations are present. Otherwise, such current switching generates strong voltage variations, which can compromise the integrity of the components and produce serious electromagnetic compatibility and susceptibility problems.
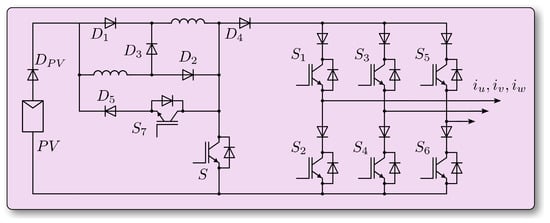
Figure 10.
Topology of the conversion system.
4.4. Compatibility of a Single DC/DC Boost Stage with the CSI Bridge
As extensively described in [,,,,], the switched-inductors circuit allows for the charging of the inductors in parallel when device S of Figure 10 is in the ON state, and allows the discharge of the accumulated current of the series inductors when device S is in the OFF state. The voltage at the input terminals of the CSI bridge can overlap with the states of device S and consequently modify the charging and discharging state of the switched inductors. For example, this happens when switch S is in the ON state and the voltage is negative. In this case, the current flows through the bridge rather than through device S. Similarly, but in an electrically symmetrical way, it is not possible to transfer current from the boost modules to the bridge when the voltage is greater than the voltage across the series inductors. As can be seen from the Section 4.2, in which the characteristics of the “SI” circuit are reported, these circumstances cannot be avoided because the correct functioning of the DC/DC stage requires that device S must be controlled with a duty-cycle adjusted up to at least a value of 0.8. At this point, we must note that the two conversion stages, the CSI bridge and the DC/DC boost, cannot be considered as independent entities. The respective regulation systems have as their primary objective, the first, i.e., the one of the bridge, the regulation of the voltage on the grid node, and the second, i.e., that one of the “SI” module, the regulation of the current on the DC-link. The regulation system that controls the module and the phase of the SVM modulator is relatively simple if the DC-link current is assumed to be constant or in any case variable in a limited range. However, it would be advisable for the current available at the DC-link to be of a value commensurate with the current requested by the load. The control system of the DC/DC boost stage requires the adjustment to the duration of the time intervals during which to charge the current inductors and transfer this current to the bridge; however, as already mentioned, these phases are subject to the value of the DC-link voltage and then to the status of the bridge devices. In short, the two conversion stages are not independent from either an electrical point of view or a logical point of view. This fact suggests two different design paths: The first involves the study and implementation of a sophisticated control system that takes into account the interactions between the two converters and is able to guarantee the voltage profile on the grid node in the case of an isolated grid, or the current requested by the load in the case of a prevailing power electricity grid, and also the optimal management of energy flows and, consequently, the best performance of the system. The second way is to look for a HW solution that makes the two systems independent. In this way, the relevant controls can be significantly simplified by managing both the energy flow on the grid node and the current on the DC-link in a simpler way. In this project the second path was followed.
Doubling Switched-Inductors
One proposal to provide independence to the two stages is to introduce a further module with switched inductors, in parallel to the first. The two modules can be controlled alternatively, i.e., while one of them discharges the current to the bridge, the other can be in the charging phase. The difficulty of coordinating the states of the boost module with the states of the bridge suggests introducing a further module with switched inductors, in parallel to the first. In this configuration, shown in Figure 11, the two modules can be controlled in an alternative way. The coordination of the states of the two SI modules with respect to the states of the bridge is shown in Figure 12, in which three bands are drawn that develop as a function of time. The central one represents the states of the bridge; it considers the “passive” free-wheeling state, indicated with FW, and the “active” state when the current is transferred to the grid, indicated with T. The other two bands, respectively, represent the status of the SI-A module and those of the SI-B module. Each of these modules can be in one of the following three states: “charging”, indicated by AC in the case of module A, “transfer”, indicated by AT, and “current holding”, indicated by ACH. The time intervals in which there is current transfer towards the bridge and from the bridge to the grid node (AT and T) must coincide in an alternative sequence, i.e., the current flow must be guaranteed alternatively by the SI modules, as indicated by the arrows. The complementary time interval for each of the SI modules, respectively AC+AFW and BC-BFW, can be managed to regulate the duty cycle of each of the modules and therefore the current accumulated by them. There is the possibility of an overlap of the AC and BC states; in this case, it is necessary to verify the electrical compatibility of this event with the photovoltaic power system. In case of incompatibility, the constraint must be introduced in the control logic. The overall scheme is certainly more complex, the number of power devices increases considerably, as do the drivers necessary to control their state; however, regulation variables are introduced that allow simpler and more precise control of both the DC current and the voltage (or current) towards the grid node.
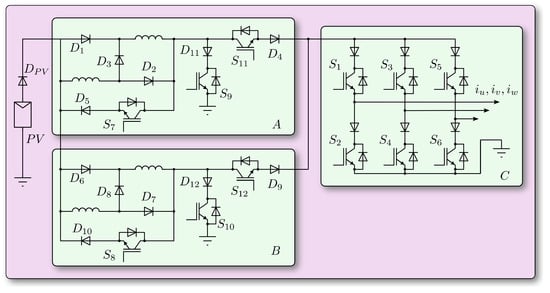
Figure 11.
Complete topology of proposed conversion system where stages A and B are the Switched Inductors modules, stage C is the CSI bridge.
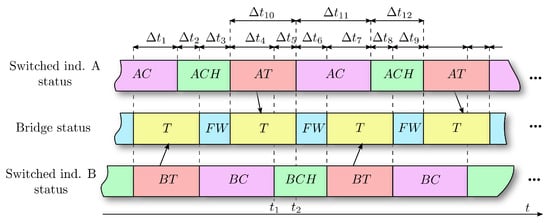
Figure 12.
Diagram of timing sequence of SI-A, SI-B, and bridge.
Table 2 reports the status of the power devices together with the status of bridge. It allows us to better explain the sequence of events and states in the intervals that follow one another over time.

Table 2.
Status of the power devices and status of bridge for each time interval.
5. Simulation Results
Below are some results obtained through simulation of the Simulink® model of the system useful for characterizing and defining the general performance in steady state. In the simulation, an isolated grid was connected, on which there is a load of 65 Ω. The capacitor bank on the same grid node consists of a star with a capacitance equal to 50 μF. The reference values of the magnitude of the space vector generated by the CSI modulator and the duty-cycle of the CSI converter have been set. In these conditions, slight distortions of the voltages present on the grid node will be visible. This is due to the absence of regulation of both the module and phase of the grid voltage and of the DC-link current module. The simulation data span 60 ms. The voltage of the photovoltaic system is generated via an increasing ramp starting from 5 ms and ending with 80 V at 80 ms. The magnitude of the current vector generated by the CSI modulator is set at 45%. The states of the SI modules are equal to each other and extend for a total of 164 μs. Each time interval, as also reported in Figure 12, has been fixed and the timing is reported in Figure 13a.
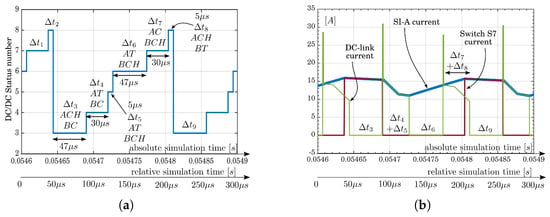
Figure 13.
Timing sequence representation of DC/DC stage and DC and module SI-A currents. (a) Timing sequence of the DC/DC stage for the simulation setup; (b) DC and SI-A current.
Figure 13b shows the current diagram of the DC-link, the current diagram in one of the inductors L of the A-SI module, and the current in the S7 device. The time interval is the same as in Figure 13a: 0.0546 s < t < 0.0549 s. Figure 14a reports the DC-link current for the entire simulation period (0.06 s) and, as a temporal and spatial reference, a diagram representing the number of the SVM sector. On the right side, the line-to-line voltages of the grid are shown, which, in this case, is assumed to be of the isolated type. The power transferred to the load is 1700 W. Figure 15 shows the path of the voltage space vector to the grid node. The voltage diagrams appear in ramp form because the DC voltage of the photovoltaic system is supposed not to be generated instantaneously but made available gradually, even if in very rapid times (the ramp starts at instant 0.005 s and reaches 80 V at instant 0.03 s). This choice was made to make the model as similar as possible to a real system, in which sudden discontinuities do not occur and therefore to favor its robustness in numerical convergence.
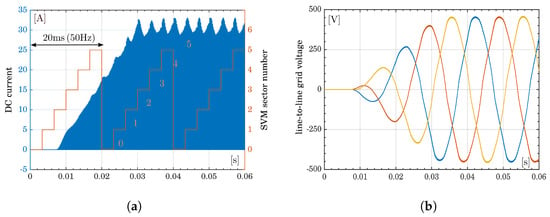
Figure 14.
DC current in a larger time frame and voltages on islanded grid. (a) DC current (red line) and sector number generated by SVM (light blue line); (b) Line to line voltage on the grid. Yellow, light blue and Red colors correspond to phases U, V and W.
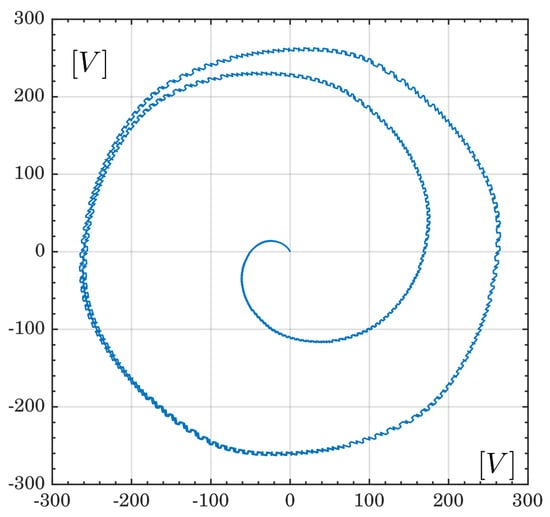
Figure 15.
Line voltage space vector over 60 ms.
6. Discussion
This paper dealt with the design procedure leading to the definition of a conversion topology that allows for the transfer of energy from a low voltage (80 V) photovoltaic system to a three-phase electrical grid with a nominal voltage of 400 V both of isolated type and of prevailing power. The target power is 3 kW. In this context, the dynamic performances of the entire conversion system will not be reported, because these will be dealt with in a future manuscript where all the control functions will be described in detail. The specifications for the construction of this conversion system were dictated by industrial and commercial needs. The requirement to make a large voltage step has, in general, significant negative implications on the performance of the entire system; however the design choices made have sought to limit energy dissipation as much as possible. From this need, a synchronized modulation strategy between the states of the bridge and the states of the SI modules has been identified. It is worth noting the following points considered key by the authors:
- The topology identified and the modulation technique described allow for an independent regulation of the DC-link current and of the current that the bridge transfers to the grid. In the case of a distributed grid, these choices favor the design of a dynamically more efficient system for the regulation of the power absorbed by the photovoltaic system and therefore the implementation of more performing MPPT strategies. In the case of an isolated grid, the punctual management of the current allows one to respond more quickly to the requests of the connected load, limiting to a minimum the circulation of current inside the conversion system and reducing the conduction losses both in the inductors and in the power devices.
- The data represented in Figure 9, together with the description of the method with which they were obtained, are useful for the characterization of a cascaded SI module with a generic voltage generator in the range of the electrical quantities that were used. Therefore, they are general data useful for the design of systems that adopt this conversion topology.
- The possibility of recirculating the current through the inductors of the DC/DC stage allows one to avoid the use of the so-called fourth leg of the CSI bridge, known in literature with the acronym CSI7 or H7 [,,], since the current coming from the SI modules is zero during the free-wheeling of the bridge, despite this typology being established with a certain frequency in the design of CSI converters and has even been defined as a “universal solution for CSI converters” [].
The Simulink® model was carefully programmed, seeking the best compromise between accuracy and acceptable computation times. In particular, ideal switches were not used, but device models with characteristics very close to real ones were chosen from the manufacturers’ libraries. The inductors were implemented taking into account the winding resistance and the skin effect phenomena at the adopted switching frequencies. The prevailing power electrical grid was modeled according to what is suggested in []. The simulation results have highlighted that the adopted conversion topology has characteristics that meet the imposed specifications. With the aim of improving the losses due to the switching and conduction of the devices, SiC type components were adopted that present significantly superior performance in terms of voltage drop in the ON-state [,,], and particular attention was paid designing switched inductors.
Application Possibilities of the Described Conversion System in Fields Other than Photovoltaic Energy Production
The proposed system has the following characteristics:
- Based on a CSI bridge;
- Reactive power regulation capability;
- High step-up capabilities;
- Not an isolated system;
- Transformerless;
- Allows for managing the energy flow from the low voltage source to a three-phase network;
- Low harmonic content of the current fed into the grid.
These characteristics are necessary and sufficient to define the applicability of the proposed conversion system architecture to other fields, obviously considering the necessary technological modifications, component sizing, and redesign of the regulation and control system. For example, a potential application field could be the use of this conversion system to support low-voltage wind generation [,,]. Another application area is advanced drives, which can benefit greatly from using a CSI step-up converter [,,]. In the automotive sector, the usefulness of CSI step-up systems for driving motors to rated speed, even with reduced DC voltage values, has been demonstrated [,]. A further application field could be front ends between distributed renewable energy systems (RES), microgrids, or charging systems for electric vehicles. As an example, the high-speed railway system can also be considered, which, in some situations where it has experienced great development, requires a study to identify alternative technical solutions to balance energy supply and demand. In such cases, a system capable of transferring energy from a relatively low voltage source to a higher voltage system could be usefully adopted []. With reference only to the DC/DC stage of the proposed conversion system, a further application field could be the energy recovery during braking of railway convoys []. Currently, the speed range for this operating mode is limited, since it is associated with a corresponding and proportional voltage range. In this case, using a step-up converter of the proposed type would significantly lower the minimum voltage limit and, therefore, allow the management of a flow of recovery energy even at lower speeds. Naturally, this solution must be subject to an in-depth study to verify its stability, robustness, and interactions with the system in which it is used, which is, by nature, very complex and hard to identify.
7. Patents
Patent Pending: Application IT102024000019174.
Author Contributions
Conceptualization, R.D.S.; methodology, R.D.S.; software, R.D.S.; validation, R.D.S. and F.M.; formal analysis, R.D.S. and F.M.; investigation, R.D.S. and F.M.; resources, R.D.S. and F.M.; data curation, R.D.S. and F.M.; writing—original draft preparation, R.D.S.; writing—review and editing, R.D.S. and F.M.; visualization, R.D.S., F.M. and F.P.; supervision, R.D.S. and F.M.; project administration, R.D.S., F.M. and F.P.; funding acquisition, R.D.S., F.M. and F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union—Next Generation EU, Mission 4 Component 1, CUP H53D23007410001, project P2022SY7LH.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors thankfully acknowledge Industrial Electronics Laboratory of University of Cassino “G. D’Angelo” for technical advice and support. The authors also thankfully acknowledge the anonymous reviewers whose comments have helped us to enhance our work.
Conflicts of Interest
Author Fabio Pellini is employed by the company CloudWise s.r.l. The company is not currently involved in the design, study, collection, analysis, interpretation of data, and writing of this article or the decision to submit it for publication. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CSI | Current source inverter |
| VSI | Voltage source inverter |
| SI | Generic switching Inductors module |
| VDC | DC-link voltage |
| S | Generic switch device of DC/DC boost stage |
| DS | Duty-cycle of one stage DC/DC |
| IL | Inductor current |
| SVM | Space vector modulation, or space vector modulator |
| Local mean value of DC-link current | |
| T | Transfer mode of CSI bridge |
| FW | Free-wheeling mode of CSI bridge |
| A-SI | Switching inductors module A |
| B-SI | Switching inductors module B |
| AC | A-SI charging state |
| ACH | A-SI current holding state |
| AT | A-SI current transfer state |
| BC/BCH/BT | The same as above but for the B-SI module |
Appendix A. Three-Dimensional Data Table Containing the Switching Status
The following table reports the data of the switching status that are referred to in:

Table A1.
Switch matrix implemented in the SVM.
Table A1.
Switch matrix implemented in the SVM.
| Device | ||||||
|---|---|---|---|---|---|---|
| 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 | |
| 1 1 1 0 1 1 1 | 0 1 0 0 0 1 0 | 0 0 0 1 0 0 0 | 1 0 0 0 0 0 1 | 0 0 0 0 0 0 0 | 0 0 1 1 1 0 0 | |
| 1 0 0 0 0 0 1 | 0 0 0 0 0 0 0 | 0 0 1 1 1 0 0 | 1 1 1 0 1 1 1 | 0 1 0 0 0 1 0 | 0 0 0 1 0 0 0 | |
| 0 0 0 0 0 0 0 | 0 0 1 1 1 0 0 | 1 1 1 0 1 1 1 | 0 1 0 0 0 1 0 | 0 0 0 1 0 0 0 | 1 0 0 0 0 0 1 | |
| 0 1 0 0 0 1 0 | 0 0 0 1 0 0 0 | 1 0 0 0 0 0 1 | 0 0 0 0 0 0 0 | 0 0 1 1 1 0 0 | 1 1 1 0 1 1 1 | |
| 0 0 0 1 0 0 0 | 1 0 0 0 0 0 1 | 0 0 0 0 0 0 0 | 0 0 1 1 1 0 0 | 1 1 1 0 1 1 1 | 0 1 0 0 0 1 0 | |
| 0 0 1 1 1 0 0 | 1 1 1 0 1 1 1 | 0 1 0 0 0 1 0 | 0 0 0 1 0 0 0 | 1 0 0 0 0 0 1 | 0 0 0 0 0 0 0 |
References
- Jasińska, E.; Jasiński, M.; Leonowicz, Z.; Martirano, L.; Gono, R.; Jasiński, M. Various Aspects of Energy Transition: Technologies, Economy, and Social Synergies to Sustainable Future. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), IEEE, Madrid, Spain, 6–9 June 2023; pp. 1–4. [Google Scholar] [CrossRef]
- UN. The Sustainable Development Agenda. Available online: https://www.un.org/sustainabledevelopment/ (accessed on 10 May 2024).
- Semenova, N.; Hassel, L.G. On the Validity of Environmental Performance Metrics. J. Bus. Ethics 2014, 132, 249–258. [Google Scholar] [CrossRef]
- Escrig-Olmedo, E.; Fernández-Izquierdo, M.; Ferrero-Ferrero, I.; Rivera-Lirio, J.; Muñoz-Torres, M. Rating the Raters: Evaluating how ESG Rating Agencies Integrate Sustainability Principles. Sustainability 2019, 11, 915. [Google Scholar] [CrossRef]
- Braccini, A.; Margherita, E. Exploring Organizational Sustainability of Industry 4.0 under the Triple Bottom Line: The Case of a Manufacturing Company. Sustainability 2018, 11, 36. [Google Scholar] [CrossRef]
- Wang, H. Investment Efficiency and Cost Analysis of New Renewable Energy Sources. In Proceedings of the 2020 IEEE Sustainable Power and Energy Conference (iSPEC), Chengdu, China, 23–25 November 2020. [Google Scholar] [CrossRef]
- Yang, Y.; Du, Z.; Zhou, X.; Chen, Y.; Zheng, L.; Xu, Y. Harmonic Stability Analysis of a System Integrated with Photovoltaic Power Generation and Energy Storage Based on Impedance Analysis Method. In Proceedings of the 2023 13th International Conference on Power and Energy Systems (ICPES), Chengdu, China, 8–10 December 2023; pp. 373–378. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Enslin, J.; Heskes, P. Harmonic Interaction Between a Large Number of Distributed Power Inverters and the Distribution Network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.; Miao, Z. Wind in Weak Grids: Low-Frequency Oscillations, Subsynchronous Oscillations, and Torsional Interactions. IEEE Trans. Power Syst. 2020, 35, 109–118. [Google Scholar] [CrossRef]
- Ali, K.; Putranto, L.M.; Imam, A.; Tumiran; Yasirroni, M. Determination of Optimal PV Energy Share Considering Voltage Stability Index. In Proceedings of the 2020 2nd International Conference on Smart Power amp; Internet Energy Systems (SPIES), Bangkok, Thailand, 15–18 September 2020. [CrossRef]
- Uzun, U.E.; Pamuk, N.; Taskin, S. Effect of Solar Photovoltaic Generation Systems on Voltage Stability. In Proceedings of the 2022 Global Energy Conference (GEC), Batman, Turkey, 26–29 October 2022. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A.; McGrath, B.P.; Kong, W.Y. Optimized Design of Stationary Frame Three Phase AC Current Regulators. IEEE Trans. Power Electron. 2009, 24, 2417–2426. [Google Scholar] [CrossRef]
- Midtsund, T.; Suul, J.A.; Undeland, T. Evaluation of current controller performance and stability for voltage source converters connected to a weak grid. In Proceedings of the 2nd International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010. [Google Scholar] [CrossRef]
- Nasiri, M.; Chandra, S.; Taherkhani, M.; McCormack, S.J. Impact of Input Capacitors in Boost Converters on Stability and Maximum Power Point Tracking in PV systems. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Virtual Conference, 20–25 June 2021. [Google Scholar] [CrossRef]
- Santra, S.B.; Chatterjee, D.; Kumar, K.; Bertoluzzo, M.; Sangwongwanich, A.; Blaabjerg, F. Capacitor Selection Method in PV Interfaced Converter Suitable for Maximum Power Point Tracking. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2136–2146. [Google Scholar] [CrossRef]
- Moradi-Shahrbabak, Z.; Bakhshai, A.; Tabesh, A. Effect of dc-link capacitor on small signal stability of grid connected PV power plants. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018. [Google Scholar] [CrossRef]
- Yan, G.; Ren, J.; Mu, G.; Jin, L.; Duan, S.; Jia, Q. DC-link voltage stability analysis for single-stage photovoltaic VSIs connected to weak grid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar] [CrossRef]
- Azmi, S.; Ahmed, K.; Finney, S.; Williams, B. Comparative analysis between voltage and current source inverters in grid-connected application. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, UK, 6–8 September 2011. [Google Scholar] [CrossRef]
- Potdukhe, K.C.; Munshi, A.P.; Munshi, A.A. Reliability prediction of new improved current source inverter (CSI) topology for transformer-less grid connected solar system. In Proceedings of the 2015 IEEE Power, Communication and Information Technology Conference (PCITC), Bhubaneswar, India, 5–17 October 2015; pp. 373–378. [Google Scholar] [CrossRef]
- Rajeev, M.; Agarwal, V. Single Phase Current Source Inverter With Multiloop Control for Transformerless Grid–PV Interface. IEEE Trans. Ind. Appl. 2018, 54, 2416–2424. [Google Scholar] [CrossRef]
- Wang, Z.; Miao, Z.; Fan, L.; Yazdani, A. Weak Grid Operation of A Grid-Following Current-Sourced PV Solar System. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, L.; Chen, P.; Yang, A.; Zhang, Q.; Wang, L.; Qian, Z.; Zhang, M.; Zhang, T. A Multilevel Asymmetric Current Source Inverter Topology Using Switched Inductor. In Proceedings of the 2022 4th International Conference on Power and Energy Technology (ICPET), Xining, China, 12–14 May 2022. [Google Scholar] [CrossRef]
- Mao, M.; Zheng, Y.; Chang, L.; Xu, H. A single-stage high gain current source inverter for grid-connected photovoltaic system. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015; pp. 1902–1907. [Google Scholar] [CrossRef]
- Mao, M.; Li, Y.; Chang, L. Optimal design and experiment validation of switching inductor based tri-state CSI. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 6923–6927. [Google Scholar] [CrossRef]
- Li, C.; Chang, L.; Mao, M. Improved SVM for High Gain Tri-state CSI to Reduce DC Side Inductor Current Ripple. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019. [Google Scholar] [CrossRef]
- Stephen, A.; Remya, K.P.; Gomathy, S. Review on Non-isolated High Gain DC-DC Converters. In Proceedings of the 2022 Third International Conference on Intelligent Computing Instrumentation and Control Technologies (ICICICT), Kannur, India, 11–12 August 2022. [Google Scholar] [CrossRef]
- Gnanasambandam, K.; Rathore, A.K.; Edpuganti, A.; Srinivasan, D. A Novel Optimal Space Vector Modulation Technique of Current Source Inverter for Solar Power Integration. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, M.; Xu, Z.; Yan, S. MPC Control of Three-Phase CSI in Unbalanced Grid. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; pp. 357–361. [Google Scholar] [CrossRef]
- Aguirre, M.P.; Calvino, L.; Valla, M.I. Multilevel Current-Source Inverter with FPGA Control. IEEE Trans. Ind. Electron. 2013, 60, 3–10. [Google Scholar] [CrossRef]
- Guo, X.; Xu, D.; Wu, B. Four-Leg Current-Source Inverter with a New Space Vector Modulation for Common-Mode Voltage Suppression. IEEE Trans. Ind. Electron. 2015, 62, 6003–6007. [Google Scholar] [CrossRef]
- Anand, S.; Gundlapalli, S.K.; Fernandes, B.G. Transformer-Less Grid Feeding Current Source Inverter for Solar Photovoltaic System. IEEE Trans. Ind. Electron. 2014, 61, 5334–5344. [Google Scholar] [CrossRef]
- Wang, W.; Gao, F.; Rui, S. Operation and modulation of H7 current source inverter with hybrid SiC and Si semiconductor switches. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015. [Google Scholar] [CrossRef]
- Lorenzani, E.; Immovilli, F.; Migliazza, G.; Frigieri, M.; Bianchini, C.; Davoli, M. CSI7: A Modified Three-Phase Current-Source Inverter for Modular Photovoltaic Applications. IEEE Trans. Ind. Electron. 2017, 64, 5449–5459. [Google Scholar] [CrossRef]
- Bendre, A.; Wallace, I.; Nord, J.; Venkataramanan, G. A current source PWM inverter with actively commutated SCRs. IEEE Trans. Power Electron. 2002, 17, 461–468. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Russo, M.; Valeri, S.; De Santis, M. LV distribution system modelling for distributed energy resources. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Catellani, S.; Bier, A.; Martin, J.; Gabriel, L.; Barruel, F. Characterization of 1.2 kV Silicon Carbide (SiC) semiconductors in hard switching mode for three-phase Current Source Inverter (CSI) prototyping in. In Proceedings of the PCIM Europe 2015, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 19–20 May 2015; pp. 1–8. [Google Scholar]
- Lee, Y.; Castellazzi, A. Discrete-time optimization of current-sensor-less control for a high-frequency all-SiC CSI converter. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Sahan, B.; Araújo, S.V.; Nöding, C.; Zacharias, P. Comparative Evaluation of Three-Phase Current Source Inverters for Grid Interfacing of Distributed and Renewable Energy Systems. IEEE Trans. Power Electron. 2011, 26, 2304–2318. [Google Scholar] [CrossRef]
- Singh, A.; Mirafzal, B. A low-voltage generator-converter topology for Direct Drive Wind Turbines. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; Volume 24, pp. 1–6. [Google Scholar] [CrossRef]
- Kavousi, A.; Fathi, S.H.; Milimonfared, J.; Soltani, M.N. Application of Boost Converter to Increase the Speed Range of Dual-Stator Winding Induction Generator in Wind Power Systems. IEEE Trans. Power Electron. 2018, 33, 9599–9610. [Google Scholar] [CrossRef]
- Wang, H.; Nayar, C.; Su, J.; Ding, M. Control and interfacing of a grid-connected small scale wind turbine generator. In Proceedings of the 2009 Australasian Universities Power Engineering Conference, Adelaide, Australia, 27–30 September 2009; pp. 1–5. [Google Scholar]
- Killeen, P.; Ghule, A.N.; Ludois, D.C. A Medium-Voltage Current Source Inverter for Synchronous Electrostatic Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1597–1608. [Google Scholar] [CrossRef]
- Fernández, E.; Coello, M. Control drive for SMPMSM in CSI converter with SiC devices. In Proceedings of the 2017 IEEE 37th Central America and Panama Convention (CONCAPAN XXXVII), Managua, Nicaragua, 15–17 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, Y.; Castellazzi, A. Implementation options of a fully SiC Buck-CSI for advanced motor drive application. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hanover, Germany, 5–9 September 2022; pp. P.1–P.11. [Google Scholar]
- Tang, L.; Su, G.J. Boost mode test of a current-source-inverter-fed permanent magnet synchronous motor drive for automotive applications. In Proceedings of the 2010 IEEE 12th Workshop on Control and Modeling for Power Electronics (COMPEL), Boulder, CO, USA, 28–30 June 2010; Volume 28, pp. 1–8. [Google Scholar] [CrossRef]
- Su, G.J.; Tang, L.; Wu, Z. Extended constant-torque and constant-power speed range control of permanent magnet machine using a current source inverter. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; Volume 137, pp. 109–115. [Google Scholar] [CrossRef]
- Ma, F.; Kuang, Y.; Wang, Z.; Huang, G.; Kuang, D.; Zhang, C. Multi-Port and -Functional Power Conditioner and Its Control Strategy with Renewable Energy Access for a Railway Traction System. Energies 2021, 14, 6146. [Google Scholar] [CrossRef]
- Chen, J.; Hu, H.; Wang, M.; Ge, Y.; Wang, K.; Huang, Y.; Yang, K.; He, Z.; Xu, Z.; Li, Y.R. Power Flow Control-Based Regenerative Braking Energy Utilization in AC Electrified Railways: Review and Future Trends. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6345–6365. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).