1. Introduction
In the northern countries, a significant proportion of fossil fuels is employed for the purpose of heating residential properties during the winter months. In the European Union, for instance, this proportion accounts for approximately two-thirds of the residential sector’s final energy consumption [
1]. Eurostat [
2] indicates that a sufficient quantity of renewable energy is available on an annual average to satisfy this demand. The implementation of cost-effective energy storage solutions would lead to a notable reduction in the reliance on fossil fuels in this sector. Long-term storage systems offer this possibility.
Various energy storage technologies based on adsorption, absorption, or chemical reactions are summarised as thermochemical storage, which can cover a wide range of applications for the utilisation of renewable heat due to their temperature range and energy density [
3].
Based on fundamental studies on the material [
4,
5,
6,
7], quicklime-based storage systems have been investigated as possible candidates for cost-effective, loss-free energy storage. Extensive work has already been carried out to shed light on aspects such as fundamental thermodynamics [
8,
9], system integration [
10], and the techno-economic aspects of the technology [
11].
The Ca(OH)
2 ⇌ CaO + H
2O reaction system has been identified as a promising material for the storage of chemical energy. The material has a high energy density of up to 215 kWh/m
3 [
10]. Furthermore, as part of the technical lime cycle, the material is inexpensive and available in large quantities. In recent years, a variety of concepts have been developed for the utilisation of lime as an energy storage medium. As outlined by Wang et al. [
12], three distinct reactor concepts have emerged. In addition to fixed-bed reactors, which are only used for basic research under laboratory conditions due to the limited possibilities for upscaling, there are also moving-bed reactors with the advantage of a continuous operation mode [
13] and fluidized-bed reactors where a batch [
14,
15] as well as a continuous operation mode is known [
16]. However, both concepts require the storage material to possess specific properties in terms of fluidisability and material feed. These systems are intended for industrial processes, as the technical complexity of these systems prevents their use for residential purposes.
A further concept known as mechanical-induced fluidization combines the advantages of fluidisation and of using unmodified material, see Risthaus et al. [
17]. In this setup, the heat transfer is significantly enhanced by fluidisation, while the reactor can be operated in batch mode with unmodified powder material. The smaller effective heat transfer surface within the reaction zone, in comparison to the aforementioned fixed bed reactors, is counteracted here by the principle of mechanical fluidisation. The material is fluidised using a ploughshare mixer, which maintains its movement continuously. This approach addresses two significant challenges associated with unmodified powder material: the low thermal conductivity of the powder and its tendency to agglomerate. Theoretically, heat transfer coefficients of up to 350 W/m
2K can be achieved [
17].
The general functional principle of lime-based thermochemical energy storage, particularly for domestic heat supply, is described in detail by Schmidt et al. [
10]. Summarising, electrical energy from grid surpluses that arise in connection with seasonal or short-term energy overproduction is used to provide heat at a temperature level of 500–550 °C and to allow a chemical reaction to take place. Theoretically, at the dehydration of Ca(OH)
2, around 40% of the supplied energy is converted in the form of reaction enthalpy of the produced CaO, which is a material property and can therefore remain constant for an unlimited time period. So if the material is prevented from further reaction, the energy can be stored for extended periods with minimum heat loss at ambient conditions [
18]. The release of energy in the form of heat is the result of an exothermic reaction of the material with H
2O.
The studies demonstrate that only a portion of the energy can be stored for long-term requirements. As a by-product of the energy-storing process, a further significant quantity of heat is turned into the form of latent and sensible heat of the produced water vapour. This heat must either be utilised immediately or stored in short-term facilities. The aforementioned concept would therefore be particularly suitable for consumers or processes that combine a base-load heat demand, a superimposed strong seasonal heat demand, and an opposite seasonal energy surplus. During periods of sufficient energy availability, the material would be charged, and the released latent and sensible heat would satisfy the base-load demand. In periods of insufficient energy availability, the chemically bonded energy can be released to meet the additional demand. The fundamental possibility to recover especially the latent energy released from this reactor type is still questionable due to the difficulties with gas–solid separation, as described by Risthaus et al. [
17].
Its low efficiency is regarded as the primary drawback of thermochemical storage technology, which ultimately renders it unfeasible from a commercial standpoint, see Abedin et al. [
19]. It is therefore important to ensure that the latent and sensible heat is actually available for short-term energy supply in order to make the entire process effective. This work demonstrates, through experimental investigation, the potential for utilising the latent heat generated during the reaction, as it would increase the total efficiency of the thermochemical storing process [
10]. As part of the study, the reactor design was adapted to enable operational procedures pertinent to the intended application to be carried out. The resulting data permitted the determination of a number of properties, including pressures, temperatures, filter permeability, conversion rates, and performance. The data obtained from this study may thus be used as a basis for the validation of numerical models for the operational strategies of long-term energy storage systems and their incorporation into existing energy supply systems [
20,
21].
2. Materials and Methods
The investigation employs a commercial Ca(OH)2 powder material, procured from Rheinkalk GmbH/Lhoist group. The analysis of the material indicates a bulk density of 380 kg/m3, a mean particle diameter (d50) of 5.1 μm, and a specific surface area of 18 m2/g. To ensure the initial conditions are consistent, a fresh batch of material is used for each test run, and the reactor is completely emptied after each test. To verify the initial material composition, thermogravimetric analysis (TGA) measurements are performed on the supplied batches. Two batches with slightly different compositions are used for the investigation. The average composition of the material is calculated to be Ca(OH)2: 88%; CaO: 5%; CaCO3: 7%. The average material loading quantity into the reactor is approximately 4967 ± 76 g.
2.1. Test Bench
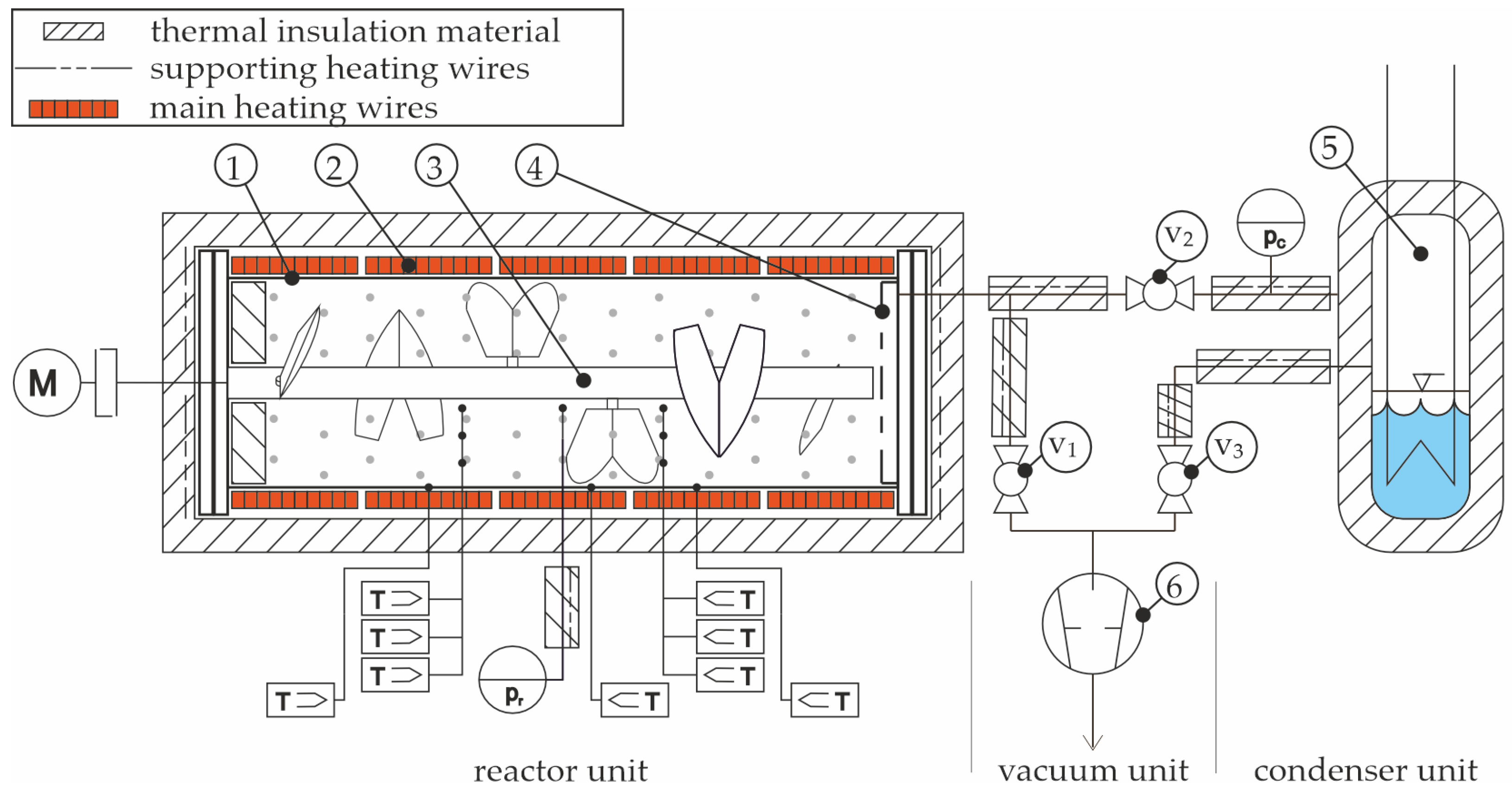
The main components and operational principles of the test bench used in the present study are described in the work of Risthaus et al. [
17]. The configuration has been adapted for the investigation described in this work, and the essential features of the current test bench configuration are described in the following paragraphs.
The test setup consists of three principal components: the reactor unit, the vacuum, and the condenser unit. The reactor is insulated with a thermal material. The reactor is furnished with five principal heating wires, which are wrapped around the reactor wall and constitute discrete heating zones along the reactor’s length. The maximum output heating power for each heating zone is 4.7 kW, as illustrated in
Figure 1 ②. Additional support heating wires with a power of 1 kW are positioned at the flanges, the clutch, and the pressure sensor supply lines. The aforementioned elements are employed to minimise heat loss and prevent condensation on the colder surfaces, respectively. The transfer of energy occurs via the reactor wall, as illustrated in
Figure 1 ①. The reactor has an inner length of 50 cm, a diameter of 20 cm, and a capacity of approximately 5 kg Ca(OH)
2 material. A rotating ploughshare mixing tool, as illustrated in
Figure 1 ③, is installed within the reactor to provide mechanical fluidisation. The reactor is airtight and can be operated at temperatures of up to 520 °C and a pressure range of 0 to 240 kPa
abs. It is only operated as a closed, airtight system.
The reactor is connected to the condenser component via a heated steam hose. During the operational phase, the produced H
2O
(g) is driven in the direction of the condenser unit due to the naturally occurring pressure gradient. In order to separate the solid and gas phases, a filter unit is installed on the inner side of the front flange, as illustrated in
Figure 1 ④. In a previous investigation, the presence of a filter cake material layer on the filter surface was observed, which resulted in a limitation of the mass flow and, consequently, the reactor power [
17]. Accordingly, the filter construction has been modified with the objective of enhancing the mass flow through the filter surface, as illustrated in
Figure 2. A static filter holder has been installed between the reactor flange and the reactor lid. The filtration process is achieved through the use of a clamped stainless-steel filter mesh, created through a twill weave with a geometric opening of 10 μm. In order to maintain the filter surface in a state free from deposits, a rotating cutting tool is connected to the rotating ploughshare and positioned in front of the filter surface, with the function of permanently removing deposits. The distance between the cutting tool and the filter surface is set in consideration of the expected thermal expansion of the material. The dimensions of the filter are as follows: inner radius: 36 mm, outer radius: 81,5 mm, resulting in a filtering surface of A
F: 0.0168 m
2. The impact of this new design is presented in the results section.
The main component of the test bench used to measure the actual conversion is the condenser unit, as illustrated in
Figure 1 ⑤. The condenser unit has a cooling power of 10 kW and a water tempering capacity. The apparatus is capable of functioning at temperatures between 10 °C and 100 °C and a pressure range from 0 kPa
abs to 240 kPa
abs. The vacuum unit consists of heated water vapour supply lines, electrical or manually operated valves (v
1, v
2, v
3), and a Busch R5 RA 0025 F vacuum pump,
Figure 1 ⑥, which is capable of providing a minimum pressure of 0.01 kPa
abs.
2.2. Measuring Technics
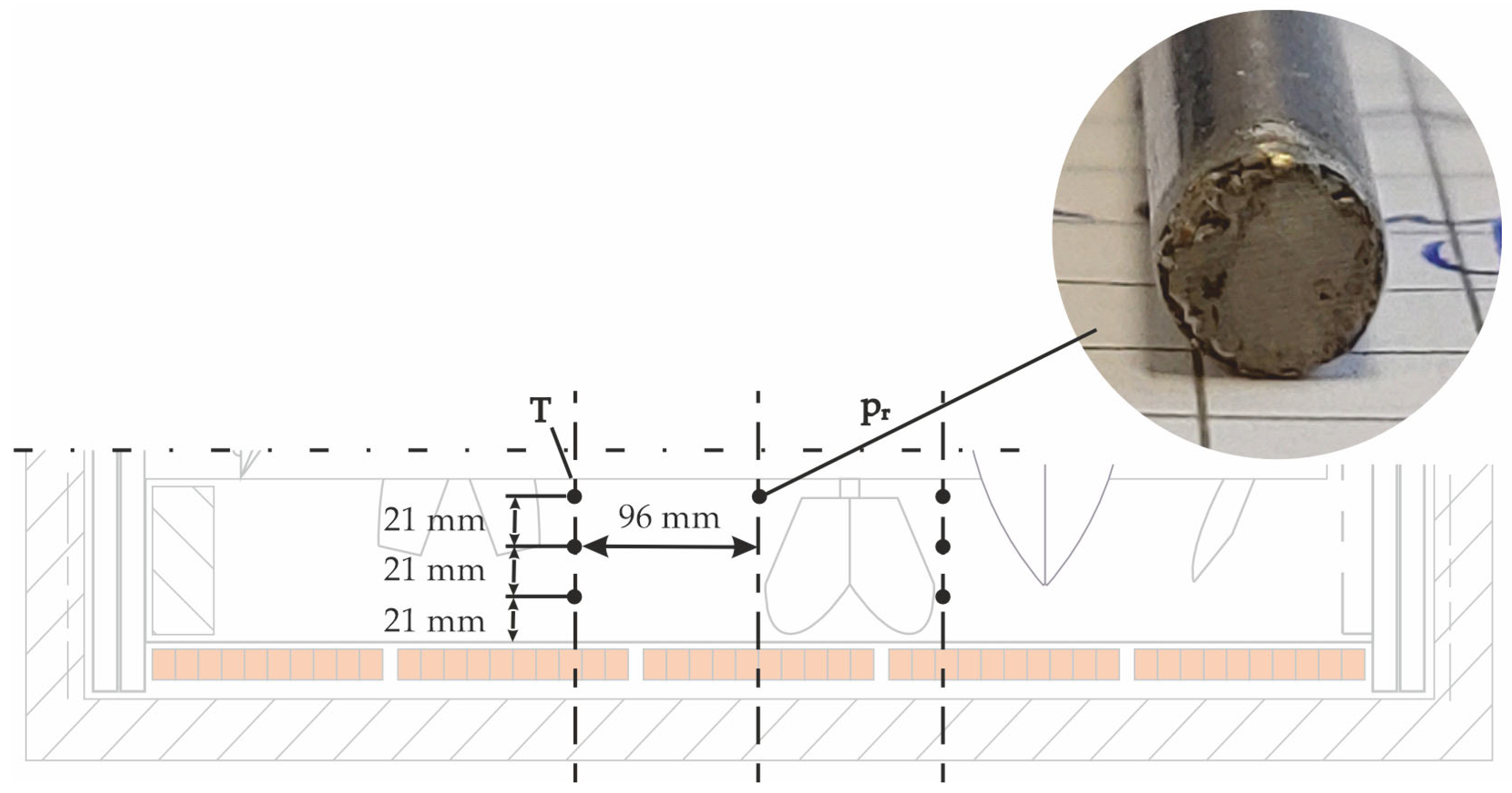
Pressure measurements are performed utilising Keller PAA-35XHTT pressure sensors, KELLER Druckmesstechnik AG, 8404 Winterthur, Switzerland, which have a range of 0 kPa
abs to 300 kPa
abs and a maximum error of ±0.6 kPa. Two pressure sensors are installed: one in the reactor (p
r,
Figure 3) and the other in proximity to the condenser unit (p
c,
Figure 1). To prevent condensation within the feed line, the reactor pressure feed line is heated externally to 100 °C. The p
r feed line comprises a steel pipe with an inner diameter of 2 mm. To prevent material accumulation and blockage of the feed line, filter material is welded to the front surface of the pipe, see
Figure 3.
The temperature measurements are performed utilising Ø 0.5 mm type K class 1 thermocouples. Three-point type K thermocouples with a diameter of 4 mm are utilised for the determination of the bulk material temperature. The sensor positions are illustrated in
Figure 3.
As the system is closed and all the total produced water vapour is condensed in the condenser, the condenser filling level is a direct method of determining the conversion and reactor performance. The condenser filling level () is measured by a microwave level sensor Vegaflex 65, VEGA Austria GmbH, 4050 Traun, Austria, with an uncertainty of ±2 mm.
The equilibrium condition of temperature and pressure in the condenser can be described using the Magnus formula.
The equilibrium formula proposed by Schaube et al. [
5] is used to describe the reaction equilibrium within the reactor.
The conversion of the reactants is defined by the following equation:
In order to gain a more representative overview, it is sufficient to consider only the change in the CaO. Adopting the assumption of a closed system and considering the relationship X
CaO = X
H2O = 1 − X
Ca(OH)2, the value of X
CaO can be calculated using the following equation:
The latent heat energy, also referred to as latent heat, is derived from the measurement of the change in condenser filling level and is calculated using the following equation:
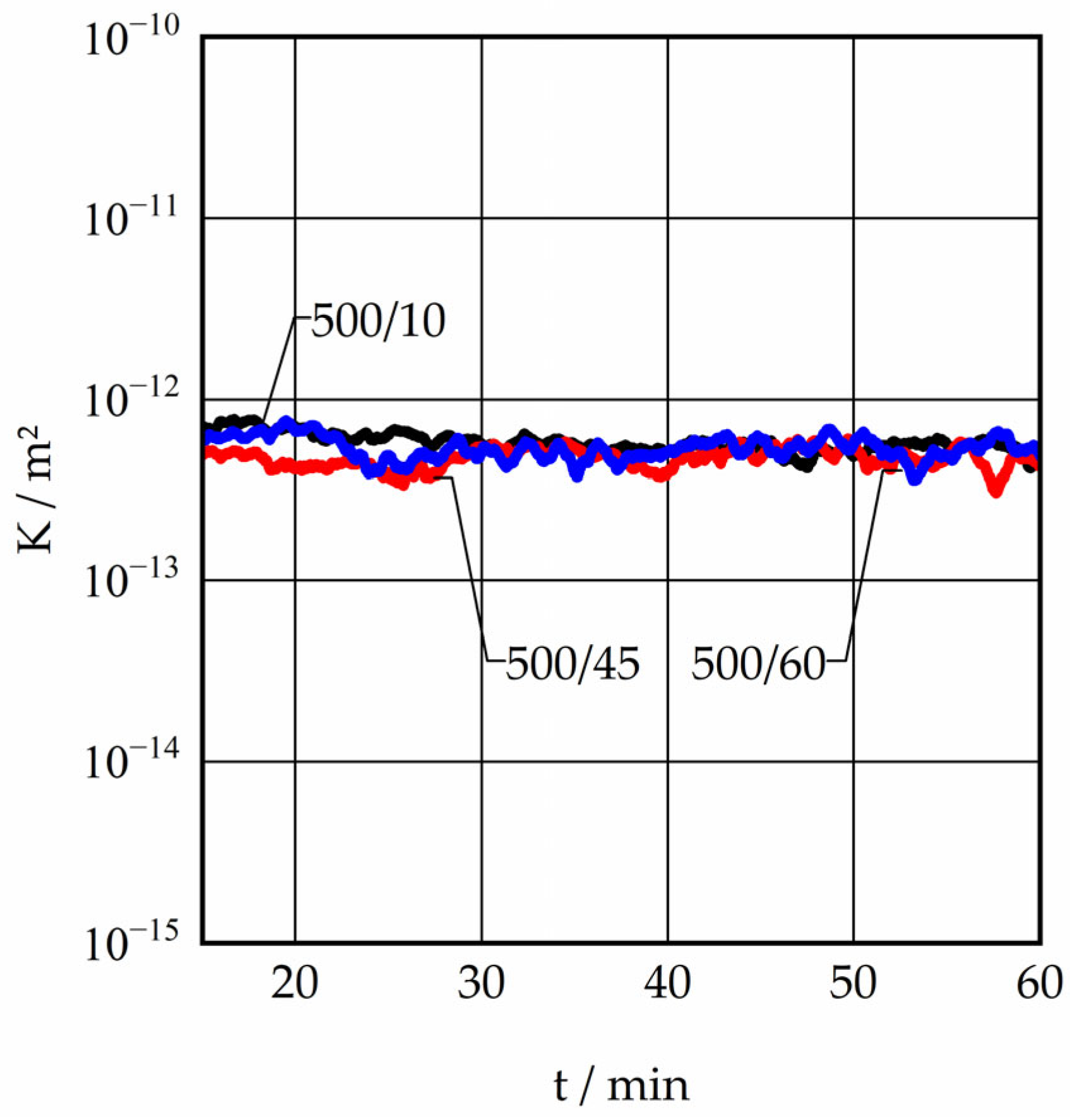
The combined permeability of the filter material and the deposit on the filter is derived from Darcy’s law and determined by the following equation:
2.3. Test Procedure
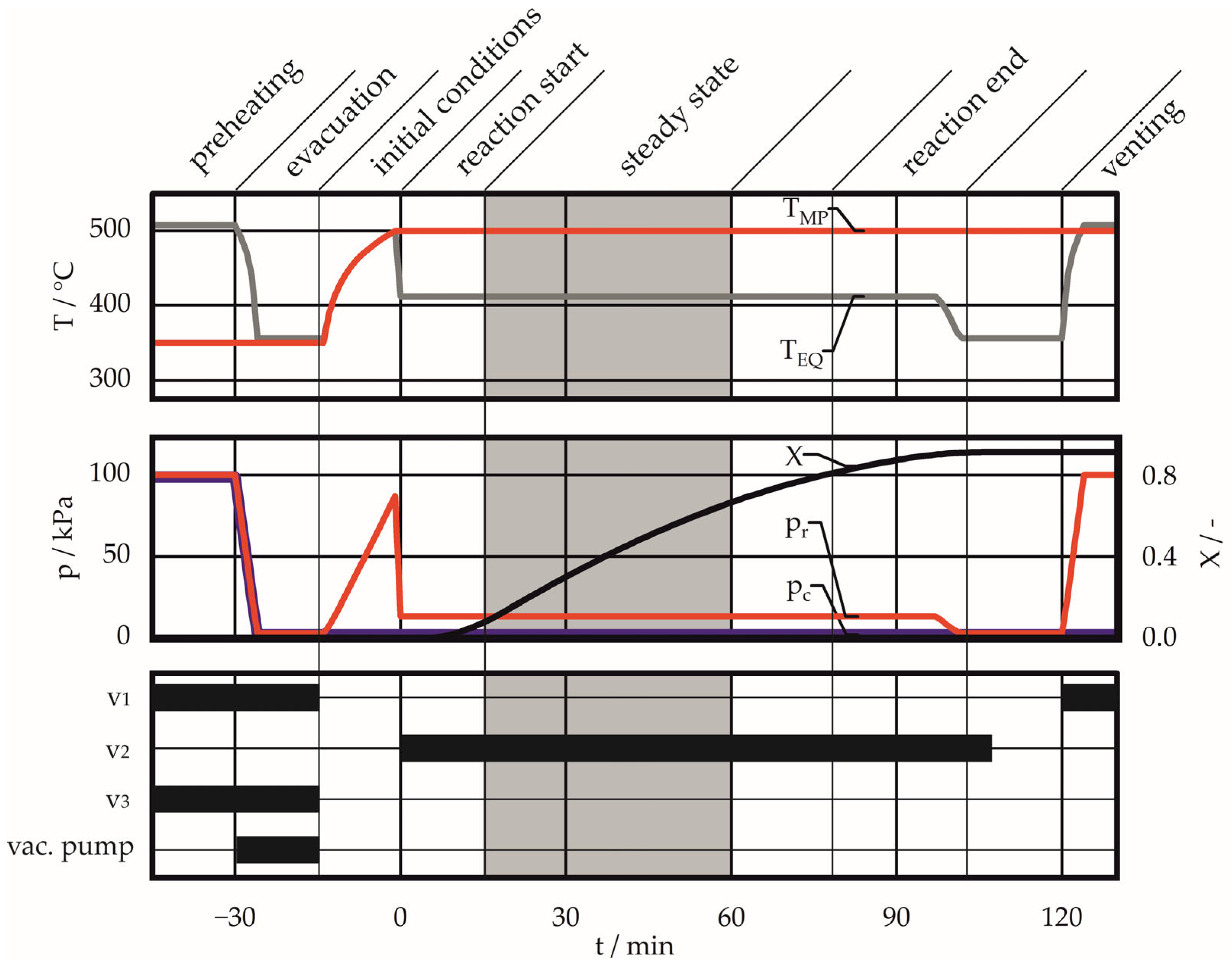
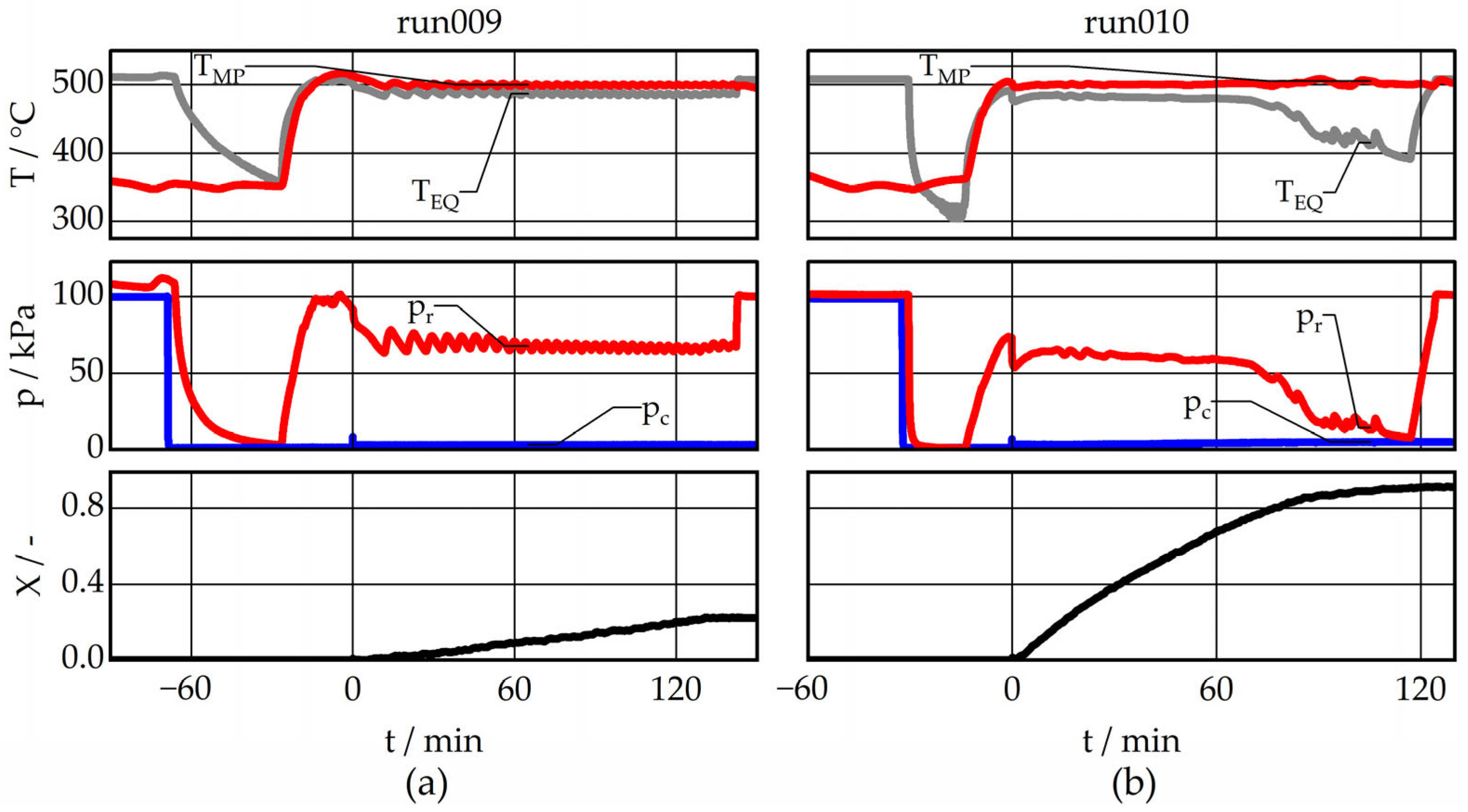
The principal focus of this investigation is to determine the feasibility of recovering latent heat during the dehydration process. Accordingly, the reactor is operated in the dehydration mode only. In order to achieve equal test conditions, the test procedure is standardised. It can be subdivided into the following process steps: loading, preheating, evacuating, reaching initial conditions, reaction start, steady state, reaction end, and venting. These are described in further detail below. The expected temperature, pressure, and conversion profiles are shown in
Figure 4. Test procedure: phases, expected profiles of p, T, X, and activation of valves and vac. pump during the dehydration process are illustrated. The grey area marks the time range of the steady state, which was considered for the calculations. Black bars show the active period (ON/OPEN).
Loading (t ≤ −45): A quantity of approximately 5 kg of Ca(OH)2 material is manually loaded into the reactor. At this time, the temperature of the material and the reactor are at ambient temperature. The initial weight and composition of the material are determined. The filter surface is cleaned of all deposits. The cutting tool is cleaned of all deposits and adjusted so that free rotation is ensured.
Pre-heating (−45 ≤ t ≤ −30): The reactor is preheated to a temperature of approximately 350 °C, while the condenser is simultaneously preheated to its initial temperature. The ploughshare mixing tool is rotating at a frequency of 250 rpm. During this phase, the condenser and reactor are connected to the environment (v1, v3 open, vacuum pump off), yet separated from each other (v2 closed). This configuration is maintained for approximately 15 min to ensure that the conditions remain in a steady state.
Evacuating (−30 ≤ t ≤ −15): The vacuum pump is connected to generate vacuum conditions in both the reactor and the condenser. This ensures the lowest possible concentration of inert gas in the system, which could disrupt the condensation process. Once the minimum pressure is reached, valves v1 and v3 are closed. At t = −15, the required test temperature of the reactor is set.
Reaction (0 ≤ t ≤ 90): The reaction starts, resulting in an increase in pressure within the reactor until a steady state is reached. Once the initial conditions have been reached, the reactor and the condenser are connected (v2 open, t = 0). A pressure drop occurs in the reactor, which is followed by condensation in the condenser. This reduces the pressure, prompting the reaction in the reactor to produce more vapour in order to maintain equilibrium. This results in a dynamic balance state within the system, accompanied by a mass flow to the condenser. From this point onwards (15 ≤ t ≤ 60), the reaction proceeds continuously, with the change in water level indicating a linear conversion progression. Once a critical quantity of Ca(OH)2 has been converted, the equilibrium cannot be maintained, and the reactor pressure tends towards the corresponding pressure in the condenser. At this point, the conversion has reached its final level (t = 100).
End of experiment (t > 100): Following a minimum period of 120 min, the heating wires are deactivated, the reactor and the condenser are separated (close v2), and the reactor is vented via v1 (t = 120). After the reactor has cooled down to 350 °C, the front reactor flange is opened, and a material sample is taken for further TGA analysis.
2.4. Measurement Matrix
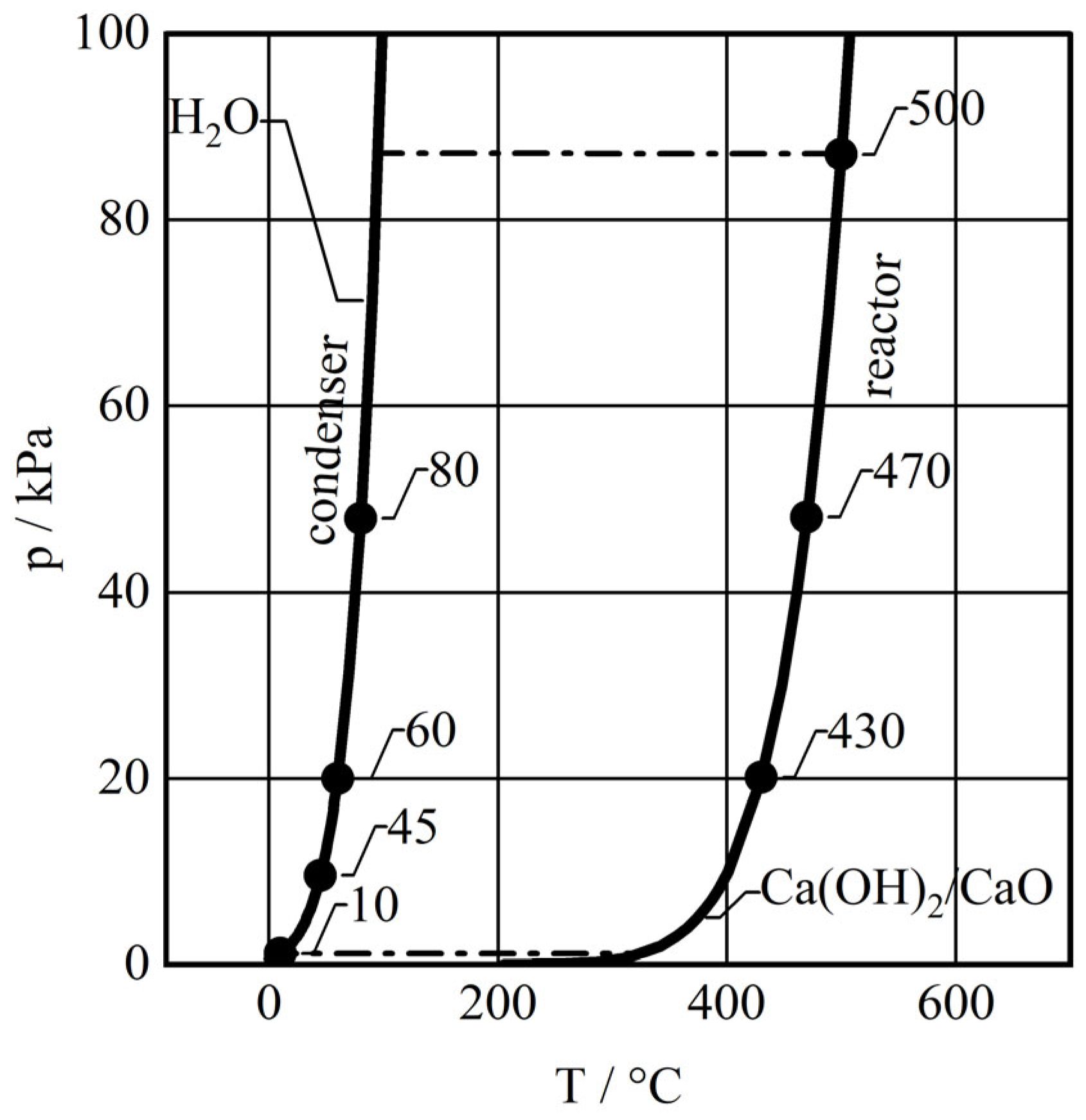
Figure 5 illustrates the operational ranges of the system. The anticipated pressures and temperatures in the reactor and condenser units are predominantly constrained by their working media characteristics. Given that the experimental conditions are analogous to those of pure water vapour atmosphere, the temperature and pressure within the reactor and condenser can be modelled using equilibrium conditions for vaporisation and the Ca(OH)
2 ⇌ CaO + H
2O reaction, respectively, see
Figure 5 solid lines.
In order to ensure optimal technical conditions for the duration of the measurement campaign, the temperature of the reactor core has been restricted to a maximum of 500 °C, while the condenser cooling limit is approximately 10 °C. These boundary conditions must also be considered (
Figure 5, stitch dotted lines). In order to ensure a reaction, it is essential to guarantee vapour mass transport, which necessitates a pressure drop between the operating point of the reactor (OPr) and the operating point of the condenser (OPc),
(Figure 5, dots).
The measurement matrix (
Table 1) was designed with consideration of potential system applications and operational conditions. As the reactor forms part of a thermochemical heat storage system, with domestic heating applications being the primary focus, the test points were derived from the typical heating circuit inlet temperatures, which range from 70–90 °C for radiator heaters in old buildings, 50–70 °C for radiator heaters in newer standards buildings, and 35–45 °C for underfloor heating systems. Furthermore, a condensation at 10 °C was used to investigate the system under conditions of minimum water vapour pressure, which can be realised in the set-up. The condenser water temperature and Ca(OH)
2 core temperature are suitable as potential control values. After considering all parameters, the selected set points are 10 °C, 45 °C, and 80 °C on the condenser and 430 °C, 470 °C, and 500 °C on the reactor side, as illustrated in
Figure 5 (dots).
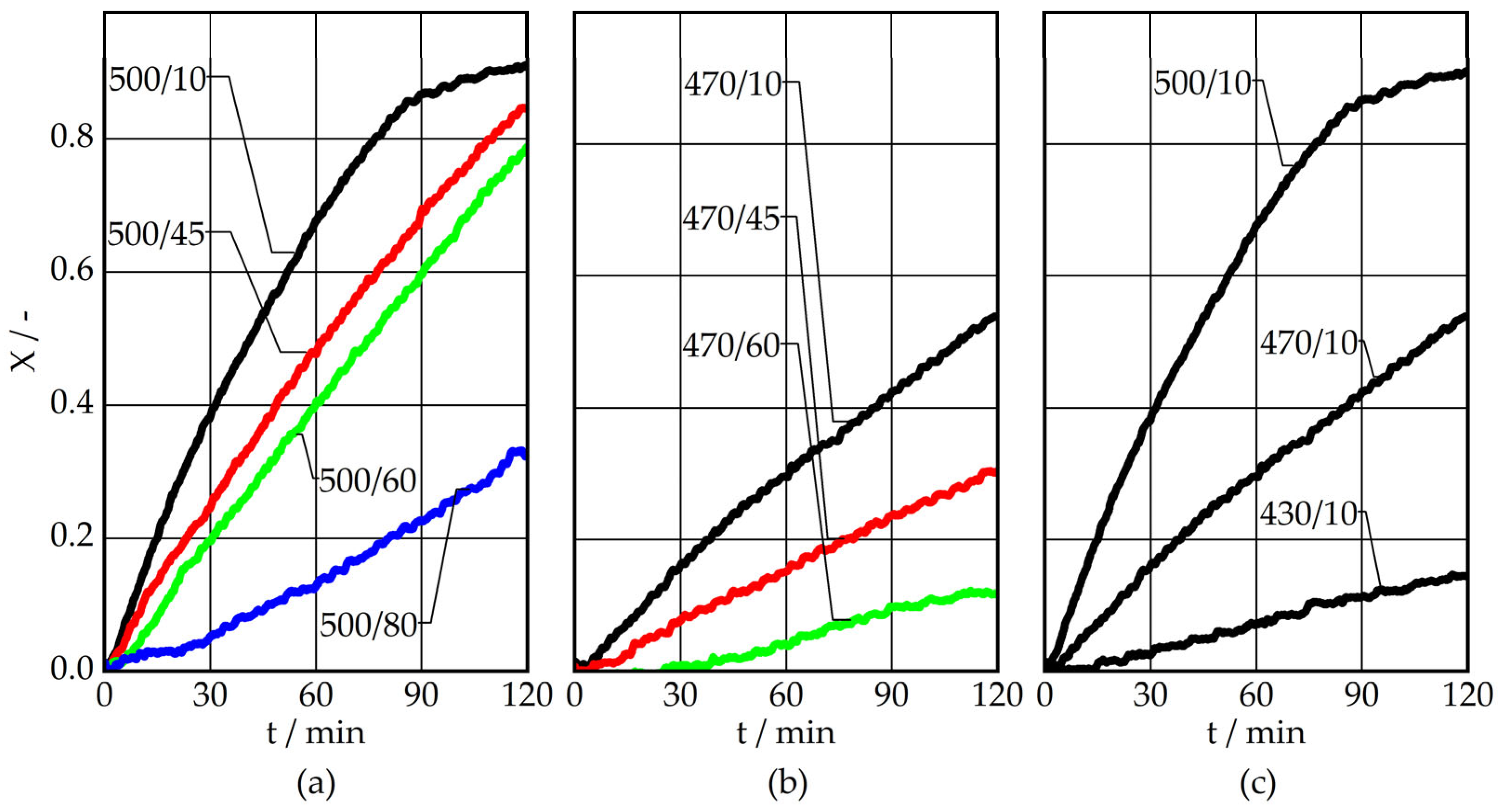
4. Conclusions
The thermal energy contained in the water vapour that is released during the charging reaction of a thermochemical energy storage system based on Ca(OH)
2 represents approximately 40% of the required charging energy. It is therefore essential that this thermal energy can be used as useful heat in the application in order to ensure the energy-efficient operation of the storage system. The primary objective of this study was to conduct an experimental investigation and demonstrate the effective recovery of the latent and heat energy produced during the dehydration reaction of Ca(OH)
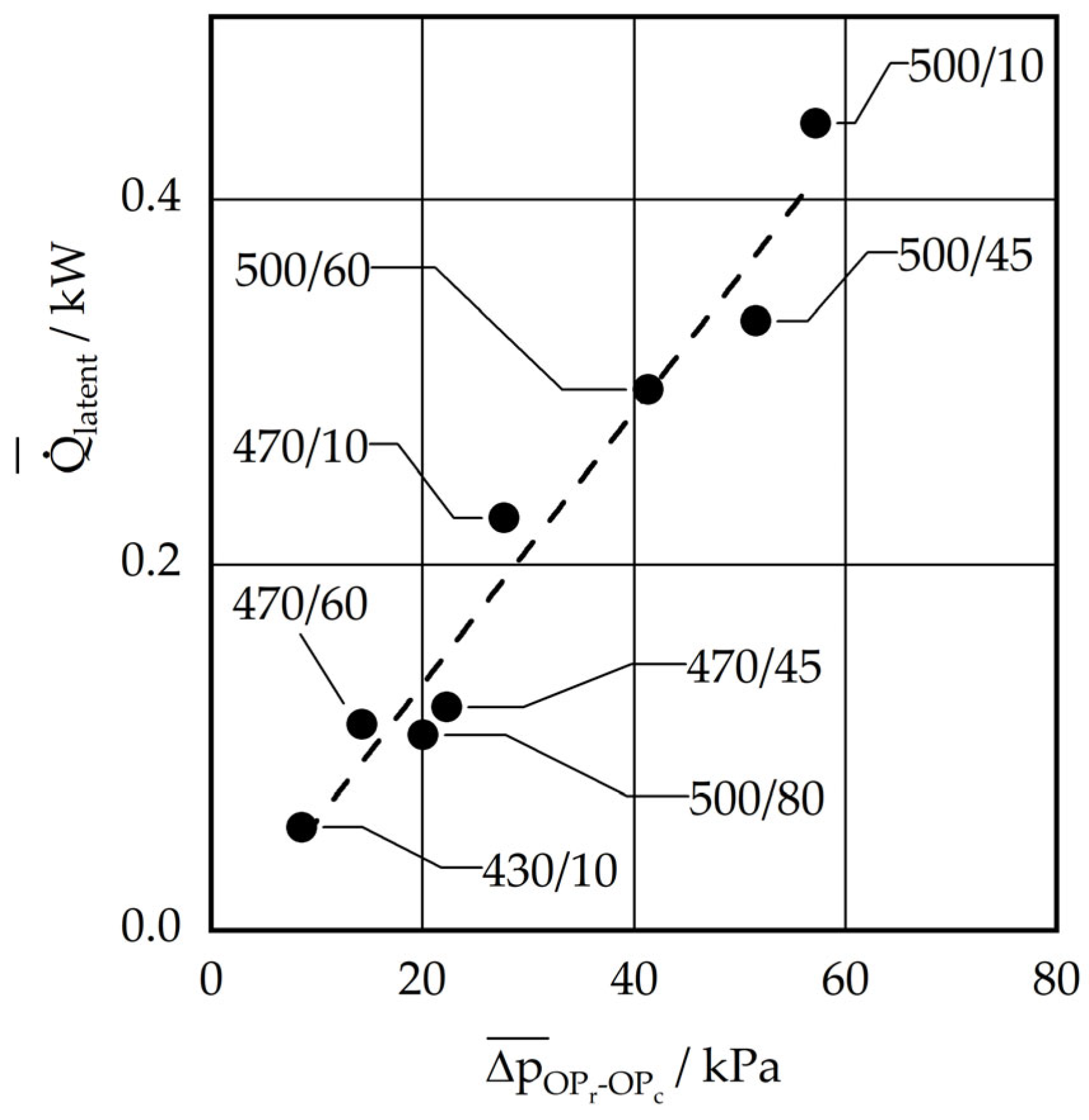
2. The recovery of heat has been demonstrated and quantified successfully at temperatures of 45 °C, 60 °C, and 80 °C. Based on the experimental verification, it can be concluded that the utilisation of this energy is feasible in applications such as district heating networks or residential hot water production, with the option of adjusting the temperature level to suit specific requirements. Furthermore, the reactor operation demonstrated that the adjustment of reaction and recovery temperature defines a potential pressure difference between the reactor and condenser. It can be postulated that higher recovery temperatures, such as 150 °C or 200 °C, would also be feasible. The reactor power presented only includes the latent heat of the water vapour that is a by-product of the energy-storing process, which according to Schmidt et al. [
10] accounts for approx. 24% of the reactor power. The power of thermochemical energy storage can be assumed to be approximately twice as high. The utilisation of the technology for seasonal energy storage for domestic applications is feasible after an upscaling of the reactor, and the combination with common heat pumps is also quite conceivable, see Weber et al. [
21]. For industrial applications as a system-relevant technology in heating networks for heat supply or electricity grids as a peak shaving technology or seasonal energy storage, a significant increase in the specific energy density of the system is required, which goes hand in hand with a significant improvement in the water vapour transport.
For further development it is sufficient to consider the pressure difference resulting from the operating temperatures and related gas velocities in the reactor design. The presented data, in conjunction with the existing thermodynamic and kinetic data, now enables the simulation of application-oriented reactor operation strategies and the extraction of reactor design constraints from the models. At the system level, the operation and integration of the storage reactor in larger energy networks can now be simulated, allowing for the analysis of the energetic and economic value of the storage system.
Furthermore, the operation of the reactor enabled the identification of significant factors pertaining to mass transfer in a mechanically fluidised bed reactor concept. It can be concluded that the filtration of gas and particles represents a significant challenge within the context of the current reactor design. The fluidisation of the particles within the reaction chamber results in their instantaneous movement in the direction of the gas flow as soon as a gas stream exits the reactor. This results in an immediate and dense clogging of the filter, which in turn causes a significant pressure drop in the filter cake. The implementation of a rotating cutting tool within the design enables the continuous cleansing of the filter throughout the operational period, thereby limiting the overall thickness of the filter cake. The enhanced gas transport resulted in a six-fold increase in performance compared to the operation without a continuously rotating cutting tool in front of the filter. Nevertheless, the findings indicated that the reactor performance remains significantly constrained by the slow mass transfer out of the reactor, which is caused by the pressure drop over the filter cake. The utilisation of rotary components in mixers and reactors is a common practice in the industrial processing of powder materials. However, depending on the design, the components may require frequent maintenance to ensure optimal functionality. It can be concluded that in general, filtration of gas and particles in a mechanically fluidised bed requires a further optimised solution. The experimental data obtained in this work can now be analysed by simulation of the gas transport in the reactor. One approach to optimising the filtration process is to enlarge the filter surface area and simultaneously reduce the thickness of the filter cake layer. Another potential direction for further research could be the specific deceleration of the gas velocity before the filter surface through a corresponding reactor design, for example, changes of the cross section at the gas outlet.