Attention-Based Load Forecasting with Bidirectional Finetuning

Abstract

Accurate load forecasting is essential for the efficient and reliable operation of power systems. Traditional models primarily utilize unidirectional data reading, capturing dependencies from past to future. This paper proposes a novel approach that enhances load forecasting accuracy by fine tuning an attention-based model with a bidirectional reading of time-series data. By incorporating both forward and backward temporal dependencies, the model gains a more comprehensive understanding of consumption patterns, leading to improved performance. We present a mathematical framework supporting this approach, demonstrating its potential to reduce forecasting errors and improve robustness. Experimental results on real-world load datasets indicate that our bidirectional model outperforms state-of-the-art conventional unidirectional models, providing a more reliable tool for short and medium-term load forecasting. This research highlights the importance of bidirectional context in time-series forecasting and its practical implications for grid stability, economic efficiency, and resource planning.

1. Introduction

Load forecasting plays a pivotal role in the management and operation of power systems, serving as the foundation for ensuring a reliable supply of electricity. The ability to accurately predict future electricity demand is crucial for maintaining grid stability, optimizing the operation of power plants, reducing operational costs, and supporting long-term infrastructure development. With the increasing complexity of power systems, driven by factors such as the integration of renewable energy sources, the rise of electric vehicles, and changing consumer behaviors, the need for precise and robust load-forecasting models has never been more critical.

Traditionally, load-forecasting models have relied on unidirectional approaches where time-series data are read and processed sequentially from past to future. These models have proven effective in capturing forward temporal dependencies, which are essential for predicting future demand based on historical consumption patterns. However, the unidirectional nature of these models limits their ability to fully leverage the rich information contained in time-series data, particularly the dependencies that may exist in the reverse temporal direction.

In recent years, attention-based models have emerged as a powerful tool for time-series forecasting, offering the ability to focus on the most relevant portions of the input data. Despite their success, these models typically follow the same unidirectional paradigm, potentially missing important contextual information that could enhance forecasting accuracy. To address this limitation, we propose a novel approach that fine tunes an attention-based model using bidirectional reading of time-series data. By incorporating both forward and backward temporal dependencies, our approach aims to provide a more comprehensive understanding of electricity consumption patterns, ultimately leading to more accurate and reliable load forecasts.

The rationale behind bidirectional fine tuning is rooted in the recognition that time-series data often contains patterns and relationships that are not solely dependent on the past but also on future events. For instance, the electricity demand on a particular day may be influenced not only by the preceding days but also by subsequent days, such as weekends, holidays, or changes in weather conditions. By reading the time-series data from both directions—left to right and right to left—the model can capture these bidirectional dependencies, enhancing its predictive capability.

In this paper, we present a detailed exploration of the proposed bidirectional fine-tuning approach. We begin by providing a mathematical framework that supports the benefits of bidirectional context in time-series forecasting. This framework demonstrates how the integration of forward and backward dependencies can potentially reduce prediction errors and improve the robustness of the model. To evaluate the performance of the proposed bidirectional model compared to traditional unidirectional models, we conducted a series of experiments on real-world load datasets. The results of the experiments reveal that our approach outperforms state-of-the-art conventional methods such as Neural Hierarchical Interpolation for Time Series (NHiTS), Long Short-Term Memory (LSTM), Temporal Convolutional Network (TCN), and Bidirectional Long Short-Term Memory (Bi-LSTM) offering a more reliable and accurate tool for load forecasting across various time horizons.

The contributions of this paper are threefold: (1) introduce a novel bidirectional fine-tuning technique for attention-based models in the context of load forecasting, (2) provide a mathematical framework for the proposed approach, and (3) demonstrate its effectiveness through empirical validation on real-world datasets. By highlighting the importance of bidirectional context in load forecasting, this research opens new avenues for improving the accuracy and reliability of time-series forecasting models with significant implications for the management and operation of power systems.

The manuscript is structured as follows. In Section 2, we provide an overview of the existing literature related to load forecasting. In Section 3, we present a mathematical analysis of the proposed bidirectional fine-tuning method. Section 4 contains the results of the numerical experiments on real-world data to evaluate the performance of the proposed method in practice. We end the paper with concluding remarks in Section 5.

2. Literature Review

Over the past decade, time-series forecasting, particularly in the context of load forecasting, has garnered significant scholarly interest. Research in power forecasting encompasses a range of methodologies, including statistical models, deep learning frameworks, and hybrid approaches. Statistical techniques primarily involve autoregressive linear regression models, while deep learning models leverage various neural network architectures that utilize a lookback window to generate predictions. Hybrid models, on the other hand, integrate multiple methods to produce a unified forecast. The majority of these methodologies focus on univariate sequences, processing the input series in a left-to-right manner. Although some bidirectional sequence processing techniques have been explored, these are predominantly limited to recurrent-based neural networks.

2.1. Statistical Models

Statistical methods have long been the cornerstone of load forecasting with traditional approaches such as Autoregressive Integrated Moving Average (ARIMA), linear regression, and exponential smoothing models being widely used [1,2,3]. These methods primarily rely on past values of the time series to predict future values, with techniques like least squares linear regression and maximum likelihood estimation, and autoregressive methods commonly employed to estimate model parameters. In recent years, there has been a rise in the use of linear regression models that incorporate a large number of input features alongside regularization techniques, notably the least absolute shrinkage and selection operator (LASSO), which minimizes the $L_1$ norm of the feature vector to enhance model performance [4,5].

Additionally, advancements have been made in the application of preprocessing techniques, such as variance stabilizing transformations [6] and the incorporation of long-term seasonal components [7], to improve forecasting accuracy. Ensemble methods, which combine multiple forecasts from the same model calibrated on different time windows, have also gained traction [8]. These methods, particularly those that analyze forecast errors and signal shapes, have been applied to both current and voltage time-series forecasting [9].

While these statistical models have proven effective, especially in short-term load forecasting due to their ability to detect linear patterns, their unidirectional framework—processing data sequentially from past to future—poses limitations in capturing more complex dependencies, particularly those influenced by future events [3,10]. Despite these limitations, statistical models continue to serve as benchmarks in the field of load forecasting, which are favored for their simplicity and ease of implementation [11]. Unlike in financial time-series forecasting, where generalized autoregressive conditional heteroskedastic (GARCH) models are prevalent, electricity load forecasting often yields more accurate results with basic autoregressive (AR) and ARIMA models [12,13].

2.2. Machine Learning and Deep Learning Approaches

The limitations of statistical models have paved the way for machine learning techniques, which offer improved forecast precision. Techniques such as support vector machines (SVMs) [3], gradient boosting machines (GBMs) [3], and convolutional neural networks (CNNs) [14] have demonstrated progress over traditional statistical models, particularly in detecting non-linear relationships in data. Recent advancements in deep learning have significantly enhanced electricity demand predictions by more accurately capturing complex temporal dependencies within data [1].

Although effective, many machine learning models continue to follow a unidirectional paradigm, focusing primarily on past data to predict future outcomes [3]. For example, Shen et al. proposed a novel deep learning forecasting model that improves prediction accuracy but still relies predominantly on past data [1].

2.3. Attention Mechanisms and Transformer Models

Relying solely on past data limits the capacity of models to account for scenarios where future events might influence past trends. To overcome such limitations, attention-based models have been introduced, significantly advancing the field of time-series forecasting [3,14]. By focusing on the most relevant portions of input data, these models enhance the ability to capture long-term dependencies [14], making them particularly well suited for load forecasting, where understanding intricate patterns over extended periods is crucial.

Despite their success, attention-based models have typically been unidirectional, which limits their ability to fully exploit the extensive information present in time-series data [15,16,17]. To address this constraint, recent studies have explored hybrid methods that combine various forecasting techniques to improve accuracy and reliability. For instance, combining CNNs with LSTM networks has shown promising results in capturing both the spatial and temporal characteristics of load data, leading to more accurate predictions [16]. Additionally, some methods have investigated transformers enhanced with temporal-aware self-attention mechanisms, further refining the ability to predict complex time-series data. While research on unidirectional fine-tuning has highlighted its practicality in scenarios where computational efficiency is prioritized while still delivering satisfactory accuracy in load-forecasting tasks [17,18], these methods allow for faster processing and reduced resource consumption, which is particularly valuable in real-time applications. However, they may not capture all dependencies in complex time-series data as effectively as bidirectional approaches.

The emergence of transfer learning techniques has enabled the leveraging of pre-trained models for new load-forecasting tasks, significantly reducing the need for large amounts of labeled data [19]. These approaches have been instrumental in power forecasting applications, showing promising results in reducing forecasting errors and improving model adaptability to changing conditions [20,21]. For instance, the NeuralForecast framework by Olivares et al. leverages state-of-the-art neural forecasting models that are pre-trained and then fine-tuned for specific tasks [21].

Recent developments in zero-shot learning have further expanded the capabilities of transfer learning by enabling models to forecast new tasks without additional training [19]. This method has demonstrated significant potential for increasing forecasting accuracy and computational efficiency particularly in dynamic and rapidly changing contexts [20].

2.4. Hybrid Models

Hybrid models, which integrate different forecasting methods, have significantly enhanced prediction accuracy. A well-known example is the combination of CNNs with LSTM networks, allowing for the capture of both spatial and temporal patterns in load data [3,16,22]. Mamun et al. provide a comprehensive review of various load-forecasting methods used in the power utility sector, covering both single-method and hybrid models. The study emphasizes the critical role of accurate load predictions in maintaining a stable power supply and efficient resource management. A range of machine learning techniques, including SVM and feedforward networks, are examined, highlighting how integrating these into hybrid models can enhance forecasting precision [3].

A study by Ghimire and colleagues proposed a hybrid model that combines Variational Mode Decomposition (VMD) with a Convolutional Attention-Based Bidirectional Long Short-Term Memory Network (CABLSTM) and Artificial Neural Networks (ANN), incorporating an error correction mechanism (EC). This VMD-CABLSTM-ANN-EC hybrid model uses VMD to decompose time-series data into intrinsic mode functions, improving prediction accuracy by capturing the non-linear and non-stationary characteristics of electricity demand. As energy systems become more complex, the need for accurate and efficient real-time load-forecasting solutions grows. Recent research focuses on developing hybrid models that balance both accuracy and computational efficiency. For example, Geng et al. proposed a model combining data decomposition techniques with attention mechanisms to improve forecasting accuracy while maintaining computational efficiency, making it suitable for high-frequency energy trading platforms [23]. Despite these significant advancements, challenges in electrical load forecasting persist. Akhtar et al. highlighted ongoing difficulties in short-term load forecasting, such as handling data sparsity, improving forecasting accuracy under uncertain conditions, and enhancing model interpretability [24]. These challenges underscore the need for continuous improvement in forecasting methods to address the increasing complexity of energy systems. Other hybrid approaches include combining one or more forecasting models into a single prediction, data decomposition, feature selection, and data clustering [25,26,27].

2.5. Bidirectional Approaches

Another significant advancement has been the introduction of bidirectional sequence processing. This approach processes data in both forward and backward directions, acknowledging that future events can influence current trends. By incorporating information from both temporal directions, models achieve a more holistic understanding of the underlying patterns in data [16,28]. Bidirectional LSTM (BiLSTM) networks, for example, have successfully captured both past and future contexts, making them well suited for applications in load forecasting [29,30]. In particular, it was shown in [29] that the BiLSTM model significantly outperformed traditional models like RNN, LSTM, and GRU, particularly in reducing errors and improving accuracy. The findings underscore the importance of bidirectional processing in capturing intricate temporal patterns in energy consumption data, making the BiLSTM model a powerful tool for planning and market management. Additionally, Yan et al. introduced a bidirectional simple recurrent unit (SRU) network with feature–temporal attention mechanisms, further enhancing prediction accuracy in integrated energy load aggregation scenarios [31].

Although bidirectional sequence processing techniques have been explored in the literature, these approaches have been predominantly limited to recurrent neural networks, such as RNN, GRU, and LSTM. These models, while effective in certain contexts, suffer from significant computational constraints and struggle to capture long-term dependencies effectively. Our proposed method leverages the attention mechanism, which offers a more efficient and scalable solution for bidirectional sequence processing. By incorporating both forward and backward temporal dependencies, our approach aims to enhance the model’s capacity to understand and predict complex patterns in load forecasting.

3. Theoretical Analysis of Bidirectional Fine-Tuning

In this section, we present a mathematical argument in support of the proposed bidirectional fine-tuning approach for improving load-forecasting accuracy. We begin by formalizing the load-forecasting problem and then demonstrate how bidirectional fine tuning enhances the model’s capacity to capture temporal dependencies, leading to more accurate predictions.

3.1. Problem Formulation

Consider a time series representing electricity load demand, $X=\{x_1,x_2,\dots ,x_T\}$, where $x_t$ denotes the load at time t. The objective of load forecasting is to predict future values $\widehat{X}=\{{\widehat{x}}_{T+1},{\widehat{x}}_{T+2},\dots ,{\widehat{x}}_{T+H}\}$, where H is the forecast horizon.

Traditional unidirectional models predict the future load based on past observations:

$${\widehat{x}}_{T+h}=f(x_1,x_2,\dots ,x_T),\mathrm{for}h=1,2,\dots ,H$$

(1)

where $f(·)$ represents the model function, which may be a neural network, a statistical model, or another type of forecasting method.

3.2. Bidirectional Fine-Tuning Approach

The proposed bidirectional approach enhances the model by incorporating information from both past and future observations. Specifically, the model is trained to predict each load value $x_t$ using both forward and backward contexts:

• Forward Model $f_f(·)$: Processes the time series from $t=1$ to $t=T$.
• Backward Model $f_b(·)$: Processes the time series from $t=T$ to $t=1$.

The forward prediction is given by

$${\widehat{x}}_t^{\left(f\right)}=f_f(x_1,x_2,\dots ,x_T)$$

(2)

The backward prediction is given by

$${\widehat{x}}_t^{\left(b\right)}=f_b(x_T,x_{T-1},\dots ,x_1)$$

(3)

The final prediction ${\widehat{x}}_t$ is a weighted combination of these two predictions:

$${\widehat{x}}_t=\alpha {\widehat{x}}_t^{\left(f\right)}+(1-\alpha ){\widehat{x}}_t^{\left(b\right)},\alpha \in [0,1]$$

(4)

where $\alpha$ is a weighting parameter that can be tuned based on the specific characteristics of the dataset.

3.3. Enhanced Feature Representation

In the unidirectional approach, the feature representation ${\varphi }_t$ at time t is derived solely from past observations:

$${\varphi }_t^{\mathrm{uni}}=W_f·{[x_1,x_2,\dots ,x_t]}^T$$

(5)

where $W_f$ is a weight matrix associated with the forward model. In the bidirectional approach, the feature representation incorporates both forward and backward contexts:

$${\varphi }_t^{\mathrm{bi}}=W_f·{[x_1,x_2,\dots ,x_t]}^T+W_b·{[x_t,x_{t-1},\dots ,x_1]}^T$$

(6)

where $W_b$ is the weight matrix for the backward model. This enhanced feature representation ${\varphi }_t^{\mathrm{bi}}$ is expected to capture more comprehensive temporal dependencies, leading to more accurate predictions.

3.4. Error Reduction and Robustness

The forecasting error in the unidirectional case can be expressed as follows:

$${\mathcal{L}}^{\mathrm{uni}}=\sum _{t=T+1}^{T+H}L(x_t,{\widehat{x}}_t^{\left(f\right)})$$

(7)

For the bidirectional model, the error is

$${\mathcal{L}}^{\mathrm{bi}}=\sum _{t=T+1}^{T+H}L\left(x_t,\alpha {\widehat{x}}_t^{\left(f\right)}+(1-\alpha ){\widehat{x}}_t^{\left(b\right)}\right)$$

(8)

Given that the bidirectional model utilizes information from both past and future, we hypothesize that it will reduce prediction errors compared to the unidirectional model:

$${\mathcal{L}}^{\mathrm{bi}}\le {\mathcal{L}}^{\mathrm{uni}}$$

(9)

The primary reason for the expected reduction in error lies in the increase in training data. By processing the time-series data in both forward and backward directions, we effectively double the size of the training data, allowing the model to learn from a more comprehensive set of patterns and dependencies.

3.5. Regularization Effect and Generalization

Bidirectional fine tuning can also be viewed as a form of regularization. By training the model to consider both directions, we effectively increase the diversity of the training data, which helps in reducing overfitting. The model learns to generalize better, resulting in improved performance on unseen data.

The variance component of the error can be reduced by combining predictions from both directions:

$$\mathrm{Var}({\widehat{x}}_t^{\mathrm{bi}})={\alpha }^2\mathrm{Var}({\widehat{x}}_t^{\left(f\right)})+{(1-\alpha )}^2\mathrm{Var}({\widehat{x}}_t^{\left(b\right)})$$

(10)

Since $\mathrm{Var}({\widehat{x}}_t^{\mathrm{bi}})$ is expected to be lower than either $\mathrm{Var}({\widehat{x}}_t^{\left(f\right)})$ or $\mathrm{Var}({\widehat{x}}_t^{\left(b\right)})$ alone, the bidirectional model exhibits improved robustness and generalization.

The mathematical analysis presented above supports the hypothesis that bidirectional fine tuning enhances the performance of load-forecasting models. By incorporating both forward and backward temporal dependencies, the proposed approach leads to richer feature representations, reduced prediction errors, and improved model robustness. The bidirectional model is thus better equipped to capture complex patterns in time-series data, making it a valuable tool for accurate and reliable load forecasting.

4. Attention-Based Forecasting

Recent advances in attention-based models have significantly expanded their application beyond natural language processing, spurring their adoption in time-series forecasting. The attention mechanism, which allows models to dynamically focus on different parts of the input data, has proven particularly effective in handling the complex temporal dependencies inherent in time-series data. Unlike traditional models that rely on fixed windows of historical data, attention-based models can learn to weigh the importance of different time steps, thus capturing both short-term fluctuations and long-term trends more effectively. This adaptability has led to the development of several implementations of the attention mechanism tailored specifically for time-series forecasting, including temporal attention, self-attention in transformers, and hybrid models that combine attention with recurrent or convolutional layers [14,22,23].

In this paper, we utilize the TimeGPT model developed by NIXTLA [19]. TimeGPT is a generative pre-trained transformer specifically designed for time-series forecasting, which is independently trained on a substantial volume of time-series data to minimize forecasting error without relying on any existing large language models. The architecture of TimeGPT features an encoder–decoder structure with multiple layers, each incorporating residual connections and layer normalization. A final linear layer maps the decoder’s output to the dimension of the forecasting window.

As a pre-trained model, TimeGPT enables zero-shot forecasting, allowing it to generate predictions without requiring task-specific training. Furthermore, the model can be fine-tuned to adapt to the unique characteristics of a specific dataset, enhancing its performance on specialized tasks. During the fine-tuning process, the model processes data in a forward direction, from left to right, to generate future predictions. In this work, we propose a bidirectional fine-tuning approach which involves reading the data in both forward and reverse directions. We hypothesize that the proposed approach will improve the forecasting accuracy due to additional patterns learned during bidirectional fine-tuning.

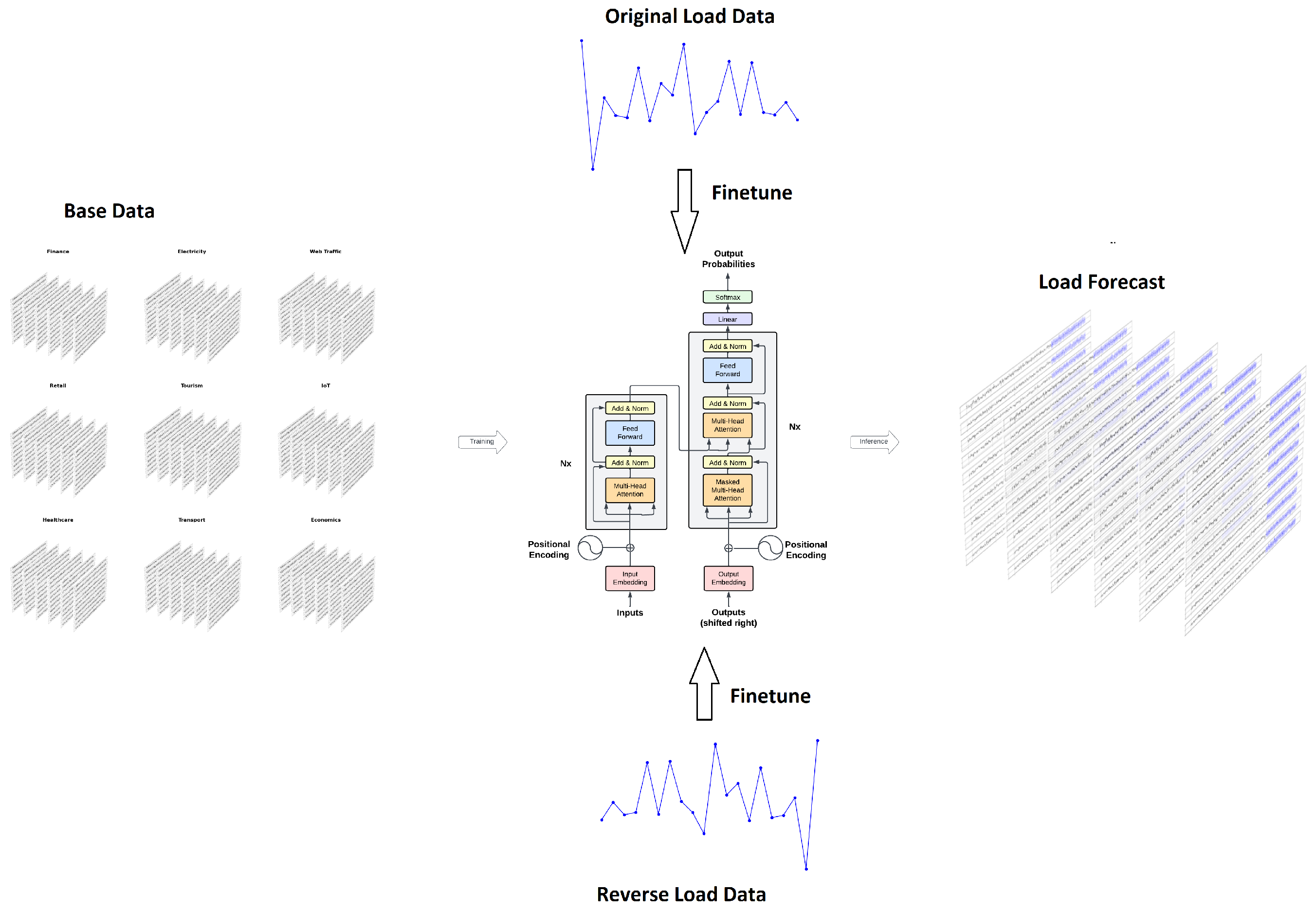
We use the attention-based model TimeGPT as the base model in the proposed method. As a pre-trained model, TimeGPT offers a robust starting point for time-series forecasting tasks. Our approach is to fine-tune the base model specifically for load forecasting using a bidirectional approach (Figure 1). This differs from traditional methods where the base model is either used without any fine tuning (zero-shot) or fine-tuned using unidirectional data only. The bidirectional fine tuning allows the model to capture temporal dependencies more effectively by considering the data in both forward and backward directions. As a result, our method enhances the model’s ability to generalize from the data, leading to improved forecasting accuracy compared to conventional techniques that rely solely on unidirectional data processing.

5. Numerical Experiments

In this section, we present the results of numerical experiments conducted to compare the performance of the proposed bidirectional approach with that of existing forecasting methods.

5.1. Benchmark Methods

To benchmark the performance of the proposed forecasting method, we utilize state-of-the-art models such as Neural Hierarchical Time Series (N-HiTS) and the Temporal Convolutional Network (TCN) alongside a traditional Long Short-Term Memory (LSTM) model. All models are implemented using the NeuralForecast Python library with default parameters applied as provided by the library [21]. In addition, we test TimeGPT in two standard modes: zero-shot forecasting and forward fine tuning. Finally, to compare the proposed approach with other existing bidirectional methods, we have included the Bidirectional Long Short-Term Memory (Bi-LSTM) model in our benchmarking process. Thus, the proposed approach is benchmarked against a total of six models:

• N-HiTS [32];
• LSTM [33];
• TCN [34];
• TimeGPT zero-shot [19];
• TimeGPT forward fine-tuning [19];
• Bi-LSTM [35].

The N-HiTS model is an advanced deep-learning architecture designed to address the challenges of time-series forecasting particularly in the presence of hierarchical structures. The core idea behind N-HiTS is to decompose time-series data into different hierarchical levels and use a series of neural networks to capture dependencies and patterns at each level. The model consists of multiple MLPs utilizing ReLU activation functions with blocks connected using a doubly residual stacking approach. The l-th block produces both a backcast output, ${\tilde{y}}_{t-L:t,l}$, and a forecast output, ${\tilde{y}}_{t+1:t+H,l}$. By incorporating multi-rate input pooling, hierarchical interpolation, and backcast residual connections, the model promotes the specialization of additive predictions across various signal bands. This design reduces memory usage and computational time, enhancing the model’s efficiency and accuracy [32].

The LSTM model is a type of Recurrent Neural Network (RNN) specifically designed to address the vanishing gradient problem commonly encountered in traditional RNNs, making it highly effective for sequential data and time-series forecasting. The basic idea behind LSTM is to maintain and regulate the flow of information over long sequences, allowing the model to remember important information while forgetting irrelevant details. The architecture of an LSTM network includes a series of LSTM cells, each containing three key components: a forget gate, an input gate, and an output gate. These gates control the cell state and hidden state of the LSTM by selectively filtering and updating information as it passes through the network. The forget gate decides what information should be discarded, the input gate determines which new information should be added, and the output gate controls what part of the current cell state should be output. The gating mechanism enables LSTM networks to capture long-term dependencies and temporal dynamics [33,36].

The TCN model is a deep learning architecture designed for sequential data processing, particularly in time-series forecasting tasks. The basic idea behind TCN is to leverage convolutional layers to capture temporal dependencies in time-series data, offering an alternative to recurrent models like LSTMs. TCN uses 1D dilated convolutions to allow the model to learn long-range dependencies while maintaining computational efficiency. The architecture is composed of multiple stacked convolutional layers with increasing dilation factors, enabling the receptive field of the network to grow exponentially with depth, thus capturing patterns over extended time horizons. TCNs also incorporate causal convolutions to ensure that the predictions for a given time step only depend on past data, preserving the temporal order. In addition, the model includes residual connections between layers to facilitate the training of deep networks, mitigating the vanishing gradient problem [34].

The Bi-LSTM model is a type of RNN designed to capture both past and future temporal dependencies in sequential data. Unlike traditional LSTMs, which only process input in one direction (from past to future), Bi-LSTM layers consist of two LSTM networks running in parallel. One processes the input sequence forward, while the other processes it backward, allowing the model to leverage context from both preceding and succeeding time steps. The architecture of Bi-LSTMs retains the gating mechanism of standard LSTMs, which helps mitigate the vanishing gradient problem and enables the model to learn long-range dependencies more effectively. By incorporating both forward and backward temporal information, Bi-LSTMs aims to provide more accurate predictions in complex sequential data scenarios [35].

5.2. Data

The numerical experiments in this study are conducted using the Australian Electricity Demand dataset [37]. This dataset contains energy demand records for five Australian regions: Victoria (VIC), New South Wales (NSW), Queensland (QUN), Tasmania (TAS), and South Australia (SA). As detailed in

Table 1. The time-series details for each region. The end time for all series is 23:00.

Region	VIC	NSW	QUN	TAS	SA
Start	2002-01-01	2002-01-01	2002-01-01	2002-01-01	2002-01-01
End	2015-02-28	2015-02-28	2015-04-01	2015-02-28	2015-03-01
Frequency	30 min	30 min	30 min	30 min	30 min

, each time series within the dataset terminates on a different date. All data are recorded at a half-hourly frequency, meaning that 48 time steps correspond to one day.

5.3. Accuracy Metrics

To measure the performance of the models, we use mean absolute error (MAE) and symmetric mean absolute percentage error (SMAPE). These are widely used metrics in time-series forecasting due to their intuitive interpretability and effectiveness in capturing forecast accuracy. MAE provides a straightforward measure of average error magnitude, offering a clear understanding of the model’s overall prediction accuracy in the same units as the data. On the other hand, SMAPE normalizes the error by the sum of actual and forecasted values, making it particularly useful for assessing the accuracy of models across datasets with varying scales. SMAPE’s symmetric nature ensures that it treats overestimation and underestimation errors equally, providing a balanced evaluation of model performance. Together, MAE and SMAPE offer complementary insights, making them valuable tools for assessing the effectiveness of forecasting models.

The MAE is computed as follows:

$$\mathrm{MAE}={\displaystyle \frac{1}{H}}\sum _{i=1}^H|x_i-{\widehat{x}}_i|$$

where $x_i$ is the actual value, ${\widehat{x}}_i$ is the forecast value of the time series, and H is the forecast horizon. The SMAPE is defined as follows:

$$\mathrm{SMAPE}={\displaystyle \frac{100\%}{H}}\sum _{i=1}^H{\displaystyle \frac{|x_i-{\widehat{x}}_i|}{\frac{|x_i|+|{\widehat{x}}_i|}{2}}}.$$

5.4. Experimental Setup

The evaluation of the proposed method is conducted in two phases. First, we forecast the final 48 time steps of each time series in the dataset. Second, we perform a more comprehensive analysis using cross-validation.

In the first phase, the last 48 time steps (equivalent to 1 day) of each series are forecasted based on an input window of preceding time steps. The size of the input window varies depending on the model. The TimeGPT-based models utilize an input window of 4800 time steps (100 days), whereas the N-HiTS, LSTM, TCN, and Bi-LSTM models use an input window of 9600 time steps (200 days), as these models require more data for training. The forecasted values are then compared to the actual values to assess the accuracy of each model.

In the second phase, we further examine the performance of the models through cross-validation. The input window sizes used in cross-validation are consistent with those used in the initial forecasting phase. We employ an expanding window strategy, gradually increasing the size of the input window from H to 10H, where $H=48$ represents the forecast horizon. The final results are reported as the average accuracy across the 10 cross-validation folds.

A summary of the setup for each model is provided in

Table 2. Model parameters used in the numerical evaluation. For transparency, the default parameter values provided by Nixtla were used in most cases.

Model	Input Window	Training	Hyperparemeters
TimeGPT zero shot	4800	No	Default
TimeGPT forward	4800	Yes	Default
TimeGPT bidirectional	4800	Yes	Default
N-HiTS	9600	Yes	Default
LSTM	9600	Yes	Default
TCN	9600	Yes	Default
Bi-LSTM	9600	Yes	Default

. The Jupyter Notebook containing the code for all experiments is publicly available on GitHub.

5.5. Results

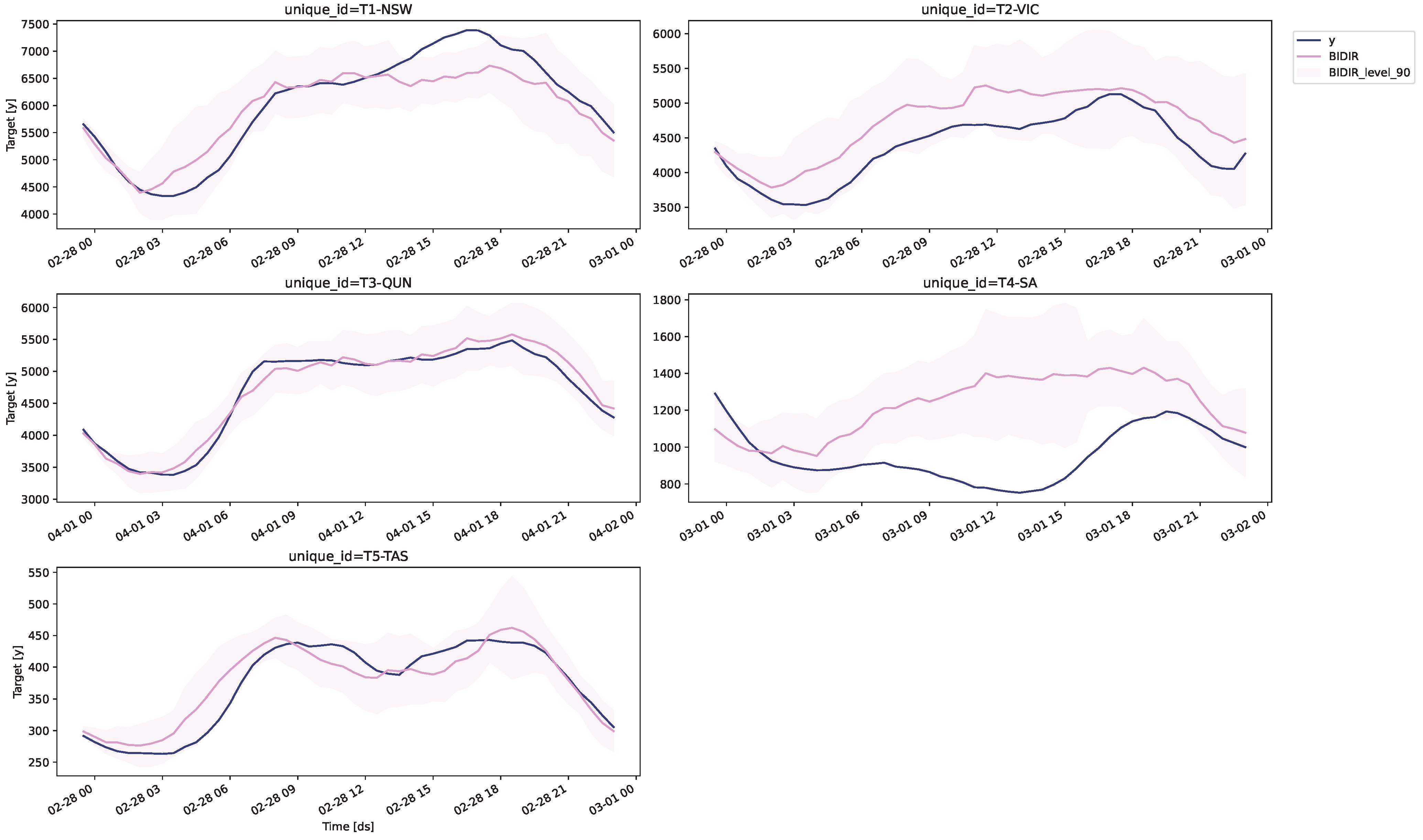
The forecasted values for the last 48 time steps in each series, obtained using the bidirectional fine-tuning approach, are presented in Figure 2. The results indicate that the forecasted values are remarkably close to the actual values across all series with the exception of South Australia (SA). Notably, the actual values of the series consistently fall within the forecasted 90% confidence interval, underscoring the accuracy of the proposed method. These findings demonstrate that the bidirectional fine-tuning approach is effective in accurately forecasting both medium and long-term horizons.

To benchmark the performance of the proposed bidirectional model (BIDIR) against existing forecasting methods, we evaluated the mean absolute error (MAE) and symmetric mean absolute percentage error (SMAPE) of the models when forecasting 48 time steps into the future.

As shown in

Table 3. Forecast MAE over 48 time steps. The bold values represent the minimum MAE.

Region	Zero	FWD	BIDIR	NHITS	LSTM	TCN	Bi-LSTM
NSW	652.74	607.87	315.55	645.93	793.62	800.15	1198.63
VIC	437.86	441.83	346.79	599.9	420.37	413.11	326.46
QUN	523.06	444.66	112.16	196	636.74	575.83	239.01
SA	328.23	332.84	293.68	219.13	225.32	256.11	480.92
TAS	48.08	49.49	19.92	24.34	57.52	56.92	27.85
Mean	397.99	375.34	217.62	337.06	426.71	420.42	454.57

, the BIDIR method achieved the lowest MAE in four out of the five series, and it also recorded the lowest mean MAE (217.62) with a significant margin over the other methods. This demonstrates the superior accuracy of the BIDIR approach in minimizing forecasting errors across different regions.

Similarly, as shown in

Table 4. Forecast SMAPE over 48 time steps. The bold values represent the minimum SMAPE.

Region	Zero	FWD	BIDIR	NHITS	LSTM	TCN	Bi-LSTM
NSW	0.056	0.053	0.026	0.052	0.067	0.068	0.174
VIC	0.05	0.051	0.039	0.064	0.048	0.048	0.074
QUN	0.058	0.049	0.012	0.021	0.07	0.064	0.054
SA	0.151	0.152	0.134	0.104	0.111	0.123	0.402
TAS	0.067	0.067	0.028	0.033	0.079	0.079	0.073
Mean	0.076	0.074	0.048	0.055	0.075	0.076	0.155

, the BIDIR method achieved the lowest SMAPE in four out of the five series. The BIDIR model also obtained the lowest mean SMAPE (0.048) with a considerable margin, further illustrating its effectiveness in reducing relative forecasting errors compared to the other models.

To gain a more comprehensive understanding of the models’ performance, we conducted cross-validation using an expanding window strategy with 10 windows. As shown in

Table 5. Cross-validation MAE using 10 windows. The bold values represent the minimum MAE.

Region	Zero	FWD	BIDIR	NHITS	LSTM	TCN	Bi-LSTM
NSW	959.72	850.12	341.17	459.92	956.11	893.380	679.72
VIC	676.81	814.36	520.41	389.32	544.29	490.291	373.15
QUN	660.38	745.05	166.7	303.92	587.66	553.552	473.58
SA	267.69	313.41	206.02	188.42	194.73	144.949	117.08
TAS	50.49	50.6	27.34	36.07	57.14	54.390	42.79
Mean	523.02	554.71	252.33	275.53	467.99	427.313	337.26

, the BIDIR method achieved the lowest MAE in three out of five series and recorded the lowest mean MAE (252.33) among all the models evaluated, reinforcing its robustness in various forecasting scenarios.

In terms of SMAPE, as presented in

Table 6. Cross-validation SMAPE using 10 windows. The bold values represent the minimum SMAPE.

Region	Zero	FWD	BIDIR	NHITS	LSTM	TCN	Bi-LSTM
NSW	0.076	0.068	0.026	0.036	0.076	0.071	0.107
VIC	0.069	0.08	0.049	0.039	0.059	0.053	0.087
QUN	0.07	0.074	0.016	0.031	0.065	0.061	0.104
SA	0.091	0.1	0.064	0.064	0.073	0.054	0.109
TAS	0.064	0.063	0.033	0.044	0.073	0.070	0.105
Mean	0.074	0.077	0.038	0.043	0.069	0.062	0.102

, the BIDIR method achieved the lowest SMAPE in three out of five series and registered the lowest mean SMAPE (0.038) across the cross-validation folds. This consistent performance across different regions and metrics underscores the BIDIR model’s capability to deliver reliable and accurate forecasts over multiple time horizons.

The results presented above demonstrate the superior performance of the proposed bidirectional fine-tuning approach across multiple evaluation metrics and forecasting scenarios. Specifically, the BIDIR method consistently achieved the lowest MAE and SMAPE in the majority of the time series, outperforming other state-of-the-art models such as TimeGPT (zero-shot and forward fine tuning), N-HiTS, LSTM, TCN, and Bi-LSTM. The BIDIR model’s ability to effectively utilize both forward and backward temporal dependencies allows it to capture complex patterns in the data, leading to significant improvements in forecast accuracy. The robustness of the BIDIR approach is further evidenced by its strong performance in cross-validation, where it maintained the lowest average error across multiple regions and time horizons. Our findings highlight the effectiveness of bidirectional fine tuning as a powerful enhancement to attention-based models, offering a reliable and accurate solution for medium- and long-term load forecasting.

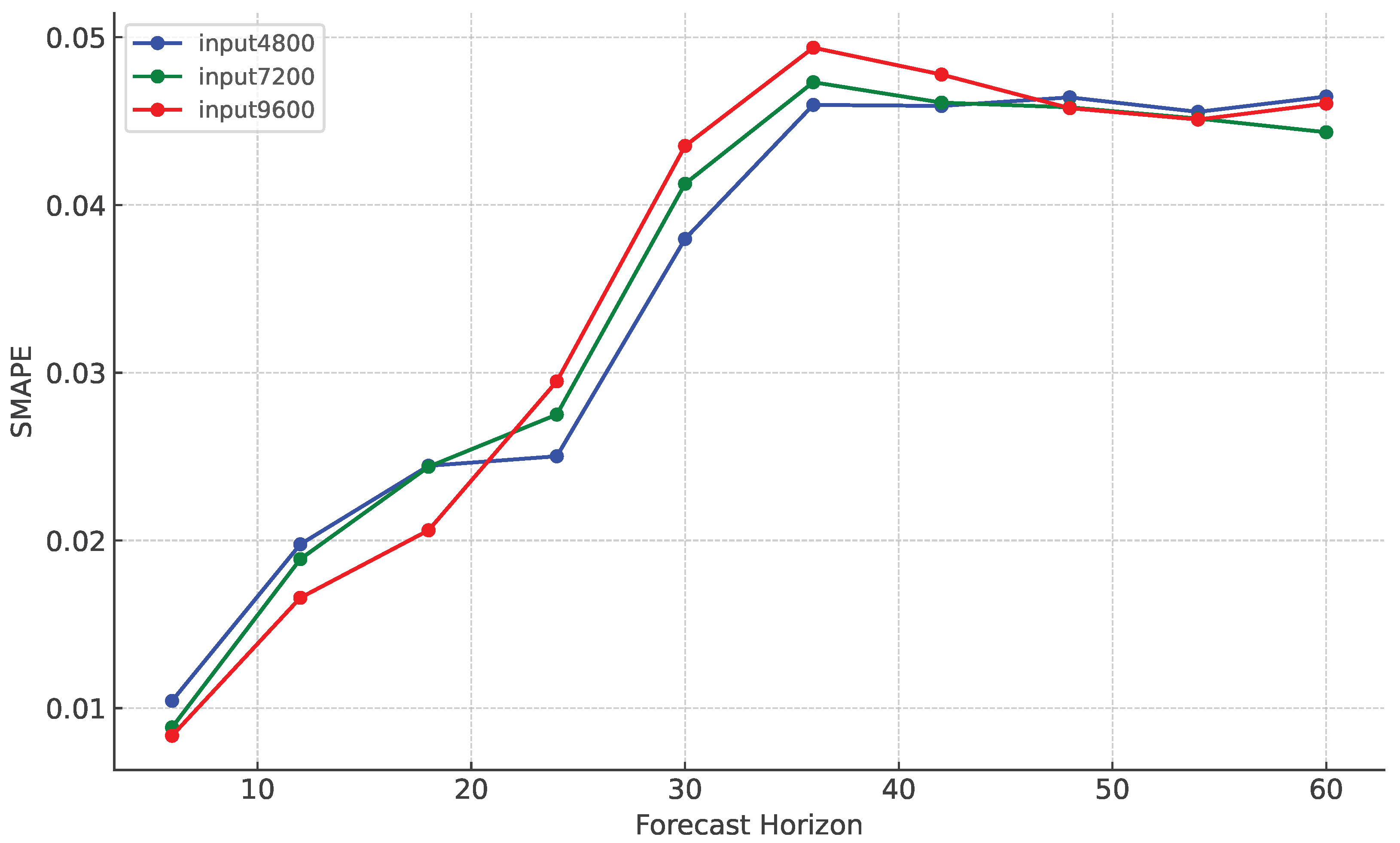
To better understand the performance of the proposed bidirectional fine-tuning model, we analyze its accuracy for different input and output ranges. Figure 3 illustrates the model’s performance, in term of SMAPE, for three different input lengths (4800, 7200, and 9600) across various forecast horizons. The mean SMAPE is calculated over the five regional time series, which is similar to the last row of Table 4. The results indicate that the performance of the model generally worsens (SMAPE increases) as the forecast horizon increases for all input lengths. This is not a surprising observation. It is a typical behavior in time-series forecasting, as the longer the forecast horizon, the greater the uncertainty and the higher the likelihood of prediction errors. In general, the farther into the future the model tries to predict, the less accurate the forecasts become, leading to an increase in SMAPE. The increase in error over time is expected due to the accumulation of forecast inaccuracies as the model moves further from the observed data. Thus, the observed trend is consistent with the inherent challenges of long-term forecasting. We also find that shorter input lengths (input4800 and input7200) generally yield lower SMAPE values in shorter forecast horizons, suggesting better accuracy in the short term. However, as the forecast horizon increases, the performance differences between input lengths become less pronounced with input 9600 approaching the accuracy of the shorter input lengths.

The training times for the results given in Table 4 are presented in

Table 7. Training times for different algorithms (in seconds).

Algorithm	Training Time
ZERO	2.24
FWD	2.95
BIDIR	14.44
NHiTS	7.38
LSTM	25.13
TCN	9.87
BiLSTM	44.44

. As shown, the proposed bidirectional model demonstrates a reasonable balance between computational efficiency and performance. While it is faster than both LSTM and Bi-LSTM models, which took 25.13 and 44.44 s respectively, it is still slower than the other benchmark models such as the ZERO (2.24 s), FWD (2.95 s), and NHiTS (7.38 s). The TCN model also performs faster at 9.87 s.

The slower execution time of the proposed bidirectional method compared to the other unidirectional models is expected, as the bidirectional model processes the data in both forward and backward directions, effectively doubling the amount of data that need to be trained. Despite this, the difference in execution time between the bidirectional model (14.44 s) and other faster models is not drastic, particularly when considering the improvement in forecasting accuracy brought by capturing temporal dependencies in both directions.

Furthermore, the training speed of the proposed model can be further optimized by leveraging GPU acceleration. Given the current setup, the execution times reflect CPU-based training, and the use of GPUs is expected to significantly reduce the computation time, making the proposed approach even more efficient in real-world applications.

5.6. Discussion

The results of our numerical experiments clearly demonstrate the effectiveness of the proposed bidirectional fine-tuning approach in the context of load forecasting. In the task of forecasting the final 48 time steps of regional electricity demand, the BIDIR method consistently outperformed other methods, achieving the lowest SMAPE in four out of the five regions and the lowest overall mean SMAPE. Similarly, the BIDIR model recorded the lowest MAE values in three out of five cases, further validating its superior predictive capability in accurately forecasting electricity load. The significant reduction in both MAE and SMAPE across multiple regions suggests that the bidirectional approach effectively captures complex temporal dependencies inherent in load data and reduces forecasting errors, particularly when compared to unidirectional models such as TimeGPT zero-shot, TimeGPT forward fine tuning, N-HiTS, LSTM, and TCN. To benchmark our proposed method against other existing bidirectional methods, we included the Bi-LSTM model in our comparative assessment. Bi-LSTM is a main representative of the class of existing bidirectional models. While the Bi-LSTM method achieved the minimum MAE on the VIC time series, it did not perform well in the overall MAE or SMAPE comparisons. Moreover, Bi-LSTM is a relatively slow algorithm, which was one of the main reasons we introduced our own bidirectional approach to improve both performance and computational efficiency. Our findings highlight the potential of bidirectional fine tuning to improve the precision of load forecasts, which is crucial for efficient grid management and planning.

The cross-validation results further reinforce the robustness and generalizability of the BIDIR method in load forecasting. By employing an expanding window strategy, we were able to assess the models’ performance across varying input window sizes, thus reflecting more realistic forecasting scenarios encountered in power system operations. The BIDIR method maintained its superiority, achieving the lowest mean MAE and SMAPE across the cross-validation folds. The consistent performance across both direct forecasting tasks and cross-validation analysis indicates that the bidirectional fine-tuning approach not only enhances immediate load-forecasting accuracy but also provides a stable and reliable model that generalizes well across different temporal patterns and forecasting horizons. The results confirm the value of incorporating attention-based bidirectional context into load-forecasting models, offering a significant advancement in the state of the art for predicting electricity demand and supporting more effective decision making in energy management and grid operations.

6. Conclusions

In this study, we have introduced a novel approach for load forecasting based on the bidirectional fine-tuning of an attention model. Our approach leverages both forward and backward temporal dependencies in time-series data, leading to improved forecasting accuracy and robustness compared to traditional unidirectional models. Through comprehensive numerical experiments, we demonstrated that our bidirectional model outperforms state-of-the-art methods such as N-HiTS, LSTM, TCN, and Bi-LSTM across various time-series data.

The proposed model’s ability to capture complex patterns in electricity consumption data and reduce forecasting errors underscores its potential as a powerful tool for medium- and long-term load forecasting. The incorporation of bidirectional context not only enhances predictive performance but also contributes to more reliable and efficient power system management. This work represents a notable advancement in the field of time-series forecasting, particularly in the context of energy demand prediction, and opens new avenues for further research on bidirectional models in other domains.

Future research may explore the integration of additional contextual information, such as weather data or economic indicators, to further refine forecasting accuracy. Additionally, the application of our bidirectional fine-tuning approach to other types of time-series data, such as financial or environmental data, could yield valuable insights and broader applicability.